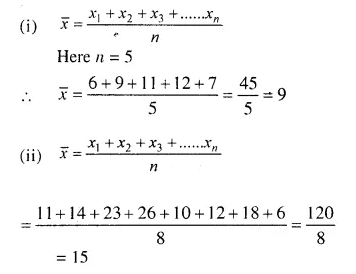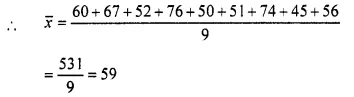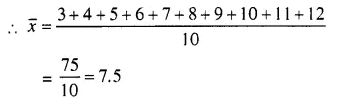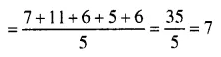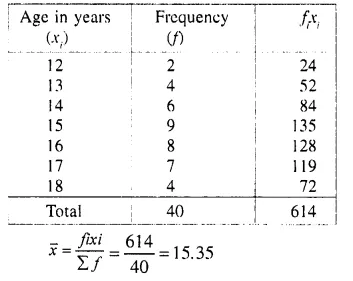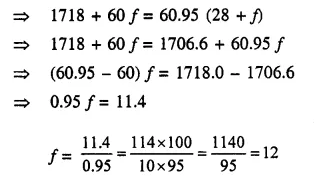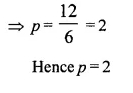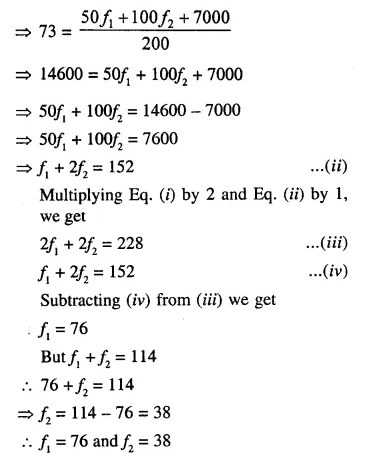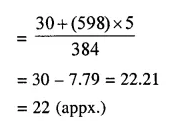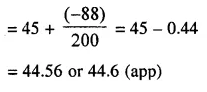Prasanna

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency (Mean, Median, Quartiles and Mode) Ex 24B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 24 Measures of Central Tendency (Mean, Median, Quartiles and Mode) Ex 24B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24E

Question 1.
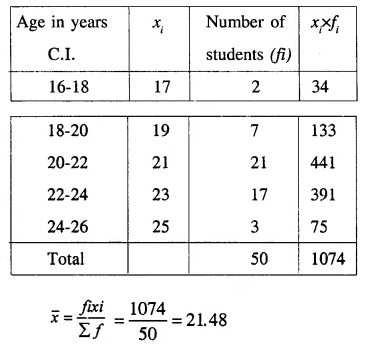
The following table gives the ages of 50 students of a class. Find the arithmetic mean of their ages.

Solution:

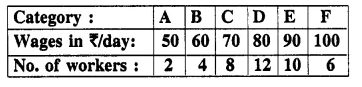
Question 2.
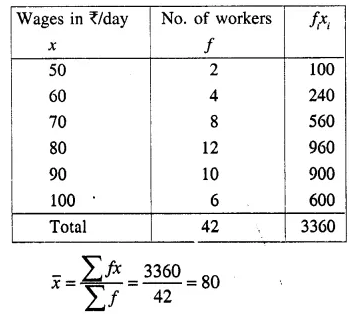
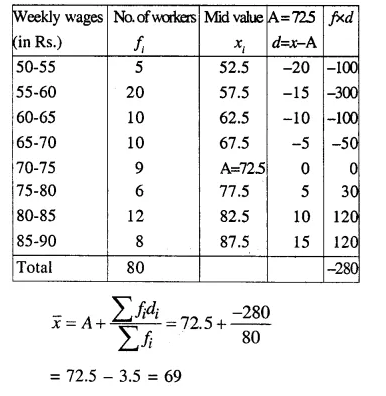
The following table gives the weekly wages of workers in a factory.

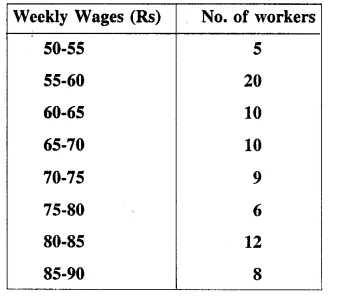
Calculate the mean by using :
(i) Direct Method
(ii) Short-Cut Method
Solution:
(i) Direct Method:

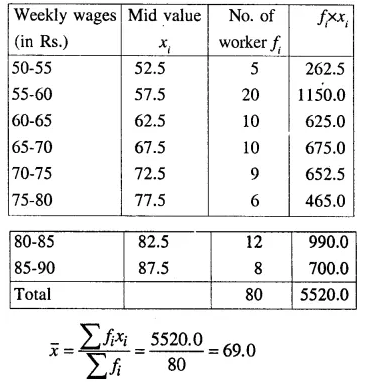
(ii) Short cut method :

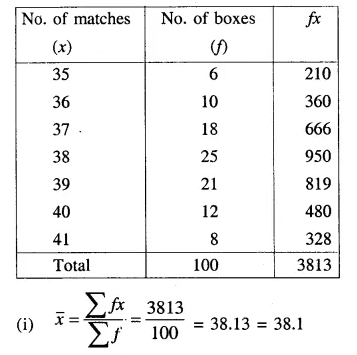
Question 3.
The following are the marks obtained by 70 boys in a class test :

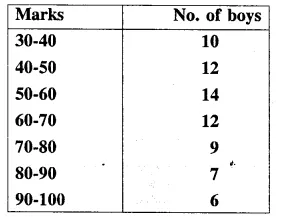
Calculate the mean by :
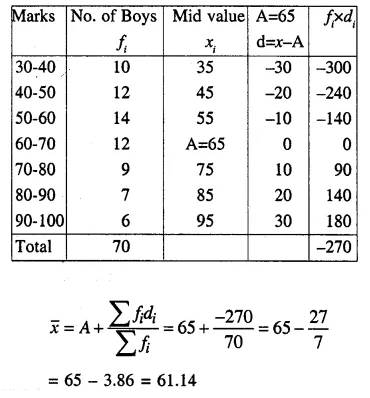
(i) Short-Cut Method
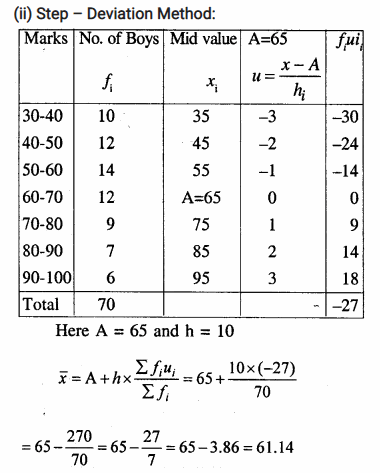
(ii) Step-Deviation Method.
Solution:
(i) Short cut Method :

(ii) Step – Deviation Method:

Question 4.
Find mean by ‘step-deviation method :

Solution:

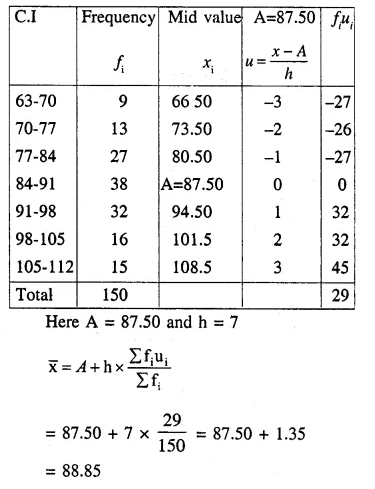
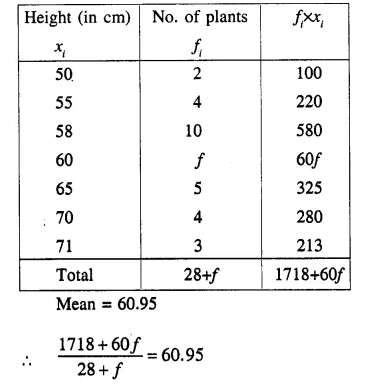
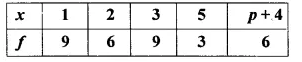
Question 5.
The mean of following frequency distribution is 21\(\frac { 1 }{ 7 }\) Find the value of ‘f ‘.

Solution:

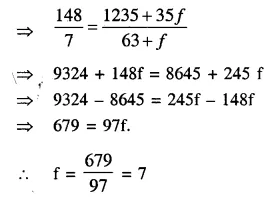
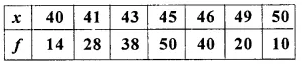
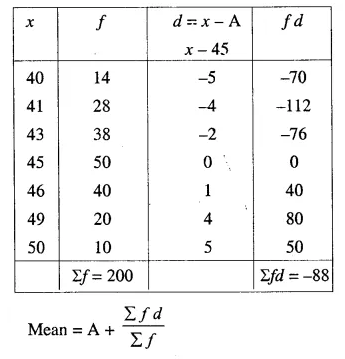
Question 6.
Using step-deviation method, calculate the mean marks of the following distribution.

Solution:
Let Assumed mean = 72.5

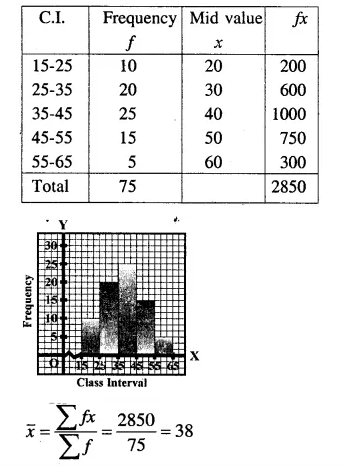
Question 7.
Using the information given in the adjoining histogram; calculate the mean.
Solution:

Question 8.
If the mean of the following observations is 54, find the value of p.

Solution:
Mean = 54

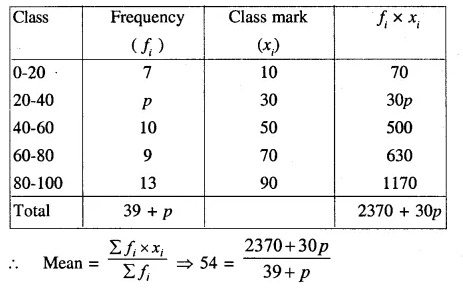
⇒ 2106 + 54p = 2370 + 30p
⇒ 54p – 30p = 2370 – 2106 ⇒ 24p = 264
p = \(\frac { 264 }{ 24 }\) = 11
Hence p = 11

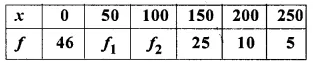
Question 9.
The mean of the following distribution is 62.8 and the sum of all the frequencies is 50. Find the missing frequencies f₁ and f₂.

Solution:
Mean = 62.8
and sum of frequencies = 50

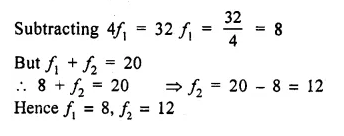
Question 10.
Calculate the mean of the distribution given below using the short cut method.

Solution:

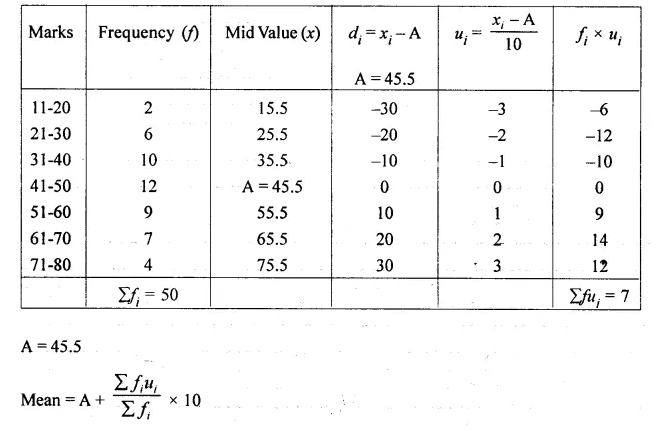
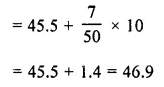
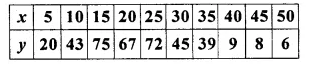
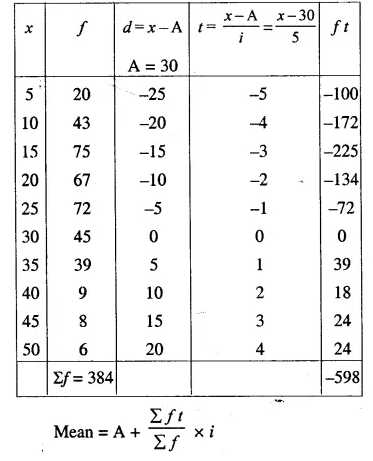
Question 11.
Calculate the mean of the following distribution :

Solution:

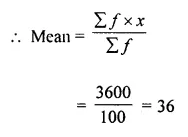
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Question 1.
In an A.P., ten times of its tenth term is equal to thirty times of its 30th term. Find its 40th term.
Solution:
In an A.P.
10T₁₀ = 30T₃₀
We know that,
If m times of mth term = n times of nth term
Then its (m + n)th term = 0
∴ 10T₁₀ = 30T₃₀
Then T₁₀₊₃₀ = 0 or T₄₀ = 0

Question 2.
How many two-digit numbers are divisible by 3 ?
Solution:
Two digits numbers are 10 to 99
and two digits numbers which are divisible
by 3 are 12, 15, 18, 21,….99
Here a = 12, d = 3 and l = 99
Now, Tn = l = a + (n – 1 )d
99 = 12 + (n – 1) x 3
=> 99 – 12 = 3(n – 1)
=> 87 = 3(n – 1)
=> \(\\ \frac { 87 }{ 3 } \) = n – 1
=> n – 1 = 29
n = 29 + 1 = 30
Number of two digit number divisible by 3 = 30

Question 3.
Which term of A.P. 5, 15, 25, will be 130 more than its 31st term?
Solution:
A.P. is 5, 15, 25,….
Let T_n = T₃₁ + 130
In A.P. a = 5, d = 15 – 5 = 10
∴ T_n = a + 30d + 130 = 5 + 30 x 10 +130
= 5 + 300 + 130 = 435
∴ n + (n – 1)d = 435
=> 5 + (n – 1) x 10 = 435
=> (n – 1) x 10 = 435 – 5 = 430
n – 1 = \(\\ \frac { 430 }{ 10 } \) = 43
n = 43 + 1 = 44
∴ The required term is 44th.

Question 4.
Find the value of p, if x, 2x + p and 3x + 6 are in A.P.
Solution:
A.P. is x, 2x + p, 3x + 6
2x + p – x = 3x + 6 – 2x + p
x + p = x – p + 6
=>2p = 6
=>p = \(\\ \frac { 6 }{ 2 } \) = 3
Hence p = 3

Question 5.
If the 3rd and the 9th terms of an arithmetic progression are 4 and – 8 respectively, which term of it is zero?
Solution:
In an A.P.
T₃ = 4 and T₉ = – 8
Let a be the first term and d be the common difference, then

Question 6.
How many three-digit numbers ate divisible by 87 ?
Solution:
Three digits numbers are 100 to 999

999 – 42 = 957
Numbers divisible by 87 will be 174,….., 957
Let n be the number of required three digit number.
Here, a = 174 and d = 87
l = 957 = a + (n – l)d
= 174 + (n – 1) x 87
=> (n – 1) x 87 = 957 – 174 = 783
n – 1 = \(\\ \frac { 783 }{ 87 } \) = 9
n = 9 + 1 = 10
There are 10 such numbers.

Question 7.
For what value of n, the nth term of A.P. 63, 65, 67,….. and nth term of A.P. 3, 10, 17,…… are equal to each other?
Solution:
We are given,
nth term of 63, 65, 67, …….
=> nth term of 3, 10, 17,…….
=> In first A.P., a₁ = 63, d₁ = 2
and in second A.P., a₂ = 3, d₂ = 1

∴ Required nth term will be 13th

Question 8.
Determine the A.P. whose 3rd term is 16 and the 7th term exceeds the 5th term by 12.
Solution:
T₃ = 16, and T₇ = T₅ + 12
Let a be the first term and d be the common difference
T₃ = a + 2d – 16 …(i)
T₇ = T₅ + 12
a + 6d = a + 4d + 12
=> 6d – 4d = 12 => 2d – 12
=> d = \(\\ \frac { 12 }{ 2 } \) = 6
and in (i),
a + 6 x 2 = 16
=> a + 12 = 16
=>a = 16 – 12 = 4
A.P. will be 4, 10, 16, 22,……

Question 9.
If numbers n – 2, 4n – 1 and 5n + 2 are in A.P., find the value of n and its next two terms.
Solution:
n – 2, 4n – 1 and 5n + 2 are in A.P.
(4n – 1) – (n – 2) = (5n + 2) – (4n – 1)
=> 4n – 1 – n + 2 = 5n + 2 – 4n + 1
=> 4n – n – 5n + 4n = 2 + 1 + 1 – 2
=>2n = 2 =>n = \(\\ \frac { 2 }{ 2 } \) = 1
4n – 1 = 4 x 1 – 1 = 4 – 1 = 3
n – 2 = 1 – 2 = – 1
and 5n + 2 = 5 x 1 + 2 = 5 + 2 = 7
A.P. is – 1, 3, 7, ……
and next 2 terms will 11, 15

Question 10.
Determine the value of k for which k² + 4k + 8, 2k² + 3k + 6 and 3k² + 4k + 4 are in A.P.
Solution:
k² + 4k+ 8, 2k² + 3k + 6 and 3k² + 4k + 4 are in A.P.
(2k² + 3k + 6) – (k² + 4k + 8)
= (3k² + 4k + 4) – (2k² + 3k + 6)
=> 2k² + 3k + 6 – k² – 4k – 8
= 3k² + 4k + 4 – 2k² – 3k – 6
=> k² – k – 2 = k² + k – 2
=> k² – k – k² – k = – 2 + 2
=> – 2k = 0
=> k = 0
Hence k = 0

Question 11.
If a, b and c are in A.P. show that :
(i) 4a, 4b and 4c are in A.P.
(ii) a + 4, b + 4 and c + 4 are in A.P.
Solution:
a, b, c are in A.P.
2b = a + c
(i) 4a, 4b and 4c are in A.P.
If 2(4b) = 4a + 4c
If 8b = 4a + 4c
If 2b = a + c which is given
(ii) a + 4, b + 4 and c + 4 are in A.P.
If 2(b + 4) = a + 4 + c + 4
If 2b + 8 = a + c + 8
If 2b = a + c which is given

Question 12.
An A.P. consists of 57 terms of which 7th term is 13 and the last term is 108. Find the 45th term of this A.P.
Solution:
Number of terms in an A.P. = 57
T₇ = 13, l= 108
To find T₄₅
Let a be the first term and d be the common difference
=> a + 6d = 13 …(i)
a + (n – 1 )d= 108
=> a + (57 – 1 )d= 108
=> a + 56d = 108
Subtracting,

Question 13.
4th term of an A.P. is equal to 3 times its term and 7th term exceeds twice the 3rd term by 1. Find the first term and the common difference.
Solution:
In A.P
T₄ = 3 x T₁
T₇ = 2 x T₃ + 1
Let a be the first term and d be the common
difference

Question 14.
The sum of the 2nd term and the 7th term of an A.P. is 30. If its 15th term is 1 less than twice of its 8th term, find the A.P.
Solution:
In an A.P.
T₂ + T₇ = 30
T₁₅ = 2T₈ – 1
Let a be the first term and d be the common difference
a + d + a + 6d = 30

Question 15.
In an A.P., if mth term is n and nth term is m, show that its rth term is (m + n – r)
Solution:
In an A.P.
T_m = n and T_n = m
Let a be the first term and d be the common difference, then
T_m = a + (m – 1 )d = n

Question 16.
Which term of the A.P. 3, 10, 17,…..will be 84 more than its 13th term?
Solution:
A.P. is 3, 10, 17,….
Here, a = 2, d = 10 – 3 = 7

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Question 1.
Which of the following sequences are in arithmetic progression?
(i) 2, 6, 10, 14, …….
(ii) 15, 12, 9, 6,…….
(iii) 5, 9, 12, 18, ……
(iv) \(\frac { 1 }{ 2 } ,\frac { 1 }{ 3 } ,\frac { 1 }{ 4 } ,\frac { 1 }{ 5 } \),…..
Solution:
(i) 2, 6, 10, 14,
Here, d = 6 – 2 = 4
10 – 6 = 4
14 – 10 = 4
∴ In each case (d) is same.
∴It is an arithmetic progression.


∴d is not the same
∴It is not an arithmetic progression

Question 2.
The nth term of a sequence is (2n – 3), find its fifteenth term.
Solution:
T_n = 2n – 3
T₁₅ = 2 x 15 – 3
= 30 – 3
= 27

Question 3.
If the pth term of an A.P. is (2p + 3); find the A.P.
Solution:
T_p = 2p + 3
T₁ = 2 x 1 + 3 = 2 + 3 = 5
T₂ = 2 x 2 + 3 = 4 + 3 = 7
T₃ = 2 x 3 + 3 = 6 + 3 = 9
∴A.P. is 5, 7, 9,…..

Question 4.
Find the 24th term of the sequence : 12, 10, 8, 6,…….
Solution:
A.P. is 12, 10, 8, 6,……
Here a = 12, d = 10 – 12 = – 2
T_n = a + (n – 1)d
T₂₄ = 12 + (24 – 1) x ( – 2)
= 12 + 23 x ( – 2)
= 12 – 46
= – 34

Question 5.
Find the 30th term of the sequence :
\(\\ \frac { 1 }{ 2 } \), 1, \(\\ \frac { 3 }{ 2 } \),….
Solution:
\(\\ \frac { 1 }{ 2 } \), 1, \(\\ \frac { 3 }{ 2 } \),….
Here a = \(\\ \frac { 1 }{ 2 } \), d = \(1- \frac { 1 }{ 2 } \)
\(\\ \frac { 1 }{ 2 } \)

Question 6.
Find the 100th term of the sequence :
√3, 2√3, 3√3,….
Solution:
√3, 2√3, 3√3,….
Here a = √3, d = 2√3 – √3 = √3

Question 7.
Find the 50th term of the sequence :
\(\\ \frac { 1 }{ n } \), \(\\ \frac { n+1 }{ n } \), \(\\ \frac { 2n+1 }{ n } \),……
Solution:
\(\\ \frac { 1 }{ n } \), \(\\ \frac { n+1 }{ n } \), \(\\ \frac { 2n+1 }{ n } \),……
=>\(\\ \frac { 1 }{ n } \), \(1+ \frac { 1 }{ n } \), \(2+ \frac { 1 }{ n } \),…..

Question 8.
Is 402 a term of the sequence :
8, 13, 18, 23,…?
Solution:
In sequence 8, 13, 18, 23,…..
a = 8 and d = 13 – 8 = 5
Let 402 be the nth term, then
402 = a + (n – 1)d = 8 + (n – 1) x 5
\(\\ \frac { 402-8 }{ 5 } \) = n – 1
=> \(\\ \frac { 394 }{ 5 } \) = n – 1
394 is not exactly divisible by 5,
∴ 402 is not its term.

Question 9.
Find the common difference and 99th term of the arithmetic progression :
\(7 \frac { 3 }{ 4 } \), \(9 \frac { 1 }{ 2 } \), \(11 \frac { 1 }{ 4 } \),…..
Solution:
\(7 \frac { 3 }{ 4 } \), \(9 \frac { 1 }{ 2 } \), \(11 \frac { 1 }{ 4 } \),…..
here a = \(7 \frac { 3 }{ 4 } \)
= \(\\ \frac { 31 }{ 4 } \)

Question 10.
How many terms are there in the series:
(i) 4, 7, 10, 13,…..148 ?
(ii) 0.5, 0.53, 0.56,…..1.1 ?
(iii) \(\\ \frac { 3 }{ 4 } \), 1, \(1 \frac { 1 }{ 4 } \),….3 ?
Solution:
(i) 4, 7, 10, 13,…..148 ?
Here a = 4, d = 7 – 4
= 3
Let 148 be the nth term, then

Question 11.
Which term of the A.P. 1 + 4 + 7 + 10 +……is 52 ?
Solution:
A.P. is 1, 4, 7, 10,……is 52
Here a = 1, d = 4 – 1 = 3
Let 52 be the nth term, then

Question 12.
If 5th and 6th terms of an A.P. are respectively 6 and 5, find the 11th term of the A.P.
Solution:
5th term (T₅) = 6
=> 6 = a + 4d
and T₆ = 5
=> 5 = a + 5d

Question 13.
If t_n represents nth term of an A.P., t₂ + t₅ – t₃ = 10 and t₂ + t₉ = 17, find its first term and its common difference.
Solution:
Let first term of an A.P. be a
and common difference = d
Then T_n is the nth term

Question 14.
Find the 10th term from the end of the A.P. 4, 9, 14,…. 254.
Solution:
We know that rth term from the end
= (n – r + 1)th from the beginning
Here, a = A, d = 9 – 4 = 5,
nth term = 254

Question 15.
Determine the arithmetic progression whose 3rd term is 5 and 7th term is 9.
Solution:
Let a be the first term and d be the common difference, then
T₃ = a + 2d – 5
T₇ = a + 6d = 9

Question 16.
Find the 31st term of an A.P. whose 10th term is 38 and 16th term is 74.
Solution:
Let a be the first term and d be the common difference, then
T₁₀ = a + 9d =38
and T₁₆ = a + 15d = 74

Question 17.
Which term of the series :
21, 18, 15, is – 81 ?
Can any term of this series be zero ? If yes, find the number of term.
Solution:
21, 18, 15, 1….. – 81
Here a = 21,d = 18 – 21 = – 3,
nth term = – 81

Question 18.
An A.P. consists of 60 terms. If the first and the last terms be 7 and 125 respectively, find the 31st term.
Solution:
Given : An A.P. consists of 60 terms
a = 7
and a₆₀ = 125
=> a + (60 – 1 )d = 125
=> 7 + 59 d = 125
=> 59d= 125 – 7
=> d = \(\\ \frac { 118 }{ 59 } \) = 2
now, a₃₁ = a + (n – 1)d
= 7 + (31 – 1) x 2
= 7 + 30 x 2
= 67

Question 19.
The sum of the 4th and the 8th terms of an A.P. is 24 and the sum of the sixth term and the tenth term is 34. Find the first three terms of the A.P.
Solution:
In an A.P.
T₄ + T₈ = 24
T₆ + T₁₀ =34
Let a be the first term and d be the common difference

Question 20.
If the third term of an A.P. is 5 and the seventh terms is 9, find the 17th term
Solution:
Let the first term of an A.P. = a
and the common difference of the given A.P. = d
As, we know that,

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.