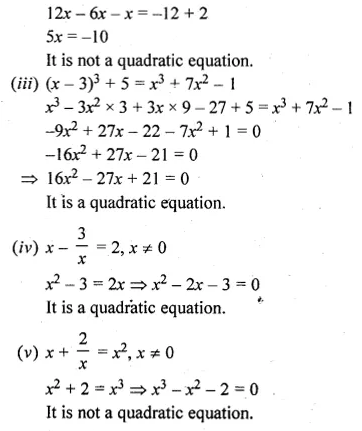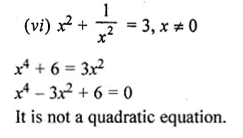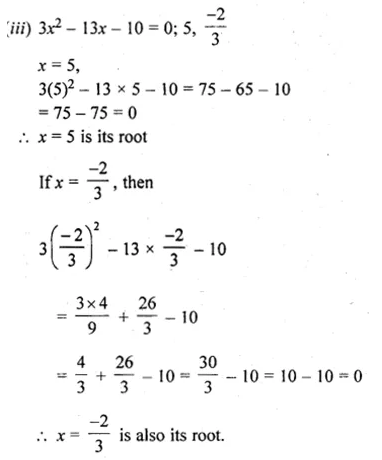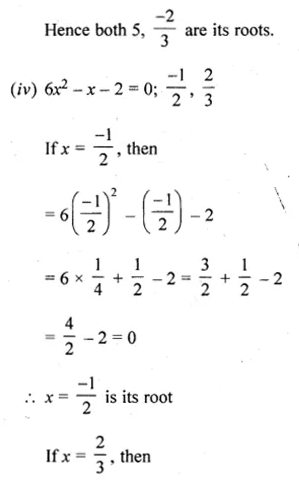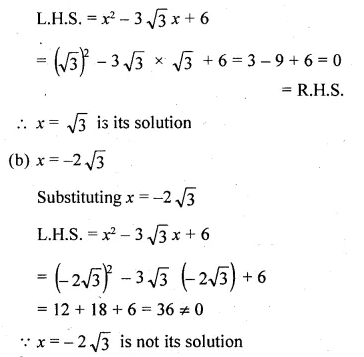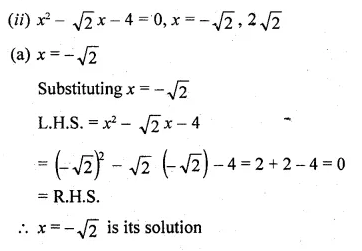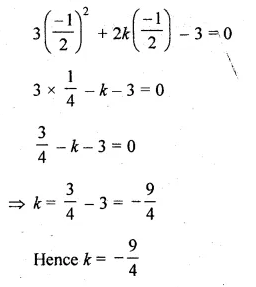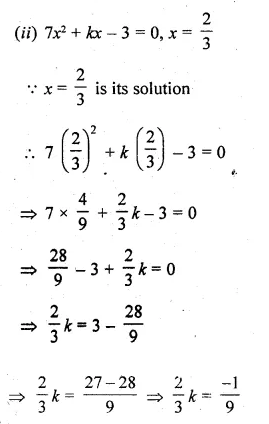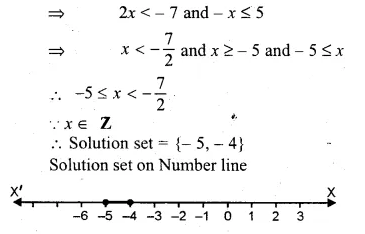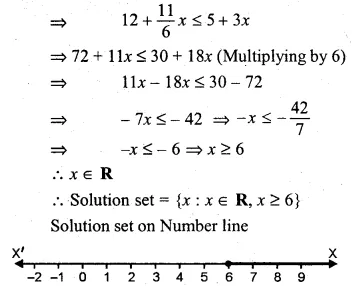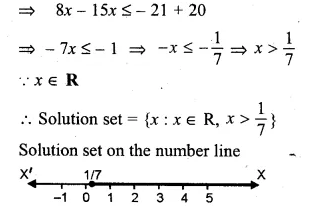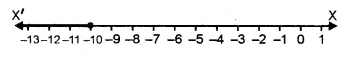Prasanna

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Solve the following equations (1 to 24) by factorization

Question 1.
(i) 4x² = 3x
(ii) \(\frac { { x }^{ 2 }-5x }{ 2 } =0\)
Solution:
(i) 4x² = 3x
x(4x – 3) = 0
Either x = 0,

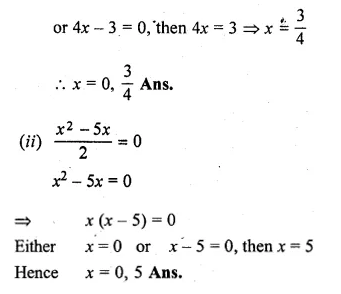
Question 2.
(i) (x – 3) (2x + 5) = 0
(ii) x (2x + 1) = 6
Solution:
(i) (x – 3) (2x + 5) = 0
Either x – 3 = 0,
Then x = 3

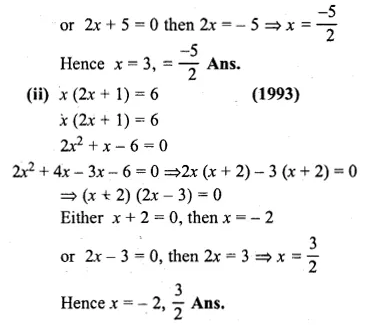
Question 3.
(i) x² – 3x – 10 = 0
(ii) x(2x + 5) = 3
Solution:
(i) x² – 3x – 10 = 0
⇒ x² – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0

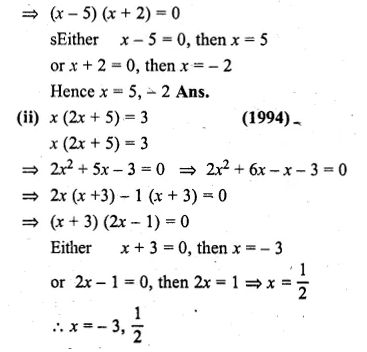
Question 4.
(i) 3x² – 5x – 12 = 0
(ii) 21x² – 8x – 4 = 0
Solution:
(i) 3x² – 5x – 12 = 0
⇒ 3x² – 9x + 4x – 12 = 0
⇒ 3x (x – 3) + 4(x – 3) = 0

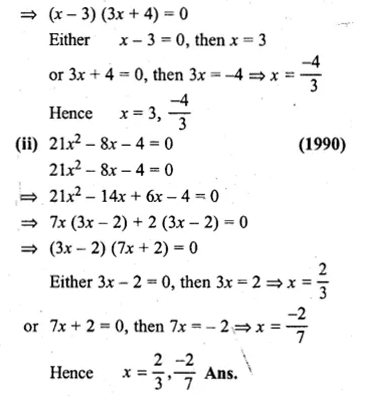
Question 5.
(i) 3x² = x + 4
(ii) x(6x – 1) = 35
Solution:
(i) 3x² = x + 4
⇒ 3x² – x – 4 = 0
⇒ 3x² – 4x + 3x – 4 = 0

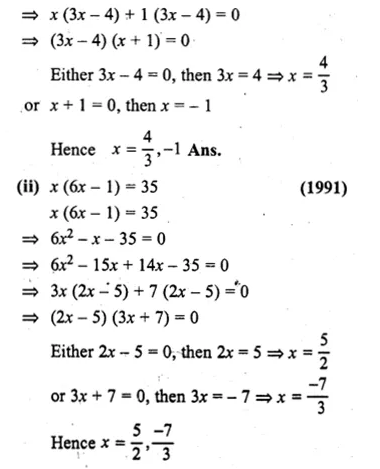
Question 6.
(i) 6p² + 11p – 10 = 0
(ii) \(\frac { 2 }{ 3 } { x }^{ 2 }-\frac { 1 }{ 3 } x=1 \)
Solution:
(i) 6p² + 11p – 10 = 0
⇒ 6p² + 15p – 4p – 10 = 0
⇒ 3p(2p + 5) – 2(2p + 5) = 0

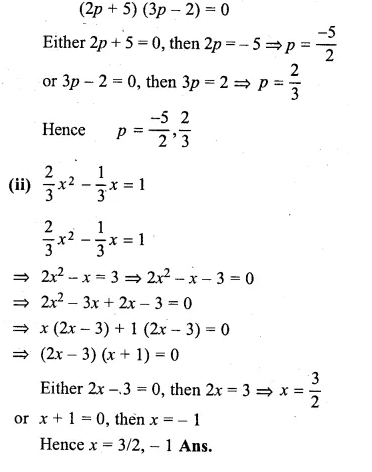
Question 7.
(i) (x – 4)² + 5² = 13²
(ii) 3(x – 2)² = 147
Solution:
(i) (x – 4)² + 5² = 13²
x² – 8x + 16 + 25 = 169

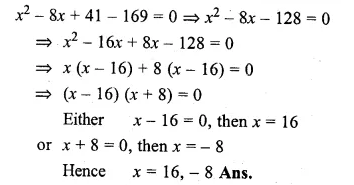
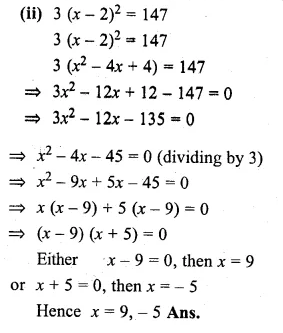
Question 8.
(i) \(\\ \frac { 1 }{ 7 } \)(3x – 5)² = 28
(ii) 3(y² – 6) = y(y + 7) – 3
Solution:
(i) \(\\ \frac { 1 }{ 7 } \)(3x – 5)² = 28
(3x – 5)² = 28 × 7
⇒ 9x² – 30x + 25 = 196

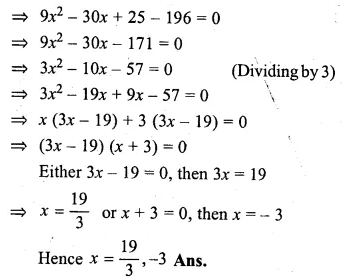
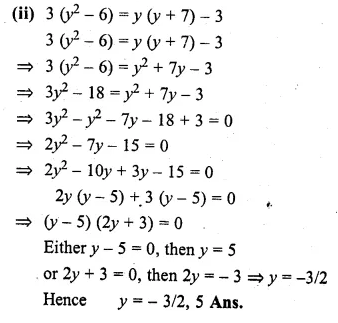
Question 9.
x² – 4x – 12 = 0,when x∈N
Solution:
x² – 4x – 12 = 0
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6) = 0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then x = 6
or x + 2 = 0, then x = -2
But -2 is not a natural number
∴ x = 6

Question 10.
2x² – 8x – 24 = 0 when x∈I
Solution:
2x² – 8x – 24 = 0
⇒ x² – 4x – 12 = 0 (Dividing by 2)
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6) = 0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then, x = 6
or x + 2 = 0, then x = – 2
Hence x = 6, – 2

Question 11.
5x² – 8x – 4 = 0 when x∈Q
Solution:
5x² – 8x – 4 = 0
∵ 5 × ( – 4) = – 20
-20 = – 10 + 2
-8 = – 10 + 2

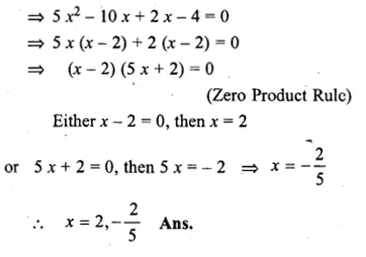
Question 12.
2x² – 9x + 10 = 0,when
(i)x∈N
(ii)x∈Q
Solution:
2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x(x – 2) – 5(x – 2) = 0

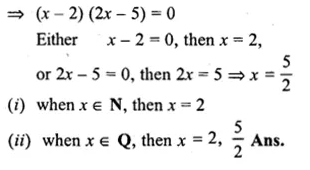
Question 13.
(i) a²x² + 2ax + 1 = 0, a≠0
(ii) x² – (p + q)x + pq = 0
Solution:
(i) a²x² + 2ax + 1 = 0
⇒ a²x² + ax + ax + 1 = 0

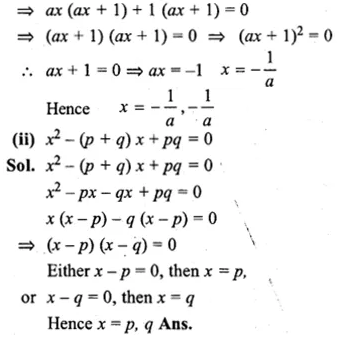
Question 14.
a²x² + (a² + b²)x + b² = 0, a≠0
Solution:
a²x² + (a² + b²)x + b² = 0
⇒ a²x(x + 1) + b²(x + 1) = 0

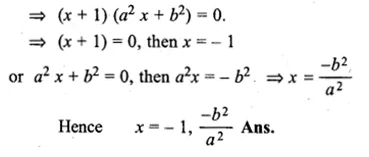
Question 15.
(i) √3x² + 10x + 7√3 = 0
(ii) 4√3x² + 5x – 2√3 = 0
Solution:
(i) √3x² + 10x + 7√3 = 0
[ ∵ √3 x 7√3 = 7 x 3 = 21]
⇒ √3x(x + √3) + 7(x + √3) = 0

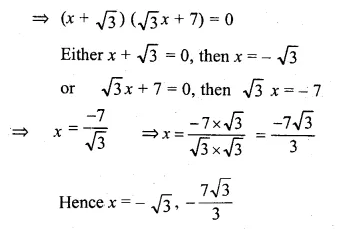
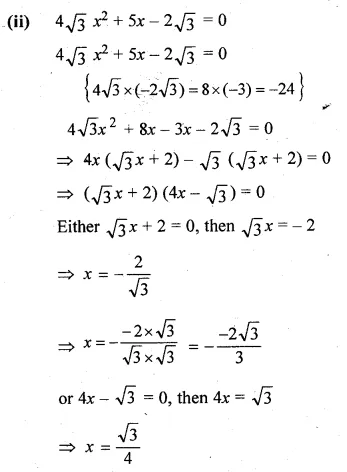
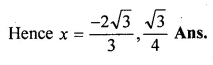
Question 16.
(i) x² – (1 + √2)x + √2 = 0
(ii) \(x+ \frac { 1 }{ x } \) = \(2 \frac { 1 }{ 20 } \)
Solution:
(i) x² – (1 + √2)x + √2 = 0
⇒ x² – x – √2x + √2 = 0

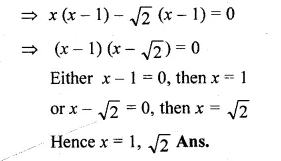
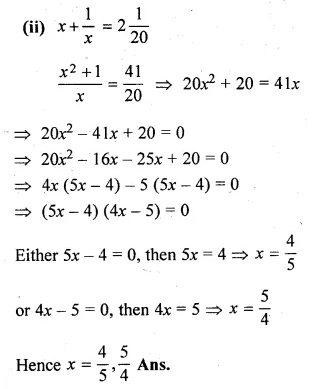
Question 17.
(i) \(\frac { 2 }{ { x }^{ 2 } } -\frac { 5 }{ x } +2=0,x\neq 0 \)
(ii)\(\frac { { x }^{ 2 } }{ 15 } -\frac { x }{ 3 } -10=0 \)
Solution:
(i) \(\frac { 2 }{ { x }^{ 2 } } -\frac { 5 }{ x } +2=0,x\neq 0 \)
⇒ 2 – 5x + 2x² = 0

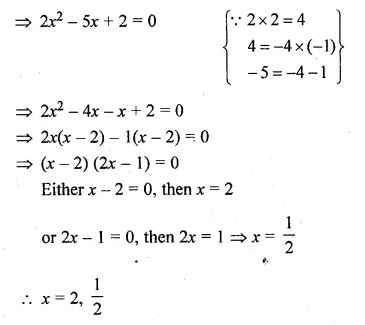
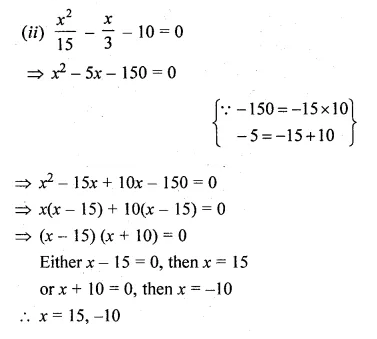
Question 18.
(i) \(3x-\frac { 8 }{ x } =2 \)
(ii) \(\frac { x+2 }{ x+3 } =\frac { 2x-3 }{ 3x-7 } \)
Solution:
(i) \(3x-\frac { 8 }{ x } =2 \)
\(\frac { { 3x }^{ 2 }-8 }{ x } =2 \)

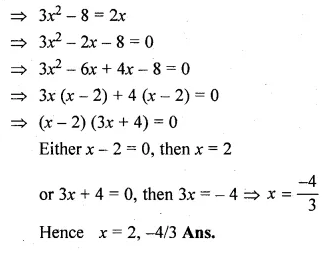
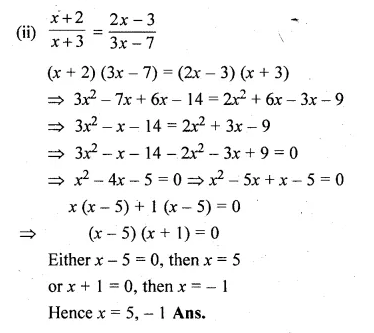
Question 19.
(i) \(\frac { 8 }{ x+3 } -\frac { 3 }{ 2-x } =2 \)
(ii) \(\frac { x }{ x-1 } +\frac { x-1 }{ x } =2\frac { 1 }{ 2 } \)
Solution:
(i) \(\frac { 8 }{ x+3 } -\frac { 3 }{ 2-x } =2 \)
\(\frac { 16-8x-3x-9 }{ (x+3)(2-x) } =2 \)

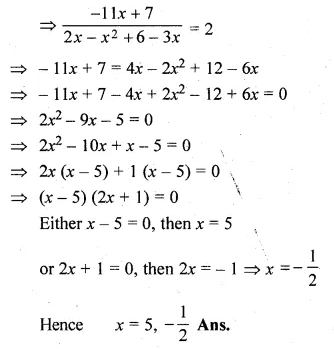
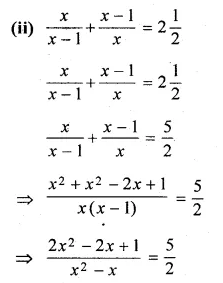
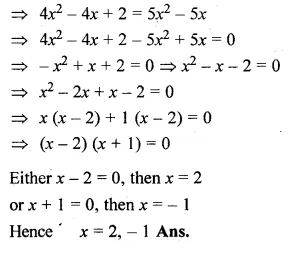
Question 20.
(i) \(\frac { x }{ x+1 } +\frac { x+1 }{ x } =\frac { 34 }{ 15 } \)
(ii) \(\frac { x+1 }{ x-1 } +\frac { x-2 }{ x+2 } =3 \)
Solution:
(i) \(\frac { x }{ x+1 } +\frac { x+1 }{ x } =\frac { 34 }{ 15 } \)
\(\frac { { x }^{ 2 }+{ x }^{ 2 }+2x+1 }{ x(x+1) } =\frac { 34 }{ 15 } \)

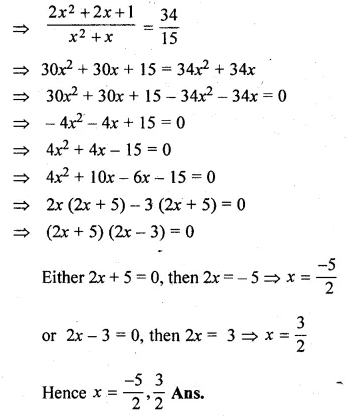
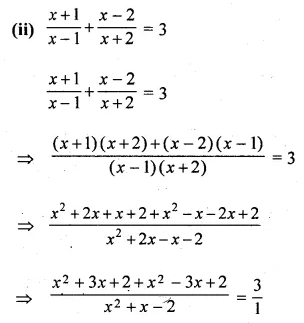
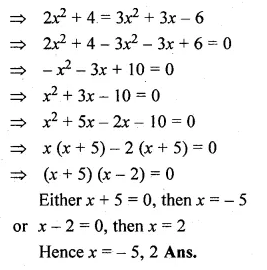
Question 21.
(i) \(\frac { 1 }{ x-3 } -\frac { 1 }{ x+5 } =\frac { 1 }{ 6 } \)
(ii) \(\frac { x-3 }{ x+3 } +\frac { x+3 }{ x-3 } =2\frac { 1 }{ 2 } \)
Solution:
(i) \(\frac { 1 }{ x-3 } -\frac { 1 }{ x+5 } =\frac { 1 }{ 6 } \)

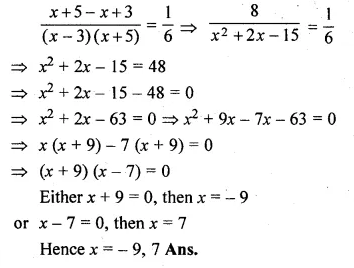
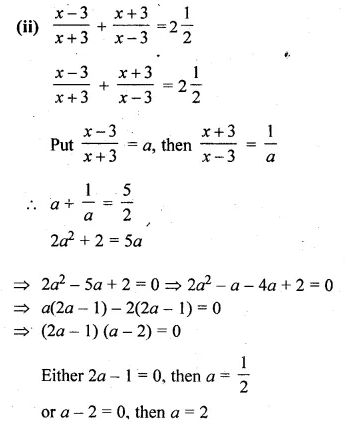
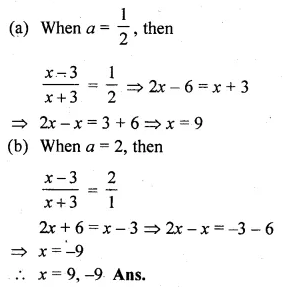
Question 22.
(i) \(\frac { a }{ ax-1 } +\frac { b }{ bx-1 } =a+b,a+b\neq 0,ab\neq 0\)
(ii) \(\frac { 1 }{ 2a+b+2x } =\frac { 1 }{ 2a } +\frac { 1 }{ b } +\frac { 1 }{ 2x } \)
Solution:
(i) \(\frac { a }{ ax-1 } +\frac { b }{ bx-1 } =a+b\)
⇒ \(\left( \frac { a }{ ax-1 } -b \right) +\left( \frac { b }{ bx-1 } -a \right) =0\)

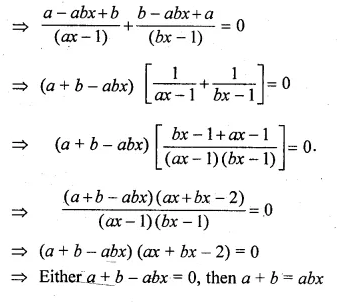
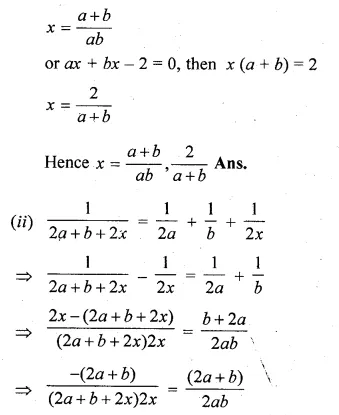
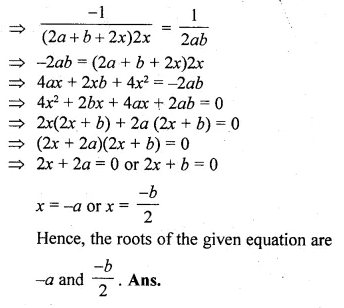
Question 23.
\(\frac { 1 }{ x+6 } +\frac { 1 }{ x-10 } =\frac { 3 }{ x-4 } \)
Solution:
\(\frac { 1 }{ x+6 } +\frac { 1 }{ x-10 } =\frac { 3 }{ x-4 } \)
⇒ \(\frac { x-10+x+6 }{ (x+6)(x-10) } =\frac { 3 }{ x-4 } \)

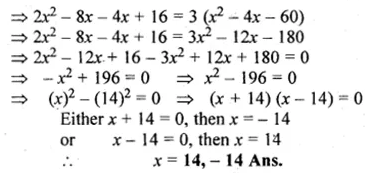
Question 24.
(i) \(\sqrt { 3x+4 } =x\)
(ii) \(\sqrt { x(x-7) } =3\sqrt { 2 } \)
Solution:
(i) \(\sqrt { 3x+4 } =x\)
Squaring on both sides

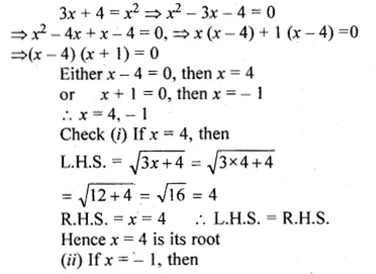
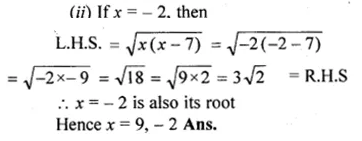
Question 25.
Use the substitution y = 3x + 1 to solve for x : 5(3x + 1 )² + 6(3x + 1) – 8 = 0
Solution:
y = 3x + 1
Now, 5(3x + 1)² + 6(3x + 1) – 8 = 0

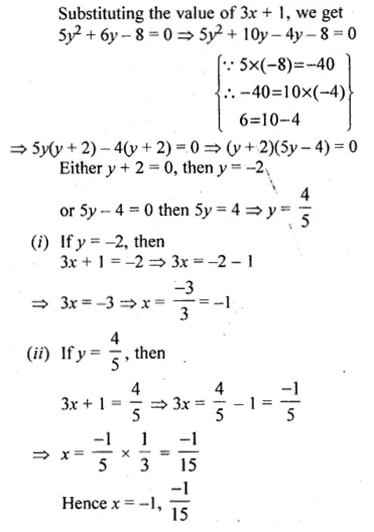
Question 26.
Find the values of x if p + 1 =0 and x² + px – 6 = 0
Solution:
p + 1 = 0, then p = – 1
Substituting the value of p in the given quadratic equation
x² + ( – 1)x – 6 = 0
⇒ x² – x – 6 = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x (x – 3) + 2 (x – 3) = 0
⇒ (x – 3) (x + 2) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = – 2
Hence x = 3, -2

Question 27.
Find the values of x if p + 7 = 0, q – 12 = 0 and x² + px + q = 0,
Solution:
p + 7 = 0, then p = – 7
and q – 12 = 0, then q = 12
Substituting the values of p and q in the given quadratic equation,
x² – 7x + 12 = 0
⇒ x² – 3x – 4x + 12 = 0
⇒ x (x – 3) – 4 (x – 3) = 0
⇒ (x – 3) (x – 4) = 0
Either x – 3 = 0, then x = 3
or x – 4 = 0, then x = 4
Hence x = 3, 4

Question 28.
If x = p is a solution of the equation x(2x + 5) = 3, then find the value of p.
Solution:
Given, x = p and x(2x + 5) = 3
Substituting the value of p, we get
p(2p + 5) = 3
⇒ 2p² + 5p – 3 = 0
⇒ 2p² + 6p – p – 3 = 0

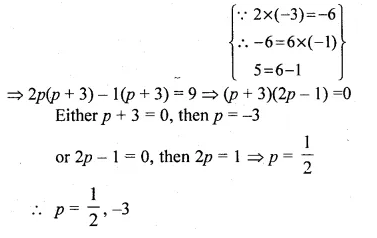
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Question 1.
Check whether the following are quadratic equations:
(i)\(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
(ii)(2x + 1) (3x – 2) = 6(x + 1) (x – 2)
(iii)\({ (x-3) }^{ 3 }+5={ x }^{ 3 }+7{ x }^{ 2 }-1\)
(iv)\(x-\frac { 3 }{ x } =2,x\neq 0\)
(v)\(x+\frac { 2 }{ x } ={ x }^{ 2 },x\neq 0\)
(vi)\({ x }^{ 2 }+\frac { 1 }{ { x }^{ 2 } } =3,x\neq 0 \)
Solution:
(i) \(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
It is a quadratic equation as it is power of 2.
(ii) (2x + 1) (3x – 2) = 6(x + 1) (x – 2)
6x² – 4x + 3x – 2 = 6(x² – 2x + x – 2)
6x² – x – 2 = 6x² – 12x + 6x – 12

Question 2.
In each of the following, determine whether the given numbers are roots of the given equations or not;
(i) x² – x + 1 = 0; 1, – 1
(ii) x² – 5x + 6 = 0; 2, – 3
(iii) 3x² – 13x – 10 = 0; 5,\(\\ \frac { -2 }{ 3 } \)
(iv) 6x² – x – 2 = 0;\(\\ \frac { -1 }{ 2 } \), \(\\ \frac { 2 }{ 3 } \)
Solution:
(i) x² – x + 1 = 0; 1, -1
Where x = 1, then
(1)² – 1 + 1 = 1 – 1 + 1 = 1 ≠ 0
∴ x = 1 does not satisfy it

Question 3.
In each of the following, determine whether the given numbers are solutions of the given equation or not:
(i) x² – 3√3x + 6 = 0; √3, – 2√3
(ii) x² – √2x – 4 = 0, x = – √2, 2√2
Solution:
(i) x² – 3√3x + 6 = 0; √3, -2√3
(a) Substituting the value of x = √3

Question 4.
(i) If \(– \frac { 1 }{ 2 } \) is a solution of the equation 3x² + 2kx – 3 = 0, find the value of k.
(ii) If \(\\ \frac { 2 }{ 3 } \) is a solution of the equation 7x² + kx – 3 = 0, find the value of k.
Solution:
(i) x = \(– \frac { 1 }{ 2 } \) is a solution of the
3x² + 2kx – 3 = 0,
Substituting the value of x in the given equation

Question 5.
(i) If √2 is a root of the equation kx² + √2 – 4 = 0, find the value of k.
(ii) If a is a root of the equation x² – (a + b)x + k = 0, find the value of k.
Solution:
(i) kx² + √2 – 4 = 0, x = √2
x = √2 is its solution

Question 6.
If \(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0, find the values of p and q.
Solution:
\(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0
Substituting the value of x = \(\\ \frac { 2 }{ 3 } \) and – 3 respectively, we get

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

Question 1.
Solve the inequation : 5x – 2 ≤ 3(3 – x) where x ∈ { – 2, – 1, 0, 1, 2, 3, 4}. Also represent its solution on the number line.
Solution:
5x – 2 < 3(3 – x)
⇒ 5x – 2 ≤ 9 – 3x
⇒ 5x + 3x ≤ 9 + 2

Question 2.
Solve the inequations :
6x – 5 < 3x + 4, x ∈ I.
Solution:
6x – 5 < 3x + 4
6x – 3x < 4 + 5
⇒ 3x <9
⇒ x < 3
x ∈ I
Solution Set = { -1, -2, 2, 1, 0….. }

Question 3.
Find the solution set of the inequation
x + 5 < 2 x + 3 ; x ∈ R
Graph the solution set on the number line.
Solution:
x + 5 ≤ 2x + 3
x – 2x ≤ 3 – 5
⇒ -x ≤ -2
⇒ x ≥ 2

Question 4.
If x ∈ R (real numbers) and – 1 < 3 – 2x ≤ 7, find solution set and represent it on a number line.
Solution:
-1 < 3 – 2x ≤ 7
-1 < 3 – 2x and 3 – 2x ≤ 7
⇒ 2x < 3 + 1 and – 2x ≤ 7 – 3
⇒ 2x < 4 and -2x ≤ 4
⇒ x < 2 and -x ≤ 2
and x ≥ -2 or -2 ≤ x
x ∈ R
Solution set -2 ≤ x < 2
Solution set on number line

Question 5.
Solve the inequation :
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le 1\frac { 3 }{ 5 } +\frac { 3x-1 }{ 7 } ,x\in R\)
Solution:
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le 1\frac { 3 }{ 5 } +\frac { 3x-1 }{ 7 } \)
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le \frac { 8 }{ 5 } +\frac { 3x-1 }{ 7 } \)

Question 6.
Find the range of values of a, which satisfy 7 ≤ – 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.
Solution:
7 < – 4x + 2 < 12
7 < – 4x + 2 and – 4x + 2 < 12

Question 7.
If x∈R, solve \(2x-3\ge x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)
Solution:
\(2x-3\ge x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)
\(2x-3\ge x+\frac { 1-x }{ 3 } \) and \(x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)

Question 8.
Find positive integers which are such that if 6 is subtracted from five times the integer then the resulting number cannot be greater than four times the integer.
Solution:
Let the positive integer = x
According to the problem,
5a – 6 < 4x
⇒ 5a – 4x < 6
⇒ x < 6
Solution set = {x : x < 6}
= { 1, 2, 3, 4, 5, 6}

Question 9.
Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is at least 3.
Solution:
Let first least natural number = x
then second number = x + 1
and third number = x + 2

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

Choose the correct answer from the given four options (1 to 5) :

Question 1.
If x ∈ { – 3, – 1, 0, 1, 3, 5}, then the solution set of the inequation 3x – 2 ≤ 8 is
(a) { – 3, – 1, 1, 3}
(b) { – 3, – 1, 0, 1, 3}
(c) { – 3, – 2, – 1, 0, 1, 2, 3}
(d) { – 3, – 2, – 1, 0, 1, 2}
Solution:
x ∈ { -3, -1, 0, 1, 3, 5}
3x – 2 ≤ 8
⇒ 3x ≤ 8 + 2
⇒ 3x ≤ 10
⇒ x ≤ \(\\ \frac { 10 }{ 3 } \)
⇒ x < \(3 \frac { 1 }{ 3 } \)
Solution set = { -3, -1, 0, 1, 3} (b)

Question 2.
If x ∈ W, then the solution set of the inequation 3x + 11 ≥ x + 8 is
(a) { – 2, – 1, 0, 1, 2, …}
(b) { – 1, 0, 1, 2, …}
(c) {0, 1, 2, 3, …}
(d) {x : x∈R,x≥\(– \frac { 3 }{ 2 } \)}
Solution:
x ∈ W
3x + 11 ≥ x + 8
⇒ 3x – x ≥ 8 – 11

Question 3.
If x ∈ W, then the solution set of the inequation 5 – 4x ≤ 2 – 3x is
(a) {…, – 2, – 1, 0, 1, 2, 3}
(b) {1, 2, 3}
(c) {0, 1, 2, 3}
(d) {x : x ∈ R, x ≤ 3}
Solution:
x ∈ W
5 – 4x < 2 – 3x
⇒ 5 – 2 ≤ 3x + 4x
⇒ 3 ≤ x
Solution set = {0, 1, 2, 3,} (c)

Question 4.
If x ∈ I, then the solution set of the inequation 1 < 3x + 5 ≤ 11 is
(a) { – 1, 0, 1, 2}
(b) { – 2, – 1, 0, 1}
(c) { – 1, 0, 1}
(d) {x : x ∈ R, \(– \frac { 4 }{ 3 } \) < x ≤ 2}
Solution:
x ∈ I
1 < 3x + 5 ≤ 11
⇒ 1 < 3x + 5
⇒ 1 – 5 < 3x

Question 5.
If x ∈ R, the solution set of 6 ≤ – 3 (2x – 4) < 12 is
(a) {x : x ∈ R, 0 < x ≤ 1}
(b) {x : x ∈ R, 0 ≤ x < 1}
(c) {0, 1}
(d) none of these
Solution:
x ∈ R
6 ≤ – 3(2x – 4) < 12
⇒ 6 ≤ – 3(2x – 4)
⇒ 6 ≤ – 6x + 12

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

Question 1.
Solve the inequation 3x -11 < 3 where x ∈ {1, 2, 3,……, 10}. Also represent its solution on a number line
Solution:
3x – 11 < 3 => 3x < 3 + 11 => 3x < 14 x < \(\\ \frac { 14 }{ 3 } \)
But x ∈ 6 {1, 2, 3, ……., 10}
Solution set is (1, 2, 3, 4}
Ans. Solution set on number line

Question 2.
Solve 2(x – 3)< 1, x ∈ {1, 2, 3, …. 10}
Solution:
2(x – 3) < 1 => x – 3 < \(\\ \frac { 1 }{ 2 } \) => x < \(\\ \frac { 1 }{ 2 } \) + 3 => x < \(3 \frac { 1 }{ 2 } \)
But x ∈ {1, 2, 3 …..10}
Solution set = {1, 2, 3} Ans.

Question 3.
Solve : 5 – 4x > 2 – 3x, x ∈ W. Also represent its solution on the number line.
Solution:
5 – 4x > 2 – 3x
– 4x + 3x > 2 – 5
=> – x > – 3
=> x < 3
x ∈ w,
solution set {0, 1, 2}
Solution set on Number Line :

Question 4.
List the solution set of 30 – 4 (2.x – 1) < 30, given that x is a positive integer.
Solution:
30 – 4 (2x – 1) < 30
30 – 8x + 4 < 30
– 8x < 30 – 30 – 4
– 8x < – 4 x > \(\\ \frac { -4 }{ -8 } \)
=> x > \(\\ \frac { 1 }{ 2 } \)
x is a positive integer
x = {1, 2, 3, 4…..} Ans.

Question 5.
Solve : 2 (x – 2) < 3x – 2, x ∈ { – 3, – 2, – 1, 0, 1, 2, 3} .
Solution:
2(x – 2) < 3x – 2
=> 2x – 4 < 3x – 2
=> 2x – 3x < – 2 + 4
=> – x < 2
=> x > – 2
Solution set = { – 1, 0, 1, 2, 3} Ans.

Question 6.
If x is a negative integer, find the solution set of \(\\ \frac { 2 }{ 3 } \)+\(\\ \frac { 1 }{ 3 } \) (x + 1) > 0.
Solution:
\(\\ \frac { 2 }{ 3 } \)+\(\\ \frac { 1 }{ 3 } \) x + \(\\ \frac { 1 }{ 3 } \) > 0
=> \(\\ \frac { 1 }{ 3 } \) x + 1 > 0
=> \(\\ \frac { 1 }{ 3 } \) x > – 1

x is a negative integer
Solution set = {- 2, – 1} Ans.

Question 7.
Solve: \(\\ \frac { 2x-3 }{ 4 } \)≥\(\\ \frac { 1 }{ 2 } \), x ∈ {0, 1, 2,…,8}
Solution:
\(\\ \frac { 2x-3 }{ 4 } \)≥\(\\ \frac { 1 }{ 2 } \)
=> 2x – 3 ≥ \(\\ \frac { 4 }{ 2 } \)

Question 8.
Solve x – 3 (2 + x) > 2 (3x – 1), x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}. Also represent its solution on the number line.
Solution:
x – 3 (2 + x) > 2 (3x – 1)
=> x – 6 – 3x > 6x – 2
=> x – 3x – 6x > – 2 + 6
=> – 8x > 4
=> x < \(\\ \frac { -4 }{ 8 } \) => x < \(– \frac { 1 }{ 2 } \)
x ∈ { – 3, – 2, – 1, 0, 1, 2}
.’. Solution set = { – 3, – 2, – 1}
Solution set on Number Line :

Question 9.
Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9} solve x – 3 < 2x – 1.
Solution:
x – 3 < 2x – 1
x – 2x < – 1 + 3 => – x < 2 x > – 2
But x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4, 5, 6, 7, 9} Ans.

Question 10.
Given A = {x : x ∈ I, – 4 ≤ x ≤ 4}, solve 2x – 3 < 3 where x has the domain A Graph the solution set on the number line.
Solution:
2x – 3 < 3 => 2x < 3 + 3 => 2x < 6 => x < 3
But x has the domain A = {x : x ∈ I – 4 ≤ x ≤ 4}
Solution set = { – 4, – 3, – 2, – 1, 0, 1, 2}
Solution set on Number line :

Question 11.
List the solution set of the inequation
\(\\ \frac { 1 }{ 2 } \) + 8x > 5x \(– \frac { 3 }{ 2 } \), x ∈ Z
Solution:
\(\\ \frac { 1 }{ 2 } \) +8x > 5x \(– \frac { 3 }{ 2 } \)

Question 12.
List the solution set of \(\\ \frac { 11-2x }{ 5 } \) ≥ \(\\ \frac { 9-3x }{ 8 } \) + \(\\ \frac { 3 }{ 4 } \),
x ∈ N
Solution:
\(\\ \frac { 11-2x }{ 5 } \) ≥ \(\\ \frac { 9-3x }{ 8 } \) + \(\\ \frac { 3 }{ 4 } \)
=> 88 – 16x ≥ 45 – 15x + 30
(L.C.M. of 8, 5, 4 = 40}
=> – 16x + 15x ≥ 45 + 30 – 88
=> – x ≥ – 13
=>x ≤ 13
x ≤ N.
Solution set = {1, 2, 3, 4, 5, .. , 13} Ans.

Question 13.
Find the values of x, which satisfy the inequation : \(-2\le \frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le 1\frac { 5 }{ 6 } \), x ∈ N.
Graph the solution set on the number line. (2001)
Solution:
\(-2\le \frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le 1\frac { 5 }{ 6 } \), x ∈ N

Question 14.
If x ∈ W, find the solution set of
\(\frac { 3 }{ 5 } x-\frac { 2x-1 }{ 3 } >1\)
Also graph the solution set on the number line, if possible.
Solution:
\(\frac { 3 }{ 5 } x-\frac { 2x-1 }{ 3 } >1\)
9x – (10x – 5) > 15 (L.C.M. of 5, 3 = 15)
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
But x ∈ W
Solution set = Φ
Hence it can’t be represented on number line.

Question 15.
Solve:
(i)\(\frac { x }{ 2 } +5\le \frac { x }{ 3 } +6\) where x is a positive odd integer.
(ii)\(\frac { 2x+3 }{ 3 } \ge \frac { 3x-1 }{ 4 } \) where x is positive even integer.
Solution:
(i) \(\frac { x }{ 2 } +5\le \frac { x }{ 3 } +6\)

Question 16.
Given that x ∈ I, solve the inequation and graph the solution on the number line :
\(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \ge 2 \) (2004)
Solution:
\(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \) and \(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \ge 2 \)

Question 17.
Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9}, find the values of x for which -3 < 2x – 1 < x + 4.
Solution:
-3 < 2x – 1 < x + 4.
=> – 3 < 2x – 1 and 2x – 1 < x + 4
=> – 2x < – 1 + 3 and 2x – x < 4 + 1
=> – 2x < 2 and x < 5
=> – x < 1
=> x > – 1
– 1 < x < 5
x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4} Ans.

Question 18.
Solve : 1 ≥ 15 – 7x > 2x – 27, x ∈ N
Solution:
1 ≥ 15 – 7x > 2x – 27
1 ≥ 15 – 7x and 15 – 7x > 2x – 27

Question 19.
If x ∈ Z, solve 2 + 4x < 2x – 5 ≤ 3x. Also represent its solution on the number line.
Solution:
2 + 4x < 2x – 5 ≤ 3x
2 + 4x < 2x – 5 and 2x – 5 ≤ 3x => 4x – 2x < – 5 – 2 ,and 2x – 3x ≤ 5

Question 20.
Solve the inequation = 12 + \(1 \frac { 5 }{ 6 } x\) ≤ 5 + 3x, x ∈ R. Represent the solution on a number line. (1999)
Solution:
12 + \(1 \frac { 5 }{ 6 } x\) ≤ 5 + 3x

Question 21.
Solve : \(\\ \frac { 4x-10 }{ 3 } \)≤\(\\ \frac { 5x-7 }{ 2 } \) x ∈ R and represent the solution set on the number line.
Solution:
\(\\ \frac { 4x-10 }{ 3 } \)≤\(\\ \frac { 5x-7 }{ 2 } \)
=> 8x – 20 ≤ 15x – 21
(L.C.M. of 3, 2 = 6)

Question 22.
Solve \(\frac { 3x }{ 5 } -\frac { 2x-1 }{ 3 } \) > 1, x ∈ R and represent the solution set on the number line.
Solution:
\(\frac { 3x }{ 5 } -\frac { 2x-1 }{ 3 } \) > 1
=> 9x – (10x – 5) > 15
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
x ∈ R.
.’. Solution set = {x : x ∈R, x < – 10}
Solution set on the number line

Question 23.
Solve the inequation – 3 ≤ 3 – 2x < 9, x ∈ R. Represent your solution on a number line. (2000)
Solution:
– 3 ≤ 3 – 2x < 9
– 3 ≤ 3 – 2x and 3 – 2x < 9
2x ≤ 3 + 3 and – 2x < 9 – 3
2x ≤ 6 and – 2x < 6 => x ≤ 3 and – x < 3 => x ≤ – 3 and – 3 < x
– 3 < x ≤ 3.
Solution set= {x : x ∈ R, – 3 < x ≤ 3)
Solution on number line

Question 24.
Solve 2 ≤ 2x – 3 ≤ 5, x ∈ R and mark it on number line. (2003)
Solution:
2 ≤ 2x – 3 ≤ 5 .
2 ≤ 2x – 3 and 2x – 3 ≤ 5
2 + 3 ≤ 2x and 2x ≤ 5 + 3
5 ≤ 2x and 2x ≤ 8.

Question 25.
Given that x ∈ R, solve the following inequation and graph the solution on the number line: – 1 ≤ 3 + 4x < 23. (2006)
Solution:
We have
– 1 ≤ 3 + 4x < 23 => – 1 – 3 ≤ 4x < 23 – 3 => – 4 ≤ 4x < 20 => – 1 ≤ x < 5, x ∈ R
Solution Set = { – 1 ≤ x < 5; x ∈ R}

Question 26.
Solve tlie following inequation and graph the solution on the number line. (2007)
\(-2\frac { 2 }{ 3 } \le x+\frac { 1 }{ 3 } <3+\frac { 1 }{ 3 } \) x∈R
Solution:
Given \(-2\frac { 2 }{ 3 } \le x+\frac { 1 }{ 3 } <3+\frac { 1 }{ 3 } \) x∈R
\(-\frac { 8 }{ 3 } \le x+\frac { 1 }{ 3 } <\frac { 10 }{ 3 } \)
Multiplying by 3, L.C.M. of fractions, we get

Question 27.
Solve the following inequation and represent the solution set on the number line :
\(-3<-\frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le \frac { 5 }{ 6 } ,x\in R\)
Solution:
\(-3<-\frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le \frac { 5 }{ 6 } ,x\in R\)

Question 28.
Solve \(\frac { 2x+1 }{ 2 } +2(3-x)\ge 7,x\in R\). Also graph the solution set on the number line
Solution:
\(\frac { 2x+1 }{ 2 } +2(3-x)\ge 7,x\in R\)

Question 29.
Solving the following inequation, write the solution set and represent it on the number line. – 3(x – 7)≥15 – 7x > \(\\ \frac { x+1 }{ 3 } \), n ∈R
Solution:
– 3(x – 7)≥15 – 7x > \(\\ \frac { x+1 }{ 3 } \), n ∈R

Question 30.
Solve the inequation :
\(-2\frac { 1 }{ 2 } +2x\le \frac { 4x }{ 3 } \le \frac { 4 }{ 3 } +2x,\quad x\in W\). Graph the solution set on the number line.
Solution:
\(-2\frac { 1 }{ 2 } +2x\le \frac { 4x }{ 3 } \le \frac { 4 }{ 3 } +2x,\quad x\in W\)

Question 31.
Solve the inequation 2x – 5 ≤ 5x + 4 < 11, where x ∈ I. Also represent the solution set on the number line. (2011)
Solution:
2x – 5 ≤ 5x + 4 < 11 2x – 5 ≤ 5x + 4
=> 2x – 5 – 4 ≤ 5x and 5x + 4 < 11
=> 2x – 9 ≤ 5x and 5x < 11 – 4
and 5x < 7
=> 2x – 5x ≤ 9 and x < \(\\ \frac { 7 }{ 5 } \)
=> 3x > – 9 and x< 1.4
=> x > – 3

Question 32.
If x ∈ I, A is the solution set of 2 (x – 1) < 3 x – 1 and B is the solution set of 4x – 3 ≤ 8 + x, find A ∩B.
Solution:
2 (x – 1) < 3 x – 1
2x – 2 < 3x – 1
2x – 3x < – 1 + 2 => – x < 1 x > – 1
Solution set A = {0, 1, 2, 3, ..,.}
4x – 3 ≤ 8 + x
4x – x ≤ 8 + 3
=> 3x ≤ 11
=> x ≤ \(\\ \frac { 11 }{ 3 } \)
Solution set B = {3, 2, 1, 0, – 1…}
A ∩ B = {0, 1, 2, 3} Ans.

Question 33.
If P is the solution set of – 3x + 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find
(i) P ∩ Q
(ii) Q – P.
Solution:
(i) – 3 x + 4 < 2 x – 3
– 3x – 2x < – 3 – 4 => – 5x < – 7

Question 34.
A = {x : 11x – 5 > 7x + 3, x ∈R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Find the range of set A ∩ B and represent it on a number line
Solution:
A = {x : 11x – 5 > 7x + 3, x ∈R}
B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Now, A = 11x – 5 > 7x + 3
=> 11x – 7x > 3 + 5
=> 4x > 8
=>x > 2, x ∈ R

Question 35.
Given: P {x : 5 < 2x – 1 ≤ 11, x∈R)
Q{x : – 1 ≤ 3 + 4x < 23, x∈I) where
R = (real numbers), I = (integers)
Represent P and Q on number line. Write down the elements of P ∩ Q. (1996)
Solution:
P= {x : 5 < 2x – 1 ≤ 11}
5 < 2x – 1 ≤ 11

Question 36.
If x ∈ I, find the smallest value of x which satisfies the inequation \(2x+\frac { 5 }{ 2 } >\frac { 5x }{ 3 } +2\)
Solution:
\(2x+\frac { 5 }{ 2 } >\frac { 5x }{ 3 } +2\)
=>\(2x-\frac { 5x }{ 3 } >2-\frac { 5 }{ 2 } \)
=>12x – 10x > 12 – 15
=> 2x > – 3
=>\(x>-\frac { 3 }{ 2 } \)
Smallest value of x = – 1 Ans.

Question 37.
Given 20 – 5 x < 5 (x + 8), find the smallest value of x, when
(i) x ∈ I
(ii) x ∈ W
(iii) x ∈ N.
Solution:
20 – 5 x < 5 (x + 8)
⇒ 20 – 5x < 5x + 40
⇒ – 5x – 5x < 40 – 20
⇒ – 10x < 20
⇒ – x < 2
⇒ x > – 2
(i) When x ∈ I, then smallest value = – 1.
(ii) When x ∈ W, then smallest value = 0.
(iii) When x ∈ N, then smallest value = 1. Ans.

Question 38.
Solve the following inequation and represent the solution set on the number line :
\(4x-19<\frac { 3x }{ 5 } -2\le -\frac { 2 }{ 5 } +x,x\in R\)
Solution:
We have
\(4x-19<\frac { 3x }{ 5 } -2\le -\frac { 2 }{ 5 } +x,x\in R\)
Hence, solution set is {x : -4 < x < 5, x ∈ R}
The solution set is represented on the number line as below.

Question 39.
Solve the given inequation and graph the solution on the number line :
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
Solution:
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
(a) 2y – 3 < y + 1
⇒ 2y – y < 1 + 3
⇒ y < 4
⇒ 4 > y ….(i)
(b) y + 1 ≤ 4y + 7

Question 40.
Solve the inequation and represent the solution set on the number line.
\(-3+x\le \frac { 8x }{ 3 } +2\le \frac { 14 }{ 3 } +2x,Where\quad x\in I\)
Solution:
Given : \(-3+x\le \frac { 8x }{ 3 } +2\le \frac { 14 }{ 3 } +2x,Where\quad x\in I\)

Question 41.
Find the greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer.
Solution:
Let the greatest integer = x
According to the condition,
2x + 7 > 3x
⇒ 2x – 3x > – 7
⇒ – x > – 7
⇒ x < 7
Value of x which is greatest = 6 Ans.

Question 42.
One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.
Solution:
Let the length of the shortest pole = x metre
Length of pole which is burried in mud = \(\\ \frac { x }{ 3 } \)
Length of pole which is in the water = \(\\ \frac { x }{ 6 } \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.