ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test
Question 1.
Check whether the following are quadratic equations:
(i)\(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
(ii)(2x + 1) (3x – 2) = 6(x + 1) (x – 2)
(iii)\({ (x-3) }^{ 3 }+5={ x }^{ 3 }+7{ x }^{ 2 }-1\)
(iv)\(x-\frac { 3 }{ x } =2,x\neq 0\)
(v)\(x+\frac { 2 }{ x } ={ x }^{ 2 },x\neq 0\)
(vi)\({ x }^{ 2 }+\frac { 1 }{ { x }^{ 2 } } =3,x\neq 0 \)
Solution:
(i) \(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
It is a quadratic equation as it is power of 2.
(ii) (2x + 1) (3x – 2) = 6(x + 1) (x – 2)
6x² – 4x + 3x – 2 = 6(x² – 2x + x – 2)
6x² – x – 2 = 6x² – 12x + 6x – 12
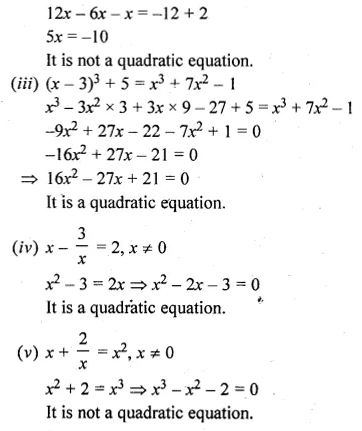
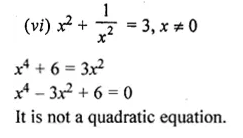
Question 2.
In each of the following, determine whether the given numbers are roots of the given equations or not;
(i) x² – x + 1 = 0; 1, – 1
(ii) x² – 5x + 6 = 0; 2, – 3
(iii) 3x² – 13x – 10 = 0; 5,\(\\ \frac { -2 }{ 3 } \)
(iv) 6x² – x – 2 = 0;\(\\ \frac { -1 }{ 2 } \), \(\\ \frac { 2 }{ 3 } \)
Solution:
(i) x² – x + 1 = 0; 1, -1
Where x = 1, then
(1)² – 1 + 1 = 1 – 1 + 1 = 1 ≠ 0
∴ x = 1 does not satisfy it

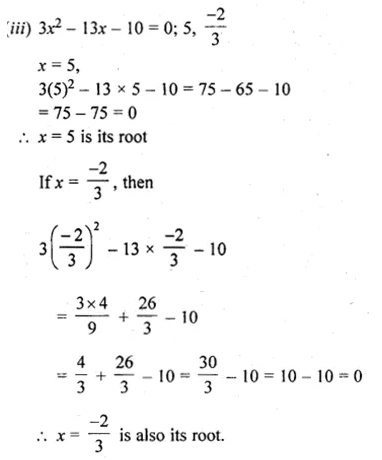
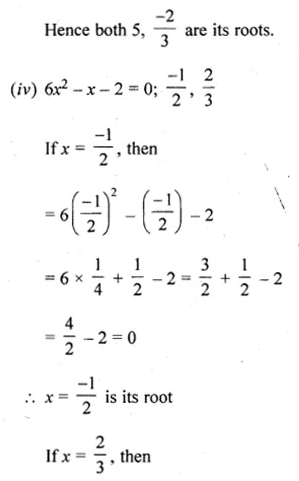

Question 3.
In each of the following, determine whether the given numbers are solutions of the given equation or not:
(i) x² – 3√3x + 6 = 0; √3, – 2√3
(ii) x² – √2x – 4 = 0, x = – √2, 2√2
Solution:
(i) x² – 3√3x + 6 = 0; √3, -2√3
(a) Substituting the value of x = √3
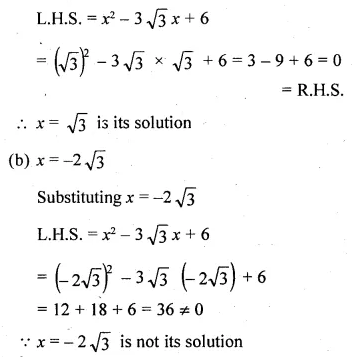
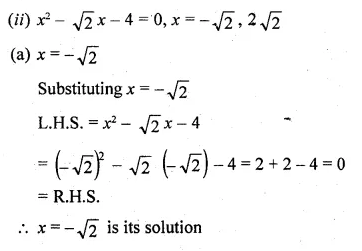

Question 4.
(i) If \(– \frac { 1 }{ 2 } \) is a solution of the equation 3x² + 2kx – 3 = 0, find the value of k.
(ii) If \(\\ \frac { 2 }{ 3 } \) is a solution of the equation 7x² + kx – 3 = 0, find the value of k.
Solution:
(i) x = \(– \frac { 1 }{ 2 } \) is a solution of the
3x² + 2kx – 3 = 0,
Substituting the value of x in the given equation
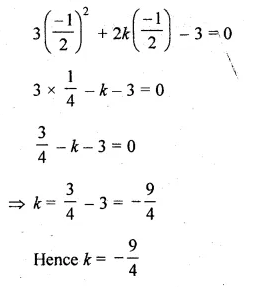
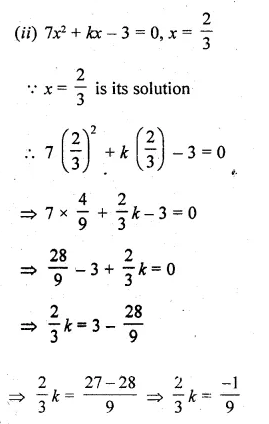
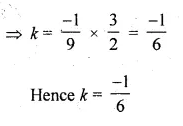
Question 5.
(i) If √2 is a root of the equation kx² + √2 – 4 = 0, find the value of k.
(ii) If a is a root of the equation x² – (a + b)x + k = 0, find the value of k.
Solution:
(i) kx² + √2 – 4 = 0, x = √2
x = √2 is its solution
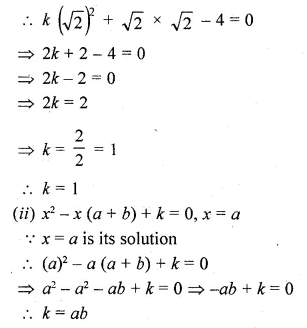
Question 6.
If \(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0, find the values of p and q.
Solution:
\(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0
Substituting the value of x = \(\\ \frac { 2 }{ 3 } \) and – 3 respectively, we get
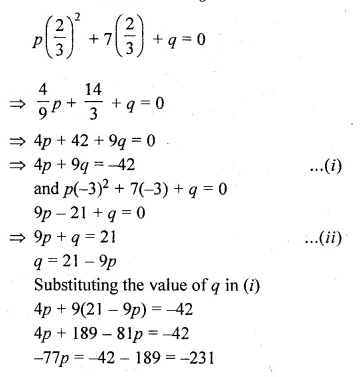
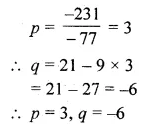
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.