ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test
Question 1.
Solve the inequation 3x -11 < 3 where x ∈ {1, 2, 3,……, 10}. Also represent its solution on a number line
Solution:
3x – 11 < 3 => 3x < 3 + 11 => 3x < 14 x < \(\\ \frac { 14 }{ 3 } \)
But x ∈ 6 {1, 2, 3, ……., 10}
Solution set is (1, 2, 3, 4}
Ans. Solution set on number line

Question 2.
Solve 2(x – 3)< 1, x ∈ {1, 2, 3, …. 10}
Solution:
2(x – 3) < 1 => x – 3 < \(\\ \frac { 1 }{ 2 } \) => x < \(\\ \frac { 1 }{ 2 } \) + 3 => x < \(3 \frac { 1 }{ 2 } \)
But x ∈ {1, 2, 3 …..10}
Solution set = {1, 2, 3} Ans.

Question 3.
Solve : 5 – 4x > 2 – 3x, x ∈ W. Also represent its solution on the number line.
Solution:
5 – 4x > 2 – 3x
– 4x + 3x > 2 – 5
=> – x > – 3
=> x < 3
x ∈ w,
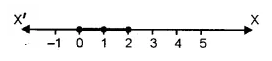
solution set {0, 1, 2}
Solution set on Number Line :
Question 4.
List the solution set of 30 – 4 (2.x – 1) < 30, given that x is a positive integer.
Solution:
30 – 4 (2x – 1) < 30
30 – 8x + 4 < 30
– 8x < 30 – 30 – 4
– 8x < – 4 x > \(\\ \frac { -4 }{ -8 } \)
=> x > \(\\ \frac { 1 }{ 2 } \)
x is a positive integer
x = {1, 2, 3, 4…..} Ans.
Question 5.
Solve : 2 (x – 2) < 3x – 2, x ∈ { – 3, – 2, – 1, 0, 1, 2, 3} .
Solution:
2(x – 2) < 3x – 2
=> 2x – 4 < 3x – 2
=> 2x – 3x < – 2 + 4
=> – x < 2
=> x > – 2
Solution set = { – 1, 0, 1, 2, 3} Ans.
Question 6.
If x is a negative integer, find the solution set of \(\\ \frac { 2 }{ 3 } \)+\(\\ \frac { 1 }{ 3 } \) (x + 1) > 0.
Solution:
\(\\ \frac { 2 }{ 3 } \)+\(\\ \frac { 1 }{ 3 } \) x + \(\\ \frac { 1 }{ 3 } \) > 0
=> \(\\ \frac { 1 }{ 3 } \) x + 1 > 0
=> \(\\ \frac { 1 }{ 3 } \) x > – 1
![]()
x is a negative integer
Solution set = {- 2, – 1} Ans.
Question 7.
Solve: \(\\ \frac { 2x-3 }{ 4 } \)≥\(\\ \frac { 1 }{ 2 } \), x ∈ {0, 1, 2,…,8}
Solution:
\(\\ \frac { 2x-3 }{ 4 } \)≥\(\\ \frac { 1 }{ 2 } \)
=> 2x – 3 ≥ \(\\ \frac { 4 }{ 2 } \)
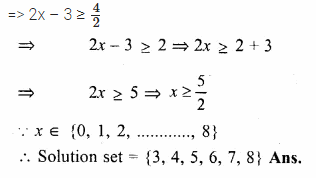
Question 8.
Solve x – 3 (2 + x) > 2 (3x – 1), x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}. Also represent its solution on the number line.
Solution:
x – 3 (2 + x) > 2 (3x – 1)
=> x – 6 – 3x > 6x – 2
=> x – 3x – 6x > – 2 + 6
=> – 8x > 4
=> x < \(\\ \frac { -4 }{ 8 } \) => x < \(– \frac { 1 }{ 2 } \)
x ∈ { – 3, – 2, – 1, 0, 1, 2}
.’. Solution set = { – 3, – 2, – 1}
Solution set on Number Line :
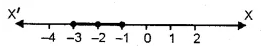
Question 9.
Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9} solve x – 3 < 2x – 1.
Solution:
x – 3 < 2x – 1
x – 2x < – 1 + 3 => – x < 2 x > – 2
But x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4, 5, 6, 7, 9} Ans.
Question 10.
Given A = {x : x ∈ I, – 4 ≤ x ≤ 4}, solve 2x – 3 < 3 where x has the domain A Graph the solution set on the number line.
Solution:
2x – 3 < 3 => 2x < 3 + 3 => 2x < 6 => x < 3
But x has the domain A = {x : x ∈ I – 4 ≤ x ≤ 4}
Solution set = { – 4, – 3, – 2, – 1, 0, 1, 2}
Solution set on Number line :
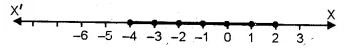
Question 11.
List the solution set of the inequation
\(\\ \frac { 1 }{ 2 } \) + 8x > 5x \(– \frac { 3 }{ 2 } \), x ∈ Z
Solution:
\(\\ \frac { 1 }{ 2 } \) +8x > 5x \(– \frac { 3 }{ 2 } \)
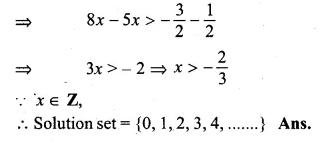
Question 12.
List the solution set of \(\\ \frac { 11-2x }{ 5 } \) ≥ \(\\ \frac { 9-3x }{ 8 } \) + \(\\ \frac { 3 }{ 4 } \),
x ∈ N
Solution:
\(\\ \frac { 11-2x }{ 5 } \) ≥ \(\\ \frac { 9-3x }{ 8 } \) + \(\\ \frac { 3 }{ 4 } \)
=> 88 – 16x ≥ 45 – 15x + 30
(L.C.M. of 8, 5, 4 = 40}
=> – 16x + 15x ≥ 45 + 30 – 88
=> – x ≥ – 13
=>x ≤ 13
x ≤ N.
Solution set = {1, 2, 3, 4, 5, .. , 13} Ans.
Question 13.
Find the values of x, which satisfy the inequation : \(-2\le \frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le 1\frac { 5 }{ 6 } \), x ∈ N.
Graph the solution set on the number line. (2001)
Solution:
\(-2\le \frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le 1\frac { 5 }{ 6 } \), x ∈ N
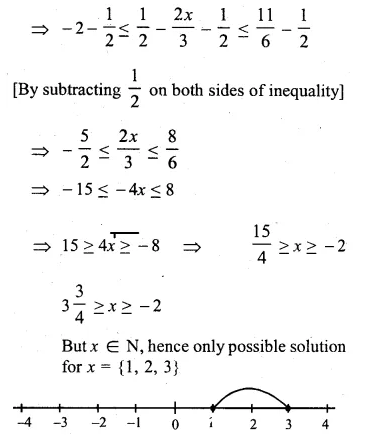
Question 14.
If x ∈ W, find the solution set of
\(\frac { 3 }{ 5 } x-\frac { 2x-1 }{ 3 } >1\)
Also graph the solution set on the number line, if possible.
Solution:
\(\frac { 3 }{ 5 } x-\frac { 2x-1 }{ 3 } >1\)
9x – (10x – 5) > 15 (L.C.M. of 5, 3 = 15)
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
But x ∈ W
Solution set = Φ
Hence it can’t be represented on number line.
Question 15.
Solve:
(i)\(\frac { x }{ 2 } +5\le \frac { x }{ 3 } +6\) where x is a positive odd integer.
(ii)\(\frac { 2x+3 }{ 3 } \ge \frac { 3x-1 }{ 4 } \) where x is positive even integer.
Solution:
(i) \(\frac { x }{ 2 } +5\le \frac { x }{ 3 } +6\)
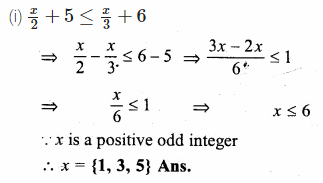
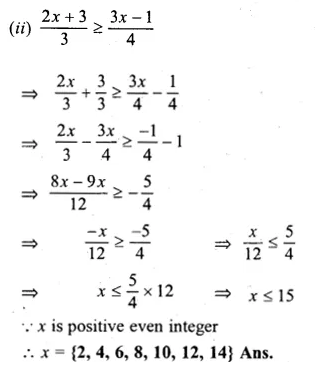
Question 16.
Given that x ∈ I, solve the inequation and graph the solution on the number line :
\(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \ge 2 \) (2004)
Solution:
\(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \) and \(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \ge 2 \)
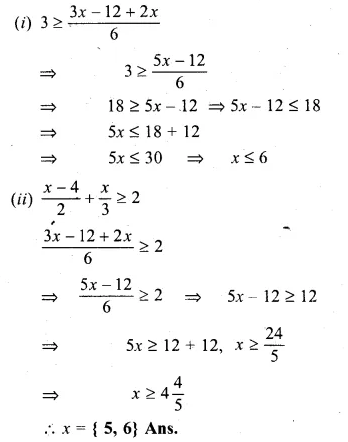
Question 17.
Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9}, find the values of x for which -3 < 2x – 1 < x + 4.
Solution:
-3 < 2x – 1 < x + 4.
=> – 3 < 2x – 1 and 2x – 1 < x + 4
=> – 2x < – 1 + 3 and 2x – x < 4 + 1
=> – 2x < 2 and x < 5
=> – x < 1
=> x > – 1
– 1 < x < 5
x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4} Ans.
Question 18.
Solve : 1 ≥ 15 – 7x > 2x – 27, x ∈ N
Solution:
1 ≥ 15 – 7x > 2x – 27
1 ≥ 15 – 7x and 15 – 7x > 2x – 27
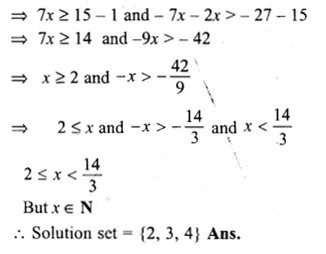
Question 19.
If x ∈ Z, solve 2 + 4x < 2x – 5 ≤ 3x. Also represent its solution on the number line.
Solution:
2 + 4x < 2x – 5 ≤ 3x
2 + 4x < 2x – 5 and 2x – 5 ≤ 3x => 4x – 2x < – 5 – 2 ,and 2x – 3x ≤ 5
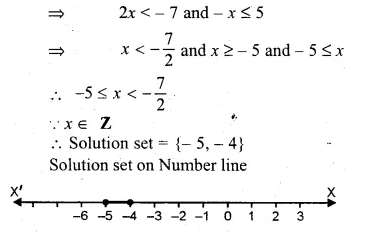
Question 20.
Solve the inequation = 12 + \(1 \frac { 5 }{ 6 } x\) ≤ 5 + 3x, x ∈ R. Represent the solution on a number line. (1999)
Solution:
12 + \(1 \frac { 5 }{ 6 } x\) ≤ 5 + 3x
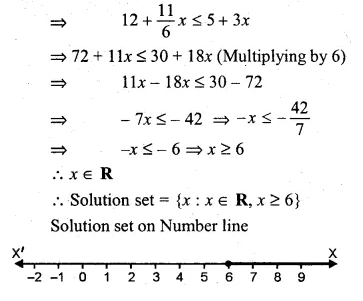
Question 21.
Solve : \(\\ \frac { 4x-10 }{ 3 } \)≤\(\\ \frac { 5x-7 }{ 2 } \) x ∈ R and represent the solution set on the number line.
Solution:
\(\\ \frac { 4x-10 }{ 3 } \)≤\(\\ \frac { 5x-7 }{ 2 } \)
=> 8x – 20 ≤ 15x – 21
(L.C.M. of 3, 2 = 6)
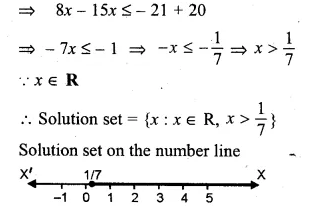
Question 22.
Solve \(\frac { 3x }{ 5 } -\frac { 2x-1 }{ 3 } \) > 1, x ∈ R and represent the solution set on the number line.
Solution:
\(\frac { 3x }{ 5 } -\frac { 2x-1 }{ 3 } \) > 1
=> 9x – (10x – 5) > 15
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
x ∈ R.
.’. Solution set = {x : x ∈R, x < – 10}
Solution set on the number line
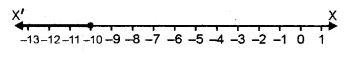
Question 23.
Solve the inequation – 3 ≤ 3 – 2x < 9, x ∈ R. Represent your solution on a number line. (2000)
Solution:
– 3 ≤ 3 – 2x < 9
– 3 ≤ 3 – 2x and 3 – 2x < 9
2x ≤ 3 + 3 and – 2x < 9 – 3
2x ≤ 6 and – 2x < 6 => x ≤ 3 and – x < 3 => x ≤ – 3 and – 3 < x
– 3 < x ≤ 3.
Solution set= {x : x ∈ R, – 3 < x ≤ 3)
Solution on number line

Question 24.
Solve 2 ≤ 2x – 3 ≤ 5, x ∈ R and mark it on number line. (2003)
Solution:
2 ≤ 2x – 3 ≤ 5 .
2 ≤ 2x – 3 and 2x – 3 ≤ 5
2 + 3 ≤ 2x and 2x ≤ 5 + 3
5 ≤ 2x and 2x ≤ 8.

Question 25.
Given that x ∈ R, solve the following inequation and graph the solution on the number line: – 1 ≤ 3 + 4x < 23. (2006)
Solution:
We have
– 1 ≤ 3 + 4x < 23 => – 1 – 3 ≤ 4x < 23 – 3 => – 4 ≤ 4x < 20 => – 1 ≤ x < 5, x ∈ R
Solution Set = { – 1 ≤ x < 5; x ∈ R}

Question 26.
Solve tlie following inequation and graph the solution on the number line. (2007)
\(-2\frac { 2 }{ 3 } \le x+\frac { 1 }{ 3 } <3+\frac { 1 }{ 3 } \) x∈R
Solution:
Given \(-2\frac { 2 }{ 3 } \le x+\frac { 1 }{ 3 } <3+\frac { 1 }{ 3 } \) x∈R
\(-\frac { 8 }{ 3 } \le x+\frac { 1 }{ 3 } <\frac { 10 }{ 3 } \)
Multiplying by 3, L.C.M. of fractions, we get

Question 27.
Solve the following inequation and represent the solution set on the number line :
\(-3<-\frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le \frac { 5 }{ 6 } ,x\in R\)
Solution:
\(-3<-\frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le \frac { 5 }{ 6 } ,x\in R\)
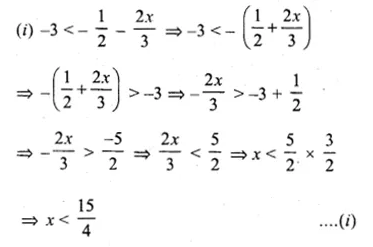

Question 28.
Solve \(\frac { 2x+1 }{ 2 } +2(3-x)\ge 7,x\in R\). Also graph the solution set on the number line
Solution:
\(\frac { 2x+1 }{ 2 } +2(3-x)\ge 7,x\in R\)
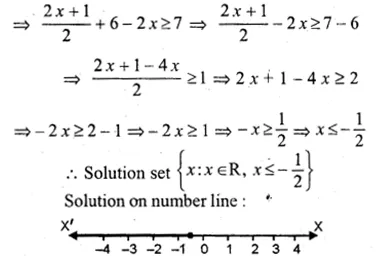
Question 29.
Solving the following inequation, write the solution set and represent it on the number line. – 3(x – 7)≥15 – 7x > \(\\ \frac { x+1 }{ 3 } \), n ∈R
Solution:
– 3(x – 7)≥15 – 7x > \(\\ \frac { x+1 }{ 3 } \), n ∈R
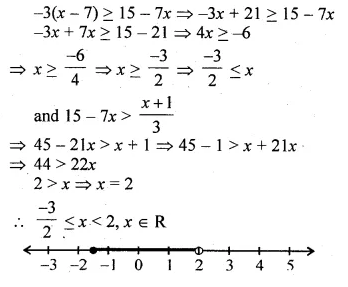
Question 30.
Solve the inequation :
\(-2\frac { 1 }{ 2 } +2x\le \frac { 4x }{ 3 } \le \frac { 4 }{ 3 } +2x,\quad x\in W\). Graph the solution set on the number line.
Solution:
\(-2\frac { 1 }{ 2 } +2x\le \frac { 4x }{ 3 } \le \frac { 4 }{ 3 } +2x,\quad x\in W\)
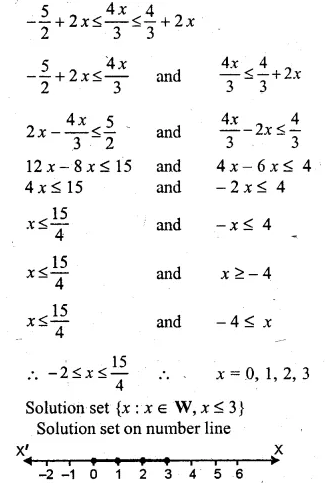
Question 31.
Solve the inequation 2x – 5 ≤ 5x + 4 < 11, where x ∈ I. Also represent the solution set on the number line. (2011)
Solution:
2x – 5 ≤ 5x + 4 < 11 2x – 5 ≤ 5x + 4
=> 2x – 5 – 4 ≤ 5x and 5x + 4 < 11
=> 2x – 9 ≤ 5x and 5x < 11 – 4
and 5x < 7
=> 2x – 5x ≤ 9 and x < \(\\ \frac { 7 }{ 5 } \)
=> 3x > – 9 and x< 1.4
=> x > – 3
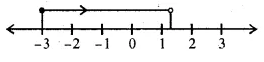
Question 32.
If x ∈ I, A is the solution set of 2 (x – 1) < 3 x – 1 and B is the solution set of 4x – 3 ≤ 8 + x, find A ∩B.
Solution:
2 (x – 1) < 3 x – 1
2x – 2 < 3x – 1
2x – 3x < – 1 + 2 => – x < 1 x > – 1
Solution set A = {0, 1, 2, 3, ..,.}
4x – 3 ≤ 8 + x
4x – x ≤ 8 + 3
=> 3x ≤ 11
=> x ≤ \(\\ \frac { 11 }{ 3 } \)
Solution set B = {3, 2, 1, 0, – 1…}
A ∩ B = {0, 1, 2, 3} Ans.
Question 33.
If P is the solution set of – 3x + 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find
(i) P ∩ Q
(ii) Q – P.
Solution:
(i) – 3 x + 4 < 2 x – 3
– 3x – 2x < – 3 – 4 => – 5x < – 7
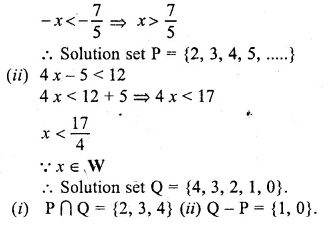
Question 34.
A = {x : 11x – 5 > 7x + 3, x ∈R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Find the range of set A ∩ B and represent it on a number line
Solution:
A = {x : 11x – 5 > 7x + 3, x ∈R}
B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Now, A = 11x – 5 > 7x + 3
=> 11x – 7x > 3 + 5
=> 4x > 8
=>x > 2, x ∈ R
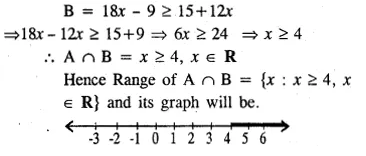
Question 35.
Given: P {x : 5 < 2x – 1 ≤ 11, x∈R)
Q{x : – 1 ≤ 3 + 4x < 23, x∈I) where
R = (real numbers), I = (integers)
Represent P and Q on number line. Write down the elements of P ∩ Q. (1996)
Solution:
P= {x : 5 < 2x – 1 ≤ 11}
5 < 2x – 1 ≤ 11

Question 36.
If x ∈ I, find the smallest value of x which satisfies the inequation \(2x+\frac { 5 }{ 2 } >\frac { 5x }{ 3 } +2\)
Solution:
\(2x+\frac { 5 }{ 2 } >\frac { 5x }{ 3 } +2\)
=>\(2x-\frac { 5x }{ 3 } >2-\frac { 5 }{ 2 } \)
=>12x – 10x > 12 – 15
=> 2x > – 3
=>\(x>-\frac { 3 }{ 2 } \)
Smallest value of x = – 1 Ans.
Question 37.
Given 20 – 5 x < 5 (x + 8), find the smallest value of x, when
(i) x ∈ I
(ii) x ∈ W
(iii) x ∈ N.
Solution:
20 – 5 x < 5 (x + 8)
⇒ 20 – 5x < 5x + 40
⇒ – 5x – 5x < 40 – 20
⇒ – 10x < 20
⇒ – x < 2
⇒ x > – 2
(i) When x ∈ I, then smallest value = – 1.
(ii) When x ∈ W, then smallest value = 0.
(iii) When x ∈ N, then smallest value = 1. Ans.
Question 38.
Solve the following inequation and represent the solution set on the number line :
\(4x-19<\frac { 3x }{ 5 } -2\le -\frac { 2 }{ 5 } +x,x\in R\)
Solution:
We have
\(4x-19<\frac { 3x }{ 5 } -2\le -\frac { 2 }{ 5 } +x,x\in R\)
Hence, solution set is {x : -4 < x < 5, x ∈ R}
The solution set is represented on the number line as below.
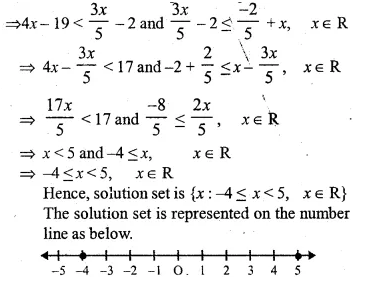
Question 39.
Solve the given inequation and graph the solution on the number line :
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
Solution:
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
(a) 2y – 3 < y + 1
⇒ 2y – y < 1 + 3
⇒ y < 4
⇒ 4 > y ….(i)
(b) y + 1 ≤ 4y + 7
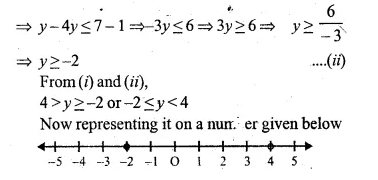
Question 40.
Solve the inequation and represent the solution set on the number line.
\(-3+x\le \frac { 8x }{ 3 } +2\le \frac { 14 }{ 3 } +2x,Where\quad x\in I\)
Solution:
Given : \(-3+x\le \frac { 8x }{ 3 } +2\le \frac { 14 }{ 3 } +2x,Where\quad x\in I\)

Question 41.
Find the greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer.
Solution:
Let the greatest integer = x
According to the condition,
2x + 7 > 3x
⇒ 2x – 3x > – 7
⇒ – x > – 7
⇒ x < 7
Value of x which is greatest = 6 Ans.
Question 42.
One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.
Solution:
Let the length of the shortest pole = x metre
Length of pole which is burried in mud = \(\\ \frac { x }{ 3 } \)
Length of pole which is in the water = \(\\ \frac { x }{ 6 } \)
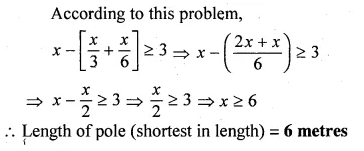
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.