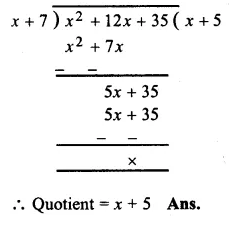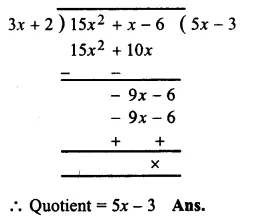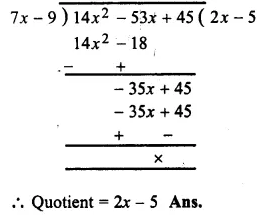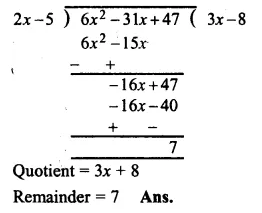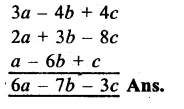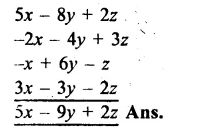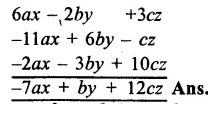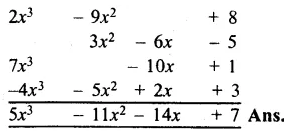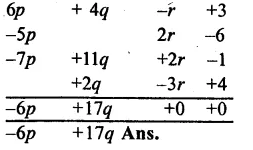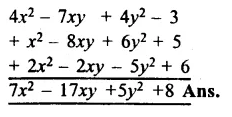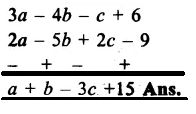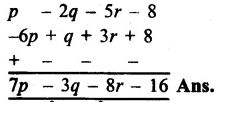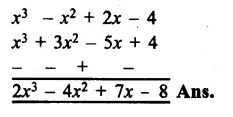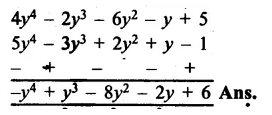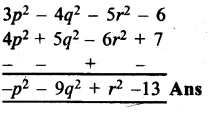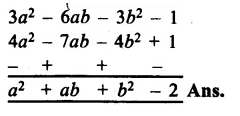RS Aggarwal Maths Solutions Class 8

RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6C.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6C
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6D
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6E

Question 1.
Solution:
(i) 24x²y³ ÷ 3xy

Question 2.
Solution:
(i)(5m³ – 30m² + 45m) ÷ 5m

Write the quotient and remainder when we divide:

Question 3.
Solution:

Question 4.
Solution:

Quotient = x – 2
Remainder = 0

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

Question 13.
Solution:

Question 14.
Solution:

Question 15.
Solution:

Hope given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6C
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6D
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6E

Find each of the following products?

Question 1.
Solution:
(5x + 7) X (3x + 4) = 5x(3x + 4) + 7(3x + 4)
= 15x² + 20x + 21x + 28 = 15x² + 41x + 28 Ans.

Question 2.
Solution:
(4x + 9) X (x – 6) = 4x(x – 6) + 9(x – 6)
= 4x² – 24x + 9x – 54
= 4x² – 15x – 54 Ans.

Question 3.
Solution:
(2x + 5) X (4x – 3) = 2x(4x – 3) + 5(4x – 3)
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15 Ans.

Question 4.
Solution:
(3y – 8) X (5y – 1) = 3y(5y – 1) – 8(5y – 1)
= 15y² – 3y – 40y + 8
= 15y² – 43y + 8 Ans.

Question 5.
Solution:
(7x + 2y) X (x + 4y)
= 7x(x + 4y) + 2y(x + 4y)
= 7x² + 28xy + 2xy + 8y²
= 7x² + 30xy + 8y² Ans.

Question 6.
Solution:
(9x + 5y) X (4x + 3y) = 9x(4x + 3y) + 5y(4x + 3y)
= 36x² + 27xy + 20xy + 15y²
= 36x² + 47xy + 15y² Ans.

Question 7.
Solution:
(3m – 4n) X (2m – 3n)
= 3m(2m – 3n) – 4n(2m – 3n)
= 6m² – 9mn – 8mn + 12n²
= 6m² – 17mn + 12n² Ans.

Question 8.
Solution:
(x² – a²) X (x – a)
= x²(x – a) – a²(x – a)
= x³ – x²a – xa² + a³ Ans.

Question 9.
Solution:
(x² – y²) X (x + 2y)
= x²(x + 2y) – y²(x + 2y)
= x³ + 2x²y – xy² – 2y³ Ans.

Question 10.
Solution:
(3p² + q²) X (2p² – 3q²)
= 3p²(2p² – 3q²) + q²(2p² – 3q²)
= 6p⁴ – 9p²q² + 2p²q² – 3q⁴
= 6p⁴ – 7p²q² – 3q⁴ Ans.

Question 11.
Solution:
(2x² – 5y²) X (x² + 3y²)
= 2x²(x² + 3y²) – 5y²(x² + 3y²)
= 2x⁴ + 6x²y² – 5x²y² – 15y⁴)
= 2x⁴ + x2y² – 15y⁴ Ans.

Question 12.
Solution:
(x³ – y³) X (x² + y²)
= x³(x² + y²) – y³(x² + y²)
= x⁵ + x³y² – x²y³ – y⁵ Ans.

Question 13.
Solution:
(x⁴ + y⁴) X (x² – y²)
= x⁴(x² – y²) + y⁴(x² – y²)
= x⁶ – x⁴y² + x²y⁴ – y⁶ Ans.

Question 14.
Solution:
\(\left( { x }^{ 4 }+\frac { 1 }{ { x }^{ 4 } } \right) \times \left( { x+ }\frac { 1 }{ { x } } \right)\)

Find each of the following products:

Question 15.
Solution:
(x² – 3x + 7) X (2x + 3)
= (x² – 3x + 7) (2x) + (x² – 3x + 7) X 3
= 2x³ – 6x + 14x + 3x² – 9x + 21
= 2x³ – 3x² + 5x + 21 Ans.

Question 16.
Solution:
(3x² + 5x – 9) X (3x – 5)
= 3x²(3x – 5x) + 5x(3x – 5) – 9(3x – 5)
= 9x³ – 15x² + 15x² – 25x – 27x + 45
= 9x³ – 52x + 45 Ans.

Question 17.
Solution:
(x² – xy + y²) X (x + y)
= (x² – xy + y²) X x + (x² – xy + y²) X y
= x³ – x²y + xy² + x²y – xy² + y³
= x³ + y³ Ans.

Question 18.
Solution:
(x² + xy + y²) X (x – y)
(x² + xy + y²) X x + (x² + xy + y²) X ( – y)
= x³ + x²y + xy² – x²y – xy² – y³
= x³ – y³ Ans.

Question 19.
Solution:
(x³ – 2x² + 5) X (4x – 1)
= (x³ – 2x² + 5) X 4x + (x³ – 2x² + 5) X ( – 1)
= 4x⁴ – 8x³ + 20x – x³ + 2x² – 5
= 4x⁴ – 9x³ + 2x² + 20x – 5 Ans.

Question 20.
Solution:
(9x² – x + 15) X (x² – 3)
(9x² – X + 15) X x² + (9x² – x + 15) X ( – 3)
= 9x⁴ – x³ + 15x² – 27x² + 3x – 45
= 9x⁴ – x³ – 12x² + 3x – 45 Ans.

Question 21.
Solution:
(x² – 5x + 8) X (x² + 2)
= (x² – 5x + 8) X x² + (x² – 5x + 8) X 2
= x⁴ – 5x³ + 8x² + 2x² – 10x + 16
= x⁴ – 5x³ + 10x² – 10x + 16 Ans.

Question 22.
Solution:
(x³ – 5x² + 3x + 1) X (x² – 3)
= (x³ – 5x² + 3x + 1) X x² + (x³ – 5x² + 3x + 1) X ( – 3)
= x⁵ – 5x⁴ + 3x³ + x² – 3x³ + 15x² – 9x – 3
= x⁵ – 5x⁴ + 16x² – 9x – 3 Ans.

Question 23.
Solution:
(3x + 2y – 4) X (x – y + 2)

Question 24.
Solution:
(x² – 5x + 8) X (x² + 2x – 3)

Question 25.
Solution:
(2x² + 3x – 7) X (3x² – 5x + 4)

Question 26.
Solution:
(9x² – x + 15) X (x² – x – 1)

Hope given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6C
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6D
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6E

Add:

Question 1.
Solution:
8ab + ( – 5ab) + (3ab) + ( – ab)
= 8ab – 5ab + 3ab – ab = 11 ab – 6ab
= 5ab Ans.

Question 2.
Solution:
7x + ( – 3x) + 5x + ( – x) + ( – 2x)
= 7x – 3x + 5x – x – 2x
= 12x – 6x = 6x Ans.

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Subtarct:

Question 9.
Solution:
-5a²b – 3a²b = – 8a²b Ans.

Question 10.
Solution:
6pq – ( – 8pq) = 6pq + 8pq

Question 11.
Solution:
– 8abc – ( – 2abc)
= – 8abc + 2abc
= – 6abc Ans.

Question 12.
Solution:
– 11p – ( – 16p)
= – 11p + 16p
= 5p Ans.

Question 13.
Solution:

Question 14.
Solution:

Question 15.
Solution:

Question 16.
Solution:

Question 17.
Solution:

Question 18.
Solution:

Question 19.
Solution:
Let length of rectangle = 5x² – 3y²
and breadth = x² + 2xy
Perimeter = 2(Length + Breadth)
= 2(5x² – 3y² + x² + 2xy)
= 2(6x² – 3y² + 2xy)
= 12x² – 6y² + 4xy Ans.

Question 20.
Solution:
Perimeter of a triangle = 6p² – 4p + 9
Sum of two sides of it = 3p² – 5p + 3 + p² – 2p + 1 = 4p² – 7p – 4
Third side = (6p² – 4p + 9) – (4p² – 7p + 4)
= 6p² – 4p + 9 – 4p² + 7p – 4
= 2p² + 3p + 5 Ans

Hope given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5D

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5D.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5A
• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5B
• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5C
• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5D

Question 1.
Solution:
5×6 is exactly divisible by 3
Sum of its digits must be divisible by 3
5 + x + 6 = 11 + x is divisible by 3
Least value of x = 1 as 12 is divisible by 3 (b)

Question 2.
Solution:
64y8 is exactly divisible by 3 then the sum of its digits must be divisible by 3
6 + 4 + y + 8 or 18 + y is divisible by 3
Least value of y = 0
18 is divisible by 3 (a)

Question 3.
Solution:
7 x 8 is exactly divisible by 9
Sum of its digits must be divisible by 9
7 + x + 8 = 15 + x must be divisible by 9
Least value of x = 3 as 15 + 3 = 18 is divisible by 9 (c)

Question 4.
Solution:
37y4 is exactly divisible by 9
The sum of its digits must be divisible by
3 + 7 + y + 4 or 14 + y is divisible by 9
Least value of y = 4
As 14 + 4 = 18 is divisible by 9 (d)

Question 5.
Solution:
4xy7 is exactly divisible by 3
The sum of its digits must be divisible by 9
or 4 + x + y + 7 or 11 + (x + y) is divisible by 9
Least value of x + y = 7
as 11 + 7 = 18 is divisible by 9 (d)

Question 6.
Solution:
x7y5 is exactly divisible by 3
Sum of its digits must be divisible by 3
x + 7 + y + 512 + (x + y) is divisible by 3
Least value of x + y = 0 as
12 + 0 = 12 is divisible by 3 (b)

Question 7.
Solution:
x4y5z is exactly divisible by 9
The sum of its digits must be divisible by 9
x + 4 + y + 5 + z or 9 + (x + y + z) must be divisible by 9
Least value of x + y + z = 0 as 9 + 0 = 9 is divisible by 9 (d)

Question 8.
Solution:
A2B5 is exactly divisible by 9
Sum of its digits must be divisible by 9
A + 2 + B + 5 = 7 + A + B is divisible by 9
Least value of A + B = 2 as 7 + 2 = 9 is divisible by 9

Question 9.
Solution:
x27y is exactly divisible by 9
The sum of its digits must be divisible by 9
x + 2 + 7 + y = x + y + 9 is divisible by 9
Least value of x + y = 0 as 0 + 99 is exactly divisible by 9 (a)

Hope given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5C.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5A
• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5B
• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5C
• RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5D

Replace A, B, C by suitable numerals.

Question 1.
Solution:
Here A can be as 6 + 7 = 13
Now 1 + 5 + 8 = 14
∴C = 1, B = 4, A = 6

Question 2.
Solution:
Here A can be 7, as 6+7 = 13
1 + B + 9 = 10 + B
∴B can be 7
∴10 + 7 = 17
1 + C + 6 = 7 + C
∴C can be 4
∴1 + 4 + 6 = 11
and 1 + 4 + 3 = 8
∴A = 7, B = 7, C = 4

Question 3.
Solution:
Here A + A + A = A
∴A can = 5
∴5 + 5 + 5 = 15
∴B = 1
Hence A = 5, B = 1

Question 4.
Solution:
6 – A = 3
1 + 5 – A = 3
5 – A = 3
∴A = 5 – 3 = 2
Now 2 – B = 7
=>12 – B = 7
∴B = 5
Hence A = 2, B = 5

Question 5.
Solution:
– 5 – A = 9 =>A = 5 – 9 or 15 – 9
= 6
∴A = 6
Now B – 1 – 8 = 5 =>B – 9 = 5
=>B = 5 + 9 = 14
∴B = 4
Now C – 1 – 2 = 2 =>C – 3 = 2
C = 2 + 3 = 5
∴A = 6, B = 4, C = 5

Question 6.
Solution:
B x 3 = B
∴B can be 5 or 0
∴5 x 3 = 15 => B = 5 or 3 x 0 =0
If B = 0, then A can be 5
∴3 x 5 = 15
∴A = 5 and C = 1
Hence A = 5, B = 0, C = 1

Question 7.
Solution:

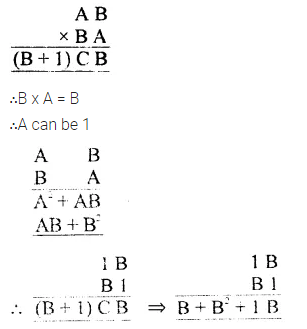
∴AB = B
=>A = 1
and A² + B² – 1 + B² + C
∴B² +1 = C
∴B² in one digit
If B = 3
∴3² + 1 = 9 + 1 = 10 = C
∴C = 0
B x 1 + 1 = B + 1 = 3 + 1
Hence A = 1, B = 3, C = 0

Question 8.
Solution:
Here we see that 6 x 9 = 54
∴A – 4 = 3 => A = 3 + 4 = 7
and 6 x 6 = 36
3B = 36 => B = 6
and C = 6
Hence A = 7, B = 6, C = 6

Question 9.
Solution:
Product of two numbers = 1 -digit number
and sum = 2-digit numbers
Let first number = x
and second number = y
∴x X y = 1-digit number
x + y = 2-digit number
By hit and hail, we sec that
1 x 9 = 9 which is I-digit number
and 1 + 9 = 10 which is 2-digit number

Question 10.
Solution:
By hit and trail method, we see that
1 + 2 + 3 = 6 and 1 x 2 x 3 = 6
1, 2 and 3 are the required whole numbers
whose sum and product is same

Question 11.
Solution:
In the given square, we have to interest the numbers from 1 to 9, such that the sum in each raw, column on diagonal to be 15
So, we complete it as given here

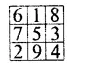
Question 12.
Solution:
We shall complete the triangle by intersecting the numbers from 1 to 6 without repetition so that the sum in each side be 12

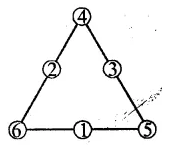
Question 13.
Solution:
The given numbers are
a, b (a + b), (a + 2b), (2a + 3b), (3a + 5b), (5a + 8b), (8a + 13b), (13a + 21b), and (21a + 34b)
Sum of there numbers = 11 (5a + 8b)
= 11 x 7th number
Now taking a = 8, b = 13, then the 10 number be 8, 13, 21, 34, 55, 89, 144, 233, 377, 610
Whose 7th number = 144
By adding these 10 numbers, we get the
sum
= 8+ 13 + 21 + 34 + 55 + 89 + 144 + 233 + 377 + 610 = 1584 and 11 x 7th number =11 x 144 , = 1584
Which is same in each case

Question 14.
Solution:
We see that in the magic box sum of 0 + 11 + 7 + 12 = 30
Now we shall complete this magic square, to get 30 as the sum in each row and column and also diagonal wise

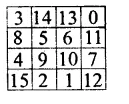
Hope given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.