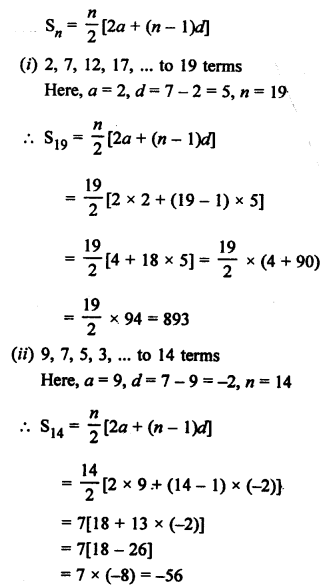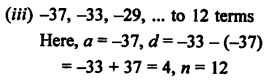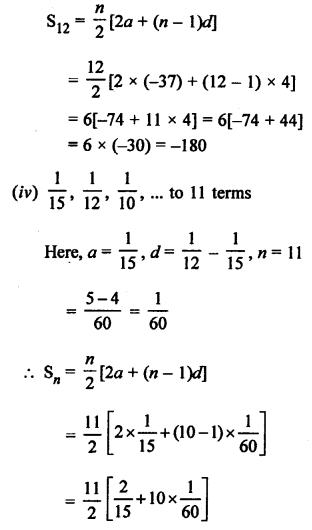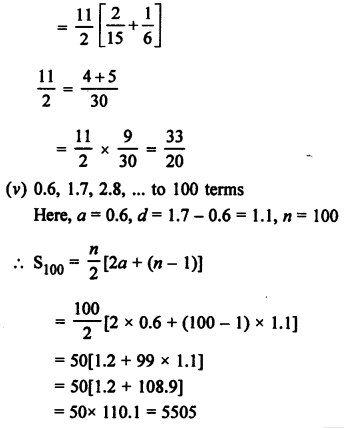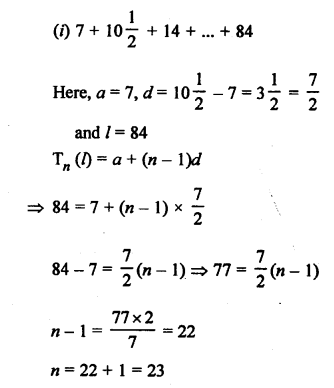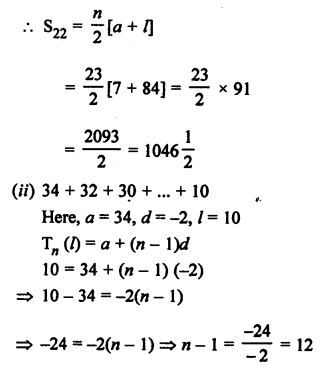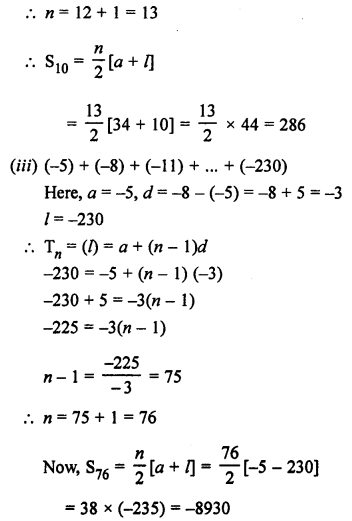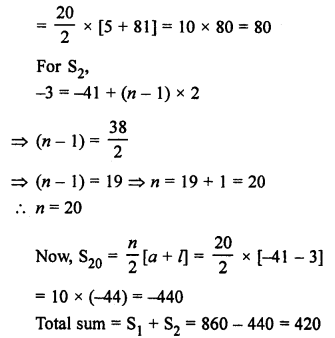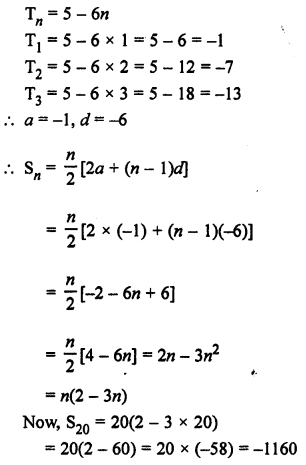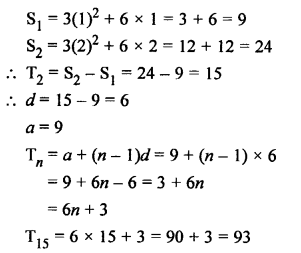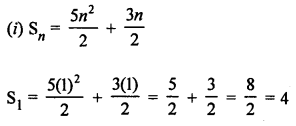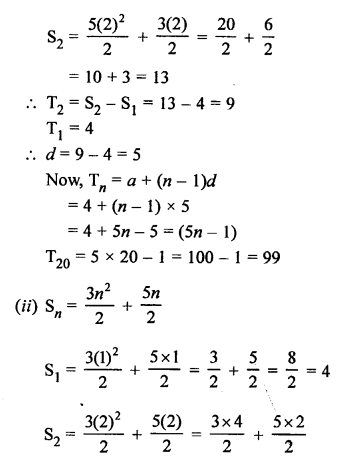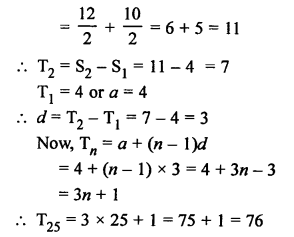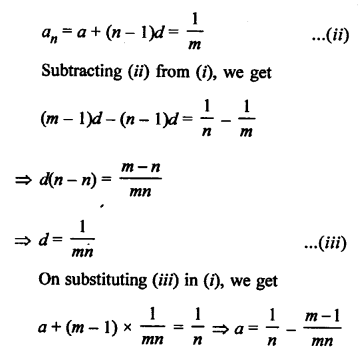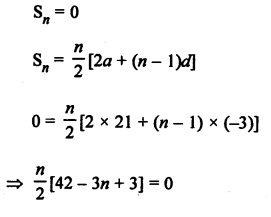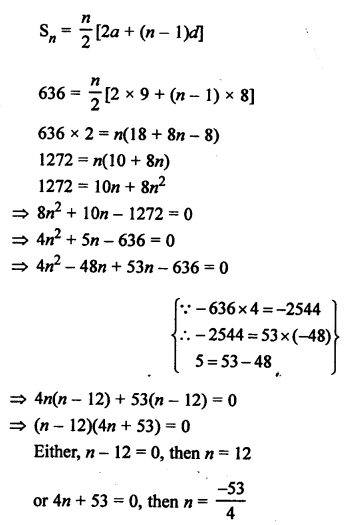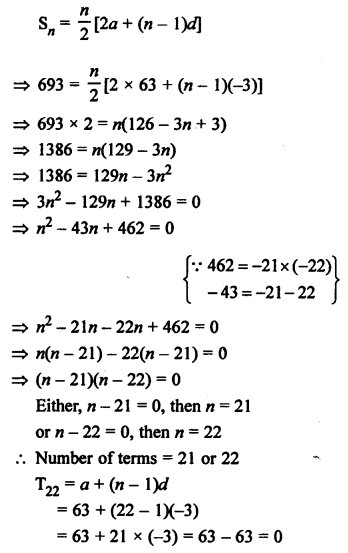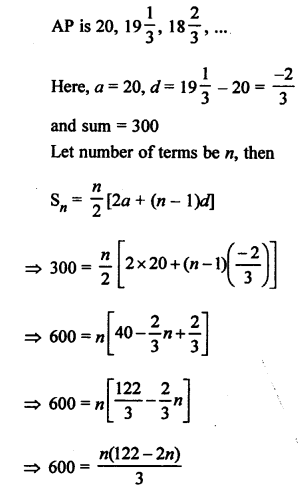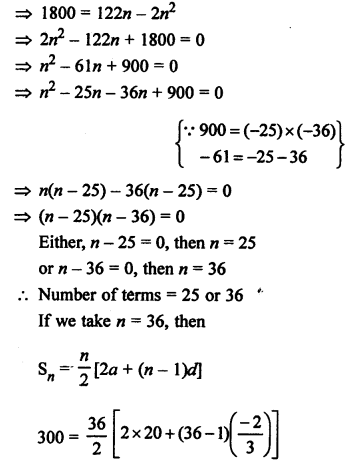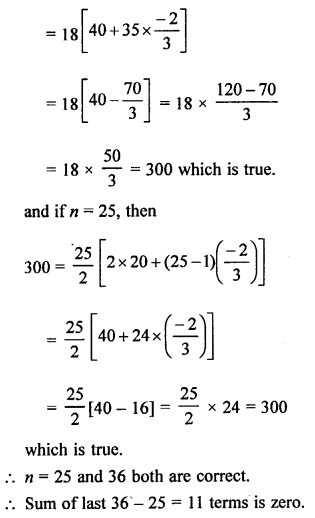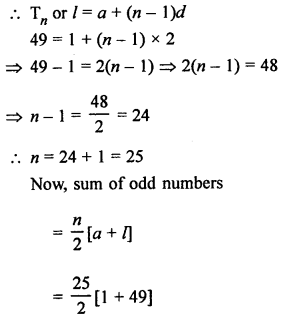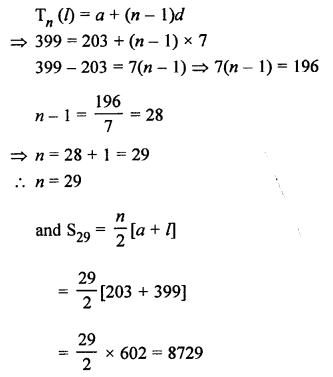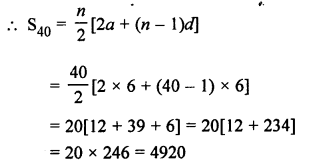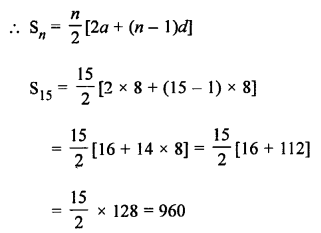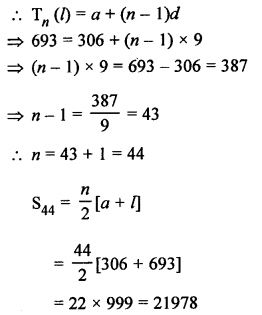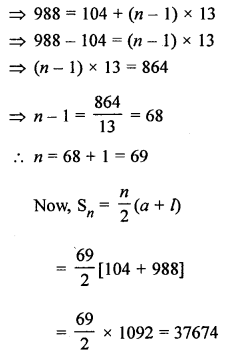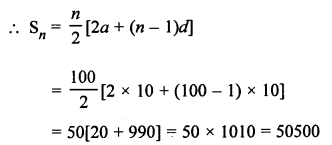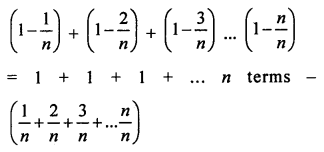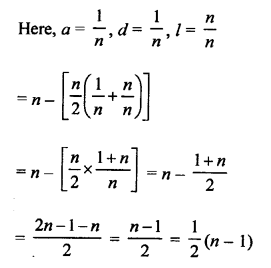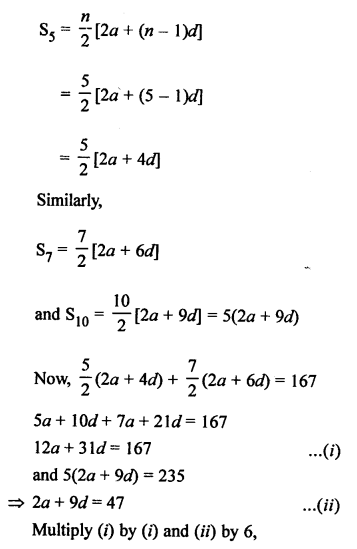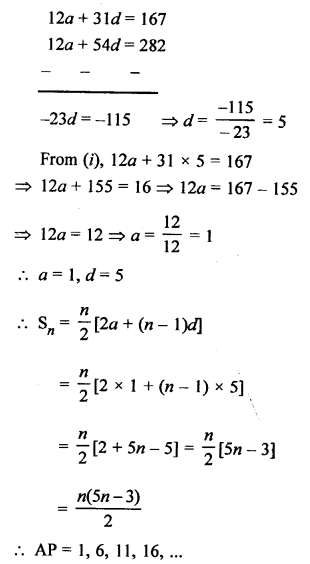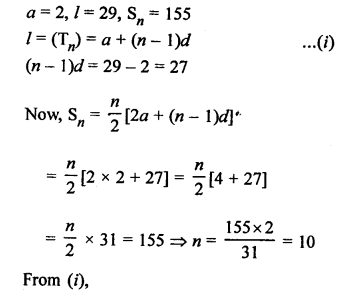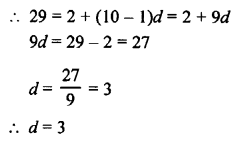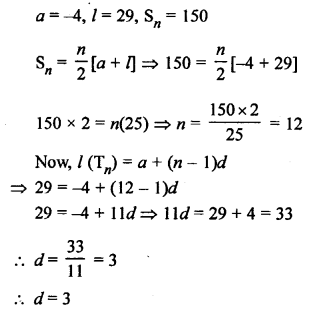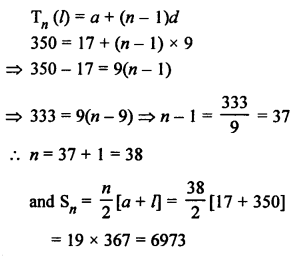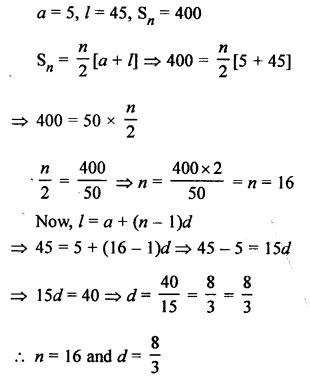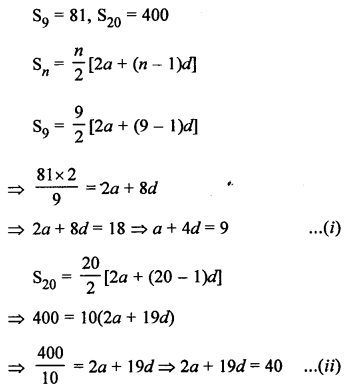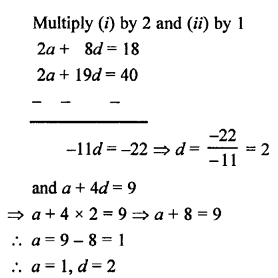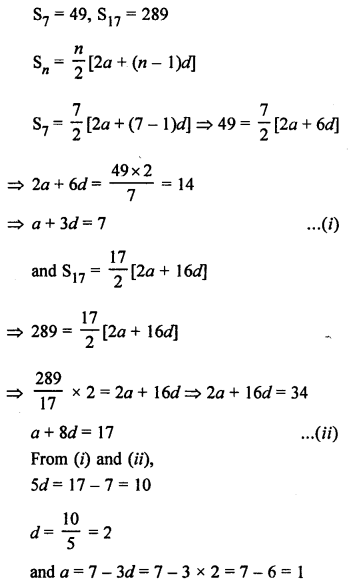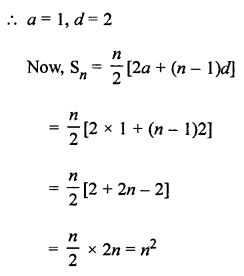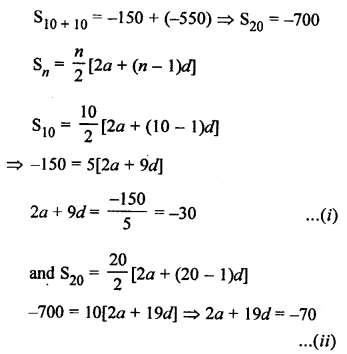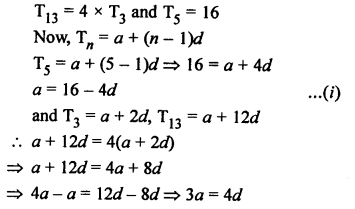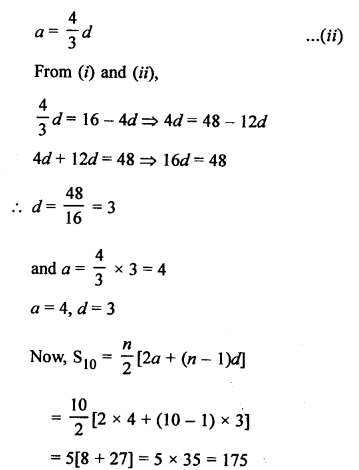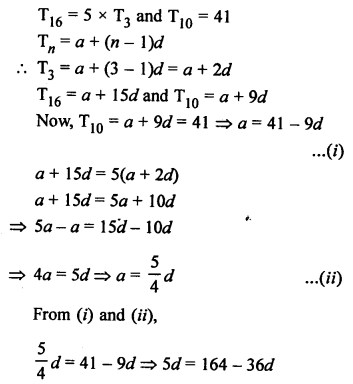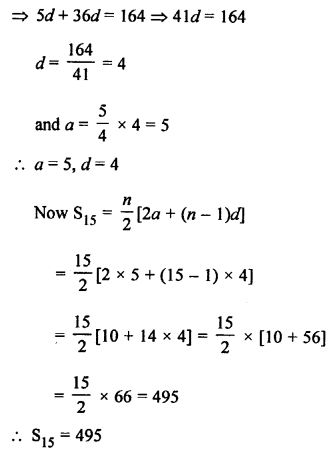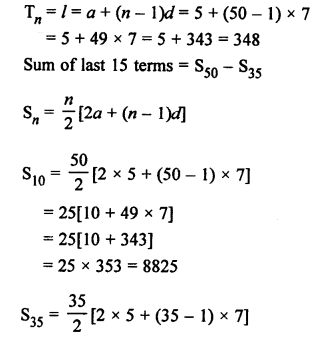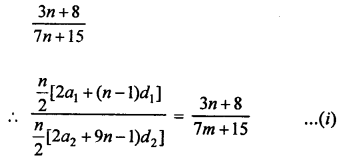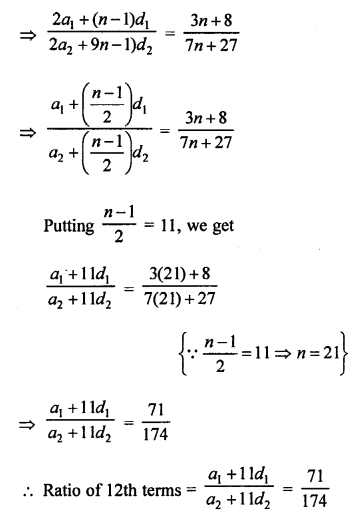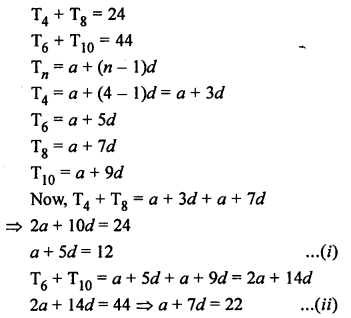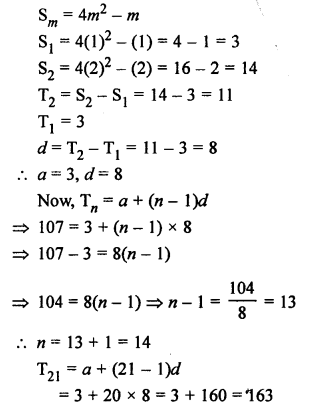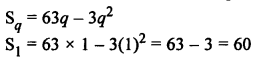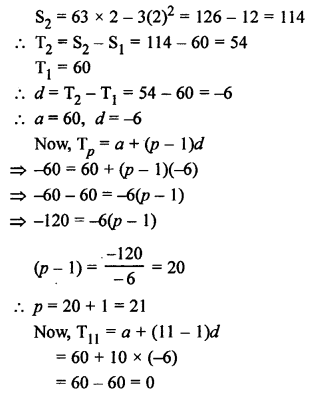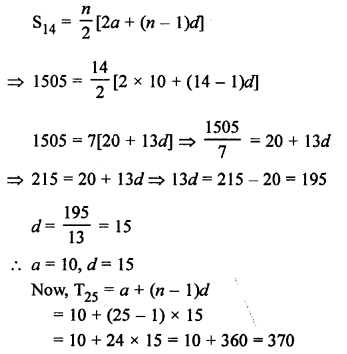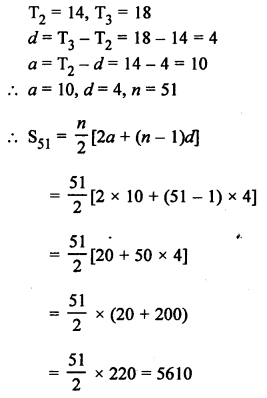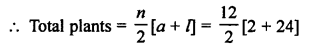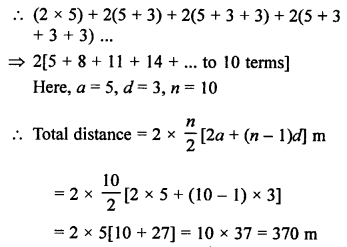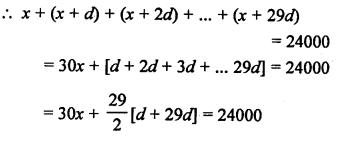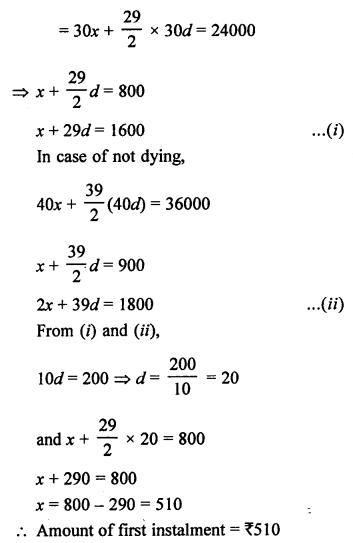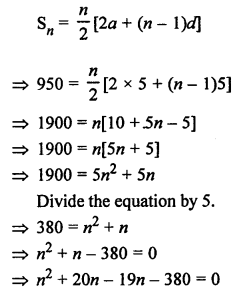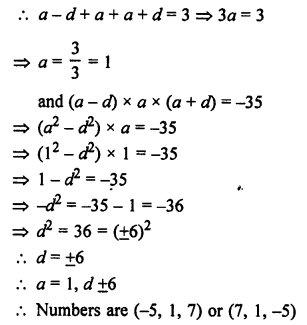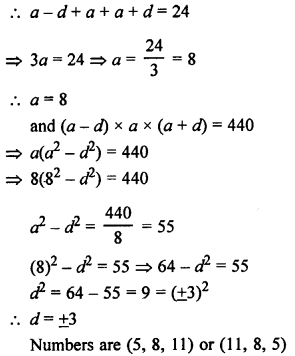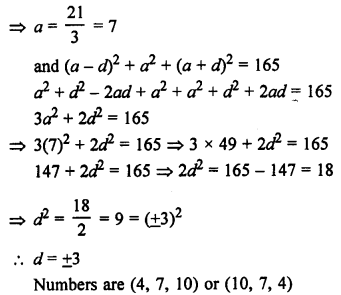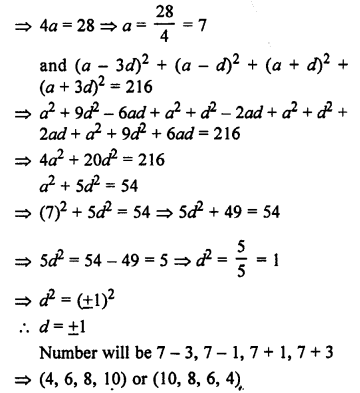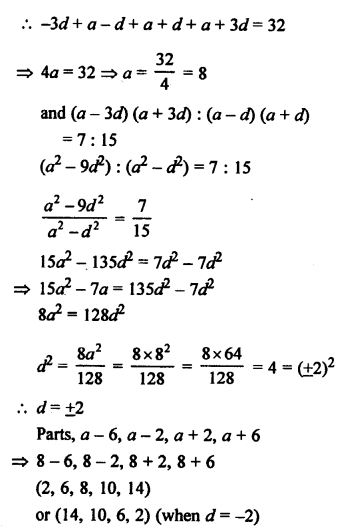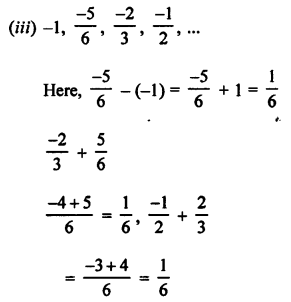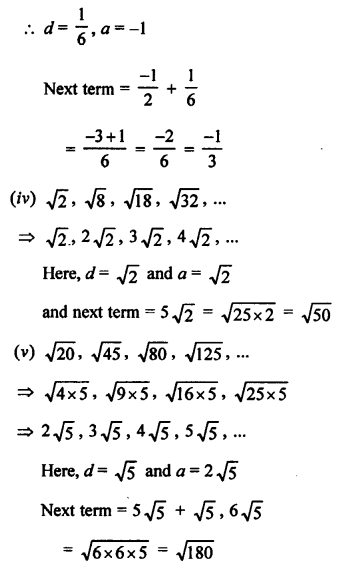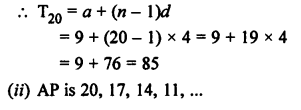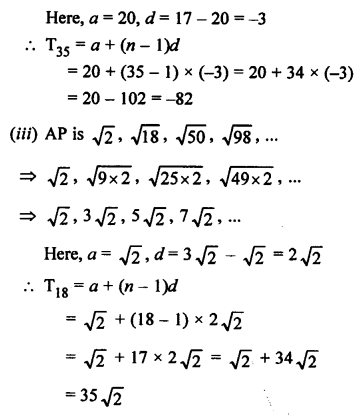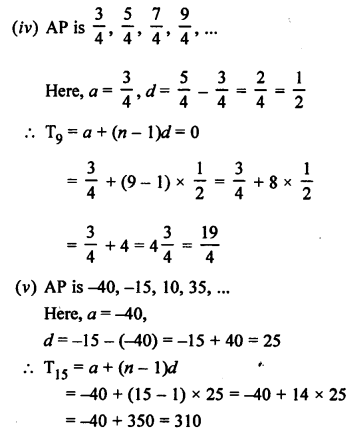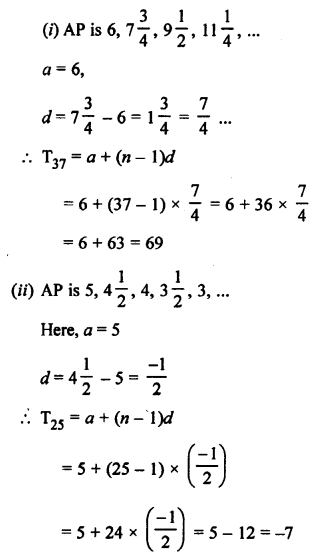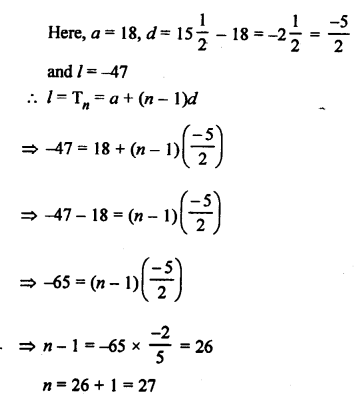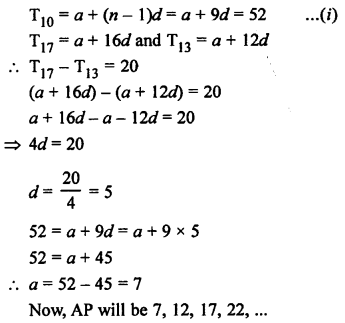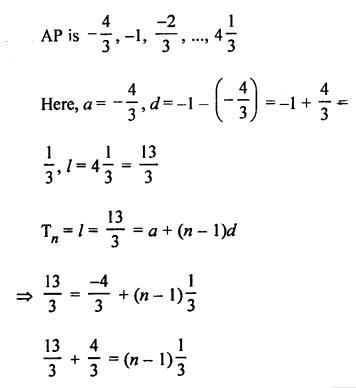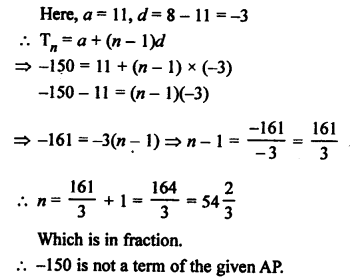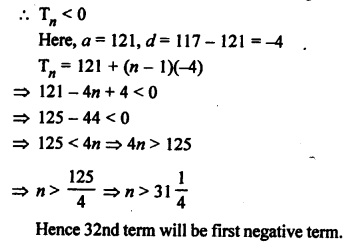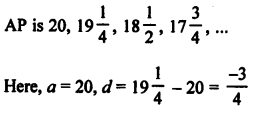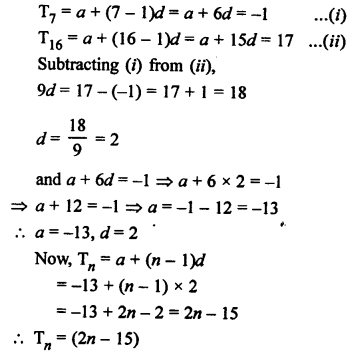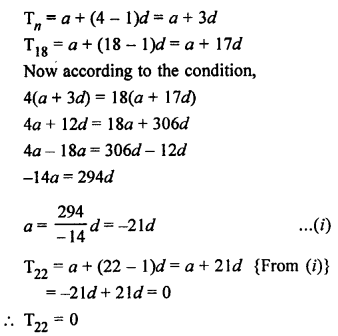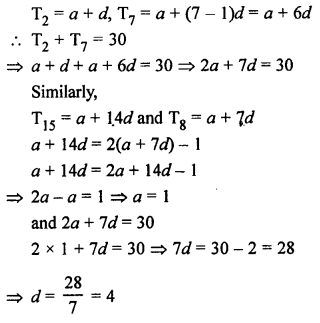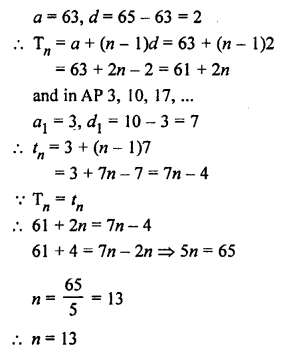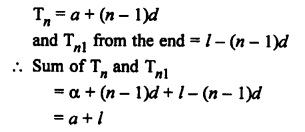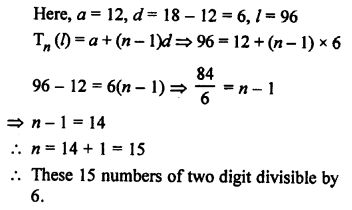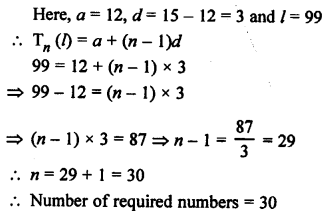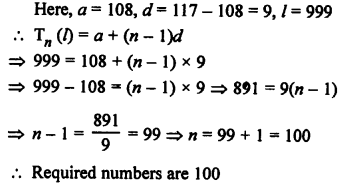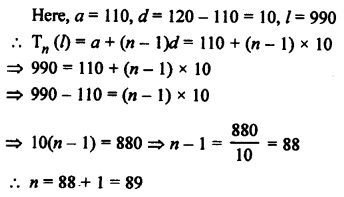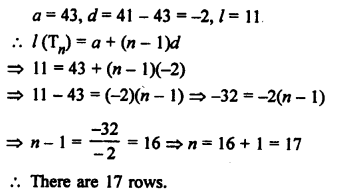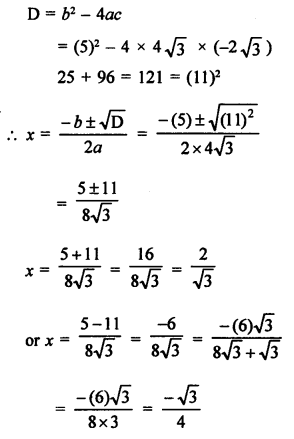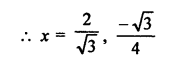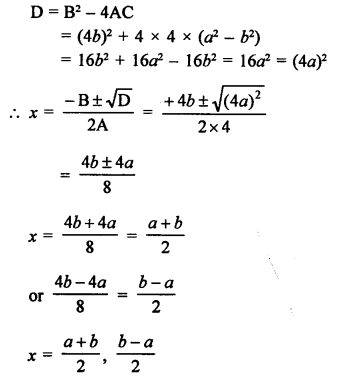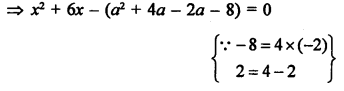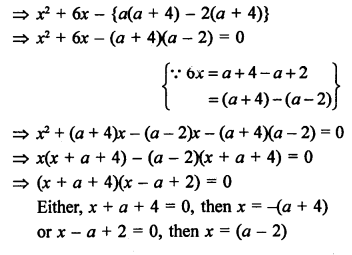RS Aggarwal Maths Solutions Class 10

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Very-Short and Short-Answer Questions
Question 1.
Solution:
(3y – 1), (3y + 5) and (5y+ 1) are in AP
(3y + 5) – (3y – 1) = (5y + 1) – (3y + 5)
⇒ 2 (3y + 5) = (5y + 1) + (3y – 1)
⇒ 6y + 10 = 8y
⇒ 8y – 6y = 10
⇒ 2y = 10
⇒ y = 5
y = 5

Question 2.
Solution:
k, (2k – 1) and (2k + 1) are the three successive terms of an AP.
(2k – 1) – k = (2k + 1) – (2k – 1)
⇒ 2 (2k – 1) = 2k + 1 + k
⇒ 4k – 2 = 3k + 1
⇒ 4k – 3k = 1 + 2
⇒ k = 3
k = 3

Question 3.
Solution:
18, a, (b – 3) are in AP
⇒ a – 18 = b – 3 – a
⇒ a + a – b = -3 + 18
⇒ 2a – b = 15

Question 4.
Solution:
a, 9, b, 25 are in AP.
9 – a = b – 9 = 25 – b
b – 9 = 25 – b
⇒ b + b = 22 + 9 = 34
⇒ 2b = 34
⇒ b= 17
a – b = a – 9
⇒ 9 + 9 = a + b
⇒ a + b = 18
⇒ a + 17 = 18
⇒ a = 18 – 17 = 1
a = 18, b= 17

Question 5.
Solution:
(2n – 1), (3n + 2) and (6n – 1) are in AP
(3n + 2) – (2n – 1) = (6n – 1) – (3n + 2)
⇒ (3n + 2) + (3n + 2) = 6n – 1 + 2n – 1
6n + 4 = 8n – 2
⇒ 8n – 6n = 4 + 2
⇒ 2n = 6
⇒ n = 3
and numbers are
2 x 3 – 1 = 5
3 x 3 + 2 = 11
6 x 3 – 1 = 17
i.e. (5, 11, 17) are required numbers.

Question 6.
Solution:
Three digit numbers are 100 to 990 and numbers which are divisible by 7 will be
105, 112, 119, 126, …, 994
Here, a = 105, d= 7, l = 994
T_n = (l) = a + (n – 1) d
⇒ 994 = 105 + (n – 1) x 7
⇒ 994 – 105 = (n – 1) 7
⇒ (n – 1) x 7 = 889
⇒ n – 1 = 127
⇒ n = 127 + 1 = 128
Required numbers are 128

Question 7.
Solution:
Three digit numbers are 100 to 999
and numbers which are divisible by 9 will be
108, 117, 126, 135, …, 999
Here, a = 108, d= 9, l = 999
T_n (l) = a + (n – 1) d
⇒ 999 = 108 + (n – 1) x 9
⇒ (n – 1) x 9 = 999 – 108 = 891
⇒ n – 1 = 99
⇒ n = 99 + 1 = 100

Question 8.
Solution:
Sum of first m terms of an AP = 2m² + 3m
S_m = 2m² + 3m
S₁ = 2(1)² + 3 x 1 = 2 + 3 = 5
S₂ = 2(2)² + 3 x 2 = 8 + 6=14
S₃ = 2(3)² + 3 x 3 = 18 + 9 = 27
Now, T₂ = S₂ – S₁ = 14 – 5 = 9
Second term = 9

Question 9.
Solution:
AP is a, 3a, 5a, …
Here, a = a, d = 2a

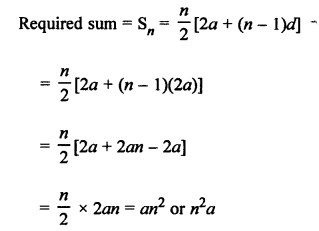
Question 10.
Solution:
AP 2, 7, 12, 17, …… 47
Here, a = 2, d = 7 – 2 = 5, l = 47
nth term from the end = l – (n – 1 )d
5th term from the end = 47 – (5 – 1) x 5 = 47 – 4 x 5 = 47 – 20 = 27

Question 11.
Solution:
AP is 2, 7, 12, 17, …
Here, a = 2, d = 7 – 2 = 5
a_n = a + (n – 1) d = 2 + (n – 1) x 5 = 2 + 5n – 5 = 5n – 3
Now, a₃₀ = 2 + (30 – 1) x 5 = 2 + 29 x 5 = 2 + 145 = 147
and a₂₀ = 2 + (20 – 1) x 5 = 2 + 19 x 5 = 2 + 95 = 97
a₃₀ – a₂₀ = 147 – 97 = 50

Question 12.
Solution:
T_n = 3n + 5
T_n-1 = 3 (n – 1) + 5 = 3n – 3 + 5 = 3n + 2
d = T_n – T_n-1 = (3n + 5) – (3n + 2) = 3n + 5 – 3n – 2 = 3
Common difference = 3

Question 13.
Solution:
T_n = 7 – 4n
T_n-1 = 7 – 4(n – 1) = 7 – 4n + 4 = 11 – 4n
d = T_n – T_n-1 = (7 – 4n) – (11 – 4n) = 7 – 4n – 11 + 4n = -4
d = -4

Question 14.
Solution:
AP is √8, √18, √32, …..
⇒ √(4 x 2) , √(9 x 2) , √(16 x 2), ………

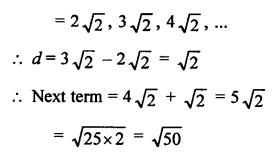
Question 15.
Solution:

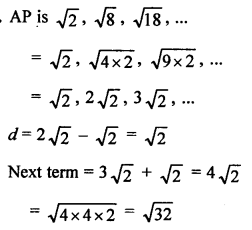
Question 16.
Solution:
AP is 21, 18, 15, …n
Here, a = 21, d = 18 – 21 = -3, l = 0
T_n (l) = a + (n – 1) d
0 = 21 + (n – 1) x (-3)
0 = 21 – 3n + 3
⇒ 24 – 3n = 0
⇒ 3n = 24
⇒ n = 8 .
0 is the 8th term.

Question 17.
Solution:
First n natural numbers are 1, 2, 3, 4, 5, …, n
Here, a = 1, d = 1

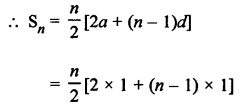
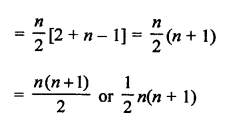
Question 18.
Solution:
First n even natural numbers are 2, 4, 6, 8, 10, … n
Here, a = 2, d = 4 – 2 = 2

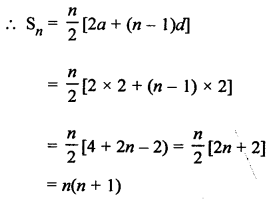
Question 19.
Solution:
In an AP
First term (a) = p
and common difference (d) = q
T₁₀ = a + (n – 1) d = p + (10 – 1) x q = (p + 9q)

Question 20.
Solution:

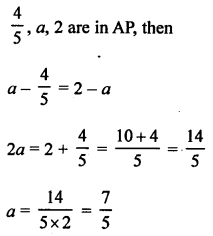
Question 21.
Solution:
2p + 1, 13, 5p – 3 are in AP, then
13 – (2p + 1) = (5p – 3) – 13
⇒ 13 – 2p – 1 = 5p – 3 – 13
⇒ 12 – 2p = 5p – 16
⇒ 5p + 2p = 12 + 16
⇒ 7p = 28
⇒ p = 4
P = 4

Question 22.
Solution:
(2p – 1), 7, 3p are in AP, then
⇒ 7 – (2p – 1) = 3p – 7
⇒ 7 – 2p + 1 = 3p – 7
⇒ 7 + 1 + 7 = 3p + 2p
⇒ 5p = 15
⇒ p = 3
P = 3

Question 23.
Solution:

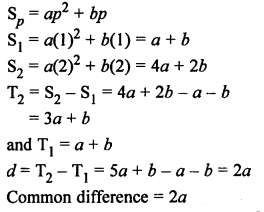
Question 24.
Solution:

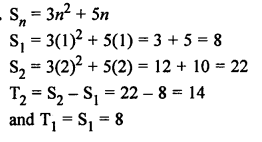
d = T₂ – T₁ = 14 – 8 = 6
Common difference = 6

Question 25.
Solution:

Question 26.
Solution:

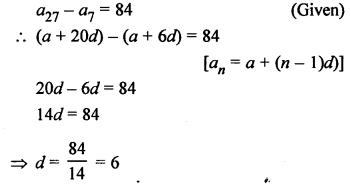
Question 27.
Solution:

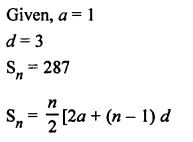
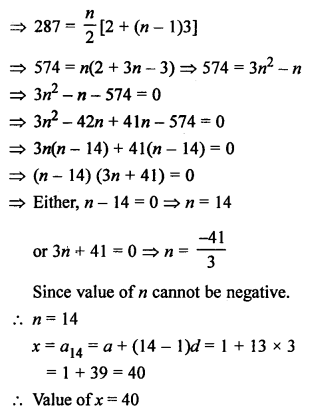
Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:
S_n = 3n² + 6n

Question 5.
Solution:
S_n = 3n² – n
S₁ = 3(1)² – 1 = 3 – 1 = 2
S₂ = 3(2)² – 2 = 12 – 2 = 10
T₂ = 10 – 2 = 8 and
T₁ = 2
(i) First term = 2
(ii) Common difference = 8 – 2 = 6
T_n = a + (n – 1) d = 2 + (n – 1) x 6
= 2 + 6n – 6 = 6n – 4

Question 6.
Solution:

Question 7.
Solution:
Let a be first term and d be the common difference of an AP.
Since, we have,
a_m = a + (m – 1) d = \(\frac { 1 }{ n }\) …(i)

Question 8.
Solution:
AP is 21, 18, 15,…
Here, a = 21,
d = 18 – 21 = -3,
sum = 0
Let number of terms be n, then

Question 9.
Solution:
AP is 9, 17, 25,…
Here, a = 9, d = 17 – 9 = 8
Sum of terms = 636
Let number of terms be n, then

Which is not possible being negative and fraction.
n = 12
Number of terms = 12

Question 10.
Solution:
AP is 63, 60, 57, 54,…
Here, a = 63, d = 60 – 63 = -3 and sum = 693
Let number of terms be n, then

22th term is zero.
There will be no effect on the sum.
Number of terms are 21 or 22.

Question 11.
Solution:

Question 12.
Solution:
Odd numbers between 0 and 50 are 1, 3, 5, 7, 9, …, 49
Here, a = 1, d = 3 – 1 = 2, l = 49

= \(\frac { 25 }{ 2 }\) x 50 = 25 x 25 = 625

Question 13.
Solution:
Numbers between 200 and 400 which are divisible by 7 will be 203, 210, 217,…, 399
Here, a = 203, d = 7, l = 399

Question 14.
Solution:
First forty positive integers are 0, 1, 2, 3, 4, …
and numbers divisible by 6 will be 6, 12, 18, 24, … to 40 terms
Here, a = 6, d = 12 – 6 = 6, n = 40 .

Question 15.
Solution:
First 15 multiples of 8 are 8, 16, 24, 32, … to 15 terms
Here, a = 8, d = 16 – 8 = 8 , n = 15

Question 16.
Solution:
Multiples of 9 lying between 300 and 700 = 306, 315, 324, 333, …, 693
Here, a = 306, d = 9, l = 693

Question 17.
Solution:
Three digit numbers are 100, 101, …, 999
and numbers divisible by 13, will be 104, 117, 130, …, 988
Here, a = 104, d = 13, l = 988
T_n (l) = a + (n – 1) d

Question 18.
Solution:
Even natural numbers are 2, 4, 6, 8, 10, …
Even natural numbers which are divisible by 5 will be
10, 20, 30, 40, … to 100 terms
Here, a = 10, d = 20 – 10 = 10, n = 100

Question 19.
Solution:

Question 20.
Solution:
Let a be the first term and d be the common difference of the AP, then

Question 21.
Solution:
Let a be the first term and d be the common difference, then

Question 22.
Solution:
Let a be the first term and d be the common difference, then

Question 23.
Solution:
In an AP
a = 17, d = 9, l = 350
Let number of terms be n, then

Question 24.
Solution:
Let a be the first term, d be the common difference, then

Question 25.
Solution:
In an AP, let a be the first term and d be the common difference, then

Question 26.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 27.
Solution:
Let a be first term and d be the common difference, then

Question 28.
Solution:
Let first term be a and d be the common difference in an AP, then

Question 29.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 30.
Solution:
Let a₁ and a₂ be the first terms of the two APs and d be the common difference, then
a₁ = 3, a₂ = 8

Question 31.
Solution:
Let a be the first term and d be the common difference, then
S₁₀ = -150

Question 32.
Solution:
Let a be the first term and d be the common difference, then

Question 33.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 34.
Solution:
(i) AP is 5, 12, 19,… to 50 terms
Here, a = 5, d = 12 – 5 = 7, n = 50

Question 35.
Solution:
Let a₁, a₂ be the first term and d₁, d₂ be common difference of the two AP’s respectively.
Given, ratio of sum of first n terms =

Question 36.
Solution:
Let a be the first term and d be the common difference of an AP.

Question 37.
Solution:

Question 38.
Solution:

Question 39.
Solution:
AP is -12, -9, -6,…, 21
Here, a = -12, d = -9 – (-12) = -9 + 12 = 3, l = 21

Question 40.
Solution:
S₁₄ = 1505
Let a be the first term and d be the common difference, then
a = 10

Question 41.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 42.
Solution:
In the school, there are 12 classes, class 1 to 12 and each class has two sections.
Each class plants double of the class
i.e. class 1 plants two plant, class 2 plants 4 plants, class 3 plants 6 plants, and so on.
So, total plants will be for each class each sections = 2 + 4 + 6 + 8 … + 24
Here, a = 2, d = 2, l = 24, n = 12

Each class has. two sections.
Plants will also be doubt
i.e. Total plants = 156 x 2 = 312

Question 43.
Solution:
In a potato race,
Bucket is at 5 m from first potato and then the distance between the two potatoes is 3m.
There are 10 potatoes.
The player, pick potato and put it in the bucket one by one.
Total distance in m to be covered, for 1st, 2nd, 3rd, … potato.

Question 44.
Solution:
Total number of trees = 25
Distance between them = 5 m in a line.
There is a water tank which is 10 m from the first tree.
A gardener waters these plants separately.
Total distance for going and coming back

Question 45.
Solution:
Total sum = ₹ 700
Number of cash prizes = 7
Each prize in ₹ 20 less than its preceding prize.
Let first prize = ₹ x
Then second prize = ₹ (x – 20)
Third prize = ₹ (x – 40) and so on.

Question 46.
Solution:
Total savings = ₹ 33000
Total period = 10 months
Each month, a man saved ₹ 100 more than its preceding of month.
Let he saves ₹ x in the first month.

Question 47.
Solution:
Total debt to be paid = ₹ 36000
No. of monthly installments = 40
After paying 30 installments, \(\frac { 1 }{ 3 }\) of his debt left
i.e. ₹ 36000 x \(\frac { 1 }{ 3 }\) = ₹ 12000
and amount paid = ₹ 36000 – ₹ 12000 = ₹ 24000
Monthly installments are in AP.
Let first installment = x
and common difference = d

Question 48.
Solution:
A contractor will pay the penalty for not doing the work in time.
For the first day = ₹ 200
For second day = ₹ 250
For third day = ₹ 300 and so on
The work was delayed for 30 days
Total penalty, he paid
200 + 250 + 300 + ….. to 30 terms
Here, a = 200, d = 50, n = 30
Total sum = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
= \(\frac { 30 }{ 2 }\) [2 x 200 + (30 – 1) x 50]
= 15 [400 + 29 x 50]
= 15 [400 + 1450]
= 15 x 1850 = ₹ 27750

Question 49.
Solution:
Child will put 5 rupee on 1st day, 10 rupee (2 x 5 rupee)
on 2nd day, 15 rupee (3 x 5 rupee) on 3rd day etc.
Total saving = 190 coins = 190 x 5 = 950 rupee
The above problem can be written as Arithmetic Progression series
5, 10, 15, 20, ……
with a = 5, d = 5, S_n = 950
Let n be the last day when piggy bank become full.

⇒ n (n + 20) – 19 (n + 20) = 0
⇒ (n + 20) (n – 19) = 0
⇒ n + 20 = 0 or n – 19 = 0
⇒ n = -20 or n = 19
cannot be negative, hence n = 19
She can put money for 19 days.
Total saving is 950 rupees.

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Question 1.
Solution:
(3k – 2), (4k – 6) and (k + 2) are three consecutive terms of an AP.
(4k – 6) – (3k – 2) = (k + 2) – (4k – 6)
⇒ 2(4k – 6) = (k + 2) + (3k – 2)
⇒ 8k – 12 = 4k + 0
⇒ 8k – 4k = 0 + 12
⇒ 4k = 12
k = 3

Question 2.
Solution:
(5x + 2), (4x – 1) and (x + 2) are in AP.
(4x – 1) – (5x + 2) = (x + 2) – (4x – 1)
⇒ 2(4x – 1) = (x + 2) + (5x + 2)
⇒ 8x – 2 = 6x + 2 + 2
⇒ 8x – 2 = 6x + 4
⇒ 8x – 6x = 4 + 2
⇒ 2x = 6
x = 3

Question 3.
Solution:
(3y – 1), (3y + 5) and (5y + 1) are the three consecutive terms of an AP.
(3y + 5) – (3y – 1) – (5y + 1) – (3y + 5)
⇒ 2(3y + 5) = 5y + 1 + 3y – 1
⇒ 6y + 10 = 8y
⇒ 8y – 6y = 10
⇒ 2y = 10
⇒ y = 5
y = 5

Question 4.
Solution:
(x + 2), 2x, (2x + 3) are three consecutive terms of an AP.
2x – (x + 2) = (2x + 3) – 2x
⇒ 2x – x – 2 = 2x + 3 – 2x
⇒ x – 2 = 3
⇒ x = 2 + 3 = 5
x = 5

Question 5.
Solution:
(a – b)², (a² + b²) and (a + b)² will be in AP.
If (a² + b²) – (a – b)² = (a + b)² – (a² + b²)
If (a² + b²) – (a² + b² – 2ab) = a² + b² + 2ab – a² – b²
2ab = 2ab which is true.
Hence proved.

Question 6.
Solution:
Let the three numbers in AP be
a – d, a, a + d
a – d + a + a + d = 15
⇒ 3a = 15
⇒ a = 5
and (a – d) x a x (a + d) = 80
a(a² – d²) = 80
⇒ 5(5² – d²) = 80
⇒ 25 – d² = 16
⇒ d² = 25 – 16 = 9 = (±3)²
d = ±3
Now, a = 5, d = +3
Numbers are 5 – 3 = 2
5 and 5 + 3 = 8
= (2, 5, 8) or (8, 5, 2)

Question 7.
Solution:
Let the three numbers in AP be a – d, a and a + d

Question 8.
Solution:
Sum of three numbers = 24
Let the three numbers in AP be a – d, a, a + d

Question 9.
Solution:
Let three consecutive in AP be a – d, a, a + d
a – d + a + a + d = 21
⇒ 3a = 21

Question 10.
Solution:
Sum of angles of a quadrilateral = 360°
Let d= 10
The first number be a, then the four numbers will be
a, a + 10, a + 20, a + 30
a + a + 10 + a + 20 + a + 30 = 360
4a + 60 = 360
4a = 360 – 60 = 300
Angles will be 75°, 85°, 95°, 105°

Question 11.
Solution:
Let the four numbers in AP be a – 3d, a – d, a + d, a + 3d, then
a – 3d + a – d + a + d + a + 3d = 28

Question 12.
Solution:
Let the four parts of 32 be a – 3d, a – d, a + d, a + 3d

Question 13.
Solution:
Let the three terms be a – d, a, a + d
a – d + a + a + d = 48
⇒ 3a = 48
⇒ a = 16
and (a – d) x a = (a + d) + 12
⇒ a(a – d) = 4 (a + d) + 12
⇒ 16 (16 – d) = 4(16 + d) + 12
⇒ 256 – 16d = 64 + 4d + 12 = 4d + 76
⇒ 256 – 76 = 4d + 16d
⇒ 180 = 20d
⇒ d = 9
Numbers are (16 – 9, 16), (16 + 9) or (7, 16, 25)

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Question 1.
Solution:
(i) 9, 15, 21, 27, …
Here, 15 – 9 = 6,
21 – 15 = 6,
27 – 21 = 6
d = 6 and a = 9
Next term = 27 + 6 = 33
(ii) 11, 6, 1, -4, …
Here, 6 – 11 = -5,
1 – 6 = -5,
-4 – 1 = -5
d = -5 and a = 11
Next term = -4 – 5 = -9

Question 2.
Solution:
(i) AP is 9, 13, 17, 21, ……
Here, a = 9, d = 13 – 9 = 4

Question 3.
Solution:

Question 4.
Solution:
If the terms are in AP, then
a₂ – a₁ = a₃ – a₂ = …….
a₂ = 3p + 1
a₁ = 2p – 1
a₃ = 11
⇒ (3p + 1) – (2p – 1) = 11 – (3p + 1)
⇒ 3p + 1 – 2p + 1 = 11 – 3p – 1
⇒ p + 2 = 10 – 3p
⇒ 4p = 8
⇒ p = 2
Then for p = 2, these terms are in AP.

Question 5.
Solution:
(i) AP is 5, 11, 17, 23, ……
Here, a = 5, d = 11 – 5 = 6
T_n = a (n – 1)d = 5 + (n – 1) x 6 = 5 + 6n – 6 = (6n – 1)
(ii) AP is 16, 9, 2, -5, ……
Here, a = 16 d = 9 – 16 = -7
T_n = a + (n – 1)d = 16 + (n – 1) (-7)
= 16 – 7n + 7 = (23 – 7n)

Question 6.
Solution:
nth term = 4n – 10
Substituting the value of 1, 2, 3, 4, …, we get
4n – 10
= 4 x 1 – 10 = 4 – 10 = -6
= 4 x 2 – 10 = 8 – 10 = -2
= 4 x 3 – 10 = 12 – 10 = 2
= 4 x 4 – 10 = 16 – 10 = 6
We see that -6, -2, 2, 6,… are in AP
(i) Whose first term = -6
(ii) Common difference = -2 – (-6) = -2 + 6 = 4
(iii) 16th term = 4 x 16 – 10 = 64 – 10 = 54

Question 7.
Solution:
In AP 6, 10, 14, 18,…, 174
Here, a = 6, d= 10 – 6 = 4
nth or l = 174
T_n = a + (n – 1)d
⇒ 174 = 6 + (n – 1) x 4
⇒ 174 – 6 = (n – 1) x 4
⇒ n – 1 = \(\frac { 168 }{ 4 }\) = 42
n = 42 + 1 = 43
Hence, there are 43 terms in the given AP.

Question 8.
Solution:
In AP 41, 38, 35,…, 8
a = 41, d = 38 – 41 = -3, l = 8
Let l be the nth term
l = T_n = a + (n – 1) d
⇒ 8 = 41 + (n – 1)(-3)
⇒ 8 – 41 = (n – 1)(-3)
⇒ n – 1 = 11
⇒ n = 11 + 1 = 12
There are 12 terms in the given AP.

Question 9.
Solution:
the AP is 8, 15\(\frac { 1 }{ 2 }\) , 13, …, -47

There are 27 terms in the given AP.

Question 10.
Solution:
Let 88 be the nth term
Now, in AP 3, 8, 13, 18, …
a = 3, d = 8 – 3 = 5
T_n = a + (n – 1) d
88 = 3 + (n – 1)(5)
⇒ 88 – 3 = (n – 1) x 5
⇒ \(\frac { 88 }{ 5 }\) = n – 1
⇒ 17 = n – 1
n= 17 + 1 = 18
88 is the 18th term.

Question 11.
Solution:
In the AP 72, 68, 64, 60, …..
Let 0 be the nth term
Here, a = 72, d = 68 – 72 = -4
T_n = a + (n – 1)d
0 = 72 + (n – 1)(-4)
⇒ -72 = -4(n – 1)
⇒ n – 1 = 18
⇒ n = 18 + 1 = 19
0 is the 19th term.

Question 12.
Solution:

n = 13 + 1 = 14
3 is the 14th term.

Question 13.
Solution:
In the AP 21, 18, 15, ……
Let -81 is the nth term
a = 21, d = 18 – 21 = -3
T_n = a + (n – 1)d
⇒ -81 = 21 + (n – 1)(-3)
⇒ -81 – 21 = (n – 1)(-3)
⇒ -102 = (n – 1)(-3)
⇒ n – 1 = 34
n = 34 + 1 = 35
-81 is the 35th term

Question 14.
Solution:
In the given AP 3, 8, 13, 18,…
a = 3, d = 8 – 3 = 5
T₂₀ = a + (n – 1)d = 3 + (20 – 1) x 5 = 3 + 19 x 5 = 3 + 95 = 98
The required term = 98 + 55 = 153
Let 153 be the nth term, then
T_n = a + (n – 1)d
⇒ 153 = 3 + (n – 1) x 5
⇒ 153 – 3 = 5(n – 1)
⇒ 150 = 5(n – 1)
⇒ n – 1 = 30
⇒ n = 30 + 1 = 31
Required term will be 31st term.

Question 15.
Solution:
AP is 5, 15, 25,…
a = 5, d = 15 – 5 = 10
T₃₁ = a + (n – 1)d = 5 + (31 – 1) x 10 = 5 + 30 x 10 = 5 + 300 = 305
Now the required term = 305 + 130 = 435
Let 435 be the nth term, then
T_n = a + (n – 1)d
⇒ 435 = 5 + (n – 1)10
⇒ 435 – 5 = (n – 1)10
⇒ n – 1 = 43
⇒ n = 43 + 1 = 44
The required term will be 44th term.

Question 16.
Solution:
Let a be the first term and d be the common difference, then

Question 17.
Solution:

T₁₆ = 6 + (16 – 1)7 = 6+ 15 x 7 = 6 + 105 = 111

Question 18.
Solution:
AP is 10, 7, 4, …, (-62)
a = 10, d = 7 – 10 = -3, l = -62
l = T_n = a + (n – 1)d
⇒ -62 = 10 + (n – 1) x (-3)
⇒ -62 – 10 = -3(n- 1)
-72 = -3(n – 1)
n = 24 + 1 = 25
Middle term = \(\frac { 25 + 1 }{ 2 }\) th = 13th term
T₁₃ = 10 + (13 – 1)(-3) = 10+ 12 x (-3)= 10 – 36 = -26

Question 19.
Solution:

Question 20.
Solution:
AP is 7, 10, 13,…, 184
a = 7, d = 10 – 7 = 3, l = 184
nth term from the end = l – (n – 1)d
8th term from the end = 184 – (8 – 1) x 3 = 184 – 7 x 3 = 184 – 21 = 163

Question 21.
Solution:
AP is 17, 14, 11, …,(-40)
Here, a = 17, d = 14 – 17 = -3, l = -40
6th term from the end = l – (n – 1)d
= -40 – (6 – 1) x (-3)
= -40 – [5 x (-3)]
= -40 + 15
= -25

Question 22.
Solution:
Let 184 be the nth term of the AP
3, 7, 11, 15, …
Here, a = 3, d = 7 – 3 = 4
T_n = a + (n – 1)d
⇒ 184 = 3 + (n – 1) x 4
⇒ 184 – 3 = (n – 1) x 4
⇒ \(\frac { 181 }{ 4 }\) = n – 1
⇒ n = \(\frac { 181 }{ 4 }\) + 1 = \(\frac { 185 }{ 4 }\) = 46\(\frac { 1 }{ 4 }\)
Which is in fraction.
184 is not a term of the given AP.

Question 23.
Solution:
Let -150 be the nth term of the AP
11, 8, 5, 2,…

Question 24.
Solution:
Let nth of the AP 121, 117, 113,… is negative

Question 25.
Solution:

Question 26.
Solution:
Let a be the first term and d be the common difference of an AP
T_n = a + (n – 1)d
T₇ = a + (7 – 1)d = a + 6d = -4 …(i)
T₁₃ = a + 12d = -16 …..(ii)
Subtracting (i) from (ii),
6d = -16 – (-4) = -16 + 4 = -12
From (i), a + 6d = -4
a + (-12) = -4
⇒ a = -4 + 12 = 8
a = 8, d = -2
AP will be 8, 6, 4, 2, 0, ……

Question 27.
Solution:
Let a be the first term and d be the common difference of an AP.
T₄ = a + (n- 1)d = a + (4 – 1)d = a + 3d
a + 3d = 0 ⇒ a = -3d
Similarly,
T₂₅ = a + 24d and T₁₁ = a + 10d = -3d + 24d = 21d
It is clear that T₂₅ = 3 x T₁₁

Question 28.
Solution:
Given, a₆ = 0
⇒ a + 5d = 0
⇒ a = -5 d
Now, a₁₅ = a + (n – 1 )d
= a + (15 – 1)d = -5d + 14d = 9d
and a₃₃ = a + (n – 1 )d = a + (33 – 1)d = -5d + 32d = 27d
Now, a₃₃ : a₁₂
⇒ 27d : 9d
⇒ 3 : 1
a₃₃ = 3 x a₁₅

Question 29.
Solution:
Let a be the first term and d be the common difference of an AP.
T_n = a + (n – 1)d
T₄ = a + (4 – 1)d = a + 3d
a + 3d = 11 …(i)
Now, T₅ = a + 4d
and T₇ = a + 6d
Adding, we get T₅ + T₇ = a + 4d + a + 6d = 2a + 10d
2a + 10d = 34
⇒ a + 5d = 17 …(ii)
Subtracting (i) from (ii),
2d = 17 – 11 = 6
⇒ d = 3
Hence, common difference = 3

Question 30.
Solution:
Let a be the first term and d be the common difference of an AP.

Question 31.
Solution:
Let a be the first term and d be the common difference, then

Question 32.
Solution:
In an AP,
Let a be the first term and d be the common difference, then

Question 33.
Solution:
Let a be the first term and d be the common difference in an AP, then

Question 34.
Solution:
In an AP,
Let d be the common difference,
First term (a) = 5
Sum of first 4 terms
= a + a + d + a + 2d + a + 3d = 4a + 6d
Sum of next 4 terms
= a + 4d + a + 5d + a + 6d + a + 7d = 4a + 22d
According to the condition,

Question 35.
Solution:
Let a be the first term and d be the common difference in an AP, then

a = 1, d = 4
AP = 1, 5, 9, 13, 17, …

Question 36.
Solution:
In AP 63, 65, 67, …..

Question 37.
Solution:
Let first term of AP = a
and common difference = d

Question 38.
Solution:
Let a be the first term and d be the common difference, then

Question 39.
Solution:
Let a be the first term and d be the common difference, then

Question 40.
Solution:
Let a be the first term and d be the common difference, then

Question 41.
Solution:
Let a be the first term, d be the common difference, then

Question 42.
Solution:
Two-digit numbers are 10 to 99 and two digit numbers divisible by 6 will be
12, 18, 24, 30, …, 96

Question 43.
Solution:
Two digit numbers are 10 to 99 and
Two digit numbers which are divisible by 3 are
12, 15, 18, 21, 24, … 99

Question 44.
Solution:
Three digit numbers are 100 to 999 and numbers divisible by 9 will be
108, 117, 126, 999

Question 45.
Solution:
Numbers between 101 and 999 which are divisible both by 2 and 5 will be
110, 120, 130,…, 990

Question 46.
Solution:
Let number of from a rows are in the flower bed, then

Question 47.
Solution:
Total amount = ₹ 2800
and number of prizes = 4
Let first prize = ₹ a
Then second prize = ₹ a – 200
Third prize = a – 200 – 200 = a – 400
and fourth prize = a – 400 – 200 = a – 600
But sum of there 4 prizes are ₹ 2800
a + a – 200 + a – 400 + a – 600 = ₹ 2800
⇒ 4a – 1200 = 2800
⇒ 4a = 2800 + 1200 = 4000
⇒ a = 1000
First prize = ₹ 1000
Second prize = ₹ 1000 – 200 = ₹ 800
Third prize = ₹ 800 – 200 = ₹ 600
and fourth prize = ₹ 600 – 200 = ₹ 400

Question 48.
Solution:
The first term between 200 and 500 divisible by 8 is 208, and last term is 496.
So, first term (a) = 208
Common difference (d) = 8
Now, an = a + (n – 1 )d
⇒ 496 = 208 + (n – 1) x 8
⇒ (n – 1) = \(\frac { 288 }{ 8 }\)
⇒ n – 1 = 36
⇒ n = 36 + 1 = 37
Hence, there are 37 integers between 200 and 500 which are divisible by 8.

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Test Yourself

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Objective Questions (MCQ)
Question 1.
Solution:
(a) x² – 3√x + 2 = 0
It is not a quadratic equation, it has a fractional power of √x
(b) x + \(\frac { 1 }{ x }\) = x²
⇒ x² + 1 = x³
It is not a quadratic equation.
(c) x² + \(\frac { 1 }{ { x }^{ 2 } }\) = 5
⇒ x⁴ + 1 + 5x²
It is not a quadratic equation.
(d) 2x² – 5x = (x – 1)²
⇒ 2x² – 5x = x² – 2x + 1
⇒ x² – 3x – 1 = 0
It is a quadratic equation. (d)

Question 2.
Solution:
(a) (x² + 1) = (2 – x)² + 3
⇒ x² + 1 = 4 + x² – 4x + 3 is not a quadratic equation.
(b) x³ – x² = (x – 1)³
⇒ x³ – x² = x³ – 3x² + 3x – 1
⇒ 3x² – x² – 3x + 1 = 0
⇒ 2x² – 3x + 1 = 0
It is a quadratic equation.
(c) 2x² + 3 = 10x – 15 + 2x² – 3x
⇒ 3x – 15 – 3 = 0
It is not a quadratic equation. (b)

Question 3.
Solution:
(a) It is a quadratic equation.
(b) (x + 2)² = 2(x² – 5)
⇒ x² + 4x + 4 = 2x² – 10
⇒ x² – 4x – 14 = 0
It is a quadratic equation.
(c) (√2 x + 3)² = 2x² + 6
⇒ 2x² + 3√2 x + 9 = 2x² + 6
⇒ 3√2 + 3 = 0
It is not a quadratic equation.
(d) (x – 1)² = 3x² + x – 2
⇒ x² – 2x +1 = 3x² + x – 2
⇒ 2x² + 3x – 3 = 0
It is a quadratic equation. (c)

Question 4.
Solution:
x = 3 is solution of 3x² + (k – 1)x + 9 = 0
It will satisfy it
3(3)² + (k – 1)(3) + 9 = 0
⇒ 27 + 3k – 3 + 9 = 0
⇒ 3k + 33 = 0
⇒ k = -11 (b)

Question 5.
Solution:
2 is one root of equation 2x² + ax + 6 = 0
It will satisfy it
2(2)² + a(2) + 6 = 0
⇒ 8 + 2a + 6 = 0
⇒ 2a = -14
⇒ a = -7
a = -7 (b)

Question 6.
Solution:
In equation x² – 6x + 2 = 0
Sum of roots = \(\frac { -b }{ a }\) = \(\frac { -(-6) }{ 1 }\) = 6 (c)

Question 7.
Solution:
In equation x² – 3x + k = 10
x² – 3x + (k – 10) = 0
Product of roots = \(\frac { c }{ a }\) = \(\frac { k – 10 }{ 1 }\) = k – 10
k – 10 = -2 then k = 10 – 2 = 8 (c)

Question 8.
Solution:
In equation 7x² – 12x + 18 = 0

Question 9.
Solution:
In equation 3x² – 10x + 3 = 0

Question 10.
Solution:
In equation 5x² + 13x + k = 0

Question 11.
Solution:
In equation kx² + 2x + 3k = 0
Sum of roots = \(\frac { -b }{ a }\) = \(\frac { -2 }{ k }\)

Question 12.
Solution:
Roots of an equation are 5, -2
Sum of roots (S) = 5 – 2 = 3
and product (P) = 5 x (-2) = -10
Equation will be
x² – (S)x + (P) = 0
⇒ x² – 3x – 10 = 0 (b)

Question 13.
Solution:
Sum of roots (S) = 6
Product of roots (P) = 6
Equation will be x² – (S)x + (P) = 0
x² – 6x + 6 = 0 (a)

Question 14.
Solution:
α and β are the roots of the equation 3x² + 8x + 2 = 0

Question 15.
Solution:
In equation ax² + bx + c = 0

Question 16.
Solution:
In equation ax² + bx + c = 0
Let α and β are the roots, then

Question 17.
Solution:
In equation 9x² + 6kx + 4 = 0, roots are equal
Let roots be α, α then

Question 18.
Solution:
In equation x² + 2 (k + 2) x + 9k = 0
Roots are equal
Let α, α be the roots, then

Question 19.
Solution:
In the equation
4x² – 3kx + 1 = 0 roots are equal
Let α, α be the roots

Question 20.
Solution:
Roots of ax² + bx + c = 0, a ≠ 0 are real and unequal if D > 0
⇒ b² – 4ac > 0 (a)

Question 21.
Solution:
In the equation ax² + bx + c = 0
D = b² – 4ac > 0, then roots are real and unequal. (b)

Question 22.
Solution:
In the equation 2x² – 6x + 7 = 0
D = b² – 4ac = (-6)² – 4 x 2 x 7 = 36 – 56 = -20 < 0
Roots are imaginary (not real) (d)

Question 23.
Solution:
In equation 2x² – 6x + 3 = 0
D = b² – 4ac = (-6)² – 4 x 2 x 3 = 36 – 24 = 12 > 0
Roots are real, unequal and irrational, (b)

Question 24.
Solution:
In equation 5x² – kx + 1 = 0
D = b² – 4ac = (-k)² – 4 x 5 x 1 = k² – 20
Roots are real and distinct
D > 0
⇒ k² – 20 > 0
⇒ k² > 20
⇒ k > √±20
⇒ k > ±2√5
⇒ k > 2√5 or k < -2√5 (d)

Question 25.
Solution:
In equation x² + 5kx + 16 = 0
D = b² – 4ac = (5k)² – 4 x 1 x 16

Question 26.
Solution:
The equation x² – kx + 1 = 0
D = b2 – 4ac = (-k)² – 4 x 1 x 1 ⇒ k² – 4
Roots are not real
D < 0
⇒ k² – 4 < 0
⇒ k² < 4
⇒k < (±2)²
⇒ k < ±2
-2 < k < 2 (c)

Question 27.
Solution:
In the equation kx² – 6x – 2 = 0

Question 28.
Solution:
Let the number be = x

Question 29.
Solution:
Perimeter of a rectangle = 82 m
and Area = 400
Let breadth (b) = x, then
Length = \(\frac { P }{ 2 }\) – x = \(\frac { 82 }{ 2 }\) – x = 41 – x
Area = lb
400 = x (41 – x) = 41x – x²
⇒ x² – 41x + 400 = 0
⇒ x² – 25x – 16x + 400 = 0
⇒ x (x – 25) – 16(x – 25) = 0
⇒ (x – 25) (x – 16) = 0
Either, x – 16 = 0, then x = 16
or x – 25 = 0, then x = 25
Breadth = 16 m (c)

Question 30.
Solution:
Let breadth of a rectangular field = x m
Then length = (x + 8) m
and area = 240 m²
x (x + 8) = 240
⇒ x² + 8x – 240 = 0
⇒ x² + 20x – 12x – 240 = 0
⇒ x (x + 20) – 12 (x + 20) = 0
⇒ (x + 20) (x – 12) = 0
Either, x + 20 = 0, then x = -20 which is not possible being negative,
or x – 12 = 0, then x = 12
Breadth = 12 m (c)

Question 31.
Solution:
2x² – x – 6 = 0

Very-Short-Answer Questions
Question 32.
Solution:
Sum of two natural numbers = 8
Let first number – x
Then second number = 8 – x
According to the condition,
x (8 – x) = 15
⇒ 8x – x² = 15
⇒ x² – 8x + 15 = 0
⇒ x² – 3x – 5x + 15 = 0
⇒ x(x – 3) – 5(x – 3) = 0
⇒ (x – 3)(x – 5) = 0
Either, x – 3 = 0, then x = 3
or x – 5 = 0, then x = 5
Natural numbers are 3, 5

Question 33.
Solution:
x = -3 is a solution of equation x² + 6x + 9 = 0 Then it will satisfy it
LHS = x² + 6x + 9 = (-3)² + 6(-3) + 9 = 9 – 18 + 9 = 0 = RHS

Question 34.
Solution:
3x² + 13x + 14 = 0
If x = -2 is its root then it will satisfy it
LHS = 3(-2)² + 13(-2) + 14 = 3 x 4 – 26 + 14 = 12 – 26 + 14 = 26 – 26 = 0 = RHS

Question 35.
Solution:
x = y is a solution of equation 3x² + 2kx – 3 = 0, then it will satisfy it

Question 36.
Solution:
2x² – x – 6 = 0
⇒ 2x² – 4x + 3x – 6 = 0

Question 37.
Solution:
3√3 x² + 10x + √3 = 0

Question 38.
Solution:
Roots of the quadratic equation 2x² + 8x + k = 0 are equal
Let α, α be its roots, then

Question 39.
Solution:
px² – 2√5 px + 15 = 0
Here, a = p, b = 2√5 p, c = 15
D = b² – 4ac = (-2√5 p)² – 4 x p x 15 = 20p² – 60p
Roots are equal.
D = 0
⇒ 20p² – 60p = 0
⇒ p² – 3p = 0
⇒ p (p – 3) = 0
p – 3 = 0, then p = 3

Question 40.
Solution:
1 is a root of equation
ay² + ay + 3 = 0 and y² + y + b = 0
Then a(1)² + a(1) + 3 = 0
⇒ a + a + 3 = 0
⇒ 2a + 3 = 0
⇒ a = \(\frac { -3 }{ 2 }\)
and 1 + 1 + b = 0
⇒ 2 + b = 0
⇒ b = -2
ab = \(\frac { -3 }{ 2 }\) x (-2) = 3
Hence, ab = 3

Question 41.
Solution:
The polynomial is x² – 4x + 1
Here, a = 1, b = -4, c = 1

Question 42.
Solution:
In the quadratic equation 3x² – 10x + k = 0

Question 43.
Solution:
The quadratic equation is
px (x – 2) + 6 = 0
⇒ px² – 2px + 6 = 0
D = b² – 4ac = (-2p)² – 4 x p x 6 = 4p² – 24p
Roots are equal
D = 0
Then 4p² – 24p = 0
⇒ 4p (p – 6) = 0
⇒ p – 6 = 0
⇒ p = 6

Question 44.
Solution:
x² – 4kx + k = 0
D = b² – 4ac = (-4k)² – 4 x 1 x k = 16k² – 4k
Roots are equal
D = 0
16k² – 4k = 0
⇒ 4k (4k – 1) = 0
⇒ 4k – 1 = 0
⇒ k = \(\frac { 1 }{ 4 }\)

Question 45.
Solution:
9x² – 3kx + k = 0
D = b² – 4ac = (-3k)² – 4 x 9 x k = 9k² – 36k
Roots are equal
D = 0
9k² – 36k = 0
9k (k – 4) = 0
Either, 9k = 0, then k = 0
or (k – 4) = 0 ⇒ k = 4
k = 0, 4

Short-Answer Questions
Question 46.
Solution:
x² – (√3 + 1) x + √3 = 0
D = b² – 4ac
= [-(√3 + 1)]² – 4 x 1 x √3
= 3 + 1 + 2√3 – 4√3
= 4 + 2√3 – 4√3
= 4 – 2√3
= 3 + 1 – 2√3
= (√3 – 1)²

Question 47.
Solution:
2x² + ax – a² = 0
D = B² – 4AC = a² – 4 x 2(-a)² = a² + 8a² = 9a²

Question 48.
Solution:
3x² + 5√5 x – 10 = 0
D = b² – 4ac = (5√5)² – 4 x 3 x (-10)
= 125 + 120 = 245 = 49 x 5 = (7√5)²

Question 49.
Solution:
√3 x² + 10x – 8√3 = 0

Question 50.
Solution:
√3 x² – 2√2 x – 2√3 = 0

Question 51.
Solution:
4√3 x² + 5x – 2√3 = 0

Question 52.
Solution:
4x² + 4bx – (a² – b²) = 0

Question 53.
Solution:
x² + 5x – (a² + a – 6) = 0
a² + a – 6 = a² + 3a – 2a – 6 = a(a + 3) – 2(a + 3) = (a + 3)(a – 2)
and 6 = (a + 3) – (a – 2)
x² + (a + 3)x – (a – 2)x – (a + 3) (a – 2) = 0
x (x + a + 3) – (a – 2) (x + a + 3) = 0
(x + a + 3)(x – a + 2) = 0
Either, x + a + 3 = 0, then x = -(a + 3)
or x – a + 2 = -0 then x = (a – 2)
x = -(a + 3) or (a – 2)

Question 54.
Solution:
x² + 6x – (a² + 2a – 8) = 0

Question 55.
Solution:
x² – 4ax + 4a² – b² = 0
4a² – b² = (2a)² – (b)² = (2a + b)(2a – b) – 4ax = (2a + b)x + (2a – b)x
x² – 4ax + 4a² – b² = x² – (2a + b)x – (2a – b)x + (2a + b)(2a – b) = 0
⇒ x (x – 2a – b) – (2a – b)(x – 2a – b) = 0
⇒ (x – 2a – b)(x – 2a + b)
Either, x – 2a – b = 0, then x = 2a + b
or x – 2a + b = 0, then x = 2a – b
Hence, x = (2a + b) or (2a – b)

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.