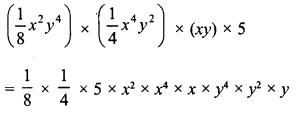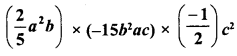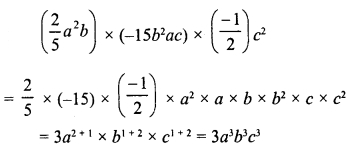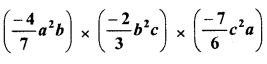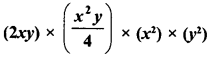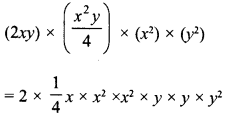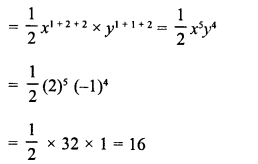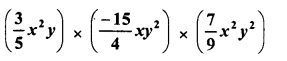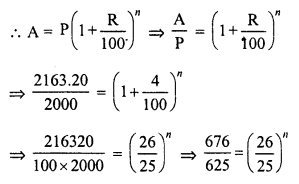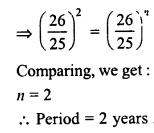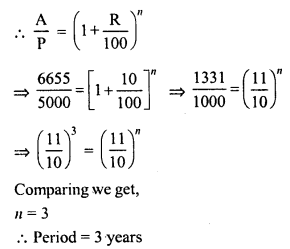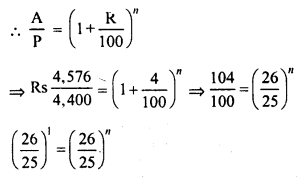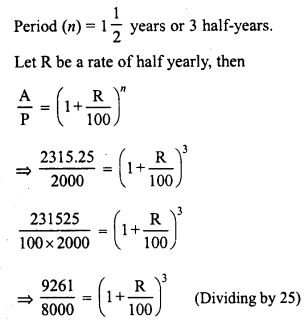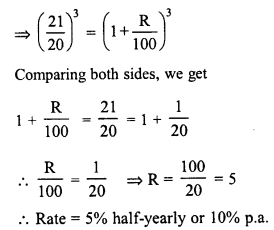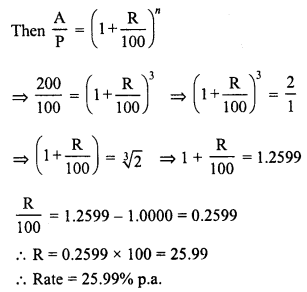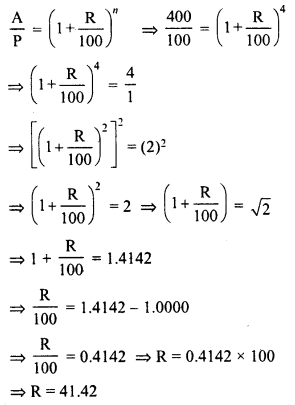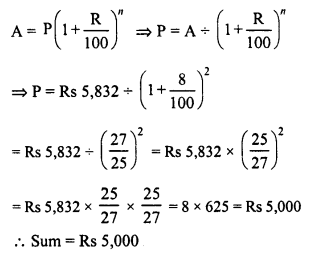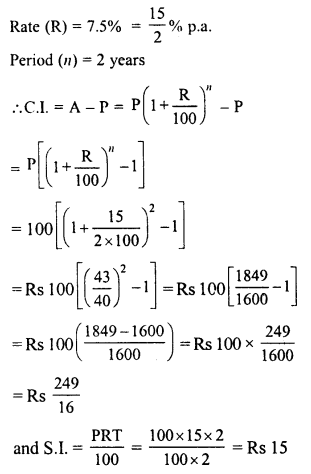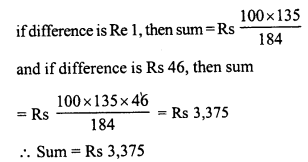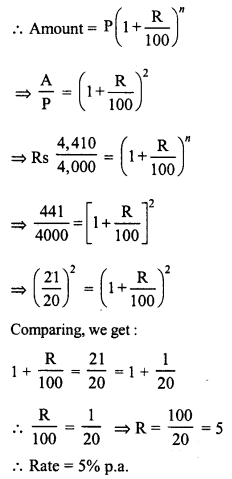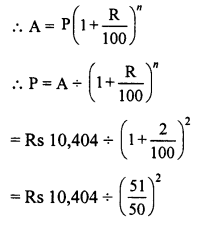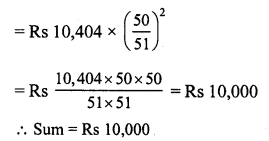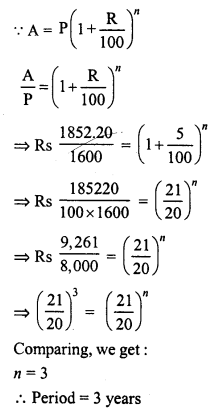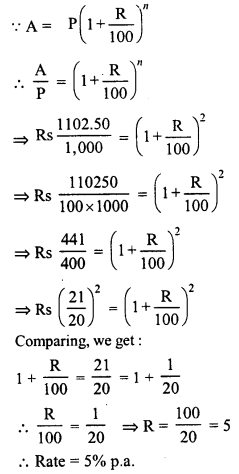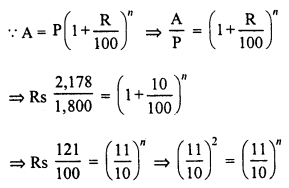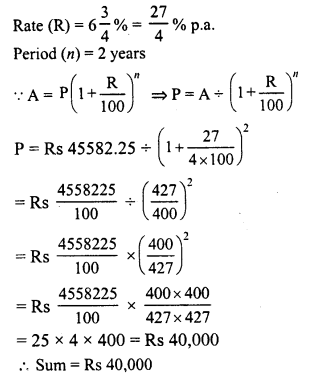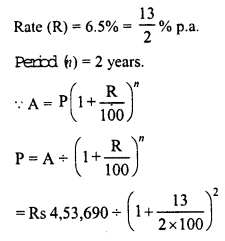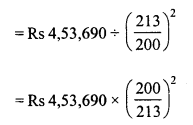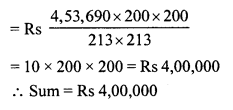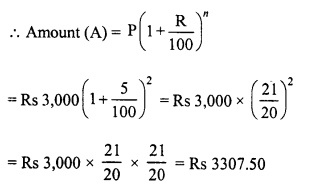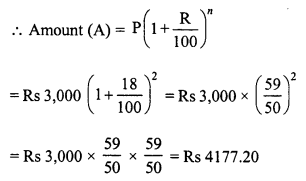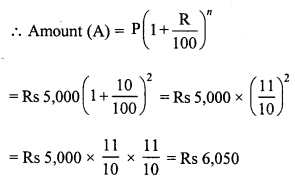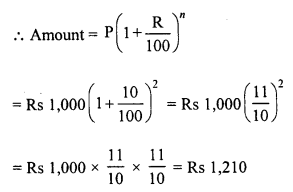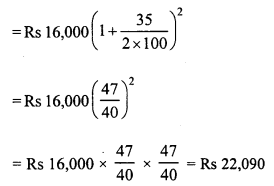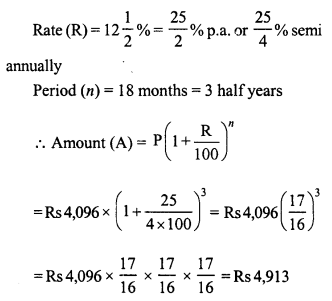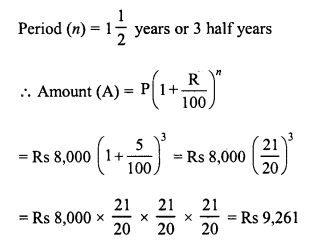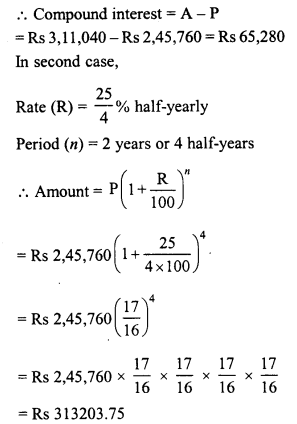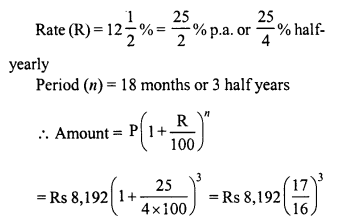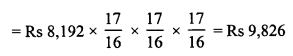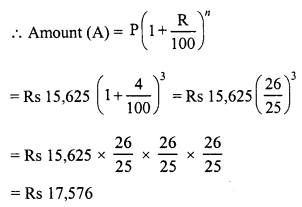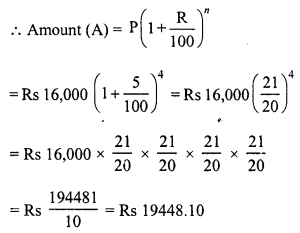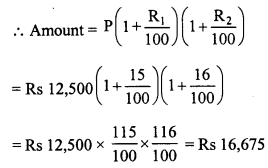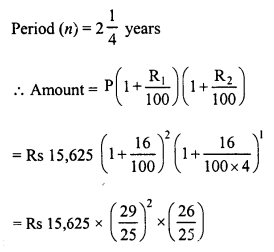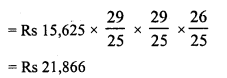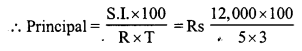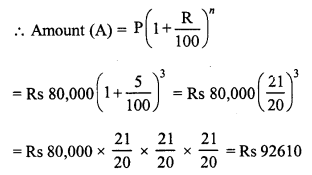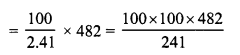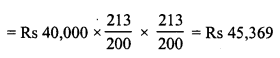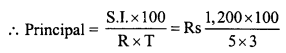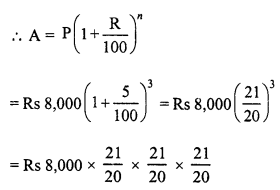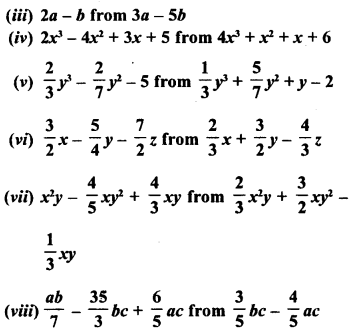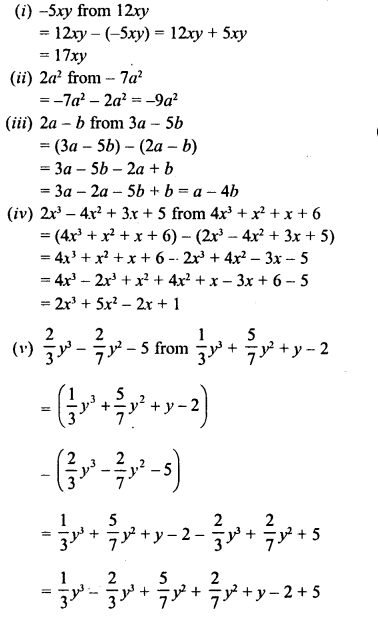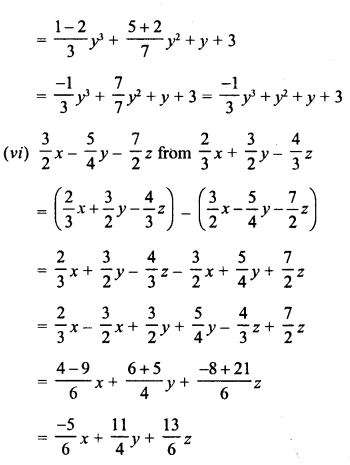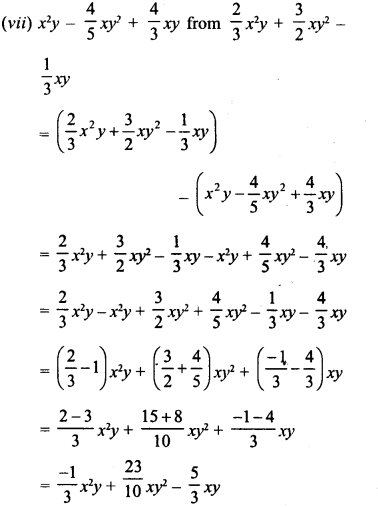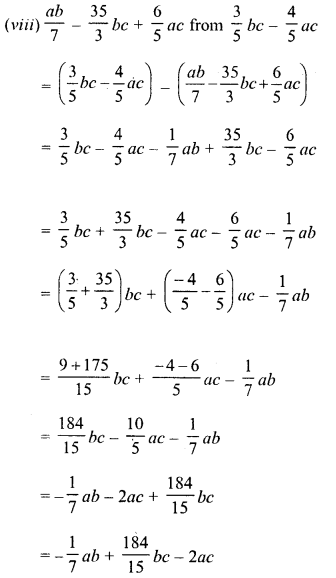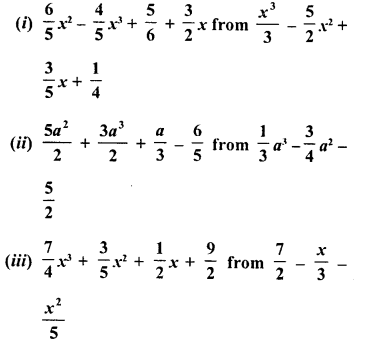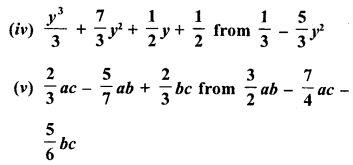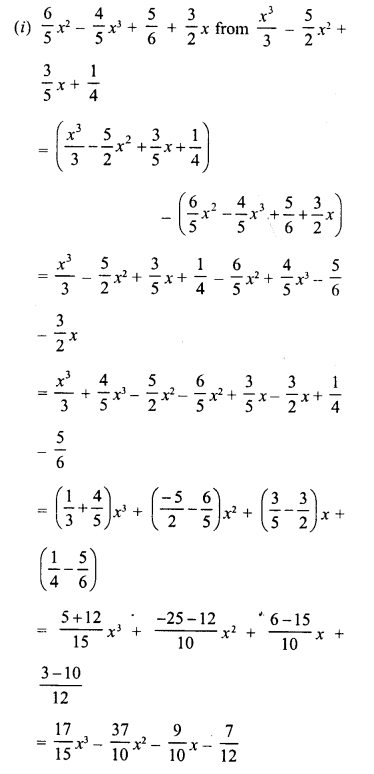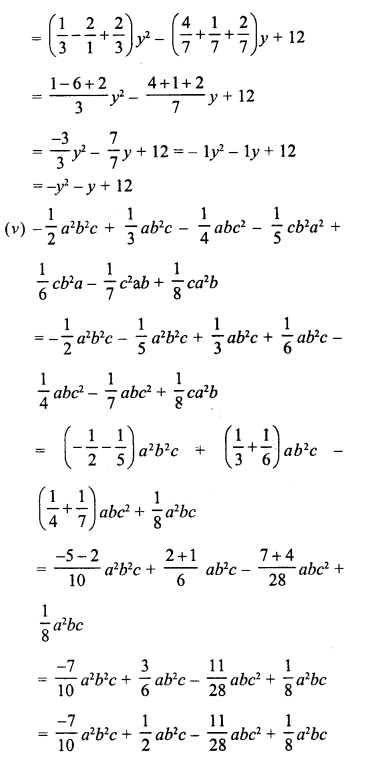RD Sharma Maths Solutions Class 8

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
The present population of a town is 28,000. If it increases at the rate of 5% per annum, what will be its population after 2 years ?
Solution:
Present population = 28000
Rate of increase (R) = 5% p.a.
Period (n) = 2 years
Population after 2 years

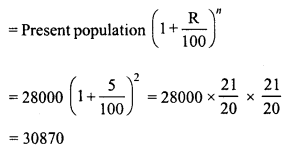
Question 2.
The population of a city is 125000. If the annual birth rate and death rate are 5.5% and 3.5% respectively, calculate the population of city after 3 years.
Solution:
Present population = 125000
Rate of birth = 5.5%
and rate of death = 3.5%
Increase = 5.5 – 3.5 = 2% p.a.
Period = 3 years.
Population after 3 years

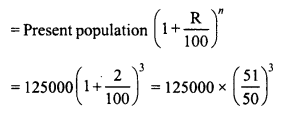
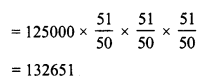
Question 3.
The present population of a town is 25000. It grows at 4%, 5% and 8% during first year, second year and third year respectively. Find its population after 3 years.
Solution:
Present population = 25000
Increase in first year = 4%
in second year= 5% and
in third year = 8%
Population after 3 years =

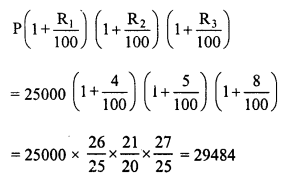
Question 4.
Three years ago, the population of a town was 50000. If the annual increase during three successive years be at the rate of 4%, 5% and 3% respectively, find the present population.
Solution:
Three years ago,
Population of a town = 50000
Annual increase in population in first year = 4%
in second year = 5%
and in third year = 3%
Present population

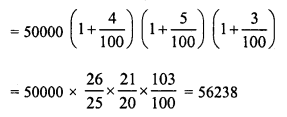
Question 5.
There is a continuous growth in population of a village at the rate of 5% per annum. If its present population is 9261, what it was 3 years ago ?
Solution:
Let 3 years ago, population = P
Present population = 9261
Rate of increase (R) = 5% p.a.
Period (n) = 3 years.

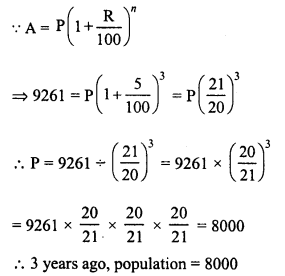
Question 6.
In a factory, the production of scooters rose to 46305 from 40000 in 3 years. Find the annual rate of growth of the production of scooters.
Solution:
Production of scooters 3 years ago (P) = 40000
Present production (A) = 46305
Period (n) = 3 years

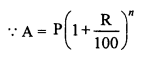
Question 7.
The annual rate of growth in population of a certain city is 8%. If its present population is 196830, what it was 3 years ago ?
Solution:
Let 3 years ago, the population of a city = P
Rate of growth (R) = 8% p.a.
Present population = 196830
Period (n) = 3 years

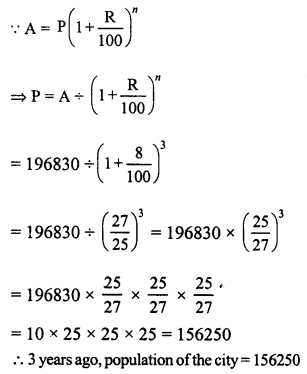
Question 8.
The population of a town increases at the rate of 50 per thousand. Its population after 2 years will be 22050. Find its present population.
Solution:
Population after 2 years = 22050
Rate of increase = 50 per thousand
Period (n) = 2 years
Let present population = P, then

Question 9.
The count of bacteria in a culture grows by 10% in the first hour, decreases by 8% in the second hour and again increases by 12% in the third hour. If the count of bacteria in the sample is 13125000, what will be the count of bacteria after 3 hours ?
Solution:
Present count of bacteria = 13125000
In first hour increase = 10%
decrease in second hour = 8%
increase in third hour = 12%
Count of bacteria after 3 hours

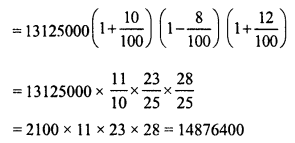
Question 10.
The population of a certain city was 72000 on the last day of the year 1998. During next year it increased by 7% but due to an epidemic it decreased by 10% in the following year. What was its population at the end of the year 2000 ?
Solution:
On the last day of 1998,
Population of a town = 72000
In the first year, increase = 7%
In the second year, decrease = 10%
Population in the last day of 2000

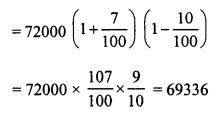
Question 11.
6400 workers were employed to construct a river bridge in four years. At the end of the first year, 25% workers were retrenched. At the end of the second year, 25% of those working at that time were retrenched. However, to complete the project in time, the number of workers was increased by 25% at the end of the third year. How many workers were working during the fourth year ?
Solution:
Number of workers at the beginning = 6400
Period = 4 years.
At the end of 1st year, workers retrenched = 25%
At the end of second year, workers retrenched = 25%
At the end of third year, workers increased = 25%
Total number of workers during the 4 years

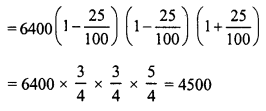
Question 12.
Aman started a factory with an initial investment of Rs 1,00,000. In the first year, he incurred a loss of 5%. However, during the second year, he earned a profit of 10% which in the third year rose to 12%. Calculate his net profit for the entire period of three years.
Solution:
Initial investment = Rs 100000
Loss in the first year = 5%
Profit in the second year = 10%
Profit in the third year = 12%
Investment at the end of 3 years

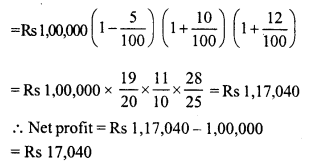
Question 13.
The population of a town increases at the rate of 40 per thousand annually. If the present population be 175760, what was the population three years ago ?
Solution:
Present population (A) = 175760
Increase rate = 40 per 1000
Period = 3 years
Let 3 years ago,
population was = P

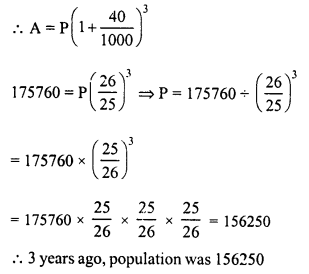
Question 14.
The production of a mixi company in 1996 was 8000 mixies. Due to increase in demand it increases its production by 15% in the next two years and after two years its demand decreases by 5%. What will be its production after 3 years ?
Solution:
Production of Mixi in 1996 = 8000
Increase in next 2 years = 15%
Decrease in the third year = 5%
Production after 3 years

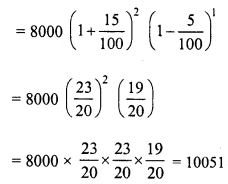
Question 15.
The population of a city increases each year by 4% of what it had been at the beginning of each year. If the population in 1999 had been 6760000, find the population of the city in (i) 2001 (ii) 1997.
Solution:
Population of a city in 1999 = 6760000
Increase = 4%
(i) Population in 2001 is after 2 years

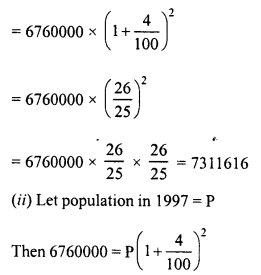
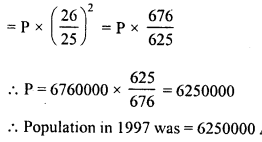
Question 16.
Jitendra set up a factory by investing Rs 25,00,000. During the first two successive years his profits were 5% and f 10% respectively. If each year the profit was on previous year’s capital, compute his total profit.
Solution:
Investment in the beginning = Rs 25,00,000
Profit during the first 2 years = 5% and 10% respectively
Investment after 2 years will be

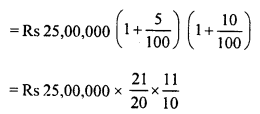
= Rs 28,87,500
Amount of profit = Rs 28,87,500 – Rs 25,00,000 = Rs 3,87,500

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Find each of the following products (1-8)
Question 1.
5x² x 4x³
Solution:
5x² x 4x³ = 5 x 4 x x² x x³
= 20x^{2 + 3} = 20x^s

Question 2.
3a² x 4b⁴
Solution:
-3a² x 4b⁴ = -3 x 4 x a²b⁴
= -12a²b⁴

Question 3.
(-5xy) x (-3x²yz)
Solution:
(-5xy) x (-3x²yz)
= (-5) x (-3)xy x x²yz
= 15x^{1 + 2}xy^{1+ 1}z= 15x³y²z

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Find each of the following products : (9-17)

Question 9.
(7ab) x (-5ab²c) x (6abc²)
Solution:
(7ab) x (-5ab²c) x (6abc²)
= 7 x (-5) x 6 x a x a x a x b x b² x b x c x c²
=-210 x a¹⁺¹⁺¹ x b¹⁺²⁺¹x c¹⁺²
=-210 x a³b⁴c³

Question 10.
(-5a) x (-10a²) x (-2a³)
Solution:
(-5a) x (-10a²) x (-2a³)
= (-5) (-10) (-2) x a x a² x a³
= -100a^{1 + 2 + 3} = -100a⁶

Question 11.
(-4x²) x (-6xy²) x (-3yz²)
Solution:
(-4x²) x (-6xy²) x (-3yz²)
= (-4) x (-6) x (-3) x² x x x y² x y xz²
= -72x²⁺¹ x y²⁺¹ x _z²
= 72x³y³z³

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.
(2.3xy) x (0.1x) x (0.16)
Solution:
(2.3xy) x (0.1x) x (0.16)
= 2.3 x 0.1 x 0.16 x x x x x y
= 0.0368x^{1 +1} x y = 0.0368x²y

Express each of the following products as a monomials and verify the result in each case for x = 1 : (18 -26)

Question 18.
(3x) x (4x) x (-5x)
Solution:

Question 19.

Solution:

Question 20.
(5x⁴) x (x²)³ x (2x)²
Solution:
(5x⁴) x (x²)³ x (2x)²
= 5x⁴ x x^{2 x 3} x 2x x 2x
= 5x⁴ * x⁶ x 4x² = 5 x 4 x x^{4 + 6 + 2}
= 20x¹²
Verification:
L.H.S. = (5x⁴) x (x²)³ x (2x)²
= 5 x (1)⁴ x [(1)²]³ x (2 x 1)²
= 5 x 1 x (1)^{2 x 3}_x (2)²
= 5 x 1⁶ x 2² = 5 x 1 x 4 = 20
R.H.S. = 20x¹² = 20 (1)¹² = 20 x 1 = 20
∴ L.H.S. = R.H.S.

Question 21.
(x²)³ x (2x) x (-4x) x 5
Solution:
(x²)³ x (2x) x (-4x) x (5)
= x^{2 x 3} X 2x X (-4x) X 5
= x⁶ x 2x x (-4x) x 5 = 2 x (-4) x 5x^{6+1 +1}
= -40x⁸
Verification
L.H.S. = (x²)³ x (2x) x (-4x) x (5)
= (1²)³ x (2 x 1) x (-4 x 1) x 5
= 1^2 x 3 x 2 x (- 4) x 5 = 1⁶ x 2 x (-4) x 5
= 1 x 2 x (-4) x 5 = -40
R.H.S. = -40x⁸ = -40 x (1)⁸
= -40 x 1 = -40
∴ L.H.S. = R.H.S.

Question 22.
Write down the product of -8x²y⁶ and – 20xy Verify the product for x = 2.5, y = 1.
Solution:
Product of -8x²y⁶ and -20xy
= (-8x²y⁶) x (-20xy)
= -8 x (-20) x² x _x x y⁶ x y = 160x^{2 + 1} x y^{6 + 1}
= 160x³y³
Verification.
L.H.S. = (-8x²y⁶) x (-20xy)
= -8 x (2.5)² x (1) x (-20 x 2.5 x 1)
= -8 x 6.25 x 1 x -20 x 2.5
= (-50) x (-50) = 2500
R.H.S. = 160 x = 160 (2.5)³ x (1)⁷
= 160 x 15.625 x 1 =2500
∴ L.H.S. = R.H.S.

Question 23.
Evaluate : (3.2x⁶y³) x (2.1x²y²) when x = 1 and y = 0.5.
Solution:
3.2x⁶y³ x 2.1x²y²
= 3.2 x 2.1 x x⁶⁺² x y³⁺²
= 6.72x⁸y⁵ = 6.72 x (1)⁸ x (0.5)⁵
= 6.72 x 1 x 0.03125
= 0.21

Question 24.
Find the value of (5x⁶) x (-1.5x²y³) x (-12xy²) when x = 1, y = 0.5.
Solution:

Question 25.
Evaluate : (2.3a⁵b²) x (1.2a²b²) when a = 1, b = 0.5.
Solution:

Question 26.
Evaluate : (-8x²y⁶) x (-20xy) for x = 2.5 and y = 1.
Solution:

Express each of the following products as a monomials and verify the result for x = 1,y = 2: (27-31)

Question 27.
(-xy³) x (yx³) x (xy)
Solution:
(-xy³) x (yx³) x (xy)
= -x x x³ x x x y³ x y x y = -x^{1 + 3 + 1} x y^{3 + 1 + 1} = -x⁵y⁵
Verification:
L.H.S. = (-xy³) x (yx³) x (xy)
= (-1 x 2³) x [2 x (1)³] x (1 X 2)
= (-1 x 8) x (2 x 1) x (1 x 2)
= -8 x 2 x 2 = -32
R.H.S. =-x⁵y⁵  = -(1)⁵ (2)⁵
= -1 x 32 =-32
∴ L.H.S. = R.H.S.

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.

Solution:

Question 32.

Solution:

Question 33.

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
On what sum will the compound interest at 5% p.a. annum for 2 years compounded annually be Rs 164 ?
Solution:
Let Principal (P) = Rs 100
Rate (R) = 5% p.a.
Period (n) = 2 years

Question 2.
Find the principal of the interest compounded annually at the rate of 10% for two years is Rs 210.
Solution:
Let principal (P) = Rs 100
Rate (R) = 10% p.a.
Period (n) = 2 years

Question 3.
A sum amounts to Rs 756.25 at 10% per annum in 2 years, compounded annually. Find the sum.
Solution:
Amount (A) = Rs 756.25
Rate (R) = 10% p.a.
Period (n) = 2 years

Question 4.
What sum will amount to Rs 4913 in 18 months, if the rate of interest is 12\(\frac { 1 }{ 2 }\) % per annum, compounded half-yearly.
Solution:
Amount (A) = Rs 4,913

Question 5.
The difference between the compound interest and simple interest on a certain sum at 15% per annum for 3 years is Rs 283.50. Find the sum.
Solution:
Let sum (P) = Rs 100
Rate (R) = 15% p.a.
Period (n) = 3 years

Question 6.
Rachna borrowed a certain sum at the rate of 15% per annum. If she paid at the end of two years Rs 1,290 as interest compounded annually, find the sum she borrowed.
Solution:
C.I. = Rs 1,290
Rate (R) = 15% p.a.
Period (n) = 2 years
Let sum (P) = Rs 100

Question 7.
The interest on a sum of Rs 2,000 is being compounded annually at the rate of 4% per annum. Find the period for which the compound interest is Rs 163.20.
Solution:
Sum (P) = Rs 2,000
C.I. = Rs 163.20
Amount (A) = P + C.I. = Rs 2000 + Rs 163.20 = Rs 2163.20
Rate (R) = 4%
Let period = n years

Question 8.
In how much time would Rs 5,000 amount to Rs 6,655 at 10% per annum compound interest ?
Solution:
Principal (P) = Rs 5,000
Amount (A) = Rs 6,655
Rate (R) = 10%
Let period = n years.

Question 9.
In what time will Rs 4,400 becomes Rs 4,576 at 8% per annum interest compounded half-yearly ?
Solution:
Principal (P) = Rs 4,400
Amount (A) = Rs 4,576
Rate (R) = 8% or 4% half-yearly
Let period = n half-years

n = 1
Period = 1 half year

Question 10.
The difference between the S.I. and C.I. on a certain sum of money for 2 years at 4% per annum is Rs 20. Find the sum.
Solution:
Difference between C.I. and S.I. = Rs 20
Rate (R) = 4% p.a.
Period (n) = 2 years
Let principal (P) = Rs 100

Question 11.
In what time will Rs 1,000 amount to Rs 1,331 at 10% per annum compound interest.
Solution:
Principal (P) = Rs 1,000
Amount (A) = Rs 1,331
Rate (R) = 10% p.a.
Let period = n year

Question 12.
At what rate percent compound interest per annum will Rs 640 amount to Rs 774.40 in 2 years ?
Solution:
Principal (P) = Rs 640
Amount (A) = Rs 774.40
Period (n) = 2 years.
Let R be the rate of interest p.a.

Question 13.
Find the rate percent per annum if Rs 2000 amount to Rs 2,662 in 1\(\frac { 1 }{ 2 }\) years, interest being compounded half-yearly ?
Solution:
Principal (P) = Rs 2,000
Amount (A) = Rs 2,662

Question 14.
Kamala borrowed from Ratan a certain rate for two years simple interest. She lent this sum at the same rate to Hari for two years compound interest. At the end of two years, she received Rs 210 as compound interest, but paid Rs 200 only as simple interest. Find the sum and the rate of interest.
Solution:
Simple interest = Rs 200
and compound interest = Rs 210.
Period = 2 years

Question 15.
Find the rate percent per annum, if Rs 2,000 amount to Rs 2,315.25, in an year and a half, interest being compounded six monthly.
Solution:
Principal (P) = Rs 2,000
Amount (A) = Rs 2315.25

Question 16.
Find the rate at which a sum of money will double itself in 3 years, if the interest is compounded annually.
Solution:
Let Principal (P) = Rs 100
then Amount (A) = Rs 200
Period (n) = 3 years
Let R be the rate % p.a.

Question 17.
Find the rate at which a sum of money will become four times the original amount in 2 years, if the interest is compounded half- yearly.
Solution:
Let Principal (P) = Rs 100
Then Amount (A) = Rs 400
Period (n) = 2 years or 4 half years
Let R be the rate % half-yearly, then

Rate % = 41.42% half yearly and 82.84% p.a.

Question 18.
A certain sum amounts to Rs 5,832 in 2 years at 8% compounded interest. Find the sum.
Solution:
Amount (A) = Rs 5,832
Let P be the sum
Rate (R) = 8% p.a.
Period (n) = 2 years

Question 19.
The difference between the compound interest and simple interest on a certain sum for 2 years at 7.5% per annum is Rs 360. Find the sum.
Solution:
Let sum (P) = Rs 100

Question 20.
The difference in simple interest and compound interest on a certain sum of money at 6\(\frac { 2 }{ 3 }\) % per annum for 3 years is Rs 46. Determine the sum.
Solution:
Let sum (P) = Rs 100

Question 21.
Ishita invested a sum of Rs 12,000 at 5% per annum compound interest. She received an amount of Rs 13,230 after n years, Find the value of n.
Solution:
Principal (P) = Rs 12,000
Amount (A) = Rs 13,230
Rate (R) = 5% p.a.
Period = n years

Question 22.
At what rate percent per annum will a sum of Rs 4,000 yield compound interest of Rs 410 in 2 years ?
Solution:
Principal (P) = Rs 4,060
C.I. = Rs 410
Amount (A) = Rs 4,000 + 410 = Rs 4,410
Let rate = R % p.a.
Period (n) = 2 years

Question 23.
A sum of money deposited at 2% per annum compounded annually becomes Rs 10404 at the end of 2 years. Find the sum deposited.
Solution:
Amount (A) = Rs 10,404
Rate (R) = 2% p.a.
Period (n) = 2 years.

Question 24.
In how much time will a sum of Rs 1,600 amount to Rs 1852.20 at 5% per annum compound interest ?
Solution:
Principal (P) = Rs 1,600
Amount (A) = Rs 1852.20
Rate (R) = 5% p.a.
Let n be the time

Question 25.
At what rate percent will a sum of Rs 1,000 amount to Rs 1102.50 in 2 years at compound interest ?
Solution:
Principal (P) = Rs 1,000
Amount (A) = Rs 1102.50 .
Period (n) = 2 years
Let R be the rate of interest p.a.

Question 26.
The compound interest on Rs 1,800 at 10% per annum for a certain period of time is Rs 378. Find the time in years.
Solution:
Principal (P) = Rs 1,800
C.I. = Rs 378
Amount (A) = P + C.I. = Rs 1,800 + 378 = Rs 2,178
Rate (R) = 10% p.a.
Let n be the period in years

Comparing, we get:
n = 2
Period = 2 years

Question 27.
What sum of money will amount to Rs 45582.25 at 6\(\frac { 3 }{ 4 }\) % per annum in two years, interest being compounded annually ?
Solution:
Amount (A) = Rs 45582.25

Question 28.
Sum of money amounts to Rs 4,53,690 in 2 years at 6.5% per annum compounded annually. Find the sum.
Solution:
Amount (A) = Rs 4,53,690

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
Compute the amount and the compound interest in each of the following by using the formula when :
(i) Principal = Rs 3,000, Rate = 5%, Time = 2 years
(ii) Principal = Rs 3,000 Rate = 18%, Time = 2 years
(iii) Principal = Rs 5,000 Rate = 10 paise per rupee per annum, Time = 2 years
(iv) Principal = Rs 2,000, Rate = 4 paise per rupee per annum, Time = 3 years.
(v) Principal = Rs 12,800, Rate = 7\(\frac { 1 }{ 2 }\) %, Time = 3 years
(vi) Principal = Rs 10,000, Rate = 20% per annum compounded half-yearly, time = 2 years
(vii) Principal = Rs 1,60,000, Rate = 10 paise per rupee per annum compounded half- yearly, Time = 2 years.
Solution:
(i) Principal (P) = Rs 3,000
Rate (R) = 5% p.a.
Time (n) = 2 years

and compound interest (C.I) = A – P = Rs 3307.50 – Rs 3,000 = Rs 307.50
(ii) Principal (P) = Rs 3,000
Rate (R) = 18% p.a.
Time (n) = 2 years

and compound interest (C.I.) = A – P = Rs 4177.20 – Rs 3,000 = Rs 1177.20
(iii) Principal (P) = Rs 5,000
Rate (R) =10 paise per rupee or 10% p.a.
Time (n) = 2 years.

C.I. = A – P = Rs 6,050 – Rs 5,000 = Rs 1,050
(iv) Principal (P) = Rs 2,000
Rate (R) = 4 paise per rupee or 4% p.a.
Time (n) = 3 years

C.I. = A – P = Rs 2249.73 – Rs 2,000 = Rs 249.73
(v) Principal (P) = Rs 12,800

C.I. = A – P = Rs 15901.40 – Rs 12,800 = Rs 3101.40
(vi) Principal (P) = Rs 10,000
Rate (R) = 20% p.a. or 10% half-yearly
Time = 2 years or 4 half-years

C.I. = A – P = Rs 14,641 – Rs 10,000 = Rs 4,641
(vii) Principal (P) = Rs 1,60,000
Rate (R) = 10 paise per rupee or 10% p.a. or 5% half-yearly
Time (n) = 2 years or 4 half-years.

C.I. = A – P = Rs 1,94,481 – Rs 1,60,000 = Rs 34,481

Question 2.
Find the amount of Rs 2,400 after 3 years, when the interest is compounded annually at the rate of 20% per annum.
Solution:
Principal (P) = Rs 2,400
Rate (R) = 20%
Time (n) = 3 years

Question 3.
Rahman lent Rs 16,000 to Rasheed at the rate of 12\(\frac { 1 }{ 2 }\) % per annum compound interest. Find the amount payable by Rasheed to Rahman after 3 years.
Solution:
Principal (P) = Rs 16,000

Question 4.
Meera borrowed a sum of Rs 1,000 from Sita for two years. If the rate of interest is 10% compounded annually find the amount that Meera has to pay back.
Solution:
Amount of loan (P) = Rs 1,000
Rate (R) = 10% p.a.
Period (n) = 2 years

Question 5.
Find the difference between the compound interest and simple interest. On a sum of Rs 50,000 at 10% per annum for 2 years.
Solution:
Principal (P) = Rs 50,000
Rate (R) = 10% p.a.
Period (n) = 2 years.

Difference between C.I. and S.I. = Rs 10,500 – Rs 10,000 = Rs 500

Question 6.
Amit borrowed Rs 16,000 at 17\(\frac { 1 }{ 2 }\) % per annum simple interest on the same day, he lent it to Ashu at the same rate but compounded annually. What does he gain at the end of 2 years ?
Solution:
Amount of loan (P) = Rs 16,000


C.I. = A – P = Rs 22,090 – Rs 16,000 = Rs 6,090
Now gain = C.I. – S.I = Rs 6,090 – 5,600 = Rs 490

Question 7.
Find the amount of Rs 4,096 for 18 months at 12\(\frac { 1 }{ 2 }\) % per annum, interest being compounded semi-annually ?
Solution:
Principal (P) = Rs 4,096

Question 8.
Find the amount and the compound interest on Rs 8,000 for 1\(\frac { 1 }{ 2 }\) years at 10% per annum, compounded half-yearly.
Solution:
Principal (P) = Rs 8,000
Rate (R) = 10% p.a. or 5% half yearly

and C.I. = A – P = Rs 9,261 – Rs 8,000 = Rs 1,261

Question 9.
Kamal borrowed Rs 57,600 from LIC against her policy at 12\(\frac { 1 }{ 2 }\) % per annum to build a house. Find the amount that she pays LIC after 1\(\frac { 1 }{ 2 }\) years if the interest is calculated half-yearly.
Solution:
Amount of loan (P) = Rs 57,600

Question 10.
Abha purchased a house from Avas Parishad on credit. If the cost of the house is Rs 64,000 and the rate of interest is 5% per annum compounded half-yearly, find the interest paid by Abha after one year and a half.
Solution:
Price of house (P) = Rs 64,000

Compound interest (C.I.) = A – P = Rs 68,921 – Rs 64,000 = Rs 4,921

Question 11.
Rakesh lent out Rs 10,000 for 2 years at 20% per annum compounded annually. How much more he could earn if the interest be compounded half-yearly ?
Solution:
Principal (P) = Rs 10,000
Rate (R) = 20% p.a. or 10% half-yearly
Period (n) = 2 years or 4 half-years


C.I. = Rs 14,400 – Rs 10,000 = Rs 4,400
Now difference in C.I. = Rs 4,641 – Rs 4,400 = Rs 241

Question 12.
Romesh borrowed a sum of Rs 2,45,760 at 12.5% per annum compounded annually. On the same day, he lent out his money to Ramu at the same rate of interest but compounded semi-annually. Find his gain after 2 years.
Solution:
In first case,
Principal (P) = Rs 2,45,760


C.I. = A – P = Rs 313203.75 – Rs 2,45,760 = Rs 67443.75
Gain = 67443.75 – Rs 65,280 = Rs2163.75

Question 13.
Find the amount that David would receive if he invests Rs 8,192 for 18 months at 12\(\frac { 1 }{ 2 }\) % per annum, the interest being compounded half-yearly.
Solution:
Principal (P) = Rs 8,192

Question 14.
Find the compound interest on Rs 15,625 for 9 months at 16% per annum, compounded quarterly.
Solution:
Principal (P) = Rs 15,625
Rate (R) = 16% p.a. or 4% quarterly
Period (n) = 9 months or 3 quarters

Compound interest = A – P = Rs 17,576 – Rs 15,625 = Rs 1,951

Question 15.
Rekha deposited Rs 16,000 in a foreign bank which pays interest at the rate of 20% per annum compounded quarterly, find the interest received by Rekha after one year.
Solution:
Principal (P) = Rs 16,000
Rate (R) = 20% p.a. or 5% quarterly
Period (n) = one year or 4 quarters

C.I. = A – P = Rs 19448.10 – Rs 16,000 = Rs 3448.10

Question 16.
Find the amount of Rs 12,500 for 2 years compounded annually, the rate of interest being 15% for the first year and 16% for the second year.
Solution:
Principal (P) = Rs 12,500
Rate (R1) = 15% p.a. for first year
R2 = 16% p.a. for second year
Period = 2 years

Question 17.
Ramu borrowed Rs 15,625 from a finance company to buy a scooter. If the rate of interest be 16% per annum compounded annually, what payment he will have to make after 2\(\frac { 1 }{ 4 }\) years ?
Solution:
Principal (P) = Rs 15,625
Rate (R) = 16%

Question 18.
What will Rs 1,25,000 amount to at the rate of 6% if interest is calculated after every 4 months for one year ?
Solution:
Principal (P) = Rs 1,25,000

Question 19.
Find the compound interest at the rate of 5% for 3 years on that principal which in 3 years at the rate of 5% per annum gives Rs 12,000 as simple interest.
Solution:
In first case,
S.I. = Rs 12,000
Rate (R) = 5% p.a.
Period (T) = 3 years

= Rs 80,000
In second case,
Principal (P) = Rs 80,000
Rate (R) = 5% p.a.
Period (n) = 3 years

C.I. = A – P = Rs 92,610 – 80,000 = Rs 12,610

Question 20.
A sum of money was lent for 2 years at 20% compounded annually. If the interest is payable half-yearly instead of yearly, then the interest is Rs 482 more. Find the sum.
Solution:
Let Sum (P) = Rs x
Rate (R) = 20% p.a. or 10% half-yearly
Period (n) = 2 years or 4 half years
In first case,

Interests = A – P = Rs 146.41 – Rs 100 = Rs 46.41
Now difference in interests = Rs 46.41 – Rs 44.00 = Rs 2.41
If difference is 2.41 then sum is 100 If difference is Rs 482, then sum

Question 21.
Simple interest on a sum of money for 2 years at 6\(\frac { 1 }{ 2 }\) % per annum is Rs 5,200. What will be the compound interest on the sum at the same rate for the same period ?
Solution:
In first case,
S.I. = Rs 5,200


Compound interest = A – P = Rs 45,369 – Rs 40,000 = Rs 5,369

Question 22.
Find the compound interest at the rate of 5% per annum for 3 years on that principal which in 3 years at the rate of 5% per annum gives Rs 1,200 as simple interest.
Solution:
In first case,
S.I. = Rs 1,200
Rate (R) = 5% p.a.
Period (T) = 3 years

In second case,
Principal (P) = Rs 8,000
Rate (R) = 5% p.a.
Period (n) = 3 years

= Rs 9,261
C.I. = A – P = Rs 9,261 – Rs 8000 = Rs 1,261

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Question 1.
Add the following algebraic expressions


Solution:

Question 2.
Subtract:
(i) -5xy from 12xy
(ii) 2a² from -7a²

Solution:

Question 3.
Take away :


Solution:

Question 4.
Subtract 3x – 4y – 7z from the sum of x – 3y + 2z and – 4X + 9y- 11z.
Solution:
Sum of x – 3y + 2z and – 4x + 9y – 11z
= x – 3y + 2z + (- 4x + 9y – 11z)
= x – 3y + 2z – 4x + 9y – 11z
= x – 4x – 3y + 9y + 2z – 11z
= – 3x + 6y – 9z
Now (-3x + 6y – 9z) – (3x – 4y – 7z)
= -3x + 6y – 9z – 3x + 4y + 7z
= -3x – 3x + 6y + 4y -9z +7z
= -6x + 10y – 2z

Question 5.
Subtract the sum of 3l- 4m – 7n² and 2l + 3m – 4n² from the sum of 9l + 2m – 3n² and -3l + m + 4n².
Solution:
Sum of 9l + 2m – 3n² and -3l + m + 4n²
= 9l + 2m – 3 n² + (-3l) + m + 4n²
= 9l + 2m – 3n² – 3l + m + 4n²
= 9l- 3l+ 2m + m – 3 n² + 4n²
= 6l + 3m + n²
and sum of 3l – 4m – 7n² and 2l +3m- 4n²
= 3l- 4m – 7n² + 2l+ 3m- 4n²
= 3l + 2l – 4m + 3m- 7n² – 4n²
= 5l -m- 11n²
Now (6l + 3m + n²) – (5l – m – 11n²)
= 6l + 3m + n² – 5l + m + 11n²
= 6l – 5l + 3m + m + n² + 11n²
= l + 4m+ 12n²

Question 6.
Subtract the sum of 2x – x² + 5 and -4x – 3 + 7x² from 5.
Solution:
5 – (2x-x² + 5-4x-3 + 7x²)
= 5 – (2x – 4x- x² + 7x² + 5-3)
= 5 – (-2x + 6x² + 2)
= 5 + 2x – 6x² – 2
= – 6x²+2x+3
= 3 + 2x – 6x²

Question 7.

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.