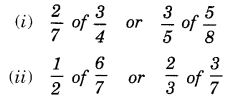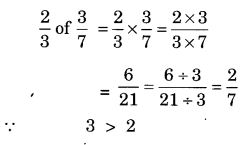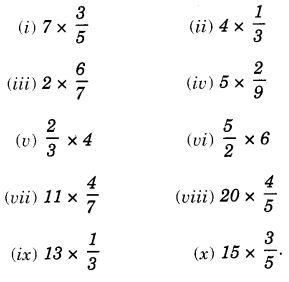NCERT Solutions for Class 7 Maths

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3.

• Fractions and Decimals Class 7 Ex 2.1
• Fractions and Decimals Class 7 Ex 2.2
• Fractions and Decimals Class 7 Ex 2.4
• Fractions and Decimals Class 7 Ex 2.5
• Fractions and Decimals Class 7 Ex 2.6
• Fractions and Decimals Class 7 Ex 2.7
• Fractions and Decimals Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3

Question 1.
Find:

Solution:

Question 2.
Multiply and reduce to lowest form (if possible):


Solution:

Question 3.
Multiply the following fractions:

Solution:

Question 4.
Which is greater:

Solution:

Question 5.
Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is \(\frac { 3 }{ 4 } \) m. Find the distance between the first and the last sapling.
Solution:

Let A, B, C and D be the four saplings planted in a row.
Distance between two adjacent saplings = \(\frac { 3 }{ 4 } \) m
∴ Distance between the first and the last sapling = AD = 3 × AB

Question 6.
Lipika reads a book for 1 \(\frac { 3 }{ 4 } \) hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?
Solution:
Hours in all required by Lipika to read the book

Question 7.
A car runs 16 km using 1 litre of petrol. How much distance will it cover using 2 \(\frac { 3 }{ 4 } \) litres of petrol?
Solution:
Distance covered by the car using 2 \(\frac { 3 }{ 4 } \) litres of petrol

Question 8.

Solution:

We hope the NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2.

• Fractions and Decimals Class 7 Ex 2.1
• Fractions and Decimals Class 7 Ex 2.3
• Fractions and Decimals Class 7 Ex 2.4
• Fractions and Decimals Class 7 Ex 2.5
• Fractions and Decimals Class 7 Ex 2.6
• Fractions and Decimals Class 7 Ex 2.7
• Fractions and Decimals Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2

Question 1.
Which of the drawings (a) to (d) show:

Solution:
(i) (d)
(ii) (b)
(iii) (a)
(iv) (c)

Question 2.
Some pictures (a) to (c) are given below. Tell which of them show:


Solution:

Question 3.
Multiply and reduce to lowest form and convert into a mixed fraction:

Solution:

Question 4.
Shade

1. \(\frac { 1 }{ 2 } \) of the circles in box (a)
2. \(\frac { 2 }{ 3 } \) of the triangles in box (b)
3. \(\frac { 3 }{ 5 } \) of the squares in box (c)

Solution:

Question 5.
Find:

Solution:

Question 6.
Multiply and express as a mixed fraction:

Solution:

Question 7.
Find

Solution:

Question 8.
Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 liters of water. Vidya consumed \(\frac { 2 }{ 5 } \) of the water. Pratap consumed the remaining water.
(i) How much water did Vidya drink?
(ii) What fraction of the total quantity of water did Pratap drink?
Solution:
(i) Quantity of water drank by Vidya

(ii) Quantity of water drank by Pratap
= 5 litres – 2 litres = 3 litres
∴ The fraction of the total quantity of water drank by Pratap

We hope the NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4.

• Integers Class 7 Ex 1.1
• Integers Class 7 Ex 1.2
• Integers Class 7 Ex 1.3
• Integers Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4

Question 1.
Evaluate each of the following:

(a) (-30)+ 10
(b) 50 + (-5)
(c) (-36) +(-9)
(d) (-49) + (49)
(e) 13 + [(- 2) + 1]
(f) 0 + (-12)
(g) (-31) + [(-30) + (-1)]
(h) [(-36)+ 12]+3
(i) [(- 6) + 5] + [(- 2) + 1].

Solution:

(a) (- 30) + 10 = – 3
(b) 50 +(-5) = – 10
(c) (-36) +(-9) = 4
(d) (- 49) + (49) = – 1
(e) 13 + [(- 2) + 1] = 13 + (- 1) = – 13
(f) 0 + (- 12) = 0
(g) (- 31) + [(- 30) + (- 1)] = (- 31) + (- 31) = 1
(h) [(- 36) + 12] + 3 = (- 3) + 3 = – 1
(i) [(- 6) + 5] + [(- 2) + 1] = (- 1) + (- 1) = 1.

Question 2.
Verify that
a + (b + c) ≠ (a + b) + (a ÷ c)
for each of the following values of a, b and c.
(a) a = 12, b = – 4, c = 2
(b) a = (- 10), b = 1, c = l.
Solution:
(a) a + (b + c) = 12 ÷ [(- 4) + 2] = 12 + (- 2) = – 6
(a ÷ b) + (a ÷ c) = 12 ÷ (- 4) + 12 ÷ 2 = -3 + 6 = 3
So, a + (b + c) ≠ (a + b) + (a + c)

(b) a ÷ (b + c) = (- 10) + (1 + 1) = (- 10) + 2 = – 5
a ÷ b + a ÷ c = (- 10) ÷ 1 + (- 10) ÷ 1 = (- 10) + (- 10) = – 20
So, a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c).

Question 3.
Fill in the blanks:

(a) 369 ÷ …….. = 369
(b) -75 ÷ …….. = – 1
(c) (- 206) ÷ ……. = 1
(d) -87 ÷ …….. = 87
(e) ……. ÷ 1 = -87
(f) ……. ÷ 48 = -1
(g) 20 ÷ …… = -2
(h) …… ÷ (4) = – 3.

Solution:

(a) 369 ÷ 1 = 369
(b) – 75 ÷ 75 = -1
(c) (- 206) ÷ (- 206) = 1
(d) – 87 ÷ – 1 = 87
(e) – 87 ÷ 1 = – 87
(f) – 48 ÷ 48 = – 1
(g) 20 ÷ (-10) = – 2
(h) – 12 ÷ (4) = – 3.

Question 4.
Write five pairs of integers (a, b) such that a + b = -3. One such pair is (6, -2) because 6 +(-2) = (-3).
Solution:
Five pairs of integers (a, b) such that a + b = -3 are (- 6, 2), (-9, 3), (12,- 4), (21, -7), (-24, 8)
Note: We may write many such pairs of integers.

Question 5.
The temperature at 12 noon was 10°C above zero. If it decreases at the rate of 2°C per hour until mid-night, at what time would the temperature be 8°C degrees below zero? What would be the temperature at mid night?
Solution:
Difference in temperatures +10 °C and -8
= [10 – (- 8)] °C = (10 + 8)° C = 18 °C
Decrease in temperature in one hour = 2°C
Number of hours taken to have temperature 8 °C below zero \(=\frac { Total\quad decrease }{ Decrease\quad in\quad one\quad hour } \)
\(=\frac { 18 }{ 2 }\)
So, at 9 P.M., the temperature will be 8 °C below zero
Temperature at mid-night = 10 °C – (2 x 12) °C
= 10°C – 24 °C = -14 °C

Question 6.
In a class test (+3) marks are given for every correct answer and (- 2) marks are given for every incorrect answer and no marks for not attempting any question.
(i) Radhika scored 20 marks. If she has got 12 correct answers, how many questions has she attempted incorrectly?
(ii) Mohini scores – 5 marks in this test, though she has got 7 correct answers. How many questions has she attempted incorrectly?
Solution:
(i) Let ‘x’ be the number of incorrect questions attempted by Radhika.
According to the question, we get
(+ 3) × 12 + x × (-2) = 20
⇒ 36 – 2x = 20
⇒ 2x = 36 – 20
⇒ x = \(\frac { 16 }{ 2 } \) = 8
Therefore, Radhika attempted 8 incorrect questions.

(ii) Let ‘x’ be the number of incorrect question attempted by Mohini.
According to the question, we get
(+ 3) × 7 + x × (- 2) = – 5
⇒ 21 – 2x = -5
⇒ 2x = 21 + 5
⇒ x = \(\frac { 26 }{ 2 } \) = 13
Therefore, Mohini attempted 13 incorrect questions.

Question 7.
An elevator descends into a mine shaft at the rate of 6m/min. If the descent starts from 10 m above the ground level, how long will it take to reach – 350 m.
Solution:
Difference in heights at two positions = 10 m – (-350 m) = 360 m
Rate of descent = 6 m/minute
∴ Time taken \(=\left( 360 \right) \div \left( 6 \right)\) minutes = 60 minutes = 1 hour
Hence, the elevator will take 1 hour to reach = 350 m.

We hope the NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3.

• Integers Class 7 Ex 1.1
• Integers Class 7 Ex 1.2
• Integers Class 7 Ex 1.4
• Integers Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3

Question 1.
Find each of the following products:
(a) 3 × (- 1)
(b) (- 1) × 225
(c) (-21) × (- 30)
(d) (- 316) × (- 1)
(e) (- 15) × 0 × (- 18)
(f) (- 12) × (- 11) × (10)
(g) 9 × (-3) × (-6)
(h) (- 18) ×(-5)× (- 4)
(i) (- 1) × (-2) × (-3) × 4
(j) (- 3) × (- 6) × (-2) × (- 1).
Solution:
(a) 3 x (- 1) = – (3 x 1) = – 3
(b) (- 1) x 225 = – (1 x 225) = – 225
(c) (- 21) x (- 30) = 21 x 30 = 630
(d) (- 316) x (- 1) = 316 x 1 = 316
(e) (- 15) x 0 x (- 18) = [(- 15) x 0]  x  (- 18) = 0 x (- 18) = 0
(f) (- 12) x (- 11) x (10) = [(- 12) x (- 11)] x (10) = (132) x (10) = 1320
(g) 9 x (- 3) x (- 6) = [9 x (- 3)] x (- 6) = (- 27) x (- 6) = 162
(h) (- 18) x (- 5) x (- 4) = [(- 18) x (- 5)] x (- 4) = 90 x (- 4) = – 360
(i) (- 1) x (- 2) x (- 3) x 4 = [(- 1) x (- 2)] x [(- 3) x 4] = (2)x (- 12) = -24
(j) (- 3) x (- 6) x (- 2) x (- 1) = [(- 3) x (- 6)] x [(- 2) x (- 1)] = (18) x (2) = 36

Question 2.
Verify the following:
(a) 18 × [7 + (- 3)] = [18 × 7] + [18 × (- 3)]
(b) (-21)×[(-4) + (-6)] = [(-21) × (-4)] + [(-21) × (-6)
Solution:
(a) 18 × [7 + (- 3)] = [18 × 7] + [18 × (- 3)]
L.H.S. = 18 × [7 + (- 3)]
= 18 × L(7 – 3)] = 18 × (4) = 18 × 4 = 72
R.H.S. = [18 × 7] + [18 × (- 3)]
= 126 + [- (18 × 3)] = 126 + (- 54) = 126 – 54 = 72
So, 18 × [7 + (- 3)]
= [18 × 7] + [18 × (- 3)]

(b) (- 21) × [(- 4) + (- 6)] = [(- 21) × (- 4)] + [(- 21) × (- 6)]
L.H.S. = (- 21) × [(- 4) + (- 6)]
= (- 21) × (- 10)
= 21 × 10 = 210
R. H.S. = [(- 21) × (- 4)] + [(- 21) × (- 6)]
= (21 × 4) + (21 × 6)
= 84 + 126 = 210
So, (- 21) × [(- 4) + (- 6)]
= [(- 21) × (- 4)] + [(- 21) × (- 6)].

Question 3.
(i) For any integer a, what is (-1)×a equal to?
(ii) Determine the integer whose product with (- 1) is
(a) – 22
(b) 37
(c) 0.
Solution:
(i) For any integer a, (-1) x a = -a.
(ii) We know that the product of any integer and (-1) is the additive inverse of an integer.
The integer whose product with (-1) is
(a) additive inverse of -22, t. e., 22.
(b) additive inverse of 37, i.e., -37.
(c) additive inverse of 0, i.e., 0.

Question 4.
Starting from (- 1) × 5, write various products showing some pattern to show (- 1) × (-1) – 1.
Solution:
(- 1) × 5 = – 5
(- 1) × 4 = – 4 [= (- 5) + 1]
(- 1) × 3 = – 3 [= (- 4) + 1]
(- 1) × 2 = – 2 [= (- 3) + 1]
(- 1) × 1 = – 1 [= (- 2) + 1]
(- 1) × 0 = 0 [= (- 1) + 1]
(- 1) × (- 1) = 1 [= 0 + 1]

Question 5.
Find the product, using suitable properties:
(a) 26 × (- 48) + (- 48) × (- 36)
(b) 8 × 53 × (- 125)
(c) 15×(-25)×(-4)×(- 10)
(d) (-41) × 102
(e) 625 × (-35) + (- 625) × 65
(f) 7 × (50 -2)
(g) (-17) × (-29)
(h) (- 57) ×(-19)+ 57.
Solution:
(a) We have, 26 x (-48) + (- 48) x (- 36)
= (- 48) x 26 + (- 48) x (- 36)
= (- 48) x [26 + (- 36)]
= (- 48) x (26 – 36)
=(- 48) x (- 10)= 480
(b) We have,
8 x 53 x (- 125) = [8 x (- 125)] x 53
= (- 1000) x 53 = – 53000
(c) We have,
15 x (- 25) x (- 4) x (- 10)
=15 x [(- 25) x (-4)] x (- 10)
= 15 x (100) x (- 10)
= (15 x 100) x (- 10)
= 1500 x (- 10) = – 15000
(d) We have,
(- 41) x 102 = (- 41) x (100 + 2)
= (- 41) x 100 + (- 41) x 2 = -4100 – 82 = – 4182
(e) We have, 625 x (- 35) + (- 625) x 65
= 625 x (- 35) + (625) x (- 65)
= 625 x [(- 35)+ (- 65)]
= 625 x (- 100) = – 62500
(f) 7 x (50 – 2) = 7 x 50 – 7 x 2
= 350 -14 =336
(g) (-17) x (- 29) = (-17) x [(- 30) + 1]
= (- 17) x (- 30) + (- 17) x 1 = 510 – 17 = 493
(h) (- 57) x (-19)+ 57 =57 x 19 + 57 x 1
= 57 x (19 +1)
= 57 x 20 = 1140

Question 6.
A certain freezing process requires that room temperature be lowered from 40°C at the rate of 5° C every hour. What will be the room temperature 10 hours after the process begins?
Solution:
Room temperature 10 hours after the process begins
= 40°C – 10 × 5°C
= 40°C – 50°C
= – (50 – 40)°C = – 10°C

Question 7.
In a class test containing 10 questions, 5 marks are awarded for every correct answer and (-2) marks are awarded for every incorrect answer and 0 for questions not attempted.
(i) Mohan gets four correct and si× incorrect answers. What is his score?
(ii) Reshma gets five correct answers and five incorrect answers, what is her score?
(iii) Heena gets two correct and five incorrect answers out of seven questions she attempts. What is her score?
Solution:
(i) Mohan gets for four correct answers 4 × 5 = 20 marks
He also gets for si× incorrect answers. 6 × (- 2) = – 12 marks.
Therefore, Mohan’s score = 20 + (- 12) = 20-12 = 8 marks.

(ii) Reshma gets for five correct answers 5 × 5 = 25 marks
She also gets for five incorrect answers 5 × (- 2) = – 10 marks Therefore, Reshma’s score = 25 + (- 10) = 25-10 = 15 marks.

(iii) Heena gets for two correct answers
2 × 5 = 10 marks.
She also gets for five incorrect answers 5 × (- 2) = – 10 marks
She didn’t attempt three questions. For these, she gets 3×0 = 0 marks
Therefore, Heena’s score = 10 + (- 10) + 0 = 10 – 10 + 0 = 0 marks.

Question 8.
A cement company earns a profit of ₹ 8 per bag of white cement sold and a loss of ₹ 5 per bag of grey cement sold.
(a) The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month. What is its profit or loss?
(b) What is the number of white cement bags it must sell to have neither profit nor loss if the number of grey bags sold is 6,400 bags.
Solution:
(a) The company sells 3,000 bags of white cement. So her profit = 3,000 × 8 = ₹ 24,000
Also, the company sells 5,000 bags of grey cement. So her loss = 5,000 × 5 = ₹ 25,000
Since 25,000 > 24,000
Therefore, the company is at a loss and the loss is = 25000 – 24000 = ₹ 1000

(b) Let ‘×’ be the number of white cement bags sold.
According to the question, we get
x × 8 = 6400 × 5
⇒ x = \(\frac { 6400\times 5 }{ 8 }\) = 800 × 5 = 4,000 bags.
Therefore, 4,000 bags of white cement must be sold to have neither profit nor loss.

Question 9.
Replace the blank with an integer to make it a true statement.

1. (a) (- 3) × …….. = 27
2. (b) 5 × …….. = -35
3. (c) …….. × (- 8) = – 56
4. (d) …….. × (- 12) = 132.

Solution:

1. (a) (-3) x (- 9) = 27
2. (b) 5 x (-7) = (-35)
3. (c) 7 x (-8) = (-56)
4. (d) (-11) x (-12) = 132

We hope the NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2.

• Integers Class 7 Ex 1.1
• Integers Class 7 Ex 1.3
• Integers Class 7 Ex 1.4
• Integers Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2

Question 1.
Write down a pair of integers whose:

(a) the sum is -7
(b) the difference is -10
(c) the sum is 0.

Solution:

(a) (-15) and 8
(b) 15 and 25.
(c) (-49) and 49

Question 2.

(a) Write a pair of negative integers whose difference gives 8.
(b) Write a negative integer and a positive integer whose sum is -5.
(c) Write a negative integer and a positive integer whose difference is -3.

Solution:

(a) (-10) and (-18)
(b) (-10) and 5
(c) (-1) and 2

Question 3.
In a quiz, team A scored – 40, 10,0 and team B scored 10, 0, – 40 in three successive rounds. Which team scored more? Can we say that we can add integers in any order?
Solution:
Total scores of team A = (- 40) + 10 + 0 = – 40 + 10 + 0 = – 30
and, total scores of team B = 10 + 0 + (- 40) = 10 + 0 – 40 = – 30
Since the total scores of each team are equal.
∴ No team scored more than the other but each has an equal score.
Yes, integers can be added in any order and the result remains unaltered.
For example, 10 + 0 + (-40) = -30 = -40 + 0 + 10

Question 4.
Fill in the blanks to make the following statements true:

1. (-5) + (-8) = (+8) + (……)
2. -53 + …… = -53.
3. 17 + …… = 0
4. [13 + (-12)] + (…… ) = 13 + [(-12) + (- 7)]
5. (- 4) + [15 + (- 3)] = [(-4) + 15] + …….

Solution:

1. (-5) + (-8) = (-8) + (- 5)
2. -53 + 0 = -53
3. 17 + (- 17) = 0
4. [13 + (- 12)] + (- 7) = 13 + [(- 12) + (-7)]
5. (- 4) + [15 + (- 3)] = [(- 4) + 15] + (- 3).

We hope the NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2, drop a comment below and we will get back to you at the earliest.