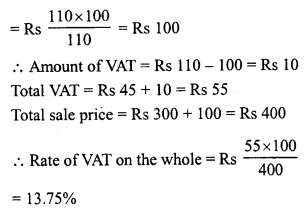Maths RD Sharma Solutions Class 8

RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III (Special Types of Quadrilaterals) Ex 17.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3

Question 1.
Which of the following statements are true for a rectangle ?
(i) It has two pairs of equal sides.
(ii) It has all its sides of equal length.
(iii) Its diagonals are equal.
(iv) Its diagonals bisect each other.
(v) Its diagonals are perpendicular.
(vi) Its diagonals are perpendicular and bisect each other.
(vii) Its diagonals are equal and bisect each other.
(viii) Its diagonals are equal and perpendicular, and bisect each other.
(ix) All rectangles are squares.
(x) All rhombuses are parallelograms.
(xi) All squares are rhombuses and also rectangles.
(xii) All squares are not parallelograms.
Solution:
(i) True.
(ii) False. (Only pair of opposite sides is equal)
(iii) True
(iv) True
(v) False (Diagonals are not perpendicular)
(vi) False (Diagonals are not perpendicular to each other)
(vii) True
(viii) False (Diagonals are equal but not perpendicular)
(ix) False (All rectangles are not square but a special type can be a square)
(x) True
(xi) True
(xii) False (All squares are parallelograms because their opposite sides are parallel and equal)

Question 2.
Which of the following statements are true for a square ?
(i) It is a rectangle.
(ii) It has all its sides of equal length.
(iii) Its diagonals bisect each other at right angle.
(iv) Its diagonals are equal to its sides.
Solution:
(i) True
(ii) True
(iii) True
(iv) False (Each diagonal of a square is greater than its side)

Question 3.
Fill in the blanks in each of the following so as to make the statement true :
(i) A rectangle is a parallelogram in which ……..
(ii) A square is a rhombus in which ……….
(iii) A square is a rectangle in which ………
Solution:
(i) A rectangle is a parallelogram in which one angle is right angle.
(ii) A square is a rhombus in which one angle is right angle.
(iii) A square is a rectangle in which adjacent sides are equal.

Question 4.
A window frame has one diagonal longer than the other. Is the window frame a rectangle ? Why or why not ?
Solution:
No, it is not a rectangle as rectangle has diagonals of equal length.

Question 5.
In a rectangle ABCD, prove that ∆ACB = ∆CAD.
Solution:
In rectangle ABCD, AC is its diagonal.

Now in ∆ACB and ∆CAD
AB = CD (Opposite sides of a rectangle)
BC = AD
AC = AC (Common)
∆ACB = ∆CAD (SSS condition)

Question 6.
The sides of a rectangle are in the ratio 2 : 3 and its perimeter is 20 cm. Draw the rectangle.
Solution:
Perimeter of a rectangle = 20 cm
Ratio in the sides = 2 : 3

Let breadth (l) = 2x
Then length (b) = 3x
Perimeter = 2 (l + b)
⇒ 20 = 2 (2x + 3x)
⇒ 4x + 6x = 20
⇒ 10x = 20
⇒ x = \(\frac { 20 }{ 10 }\) = 2
Length = 3x = 3 x 2 = 6
and breadth = 2x = 2 x 2 = 4 cm
Steps of construction:
(i) Draw a line segment AB = 6 cm.
(ii) At A and B draw perpendicular AX and BY.
(iii) Cut off from AX and BY,
AD = BC = 4 cm.
(iv) Join CD.
Then ABCD is the required rectangle.

Question 7.
The sides of a rectangle are the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
Solution:
Perimeter of a rectangle = 90 cm.

Ratio in sides = 4 : 5
Let first side = 4x
Then second side = 5x
Perimeter = 2 (l + b)
⇒ 2 (4x + 5x) = 90
⇒ 2 x 9x = 90
⇒ 18x = 90
⇒ x = 5
First side = 4x = 4 x 5 = 20 cm
and second side = 5x = 5 x 5 = 25 cm

Question 8.
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
Solution:
In rectangle ABCD, AB = 12 cm and AD = 5 cm

BD is its diagonal.
Now, in right angled ∆ABD,
BD² = AB² + AD² (Pythagoras theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
BD = 13 cm
Length of diagonal = 13 cm

Question 9.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8 cm

(ii) At B, draw a perpendicular BX
(iii) With centre A and radius 10 cm, draw an arc which intersects BX at C.
(iv) With centre C and radius equal to AB and with centre A and radius equal to BC, draw arcs which intersect at D.
(v) Join AD, AC, CD and BD.
Then ABCD is the required rectangle.

Question 10.
Draw a square whose each side measures 4.8 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4.8 cm.

(ii) At A and B, draw perpendiculars AX and BY.
(iii) Cut off AD = BC = 4.8 cm
(iv) Join CD.
Then ABCD is the required square.

Question 11.
Identify all the quadrilaterals that have:
(i) Four sides of equal length.
(ii) Four right angles.
Solution:
(i) A quadrilateral whose four sides are equal can be a square or a rhombus.
(ii) A quadrilateral whose four angle are right angle each can be a square or a rectangle.

Question 12.
Explain how a square is
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle ?
Solution:
(i) A square is a quadrilateral as it has four sides and four angles.
(ii) A square is a parallelogram, because its opposite sides are parallel and equal.
(iii) A square is a rhombus because it has all sides equal and opposite sides are parallel.
(iv) A square is a rectangle as its opposite sides are equal and each angle is of 90°.

Question 13.
Name the quadrilaterals whose diagonals:
(i) bisect each other
(ii) are perpendicular bisector of each other
(iii) are equal.
Solution:
(i) A quadrilateral whose diagonals bisect each other can be a square, rectangle, rhombus or a parallelogram.
(ii) A quadrilateral whose diagonals are perpendicular bisector of each other can be a square or a rhombus.
(iii) A quadrilateral whose diagonals are equal can be a square or a rectangle.

Question 14.
ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.
Solution:
In ∆ABC, ∠B = 90°.
O is the mid-point of AC i.e. OA = OC.

BO is joined.
Now, we have to prove that OA = OB = OC
Produce BO to D such that OD = OB.
Join DC and DA.
In ∆AOB and ∆COD
OA = OC (O is the mid point of AC)
OB = OD (Construction)
∠AOB = ∠COD (Vertically opposite angles)
∆AOB = ∆COD (SAS condition)
AB = CD (c.p.c.t.) …..(i)
Similarly, we can prove that
∆BOC = ∆AOD
BC = AD …….(ii)
From (i) and (ii)
ABCD is a rectangle.
But diagonals of a rectangle bisect each other and are equal in length.
AC and BD bisect each other at O.
OA = OC = OB.
O is equidistant from A, B and C.

Question 15.
A mason has made a concrete slap. He needs it to be rectangular. In what different ways can he make sure that it is a rectangular ?
Solution:
By definition, a rectangle has each angle of 90° and their diagonals are equal.
The mason will check the slab whether it is a rectangular in shape by measuring that
(i) its each angle is 90°
(ii) its both diagonals are equal.

Hope given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III (Special Types of Quadrilaterals) Ex 17.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3

Question 1.
Which of the following statements are true for a rhombus ?
(i) It has two pairs of parallel sides.
(ii) It has two pairs of equal sides.
(iii) It has only two pairs of equal sides.
(iv) Two of its angles are at right angles.
(v) Its diagonals bisect each other at right angles.
(vi) Its diagonals are equal and perpendicular.
(vii) it has all its sides of equal lengths.
(viii) It is a parallelogram.
(ix) It is a quadrilateral.
(x) It can be a square.
(xi) It is a square.
Solution:
(i) True
(ii) True
(iii) False (Its all sides are equal)
(iv) False (Opposite angles are equal)
(v) True
(vi) False (Diagonals are not equal)
(vii) True
(viii) True
(ix) True
(x) True (It is a rhombus)
(xi) False

Question 2.
Fill in the blanks, in each of the following, so as to make the statement true:
(i) A rhombus is a parallelogram in which ………..
(ii) A square is a rhombus in which ………..
(iii) A rhombus has all its sides of …….. length.
(iv) The diagonals of a rhombus each ………. other at ………. angles.
(v) If the diagonals of a parallelogram bisect each other at right angles, then it is a ………..
Solution:
(i) A rhombus is a parallelogram in which adjacent sides are equal.
(ii) A square is a rhombus in which one angle is right angle.
(iii) A rhombus has all its sides of equal length.
(iv) The diagonals of a rhombus bisect each other at right angles.
(v) If the diagonals of a parallelogram bisect each other at right angles, then it is a rhombus.

Question 3.
The diagonals of a parallelogram are not perpendicular. Is it a rhombus ? Why or why not ?
Solution:
By definition of a rhombus, its diagonals bisect each other at right angle.
So, the given parallelogram is not a rhombus.

Question 4.
The diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus. If your answer is ‘No’, draw a figure to justify your answer.
Solution:
The diagonals of a quadrilateral are perpendicular to each.

It is not always possible to be a rhombus. It can be of the diagonals bisect each other at right angles and if not, then it is not rhombus as shown in the figure given above:

Question 5.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
Solution:
In rhombus ABCD, diagonals AC and BD intersect each other at O.

∠ACB = 40°, we have to find ∠ADB.
BD || AD and AC.is its transversal..
∠ACB = ∠CAD (Alternate angles)
Now in ∆AOD
∠OAD + ∠AOD + ∠ADO = 180° (Sum of angles of a triangle)
⇒ 40° + 90° + ∠ADO = 180°
⇒ 130° + ∠ADO = 180°
⇒ ∠ADO = 180° – 130° = 50°
∠ADB = 50°

Question 6.
If the diagonals of a rhombus are 12 cm and 16 cm, find the length of each side.
Solution:
In rhombus ABCD, diagonals AC and BD bisect each other at O at right angles.

AC = 16 cm, BD = 12 cm
AO = OC = \(\frac { 16 }{ 2 }\) = 8 cm
BO = OD = \(\frac { 12 }{ 2 }\) = 6 cm.
Now, in right angled ∆AOB,
AB² = AO² + BO² = (8)² + (6)² = 64 + 36 = 100 = (10)²
AB = 10 cm
Each side of rhombus = 10 cm

Question 7.
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
Solution:
(i) Draw a line segment AC =10 cm.

(ii) Draw its perpendicular bisector and cut off OB = OD = 3 cm (\(\frac { 1 }{ 2 }\) of 6 cm).
(iii) Join AB, BC, CD and DA.
Then ABCD is the required rhombus.

Question 8.
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
Solution:
Steps of construction
(i) Draw a line segment AB = 3.5 cm.

(ii) Draw a ray BX making an angle of 40° at B and cut off BC = 3.5 cm.
(iii) With centres C and A, and radius 3.5 cm. Draw arcs intersecting each other at D.
(iv) Join AD and CD.
Then ABCD is a required rhombus.

Question 9.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
Solution:
(i) Draw a line segment AB = 4 cm.
(ii) At B, draw a perpendicular BX and cut off BL = 3.2 cm.

(iii) At L, draw a line LY parallel to AB.
(iv) With centres B and radius 4 cm, draw an arc intersecting the line LY at C.
(v) With centre C cut off CD = 4 cm.
(vi) Join BC and AD.
Then ABCD is the required rhombus.

Question 10.
Draw a rhombus ABCD if AB = 6 cm and AC = 5 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 6 cm.
(ii) With centre A and radius 5 cm and with centre B and radius 6 cm, draw arcs intersecting each other at C.

(iii) Join AC and BC.
(iv) Again with centres C and A and radius 6 cm, draw arcs intersecting each other at D.
(v) Join AD and CD.
Then ABCD is the required rhombus.

Question 11.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC = ∆DOC ? State the congruence condition used ?
(ii) Also state, if ∠BCO = ∠DCO.
Solution:
In rhombus ABCD, diagonals AC and BD bisect each other at O.

(i) Now in ∆BOC and ∆DOC
OC = OC (Common)
BC = CD (Sides of rhombus)
OB = OC (Diagonals bisect each other at O)
∆BOC = ∆DOC (SSS. condition)
(ii) ∠BCO = ∠DCO

Question 12.
Show that each diagonal of a rhombus bisects the angle through which it passes:
Solution:
In rhombus ABCD, AC is its diagonal we have to prove that AC bisects ∠A and ∠C.

Now, in ∆ABC and ∆ADC
AC = AC (Common)
AB = CD (Sides of a rhombus)
BC = AD
∆ABC = ∆ADC (SSS condition)
∠BAC = ∠DAC and ∠BCA = ∠DCA (c.p.c.t.)
Hence AC bisects the angle A.
Similarly, by joining BD, we can prove that BD bisects ∠B and ∠D.
Hence each diagonal of a rhombus bisects the angle through which it passes.

Question 13.
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
Solution:
In rhombus ABCD,

AB = 10 cm, diagonal BD = 16 cm.
Draw diagonal AC which bisects BD at O at right angle.
BO = OD = 8 cm and AO = OC.
Now in ∆AOB,
AB² = AO² + BO²
⇒ (10)² = AO² + (8)²
⇒ 100 = AO² – 64
⇒ AO² = 100 – 64 = 36 = (6)²
AO = 6.
AC = 2AO = 2 x 6 = 12 cm

Question 14.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral ?
Solution:
In a quadrilateral ABCD, diagonals AC and BD bisect each other at right angles.
AC = 8 cm and BD = 6 cm.

AO = OC = 4 cm and BO = OD = 3 cm
Now, in right ∆AOB,
AB² = AO² + BO² = (4)² + (3)² = 16 + 9 = 25 = (5)²
AB = 5 cm
Hence each side of quadrilateral will be 5 cm.

Hope given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III (Special Types of Quadrilaterals) Ex 17.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3

Question 1.
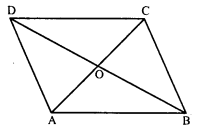
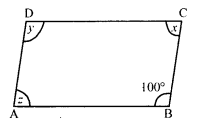
Given below is a parallelogram ABCD. Complete each statement along with the definition or property used:
(i) AD = ………
(ii) ∠DCB = ……….
(iii) OC’ = …….
(iv) ∠DAB + ∠CDA = …….

Solution:
(i) AD = BC
(ii) ∠DCB = ∠ADC

(iii) OC = OA
(iv) ∠DAB + ∠CDA = 180°

Question 2.
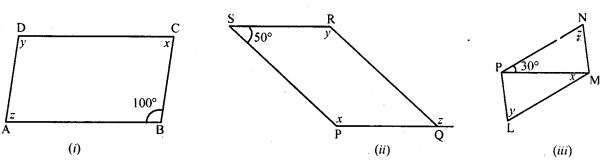
The following figures are parallelograms. Find the degree values of the unknowns x,y, z.


Solution:
In a parallelogram, opposite angles are equal and sum of adjacent angle is 180°.
(i) In parallelogram ABCD,
∠B = 100°
∠A = ∠C = 180° (Co-interior angles)

⇒ x + 100° = 180°
⇒ x = 180° – 100°
⇒ x = 80°
But ∠A = ∠C and ∠B = ∠D (Opposite angles)
A = x
⇒ z = x
⇒ z = 80°
and ∠D = ∠B
⇒ y = 100°
x = 80°, y = 100° and z = 80°
(ii) In parallelogram PQRS, side PQ is produced to T.

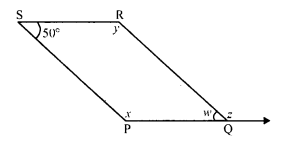
∠S = 50°
∠PQR = ∠S (Opposite angles)
w = 50°
But ∠P + ∠PQR = 180° (Sum of adjacent angles)
⇒ x + 50° = 180°
⇒ x = 180° – 50° = 130°
⇒ But ∠P = ∠R (Opposite angles)
x = y
⇒ y = 130°
But w + z = 180° (A linear pair)
⇒ 50° + z = 180°
⇒ z = 180° – 50° = 130°
⇒ x = 130°, y = 130°, ∠ = 130
(iii) In parallelogram LMNP, PM is its diagonal ∠NPM = 30°, ∠PMN = 90°

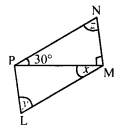
PN || LM (Opposite sides of a parallelogram) and PM is its transversal
∠NPM = ∠PML
⇒ 30° = x
x = 30°
In ∆PMN,
∠P = 30°, ∠M = 90°
But ∠P + ∠M + ∠N = 180° (Sum of angles of a triangle)
⇒ 30° + 90° + z = 180°
⇒ 120° + z = 180°
⇒ z = 180° – 120° = 60°
But ∠L = ∠N (Opposite angles of a parallelogram)
y = z
⇒ y = 60°
Hence x = 30°, y = 60° and ∠ = 60°
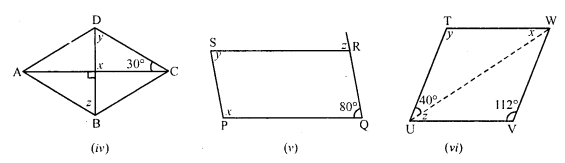
(iv) In rhombus ABCD, diagonals AC and BD bisect each other at right angles.

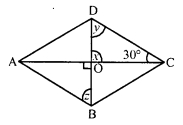
x = 90°
In ∆OCD,
∠O + ∠C + ∠D = 180°
⇒ 90° + 30° + y = 180°
⇒ 120° + y = 180°
⇒ y = 180° – 120° = 60°
y = 60°
CD || AB, BD is the transversal
y = z (Alternate angles)
z = 60°
Hence x = 90°, y = 60° and z = 60°
(v) In parallelogram PQRS, side QR is produced to T

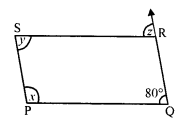
∠Q = 80°
∠P + ∠Q = 180° (Sum of adjacent angles)
⇒ x + 80° = 180°
⇒ x = 180° – 80° = 100°
∠Q = ∠S (Opposite angles of a parallelogram)
⇒ 80° = y
⇒ y = 80°
PQ || SR and QRT is transversal
∠TRS = ∠RQP (Corresponding angles)
⇒ ∠ = 80°
Hence x = 100°, y = 80° and z = 80°
(vi) In parallelogram TUVW, UW is its diagonal

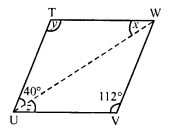
∠TUW = 40° and ∠V = 112°
∠T = ∠V (Opposite angles)
y = 112°
In ∆TUW,
∠T + ∠V + ∠W = 180° (Sum of angles of a parallelogram)
⇒ y + 40° + x = 180°
⇒ 112° + 40° + x = 180°
⇒ 152° + x = 180°
⇒ x = 180° – 152° = 28°
UV || TW and UW is its transversal
∠WUV = ∠TWU (Alternate angles)
⇒ z = x
⇒ z = 28°
Hence x = 28°, y = 112°, z = 28°

Question 3.
Can the following figures be parallelograms. Justify your answer.

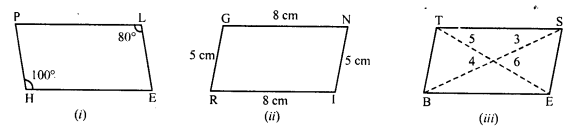
Solution:
(i) In quadrilateral PLEH
∠H = 100°, ∠L = 80°
But there are opposite angles
∠H ≠ ∠L
PLEH is not a parallelogram.
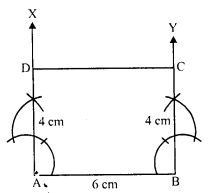
(ii) In quadrilateral GNIR,
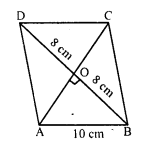
RI = 8 cm, GN = 8 cm, RG = 5 cm and IN = 5 cm
PI = GH and RG = IN
But there are opposite sides of the quadrilateral.
GNIR is a parallelogram.
(iii) In quadrilateral BEST,
BS and ET are its diagonals
But these diagonal do not bisect each other.
BEST is not a parallelogram

Question 4.
In the adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the geometrical truths you use to find them.

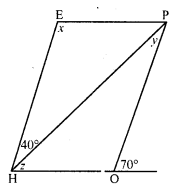
Solution:
In the figure, HOPE is a parallelogram in which HG is produced and HP is the diagonal

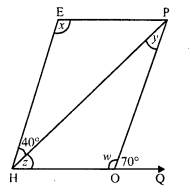
∠EHP = 40° and ∠POQ = 70°
But ∠POQ + ∠POH = 180° (Linear pair)
⇒ 70° + w = 180°
⇒ w = 180° – 70° = 110°
But ∠E = ∠POE (Opposite angles of a parallelogram)
x = 110°
HE || OP and HP is its transversal.
∠EHP = ∠HPO (Alternate angles)
⇒40° = y
⇒ y = 40°
In ∆PHO,
Ext. ∠POQ = ∠PHO + ∠HPO
⇒ 70° = z + y
⇒ 70° = z + 40°
⇒ z = 70° – 40° = 30°
Hence x = 110°, y = 40°, z = 30°

Question 5.
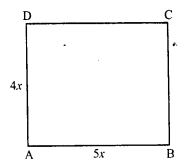
In the following figures GUNS and RUNS are parallelograms. Find x and y.

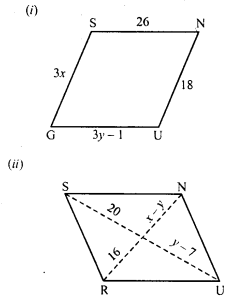
Solution:
(i) In parallelogram GUNS,
Opposite sides are parallel and equal
3x = 18
⇒ x = 6
and 3y – 1 = 26
⇒ 3y = 26 + 1 = 27
⇒ y = 9
x = 6, y = 9
(ii) Diagonals of a parallelogram bisect each other.
y – 7 = 20
⇒ y = 20 + 7 = 27
and x – 27 = 16
⇒ x – 27 = 16
⇒ x = 16 + 27 = 43
x = 43, y = 27

Question 6.
In the following figure RISK and CLUE are parallelograms. Find the measure of x.

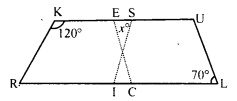
Solution:
In the figure, RISK and CLUE are parallelograms
∠K = 120° and ∠L = 70°
In parallelogram RISK

RK || IS
∠RKS = ∠ISU (Corresponding angles)
⇒ ∠ISU = 120°
In parallelogram CLUE,
∠E = ∠L (Opposite angles of a parallelogram)
∠E = 70° (∠L = 70°)
Now in ∆EOS,
Ext. ∠ISU = x + ∠E
⇒ 120° = x + 70°
⇒ x = 120° – 70° = 50°
x = 50°

Question 7.
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram.
Solution:
In parallelogram ABCD,

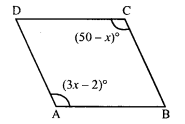
∠A = (3x – 2)° and ∠C = (50 – x)°
∠A = ∠C (Opposite angles of a parallelogram)
⇒ 3x – 2° = 50° – x
⇒ 3x + x = 50° + 2°
⇒ 4x = 52°
x = 13°

Question 8.
If an angle of a parallelogram is two- third of its adjacent angle, find the angles of the parallelogram.
Solution:
Let the parallelogram is ABCD and ∠A of a parallelogram ABCD be x

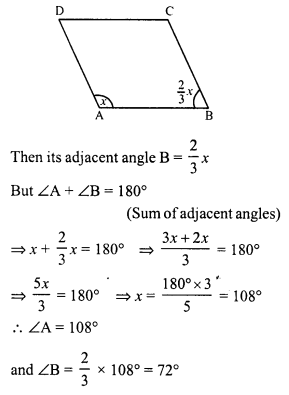
Hence other angles will be
∠C = ∠A = 108° (Opposite angles)
and ∠D = ∠B = 72° (Opposite angles)
Hence ∠A = 108°, ∠B = 72°, ∠C = 108° and ∠D = 72°

Question 9.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles ?
Solution:
Let in parallelogram ABCD,

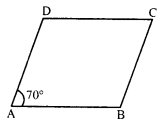
∠A = 70°
But ∠A + ∠B= 180° (Sum of adjacent angles)
⇒ 70° + ∠B = 180°
⇒ ∠B = 180° – 70°
⇒ ∠B = 110°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 70° and ∠D = 110°
Hence ∠B = 110°, ∠C = 70° and ∠D = 110°

Question 10.
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
Solution:
Let in parallelogram ABCD,

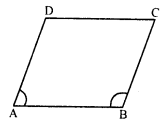
∠A : ∠B = 1 : 2
Let ∠A = x, then ∠B = 2x
But ∠A + ∠B = 180° (Sum of adjacent angles)
⇒ x + 2x = 180°
⇒ 3x = 180°
∠A = x = 60°
and ∠B = 2x = 2 x 60°= 120°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 60° and ∠D = 120°
Hence ∠A = 60°, ∠B = 120°, ∠C = 60° and ∠D = 120°

Question 11.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
Solution:
In parallelogram ABCD,

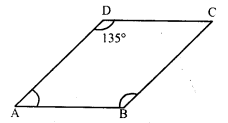
∠D = 135°
But ∠A + ∠D= 180° (Sum of adjacent angles)
∠A + 135° = 180°
∠A = 180° – 135° = 45°
But ∠B = ∠D (Opposite angles)
∠B = 135°
Hence ∠A = 45° and ∠B = 135°

Question 12.
ABCD is a parallelogram in which ∠A = 70°, compute ∠B, ∠C and ∠D.
Solution:
In parallelogram ABCD,

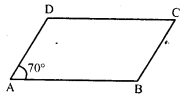
∠A = 70°
But ∠A + ∠B = 180° (Sum of adjacent angles)
⇒ 70° + ∠B = 180°
⇒ ∠B = 180° – 70° = 110°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 70° and ∠D = 110°
Hence ∠B = 110°, ∠C = 70° and ∠D = 110°

Question 13.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
Solution:
Let in parallelogram

∠A + ∠C = 130°
But ∠A = ∠C (Opposite angles)
⇒ ∠C = \(\frac { 130 }{ 2 }\) = 65°
∠B + ∠D = 180° (Sum of adjacent angles)
⇒ 65° + ∠B = 180°
⇒ ∠B = 180° – 65° = 115°
⇒ ∠B = 115°
But ∠D = ∠B (Opposite angles)
∠D = 115°
Hence ∠A = 65°, ∠B = 115°, ∠C = 65° and ∠D = 115°

Question 14.
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram ? What special type of parallelogram is it ?
Solution:
All the angles of a quadrilateral are equal and sum of the four angles = 360°
Each angle will be = \(\frac { 360 }{ 4 }\) = 90°
Let in quadrilateral ABCD,
∠A = ∠B = ∠C = ∠D = 90°
It is a parallelogram as opposite angles are equal
i.e., ∠A = ∠C and ∠B = ∠D.
Each angle is of 90°
This parallelogram is a rectangle.

Question 15.
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
Solution:
Length of two adjacent sides = 4 cm and 3 cm
i.e., l = 4 cm and b = 3 cm
Perimeter = 2 (l + b) = 2 (4 + 3) cm = 2 x 7 = 14 cm

Question 16.
The perimeter of a parallelogram is 150 cm. One of its sides is greater ii.au the other by 25 cm. Find the length of the sides of the parallelogram.
Solution:
Perimeter of a parallelogram = 150 cm
Let l he the longer side and b be the shorter side
l = b + 25 cm.
⇒ 2 (l + b) = 150
⇒ l + b = 75
⇒ b + 25 + b = 75
⇒ 2b = 75 – 25 = 50
⇒ b = 25
l = b + 25 = 25 + 25 = 50
Sides are 50 cm, 25 cm

Question 17.
The shorter side of a parallelogram is 4.8 cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
Solution:
In a parallelogram shorter side (b) = 4.8 cm.
longer side (l) = 4.8 + \(\frac { 1 }{ 2 }\) x 4.8
= 4.8 + 2.4 = 7.2 cm
Perimeter = 2 (l + b) = 2 (7.2 + 4.8) cm = 2 x 12.0 = 24 cm

Question 18.
Two adjacent angles of a parallelogram are (3x – 4)° and (3x + 10)°. Find the angles of the parallelogram.
Solution:
Let in parallelogram ABCD,

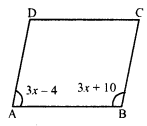
∠A = (3x + 4)° and ∠B = (3x + 10)°
But ∠A + ∠B = 180° (Sum of adj adjacent angles)
⇒ 3x – 4 + 3x + 10 = 180°
⇒ 6x + 6° = 180°
⇒ 6x = 180° – 6° = 174°
⇒ x = 29°
∠A = 3x – 4 = 3 x 29 – 4 = 87° – 4° = 83°
∠B = 3x + 10 = 3 x 29° + 10° = 87° + 10° = 97°
But ∠C = ∠A and ∠D = ∠B (Opposite angles)
∠C = 83° and ∠D = 97°
Hence ∠A = 83°, ∠B = 97°, ∠C = 83° and ∠D = 97°

Question 19.
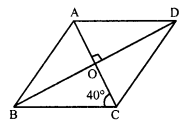
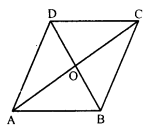
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°.
Find : ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
Solution:
In parallelogram ABCD, diagonal AC and ED bisect each other at O.

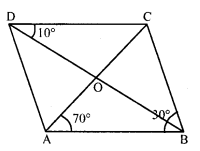
∠ABC = 30°, ∠CAB = 70° and ∠BDC = 10°
∠ADC = ∠ABC = 30° (Opposite angles)
and ∠ADB = ∠ADC – ∠BDC = 30° – 10° = 20°
AB || DC and AC is the transversal
∠ACD = ∠CAB = 70°(Altemate angles)
AB || DC and BD is transversal
∠CDB = ∠ABD = 10°(Altemate angles)
In ∆ABC
∠CAB + ∠ABC + ∠BCA = 180° (Sum of anlges of a triangle)
⇒ 70° + 30° + ∠BCA = 180°
⇒ 100° + ∠BCA = 180°
∠BCA = 180° – 100° = 80°
∠BCD = ∠BCA + ∠ACD = 80° + 70° = 150°
∠BCD = ∠DAB (Opposite angles)
⇒ ∠DAB = 150° and ∠CAD = 150° – 70° = 80°
In ∆OCD,
∠ODC + ∠OCD + ∠COD = 180° (Angles of a triangle)
⇒ ∠ACD + ∠ACD + ∠COD = 180°
⇒ 70° + 10° + ∠COD = 180°
⇒ 80° + ∠COD = 180°
⇒ ∠COD = 180° – 80° = 100°
∠COD = 100°
But ∠AOD + ∠COD = 180° (Linear pair)
⇒ ∠AOD + 100° = 180°
⇒ ∠AOD = 180° – 100° = 80°
⇒ ∠AOD = 80°
But ∠AOB = ∠COD
and ∠BOC = ∠AOD (Vertically opposite angles)
∠AOB = 100° and ∠BOC = 80°
Hence ∠DAB = 150°, ∠ADC = 30°, ∠BCD = 150°
∠AOD = 80° ∠DOC = 100°
∠BOC = 80° ∠AOB = 100°
∠ACD = 70°, ∠CAB = 70°, ∠AD = 20°, ∠ACB = 80°, ∠DBC = 20°, ∠DBA = 10

Question 20.
Find the angles marked with a question mark shown in the figure.

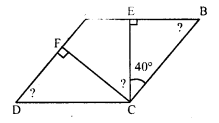
Solution:
In parallelogram ABCD,

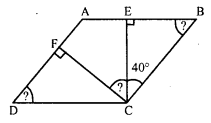
CE ⊥ AB and CF ⊥ AD
∠BCE = 40°
In ∆BCE,
∠BCE + ∠CEB + ∠EBC = 180° (Sum of angles of a triangle)
⇒ 40° + 90° + ∠EBC = 180°
⇒ 130° + ∠EBC = 180°
⇒ ∠EBC = 180° – 130° = 50°
or ∠B = 50°
But ∠D = ∠B (Opposite angles)
∠D = 50° or ∠ADC = 50°
Similarly in ∆DCF,
∠DCF + ∠CFD + ∠FDC = 180°
⇒ ∠DCF + 90° + 50° = 180°
⇒ ∠DCF + 140° = 180°
⇒ ∠DCF = 180° – 140° = 40°
But ∠C + ∠B= 180° (Sum of adjacent angles)
⇒ ∠BCE + ∠ECF + ∠DCF + ∠B = 180°
⇒ 40° + ∠ECF + 40° + 50° = 180°
⇒ ∠ECF + 130° = 180°
⇒ 40° + ∠ECF + 40° + 50° = 180°
⇒ ∠ECF + 130° = 180°
⇒ ∠ECF = 180° – 130° = 50°
∠ECF = 50°

Question 21.
The angle between the altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
Solution:
In parallelogram ABCD,

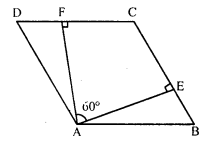
∠A is an obtused angle
AE ⊥ BC and AF ⊥ DC
∠EAF = 60°
In quadrilateral AECF,
∠EAF + ∠F + ∠C + ∠E = 360° (Sum of angles of a quadrilateral)
⇒ 60° + 90° + ∠C + 90° = 360°
⇒ 240° + ∠C = 360°
⇒ ∠C = 360° – 240° = 120°
∠C = 120°
But ∠A = ∠C (Opposite angles)
∠A = 120°
But ∠A + ∠B = 180° (Sum of adjacent angles)
⇒ 120° + ∠B = 180°
⇒ ∠B = 180° – 120° = 60°
∠B = 60°
But ∠D = ∠B (Opposite angles)
∠D = 60°
Hence ∠A = 120°, ∠B = 60°, ∠C = 120° and ∠D = 60°

Question 22.
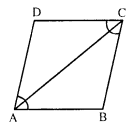
In the figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F ?

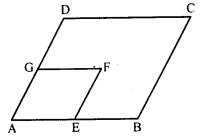
Solution:
In the parallelogram ABCD,
∠A = ∠C …..(i) (Opposite angles of a parallelogram)
Similarly in parallelogram AEFG,
∠A = ∠F …(ii)
From (i) and (ii),
∠C = ∠F = 55° (∠C = 55°)
Hence ∠F = 55°

Question 23.
In the figure, BDEF and DCEF are each a parallelogram. It is true that BD = DC ? Why or why not ?

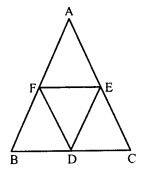
Solution:
In parallelogram BDEF,
BD = EF ……(i) (Opposite sides of a parallelogram)
Similarly, in parallelogram DCEF
DC = EF
From (i) and (ii),
BD = DC
Hence it is true that BD = DC.

Question 24.
In the figure, suppose it is known that DE = DF. Then is ∆ABC isosceles ? Why or why not ?
Solution:
In parallelogram BDEF,

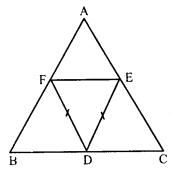
∠B = ∠E ……(i) (Opposite angles of a parallelogram)
Similarly, in parallelogram DCEF,
∠C = ∠F ……(ii)
But DE = DF (Given)
In ∆DEF
∠E = ∠F
From (i) and (ii),
∠B = ∠C
AC = AB (Sides opposite to equal angles)
∆ABC is an isosceles triangle.

Question 25.
Diagonals of parallelogram ABCD intersect at O as shown in the figure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY = ∆DOX
Now, state if XY is bisected at O.
Solution:
In parallelogram ABCD,

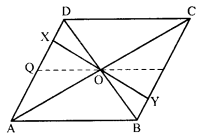
diagonals AC and BP intersect each other at O
O is the mid-point of AC and BD.
Through O, XY is draw such that X lies on AD and Y, on BC.
(i) OB = OD (O is mid-point of BD)
(ii) AD || BC and BD is transversal
∠OBY = ∠ODX (Alternate angles)
(iii) ∠BOY = ∠DOX (Vertically opposite angles)
(iv) Now in ∆BOY and ∆DOX,
OB = OD
∠OBY = ∠ODX
∠BOY = ∠DOX
∆BOY = ∆DOX (ASA axiom)
OY = OX (c.p.c.t.)
Hence XY is bisected at O.

Question 26.
In the figure ABCD is a parallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same.
(i) ∠A = ∠C
(ii) ∠FAB = \(\frac { 1 }{ 2 }\) ∠A
(iii) ∠DCE = \(\frac { 1 }{ 2 }\) ∠C
(iv) ∠CEB = ∠FAB
(v) CE || AF.
Solution:
In parallelogram ABCD,
CE is the bisector of ∠C and and AF is the bisector of ∠A.

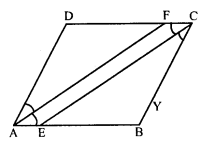
(i) ∠A = ∠C (Opposite angles of a parallelogram)
(ii) AF is the bisector of ∠A
∠FAB = \(\frac { 1 }{ 2 }\) ∠A
(iii) CE is the bisector of ∠C
∠DCE = \(\frac { 1 }{ 2 }\) ∠C
(iv) From (i), (ii) and (iii)
∠FAB = ∠DCE
(v) ∠FAB = ∠DCE
But these are opposite angles of quadrilateral AECF
AB or AE || DC or FC
AECF is a parallelogram
CE || AF
Hence proved

Question 27.
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM ? Why or why not ?
Solution:
In parallelogram ABCD, diagonals AC and BD intersect each other at O.

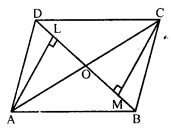
O is the mid-point of AC and BD.
AL ⊥ BD and CM ⊥ BD.
In ∆ALO and ∆CMO
∠L = ∠M (Each 90°)
∠AOL = ∠COM (Vertically opposite angles)
AO = CO (O is mid-point of AC)
∆ALO = ∆CMO (AAS axiom)
AL = CM (c.p.c.t.)
Hence proved

Question 28.
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE ?
Solution:
In parallelogram ABCD,

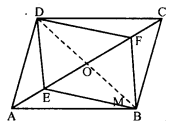
AC is its diagonal. E and F are points on AC such that AE = CF
Join EB, BF, FD and DE .
Join also diagonal BD which intersects AC at O
O is the mid-point of AC and BD
AO = OC
But AE = CF
⇒ AO – AE = CO – CF
⇒ EO = OF
But BO = OD (O is mid-point of BD)
Diagonals EF and BD of quadrilateral bisect each other at O.
BFDE is a parallelogram.

Question 29.
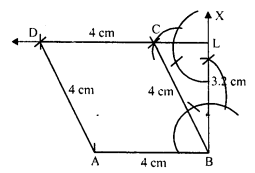
In a parallelogram ABCD, AB = 10 cm, AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
Solution:
AB || DC

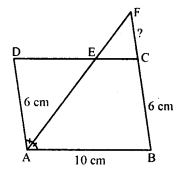
∠DEA = ∠EAB (Alternate angles)
= ∠DAE (EA is bisector of ∠A)
In ∆DAE,
∠DEA = ∠DAE
AD = DE = 6 cm
But DE = AB = 10 cm.
EC = DC – DE = 10 – 6 = 4 cm
AD || BC or BF and AF is transversal
∠DAE = ∠EFC (Alternate angle)
But ∠DAE = ∠DEA Prove
= ∠FEC (DEA = FEC vertically opposite angles)
In ∆ECF,
CE = CF = 4 cm (CE = 4 cm)

Hope given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Question 1.
Identify the terms, their co-efficients for each of the following expressions.
(i) 7x²yz – 5xy
(ii) x² + x + 1
(iii)3x²y² – 5x²y² + z² + z²
(iv) 9 – ab + be-ca
(v) \(\frac { a }{ 2 } +\frac { b }{ 2 }\)-ab
(vi)2x – 0.3xy + 0.5y
Solution:
(i) Co-efficient of 7x²yz = 7
co-efficient of -5xy = -5
(ii) Co-efficient of x¹ = 1
co-efficient of x = 1
co-efficient of 1 = 1
(iii) Co-efficient of 3x²_y² = 3
co-efficient of -5x²y²z² = -5
co-efficient of z² – 1
(iv) Co-efficient of 9 = 9
co-efficient of -ab = -1
co-efficient of be = 1
co-efficient of -ca = -1
(v) Co-efficient of \(\frac { a }{ 2 } =\frac { 1 }{ 2 }\)
Co-efficient of \(\frac { b }{ 2 } =\frac { 1 }{ 2 }\)
co-efficient of -ab = -1
(vi) co-efficient of 0.2x = 0.2
co-efficient of-0.3xy = -0.3
co-efficient of 0.5y = 0.5

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any category ?
(i) x+y
(ii) 1000
(iii) x + x² + x³ + x⁴
(iv) 7 + a + 5b
(v) 2b – 3 b²    
(vi) 2y – 3y² +4y³
(vii) 5x – 4y + 3x
(viii) 4a – 15a²
(ix) xy+yz + zt + tx
(x)   pqr
(xi) p²q + pq²       
(xii)  2p + 2 q
Solution:
Monomials are (ii), (x)
Binomials are (i), (v), (viii), (xi), (xii)
Trinomials are (iv), (vi) and (vii)
None of these are (iii) and (ix)

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.1
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.2
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.3

Question 1.
The list price of a refrigerator is Rs 9700. If a value added tax of 6% is to be charged on it, how much one has to pay to buy the refrigerator ?
Solution:
List price of refrigerator = Rs 9700
Rate of VAT = 6%
Amount of VAT = Rs. \(\frac { 9700 x 6 }{ 100 }\) = Rs 582
Total price to be paid = Rs 9700 + 582 = Rs 10282

Question 2.
Vikram bought a watch for Rs 825. If this amount includes 10% VAT on the list price, what was the list price of the watch ?
Solution:
Price of watch including VAT = Rs 825
Rate of VAT = 10%

Question 3.
Aman bought a shirt for Rs 374.50 which includes 7% VAT. Find the list price of the shirt.
Solution:
Cost price of the shirt = Rs 374.50
Rate of VAT = 7%

Question 4.
Rani purchases a pair of shoes whose sale price is Rs 175. If he pays a VAT at the rate of 7%, how much amount does he pays as VAT. Find the net value of the pair of shoes.
Solution:
Sale price of a pair of shoes = Rs 175
Rate of VAT = 7%
Total VAT paid = Rs. \(\frac { 175 x 7 }{ 100 }\) = Rs 12.25
and total amount paid = Rs 175 + Rs 12.25 = Rs 187.25

Question 5.
Swarna paid Rs 20 as VAT on a pair of shoes worth Rs 250. Find the rate of VAT.
Solution:
Amount of VAT paid = Rs 20
Price of the pair of shoes = Rs 250
Rate of VAT = \(\frac { 20 x 100 }{ 250 }\) = 8%

Question 6.
Sarita buys goods worth Rs 5,500. She gets a rebate of 5% on it. After getting the rebate if VAT at the rate of 5% is charged, find the amount she will have to pay for the goods.
Solution:
Price of goods = Rs 5,500
Rate of rebate = 5%
Sales price after rebate

= Rs 5,225
Rate of VAT = 5%
Amount of VAT

Amount to be paid after paying VAT = Rs 5,225 + 261.25 = Rs 5486.25

Question 7.
The cost of furniture inclusive of VAT is Rs 7,150. If the rate of VAT is 10%, find the original cost of the furniture.
Solution:
Cost of furniture including VAT = Rs 7,150
Rate of VAT = 10%
Original cost of furniture

Question 8.
A refrigerator is available for Rs 13,750 including VAT. If the rate of VAT is 10%, find the original cost of refrigerator.
Solution:
Cost of refrigerator including VAT = Rs 13,750
Rate of VAT = 10%
Actual price of refrigerator

Question 9.
A colour TV is available for Rs 13,440 inclusive of VAT. If the original cost of TV is Rs 12,000, find the rate of VAT.
Solution:
Cost of TV including VAT = Rs 13,440
Actual cost = Rs 12,000
Amount of VAT = Rs 13,440 – Rs 12,000 = Rs 1,440

Question 10.
Reena goes to a shop to buy a radio, costing Rs 2,568. The rate of VAT is 7%. She tells the shopkeeper to reduce the price of the radio such that she has to pay Rs 2,568 inclusive of VAT. Find the reduction needed in the price of radio.
Solution:
Price of radio inclusive of VAT = Rs 2,568
Rate of VAT = 7%

But the cost of radio in the beginning = Rs 2,568
Reduction = Rs 2568 – Rs 2,400 = Rs 168

Question 11.
Rajat goes to a departmental store and buys the following articles :

Calculate the total amount he has to pay to the store.
Solution:
Price of 2 pairs of shoes @ Rs 800 = Rs800 x 2 = Rs 1,600
Rate of VAT = 5%


Total amount to be paid = Rs 1,680 + Rs 1,590 + Rs 1,352 = Rs 4,622

Question 12.
Ajit buys a motorcycle for Rs 17,600 including value added tax. If the rate of VAT is 10%, what is the sale price of the motorcycle ?
Solution:
Cost price of motorcycle (including VAT) = Rs 17,600
Rate of VAT = 10%
Sale price of motorcycle

Question 13.
Manoj buys a leather coat costing Rs 900 at Rs 990 after paying the VAT. Calculate the VAT charged on the cost.
Solution:
Cost price of coat = Rs 900
And sale price including VAT = Rs 990
Amount of VAT = Rs 990 – Rs 900 = Rs 90
Rate of VAT = \(\frac { 90 x 100 }{ 900 }\) = 10%

Question 14.
Rakesh goes to a departmental store and purchases the following articles:
(i) biscuits and bakery products costing Rs 50, VAT @ 5%.
(ii) medicines costing Rs 90. VAT @ 10%,
(iii) clothes costing Rs 400, VAT @ 1% and
(iv) cosmetics costing Rs 150, VAT @ 10% Calculate the total amount to be paid by Rakesh to the store.
Solution:
(i) Cost of biscuits and bakery product = Rs 50
VAT = 5%

Total amount of the bill = Rs 52.50 + Rs 99 + Rs 404 + Rs 165 = Rs 720.50

Question 15.
Rajeeta purchased a set of cosmetics. She paid Rs 165 for it including VAT. If the rate of VAT is 10%, find the sale price of the set.
Solution:
Total price of set including VAT = Rs 165
Rate of VAT = 10%

Question 16.
Sunita purchases a bicycle for Rs 660. She has paid a VAT of 10%. Find the list price of bicycle.
Solution:
Cost price of bicycle including VAT = Rs. 660
Rate of VAT = 10%

Question 17.
The sales price of a television inclusive of VAT is Rs 13,500. If VAT is charged at the rate of 8% of the list price, find the list price of the television.
Solution:
Sale price of television including VAT = Rs 13,500
Rate of VAT = 8%

Question 18.
Shikha purchased a car with a marked price of Rs 2,10,000 at a discount of 5%. If VAT is charged at the rate of 10%, find the amount Shikha had paid for purchasing the car.
Solution:
Marked price of car = Rs 2,10,000
Rate of discount = 5%

Question 19.
Sharuti bought a set of cosmetic items for Rs 345 including 15% value added tax and a purse for Rs 110 including 10% VAT. What percent is the VAT charged on the whole transactions ?
Solution:
Cost price of set = Rs 345
VAT = 15%

Question 20.
List price of a cooler is Rs 2,563. The rate of VAT is 10%. The customer requests the shopkeeper to allow a discount in the price of the cooler to such an extent that the price remains Rs 2,563 inclusive of VAT. Find the discount in the price of the cooler.
Solution:
List price of cooler = Rs. 2,563
On request the price of cooler is paid Rs 2,563 including VAT
VAT = 10%

Amount of discount = Rs 2,563 – Rs 2,330 = Rs 233

Question 21.
List price of a washing machine is Rs 9,000. If the dealer allows a discount of 5% on the cash payment, how much money will a customer pay to the dealer in cash, if the rate of VAT is 10%.
Solution:
List price of washing machine = Rs 9,000
Rate of discount = 5%
Amount after giving discount

Hope given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.