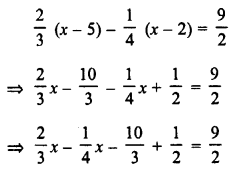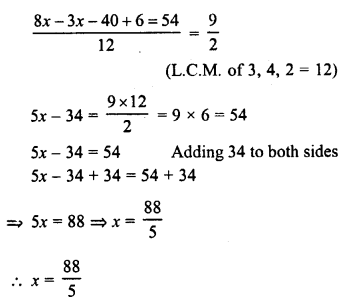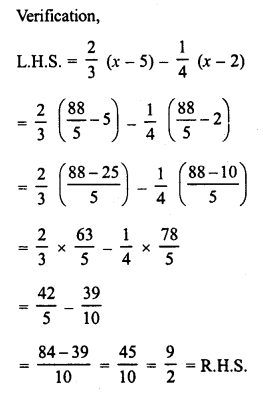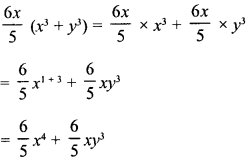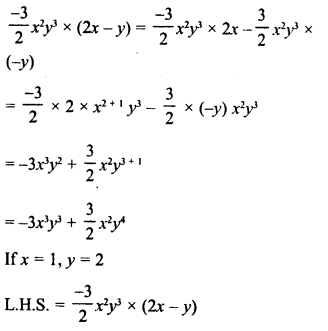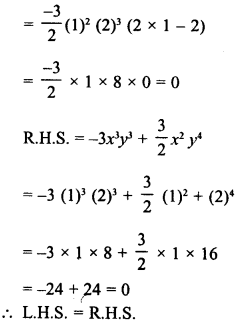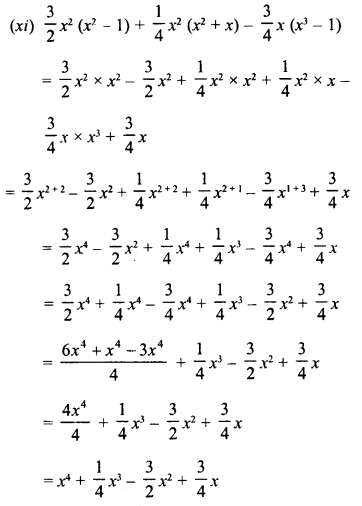Maths RD Sharma Solutions Class 8

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
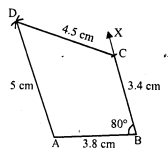
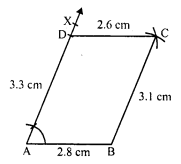
Construct a quadrilateral ABCD, in which AB = 6 cm, BC = 4 cm, CD = 4 cm, ZB = 95° and ∠C = 90°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4 cm.

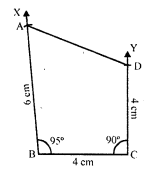
(ii) At B, draw a ray BX making an angle of 95° and cut off BA = 6 cm.
(iii) At C, draw a ray CY making an angle of 90° and cut off CD = 4 cm.
(iv) Join AD.
Then ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD, where AB = 4.2 cm, BC = 3.6 cm, CD = 4.8 cm, ∠B = 30° and ∠C = 150°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.6 cm.
(ii) At B, draw a ray BX making an angle of 30° and cut of BA = 4.2 cm.
(iii) At C, draw another ray CY making an angle of 150° and cut off CD = 4.8 cm.

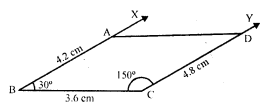
(iv) Join AD.
Then ABCD is the required quadrilateral.

Question 3.
Construct a quadrilateral PQRS, in which PQ = 3.5 cm, QR = 2.5 cm, RS = 4.1 cm, ∠Q = 75° and ∠R = 120°.
Solution:
Steps of construction :
(i) Draw a line segment QR = 2.5 cm.

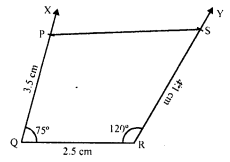
(ii) At Q, draw a ray QX making an angle of 75° and cut off QP = 3.5 cm.
(iii) At R, draw another ray RY making an angle of 120° and cut off RS = 4.1 cm.
(iv) Join PS.
Then PQRS is the required quadrilateral.

Question 4.
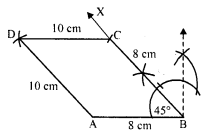
Construct a quadrilateral ABCD given BC = 6.6 cm, CD = 4.4 cm, AD = 5.6 cm and ∠D = 100° and ∠C = 95°.
Solution:
Steps of construction :
(i) Draw a line segment CD = 4.4 cm.

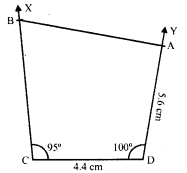
(ii) At C, draw a ray CX making an angle of 95° and cut off CB = 6.6 cm
(iii) At D, draw another ray DY making an angle of 100° and cut off DA = 5.6 cm.
(iv) Join AB.
Then ABCD is the required quadrilateral.

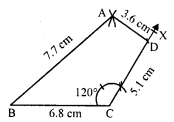
Question 5.
Construct a quadrilateral ABCD in which AD = 3.5 cm, AB = 4.4 cm, BC = 4.7 cm, ∠A = 125° and ∠B = 120°.
Solution:
Steps of construction :
(i) Draw a line segment AB 4.4 cm.

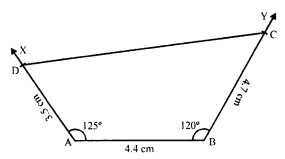
(ii) At A, draw a ray AX making an angle of 125° and cut off AD = 3.5 cm.
(iii) At B, draw another ray BY making an angle of 120° and cut off BC = 4.7 cm.
(iv) Join CD.
Then ABCD is the required quadrilateral.

Question 6.
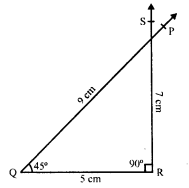
Construct a quadrilateral PQRS in which ∠Q = 45°, ∠R = 90°, QR = 5 cm, PQ = 9 cm and RS = 7 cm.
Solution:
Steps of construction :
This quadrilateral is not possible to construct as shown in the figure.

Question 7.
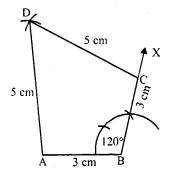
Construct a quadrilateral ABCD in which AB = BC = 3 cm, AD = 5 cm, ∠A = 90° and ∠B = 105°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 3 cm.

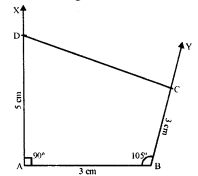
(ii) At A, draw a ray AX making an angle of 90° and cut off AD = 5 cm.
(iii) At B, draw another ray BY making an angle of 105° and cut off BC = 3 cm.
(iv) Join CD.
Then ABCD is the required quadrilateral.

Question 8.
Construct a quadrilateral BDEF where DE = 4.5 cm, EF = 3.5 cm, FB = 6.5 cm and ∠F = 50° and ∠E = 100°
Solution:
Steps of construction :
(i) Draw a line segment EF = 3.5 cm.
(ii) At E, draw a ray EX making an angle of 100° and cut off ED = 4.5 cm.
(iii) At F, draw another ray FY making an angle of 45° and cut off FB = 6.5 cm.
(iv) Join DB.

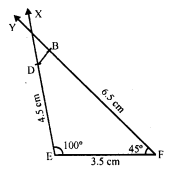
Then BDEF is the required quadrilateral.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.4 cm, CD = 4.5 cm, AD = 5 cm and ∠B = 80°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 3.8 cm.
(ii) At B, draw a ray BX making an angle of 80° and cut off BC = 3.4 cm.
(iii) With centre A and radius 5 cm and with centre C and radius 4.5 cm, draw arcs which intersect each other at D.
(iv) Join CD and AD.

ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD given that AB = 8 cm, BC = 8 cm, CD = 10 cm, AD = 10 cm and ∠A = 45°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8 cm.

(ii) At A, draw a ray AX making an angle of 45° and cut off BC = 8 cm.
(iii) With centre A and C and radius 10 cm, draw arcs intersecting each other at D.
(iv) Join AD, CD.
Then ABCD is the required quadrilateral.

Question 3.
Construct a quadrilateral ABCD in which AB = 7.7 cm, BC = 6.8 cm, CD = 5.1 cm, AD = 3.6 cm and ∠C = 120°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6.8 cm.

(ii) At C, draw a ray CX making an angle of 120° and cut off CD = 5.1 cm.
(iii) With centre B and radius 7.7 cm and with centre D and radius 3.6 cm draw arcs which intersect each other at A.
(iv) Join AD and AB.
Then ABCD is the required quadrilateral.

Question 4.
Construct a quadrilateral ABCD in which AB = BC = 3 cm, AD = CD = 5 cm and ∠B = 120°
Solution:
Steps of construction :
(i) Draw a line segment AB = 3 cm.

(ii) At B, draw a ray BX making an angle of 120° and cut off BC = 3 cm.
(iii) With centres A and C, and radius 5 cm, draw arcs intersecting each other at D.
(iv) Join AD and CD.
Then ABCD is the required quadrilateral.

Question 5.
Construct a quadrilateral ABCD in which AB = 2.8 cm, BC = 3.1 cm, CD = 2.6 cm and DA = 3.3 cm and ∠A = 60°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 2.8 cm.

(ii) At A draw a ray AX making an angle of 60° and cut off AD = 3.3 cm.
(iii) With centre B and radius 3.1 cm and with centre D and radius 2.6 cm, draw arc which intersect each other at C.
(iv) Join CB and CD.
Then ABCD is the required quadrilateral.

Question 6.
Construct a quadrilateral ABCD in which AB = BC = 6 cm, AD = DC = 4.5 cm and ∠B = 120°.
Solution:
Steps of construction:
The construction is not possible to draw as arcs of radius 4.5 cm from A and C, do not intersect at any point.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.0 cm, AD = 2.3 cm, AC = 4.5 cm and BD = 3.8 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 3.8 cm.
(ii) With centre A and radius 2.3 cm and with centre B and radius 3.8 cm draw arcs intersecting each other at D.

(iii) Join AD and BD.
(iv) Again with centre A and radius 4.5 cm and with centre B and radius 3 cm, draw arcs intersecting each other at C.
(v) Join AC and BC and also CD.
Then ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD in which BC = 7.5 cm, AC = AD = 6 cm, CD = 5 cm and BD = 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment CD = 5 cm.

(ii) With centre C and D and radius 6 cm, draw line segments intersecting each other at A.
(iii) Join AC and AD.
(iv) Again with centre C and radius 7.5 cm and with centre D and radius 10 cm, draw arcs intersecting each other at B.
(v) Join CB, CA, DA, DB and AB.
Then ABCD is the required quadrilateral.

Question 3.
Construct a quadrilateral ABCD, when AB = 3 cm, CD = 3 cm, DA = 7.5 cm, AC = 8 cm and BD = 4 cm.
Solution:
Steps of construction :
This quadrilateral is not possible as
BD = 4 cm, AB = 3 cm and AD = 7.5 cm
The sum of any two sides of a triangle is greater than the third side.
But BD + AD = 4 + 3 = 7 cm
BD + AD < AD

Question 4.
Construct a quadrilateral ABCD given AD = 3.5 cm, BC = 2.5 cm, CD = 4.1 cm, AC = 7.3 cm and BD = 3.2 cm.
Solution:
Steps of construction :
(i) Draw a line segment CD = 4.1 cm.
(ii) With centre C and radius 7.3 cm and with centre D and radius 3.5 cm, draw arcs intersecting each other at A.

(iii) Join AC and AD.
(iv) Again with centre C and radius 2.5 cm and with centre D and radius 3.2 cm, draw arcs intersecting each other at B.
(v) Join CB’, and DB’ and join AB’.
Then ABCD is the required quadrilateral.

Question 5.
Construct a quadrilateral ABCD given AD = 5 cm, AB = 5.5 cm, BC = 2.5 cm, AC = 7.1 cm and BD = 8 cm.
Solution:
Steps of construction:
(i) Draw a line segment AB = 5 cm.

(ii) With centre A and radius 7.1 cm and with centre B and radius 2.5 cm, draw arcs which intersect each other at C.
(iii) Join AC and BC.
(iv) Again with centre A and radius 5 cm and with centre B and radius 8 cm, draw arcs which intersect each other at D.
(v) Join AD and BD and CD.
Then ABCD is the required quadrilateral.

Question 6.
Construct a quadrilateral ABCD in which BC = 4 cm, CA = 5.6 cm, AD = 4.5 cm, CD = 5 cm and BD = 6.5 cm.
Solution:
Steps of construction:
(i) Draw a line segment CD = 5 cm.

(ii) With centre C and radius 5.6 cm and with centre D and radius 4.5 cm, draw arcs which intersect each other at A.
(iii) Join AC and AD.
(iv) Again with centre C and radius 4 cm and with centre D and radius 6.5 cm, draw arcs which intersect each other at B.
(v) Join BC and BD and AB.
Then ABCD is the required quadrilateral.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1

Other Exercises

• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.2
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.3
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4

Solve each of the following equations and also verify your solution :
Question 1.
9\(\frac { 1 }{ 4 }\) = y – 1\(\frac { 1 }{ 3 }\)
Solution:

Question 2.
\(\frac { 5x }{ 3 }\) + \(\frac { 2 }{ 5 }\) = 1
Solution:

Question 3.
\(\frac { x }{ 2 }\) + \(\frac { x }{ 3 }\) + \(\frac { x }{ 4 }\) = 13
Solution:

Question 4.
\(\frac { x }{ 2 }\) + \(\frac { x }{ 8 }\) = \(\frac { 1 }{ 8 }\)
Solution:

Question 5.
\(\frac { 2x }{ 3 }\) – \(\frac { 3x }{ 8 }\) = \(\frac { 7 }{ 12 }\)
Solution:

Question 6.
(x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1) = 0
Solution:
(x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1) = 0
⇒ [x² + (2 + 3) x + 2 x 3] + [x² + (-3 – 2) x + (-3) (-2)] – 2x² – 2x = 0
⇒ x² + 5x + 6 + x² – 5x + 6 – 2x² – 2x = 0
⇒ x² + x² – 2x² + 5x – 5x – 2x + 6 + 6 = 0
⇒ -2x + 12 = 0
Subtracting 12 from both sides,
-2x + 12 – 12 = 0 – 12
⇒ -2x = -12
Dividing by -2,
x = 6
Verification:
L.H.S. = (x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1)
= (6 + 2) (6 + 3) + (6 – 3) (6 – 2) – 2 x 6 (6 + 1)
= 8 x 9 + 3 x 4 – 12 x 7
= 72 + 12 – 84
= 84 – 84
= 0
= R.H.S.

Question 7.
\(\frac { x }{ 2 }\) – \(\frac { 4 }{ 5 }\) + \(\frac { x }{ 5 }\) +\(\frac { 3x }{ 10 }\) = \(\frac { 1 }{ 5 }\)
Solution:

Question 8.
\(\frac { 7 }{ x }\) + 35 = \(\frac { 1 }{ 10 }\)
Solution:

Question 9.
\(\frac { 2x – 1 }{ 3 }\) – \(\frac { 6x – 2 }{ 5 }\) = \(\frac { 1 }{ 3 }\)
Solution:

Question 10.
13 (y – 4) – 3 (y – 9) – 5 (y + 4) = 0
Solution:
13 (y – 4) – 3 (y – 9) – 5 (y + 4) = 0
⇒ 13y – 52 – 3y + 27 – 5y – 20 = 0
⇒ 13y – 3y – 5y – 52 + 27 – 20 = 0
⇒ 13y – 8y – 72 + 27 = 0
⇒ 5y – 45 = 0
Dividing by 5,
y = 9
Verification:
L.H.S. = 13 (y – 4) – 3 (y – 9) – 5 (y + 4)
= 13 (9 – 4) – 3 (9 – 9) – 5 (9 + 4)
= 13 x 5 – 3 x 0 – 5 x 13
= 65 – 0 – 65
= 0
= R.H.S.

Question 11.
\(\frac { 2 }{ 3 }\) (x – 5) – \(\frac { 1 }{ 4 }\) (x – 2) = \(\frac { 9 }{ 2 }\)
Solution:

Hope given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Find the following products 

Question 1.
2a³ (3a + 5b)
Solution:
2a³ (3a + 5b) = 2a³ x 3a + 2a³ x 5b
= 6a^{3 +1} + 10a³b
= 6a⁴ + 10a³b

Question 2.
-11a (3a + 2b)
Solution:
-11a (3a + 2b) = -11a x 3a – 11a x 2b
= -33a²– 22ab

Question 3.
-5a (7a – 2b)
Solution:
-5a (7a – 2b) = -5a x 7a- 5a x (-2b)
= -35a² + 10ab

Question 4.
-11y² (3y + 7)
Solution:
-11y² (3y + 7) = -11y² x 3y – 11y² x 7
= -33y²⁺¹-77y²
= 33y³-77y²

Question 5.
\(\frac { 6x }{ 5 }\) (x³+y³)
Solution:

Question 6.
xy (x³-y³)
Solution:
xy (x³ – y³) =xy x x³ – xy x y³
= x^{1 + 3} x y – x x y¹⁺³
= x⁴y – xy⁴

Question 7.
0.1y (0.1x⁵ + 0.1y)
Solution:
0.1y (0.1x⁵ + 0.1y) = 0.1y x 0.1x⁵ + 0.1y x 0.1y
= 0.01x⁵y + 0.01y²

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.
5x (10x²y – 100xy²)
Solution:
5x (10x²y – 100xy²)
= 1.5x x 10x²y – 1.5x x 100xy²
= 15x^{1 + 2}y- 150x¹⁺¹ x y²
15 x³y- 150x² y²

Question 12.
4.1xy (1.1x-y)
Solution:
4.1xy (1.1x-y) = 4.1xy x 1.1x – 4.1xy x y
= 4.51x²y-4.1xy²

Question 13.

Solution:

Question 14.

Solution:

Question 15.
\(\frac { 4 }{ 3 }\) a (a² + 6² – 3c²)
Solution:

Question 16.
Find the product 24x² (1 – 2x) and evaluate its value for x = 3.
Solution:
24x² (1 – 2x) = 24x² x 1 + 24x² x (-2x)
= 24x² + (-48x²⁺¹)
= 24x² – 48x³
If x = 3, then
= 24 (3)² – 48 (3)³
= 24 x 9-48 x 27 = 216- 1296
= -1080

Question 17.
Find the product of -3y (xy +y²) and find its value for x = 4, and y = 5.
Solution:
-3y (xy + y²) = -3y x xy – 3y x y²
= -3xy² -3y^{2 +1}  = -3xy² – 3y³
If x = 4, y = 5, then
= -3 x 4 (5)² – 3 (5)³ = -12 x 25 – 3 x 125
= -300 – 375 = – 675

Question 18.
Multiply – \(\frac { 3 }{ 2 }\) x²y³ by (2x-y) and verify the answer for x = 1 and y = 2.
Solution:

Question 19.
Multiply the monomial by the binomial and find the value of each for x = -1, y = 25 and z =05 :
(i) 15y² (2 – 3x)
(ii) -3x (y² + z²)
(iii) z² (x – y)
(iv) xz (x² + y²)
Solution:

Question 20.
Simplify :
(i) 2x² (at¹ – x) – 3x (x⁴ + 2x) -2 (x⁴ – 3x²)
(ii) x³y (x² – 2x) + 2xy (x³ – x⁴)
(iii) 3a² + 2 (a + 2) – 3a (2a + 1)
(iv) x (x + 4) + 3x (2x² – 1) + 4x² + 4
(v) a (b-c) – b (c – a) – c (a – b)
(vi) a (b – c) + b (c – a) + c (a – b)
(vii) 4ab (a – b) – 6a² (b – b²) -3b² (2a² – a) + 2ab (b-a)
(viii) x² (x² + 1) – x³ (x + 1) – x (x³ – x)
(ix) 2a² + 3a (1 – 2a³) + a (a + 1)
(x) a² (2a – 1) + 3a + a³ – 8
(xi) \(\frac { 3 }{ 2 }\)-x² (x² – 1) + \(\frac { 1 }{4 }\)-x² (x² + x) – \(\frac { 3 }{ 4 }\)x (x³ – 1)
(xii) a²b (a – b²) + ab² (4ab – 2a²) – a³b (1 – 2b)
(xiii )a²b (a³ – a + 1) – ab (a⁴ – 2a² + 2a) – b (a³– a² -1)
Solution:
(i) 2x² (x³ -x) – 3x (x⁴ + 2x) -2 (x⁴ – 3x²)
= 2x² x x³-2x²x x-3x x x⁴-3x x 2x-2x⁴ + 6x²
= 2x^{2 + 3}– 2x^{2 +1} – 3x^{,1+ 4}-6x^,1+1 -2x⁴ + 6x²
= 2x⁵ – 2x³ – 3x⁵ — 6x² – 2x⁴ + 6x²
= 2x⁵ – 3x⁵ – 2a⁴ – 2x³ + 6x² – 6x²
= -x⁵ – 2x⁴ – 2x³ + 0
= -x⁵-2x⁴-2x³
(ii) x³y (x² – 2x) + 2xy (x³ – x⁴)
= x³y x x² – x³y x 2x + 2ay x ac³ – 2xy x x⁴
= x^{3 + 2}y-2x^{3 + 1} y + 2x^{1 + 3}y – 2yx⁴⁺¹
= x⁵y – 2x⁴y + 2x⁴y – 2yx⁵
= -x⁵y
(iii) 3a² + 2 (a + 2) – 3a (2a + 1)
= 3a² + 2a + 4 – 6a² – 3a
= 3a² – 6a² + 2a – 3a + 4
= -3a² – a + 4
(iv) x (x + 4) + 3x (2x² – 1) + 4x² + 4
= x² + 4x + 3x x 2x² – 3x x 1 + 4x² + 4
= x² + 4x + 6x^{2 +1} – 3x + 4x² + 4
= x² + 4x + 6x³ – 3x + 4x² + 4
= 6a³ + 4x² + x² + 4x – 3x + 4
= 6x³ + 5x² + x + 4
(v) a (b – c)-b (c – a) – c (a – b)
= ab – ac – be + ab – ac + bc
= 2ab – 2ac
(vi) a (b – c) + b (c – a) + c (a – b)
= ab – ac + bc – ab + ac – bc
= ab – ab + bc – be + ac – ac
= 0
(vii) 4ab (a – b) – 6a² (b – b²) -3b² (2a² – a) + 2ab (b – a)
= 4a²b – 4ab² – 6a²b + 6a²b² – 6a²b² + 3ab² + 2ab² – 2a²b
= 4a²b- 6a²b – 2 a²b – 4ab² + 3 ab² + 2ab² + 6a²b² – 6a²b²
= 4a²b – 8a²b – 4ab² + 5 ab² + 0
= – 4a²b + ab²
(viii) x² (x² + 1) – x³ (x + 1) – x (x³ – x)
= x^{2 + 2} + x² – x^{3 + 1} – x³ – x^{1 + 3} + x^{1 + 1}
= x⁴ + x²-x⁴-x³-x⁴ + x²
= x⁴-x⁴-x⁴-x³ + x² + x²
= -x⁴ – x³ + 2x²
(ix) 2a² + 3a (1 – 2a³) + a (a + 1)
= 2a² + 3 a – 3 a x 2a³ + a² + a
= 2a² + 3a – 6a^{1 + 3} + a² + a
= 2a² + 3a – 6a⁴ + a² + a
= -6a⁴ + 3a² + 4a
(x) a² (2a – 1) + 3a + a³ – 8
= 2 a² x a – a² x 1+3a + a³-8
= 2a³ – a² + 3a + a³ – 8
= 2a³ + a³ – a² + 3a – 8
= 3a³ – a² + 3a – 8

(xii) a²b (a – b²) + ab² (4ab – 2a²) – a³b (1 – 2b)
= a²b x a – a²b x b¹ + ab² x 4ab – ab¹ x2a² -a³b x 1 + a³b x 2b
= a²⁺¹ b-a²b^{2 +1}+ 4a^{1 +1} b^{2 +1} -2a²⁺¹ b²-a³b + 2a³b^{1 +1}
= a’b – a²b³ + 4a²b³ – 2a³b² – a³b + 2a³b²
= a³b – a³b – a²b³ + 4a²b³ – 2a³b² + 2a³b²
= 0 + 3a²b³ + 0 = 3 a²b³
(xiii) a²b (a³ – a + 1) – ab (a⁴ – 2a² + 2a) – b (a³ -a²– 1)
= a²b x _a³ – a²b x _a + a²b – ab x a² + ab x 2a² – ab x 2a- ba³ + ba² + b
= a^2+ 3b – a²⁺¹ b + a²b -a^{1 + 4}b + 2a^{1 + 2}b- 2a¹⁺¹ b- a³b + a²b + b
= a⁵b – a³b + a²6 – a⁵b + 2a³b – 2a²b – a³b + a²b + b
= a⁵b – a³b + 2a³b – a³6 – a³b + a²b – 2a²b + a²b + b
= a³b – a⁵b + 2a³b – 2a³b + 2a²b-2a²b + b
= 0 + 0 + 0 + b = b

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.