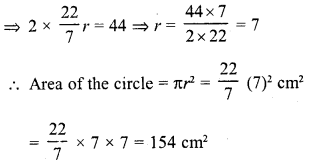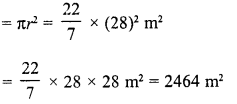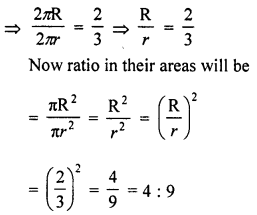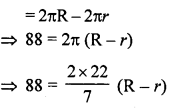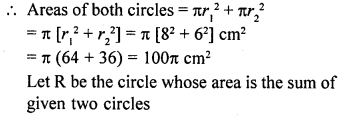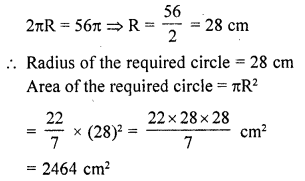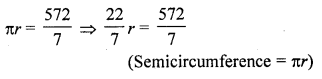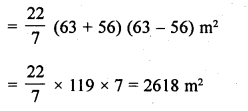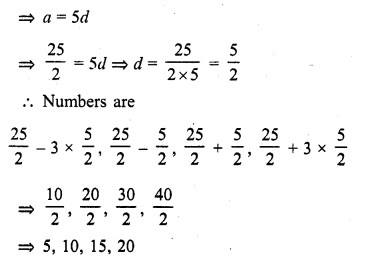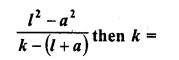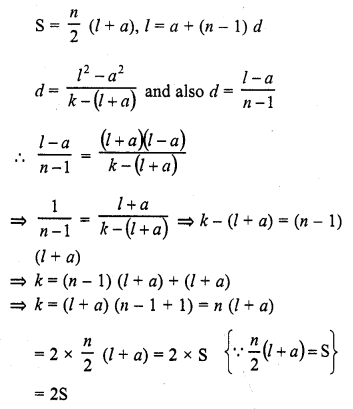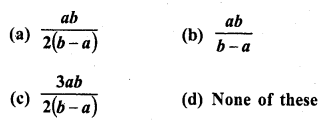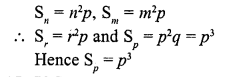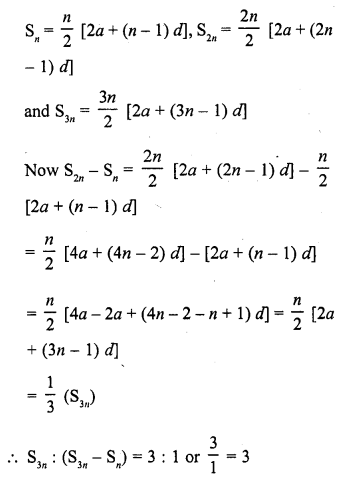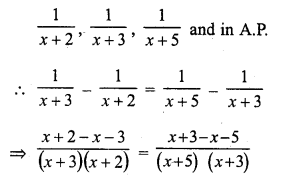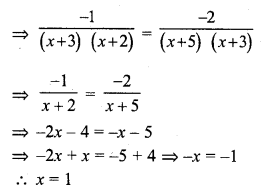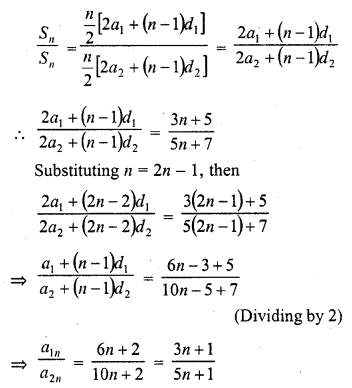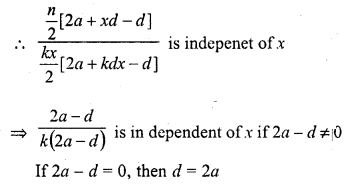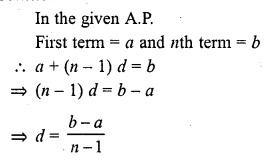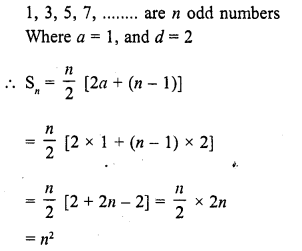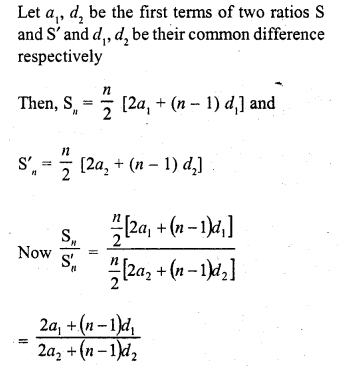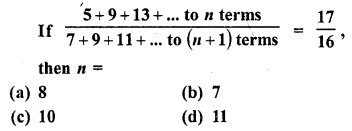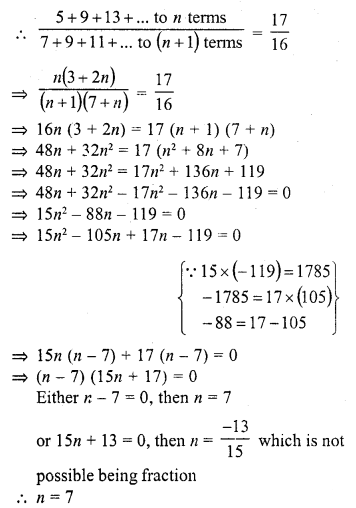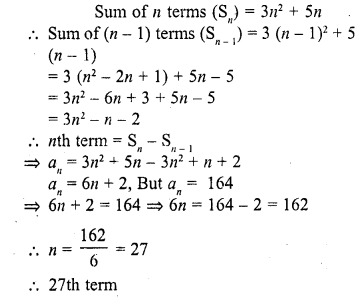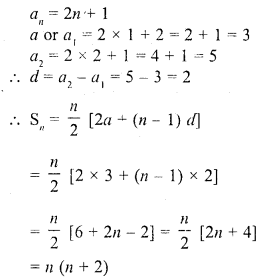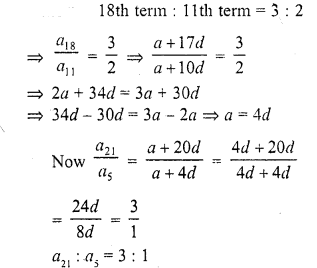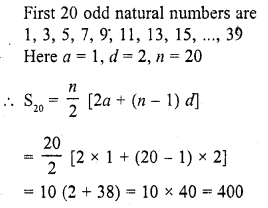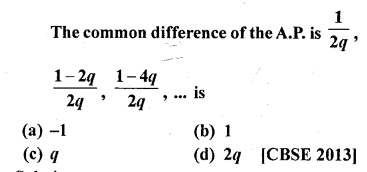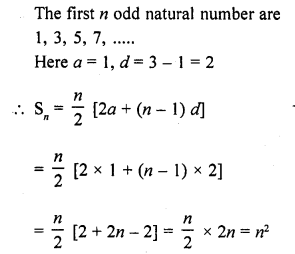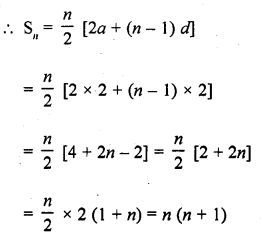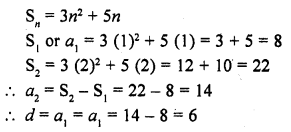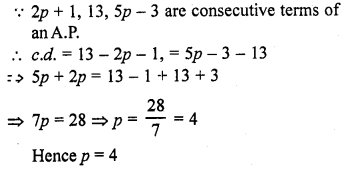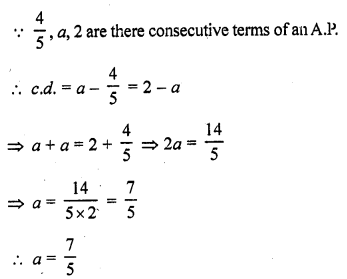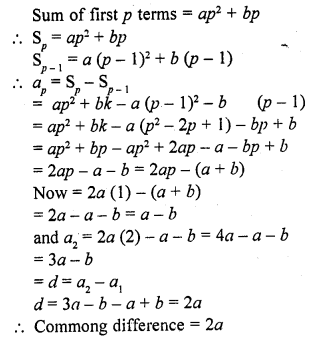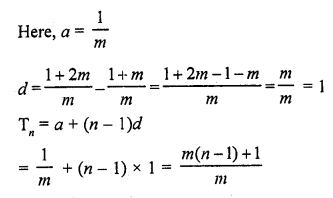Maths RD Sharma Solutions Class 10

RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.3
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.4
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS

Question 1.
Find, in terms of π the length of the arc that subtends an angle of 30° at the centre of a circle of radius 4 cm.
Solution:
Radius of the circle (r) = 4 cm
Angle at the centre subtended an arc = 30°

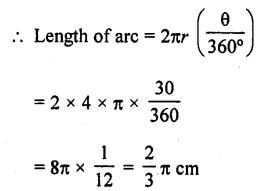
Question 2.
Find the angle subtended at the centre of a circle of radius 5 cm by an arc of length \((\frac { 5\pi }{ 3 } \) cm.
Solution:
Radius of the circle (r) = 5 cm 571
Length of arc = \(\frac { 5\pi }{ 3 }\) cm
Let θ be the angle subtended by the arc, then

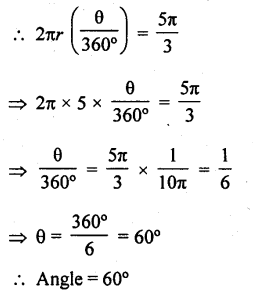
Question 3.
An arc of length 20tc cm subtends an angle of 144° at the centre of a circle. Find the radius of the circle.
Solution:
Length of an arc = 20π cm
Angle subtended by the arc = 144°
Let r be the radius of the circle, then

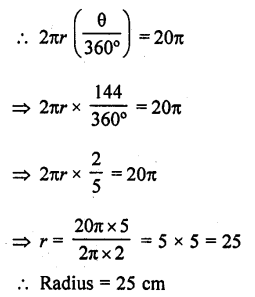
Question 4.
An arc of length 15 cm subtends an angle of 45° at the centre of a circle. Find in terms of π ; the radius of the circle.
Solution:
Length of arc = 15 cm
Angle subtended at the centre = 45°
Let r be the radius of the circle, then

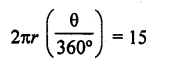
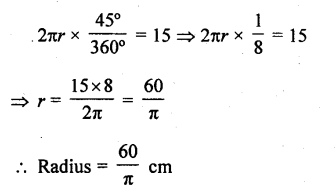
Question 5.
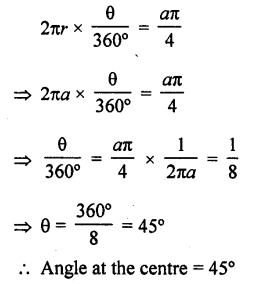
Find the angle subtended at the centre of a circle of radius ‘a’  by an arc of length \((\frac { a\pi }{ 4 } )\)  cm.
Solution:
Radius of the circle (r) = a cm
Length of arc = \(\frac { a\pi }{ 4 }\)   cm
Let θ be the angle subtended by the arc at the centre, then

Question 6.
A sector of a circle of radius 4 cm contains an angle of 30°. Find the area of the sector.
Solution:
Radius of the sector of a circle (r) = 4 cm
Angle at the centre (θ) = 30°

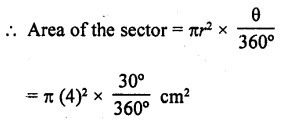
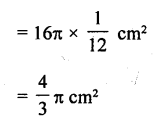
Question 7.
A sector of a circle of radius 8 cm contains an angle of 135°. Find the area of the sector.
Solution:
Radius of the sector of the circle (r) = 8 cm
Angle at the centre (θ) = 135°

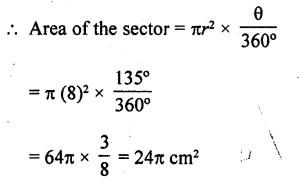
Question 8.
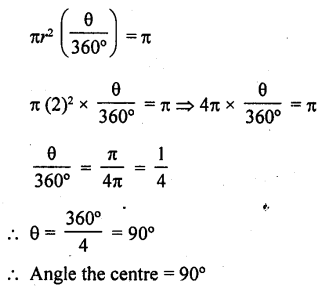
The area of a sector of a circle of radius 2 cm is 7 is cm². Find the angle contained by the sector.
Solution:
Area of the sector of a circle =π cm²
Radius of the circle (r) = 2 cm
Let 0 be the angle at the centre, then

Question 9.
The area of a sector of a circle of radius 5 cm is 5π cm². Find the angle contained by the sector.
Solution:
Area of the sector of a circle = 5π cm²
Radius of the circle (r) = 5 cm
Let 9 be the angle at the centre, then

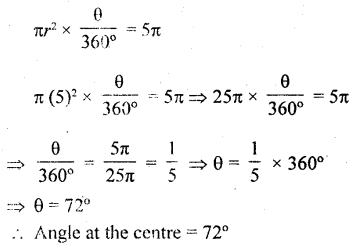
Question 10.
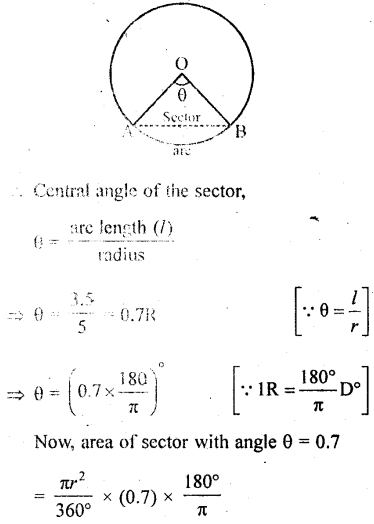
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm. [NCERT Exemplar]
Solution:
Let the central angle of the sector be θ.
Given that, radius of the sector of a circle (r) = 5 cm
and arc length (l) = 3.5 cm

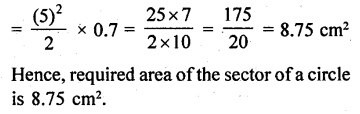
Question 11.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of the arc and area of the sector.
Solution:
Radius of the circle (r) = 25 cm
Angle at the centre (θ) = 72°

Question 12.
The perimeter of a sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
Solution:
Radius of the circle (r) = 5.7 m
Perimeter of the sector = 27.2 m
Length of the arc = Perimeter – 2r
= (27.2 – 2 x 5.7) m
= 27.2 – 11.4 = 15.8 m
Let θ be the central angle, then

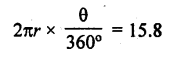
Question 13.
The perimeter of a certain sector of a circle of radius 5.6 cm is 27.2 m. Find the area of the sector.
Solution:
Radius of the sector (r) = 5.6 cm
and perimeter of the sector = 27.2 cm
∴ Length of arc = Perimeter – 2r
= 27.2 – 2 x 5.6
= 27.2- 11.2= 16.0 cm
∴ θ be the angle at the centre, then

Question 14.
A sector is cut-off from a circle of radius 21 cm. The angle of the sector is 120°. Find the length of its arc and the area.
Solution:
Radius of the sector of a circle (r) = 21 cm
Angle at the centre = 120°

Question 15.
The minute hand of a clock is \(\sqrt { 21 } \)  cm long, Find the area described by the minute hand on the face of the clock between 7.00 A.M. and 7.05 A.M.
Solution:
Length of minute hand of a clock (r) = \(\sqrt { 21 }\)  cm
Period = 7 a.m. to 7.05 a.m. 5 minutes

Question 16.
The minute hand of a clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 8.00 A.M. and 8.25 A.M.
Solution:
Length of minute hand of a clock (r) = 10 cm
Period = 8 A.M. to 8.25 A.M. = 25 minutes

Question 17.
The sector of 56° cut out from a circle contains area 4.4 cm², Find the radius of the circle.
Solution:
Area of a sector = 4.4 cm²
Central angle = 56°                                        ‘
Let r be the radius of the sector of the circle, then

Question 18.
Area of a sector of central angle 200° of a circle s 770²cm. Find the length of the corresponding are of this sector.
Solution:
Let the radius of the sector AOBA be r.
Given that, Central angle of sector AOBA = θ = 200°
and area of the sector AOBA = 770 cm²

Question 19.
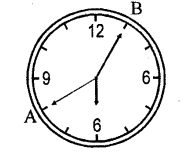
The length of minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6:05 am and 6:40 am.           [NCERT Exemplar]
Solution:
We know that, in 60 min, minute hand revolving = 360°
In 1 min, minute hand revolving = \(\frac { 360\circ }{ 60\circ }\)

Question 20.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [CBSE 2013]
Solution:
Length of minute hand (r)= 14 cm
Area swept by the minute hand in 5 minutes

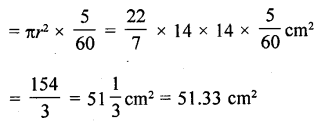
Question 21.
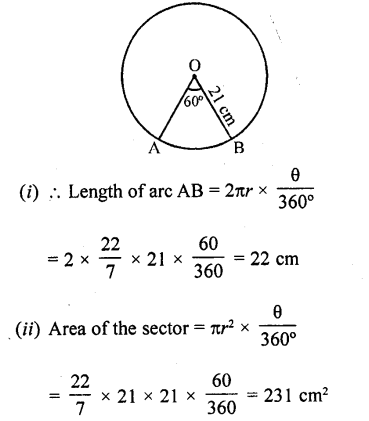
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find (0 the length of the arc (ii) area of the secter formed by the arc. (Use π = 22/7) [CBSE 2013]
Solution:
Radius of a circle (r) = 21 cm
Angle at the centre = 60°

Question 22.
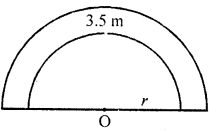
From a circular piece of cardboard of radius 3 cm two sectors of 90° have been cut off. Find the perimeter of the remaining portion nearest hundredth centimeters (Take π = 22/7).
Solution:
Radius of the circular piece of cardboard (r) = 3 cm

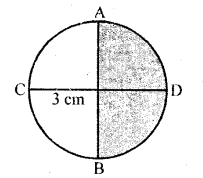
∴ Two sectors of 90° each have been cut off
∴ We get a semicular cardboard piece
∴ Perimeter of arc ACB

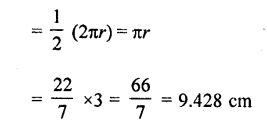
Question 23.
The area of a sector is one-twelfth that of the complete circle. Find the angle of the sector.
Solution:
Let r be the radius of the circle and 0 be the central angle of the sector of the circle Then area of circle = πr²

Question 24.
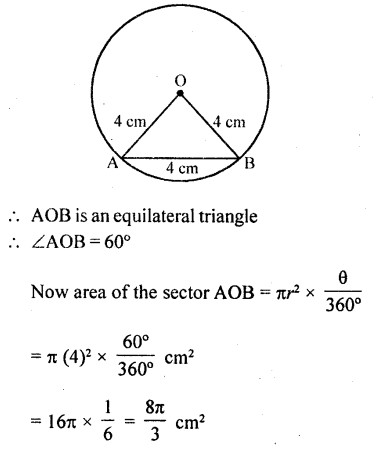
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by the chord AB.
Solution:
Radius of the circle with centre O (r) = 4 cm
Length of chord AB = 4 cm

Question 25.
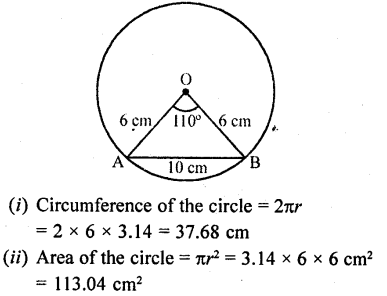
In a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110° at the centre of the circle. Find 
(i)  the circumference of the circle,
(ii) the area of the circle,
(iii) the length of the arc AB,
(iv) the area of the sector OAB.
Solution:
Radius of the circle (r) = 6 cm
Length of chord = 10 cm
and central angle (θ) =110°

Question 26.
Figure, shows a sector of a circle, centre O, containing an angle θ°. Prove that :

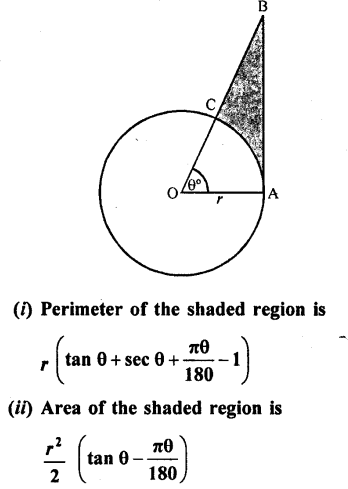
Solution:
Radius of the circle = r
Arc AC subtends ∠θ at the centre of the
circle. OAB is a right triangle
In the right ΔOAB,

Question 27.
Figure, shows a sector of a circle of radius r cm containing an angle θ°. The area of the sector is A cm² and perimeter of the sector is 50 cm. Prove that

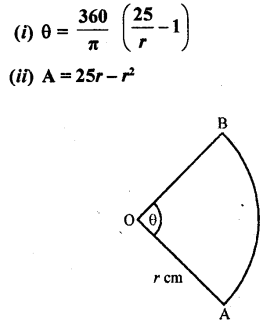
Solution:
Radius of the sector of the circle = r cm
and angle at the centre = 0
Area of sector OAB = A cm²
and perimeter of sector OAB = 50 cm

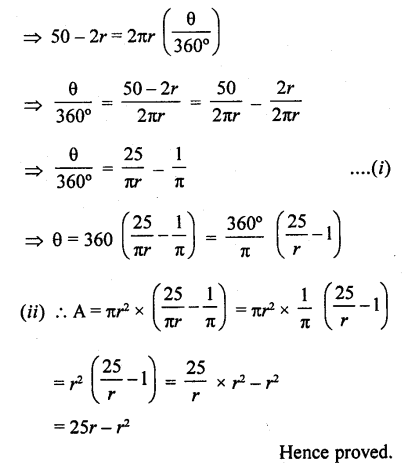
Hope given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS

Question 1.
On which axis do the following points lie?
(i) P (5, 0)
(ii) Q (0 – 2)
(iii) R (-4, 0)
(iv) S (0, 5)
Solution:
(i) P (5, 0)
Its ordinate or y-axis is 0. It lies on x-axis
(ii) Q (0 – 2)
Its abscissa or x-axis is 0. It lies on y-axis
(iii) R (-4, 0)
Its ordinate is 0 It lies on x-axis
(iv) S (0, 5)
Its abscissa is 0. It lies on y-axis

Question 2.
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when
(i) A coincides with the origin and AB and AD are along OX and OY respectively.
(ii) The centre of the square is at the-origin and coordinate axes are parallel to the sides AB and AD respectively.
Solution:
ABCD is a square whose side is 2a
(i) A coincides with origin (0, 0)
AB and AD are along OX and OY respectively
Co-ordinates of A are (0, 0), of B are (2a, 0) of C are (2a, 2a) and of D are (0, 2a)
(ii) The centre of the square is at the origin (0, 0) and co-ordinates axes are parallel to the sides AB and AD respectively.
Then the co-ordinates of A are (a, a) of B are (-a, a), of C are (-a, -a) and of D are (a, -a) as shown in the figure given below :

Question 3.
The base PQ of two equilateral triangles PQR and PQR’ with side 2a lies along y- axis such.that the mid-point of PQ is at the origin. Find the coordinates of the vertices R and R’ of the triangles.
Solution:
∆PQR and PQR’ are equilateral triangles with side 2a each and base PQ and mid of point of PQ is 0 (0, 0) and PQ lies along y-axis

Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.3
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.4
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS

Question 1.
Find the circumference and area of a circle of radius 4.2 cm.
Solution:
Radius of a circle = 4.2 cm

Question 2.
Find the circumference of a circle whose area is 301.84 cm².
Solution:
Area of a circle = 301.84 cm²
Let r be the radius, then πr² = 301.84

Question 3.
Find the area of a circle whose circum­ference is 44 cm.
Solution:
Circumference of a circle = 44 cm
Let r be the radius,
then 2πr = circumference

Question 4.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the circum­ference of the circle. (C.B.S.E. 1996)
Solution:
Let r be the radius of the circle
∴  Circumference = 2r + 16.8 cm
⇒  2πr = 2r + 16.8
⇒  2πr – 2r = 16.8

Question 5.
A horse is tied to a pole with 28 m long string. Find the area where the horse can graze. (Take π = 22/7)
Solution:
Radius of the circle (r) = Length of the rope = 28 m .
Area of the place where the horse can graze

Question 6.
A steel wire when bent in the form of a square encloses an area of 121 cm². If the same wire is bent in the form of a circle, find the area of the circle.  (C.B.S.E. 1997)
Solution:
Area of square formed by a wire =121 cm²
∴ Side of square (a) = \(\sqrt { Area } \)  = \(\sqrt { 121 } \)  = 11 cm Perimeter of the square = 4 x side = 4 x 11 = 44 cm
∴Circumference of the circle formed by the wire = 44cm
Let r be the radius

Question 7.
The circumference of two circles are in the ratio 2 : 3. Find the ratio of their areas.
Solution:
Let R and r be the radii of two circles and their ratio between them circumference = 2 : 3

Question 8.
The sum of radii of two circles is 140 cm and the difference of their circum­ferences is 88 cm. Find the diameters of the circles.
Solution:
Let R and r be the radii of two circles Then R + r = 140 cm  …….(i)
and difference of their circumferences

Question 9.
Find the radius of a circle whose circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm. [NCERT Exemplar]
Solution:
Let the radius of a circle be r.
Circumference of a circle = 2πr
Let the radii of two circles are r₁ and r₂ whose
values are 15 cm and 18 cm respectively.
i.e., r₁ = 15 cm and r₂ = 18 cm
Now, by given condition,
Circumference of circle = Circumference of first circle + Circumference of second circle
⇒   2πr = 2π r₁ + 2πr₂ =
⇒  r = r₁ + r₂
⇒   r = 15 + 18
∴ r = 33 cm
Hence, required radius of a circle is 33 cm.

Question 10.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having its area equal to the sum of the areas of the two circles.
Solution:
Radius of first circle (r₁) = 8 cm
and radius of second circle (r₂) = 6 cm

Question 11.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius and area of the circle which has its circumference equal to the sum of the circumferences of the two circles.
Solution:
Radius of the first circle (r₁) = 19 cm
and radius of the second circle (r₂) = 9 cm S
um of their circumferences = 2πr₁ + 2πr₂
= 2π (r₁ + r₂) = 2π (19 + 9) cm
= 2π x 28 = 56π cm
Let R be the radius of the circle whose circumference is the sum of the circum­ferences of given two circles, then

Question 12.
The area of a circular playground is 22176 m². Find the cost of fencing this ground at the rate of ₹50 per metre.  [NCERT Exempiar]
Solution:
Given, area of a circular playground  = 22176 m²

Question 13.
The side of a square is 10 cm. Find the area of circumscribed and inscribed circles.
Solution:
ABCD is a square whose each side is 10 cm
∴  AB = BC = CD = DA = 10 cm
AC and BD are its diagonals

Question 14.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
Solution:
Let r be the radius of the circle a be the side of the square

Question 15.
The area of a circle inscribed in an equilateral triangle is 154 cm². Find the perimeter of the triangle. (Use π = 22/7 and \(\sqrt { 3 } \)  = 1.73)
Solution:
Area of the inscribed circle of ΔABC = 154 cm²

Question 16.
A field is in the form of a circle. A fence is to be erected around the field. The cost of fencing would be ₹2640 at the rate of ₹12 per metre. Then, the field is to be thoroughly ploughed at the cost of ₹0.50 per m². What is the amount required to plough the field ? (Take π = 22/7)
Solution:
Cost of the fencing the circular field = ₹2640
Rate = ₹12 per metre 2640
∴ Circumference = \((\frac { 2640 }{ 12 } )\) = 220 m
Let r be the radius of the field, then = 2πr = 220

Question 17.
A park is in the form of a rectangle 120 m x 100 m. At the centre of the park there is a circular lawn. The area of park excluding lawn is 8700 m². Find the radius of the circular lawn. (Use π = 22/7).
Solution:
Area of the park excluding lawn = 8700 m²
Length of rectangular park = 120 m
and width = 100 m

∴ Area of lawn = l x b
= 120 x 100 m² = 12000 m²
Let r be the radius of the circular lawn, then area of lawn = πr²

Question 18.
A car travels 1 kilometre distance in which each wheel makes 450 complete revolutions. Find the radius of the its wheels.
Solution:
Distance covered by the car in 450 revolutions = 1 km = 1000 m
∴ Distance covered in 1 revolution = \((\frac { 1000 }{ 450 } )\)
= \((\frac { 20 }{ 9 } )\) m

Question 19.
The area of enclosed between the concentric circles is 770 cm². If the radius of the outer circle is 21 cm, find the radius of the inner circle.
Solution:
Area of enclosed between two concentric circles = 770 cm²
Radius of the outer circle (R) = 21 cm

Question 20.
An archery target has three regions formed by the concentric circles as shown in the figure. If the diameters of the concentric circles are in the ratio 1:2:3, then find the ratio of the areas of three regions.[NCERT Exemplar]

Solution:
Let the diameters of concentric circles be k, 2k , 3k

Question 21.
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr? [NCERT Exemplar]
Solution:
Given, radius of wheel, r = 35 cm
Circumference of the wheel = 2πr
= 2 x \((\frac { 22 }{ 7 } )\) x 35 = 220 cm
But speed of the wheel = 66 kmh^-1
= \((\frac { 66 x 1000 }{ 60 } )\) m/ mm
= 1100 x 100 cm min^-1
= 110000 cm min^-1
∴ Number of revolutions in 1 min
= \((\frac { 110000 }{ 220 } )\)= 500 revolution
Hence, required number of revolutions per minute is 500.

Question 22.
A circular pond is 17.5 m in diameter. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of ₹25 per m². [NCERT Exemplar]
Solution:
Given that, a circular pond is surrounded by a wide path.
The diameter of circular pond = 17.5 m

Question 23.
A circular park is surrounded by a rod 21 m wide. If the radius of the park is 105 m, find the area of the road. [NCERT Exemplar]
Solution:
Given that, a circular park is surrounded by a road.
Width of the road = 21 m
Radius of the park (r₁) = 105 m

.’. Radius of whole circular portion (park + road),
r_e = 105 + 21 = 126 m
Now, area of road = Area of whole circular portion – Area of circular park
= πr² – πr²             [∵ area of circle = πr²]

Question 24.
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.  [NCERT Exemplar]
Solution:
Let the side of a square be a and the radius of circle be r.
Given that, length of diagonal of square = 8 cm

Question 25.
A path of 4 m width runs round a semi­circular grassy plot whose circumference is 81 \((\frac { 5 }{ 7 } )\)m. Find:
(i) the area of the path
(ii) the cost of gravelling the path at the rate of ₹1.50 per square metre
(iii) the cost of turfing the plot at the rate of 45 paise per m².
Solution:
Width of path around the semicircular grassy plot = 4 m
Circumference of the plot = 81 \((\frac { 5 }{ 7 } )\)m
= \((\frac { 572 }{ 7 } )\) m
Let r be the radius of the plot, then

Question 26.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle, such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles. Find the radius of the third circle correct to one decimal place.
Solution:
Radius of first circle (r₁) = 3.5 cm
Radius of second circle (r₂) = 7 cm

Question 27.
A path of width 3.5 m runs around a semi­circular grassy plot whose perimeter is 72 m. Find the area of the path. (Use π = 22/7)                   [CBSE 2015]
Solution:
Perimeter of semicircle grassy plot = 72 m

Let r be the radius of the plot

Question 28.
A circular pond is of diameter 17.5 m. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of ₹25 per square metre (Use π = 3.14)               [CBSE 2014]
Solution:
Diameter of circular pond (d) = 17.5 m
Radius (r) =\((\frac { 1725 }{ 2 } )\) = 8.75 m
Width of path = 2m
∴  Radius of outer cirlce (R) = 8.75 + 2 = 10.75 m
Area of path = (R² – r²)π
= [(10.75)² – (8.75)²](3.14)
= 3.14(10.75 + 8.75) (10.75 – 8.75)
= 3.14 x 19.5 x 2 = 122.46 m²
Cost of 1 m² for constructing the path ₹25 m²
∴  Total cost = ₹ 122.46 x 25 = ₹3061.50

Question 29.
The outer circumference of a circular race-track is 528 m. The track is every­where 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre (Use π= 22/7).
Solution:
Let R and r be the radii of the outer and inner of track.
Outer circumference of the race track = 528 m

Question 30.
A road which is 7 m wide surrounds a circular park whose circumference is 352 m. Find the area of the road.
Solution:
Width of the road = 7 m

Circumference of the park = 352 m
Let r be the radius, then 2πr = 352

Question 31.
Prove that the area of a circular path of uniform width surrounding a circular region of radius r is πh(2r + h).
Solution:
Radius of inner circle = r
Width of path = h
∴ Outer radius (R) = (r + h)
∴ Area of path = πR² – πr²
= π {(r + h)² – r²}
= π {r² + h² + 2rh – r²}
= π {2rh + h²}
= πh (2r + h) Hence proved.

Hope given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.3
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.4
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.5
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

Mark the correct alternative in each of the following :
Question 1.
If 7th and 13th terms of an A.P. be 34 and 64 respectively, then its 18th term is
(a) 87
(b) 88
(c) 89
(d) 90
Solution:
(c) 7th term (a₇) = a + 6d = 34
13th term (a₁₃) = a + 12d = 64
Subtracting, 6d = 30 => d = 5
and a + 12 x 5 = 64 => a + 60 = 64 => a = 64 – 60 = 4
18th term (a₁₈) = a + 17d = 4 + 17 x 5 = 4 + 85 = 89

Question 2.
If the sum of p terms of an A.P. is q and the sum of q terms is p, then the sum of (p + q) terms will be
(a) 0
(b) p – q
(c) p + q
(d) – (p + q)
Solution:
(d)

Question 3.
If the sum of n terms of an A.P. be 3n² + n and its common difference is 6, then its first term is
(a) 2
(b) 3
(c) 1
(d) 4
Solution:
(d)

Question 4.
The first and last terms of an A.P. are 1 and 11. If the sum of its terms is 36, then the number of terms will be
(a) 5
(b) 6
(c) 7
(d) 8
Solution:
(b) First term of an A.P. (a) = 1
Last term (l) = 11
and sum of its terms = 36
Let n be the number of terms and d be the common difference, then

Question 5.
If the sum of n terms of an A.P. is 3n² + 5n then which of its terms is 164 ?
(a) 26th
(b) 27th
(c) 28th
(d) none of these
Solution:
(b)

Question 6.
If the sum of it terms of an A.P. is 2n² + 5n, then its nth term is
(a) 4n – 3
(b) 3n – 4
(c) 4n + 3
(d) 3n + 4
Solution:
(c)

Question 7.
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is :
(a) 13
(b) 9
(c) 21
(d) 17
Solution:
(c)

Question 8.
If four numbers in A.P. are such that their sum is 50 and the greatest number is 4 times the least, then the numbers are
(a) 5, 10, 15, 20
(b) 4, 10, 16, 22
(c) 3, 7, 11, 15
(d) None of these
Solution:
(a)
4 numbers are in A.P.
Let the numbers be
a – 3d, a – d, a + d, a + 3d
Where a is the first term and 2d is the common difference
Now their sum = 50
a – 3d + a – d + a + d + a + 3d = 50
and greatest number is 4 times the least number
a + 3d = 4 (a – 3d)
a + 3d = 4a – 12d
4a – a = 3d + 12d
=> 3a = 15d

Question 9.
Let S denotes the sum of n terms of an A.P. whose first term is a. If the common difference d is given by d = S_n – k S_n-1 + S_n-2 then k =
(a) 1
(b) 2
(c) 3
(d) None of these
Solution:
(b)

Question 10.
The first and last term of an A.P. are a and l respectively. If S is the sum of all the terms of the A.P. and the common difference is given by

(a) S
(b) 2S
(c) 3S
(d) None of these
Solution:
(b)

Question 11.
If the sum of first n even natural number is equal to k times the sum of first n odd natural numbers, then k =

Solution:
(d)

Question 12.
If the first, second and last term of an A.P. are a, b and 2a respectively, its sum is

Solution:
(c)

Question 13.
If S₁ is the sum of an arithmetic progression of ‘n’ odd number of terms and S₂ is the sum of the terms of the

Solution:
(a)

Question 14.
If in an A.P., S_n = n²p and S_m = m²p, where S denotes the sum of r terms of the A.P., then S_p is equal to
(a) \(\frac { 1 }{ 2 }\) p³
(b) mnp
(c) p³
(d) (m + n) p²
Solution:
(c)

Question 15.
If Sn denote the sum of the first n terms of an A.P. If S_2n = 3S_n , then S_3n : S_n is equal to
(a) 4
(b) 6
(c) 8
(d) 10
Solution:
(b)

Question 16.
In an AP, S_p = q, S_q = p and S denotes the sum of first r terms. Then, S_p+q is equal to
(a) 0
(b) – (p + q)
(c) p + q
(d) pq
Solution:
(c) In an A.P. S_p = q, S_q = p
S_p+q = Sum of (p + q) terms = Sum of p term + Sum of q terms = q + p

Question 17.
If S_n denotes the sum of the first r terms of an A.P. Then, S_3n : (S_2n – S_n) is
(a) n
(b) 3n
(b) 3
(d) None of these
Solution:
(c)

Question 18.
If the first term of an A.P. is 2 and common difference is 4, then the sum of its 40 term is
(a) 3200
(b) 1600
(c) 200
(d) 2800
Solution:
(a)

Question 19.
The number of terms of the A.P. 3, 7,11, 15, … to be taken so that the sum is 406 is
(a) 5
(b) 10
(c) 12
(d) 14
Solution:
(d)

Question 20.
Sum of n terms of the series

Solution:
(c)

Question 21.
The 9th term of an A.P. is 449 and 449th term is 9. The term which is equal to zero is
(a) 50th
(b) 502th
(c) 508th
(d) None of these
Solution:
(d)

Question 22.

Solution:
(c)

Question 23.

Solution:
(b) S_n is the sum of first n terms
Last term nth term = S_n – S_n-1

Question 24.
The common difference of an A.P., the sum of whose n terms is S_n, is

Solution:
(a)

Question 25.

Solution:
(b)
In first A.P. let its first term be a₁ and common difference d₁
and in second A.P., first term be a₂ and common difference d₂, then

Question 26.

Solution:
(b)

Question 27.
If the first term of an A.P. is a and nth term is b, then its common difference is

Solution:
(b)

Question 28.
The sum of first n odd natural numbers is
(a) 2n – 1
(b) 2n + 1
(c) n²
(d) n² – 1
Solution:
(c)

Question 29.
Two A.P.’s have the same common difference. The first term of one of these is 8 and that of the other is 3. The difference between their 30th terms is
(a) 11
(b) 3
(c) 8
(d) 5
Solution:
(d) In two A.P.’s common-difference is same
Let A and a are two A.P. ’s
First term of A is 8 and first term of a is 3
A₃₀ – a₃₀ = 8 + (30 – 1) d – 3 – (30 – 1) d
= 5 + 29d – 29d = 5

Question 30.
If 18, a, b – 3 are in A.P., the a + b =
(a) 19
(b) 7
(c) 11
(d) 15
Solution:
(d) 18, a, b – 3 are in A.P., then a – 18 = -3 – b
=> a + b = -3 + 18 = 15

Question 31.
The sum of n terms of two A.P.’s are in the ratio 5n + 4 : 9n + 6. Then, the ratio of their 18th term is

Solution:
(a)

Question 32.

Solution:
(b)

Question 33.
The sum of n terms of an A.P. is 3n² + 5n, then 164 is its
(a) 24th term
(b) 27th term
(c) 26th term
(d) 25th term
Solution:
(b)

Question 34.
If the nth term of an A.P. is 2n + 1, then the sum of first n terms of the A.P. is
(a) n (n – 2)
(b) n (n + 2)
(c) n (n + 1)
(d) n (n – 1)
Solution:
(b)

Question 35.
If 18th and 11th term of an A.P. are in the ratio 3 : 2, then its 21st and 5th terms are in the ratio
(a) 3 : 2
(b) 3 : 1
(c) 1 : 3
(d) 2 : 3
Solution:
(b)

Question 36.
The sum of first 20 odd natural numbers is
(a) 100
(b) 210
(c) 400
(d) 420 [CBSE 2012]
Solution:
(c)

Question 37.

Solution:
(a)

Question 38.

Solution:
(c)

Question 39.
The common difference of the A.P. \(\frac { 1 }{ 2b }\) ,

Solution:
(d)

Question 40.
If k, 2k – 1 and 2k + 1 are three consecutive terms of an AP, the value of k is
(a) -2
(b) 3
(c) -3
(d) 6 [CBSE 2014]
Solution:
(b) (2k – 1) – k = (2k + 1) – (2k- 1)
2k – 1 – k = 2
=> k = 3

Question 41.
The next term of the A.P. , √7 , √28, √63, …………
(a) √70
(b) √84
(c) √97
(d) √112 [CBSE 2014]
Solution:
(d)

= √(l6 x 7)= √112

Question 42.
The first three terms of an A.P. respectively are 3y – 1, 3y + 5 and 5y + 1. Then, y equals
(a) -3
(b) 4
(c) 5
(d) 2 [CBSE 2014]
Solution:
(c) 2 (3y + 5) = 3y – 1 + 5y + 1
(If a, b, c are in A.P., b – a = c – b=> 2b = a + c)
=> 6y + 10 = 8y
=> 10 = 2y
=> y = 5

Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.3
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.4
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.5
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
Define an arithmetic progression.
Solution:
A sequence a₁, a₂, a₃, …, an is called an arithmetic progression of then exists a constant d
Such that a₂ – a₁ = d, a₃ – a₂ = d, ………… a_n – a_n-1 = d
and so on and d is called common difference

Question 2.
Write the common difference of an A.P. whose nth term is a_n = 3n + 7.
Solution:
a_n = 3n + 7
a₁ = 3 x 1 + 7 = 3 + 7 = 10
a₂ = 3 x 2 + 7 = 6 + 7 = 13
a₃ = 3 x 3 + 7 = 9 + 7 = 16
d = a₃ – a₂ or a₂ – a₁ = 16 – 13 = 3 or 13 – 10 = 3

Question 3.
Which term of the sequence 114, 109, 104, … is the first negative term ?
Solution:
Sequence is 114, 109, 104, …..
Let a_n term be negative

Question 4.
Write the value of a₃₀ – a₁₀ for the A.P. 4, 9, 14, 19, …………
Solution:

Question 5.
Write 5th term from the end of the A.P. 3, 5, 7, 9,…, 201.
Solution:

= 3 + 190 = 193
5th term from the end = 193

Question 6.
Write the value of x for which 2x, x + 10 and 3x + 2 are in A.P.
Solution:

Question 7.
Write the nth term of an A.P. the sum of whose n terms is S_n.
Solution:
Sum of n terms = S_n
Let a be the first term and d be the common difference a_n =S_n – S_n-1

Question 8.
Write the sum of first n odd natural numbers.
Solution:

Question 9.
Write the sum of first n even natural numbers.
Solution:
First n even natural numbers are
2, 4, 6, 8, ……….
Here a = 2, d = 2

Question 10.
If the sum of n terms of an A.P. is S_n = 3n² + 5n. Write its common difference.
Solution:

Question 11.
Write the expression for the common difference of an A.P. Whose first term is a and nth term is b.
Solution:
First term of an A.P. = a
and a_n = a + (n – 1) d = b .
Subtracting, b – a = (n – 1) d
d = \(\frac { b – a }{ n – 1 }\)

Question 12.
The first term of an A.P. is p and its common difference is q. Find its 10th term. [CBSE 2008]
Solution:
First term of an A.P. (a) = p
and common difference (d) = q
a₁₀ = a + (n – 1) d
= p + (10 – 1) q = p + 9q

Question 13.
For what value of p are 2p + 1, 13, 5p – 3 are three consecutive terms of an A.P.? [CBSE 2009]
Solution:

Question 14.
If \(\frac { 4 }{ 5 }\), a, 2 are three consecutive terms of an A.P., then find the value of a.
Solution:

Question 15.
If the sum of first p term of an A.P. is ap² + bp, find its common difference.
Solution:

Question 16.
Find the 9th term from the end of the A.P. 5, 9, 13, …, 185. [CBSE 2016]
Solution:
Here first term, a = 5
Common difference, d = 9 – 5 = 4
Last term, l = 185
nth term from the end = l – (n – 1) d
9th term from the end = 185 – (9 – 1) 4 = 185 – 8 x 4 = 185 – 32 = 153

Question 17.
For what value of k will the consecutive terms 2k + 1, 3k + 3 and 5k – 1 form on A.P.? [CBSE 2016]
Solution:
(3k + 3) – (2k + 1) = (5k – 1) – (3k + 3)
3k + 3 – 2k – 1 = 5k – 1 – 3k – 3
k + 2 = 2k – 4
2k – k = 2 + 4
k = 6

Question 18.
Write the nth term of the A.P.
\(\frac { 1 }{ m }\) , \(\frac { 1 + m }{ m }\) , \(\frac { 1 + 2m }{ m }\) , ……… [CBSE 2017]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.