RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.3
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.4
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS
Question 1.
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
(a) π/2
(b) 2π
(c) 2
(d) 4
Solution:
Let r be the radius of the circle, then Circumference = 2πr
and area = πr²
But 2πr= πr²
∴ 2r = r²
⇒ r = 2
Diameter = 2r = 2 x 2 = 4 (d)
Question 2.
If the difference between the circum-ference and radius of a circle is 37 cm., then using π = \(\frac { 22 }{ 7 }\) the circumference (in cm) of the circle is
(a) 154
(b) 44
(c) 14
(d) 7 [CBSE 2013]
Solution:
Difference between circumference and radius of a circle = 37 cm
∴ 2πr-r = 37

Question 3.
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form of a square, then its area will be
(a) 3520 cm²
(b) 6400 cm²
(c) 7744 cm²
(d) 8800 cm²
Solution:
Radius of a circular wire (r) = 56 cm
Circumference = 2πr = 2 x \(\frac { 22 }{ 7 }\) x 56 cm = 352 cm
Now perimeter of square = 352 cm
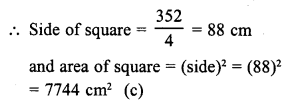
Question 4.
If a wire is bent into the shape of a square, then the area of the square is 81 cm². When wire is bent into a semicircular shape, then the area of the semi-circle will be
(a) 22 cm²
(b) 44 cm²
(c) 77 cm²
(d) 154 cm²
Solution:
Area of a square wire = 81 cm²
∴ Side of square = \(\sqrt { Area } \) = \(\sqrt { 81 } \) cm = 9 cm ard per in eret of square =4a = 4 x 9 = 36cm
Perimeter of semicircular wire whose bent = 36 cm
Let r be the radius, then
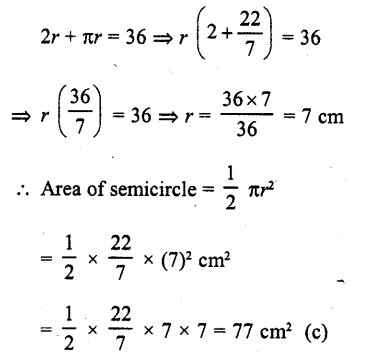
Question 5.
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
(a) 20 m
(b) 21 m
(c) 22 m
(d) 24 m
Solution:
Let R and r be the radii of the outer and inner circles of the park, then 2πR – 2πr = 132
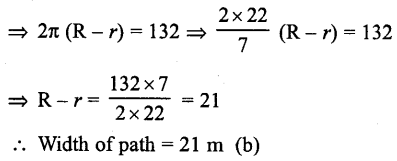
Question 6.
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
(a) 2800
(b) 4000
(c) 5500
(d) 7000
Solution:
Radius of the wheel (r) = 0.25 m = 25 cm
Circumference of the wheel

Question 7.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
(a) 55 m
(b) 110 m
(c) 220 m
(d) 230 m
Solution:
Ratio in the outer and inner perimeter of a circular path = 23 : 22
Width of path = 5 m
Let R and r be the radii of outer and inner path then R- r = 5 m ….(i)
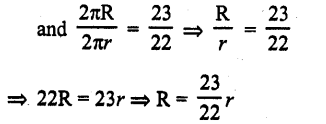
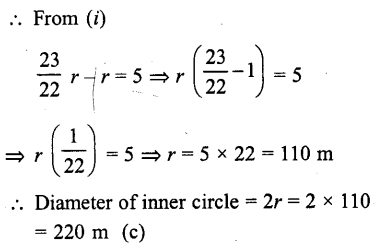
Question 8.
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is

Solution:
Circumference of a circle (c) = 100 cm
Diagonal of square which is inscribed in the circle

Question 9.
The area of the incircle of an equilateral triangle of side 42 cm is :
(a) 22 73 cm²
(b) 231 cm²
(c) 462 cm²
(d) 924 cm²
Solution:
Side of an equilateral triangle (a) = 42 cm
Radius of inscribed circle = \(\frac { 1 }{ 3 }\) x altitude
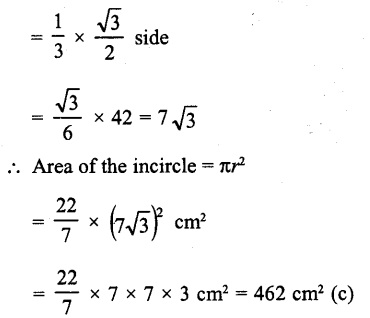
Question 10.
The area of incircle of an equilateral triangle is 154 cm2. The perimeter of the triangle is
(a) 71.5 cm
(b) 71.7 cm
(c) 72.3 cm
(d) 72.7 cm
Solution:
Area of incircle of an equilateral triangle = 154 cm²

Question 11.
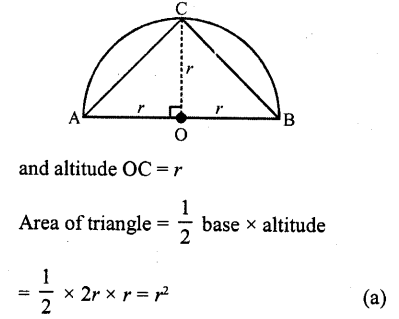
The area of the largest triangle that can be inscribed in a semi-circle of radius r. is
(a) r²
(b) 2 r²
(c) r³
(d) 2r³
Solution:
The largest triangle inscribed in a semi-circle of radius r, can be ΔABC as shown in the figure, whose base = AB = 2r
Question 12.
The perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is
(a) 70 cm²
(b) 140 cm²
(c) 210 cm²
(d) 420 cm²
Solution:
The perimeter of a triangle = 30 cm
and circumference of its incircle = 88 cm

Question 13.
The area of a circle is 220 cm², the area of a square inscribed in it is
(a) 49 cm²
(b) 70 cm²
(c) 140 cm²
(d) 150 cm²
Solution:
Area of a circle = 220 cm²

Question 14.
If the circumference of a circle increases from 4π to 8π, then its area is
(a) halved
(b) doubled
(c) tripled
(d) quadrupled
Solution:
In first case circumference of a circle = 4π

Question 15.
If the radius of a circle is diminished by 10%, then its area is diminished by
(a) 10%
(b) 19%
(c) 20%
(d) 36%
Solution:
Let in first case radius of a circle = r
Then area = πr²
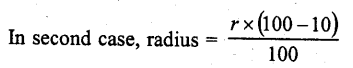

Question 16.
If the area of a square is same as the area of a circle, then the ratio of their perimeter, in terms of 7t, is

Solution:
Let side of square = a
Perimeter = 4 a
Then area = a²
∴ Area of circle = a²

Question 17.
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
(a) 2r
(b) r²
(c) r
(d) \(\sqrt { r } \)
Solution:
Radius of semicircule = r
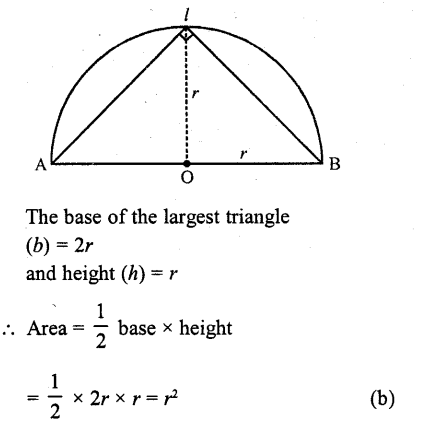
Question 18.
The ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is
(a) π : \(\sqrt { 2 } \)
(b) π : \(\sqrt { 3 } \)
(c) \(\sqrt { 3 } \) :π
(d) \(\sqrt { 2 } \) : π
Solution:
Let side of equilateral triangle = a
Then area = \(\frac { \sqrt { 3 } }{ 4 }\) a²
Diameter of circle = a
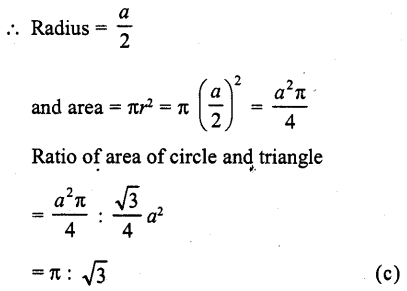
Question 19.
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then r1² + r2²
(a) >r²
(b) = r²
(c) < r²
(d) None of these
Solution:
Sum of area of two circles with radii r1 and r2
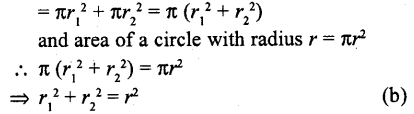
Question 20.
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
(a) 10 cm
(b) 12 cm
(c) 14 cm
(d) 16 cm
Solution:
Perimeter of a semicircle = 36 cm
Let d be its diameter, then
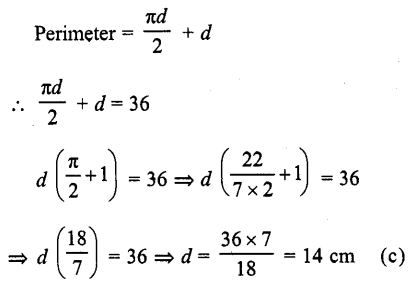
Question 21.
The perimeter of the sector OAB shown in the fiugre, is
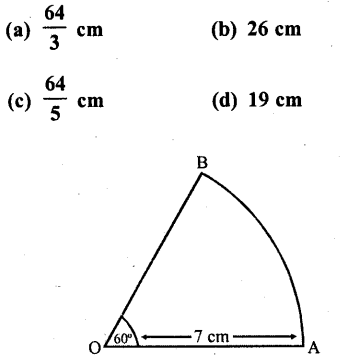
Solution:
Radius of sector of 60° = 7 cm
∴ Perimeter = arc AB + 2 r
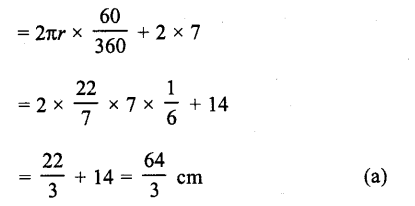
Question 22.
If the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is
(a) 58 cm²
(b) 52 cm²
(c) 25 cm²
(d) 56 cm²
Solution:
Radius of a sector = 6.5 cm
and perimeter = 29 cm

Question 23.
If the area of a sector of a circle bounded by an arc of length 5K cm is equal to 20K cm², then its radius is
(a) 12 cm
(b) 16 cm
(c) 8 cm
(d) 10 cm
Solution:
Let r be the radius, then
Length of the arc of sector of θ angle = 5π
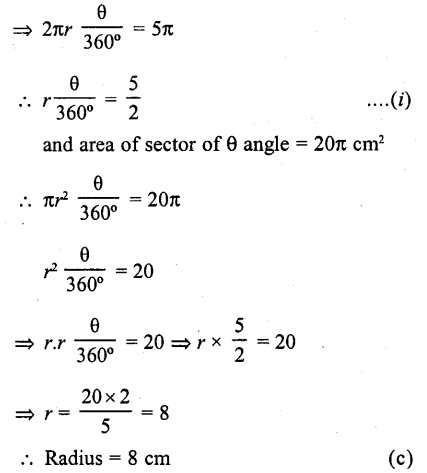
Question 24.
The area of the circle that can be inscribed in a square of side 10 cm is
(a) 40π cm²
(b) 30π cm²
(c) 100π cm²
(d) 25π cm²
Solution:
Side of square = 10 cm
∴ Diameter of the inscribed circle = 10 cm
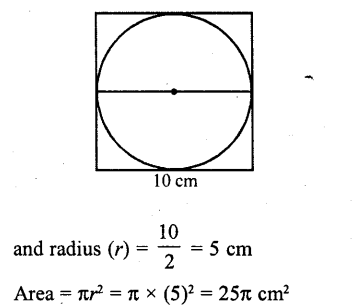
Question 25.
If the difference between the circumference
(a) 154 cm²
(b) 160 cm²
(c) 200 cm²
(d) 150 cm²
Solution:
Let r be the radius of a circle then circum-ference = 2πr
∴ 2πr-r = 37
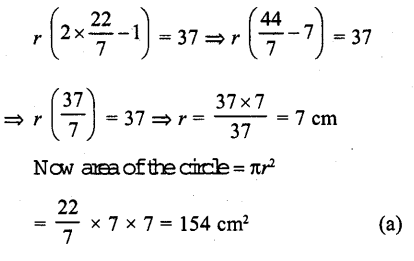
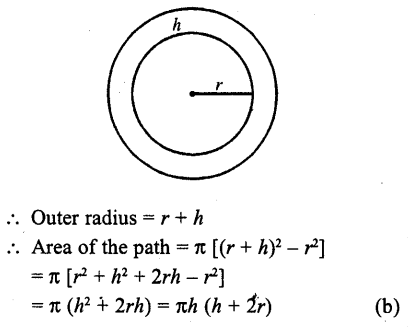
Question 26.
The area of a circular path of uniform width h surrounding a circular region of radius r is
(a) π (2r + h) r
(b) π (2r + h) h
(c) π (h + r)r
(d) π (h + r) A
Solution:
Let r be the radius of inner circle h is the width of circular path
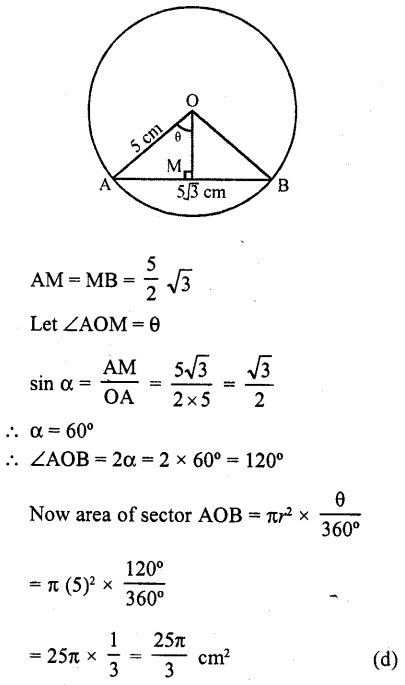
Question 27.
If AB is a chord of length 5\(\sqrt { 3 } \) cm of a circle with centre O and radius 5 cm, then area of sector OAB is


Solution:
Radius of the circle (r) = 5 cm
AB is a chord = 5\(\sqrt { 3 } \)
Draw OM ⊥ AB which bisects the chord AB at M
Question 28.
The area of a circle whose area and circumference are numerically equal, is
(a) 2π sq. units
(b) 4π sq. units
(c) 6π sq. units
(d) 8π sq. units
Solution:
Let radius of the circle = r
∴ Area = πr²
and circumference = 2πr
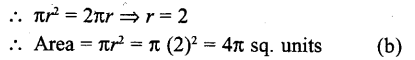
Question 29.
If diameter of a circle is increased by 40%, then its area increases by
(a) 96%
(b) 40%
(c) 80%
(d) 48%
Solution:
Let the diameter of a circle in first case = 2r
Then radius = r
Area = πr²

Question 30.
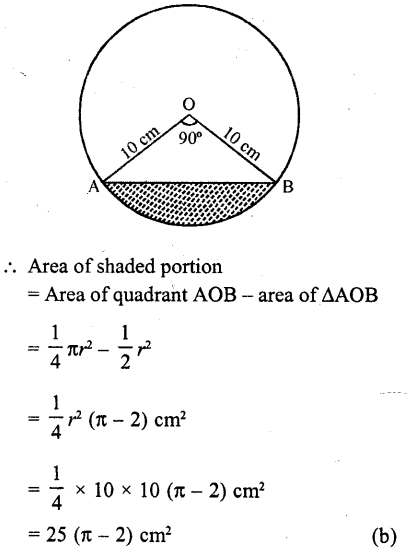
In the figure, the shaded area is
(a) 50 (π – 2) cm²
(b) 25 (π – 2) cm²
(c) 25 (π + 2) cm²
(d) 5 (π – 2) cm²
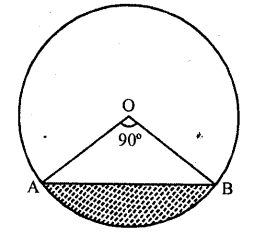
Solution:
In the figure, ∠AOB = 90°
and radius of the circle = 10 cm
Question 31.
In the figure, the area of the segment PAQ is
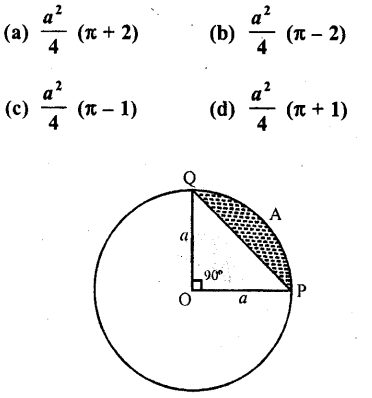
Solution:
a is the radius of the circle arc PAQ subtends angle 90° at the centre
∴ Area of segment PAQ
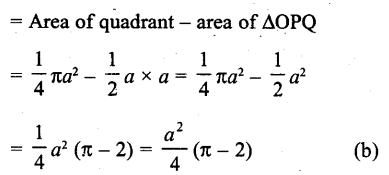
Question 32.
In the figure, the area of segment ACB is
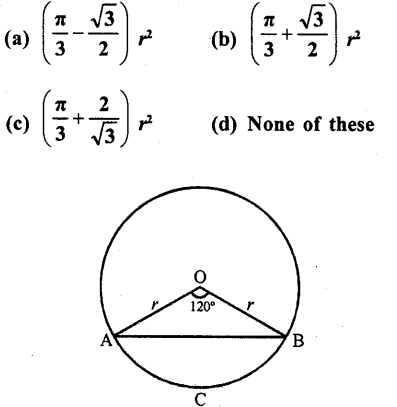
Solution:
r is the radius of the circle and arc ACB subtends angle of 120° at the centre
Area of segment ACB = r
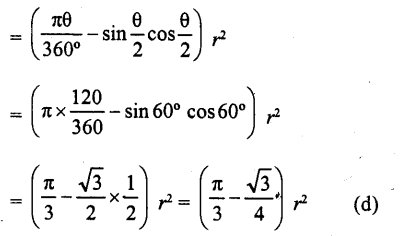
Question 33.
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20rc cm², then the radius of the circle is
(a) 12 cm
(b) 16 cm
(c) 8 cm
(d) 10 cm
Solution:
Length of arc = 5π cm
area of sector = 20π cm²
Let the angle at the centre be θ
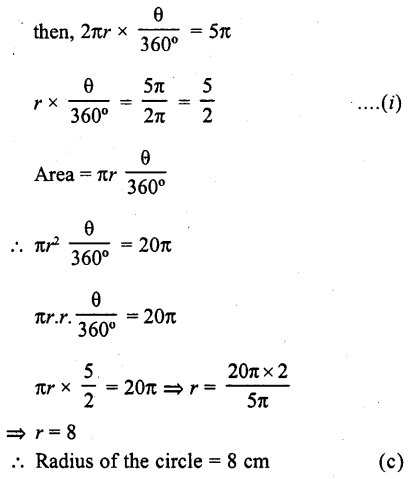
Question 34.
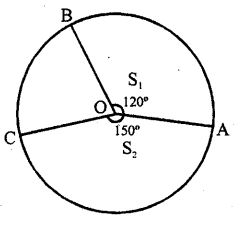
In the figure, the ratio of the areas of two sectors S1 and S2 is
(a) 5 : 2
(b) 3 : 5
(c) 5 : 3
(d) 4 : 5
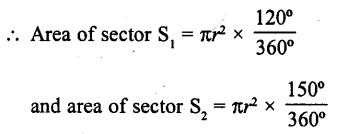
Solution:
Let r be the radius of the circle
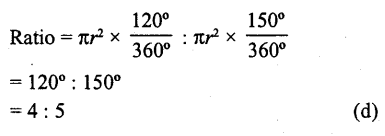
Question 35.
If the area of a sector of a circle is \(\frac { 5 }{ 18 }\) of the area of the circle, then the sector angle is equal to
(a) 60°
(b) 90°
(c) 100°
(d) 120°
Solution:
Area of sector of a circle = \(\frac { 5 }{ 18 }\) x area of circle
Let θ be its angle at the centre and r be radius
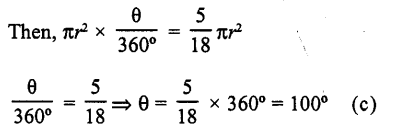
Question 36.
If the area of a sector of a circle is \(\frac { 7 }{ 20 }\) of the area of the circle, then the sector angel is equal to
(a) 110°
(b) 130°
(c) 100°
(d) 126°
Solution:
Area of sector of a circle = \(\frac { 7 }{ 20 }\) of the area of the circle
Let r be the radius and θ be its angle at the centre
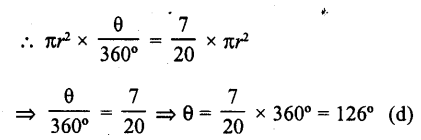
Question 37.
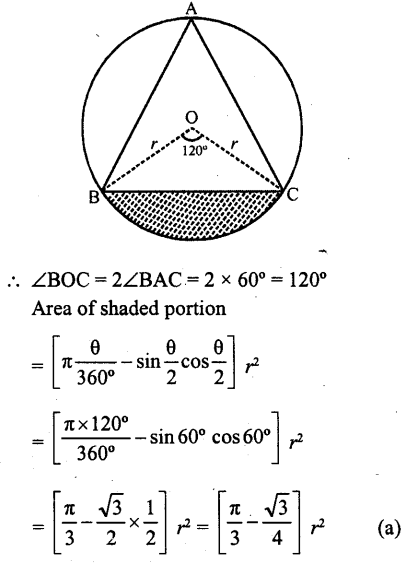
In the figure, if ABC is an equilateral triangle, then shaded area is equal to?
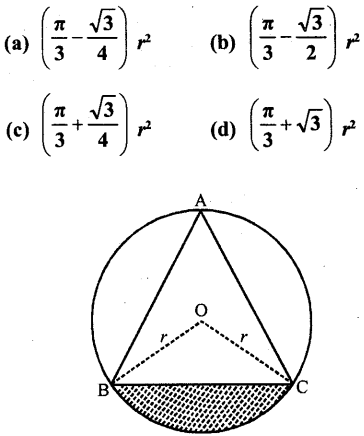
Solution:
ΔABC is an equilateral triangle inscribed in a circle with centre O and radius r
BO and CO are joined
Question 38.
In the figure, the ara of the shaded region is
(a) 3π cm²
(b) 6π cm²
(c) 9π cm²
(d) 7π cm²
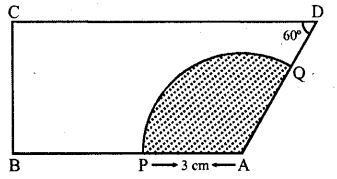
Solution:
In the figure, ∠B = ∠C = 90°, ∠D = 60?
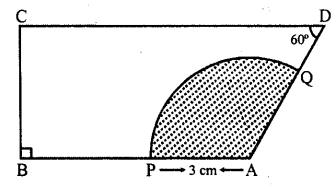
∴ ∠A= 360° – (90° + 90° + 60°) = 360° – 240° = 120°
Radius of the sector = 3 cm
∴Area of shaded portion
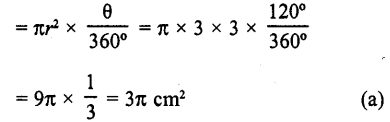
Question 39.
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is
(a) 13 : 22
(b) 14 : 11
(c) 22 : 13
(d) 11 :14
Solution:
Let side of square = a units
∴ Area = a² sq. units
and perimeter = 4a units
Now perimeter of circle = 4a units
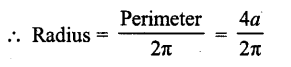

Question 40.
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is

Solution:
Radius of circle (R) = 20 cm
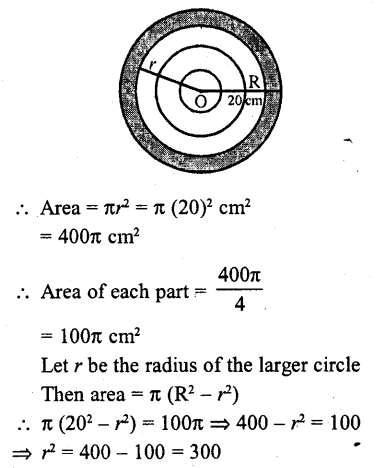
![]()
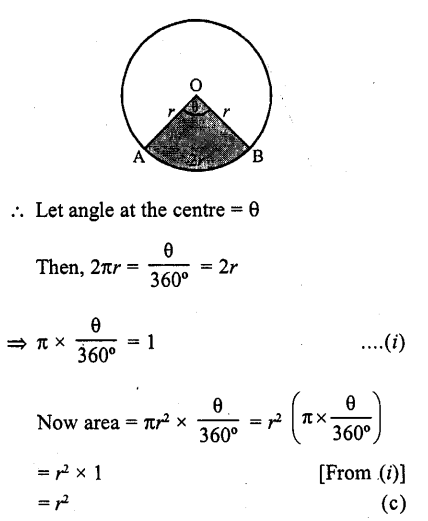
Question 41.
The area of a sector whose perimeter is four times its radius r units, is

Solution:
Radius of sector = r
Perimeter = 4r
and length of arc = 4r – 2r = 2r
Question 42.
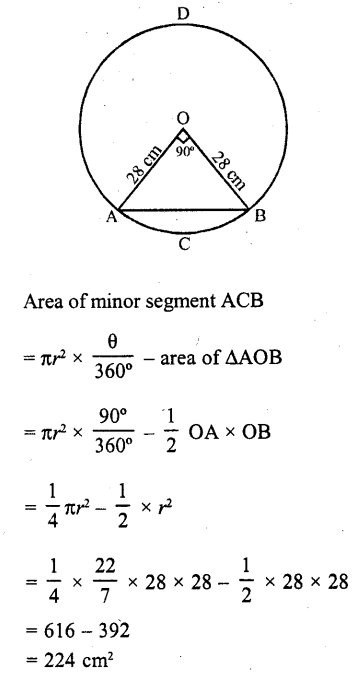
If a chord of a circle of radius 28 cm makes an angle of 90° at the centre, then the area of the major segment is
(a) 392 cm²
(b) 1456 cm²
(c) 1848 cm²
(d) 2240 cm²
Solution:
A chord AB makes an angle of 90° at the centre
Radius of the circle = 28 cm

Question 43.
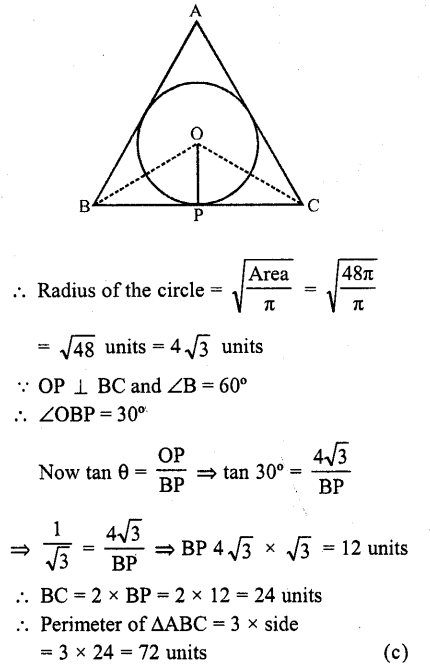
If the area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the trianlge is
(a) 17\(\sqrt { 3 } \) units
(b) 36 units
(c) 72 units
(d) 48\(\sqrt { 3 } \) units
Solution:
Area of a circle inscribed in an equilateral triangle = 48π sq. units
Question 44.
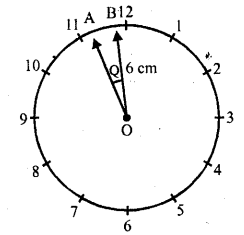
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
(a) 2.75 cm²
(b) 5.5 cm²
(c) 11 cm²
(d) 10 cm²
Solution:
Length of hour hand of a clock (r) = 6 cm
Time 11.20 am to 11.55 am = 35 minutes

Question 45.
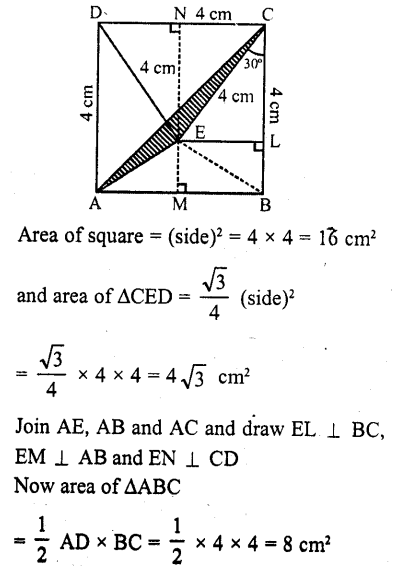
ABCD is a square of side 4 cm. If ? is a point in the interior of the square such that ΔCED is equilateral, then area of ΔACEis
(a) 2 (\(\sqrt { 3 } \) – 1) cm²
(b) 4 (\(\sqrt { 3 } \) -1) cm²
(c) 6(\(\sqrt { 3 } \)-1)cm²
(d) 8(\(\sqrt { 3 } \)-1)cm²
Solution:
Side of square ABCD = 4 cm
and side of equilateral ΔCED = 4 cm

Question 46.
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the larger circle (in cm) is
(a) 34
(b) 26
(c) 17
(d) 14
Solution:

Question 47.
If π is taken as 22/7, the-distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is (a) 2.2
(b) 1.1
(b) 9.625
(d) 96.25 [CBSE 2013]
Solution:
Diameter of a wheel = 35 cm = \(\frac { 35 }{ 100 }\) m
Circumference of the wheel = πd
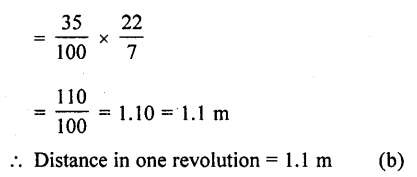
Question 48.
ABCD is a rectangle whose three vertices are B (4, 0), C (4, 3) and D (0, 3). The length of one of its diagonals is
(a) 5
(b) 4
(c) 3
(d) 25 [CBSE 2014]
Solution:
Three vertices of a rectangle ABCD are B (4,0), C (4, 3) and D (0, 3) length of one of its diagonals
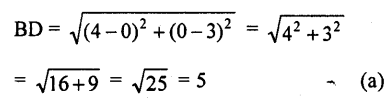
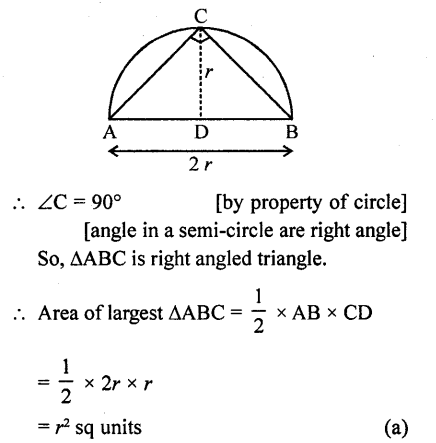
Question 49.
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is

Solution:
Take a point C on the circumference of the semi-circle and join it by the end points of diameter A and B.
Question 50.
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then

Solution:
According to the given condition,
Area of circle = Area of first circle + Area of second circle.

Question 51.
If the sum of the circumference of two circles with radii r, and r2 is equal to the circumference of a circle of radius r, then
Solution:
According to the given condition, Circumference of circle = Circumference of first circle + Circumference of second circle
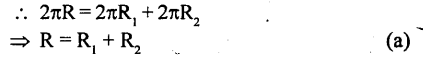
Question 52.
If the circumference of a circle and the perimeter of a square are equal, then
(a) Area of the circle = Area of the square
(b) Area of the circle < Area of the square
(c) Area of the circle > Area of the square
(d) Nothing definite can be said
Solution:
According to the given condition, Circumference of a circle = Perimeter of square 2 πr = 4 a
[where, r and a are radius of circle and side of square respectively]

Question 53.
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is
(a) 22 : 7
(b) 14 : 11
(c) 7 : 22
(d) 11 : 14
Solution:
Let radius of circle be r and side of a square be a
According to the given condition,
Perimeter of a circle = Perimeter of a square
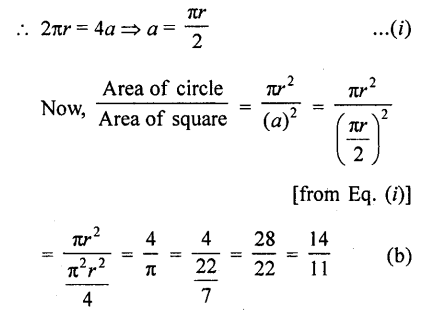
Hope given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.