Class 8 Maths RD Sharma Solutions

RD Sharma Class 8 Solutions Chapter 16 Understanding Shapes II (Quadrilaterals) Ex 16.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 16 Understanding Shapes II Ex 16.1

Question 1.
Define the following terms:
(i) Quadrilateral
(ii) Convex Quadrilateral.
Solution:
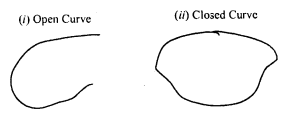
(i) Quadrilateral: A closed figure made of four line segments is called a quadrilateral such that:

(a) no three points of them are collinear
(b) the line segments do not intersect except at their ends points.
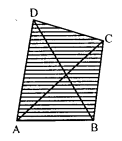
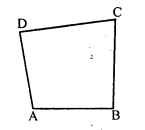
(ii) Convex quadrilateral: A quadrilateral is called a convex quadrilateral of the line containing any side of the quadrilateral has the remaining vertices on the same side of it. In the figure, quadrilateral ABCD is a convex quadrilateral.

Question 2.
In a quadrilateral, define each of the following:
(i) Sides
(ii) Vertices
(iii) Angles
(iv) Diagonals
(v) Adjacent angles
(vi) Adjacent sides
(vii) Opposite sides
(viii) Opposite angles
(ix) Interior
(x) Exterior
Solution:
(i) Sides: In a quadrilateral ABCD, form line segments AB, BC, CD and DA are called sides of the quadrilateral.
(ii) Vertices : The ends points are called the vertices of the quadrilateral. Here in the figure, A, B, C and D are its vertices.
(iii) Angles: A quadrilateral has four angles which are at their vertices. In the figure, ∠A, ∠B, ∠C and ∠D are its angles.
(iv) Diagonals: The line segment joining the opposite vertices is called diagonal. A quadrilateral has two diagonals.
(v) Adjacent Angles : The angles having a common arm (side) are called adjacent angles.
(vi) Adjacent sides : If two sides of a quadrilateral have a common end-point, these are called adjacent sides.
(vii) Opposite sides: If two sides do not have a common end-point of a quadrilateral, they are called opposite sides.
(viii) Opposite angles : The angles which are not adjacent are called opposite angles.
(ix) Interior: The region which is surrounded by the sides of the quadrilateral is called its interior.
(x) Exterior : The part of the plane made up by all points as the not enclosed by the quadrilateral, is called its exterior.

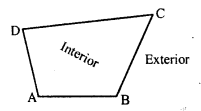
Question 3.
Complete each of the following, so as to make a true statement:
(i) A quadrilateral has ………… sides.
(ii) A quadrilateral has ………… angles.
(iii) A quadrilateral has ……….. vertices, no three of which are …………
(iv) A quadrilateral has …………. diagonals.
(v) The number of pairs of adjacent angles of a quadrilateral is ………….
(vi) The number of pairs of opposite angles of a quadrilateral is ……………
(vii) The sum of the angles of a quadrilateral is …………
(viii) A diagonal of a quadrilateral is a line segment that joins two ………. vertices of the quadrilateral.
(ix) The sum of the angles of a quadrilateral is …………. right angles.
(x) The measure of each angle of a convex quadrilateral is …………. 180°.
(xi) In a quadrilateral the point of intersection of the diagonals lies in ………….. of the quadrilateral.
(xii) A point is in the interior of a convex quadrilateral, if it is in the ……….. of its two opposite angles.
(xiii) A quadrilateral is convex if for each side, the remaining …………. lie on the same side of the line containing the side.
Solution:
(i) A quadrilateral has four sides.
(a) A quadrilateral has four angles.
(iii) A quadrilateral has four vertices, no three of which are collinear .
(iv) A quadrilateral has two diagonals.
(v) The number of pairs of adjacent angles of a quadrilateral is four .
(vi) The number of pairs of opposite angles ot a quadrilateral is two.
(vii) The sum of the angles of a quadrilateral is 360°.
(viii) A diagonal of a quadrilateral is a line segment that join two opposite vertices of the quadrilateral.
(ix) The sum of the angles of a quadrilateral is 4 right angles.
(x) The measure of each angle of a convex quadrilateral is less than 180°.
(xi) In a quadrilateral the point of intersection of the diagonals lies in interior of the quadrilateral.
(xii) A point is in the interior of a convex quadrilateral, if it is in the interior of its two opposite angles.
(xiii) A quadrilateral is convex if for each side, the remaining vertices lie on the same side of the line containing the side.

Question 4.
In the figure, ABCD is a quadrilateral.
(i) Name a pair of adjacent sides.
(ii) Name a pair of opposite sides.
(iii) How many pairs of adjacent sides are there?
(iv) How many pairs of Opposite sides are there ?

(v) Name a pair of adjacent angles.
(vi) Name a pair of opposite angles.
(vii) How many pairs of adjacent angles are there ?
(viii) How many pairs of opposite angles are there ?
Solution:
In the figure, ABCD is a quadrilateral
(i) Pairs of adjacent sides are AB, BC, BC, CD, CD, DA, DA, AB.
(ii) Pairs of opposite sides are AB and CD; BC and AD.
(iii) There are four pairs of adjacent sides.
(iv) There are two pairs of opposite sides.
(v) Pairs of adjacent angles are ∠A, ∠B; ∠B, ∠C; ∠C, ∠D; ∠D, ∠A.
(vi) Pairs of opposite angles are ∠A and ∠C; ∠B and ∠D.
(vii) There are four pairs of adjacent angles.
(viii) There are two pairs of opposite angles.

Question 5.
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
Solution:
Sum of four angles of quadrilateral is 360°
110° + 12° + 55° + x° = 360°
⇒ 237° + x° = 360°
⇒ x° = 360° – 237° = 123°
x = 123°

Question 6.
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
Solution:
The sum of four angles of a quadrilateral = 360°
Three angles are 110°, 50° and 40°
Let fourth angle = x
Then 110° + 50° + 40° + x° = 360°
⇒ 200° + x° = 360°
⇒ x = 360° – 200° = 160°
x = 160°

Question 7.
A quadrilateral has three acute angles each measures 80°. What is the measure of fourth angle ?
Solution:
Sum of four angles of a quadrilateral = 360°
Sum of three angles having each angle equal to 80° = 80° x 3 = 240°
Let fourth angle = x
Then 240° + x = 360°
⇒ x° = 360° – 240°
⇒ x° = 120°
Fourth angle = 120°

Question 8.
A quadrilateral has all its four angles of the same measure. What is the measure of each ?
Solution:
Let each equal angle of a quadrilateral = x
4x° = 360°
⇒ x° = \(\frac { 360 }{ 4 }\) = 90°
Each angle will be = 90°

Question 9.
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles ?
Solution:
Measures of two angles each = 65°
Sum of these two angles = 2 x 65°= 130°
But sum of four angles of a quadrilateral = 360°
Sum of the remaining two angles = 360° – 130° = 230°
But these are equal to each other
Measure of each angle = \(\frac { 230 }{ 2 }\) = 115°

Question 10.
Three angles of a quadrilateral are equal. Fourth angle is of measure 150°. What is the measure of equal angles ?
Solution:
Sum of four angles of a quadrilateral = 360°
One angle = 150°
Sum of remaining three angles = 360° – 150° = 210°
But these three angles are equal
Measure of each angle = \(\frac { 210 }{ 3 }\) = 70°

Question 11.
The four angles of a quadrilateral are as 3 : 5 : 7 : 9. Find the angles.
Solution:
Sum of four angles of a quadrilateral = 360°
and ratio in angles = 3 : 5 : 7 : 9
Let first angles = 2x
Then second angle = 5x
third angle = 7x
and fourth angle = 9x
3x + 5x + 7x + 9x = 360°
⇒ 24x = 369°
⇒ x = \(\frac { 360 }{ 24 }\) = 15°
First angle = 3x = 3 x 15° = 45°
second angle = 5x = 5 x 15° = 75°
third angle = 7x = 7 x 15° = 105°
and fourth angle = 9x = 9 x 15° = 135°

Question 12.
If the sum of the two angles of a quadrilateral is 180°, what is the sum of the remaining two angles ?
Solution:
Sum of four angles of a quadrilateral = 360°
and sum of two angle out of these = 180°
Sum of other two angles will be = 360° – 180° = 180°

Question 13.
In the figure, find the measure of ∠MPN.

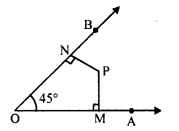
Solution:
In the figure, OMPN is a quadrilateral in which
∠O = 45°, ∠M = ∠N = 90° (PM ⊥ OA and PN ⊥ OB)
Let ∠MPN = x°
∠O + ∠M + ∠N + ∠MPN = 360° (Sum of angles of a quadrilateral)
⇒ 45° + 90° + 90° + x° = 360°
⇒ 225° + x° = 360°
⇒ x° = 360° – 225°
⇒x = 135°
∠MPN = 135°

Question 14.
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles ?
Solution:
The sides of a quadrilateral ABCD are produced in order, forming exterior angles ∠1, ∠2, ∠3 and ∠4.

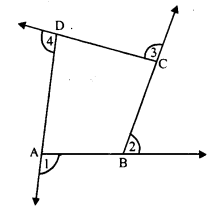
Now ∠DAB + ∠1 = 180° (Linear pair) ……(i)
Similarly,
∠ABC + ∠2 = 180°
∠BCD + ∠3 = 180°
and ∠CDA + ∠4 = 180°
Adding, we get
∠DAB + ∠1 + ∠ABC + ∠2 + ∠BCD + ∠3 + ∠CDA + ∠4 = 180° + 180° + 180° + 180° = 720°
⇒ ∠DAB + ∠ABC + ∠CDA + ∠ADC + ∠1 + ∠2 + ∠3 + ∠4 = 720°
But ∠DAB + ∠ABC + ∠CDA + ∠ADB = 360° (Sum of angles of a quadrilateral)
360° + ∠1 + ∠2 + ∠3 + ∠4 = 720°
⇒ ∠l + ∠2 + ∠3 + ∠4 = 720° – 360° = 360°
Sum of exterior angles = 360°

Question 15.
In the figure, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
Solution:
In quadrilateral ABCD,

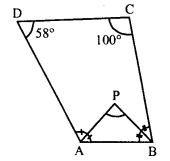
∠D = 50°, ∠C = 100°
PA and PB are the bisectors of ∠A and ∠B.
In quadrilateral ABCD,
∠A + ∠B + ∠C + ∠D = 360° (Sum of angles of a quadrilateral)
⇒ ∠A + ∠B + 100° + 50° = 360°
⇒ ∠A + ∠B + 150° = 360°’
⇒ ∠A + ∠B = 360° – 150° = 210°
and \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B = \(\frac { 210 }{ 2 }\) = 105°
(PA and PB are bisector of ∠A and ∠B respectively)
∠PAB + ∠PBA = 105°
⇒ ∠PAB + ∠PBA + ∠APB = 180° (Sum of angles of a triangle)
⇒ 105° + ∠APB = 180°
⇒ ∠APB = 180° – 105° = 75°
∠APB = 75°

Question 16.
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
Solution:
Sum of angles A, B, C and D of a quadrilateral = 360°
i.e. ∠A + ∠B + ∠C + ∠D = 360°
But ∠A = ∠B = ∠C = ∠D = 1 : 2 : 4 : 5

Let ∠A = x,
Then ∠B = 2x
∠C = 4x
∠D = 5x
x + 2x + 4x + 5x = 360°
⇒ 12x = 360°
⇒ x = \(\frac { 360 }{ 12 }\) = 30°
∠A = x = 30°
∠B = 2x = 2 x 30° = 60°
∠C = 4x = 4 x 30° = 120°
∠D = 5A = 5 x 30° = 150°

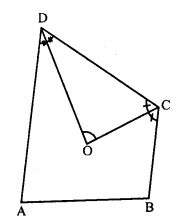
Question 17.
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD = \(\frac { 1 }{ 2 }\) (∠A + ∠B).
Solution:
In quadrilateral ABCD,

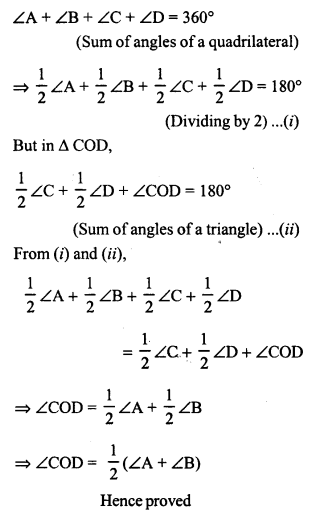
Question 18.
Find the number of sides of a regular polygon when each of its angles has a measures of
(i) 160°
(ii) 135°
(iii) 175°
(iv) 162°
(v) 150°.
Solution:
In a n-sided regular polygon, each angle

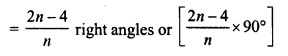
Question 19.
Find the number of degrees in each exterior angle of a regular pentagon.
Solution:
In a pentagon or a polygon, sum of exterior angles formed by producing the sides in order, is four right angles or 360°
Each exterior angle = \(\frac { 360 }{ 5 }\) = 72°

Question 20.
The measure of angles of a hexagon are x°, (x – 5)° (x – 5)°, (2x – 5)°, (2x – 5)°, (2x + 20)°. Find the value of x.
Solution:
We know that the sum of interior angels of a hexagon = 720° (180° x 4)
⇒ x + x – 5 + x – 5 + 2x – 5 + 2x – 5 + 2x + 20 = 720°
⇒ 9x – 20 + 20 = 720
⇒ 9x = 720
⇒ x = \(\frac { 720 }{ 9 }\) = 80°
x = 80°

Question 21.
In a convex hexagon, prove that the sum of all interior angles is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
Solution:
In a convex hexagon ABCDEF, its sides AB, BG, CD, DE, EF and FA are produced in order forming exterior angles a, b, c, d, e, f

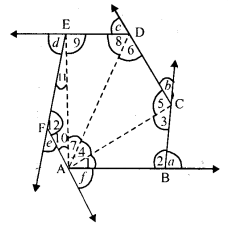
∠a + ∠b + ∠c + ∠d + ∠e + ∠f = 4 right angles (By definition)
By joining AC, AD, and AE, 4 triangles ABC, ACD, ADE and AEF are formed
In ∆ABC,
∠1 + ∠2 + ∠3 = 180° = 2 right angle (Sum of angles of a triangle) …… (i)
Similarly,
In ∆ACD,
∠4 +∠5 + ∠6 = 180° = 2 right angles
In ∆ADE,
∠1 + ∠8 + ∠9 = 2 right angles …(iii)
In ∆AEF,
∠10 + ∠11 + ∠12 = 2 right angles …(iv)
Joining (i), (ii), (iii) and (iv)
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 + ∠9 + ∠10 + ∠11 + ∠12 = 8 right angles
⇒ ∠2 + ∠3 + ∠5 + ∠6 + ∠8 + ∠9 + ∠11 + ∠12 + ∠1 + ∠4 + ∠7 + ∠10 = 8 right angles
⇒ ∠B + ∠C + ∠D + ∠E +∠F + ∠A = 8 right angles
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 2 (∠a + ∠b + ∠c + ∠d + ∠e + ∠f)
Sum of all interior angles = 2(the sum of exterior angles)
Hence proved.

Question 22.
The sum of the interior angles of a polygon is three times the sum of its exterior angles. Determine the number of sides of the polygon.
Solution:
Let number of sides of a regular polygon = n
Each interior angle = \(\frac { 2n – 4 }{ n }\) right angles
Sum of all interior angles = \(\frac { 2n – 4 }{ n }\) x n
right angles = (2n – 4) right angles
But sum of exterior angles = 4 right angles
According to the condition,
(2n – 4) = 3 x 4 (in right angles)
⇒ 2n – 4 = 12
⇒ 2n = 12 + 4 = 16
⇒ n = 8
Number of sides of the polygon = 8

Question 23.
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
Solution:
Ratio in exterior angle and interior angles of a regular polygon = 1 : 5
But sum of interior and exterior angles = 180° (Linear pair)

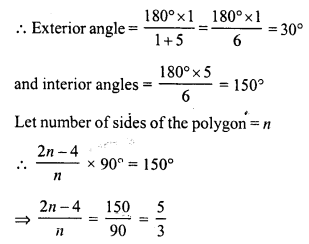
By cross multiplication:
6n – 12 = 5n
⇒ 6n – 5n = 12
⇒ n = 12
Number of sides of polygon is 12

Question 24.
PQRSTU is a regular hexagon. Determine each angle of ∆PQT.
Solution:
In regular hexagon, PQRSTU, diagonals PT and QT are joined.

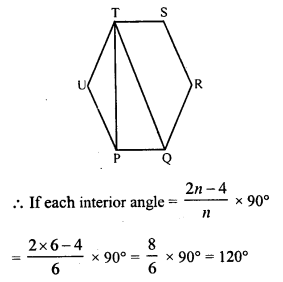
In ∆PUT, PU = UT
∠UPT = ∠UTP
But ∠UPT + ∠UTP = 180° – ∠U = 180° – 120° = 60°
∠UPT = ∠UTP = 30°
∠TPQ = 120° – 30° = 90° (QT is diagonal which bisect ∠Q and ∠T)
∠PQT = \(\frac { 120 }{ 2 }\) = 60°
Now in ∆PQT,
∠TPQ + ∠PQT + ∠PTQ = 180° (Sum of angles of a triangle)
⇒ 90° + 60° + ∠PTQ = 180°
⇒ 150° + ∠PTQ = 180°
⇒ ∠PTQ = 180° – 150° = 30°
Hence in ∆PQT,
∠P = 90°, ∠Q = 60° and ∠T = 30°

Hope given RD Sharma Class 8 Solutions Chapter 16 Understanding Shapes II Ex 16.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I (Polygons) Ex 15.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I Ex 15.1

Question 1.
Draw rough diagrams to illustrate the following:
(i) Open curve
(ii) Closed curve
Solution:

Question 2.
Classify the following curves as open or closed.

Solution:
Open curves : (i), (iv) and (v) are open curves.
(ii) , (iii), and (vi) are closed curves.

Question 3.
Draw a polygon and shade its interior. Also draw its diagonals, if any.
Solution:
In the given polygon, the shaded portion is its interior region AC and BD are the diagonals of polygon ABCD.

Question 4.
Illustrate, if possible, each one of the following with a rough diagram:
(i) A closed curve that is not a polygon.
(ii) An open curve made up entirely of line segments.
(iii) A polygon with two sides.
Solution:
(i) Close curve but not a polygon.

(ii) An open curve made up entirely of line segments.

(iii) A polygon with two sides. It is not possible. At least three sides are necessary

Question 5.
Following are some figures : Classify each of these figures on the basis of the following:


(i) Simple curve
(ii) Simple closed curve
(iii) Polygon
(iv) Convex polygon
(v) Concave polygon
(vi) Not a curve
Solution:
(i) It is a simple closed curve and a concave polygon.
(ii) It is a simple closed curve and convex polygon.
(iii) It is neither a curve nor polygon.
(iv) it is neither a curve not a polygon.
(v) It is a simple closed curve but not a polygon.
(vi) It is a simple closed curve but not a polygon.
(vii) It is a simple closed curve but not a polygon.
(viii) It is a simple closed curve but not a polygon.

Question 6.
How many diagonals does each of the following have ?
(i) A convex quadrilateral
(ii) A regular hexagon
(iii) A triangle.
Solution:
(i) A convex quadrilateral
Here n = 4

Question 7.
What is a regular polygon ? State the name of a regular polygon of:
(i) 3 sides
(ii) 4 sides
(iii) 6 sides.
Solution:
A regular polygon is a polygon which has all its sides equal and so all angles are equal,
(i) 3 sides : It is an equilateral triangle.
(ii) 4 sides : It is a square.
(iii) 6 sides : It is a hexagon.

Hope given RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I Ex 15.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
Mr. Cherian purchased a boat for Rs 16,000. If the total cost of the boat is depreciating at the rate of 5% per annum, calculate its value after 2 years.
Solution:
Cost of boat = Rs 16,000
Rate of depreciating = 5% p.a.
Period = 2 years
Value of boat after 2 years

Question 2.
The value of a machine depreciates at the rate of 10% per annum. What will be its value 2 years hence, if the present value is Rs 1,0,000 ? Also, find the total depreciation during this period.
Solution:
Present value of machine = Rs 1,00,000
Rate of depreciation = 10% p.a.
Period (n) = 2 years
Value of machine after 2 years

Question 3.
Pritam bought a plot of land for Rs 6,40,000. Its value is increasing by 5% of its previous value after every six months. What will be the value of the plot after 2 years ?
Solution:
Present value of plot = Rs 6,40,000
Increase = 5% per half year
Period (n) = 2 years or 4 half years

Question 4.
Mohan purchased a house for Rs 30,000 and its value is depreciating at the rate of 25% per year. Find the value of the house after 3 years.
Solution:
Present value of the house (P) = Rs 30,000
Rate of depreciation = 25% p.a.
Period (n) = 3 years
Value of house after 3 years

Question 5.
The value of a machine depreciates at the rate of 10% per annum. It was purchased 3 years ago. If its present value is Rs 43,740, find its purchased price.
Solution:
Let the purchase price of machine = Rs P
Rate of depreciation = 10% p.a.
Period (n) = 3 years.
and present value = Rs 43,740

Question 6.
The value of a refrigerator which was purchased 2 years ago, depreciates at 12% per annum. If its present value is Rs 9,680, for how much was it purchased ?
Solution:
Let the refrigerator was purchased for = Rs P
Rate of depreciation (R) = 12% p.a.
Period (n) = 2 years
and present value (A) = Rs 9,680

Question 7.
The cost of a TV set was quoted Rs 17,000 at the beginning of 1999. In the beginning of2000, the price was hiked by 5%. Because of decrease in demand the cost was reduced by 4% in the beginning of 2001. What is the cost of the TV set in 2001 ?
Solution:
List price of TV set in 1999 = Rs 17,000
Rate of hike in 2000 = 5%
Rate of decrease in 2001 = 4%
Price of TV set in 2001

Question 8.
Ashish started the business with an initial investment of Rs 5,00,000. In the first year, he incurred a loss of 4%. However, during the second year he earned a profit of 5% which in third year, rose to 10%. Calculate the net profit for the entire period of 3 years.
Solution:
Initial investment = Rs 5,00,000
In the first year, rate of loss = 4%
In the second year, rate of gain = 5%
and in the third year, rate of gain = 10%
Investment after 3 years

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
Construct a quadrilateral ABCD in which AB = 4.4 cm, BC = 4 cm, CD = 6.4 cm, DA = 3.8 cm and BD = 6.6 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4.4 cm.

(ii) With centre A and radius 3.8 cm and with centre B and radius 6.6 cm, draw arcs intersecting each other at D.
(iii) With centre B and radius 4 cm, and with centre D and radius 6.4 cm, draw arcs intersecting each other at C on the other side of BD.
(iv) Join AD, BD, BC and DC.
The ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD such that AB = BC = 5.5 cm, CD = 4 cm, DA = 6.3 cm and AC = 9.4 cm. Measure BD.
Solution:
(i) Draw a line segment AC = 9.4 cm.
(ii) With centre A and C and radius 5.5 cm, draw arcs intersecting each other at B.
(iii) Join AB and CB.
(iv) Again with centre A and radius 6.3 cm, and with centre C and radius 4 cm, draw arcs intersecting each other at D below the line segment AC.

(v) Join AD and CD.
Then ABCD is the required quadrilateral. On measuring BD, it is 5 cm.

Question 3.
Construct a quadrilateral XYZW in which XY = 5 cm, YZ = 6 cm, ZW = 7 cm, WX = 3 cm and XZ = 9 cm.
Solution:
Steps of construction :
(i) Draw a line segment XZ = 9 cm.
(ii) With centre X and radius 3 cm and with centre Z and radius 7 cm, draw arcs intersecting each other at W.

(iii) Join XW and ZW.
(iv) Again with centre X and radius 5 cm and with centre Z and radius 6 cm, draw arcs, intersecting each other at Y below the line segment XZ.
(v) Join XY and ZY.
Then XYZW is the required quadrilateral.

Question 4.
Construct a parallelogram PQRS such that PQ = 5.2 cm, PR = 6.8 cm and QS = 8.2 cm.
Solution:
Steps of construction:
In a parallelogram, diagonals bisect each other. Now
(i) Draw a line segment PQ = 5.2 cm.
(ii) With centre P and radius 3.4 cm (\(\frac { 1 }{ 2 }\) of PR) and with centre Q and radius 4.1 cm (\(\frac { 1 }{ 2 }\) of QS) draw arcs intersecting each other at O.

(iii) Join PQ and QO and produced them to R and S respectively such that PO = OR and QO = OS.
(iv) Join PS, SR and RQ.
Then PQRS is the required parallelogram.

Question 5.
Construct a rhombus with side 6 cm and one diagonal 8 cm. Measure the other diagonal.
Solution:
Steps of construction :
Sides of a rhombus are equal.
(i) Draw a line segment AC = 8 cm.

(ii) With centres A and C and radius 6 cm, draw two arcs above the line segment AC and two below the line segment AC, intersecting each other at D and B respectively.
(iii) Join AB, AD, BC and CD.
Then ABCD is the required rhombus.
JoinBD.
On measuring BD, it is approximately 9 cm

Question 6.
Construct a kite ABCD in which AB = 4 cm, BC = 4.9 cm and AC = 7.2 cm.
Solution:
Steps of construction :
(i) Draw a line segment AC = 7.2 cm.

(ii) With centre A and radius 4 cm draw an arc.
(iii) With centre C and radius 4.9 cm, draw another arc which intersects the first arc at B and D.
(iv) Join AB, BC, CD and DA.
Then ABCD is the required kite.

Question 7.
Construct, if possible, a quadrilateral ABCD given, AB = 6 cm BC = 3.7 cm, CD = 5.7 cm, AD = 5.5 cm and BD = 6.1 cm. Give reasons for not being able to construct, if you cannot.
Solution:
Steps of construction :
(i) Draw a line segment BD = 6.1 cm.
(ii) With centre B and radius 6 cm and with centre D and radius 5.5 cm, draw arcs intersecting at A.
(iii) Join AB and AD.
(iv) Again with centre B and radius 3.7 cm and with centre D and radius 5.7 cm, draw two arcs intersecting each other at C below the BD.

(v) Join BC and DC.
Then ABCD is the required quadrilateral.

Question 8.
Construct, if possible a quadrilateral ABCD in which AB = 6 cm, BC = 7 cm, CD = 3 cm, AD = 5.5. cm and AC = 11 cm. Give reasons for not being able to construct, if you cannot.
Solution:
Steps of construction:
It is not possible to construct this quadrilateral ABCD because
AD + DC = 5.5 cm + 3 cm = 8.5 cm
and AC = 11 cm
AD + DC < AC.
But we know that in a triangle,
Sum of two sides is always greater than its third side.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Multiply:

Question 1.
(5x + 3) by (7x + 2)
Solution:
(5x + 3) x (7x + 2)
= 5x (7x + 2) + 3 (7x + 2)
= 35x² + 10x + 21x + 6
= 35x² + 31x + 6

Question 2.
(2x + 8) by (x – 3)
Solution:
(2x + 8) x (x – 3)
= 2x (x – 3) + 8 (x – 3)
= 2x² – 6x + 8x – 24
= 2x² + 2x – 24

Question 3.
(7x +y) by (x + 5y)
Solution:
(7x + y) x (x + 5y)
= 7x (x + 5y) + y (x + 5y)
= 7x² + 35xy + xy + 5y²
=7x² + 36xy + 5y²

Question 4.
(a – 1) by (0.1a² + 3)
Solution:
(a – 1) x (0.1a² + 3)
= a (0.1a² + 3) – 1 (0.1a²+ 3)
= 0.1a³ + 3a-0.1a²-3
= 0.1a³ – 0.1a² + 3a-3

Question 5.
(3x² +y²) by (2x² + 3y²)
Solution:
(3x²+y²) x (2x² + 3y²)
= 3x² (2x² + 3y²) + y²(2x² + 3y²)
= 6x^{2 +2} + 9x²y² + 2x²y² + 3y^{2 + 2}
= 6x⁴ + 11 x²y² + 3y⁴

Question 6.

Solution:

Question 7.
(x⁶-y⁶) by (x²+y²)
Solution:
(x⁶ – y⁶) x (x² + y²)
= x⁶ (x² + y²) – y⁶ (x² + y²)
= x⁶ x x² + x⁶y² – x²y⁶ -y⁶ x y²
= x^{6 + 2} + x⁶y² – x²y⁶ – y^{6 +2}
= x  + x⁶y² – x²y⁶ – y⁸

Question 8.
(x² + y²) by (3a+2b)
Solution:
(x² + y²) x (3a + 2b)
= x² (3a + 2b) + y² (3a + 2b)
= 3x²a + 2x²b + 3y²a + 2y²b
3ax² + 3av² + 2bx² + 2by²

Question 9.
[-3d + (-7ƒ)] by (5d +ƒ)
Solution:
[-3d + (-7ƒ)] x (5d +ƒ)
= -3d x (5d +ƒ) + (-7ƒ) x (5d +ƒ)
= -15d²-3dƒ- 35dƒ- 7ƒ²
= -15d² – 38dƒ- 7ƒ²

Question 10.
(0.8a – 0.5b) by (1.5a -3b)
Solution:
(0.8a – 0.5b) x (1.5a-3b)
= 0.8a x (1.5a – 36) – 0.56 (1.5a -3b)
= 1.2a² – 2.4ab – 0.75ab + 1.5b²
= 1.2a²-3.15ab+ 1.5b²

Question 11.
(2x² y² – 5xy²) by (x² -y²)
Solution:
(2x² y² – 5xy²) x (x² -y²)
= 2x²y² (x² – y²) – 5x_y² (x² – y²)
= 2x²y² x x² – 2x²y² xy²– 5xy² x x² + 5x² xy²
= 2x^{2 + 2} y²– 2x² x y^{2 + 2}– 5x¹⁺² y²+5xy^{2 + 2}
= 2x⁴y²– 2x²y⁴ – 5x³y²+ 5xy⁴

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.
(2x²-1) by (4x³ + 5x²)
Solution:
(2x²-1)x(4x³ + 5x²)
= 2x² x (4x³ + 5x²) – 1 (4x³ + 5x²)
= 2x² x 4x³ + 2x² x 5x² – 4x³ – 5x²
= 8x^{2 + 3} + 10x^{2 + 2}-4x³-5x²
= 8x⁵ + 10x⁴ – 4x³ – 5x²

Question 16.
(2xy + 3y²) (3y² – 2)
Solution:
(2xy + 3y²) (3y² – 2)
= 2xy x (3y²-2) + 3y² x (3y²-2)
= 2xy x Zy²+ 2xy x (-2) + Zy² x Zy² – Zy² x 2
= 6xy^{1 + 2}– 4xy + 9y^{2 + 2}– 6y²
= 6xy³ – 4xy + 9y⁴– 6y²
Find the following products and verify the result for x = -1, y = -2 :

Question 17.
(3x-5y)(x+y)
Solution:
(3x-5y)(x+y)
= 3x x (x + y) – 5y x (x + y)
= 3x x x + 3x x y-5y x x-5y x y
= 3x² + 3xy – 5xy – 5y²
= 3x² – 2xy – 5y²
Verfification:
x = -1,y = -2
L.H.S. = (3x-5y)(x+y)
= [3 (-1) -5 (-2)] [-1 – 2]
= (-3 + 10) (-3) = 7 x (-3) = -21
R.H.S. = 3x² – 2xy – 5y²
= 3 (-1)² – 2 (-1) (-2) -5 (-2)²
=3×1-4-5×4=3-4-20
= 3-24 = -21
∴ L.H.S. = R.H.S.

Question 18.
(x²y-1) (3-2x²y)
Solution:
(x²y-1) (3-2x²y)
= x²y (3 – 2x²y) -1(3-2x²y)
= x²y x 3 – x²y x 2x²y – 1 x 3 + 1 x 2x²y
= 3x²y-2x^{2 + 2}x y^{1 +1}-3 + 2x²y
= 3x²y – 2x⁴y²– 3 + 2x²y
= 3x²y + 2x²y – 2x⁴y² – 3
= 5x²y – 2x⁴y² – 3
Verification : (x = -1, y = -2)
L.H.S. = (x²y – 1) (3 – 2x²y)
= [(-1)² x (-2) -1] [3 – 2 x (-1)2 x (-2)]
= [1 x (-2) -1) [3 – 2 x 1 x (-2)]
= (-2 – 1) (3 + 4) = -3 x 7 = -21
R.H.S. = 5x²y – 2x⁴y² – 3
= 5 (-1)² (-2) -2 (-1)⁴ (-2)² -3
5 x 1 (-2) – 2 (1 x 4) -3
= -10-8-3 = -21
∴ L.H.S. = R.H.S

Question 19.

Solution:

Simplify :

Question 20.
x² (x + 2y) (x – 3y)
Solution:
x² (x + 2y) (x – 3y)
= x² [x (x – 3y) + 2y (x – 3y)]
= x² [x² – 3xy + 2xy – 6y²]
= x² [x² – xy – 6y²)
= x² x x² – x² x xy – x²6y²
= x⁴ – x³y – 6x²y²

Question 21.
(x² – 2y²) (x + 4y)
Solution:
(x² – 2y²) (x + 4y) x²y²
= [x² (x + 4y) -2y² (x + 4y)] x²y²
= (x³ + 4x²y – 2xy² – 8y³) x²y²
= x²y² x x³ + x²y² x 4x²y – 2x²y² x xy² – 8x²y² x y³
= x^{2 +3} y² + 4x^{2 + 2} y^{2 +1} – 2x^{2 +1} y^{2+ 2} – 8x²y²⁺³
= xy + 4⁴xy³ – 2x³y⁴ – 8x²y⁵

Question 22.
a²b² (a + 2b) (3a + b)
Solution:
a²b² (a + 2b) (3a + b)
= a²b² [a (3a + b).+ 2b (3a + b)]
= a²b² [3a² + ab + 6ab + 2b²]
= a²b² [3a² + lab + 2b²]
= a²b² x 3a² + a²b² x 7ab + a²b² x 2b²
= 3a^{2 + 2}b² + 7a²⁺¹ b²⁺¹+ 2a²b^{2 + 2}
= 3a⁴b² + 7a³b³ + 2a²b⁴

Question 23.
x² (x-y) y² (x + 2y)
Solution:
x² (x -y) y² (x + 2y)
= [x² x x – x² x y] [y² x x + y² x 2y]
= (x³ – x²y) (xy² + 2y³)
= x³ (xy² + 2y³) – x²y (xy² + 2y³)
= x³ x xy² + x³ x 2y³ – x²y x xy² – x²y x 2y³
= x^{3 +1} y² + 2x³y³ – x^{2 +1} y^{1+ 2} – 2x²y^{1 + 3}
= x⁴y² + 2x³y³ – x³y³ – 2x²y⁴
= x⁴y² + x³y³ – 2x²y⁴

Question 24.
(x³ – 2x² + 5x-7) (2x-3)
Solution:
(x³ – 2x² + 5x – 7) (2x – 3)
= (2x – 3) (x³ – 2x² + 5x – 7)
= 2x (x³ – 2x² + 5x – 7) -3 (x³ – 2x² + 5x – 7)
= 2x x x³ – 2x x 2x² + 2x x 5x – 2x x 7 -3 x x³ – 3 x (-2x²) – 3 x 5x – 3 x (-7)
= 2x⁴-4x³ + 10x²– 14x-3x³ + 6x²– 15x + 21
= 2x⁴ – 4x³ – 3x³ + 10x² + 6x²– 14x- 15x + 21
= 2x⁴-7x³ + 16x²-29x+ 21

Question 25.
(5x + 3) (x – 1) (3x – 2)
Solution:
(5x + 3) (x – 1) (3x – 2)
= (5x + 3) [x (3x – 2) -1 (3x – 2)]
= (5x + 3) [3x² – 2x – 3x + 2]
= (5x + 3) [3x² – 5x + 2]
= 5x (3x² – 5x + 2) + 3 (3x² – 5x + 2)
= (5x x 3x² – 5x x Sx + 5x x 2)+ [3 x 3x² + 3 x (-5x) + 3×2]
= 15x³ – 25x² + 10x + 9x² – 15x + 6
= 15x³ – 25x² + 9x² + 10x – 15x + 6
= 15x³ – 16x² – 5x + 6

Question 26.
(5-x) (6-5x) (2-x)
Solution:
(5-x) (6-5x) (2-x)
= [5 (6 – 5x) -x (6 – 5x)] (2 – x)
= [30 – 2$x – 6x + 5x²] (2 – x)
= (30 – 3 1x + 5x²) (2-x)
= 2 (30 – 31x + 5x²) – x (30 – 31x + 5x²)
= 60 – 62x + 10x² – 30x + 3 1x² – 5x³
= 60 – 62x – 30x + 10x² + 3 1x² – 5x³
= 60 – 92x + 41x² – 5x³

Question 27.
(2x² + 3x – 5) (3x² – 5x + 4)
Solution:
(2x² + 3x – 5) (3x² – 5x + 4)
= 2x² (3x² – 5x + 4) + 3x (3x² – 5x + 4) -5 (3x² – 5x + 4)
= 2x² x 3x² – 2x² x 5x + 2x² x 4 + 3x x 3x² – 3x x 5x + 3x x 4 – 5 x 3x² – 5 (-5x) -5×4
= 6x⁴ – 10x³ + 8x² + 9x³ – 15x² + 12x – 15x² + 25x-20
= 6x⁴ – 10x³ + 9x³ + 8x² – 15x² – 15x² + 12x + 25x – 20
= 6x⁴ – x³ – 22x² + 37x – 20

Question 28.
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
Solution:
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
= 3x (2x – 3) -2 (2x – 3) + 5x (x + 1) – 3 (x + 1)
= 6x² – 9x – 4x + 6 + 5x² + 5x – 3x – 3
= 6x² + 5x² – 9x – 4x + 5x – 3x + 6 – 3
= 11x²– 11x + 3

Question 29.
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
Solution:
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
= [5x (x + 2) -3 (x + 2)] – [2x (4x – 3) + 5 (4x – 3)]
= [5x² + 1 0x – 3x – 6] – [8x² – 6x + 20x -15]
= (5x² + 7x – 6) – (8x² + 14x – 15)
= 5x² + lx – 6 – 8x² – 14x + 15
= 5x² – 8x² + 7x – 14x – 6 + 15
= -3x² – 7x + 9

Question 30.
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
Solution:
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
= [3x (4x + 3y) + 2y (4x + 3y)]-[2x (7_x-3y)-y(7_x-3y)]
= (12x² + 9xy + 8xy + 6y²) – (14x² – 6xy – 7xy + 3y²)
= (12x² + 17xy + 6y²) – (14x² – 13xy + 3y²)
= 12x² + 17xy + 6y² – 14x² + 13xy – 3y²
= 12x² – 14x² + 17xy + 13xy + 6y² – 3y²
= -2x² + 30xy + 3y²
= -2x² + 3y² + 30xy

Question 31.
(x²-3x + 2) (5x- 2) – (3x² + 4x-5) (2x- 1)
Solution:
(x²-3x + 2) (5x- 2) – (3x² + 4x-5) (2x- 1)
= [5x (x² – 3x + 2) -2 (x² – 3x + 2)] – [2x (3x² + 4x – 5) -1 (3x² + 4x – 5)]
= [5x³ – 15x² + 10x – 2x² + 6x – 4] – [6x³ + 8x² – 10x – 3x² – 4x + 5]
= [5x³ – 15x² – 2x² + 10xc + 6x – 4] – [6x³ + 8x² – 3x² – 10x – 4x + 5]
= (5x³ – 17x² + 16x-4) – (6x³ + 5x² – 14x + 5)
= 5x³ – 17x² + 16x – 4 – 6x³ – 5x² + 14x – 5
= 5x³ – 6x³ – 17x² – 5x² + 16x + 14x – 4 – 5
= -x³ – 22x² + 30x – 9

Question 32.
x³ – 2x² + 3x – 4) (x – 1) – (2x – 3) (x² – x + 1)
Solution:
(x³ – 2x² + 3x – 4) (x – 1) – (2x – 3) (x² – x + 1)
= [x (x³ – 2x² + 3x – 4) – 1 (x³ – 2x² + 3x – 4)] – [2x (x² – x + 1) – 3 (x² – x + 1)]
= [x⁴ – 2x³ + 3x² – 4x – x³ + 2x² – 3x + 4] [2x³ – 2x² + 2x – 3x² + 3x – 3]
= (x⁴ – 2x³ – x³ + 3x² + 2x² – 4x – 3x + 4) (2x³ – 2x² – 3x² + 2x + 3x – 3)
= (x⁴ – 3x³ + 5x² – 7x + 4) – (2x³ – 5x² + 5x – 3)
= x⁴ – 3x³ + 5x² – 7x + 4 – 2x³ + 5x² – 5x + 3
= x⁴ – 3x³ – 2x³ + 5x² + 5x² – 7x – 5x + 4 + 3
= x⁴ – 5x³ + 10x² – 12x + 7

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.