Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion (Including Properties and Uses) Ex 7B
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7B.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D
Question 1.
Find the fourth proportional to :
(i) 1.5, 4.5 and 3.5
(ii) 3a, 6a² and 2ab²
Solution:
(i) Let x be the fourth proportional to 1.5, 4.5

Question 2.
Find the third proportional to :
(i) 2\(\frac { 2 }{ 3 }\) and 4
(ii) a – b and a² – b²
Solution:

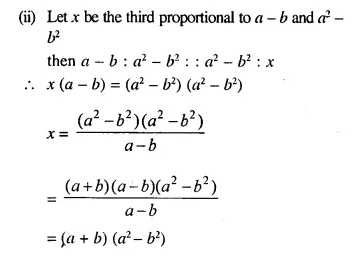
Question 3.
Find the mean proportional between :
(i) 6 + 3√3 and 8 – 4√3
(ii) a – b and a3 – a²b.
Solution:
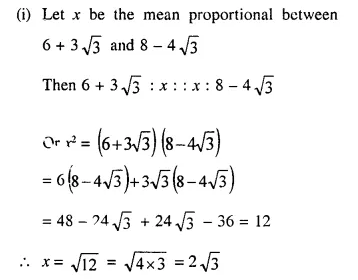
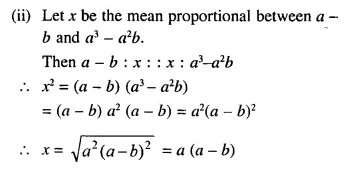
Question 4.
If x + 5 is the mean proportion between x + 2 and x + 9 ; find the value of x.
Solution:
x + 5 is the mean proportion between x + 2 and x + 9
(x + 5)² = (x + 2) (x + 9) {b² = ac}
⇒ x² + 10x + 25 = x² + 11x + 18
⇒ x² + 10x – x² – 11x = 18 – 25
⇒ -x = -7
⇒ x = 7
Hence x = 7
Question 5.
If x², 4 and 9 are in continued proportion, find x.
Solution:
x², 4 and 9 are in continued proportion
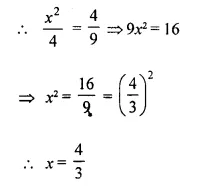
Question 6.
What least number must be added to each of the numbers 6, 15, 20 and 43 to make them proportional. (2005, 2013)
Solution:
Let x to be added to each number then 6 + x, 15 + x, 20 + x and 43 + x are in proportion.
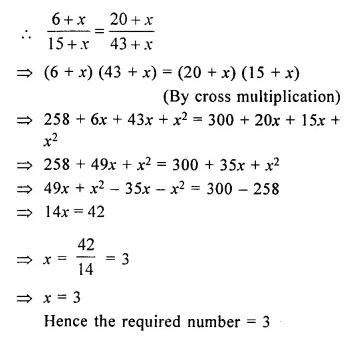
Question 7.

Solution:
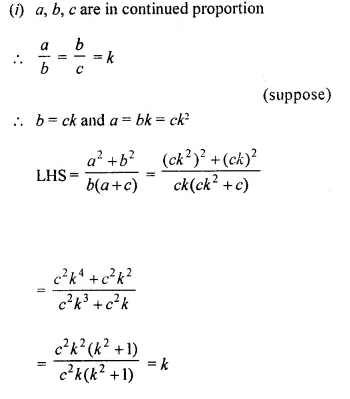

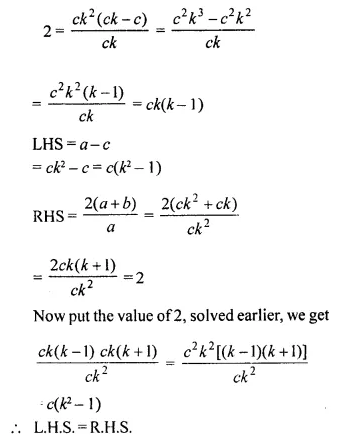

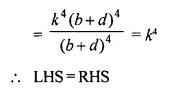
Question 8.
What least number must be subtracted from each of the numbers 7,17 and 47 so that the remainders are in continued pro-portion ?
Solution:
Let x be subtracted from each of the numbers 7, 17 and 47.
Then 7 – x, 17 – x and 47 – x are in continued proportion.
7 – x : 17 – x : : 17 – x : 47 – x
⇒ (7 – x) (47 – x) = (17 – x) (17 – x)
⇒ 329 – 7x – 47x + x² = 289 – 17x – 17x + x²
⇒ -7x – 47x + x² + 17x + 17x – x² = 289 – 329
⇒ -54x + 34x = – 40
⇒ -20x = -40
⇒ x = 2
2 is to be the subtracted
Question 9.
If y is the mean proportional between x and z; show that xy + yz is the mean proportional between x² + y² and y² + z².
Solution:
y is the mean proportional between x and z.
y² = xz
Now, we have to prove that
xy + yz is the mean proportional between x² + y² and y² + z²
i.e., (xy + yz)² = (x² + y²) (y² + z²)
L.H.S. (xy + yz)² = [y(x + z)]² = y² (x + z)² = xz (x + z)²
R.H.S. (x² + y²) (y² + z²) = (x² + xz) (xz + z²) = x (x + z) z (x + z) = xz (x + z)²
L.H.S. = R.H.S.
Hence proved.
Question 10.
If q is the mean proportional between p and r, show that: pqr (p + q + r)3 = (pq + qr + pr)3.
Solution:
q is the mean proportional between p and r,
q² = pr
Now L.H.S. = pqr (p + q + r)3
= qq² (p + q + r)3
= q3 (p + q + r)3
= [q(p + q + r)]3
= (pq + q² + qr)3
= (pq + pr + qr)3
= (pq + qr + pr)3
= R.H.S.
Question 11.
If three quantities are in continued proportion; show that the ratio of the first to the third is the duplicate ratio of the first to the second.
Solution:
Let x, y and z are three quantities which are
in continued proportion
Then x : y : y : z ⇒ y² = zx
Now, we have to prove that
x : z = x² : y² or xy² = zx²
L.H.S. = xy² = x x zx (y² = zx)
= x² z = R.H.S.
Hence Proved.
Question 12.
If y is the mean proportional between x and z, prove that:
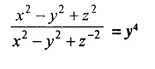
Solution:

Question 13.
Given four quantities a, b, c and d are in proportion. Show that:
(a – c) b² : (b – d) cd = (a² – b² – ab) : (c² – d² – cd)
Solution:
a, b, c and d are in proportion Then a : b :: c : d
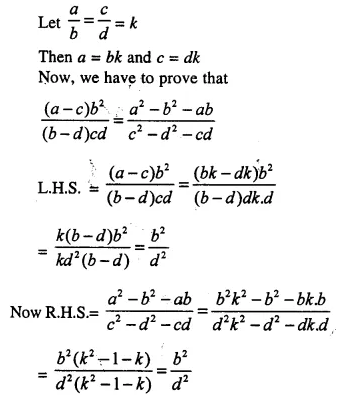
Question 14.
Find two numbers such that the mean proportional between them is 12 and the third proportional to them is 96.
Solution:
Let a and b be the two numbers, whose mean proportional is 12

Question 15.

Solution:

Question 16.
If p : q = r : s ; then show that: mp + nq : q = mr + ns : s.
Solution:
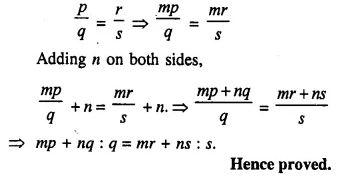
Question 17.
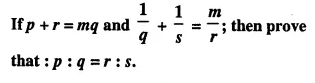
Solution:
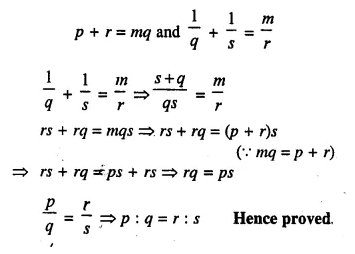
Question 18.
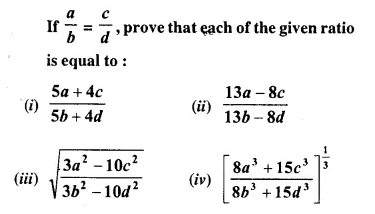
Solution:
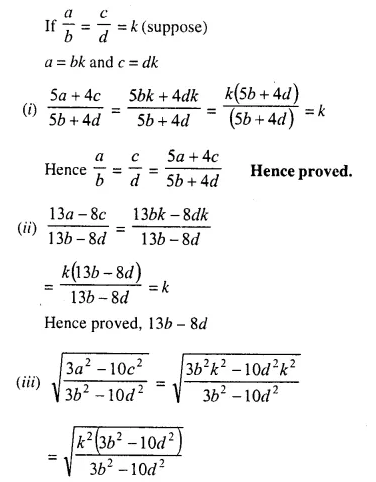

Question 19.
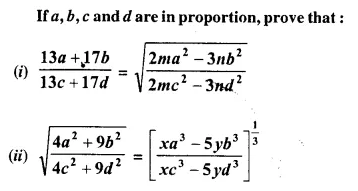
Solution:
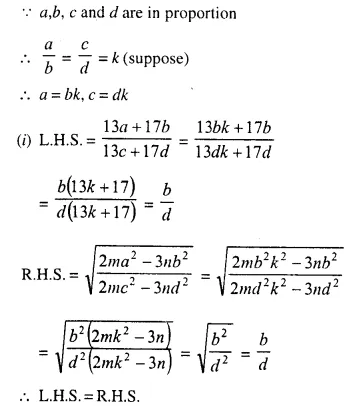
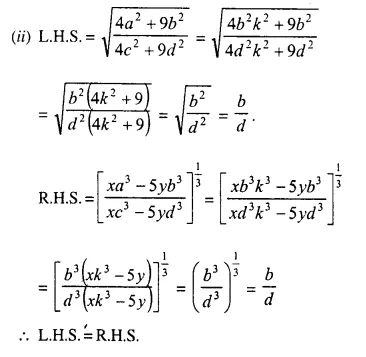
Question 20.
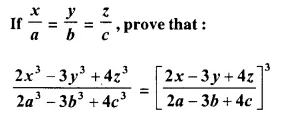
Solution:
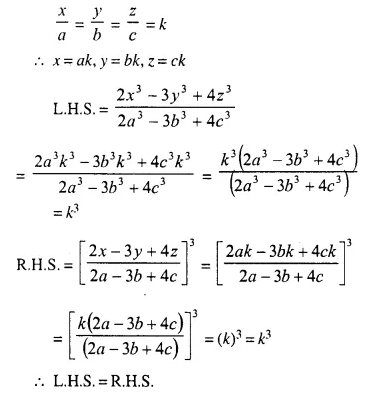
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.