RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A
These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A.
Other Exercises
- RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A
- RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9B
- RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9C
Question 1.
Solution:
Let x be the given number, then
(i) 5x = 40
(ii) x + 8 = 15
(iii) 25 – x = 7
(iv) x – 5 = 3
(v) 3x – 5 = 16
(vi) x – 12 = 24
(vii) 19 – 2x = 11
(viii) \(\\ \frac { x }{ 8 } \) = 7
(ix) 4x – 3 = 17
(x) 6x = x + 5
Question 2.
Solution:
(i) 7 less than from the number x is 14.
(ii) Twice the number y is 18.
(iii) 11 increased by thrice the number x is 17.
(iv) 3 less than twice the number x is 13.
(v) 30 less than 12 times the number is 6.
(vi) Quotient of twice the number z and 3 is
Question 3.
Solution:
(i) The given equation is 3x – 5 = 7
Substituting x = 4, we get
L.H.S. = 3 x – 5
= 3 x 4 – 5
= 12 – 5
= 7 = R.H.S.
It is verified that x = 4 is the root of the given equation.
(ii) The given equation is 3 + 2 x = 9
Substituting x = 3, we get L.H.S. = 3 + 2x
= 3 + 2 x 3
= 3 + 6 = 9
= R.H.S.
It is verified that x = 3 is the root of the given equation.
(iii) The given equation is 5x – 8 = 2x – 2
Substituting x = 2, we get
L.H.S. = 5x – 8
=5 x 2 – 8
= 10 – 8
= 2
R.H.S. = 2x – 2
= 2 x 2 – 2
= 4 – 2
= 2
L.H.S. = R.H.S.
Hence, it is verified that x = 2, is the root of the given equation.
(iv) The given equation is 8 – 7y = 1 Substituting y = 1, we get L.H.S. = 8 – 7y
= 8 – 7 x 1
= 8 – 7
= 1
= R.H.S.
Hence, it verified that y = 1 is the root of the given equation.
(v) The given equation is \(\\ \frac { z }{ 7 } \) = 8
Substituting the value of z = 56, we get
L.H.S.= \(\\ \frac { 56 }{ 7 } \)
= 8
= R.H.S.
Hence, it is verified that z = 56 is the root of the given equation.
Question 4.
Solution:
(i) The given equation is y + 9 = 13
We try several values of y and find L.H.S. and the R.H.S. and stop when L.H.S. = R.H.S.

When y = 4, we have L.H.S. = R.H.S.
So y = 4 is the solution of the given equation.
(ii) The given equation is x – 1 = 10
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
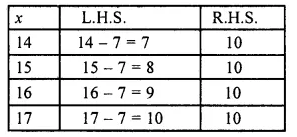
When x = 17, we hive L.H.S. = R.H.S
So x = 17 is the solution of the given equation.
(iii) The given equation is 4x = 28
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When x = 7, we have L.H.S. = R.H.S.
So x = 7 is the solution of the given equation.
(iv) The given equation is 3y = 36
We guess and try several values of y to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When y = 12, we have L.H.S. = R.H.S.
So y = 12 is the solution of the given equation.
(v) The given equation is 11 + x = 19
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When x = 8, we have L.H.S. = R.H.S.
So, x = 8 is the solution of the given equation.
(vi) The given equation is \(\\ \frac { x }{ 3 } \) = 4
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
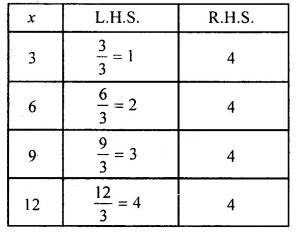
When x = 12, we have L.H.S. = R.H.S.
So, x = 12 is the solution of the given equation.
(vii) The given equation is 2 x – 3 = 9
We guess and try several values of x to find L.H.S. and R.H.S. and stop when

.’. When x = 6, we have L.H.S. = R.H.S.
So, x = 6 is the solution of the given equation.
L.H.S. = R.H.S.
(viii) The given equation is \(\\ \frac { 1 }{ 2 } \) x + 7 = 11
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.
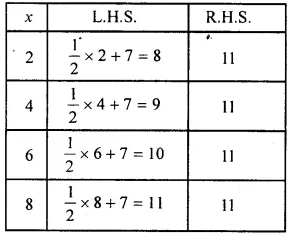
When x = 8, we have L.H.S. = R.H.S.
So, x = 8 is the solution of the given equation.
(ix) The given equation is 2y + 4 = 3y (x)
We guess and try several values of z to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When y = 4, we have L.H.S. = R.H.S. So, y = 4 is the solution of the given equation
(x) The given equation is z – 3 = 2z – 5
We guess and try several values of z to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S
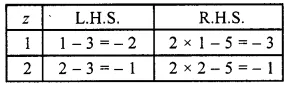
When z = 2, we have L.H.S. = R.H.S. So, z = 2 is the solution of the given equation.
Hope given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.