RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1
- RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
- RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
- RD Sharma Class 10 Solutions Chapter 8 Circles MCQS
Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
In the figure, PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB = 10 cm and CQ = 2 cm, what is the length PC ?
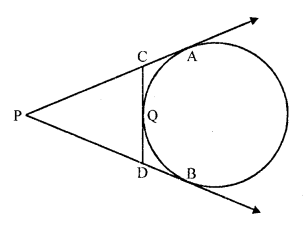
Solution:
In the figure, PA and PB are the tangents to the circle drawn from P
CD is the third tangent to the circle drawn at Q
PB = 10 cm, CQ = 2 cm
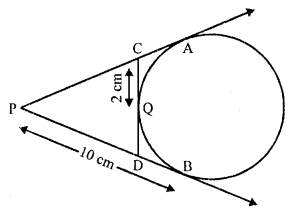
PA and PB are tangents to the circle
PA = PB = 10 cm
Similarly CQ and CA are tangents to the circle
CQ = CA = 2 cm
PC = PA – CA = 10 – 2 = 8 cm
Question 2.
What is the distance between two parallel tangents of a circle of radius 4 cm ?
Solution:
TT’ and SS’ are two tangents of a circle with centre O and radius 4 cm and TT’ || SS’
OP and OQ are joined
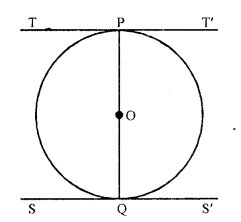
Now OP is the radius and TPT’ is the tangent
OP ⊥ TPT’
Similar OQ ⊥ SS’
But TT’ || SS’
POQ is the diameter
Which is 4 x 2 = 8 cm
Distance between the two parallel tangents is 8 cm
Question 3.
The length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What is the radius of the circle ?
Solution:
PA is a tangent to the circle from P at a distance of 5 cm from the centre O
PA = 4 cm
OA is joined and let OA = r
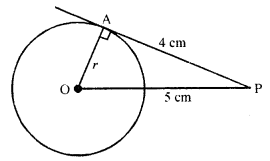
Now in right ∆OAP,
OP² = OA² + PA²
=> (5)² = r² + (4)²
=> 25 = r + 16
=> r² = 25 – 16 = 9 = (3)²
r = 3
Radius of the circle = 3 cm
Question 4.
Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in the following figure. If they are inclined to each other at an angle of 100°, then what is the value of ∠POQ ?
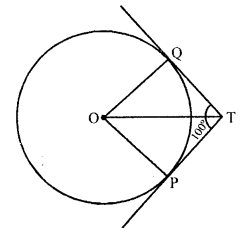
Solution:
TP and TQ are the tangents from T to the circle with centre O and ∠PTQ = 100°
OT, OP and OQ are joined
OP and OQ are radius
OP ⊥ PT and OQ ⊥ QT
Now in quadrilateral OPTQ,
∠POQ + ∠OPT + ∠PTQ + ∠OQT = 360° (Sum of angles of a quadrilateral)
=> ∠POQ + 90° + 100° + 90° = 360°
=> ∠POQ + 280° = 360°
=> ∠POQ = 360° – 280° = 80°
Hence ∠POQ = 80°
Question 5.
What is the distance between two parallel tangents to a circle of radius 5 cm?
Solution:
In a circle, the radius is 5 cm and centre is O
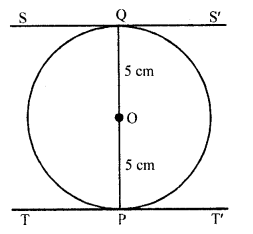
TT’ and SS’ are two tangents at P and Q to the circle
Such that TT’ || SS’
Join OP and OQ
OP is radius and TPT’ is the tangent
OP ⊥ TT’
Similarly OQ ⊥ SS’
POQ is the diameter of the circle
Now length of PQ = OP + OQ = 5 + 5 = 10 cm
Hence distance between the two parallel tangents = 10 cm
Question 6.
In Q. No. 1, if PB = 10 cm, what is the perimeter of ∆PCD ?
Solution:
In the figure, PB = 10 cm, CQ = 2 cm
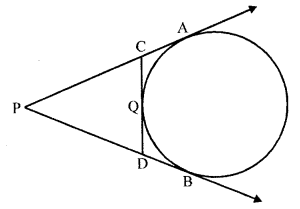
PA and PB are tangents to the give from P
PA = PB = 10 cm
Similarly, CA and CQ are the tangents
CA = CQ = 2 cm
and DB and DQ are the tangents
DB = DQ
Now, perimeter of ∆PCD
PC + PD + CQ + DQ
= PC + CQ + PD + DQ
= PC + CA + PD + DB {CQ = CA and DQ = DB}
= PA + PB = 10 + 10 = 20 cm
Question 7.
In the figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then find the length of BR. (C.B.S.E. 2009)
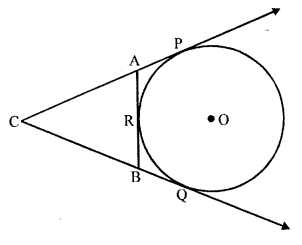
Solution:
Given : In the figure, CP and CQ are tangents to a circle with centre O
ARB is a third tangent to the circle at R
CP = 11 cm, BC = 7 cm
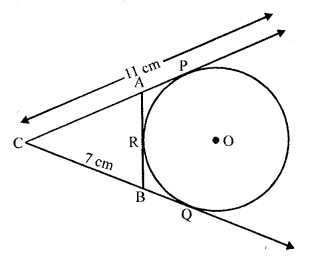
To find : The length of BR
BQ and BR are tangents to the circle drawn from B
BQ = BR ….(i)
Similarly CQ = CP
=> BC + BQ = CP = 11 (CP = 11 cm and BC = 7 cm)
=> 7 + BQ = 11
=> BQ = 11 – 7
BQ = 4 cm
But BQ = BR
BR = 4 cm
Question 8.
In the figure, ∆ABC is circumscribing a circle. Find the length of BC. (C.B.S.E. 2009)
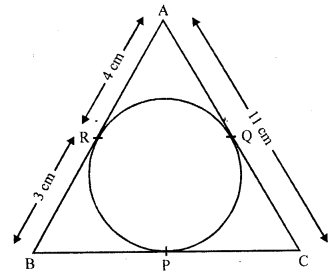
Solution:
∆ABC is circumscribing a circle which touches it at P, Q and R
AC = 11 cm, AR = 4 cm, BR = 3 cm
Now we have to find BC
AR and AQ are tangents to the circle from A
AQ = AR = 4 cm
Then CQ = AC – AQ = 11 – 4 = 7 cm
Similarly,
CP and CQ are tangents from C
CP = CQ = 7 cm
and BP and BR are tangents from B
BP = BR = 3 cm
Now BC = BP + CP = 3 + 7 = 10 cm
Question 9.
In the figure, CP and CQ are tangents from an external point C to a circle with centre O. AB is another tangent which touches the circle at R. If CP = 11 cm and BR = 4 cm, find the length of BC. [CBSE 2010]
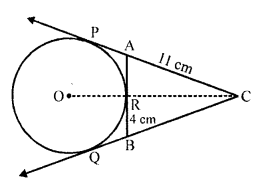
Solution:
CP and CQ are the tangents to the circle from C.
AB is another tangent to the same circle which touches at R and meets the first two tangents at A and B. O is the centre of the circle.
OC is joined
CP = 11 cm, BR = 4 cm
CP and CQ are tangents to the circle
CP = CQ = 11 cm
Similarly from B, CR and BQ are the tangents
BQ = BR = 4 cm
Now BC = CQ – BQ = 11 – 4 = 7 cm
Question 10.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
Two concentric circles with centre O, have radii 5 cm and 3 cm
AB is a chord which touches the smaller circle at P
OP is joined which is radius of smaller circle
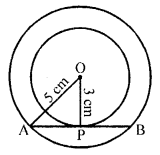
P is mid-point of AB
OP = 3 cm and OA = 5 cm
Now in right ∆OAP
OA² = OP² + AP²
(5)² = (3)² + AP²
=> 25 = 9 + AP²
=> AP² = 25 – 9 = 16 = (4)²
AP = 4 cm
AB = 2 AP = 2 x 4 cm = 8 cm
Question 11.
In the given figure, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB. [CBSE 2015]
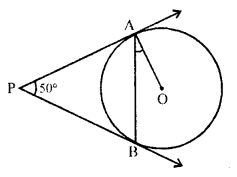
Solution:
In the given figure,
PA and PB are tangents to the circle from P
PA = PB
∠APB = 50°, OA is joined
To find ∠OAB
In ∆PAB
PA = PB
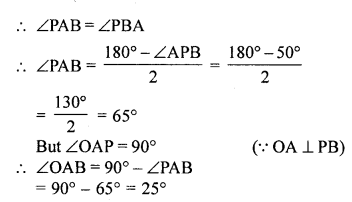
Question 12.
In the figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT = 60°. Then, find ∠PRQ. [NCERT Exemplar]
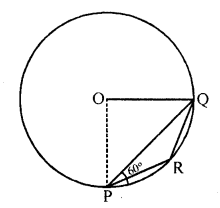
Solution:
∠OPQ = ∠OQP = 30°, i.e., ∠POQ = 120°
Also, ∠PRQ = \(\frac { 1 }{ 2 }\) reflex ∠POQ
Question 13.
In the figure, PQL and PRM are tangents to the circle with centre O at the points Q and R respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then, find ∠QSR. [NCERT Exemplar]
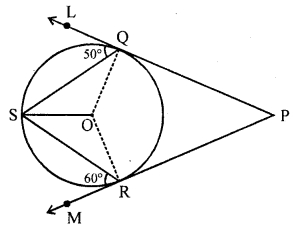
Solution:
Here ∠OSQ = ∠OQS = 90° – 50° = 40°
and ∠RSO = ∠SRO = 90° – 60° = 30°.
Therefore, ∠QSR = 40° + 30° = 70°
Question 14.
In the figure, BOA is a diameter of a circle and the tangent at a point P meets BA produced at T. If ∠PBO = 30°, then find ∠PTA. [NCERT Exemplar]
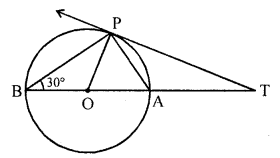
Solution:
As ∠BPA = 90°,
∠PAB = ∠OPA = 60°
Also OP ⊥ PT.
Therefore, ∠APT = 30°
and ∠PTA = 60° – 30° = 30°
Hope given RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.