RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.
Prove the following trigonometric identities :
Question 1.
(1 – cos2 A) cosec2 A = 1
Solution:
(1 – cos2 A) cosec2 A = 1
L.H.S. = (1 – cos2 A) cosec2 A = sin2 A cosec2 A (∵ 1 – cos2 A = sin2 A)
= (sin A cosec A)2 = (l)2 = 1 = R.H.S. {sin A cosec A = 1 }
Question 2.
(1 + cot2 A) sin2 A = 1
Solution:
(1 + cot2 A) sin2 A = 1
L.H.S. = (1 + cot2 A) (sin2 A)
= cosec2 A sin2 A {1 + cot2 A = cosec2 A}
= [cosec A sin A]2
= (1)2= 1 = R.H.S. (∵ sin A cosec A = 1
Question 3.
tan2 θ cos2 θ = 1- cos2 θ
Solution:
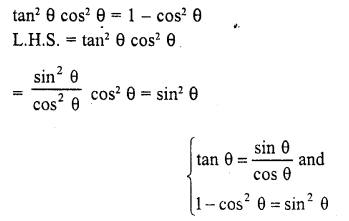
![]()
Question 4.
![]()
Solution:
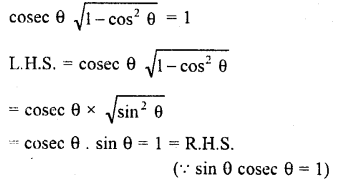
Question 5.
(sec2 θ – 1) (cosec2 θ – 1) = 1
Solution:
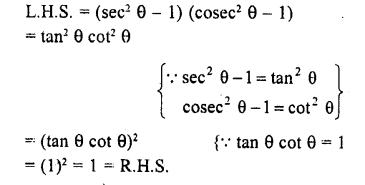
Question 6.
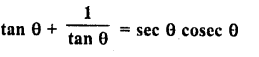
Solution:

Question 7.
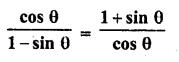
Solution:
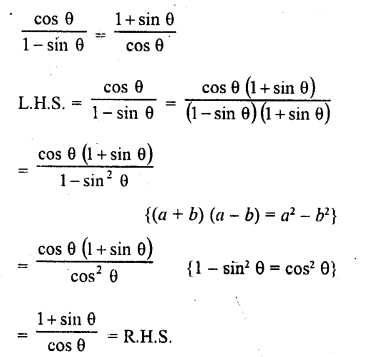
Question 8.
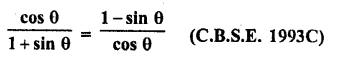
Solution:
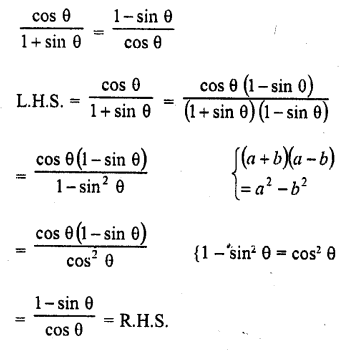
Question 9.
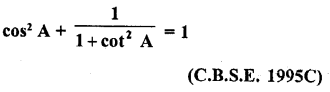
Solution:
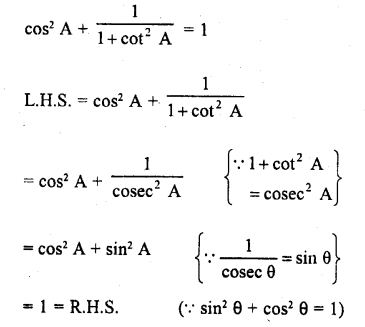
Question 10.
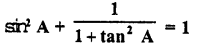
Solution:
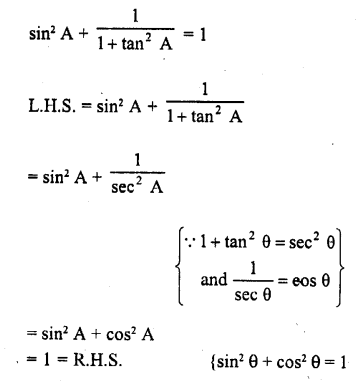
Question 11.
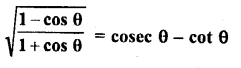
Solution:
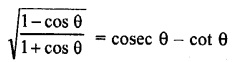
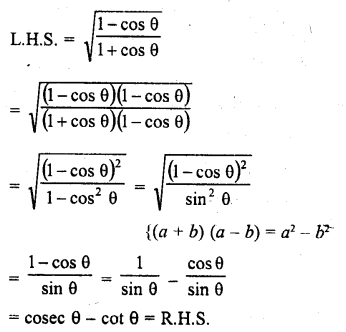
Question 12.
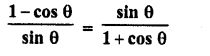
Solution:
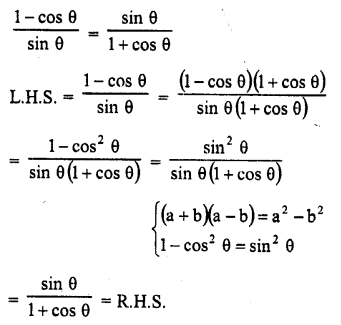
Question 13.
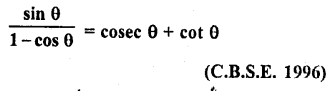
Solution:
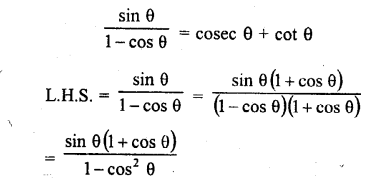
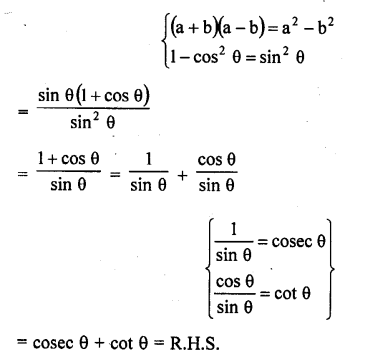
Question 14.
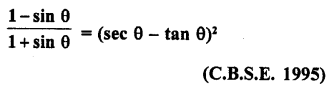
Solution:
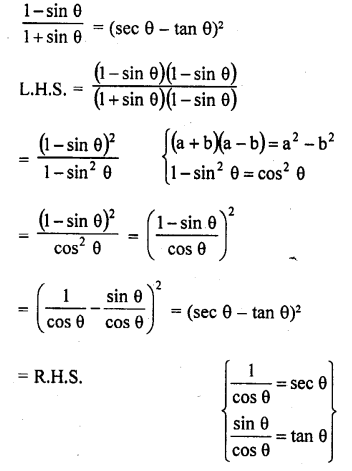
Question 15.
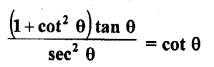
Solution:

Question 16.
tan2 θ – sin2 θ = tan2 θ sin2 θ
Solution:
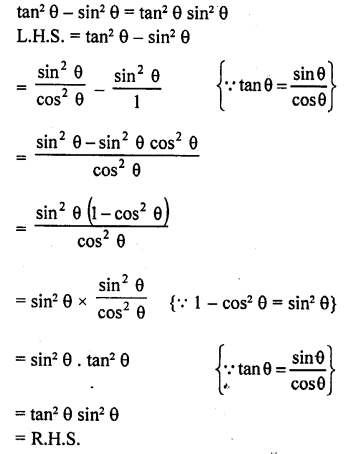
Question 17.
(sec θ + cos θ ) (sec θ – cos θ ) = tan2 θ + sin2 θ
Solution:
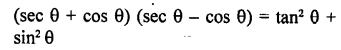
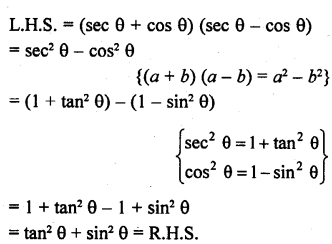
Question 18.
(cosec θ + sin θ) (cosec θ – sin θ) = cot2 θ + cos2 θ
Solution:
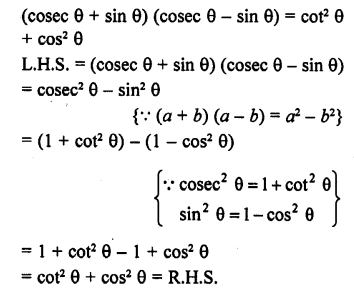
Question 19.
sec A (1 – sin A) (sec A + tan A) = 1 (C.B.S.E. 1993)
Solution:
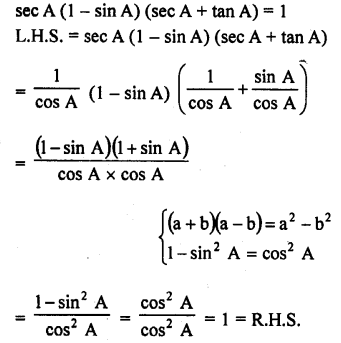
Question 20.
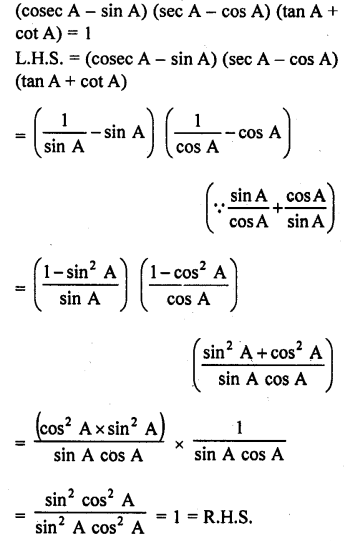
(cosec A – sin A) (sec A – cos A) (tan A + cot A) = 1
Solution:
Question 21.
(1 + tan2 θ) (1 – sin θ) (1 + sin θ) = 1
Solution:
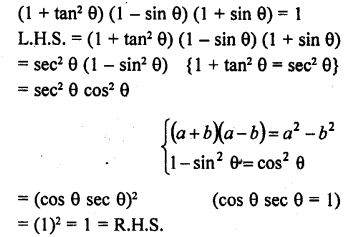
Question 22.
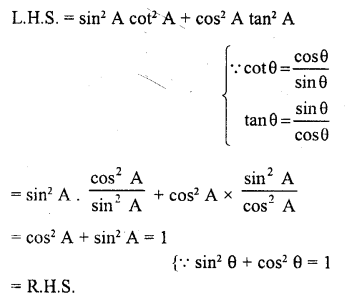
sin2 A cot2 A + cos2 A tan2 A = 1 (C.B.S.E. 1992C)
Solution:
![]()
Question 23.
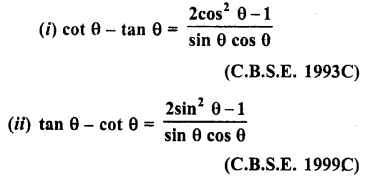
Solution:
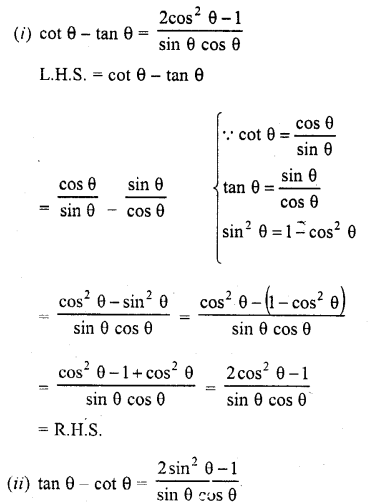
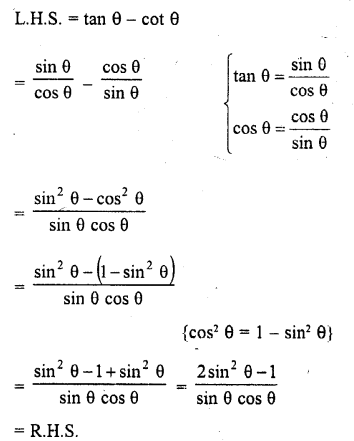
Question 24.
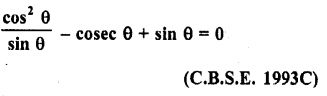
Solution:
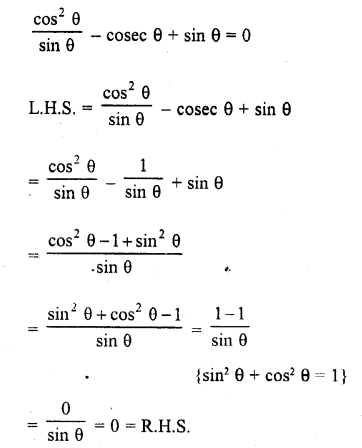
Question 25.
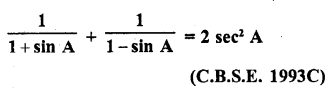
Solution:

Question 26.
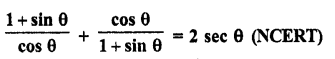
Solution:
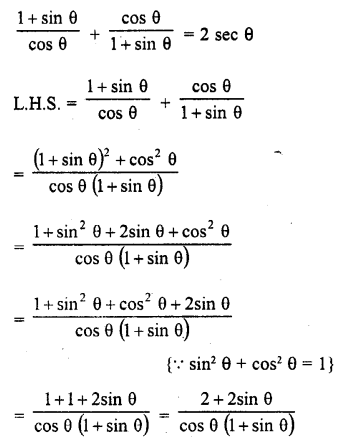
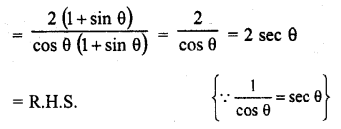
Question 27.
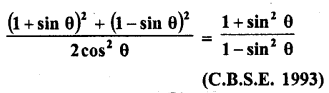
Solution:
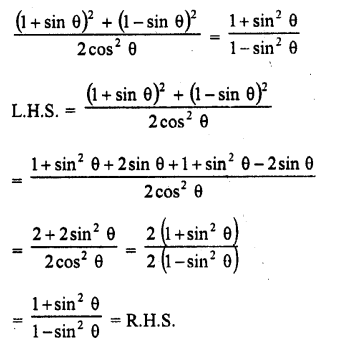
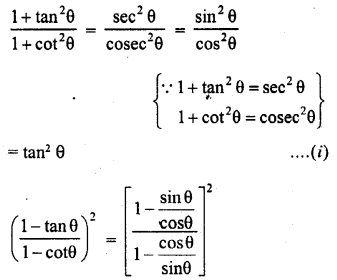
Question 28.
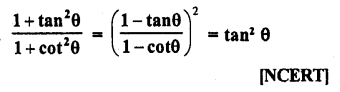
Solution:

Question 29.
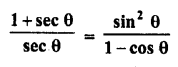
Solution:

Question 30.
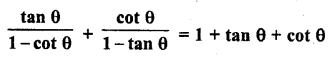
Solution:
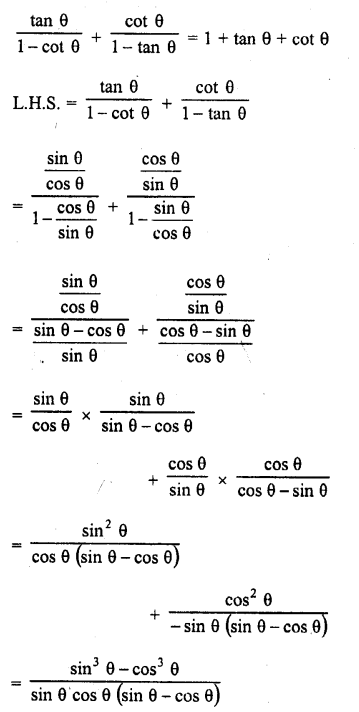
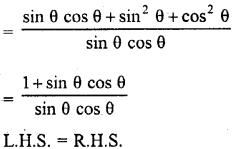
Question 31.
sec6 θ= tan6 θ + 3 tan2 θ sec2 θ + 1
Solution:
Question 32.
cosec6 θ = cot6 θ+ 3cot2θ cosec2 θ + 1
Solution:
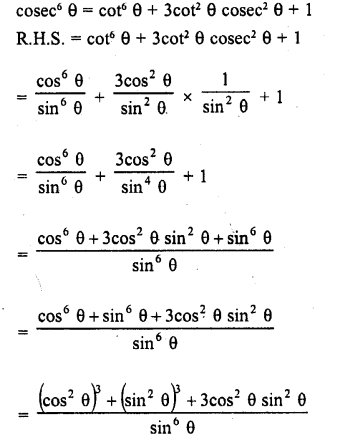
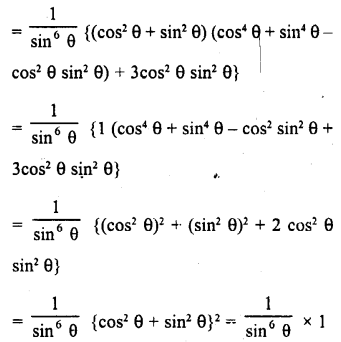
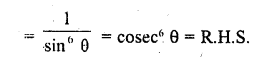
Question 33.
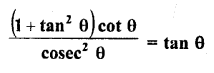
Solution:
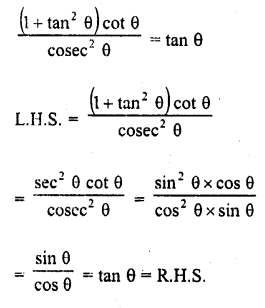
Question 34.
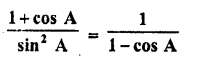
Solution:

Question 35.
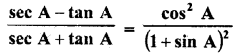
Solution:

Question 36.
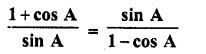
Solution:
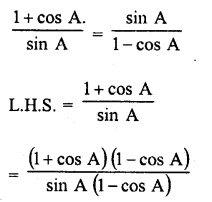
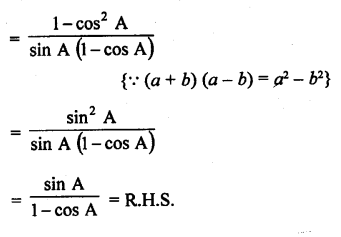
Question 37.
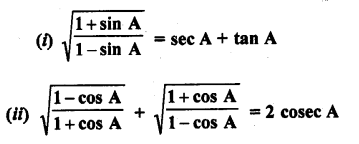
Solution:


Question 38.

Solution:

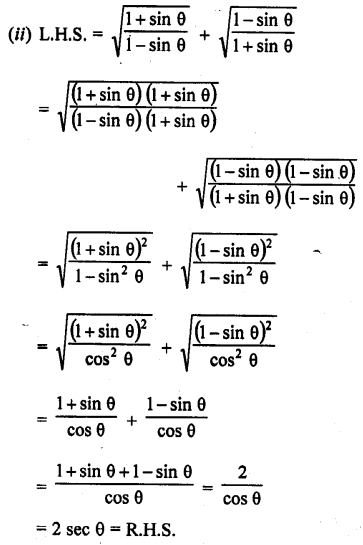
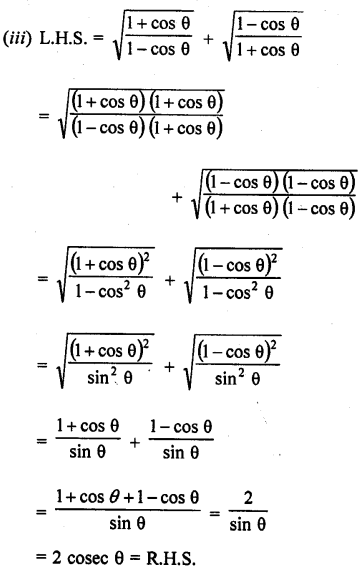
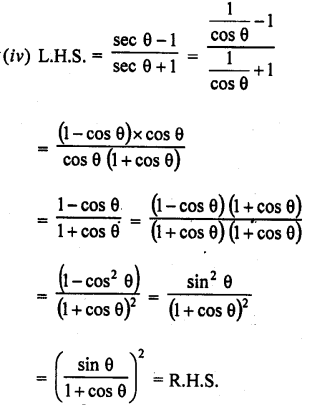
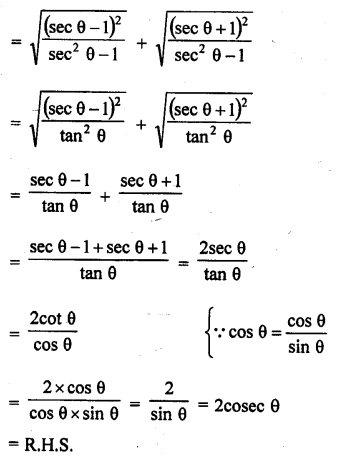
Question 39.
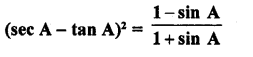
Solution:

Question 40.
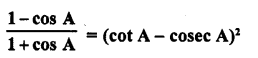
Solution:
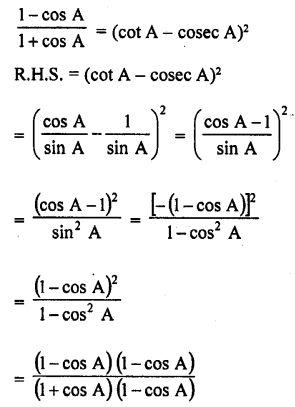

Question 41.
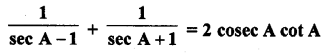
Solution:
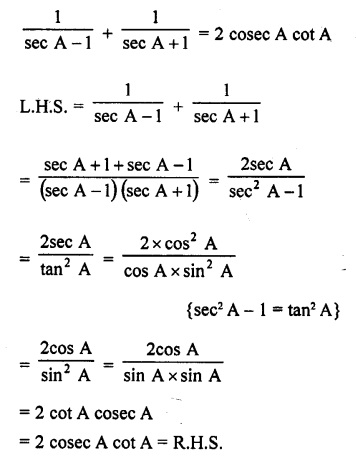
Question 42.
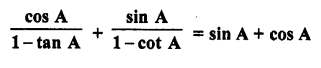
Solution:
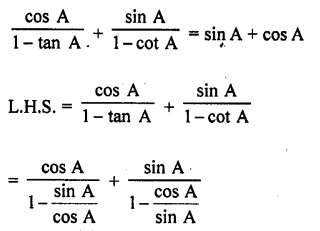
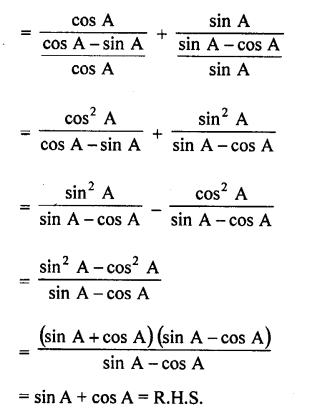
Question 43.
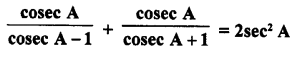
Solution:

Question 44.
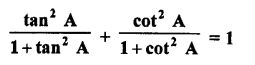
Solution:
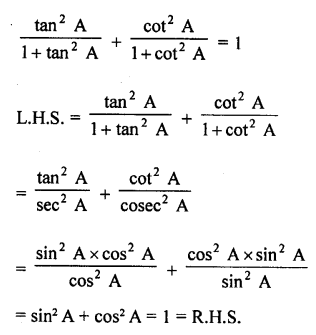
Question 45.
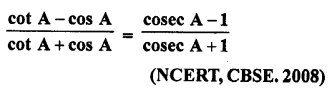
Solution:
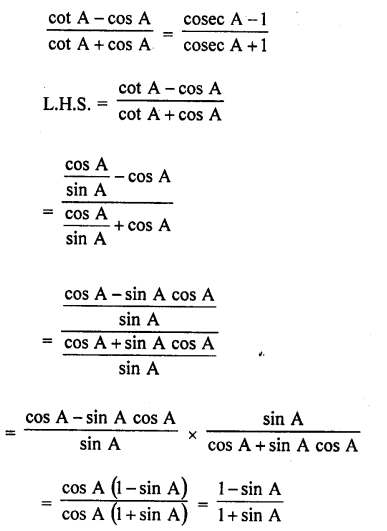

Question 46.
Solution:
Question 47.
Solution:
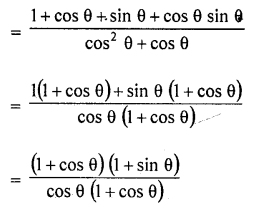

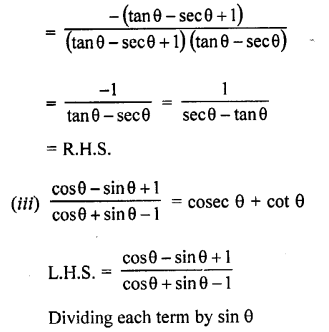

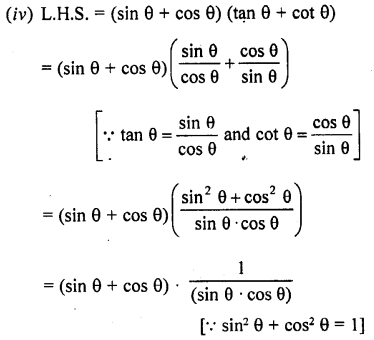
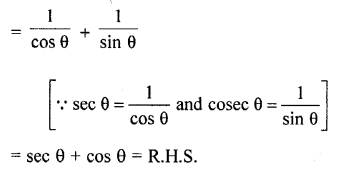
Question 48.
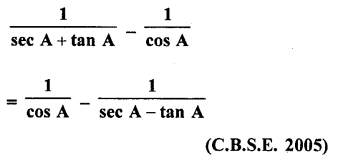
Solution:
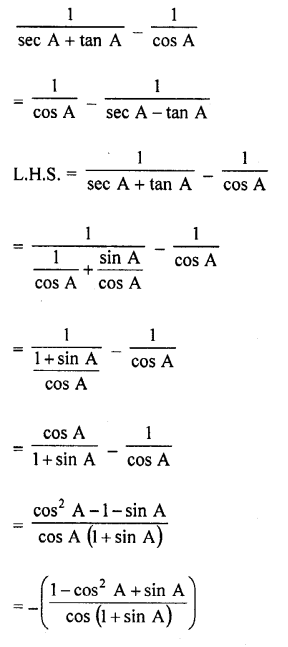

Question 49.
tan2 A + cot2 A = sec2 A cosec2 A – 2
Solution:
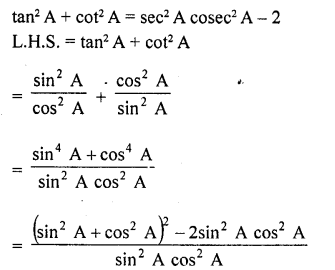
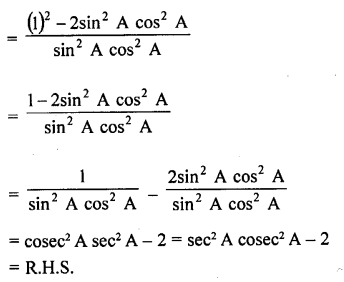
Question 50.
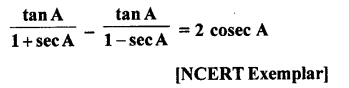
Solution:

Question 51.
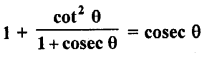
Solution:
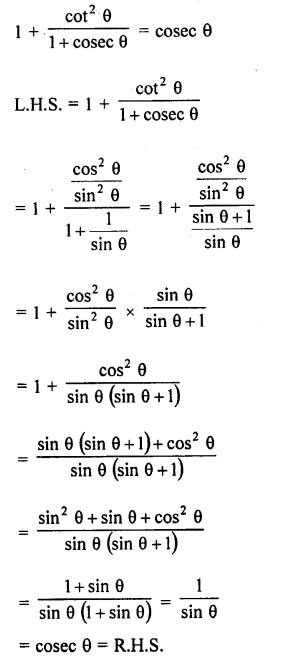
Question 52.
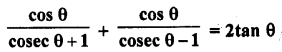
Solution:
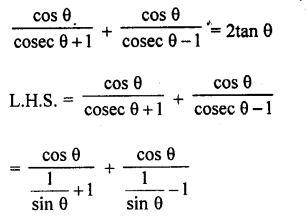
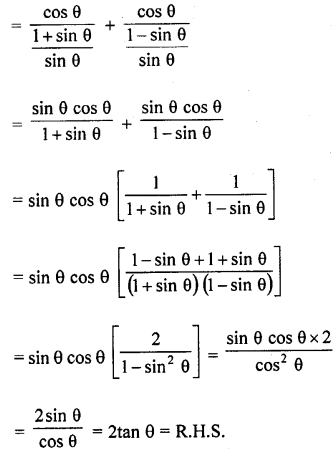
Question 53.
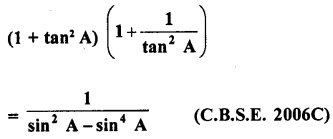
Solution:
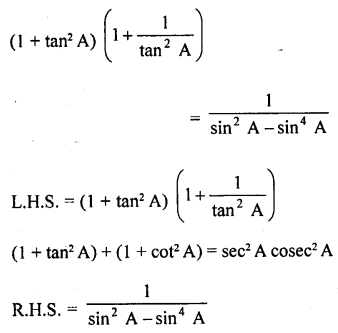
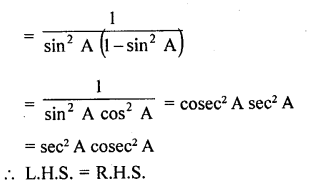
Question 54.
sin2 A cos2 B – cos2 A sin2 B = sin2 A – sin2 B.
Solution:
L.H.S. = sin2 A cos2 B – cos2 A sin2 B
= sin2 A (1 – sin2 B) – (1 – sin2 A) sin2 B
= sin2 A – sin2 A sin2 B – sin2 B + sin2 A sin2 B
= sin2 A – sin2 B
Hence, L.H.S. = R.H.S.
Question 55.
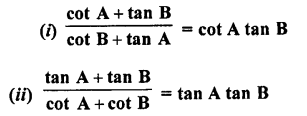
Solution:


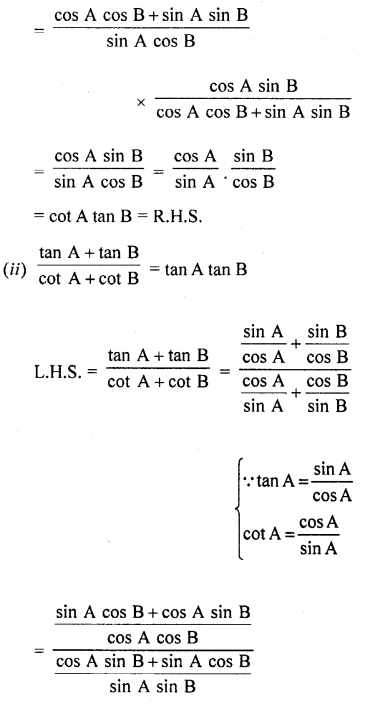
Question 56.
cot2 A cosec2 B – cot2 B cosec2 A = cot2 A – cot2 B
Solution:
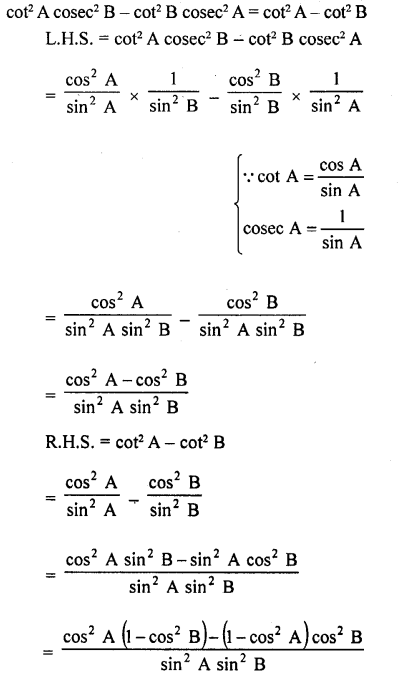
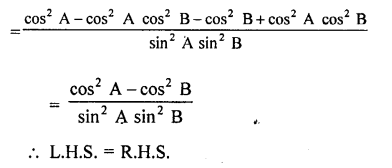
Question 57.
tan2 A sec2 B – sec2 A tan2 B = tan2 A – tan2 B
Solution:
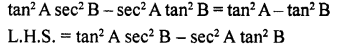
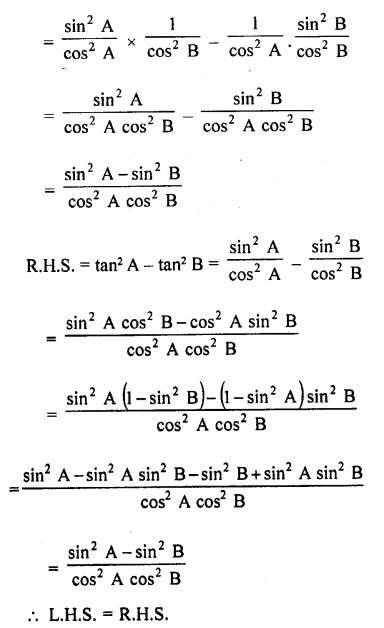
Prove the following identities: (58-75)
Question 58.
If x = a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x1 – y2 = a2 – b1. [C.B.S.E. 2001, 20O2C]
Solution:
x – a sec θ + b tan θ
y = a tan θ + b sec θ
Squaring and subtracting, we get
x2-y2 = {a sec θ + b tan θ)2 – (a tan θ + b sec θ)2
= (a2 sec2 θ + b2 tan2 θ + 2ab sec θ x tan θ) – (a2 tan2 θ + b2 sec2 θ + 2ab tan θ sec θ)
= a2 sec2 θ + b tan2 θ + lab tan θ sec θ – a2 tan2 θ – b2 sec2 θ – 2ab sec θ tan θ
= a2 (sec2 θ – tan2 θ) + b2 (tan2 θ – sec2 θ)
= a2 (sec2 θ – tan2 θ) – b2 (sec2 θ – tan2 θ)
= a2 x 1-b2 x 1 =a2-b2 = R.H.S.
Question 59.
If 3 sin θ + 5 cos θ = 5, prove that 5 sin θ – 3 cos θ = ±3
Solutioon:

Question 60.
If cosec θ + cot θ = mand cosec θ – cot θ = n,prove that mn= 1
Solution:
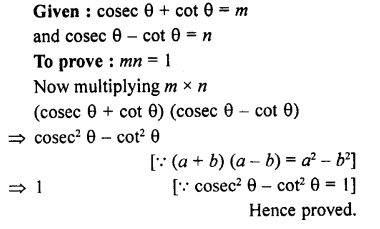
Question 61.
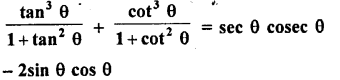
Solution:
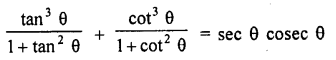
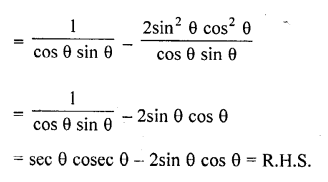
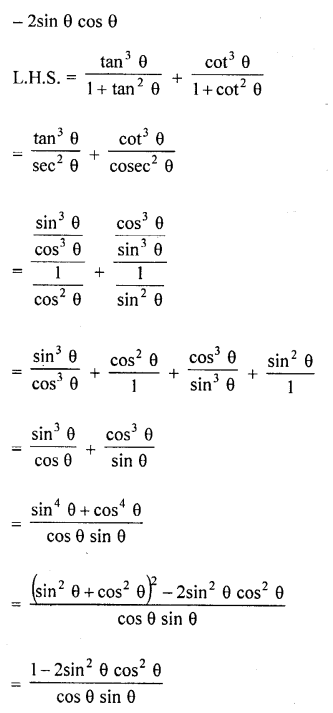
Question 62.
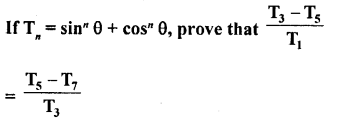
Solution:
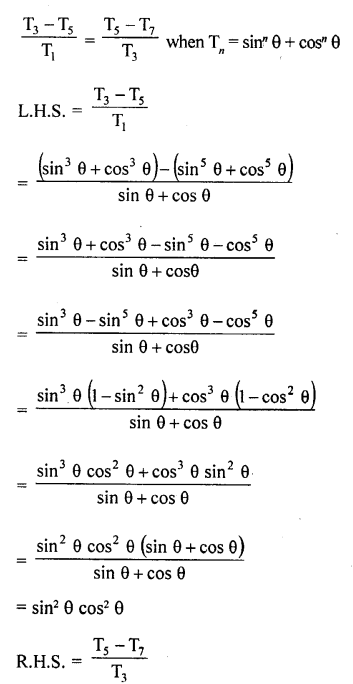
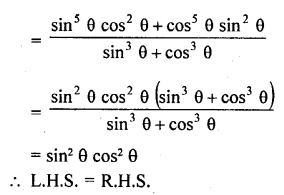
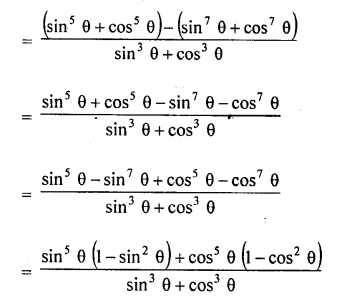
Question 63.
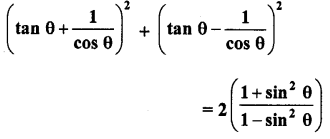
Solution:
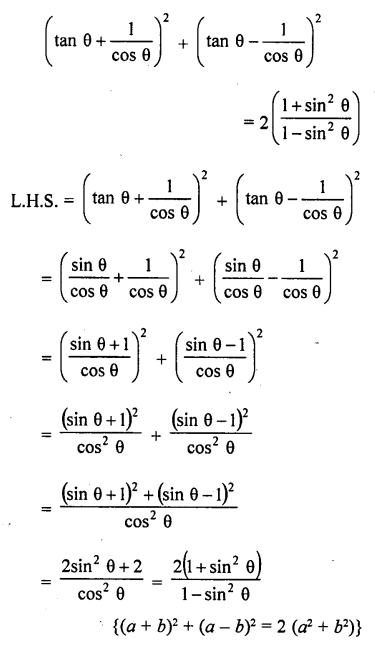
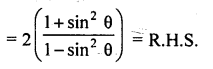
Question 64.
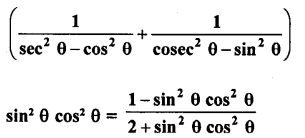
Solution:
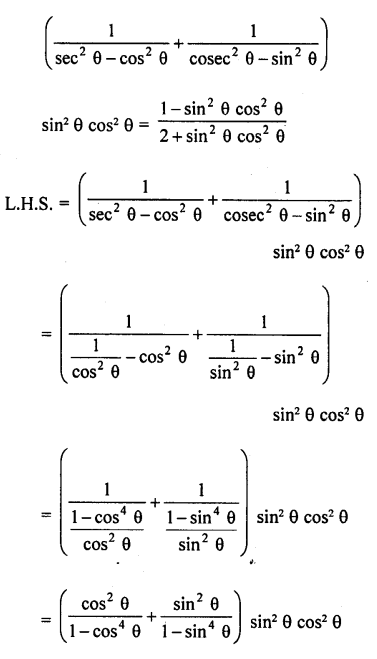
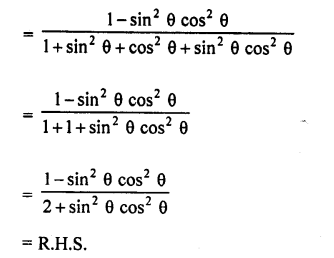
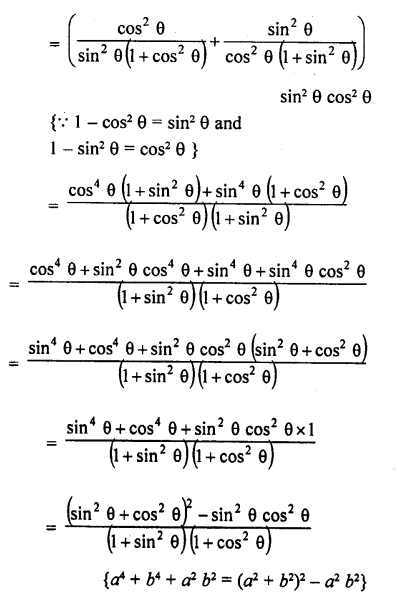
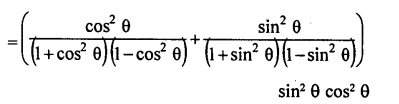
Question 65.
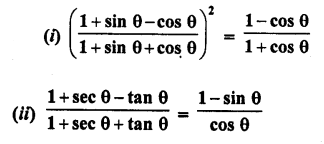
Solution:
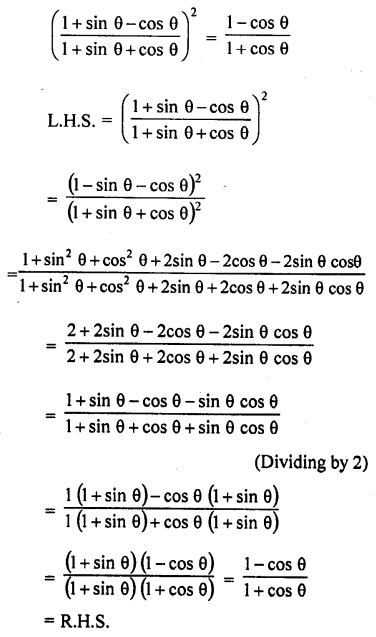
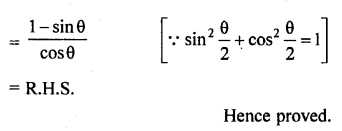
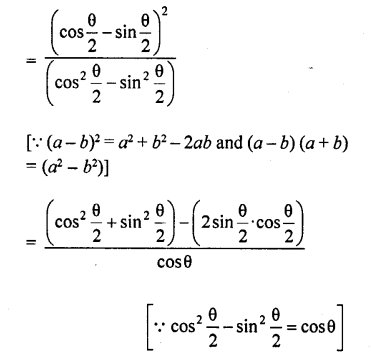
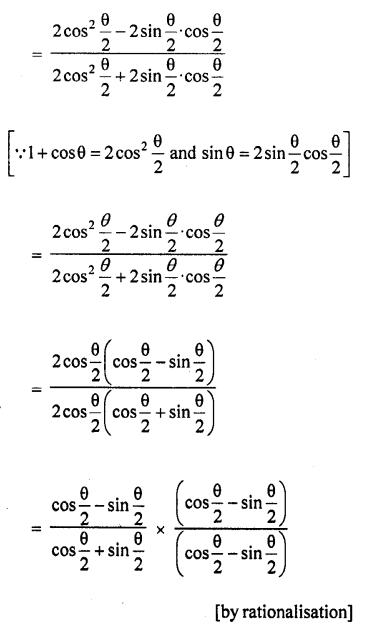
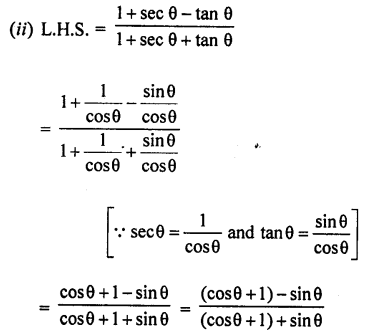
Question 66.
(sec A + tan A – 1) (sec A – tan A + 1) = 2 tan A
Solution:
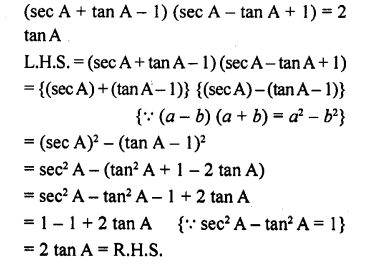
Question 67.
(1 + cot A – cosec A) (1 + tan A + sec A) = 2
Solution:


Question 68.
(cosec θ – sec θ) (cot θ – tan θ) = (cosec θ + sec θ) (sec θ cosec θ-2)
Solution:
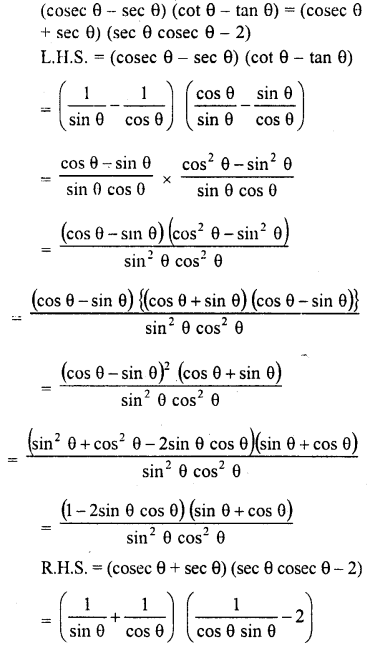
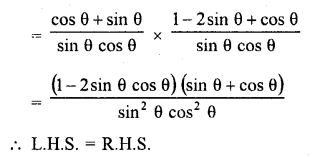
Question 69.
(sec A – cosec A) (1 + tan A + cot A) = tan A sec A – cot A cosec A
Solution:

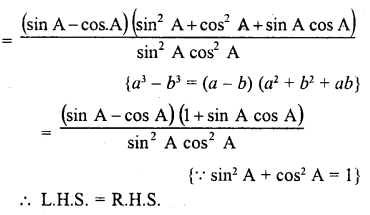
Question 70.
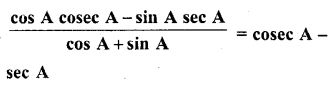
Solution:

Question 71.
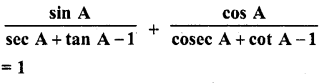
Solution:
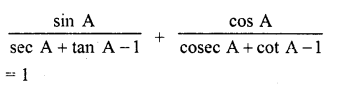

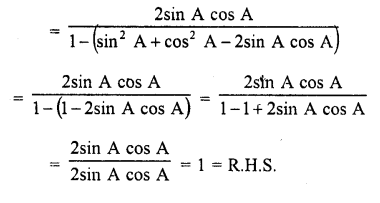
Question 72.
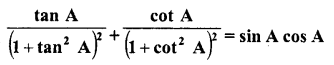
Solution:
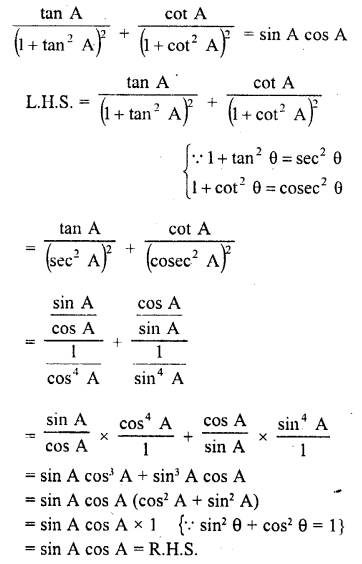
Question 73.
sec4 A (1 – sin4 A) – 2tan2 A = 1
Solution:
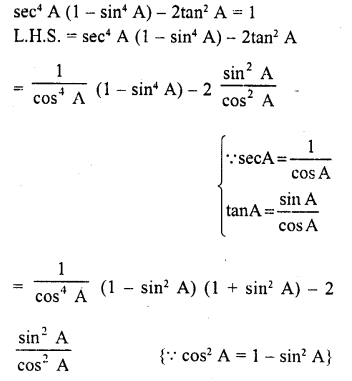
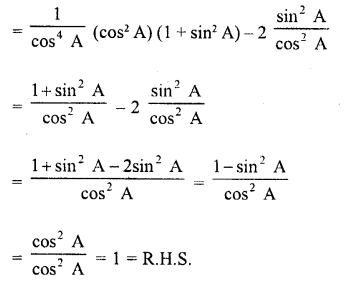
Question 74.
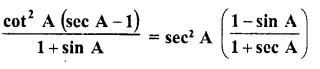
Solution:

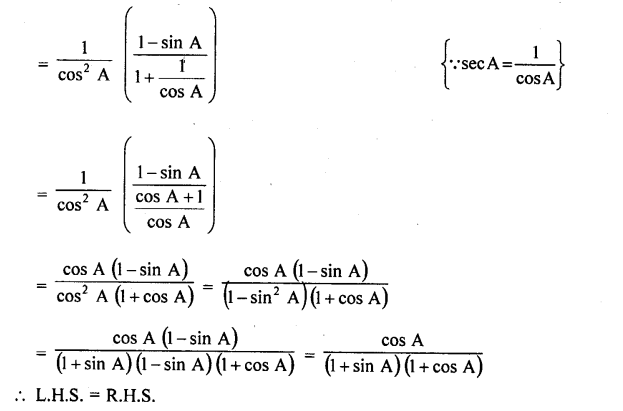
Question 75.
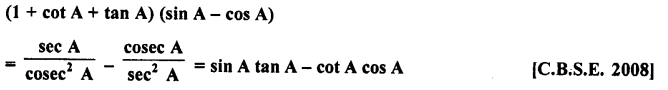
Solution:

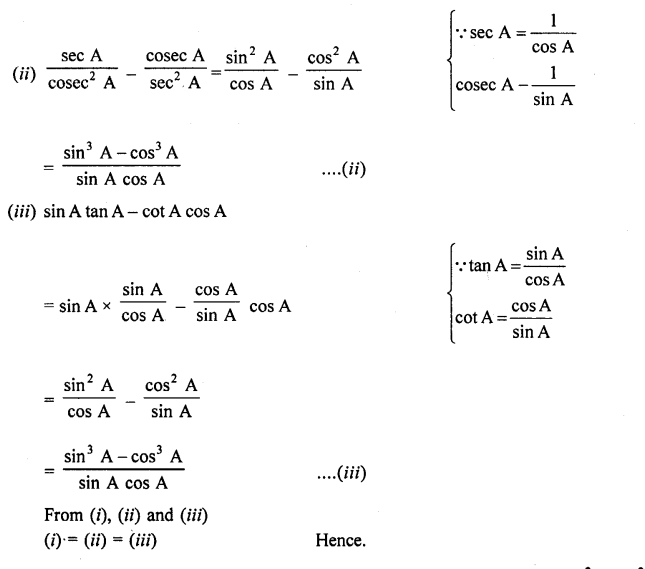
Question 76.
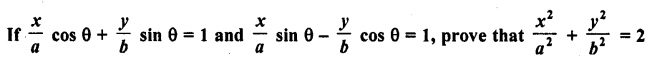
Solution:
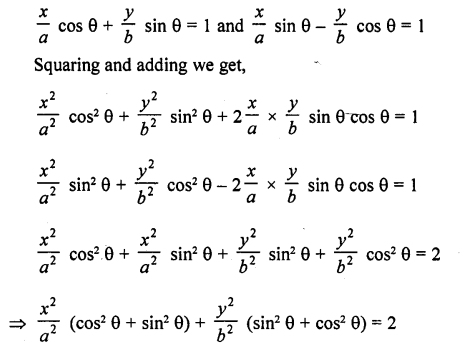
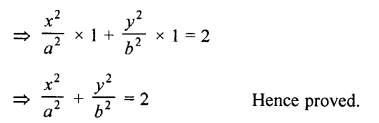
Question 77.
If cosec θ – sin θ = a3, sec θ – cos θ = b3, prove that a2b2 (a2 + b2) = 1
Solution:
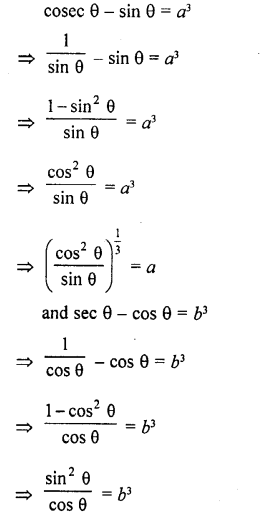
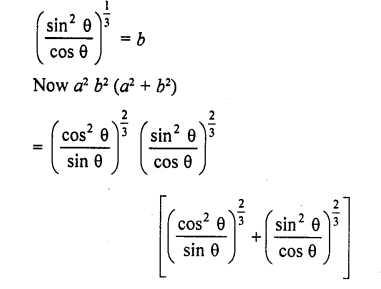
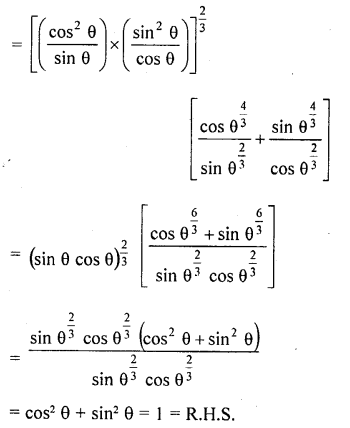
Question 78.
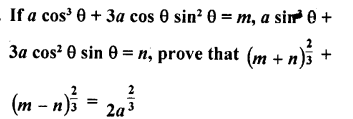
Solution:

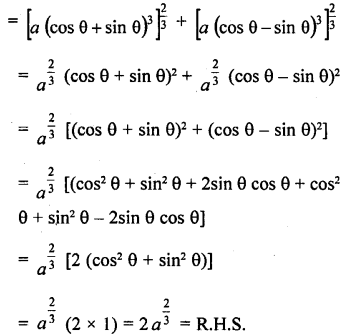
Question 79.
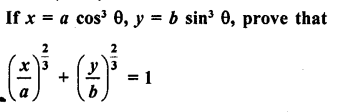
Solution:
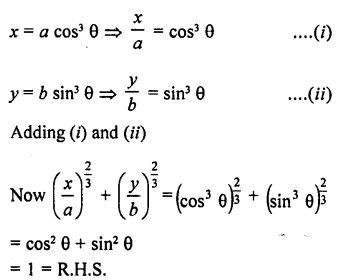
Question 80.
If a cos θ + b sin θ = m and a sin θ – b cos θ = n, prove that a2 + b2 = m2 + n2
Solution:
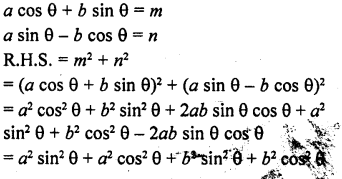
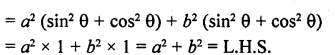
Question 81.
If cos A + cos2 A = 1, prove that sin2 A + sin4 A = 1
Solution:
cos A + cos2 A = 1
⇒ cos A = 1 – cos2 A
⇒cos A = sin2 A
Now, sin2 A + sin4 A = sin2 A + (sin2 A)2
= cos A + cos2 A = 1 = R.H.S.
Question 82.
If cos θ + cos2 θ = 1, prove that
sin12 θ + 3 sin10 θ + 3 sin8 θ + sin6 θ + 2 sin4 θ + 2 sin2 θ-2 = 1
Solution:
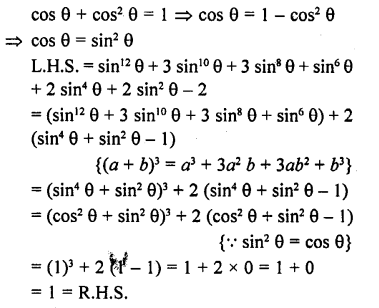
Question 83.
Given that :
(1 + cos α) (1 + cos β) (1 + cos γ) = (1 – cos α) (l – cos β) (1 – cos γ)
Show that one of the values of each member of this equality is sin α sin β sin γ
Solution:
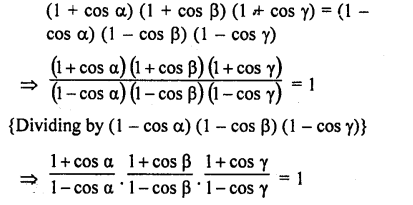
Question 84.
Solution:
Question 85.
Solution:
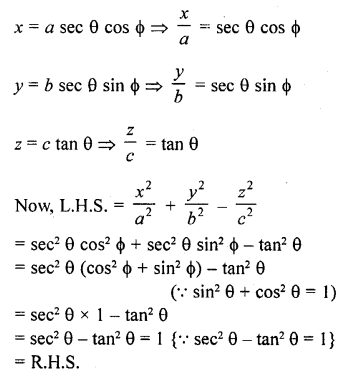
Question 86.
If sin θ + 2cos θ = 1 prove that 2sin θ – cos θ = 2. [NCERT Exemplar]
Solution:
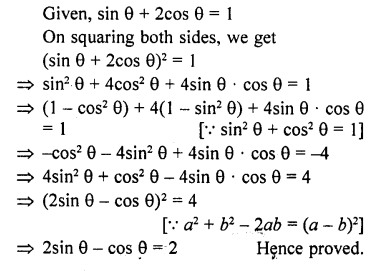
Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.