ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Ex 11
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test
Choose the correct answer from the given four options (1 to 12) :
Question 1.
The points A (9, 0), B (9, 6), C ( – 9, 6) and D ( – 9, 0) are the vertices of a
(a) rectangle
(b) square
(c) rhombus
(d) trapezium
Solution:
A (9, 0), B (9, 6), C (-9, 6), D (-9, 0)
AB² = (x2 – x1)² + (y2 – y1)²
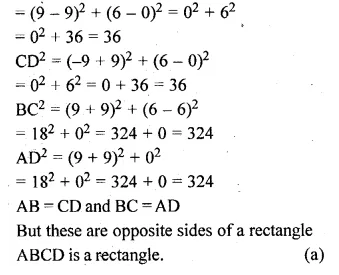
Question 2.
The mid-point of the line segment joining the points A ( – 2, 8) and B ( – 6, – 4) is
(a) ( – 4, – 6)
(b) (2, 6)
(c) ( – 4, 2)
(d) (4, 2)
Solution:
Mid-point of the line segment joining the points A (-2, 8), B (-6, -4)
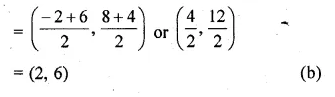
Question 3.
If \(P\left( \frac { a }{ 3 } ,4 \right) \) segment joining the points Q ( – 6, 5) and R ( – 2, 3), then the value of a is
(a) – 4
(b) – 6
(c) 12
(d) – 12
Solution:
\(P\left( \frac { a }{ 3 } ,4 \right) \) is mid-point of the line segment
joining the points Q (-6, 5) and R (-2, 3)
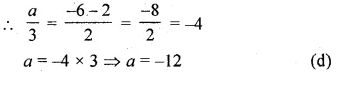
Question 4.
If the end points of a diameter of a circle are A ( – 2, 3) and B (4, – 5), then the coordinates of its centre are
(a) (2, – 2)
(b) (1, – 1)
(c) ( – 1, 1)
(d) ( – 2, 2)
Solution:
End points of a diameter of a circle are (-2, 3) and B (4,-5)
then co-ordinates of the centre of the circle
= \(\left( \frac { -2+4 }{ 2 } ,\frac { 3-5 }{ 2 } \right) or\left( \frac { 2 }{ 2 } ,\frac { -2 }{ 2 } \right) \)
= (1, -1) (b)
Question 5.
If one end of a diameter of a circle is (2, 3) and the centre is ( – 2, 5), then the other end is
(a) ( – 6, 7)
(b) (6, – 7)
(c) (0, 8)
(d) (0, 4)
Solution:
One end of a diameter of a circle is (2, 3) and centre is (-2, 5)
Let (x, y) be the other end of the diameter
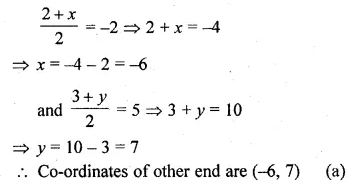
Question 6.
If the mid-point of the line segment joining the points P (a, b – 2) and Q ( – 2, 4) is R (2, – 3), then the values of a and b are
(a) a = 4, b = – 5
(b) a = 6, b = 8
(c) a = 6, b = – 8
(d) a = – 6, b = 8
Solution:
the mid-point of the line segment joining the
points P (a, b – 2) and Q (-2, 4) is R (2, -3)
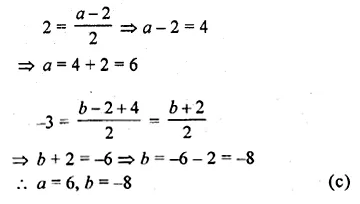
Question 7.
The point which lies on the perpendicular bisector of the line segment joining the points A ( – 2, – 5) and B (2, 5) is
(a) (0, 0)
(b) (0, 2)
(c) (2, 0)
(d) ( – 2, 0)
Solution:
the line segment joining the points A (-2, -5) and B (2, -5), has mid-point
= \(\left( \frac { -2+2 }{ 2 } ,\frac { -5+5 }{ 2 } \right) \) = (0, 0)
(0, 0) lies on the perpendicular bisector of AB. (a)
Question 8.
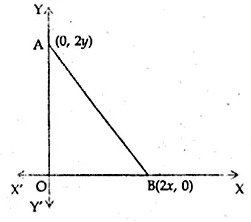
The coordinates of the point which is equidistant from the three vertices of ∆AOB (shown in the given figure) are
(a) (x, y)
(b) (y, x)
(c) \(\left( \frac { x }{ 2 } ,\frac { y }{ 2 } \right) \)
(d) \(\left( \frac { y }{ 2 } ,\frac { x }{ 2 } \right) \)
Solution:
In the given figure, vertices of a ∆OAB are (0, 0), (0, 2y) and (2x, 0)
The point which is equidistant from O, A and B is the mid-point of AB.
∴ Coordinates are \(\left( \frac { 0+2x }{ 2 } ,\frac { 2y+0 }{ 2 } \right) \) or (x, y) (a)
Question 9.
The fourth vertex D of a parallelogram ABCD whose three vertices are A ( – 2, 3), B (6, 7) and C (8, 3) is
(a) (0, 1)
(b) (0, – 1)
(c) ( – 1, 0)
(d) (1, 0)
Solution:
ABCD is a ||gm whose vertices A (-2, 3), B (6, 7) and C (8, 3).
The fourth vertex D will be the point on which diagonals AC and BD
bisect each other at O.
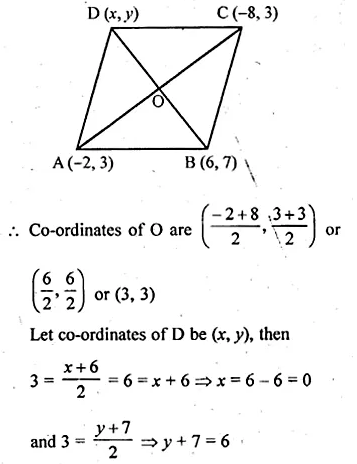
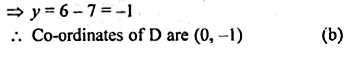
Question 10.
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, – 5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(a) (0, – 5) and (2, 0)
(b) (0, 10) and ( – 4, 0)
(c) (0, 4) and ( – 10, 0)
(d) (0, – 10) and (4, 0)
Solution:
A line intersects y-axis at P and x-axis a Q.
R (2, -5) is the mid-point
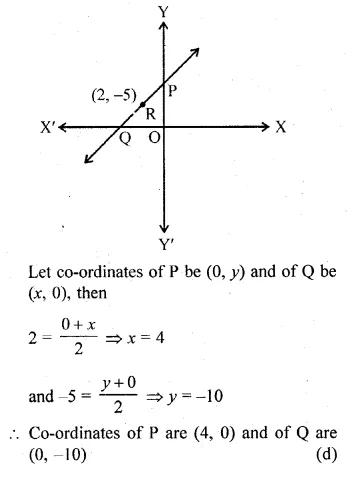
Question 11.
The points which divides the line segment joining the points (7, – 6) and (3, 4) in the ratio 1 : 2 internally lies in the
(a) Ist quadrant
(b) IInd quadrant
(c) IIIrd quadrant
(d) IVth quadrant
Solution:
A point divides line segment joining the points
A (7, -6) and B (3, 4) in the ratio 1 : 2 internally.
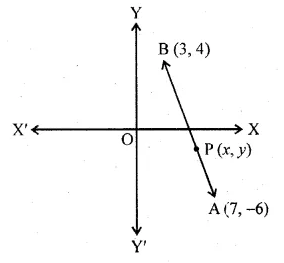
Let (x, y) divides it in the ratio 1 : 2
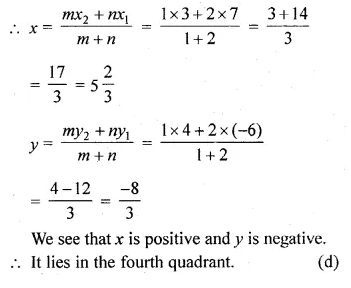
Question 12.
The centroid of the triangle whose vertices are (3, – 7), ( – 8, 6) and (5, 10) is
(a) (0, 9)
(b) (0, 3)
(c) (1, 3)
(d) (3, 3)
Solution:
Centroid of the triangle whose Vertices are (3, -7), (-8, 6) and (5, 10) is
\(\left( \frac { 3-8+5 }{ 3 } ,\frac { -7+6+10 }{ 3 } \right) or\left( 0,\frac { 9 }{ 3 } \right) \)
or (0, 3) (b)
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.