Continuity and Differentiable Class 12 MCQs Questions with Answers
Continuity And Differentiability Class 12 MCQ Question 1.
If f(x) = 2x and g(x) = \(\frac{x^{2}}{2}+1\) then which of the following can be a discontinuous function?
(A) f(x) + g(x)
(B) f(x) – g(x)
(C) f(x).g(x)
(D) \(\frac {f(x)}{g(x) }\)
Answer:
(D) \(\frac {f(x)}{g(x) }\)
Explanation:
Since f(x) = 2x and g(x) = \(\frac{x^{2}}{2}+1\) are continuous functions, then by using the algebra of continuous functions, the functions fix) + g(x), fix) – g(x), f(x),g(x) are also continuous functions but \(\frac {f(x)}{g(x) }\) Is discontinuous function at x = 0
Continuity And Differentiability MCQ Question 2.
The function f(x) = \(\frac{4-x^{2}}{4 x-x^{3}}\)
(A) discontinuous at only one point
(B) discontinuous at exactly two points
(C) discontinuous at exactly three points
(D) none of these
Answer:
(C) discontinuous at exactly three points
Explanation:
Given that,
f(x) = \(\frac{4-x^{2}}{4 x-x^{3}}\) then it is discontinuous if
⇒ 4x – x2 = 0
⇒ x(4 – x2) = 0
x(2 + x)(2 – x)= 0
x = 0,-2,2
Thus, the given function is discontinuous at exactly three points.
![]()
MCQ On Continuity And Differentiability Class 12 Question 3.
The function(x) cot xis discontinuous on the set
(A) {x = nπ; n∈Z)
(B) {x = 2nπ; n∈Z}
(C) {x = (2n + 1); n∈z}
(D) {x = \(\frac {nπ}{2}\);n∈z}
Answer:
(A) {x = nπ; n∈Z)
Explanation:
Given that
f(x) = Cot x \(\frac{\cos x}{\sin x}\)
it is discontinuous at
sin x = 0
x = nπ, n∈z
Thus, the given function h diacontIrnus at
{x = nπ: n∈z).
Differentiation MCQ Class 12 Question 4.
f(x) =
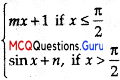
is continuous at x = \(\frac{π}{2}\) then
(A) m = 1,n = 0
(B) m = \(\frac{nπ}{2}\) + 1
(C) n = \(\frac{mπ}{2}\)
(D) m = n = \(\frac{π}{2}\)
Answer:
(C) n = \(\frac{mπ}{2}\)
Given that,
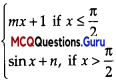
is continuous function at x then
LHL = RHL
⇒ \(\lim _{x \rightarrow \frac{\pi}{2}^{-}} f(x)=\lim _{x \rightarrow \frac{\pi^{+}}{2}} f(x)\)
⇒ \(\lim _{h \rightarrow 0} f\left(\frac{\pi}{2}-h\right)=\lim _{h \rightarrow 0} f\left(\frac{\pi}{2}+h\right)\)
⇒ \(\lim _{h \rightarrow 0} m\left(\frac{\pi}{2}-h\right)+1=\lim _{h \rightarrow 0} \sin \left(\frac{\pi}{2}+h\right)+n\)
⇒ \(\lim _{h \rightarrow 0} m\left(\frac{\pi}{2}-h\right)+1=\lim _{h \rightarrow 0} \cos h+n\)
⇒ m(\(\frac{π}{2}\)) + 1 = 1 + n
⇒ n = \(\frac{mx}{2}\))
Class 12 Maths Chapter 5 MCQ Question 5.
if y = Ae5x + Be5x, then \(\frac{d^{2} y}{d x^{2}}\) is equal to
(A) 25 y
(B) 5 y
(C) -25 y
(D) 15 y
Answer:
(A) 25 y
Explanation:
y = Ae5x + Be5x
\(\frac{dx}{dy}\) = 5Ae5x – 5Be5x
\(\frac{d^{2} y}{d x^{2}}\) = 25Ae5x – 25Be5x
= 25 y
![]()
MCQ On Differentiation Class 12 Question 6.
If y = log \(\left(\frac{x^{2}}{e^{2}}\right)\), then \(\frac{d^{2} y}{d x^{2}}\) equals
(A) \(-\frac{1}{x}\)
(B) \(-\frac{1}{x^{2}}\)
(C) \(\frac{2}{x^{2}}\)
(D) \(-\frac{2}{x^{2}}\)
Answer:
(D) \(-\frac{2}{x^{2}}\)
Explanation:
Given, y = \(\left(\frac{x^{2}}{e^{2}}\right)\)
⇒ y = 2 \(2 \log _{e} x-\log _{e} e^{2}\)
⇒ y = 2 \(2 \log _{e} x-2\)
⇒ \(\frac{d y}{d x}=\frac{2}{x}\)
⇒ \(\frac{d^{2} y}{d x^{2}}=\frac{-2}{x^{2}}\)
MCQ Questions On Differentiation Class 12 Question 7.
The set of points where the function f given by f(x) = |2x -1| sin x is differentiable is
(A) R
(B) R – \(\frac{1}{2}\)
(C) (0, ∞)
(D) none of these
Answer:
(B) R – \(\frac{1}{2}\)
Explanation:
Given that,
f(x) = |2x -1| sin x
The function sin x is differentiable.
The function |2x -1| is differentiable, except
2x – 1 = 0
Thus, the given function dIffeintiable R – \(\frac{1}{2}\).
![]()
MCQ Of Continuity And Differentiability Class 12 Question 8.
The function f(x) = \(e^{|x|}\) is
(A) continuous everywhere but not differentiable at x = 0
(B) continuous and differentiable everywhere
(C) not continuous at x = 0
(D) none of these
Answer:
(B) continuous and differentiable everywhere
Explanation:
Given that.
f(x) = \(e^{|x|}\)
The functions e’ and 1×1 are continuous functions for all real value of x. Since? is differentiable everywhere but |x| non-differentiable a |x| = 0. Thus, the given functions f(x) = \(e^{|x|}\) is continuous everywhere but not differentiable at x = 0.
MCQ Of Differentiation Class 12 Question 9.
Let f(x) = |sin x|, then
(A) f is everywhere differentiable
(B) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z.
(C) f is everywhere continuous but not differentiable at x = (2n + 1) \(\frac{π}{2}\) n € Z.
(D) none of these
Answer:
(B) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z.
Explanation:
Given that,
f(x) = |sin x|
The functions lxi and sin x are continuous function for afl real value of x.
Thus, the function f(x) = |sin x| is continuous Funon evey where.
Now, |x| is non-differentiable function at x = 0.
Since f(x) = |sin x| is non-differentiabLe function
at sin x = 0
Thus, f is everywhere continuous but not
differentiable at x = nπ, n ∈ Z.
MCQ Of Chapter 5 Maths Class 12 Question 10.
II y = log\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\) then \(\frac {dy}{dx}\) is equal to
(A) \(\frac{4 x^{3}}{1-x^{4}}\)
(B) \(\frac{-4 x}{1-x^{4}}\)
(C) \(\frac{1}{4-x^{4}}\)
(D) \(\frac{-4 x^{3}}{1-x^{4}}\)
Answer:
(B) \(\frac{-4 x}{1-x^{4}}\)
Explanation:
Given that,
y = log \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
y = log \(\log \left(1-x^{2}\right)-\log \left(1+x^{2}\right)\)
Differentiate with respect to x,we have
= \(\frac{d y}{d x}=\frac{d}{d x}\left[\log \left(1-x^{2}\right)\right]-\frac{d}{d x}\left[\log \left(1+x^{2}\right)\right]\)
= \(\log \left(1-x^{2}\right)-\log \left(1+x^{2}\right)\)
= \(-2 x\left(\frac{2}{\left(1-x^{2}\right)\left(1+x^{2}\right)}\right)\)
= \(-\frac{4 x}{1-x^{4}}\)
![]()
Continuity MCQ Chapter 5 Maths Class 12 Question 11.
If y = \(\sqrt{\sin x+y}\). then \(\frac{d y}{d x}\)is equal to
(A) \(\frac{\cos x}{2 y-1}\)
(B) \(\frac{\cos x}{1-2 y}\)
(C) \(\frac{\sin x}{1-2 y}\)
(D) \(\frac{\sin x}{2 y-1}\)
Answer:
(A) \(\frac{\cos x}{2 y-1}\)
Explanation:
Given that.
y = \(\sqrt{\sin x+y}\)
y2 = sin x + y
Differentiate with respect to x, we have
2y \(\frac{d y}{d x}\) = cos x + \(\frac{d y}{d x}\)
(2y – 1) \(\frac{d y}{d x}\) = cos x
\(\frac{d y}{d x}\) = \(\frac{\cos x}{2 y-1}\)
Class 12 Continuity And Differentiability MCQ Question 12.
The derivative of cos-1(2x2 – 1) w.r.t. cos-1 x is
(A) 2
(B) \(\frac{-1}{2 \sqrt{1-x^{2}}}\)
(C) \(\frac{2}{x}\)
(D) 1 – x2
Answer:
(A) 2
Explanation:
Let
And u = cos -1(2x2 – 1)
⇒ \(\frac{d u}{d x}=\frac{4 x}{\sqrt{1-\left(2 x^{2}-1\right)^{2}}}\)
⇒ \(\frac{d u}{d x}=-\frac{4 x}{\sqrt{1-4 x^{4}+4 x^{2}-1}}\)
⇒ \(\frac{d u}{d x}=-\frac{4 x}{\sqrt{1-4 x^{4}+4 x^{2}-1}}\)
⇒ \(\frac{d u}{d x}=-\frac{4 x}{\sqrt{-4 x^{4}+4 x^{2}}}\)
⇒ \(\frac{d u}{d x}=-\frac{2}{\sqrt{1-x^{2}}}\)
And υ = cos-1x
\(\frac{d v}{d x}=-\frac{1}{\sqrt{1-x^{2}}}\)
thus, \(\frac{d v}{d x}\) = 2
Class 12 Maths Continuity And Differentiability MCQ Question 13.
x × t2 and y = t3 then is \(\frac{d^{2} y}{d x^{2}}\) is
(A) \(\frac{3}{2}\)
(B) \(\frac{3}{4 t}\)
(C) \(\frac{3}{2 t}\)
(D) \(\frac{3}{4}\)
Answer:
(A) \(\frac{3}{2}\)
Explanation:
Given that,
x = t2 and y = t2
then \(\frac{d x}{d t}\) = 2t and \(\frac{d x}{d t}\) = 3t2
Thus,
\(\frac{d y}{d x}=\frac{3 t^{2}}{2 t}=\frac{3 t}{2}\)
⇒ \(\frac{d^{2} y}{d x^{2}}=\frac{3}{2}\)
![]()
Assertion And Reason Based MCQs (1 Mark each)
Directions: in the following questions, A statemeni of Assertion (A) is followed by a statement ol
Reason (R). Mark the correct choice as.
(A) Both A and R are true and R is the corred ep1anation of A
(B) Both A and R are true but R is NOT the corred explanation of A
(C) A is true but R is false
(D) A is false and R is True
MCQ On Continuity And Differentiability Class 12 Question 1.
Assertion (A): sin xl is continuous for all x R.
Reason (R): sin x and 1×1 are continuous in R.
Answer:
(A) Both A and R are true and R is the corred ep1anation of A
Explanation:
sin x and 1×1 are continuous in R.
hence R is true.
Consider the functions f(x) = sin x and g(x) = |x| both of which are continuous ¡n R.
gof (x) – g(f(x)) = g(sin x) – |sin x|
Since f(x) and g(x) are continuous in R. gof(x) is
also continuous In R.
Hence A is true.
R Is the correct explanation of A.
![]()
MCQ Of Continuity And Differentiability Class 12 Question 2.
Assertion (A): f(x) = tan x is continuous at x = \(\frac {π}{2}\)
Reason (R) g(x) = x2 is continuous at x = \(\frac {π}{2}\)
Answer:
(D) A is false and R is True
Explanation:
g(x) – x2 is a polynomial function. It is continuous for afl x ∈ R.
Hence R is frue.
f(x) = tan x is not defined when x = \(\frac {π}{2}\)
Therefore f(\(\frac {π}{2}\))does not exist and hence f(x) is not continuous at x =\(\frac {π}{2}\)
A is false.
MCQs On Continuity And Differentiability Question 3.
Consider the function
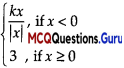
which is continuous at x = 0.
Assertion (A): The rue of k is -3.
Reason (R):
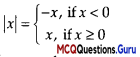
Answer:
(A) Both A and R are true and R is the corred ep1anation of A
Explanation:
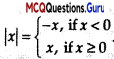
This is the definition for modulus function and
hence true.
Hence R is true.
Since f is continuous at x = 0,
\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
Here f(0) = 3,
\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
LHL = \(\lim _{x \rightarrow 0^{-}} f(x)\)
= \(\lim _{x \rightarrow 0^{-}} \frac{k x}{|x|}=\lim _{x \rightarrow 0^{-}-x} \frac{k x}{-x}=-k\)
∴ -k = 3 or k = 3
Hence A Is true.
R is the correct explanation of A.
Class 12 Maths Ch 5 MCQ Question 4.
Consider the function
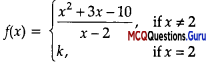
which is continuous at x = 2.
Assertion (A): The value of k is 0.
Reason (R): fix) is continuous at z = a, if
\(\lim _{x \rightarrow a} f(x)=f(a)\)
Answer:
(D) A is false and R is True
Explanation:
f(x) is continuous at x = a,if \(\lim _{x \rightarrow a} f(x)=f(a)\)
R is true.
\(\lim _{x \rightarrow 2} f(x)=f(2)=k\)
\(\lim _{x \rightarrow 2} \frac{(x+5)(x-2)}{x-2}=k\)
∴ K = 7
MCQ On Continuity And Differentiability Pdf Question 5.
Assertion (A): | sin x| is continuous at x = 0
Reason (R): |sin x| is differentiable at x = 0.
Answer:
(C) A is true but R is false
Explanation:
Since sin x and |x| are continuous functions in R, |sin x| is continuous at x = 0.
Hence A is true.
|sin x| = \(\begin{cases}-\sin x, & \text { if } x<0 \\ \sin x, & \text { if } x \geq 0\end{cases}\)
f (0) = |sin 0| = 0
LHD = f(0–) = \(\lim _{x \rightarrow 0} \frac{-\sin x-0}{x}\) = -1
RHÐ = f (0–) = \(\lim _{x \rightarrow 0} \frac{\sin x-0}{x}\) = 1
At x = 0, LHD ≠ RHD.
So f(x) is not differentiable at x = 0.
Hence Ris is false..
![]()
Ch 5 Maths Class 12 MCQ Question 6.
Assertion (A):ftx) [xJ is not differentiable at x 2.
Reason (R): f(x) = [xJ is not continuous at x = 2.
Answer:
(A) Both A and R are true and R is the corred ep1anation of A
Explanation:
f(x) = [x] is not continuous when x is an integet
So f [x] is not continuous at x = 2. Hence R is true.
A differentiable function is always continuous.
Since f(x) [x] is not continuous at x – 2, it is
also not differentiable at x = 2.
Hence A is true.
R is the correct explanation of A.
![]()
Question 7.
Assertion (A): A continuous function is always differentiable.
Reason (R): A differentiable function is always continuous,
Answer:
(D) A is false and R is True
Explanation:
The function f(x) is differentiable at
x = a, If it is continuous at x = a and
LHD = RHD at x = a.
A differentiable function Is always continuous.
Hence R is true.
A continuous function need not be always differentiable.
For example, |x| is continuous at x = 0, but not differentiable at x = 0.
Hence A is laise.
Question 8.
Assertion (A): If y = sin-1 (6 × \(\sqrt{1-9 x^{2}}\)), then \(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^{2}}}\)
Reason (R): sin-1(6 x \(\sqrt{1-9 x^{2}}\)) = sin-1(sin 2x)
Answer:
(C) A is true but R is false
Explanation:
put 3x = sin θ or θ = sin-1 3x
y = sin-1(6 x \(\sqrt{1-9 x^{2}}\)) = sin-1(sin 2θ)
= 2θ
= 2 sin-1 3x
∴ \(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^{2}}}\)
A is,true. R is false.
Case-Based MCQs
Attempt any four sub-parts from each question.
Each sub-part carries 1 mark.
I. Read the following test and answer the following questions on the basis of the same:
Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chart The chain rule says that if h and g arc functions and
f(x) = g(h(x)), then

Let f(x) = sin x and g(x) = x3
Question 1.
fog (x) = ……………
(A) sin x3
(B) sin3 x
(C) sin 3x
(D) 3 sin x
Answer:
(A) sin x3
Explanation:
f0g(x) = f(g(x))
= f(x3)
= sin(x3)
![]()
Question 2.
gof(x) = ……………..
(A) sin x3
(B) sin3 x
(C) sin 3x
(D) 3 sin x
Answer:
(B) sin3 x
Explanation:
gof(x) = g(f(x))
= g(sin x)
= sin3x
Question 3.
\(\frac{d}{d x}\left(\sin ^{3} x\right)\) = ……………
(A) cos 3x
(B) 3 sin x cos x
(C) 3 sin x cos x
(D) – cos3x
Answer:
(C) 3 sin x cos x
Explanation:
\(\frac{d}{d x}\left(\sin ^{3} x\right)\) = 3 sin2 × \(\frac{d}{d x}(\sin x)\)
= 3 sin2 x cos x
= 3sin2x cosx
Question 4.
\(\frac{d}{d x}(\sin 2 x)\) at x = \(\frac {π}{2}\) is …………
(A) cos (x2)
(B) – cos(x2)
(C) 3x2 sin (x3)
(D) 3x2cos (x3)
Ans
(D) 3x2cos (x3)
Explanation:
\(\frac{d}{d x}\left(\sin x^{3}\right)=\cos x^{3} \frac{d}{d x}\left(x^{3}\right)\)
= 3x 2 cos x3
Question 5.
– \(\frac{d}{d x}(\sin 2 x)\) at x = \(\frac {π}{2}\) is …………
(A) 0
(B) 1
(C) 2
(D) -2
Answer:
(D) -2
Explanation:
\(\frac{d}{d x}(\sin 2 x)\) = \(\cos 2 x \frac{d}{d x}(2 x)\)
= cos 2x
\(\left.\frac{d}{d x}(\sin 2 x)\right|_{x=\frac{\pi}{4}}\) = 2 cos 2 x \(\frac {π}{2}\) = 2 cos π
= 2(-1) = -2
II. Read the following text and answer the following questions on the basis of the same:
A potter made a mud vessel, where the shape 01 the pot is based on f(x) = |x – 3| + |x – 2|, where f(x) represents the height of the pot.
Question 1.
When z > 4 what will be the height in terms of x?
(A) x – 2
(B) x – 3
(C) 2x – 5
(D) 5 – 2x
Answer:
(C) 2x – 5
Explanation:
The given function can be written as
f(x) = \(\begin{cases}5-2 x, & \text { if } x<2 \\ 1, & \text { if } 2 \leq x<3 \\ 2 x-5, & \text { if } x \geq 3\end{cases}\) When x > 4, f(x) = 2x – 5
![]()
Question 2.
Will the slope vary with z value?
(A) Yes
(B) No
(C) Cant say
(D) Incomplete data
Answer:
(A) Yes
Explanation:
f'(x) = \(\begin{cases}-2, & \text { if } x<2 \\ 0, & \text { if } 2 \leq x<3 \\ 2, & \text { if } x \geq 3\end{cases}\)
Question 3.
What is \(\frac {dy}{dx}\) at x = 3
(A) 2
(B) -2
(C) Function is not differentiable
(D) 1
Answer:
(C) Function is not differentiable
Explanation:
f(x) is not differentiable at x = 2 and x = 3.
Question 4.
When the value of r lies between (2, 3) then the function is
(A) 2x – 5
(B) 5 – 2x
(C) 1
(D) 5
Answer:
(C) 1
Explanation:
In (2. 3),f(x) = 1
Question 5.
if the potier is trying to make a pot using the function f(x) = [x] will he get a pot or not? Why?
(A) Yes, because it is a continuous function
(B) Yes. because it is not continuous
(C) No, because it is a Continuous function
(D) No, because it is not continuous
Answer:
(D) No, because it is not continuous
Explanation:
[x] is not continuous at integral values of x.