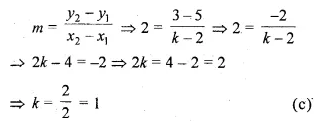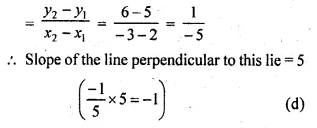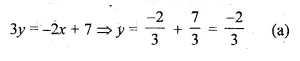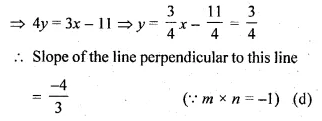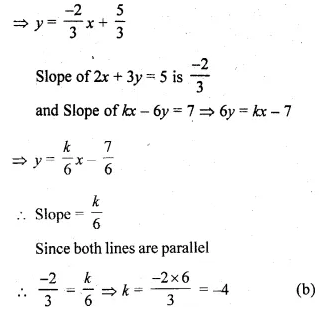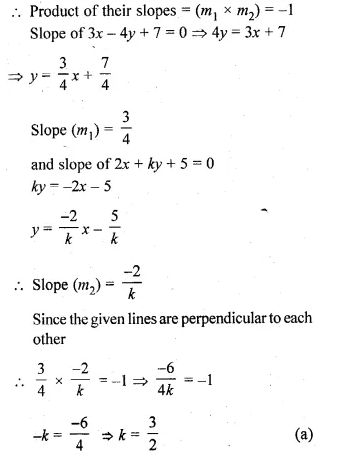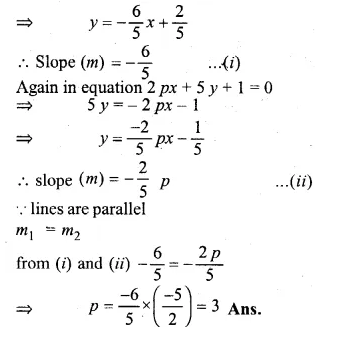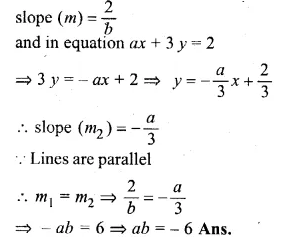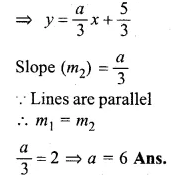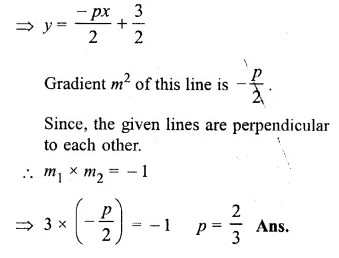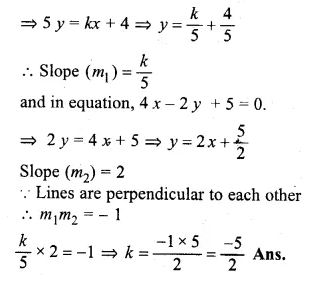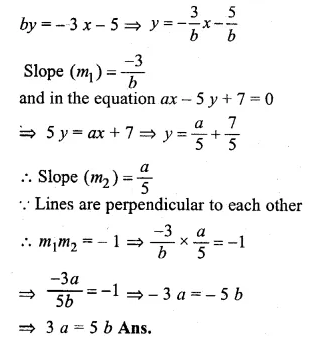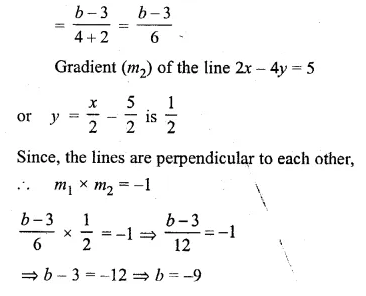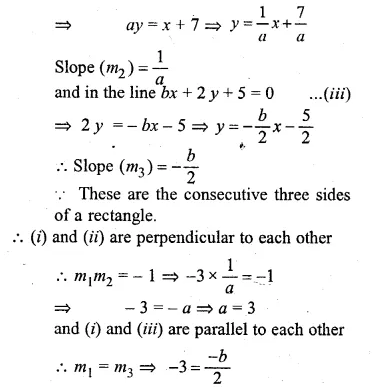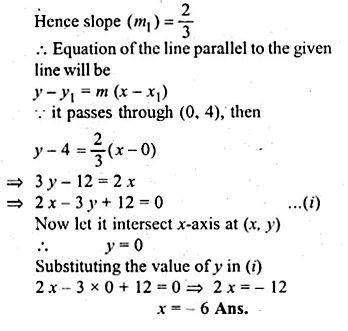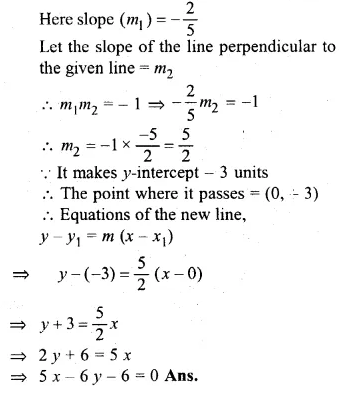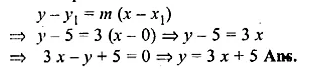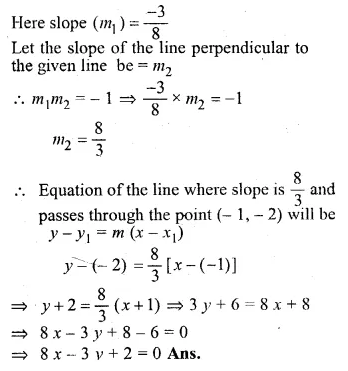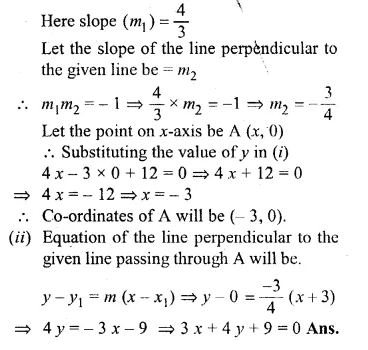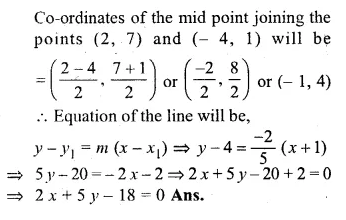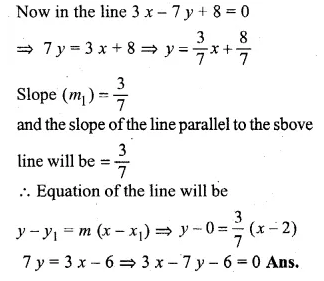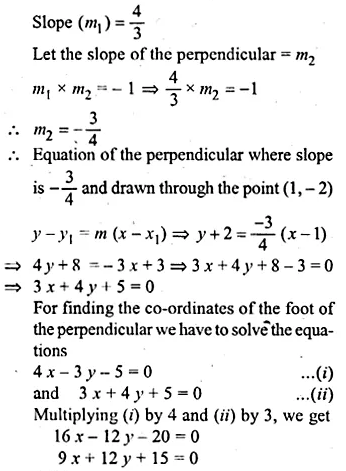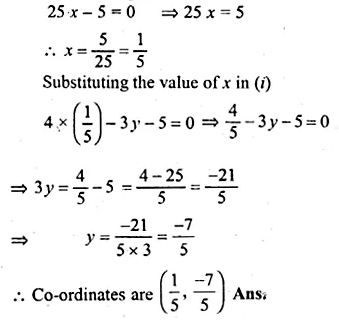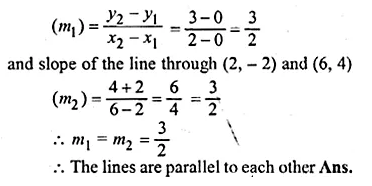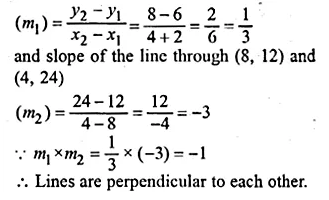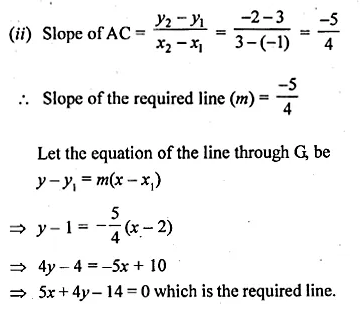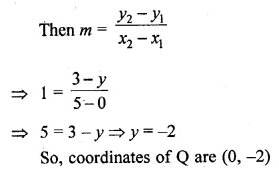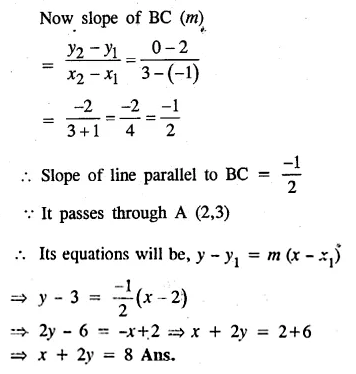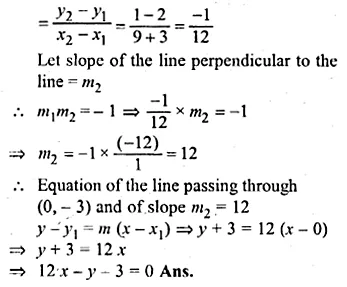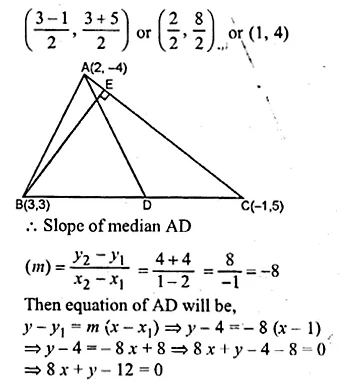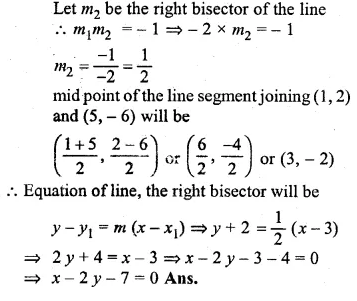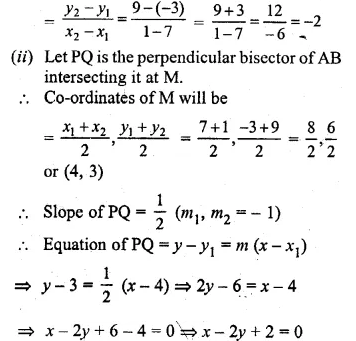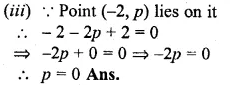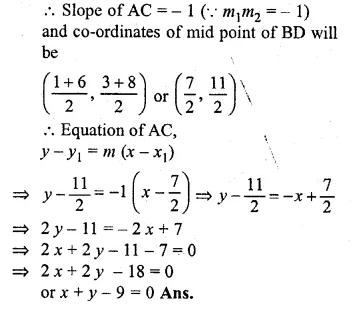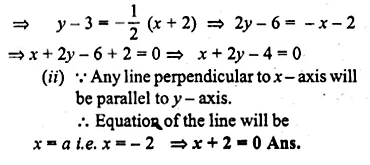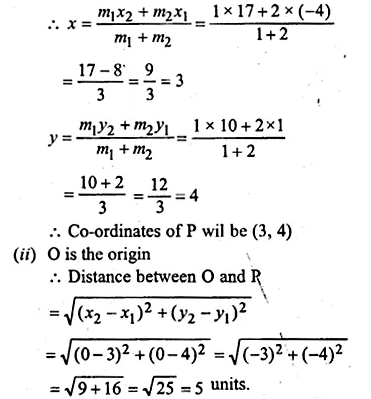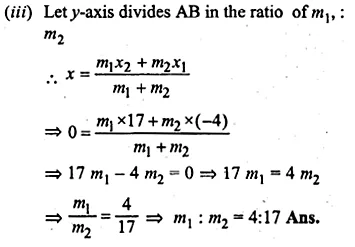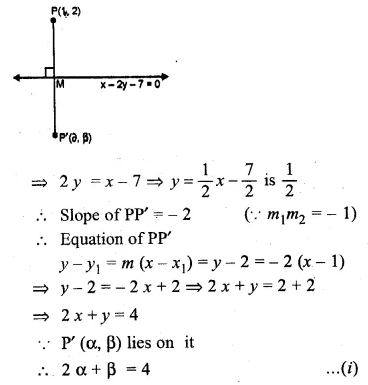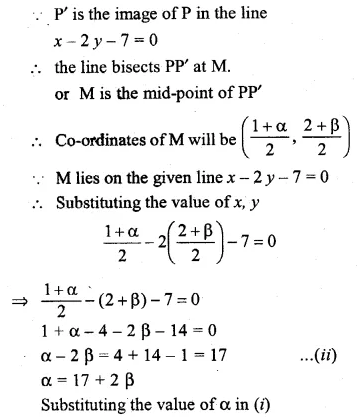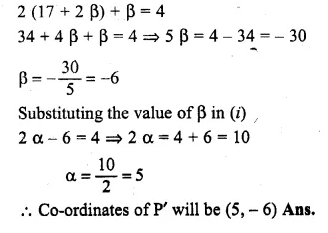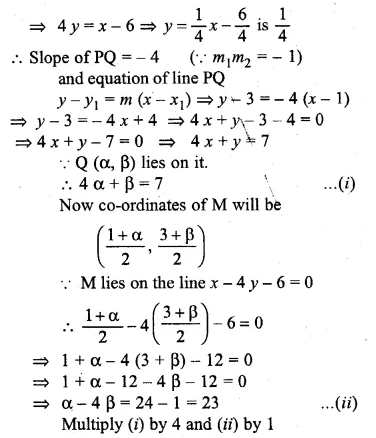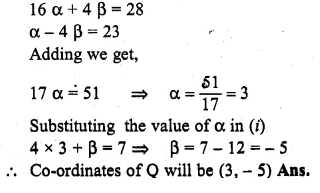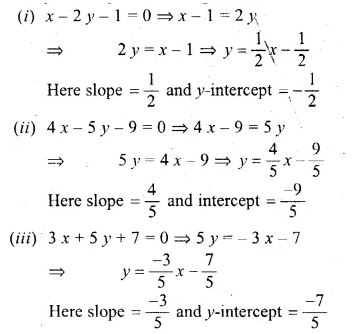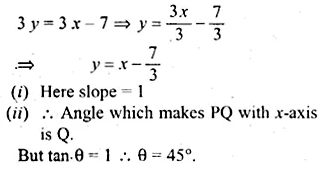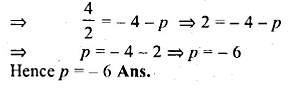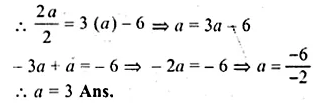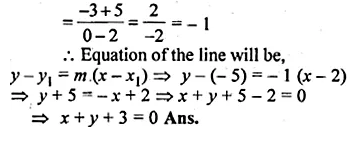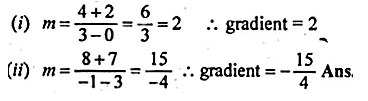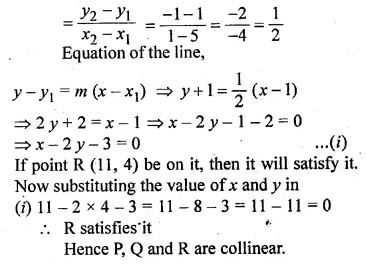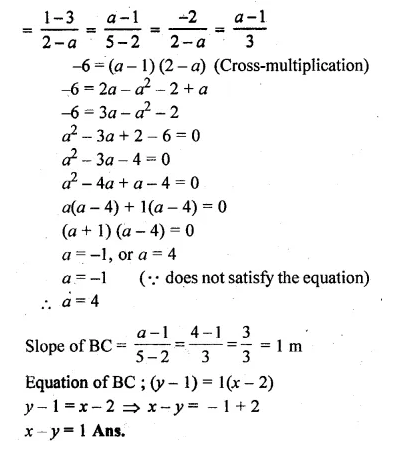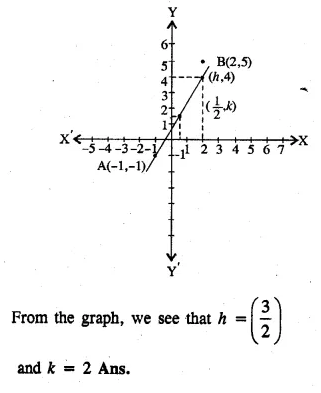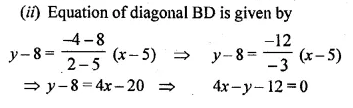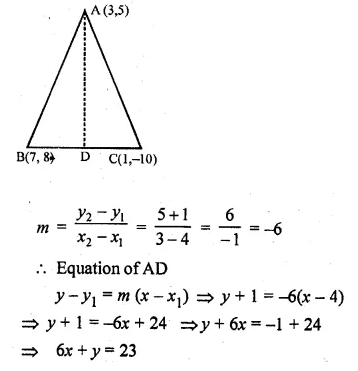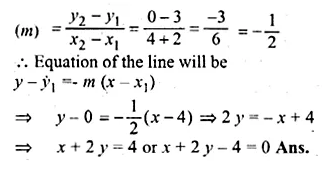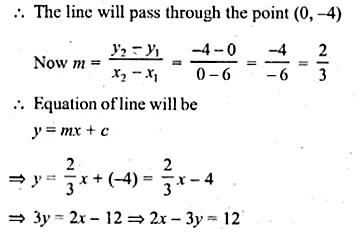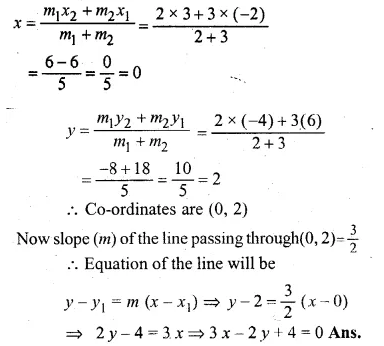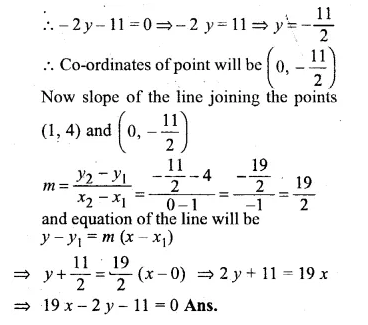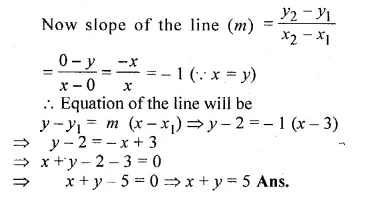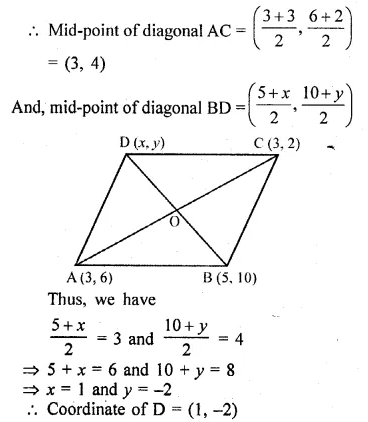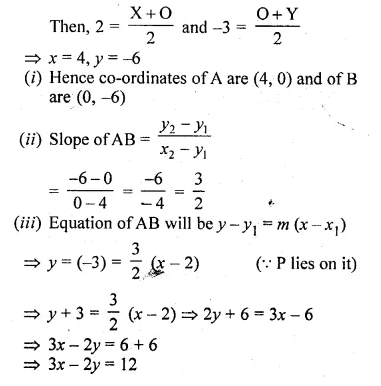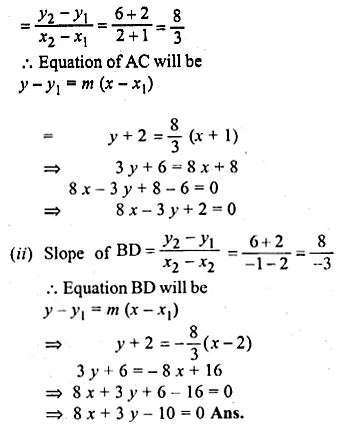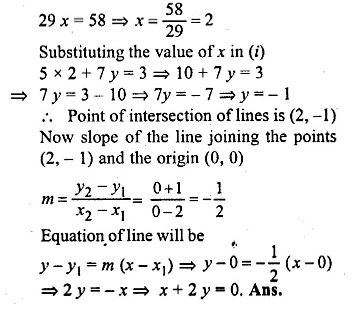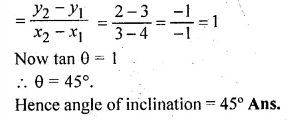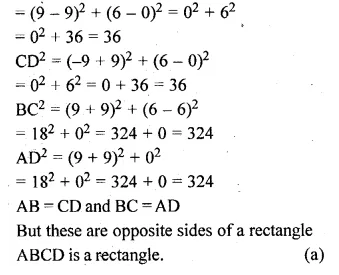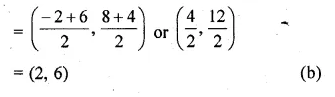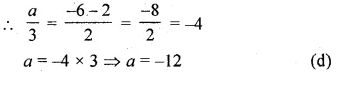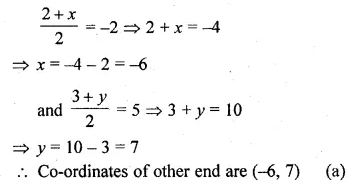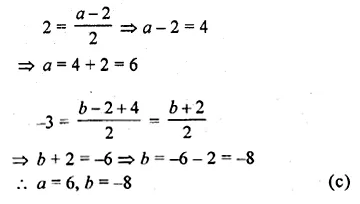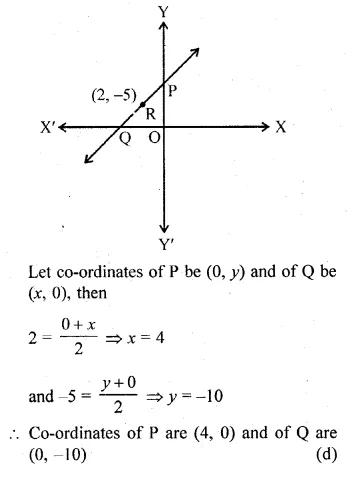ICSE Class 10

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Choose the correct answer from the given four options (1 to 13) :

Question 1.
The slope of a line parallel to y-axis is
(a) 0
(b) 1
(c) – 1
(d) not defined
Solution:
Slope of a line parallel to y-axis is not defined. (b)

Question 2.
The slope of a line which makes an angle of 30° with the positive direction of x-axis is
(a) 1
(b) \(\frac { 1 }{ \sqrt { 3 } } \)
(c) √3
(d) \(– \frac { 1 }{ \sqrt { 3 } } \)
Solution:
Slope of a line which makes an angle of 30°
with positive direction of x-axis = tan 30°
= \(\frac { 1 }{ \sqrt { 3 } } \) (b)

Question 3.
The slope of the line passing through the points (0, – 4) and ( – 6, 2) is
(a) 0
(b) 1
(c) – 1
(d) 6
Solution:
Slope of the line passing through the points (0, -4) and (-6, 2)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { 2+4 }{ -6-0 } =\frac { 6 }{ -6 } =-1 \) (c)

Question 4.
The slope of the line passing through the points (3, – 2) and ( – 7, – 2) is
(a) 0
(b) 1
(c) \(– \frac { 1 }{ 10 } \)
(d) not defined
Solution:
Slope of the line passing through the points (3, -2) and (-7, -2)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -2+2 }{ -7-3 } =\frac { 0 }{ -10 } =0 \) (a)

Question 5.
The slope of the fine passing through the points (3, – 2) and (3, – 4) is
(a) – 2
(b) 0
(c) 1
(d) not defined
Solution:
The slope of the line passing through (3, -2) and (3, -4)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -4+2 }{ 3-3 } =\frac { -2 }{ 0 } \) (d)

Question 6.
The inclination of the line y = √3x – 5 is
(a) 30°
(b) 60°
(c) 45°
(d) 0°
Solution:
The inclination of the line y = √3x – 5 is
√3 = tan 60° = 60° (b)

Question 7.
If the slope of the line passing through the points (2, 5) and (k, 3) is 2, then the value of k is
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
Slope of the line passing through the points (2, 5) and (k, 3) is 2, then

Question 8.
The slope of a line parallel to the line passing through the points (0, 6) and (7, 3) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
Slope of the line parallel to the line passing through (0, 6) and (7, 3)
Slope of the line = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { 3-6 }{ 7-0 } =\frac { -3 }{ 7 } \) (b)

Question 9.
The slope of a line perpendicular to the line passing through the points (2, 5) and ( – 3, 6) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
Slope of the line joining the points (2, 5), (-3, 6)

Question 10.
The slope of a line parallel to the line 2x + 3y – 7 = 0 is
(a) \(– \frac { 2 }{ 3 } \)
(b) \(\\ \frac { 2 }{ 3 } \)
(c) \(– \frac { 3 }{ 2 } \)
(d) \(\\ \frac { 3 }{ 2 } \)
Solution:
The slope of a line parallel to the line 2x + 3y – 7 = 0
slope of the line

Question 11.
The slope of a line perpendicular to the line 3x = 4y + 11 is
(a) \(\\ \frac { 3 }{ 4 } \)
(b) \(– \frac { 3 }{ 4 } \)
(c) \(\\ \frac { 4 }{ 3 } \)
(d) \(– \frac { 4 }{ 3 } \)
Solution:
slope of a line perpendicular to the line 3x = 4y + 11 is

Question 12.
If the lines 2x + 3y = 5 and kx – 6y = 7 are parallel, then the value of k is
(a) 4
(b) – 4
(c) \(\\ \frac { 1 }{ 4 } \)
(d) \(– \frac { 1 }{ 4 } \)
Solution:
lines 2x + 3y = 5 and kx – 6y = 7 are parallel
Slope of 2x + 3y = 5 = Slope of kx – 6y = 7
⇒ 3y – 2x + 5

Question 13.
If the line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other, then the value of k is
(a) \(\\ \frac { 3 }{ 2 } \)
(b) \(– \frac { 3 }{ 2 } \)
(c) \(\\ \frac { 2 }{ 3 } \)
(d) \(– \frac { 2 }{ 3 } \)
Solution:
line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0
are perpendicular to each other

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Question 1.
State which one of the following is true : The straight lines y = 3x – 5 and 2y = 4x + 7 are
(i) parallel
(ii) perpendicular
(iii) neither parallel nor perpendicular.
Solution:
Slope of line y = 3x – 5 = 3
and slope of line 2y = 4x + 7
⇒ y = 2x + \(\\ \frac { 7 }{ 2 } \) = 2.
∴ Slope of both the lines are neither equal nor their product is – 1.
∴ These line are neither parallel nor perpendicular.

Worksheets for Class 10 Maths

Question 2.
If 6x + 5y – 7 = 0 and 2px + 5y + 1 = 0 are parallel lines, find the value of p.
Solution:
In equation
6x + 5 y – 7 = 0
⇒ 5y = -6x + 7

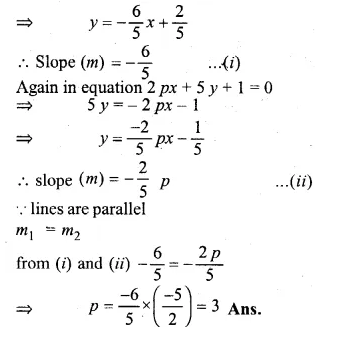
Question 3.
Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel. Find the relation connecting a and b. (1991)
Solution:
In equation 2x – by + 5 = 0
⇒ – by = – 2x – 5
⇒ y = \(\\ \frac { 2 }{ b } \) + \(\\ \frac { 5 }{ b } \)

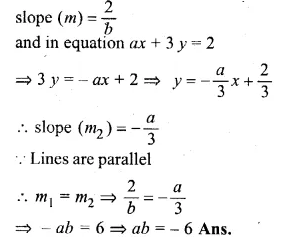
Question 4.
Given that the line \(\\ \frac { y }{ 2 } \) = x – p and the line ax + 5 = 3y are parallel, find the value of a. (1992)
Solution:
In equation y = x – p
⇒ y = 2x – 2p
Slope (m₁) = 2
In equation ax + 5 = 3y

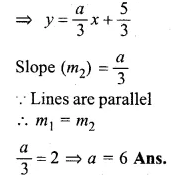
Question 5.
If the lines y = 3x + 7 and 2y + px = 3 perpendicular to each other, find the value of p. (2006)
Solution:
Gradient m₁ of the line y = 3x + 7 is 3
2y + px = 3

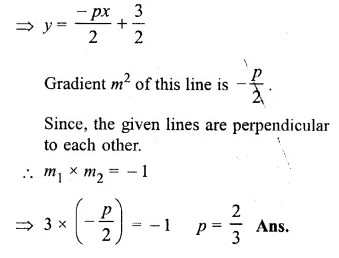
Question 6.
Find the value of k for which the lines kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other. (2003)
Solution:
Given
In equation, kx – 5y + 4 = 0

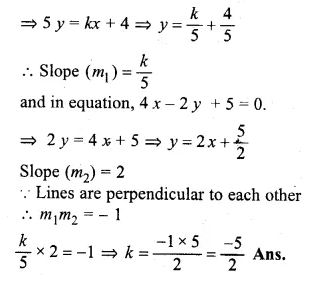
Question 7.
If the lines 3x + by + 5 = 0 and ax – 5y + 7 = 0 are perpendicular to each other, find the relation connecting a and b.
Solution:
Given
In the equation 3x + by + 5 = 0

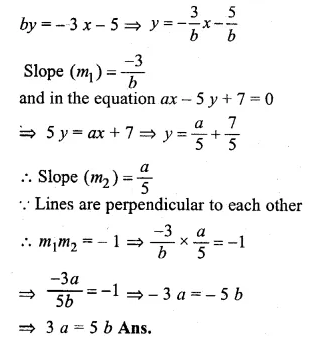
Question 8.
Is the line through ( – 2, 3) and (4, 1) perpendicular to the line 3x = y + 1 ?
Does the line 3x = y + 1 bisect the join of ( – 2, 3) and (4, 1). (1993)
Solution:
Slope of the line passing through the points
(-2, 3) and (4, 1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-x_{ 1 } } \)

Hence the line 3x = y + 1 bisects the line joining the points (-2, 3), (4, 1).

Question 9.
The line through A ( – 2, 3) and B (4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
Gradient (m₁) of the line passing through the
points A (-2, 3) and B (4, b)

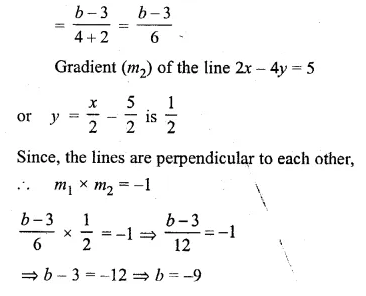
Question 10.
If the lines 3x + y = 4, x – ay + 7 = 0 and bx + 2y + 5 = 0 form three consecutive sides of a rectangle, find the value of a and b.
Solution:
In the line 3x + y = 4 …(i)
⇒ y = – 3x + 4
Slope (m₁) = – 3
In the line x – ay + 7 = 0…..(ii)

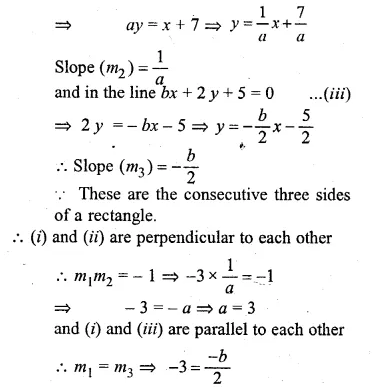
⇒ -b = -6 ⇒ b = 6
Hence a = 3, b = 6

Question 11.
Find the equation of a line, which has the y-intercept 4, and is parallel to the line 2x – 3y – 7 = 0. Find the coordinates of the point where it cuts the x-axis. (1998)
Solution:
In the given line 2x – 3y – 7 = 0
⇒ 3y = 2x – 7
⇒ \(y=\frac { 2 }{ 3 } x-\frac { 7 }{ 3 } \)

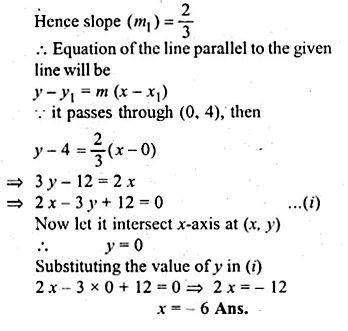
Question 12.
Find the equation of a straight line perpendicular to the line 2x + 5y + 7 = 0 and with y-intercept – 3 units.
Solution:
In the line 2x + 5y + 7 = 0
⇒ 5y = – 2x – 7
⇒ \(y=\frac { -2 }{ 5 } x-\frac { 7 }{ 5 } \)

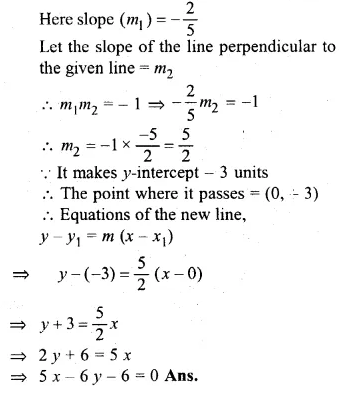
Question 13.
Find the equation of a st. line perpendicular to the line 3x – 4y + 12 = 0 and having same y-intercept as 2x – y + 5 = 0.
Solution:
In the given line 3x – 4y + 12 = 0
⇒ 4y = 3x + 12
⇒ y = \(\\ \frac { 3 }{ 4 } x+3\)

Question 14.
Find the equation of the line which is parallel to 3x – 2y = – 4 and passes through the point (0, 3). (1990)
Solution:
In the given line 3x – 2y = – 4
⇒ 2y = 3x + 4
⇒ y = \(\\ \frac { 3 }{ 2 } x+2\)

Question 15.
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0. (1999)
Solution:
In the given equation 3x + 5y + 15 = 0
⇒ 5y = – 3x – 15
⇒ y = \(\\ \frac { -3 }{ 5 } x-3\)

Question 16.
The equation of a line is y = 3x – 5. Write down the slope of this line and the intercept made by it on the y-axis. Hence or otherwise, write down the equation of a line which is parallel to the line and which passes through the point (0, 5).
Solution:
In the given line y = 3x – 5
Here slope (m₁) = 3
Substituting x = 0, then y = – 5
y-intercept = – 5
The slope of the line parallel to the given line
will be 3 and passes through the point (0, 5).
Equation of the line will be

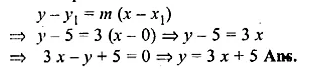
Question 17.
Write down the equation of the line perpendicular to 3x + 8y = 12 and passing through the point ( – 1, – 2).
Solution:
In the given line 3x + 8y = 12
⇒ 8y = -3x + 12
⇒ \(y=\frac { -3 }{ 8 } x+\frac { 12 }{ 8 } \)

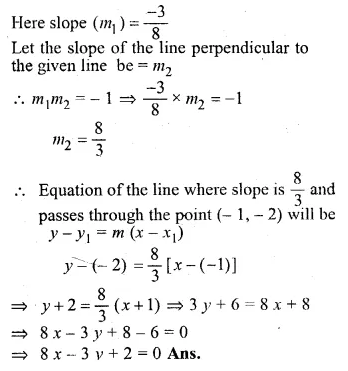
Question 18.
(i) The line 4x – 3y + 12 = 0 meets the x-axis at A. Write down the co-ordinates of A.
(ii) Determine the equation of the line passing through A and perpendicular to 4x – 3y + 12 = 0. (1993)
Solution:
(i) In the line 4x – 3y + 12 = 0 …(i)
3y = 4x + 12
⇒ y = \(\\ \frac { 4 }{ 3 } x+4\)

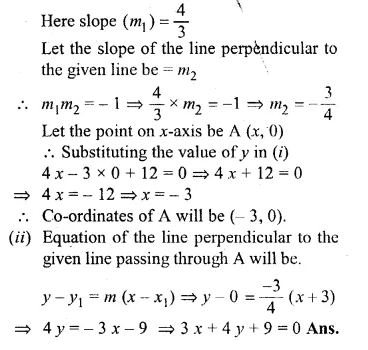
Question 19.
Find the equation of the line that is parallel to 2x + 5y – 7 = 0 and passes through the mid-point of the line segment joining the points (2, 7) and ( – 4, 1).
Solution:
The given line 2x + 5y – 7 = 0
5y = -2x + 7
⇒ \(y=\frac { -2 }{ 5 } x+\frac { 7 }{ 5 } \)

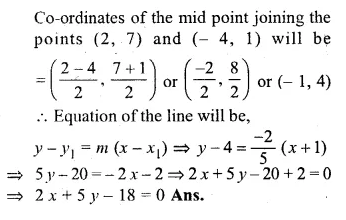
Question 20.
Find the equation of the line that is perpendicular to 3x + 2y – 8 = 0 and passes through the mid-point of the line segment joining the points (5, – 2), (2, 2).
Solution:
In the given line 3x + 2y – 8=0
⇒ 2y = – 3x + 8
⇒ y = \(\\ \frac { -3 }{ 2 } x+4\)

Question 21.
Find the equation of a straight line passing through the intersection of 2x + 5y – 4 = 0 with x-axis and parallel to the line 3x – 7y + 8 = 0.
Solution:
Let the point of intersection of the line 2x + 5y – 4 = 0 and x-axis be (x, 0)
Substituting the value of y in the equation
2x + 5 × 0 – 4 = 0
⇒ 2x – 4 = 0
⇒ 2x = 4
⇒ x = \(\\ \frac { 4 }{ 2 } \) = 2
Coordinates of the points of intersection will be (2, 0)

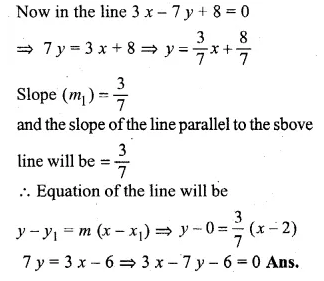
Question 22.
The equation of a line is 3x + 4y – 7 = 0. Find
(i) the slope of the line. .
(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0. (2010)
Solution:
(i) Equation of the line is 3x + 4y – 1 = 0
⇒ 4y = 7 – 3x

Question 23.
Find the equation of the line perpendicular from the point (1, – 2) on the line 4x – 3y – 5 = 0. Also find the co-ordinates of the foot of perpendicular.
Solution:
In the equation 4x – 3y – 5 = 0,
⇒ 3y = 4x – 5
⇒ \(y=\frac { 4 }{ 3 } x-\frac { 5 }{ 3 } \)

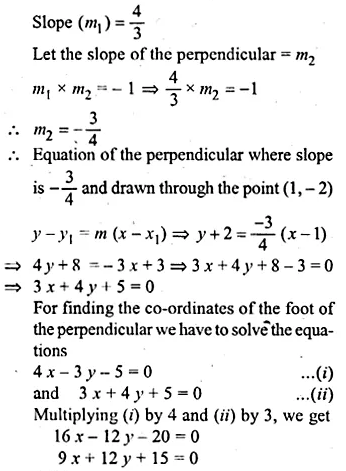
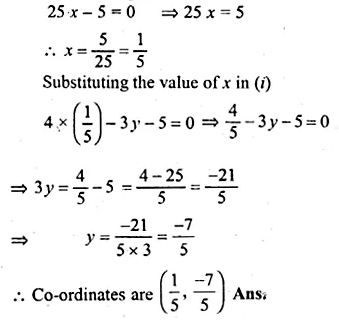
Question 24.
Prove that the line through (0, 0) and (2, 3) is parallel to the line through (2, – 2) and (6, 4).
Solution:
Given that
Slope of the line through (0, 0) and (2, 3)

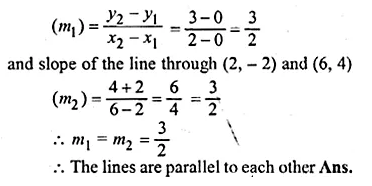
Question 25.
Prove that the line through,( – 2, 6) and (4, 8) is perpendicular to the line through (8, 12) and (4, 24).
Solution:
Given that
Slope of the line through (-2, 6) and (4, 8)

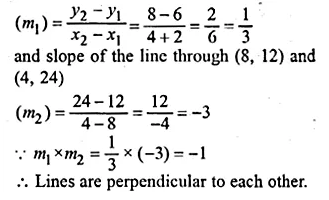
Question 26.
Show that the triangle formed by the points A (1, 3), B (3, – 1) and C ( – 5, – 5) is a right angled triangle by using slopes.
Solution:
Slope (m₁) of line by joining the points
A(1, 3), B (3, -1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ x_{ 2 }-{ x }_{ 1 } } \)

Question 27.
Find the equation of the line through the point ( – 1, 3) and parallel to the line joining the points (0, – 2) and (4, 5).
Solution:
Slope of the line joining the points (0, -2) and (4, 5) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ x_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 5+2 }{ 4-0 } =\frac { 7 }{ 4 } \)
Slope of the line parallel to it passing through (-1, 3) = \(\\ \frac { 7 }{ 4 } \)

Question 28.
A ( – 1, 3), B (4, 2), C (3, – 2) are the vertices of a triangle.
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC
Solution:
Given, A (-1, 3), B (4, 2), C (3, -2)
(i) Coordinates of centroid G

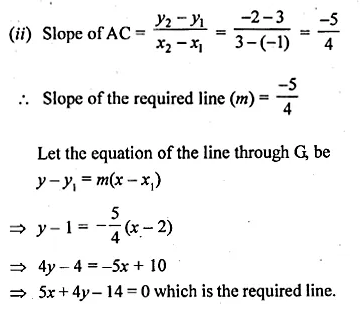
Question 29.
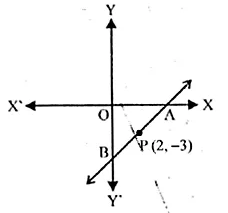
The line through P (5, 3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the coordinates of Q.

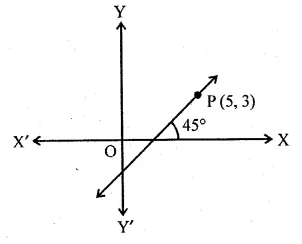
Solution:
(i) Here θ = 45°
So, slope of the line = tan θ = tan 45° = 1
(ii) Equation of the line through P and Q is
y – 3 = 1(x – 5) ⇒ y – x + 2 = 0
(iii) Let the coordinates of Q be (0, y)

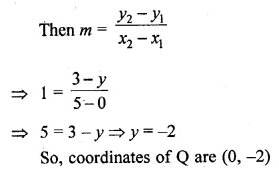
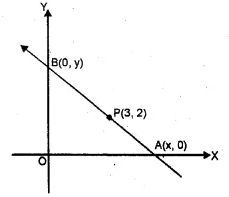
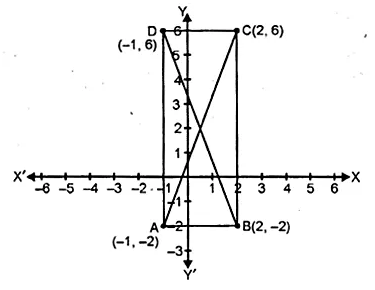
Question 30.
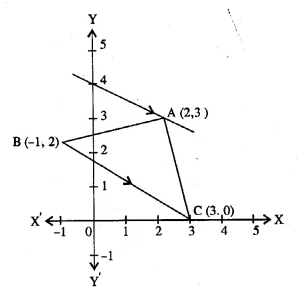
In the adjoining diagram, write down
(i) the co-ordinates of the points A, B and C.
(ii) the equation of the line through A parallel to BC. (2005)

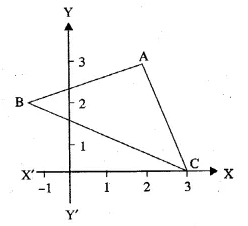
Solution:
From the given figure, it is clear that
co-ordinates of A are (2, 3) of B are ( -1, 2)
and of C are (3, 0).

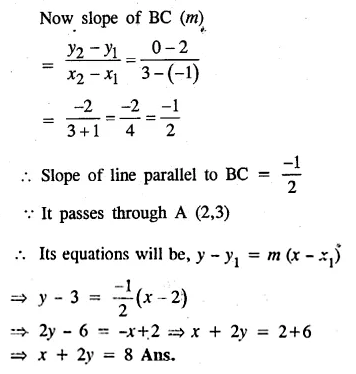
Question 31.
Find the equation of the line through (0, – 3) and perpendicular to the line joining the points ( – 3, 2) and (9, 1).
Solution:
The slope (m₁) of the line joining the points (-3, 2) and (9, 1)

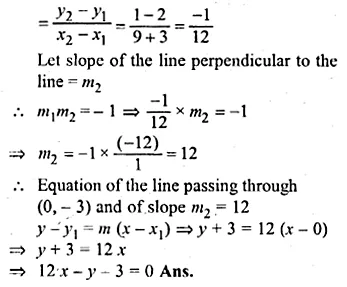
Question 32.
The vertices of a triangle are A (10, 4), B (4, – 9) and C ( – 2, – 1). Find the equation of the altitude through A. The perpendicular drawn from a vertex of a triangle to the opposite side is called altitude.
Solution:
Vertices of ∆ABC are A (10, 4), B (4, -9) and C( – 2, – 1)
Slope of the line BC (m₁) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)

Question 33.
A (2, – 4), B (3, 3) and C ( – 1, 5) are the vertices of triangle ABC. Find the equation of :
(i) the median of the triangle through A
(ii) the altitude of the triangle through B
Solution:
(i) D is the mid-point of BC
Co-ordinates of D will

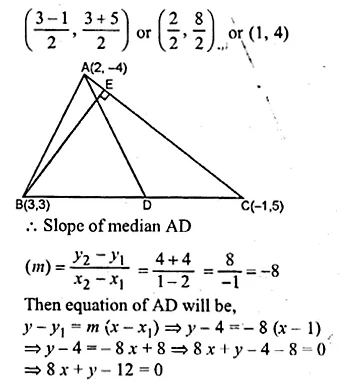
Question 34.
Find the equation of the right bisector of the line segment joining the points (1, 2) and (5, – 6).
Solution:
Slope of the line joining the points (1, 2) and (5, -6)
\({ m }_{ 1 }=\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -6-2 }{ 5-1 } =\frac { -8 }{ 4 } =-2\)

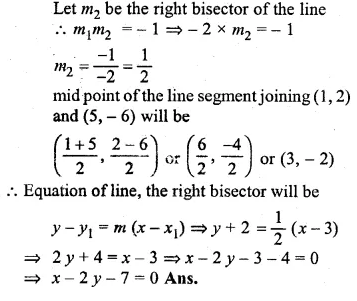
Question 35.
Points A and B have coordinates (7, – 3) and (1, 9) respectively. Find
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of ‘p’ if ( – 2, p) lies on it.
Solution:
Coordinates of A are (7, -3), of B = (1, 9)
(i) ∴ slope (m)

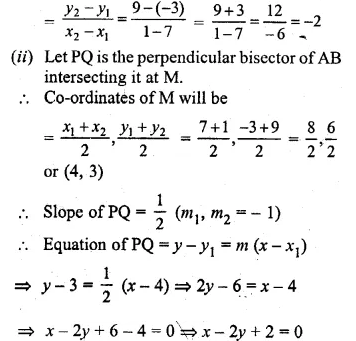
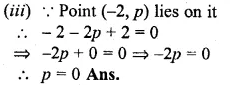
Question 36.
The points B (1, 3) and D (6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.
Solution:
Slope of BD (m₁) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 8-3 }{ 6-1 } =\frac { 5 }{ 5 } =1\)
Diagonal AC is perpendicular bisector of diagonal BD

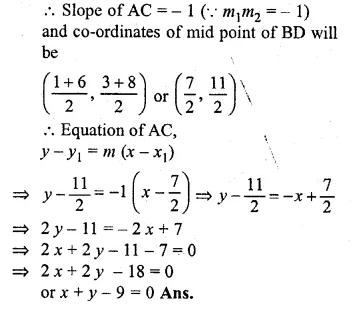
Question 37.
ABCD is a rhombus. The co-ordinates of A and C are (3, 6) and ( – 1, 2) respectively. Write down the equation of BD. (2000)
Solution:
Co-ordinates of A (3, 6), C (-1, 2)
Slope of AC (m₁) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 2-6 }{ -1-3 } =\frac { -4 }{ -4 } =1\)

Question 38.
Find the equation of the line passing through the intersection of the lines 4x + 3y = 1 and 5x + 4y = 2 and
(i) parallel to the line x + 2y – 5 = 0
(ii) perpendicular to the x-axis.
Solution:
4x + 3y = 1 …(i)
5x + 4y = 2 …(ii)
Multiplying (i) by 4 and (ii) by 3

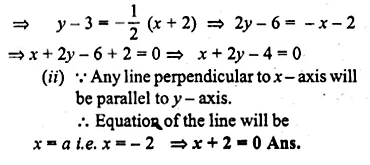
Question 39.
(i) Write down the co-ordinates of the point P that divides the line joining A ( – 4, 1) and B (17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP where 0 is the origin
(iii) In what ratio does the y-axis divide the line AB?
Solution:
(i) Co-ordinate A (-4, 1) and B (17, 10) P divides it in the ratio of 1 : 2
Let the co-ordinates of P will be (x, y)

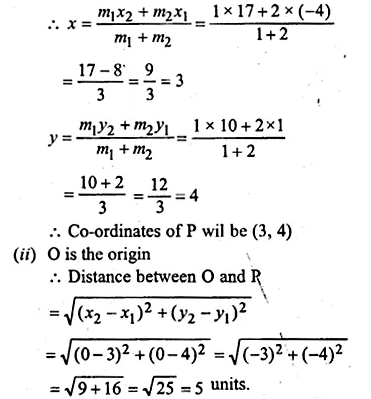
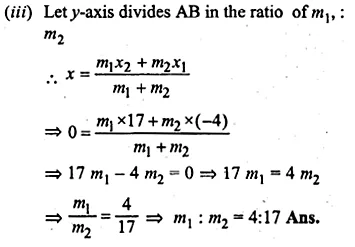
Question 40.
Find the image of the point (1, 2) in the line x – 2y – 7 = 0
Solution:
Draw a perpendicular from the point P(1, 2) on the line, x – 2y – 7 = 0
Let P’ is the image of P and let its
co-ordinates sue (α, β) slope of line x – 2y – 7 = 0

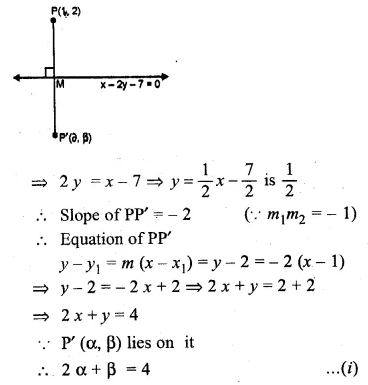
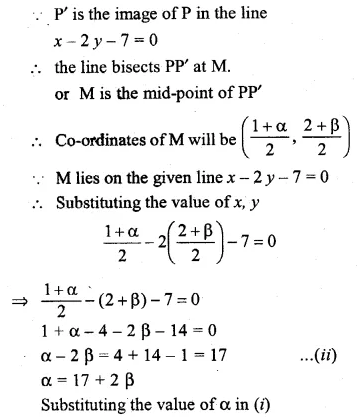
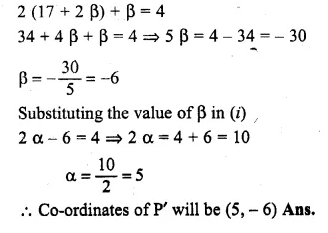
Question 41.
If the line x – 4y – 6 = 0 is the perpendicular bisector of the line segment PQ and the co-ordinates of P are (1, 3), find the co-ordinates of Q.
Solution:
Let the co-ordinates of Q be (α, β) and let the line x – 4y – 6 = 0 is the

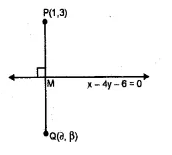
perpendicular bisector of PQ and it intersects the line at M.
M is the mid point of PQ Now slope of line x – 4y – 6 = 0

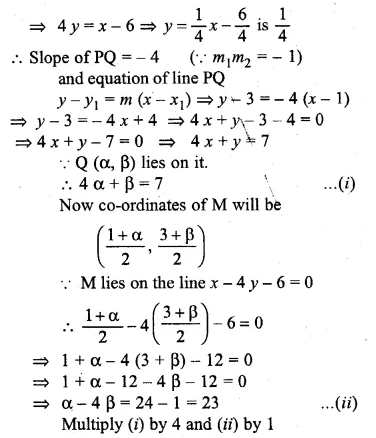
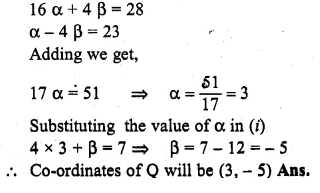
Question 42.
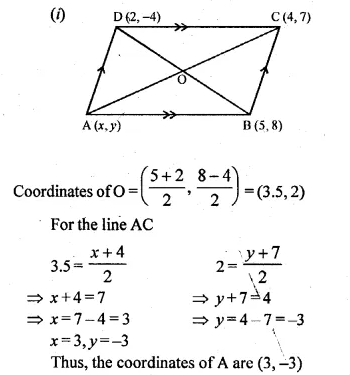
OABC is a square, O is the origin and the points A and B are (3, 0) and (p, q). If OABC lies in the first quadrant, find the values of p and q. Also write down the equations of AB and BC.
Solution:
OA = \(\sqrt { { (3-0) }^{ 2 }+{ (0-0) }^{ 2 } } \)
\(\sqrt { { (3-0) }^{ 2 }+{ (0) }^{ 2 } } \)

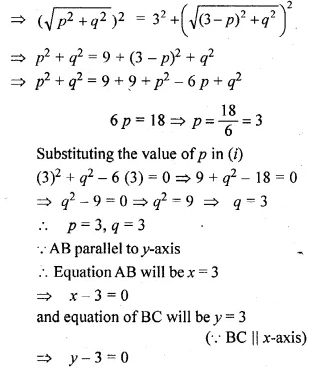
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Question 1.
Find the slope of a line whose inclination is
(i) 45°
(ii) 30°
Solution:
(i) tan 45° = 1
(ii) tan 30° = \(\frac { 1 }{ \sqrt { 3 } } \)

Question 2.
Find the inclination of a line whose gradient is
(i) 1
(ii) √3
(iii) \(\frac { 1 }{ \sqrt { 3 } } \)
Solution:
(i) tan θ = 1 ⇒ θ = 45°
(ii) tan θ = √3 ⇒ θ = 60°
(iii) tan θ = \(\frac { 1 }{ \sqrt { 3 } } \) ⇒ θ = 30°

Question 3.
Find the equation of a straight line parallel 1 to x-axis which is at a distance
(i) 2 units above it
(ii) 3 units below it.
Solution:
(i) A line which is parallel to x-axis is y = a
⇒ y = 2
⇒ y – 2 = 0
(ii) A line which is parallel to x-axis is y = a
⇒ y = -3
⇒ y + 3 = 0

Question 4.
Find the equation of a straight line parallel to y-axis which is at a distance of:
(i) 3 units to the right
(ii) 2 units to the left.
Solution:
(i) The equation of line parallel to y-axis is at a distance of 3 units to the right is x = 3 ⇒ x – 3 = 0
(ii) The equation of line parallel to y-axis at a distance of 2 units to the left is x = -2 ⇒ x + 2 = 0

Question 5.
Find the equation of a straight line parallel to y-axis and passing through the point ( – 3, 5).
Solution:
The equation of the line parallel to y-axis passing through ( – 3, 5) to x = -3
⇒ x + 3 = 0

Question 6.
Find the equation of the a line whose
(i) slope = 3, y-intercept = – 5
(ii) slope = \(– \frac { 2 }{ 7 } \), y-intercept = 3
(iii) gradient = √3, y-intercept = \(– \frac { 4 }{ 3 } \)
(iv) inclination = 30°,y-intercept = 2
Solution:
Equation of a line whose slope and y-intercept is given is
y = mx + c
where m is the slope and c is the y-intercept
(i) y = mx + c
⇒ y = 3x + (-5)
⇒ y = 3x – 5

Question 7.
Find the slope and y-intercept of the following lines:
(i) x – 2y – 1 = 0
(ii) 4x – 5y – 9 = – 0
(iii) 3x +5y + 7 = 0
(iv) \(\frac { x }{ 3 } +\frac { y }{ 4 } =1\)
(v) y – 3 = 0
(vi) x – 3 = 0
Solution:
We know that in the equation
y = mx + c, m is the slope and c is the y-intercept.
Now using this, we find,

Question 8.
The equation of the line PQ is 3y – 3x + 7 = 0
(i) Write down the slope of the line PQ.
(ii) Calculate the angle that the line PQ makes with the positive direction of x-axis.
Solution:
Equation of line PQ is 3y – 3x + 7 = 0
Writing in form of y = mx + c

Question 9.
The given figure represents the line y = x + 1 and y = √3x – 1. Write down the angles which the lines make with the positive direction of the x-axis. Hence determine θ.

Solution:
Slope of the line y = x + 1 after comparing
it with y = mx + c, m = 1

Question 10.
Find the value of p, given that the line \(\frac { y }{ 2 } =x-p\) passes through the point ( – 4, 4) (1992).
Solution:
Equation of line is \(\frac { y }{ 2 } =x-p\)
It passes through the points (-4, 4)
It will satisfy the equation

Question 11.
Given that (a, 2a) lies on the line \(\frac { y }{ 2 } =3x-6\) find the value of a.
Solution:
∵ Point (a, 2a) lies on the line
\(\frac { y }{ 2 } =3x-6\)
∴this point will satisfy the equation

Question 12.
The graph of the equation y = mx + c passes through the points (1, 4) and ( – 2, – 5). Determine the values of m and c.
Solution:
Equation of the line is y = mx + c
∴ it passes through the points (1, 4)
∴ 4 = m x 1 + c
⇒ 4 = m + c
⇒ m + c = 4 … (i)
Again it passes through the point (-2, -5)
∴ 5 = m (-2) + c
⇒ 5 = -2 m + c
⇒ 2m – c = 5 …(ii)
Adding (i) and (ii)
3m = 9
⇒ m = 3
Substituting the value of m in (i)
3 + c = 4
⇒ c = 4 – 3 = 1
Hence m = 3, c = 1

Question 13.
Find the equation of the line passing through the point (2, – 5) and making an intercept of – 3 on the y-axis.
Solution:
∴ The line intersects y-axis making an intercept of -3
∴ the co-ordinates of point of intersection will be (0, -3)
Now the slope of line (m) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)

Question 14.
Find the equation of a straight line passing through ( – 1, 2) and whose slope is \(\\ \frac { 2 }{ 5 } \).
Solution:
Equation of the line will be
\(y-{ y }_{ 1 }=m(x-{ x }_{ 1 }) \)
\(y-2=\frac { 2 }{ 5 } (x+1)\)
⇒ 5y – 10 = 2x + 2
⇒ 2x – 5y + 2 + 10 = 0
⇒ 2x – 5y + 12 = 0

Question 15.
Find the equation of a straight line whose inclination is 60° and which passes through the point (0, – 3).
Solution:
The equation of line whose slope is wand passes through a given point is
\(y-{ y }_{ 1 }=m(x-{ x }_{ 1 }) \)
Here m = tan 60° = √3 and point is (0, -3)
∴ y + 3 = √3 (x – 0)
⇒ y + 3 = √3x
⇒ √3x – y – 3 = 0

Question 16.
Find the gradient of a line passing through the following pairs of points.
(i) (0, – 2), (3, 4)
(ii) (3, – 7), ( – 1, 8)
Solution:
m = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
Given
(i) (0, -2), (3, 4)
(ii) (3, -7), (-1, 8)

Question 17.
The coordinates of two points E and F are (0, 4) and (3, 7) respectively. Find :
(i) The gradient of EF
(ii) The equation of EF
(iii) The coordinates of the point where the line EF intersects the x-axis.
Solution:
Co-ordinates of points E (0, 4) and F (3, 7) are given, then
(i) The gradient of EF

Question 18.
Find the intercepts made by the line 2x – 3y + 12 = 0 on the co-ordinate axis.
Solution:
Putting y = 0, we will get the intercept made on x-axis,
2x – 3y + 12 = 0
⇒ 2x – 3 × 0 + 12 = 0
⇒ 2x – 0 + 2 = 0
⇒ 2x = -12
⇒ x = -6
and putting x = 0, we get the intercepts made on y-axis,
2x – 3y + 12 = 0
⇒ 2 × 0 – 3y + 12 = 0
⇒ -3y = -12
⇒ \(y= \frac { -12 }{ -3 } \) = 4

Question 19.
Find the equation of the line passing through the points P (5, 1) and Q (1, – 1). Hence, show that the points P, Q and R (11, 4) are collinear.
Solution:
The two given points are P (5, 1), Q(1, -1).
∴ Slope of the line (m)

Question 20.
Find the value of ‘a’ for which the following points A (a, 3), B (2,1) and C (5, a) are collinear. Hence find the equation of the line.
Solution:
Given That
A(a, 3), B (2, 1) and C (5, a) are collinear.
Slope of AB = Slope of BC

Question 21.
Use a graph paper for this question. The graph of a linear equation in x and y, passes through A ( – 1, – 1) and B (2, 5). From your graph, find the values of h and k, if the line passes through (h, 4) and (½, k). (2005)
Solution:
Points (h, 4) and (½, k) lie on the line passing
through A(-1, -1) and B(2, 5)

Question 22.
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, – 4). Find
(i) the coordinates of A
(ii) the equation of the diagonal BD.
Solution:
Given that
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, -4)

Question 23.
In ∆ABC, A (3, 5), B (7, 8) and C (1, – 10). Find the equation of the median through A.
Solution:
AD is median
⇒ D is mid point of BC
∴ D is \(\left( \frac { 7+1 }{ 2 } ,\frac { 8-10 }{ 2 } \right) \)
i.e (4, -1)
slope of AD

Question 24.
Find the equation of a line passing through the point ( – 2, 3) and having x-intercept 4 units. (2002)
Solution:
x-intercept = 4
∴ Co-ordinates of the point will be (4, 0)
Now slope of the line passing through the points (-2, 3) and (4, 0)

Question 25.
Find the equation of the line whose x-intercept is 6 and y-intercept is – 4.
Solution:
x-intercept = 6
∴ The line will pass through the point (6, 0)
y -intercept = -4 ⇒ c = -4

Question 26.
Write down the equation of the line whose gradient is \(\\ \frac { 1 }{ 2 } \) and which passes through P where P divides the line segment joining A ( – 2, 6) and B (3, – 4) in the ratio 2 : 3. (2001)
Solution:
P divides the line segment joining the points
A (-2, 6) and (3, -4) in the ratio 2 : 3
∴ Co-ordinates of P will be

Question 27.
Find the equation of the line passing through the point (1, 4) and intersecting the line x – 2y – 11 = 0 on the y-axis.
Solution:
line x – 2y – 11 = 0 passes through y-axis
x = 0,
Now substituting the value of x in the equation x – 2y – 11 = 0

Question 28.
Find the equation of the straight line containing the point (3, 2) and making positive equal intercepts on axes.
Solution:

Let the line containing the point P (3, 2)
passes through x-axis at A (x, 0) and y-axis at B (0, y)
OA = OB given
∴ x = y

Question 29.
Three vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find:
(i) the coordinates of the fourth vertex D.
(ii) length of diagonal BD.
(iii) equation of side AB of the parallelogram ABCD. (2015)
Solution:
Three vertices of a parallelogram ABCD taken in order are
A (3, 6), B (5, 10) and C (3, 2)
(i) We need to find the co-ordinates of D
We know that the diagonals of a parallelogram bisect each other
Let (x, y) be the co-ordinates of D

Question 30.
A and B arc two points on the x-axis and y-axis respectively. P (2, – 3) is the mid point of AB. Find the

(i) the co-ordinates of A and B.
(ii) the slope of the line AB.
(iii) the equation of the line AB. (2010)
Solution:
Points A and B are on x-axis and y-axis respectively
Let co-ordinates of A be (X, O) and of B be (O, Y)
P (2, -3) is the midpoint of AB

Question 31.
Find the equations of the diagonals of a rectangle whose sides are x = – 1, x = 2 , y = – 2 and y = 6.

Solution:
The equations of sides of a rectangle whose equations are
x₁ = -1, x₂ = 2, y₁ = -2, y₂ = 6.
These lines form a rectangle when they intersect at A, B, C, D respectively
Co-ordinates of A, B, C and D will be
(-1, -2), (2, -2), (2, 6) and (-1, 6) respectively.
AC and BD are its diagonals
(i) Slope of the diagonal AC

Question 32.
Find the equation of a straight line passing through the origin and through the point of intersection of the lines 5x + 1y – 3 and 2x – 3y = 7
Solution:
5x + 7y = 3 …(i)
2x – 3 y = 7 …(ii)
Multiply (i) by 3 and (ii) by 7,
15x + 21y = 9
14x – 21y = 49
Adding we get,

Question 33.
Point A (3, – 2) on reflection in the x-axis is mapped as A’ and point B on reflection in the y-axis is mapped onto B’ ( – 4, 3).
(i) Write down the co-ordinates of A’ and B.
(ii) Find the slope of the line A’B, hence find its inclination.
Solution:
A’ is the image of A (3, -2) on reflection in the x-axis.
∴ Co-ordinates of A’ will be (3, 2)
Again B’ (- 4, 3) in the image of A’, when reflected in the y-axis
∴ Co-ordinates of B will be (4, 3)
(ii) Slope of the line joining, the points A’ (3, 2) and B (4, 3)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Ex 11
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

Question 1.
The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of the point C are (0, – 3). If origin is the mid-point of the base BC, find the coordinates of the points A and B
Solution:
Base BC of an equilateral ∆ABC lies on y-axis
co-ordinates of point C are (0, – 3),
origin (0, 0) is the mid-point of BC.

Question 2.
A and B have co-ordinates (4, 3) and (0, 1), Find
(i) the image A’ of A under reflection in the y – axis.
(ii) the image of B’ of B under reflection in the lineAA’.
(iii) the length of A’B’.
Solution:

(i) Co-ordinates of A’, the image of A (4, 3)
reflected in y-axis will be ( – 4, 3).
(ii) Co-ordinates of B’ the image of B (0, 1)
reflected in the line AA’ will be (0, 5).
(iii) Length A’B’

Question 3.
Find the co-ordinates of the point that divides the line segment joining the points P (5, – 2) and Q (9, 6) internally in the ratio of 3 : 1.
Solution:
Let R be the point whose co-ordinates are (x, y)
which divides PQ in the ratio of 3:1.

Question 4.
Find the coordinates of the point P which is three-fourth of the way from A (3, 1) to B ( – 2, 5).
Solution:
Co-ordinates of A (3, 1) and B ( – 2, 5)
P lies on AB such that

Question 5.
P and Q are the points on the line segment joining the points A (3, – 1) and B ( – 6, 5) such that AP = PQ = QB. Find the co-ordinates of P and Q.
Solution:
Given
AP = PQ = QB

Question 6.
The centre of a circle is (α + 2, α – 5). Find the value of a given that the circle passes through the points (2, – 2) and (8, – 2).
Solution:
Let A (2, -2), B (8, -2) and centre of the circle be
O (α + 2, α – 5)

Question 7.
The mid-point of the line joining A (2, p) and B (q, 4) is (3, 5). Calculate the numerical values of p and q.
Solution:
Given
(3, 5) is the mid-point of A (2, p) and B (q, 4)

Question 8.
The ends of a diameter of a circle have the co-ordinates (3, 0) and ( – 5, 6). PQ is another diameter where Q has the coordinates ( – 1, – 2). Find the co-ordinates of P and the radius of the circle.
Solution:
Let AB be the diameter where co-ordinates of
A are (3, 0) and of B are (-5, 6).
Co-ordinates of its origin O will be

Question 9.
In what ratio does the point ( – 4, 6) divide the line segment joining the points A( – 6, 10) and B (3, – 8) ?
Solution:
Let the point (-4, 6) divides the line segment joining the points
A (-6, 10) and B (3, -8), in the ratio m : n

Question 10.
Find the ratio in which the point P ( – 3, p) divides the line segment joining the points ( – 5, – 4) and ( – 2, 3). Hence find the value of p.
Solution:
Let P (-3, p) divides AB in the ratio of m₁ : m₂ coordinates of
A (-5, -4) and B (-2, 3)

Question 11.
In what ratio is the line joining the points (4, 2) and (3, – 5) divided by the x-axis? Also find the co-ordinates of the point of division.
Solution:
Let the point P which is on the x-axis, divides the line segment
joining the points A (4, 2) and B (3, -5) in the ratio of m₁ : m₂.
and let co-ordinates of P be (x, 0)

Question 12.
If the abscissa of a point P is 2, find the ratio in which it divides the line segment joining the points ( – 4 – 3) and (6, 3). Hence, find the co-ordinates of P.
Solution:
Let co-ordinates of A be (-4, 3) and of B (6, 3) and of P be (2, y)
Let the ratio in which the P divides AB be m₁ : m₂

Question 13.
Determine the ratio in which the line 2x + y – 4 = 0 divide the line segment joining the points A (2, – 2) and B (3, 7). Also find the co-ordinates of the point of division.
Solution:
Points are given A (2, -2), B (3, 7)
and let the line 2x + y – 4 = 0 divides AB in the ratio m₁ : m₂
at P and let co-ordinates of

Question 14.
The point A(2, – 3) is reflected in the v-axis onto the point A’. Then the point A’ is reflected in the line x = 4 onto the:point A”.
(i) Write the coordinates of A’ and A”.
(ii) Find the ratio in which the line segment AA” is divided by the x-axis. Also find the coordinates of the point of division.
Solution:
A’ is the reflection of A(2, -3) in the x-axis
(i) ∴ Co-ordinates of A’ will be (2, 3)
Draw a line x = 4 which is parallel to y-axis
A” is the reflection of A’ (2, 3)
∴Co-ordinates OA” will be (6, 3)
(ii) Join AA” which intersects x-axis at P whose
co-ordinate are (4, 0)
Let P divide AA” in the ratio in m₁ : m₂

Hence P(4, 0) divides AA” in the ratio 1 : 1

Question 15.
ABCD is a parallelogram. If the coordinates of A, B and D are (10, – 6), (2, – 6) and (4, – 2) respectively, find the co-ordinates of C.
Solution:
Let the co-ordinates of C be (x, y) and other three vertices
of the given parallelogram are A (10, – 6), B, (2, – 6) and D (4, – 2)
∴ ABCD is a parallelogram
Its diagonals bisect each other.
Let AC and BD intersect each other at O.
∴O is mid-points of BD
∴ Co-ordinates of O will be

Question 16.
ABCD is a parallelogram whose vertices A and B have co-ordinates (2, – 3) and ( – 1, – 1) respectively. If the diagonals of the parallelogram meet at the point M(1, – 4), find the co-ordinates of C and D. Hence, find the perimeter of the parallelogram. find the perimeter of the parallelogram.
Solution:
ABCD is a || gm , m which co-ordinates of A are (2, -3) and B (-1, -1)
Its diagonals AC and BD bisect each other at M (1, -4)
∴ M is the midpoint of AC and BD
Let co-ordinates of C be (x₁, y₁) and of D be (x₂, y₂)
when M is the midpoint of AC then

Question 17.
In the adjoining figure, P (3, 1) is the point on the line segment AB such that AP : PB = 2 : 3. Find the co-ordinates of A and B.

Solution:
A lies on x-axis and
B lies on y-axis
Let co-ordinates of A be (x, 0) and B be (0, y)
and P (3, 1) divides it in the ratio of 2 : 3.

Question 18.
Given, O, (0, 0), P(1, 2), S( – 3, 0) P divides OQ in the ratio of 2 : 3 and OPRS is a parallelogram.
Find : (i) the co-ordinates of Q.
(ii)the co-ordinates of R.
(iii) the ratio in which RQ is divided by y-axis.

Solution:
(i) Let co-ordinates of Q be (x’, y’) and of R (x”, y”)
Point P (1, 2) divides OQ in the ratio of 2 : 3

Question 19.
If A (5, – 1), B ( – 3, – 2) and C ( – 1, 8) are the vertices of a triangle ABC, find the length of the median through A and the co-ordinates of the centroid of triangle ABC.
Solution:
A (5, -1), B (-3, -2) and C (-1, 8) are the vertices of ∆ABC
D, E and F are the midpoints of sides BC, CA and AB respectively
and G is the centroid of the ∆ABC

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Ex 11
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

Choose the correct answer from the given four options (1 to 12) :

Question 1.
The points A (9, 0), B (9, 6), C ( – 9, 6) and D ( – 9, 0) are the vertices of a
(a) rectangle
(b) square
(c) rhombus
(d) trapezium
Solution:
A (9, 0), B (9, 6), C (-9, 6), D (-9, 0)
AB² = (x₂ – x₁)² + (y₂ – y₁)²

Question 2.
The mid-point of the line segment joining the points A ( – 2, 8) and B ( – 6, – 4) is
(a) ( – 4, – 6)
(b) (2, 6)
(c) ( – 4, 2)
(d) (4, 2)
Solution:
Mid-point of the line segment joining the points A (-2, 8), B (-6, -4)

Question 3.
If \(P\left( \frac { a }{ 3 } ,4 \right) \) segment joining the points Q ( – 6, 5) and R ( – 2, 3), then the value of a is
(a) – 4
(b) – 6
(c) 12
(d) – 12
Solution:
\(P\left( \frac { a }{ 3 } ,4 \right) \) is mid-point of the line segment
joining the points Q (-6, 5) and R (-2, 3)

Question 4.
If the end points of a diameter of a circle are A ( – 2, 3) and B (4, – 5), then the coordinates of its centre are
(a) (2, – 2)
(b) (1, – 1)
(c) ( – 1, 1)
(d) ( – 2, 2)
Solution:
End points of a diameter of a circle are (-2, 3) and B (4,-5)
then co-ordinates of the centre of the circle
= \(\left( \frac { -2+4 }{ 2 } ,\frac { 3-5 }{ 2 } \right) or\left( \frac { 2 }{ 2 } ,\frac { -2 }{ 2 } \right) \)
= (1, -1) (b)

Question 5.
If one end of a diameter of a circle is (2, 3) and the centre is ( – 2, 5), then the other end is
(a) ( – 6, 7)
(b) (6, – 7)
(c) (0, 8)
(d) (0, 4)
Solution:
One end of a diameter of a circle is (2, 3) and centre is (-2, 5)
Let (x, y) be the other end of the diameter

Question 6.
If the mid-point of the line segment joining the points P (a, b – 2) and Q ( – 2, 4) is R (2, – 3), then the values of a and b are
(a) a = 4, b = – 5
(b) a = 6, b = 8
(c) a = 6, b = – 8
(d) a = – 6, b = 8
Solution:
the mid-point of the line segment joining the
points P (a, b – 2) and Q (-2, 4) is R (2, -3)

Question 7.
The point which lies on the perpendicular bisector of the line segment joining the points A ( – 2, – 5) and B (2, 5) is
(a) (0, 0)
(b) (0, 2)
(c) (2, 0)
(d) ( – 2, 0)
Solution:
the line segment joining the points A (-2, -5) and B (2, -5), has mid-point
= \(\left( \frac { -2+2 }{ 2 } ,\frac { -5+5 }{ 2 } \right) \) = (0, 0)
(0, 0) lies on the perpendicular bisector of AB. (a)

Question 8.
The coordinates of the point which is equidistant from the three vertices of ∆AOB (shown in the given figure) are
(a) (x, y)
(b) (y, x)
(c) \(\left( \frac { x }{ 2 } ,\frac { y }{ 2 } \right) \)
(d) \(\left( \frac { y }{ 2 } ,\frac { x }{ 2 } \right) \)

Solution:
In the given figure, vertices of a ∆OAB are (0, 0), (0, 2y) and (2x, 0)
The point which is equidistant from O, A and B is the mid-point of AB.
∴ Coordinates are \(\left( \frac { 0+2x }{ 2 } ,\frac { 2y+0 }{ 2 } \right) \) or (x, y) (a)

Question 9.
The fourth vertex D of a parallelogram ABCD whose three vertices are A ( – 2, 3), B (6, 7) and C (8, 3) is
(a) (0, 1)
(b) (0, – 1)
(c) ( – 1, 0)
(d) (1, 0)
Solution:
ABCD is a ||gm whose vertices A (-2, 3), B (6, 7) and C (8, 3).
The fourth vertex D will be the point on which diagonals AC and BD
bisect each other at O.

Question 10.
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, – 5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(a) (0, – 5) and (2, 0)
(b) (0, 10) and ( – 4, 0)
(c) (0, 4) and ( – 10, 0)
(d) (0, – 10) and (4, 0)
Solution:
A line intersects y-axis at P and x-axis a Q.
R (2, -5) is the mid-point

Question 11.
The points which divides the line segment joining the points (7, – 6) and (3, 4) in the ratio 1 : 2 internally lies in the
(a) Ist quadrant
(b) IInd quadrant
(c) IIIrd quadrant
(d) IVth quadrant
Solution:
A point divides line segment joining the points
A (7, -6) and B (3, 4) in the ratio 1 : 2 internally.

Let (x, y) divides it in the ratio 1 : 2

Question 12.
The centroid of the triangle whose vertices are (3, – 7), ( – 8, 6) and (5, 10) is
(a) (0, 9)
(b) (0, 3)
(c) (1, 3)
(d) (3, 3)
Solution:
Centroid of the triangle whose Vertices are (3, -7), (-8, 6) and (5, 10) is
\(\left( \frac { 3-8+5 }{ 3 } ,\frac { -7+6+10 }{ 3 } \right) or\left( 0,\frac { 9 }{ 3 } \right) \)
or (0, 3) (b)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.