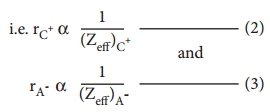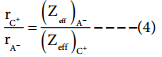Chemistry

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Periodic Trends in Chemical Properties:

So far, we have studied the periodicity of the physical properties such as atomic radius, ionisation enthalpy, electron gain enthalpy and electronegativity. In addition, the chemical properties such as reactivity, valence, oxidation state etc… also show periodicity to certain extent.

In this section, we will discuss briefly about the periodicity in valence (oxidation state) and anomalous behaviour of second period elements (diagonal relationship).

Valence or Oxidation States

The valence of an atom is the combining capacity relative to hydrogen atom. It is usually equal to the total number of electrons in the valence shell or equal to eight minus the number of valence electrons. It is more convenient to use oxidation state in the place of valence.

Periodicity of Valence or Oxidation States

The valence of an atom primarily depends on the number of electrons in the valence shell. As the number of valence electrons remains same for the elements in same group, the maximum valence also remains the same. However, in a period the number of valence electrons increases, hence the valence also increases.

In addition to that some elements have variable valence. For example, most of the elements of group 15 which have 5 valence electrons show two valences 3 and 5. Similarly transition metals and inner transition metals also show variable oxidation states.

Anomalous Properties of Second Period Elements:

As we know, the elements of the same group show similar physical and chemical properties. However, the first element of each group differs from other members of the group in certain properties. For example, lithium and beryllium form more covalent compounds, unlike the alkali and alkali earth metals which predominantly form ionic compounds.

The elements of the second period have only four orbitals (2s & 2p) in the valence shell and have a maximum co-valence of 4, whereas the other members of the subsequent periods have more orbitals in their valence shell and shows higher valences. For example, boron forms BF₄^– and aluminium forms AlF₆^3-.

Diagonal Relationship

On moving diagonally across the periodic table, the second and third period elements show certain similarities. Even though the similarity is not same as we see in a group, it is quite pronounced in the following pair of elements.

The similarity in properties existing between the diagonally placed elements is called ‘diagonal relationship’.

Periodic Trends and Chemical Reactivity:

The physical and chemical properties of elements depend on the valence shell electronic configuration as discussed earlier. The elements on the left side of the periodic table have less ionisation energy and readily lose their valence electrons.

On the other hand, the elements on right side of the periodic table have high electron affinity and readily accept electrons. As a consequence of this, elements of these extreme ends show high reactivity when compared to the elements present in the middle. The noble gases having completely filled electronic configuration neither accept nor lose their electron readily and hence they are chemically inert in nature.

The ionisation energy is directly related to the metallic character and the elements located in the lower left portion of the periodic table have less ionisation energy and therefore show metallic character. On the other hand the elements located in the top right portion have very high ionisation energy and are nonmetallic in nature.

Let us analyse the nature of the compounds formed by elements from both sides of the periodic table. Consider the reaction of alkali metals and halogens with oxygen to give the corresponding oxides.

4 Na + O₂ → 2 Na₂O
2 Cl₂ + 7O₂ → 2 Cl₂O₇

Since sodium oxide reacts with water to give strong base sodium hydroxide, it is a basic oxide. Conversely Cl₂O₇ gives strong acid called perchloric acid upon reaction with water So, it is an acidic oxide.

Na₂O + H₂O → 2NaOH
Cl₂O₇ → 2 Cl₂O₇

Thus, the elements from the two extreme ends of the periodic table behave differently as expected. As we move down the group, the ionisation energy decreases and the electropositive character of elements increases. Hence, the hydroxides of these elements become more basic. For example, let us consider the nature of the second group hydroxides:

Be(OH)₂ amphoteric; Mg(OH)₂ weakly basic; Ba(OH)₂ strongly basic

Beryllium hydroxide reacts with both acid and base as it is amphoteric in nature.

Be(OH)₂ + 2HCl → BeCl₂ + 2H₂O
Be(OH)₂+ 2 NaOH → Na₂BeO₂ + 2H₂O.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Periodic Trends in Properties

As discussed earlier, the electronic configuration of the elements shows a periodic variation with increase in atomic numbers. Similarly a periodic trend is observed in physical and chemical behaviour of elements. In this section, we will study the periodic trends in the following properties of elements.

• Atomic Radius
• Ionic Radius
• Ionisation Enthalpy (energy)
• Electron Gain Enthalpy (Electron Affinity)
• Electronegativity

Atomic Radius

Atomic radius of an atom is defined as the distance between the centre of its nucleus and the outermost shell containing the valence electron.

It is not possible to measure the radius of an isolated atom directly. Except for noble gases, usually atomic radius is referred to as covalent radius or metallic radius depending upon the nature of bonding between the concerned atoms.

Covalent Radius

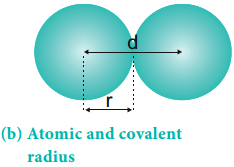
It is one-half of the internuclear distance between two identical atoms linked together by a single covalent bond. Inter nuclear distance can be determined using x-ray diffraction studies.

Example:

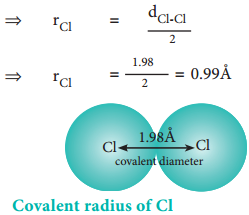
The experimental internuclear distance in Cl₂ molecule is 1.98 Å. The covalent radius of chlorine is calculated as below.

d_Cl-Cl = r_Cl + r_Cl
⇒ d_Cl-Cl = 2r_Cl

The formation of covalent bond involves the overlapping of atomic orbitals and it reduces the expected internuclear distance. Therefore covalent radius is always shorter than the actual atomic radius.

In case of hetero nuclear diatomic molecules, the covalent radius of individual atom can also be calculated using the internuclear distance (d_A-B) between two different atoms A and B. The simplest method proposed by Schomaker and Stevenson is as follows.

d_A-B = r_A + r_B – 0.09 (x_A – x_B)

where χ_A and χ_B are the electronegativities of A and B respectively in Pauling units. Here χ_A > χ_B and
radius is in Å.

Let us calculate the covalent radius of hydrogen using the experimental d_H-Cl value is 1.28 Å and the covalent radius of chlorine is 0.99 Å. In pauling scale the electronegativity of chlorine and hydrogen are 3 and 2.1 respectively.

d_H-Cl = r_H + r_Cl – 0.09 (x_Cl – x_H)
1.28 = r_H + 0.99 – 0.09 (3 – 2.1)
1.28 = r_H + 0.99 – 0.09 (0.9)
1.28 = r_H + 0.99 – 0.081
1.28 = r_H + 0.909
∴ r_H = 1.28 – 0.909 = 0.371 Å

Metallic Radius

It is defied as one-half of the distance between two adjacent metal atoms in the closely packed metallic crystal lattice. For example, the distance between the adjacent copper atoms in solid copper is 2.56 Å and therefore the metallic radius of copper is \(\frac{2.56}{2}\) = 1.28 Å

The metallic radius can be calculated using the unit cell length of the metallic crystal. You will study the detailed calculation procedure in XII standard solid state unit.

Periodic Trends in Atomic Radius

Variation in Periods

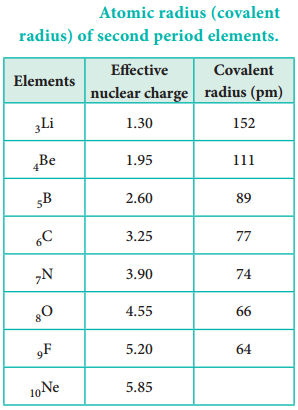
Atomic radius tends to decrease in a period. As we move from left to right along a period, the valence electrons are added to the same shell. The simultaneous addition of protons to the nucleus, increases the nuclear charge, as well as the electrostatic attractive force between the valence electrons and the nucleus. Therefore atomic radius decreases along a period.

Effective Nuclear Charge

In addition to the electrostatic forces of attraction between the nucleus and the electrons, there exists repulsive forces among the electrons. The repulsive force between the inner shell electrons and the valence electrons leads to a decrease in the electrostatic attractive forces acting on the valence electrons by the nucleus. Thus, the inner shell electrons act as a shield between the nucleus and the valence electrons. This effect is called shielding effect.

The net nuclear charge experienced by valence electrons in the outermost shell is called the effective nuclear charge. It is approximated by the below mentioned equation.

Z_eff = Z – S

Where Z is the atomic number and ‘S’ is the screening constant which can be calculated using Slater’s rules as described below.

Step 1:

Write the electronic configuration of the atom and rearrange it by grouping ns and np orbitals together and others separately in the following form. (1s) (2s, 2p) (3s, 3p) (3d) (4s, 4p) (4d) (4f) (5s, 5p) …

Step 2:

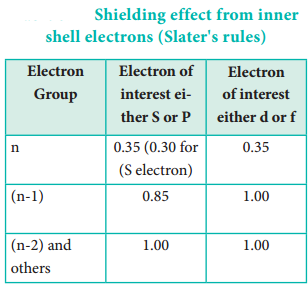
Identify the group in which the electron of interest is present. The electron present right to this group does not contribute to the shielding effect. Each of the electrons within the identified group (denoted by ‘n’) shields to an extent of 0.35 unit of nuclear charge. However, it is 0.30 unit for 1s electron.

Step 3:

Shielding of inner shell electrons. If the electron of interest belongs to either s or p orbital,

• Each electron within the (n-1) group shields to an extent of 0.85 unit of nuclear charge, and
• Each electron within the (n-2) group (or) even lesser group (n-3), (n-4) etc … completely shields i.e. to an extent of 1.00 unit of nuclear charge.

If the electron of interest belongs to d or f orbital, then each of electron left of the group of electron of interest shields to an extent of 1.00 unit of nuclear charge.

Step 4:

Summation of the shielding effect of all the electrons gives the shielding constant ‘S’

Example:

Let us explain the calculation of effective nuclear charge on 4s electron and 3d electron in scandium. The electronic configuration of scandium is 1s², 2s², 2p⁶, 3s², 3p⁶, 4s², 3d¹. we can rearrange as below.

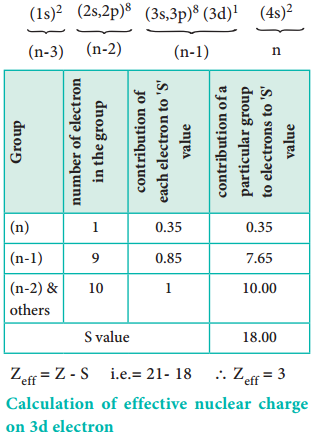
Calculation of Effective Nuclear Charge on 3d Electron

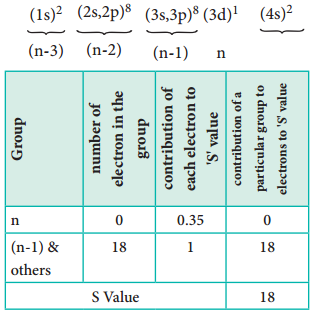
∴ Z_eff = Z – S i.e. = 21 – 8 ∴Z_eff = 3

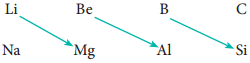
Variation in Group

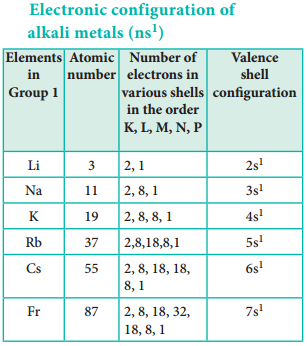
In the periodic table, the atomic radius of elements increases down the group. As we move down a group, new shells are opened to accommodate the newly added valence electrons. As a result, the distance between the centre of the nucleus and the outermost shell containing the valence electron increases. Hence, the atomic radius increases. The trend in the variation of the atomic radius of the alkali metals down the group os shown below.

Ionic Radius

It is defined as the distance from the centre of the nucleus of the ion up to which it exerts its influence on the electron cloud of the ion. Ionic radius of uni-univalent crystal can be calculated using Pauling’s method from the inter ionic distance between the nuclei of the cation and anion. Pauling assumed that ions present in a crystal lattice are perfect spheres, and they are in contact with each other. Therefore,

d = r_C⁺ + r_A^– ………………… (1)

Where d is the distance between the centre of the nucleus of cation C⁺ and anion A^– and r_C⁺, r_A^– are the radius of the cation and anion respectively.

Pauling also assumed that the radius of the ion having noble gas electronic configuration (Na⁺ and Cl^– having
1s² 2s², 2p⁶ configuration) is inversely proportional to the effective nuclear charge felt at the periphery of
the ion.

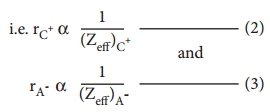
Where Z_eff is the effective nuclear charge and Z_eff = Z – S

Dividing the equation 2 by 3

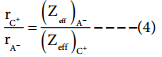
On solving equation (1) and (4) the values of r_C⁺ and r_A^– can be obtained

Let us explain this method by calculating the ionic radii of Na⁺ and F^– in NaF crystal whose interionic distance is equal to 231 pm.

Ionisation Energy

It is defined as the minimum amount of energy required to remove the most loosely bound electron from the valence shell of the isolated neutral gaseous atom in its ground state. It is expressed in kJ mol^-1 or in electron volts (eV). M_(g) + IE₁ → M⁺_(g) + 1 e^–

Successive Ionisation Energies

The minimum amount of energy required to remove an electron from a unipositive cation is called second ionisation energy. It is represented by the following equation.

M⁺_(g) + IE₂ → M²⁺_(g) + 1e^–

In this way we can define the successive ionisation energies such as third, fourth etc.

The total number of electrons are less in the cation than the neutral atom while the nuclear charge remains the same. Therefore the effective nuclear charge of the cation is higher than the corresponding neutral atom. Thus the successive ionisation energies, always increase in the following order

IE₁ < IE₂ < IE₃ < …..

Periodic Trends in Ionisation Energy

The ionisation energy usually increases along a period with few exceptions. As discussed earlier, when we move from left to right along a period, the valence electrons are added to the same shell, at the same time protons are added to the nucleus.

This successive increase of nuclear charge increases the electrostatic attractive force on the valence electron and more energy is required to remove the valence electron resulting in high ionisation energy.

Let us consider the variation in ionisation energy of second period elements. The plot of atomic number vs ionisation energy is given below.

In the following graph, there are two deviation in the trends of ionisiation energy. It is expected that boron has higher ionisation energy than beryllium since it has higher nuclear charge. However, the actual ionisation energies of beryllium and boron are 899 and 800 kJ mol^-1 respectively contrary to the expectation. It is due to the fact that beryllium with completely filled 2s orbital, is more stable than partially filled valence shell electronic configuration of boron. (2s², 2p¹)

The electronic configuration of beryllium (Z=4) in its ground state is 1s², 2s² and that of boran is (Z = 5) 1s² 2s² 2p¹

Similarly, nitrogen with 1s², 2s², 2p³ electronic configuration has higher ionisation energy (1402 kJ mol^-1) than oxygen (1314 kJ mol^-1). Since the half filled electronic configuration is more stable, it requires higher energy to remove an electron from 2p orbital of nitrogen. Whereas the removal one 2p electron from oxygen leads to a stable half filled configuration. This makes comparatively easier to remove 2p electron from oxygen.

Periodic Variation in Group

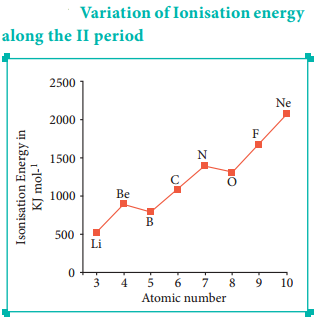
The ionisation energy decreases down a group. As we move down a group, the valence electron occupies new shells, the distance between the nucleus and the valence electron increases. So, the nuclear forces of attraction on valence electron decreases and hence ionisation energy also decreases down a group.

Ionisation Energy and Shielding Effect

As we move down a group, the number of inner shell electron increases which in turn increases the repulsive force exerted by them on the valence electrons, i.e. the increased shielding effect caused by the inner electrons decreases the attractive force acting on the valence electron by the nucleus. Therefore the ionisation energy decreases. Let us understand this trend by considering the ionisation energy of alkali metals.

Electron Affinity

It is defined as the amount of energy released (required in the case noble gases) when an electron is added to the valence shell of an isolated neutral gaseous atom in its ground state to form its anion. It is expressed in kJ mol^-1

A + e^– → A^– + EA

Variation of Electron Affinity in a Period:

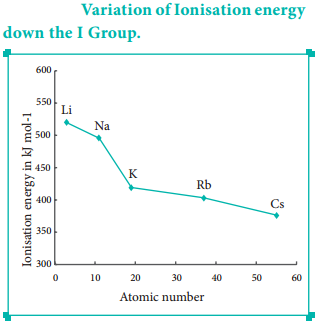
The variation of electron affinity is not as systematic as in the case of ionisation energy. As we move from alkali metals to halogens in a period, generally electron affinity increases, i.e. the amount of energy released will be more. This is due to an increase in the nuclear charge and decrease in size of the atoms.

However, in case of elements such as beryllium (1s², 2s²), nitrogen (1s², 2s², 2p³) the addition of extra electron will disturb their stable electronic configuration and they have almost zero electron affinity.

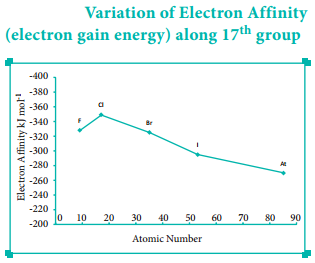
Noble gases have stable ns², np⁶ configuration, and the addition of further electron is unfavourable and requires energy. Halogens having the general electronic configuration of ns², np⁵ readily accept an electron to get the stable noble gas electronic configuration (ns², np⁶), and therefore in each period the halogen has high electron affinity. (high negative values)

Variation of Electron Affinity in a Group:

As we move down a group, generally the electron affinity decreases. It is due to increase in atomic size and the shielding effect of inner shell electrons. However, oxygen and fluorine have lower affinity than sulphur and chlorine respectively.

The sizes of oxygen and fluorine atoms are comparatively small and they have high electron density. Moreover, the extra electron added to oxygen and fluorine has to be accommodated in the 2p orbital which is relatively compact compared to the 3p orbital of sulphur and chlorine so, oxygen and fluorine have lower electron affinity than their respective group elements sulphur and chlorine.

Electronegativity

It is defined as the relative tendency of an element present in a covalently bonded molecule, to attract the shared pair of electrons towards itself. Electronegativity is not a measurable quantity. However, a number of scales are available to calculate its value. One such method was developed by Pauling, he assigned arbitrary value of electronegativities for hydrogen and fluorine as 2.1 and 4.0 respectively. Based on this the  electronegativity values for other elements can be calculated using the following expression

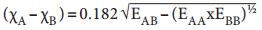
Where E_AB, E_AA and E_BB are the bond dissociation energies (K cal) of AB, A₂ and B₂ molecules respectively.

The electronegativity of any given element is not a constant and its value depends on the element to which it is covalently bound. The electronegativity values play an important role in predicting the nature of the bond.

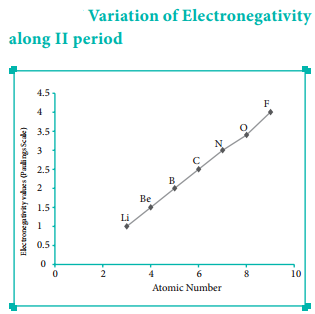
Variation of Electronegativity in a Period:

The electronegativity generally increases across a period from left to right. As discussed earlier, the atomic radius decreases in a period, as the attraction between the valence electron and the nucleus increases. Hence the tendency to attract shared pair of electrons increases. Therefore, electronegativity also increases in a period.

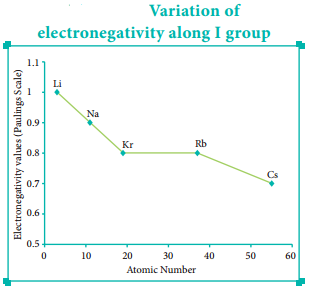
Variation of Electronegativity in a Group:

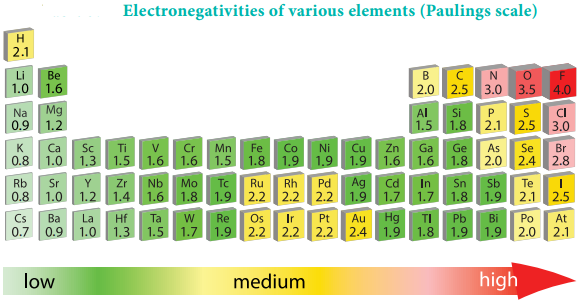
The electronegativity generally decreases down a group. As we move down a group the atomic radius increases and the nuclear attractive force on the valence electron decreases. Hence, the electronegativity decreases.

Noble gases are assigned zero electronegativity. The electronegativity values of the elements of s-block show the expected decreasing order in a group. Except 13^th and 14^th group all other p-block elements follow the expected decreasing trend in electronegativity.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Grouping of Elements Based on Electronic Configurations

In the modern periodic table, the elements are organised in 7 periods and 18 groups based on the modern periodic law. The placement of element in the periodic table is closely related to its outer shell electronic configuration. Let us analyse the change in the electronic configuration of elements along the periods and down the groups.

Variation of Electronic Configuration Along the Periods

We have already learnt that each period starts with the element having general outer electronic configuration ns¹ and ends with ns², np⁶ where n is the period number. The first period starts with the filling of valence electrons in 1s orbital, which can accommodate only two electrons.

Hence, the first period has two elements, namely hydrogen and helium. The second period starts with the filling of valence electrons in 2s orbital followed by three 2p orbitals with eight elements from lithium to neon. The third period starts with filling of valence electrons in the 3s orbital followed by 3p orbitals.

The fourth period starts with filling of valence electrons from 4s orbital followed by 3d and 4p orbitals in accordance with Aufbau principle. Similarly, we can explain the electronic configuration of elements in the subsequent periods (Table 3.10).

In the fourth period the filling of 3d orbitals starts with scandium and ends with zinc. These 10 elements are called first transition series. Similarly 4d, 5d and 6d orbitals are filled in successive periods and the corresponding series of elements are called second, third and fourth transition series respectively.

In the sixth period the filling of valence electrons starts with 6s orbital followed by 4f, 5d and 6p orbitals. The filling up of 4f orbitals begins with Cerium (Z=58) and ends at Lutetium (Z=71). These 14 elements constitute the first inner-transition series called Lanthanides.

Similarly, in the seventh period 5f orbitals are filled, and it’s -14 elements constitute the second inner transition series called Actinides. These two series are placed separately at the bottom of the modern periodic table.

Variation of Electronic Configuration in the Groups:

Elements of a group have similar electronic configuration in the outer shell. The general outer electronic configurations for the 18 groups are listed in the Table 3.11. The groups can be combined as s, p, d and f block elements on the basis of the orbital in which the last valence electron enters.

The elements of group 1 and group 2 are called s-block elements, since the last valence electron enters the ns orbital. The group 1 elements are called alkali metals while the group 2 elements are called alkaline earth metals.

These are soft metals and possess low melting and boiling points with low ionisation enthalpies. They are highly reactive and form ionic compounds. They are highly electropositive in nature and most of the elements imparts colour to the flame. We will study the properties of these group elements in detail in subsequent chapters.

The elements of groups 13 to 18 are called p-block elements or representative elements and have a general electronic configuration ns², np^1-6. The elements of the group 16 and 17 are called chalcogens and halogens respectively.

The elements of 18^th group contain completely filled valence shell electronic configuration (ns², np⁶) and are called inert gases or nobles gases. The elements of p-block have high negative electron gain enthalpies. The ionisation energies are higher than that of s-block elements. They form mostly covalent compounds and shows more than one oxidation states in their compounds.

The elements of the groups 3 to 12 are called d-block elements or transition elements with general valence shell electronic configuration ns^1-2, (n-1)d^1-10. These elements also show more than one oxidation state and form ionic, covalent and co-ordination compounds. They can form interstitial compounds and alloys which can also act as catalysts. These elements have high melting points and are good conductors of heat and electricity.

The lanthanides (4f^1-14, 5d^0-1, 6s²) and the actinides (5f^0-14, 6d^0-2, 7s²) are called f-block elements. These elements are metallic in nature and have high melting points. Their compounds are mostly coloured. These elements also show variable oxidation states.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Nomenclature of Elements with Atomic Number Greater than 100

Usually, when a new element is discovered, the discoverer suggests a name following IUPAC guidelines which will be approved after a public opinion. In the meantime, the new element will be called by a temporary name coined using the following IUPAC rules, until the IUPAC recognises the new name.

1. The name was derived directly from the atomic number of the new element using the following numerical roots.

Notation for IUPAC Nomenclature of Elements

2. The numerical roots corresponding to the atomic number are put together and ‘ium’ is added as suffix

3. The final ‘n’ of ‘enn’ is omitted when it is written before ‘nil’ (enn + nil = enil) similarly the final ‘i’ of ‘bi’ and ‘tri’ is omitted when it written before ‘ium’ (bi + ium = bium; tri + ium = trium)

4. The symbol of the new element is derived from the first letter of the numerical roots.

The following table illustrates these facts.

To overcome all these difficulties, IUPAC nomenclature has been recommended for all the elements with Z > 100. It was decided by IUPAC that the names of elements beyond atomic number 100 should use Latin words for their numbers. The names of these elements are derived from their numerical roots.

Fermium is a synthetic element with the symbol Fm and atomic number 100. It is an actinide and the heaviest element that can be formed by neutron bombardment of lighter elements, and hence the last element that can be prepared in macroscopic quantities, although pure fermium metal has not yet been prepared.

The twelve elements of nature are Earth, Water, Wind, Fire, Thunder, Ice, Force, Time, Flower, Shadow, Light and Moon.

Uranium

The heaviest element known to occur in nature is uranium, which contains only 92 protons, putting it 30 places below the putative new element in the periodic table. In the laboratory, physicists have managed to create elements up to 118, but they are all highly unstable.

The fifth element on top of earth, air, fire, and water, is space or aether. It was hard for people to believe that the stars and everything else in space were made of the other elements, so space was considered as a fifth element.

According to ancient and medieval science, aether also spelled ether, aither, or ether and also called quintessence (fifth element), is the material that fills the region of the universe above the terrestrial sphere.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Moseley’s Work and Modern Periodic Law

In 1913, Henry Moseley studied the characteristic X-rays spectra of several elements by bombarding them with high energy electrons and observed a linear correlation between atomic number and the frequency of X-rays emitted which is given by the following expression.

\(\sqrt{υ}\) = a(Z – b)

Where, υ is the frequency of the X-rays emitted by the element with atomic number ‘Z’; a and b are constants and have same values for all the elements.

The plot of \(\sqrt{υ}\) against Z gives a straight line. Using this relationship, we can determine the atomic number of an unknown (new) element from the frequency of X-ray emitted. Based on his work, the modern periodic law was developed which states that, “the physical and chemical properties of the elements are periodic functions of their atomic numbers.” Based on this law, the elements were arranged in order of their increasing atomic numbers.

This mode of arrangement reveals an important truth that the elements with similar properties recur after regular intervals. The repetition of physical and chemical properties at regular intervals is called periodicity.

Modern Periodic Table

The physical and chemical properties of the elements are correlated to the arrangement of electrons in their outermost shell (valence shell). Different elements having similar outer shell electronic configuration possess similar properties. For example, elements having one electron in their valence shell s-orbital possess similar physical and chemical properties. These elements are grouped together in the modern periodic table as first group elements.

Similarly, all the elements are arranged in the modern periodic table which contains 18 vertical columns and 7 horizontal rows. The vertical columns are called groups and the horizontal rows are called periods. Groups are numbered 1 to 18 in accordance with the IUPAC recommendation which replaces the old numbering scheme IA to VIIA, IB to VIIB and VIII.

Each period starts with the element having general outer electronic configuration ns¹ and ends with ns² np⁶.
Here ‘n’ corresponds to the period number (principal quantum number). The aufbau principle and the  electronic configuration of atoms provide a theoretical foundation for the modern periodic table.