Chemistry

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Wave Particle Duality of Matter

Albert Einstein proposed that light has dual nature. i.e. light photons behave both like a particle and as a wave. Louis de Broglie extended this concept and proposed that all forms of matter showed dual character. To quantify this relation, he derived an equation for the wavelength of a matter wave. He combined the following two equations of energy of which one represents wave character (hυ) and the other represents the particle nature (mc²).

(i) Planck’s quantum hypothesis:
E = hυ ……………. (2.6)

(ii) Einstein’s mass-energy relationship
E = mc² …………….. (2.7)

From (2.6) and (2.7)

hν = mc²
hc/λ = mc²
λ = h/mc …………….. (2.8)

The equation 2.8 represents the wavelength of photons whose momentum is given by mc (Photons have zero rest mass)

For a particle of matter with mass m and moving with a velocity v, the equation 2.8 can be written as
λ = h/mv ………………. (2.9)

This is valid only when the particle travels at speeds much less than the speed of Light.

This equation implies that a moving particle can be considered as a wave and a wave can exhibit the properties (i.e momentum) of a particle. For a particle with high linear momentum (mv) the wavelength will be so small and cannot be observed. For a microscopic particle such as an electron, the mass is of the order of 10^-31 kg, hence the wavelength is much larger than the size of atom and it becomes significant.

Let us understand this by calculating de Broglie wavelength in the following two cases:

• A 6.626 kg iron ball moving at 10 ms^-1
• An electron moving at 72.73 ms^-1

λ_ironball= h/mv

λ_electron= h/mv

For the electron, the de Broglie wavelength is significant and measurable while for the iron ball it is too small to measure, hence it becomes insignificant.

According to the de Broglie concept, the electron that revolves around the nucleus exhibits both particle and wave character. In order for the electron wave to exist in phase, the circumference of the orbit should be an integral multiple of the wavelength of the electron wave. Otherwise, the electron wave is out of phase.

Circumference of the orbit = nλ

2πr = nλ ……………… (2.10)
2πr = nh/mv

Rearranging,
mvr = nh/2π …………… (2.11)

Angular momentum = nh/2π

The above equation was already predicted by Bohr. Hence, De Broglie and Bohr’s concepts are in agreement with each other.

Davison and Germer Experiment:

The wave nature of electron was experimentally confirmed by Davisson and Germer. They allowed the accelerated beam of electrons to fall on a nickel crystal and recorded the diffraction pattern. The resultant diffraction pattern is similar to the x-ray diffraction pattern. The finding of wave nature of electron leads to the development of various experimental techniques such as electron microscope, low energy electron diffraction etc.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Introduction to Atom Models

Let us recall the history of the development of atomic models from the previous classes. We know that all things are made of matter. The basic unit that makes up all matter is atom. The word ‘atom’ has been derived from the Greek word ‘a – tomio’ meaning nondivisible.

Atom was considered as nondivisible until the discovery of subatomic particles such as electron, proton and neutron. J. J. Thomson’s cathode ray experiment revealed that atoms consist of negatively charged particles called electrons.

He proposed that atom is a positively charged sphere in which these electrons are embedded like the seeds in the watermelon. Later, Rutherford’s α-ray scattering experiment results proved that Thomson’s model was wrong. Rutherford bombarded a thin gold foil with a stream of fast moving α-particles. It was observed that

1. Most of the α-particles passed through the foil
2. Some of them were deflected through a small angle and
3. Very few α-particles were reflected back by 180°

Based on these observations, he proposed that in an atom there is a tiny positively charged nucleus and the electrons are moving around the nucleus with high speed. The theory of electromagnetic radiation states that a moving charged particle should continuously loose its energy in the form of radiation.

Therefore, the moving electron in an atom should continuously loose its energy and finally collide with nucleus resulting in the collapse of the atom. However, this doesn’t happen and the atoms are stable. Moreover, this model does not explain the distribution of electrons around the nucleus and their energies.

Bohr Atom Model:

The work of Planck and Einstein showed that the energy of electromagnetic radiation is quantised in units of hν (where ν is the frequency of radiation and h is Planck’s constant 6.626 × 10^-34 Js). Extending Planck’s quantum hypothesis to the energies of atoms, Niels Bohr proposed a new atomic model for the hydrogen atom. This model is based on the following assumptions:

1. The energies of electrons in an atom are quantised.

2. The electron is revolving around the nucleus in a certain circular path of fixed energy called stationary orbit.

3. Electron can revolve only in those orbits in which the angular momentum (mvr) of the electron must be equal to an integral multiple of h/2π.

i.e. mvr = nh/2π ……………… (2.1)
where n = 1, 2, 3, … etc.,

4. As long as an electron revolves in the fixed stationary orbit, it doesn’t lose its energy. However, when an electron jumps from higher energy state (E₂) to a lower energy state (E₁), the excess energy is emitted as radiation. The frequency of the emitted radiation is

E₂ – E₁ = hυ
and
υ = \(\frac{(E₂)-E₁)}{h}\) ………………. (2.2)

Conversely, when suitable energy is supplied to an electron, it will jump from lower energy orbit to a higher energy orbit.

Applying Bohr’s postulates to a hydrogen like atom (one electron species such as H, He⁺ and Li²⁺ etc..) the radius of the n^th orbit and the energy of the electron revolving in the n^th orbit were derived.

The results are as follows:

The detailed derivation of r_n and E_n will be discussed in 12^th standard atomic physics unit.

Limitation of Bohr’s Atom Model:

The Bohr’s atom model is applicable only to species having one electron such as hydrogen, Li²⁺ etc… and not applicable to multi electron atoms. It was unable to explain the splitting of spectral lines in the presence of magnetic field (Zeeman effect) or an electric field (Stark effect).

Bohr’s theory was unable to explain why the electron is restricted to revolve around the nucleus in a fixed orbit in which the angular momentum of the electron is equal to nh/2π and a logical answer for this, was provided by Louis de Broglie.

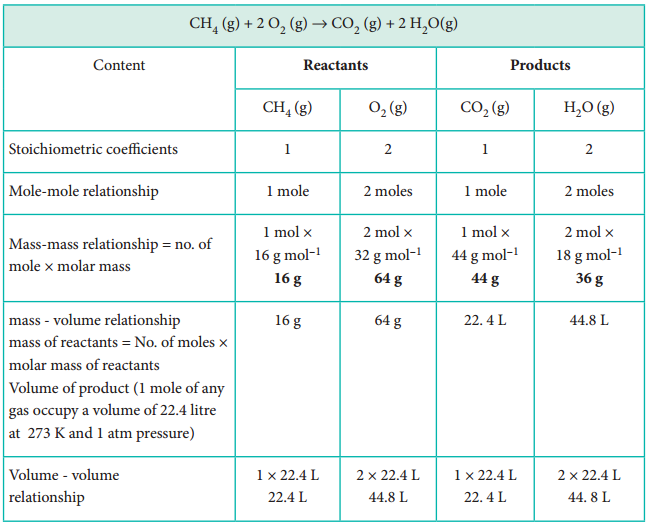
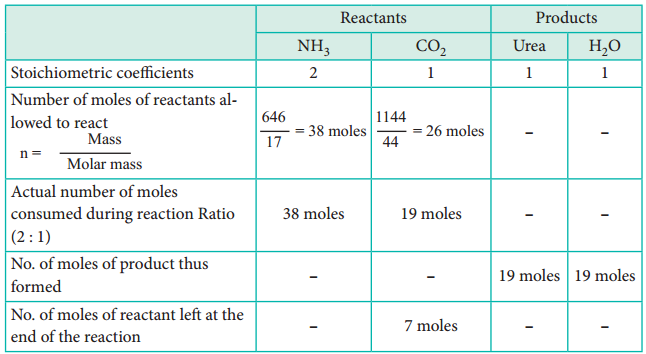
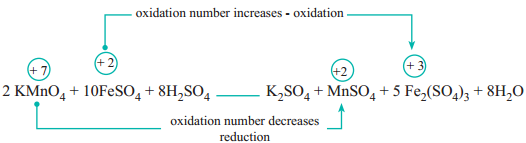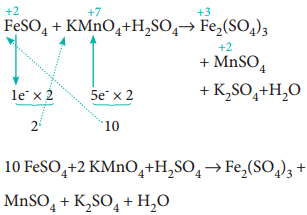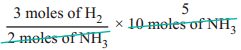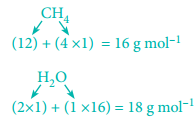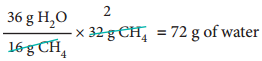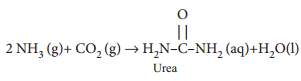Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Oxidation Number Defination and Examples

It is defined as the imaginary charge left on the atom when all other atoms of the compound have been removed in their usual oxidation states that are assigned according to set of rules. A term that is often used interchangeably with oxidation number is oxidation state.

1. The oxidation state of a free element (i.e. in its uncombined state) is zero.
Example: each atom in H₂, Cl₂, Na, S₈ have the oxidation number of zero.

2. For a monatomic ion, the oxidation state is equal to the net charge on the ion.

Example:

The oxidation number of sodium in Na⁺ is +1.

The oxidation number of chlorine in Cl^– is -1.

3. The algebric sum of oxidation states of all atoms in a molecule is equal to zero, while in ions, it is equal to the net charge on the ion.

Example:

In H₂SO₄; 2 × (oxidation number of hydrogen) + (oxidation number of S) + 4 (oxidation number of oxygen) = 0.

In SO₄^2-; (oxidation number of S) + 4 (oxidation number of oxygen) = – 2.

4. Hydrogen has an oxidation number of +1 in all its compounds except in metal hydrides where it has – 1 value.

Example:

Oxidation number of hydrogen in hydrogen chloride (HCl) is + 1.
Oxidation number of hydrogen in sodium hydride (NaH) is -1.

5. Fluorine has an oxidation state of – 1 in all its compounds.

6. The oxidation state of oxygen in most compounds is – 2. Exceptions are peroxides, super oxides and compounds with fluorine.

Example:

Oxidation number of oxygen,

(i) in water (H₂O) is – 2.

(ii) in hydrogen peroxide (H₂O₂) is -1.
2 (+ 1) + 2x = 0;
⇒ 2x = – 2;
⇒ x = – 1

(iii) in super oxides such as KO₂ is – 1
+1 + 2x = 0;
2x = – 1;
x = – 1/2

(iv) in oxygen difloride (OF₂) is + 2.
x + 2 (- 1) = 0;
x = + 2

7. Alkali metals have an oxidation state of + 1 and alkaline earth metals have an oxidation state of + 2 in all their compounds.

Calculation of Oxidation Number Using the Above Rules.

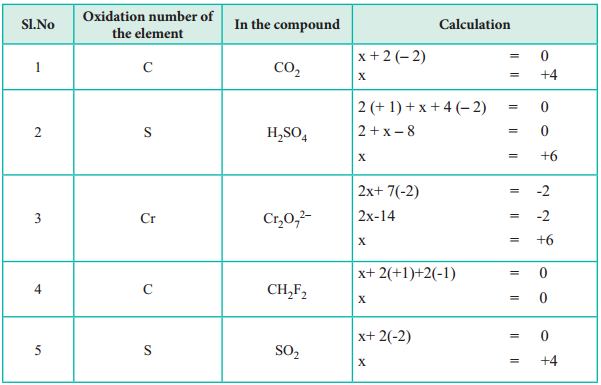
Redox Reactions in Terms of Oxidation Numbers

During redox reactions, the oxidation number of elements changes. A reaction in which oxidation number of the element increases is called oxidation. A reaction in which it decreases is called reduction.

Consider the following reaction

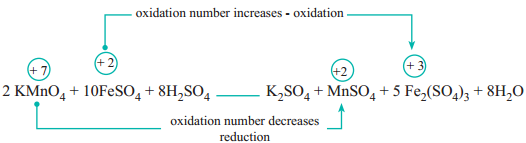
In this reaction, manganese in potassium permanganate (KMnO₄) favours the oxidation of ferrous sulphate (FeSO₄) into ferric sulphate (Fe₂(SO₄)₃ by gaining electrons and thereby gets reduced. Such reagents are called oxidising agents or oxidants. Similarly, the reagents which facilitate reduction by releasing electrons and get oxidised are called reducing agents.

Types of Redox Reactions

Redox reactions are classified into the following types.

1. Combination Reactions:

Redox reactions in which two substances combine to form a single compound are called combination reaction.

Example:

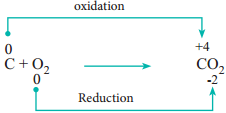
2. Decomposition Reactions:

Redox reactions in which a compound breaks down into two or more components are called decomposition reactions. These reactions are opposite to combination reactions. In these reactions, the oxidation number of the different elements in the same substance is changed.

Example

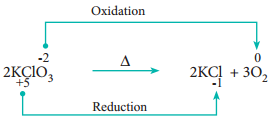
3. Displacement Reactions:

Redox reactions in which an ion (or an atom) in a compound is replaced by an ion (or atom) of another element are called displacement reactions. They are further classified into

• Metal Displacement Reactions
• Non-Metal Displacement Reactions

Metal Displacement Reactions:

Place a zinc metal strip in an aqueous copper sulphate solution taken in a beaker. Observe the solution, the intensity of blue colour of the solution slowly reduced and finally disappeared. The zinc metal strip became coated with brownish metallic copper. This is due to the following metal displacement reaction.

Non-Metal Displacement

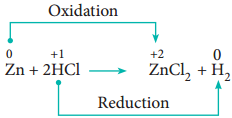
4. Disproportionation Reaction (Auto Redox Reactions)

In some redox reactions, the same compound can undergo both oxidation and reduction. In such reactions, the oxidation state of one and the same element is both increased and decreased. These reactions are called disproportionation reactions.

Examples

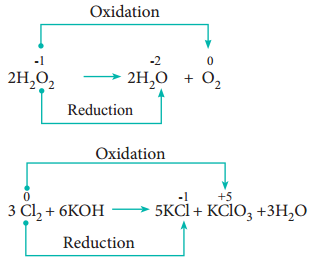
5. Competitive Electron Transfer Reaction

In metal displacement reactions, we learnt that zinc replaces copper from copper sulphate solution. Let us examine whether the reverse reaction takes place or not. As discussed earlier, place a metallic copper strip in zinc sulphate solution. If copper replaces zinc from zinc sulphate solution, Cu²⁺ ions would be released into the solution and the colour of the solution would change to blue.

But no such change is observed. Therefore, we conclude that among zinc and copper, zinc has more tendency to release electrons and copper to accept the electrons.

Let us extend the reaction to copper metal and silver nitrate solution. Place strip of metallic copper in sliver nitrate solution taken in a beaker. After some time, the solution slowly turns blue. This is due to the formation of Cu²⁺ ions, i.e. copper replaces silver from silver nitrate.

The reaction is,

It indicates that between copper and silver, copper has the tendency to release electrons and silver to accept electrons.

From the above experimental observations, we can conclude that among the three metals, namely, zinc, copper and silver, the electron releasing tendency is in the following order.

Zinc > Copper > Silver

This kind of competition for electrons among various metals helps us to design (galvanic) cells. In XII standard we will study the galvanic cell in detail.

Balancing (the Equation) of Redox Reactions

The two methods for balancing the equation of redox reactions are as follows.

• The oxidation number method
• Ion-electron method / half reaction method.

Both are based on the same principle:

In oxidation – reduction reactions the total number of electrons donated by the reducing agent is equal to the total number of electrons gained by
the oxidising agent.

Oxidation Number Method

In this method, the number of electrons lost or gained in the reaction is calculated from the oxidation numbers of elements before and after the reaction. Let us consider the oxidation of ferrous sulphate by potassium permanganate in acid medium. The unbalanced chemical equation is,

FeSO₄ + KMnO₄ + H₂SO₄ → Fe₂(SO₄)₃ + MnSO₄ + K₂SO₄ + H₂O

Step 1

Using oxidation number concept, identify the reactants (atom) which undergo oxidation and reduction.

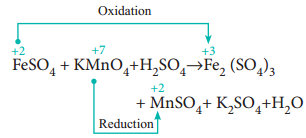
(a) The oxidation number of Mn in KMnO₄ changes from +7 to +2 by gaining five electrons.

(b) The oxidation number of Fe in FeSO₄ changes from +2 to +3 by loosing one electron.

Step 2

Since, the total number of electrons lost is equal to the total number of electrons gained, equate, the number of electrons, by cross multiplication of the respective formula with suitable integers on reactant side as below. Here, the product Fe₂(SO₄)₃ contains 2 moles of iron, So, the Coefficients 1e^– & 5e^– are multiplied by the number ‘2’.

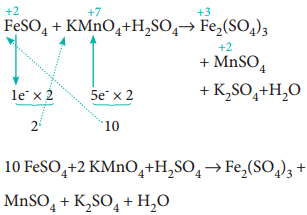
10 FeSO₄ + 2 KMnO₄ + H₂SO₄ → Fe₂(SO₄)₃ + MnSO₄ + K₂SO₄ + H₂O

Step 3

Balance the reactant / Product Oxidised / Reduced

Now, based on the reactant side, balance the products (ie oxidised and reduced).The above equation becomes

10FeSO₄ + 2KMnO₄ + H₂SO₄ → 5Fe₂(SO₄)₃ + 2MnSO₄ + K₂SO₄ + H₂O

Step 4

Balance the other elements except H and O atoms. In this case, we have to balance K and S atoms but K is balanced automatically.

Reactant Side:

10 ‘S’ atoms (10 FeSO₄)

Product Side:

18 ‘S’ atoms

5Fe₂(SO₄)₃ + 2MnSO₄ + K₂SO₄

15S + 2S + 1S = 18S

Therefore the difference 8-S atoms in reactant side, has to be balanced by multiplying H₂SO₄ by ‘8’ The equation now becomes,

10FeSO₄ + 2KMnO₄ + 8H₂SO₄ → 5Fe₂(SO₄)₃ + 2MnSO₄ + K₂SO₄ + H₂O

Step 5

Balancing ‘H’ and ‘O’ atoms

Reactant side ’16’-H atoms (8H₂SO₄ i.e. 8 × 2H = 16 ‘H’)

Product side ‘2’ – H atoms (H₂O i.e. 1 × 2H = 2 ‘H’)

Therefore, multiply H₂O molecules in the product side by ‘8’

10 FeSO₄ + 2 KMnO₄ + 8 H₂SO₄ → 5 Fe₂(SO₄)₃ + 2 MnSO₄ + k₂SO₄ + 8H₂O

The oxygen atom is automatically balanced. This is the balanced equation.

Ion – Electron Method

This method is used for ionic redox reactions.

Step 1

Using oxidation number concept, find out the reactants which undergo oxidation and reduction.

Step 2

Write two separate half equations for oxidation and reduction reaction, Let us consider the same example which we have already discussed in
oxidation number method.

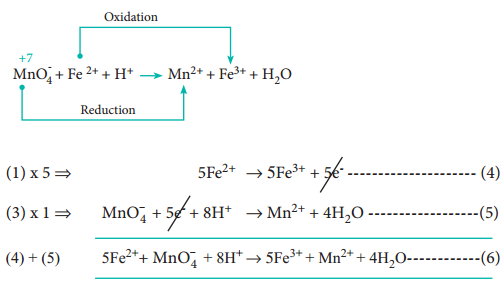
KMnO₄ + FeSO₄ + H₂SO₄ → MnSO₄ + Fe₂(SO₄)₃ + K₂SO₄ + H₂O

The ionic form of this reaction is,

The two half reactions are,

Fe²⁺ → Fe³⁺ + 1e^– ………………….. (1)
and
MnO^–₄ + 5e^– → Mn²⁺ …………………. (2)

Balance the atoms and charges on both sides of the half reactions.

Equation (1) ⇒ No changes i.e.,

Fe²⁺ → Fe³⁺ + 1e^– ………………….. (1)

Equation (2) ⇒ 4’O’ on the reactant side, therefore add 4H₂O on the product side, to balance ‘H’ – add, 8H⁺ in the reactant side

MnO^–₄ + 5e^– + 8H⁺ → Mn²⁺ + 4H₂O ……………… (3)

Step 3

Equate both half reactions such that the number of electrons lost is equal to number of electrons gained. Addition of two half reactions gives the balanced equation represented by equation (6).

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Redox Reaction Examples, Types and Applications

When an apple is cut, it turns brown after sometime. Do you know the reason behind this colour change? It is because of a chemical reaction called oxidation. We come across oxidation reactions in our daily life. For example

1. Burning of LPG gas
2. Rusting of iron
3. Oxidation of carbohydrates, lipids, etc. into CO₂ and H₂O to produce energy in the living organisms.

All oxidation reactions are accompanied by reduction reactions and vice versa. Such reactions are called redox reactions. As per the classical concept, addition of oxygen (or) removal of hydrogen is called oxidation and the reverse is called reduction.

Fig. 1.4 Oxidation reactions in daily life

Consider the following two reactions.

Reaction 1:
4 Fe + 3O₂ → 2 Fe₂O₃

Reaction 2:
H₂S + Cl₂ → 2 HCl + S

Both these reactions are oxidation reactions as per the classical concept. In the first reaction which is responsible for the rusting of iron, the oxygen adds on to the metal, iron. In the second reaction, hydrogen is removed from Hydrogen sulphide (H₂S). Identity which species gets reduced.

Consider the following two reactions in which the removal of oxygen and addition of hydrogen take place respectively. These reactions are called reduction reactions as per the classical concept.

CuO + C → Cu + CO (Removal of oxygen from cupric oxide)

S + H₂ → H2S (Addition of hydrogen to sulphur)

Oxidation-reduction reactions i.e. redox reactions are not always associated with oxygen or hydrogen. In such cases, the process can be explained on the basis of electrons. The reaction involving loss of electron is termed oxidation and gain of electron is termed reduction.

For example,

Fe²⁺ → Fe³⁺ + e^– (loss of electron-oxidation).
Cu²⁺ + 2e^– → Cu (gain of electron-reduction)

Redox reactions can be better explained using oxidation numbers.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

What is Stoichiometry? Balancing Equations

Have you ever noticed the preparation of kesari at your home? In one of the popular methods for the preparation of kesari, the required ingredients to prepare six cups of kesari are as follows.

1. Rava – 1 Cup
2. Sugar – 2 Cups
3. Ghee – \(\frac{1}{2}\) Cup
4. Nuts and Dry Fruits – \(\frac{1}{4}\) Cup

Otherwise,

1 cup rava + 2 cups sugar + \(\frac{1}{2}\) cup ghee + \(\frac{1}{4}\) cup nuts and dry fruits → 6 cups kesari.

From the above information, we will be able to calculate the amount of ingredients that are required for the preparation of 3 cups of kesari as follows

Alternatively, we can calculate the amount of kesari obtained from 3 cups rava as below.

Similarly, we can calculate the required quantity of other ingredients too. We can extend this concept to perform stoichiometric calculations for a chemical reaction. In Greek, stoicheion means element and metron means measure that is, stoichiometry gives the numerical relationship between chemical quantities in a balanced chemical equation.

By applying the concept of stoichiometry, we can calculate the amount of reactants required to prepare a specific amount of a product and vice versa using balanced chemical equation.

Let us consider the following chemical reaction.
C(s) + O₂(g) → CO₂(g)

From this equation, we learnt that 1 mole of carbon reacts with 1 mole of oxygen molecule to form 1 mole of carbon dioxide.

1 mole of C ≡ 1 mole of O₂
≡ 1 mole of CO₂

The symbol ‘≡’ means ‘stoichiometrically 6 cups of Kesari equal to’

Stoichiometric Calculations:

Stoichiometry is the quantitative relationship between reactants and products in a balanced chemical equation in moles. The quantity of reactants and products can be expressed in moles or in terms of mass unit or as volume. These three units are inter convertible.

Let us explain these conversions by considering the combustion reaction of methane as an example. The balanced chemical equation is,

CH₄ (g) + 2 O₂ (g) → CO₂ (g) + 2 H₂O(g)

Calculations Based on Stoichiometry

1. How many moles of hydrogen is required to produce 10 moles of ammonia?

The balanced stoichiometric equation for the formation of ammonia is

N₂(g) + 3H₂ (g) → 2 NH₃ (g)

As per the stoichiometric equation, to produce 2 moles of ammonia, 3 moles of hydrogen are required

∴ to produce 10 moles of ammonia, 3 moles of hydrogen are required

= 15 moles of hydrogen are required.

2. Calculate the amount of water produced by the combustion of 32 g of methane.

CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(g)

As per the stoichiometric equation,

Combustion of 1 mole (16 g) CH₄ produces 2 moles (2 × 18 = 36 g) of water.

Combustion of 32 g CH₄ produces

3. How much volume of carbon dioxide is produced when 50 g of calcium carbonate is heated completely under standard conditions?

The balanced chemical equation is,

As per the stoichiometric equation,

1 mole (100g) CaCO₃ on heating produces 1 mole CO₂

At STP, 1 mole of CO₂ occupies a volume of 22.7 litres

∴ At STP, 50 g of CaCO₃ on heating produces,

= 11.35 litres of CO₂

4. How much volume of chlorine is required to form 11.2 L of HCl at 273 K and 1 atm pressure?

The balanced equation for the formation of HCl is

H₂(g) + Cl₂(g) → 2 HCl (g)

As per the stoichiometric equation under given conditions,

To produce 2 moles of HCl, 1 mole ofchlorine gas is required

To produce 44.8 litres of HCl, 22.4 litres of chlorine gas are required.

∴ To produce 11.2 litres of HCl,

= 5.6 litres of chlorine are required.

5. Calculate the percentage composition of the elements present in magnesium carbonate. How many kilogram of CO₂ can be obtained by heating 1 kg of 90% pure magnesium carbonate.

The balanced chemical equation is

Molar mass of MgCO₃ is 84 g mol^-1.

84 g MgCO₃ contain 24 g of Magnesium.

∴ 100 g of MgCO₃ contain

= 28.57 g Mg.

i.e. percentage of magnesium
= 28.57 %.

84 g MgCO₃ contain 12 g of carbon

∴ 100 g MgCO₃ contain

= 14.29 g of carbon.

∴ Percentage of carbon
= 14.29 %.

84 g MgCO₃ contain 48 g of oxygen
∴ 100 g MgCO₃ contains

∴ Percentage of oxygen
= 57.14 %.

As per the stoichiometric equation,

84 g of 100 % pure MgCO3 on heating gives 44 g of CO₂.

∴ 1000 g of 90 % pure MgCO₃ gives

= 471.43 g of CO₂
= 0.471 kg of CO₂

Limiting Reagents:

Earlier, we learnt that the stoichiometry concept is useful in predicting the amount of product formed in a given chemical reaction. If the reaction is carried out with stoichiometric quantities of reactants, then all the reactants will be converted into products.

On the other hand, when a reaction is carried out using non-stoichiometric quantities of the reactants, the product yield will be determined by the reactant that is completely consumed. It limits the further reaction from taking place and is called as the limiting reagent. The other reagents which are in excess are called the excess reagents.

Recall the analogy that we used in stoichiometry concept i.e. kesari preparation, As per the recipe requirement, 2 cups of sugar are needed for every cup of rava. Consider a situation where 8 cups of sugar and 3 cups of rava are available (all other ingredients are in excess), as per the cooking recipe, we require 3 cups of rava and 6 cups of sugar to prepare 18 cups of kesari.

Even though we have 2 more cups of sugar left, we cannot make any more quantity of Kesari as there is no rava available and hence rava limits the quantity of Kesari in this case. Extending this analogy for the  chemical reaction in which three moles of sulphur are allowed to react with twelve moles of fluorine to give sulphur hexafluoride.

The balanced equation for this reaction is, S + 3F₂ → SF₆

As per the stoichiometry,

1 mole of sulphur reacts with 3 moles of fluorine to form 1 mole of sulphur hexafluoride and therefore 3 moles of sulphur reacts with 9 moles of fluorine to form 3 moles of sulphur hexafluoride. In this case, all available sulphur gets consumed and therefore it limits the further reaction. Hence sulphur is the limiting reagent and fluorine is the excess reagent. The remaining three moles of fluorine are in excess and do not react.

Urea, a commonly used nitrogen based fertilizer, is prepared by the reaction between ammonia and carbon dioxide as follows.

In a process, 646 g of ammonia is allowed to react with 1.144 kg of CO₂ to form urea.

1. If the entire quantity of all the reactants is not consumed in the reaction which is the limiting reagent?
2. Calculate the quantity of urea formed and unreacted quantity of the excess reagent.

The balanced equation is

2 NH₃ + CO₂
↓
H₂NCONH₂ + H₂O

Answer:

1. The entire quantity of ammonia is consumed in the reaction. So ammonia is the limiting reagent. Some quantity of CO₂ remains
unreacted, so CO₂ is the excess reagent.

2. Quantity of urea formed

= number of moles of urea formed × molar mass of urea
= 19 moles × 60 g mol^-1
= 1140 g
= 1.14 kg

Excess reagent leftover at the end of the reaction is carbon dioxide.

Amount of carbon dioxide leftver

= number of moles of CO₂ left over × molar mass of CO₂
= 7 moles × 44 g mol^-1
= 308 g.