CBSE Notes

By going through these CBSE Class 12 Chemistry Notes Chapter 3 Electrochemistry, students can recall all the concepts quickly.

Electrochemistry Notes Class 12 Chemistry Chapter 3

Electrochemical Cell: It is a device to convert the chemical energy of a spontaneous redox reaction into electrical energy. It is also called Galvanic Or Voltaic Cell. One such example of an electrochemical cell is Daniel Cell.

Daniel’s cell converts the chemical energy liberated during the redox reactions.
Zn (s) + Cu²⁺ (aq) → Zn²⁺ (aq) + Cu (s) into electrical energy and has an electrical potential [E.M.F. ] equal to 1.1 volt when concentration of both Zn²⁺ and Cu²⁺ ions is unity (1 mol dm^-3)

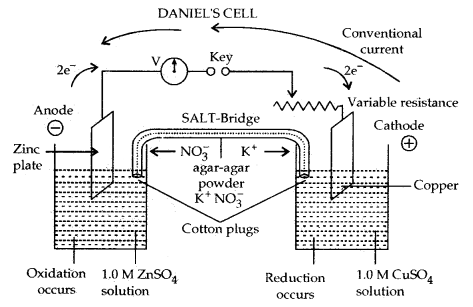
In the left-hand beaker, oxidation occurs. Zn plate dissolves to form Zn²⁺. Zn plate loses weight
Oxidation Half-reaction:
At anode: Zn (s) → Zn²⁺ (aq) + 2e^–

Reduction Half-Reaction: In the right-hand beaker reduction occurs. Cu²⁺ ions from the solution deposit on the copper plate. It gains weight.
At Cathode: Cu²⁺ (aq) + 2e^– → Cu (s)

Electrons flow from zinc plate to copper plate in the external circuit. Conventional current flows from copper to zinc plate (as. shown above) Combining the two half-reactions, we get the complete cell reaction or redox reaction.
Zn (s) + Cu²⁺ (aq) → Zn²⁺ (aq) + 2e^–

Electrolytic Cell: It is a device to convert electrical energy from an external source to produce a chemical change. In the above cell if E_ext is > 1.1. the reaction will again start but in the opposite reaction. It now will function as an electrolytic cell.

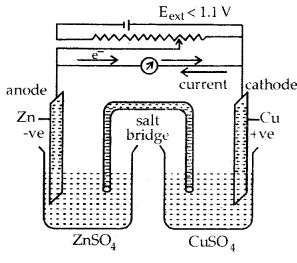
(a) when Eext < 1.1 V

1. Electrons flow from Zn rod to Cu rod hence current flows from Cu to Zn.
2. Zn dissolves at anode and copper deposits at the cathode.

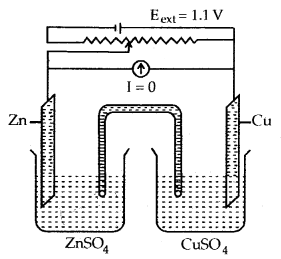
(b) when E_ext = 1.1 V

1. No flow of electrons or current.
2. No chemical reaction.

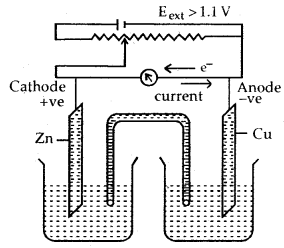
Functioning of Daniell cell when external voltage E_ext opposing the cell potential is applied.
(c) When E_ext > 1.1 V

1. Electrons flow from Cu to Zn arid current flows from Zn to Cu.
2. Zinc is deposited at the zinc electrode and copper dissolves at the copper electrode

In the electrochemical cell at each electrode-electrolyte interface, there is a tendency of metal ions from the solution to deposit on the metal electrode trying to make it positively charged. At the same time, metal atoms of the electrode have a tendency to go into the solution as ions and leave behind the electrons at the electrode trying to make it negatively charged.

At equilibrium, there is a separation of charges and depending on the tendencies of the two opposing reactions, the electrode may be positively or negatively charged with respect to the solution. A potential difference develops between the electrode and the electrolyte which is called Electrode Potential.

When the concentration of all species involved in half-cells is unity, the electrode potential is called Standard Electrode Potential.

According to the IUPAC convention, standard reduction potentials are now called standard electrode potentials. In a galvanic cell, the half¬cell in which oxidation takes place is called Anode and it has a negative potential with respect to the solution. The other half-cell in which reduction takes place is called Cathode and it has a positive potential with respect to the solution. The direction of the flow of current is opposite to that of the flow of electrons.

The cell potential is the difference between the electrode potentials (reduction potentials) of the cathode and anode. It is called electromotive force (emf) of the cell when no current flows through the circuit. Internally the two half-cells/beakers are connected through the salt bridge.
E_cell = E_right – E_left

In the Cu^– AgNO₃ cell cell reaction is
Cu (s) + 2 Ag⁺ (aq) → Cu²⁺ (aq) + 2 Ag (s)
At anode: Cu (s) → Cu²⁺ (aq) + 2 e^–] oxidation
At cathode: 2 Ag⁺ (aq) + 2 e^– → 2Ag (s)] reduction

Here Ag electrode acts as cathode and copper electrode, as anode.
The cell can be represented by
Cu (s) | Cu²⁺ (aq) || Ag⁺ (aq) | Ag (s)
E_cell = E_right – E_left
= E_Ag⁺/Ag – E_Cu²⁺/Cu

Similarly Daxtiel cell can be represented by
Zn (s) | Zn²⁺ (aq) || Cu²⁺ (aq)| Cu (s)
E_cell = E_right – Eleft
= E_Cu²⁺/Cu – E_Zn²⁺/Zn
Measurement of Electrode Potential: The measurement of the potential of half-cells is not possible.

Only the difference between the two half-cell potentials can be determined that gives the e.m.f. of the cell. By arbitrarily fixing the electrode potential of one half-cell, that of the other can be determined.

According to the convention, Standard Hydrogen Electrode represented by Pt (s), H₂(g), H₂(g)/H⁺ (aq) is assigned a zero potential at all temperatures according to the reaction
H⁺(aq) + e^– → H₂(g)

Standard Hydrogen Electrode: It consists of platinum wire sealed in a glass tube arid has a platinum foil attached to it. The foil is coated with finely divided platinum and acts as a platinum electrode. It is dipped into an acid solution containing H⁺ ions in 1 M concentration (1M HCl). Pure H₂ gas at 1 bar pressure is constantly bubbled into the solution at a constant temperature of 298 K. The following reaction occurs in the half-cell depending upon whether it acts as an anode or as a cathode.

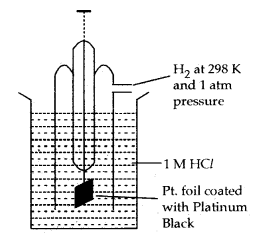
Normal Hydrogen Electrode (NHE)

If S.H.E. (orN.H.E.) acts as Anode
H₂(g) → 2H⁺ (aq) + 2e^– oxidation half reaction

If S.H.E. (or N..H.E.) acts as Cathode
2H⁺ (aq) + 2e^– → H₂ (g)] reduction half reaction

The standard hydrogen electrode is also regarded as a reversible electrode with respect to H+ ions:
H₂(g) ⇌ 2H⁺ (aq) + 2e^–

Arbitrarily, the standard electrode potential of this electrode is fixed to be 0.000 V.
The electrode potential of an electrode can be determined by connecting this half-cell with a standard hydrogen electrode.

The electrode potential of a metal electrode as determined with respect to S.H.E. (or N.H.E.) is called Standard Electrode Potential E°.

Conventionally: The reduction (standard) potential of an electrode that acts as a Cathode when attached to S.H.E. is given a positive sign, e.g., Cu/Cu⁺⁺ electrode when attached to S.H.E. acts as a cathode.

Let us calculate the electrode (reduction) potential of Zn/Zn²⁺. The cell will be
Zn (s) | Zn²⁺_1.0 (aq)| | H⁺ _1.0 (aq), H₂ (g), Pt(s).

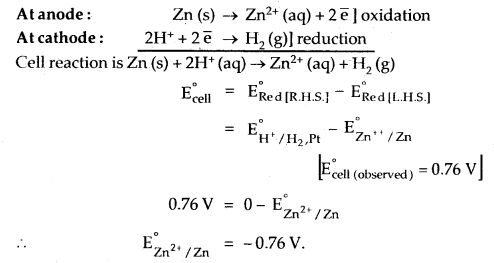
Let us measure the electrode potential of Cu/Cu²⁺ electrode concentration of Cu²⁺ is 1.0 M and the pressure of H₂ gas is one bar. At 298 K, the emf of the cell

Standard hydrogen electrode 11 second half cell.
E°_cell = E°_R – E°_L
0.34 = E°_Cu⁺⁺ – 0 [emf of the cell = 0.34 V]
∴ E_Red° of Cu electrode dipping in Cu²⁺ ions = 0.34 V

Electrochemical Series or The Standard Electrode Potentials at 298 K: Ions are present as aqueous species and H₂O as liquid, gases and solids are shown by aq, g and s.

1. A negative Ev means that the redox couple is a stronger reducing agent than the H⁺/ H₂ couple.
2. A positive Ev means that the redox couple is a weaker reducing agent than the H⁺/H₂ couple.

Applications Of Electrochemical Series:
1. Relative strength of oxidizing and reducing agents: In this series, metals are arranged in the decreasing order of their standard electrode potentials or decreasing order of their oxidizing character. e.g. Li⁺ (aq) which has least reduction potential (- 3.05) is the weakest oxidizing agent and F₂ (g) which has maximum value of p_Red = + 2.85 is the strongest oxidizing agent.

On the other hand, Li metal which has the highest standard oxidation potential (= + 3.05) is the strongest reducing agent while F- ( E°_ox = – 2.85 V) is the least reducing agent.

2. Calculation of e.m.f. of the cell: The e.m.f. of the desired cell can be calculated knowing the standard reducing potentials of the two half cells constituting the cell from the electrochemical series.
E°_cell = E°_Red [RIGHT] – E°Red [LEFT]
e.g. Zn (s) | Zn²⁺ (1.0 M) || Cu²⁺ (1.0 M) | Cu (s).
E°_cell = E°_Cu²⁺,_Cu – E°_Zn²⁺,_Zn.
= 0.34 – (- 0.76) V = 1.10 V

3. Predicting feasibility of redox reaction: In general, a redox reaction is feasible only if the species which has higher standard reduction potential is reduced i.e., accepts the electrons and the species which has lower reduction potential is oxidized i.e., loses the electrons. Otherwise, a redox reaction is not feasible. In other words, the species to release the electrons must have lower reduction potentials as compared to the species which is to accept electrons. In a nutshell, if the e.m.f. of the hypothetical cell is +ve, a redox reaction takes place; if it is – ve, a redox reaction is not feasible.

4. To predict whether a metal can librate H₂(g) from acid or not. The metals which have only negative reduction potentials, i.e., are lying above N.H.E. in the electrochemical series, can only liberate H₂ (g) from dilute acid solutions.

Nernst Equation: The relationship between electrode potentials and the concentration of the electrolytic solutions is called Nernst Equation.
1. The Nernst Equation is
E = E° + \(\frac{\mathrm{RT}}{\mathrm{nF}}\) In [Mn+]/[M] Since[M] = 1
E = E° + \(\frac{2.303 \mathrm{RT}}{\mathrm{nF}}\) log [Mn+]
E = reduction electrode potential
E° = reduction electrode potential in standard state [1 M solution of metal ions at 298 K]
R = Gas constant = 8.314 JK-1.M0l-1
T = Temperature
n = no. of electrons accepted during the change
| F | = Faraday t = 96500 C.

Putting the values of R, T = 298 K; F
| E | = E° + \(\frac{0.059}{\mathrm{n}}\) log [Mn+]

For the complete cell reaction
Zn (s) + Cu²⁺(aq) ⇌ Zn²⁺ (aq) + Cu (s)

2. Calculation of Gibbs free energy/Maximum work that can be obtained from the Galvanic cell
ΛG° = – n F E°elI = – 2.303 RT log Kc
where AG° is the standard Gibbs energy change in Gibbs function
n = number of moles of electrons involved in the cell reaction
F = Faraday = 96,500 coulombs
R = Gas Constant
Kc = Equilibrium constant.

Conductance of Electrolytic Solutions:
Resistance R (ohm) = \(\frac{\text { Potential Difference in volts }}{\text { Current strength in amperes }}\)

Resistance can be measured by the principle of the Wheatstone bridge. It depends upon the length and inversely on the area of cross-section A of the wire.
R ∝ l
R ∝ \(\frac{l}{\mathrm{~A}}\)
or
R = ρ\(\frac{l}{\mathrm{~A}}\);
where ρ (rho) is called specific resistance/Resistivity.

The resistivity of a substance is its resistance to the passage of electricity when it is one metre long and its area of cross-section is one m2.

The inverse of resistance R is called conductance.
Conductance = \(\frac{1}{\mathrm{R}}=\frac{\mathrm{A}}{\rho l}=\frac{\mathrm{A} \kappa}{l}\) ( κ = Kappa)

The SI unit of conductance is Siemens.
1S = 1 ohm^-1 = mho = Ω^-1.

The inverse of resistivity is called Conductivity or Specific Conductance.
SI unit of conductivity is Sm-1, but often (Greek Kappa) is expressed in S cm^-1.

The magnitude of conductivity varies a great deal and depends upon the nature of the material. It also depends upon the temperature and pressure of measurement.

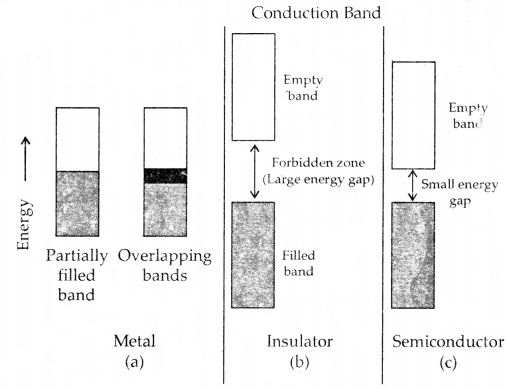
Materials are classified as

1. Conductors,
2. Insulators,
3. Semi-conductors depending upon the magnitude of their conductivity.

Metals and their alloys have very large conductivity and are known as conductors. Certain, non-metals like carbon black, graphite and some organic polymers are also electronically conductors. Substance like glass, ceramics etc. have very low conductivity are known as insulators. Substance like silicon, doped silicon, gallium arsenide is semi-conductors. Electrical conductance ( through metals called metallic or electronic conductance is due to the flow of mobile electrons.

The metallic conductance depends upon,

1. The nature and structure of the metal.
2. The number of valence electrons per atom.
3. Temperature. It decreases with an increase in temperature.
4. The composition of the metallic conductor remains unchanged.

Electrolytic or Ionic Conductance: When electrolytes are dissolved in water, they furnish their own ions in the solution. They conduct electricity through their ions in the solution and is called electrolytic or ionic conductance.

The conductivity of electrolytic or ionic solutions depends upon:

1. The nature of the electrolyte added
2. Size of the ions produced and their solvation.
3. The nature of the solvent and its viscosity.
4. The concentration of the electrolyte.
5. Temperature conductivity increases with an increase in temperature.
6. It leads to a change in its composition with the passage of direct current through the solution over a prolonged period.

Measurement of Conductivity of Ionic Solutions: It is based upon the measurement of resistance by a wheat stone bridge. The cell is called a conductivity cell.

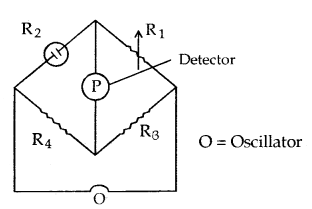
Unknown resistance of the cell R2 = \(\frac{\mathrm{R}_{1} \mathrm{R}_{4}}{\mathrm{R}_{3}}\)
Conductance C of the cell = \(\frac{1}{\mathrm{R}_{2}}\)

Cell Constant = \(\frac{\text { Specific conductance }}{\text { Observated conductance }}\)

Molar Conductivity: It is the conducting power of all ions obtained by dissolving 1 mole of an electrolyte in a given volume of the solution,

Molar conductivity = Λm = \(\frac{x}{c}\)
= \(\frac{\mathrm{Sm}^{-1}}{1000 \mathrm{Lm}^{-3} \times \text { molarity }\left(\mathrm{mL}^{-1}\right)}\)
= S m² mol^-1

Variation of Conductivity and Molar Conductivity with concentration: Both conductivity and molar conductivity change with the concentration of the electrolyte. Conductivity always decreases with the decrease in concentration both for weak and strong electrolytes. This can be explained by the fact that the number of ions per unit volume that carry the current in a solution decreases on dilution. The conductivity of a solution at any given concentration is the conductance of one unit volume of solution kept between two platinum electrodes with a unit area of cross-section and at a distance of unit length. This is clear from the equation:

C = \(\frac{\mathrm{κA}}{l}\)= κ (both A and l are unity in their appropriate Units in m or cm)

Molar conductivity of a solution at a given concentration is the conductance of volume V of a solution containing one mole of electrolyte kept between two electrodes with an area of cross-section A and distance of unit length. Therefore,
Λ_m = \(\frac{\mathrm{κA}}{l}\)= κ
Since l = 1 and A = V (volume containing 1 mole of electrolyte)
Λ_m = κV

Molar conductivity increases with a decrease in concentration. This is because the total volume, V, of a solution containing one mole of electrolyte also increases. It has been found that a decrease in κ on dilution of a solution is more than compensated by an increase in its volume.

Physically, it means that at a given concentration, Λm can be defined as the conductance of the solution of an electrolyte kept between the electrodes of a conductivity cell at a unit distance but having an area of cross-section large enough to accommodate sufficient volume of solution that contains one mole of the electrolyte. When concentration approaches zero, the molar conductivity is known as limiting molar conductivity and is represented by the symbol Λ°_m The variation in Λm with concentration is different for strong and weak electrolytes.

Strong Electrolytes: For strong electrolytes, A increases slowly with dilution and can be represented by the equation :
Λ_m = Λ°_m – A c^1/2
It can be seen that if we plot Λm against c^1/2, we obtain a straight line with an intercept equal to and slope equal to ‘A’. The value of the constant ‘A’ for a given solvent and temperature depends on the type of electrolyte i.e., the charges on the cation and anion produced on the dissociation of the electrolyte in the solution. Thus, NaCl, CaCl₂, MgS04 are known as 1-1, 2-1 and 2-2 electrolytes respectively. All electrolytes Of a particular type have the same value for ‘A’.

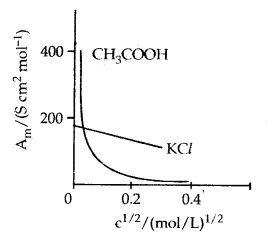
Molar conductivity versus c^1/2 for acetic acid (weak electrolyte) and potassium chloride (strong electrolyte) in aqueous solutions.

Kohlrausch law of independent migration of ions. The law states that limiting molar conductivity of an electrolyte can be represented as the sum of the individual contributions of the anion and cation of the electrolyte. Thus, if λ°_Na and λ°_Cl^– are limiting molar conductivity of the sodium and chloride ions respectively, then the limiting molar conductivity for sodium chloride is given by the equation :
Λ°_m(NaCl) = λ°_Na + λ°_Cl^–

In general: Λ°_m = v₊ λ°₊ + n_– λ°_–
Here λ°₊ and λ°_– are the limiting molar conductivities of the cation and anion respectively.

Weak Electrolytes: Weak electrolytes like acetic acid have a lower degree of dissociation at higher concentration and hence for such electrolytes, the change in Λ_m with dilution is due to an increase in the degree of dissociation and consequently the number of ions in the total volume of solution that contains 1 mol of electrolyte. In such cases, Λ_m increases steeply on dilution, especially near lower concentrations.

Therefore, Λ°m cannot be obtained by extrapolation of Λm to zero concentration. At infinite dilution (i.e., concentration c → zero) electrolyte 5 dissociates completely (α = 1), but at such low concentration, the conductivity of the solution is so low that it cannot be measured accurately. Therefore, Λ°_m for weak electrolytes is obtained by using Kohlrausch law of independent migration of ions. At any concentration c, if a is the degree of dissociation then it can be approximated to the ratio of molar conductivity A m at the concentration c to limiting molar conductivity, Λ°_m.

Thus we have:
α = \(\frac{\Lambda_{\mathrm{m}}}{\Lambda_{\mathrm{m}}^{\circ}}\)
But we know that for a weak electrolyte like acetic acid,

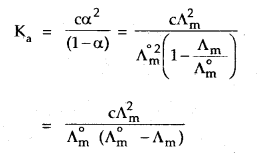
Applications of Kohlrausch law: Using Kohlrausch law of independent migration of ions, it is possible to calculate Λ°_m for any electrolyte from the λ° of individual ions. Moreover, for weak electrolytes like acetic acid, it is possible to determine the value of its dissociation constant once we know the Λ°_m and Λ_m at a given concentration c

Electrolytic Cells and Electrolysis: In an electrolytic cell external source of voltage is used to bring about a chemical reaction. The electrochemical processes are of great importance in the laboratory and the chemical industry. One of the simplest electrolytic cells consists of two copper strips dipping in an aqueous solution of copper sulphate. If a DC voltage is applied to the two electrodes, then Cu²⁺ ions discharge at the cathode (negatively charged) and the following reaction takes place:
Cu²⁺ (aq) + 2e^– → Cu (s)
Copper metal is deposited on the cathode. At the anode copper is converted into Cu²⁺ ions by the reaction:
Cu (s) → Cu²⁺ (s) + 2e^–

Thus copper is dissolved (oxidised) at the anode and deposited (reduced) at the cathode. This is the basis for an industrial process in which impure copper is converted into the copper of high purity. The impure copper is made an anode that dissolves on passing current and pure copper is deposited at the cathode.

Many metals like Na, Mg, Al, etc. are produced on large scale by electrochemical reduction of their respective cations where no suitable chemical reducing agents are available for this purpose. Sodium and magnesium metals are produced by the electrolysis of their fused chlorides and aluminium is produced by electrolysis of aluminium oxide in presence of cryolite.

Faraday’s Laws of Electrolysis:
1. First Law: The amount of chemical reaction which occurs at any electrode during electrolysis by a current is proportional to the quantity of electricity passed through the electrolyte (solution or melt).

2. Second Law: The amounts of different substances liberated by the same quantity of electricity passing through the electrolytic solution are proportional to their chemical equivalent weights (Atomic Mass of Metal. Number of electrons required to reduce the cation).

Some Commercial Cells: The electrochemical cells can be used to generate electricity and these are called batteries. The battery is generally used for two or more galvanic cells connected in series.

There are two types of commercial cells:

1. Primary cells, in which electrode reactions cannot be reversed by external energy source. Therefore, these are not chargeable. For example, dry cell, mercury cell.
2. Secondary cells are those which can be recharged. For example, lead storage cell, nickel-cadmium cell.

→ Fuel Cells: These are voltaic cells in which the reactants are continuously supplied to the electrodes. These are designed to convert the energy from the combustion of fuels such as H₂, CO, CH₄ etc. directly into electrical energy. A common example is a hydrogen-oxygen fuel cell.

→ Corrosion: The process of deterioration of a metal as a result of its reaction with air or water surrounding it is called corrosion. In the case of iron, corrosion is called rusting. Chemically rust is a hydrated form of ferric oxide, Fe₂O₃ x H₂O. It is caused by moisture, carbon dioxide and oxygen present in the air.

The chemistry of corrosion is essentially an electrochemical phenomenon. At a particular spot of an iron object, oxidation takes place and that place behaves as an anode:
Anode 2 Fe(s) → 2Fe²⁺ + 4e^– E°_Fe²⁺/Fe = – 0.44 V

Electrons released at anodic spot move through the metal and go to another spot on the metal and reduce oxygen in presence of H⁺ (which is believed to be .available from H2C03 formed due to dissolution of carbon dioxide from the air into water. Hydrogen ion in water may also be available due to the dissolution of other acidic oxides from the atmosphere).

This spot behaves as cathode with the reaction Cathode:
O₂(g) + 4H⁺ (aq) + 4e^– → 2 H₂O
E_H⁺|O2|H2O = 1.23V

The overall reaction being:
2Fe(s) + O₂(g) + 4H⁺ (aq) → 2Fe₂ (aq) + 2 H₂O (l)
E^V_cell = 1.67 V

The ferrous ions are further oxidised by atmospheric oxygen to ferric ions which come out as rust in the form of hydrated ferric oxide (Fe₂O₂ . x H₂0) and with further production of hydrogen ions.

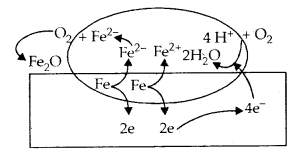
Corrosion of iron in the atmosphere

Oxidation: Fe (s) → Fe²⁺ (aq) + 2e^–
Reduction: O₂(g) + 4H⁺ (aq) + 4e^– → 2H₂O (1)

Atmospheric
oxidation : 2 Fe²⁺ (aq) + 2H₂O (l) + 1/2 O₂ (g) → Fe₂O₃ (s) + 4H⁺ (aq)

Prevention of Corrosion: The rusting of iron can be prevented or decreased by the following methods:
1. Barrier protection: In this method a barrier is placed between the iron and the atmospheric air by coating the surface with paint, applying a thin film of oil or grease or electroplating.

2. Sacrificial protection: In this method, iron is protected by covering it with a layer of metal more active than iron such as zinc, tin, etc. The process of covering iron with zinc is called galvanization.

3. Electrical protection: In this method, the iron is connected with a more active metal like magnesium or zinc.

4. Using anti-rust solution: To retard the corrosion of iron certain anti-rust solutions such as alkaline phosphates and alkaline chromates are used.

Commercial Production of Chemicals: Many metals and their compounds are prepared by using basic principles of electrolysis:

Na is prepared by the electrolysis of molten Na⁺ Cl^– by Down’s Cell

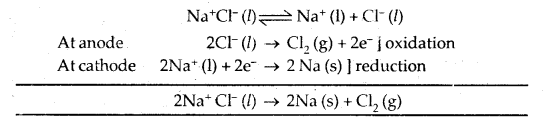
Mg is prepared from fured Mg Cl₂
MgCl₂(Z) ⇌ Mg²⁺ (l) + 2 Cl^– (l)
At anode 2Cl^– → Cl₂ (g) + 2e^–
At cathode Mg²⁺ + 2e^– → Mg (s).

The Hydrogen Economy: Both the production of hydrogen by electrolysis of water
2 H₂O (l) → 2H₂ (g) + O₂ (g) and hydrogen combustion in a fuel cell
2 H₂ (g) + O₂ (g) 2H₂O (l). will be important in future. Both are based on electrochemical principles.

By going through these CBSE Class 12 Chemistry Notes Chapter 2 Solutions, students can recall all the concepts quickly.

Solutions Notes Class 12 Chemistry Chapter 2

Solution: It is a homogeneous mixture of two or more components whose composition may be varied within limits. The component present in the largest quantity is known as Solvent. One or more components present in the solution other than the solvent are called Solutes. Solutions consisting up of two components only are called Binary Solutions.

In all there are 9 types of solutions:
Expressing Concentration of Solutions
1. Mass Percentage (W/W):
Mass of the comp, in solution
Mass % of a component= \(\frac{\text { Mass of the comp. in solution }}{\text { Total mass of solution }}\) × 100

2. Volume Percentage (V/V):
Volume % of a component = \(\frac{\text { Volume of the component }}{\text { Total volume of solution }}\) × 100
The total volume of the solution

3. Mass by volume percentage (W/V):
It is the mass of solute dissolved in 100 mL of the solution.

4. Parts per million (ppm):
Parts per million
\(\frac{\text { No. of parts of the component }}{\text { Total no. of parts of all components of the solution }}\) × 10⁶

5. Mole Fraction:
Mole fraction of a component (x) = \(\frac{\text { No. of moles of the component }}{\text { Total no. of moles of all components }}\)

If there are 2 components in a binary solution of A and B.
x_A = \(\frac{n_{A}}{n_{A}+n_{B}}\)
x_B = \(\frac{n_{B}}{n_{A}+n_{B}}\)
[where nA and nB are the no. of moles of A and B respectively]
x_A + xB_B = 1

For a solution containing i no. of components
x_i = \(\frac{n_{i}}{n_{1}+n_{2}+\ldots n_{i}}=\frac{n_{i}}{\Sigma n_{i}}\)

6. Molarity (M): Molarity is defined as the no. of moles of the solute dissolved in one litre (or one cubic decimetre) of solution.
Molarity (M) = \(\frac{\text { Moles of solute }}{\text { Volume of solution in litre }}\)
= \(\frac{\text { Strength of solute per litre of solution }}{\text { Molar mass of the solute }}\)

7. Molality (m): It is defined as the no. of moles of the solute per 1000 g [l kg] of the solvent.
Molality (m) = \(\frac{\text { Moles of solute }}{\text { Mass of solvent in } \mathrm{kg}}\)
= \(\frac{\text { Strength of the solute per } 1000 \mathrm{~g} \text { of solvent }}{\text { Molar mass of the solute }}\)

Mass %, ppm, mole fraction and molality are independent of temperature, whereas molarity depends upon temperature.

Solubility: The solubility of a substance is its maximum amount that can be dissolved in a given amount of solvent at a given temperature. It depends upon the nature of solute and solvent as well as temperature and pressure.

→ Solubility of a solid in a Liquid: In general, polar solutes dissolve in polar solvents and non-polar solutes in non-polar solvents. Like Dissolves Like. In general, a solute dissolves in a solvent if the intermolecular interactions are similar.
Solute + Solvent → Solution

→ Saturated Solution: A solution is said to be saturated if no more of the solute can be dissolved in it at a particular temperature and pressure.

→ Effect of Temperature on Solubility: The solubility of a solid in a liquid is significantly affected by temperature changes. If the process of dissolution in a nearly saturated solution is endothermic (Δsol H > 0), the solubility should increase with rising temperature and if it is exothermic (Δsol H < 0), the solubility should decrease.

→ Effect of Pressure: Pressure does not have any significant effect on the solubility of solids in liquids. It is so because solids and liquids are highly incompressible and practically remain unaffected by changes in pressure.

→ Solubility of a Gas in a Liquid: The solubility of gases in liquids is greatly affected by pressure and temperature. The solubility of gases increases with the increase of pressure.

Henry’s Law: It states, “At a constant temperature, “The solubility of a gas in a liquid is directly proportional to the pressure of the gas.”

Dalton also concluded, “The solubility of a gas in a liquid solution is a function of the partial pressure of the gas.”
In other words, “The mole fraction of the gas in the solution is proportional to the partial pressure of the gas over the solution.”

The most commonly used form of Henry’s law states “The partial pressure of the gas in the vapour phase (p) is proportional to the mole fraction of the gas (x) in the solution.”
p = K_Hx

Where KH is Henry’s law constant and it is a function of the nature of the gas.

Solubility of a gas in a liquid decreases with an increase in temperature. It is due to this reason that aquatic species like fish are more comfortable in cold waters rather than warm water.

Applications of Henry’s Law:

1. Pressure is kept high to increase the solubility of CO₂ in soft drinks.
2. Deep-sea divers experience bends or decompression sickness due to greater solubility of N₂ and O₂ in blood. O₂ is dissolved in the blood and other body fluids and N₂ will remain dissolved and will form bubbles when the diver comes to the atmospheric pressure. Hence N₂ in compressed air is’ replaced by He which is much less soluble in biological fluids.
3. In the function of lungs: Due to the partial pressure of O₂ being high when it enters the lungs, it combines with haemoglobin to form oxyhaemoglobin. The partial pressure of O₂ in tissues is low. Hence O₂ is released from oxyhaemoglobin which is utilised for functions of cells

Vapour Pressure of Liquid-Liquid Solutions: In a binary solution of two volatile liquids in a closed vessel, let Ptotal, p₁ and p₂ denote total vapour of the solution, partial vapour pressures of the two compounds and x₁ and x₂ their mole fractions, then according to Raoult’s Law.
p₁ ∝ x₁
and p₁ = p₁° × x₁
where p₁° is the V.P. of pure component 1

Similarly p₂ = p₂° × x₂
where p₂° is the V.P. of pure component 2

[Raoult’s Law states “For a solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.”]

Now according to Dalton’s law of partial pressures.
P_total = P₁ + P₂
= p₁° + p₂° x₂
= (1 – x₂)p° + x₂ p°
= P₁° + ( P₂° – P₁° )x₂.

Following conclusions can be drawn from the above equations

1. Total vapour pressure over the solution can be related to the mole fraction of any one component.
2. Total vapour pressure over the solution varies linearly with the mole fraction of component 2.
3. Depending upon the vapour pressure of the pure components 1 and 2, total vapour pressure over the solution decreases or increases with the increase of the mole fraction of component 1.

Assuming component 1 to be less volatile than component 2, the minimum value of p_total is p° and the maximum value p° (i.e. p° < p° ), a graph can be drawn between the mole fraction and their vapour pressures in solution.

The composition of the vapour phase in equilibrium with the solution is determined by the partial pressure of the components. If y₁ and y₂ are the mole fractions of the components 1 and 2 in the vapour phase, then, using Dalton’s law of partial pressures
P₁ = y₁ Ptotal
P₂ = y₂ Ptotal
In general P_i = y_i P_total

It can be concluded: At the equilibrium vapour phase will be always richer in the component which is more volatile.
Raoult’s law is a special case of Henry’s law

According to Raoult’s law p_i = x_i pi°
According to Henry’s Law p = K_H × x

Here only the proportionality constant K_H differs from p_i°. Thus Raoult’s law becomes a special case of Henry’s law in which K_H becomes equal to P_i°.

Ideal and Non-Ideal Solution: A solution that obeys Raoult’s Law at all concentrations and at all temperatures is called an Ideal Solution. Herein the magnitude of solute-solvent interactions is the same as the magnitude and solvent of the solute-solute interaction- solvent interactions magnitude in the two components.

For ideal solutions enthalpy on mixing remains the same,
i.e., ΔH_Mix = 0

For such solutions, there is no change in volume on mixing the two components
i.e., ΔV_Mix = 0

Non-Ideal Solutions are those which do not obey Raoult’s Law: For such solutions, the magnitude of solute-solvent interactions is either greater than or less than the magnitude of solute-solute or solvent-solvent interactions in the pure components.

Additionally, during solution formation either heat is evolved or absorbed.
i.e.; ΔH_Mix = +Ve
or
ΔH_Mix = -Ve [or ΔH_Mix ≠ 0]
Moreover, there is a volume change in mixing
ΔH_Mix ≠ 0

Examples of ideal solutions:

1. n-hexane + n-heptane
2. Benzene + Toluene
3. Chlorbenzene + bromobenzene
4. CCl₄ + SiCl₄
5. CH₃OH + C₂H₅OH.

Examples of Non-ideal solutions:

Colligative Properties: These properties depend only on the number of solute particles, but not on the nature of the solute.
They are

1. Relative lowering of vapour pressure
2. Elevation in boiling points
3. Depression in freezing point
4. Osmotic pressure.

1. Relative lowering of vapour pressure: The relative lowering of the vapour pressure of a dilute solution (which, for all intents and purposes, is an ideal solution) is equal to the mole fraction of the solute at a given temperature.
If x_A = Mole fraction of the solvent
x_B = Mole fraction of the solute
P_A = Vapour pressure of the pure solvent
P_B = Vapour pressure of the solution

\(\frac{P_{A}^{\circ}-P_{A}}{P_{A}^{\circ}}\) is called the relative lowering of vapour pressure
W_A = Mass of comp. A
M_A = M. mass of comp. A
W_B = Mass of comp. B
M_B = M. mass of comp. B

From relative lowering in vapour pressure, the molar mass of solute can be calculated as:
M_B = \(\frac{W_{\mathrm{B}} \times \mathrm{M}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}} \times \frac{\mathrm{P}_{\mathrm{A}}^{\circ}-\mathrm{P}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{A}}^{\circ}}}\)

2. Elevation in boiling: The boiling point of a liquid may be defined as the temperature at which its vapour pressure becomes equal to atmospheric pressure. When a non-volatile solute is added to a solvent, the solution boils at a higher temperature than the pure solvent.

If T_b° is the boiling point of the pure solvent and T_b is the boiling point of the solution, then elevation in boiling point,
ΔT_b = T_b – T_b° = K_b × m
where m is the molality of the solution and K_b is molal elevation constant or ebullioscopic constant of the solvent.

Molal elevation in boiling point is defined as the elevation in boiling point produced when 1 mole of a solute is dissolved in 1000 g of the solvent.

The molar mass of the solute can be calculated from the elevation in boiling point as
M_B = \(\frac{\mathrm{K}_{\mathrm{b}} \times \mathrm{W}_{\mathrm{B}} \times 1000}{\Delta \mathrm{T}_{\mathrm{b}} \times \mathrm{W}_{\mathrm{A}}}\)

The molar elevation constant is expressed as
K_b = \(\frac{\mathrm{RT}_{\mathrm{b}}^{\circ} \mathrm{M}}{\Delta \mathrm{H}_{\mathrm{vap}} \times 1000}\)
or
= \(\frac{\mathrm{RT}_{\mathrm{b}}^{\circ}}{\Delta \mathrm{h}_{\mathrm{vap}} \times 1000}\)

where T_b° is the boiling point of the solvent, M is the molar mass of the solvent, R is gas constant and ΔH_vap is the enthalpy of vaporisation of the pure solvent. Δh_vap is the enthalpy of vaporisation per gram as

Δh_vap = \(\frac{\Delta \mathrm{H}_{\mathrm{vap}}}{\mathrm{M}}\)

The vapour pressure curve of the solution lies below the curve for pure solvent. The diagram shows that ΔT_b denotes the elevation of the boiling point of a solvent in the solution.

3. Depression in freezing point: The freezing point of a liquid may be defined as the temperature at which solid and the liquid states of the same substance have the same vapour pressure. When a non-volatile solute is added to a solvent, the freezing point of the solution is always less than the freezing point of the pure solvent.

If T_f° is the freezing point of the pure solvent and T_f is the freezing point of the solution, then depression in freezing point,
ΔT_f = T_f° – T_f = K_f. m
where K_f = molal depression constant or cryoscopic constant
m = molality of the solution

Molal depression constant (K_f) is the depression in freezing point produced when 1 mole of solute is dissolved in 1000 g of the solvent.

Molar mass of solute from depression in freezing point may be calculated as
M_B = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{W}_{\mathrm{B}} \times 1000}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{W}_{\mathrm{A}}}\)

The molal depression constant is
K_f = \(\frac{\mathrm{RT}_{\mathrm{f}}^{\circ} \mathrm{M}}{\Delta \mathrm{H}_{\mathrm{t}} \times 1000}\)
or
= \(\frac{R T_{f}^{\circ} f}{\Delta h_{f} \times 1000}\)
where R is gas constant, Tf° is the freezing point of the solvent, M is the molar mass and ΔHf is the enthalpy of fusion of the solvent, Δhf is the enthalpy of fusion per gram and is

Δh_f = \(\frac{\Delta \mathrm{H}_{\mathrm{f}}}{\mathrm{M}}\)

Diagram showing ΔT_f depression of the freezing point of a solvent in a solution.

4. Osmotic pressure: The phenomenon of the flow of solvent through a semi-permeable membrane from pure solvent to the solution ‘ is called osmosis. The osmotic pressure may be defined as the excess pressure which must be applied to a solution to prevent the passage of solvent into it through a semi-permeable membrane. The osmotic pressure for a solution (TC) is
π = c RT
where c is the molar concentration, R is the gas constant and T is the temperature.

Molar mass of a solute from the osmotic pressure may be calculated as:
MB = \(\frac{W_{B} R T}{V \times \pi}\)

→ Isotonic solutions: The solutions having the same osmotic pressure are called isotonic.

→ Abnormal Molar Masses: Colligative properties depend upon the number of solute particles. Therefore, in case of those solutions which undergo dissociation or association in solution, the colligative properties will be different
Van t Hoff factor = \(\frac{\text { Observed colligative property }}{\text { Normal value of colligative property }}\)
= \(\frac{\pi_{\text {obs }}}{\pi_{\text {nor }}}=\frac{\Delta \mathrm{T}_{\mathrm{b}(\mathrm{obs})}}{\Delta \mathrm{T}_{\mathrm{b}(\mathrm{nor})}}=\frac{\Delta \mathrm{T}_{\mathrm{f}(\mathrm{obs})}}{\Delta \mathrm{T}_{\mathrm{f}(\text { nor })}}\)

→ The principle of measuring osmotic pressure: The pressure in excess of atmospheric pressure that must be applied to the solution to prevent it from rising in the tube is the osmotic pressure. This will also be equal to”hydrostatic pressure of the liquid column of height, h.

Since colligative property is inversely proportional to the molar mass of the solute, therefore,
i = \(\frac{\text { Normal molar mass }}{\text { Observed molar mass }}\)

∴ Observed Osmotic pressure, π = i × \(\frac{n}{V}\) RT
Observed elevation in B.Pt. ΔT_b = i × K_b × m
Observed depression in F.Pt. ΔT_f = i × K_f × m where m = molality of the solution

Reverse Osmosis and water purification: The direction of Osmosis can be reversed if a pressure larger than the osmotic pressure is applied to the solution, side. That is, now the pure solvent flows out of the solution tiìrough the semi-permeable membrane (SPM).

This phenomenon is called Reverse Osmosis and is of great utility. Reverse osmosis is used for the Desalination of seawater. The pressure required for reverse osmosis is quite high and a workable porous membrane is a film of cellulose acetate placed over suitable support. Cellulose acetate is permeable to water but impermeable to impurities and ions present in seawater.

Reverse osmosis occurs when a pressure larger than the osmotic pressure is applied to the solution.

By going through these CBSE Class 12 Chemistry Notes Chapter 1 The Solid State, students can recall all the concepts quickly.

The Solid State Notes Class 12 Chemistry Chapter 1

A solid is defined as that form of matter which possesses rigidity and hence possesses a definite shape and a definite volume.

The following are the characteristic properties of the solid-state:

1. They have definite mass, volume, and shape.
2. Intermolecular distances are short.
3. Intermolecular forces are strong.
4. Their constituent particles (atoms, molecules, or ions) have fixed positions and can only oscillate about their mean positions.
5. They are incompressible and rigid.

Solids can be classified into two classes:
1. Crystalline Solids: The substances whose constituents are arranged in a definite orderly arrangement are called crystalline solids. For example, NaCl, S, diamond, sugar, etc. The crystalline substances have sharp melting points and have physical properties different in different directions, i.e., crystalline substances are ANISOTROPIC. They have long-range and short-range orders.

2. Amorphous Substances: The substances whose constituents are not arranged in an orderly arrangement are called amorphous substances. For example, glass, rubber, fused silica, plastics, etc. They do not have sharp melting points and their physical properties are the same in all directions, i.e., there are ISOTROPIC. They have short-range orders.

The difference in their characteristics are:

Classification of Crystalline Solids:
1. Molecular solids: These solids have molecules as constituent particles.

They are further subdivided into.
→ Non-polar molecular solids: They comprise either atoms, e.g., argon and helium, or the molecules formed by non-polar covalent bonds, for example, -H₂, Cl₂, and I₂. They are held by weak dispersion forces or London forces. These solids are soft and non-conductors of electricity. They have low melting points and are usually liquids or gases at room temperature and pressure.

→ Polar molecular solids: The molecules of substances like HCl and SO₂ etc. are formed by polar covalent bonds. The molecules in such solids are held together by relatively stronger dipole-dipole interactions. They are soft solids and non-conductors of electricity. Their melting points are higher than non-polar molecular solids. They are mostly liquids and gases at room temperature and pressure. Solid SO₂ and solid NH₃, are some of the examples of such solids.

→ Hydrogen bonded molecular solids: The molecules of such solids contain polar-covalent bonds between H and F, O or N atoms. Strong hydrogen bonds bind the molecules of such solids like H₂O (ice). They are non-conductors of electricity. Generally, they are volatile liquids or soft solids under room temperature and pressure.

2. Ionic Solids: They comprise ions. They are formed by three-dimensional arrangements of cations and anions bound by strong Coulombic forces. These solids are hard and brittle. They have high melting and boiling points. Since ions are not free to move they are electrical insulators in the solid-state. These ions become mobile in molten or aqueous states. Hence they conduct electricity in their molten or aqueous state.

3. Metallic Solids: Metals are an orderly collection of positive ions (kernels) surrounded by and held together by a sea of mobile or free electrons. These mobile electrons are responsible for the high electrical and thermal conductivity of metals. They are also responsible for the color and luster of metals. Metals are highly malleable and ductile.

4. Covalent or Network Solids: A wide variety of crystalline solids of non-metals results from the formation of covalent bonds between adjacent atoms throughout the crystal. They are giant-sized molecules. Covalent bonds are strong and directional in nature. Such solids are hard and brittle. They have extremely high melting points and even decompose before melting. They are insulators and do not conduct electricity. Diamond and silicon carbide (SiC) are typical examples of such solids. Graphite is soft and conductor of electricity.

The different properties of the four types of solids are listed in the table below:
Crystal Lattices and Unit Cells: A regular three-dimensional arrangement of points in space is called a Crystal Lattice.

There are only 14 possible three-dimensional lattices. These are called Bra Vais Lattices.

Characteristics of a crystal lattice

1. Each point in a lattice is called a lattice point or lattice site.
2. Each point in a crystal lattice represents one constituent particle which may be an atom, molecule, or ion.
3. Lattice points are joined by straight lines to bring out the geometry of the lattices.

Unit Cell is the smallest portion of a crystal lattice which, when repeated in different directions venerates the entire lattice.

Table: Different Types Of Solids:

A unit cell is characterized by

1. Its dimensions along the three edges a, b and c. These edges may or may not be mutually perpendicular.
2. Angles between the edges, α (between b and c), β (between a and c), and γ (between a and b). Thus a unit cell is characterized by 6 parameters: a, b, c, α, β and γ.

These parameters of a typical unit cell are shown in the figure below:

Illustration of parameters of a unit cell

Primitive And Centered Unit Cells:
Unit cells can be broadly divided into two categories, primitive and centered unit cells.
1. Primitive Unit Cells: When constituent particles are present only on the corner positions of a unit cell, it is called a primitive unit cell.

2. Centered Unit Cells: When a unit cell contains one or more constituent particles present at positions other than corners in addition to those at comers, it is called a centered unit cell.

Centered unit cells are of three types:
(a) Body-Centered Unit Cells: Such a unit cell contains one constituent particle (atom, molecules, or ion) at its body center beside the ones that are at its corners.

(b) Face-Centered Unit Cells: Such a unit cell contains one constituent particle present at the center of its face, besides the ones that are at its corners

(c) End-Centered Unit Cells: In such a unit cell, one constituent particle is present at the center of any two opposite faces besides the ones present at its corners.

In all, there are seven types of primitive unit cells.

Table 1.2: Seven primitive unit cells and their possible variations as centered units

Unit Cells Of 14 Types Of Bra Vais Lattices:

→ The three cubic lattices: all sides of name length angles between faces all 90°

→ The two tetragonal: one side different in length to the other two angles between faces all 90°

→ The four orthorhombic lattices: unequal sides; angles between faces all 90°

→ The two monoclinic lattice: unequal sides; two faces have angles different to 90°

Number Of Atoms In A Unit Cell:
1. Primitive Cubic Unit Cell: Primitive cubic unit cell has atoms only at its corner. Each atom at a comer is shared between eight adjacent unit cells as shown in the figure below, four-unit cells in the same layer and four-unit cells of the upper (or lower) layer. Therefore only l /8th of an atom (molecule or ion) actually belongs to a particular unit cell.

In all, since each cubic unit cell has 8 atoms on its corners, the total number of atoms in one unit cell is 8 × \(\frac{1}{8}\) = 1 atom.

In a simple cubic unit cell, each corner atom is shared between 8 unit cells.

2. Body-Centered Cubic Unit Cell: A body-centered cubic (bcc) unit cell has an atom at each of its corners and also one atom at its body center. Fig. depicts such a structure.

(a) open structure
(b) space-filling model and
(c) the unit cell with portions of atoms actually belonging to it.

It can be seen that the atom at the body center wholly belongs to the unit cell in which it is present. Thus in a body-centered cubic (bcc) unit cell:

1. 8 corners × \(\frac{1}{8}\) per corner atom = 8 × \(\frac{1}{8}\) = 1 atom
2. 1 body centre atom = 1 × 1 = 1 atom
   ∴ Total number of atoms per unit cell = 2 atoms

3. Face Centered Cubic unit cell: A face-centered cubic (fee) unit cell contains atoms at all the comers and at the center of all the faces of the cube. Each atom located at the face-center is shared between two adjacent unit cells and only \(\frac{1}{2}\) of each atom belong. to a unit cell. The figure below depicts such a structure.

(a) open structure
(b) space-filling model and
(c) the unit cell with portions of atoms actually belonging to it.

Thus in a face-centered cubic face unit cell.

1. 8 corners × \(\frac{1}{8}\) per corner atom = 8 × \(\frac{1}{8}\) = 1 atom
2. 6 face-centered atoms × \(\frac{1}{2}\) atom per unit cell = 6 × \(\frac{1}{2}\) = 3 atoms
   ∴ Total number of atoms per unit cell = 4 atoms

Close Packing Of Particles:
There are two common types of close packing of particles in a crystalline substance.
→ Hexagonal Close-Packing: This type of packing is referred to as the ABABA arrangement.

→ Cubic Close-Packing: This type of packing is referred to as

ABC ABC arrangement. In both types of packing, 74% of the available space is occupied by spheres.

Interstitial Sites: Two important interstitial sites are:
1. Tetrahedral Sites: When a sphere in the second layer is placed above three spheres that are touching each other, a tetrahedral site is formed. There are two tetrahedral sites for each sphere.

2. Octahedral Site: This type of site is formed at the center of six spheres and is produced by two sets of equilateral triangles which point in opposite directions. There is one octahedral site for each sphere.

Coordination Number And Radius Ratio: The ratio of the radius of the cation to the radius of an anion is called the Radius Ratio.
Radius ratio =\(\frac{\gamma_{+}}{\gamma}\); where γ+: radius of cation
γ-: radius of anion

→ It is very important to determine the structure of IONIC SOLIDS like Na⁺ Cl^–, Cs₄Cl^–, etc.

→ The number of spheres that are touching a given sphere is called the Coordination Number.

→ It may be remembered that coordination numbers of 4,6,8 and 12 are very common in various types of crystals.

Radius’Ratios in Crystals

It may be mentioned here that, although a large number of ionic substances obey this rule, there are many exceptions to this rule.

Structure of Sodium Chloride (NaCl) Rock-Salt Structure: It has a cubic closed packed structure i.e. face-centered cubic.

1. The Na⁺ ions (represented by o) occupy the octahedral holes in the ccp lattice of Cl^– ions (represented by •)
2. Each Na⁺ is surrounded by 6 Cl^– and vice-versa.
3. Na⁺ and Cl^– have 6: 6 fold coordination.

Table 1.3: Some Cubic Ionic Solids

Caesium Chloride (CsCl) Structure

1. In this structure, the Cl^– ions are at the comers of a cube whereas Cs₄ ion is at the center of the cube or vice versa as shown.
2. This structure has 8: 8 coordination, i.e., each Cs⁺ ion is touching eight Cl^– ions, and each Cl^– ion is touching eight Cs⁺ ions.
3. For exact fitting of Cs ions in, the cubic voids the ratio \(\frac{\mathrm{r}_{\mathrm{Cs}^{+}}}{\mathrm{r}_{\mathrm{Cl}^{-}}}\) should he equal to 0.732, however, actually the ratio is slightly larger (0.932). Therefore, packing of C1 ions slightly opens up to accommodate Cs4 ions.
4. The unit cell of caesium chloride has one Cs+ ion and one Cl~ ion as calculated below:
   .No. of Cl- ions = 8 (At corners) × \(\frac{1}{8}\) = 1
   No. of Cs+ ions = 1 (At the body centre) × 1 = 1
   Thus, no. of CsCl units per unit cell is 1.

Examples of the compounds having this type of structure are CsBr, Csl, TICl, and TIBr.

Cesium chloride structure

It may be mentioned here that temperature and pressure also affect the structure of an ionic solid. For example, at ordinary temperatures and pressures, chlorides, bromides, and iodides of lithium, sodium, potassium, and rubidium possess the NaCl structure with 6: 6 coordination.

It is observed that on the application of high pressure they transform to the CsCl structure with 8: 8 coordination. Thus, high pressure increases the coordination number. Ort the other hand, CsCl on heating transforms to the NaCl structure at 760 K. Thus, at higher temperature coordination number decreases.

Point Defects in Crystals: Ideal crystals with the perfect arrangement of constituents are found only at 0°K. Above this temperature, all crystalline solids have some defects in the arrangement of their unit. An ideal crystal of A⁺ B^– type may be represented as shown in Fig.

Ideal Crystal A⁺ B^–

Defects in the crystals may give rise to
(A) Stoichiometric and
(B) Nonstoichiometric structures

(A) Stoichiometric structures: The compound A⁺ B^– is stoichiometric if it contains an equal number of ions A⁺ and B^– as suggested by the chemical formula of the compound. There are three types of defects in stoichiometric structures:
1. Schottky Defect. This defect consists of vacancies at cation sites and an equal number of vacancies at anion sites. It is predominant in compounds with high coordination numbers and where the ions are of similar size. ‘

2. Frenkel Defect. This defect consists of vacancies at cation sites in which the cation moves to another position in between two layers called interstitial sites. This defect is most predominant in compounds which have low coordination number and ions of different sizes.

3. Interstitial Defect: When some constituent particles occupy an interstitial site the crystal is said to have an interstitial defect. This defect increases the density of the substance.

(B) Nonstoichiometric Compounds: The compounds in which the ratio of the number of atoms of A⁺ to the number of atoms of B^– does not correspond to a simple whole number as suggested by the formula, are called nonstoichiometric compounds.

The nonstoichiometric defects are of two types:
1. Metal excess defects. In these defects, positive ions are in excess and arise due to.
(a) Anion vacancies: Vacancies at anion sites and their electrons remain trapped.

(b) Cation occupying Interstitial sites: Excess cations are present in interstitial sites and an equal number of electrons trapped.

2. Metal deficient defects. This arises due to
(a) Cation vacancies: Vacancies at cation sites and the extra negative charge is balanced by extra charge (higher oxidation state) of an equal number of some cations.

(b) Anion occupying Interstitial sites: Excess anions are present in interstitial sites and the corresponding increase in negative charge is balanced by oxidation of an equal number of cations to higher oxidation states.

1. Anion vacancy and electron remain trapped.
2. Cation occupying the interstitial site and electron trapped

2. (i) Cation vacancy and one A⁺ changes to A²⁺ . 2. (ii) Anion occupying the intertidal site and one A⁺ changes to A²⁺

Non-Stoichiometric Structures:
The examples of non-stoichiometric defects are in the crystals of FeO where the composition is Fe_0.93O to Fe_0.96O. This behavior is mostly found in Transition metals compounds. Electrons trapped in anionic vacancies are referred to as F-CENTRES [from the farbe-the German word for color]

It may be mentioned here that metal excess compounds and metal deficient compounds both act as semiconductors. Metal excess compounds conduct electricity through normal electron conduction mechanisms and are therefore n-type semiconductors. Metal deficient compounds conduct electricity through a positive hole conduction mechanism and are therefore p-type semiconductors.

Point Defects due to the Presence of Foreign Atoms:
So far we have discussed point defects where there are no foreign atoms. Foreign atoms can occupy interstitial or substitutional sites in a crystal. Solid solutions of group 13 or group 15 impurities with group 14 elements such as silicon or germanium are of great interest in the electronic industry as they are used to make transistors.

The group 13 elements such as AI and Ga and the group 15 elements such as P and As form substitutional solid solutions with Si and Ge. The group 15 elements have five valence electrons. After forming the four covalent bonds with the group 14 elements, one excess electron is left on them. The excess electrons give rise to electronic conduction (n-type conduction).

The group 13 elements have only three valence electrons. They combine with group 14 elements resulting in the formation of an electron-deficient bond or a hole. These holes give rise to positive hole conduction (p-type conduction). Silicon and germanium doped with group 13 or group, 15 elements impurities act as semi-conductors and have fairly high electrical conductivity. This type of conduction is known as extrinsic / conduction.

Introduction of a cation vacancy in NaCl by substitution of Na⁺ with Sr²⁺ ion.

Defects in the ionic solids may be introduced by adding impurity ions. If the impurity ions have a different valence state than that of the host ions, vacancies are created. For example, the addition of SrCl₂ to NaCl yields solid solutions where the divalent cation occupies Na⁺ sites and produces cation vacancies equal to the number of the divalent ions occupying substitutional sites. Similarly, AgCl crystals can be doped with CdCl₂ to produce impurity defects in a like-wise manner.

Electrical Properties: Solids exhibit an amazing range of electrical conductivities, extending over 27 orders of magnitude ranging from 10^-20 to 10⁷ ohm^-1 m^-1. Solids can be classified into three types on the basis of their conductivities.

1. Conductors: The solids with conductivities ranging between 10⁴ to 10⁷ ohm^-1 m^-1 are called conductors. Metals have conductivities in the order of 107 ohm’m1 and are good conductors.
2. Insulators: These are the solids with very low conductivities ranging between 10^-20 to 10^-10 ohm^-1 m^-1.
3. Semiconductors: These are the solids with conductivities in the intermediate range from 10^-6 to 10⁴ ohm^-1 m^-1.

Conduction of Electricity in Metals: A conductor may conduct electricity through the movement of electrons or ions. Meta (lie conductors belong to the former category and electrolytes to the latter.

Metals conduct electricity in solid as well as in the molten state. The conductivity of metals depends upon the number of valence electrons available per atom. The atomic orbitals of metal atoms from molecular orbitals are so close in energy to each other as to form a band. If this band is partially filled or it overlaps with a higher energy unoccupied conduction band, then electrons can flow easily under an applied electric field and the metal shows conductivity (Fig (a) below).

If the gap between the filled valence band and the next higher unoccupied band (conduction band) is large, electrons cannot jump to it and such a substance has very small conductivity and it behaves as an insulator. (Fig. (b) below)

Distinction among (a) metals, (b) insulators and (c) semi-conductors.
In each case, an unshaded area represents a conduction band.

Conduction of Electricity in semiconductors: In the case of semiconductors, the tire gap between the valence band and conduction band is small (Fig. c). Therefore, some electrons may jump to the conduction band and show some conductivity. The electrical conductivity of semiconductors increases with rising temperature since more electrons can jump to the conduction band. Substances like silicon and germanium show this type of behavior and are called intrinsic semiconductors.

The conductivity of these intrinsic semiconductors is too low to be of practical use. Their conductivity is increased by adding an appropriate amount of suitable impurity. This process is called doping. Doping can be done with an impurity that is electron-rich or electron deficit as compared to the intrinsic semiconductor silicon or germanium. Such impurities introduce electronic defects in them.

Magnetic Properties: Solids can be classified into different types depending upon their behavior towards magnetic fields. The substances which are weakly repelled by a magnetic field are called diamagnetic substances. For example, TiO₂ and NaCl. Diamagnetic substances have all their electrons paired.

The substances which are weakly attracted by a magnetic field are called paramagnetic substances. These substances have permanent magnetic dipoles due to the presence of some species (atoms, ions, or molecules) with unpaired electrons. The paramagnetic substances lose their magnetism in the absence of a magnetic field. For example, TiO, VO, and CuO.

The substances which are strongly attracted by a magnetic field are called ferromagnetic substances. These substances show permanent magnetism even in the absence of a magnetic field. Some examples of ferromagnetic solids are iron, cobalt, nickel, and CEO.

Ferromagnetism arises due to the spontaneous alignment of magnetic moments of ions or atoms in the same direction. Alignment of magnetic moments in opposite direction in a compensatory manner and resulting in a zero magnetic moment (due to an equal number of parallel and antiparallel magnetic dipoles) give rise to antiferromagnetism.

For example, MnO, Mn₂O₃, and MnO₂ are antiferromagnetic. Alignment of magnetic moments in opposite directions resulting in a net magnetic moment (due to an unequal number of parallel and antiparallel magnetic dipoles) gives rise to ferrimagnetism.

For example, FeX > 4 is ferrimagnetic.

Alignment of magnetic dipoles in (a) ferromagnetic, (b) anti-ferromagnetic, and (c) ferrimagnetic substances.

Ferromagnetism and paramagnetic substances change into I paramagnetic substances at higher temperatures due to the randomization of spins. Fe₃O₄ which is ferrimagnetic at room temperature becomes paramagnetic at 850 K.

By going through these CBSE Class 12 Biology Notes Chapter 16 Environmental Issues, students can recall all the concepts quickly.

Environmental Issues Notes Class 12 Biology Chapter 16

→ An increase in the human population is exerting tremendous pressure on our natural resources and is also contributing to pollution of air, water, and soil.

→ Pollution is referred to any undesirable change in physical, chemical, or biological characteristics of air, land, water, or soil. The agents that bring about such undesirable change are called pollutants. To control environmental pollution, the Government of India has passed the Environmental (Protection) Act, 1986. This Act is to protect the quality of the environment.

→ Air pollution primarily results from the burning of fossil fuel, e.g., coal and petroleum, in industries and in automobiles. Air pollution is harmful to both animals and plants. Strict measures should be taken to keep our air clean.

→ The most common source of pollution of water bodies is domestic sewage. It reduces dissolved oxygen but increases biochemical oxygen demand of receiving water.

→ Domestic sewage is rich in nitrogen and phosphorus. It causes eutrophication and nuisance algae bloom.

• Industrial water waste is rich in toxic chemicals such as heavy metals and organic compounds. It can harm living organisms.
• Municipal solid wastes also can create problems.

→ A few toxic substances often present in industrial wastewaters can undergo biological magnification in the aquatic food chain Increase in concentration of the toxicant at successive trophic levels refers to biomagnification. This is due to a toxic substance accumulated by an organism that cannot be metabolized or excreted, and thus, passes on the next higher trophic level. This phenomenon is well known for mercury arid DDT.

Biomagnification of DDT in an aquatic food chain

Eutrophication refers to the natural aging of a lake by the biological enrichment of its waters. Wastewater including sewage can be treated in an integrated manner, by utilizing a mix of artificial and natural processes. Disposal of hazardous waste like defunct ships, radioactive wastes, and e-wastes requires additional effort.

→ Soil pollution is due to agricultural chemicals such as pesticides, insecticides, etc., and leachates from solid wastes deposited over it.

→ The major environmental issue of global nature is the increasing greenhouse effect. It is a naturally occurring phenomenon that is responsible for heating of earth’s surface and atmosphere. Without the greenhouse effect, the average temperature at the surface of the earth would have been -18°C rather than the present average of 15°C. Increased pollution on the earth is increasing the greenhouse effect, which is warming the earth.

→ The enhanced greenhouse effect is mainly due to increased emission of carbon dioxide, methane, nitrous oxide, CFCs, and deforestation. These pollutants and depleting the ozone layer. The effects may be changed in rainfall pattern, increase in global temperature and besides deleteriously will affect living organisms. The ozone layer in the stratosphere is depleting due to the emission of CFCs. The ozone layer protects us from the harmful effects of the UV rays of the sun. The depletion of the ozone layer can increase the risk of skin cancer, mutation, and other disorders.

→ Pollution: Undesirable change in physical. chemical or biological characteristics of air, land, water, or salt.

→ Pollutants: Agents which bring undesirable change in the abiotic components of the environment.

→ CNG: Compressed Natural Gas.

→ Noise: Undesirable high level of sound.

→ BOD: Biochemical Oxygen Demand.

→ Biomagnification: Increase in the concentration of the toxicant at successive trophic levels.

→ Eutrophication: Refers to the natural aging of a lake by biological enrichment of its water.

→ Solid wastes: Everything that goes out ¡n trash.

→ Municipal solid waste: Waste from homes, offices, hospitals, schools, etc. that are collected and disposed of by the municipality.

→ Electronic wastes: Irreparable computer and other electronic goods.

→ CFCs: Chlorofluorocarbons.

→ Snow blindness: Inflammation of the cornea.

→ Soil erosion: Removal of topsoil by natural agents such as wind, water, etc.

→ Reforestation: Process of restoring a forest.

By going through these CBSE Class 12 Biology Notes Chapter 15 Biodiversity and Conservation, students can recall all the concepts quickly.

Biodiversity and Conservation Notes Class 12 Biology Chapter 15

→ Biodiversity refers to the sum total of diversity that exists at all levels of biological organization.

→ Biodiversity is the term popularized by sociobiologist Edward Wilson to describe the combined diversity at all the levels of biological organization.

Some important are as follows:

• Genetic diversity
• Species diversity
• Ecological diversity

→ More than 1.5 million species have been recorded in the world, but there might still be more than 6 million species on earth waiting to be discovered and named. Of the named species >70 percent are animals of which 70 percent are insects. Among all the species, combined, the group fungi have more than all vertebrate species combined. In India, more than 45,000 species of plants and twice as many species of animals are found. Thus, it is one of the 12 mega diversity countries of the world.

Representing global biodiversity: proportional number of species of major taxa of plants. invertebrates and vertebrates

→ The diversity of plants and animals is not uniform throughout the world. For many groups of animals or plants, there are interesting patterns in diversity, the most well-known being th£ latitudinal gradient in diversity. Tropics harbor more species than temperate or polar areas. Colombia located near the equator has nearly 1,400 species of birds while New York at 41°N has 105 species and Greenland at 71°N only 56 species.

→ The relation between species richness and area for a wide variety of taxa (angiosperm plants, birds, bats, freshwater fishes) turns out to be a rectangular hyperbola (Fig.).

Showing species-area relationship on a logarithmic scale. the relationship is a straight line described by the equation.
logS = log C + Z log A
where S = species richness
A = area
Z = slope of the line
C = Y-intercept

→ Species richness contributes to the well-being of an ecosystem. Rich biodiversity is hot only essential for ecosystem health but imperative for the very survival of the human race on this planet.

→ Conserving biodiversity is narrowly utilitarian, broadly utilitarian, and ethical. Besides the direct benefits (food, fiber, firewood, pharmaceuticals, etc.) there are many indirect benefits we receive through the ecosystem. Services such as pollination, pest control, climate moderation, and flood control. It is our moral responsibility to take good care of the earth’s biodiversity and pass it on in good order to our next generation.

→ There are four major causes of biodiversity losses.
There are:

• Habitat loss and fragmentation
• Over-exploitation
• Alien species invasions
• Co-extinctions

→ Biodiversity conservation can be taken in situ and ex-situ. In in. situ conservation, the endangered species are protected in their habitat so that the entire ecosystem is protected. Ex-situ conservation methods include protective maintenance of threatened species in zoological parks and botanical gardens, in vitro fertilization, cryopreservation of gametes, and tissue culture propagation.

→ Biodiversity: Totality of genes. species and ecosystems of a region.

→ Conservation: Preservation of biodiversity. It may be in situ or ex-situ.

→ Ecological diversity: Variation of habitats, community types, and abiotic environments present in a given area.

→ Extinction: The complete disappearance of any species from the biosphere by natural causes.

→ Exotic species: Species introduced into an ecosystem to which they are not native.

→ Fragmentation: The process of reduction of habitat into smaller scattered patches.

→ Genetic diversity: Total number of genetic characteristics either expressed or in all the individuals of a particular area.

→ Species diversity: The diversity at the species level.

→ Hot spots: Areas that are extremely rich in species, and under constant threat.

→ Endemism: Species confined to that region and not found anywhere else.