CBSE Notes

By going through these CBSE Class 11 Physics Notes Chapter 7 Systems of Particles and Rotational Motion, students can recall all the concepts quickly.

Systems of Particles and Rotational Motion Notes Class 11 Physics Chapter 7

→ C.M. of a body or a system may or may not lie inside the body.

→ The momentum of the C.M. of the system remains constant if the external force acting on it is zero.

→ C.M. of the system moves with a constant velocity if the external force on the system is zero.

→ Only the angular component of the force gives rise to torque.

→ Both angular momentum and torque are vector quantities.

→ The rotatory cum translatory motion of a ring, disc, cylinder, spherical shell, or solid sphere on a surface is called rolling.

→ The axis of rotation of the rolling body is parallel to the plane on which it rolls.

→ When the angular speed of all the particles of the rolling body is the same, it is called rolling without slipping.

→ The linear speed of different particles is different, although the angular speed is the same for all the particles.

→ K.E. is the same for all bodies having the same m, R, and ω.

→ Total energy and rotational kinetic energy are maximum for the ring and minimum for the solid sphere.

→ For ring K_r = K_t, K_r = \(\frac{1}{2}\) K_t for disc, K_r = 66%Kt for spherical shell and for solid sphere K_r = 40% of K_t.

→ The body rolls down the inclined plane without slipping only when the coefficient of limiting friction (p) bears the following relation:
µ ≥ (\(\frac{\mathrm{K}^{2}}{\mathrm{~K}^{2}+\mathrm{R}^{2}}\)) tan θ

→ The relative values of p for rolling without slipping down the inclined plane are as follows :
μ_ring > μ_shell > μ_disc > μ_{solid sphere}

→ When a body roll Is without slipping, no work is done against friction.

→ A body may roll with slipping if friction is less than a particular value and it may roll without slipping if the friction is sufficient.

→ M.I. is not a scalar quantity because for the same body its values are different for different orientations of the axis of rotation.

→ M.I. is defined w.r.t. the axis of rotation.

→ M.I. is not a vector quantity because the clockwise or anticlockwise direction is not associated with it.

→ The radius of gyration depends on the mass and the position of the axes of rotation.

→ M.I. depends on the position of the axis of rotation.

→ The theorem of ⊥ar axes is applicable to thin laminae like a sheet, disc, ring, etc.

→ The theorem of || axes is applicable to all types of bodies.

→ M.I. about the axis in a particular direction is least when the axis of rotation passes through the C.M.

→ A pair of equal and opposite forces with different lines of action is known as a couple.

→ A body may be in partial equilibrium i.e. it may be in translational. equilibrium and not in rotational equilibrium or vice-versa.

→ If the sum of forces is zero, it is said to be in translational equilibrium. 0 If the sum of moments of forces about C.G. is zero then it is said to be in rotational equilibrium.

Important Formulae:
→ Position vector of C.M. of a system of two particles is
R_cm = \(\frac{\mathrm{m}_{1} \mathbf{r}_{1}+\mathrm{m}_{2} \mathbf{r}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\)

→ Position vector of C.M of a system of two particles of equal masses is
R_cm = \(\frac{\mathbf{r}_{1}+\mathbf{r}_{2}}{2}\)

→ Torque acting on a particle is given by
τ = r × p

→ Angular momentum is given by
L = r × p
or
L = mv r = Iω = mr² ω

→ τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}\)

→ τ = Iα

→ I₁ω₁ = I₂ω₂
or
\(\frac{I_{1}}{T_{1}}=\frac{I_{2}}{T_{2}}\)

→ K.E. of rotation, K_t = \(\frac{1}{2}\)Iω²

→ Power in rotational motion, P = τω

→ According to theorem of perpendicular axes,
I_z = I_x + I_y

→ According to theorem of || axes, 1 = I_c + mh²

→ K.E. of a body rolling down an inclined plane is given by
E = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\) Iω² = K_t + K_r

→ \(\frac{K_{r}}{K_{t}}=\frac{\frac{1}{2} I \omega^{2}}{\frac{1}{2} m v^{2}}=\frac{\frac{1}{2} m K^{2} \omega^{2}}{\frac{1}{2} m v^{2}}\)

= \(\frac{\mathrm{K}^{2} \omega^{2}}{\mathrm{R}^{2} \omega^{2}}=\frac{K^{2}}{\mathrm{R}^{2}}\)

→ \(\frac{\mathrm{K}_{\mathrm{r}}}{\mathrm{E}}=\frac{\frac{1}{2} \mathrm{mK}^{2} \omega^{2}}{\frac{1}{2} \mathrm{~m}\left(\mathrm{R}^{2}+\mathrm{K}^{2}\right) \omega^{2}}=\frac{\mathrm{K}^{2}}{\mathrm{~K}^{2}+\mathrm{R}^{2}}\)

→ \(\frac{K_{t}}{E}=\frac{R^{2}}{R^{2}+K^{2}}\)

→ If inclined plane is smooth, then the body will slide down and on reaching the bottom, its sliding velocity (V_s) is given by
V_s = \(\sqrt{2 \mathrm{gh}}\) and acceleration is a_s = g sin θ.

→ For rough inclined plane :
V_r = \(\frac{\sqrt{2 \mathrm{gh}}}{\sqrt{1+\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}}}\)

→ The acceleration of the body rolling down the inclined plane is
a_r = \(\frac{g \sin \theta}{\sqrt{1+\frac{K^{2}}{R^{2}}}}\)

→ Time taken to reach the bottom is t_s = \(\sqrt{\frac{2 l}{a_{s}}}\) and t_r = \(\sqrt{\frac{2 l}{a_{r}}}\)

→ If a particle of mass m is moving along a circular path of radius r with acceleration ‘a’, then
τ = mr² α
Where α = \(\frac{a}{r}\)

→ The value of \(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\) for different bodies are as follows:

By going through these CBSE Class 11 Physics Notes Chapter 6 Work, Energy and Power, students can recall all the concepts quickly.

Work, Energy and Power Notes Class 11 Physics Chapter 6

→ The total work done in the uniform speed of a body is zero i.e. if work is done is zero then the speed of the body is uniform.

→ In doing work in stretching or compressing a spring and by a falling body, the variable forces involved are restoring force and force of gravitation.

→ Work is done by a force on a body over a certain displacement.

→ The change in kinetic energy of an object is equal to the work done on it by the net force.

→ No work is done by the force if it acts perpendicular to the displacement of the body.

→ The total mechanical energy of a system is conserved if the forces doing work on it are conservative.

→ Energy can exist in various forms such as mechanical energy, heat energy, light energy, sound energy, etc.

→ The motion of a simple pendulum is an example of the conversion of P.E. into K.E. and vice-versa.

→ A body possesses chemical energy due to the chemical bonding of its atoms.

→ A body possesses heat energy due to the disorderly motion of its molecules.

→ The mass-energy equivalence formula describes energies to all masses (E = mc²) and masses to all energies (\(\frac{\mathrm{E}}{\mathrm{c}^{2}}\) = m)

→ The P.E. which an elevator loses in coming down from an upper story of the building to stop at the ground floor is used up to lift up the counter-poise weight.

→ When a very light body in motion collides with a heavy stationary body in an elastic collision, the lighter one rebounds back with the same speed without the heavy body being displaced.

→ When a body moving with some velocity undergoes elastic collision with another similar body at rest, then there is an exchange of their velocities after collision i.e. first one comes to rest and the second starts moving with the velocity of the first one.

→ 1 J = 10⁷ erg.

→ Joule (J) and erg are the S.I. and C.G.S. units of work and energy. Energy is the capacity of the body to do the work.

→ The area under the force-displacement graph is equal to the work done.

→ Work done by the gravitational or electric force does not depend on the nature of the path followed.

→ It depends only on the initial and final positions of the path of the body.

→ Power is measured in horsepower (h.p.). It is the fps unit of power used in engineering.

→ 1 h.p. = 746 W.

→ Watt (W) is the S.I. unit of power.

→ The area under the force-velocity graph is equal to the power dissipated. Body or external agency dissipates power against friction.

→ If the rails are on a plane surface and there is no friction, the power dissipated by the engine is zero.

→ When a body moves along a circular path with constant speed, its kinetic energy remains constant.

→ K.E. of a body can’t change if the force acting on a body is perpendicular to the instantaneous velocity. ,

→ K.E. is always positive.

→ If a machine gun fires n bullets per second with kinetic energy K, then the power of the machine gun is P = nK.

→ The force required to hold the machine gun in the above case is
F = nv = n \(\sqrt{2 \mathrm{mK}}\)

→ When work is done on a body, it’s K.E. or P.E. increases.

→ When work is done by a body, its P.E. or K.E. decreases.

→ Mass and energy are interconvertible.

→ K.E. can change into P.E. and vice-versa.

→ One form of energy can be changed into other forms according to the law of conservation of energy.

→ When a body falls, its P.E. is converted into its K.E.

→ The collision generally occurs for every small interval of time.

→ Physical contact between the colliding bodies is not essential for the collision.

→ The mutual forces between the colliding bodies are action and reaction pair.

→ Momentum and total energy are conserved during elastic collisions.

→ The collision is said to be elastic when the K.E. is conserved.

→ Inelastic collisions the forces involved are conservative.

→ Elastic collisions, the K.E. or mechanical energy is not converted into any other form of energy.

→ Elastic collisions produce no sound or heat.

→ There is no difference between the elastic and perfectly elastic collisions.

→ In the elastic collisions, the relative velocity before the collision is equal to the relative velocity after collision i.e. u₁ – u₂ = v₂ – v_1.

→ The collision is said to be inelastic when the K.E. is not conserved.

→ Head-on collisions are called one-dimensional collisions.

→ When the momentum of a body increases by a factor n, then its K.E. is increased by a factor n².

→ If the speed of a vehicle is made n-times then its stopping distance becomes n² times.

→ Work: Work is said to be done if a force acting on a body displaces it by some distance along the line of action of the force.

→ Energy: It is defined as the capacity of a body to do work.

→ K.E.: It is defined as the energy possessed by a body due to its motion.

→ P.E.: It is defined as the energy possessed by a body due to its position or configuration.

→ Gravitational P.E.: It is defined as the energy possessed by a body due to its position above the surface of death.

→ Power: It is defined as the time rate of doing work.

→ Work-energy theorem: It states that the work is done by a force acting on a body is equal to the change in its K.E.

→ Law of conservation of energy: Total energy of the universe always remains constant.

→ Instantaneous Power: It is the limiting value of the average power of an agent in a small time interval tending to zero.

→ Mass-energy Equivalence: E = mc².

→ Elastic collision: The collision is said to be elastic if both momentum and the K.E. of the system remain conserved.

→ Elastic collision in one dimension: The collision is said to be one-dimensional if the colliding bodies move along the same straight line after the collision.

→ In-elastic collision: It is defined as the collision in which K.E. does not remain conserved.

→ Transformation of energy: It is defined as the phenomena of change of energy from one form to the other.

→ Coefficient of restitution: It is defined as the ratio of the velocity of separation to the velocity of approach i.e.
e = \(\frac{v_{2}-v_{1}}{u_{1}-u_{2}}\)

→ Moderator: It is defined as a substance used in atomic reactors to slow down fast-moving neutrons to make them thermal neutrons. e.g. graphite and heavy water are moderators

→ 1 eV: It is defined as the energy acquired by an electron when a potential difference of 1 volt is applied
i. e. 1 eV = 1.6 × 10^-19 c × 1 V
= 1.6 × 10^-19 J

Important Formulae:
→ Work done by F in moving a body by S is
W = F . S = FS cos θ

→ P = \(\frac{W}{t}\)

→ Instantaneous power is P = F.v

→ K.E. = \(\frac{1}{2}\)mv².

→ P.E. = mgh.

→ P.E. of a spring is given by = \(\frac{1}{2}\)kx².
where k = force constant, x = displacement i.e. extension or compression produced in the spring. .

→ E = mc².

→ Velocities of the two bodies after collisions are given by
v₁ = \(\frac{m_{1}-\dot{m}_{2}}{m_{1}+m_{2}}\)u₁ + \(\frac{2 m_{2}}{m_{1}+m_{2}}\)u₂
and
v₂ = \(\frac{m_{2}-\dot{m}_{1}}{m_{1}+m_{2}}\)u₂ + \(\frac{2 m_{2}}{m_{1}+m_{2}}\)u₁

→ Power of an engine pulling a train on rails having coefficient of friction p is given by:
P = μ mg v.
where μ = coefficient of friction.
m = mass of train,
v = velocity of train.

→ Power of engine on an inclined plane pulling the train up is
P = (μ cos θ + sin θ)mg v

→ And pulling down the inclined plane is
P = (μ cos θ – sin θ)mg v

→ Work against friction in above cases when the body moves down the inclined plane is W = m.g.(sin θ – μ cos θ)S

→ When body moves up the incline,
W = mg(μ cos θ + sin θ)S

→ % efficiency (n%) = \(\frac{\text { Poweroutput }}{\text { Powerinput }}\) × 100
= \(\frac{\text { Output energy }}{\text { Input energy }}\) × 100

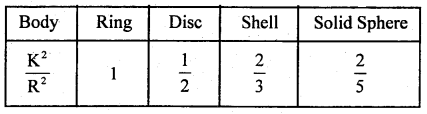
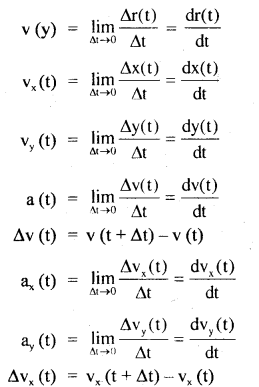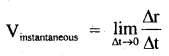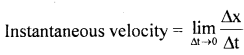By going through these CBSE Class 11 Physics Notes Chapter 5 Law of Motion, students can recall all the concepts quickly.

Law of Motion Notes Class 11 Physics Chapter 5

→ Inertia is proportional to the mass of the body.

→ The force causes acceleration.

→ In the absence of force, a body moves along a straight-line path.

→ If the net external force on a body is zero, its acceleration is zero. Acceleration can be non-zero only if there is a net external force on the body.

→ If a body moves along a curved path, then it is certainly acted upon by a force.

→ C.G.S. and S.I. absolute units of force are dyne and newton (N) respectively and 1 N = 10⁵ dynes.

→ C.G.S. and S.I. gravitational units of force are gm wt. and kg wt. (i.e. kilogram weight) respectively and 1 kg wt = kgf.

→ 1 gm wt = 1 gmf, 1 kg f = 10³ gm f.

→ 1 kg f = 9.8 N.

→ 1 gm f = 1 gm wt = 980 dyne.

→ Impulse = change in momentum.

→ Four types of forces exist in nature, they are gravitational force (F_g), electromagnetic force (F_em), weak force (F_w), and nuclear force (F_n).

→ F_g: F_em: F_w: F_n:: 1: 1025: 1036: 1038.

→ Rocket works on the principle of conservation of linear momentum.

→ Rocket ejects gases backward and as a result, acquires a forward momentum.

→ If Δm is the mass of the gas ejected backward in time At with speed u, then the force acting on the rocket will be:
F = u \(\frac{\Delta m}{\Delta t}\)

→ When a force acting on a particle is always perpendicular to its velocity, then the path followed by the particle is a circle.

→ In a uniform circular motion, the magnitude of velocity always remains constant and only its direction changes continuously.

→ If a body moves with a vertical acceleration a, then its apparent weight is given by:
R = m (g – a)

→ The weight of a body measured by the spring balance in a lift is equal to the apparent weight.

→ The apparent weight of a body falling freely is zero because for it, a = g. It is the case of weightlessness.

→ If the lift falls with a < g, the apparent weight of the body decreases.

→ If the lift accelerates upwards, the apparent weight of the body increases.

→ The true weight of the body = mg.

→ If the lift rises or falls with constant speed, then apparent weight = true weight

→ If the person climbs up along the rope with acceleration ‘a’, then tension in the rope will be T = m (g + a).

→ If the person climbs down along the rope with acceleration ‘a’, then tension in the rope will be T = m (g – a).

→ If the person climbs up or down the rope with uniform velocity, then tension in the string, T = mg.

→ If a body starting from rest moves along a smooth inclined plane of length l, height h and having an angle of inclination 0, then:
1. Its acceleration down the plane is g sin θ.

2. Its velocity at the bottom of the inclined plane will be
\(\sqrt{2 \mathrm{gh}}=\sqrt{2 \mathrm{~g} l \sin \theta}\)

3. Time taken to reach the bottom will be:
t = \(\sqrt{\frac{2 l}{g \sin \theta}}=\left(\frac{2 l^{2}}{g h}\right)^{\frac{1}{2}}\)

= \(\left(\frac{2 \mathrm{~h}}{\mathrm{~g} \sin \theta}\right)^{\frac{1}{2}}=\frac{1}{\sin \theta}\left(\frac{2 \mathrm{~h}}{\mathrm{~g}}\right)^{\frac{1}{2}}\)

4. If the angle of inclination is changed keeping the length constant, then:
\(\frac{\mathrm{t}_{1}}{\mathrm{t}_{2}}=\left(\frac{\sin \theta_{2}}{\sin \theta_{1}}\right)^{\frac{1}{2}}\)

5. If the angle of inclination is changed keeping the height constant, then
\(\frac{\mathrm{t}_{1}}{\mathrm{t}_{2}}=\frac{\sin \theta_{2}}{\sin \theta_{1}}\)

→ A system or a body is said to be in equilibrium when the net force acting on it is zero.

→ If the vector sum of a number of forces acting on a body is zero, then it is said to be in equilibrium.

→ Friction acts opposite to the direction of motion of the body and parallel to the surfaces in contact.

→ Friction depends on the nature of surfaces in contact.

→ Friction is more when the surfaces in contact are rough.

→ Friction is a necessary evil it causes the dissipation of energy. But we need.

→ Friction is of different types such as static friction, kinetic (sliding or rolling) friction, dry friction, wet friction.

→ Static friction is a variable force.

→ The maximum value of static friction is called limiting friction.

→ Static friction is equal and opposite to the force applied to the body.

→ When the applied force is equal to the limiting friction, the body begins to slide.

→ The kinetic friction is less than the limiting friction.

→ The friction on a rolling body is called rolling friction.

→ The rolling friction is less than sliding friction.

→ Friction is a self-adjusting force.

→ The limiting friction is directly proportional to the normal reaction i. e. F ∝ R.

→ The net reactive force acting perpendicular to the surface is called normal reaction (R) and is equal to the force with which the two bodies are pressed against each other.

→ The ratio of limiting friction (F) to the normal reaction (R) is called the coefficient of limiting friction (μ_l) i.e. μ_l = F/R.

→ The limiting friction is independent of the shape or area of surfaces in contact if R = constant.

→ μ_l is a dimensionless constant. It depends on the nature of the surfaces in contact. It is independent of the normal reaction.

→ No work is done against static friction.

→ The kinetic friction opposes the motion of the body.

→ Static friction is the frictional force that comes into play when a body tends to move on the surface of another body.

→ Static friction is due to the interlocking of microscopic projections on the surface of the body.

→ The change from static to kinetic friction is by a stick and slip process. The slip is a break away from the static condition.

→ Sticking is caused by the second interlocking.

→ Kinetic friction is a constant force.

→ It is independent of the applied force.

→ The coefficient of kinetic friction is equal to the ratio of kinetic friction (F_k) to the normal reaction (R) i.e. μ_k = F_k/R.

→ F_k is independent of the area of contact between two bodies.

→ Work is done against kinetic friction.

→ Coefficient of rolling friction (μ_r) = \(\frac{\mathrm{F}_{\mathrm{r}}}{\mathrm{R}}=\frac{\text { rolling friction }}{\text { normal reaction }}\)

→ μ_r < μ_k < μ_s.

→ The friction between two solid surfaces is called dry friction.

→ The friction between a solid surface and a liquid surface is called wet friction.

→ The dry friction causes squeaking of the surfaces trying to move over each other.

→ The dry friction can also cause pleasant sound e.g. the bow under-going stick and slip motion on the string of violin causes pleasant sound.

→ Friction can be decreased by converting dry friction to wet friction.

→ Friction may increase if the surfaces are highly polished. This happens due to cold welding together of the polished surfaces.

→ The angle between the normal reaction and the resultant force of friction and the normal reaction is called the angle of friction (θ).

→ µ = tan θ i.e. coefficient of friction = tan θ.

→ The angle of the inclined plane at which the body placed on it just begins to slide down is called the angle of repose (α) or angle of sliding.

→ µ = tan α.

→ Also α = θ.

→ When a body rotates, all its particles describe circular paths about a line called the axis of rotation.

→ The centers of circles described by the different particles of the rotating body lie on the axis of rotation.

→ The Axis of rotation is perpendicular to the plane of rotation.

→ For uniform circular motion, we have

1. a_c = v²/r = rω²
2. v = rω
3. a ∝ r

where α = angular acceleration.

→ When a body rotates with uniform velocity, its different particles have centripetal acceleration directly proportional to the radius i.e. a_c ∝ r.

→ There can be no circular motion without centripetal force.

→ Centripetal force can be a mechanical, electrical, or magnetic force.

→ In a uniform circular motion, the magnitude of momentum, velocity, and kinetic energy remains constant.

→ Centrifugal force is the pseudo force that is equal and opposite to the centripetal force. It is directed away from the center along the radius.

→ The centrifugal force appears to act on the agency which exerts the centripetal force.

→ The centrifugal force cannot balance the centripetal force because they act on different bodies.

→ The railway tracks and roads are banked for safe turning. The banking angle θ for safe turning is tan θ = \(\frac{\mathbf{v}^{2}}{r g}\) . Also tan θ = \(\frac{\mathrm{h}}{\mathrm{d}}\)
where d = width of road
h = height of the outer edge of the road above the inner edge

→ Maximum speed of the car without overturning when it moves on a circular banked road of radius r is
u_max = \(\sqrt{\frac{\mathrm{grd}}{\mathrm{h}}}\)
when d = \(\frac{1}{2}\) of the distance between two wheels of the car.

→ When a particle of mass m, tied to a string of length is rotated in a horizontal plane with a speed ‘y’, the tension is given by
T = \(\frac{m v^{2}}{r}\)

→ When the string breaks, the particle moves away from the center but tangentially.

→ K.E. of a body rotating in a vertical plane is different at different points.

→ The angle through which the outer edge of the road track is raised above the inner edge is called the angle of banking of roads/ tracks.

→ For safe going of the vehicle round the circular level road, the required condition is:
μ ≤ \(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\)

→ A simple pendulum oscillates in a vertical plane. It will oscillate only if its motion is in the lower semi-circle.

→ For oscillation, the velocity at the lowest point L must be such that the velocity reduces to zero at points M₁ and M₂.

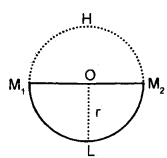
Thus, \(\frac{1}{2}\)mv_e² = mgr
or
v_e = \(\sqrt{2 \mathrm{gr}}\)
i.e v_e ≤ \(\sqrt{2 \mathrm{gr}}\)

→ If v_e > \(\sqrt{2 \mathrm{gr}}\) it will not then oscillate in the lower semi-circle.

→ Minimum velocity that a body should have at the lowest point (L) and highest point (H) of a vertical circle for looping it are
v₁ = \(\sqrt{5 \mathrm{gr}}\) and v₂ = \(\sqrt{\mathrm{gr}}\)
where v₁ and v₂ are velocities at L and H points respectively. Maximum speed with which a vehicle can take a safe turn on a level road is v = \(\sqrt{\mu \mathrm{gr}}\).

→ Maximum speed of the vehicle with which it can take a safe turn on a banked road is given by
v = \(\sqrt{rgθ}\)

→ Sufficient force of friction is there between the tyres of the vehicle and the banked road, then the maximum speed of the vehicle for taking a safe turn is given by

v_max = \(\left(rg\frac{\mu_{\mathrm{s}}+\tan \theta}{1-\mu_{\mathrm{s}} \tan \theta}\right)^{\frac{1}{2}}\)

→ The first law is also called the law of inertia according to which the state of rest or uniform motion of a body remains the same unless acted upon by an external force.

→ The action and reaction always occur in pairs.

→ The position of an event or particle is measured by using a system of coordinates called a frame of reference.

→ There are two types of frame of reference

1. inertial and
2. non-inertial (or accelerated frame of reference).

→ A frame of reference with uniform motion with respect to another inertial frame of reference is also the inertial frame of reference in which the body is situated and obey’s Newton’s law of motion.

→ Inertia: A body at rest or in uniform motion continues in its state unless acted upon by an external force.

→ Force: Force is the action that changes or tends to change the state of rest or uniform motion of a rigid body along a straight line.

→ Rigid body: A body whose various particles move through the same distance parallel to each other under the action of external force i.e. there is no relative motion amongst the various particles of the body under the action of an external force is called a rigid body.

→ Linear momentum (p).: The quantity of motion possessed by a body is called its momentum Mathematically the linear momentum of the body is equal to the product of its mass and velocity i.e.
p = mv

→ Retardation: The quantity of hindrance in the motion of a body is called retardation and the force which retards the body is called retarding force.

→ Newton’s first law of motion: A body continues in its state of rest or uniform motion along a straight line in the absence of external force.

This is called Newton’s first law of motion.
\(\overrightarrow{\mathrm{F}}\) ∞ \(\frac{\mathrm{d}(\overrightarrow{\mathrm{p}})}{\mathrm{dt}}\)
or
\(\overrightarrow{\mathrm{F}}\) = k m\(\overrightarrow{\mathrm{a}}\)

In non-relativistic dynamics \(\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\overrightarrow{\mathrm{a}}\), the acceleration of the body or particle.

When force F, mass m and acceleration arc measured in Newton, kilogram and meter per second respectively. i.e. in S.L units. so that
\(\overrightarrow{\mathrm{F}}\) = m \(\overrightarrow{\mathrm{a}}\)

Its scalar from is F = ma

→ Newton (N): It is the SI unit of measurement of force. One newton is that force that causes an acceleration of 1 ms 2 in a rigid body of mass 1 kg.
∴ 1 N = 1 kg × 1 ms^-2

→ Impulse: The impact of force is called impulse. Mathematically impulse = F × Δt = force × time. So impulse = m(Δv).

→ The inertia of rest: The property of a body to be unable to change its state of rest itself is called the inertia of rest,

→ The inertia of motion: The property of a body by virtue of which it cannot change by itself its state of uniform motion is called inertia of motion.

→ The inertia of direction: The property of a body by virtue of which it cannot change its own direction of motion is called the direction of inertia.

→ Newton’s third law of motion: States that “To every action, there is an equal and opposite reaction.”
F_BA = – F_AB
where F_AB = force exerted on body 8 by body A, and F_BA = force exerted on body A by body B.

→ Law of conservation of linear momentum: The linear momentum of an isolated system of bodies or particles is always conserved, that is it remains constant.

→ Static equilibrium: A body is said to be in static equilibrium if the vector sum of all the forces acting on it is zero. This is a necessary and sufficient condition for a point object only.

→ Lubricants: The substances which are applied to the surfaces to reduce friction are called lubricants.

Important Formulae:
→ Linear momentum of a body of mass m and moving with a velocity v is: p = mv

→ Change in momentum, Δp = m Δ v

→ If two objects of masses M and m have same momentum, then
\(\frac{M}{m}=\frac{v}{V}\)

→ F = ma

→ Resultant of two forces F, and F2 acting simultaneously at angle θ is given by F = F₁ + F₂
The magnitude of F is given by parallelogram law of vectors
F = \(\sqrt{F_{1}^{2}+F_{2}^{2}+2 F_{1} F_{2} \cos \theta}\)

→ The orthogonal components of F and a are:
F = F_xi + F_yj + F_zk
and a = a_xi + a_yj + a_zk

→ Inertial mass, m₁ = \(\frac{\mathrm{F}}{\mathrm{a}}\)

→ Gravitational mass, mg = \(\frac{\mathrm{F}}{\mathrm{g}}\)

→ Impulse I = FΔt = mΔv

→ Newton’s third law of motion:
F₁₂ = – F₂₁
or
m₁a₁ = – m₂a₂

→ Equilibrium of body under three concurrent forces:
F₁ + F₂ + F₃ = 0
Or
F₃ = – (F₁ +F₂)

→ Simple pulley: a = acceleration of masses m₁ and m₂
= \(\left(\frac{m_{2}-m_{1}}{m_{1}+m_{2}}\right)\)
If m₂ > m₁

Tension in the string connecting the two masses and passing over the pulley is given by
T = \(\left(\frac{2 m_{1} m_{2}}{m_{1}+m_{2}}\right)\)g

→ Solving problems using Free Body Diagram Technique:

1. Draw a simple neat diagram of the system as per the given problem.
2. Isolate the object of interest. This is now called a free body.
3. Consider all the external forces acting on the free body and mark them by arrows touching the free body with their line of action clearly represented.
4. Now apply Newton’s second law of motion.
5. In a non-inertial frame consider the pseudo forces like real forces acting on the object in addition to other external forces. The direction of such a force will be opposite to the direction of acceleration of the frame of reference.

By going through these CBSE Class 11 Physics Notes Chapter 4 Motion in a Plane, students can recall all the concepts quickly.

Motion in a Plane Notes Class 11 Physics Chapter 4

→ All physical quantities having direction are not vectors.

→ The following quantities are neither scalars nor vectors: Relative density, density, frequency, stress, strain, pressure, viscosity, modulus of elasticity, Poisson’s ratio, specific heat, latent leat, a moment of Inertia, loudness, spring constant, Boltzman constant, Stefan’s constant, Gas constant, Gravitational constant, Plank’s constant, Rydberg’s constant etc.

→ A vector can have only two rectangular components in a plane and only three rectangular components in space.

→ Vectors cannot be added or subtracted or divided algebraically.

→ Division of two vectors is not allowed.

→ A vector can have any number of components (even infinite in number but a minimum of two components).

→ Two vectors can be added graphically by using head to tail method or by using the parallelogram or triangle law method.

→ A vector multiplied by a real number gives another vector having a magnitude equal to real number times the magnitude of the given vector and having direction same or opposite depending upon whether the number is positive or negative.

→ Multiplication of a vector by -1 reverses its direction.

→ If A + B = C or A + B + C = 0, then A, B and C are in one place.

→ Vector addition obeys commutative law
i.e. A + B = B + A

→ Vector addition obeys associative law
i.e. (A + B) + C = A + (B + C)

→ Subtraction of B from A is defined as the sum of
– B + A i.e. A – B = A + (-B)

→ The angle between two equal vectors is zero.

→ The angle between -ve vectors is 180°.

→ Unit vector  = \(\frac{\mathbf{A}}{|\mathbf{A}|}\) .

→ The magnitude of  = 1.

→ The direction of A is the same as that of the given vector along which it acts.

→ The resultant of two vectors of unequal magnitudes can never be a null vector.

→ î, ĵ, k̂ are the unit vectors acting mutually perpendicular to each other along X, Y and Z axes respectively and are called orthogonal unit vectors.

→ î.î = ĵ.ĵ = k̂.k̂ = 1

→ î.ĵ = ĵ.k̂ = k̂.î = 0

→ î × î = ĵ × ĵ = k̂ × k̂-= 0

→ î × ĵ = k̂, ĵ × k̂ = î, k̂ × î = ĵ

→ A × A = 0 , Also A – A = 0
But A × A ≠ A – A as A × A ⊥ A and A – A is collinear with A.

→ The cross product:

1. Is not commutative (i.e. don’t obey commutative law):
   i. e. A × B ≠ B × A
   = B × A (anticommutative law)
2. obeys distributive law i.e.
   A × (B + C) = A × B + A × C

→ Vectors lying in the same plane are called co-planer vectors.

→ Vectors are added according to triangle law, parallelogram law, and polygram law of vector addition.

→ The maximum resultant of two vectors A and B is
|R_max| = |A| + |B|

→ The minimum resultant of two vectors A and B is
|R_max| = |A| – |B|

→ The minimum number of vectors lying in the same plane whose results can be zero is 3.

→ The minimum number of vectors that are not co-planar and their results can be zero is 4.

→ A minimum number of collinear vectors whose resultant can be zero is 2.

→ A vector in component form is A = A_xî + A_yĵ +A_zk̂

→ Magnitude of A is = \(\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}\).

→ A projectile is any object thrown with some initial velocity and then it moves under the effect of gravity alone.

→ The trajectory is the path followed by the projectile during its flight.

→ Its trajectory is always parabolic in nature.

→ Two-dimensional motion: The motion of an object in a plane is a two-dimensional motion such as the motion of an arrow shot at some angle and then moving under gravity.

→ Three-dimensional motion: The motion of an object in space is called a three-dimensional motion, for example, the motion of a free gas molecule.

→ Scalar quantities: The quantities which do not need direction for their description are called scalar quantities. Only the magnitude of the quantity is needed to express them correctly. Such quantities are distance, mass, density, energy, temperature etc.

→ Vector quantities: The quantities which need both magnitude and direction for their correct description are called vector quantities. They also obey the law of the addition of vectors. For example displacement, velocity, acceleration, force, momentum etc. are vector quantities.

→ Triangle law of vector addition: If the two vectors are represented by the two adjacent sides of a triangle taken in order, their resultant is given in magnitude and direction by the third side of the triangle taken in the opposite order.

→ Parallelogram law of vector addition: If two vectors acting simultaneously at a point are represented by the two adjacent sides of a parallelogram, then their resultant is completely given in magnitude and direction by the diagonal of the parallelogram passing through that point.

→ Unit vector: A unit vector is a vector in the direction of a given vector whose magnitude is unity. It is represented by a cap or a hat over letter e.g. n̂, î, ĵ, k̂, x̂, ŷ, ẑ etc. The unit vectors in the cartesian coordinate system along the three axes are generally written as î, ĵ and k̂ such that |î| = |ĵ| = |k̂| = 1.

→ Uniform velocity: The uniform or constant velocity is the one in which the moving object undergoes equal displacements in equal intervals of time.

→ Speed: The magnitude of velocity is known as speed. It is the distance travelled divided by the time taken.

→ Uniform acceleration: When the velocity of an object changes by equal amounts in equal intervals of time, the object is said to be having uniform acceleration.

→ Projectile: Projectile is a particle or an object projected with some initial velocity and then left to move under gravity alone.

→ The uniform circular motion: The motion of an object in a circular path with constant speed and constant acceleration (magnitude) is called a uniform circular motion.

→ Equal vectors: Two vectors are said to be equal if they have the same magnitude and act in the same direction.

→ Negative vector: A vector having the same magnitude as the given vector but acting in exactly the opposite direction is called a negative vector.

→ Co-initial vectors: Vectors starting from the same initial point are called co-initial vectors.

→ Zero vector or Null vector: The vector whose magnitude is zero but the direction is uncertain (or arbitrary) is called a zero or null vector. It is represented by 0.

→ Collinear vectors: Two vectors acting along the same or parallel lines in the same or opposite directions are called collinear vectors.

→ Fixed vector: A vector whose tail point or initial point is fixed is called a fixed vector.

→ Free vector: A vector whose initial point or tail is not fixed is called a free vector.

→ Polygon law of addition of vectors: It states that if a number of vectors are represented by the sides of a polygon taken in the same order, then their resultant is given completely by the closing side of the polygon taken in the opposite order.

→ Rectangular components of a vector in a plane: The resolution of a vector into two mutually perpendicular components in a plane is called rectangular resolution and each component is called a rectangular component.

→ Rectangular components in a plane: The components of a vector along three mutually perpendicular axes are called the rectangular component of a vector in space.

→ Scalar product of vectors: If the multiplication of two vectors yields a scalar quantity, the multiplication is called a scalar or dot product. This is because of the fact that multiplication is denoted by a dot (.) between the multiplying vectors e.g. A.B = AB cos θ, where θ is the angle between the two vectors.

→ Cross or vector product: When the multiplication of two vectors is shown by a cross (×) between them, it is called a cross product. The resultant is also a vector quantity e.g. A × B = C. This multiplication is, therefore, also known as the vector product.

Important Formulae:
→ Uniform circular motion: Time period T second, frequency
v = \(\frac{1}{T}\)
Angular velocity ω = \(\frac{θ}{T}\),
ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πv,
v = \(\frac{1}{T}\),
θ = \(\frac{l}{r}\)
or
l = rθ.

→ Angular acceleration: α = \(\frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}=\frac{d \omega}{d t}\)
average acceleration, a_av = \(\frac{v_{2}-v_{1}}{t_{2}-t_{1}}\)
Average angular acceleration,

→ Time for maximum height: t = \(\frac{\mathrm{u} \sin \theta}{\mathrm{g}}\)

→ Angle of projection of maximum horizontal range:
θ = \(\frac{π}{4}\) or 45°.

→ Angles for same range θ, (\(\frac{π}{2}\) – θ)

→ General position – velocity – acceleration relations:
Δr (t) = r(t + Δt) – r(t)
v(t) = \(\frac{\Delta \mathrm{x}(\mathrm{t})}{\Delta \mathrm{t}}\);

vx(t) = \(\frac{\Delta \mathrm{x}(\mathrm{t})}{\Delta \mathrm{t}}\),

vy(t) = \(\frac{\Delta \mathrm{y}(\mathrm{t})}{\Delta \mathrm{t}}\)

Δx(t) = x(t + Δt) – x(t)
Δy(t) = y(t + Δt) – y(t)

→ Since: A.A = A², so

• î.î =1,
• ĵ.ĵ =1,
• k̂.k̂ =1

As î, ĵ and k̂ are mutually perpendicular so
î.ĵ = ĵ.k̂ =0,
k̂.î = 0

→ A.(B + C) = A.B. +A.C

→ Vector product:
A × B = C = |A| |B|sin θ n̂
In cartesian coordinates,
A × B = (A_xî + A_yĵ + A_zk̂) × (B_xî + B_yĵ + B_zk̂)
= (A_yB_z – A_zB_y) î + (A_zB_x – A_xB_z)ĵ + (A_xB_y – A_yB_x)k̂
= \(\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\
\mathrm{A}_{\mathrm{x}} & \mathrm{A}_{\mathrm{y}} & \mathrm{A} \\
\mathrm{B}_{\mathrm{x}} & \mathrm{B}_{\mathrm{y}} & \mathrm{B}
\end{array}\right|\)

→ A × B ≠ B × A
= -B × A

→ |A × B|² + |A . B|² = 2|\(\overrightarrow{\mathrm{A}}\)|²|\(\overrightarrow{\mathrm{B}}\)|²

→ Direction cosines:
cos α = \(\frac{A_{x}}{A}\) = l,
cos β = \(\frac{A_{y}}{A}\) = m, and
cos γ = \(\frac{A_{z}}{A}\) = n

→ l² + m² + n² = 1

→ Velocity: v = vxi + vyj

→ Speed: v = |v| = (v_x² + v_y²)^1/2 .

→ Distance travelled in time t:
x(t)î + y(t)ĵ = x(0)î + y(0)ĵ + (v_xî + v_yĵ)t

→ x (t) = x (0) + v_xt

→ y (t) = y (0) + v_yt

→ Average velocity:
V_average = \(\frac{\left|r\left(t^{\prime}\right)-r(t)\right|}{t^{\prime}-t}=\frac{r_{12}}{\left(t_{2}-t_{1}\right)}=\frac{\Delta r}{\Delta t}\)

→ Instantaneous velocity:

→ Scalar product of A and B is
A . B = AB cos θ, where θ = angle between A and B.

→ Scalar (or Dot) product always gives a scalar quantity.

→ When A. B = 0 then A and B are perpendicular to each other.

→ A . B in component form is
A.B = A_xB_x + A_yB_y + A_zB_z.

→ Cross product of A and B is
A × B = (AB sin θ) n̂ = C
where n̂ = unit vector ⊥ to the plane containing A and B i.e. n̂ acts along C.

→ If we move anticlockwise, n is vertically upward i.e. +ve.

→ If we move clockwise, n vertically downward i.e. -ve.

→ Maximum height attained by the projectile fired at an angle 0 with the horizontal with velocity u is
H = \(\frac{\mathbf{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}\)

→ Time of flight = T = \(\frac{2 u \sin \theta}{g}\)

→ Time of maximum height attained = Time of ascent = Time of descent = \(\frac{u \sin \theta}{g}\)

→ Horizontal range of the projectile is R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\)

→The range of projectile is maximum if θ = 45°.

→ Rmax = \(\frac{\mathrm{u}^{2}}{\mathrm{~g}}\)

→ When the range is maximum, the maximum height attained by the projectile (Hm) is
H_m = \(\frac{u^{2}}{4 g}=\frac{R_{\max }}{4}\)

→ For R_max , T_max = \(\frac{\mathrm{u}}{\sqrt{2} \mathrm{~g}}\)

→ When θ = 90, H_max = \(\frac{u^{2}}{2 g}\) and is twice the maximum height attained by the projectile when range is maximum.

→ For θ = 90°, Time of flight is Maximum = \(\frac{2 \mathrm{u}}{\mathrm{g}}\)

→ Horizontal range is same for two angles of projections i.e. θ and 90 – θ with the horizontal.

→ If an object is moving in a plane with constant acceleration a, then a = \(\sqrt{\mathrm{a}_{\mathrm{x}}^{2}+\mathrm{a}_{\mathrm{y}}^{2}}\)

→ If r0 be the position vector of a particle moving in a plane at time t = 0, then at any other time t, its position vector will be
r = r_o + v_ot + \(\frac{1}{2}\) at²
where v0 = its velocity at t = 0.

→ Its velocity at time t will be v = v_o + at.

→ When the object moves in a circular path at constant speed, then its motion is called uniform circular motion. The angle described by the rotating particle is called angular displacement.

→ Angular displacement, Δθ = \(\frac{\Delta l}{\mathrm{r}}\) .

→ Angular velocity, ω = \(\frac{\Delta \theta}{\Delta \mathrm{t}}\)

Instantaneous angular velocity, ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)

ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πv (∵ v = \(\frac{1}{T}\))

Angular velocity (ω) of a rigid body rotating about a given axis is constant, so v is different for different particles of the body.

Angular acceleration α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}\)

Tangential acceleration is a₁ = α × r and a_t is directed along the tangent to the circular path.

→ Centripetal acceleration (a_c) is given by a_c = \(\vec{\omega}\) × v and it is directed towards the centre of the circular path. Thus acceleration of the particle is
a = a_t + a_c
then a_t ⊥ a_c
∴ |a| = \(\sqrt{a_{1}^{2}+a_{c}^{2}}\)

→ Also \(\vec{\omega}\) ⊥v as to and a are parallel to Δθ. i.e. they are directed along the axis of rotation
Hence a_c = ω v sin 90
ac = ω v = ω . rω = rω²
= \(\frac{v^{2}}{r}\)

→ Centripetal force, F_c = ma_c = \(\frac{m v^{2}}{r}\) = mrω².

→ Fc is always directed towards the centre of the circular path.

→ The Axis of rotation is perpendicular to the plane of rotation.

→ There can be no circular motion without centripetal force. Centripetal force can be a mechanical, electrical or magnetic force in nature.

→ Fc is always ⊥ to the velocity of the particle.

→ θ, ω, α are called axial vectors or pseudo vectors.

→ Tangential acceleration is equal to the product of angular acceleration and the radius of the circular path i.e. at = rα.

By going through these CBSE Class 11 Physics Notes Chapter 3 Motion in a Straight Line, students can recall all the concepts quickly.

Motion in a Straight Line Notes Class 11 Physics Chapter 3

→ Mechanics is divided into three main branches: Statics, Kinematics and Dynamics.

→ Distance is a scalar quantity.

→ Displacement is a vector quantity.

→ An object is said to be in motion if it changes its position w.r.t. its surroundings as time passes.

→ An object is said to be at rest or it does not change its position w.r.t. its surroundings as time passes.

→ Both rest and motion are relative terms.

→ Distance travelled by a moving body can never be zero or negative i.e. it is always positive.

→ Displacement can be positive, negative or zero.

→ The magnitude of displacement = distance only if a body moves in a straight line without a change in direction.

→ The magnitude of the displacement of a body is the minimum possible distance, so distance ≥ displacement.

→ Speed is a scalar quantity.

→ Velocity is a vector quantity.

→ When a body moves with variable speed, then the average speed of the body is calculated as:
Average speed = \(\frac{\text { Total distance travelled by the body }}{\text { Total time taken }}\)

→ When a body moves with variable velocity, then the average velocity of the body is calculated as:
Average velocity = \(\frac{\text { Total displacement }}{\text { Total time taken }}\)

→ Distance travelled by an object in a given time interval is equal to the area under the velocity-time graph.

→ The direction of velocity and acceleration may not necessarily be the same.

→ The velocity and acceleration of a body may not be zero simultaneously. When the body is in equilibrium, its acceleration is zero.

→ In one, two and three dimensional motions, the object changes its position w.r.t. one, two and three coordinate axes respectively.

→ At a particular instant of time, any point may be chosen as a reference or zero points.

→ The events taking place before the zero time are assigned negative number and events after zero are assigned +ve number.

→ A suitable unit of time say, second, minute or hour may be chosen. In fact, zero points of time and unit of time are chosen according to one’s convenience.

→ The position is also measured with respect to a chosen zero position or origin on the path line.

→ Positions to the right of origin are represented by a positive number and a unit.

→ The position to the left of the origin is represented by a negative number and the unit.

→ For motion in the vertical direction, we can use ‘up’ or ‘down’ instead of ‘right’ and ‘left’.

→ The position is always stated with respect to time,

→ x (t) shows that x is a function of time t.

→ The shift in position x (t’) – x (t) is called the displacement.

→ The rate of change, of displacement, is called velocity.

→ The motion in which an object covers equal distances in equal intervals of time is called uniform motion.

→ Uniform motion may be represented by a straight line parallel to the time axis in a velocity-time graph.

→ It is also represented by a straight line inclined at some angle. The magnitude of velocity is speed.

→ The velocity of a body w.r.t. another body is called its relative velocity.

→ The x-t graph is a straight line parallel to the time axis for a stationary object.

→ Uniformly accelerated motion is a non-uniform motion.

→ When the velocity of the body decreases with time it is said to be decelerated or retarded.

→ When a particle returns to the starting point, its average velocity is zero but the average speed is not zero.

→ For one dimensional motion, the angle between acceleration and velocity is either zero or 180°. It may also change with time.

→ For two dimensional motion, the angle between acceleration and velocity is other than 0° or 180°. It may also change with time.

→ If the angle between a and v is 90°, the path of motion is a circle.

→ If the angle between a and v is other than 0° or 180°, the path of the particle is a curve.

→ For motion with constant acceleration, the graph between x and t is a parabola.

→ For uniform motion, the average velocity is equal to the instantaneous velocity.

→ Statics: It deals with the law of composition of forces and with the conditions of equilibrium of solid, liquid and gaseous states of the objects.

→ Kinematics: It is the branch of mechanics that deals with the study of the motion of objects without knowing the cause of their motion.

→ Dynamics: It is the branch of mechanics that deals with the study of the motion of objects by taking into account the cause of their motion.

→ Point object: It is defined as an object having its dimensions much smaller as compared to the distance covered by it.

→ Acceleration: It is defined as the change in velocity with time i. e.

→ Speed: Theatre of covering distance with time is called speed i.e.
speed = \(\frac{\text { Distance }}{\text { Time }}\)

→ Average speed: It is the ratio of total path length traversed and the corresponding time interval.

→ Velocity: The rate of change of displacement is called velocity.

→ Average velocity: When an object travels with different velocities, its rate of motion is measured by its average velocity.
Average velocity = \(\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=\frac{\Delta x}{\Delta t}\)

→ Instantaneous velocity: The velocity of the object at any particular instant of time is known as instantaneous velocity.

→ V_inst = \(\frac{\mathrm{dx}}{\mathrm{dt}}\)

→ Uniform velocity: A motion in which the velocity of the moving object is constant is called uniform and the velocity is called the uniform velocity. In uniform motion, the object covers equal distances in equal intervals of time along a straight line.

→ Relative velocity: The rate of change in the relative position of an object with respect to the other object is known as the relative velocity of that object.

→ Acceleration: The time rate of change of velocity is known as acceleration.

→ Average acceleration: It is defined as the change in velocity divided by the time interval.
a_av = \(\frac{\text { Final velocity – Initial velocity }}{\text { Change in time }}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\frac{\Delta v}{\Delta t}\)

→ Instantaneous acceleration: The acceleration of an object at any instant of time is called instantaneous acceleration. It is also the limiting value of average acceleration.

→ Retardation: The negative acceleration due to which the body slows down is known as deacceleration or retardation.

→ Non-uniform motion: An object is said to have non-uniform motion when its velocity changes with time even though it has a constant acceleration.

Important Formulae:
→ Displacement in time from t to t’ = x(t’) – x (t)

→ Average velocity, vav = \(\frac{\mathrm{x}\left(\mathrm{t}^{\prime}\right)-\mathrm{x}(\mathrm{t})}{\mathrm{t}-\mathrm{t}}=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}\)

→ The relative velocity of a body A w.r.t. another body B when they are moving along two parallel straight paths in the same direction is V_AB = V_A – V_B and if they are movinig in opposite direction, then V_AB = V_A – (-V_B) = V_A + V_B.

Average Speed V_av = \(\frac{\mathrm{S}_{1}+\mathrm{S}_{2}}{\left(\frac{\mathrm{S}_{1}}{\mathrm{v}_{1}}+\frac{\mathrm{S}_{2}}{\mathrm{v}_{2}}\right)}\)
Where S₁ is the distance travelled with velocity v₁ and S₂ is the distant travelled with velocity v₂.

→ If S₁ = S₂, then vav = \(\frac{2 v_{i} v_{2}}{v_{1}+v_{2}}=\frac{2}{\frac{1}{v_{1}}+\frac{1}{v_{2}}}\)

→ Average speed of a body when it travels with speeds v₁, v₂, v₃…..v_n in time intervals t₁, t₂, t₃,… t_n, respectively is given by
V_av = \(\frac{v_{1} t_{1}+v_{2} t_{2}+v_{3} t_{3}+\ldots .+v_{n} t_{n}}{t_{1}+t_{2}+t_{3}+\ldots+t_{n}}=\frac{\sum_{i=1}^{n} v_{i} t_{i}}{\sum_{i=1}^{n} t_{i}}\)

→ Distance travelled by a body moving with uniform velocity is S = ut.

→ Velocity of an object after a time t in uniformly accelerated motion is, v = u + at.

→ Distance covered by an object after a time t in accelerated motion is, S = ut + \(\frac{1}{2}\)at².

→ Velocity of an object after covering a distance S in uniformly accelerated motion is, v² – u² = 2aS.

→ Distance covered in nth second by a uniformly accelerated object
Snth = u + \(\frac{a}{2}\)(2n – 1)

→ Total time a flight = Time of Ascent + Time of descent.

→ Time of Ascent = Time of descent.