CBSE Notes

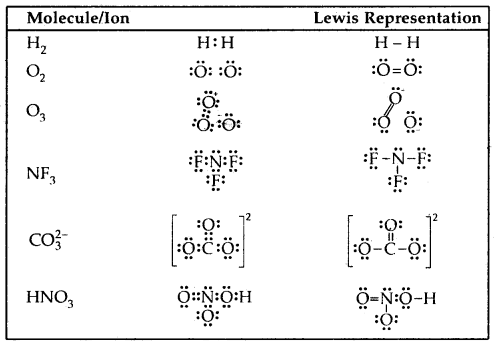
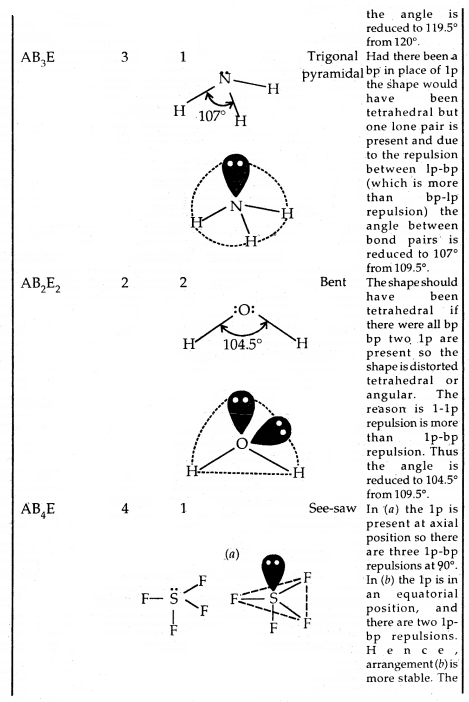
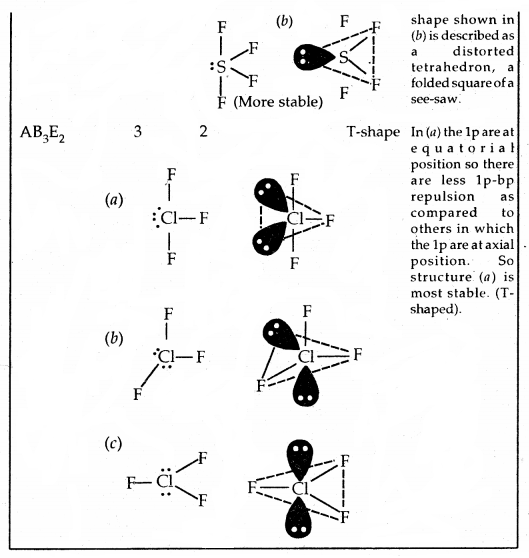
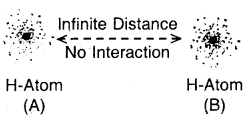
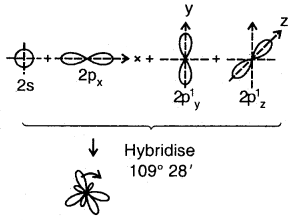
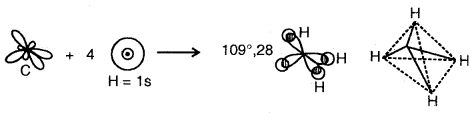
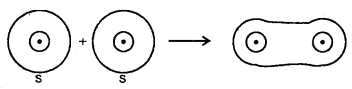
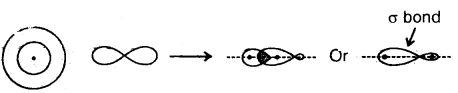
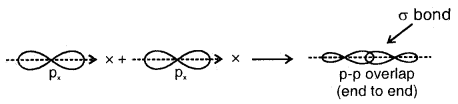
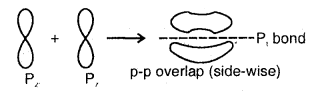
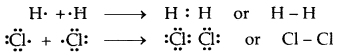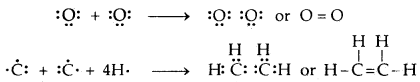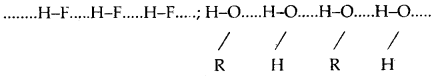By going through these CBSE Class 11 Chemistry Notes Chapter 5 States of Matter, students can recall all the concepts quickly.

States of Matter Notes Class 11 Chemistry Chapter 5

Most of the observable characteristics of chemical systems represent the bulk properties of matter. These are the properties associated with a collection of a large number of atoms, ions or molecules. For example, an individual molecule of a liquid does not boil, but the bulk boils.

Intermolecular Forces: Intermolecular forces are the forces of attraction and repulsion between interacting particles (atoms and molecules). This term does not include electrostatic forces that exist between the two oppositely charged ions and the forces that hold the atoms together in a molecule, i.e., a covalent bond.

Attractive intermolecular forces are known as van der Waals forces. They vary considerably in magnitude and include:

1. Dispersion or London forces
2. Dipole-dipole forces
3. Dipole-induced-dipole forces
4. A particularly strong type of dipole-dipole interaction is hydrogen bonding. But only a few elements (F, O, N) can participate in hydrogen bond formation.

Attractive forces between an ion and a dipole are known as ion-dipole forces and these are not van der Waals forces.

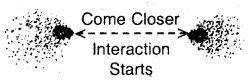
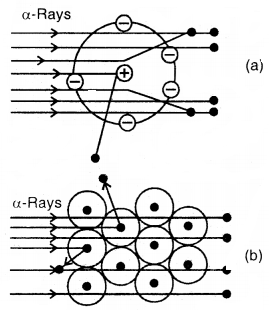
Dispersion Forces or London Forces: Atoms and non-polar molecules are electrically symmetrical and have no dipole moment because their electronic charge cloud is symmetrically distributed. But a dipole may develop momentarily even in such atoms and molecules. Suppose we have two atoms A and B close to each other [Fig. (a)]. It may so happen that momentarily electronic charge distribution in one of the atom A becomes unsymmetrical [Fig. (b) and (c)]. This results in the development of instantaneous dipole on atom A, for a very short time. This distorts the electron results a dipole is included in the atom.

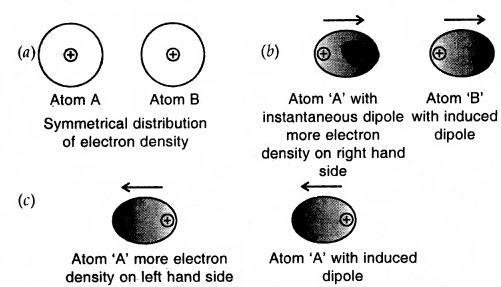
Dispersion forces of London forces between atoms

The temporary dipole of atom ‘A’ and ‘B’ attract each other. Similarly, temporary dipoles are induced in molecules also. This force of attraction was first calculated by the German physicist Fritz London. For this reason force of attraction between two temporary dipoles is known as the London forces. Another name for this force is dispersion force.

These forces are always attractive and interaction energy is inversely proportional to the sixth power of the distance between two interacting particles (i.e., \(\frac{1}{r^{6}}\) where r is the distance between two particles). These forces are important only at short distances (~ 500 pm) and the magnitude of the force depends on the polarisability of the particle. Dispersion forces are present among all particles.

Dipole-Dipole Forces:
Dipole-dipole forces act between molecules possessing permanent dipole. Ends of the dipole possess “partial charges” and these charges are shown by the Greek letter delta (5) Partial charges are always less than the unit charge (1.6 × 10^-19 C) because of the electron sharing effect.

The polar molecules interact with neighbouring molecules. This interaction is weak compared to ion-ion interaction because only partial charges are involved. The interaction energy decreases with the increase of distance between the dipoles. It is proportional to \(\frac{1}{r^{6}}\) where r is the distance between polar molecules. Besides dipole-dipole interaction, polar molecules can interact by London forces also. Thus the cumulative effect is that total of intermolecular forces in polar molecules increase. Fig. shows electron cloud distribution in the dipole of hydrogen chloride.

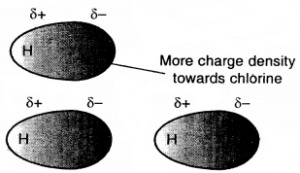
(a) Distribution of electron cloud in HCl a polar molecule
(b) Dipole-dipole interaction between two HCl molecules

Dipole-Induced Dipole Forces
This type of attractive forces operates between polar molecules having permanent dipole and molecules lacking permanent dipole. The permanent dipole of the polar molecule induces dipole of the electrically neutral molecule by deforming its electronic cloud.

Thus induced dipole is developed in the other molecule. In this case, also interaction energy is proportional to -4 where r is the distance between two molecules Induced dipole moment depends UpOn the dipole moment present in the permanent dipole and the polarizability of the electrically neutral molecule.

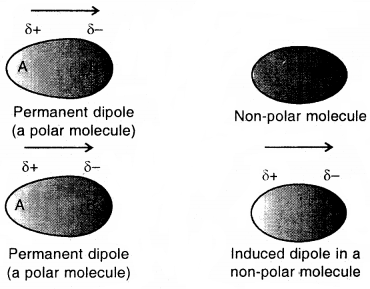
Dipole-induced dipole interaction between a permanent dipole and induced dipole

In this case, the cumulative effect of dispersion forces and dipole- included dipole interactions exists.

Hydrogen Bond
The bond formed between the hydrogen atom of one molecule with the more electronegative atom (like N, O or F) of another molecule is called a hydrogen bond Such a molecule is highly polar. The electronegative atom of the covalent bond possesses lone pair of electrons. When two such molecules containing these type of bonds come close to each other, the hydrogen of one molecule is attracted towards the electronegative atom of the other molecule This interaction is represented by a dotted line and is called a hydrogen bond.

The energy of hydrogen bond varies between 10 to 100 kJ mol^-1. This is a very significant amount of energy, therefore hydrogen bonds are a powerful force in determining the structure and properties of many compounds. The strength of the hydrogen bond is determined by the Coulomb interaction between the lone-pair electrons of the electronegative atom and the hydrogen atom. The following diagram shows the formation of the hydrogen bond.

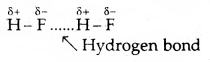
The intermolecular forces discussed so far are all attractive. Molecules also exert repulsive forces on one another. When two molecules are brought into close contact with each other, the repulsion between the electrons and between the nuclei in the molecules come into play. The magnitude of the repulsion rises very rapidly as the distance separating the molecules decreases. This is the reason that liquids and solids are hard to compress. In these states molecules are already in close contact, therefore they resist further compression.

→ Thermal Energy: Thermal energy is the energy of a body arising from the motion of its atoms or molecules. It is directly proportional to the temperature of the substance. It is the measure of the average kinetic energy of the particles of the matter and is thus responsible for the movement of particles. The movement of particles is called thermal motion.

Intermolecular Forces Vs Thermal Interactions
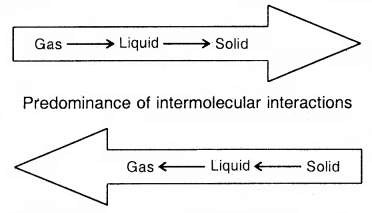
Intermolecular forces tend to keep molecules together but the thermal energy of the molecules tend to keep them apart. Three states of matter are the result of a balance between intermolecular forces and the thermal energy of the molecules.

The predominance of thermal energy and the molecular interaction energy of a substance in three states is depicted as follows:

The Gaseous State: Only 11 elements in the periodic table exist in the form of gases under normal conditions:

Gases are classified by the following properties.

1. Gases are the most compressible out of all the 3 states of matter.
2. Gases exert pressure equally in all directions.
3. Gases have a much lower density than solids and liquids.
   
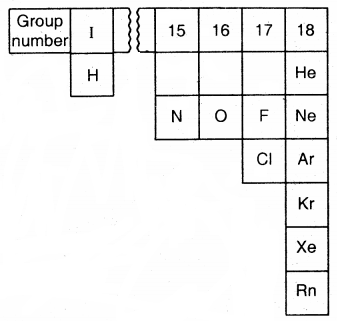
   elements that exist as gases
4. They assume the volume and shape of the container in which they are kept.
5. Gases mix evenly, and completely without any mechanical help.

Gas Law: Boyle’s Law (Pressure-Volume Relationship)
“Volume of a given mass of a gas is inversely proportional to its pressure provided the temperature is kept constant.”
V ∝ \(\frac{1}{P}\) (mass and temperature kept constant)
or
PV = constant = k
or
P₁V₁ = P₂V₂, where P₁V₁ are the initial pressure and volume of the gas. P₂ and V₂ are the final values.

The value of k depends upon the amount of the gas, temperature of the gas, its nature and the units in which P and V are expressed.
Graphical Representation of Boyle’s Law

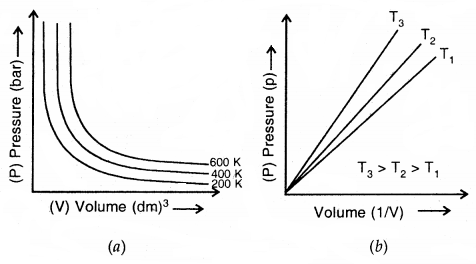
(a) Graph of Pressure Vs Volume (b) Graph of pressure p Vs \(\frac{1}{V}\)

Each curve in (a) above corresponds to a different constant temperature and is known as an Isotherm

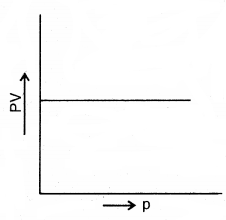
(c) Graph of PV against P

1. A plot of P versus V at constant temperature for a fixed mass of gas would be a rectangular hyperbola (a)
2. A plot of P versus \(\frac{1}{v}\) at constant temperature for a fixed mass of gas would be a straight line passing through the origin (b)
3. A plot of P versus PV at a constant temperature. In a fixed mass of a gas is a straight line parallel to the pressure axis:

Relationship between density and pressure

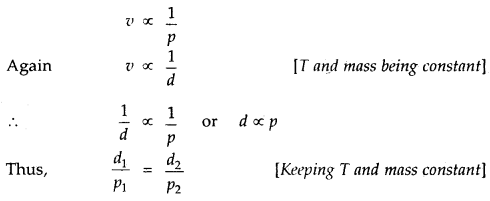
Charle’s Law (Temp. Volume Relationship): The law states, “At constant pressure, the volume of a given mass of a gas increases or decreases by \(\frac{1}{273.15}\) of its volume at 0°C and 1°C rise or fall in temperature.” Thus if the volume of the gas at 0°C and at t°C is V_o and V_t. Then

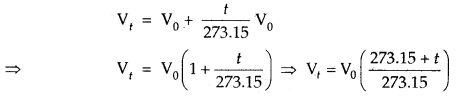
At this stage, we define a new scale of temperature such that f°C on the new scale is given by T = 273.15 + t and 0°C will be given by T_o = 273.15. This new temperature scale is called the Kelvin temperature scale or Absolute temperature scale. It can be represented as follows:

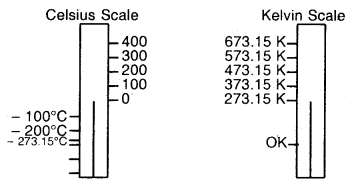
Relationship between Kelvin Scale and Celsius Scale

One degree Celsius (1 °C) is equal to one Kelvin (K) in magnitude (Note that degree sign is not used while writing the temperature in absolute temperature scale, i.e. Kelvin scale). Only the position of zero has been shifted. Kelvin scale of temperature is also called the Thermodynamic scale of temperature and is used in all scientific works.

Thus we add 273 (more precisely 273.15) to Celsius temperature to obtain temperature at Kelvin scale.

A graph of volume Vs temperature at Kelvin scale will look like as shown.

If we write Tf = 273.15 + t and T_o = 273.15 in the equation we obtain the relationship
V_t = V_o(\(\frac{\mathrm{T}_{t}}{\mathrm{~T}_{0}}\))
⇒ \(\frac{V_{t}}{V_{0}}=\frac{T_{t}}{T_{0}}\)

Thus we can write a general equation as follows:
\(\frac{V_{2}}{V_{1}}=\frac{T_{2}}{T_{1}}\)
or
\(\frac{V}{T}\) = constant = k

Each line of V vs T graph is called Isobar

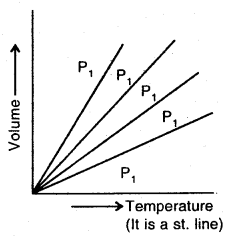
At constant pressure for a given mass of a gas
V ∝ T
or
V = kT (where k is a constant, the value of k depends upon nature and amount of the gas)
or
\(\frac{V}{T}\) = constant

If V₁ = initial volume of the gas
T₁ = initial temperature (absolute)
V₂ = Final volume
T₂ = Final temperature .
Then \(\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\) (mass and pressure kept constant)

Relationship between density and temperature
V ∝ T
or
\(\frac{1}{d}\) ∝ T
or
dT = constant
or
d₁T₁ = d₂T₂

Gay-Lussac’s Law (Pressure-Temperature Relationship): It states that at constant volume, the pressure of a given mass of a gas varies directly with temperature on the Kelvin scale
Mathematically P ∝ T
It is also called Amonton’s Law
or
\(\frac{P}{T}\) = constant

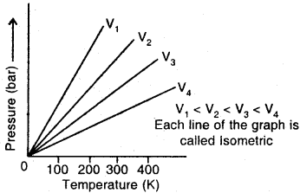
Pressure Vs Temperature (K) graph (Isometrics) of a gas

Avogadro’s Law (Volume-Amount Relationship)
It states, “Equal volumes of all gases under similar conditions of temperature and pressure contain an equal number of molecules.”

Mathematically v ∝ n where n = no. of moles of the gas if T and P are constant.
n = \(\frac{m}{M}\); where n = number of moles of gas
m = mass of the gas;
M = Molar mass of the gas

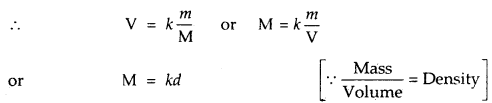
where d is the density of the gas.

Thus the density of a gas is directly proportional to its formula mass.

Avogadro’s number or Avogadro’s constant is the number of particles present in 1 mole of a substance. This number is 6.023 × 10²³.

One mole of each gas will have volume = 22.4 L at STP.

A gas that follows Boyle’s Law, Charle’s and Avogadro’s law strictly is called an ideal gas. Such gas is a hypothetical gas. It is assumed that intermolecular forces are not present between the molecules of an ideal gas. Real gases follow these laws only under certain specific conditions when forces of interaction are practically negligible. In all other situations, these deviate from ideal behaviour.

Ideal Gas Equation

1. At constant T and n, V ∝ \(\frac{1}{P}\) Boyle’s Law
2. At constant P and n, V ∝ T Charle’s Law
3. At constant T and P, V ∝ n Avogadro’s Law
   Thus
   
   On rearrangingPV= nRT … (1)

R is called Gas Constant. It is the same for all gases. Therefore, it is called Universal Gas Constant, equation (1) above is called Ideal Gas Equation.

The value of R for 1 Mole of an ideal gas can be calculated ai 273.15 K and 1 atm (1.013 × 10⁵ Pascal) [Most of the real gases behave like ideal gases under these conditions) as follows.
R = \(\frac{\left(1.0325 \times 10^{5} \mathrm{~Pa}\right) \times\left(22.41383 \times 10^{-3} \mathrm{~m}^{3} / \mathrm{mol}\right)}{298.15 \mathrm{~K}}\)
= 8.31441 Pa m³ k^-1 mol^-1
= 8.3144 JK^-1 mol^-1

[For one mole V = 22.413832 for all gases at STP] For all practical purposes approximate value of R, i.e., 8.314 JK^-1 mol^-1 can be used.

In the equation PV = nRT

• P and T are Intensive properties. Intensive properties are independent of the ‘quantity’ or ‘bulk’ of the substance.
• n and V are Extensive properties. Extensive properties are dependent upon the ‘quantity’ or ‘bulk’ of the substance.

If temperature, volume and pressure of a fixed amount of the gas vary from T₁, V₁ and P₁ to T₂, V₂ and P₂.
Then \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}\) = nR and \(\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\) = nR
or
\(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)

It is called General Gas Equation or Combined gas law. Density and Molar Mass of a Gaseous substance

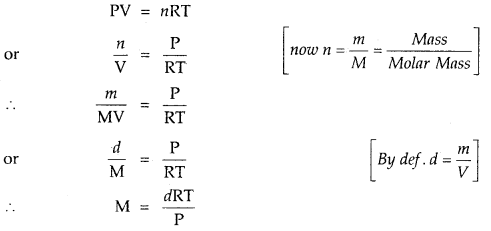
Dalton’s Law of Partial Pressures: The law states, “Total pressure exerted by a mixture of non-reacting gases is equal to the sum of partial pressures exerted by the individual gases-all measurement being made at the same temperature.” Thus at constant temperature and volume:

P_Total = p₁ + p₂ + p₃ + ………; P_Total = Total pressure.
p₁, p₂, …. are the partial pressures of the different non-reacting gases. ,

Gases are generally collected over water. The pressure of dry gas can be calculated by subtracting the vapour pressure of water from the moist gas which contains water vapours also. The pressure exerted by saturated water vapour is called aqueous tension.
P_{dry gas} = P_Total – Aqueous tension

Partial pressure in terms of mole fraction: Suppose three gases, enclosed in the volume V, exert partial pressure p₁, p₂ and p₃ respectively. Then
p₁ = \(\frac{n_{1} \mathrm{RT}}{\mathrm{V}}\)
p₂ = \(\frac{n_{2} \mathrm{RT}}{\mathrm{V}}\)
p₃ = \(\frac{n_{3} \mathrm{RT}}{\mathrm{V}}\)
where n1, n2 and n3 are number of moles of these gases. Thus expression for total pressure will be
P_Total = P₁ + P₂ + P₃
= n₁\(\frac{\mathrm{RT}}{\mathrm{V}}\) + n₂\(\frac{\mathrm{RT}}{\mathrm{V}}\) + n₃\(\frac{\mathrm{RT}}{\mathrm{V}}\)

= (n₁ + n₂ + n₃)\(\frac{\mathrm{RT}}{\mathrm{V}}\)
On dividing p₁ by P_Total we get
\(\frac{p_{1}}{P_{\text {Total }}}=\left(\frac{n}{n_{1}+n_{2}+n_{3}}\right) \frac{\mathrm{RTV}}{\mathrm{RTV}}=\frac{n_{1}}{n_{1}+n_{2}+n_{3}}\) = x₁

x₁ is called mole fraction of first gas
Thus, p₁ = x₁ P_Total.

Similarly, for the other two gases, we can write
P₂ = x₂P_Total and P₃ = x₃P_Total

Thus a general equation can be written as
p_i = x_i P_Total

where p_ix_i, and P_Totalare partial pressure and mole fraction of with gas and total pressure of the gas mixture respectively. If the total pressure of the gases is known, the equation can be used to find out the pressure exerted by the individual gas.

Molar Volume of the gas under different conditions
(a) Standard temperature and pressure (STP) conditions are 0° C or 273,15 K and one atmospheric pressure. Under these conditions, 1 mole of the gas occupies a volume of 22.413996 L = 22.4 L or 22400 mL.

When STP conditions are taken as 0°C and 1 bar pressure [as 1 bar < 1 atom and 1 bar = 0.987 atm) molar volume is slightly higher and = 22.71098 L mol^-1 = 22.7 L mol^-1 or 22700 mL.

→ Standard Ambient Temperature and Pressure (SATP): Conditions are also used in some scientific works. SATP conditions mean 298.15 K and 1 bar (i.e. exactly 10s Pa). At SATP (1 bar and 298.15 K), the molar volume of an ideal gas is 22.789 mol^-1 or 22800 mL.

→ Graham’s Law of Effusion/Diffusion: It states, “Under similar conditions of temperature and pressure, rate of diffusion of a gas is inversely proportional to the square root of the density of a gas.”

Mathematically R_d ∝ \(\sqrt{\frac{1}{d}}\)
R_d = Rate of diffusion, d = density of the gas
Rate of diffusion R_d = R\(\sqrt{\frac{1}{d}}\)

If two gases A and B diffuse under similar conditions of temperature and pressure rate r_A and r_B respectively and their densities are dA and dB respectively then
r_A = k\(\sqrt{\frac{1}{d_{\mathrm{A}}}}\)
r_B = k\(\sqrt{\frac{1}{d_{\mathrm{B}}}}\)

On dividing r_A and r_B we obtain
\(\frac{r_{\mathrm{A}}}{r_{\mathrm{B}}}=\sqrt{\frac{d_{\mathrm{B}}}{d_{\mathrm{A}}}}=\sqrt{\frac{d_{\mathrm{B}} \mathrm{V}}{d_{\mathrm{A}} \mathrm{V}}}=\sqrt{\frac{\mathrm{M}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{A}}}}\)
where V is the volume of gas A and gas B which undergoes diffusion and MA and MB are molecular masses of gas A and gas B respectively. Rate of diffusion should be proportional to the average speed of the molecules of a gas. If average speed of molecules of gas A and gas B are n_A and n_B then
\(\frac{u_{\mathrm{A}}}{u_{\mathrm{B}}}=\sqrt{\frac{\mathrm{M}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{A}}}}\)

Above equation can be used to determine the molar mass of gases.

→ Student’s Note: Though Graham’s Law of Diffusion is not included in the CBSE syllabus, but students are advised to go through it for various competitive examinations.

Kinetic Molecular Theory of Gases Postulates. Assumption of Kinetic Theory of Gases
1. Every gas is made up of a large number of extremely small particles called molecules. All the molecules of a particular gas are identical in mass and size and differ, in these from gas to gas.

2. The molecules of a gas are separated from each other by large distances so that the actual volume of the molecules is negligible as compared to the total volume of the gas.

3. The distances of separation between the molecules are so large that the forces of attraction or repulsion between them are negligible.

4. The force of gravitation on the molecules is also supposed to be negligible.

5. The molecules are supposed to be moving continuously in different directions with different velocities. Hence they keep on colliding with one another (called molecular collisions) as well as on the walls of the containing vessel.

6. The pressure exerted on the walls of the containing vessel is due to the bombardment of the molecules on the walls of the containing vessel.

7. The molecules are supposed to be perfectly elastic hard spheres so that no energy is wasted when the molecules collide with one another or with the walls of the vessel. The energy may, however, be transferred from some molecules to the other on collision.

8. Since the molecules are moving with different velocities, they possess different kinetic energies. However, the average kinetic energy of the molecules of a gas is directly proportional to the absolute temperature of the gas.

The behaviour of Real Gases
Deviation from ideal gas behaviour: A gas that obeys the ideal gas equation. (PV = nRT) at all temperatures and pressure is called Ideal Gas or Perfect Gas. Actually, none of the known gases obeys the ideal gas equation under all conditions of temperature and pressure. Such gases which do not obey the gas equation are called Real Gases.

However, most of the gases follow the ideal gas equation at low pressures and high temperatures. Appreciable deviation from the ideal gas behaviour is observed at low temperature and high pressure.

The temperature at which a real gas obeys the ideal gas law over an appreciable range of pressure is called Boyle Temperature or Boyle Point. Boyle point of a gas depends upon its nature.

A gas deviates from ideal behaviour when the product of the observed pressure and volume (P × V) is lower or higher than that expected from the ideal gas equation. Thus for a gas showing deviations from ideal behaviour (PV) observed < nRT
or
(PV)observed > nRT

Thus, to describe the behaviour of real gases, the ideal gas equation should be modified. This is conveniently done by inviting the ideal gas equation ‘in’ the form PV = Z(nRT).
or
Z = \(\frac{P V}{n R T}\)

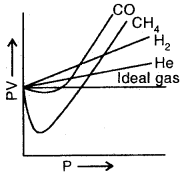
The plot of PV Vs Pressure for real and ideal gas

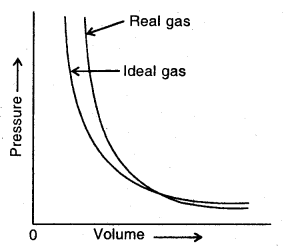
The plot of Pressure Vs Volume for real gas and ideal gas

Where Z can have a value of one, less than one or more than one. The factor Z is called Compressibility Factor.
(a) When Z = 1, then PV = nRT, i.e., the gas shows an ideal gas behaviour. For an ideal gas Z = 1 under all conditions of temperature and pressure.
(b) When Z < 1, the observed PV value is less than the value for an ideal gas. Thus the gas shows a negative deviation when Z < 1.
(c) When Z > 1, the observed PV value is higher than that for an ideal gas. So when Z > 1, the gas shows positive deviations.

Equation of state for Real Gases (Van der Waal’s equation)
The van der Waal’s equation for one mole of a real gas is written
(P + \(\frac{a}{v^{2}}\))(v-b) = RT
If n moles of a real gas is taken

The equation becomes
(P + \(\frac{a n^{2}}{v^{2}}\))(v – b) = nRT
Here ‘a’ and ‘b’ are called van der Waals parameters or constants which vary from gas to gas. Their value depends upon the gas nature.

The cause of the deviation is actually due to two faulty assumptions of the kinetic theory
They are

• There is no force of attraction and repulsion between the molecules of a gas.
• The volume of the molecules of a gas is negligibly small as compared to the empty space between them.

Derivation of van der Waal’s equation
1. Correction for volume: Suppose the volume occupied by the gas molecules is v. When the molecules are moving, their effective volume is four times the actual volume i.e., 4v. Let us called it b i.e. b = 4v (called excluded volume of co-volume). Thus the free volume available to the gas molecules for movement i.e.

Corrected volume = (V – b) for one mole
= (V – rib) for n moles

2. Correction for pressure. A molecule (A) lying within the vessel is attracted equally by other molecules on all sides but a molecule near the wall (B) is attracted (pulled back) by the molecules inside (Fig.) Hence it exerts less pressure. In other words, the observed pressure is less than the ideal pressure. Hence

Corrected pressure = P + p

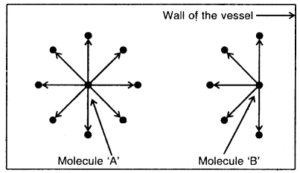
Backward pull on molecule B by other molecules

Evidently, the correction term p is proportional to density of the gas near the wall and the density of the gas inside i.e.
p ∝ (density)²
or
p ∝ d²
But d ∝ \(\frac{1}{V}\) for one mole
or
d ∝ \(\frac{1}{\mathrm{~V}^{2}}\) for 1 mole
or
p = \(\frac{a}{\mathrm{~V}^{2}}\)
or
p ∝ \(\frac{n^{2}}{\mathrm{~V}^{2}}\) for n moles
or
p = \(\frac{a n^{2}}{V^{2}}\)

∴ Corrected pressure = (P + \(\frac{a}{\mathrm{~V}^{2}}\)) for 1 mole
= (P + \(\frac{a n^{2}}{V^{2}}\)) for n moles
where a is constant depending upon the nature of the gas.

Substituting the correct values of volume and pressure in the ideal gas equation we get
(P + \(\frac{a}{\mathrm{~V}^{2}}\))(V – b) = RT for 1 mole
or
(P + \(\frac{a n^{2}}{V^{2}}\))(V – nb) = nRT for n moles

Significance of van der Waal’s constants
1. van der Waal’s constant ‘a’: Its value is a measure of the magnitude of the attractive forces among the molecules of the gas. The greater the value of ‘a’, the larger is the intermolecular forces of attraction.

2. van der Waal’s constant ‘b’: Its value is a measure of the effective size of the gas molecules. Its value is equal to four times the actual volume of the gas molecules. It is called excluded volume or co-volume.

Units of van der Waal’s constant
1. Units of ‘a’. As p = \(\frac{a n^{2}}{V^{2}}\)
∴ a = \(\frac{p \times V^{2}}{n^{2}}\)
= atm L² mol² or bar dm⁶ mol^-2

2. Units of ‘b’. As volume correction
v = nb,
∴ b = \(\frac{v}{n}\) = K mol^-1dm³mol^-1.

Explanation of the behaviour of Real gases by van der Waal’s equation
1. At very low pressure, V is very large. Hence the correction term a.V² is so small that it can also be neglected in comparison to V. Thus van der Waal’s equation reduces to the form PV = RT. This explains why at very low pressures, the real gases behave like ideal gases.

2, At moderate pressures, V decreases. Hence a/V² increases and cannot be neglected. However, V is still large enough in comparison to ‘b’ so that ’b’ can be neglected. Thus van der Waal’s equation becomes

Thus compressibility factor is less than 1. As pressure is increased at a constant temperature, V decreases so that the factor n/RTV increases. This explains why initially a dip in the plot of Z versus P is observed.

3. AT high pressures, V is so small that ‘b’ cannot be neglected in comparison to V. The factor a/V² is no doubt large but as P is very high, a/V² can be neglected in comparison to P. Thus van der Waal’s equation reduces to the form
P(V -b) = RT
or
PV = RT + Pb ⇒ \(\frac{\mathrm{PV}}{\mathrm{RT}}\) = 1 + \(\frac{\mathrm{P} b}{\mathrm{RT}}\)
or
Z = 1 + \(\frac{\mathrm{P} b}{\mathrm{RT}}\)

Thus compressibility factor is greater than 1. As P is increased (at constant T), the factor Pb/RT increases. This explains why after minima in the curves, the compressibility fact of increases continuously with pressure.

4. At high temperatures, V is very large (at a given pressure) so that both the correction factors (a/V² and b) become negligible as in case (i). Hence at high temperature, real gases behave like an ideal gas.

→ Explanation of the exceptional behaviour of hydrogen and helium may be seen that for H₂ and He, the compressibility factor Z is always greater than l and increases with the increase of pressure: This is because H₂ and He being very small molecules, the intermolecular forces of attraction in them are negligible i.e., V is very very small so that a/V² is negligible
P(V -b) = RT
or
PV = RT + Pb
or
\(\frac{\mathrm{PV}}{\mathrm{RT}}\) = 1 + \(\frac{\mathrm{PB}}{\mathrm{RT}}\)

Thus, \(\frac{\mathrm{PV}}{\mathrm{RT}}\) i.e., Z > 1 and increases with increase in the value of P at constant.

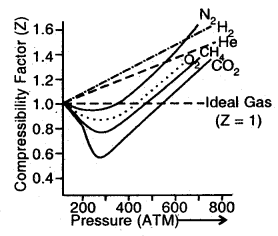
(a) Z vs P for different gases

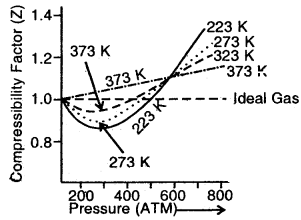
(b) Z as P to N₂ gas at different temperatures

Plots in Fig. (b) show that as the temperature increases, the minimum in the curve shifts upwards. Ultimately, a temperature is reached at which the value of Z remains close to 1 over an appreciable range of pressure. For example, in the case of N₂ at 323 K, the value of Z remains close to 1 up to nearly 100 atmospheres.

For a real gas Z = \(\frac{p V_{\text {real }}}{n \mathrm{RT}}\) ……….(1)
If the gas shows ideal behaviour then
V ideal = \(\frac{nRT}{p}\)
On putting the value of \(\frac{nRT}{p}\) in the above equation (1)
Z = \(\frac{\mathrm{V}_{\text {real }}}{\mathrm{V}_{\text {ideal }}}\)

Thus compressibility factor may also be defined as the ratio of actual molar volume of a gas to the molar volume of it if it were ideal at that temperature and pressure.

→ Liquefaction of Gases and Critical Point: At high pressures and lower temperatures deviation from ideal behaviour for gases is observed. At high pressures, molecules of the gas come closer and attractive forces start operating. As the temperature is lowered further, the attractive forces draw the molecules together to form a ‘liquid’. This temperature is called liquefaction temperature. It depends upon the nature of the gas and its pressure.

The critical temperature for gas is that temperature above which it is not possible to liquefy it, however large is the pressure applied on it. CO₂ gas remains a gas even when a pressure of 73 atmospheres is applied to it. However at this pressure when it is cooled to 30.98°C, it starts liquifying. So for CO₂ 30.98°C is its critical temperature. The volume of a gas at critical temperature is called its critical volume and pressure (73 atm. for CO₂) is critical pressure.

Critical pressure is the pressure required to liquefy the gas at the critical temperature. All three of them are collectively called critical constants of the gas and are represented by Tc, Pc and Vc. For example, critical constants of CO₂ are:
T_c = 31.1°C, P_c = 73.9 atm, V_c = 95.6 cm³ mol^-1

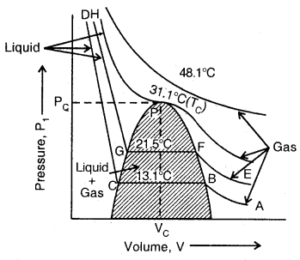
Isotherms of CO₂ (From Andrew’s experiment)

At the lowest temperature employed i.e., 13.1°C, at low pressure. CO₂ exists as a gas, as shown at point A. As the pressure is increased, the volume of the gas starts. Hence volume decreases rapidly along with BC because the liquid has much less volume than gas. At point C, liquefaction is complete. Now the increase in pressure has very little effect upon volume because liquids are very little compressible.

Hence a step curve CD is obtained. As the temperature is increased, the horizontal portion becomes smaller and smaller and at 31.1°C it is reduced at a point, P. This means that above 31.1°C, the gas cannot be liquefied at all, however, high pressure may be applied. Thus 31.1°C, is the critical temperature. The corresponding pressure to liquefy the gas at the critical temperature is its critical pressure, P (i.e., 73.9 atm). The volume occupied by 1 mole of the gas under these conditions is its critical volume, V. (i.e., 95.6 ml).

→ Liquid State: In liquids, intermolecular forces of attraction are much large than in gases. Unlike gases, liquids have a definite volume, but no definite shape. The molecules in a liquid are in constant random motion. The average kinetic energy of the molecules in a liquid is proportional to absolute temperature.

→ Vapour Pressure: Vapour pressure of a liquid at any temperature is the pressure exerted by the vapour present above the liquid in equilibrium with the liquid. The magnitude of vapour pressure depends upon the nature of, liquid and temperature. At equilibrium between the liquid and the vapour phase, the vapour pressure becomes steady or constant and at this stage, it is called Equilibrium Vapour Pressure or saturated vapour pressure.

The Boiling Point of a liquid is the temperature at which its vapour pressure becomes equal to external pressure. At 1 atm pressure boiling temperature is called the normal boiling point. If pressure is one bar, then the boiling point is called standard boiling point standard boiling point of a liquid is slightly lower than the normal boiling point (because 1 bar < 1 atm)

The normal boiling point of water is 100°C (373 K) and its standard boiling point is 99.6°C (373.6 K).

The Vapour pressure of a liquid increases with an increase in temperature, with more molecules of the liquid going into the vapour phase, the liquid becomes less dense and the density of the vapour phase increases. When the density of the liquid and vapours becomes the same the clear boundary between the liquid and the vapour disappears. This temperature is called the critical temperature of the liquid.

→ Surface Tension: The surface tension of a liquid is defined as the tangential force acting along the surface of a liquid at right angles along one unit length drew on the surface of the liquid.

It is the work done to increase the free surface area of any liquid by one unit at constant temperature and pressure.

The S.I. unit of surface tension is Nm^-1. The C.G.S. unit of surface tension is dyne^-1 cm^-1. The lowest energy state of the liquid will be when its surface area is minimum. Spherical shape satisfies this condition. Hence raindrops or mercury drops are spherical in shape. Liquids tend to rise in the capillary due to surface tension. Surface tension decreases as the temperature is raised. It has dimensions of kg s^-2. In terms of surface energy per unit area, its dimensions are Jm^-2. ,

→ Viscosity: Viscosity is a measure of resistance that arise due to the internal friction between layers of fluid as they slip past one another. It is the internal resistance to the flow of liquid. The liquids which flow rapidly have low internal resistance and hence are said to be less viscous, i.e., their viscosity is low. On the other hand, the liquids which flow slowly have high internal resistance and hence are said to be more viscous, i.e., their viscosity is high The viscosity of honey or glycerol is higher than, say, water.

The coefficient of viscosity is defined as the force applied per unit area which will maintain a unit relative velocity between the two layers of a liquid at unit distance from each other. It is represented by q. Liquids having low q values are called mobile while those having high q value are termed as viscous.

If f is the force required to maintain the flow of layers, then
f ∝ A [A is the area of contact]
f ∝ \(\frac{d u}{d Z}\)
or
f = ηA\(\frac{d u}{d Z}\); η is called coefficient of viscosity.

S.I. unit of viscosity coefficient is 1 newton second per square metre [Nsm^-2]

In the CGS system, its unit is poise
1 poise = 1 gm cm^-1 s^-1 = 10^-1 kg m^-1 s^-1

Viscosity decreases with an increase in temperature. Hydrogen bonding and van der Waal’s forces are strong enough to cause High viscosity.

→ van der Waals forces: Attractive intermolecular forces between interacting particles (atoms and molecules) are called van der Waals forces.

→ Dispersion Force/London Force: Atoms and non-polar molecules are electrically symmetrical and hence no dipole moment. But a dipole may develop momentarily even in such atoms and molecules. This force of attraction between two temporary dipoles is called the London force or dispersion force.

→ Dipole-Dipole Forces: Dipole-dipole forces act between the molecules possessing permanent dipole. The polar molecules interact with neighbouring molecules as in the case of HCl molecules.

→ Dipole-induced Dipole Forces: This type of attractive forces operate between the polar molecules having permanent dipole and the molecules lacking permanent dipole. The permanent dipole of the polar molecule induces dipole on the electrically neutral molecule by deforming its electronic cloud Thus an induced dipole is developed in the other molecule.

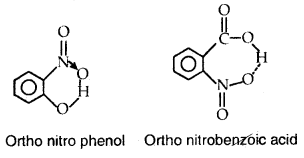
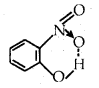
→ Hydrogen Bond: It is a special case of dipole-dipole interaction It is present in molecules having H-atom attached to a small-sized highly electronegative atom like F, O, N. The highly electronegative attracts H-atom of the neighbouring molecule through electrostatic force of attraction It is a weak bond and present in molecules like I IF, FRO, R-OH etc.

→ Thermal Energy: It is the energy of a body arising due to the motion of its atoms or molecules.

→ Boyle’s Law: At constant temperature, the volume of a given mass of a gas is inversely proportional to its pressure.

→ Charles’ Law: Pressure remaining constant, the volume of a given mass of a gas is directly proportional to its absolute temperature.

→ Isotherm: Each curve obtained on plotting different values of, pressure against volume at constant temperature is called Isotherm.

→ Isobar: Each line of the volume vs temperature graph at constant j pressure is called Isobar.

→ Kelvin temperature/Absolute temperature scale. It is obtained by adding 273.15 to the temperature on the Celsius scale.
Kelvin-Tem. = T = t°C + 273.15. It is also called the Thermodynamic ’ scale.

→ Absolute zero: The volume of all gases becomes zero at – 273.15°C. The lowest hypothetical or imaginary temperature at which gases cease to exist is called absolute zero.

→ Gay-Lussac’s Law: At constant volume, the pressure of a given j mass of a gas varies directly with the pressure.

→ Isochore: Each line of the graph obtained by plotting pressure vs Kelvin temperature at constant volume is called.Isochore.

→ Avogadro’s Law: Equal volumes of all gases under the similar condition of temperature and pressure contain an equal number of molecules.

→ Avogadro’s constant: The number of molecules in one mole of a gas is – 6.022 × 10²³ and the number 6.022 × 10²³ is called Avogadro’s constant.

→ Ideal Gas Equation.
PV = nRT
where P = Pressure,
V = volume,
R = Universal gas constant
n = no. of moles,
T = absolute temperature

For 1 mole of an ideal gas PV = RT.

Combined gas law \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)

→ Dalton’s Law of Partial Pressures: The total pressure exerted by the mixture of non-reactive gases is equal to the sum of partial pressures exerted by individual gases under similar conditions of temperature and volume.

→ Aqueous Tension: Pressure exerted by the saturated water vapour is called Aqueous Tension. ,

→ Compressibility Factor: The deviation of a gas from ideal behaviour can be measured in terms of compressibility factor Z which is the ratio of product pV and nRT.
Z = \(\frac{pV}{nRT}\)

→ Boyle Point or Boyle Temperature: The temperature at which a real gas obeys the ideal gas law is called Boyle point/temperature.

→ Critical Temperature: The temperature above which a gas cannot be liquified, however large may be the pressure applied on it.
Or
It is a temperature below which a gas can be liquified with the application of pressure is called its critical temperature (T_c) Critical Pressure: The pressure required to liquefy a gas at its critical temperature is called its critical pressure (P_c).

→ Critical Volume: The volume possessed by gas at its critical temperature is called its critical volume (V_c).

→ Boiling Point: It is a temperature at which the vapour pressure of a liquid becomes equal to external pressure.

→ Normal Boiling Point: At 1 atmospheric pressure, the boiling temperature of a liquid is called its normal boiling point.

→ Standard Boiling Point: If the pressure is 1 bar, the boiling temperature of the liquid is called standard boiling point, the standard boiling point of a liquid is slightly lower than the normal boiling point (as 1 bar is slightly < 1 atm).

→ Surface Tension: It is defined as the force acting per unit length perpendicular to the line drawn on the surface of the liquid.

→ Unit: Surface Tension (γ-Gamma) in S.I. scale = Nm^-1 V Its dimensions are kgs^-2.

→ Viscosity: It is a measure of the resistance of the flow of a liquid which arises due to internal friction between layers of it as they slip past one another while liquid flows.

Important Formulae
→ Boyle’s Law: At T constant
V ∝ \(\frac{1}{P}\)
or
PV = constant
If P₁, V₁ are the initial pressure, the volume of a gas at constant temperature and P₂, V₂ are its final pressure and volume respectively.
then P₁V₁ = P₂V₂

→ Charles’ Law: At constant pressure
V ∝ T, where T is the absolute temperature
or
\(\frac{V}{T}\) = Constant
or
\(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\)
or
\(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}=\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}\)
Gay Lassac’s Law : P ∝ T if volume is kept constant
or
\(\frac{P}{T}\) = constant

→ Ideal Gas Equation:
PV = nRT

→ Combined Gas Law:
\(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)

→ Coefficient of Viscosity : If the velocity of the layer at a distance dZ is changed by a value du, then velocity gradient is given by the amount \(\frac{d u}{d Z}\). The force required lo maintain the flow of layers is proportional to the area of contact of layers and velocity gradient,
i.e., f ∝ A [A is the area of contact]
f ∝ \(\frac{d u}{d Z}\)
∴ f ∝ A\(\frac{d u}{d Z}\)
or
f = ηA\(\frac{d u}{d Z}\)

where η is proportionality constant called coefficient of viscosity.
If A = 1 \(\frac{d u}{d Z}\) = 1
then f = η
Therefore, the Coefficient of viscosity is defined as the force when the velocity gradient is unity and the area of contact is unity.

SI unit of viscosity coefficient is 1 newton sec m^-2
= Ns m^-2 = pascal second
1 Pa s = 1 kg m^-1 s^-1

In CGS system coefficient of viscosity is poise
1 poise = 1 g cm^-1 s^-1 = 10^-1 kg m^-1 s^-1.

By going through these CBSE Class 11 Chemistry Notes Chapter 4 Chemical Bonding and Molecular Structure, students can recall all the concepts quickly.

Chemical Bonding and Molecular Structure Notes Class 11 Chemistry Chapter 4

Chemical Bond: The attractive force which holds various constituents (atoms, ions, etc.) together in different chemical species is called.a chemical bond.

There are various theories to explain the formation of a chemical bond. They are

1. Kossel-Lewis approach.
2. Valence-Shell Electron-Pair Repulsion (VSEPR) Theory
3. Valence Bond (VB) Theory
4. Molecular Orbital Theory.

Kossel-Lewis Approach to Chemical Bonding: All noble gases [except He] have 8 electrons in their valence shells. They are chemically inactive. In the case of all other elements, there are less than 3 electrons in the valence shells of their atoms, and hence they are chemically reactive.

“The atoms of different elements combine with each other in order to complete their respective octets (i.e8 electrons in their outermost shell) or duplet (i.e., the outermost shell having 2 electrons in case of H, Li, and Be) to attain stable inert gas configuration”.

Lewis Symbols: Writing symbols of elements with valence shell electrons represented by dots are called Lewis Symbols.

→ Significance: The number1 of valence electrons helps to calculate the common or Group Valence of the element. The group valence of the elements is generally either equal to the number of dots in Lewis Symbols or 8 minus the number of dots or valence electrons.

Facts for chemical bonding (Kossel)

1. The highly electronegative halogens and highly electropositive alkali metals are separated by noble gases in the periodic table.
2. The formation of a negative ion and a positive ion is due to the gain or loss of electrons by atoms.
3. The negative and positive ions thus formed attain the nearest noble gas configuration. The noble gases (with the exception of He which has a duplet of electrons) have a particularly stable outer shell configuration of eight (Octet) electrons, ns²np⁶.
4. The negative and positive ions are stabilized by electrostatic attraction.

Electrovalent or Ionic Bond: When a bond is formed by complete transference of electrons from one atom to another so as to complete their octets or duplets the bond is called an ionic or electrovalent bond. For example

→ Formation of Calcium chloride

→ Formation of MgO

The no. of electrons gained or lost during the formation of an ionic bond is called the electro valency of the elements.

Factors favoring the formation of an ionic bond.

1. Atom going to lose electrons must have low ionization enthalpy so that it can lose electrons readily. Elements of I and II. groups prefer to form, ionic bonds because they have low values of Ionisation enthalpy.
2. Elements that accept electrons must have a High Negative Value of electron gain enthalpy so that they can retain the electrons. Halogens have high values of E.G. enthalpy.
3. Lattice enthalpy should be high. This, in turn, depends upon.
   (a) Charge on the ion: Greater the charge on the ion, greater the lattice energy.
   (b) Size of the ions: Smaller the size of the ion, the greater the lattice energy.

→ Octet Rule: According to the electronic theory of chemical bonding as developed by Kossel and Lewis, atoms can combine either by transfer of valence electron’s from one atom to another (gain or loss) or by sharing valence electrons in order to have an octet in their valence shells. This is known as the Octet rule.

→ Covalent Bond: A covalent bond is formed as a result of the mutual sharing of electrons between the two atoms to complete their octet or duplet. No. of electrons contributed by each atom is called covalency.

If one pair of electrons (one electron from each atom) is mutually shared between the two atoms, a single covalent bond is formed.

If two pairs of electrons (two electrons from each atom) are mutually shared between the two atoms, a double covalent bond is formed.

If three pairs of electrons (three electrons from each atom) are mutually shared between the two atoms.


Lewis Representation of Simple Molecules (the Lewis Structures)
The Lewis dot structures provide a picture of bonding in molecules and ions in terms of the shared pairs of electrons and the octet rule. While such a picture may not explain the bonding and behavior of a molecule completely, it does help in understanding the formation and properties of the molecules to a large extent. Writing of Lewis dot structure m molecules is, therefore, very useful.

The Lewis-dot-structures can be written by adopting the following steps:
1. The total number of electrons required for writing the
structures is obtained by adding the valence electrons of the combining atoms. For example, in the CH₄ molecule, there are eight valence electrons available .for bonding (4 from carbon and 4 from the four hydrogen atoms).

2. For anions, each negative charge would mean the addition of one electron. For cations, each positive charge would result in the subtraction of one electron from the total number of valence electrons. For example, for the CO₃^2- ion, the 2- charges indicate that there are two additional electrons than those provided by the neutral atoms. For NH₄⁺ ion, 1+ charge indicates the loss of the electrons from the group of neutral atoms.

3. Knowing the chemical symbols of the combining atoms and
having knowledge of the skeletal structure of the compound (known or guessed intelligently), it is easy to distribute the total number of electrons as bonding shared pairs between the atoms in proportion to the total bonds.

4. In general the least electronegative atom occupies the central position in the molecule/ion. For example in the NF^–₃ and CO₃^2-, nitrogen and carbon are the central atoms whereas fluorine and oxygen occupy the terminal positions.

5. After accounting for the shared pairs of electrons for single bonds, the remaining electron pairs are either utilized for multiple bonding or remain as the lone pairs. The basic requirement being that each bonded atom gets an octet of electrons.

→ Lewis representation of a few molecules/ions are given in the table below:

Table: The Lewis Representation of Some Molecules

Each H atom attains the configuration of helium (a duplet of electrons)

→ Formal Charge: Lewis dot structures, generally, do not represent the actual shape of the molecules.

The formal charge of an atom in a polyatomic molecule or ion is the difference between the number of valence electrons in that atom in an isolated state or free State and the no. of electrons assigned to that atom in the Lewis structure.

Formal charge (F.C) on an atom in a Lewis structure = [total no. of valence electrons in the free atom] – [total no. of non-bonding or lone pair of electrons] – \(\frac{1}{2}\) [total no. of bonding (shared) electrons]

The molecule of O₃ can be considered

The atoms have been numbered 1. 2 and 3

The formal charge on

1. the central atom O marked 1
   = 6 – 2 – \(\frac{1}{2}\) [6] = + 1
2. the end O atom marked 2 = 6 – 4 – \(\frac{1}{2}\)[4] = 0
3. the end O atom marked 3 = 6 – 6 – \(\frac{1}{2}\)(2) = – 1

Hence we represent O₃ along with formal charges as follows:

Generally, the lowest energy structure is the one with the smallest formal charges on the atoms. The formal charge is a factor based on a pure covalent view of bonding in which electron pairs are shared equally by neighboring atoms.

Limitations of the Octet Rule: It is mainly useful to understand the structures of organic compounds and applies to the elements of the second period of the periodic table. But it is not universal.

1. The incomplete octet of the central atom: In some compounds, the number of electrons surrounding the central atom is less than eight. This especially is the case with elements having less than four valence electrons. Examples are LiCl, BeH₂ and BCl₃

Li, Be and B have 1, 2, and 3 valence electrons only. Other such compounds are AlCl₃ and BF₃.

2. Odd electrons molecules: In molecules with an odd number of electrons like nitric oxide, NO, and nitrogen oxide, NO₂, the octet rule is not satisfied for all the atoms.

3. The expanded octet Elements in and beyond the third period of the periodic table have, apart from 3s and 3p orbitals, 3d orbitals are available for bonding. In a number of compounds of these elements, there are more than eight valence electrons around the central atom. This is termed the expanded octet. The octet rule does not apply in such cases.

Some of the examples of such compounds and PF₃, SF₆, H₂SO_4, and a number of coordination compounds.

4. It is clear that the octet rule is based upon the chemical inertness of noble gases. However, some noble gases (Xenon and Krypton) also combine with oxygen and fluorine to form a number of compounds like XeF₂, XeF₄, SeOF₂, KIF_2, etc.

5. The theory does not account for the shape of molecules.

6. It does not explain the relative stability of the molecules being totally silent about the energy of a molecule.

Ionic or Electrovalent Bond: An ionic (or electrovalent) bond is formed by a complete transfer of one or more electrons from the atom of metal to that of a non-metal.

As a result of this electron transfer, the following changes occur in the reacting atoms.
(a) Both the atoms acquire stable noble gas configuration.
(b) The atom that loses its electrons becomes positively charged ions called a cation, whereas the atoms which gain these electrons becomes negatively charged ion called an anion.
(c) The two oppositely charged ions, i.e., ‘he cation and the anion, are then held together by the Coulomb forces of attraction to form an ionic bond.

Thus, an ionic bond that may be defined as the Coulomb force of attraction which holds the oppositely charged ions together is called an ionic bond.
1. Lattice Enthalpy (Lattice energy): The Lattice enthalpy of an ionic solid is defined as the energy required to completely separate one mole of a solid ionic compound into gaseous constituent ions. For example, the lattice enthalpy of NaCl is 788 kJ mol^-1. This means that 788 kJ of energy is required to separate to an infinite distance 1 mol of solid NaCl into 1 mol of Na⁺ (g) and mole of Cl^– (g).

For two atoms to form an ionic bond, the following factors are necessary

1. Low ionization enthalpy. The atom going to lose electrons must have a low value of ionization enthalpy.
2. High electron gain enthalpy. The atom going to accept electrons must have a high negative value of electron gain enthalpy.
3. High lattice enthalpy. The lattice energy of the compound should be high. The greater the charge on the ion and the smaller the size, the greater is the lattice enthalpy.

An ionic bond is formed if lattice energy and electron affinity took together are greater than ionization energy. The larger the negative value of lattice energy greater is than the stability of the ionic compound. The stability of an ionic compound is provided by its enthalpy of lattice formation and not simply by achieving an octet of electrons around the ionic species in a gaseous state.

Example of Ionic Bond

One Na⁺ is surrounded by C Cl^– ions and vice-versa Rock Salt Structure
1. Na⁺ Cl^– (Ionic Solid)


2. MgO

3. CaF2

Properties of Ionic solids:

1. Ionic compounds are solids, whereas covalent compounds can be solids, liquids, or gases.
2. Ionic compounds do not contain molecules but are made up of ions, whereas covalent compounds are molecular.
3. Ionic compounds have high melting points and boiling points due to strong electrostatic forces of attraction between ions. Covalent compounds, on the other hand, have low melting points and boiling points.
4. Ionic compounds are generally soluble in water or any polar
   solvent whereas covalent compounds are insoluble in water, but soluble in non-polar solvents.
5. Ionic compounds take part in ionic reactions whereas covalent compounds take part in molecular reactions.
6. Ionic bonds are non-directional in nature, whereas covalent bonds have directional characteristics.

Bond Parameters
1. Bond length: Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule. Bond lengths are measured by spectroscopic, X-ray diffraction, and electron diffraction techniques. Each atom of the bonded pair contributes to the bond length (Fig.) In the case of a covalent bond, the contribution from each atom is called the covalent radius of that atom.

The bond length in a covalent molecule AB
R = r_A + r_B (R is the bond length and r_A and r_B are the covalent radii of atoms A and B respectively)

The covalent radius is measured approximately as the radius of an atom’s core which is in contact with the core of an adjacent atom in a bonded situation. The covalent radius is half of the distance between two similar atoms joined by a covalent bond in the same molecule.

The van der Waals radius represents the overall size of the atom which includes its valence shell in a nonbonded situation. Further, the van der Waals radius is half of the distance between two similar atoms in separate molecules in a solid. Covalent and van der Waals radii of chlorine and depicted in Fig.

Covalent and van der Waals radii in a chlorine molecule. The inner circles correspond to the size of the chlorine atom (r_vdw and r₀ are van der Waals and covalent radii respectively)

2. Bond angle: It is defined as the angle between the orbitals containing bonding electron pairs around the central atom in a molecule/complexion. For example, the bond angle in water can be represented as under:

3. Bond enthalpy: It is defined as the amount of energy required to break one mole of bonds of a particular type between two atoms in a gaseous state.

The unit of bond enthalpy is kJ mol^-1 For example H-H bond enthalpy in hydrogen molecule is 435.8 kJ mol^-1
H₂ (g) → H (g) + H (g); ΔH = 435.8 kj mol^-1

4. Bond order: In the Lewis description of the covalent bond the bond order is given by the number of bonds between the two atoms in a molecule. The bond order in H₂ is one, in O₂ it is two and in N₂ it is three.

Isoelectronic molecules and ions have identical bond orders. For example F₂ and O₂^2- have bond order = 1.N₂, CO and NO⁺ have bond order 3.

The stabilities of molecules can be understood by the statement. With the increase in bond order, bond enthalpy increases and bond length decreases.

5. Resonance structures: According to the concept of resonance, whenever a single Lewis structure cannot describe a molecule accurately, a number of structures with similar energy, positions of nuclei, bonding, and non-bonding pairs of electrons are taken as the canonical structures of the resonance hybrid which describes the molecule accurately. Thus for Cl the two structures shown below constitute the canonical structures and their hybrid, (III, below) represents the structure of O, more accurately. Resonance is represented by a double-headed arrow.

Resonance in O₃ molecule. I and II represent the two canonical forms III is the resonance hybrid.

Some of the other examples of resonance structures are provided by the carbonate ion and the carbon dioxide molecule.
1. Carbonate ion (CO₃)

2. Carbon-dioxide

6. Electronegativity: The electronegativity is the ability of an atom of an element in a molecule to attract electrons towards itself in a shared pair of electrons.

Table: Difference between electronegativity and electron affinity (electron gain enthalpy)

7. Polarity of Bonds: An ionic bond is formed due to the complete transfer of electrons from one atom to another. A covalent bond is formed due to the mutual sharing of electrons. A covalent bond between two atoms of different elements is called a polar covalent bond. A polar bond is partly covalent bond and partly ionic. The percentage of ionicity in a covalent bond is called the percentage ionic character in that bond. The ionic character in a bond is expressed in terms of bond dipole moment (μ).

The dipole moment of a bond depends upon the difference in the electronegativity of the two atoms held together by the chemical bond.

The dipole moment of two and opposite charges is given by the product of the charge and the distance separating them. Thus
Dipole moment, μ = charge (q) × Distance separation (r)
= q × r

In the HCl molecule, the chlorine is more electronegative. Therefore, the bonding electrons lie closer to the chlorine atom. As a result, H- atom develops a slight positive (+q) and Cl^– atom a slight negative (-q) charge, thereby generating a dipole in the HC1 molecule.

For non-polar bonds, there is no charge separation. Therefore, q = 0. As a result, the dipole moment of a non-polar bond is zero.

Dipole moment and the ionic character in bonds: Ionic character in a covalent bond depends upon the difference between the electronegativity of two atoms. The greater the electronegativity difference, the greater is the charge separation, and therefore, the greater is the ionic character in the bond.

The valence shell electron pair repulsion (VSEPR) theory: The main postulates of the VSEPR theory are:

1. Pairs of electrons in the valence shell of a central atom repel each other.
2. These pairs of electrons tend to occupy positions in space that minimize repulsion and thus maximize distances between them.
3. The valence shell is taken as a sphere with the electron pairs localizing on the spherical surface at a maximum distance away from one another.
4. Multiple bonds are treated as if it is a single electron pair and the two or the three electron pairs of multiple bonds are treated as single super pair.
5. Where two or more resonance structures can depict a molecule, the VSEPR model is applicable to any such structure.

Predicting the shape of molecules on the basis of VSEPR theory: According to the VSEPR theory/the geometry of a molecule is determined by the number of electron pairs around the central atom. So to predict the geometry of the molecules, no. of electron pairs (both shared and one pair) should be known.

The repulsive interactions of electron pairs decrease in the order l – l – p > l – pb – p > b – pb – p repulsions.

The geometry of Molecules in which the Central Atom has No Lone Pair of Electrons


Shapes (Geometries) of some simple molecules/ions with central Ions having One or More Lone Pairs of Electron (E)


Shapes of Molecules containing Bond Pair and Lone Pair



Valence Bond Theory: The main postulates of the valence bond theory are:

1. A covalent bond is formed due to the overlap of the outermost half-filled orbitals of the combining atoms. The strength of the bond is determined by the extent of overlap.
2. The two half-filled orbitals involved in the covalent bond formation should contain electrons with opposite spins. The two electrons then move under the influence of both nuclei.
3. The completely-filled orbitals (orbitals containing two paired electrons) do not take part in the bond formation.
4. An s-orbital does not show any preference for direction. The non-spherical orbitals such as p-and d-orbitals tend to form bonds in the direction of the maximum overlap, i.e., along the orbitals axis.
5. Between the two orbitals of the same energy; the orbital which is non-spherical (e.g., p- and d-orbitals forms stronger bonds than the orbitals which are spherically symmetrical, e.g., s-orbital.
6. The valence of an element is equal to the number of half-filled orbitals present in it.

In the valence bond model, the stability of a molecule is explained in terms of the following type of interactions:
(a) electron-nuclei attraction interactions, i.e., the electrons of one atom are attracted by the nucleus of the other atom also.
(b) electron-electron repulsive interactions, i.e., electrons of one atom are repelled by the electrons of the other atom.
(c) nucleus-nucleus repulsive interactions, i.e., the nucleus of one atom is repelled by the nucleus of the other atom.

Valence Bond Description of Hydrogen molecule: A hydrogen molecule is a stable molecule. That is why one mole of H₂ molecules requires energy equal to 433 kJ to dissociate into hydrogen atoms, viz.
H₂ (g) + 433 kJ → 2H (g)

The formation of a hydrogen molecule from two hydrogen atoms may be considered to take place through the following steps:
Step 1. Consider two hydrogen atoms H_A and H_B at large separation from each other, so that there is no interaction between them. Since, there is no interaction between the two H atoms, hence the total energy is equal to the sum of the energies of the two H atoms. (Fig. a)

(a) No interactions at large distances

Step 2. Now, let the two H atoms approach each other. When the two atoms come closer new attractive and repulsive forces begin to operate. The electrons of one atom are attracted by the nucleus of the other atom. At this stage, both the electrons are attracted by both nuclei. Since, attractive interactions lead to a decrease of energy, hence as the two

(b) Interactions start as atoms come closer.
atoms approach each other the energy of the system starts decreasing. (Fig. b, e, d).

Step 3. When two hydrogen atoms, H_A and H_B come still closer the electron-electron (e^–_A — e^–_B) and the nucleus- nucleus repulsive interactions start operating. The repulsive interaction tends to increase energy. As long as the attractive interactions are stronger than the repulsive interactions, the energy of the system continues to decrease.

At a certain distance between the two atoms, the attractive and repulsive interaction balance each other, and the energy of the system attains a minimum value. At the state, two H atoms have a fixed distance between them and form a stable H₂ molecule. The internuclear separation when the energy of the system is minimum is called bond length The H—H bond length in H₂(g) is 75 pm (0.74 A).

New forces of attraction and repulsion between two H-atoms approaching each other

Step 4. Now, if the two H- atoms in an H₂ molecule are formed to come closer than the equilibrium internuclear separation (bond length: 74 pm), the repulsive forces start predominating and as a result, the energy of the system increases very sharply (Fig. above)

(d) Potential energy diagram showing the variation of energy with the internuclear distance between two H-atoms

2. Overlap of atomic orbitals: Various types of atomic orbitals overlap leading to the formation of covalent bonds are:
(a) s-s overlap: In this type of overlap, half-filled s-orbital of the two combining atoms overlap each other.

(b) s-p overlap: Here a half-filled s-orbital of one atom overlaps with one of the p-orbitals having only one electron in it.

(c) p-p overlap along the orbital axis: This is called head-on, end-on, or end-to-end linear overlap. Here, the overlap of the two half-filled p-orbitals takes place along the line joining the two nuclei.

(d) p-p sideways overlap: This is also called lateral overlap, in this type of overlap, two p-orbitals overlap each other along a line perpendicular to the internuclear axis, i.e., the two overlapping p- orbitals are parallel to each other.

The p-p sideways overlap

Hybridization of Atomic Orbitals:
Hybridization: It may be defined as the phenomenon of mixing of orbitals of nearly the same energy so as to redistribute their energies and to give rise to new orbitals of equivalent energies and shapes.

The new orbitals that are formed are called hybridized or hybrid orbitals. As a general rule, the number of hybrid orbitals produced from hybridization is equal to the number of orbitals that are mixed together. For example, when an s orbital is mixed with a p orbital two sp hybrid orbitals are produced. The two orbitals lie in a straight line and make an angle of 180°. Examples of molecules with sp hybrid orbitals are BeF₂ and CH ≡ CH (acetylene).

The ground state configuration of the boron is 1 s²2s²2p¹_x. If one of the 2s electrons is promoted to an orbital of a little higher energy, say 2p¹_y orbital, then the configuration 1s² 2s¹ 2p¹ 2p¹_y would result. The three equivalent orbitals formed from one 2s and two 2p orbitals are called sp² hybrid orbitals, which are coplanar and directed at an angle of 120° to each other as shown. The orbitals form a stronger bond than the sp orbitals.

sp³ Hybridization: The ground state configuration of carbon = 6 = 1s², 2s², 2p_x¹ 2p¹_y


4sp³ hybrid orbitals of C

The four sp³ hybrid orbitals are directed towards the four corners of the tetrahedron. The bond angles are 109°28′.

Example of sp³ hybridization: Shape of CH₄
The shape of CH₄ Molecule

4sp³ hybrid orbitais of C

Sigma (σ) and Pi (π) bonds
1. Sigma (σ) Bond: It is formed as a result of s-s, s-p, or p-p overlap axially or on the internuclear axis. A sigma bond îs strong as a result of overlapping on the internuclear axis.
1. Combination of s-orbitais

2. Combina Lion of s- and p- orbitais bond

3. End to end combination of two p-orbitals

2. Pi (π) Bond: When a bond is formed by the lateral or sideways overlapping of atomic orbitals, it is known as a pi (π) bond. A π bond is weaker than a bond as the overlapping is not effective and is made up of two half-electron-clouds, 1/2 above and 1/2 below the internuclear axis. It is always present in addition to a_o bond in molecules containing a double bond or a triple bond. Between two atoms forming a single covalent bond, it has to be a bond. A Pi (π) bond has no primary effect on the direction of the bond. It however shortens the internuclear distance.

The relative bond strength.has the order p-p < s-p < s-s

In addition to the sp hybridization in BeF2 sp² hybridization in BF3 and sp³ hybridization in CH4, we have hybridization involving d-orbitals also.

The elements of the third period contain d-orbitals also in addition to s and p orbitals. The 3d orbitals are comparable in energy to 3s and 3p orbitals.

Due to the availability of d orbitals, valencies of 5, 6, and 7 are also expected.
1. sp³d hybridization. This involves the mixing of one s three p and one d-orbitals. These orbitals hybridize to form five sp³d hybrid orbitals which are directed towards the corners of a regular trigonal bipyramidal geometry. For example, PF₅ has this geometry.

2. sp³d² hybridization. This involves the mixing of one-s orbital, three p, and two d-orbitals. These six orbitals hybridize to form, six sp³d² hybrid orbitals which are directed towards the corners of an octahedral geometry. For example, the SF₆ molecule has octahedral geometry.

3. sp³d³ hybridization. This involves the mixing of one s, three p, and three-d orbitals forming seven sp³d³ hybrid orbitals. These adopt pentagonal bipyramidal geometry. For example, IF₇ has this geometry.

4. dsp² hybridization. In this case, one d(^{d_x2_{– y}2}), one, and two p orbitals get hybridized to form four dsp2 hybrid orbitals. These hybrid orbitals have square planar geometry. For example [Ni(CN)₄]^2- ion.

Molecular Orbital Theory: Molecular orbital theory was developed by Hund and Milliken in 1932. The basic idea of molecular orbitals theory is that atomic orbitals of individual atoms combine to form molecular orbitals. The electrons in molecules are present in these molecular orbitals which are associated with several nuclei. These molecular orbitals are filled in the same way as the atomic orbitals in atoms are filled.

The molecular orbitals are formed by the combination of atomic orbitals of the bonded atoms.

The salient features of the Molecular orbital theory are:

1. The electrons in a molecule are present in the various molecular orbitals as the electrons of atoms are present in the various atomic orbitals.
2. The atomic orbitals of comparable energies and proper symmetry combine to form molecular orbitals.
3. While an electron in an atomic orbital is influenced by one nucleus, in a molecular orbital, it is influenced by two or more nuclei depending upon the number of atoms in the molecule. Therefore, we can call- a molecule orbital Polycentric.
4. The no. of MOs formed is equal to the no. of combining AOs. When two atomic orbitals combine, two MOs are formed. One is called bonding molecular orbital and the other is called an antibonding molecular orbital.
5. The bonding MO has lower energy and hence greater stability than the corresponding antibonding MO.
6. Just as the electron probability distribution around a nucleus in an atom is given by an atomic orbital the electron probability distribution around a group of nuclei in a molecule is given by a molecular orbital.
7. The MOs obey the Aufbau principle, Pauli Exclusion principle, and Hund’s rule like AOs.

Formation of Molecular Orbitals/Linear Combination of Atomic Orbitals (ICAO)
If φ_A and φ_B represent the wave functions of atomic orbitals A and B of hydrogen atoms forming hydrogen molecule, then
φ_MO = φ_A ± φ_B
Therefore the two molecular orbitals a and a* are formed as follows:
σ = φ_A + φ_B
σ* = φ_A – φ_B
where σ is called bonding molecular orbital and σ* is called an antibonding molecular orbital.

For example, s-orbitals of two hydrogen atoms combine to form two MOs — σ_1s and σ*_1s (bonding and antibonding MOs).

Similarly, 2s atomic orbitals may combine to form two MOs: σ2s and σ*2s.
If the 2 axes is assumed to be the internuclear axis, then 2p atomic orbitals combine to form sigma orbitals. The 2p_z atomic orbitals combine to form aMOs (σ2p_z, σ*2p_z) while 2p_x and 2p_y orbitals combine to form nMOs (π2p_x, π*2p_x, π2p_y, π*2p_y).

Energy Level Diagrams for Molecular Orbitals: 1s, 2s and 2p orbitals of two atoms combine to form bonding MOs: σ1s, σ2s, σ2p_z, π2p_x, π2p_y. and antibonding MOs:

σ*l s,’ σ*2s, σ*2p_z, π*2p_x and π*2p_y. The energy levels of these molecular orbitals have been determined experimentally by spectroscopic methods. It is observed that for diatomic molecules of the second period Li2 to Ne2 there are two types of energy levels of MOs. For molecules Li₂, Be₂, B₂, C_2, and N₂ the sequence of energies of MOs may be written as
σ1s, σ*ls, σ2s, σ*2s, π2p_x = π2p_y, σ2p_z, π*2p_x π*2p_y, σ*2p_z

On the other hand, for the molecule 02, F2 and Ne2.the sequence of energies of MOs are:
σ1s, σ1s, σ2s, σ*2s, σ2p_z, π2p_x = π2p_y, π*2p_x = π*2p_y, σ*2p_z.

The main difference between the two types of sequences is that for molecules O₂, F₂ and Ne₂, the σ2p_z MO is lower in energy than π2p_x and π2p_y MOs while in the case of molecules Li₂, Be₂, B₂, C_2, and N₂, σ2p_z MOs higher energy than π2p_x arid π2p_y MOs.

Bond Order: It is defined as the number of covalent bonds in a molecule. Bond order can .be calculated from the number of electrons in bonding and antibonding molecular orbitals as:

Bond order = \(\frac{\text {No. of electrons in bonding MOs-No. of electrons in anit-bonding MOs }}{2}\)
or
= \(\frac{\mathrm{N}_{b}-\mathrm{N}_{a}}{2}\)

The bond orders of 1, 2, or 3 correspond to the single, double, or triple bonds. But bond order may be fractional also in some cases.

Information Conveyed by Bond Order.

1. If the value of bond order is positive; it indicates a stable molecule and if the value of bond order is negative or zero, it means that the molecule is unstable.
2. The stability of a molecule is measured by its bond
   dissociation energy. But the bond dissociation energy is directly proportional to the bond order.
3. Bond order is inversely proportional to the bond length. The higher the bond order value, the smaller is the bond length.
4. If all electrons are doubly occupied in different molecular orbitals the molecule is diamagnetic. If there are one or more unpaired electrons, it is paramagnetic like O₂.

Conditions for the combination of Atomic Orbitals:

1. The combining atomic orbitals must have the same or nearly the same energy. This means that Is orbital can combine with another 1s, but not with 2s orbitals because the energy of 2s is appreciably higher than that of Is.
2. The combining atomic orbitals must have the same symmetry as the molecular axis.
3. The combining atomic orbitals must overlap to the maximum extent. In this type, sigma (σ) molecular orbitals are symmetrical around the bond axis while pi (π) molecular orbitals are not symmetrical. If the internuclear axis is taken to be in the Z-direction it can be seen that a linear combination of 2p_z-orbitals of two atoms also produces two sigma molecular orbitals σ2pz and σ*2p_z.

Molecular orbitals obtained from 2p_x and 2p_y orbitals are not symmetrical around the bond axis because of the positive lobes above and negative lobes below the molecular plane. Such molecular orbitals are labeled as π and π*. A π bonding MO has a large electron density above and below the internuclear axis. The σ* antibonding MO has a node between the nuclei.

Contoursmnd energies of bonding and antibonding molecular orbitals formed through combinations of (a) Is atomic orbitals; (b) 2p_z atomic orbitals and (c) 2p_x atomic orbitals

Molecular Orbital Electronic Configurations: Molecular orbital electronic configurations of some molecules/ions are given below:

→ Hydrogen Bond: The attractive force which binds the hydrogen atom of one molecule with the electronegative atom (F, O, N) of another molecule is known as a hydrogen bond.

A hydrogen bond is weaker than a covalent bond. The strength of a hydrogen bond ranges from 10 – 40 kJ mol^-1 while that of a normal covalent bond is of the order of 400 kJ mol^-1

Cause of formation of the hydrogen bond. When hydrogen is bonded to a strongly electronegative element, A (such as F, O, or N) the electron pair shared between the two atoms lies far away from the hydrogen atom. As a result, the hydrogen atom becomes highly electropositive with respect to the other atom, A.

Since the electrons are displaced towards A, it acquires partial charge (δ⁺). In other words, the bond H-A becomes polar and may be represented as H^δ+ – A^δ–. The electrostatic force of attraction between positively charged hydrogen- atom of one molecule and negatively charged atom of neighboring molecule results in the formation of the hydrogen bond. This may be represented as:

Conditions for Hydrogen Bonding: The conditions for hydrogen bonding are:

1. The molecule must contain a hydrogen atom attached to the highly electronegative atom (F, O, or N).
2. The size of the electronegative atom should be quite small. (HF), water (H₂O), ammonia (NH,) alcohols (ROH), carboxylic acids (RCOOH), amines (RNH₂), etc. Due to hydrogen bonding, some of the properties of these molecules are influenced.

→ Types of Hydrogen Bonds: Hydrogen bonding may be classified into two types.
(a) Intermolecular hydrogen bond: It is a hydrogen bond formed between two different molecules of the sai^e or different substances. This type of linking results in the association of molecules and increases the melting point, boiling point, viscosity, solubility, etc.

(b) Intramolecular hydrogen bond: Intramolecular hydrogen bond is formed between the hydrogen atom and the highly electronegative atom (F, O, or N) present in the same molecule. An intramolecular hydrogen bond results in the cyclization of the molecules and prevents their association. Consequently, the effect of intramolecular hydrogen bonds on physical properties is negligible.

For example, intramolecular hydrogen bonds are present in molecules such as o-nitro phenol, o-nitro benzoic acid, etc.
Ortho nitro phenol Ortho nitrobephobic acid

→ Chemical Bond: The force which holds the constituent atoms together with a molecule is called a chemical bond.

→ Electrovalent or Ionic bond: A bond formed by the complete transference of electrons from one atom to another to acquire the stable electronic configuration of the nearest gas is called an Ionic bond.

→ Electrovalency: The number of electrons so transferred (gained or lost) is called the electrovalency of the element.

→ Covalent Bond: When two atoms share the electrons mutually in order to complete their octet or duplet, the bond so formed is called a covalent bond.

→ Coordinate Bond: When the electron pair shared between the two atoms is donated by one of the two atoms, it is called a coordinate bond.

→ Sigma (σ) bond: When a bond is formed between the two atoms by the overlap of their atomic orbitals along the internuclear axis (end to end of head-on overlap) the bond so formed is called sigma (σ) bond.
It is due to s-s, s-p, p-p overlap.

→ Pi (π) Bond: It is formed by the side-wise or lateral overlap of only p-orbitals in a direction perpendicular to the internuclear axis.

1. Pi (π) bond is weaker than a sigma (σ) bond.
2. Whenever a Pi (π) bond is formed, it is formed in addition to a sigma (σ) bond in multiple bonds (a double or triple bond)
3. A single bond between the 2 atoms is always a sigma (σ) bond.

→ Bond length: The average distance between the centers of the nuclei of the two bonded atoms is called it’s the bond length.

→ Bond Enthalpy (Bond Energy): The energy required to break one mole of a particular type of bond so as to separate them into gaseous atoms is called bond dissociation energy or bond energy.

→ Dipole Moment: The product of the magnitude of charge (q) and the distance (d) between the centers of charges is called a dipole moment. Mathematically
Dipole moment = µ = q × d

→ Hybridization: It is the phenomenon of mixing of the atomic orbitals belonging to the same atom but having slightly different energies so that redistribution of energy takes place between them resulting in the formation of new orbitals of equal energies and identical shapes.

→ Hydrogen bonding: It can be defined as the attractive force which binds the hydrogen atom of one molecule with the more electronegative atom (like F, O, or N) of another molecule.

1. Intermolecular hydrogen bond: It is formed between two different molecules of the same or different compounds like H-bonds in water (H₂O), alcohol (R-OH), and HF.
2. Intramolecular hydrogen bond: It is formed between the H atom and the more electronegative atom (F, O, or N) within the same molecule as in o-nitrophenol.

→ Ionic compound: It is a three-dimensional aggregation of positive and negative ions in an ordered arrangement called the crystal lattice.

→ Valence Shell Electron Pair Repulsion (VSEPR) Theory: According to this theory used to explain the geometrical shapes of molecules-molecular geometry is determined by repulsions between lone pairs and bond pairs as follows: The order of these repulsions is lone pair-lone pair > lone pair-bond pair > bond pair-bond pair.

→ Bond Angle: It is defined as the angle between the orbitals containing bonding electron pairs around the central atom in a molecule or complexion.

The bond angle in the water of H-O-H is 104.5° as shown above.

→ Bond enthalpy: It is defined as the amount of energy required to break one mole of bonds of a particular type between two atoms in a gaseous state. The unit of bond enthalpy is kJ m-1.

→ Bond order: In the Lewis description of covalent bond, the Bond order is given by the number of bonds between the two atoms in a molecule, e.g., bond orders in H₂ (H-H), O₇(O = O), and N₂(N = N) are 1, 2 and 3 respectively.

→ Resonance: Whenever a single Lewis structure cannot explain all the observed properties of a molecule, a number of structures with almost similar energy, positions of the nuclei, bonding, and non-bonding pairs of electrons are taken as the canonical structures of the hybrid which describes the molecule accurately.

By going through these CBSE Class 11 Chemistry Notes Chapter 3 Classification of Elements and Periodicity in Properties, students can recall all the concepts quickly.

Classification of Elements and Periodicity in Properties Notes Class 11 Chemistry Chapter 3

Why do we need to Classify Elements?
At present 114 elements are known. Efforts to synthesise new elements are continuing. It is very difficult to study such a large number of elements individually and to study their properties separately. The necessity was felt to organise their knowledge in a systematic way by classifying the elements.

Genesis of Periodic Classification: Classification of elements into groups led to the development of Periodic Law and Periodic Table.

J. Dobereiner was the first who made several groups of three elements (Triads). In each case he noticed the middle element of each of the Triads had an atomic weight about halfway between the atomic weights of the other two elements. Also, the properties of the middle element were in between these of the other two elements. He referred to them as the Law of Triads. It worked for only a few elements.

Dobereiner’s Triads:

J.A. Newlands propounded the Law of Octaves. He arranged the elements in increasing order of their atomic weights and noted that every eighth element has properties similar to the first element like the octaves of music – sa, re, ga, ma, pa, dha, nee, sa Newland’s Law of Octaves seemed to be true only for elements up to calcium.

Newlands Octaves:

Russian chemist Mendeleev and German chemist Lothar Meyer working independently, let to the Periodic Law as we know it today. Mendeleev succeeded in arranging the elements in vertical columns called groups and horizontal rows called periods in his table based upon the increasing order of their atomic masses. He gave his well- known law:

”The properties of the elements are a periodic function of their atomic weights”. It was called Mendeleev law. He realised that .some of the elements did not fit in with his scheme of classification if the order of atomic weights was strictly followed. He ignored the order of atomic weights and placed the elements -with similar properties together. For example, iodine with a lower atomic weight than that of tellurium (Group VI) was placed in Group VII along with other halogens F, Cl, Br because of similarities in properties.

He left some gaps for elements that were yet undiscovered. For example, both gallium (Ga) and germanium (Ge) were unknown at his time: He left the gap below aluminium and a gap below silicon and called these elements Eka-Aluminium and Eka-Silicon. The boldness of Mendeleev’s quantitative predictions and their eventual success made him and his Periodic Table famous. Mendeleev’s periodic table published in 1905 is shown.

Characteristics of Mendeleev’s Periodic Table:
It consists up of

1. Eight vertical columns called groups. Except for the VIII group, each group is. further subdivided in A and B. This subdivision is made on the basis of difference in their properties.
2. Six horizontal row called periods.

Significance of Mendeleev’s Periodic Table

1. Instead of studying properties of elements separately, they can be studied in groups containing elements with the same properties. It led to the systematic study of the elements.
2. Prediction of new elements. At his time only 56 elements were known. He left blank spaces or groups for unknown elements.
3. Mendeleev’s periodic table corrected the doubtful atomic weights.

Defects in the Mendeleev’s Periodic Table

1. Hydrogen was placed in group IA. However, it resembles both groups IA elements (alkali metals) and group VII A (halogens). Therefore the position of hydrogen in the periodic table is Anomalous or Controversial.
2. Anomalous pairs of elements. Some elements with higher atomic weight like Argon (39.9) precede potassium (39.1) with lower atomic weight.
3. Based upon atomic weights, isotopes of an element could not be assigned to different groups. They have been assigned only one position in a group.
4. Some dissimilar elements are grouped together while some similar elements are placed in different groups. For example, alkali metals in group IA which are highly reactive are in the same group as coinage metals like Cu, Ag, Au of group IB. At the same time, certain chemically similar elements like Cu (group IB) and Hg (group IIB) have been placed in different groups.
5. Position of elements of group VIII. No proper place has been allotted to nine elements of group VIII which have been arranged in three triads without any justification.

Mendeleev’s Periodic Table published in 1905

Modern Periodic Law and the present form of the Periodic Table.
Modern Period Law: The physical and chemical properties of the elements are periodic functions of their atomic number.

According to the recommendations of IUPAC, the groups are numbered from 1 to 18 replacing the older notation of groups 0, 1A, II A

There are 7 periods. The first period contains 2 elements. The subsequent periods contain 8, 8, 18, 18 32 elements respectively. The 7th period is incomplete and like the 6th period would have a theoretical maximum of 32 elements. In this form of Periodic Table, the elements of both the sixth and seventh periods (lanthanoids and actinoids respectively) are placed in Separate panels at the bottom.

Long Form of Periodic Table
General characteristics of the long form of the Periodic table:
1. There are in all, 18 vertical columns or 18 groups in the long-form periodic table.

2. These groups are numbered from 1 to 18 starting from the left.

3. There are seven horizontal rows called periods in the long-form periodic table. Thus, there are seven periods in the long-form periodic table.

4.  The elements of group 1, 2 .and 13 to 17 are called the main group elements. These are also called typical or representative or normal elements.

5. The elements of group 3 to 12 are called transition elements.

6. Elements with atomic number 58 to 71 (Ce to Lu) occurring after lanthanum (La) are called Lanthanides. Elements with atomic numbers 90 to 103 (Th to Lr) are called Actinides. These elements are called f-block elements and also inner-transition elements.


Long-form of the Periodic Table of the EIenient with their atomic numbers and ground state outer
electronic configurations. The groups are numbered i-18 in accordance with the 1984 IUPAC recommendations. this notation replaces the old numbering scheme of IA-VIIA, 4dIII, IB—VIIB and I) for the elements.

Nomenclature of the Elements with Atomic No. > 100
Table: Nomenclature of elements with atomic number above 103

Notation for IUPAC Nomenclature of Elements

Electronic Configuration of the Elements and Periodic Table: In the long-form periodic table, the elements are arranged in the order of their atomic numbers. An atomic number of an element is equal to the number of protons inside the nucleus of its atom. In an atom, the number of electrons is equal to the number of protons (hence equal to the atomic number). As a result, there is a close connection between the electronic configurations of the elements and the long form of the periodic table.

Table: The relationship between the electronic configuration of electrons and their positions in the periodic

Electronic Configuration in Periods: The period indicates the value of n- for the outermost or valence shell. In other words, a successive period in the Periodic Table is associated with the filling of the next higher principal energy level (n = 1, n = 2, etc.). It can be readily seen that the number of elements in each period is twice the number of atomic orbitals available in the energy level that is being filled.

→ The first period (n = 1) starts with the filling of the lowest level (1s) and therefore has two elements hydrogen (1s¹) and helium (1s²) when the first shell (K) is completed. The second period (n = 2) starts with lithium and the third electron and has the electronic configuration 1s22s2. Starting from the next element boron, the 2p orbitals are filled with electrons when the L shell is complete at neon (2s²2p⁶).

→ Thus there are 8 elements in the second period. The third period (n = 3) begins at sodium, and the added electron enters a 3s orbital. Successive filling of 3s and 3p orbitals gives rise to the third period 8 elements from sodium to argon. The fourth period (n = 4) starts at potassium, and the added electrons fill up the 4s orbital.

→ Now you may note that before the 4p orbital is filled, filling up of 3d orbitals becomes energetically favourable and we come from scandium (Z = 21) which has the electronic configuration 3d¹, 4s². The fourth period ends at krypton with the filling up the ‘Ip orbitals. Altogether we have 18 elements in this fourth period. The fifth period (n = 5) beginning with rubidium is similar to the fourth period and contains the 4d transition Serietarting at yttrium (Z = 39). This period ends al xenon with the filling up of the Sp orbitals.

→ The sixth period (n = 6) contains 32 elements and successive electrons enter 6s, 4f, Sd and 6p orbitals, in the order-filling up of the 4f orbitals begins with caesium (Z = 58) and ends at lutetium (Z = 71) Lo give 4f-inner transition series which is called lanthanoid sêries. The seventh period (n = 7) is similar to the sixth period with the successive filling up of the 7s, 5f, 6d and 7p orbitals and includes most of the man-made radioactive elements.

→ This period will end at the elements with atomic number 118 which would belong to the noble gas family. Filling up of the 5f orbital after actinium (Z = 80) gives the 5f-inner transition series known as the actinoid series. The 4f- and 5f- transition series of elements are placed separately in the Periodic Table to maintain its structure and to preserve the principle classification by keeping elements with similar properties in a single column.

Thus it can be seen that the properties oían element have periodic dependence upon its atomic number and not on relative atomic mass. All the elements in the same group have the same number of electrons (ns¹ in alkali metals) in their valence shells and thus have, same properties.

Electronic Configurations and Types of Elements s-, p-, d-, f-Blocks:
The Aufbau (build-up) principle and the electronic configuration of atoms provide a theoretical foundation for periodic classification. The elements in a vertical column of the Periodic Table constitute a group or family and exhibit similar chemical behaviour. This similarity arises because these elements have the same number and same distribution of electrons in their outermost orbitals. We can classify the elements into four blocks viz., s-block, p-block, d- block and f-block depending on the type of atomic orbitals that are being filled with electrons. We notice two exceptions to this categorization.

Strictly, helium belongs to the s-block but its positioning in the p-block along with another group of 18 elements is justified because it has a completely filled valence shell (1s²) and as a result, exhibits properties characteristic of other noble gases. The other exception is hydrogen. It has alone s-electron and hence can be placed in group-1 (alkali metals). It can also gain an electron to achieve a noble gas arrangement and hence it can behave similarly to group 17 (halogen family) elements. Because it is a special case, hydrogen is placed separately at the top of the Periodic Table.

→ The s-Block Elements: The elements of group 1 (alkali metals) and group 2 (alkaline earth metals) which have ns1 and ns² outermost electronic configuration belong to the s-Block Elements. They are all reactive metals with low ionization enthalpies. They lose the outermost electron(s) readily to form + lions (in the case of alkali metals) or + 2ion (in the case of alkaline earth metals). The metallic character and the reactivity increase as we go down the group. Because of high reactivity, they are never found pure in nature. The compounds of the s-block elements, with the exception of those of lithium and beryllium, are predominantly ionic.

→ The p-Block Elements: The p-Block Elements comprise those belonging to groups 13 to 18 and these together with the s-block elements are called the Representative Elements or Main Group Elements. The outermost electronic configuration varies from nsTnpl to ns²np⁶ in each period. At the end of each period is noble gas elements with a closed valence shell ns2np6 configuration.

All the orbitals in the valence shell of the noble gases are completely filled by electrons and it is very difficult to alter this stable arrangement by the addition or removal of electrons. The noble gases thus exhibit very low chemical reactivity Preceding the noble gas family are two chemically important groups of non-metals. They are the halogens (Group 17) and the chalcogens (Group 16).

These two groups of elements have high negative electron gain enthalpies and readily add one or two electrons respectively to attain the stable noble gas configuration. The non-metallic character increases as we move from left to right across a period and the metallic character increases as we go down the group.

→ The d-Block Elements (Transition Elements): These are the elements of Group 3 to 12 in the centre of the Periodic Table These are characterised by the filling of inner (n – 1) d orbitals by electrons and are therefore referred to as d-Block Elements. These elements have the outer electronic configuration (n – 1)d^1-10ns^1-2. They are all metals. They mostly form coloured ions, exhibit variable valence (oxidation .states), paramagnetism and are often used as catalysts.

However, Zn > Cd and Hg which have, the electronic configuration, (n – 1)d¹⁰ns² do not show most of the properties of transition elements. In a way, transition metals form a bridge between the chemically active metals of s-block elements and the less active metals of Groups 13 and 14 and thus take their familiar name “transition elements”.

→ The f-Block Elements (Inner-Transition Elements): The two rows of elements at the bottom of the Periodic Table, called the Lanthanoids, Ce (Z = 58) – Lu (Z = 71) and Actinoids, Th (Z = 90) – Lr (Z = 103) are characterised by the outer, electronic configuration (n – 2)f^1-14(n – 1)d^0-1 ns². The last electron added to each element is an f-electron.

These two series of elements are hence called the inner- transition elements (f-Block Elements). They are all metals. Within each series, the properties of the elements are quite similar. The chemistry of the early -actinoids .is more complicated than the corresponding lanthanoids, due to a large number of oxidation states possible for these actinoid elements.

Actinoid elements are radioactive. Many of the actinoid elements have been made only in nanogram quantities or even less by nuclear reactions and their chemistry is not fully studied. The elements after uranium are called transuranium elements.

The Lanthnoids show predominantly an oxidation state of + 3 (with a few exceptions + 2 or + 4) whereas Actinoids show variable oxidation states.

Metals, Non-Metals and Metalloids: The elements can be divided into Metals and Non-metals. Metals comprise more than 78% of all known elements and appear on the left side of the Periodic Table. Metals are usually solids at room temperature (mercury is an exception; gallium and caesium also have very low melting point 300K and 302K respectively). Metals usually have high melting and boiling points. They are good conductors of heat and electricity. They are malleable (can be flattened into thin sheets by hammering) and ductile (can be drawn into wires). In contrast, non-metals are located at the top right-hand side of the Periodic Table.

In fact, in a horizontal row, the property of elements change from metallic on the left to non-metals on the right. Non-metals are usually solids or gases at room temperature with low melting and boiling points (boron and carbon are exceptions). They are poor conductors of heat and electricity. Most non-metallic solids are brittle and are neither malleable nor ductile. The elements become more metallic as we go down a group; the non-metallic character increases as one goes from left to right across the Periodic Table.

The change from metallic to non-metallic character is not abrupt. The elements (e.g.r silicon, germanium, arsenic, antimony and tellurium) bordering this line and running diagonally across the Periodic Table show properties that are characteristic of both metallic and non-metals. These elements are called Semi-Metals or Metalloids.

Periodic Trends in Properties of Elements:
1. Ionization Enthalpy: The amount of energy required to remove the most loosely bound electron from an isolated gaseous atom in its ground state is called ionisation enthalpy.
X (g) → X(g) + e^–

The energy required to remove the first electron is known as the first ionization enthalpy and the second electron is the second ionization enthalpy and so on. The second ionization enthalpy is always greater than The first ionization enthalpy because once an electron is removed, it becomes a positive ion and its nucleus has increased attraction for electrons. This makes it more difficult to remove the second electron.

Ionization enthalpy decreases from top to bottom in a group and increases horn left to right in a period. Thus Cs has the lowest ionization enthalpy and fluorine has the highest ionization enthalpy. Thus IE₃ > IE₂ > IE₁. IE of Li > Na > K > Rb > Cs and IE of Li in 2nd Period is lowest, whereas that of Na is highest.

The ionization enthalpy depends on two factors:

1. The attraction of electrons to the nucleus.
2. The repulsion of electrons from each other.

Screening or Shielding effect: A valence electron in a multi-electron atom is pulled by the nucleus And repelled by the other electrons in the core (inner shells). Thus the effective pull on the electron will be the pull due to the positive nucleus, less the repulsion due to core electrons.

The effective repulsive effect to the core electrons is called the screening or shielding effect. For example, the 2s electron in lithium is shielded by the inner core of Is electrons. As a result valence electron experiences a net positive charge less than + 3. In general, shielding is effective when the orbitals in the inner shells are completely filled.

2. Electron Gain (Enthalpy ΔegH): It is defined as the enthalpy change when a neutral gaseous atom takes up extra electrons to form an anion.
X(g) + e^– → X^– (g)

The value of electron gain enthalpy depends upon the atomic size, nuclear charge etc. with an increase in size, the electron gain enthalpy decreases as the nuclear attraction decreases. Thus electron gain enthalpy generally decreases in going from top to bottom in a group (F < Cl > Br > I). In a period from left to right, the electron gain enthalpy generally increases due to an increase in nuclear charge.

Thus halogens have very high electron affinity. However, the electron affinity of fluorine is less than that of chlorine. This is because fluorine has a small atomic size (only two shells). Also, electron repulsion is more in the case of fluorine, because of mutual electron-electron repulsions.

Factors affecting electron gain enthalpy:

1. Atomic size: Smaller the atom, the greater is the magnitude of the electron gain enthalpy. This is because the added electron can go closer to the nucleus and as a result releases more energy.
2. Effective nuclear charge: Greater the nuclear charge, the larger is the magnitude of electron gain enthalpy. This is because the electron would experience stronger attraction by virtue of a higher nuclear charge.
3. Electronic configuration of the atom: An atom with a stable electronic configuration has a little or no tendency to add another electron. As a result, such elements have zero, or nearly zero electron gain enthalpy.

Periodic Variation of Electron gain enthalpy:
1. Variation of electron gain enthalpy in a group: The magnitude of the electron gain enthalpy of elements decreases in going from top to bottom in a group. However, the electron gain enthalpy of fluorine is lower than that of chlorine.

On moving from top to the bottom of a group,
(a) the-atomic size increases and
(b) the nuclear charge also increases.

The effect of these factors is opposite to each other. In group, the effect of an increase in the atomic size outweighs the effect of the increased nuclear charge. As a result, the tendency to accept an electron in its valency. shell and hence the magnitude of electron gain enthalpy decreases as we go down the group.

2. Variation of electron gain Enthalpy in a period: The magnitude of electron gain enthalpy increases across a period is going from left to right.

On moving from left to right in a period, the size of the atoms decreases, and the effective nuclear charge increases. Both these factors increase the force of attraction exerted by the nucleus on the electrons. As a result, the atom has a greater tendency to gain an extra electron from outside and therefore, the magnitude of electron gain enthalpy increases in going from left to right. However, some elements in each period show an exception to such periodicity. For example, Be, Mg, N, P and noble gases show very low, or even zero electron gain enthalpies.

Periodic Variation of Atomic and Ionic Radii: Atomic radius is one half of the distance between the nuclei of two identical atoms in a molecule bonded by a single bond. In a period, as, we move from left to right, the number of shells remain the same but as more electrons are added the nuclear charge increases.

This results in an increase in the number attraction for the electrons, which in turn brings about a decrease in the radius of the elements in a period. Thus, the radius decreases along a period (from left to right). However, in a group from top to bottom; the number of shells increases, therefore, the radius also increases, e.g., r_Li < r_Na < r_K < r_Rb < … etc.

→ Ionic Radius: Ionic radius may be defined as “the effective distance from the centre and*nucleus of an ion up to which it has an influence on its electron cloud”.

→ Variation of Ionic radii in a group: The ionic radii of the ions belonging to the same group of elements and having identical charges, increases in going from top to bottom in a group. For example, the radii of the monovalent alkali metal ions increase from Li⁺ to Cs⁺.

→ Variation of the radii of isoelectronic ions: Atoms/ions of different elements having the same number of electrons are called isoelectronic ions. In other words, the ions which have the same number of electrons but different nuclear charges are called isoelectronic ions. The size of such ions depends upon the nuclear charge (as the total number of electrons remains the same).
Thus N^3- > O^2- > F^– > Na⁺ > Mg²⁺ > Al³⁺
Thus for isoelectronic ions, the ionic size decreases as the nuclear charge increases.

Cations are always smaller than their parent atoms because of

1. the disappearance of the valence shell in some cases
2. increase in effective nuclear charge.
   Thus Na⁺ < Na and Mg²⁺ < Mg.

Anions are always bigger in size than their parent atom. With the addition of one or more electrons to an atom, the effective nuclear charge per electron decreases. The electron cloud thus increases leading to an increase in the size of the anion.
Thus, F^– > F; Cl^– > Cl; O^2- > O; S^2- > S and so on.

→ Electronegativity: The ability of an atom in a chemical compound to attract the shared pair of electrons towards itself is called Electronegativity. It is not a measurable quantity, unlike IE and electron gain enthalpy. L Pauling gave numerical values of electronegativities to elements. F has been given a value of 4.0 arbitrarily, the highest in the periodic table. Electronegativity values are not constant. Electronegativity generally decreases from top to bottom in a group and increases across a period from left to right.

Electronegativity values (Pauling scale) across a period

Within a Group

Periodicity of Valence: Valence is the most characteristic property of the elements and is based upon electronic configurations. The valence of representative elements is usually (though not necessarily) equal to the number of valence electrons arid or equal to eight minus the number of outermost electrons.

→ Anomalous Behaviour of Second Period Elements:
The first element of each of the groups 1 (lithium) and 2 (beryllium) and groups 13-17 (boron to fluorine) differs in many respects from the other, members of their respective group. For example, lithium unlike other alkali metals, .and beryllium unlike other alkaline earth metals, form compounds with pronounced covalent character, the other members of these groups predominantly form ionic compounds.

In fact, the behaviour of lithium and beryllium is more similar to the second element of the following group i.e., magnesium and aluminium, respectively. This sort of similarity is commonly referred to as a diagonal relationship in the periodic properties.

→ What are the reasons for the different chemical behaviour Of the first members of a group of elements in the s- and p- blocks compared to that of the subsequent members in the same group?

The anomalous behaviour is attributed to their small size) large charge/radius ratio and high electronegativity of the elements. In addition, the first member of the group has only four valence orbitals (2s and 2p) available for bonding, whereas the second member of the groups has nine valence orbitals (3s, 3p, 3d). As a consequence of this, the maximum covalency of the first member of each group is 4, whereas the other members of the groups can expand their valence shell to accommodate more than four pairs of electrons.

Furthermore, the first member of p-block elements displays greater ability to form p_π – p_π multiple bonds to itself (e.g., C = C, C ≡ G, N = N, N ≡ N) and to other second period elements (e.g., C = O, C = N, C ≡ N, N = O) compared to subsequent members of the same group.

1. Lothar-Meyer Arrangement of Elements: When plotting a graph between the atomic volumes (gram atomic weight divided by density) and atomic weights of the elements he observed that the elements with similar properties occupied similar positions on the curve.

2. Mendeleev’s Periodic Law: The physical and chemical properties of elements are a periodic function of their atomic weights.

3. Moseley’s/Modem Periodic Law: The physical and chemical properties of the elements are a periodic function of their atomic numbers.

4. Periodicity of Properties of Elements: According to Modem Periodic Law the properties of the elements are repeated after certain regular intervals when these elements are arranged in order of their increasing atomic numbers. These regular intervals 2, 8, 8, 18, 18, 32 are called Magic Numbers.

5. Cause of Periodicity: The cause of periodicity in properties is the repetition of similar electronic configurations of the valence shells after certain regular intervals.

6. Groups: The vertical columns of elements in the periodic table are called Groups.

7. Periods: The horizontal rows of elements in the periodic table are called Periods:

→ There are 18 groups and 7 periods in the Modern Periodic Table
1. s-block Elements: These are the elements in which the last electron enters the s-subshell of the valence orbit.

2. p-Block Elements: The p-block elements are those in which the last electron enters the p-subshell of the vaLence orbit. The elements of groups 13, 14, 15, 16, 17, 18 (excluding helium) in which p-orbitals are being progressively filled in are called p-block elements. Since each group has five elements, therefore, ¡ri all, there are 30 p-block elements in the periodic table.

The elements of the 18th group are called noble gases.
General outer shell electronic configuration of p-block elements: ns2 np1 6

3. d-Block Elements: Elements in which the last electron enters any one of the five d-orbitals of their respective penultimate, i.e., (n – 1)the shells are called d-bock elements.

Transition Elements: Since the properties of these elements are midway between those of s-block and p-block elements, they are called Transition Elements.

General outer shell electronic confìguration of d-block elements: (n—1)d^1-10 n².
Zn, Cd, Hg do not show most of the properties of transition elements.

4. f-Block Elements: Elements in which the last electron enters any onè o the seven f-orbitals of their respective ante-penultimate shells are called f-block elements. In all these elements, the s-orbital of the last shell (n.) is completely filled, the d-orbital of the penultimate (n – 1) shell invariably contains zero or one electron but the J-orbitals of the antepenultimate (n – 2) shell (being lower in energy than d – orbitals of the penultimate shell) gets progressively filled in. Hence

General outer shell electronic configuration.off-block elements: (n – 2)^0-14 (n – 1) d^0-1 ns²

→ They are called Lanthanides/Lanthanones/Lanthanoids. In their case, the antepenultimate 4/subshell is being filled up.

→ They are called Actinides/Actinones/Actinoids if their antepenultimate 5/subshell is being b lied up.

All the actinoids are radioactive elements.

→ Elements from neptunium to lawrencium (₉₃Np – ₁₀₃Lr) which have been prepared artificially through nuclear reactions are called Transuranic or Transuranium elements as (hey follow uranium in the periodic table.

→ Metalloids: The elements like silicon, germanium, arsenic, antimony and tellurium (Si, Ge, As, Sb, Te) which show the properties of both metals and non-metals are called Metalloids.

→ Ionization Enthalpy: The minimum amount of energy required to remove the most loosely bound electron from an isolated gaseous atom of an element is called it’s Ionization Energy/Ionization Potential/Ionization Enthalpy.
M (g) + energy → M+ (g) + e^– (g)

→ Units of I.E.: electron volts (eV) per atom
or
kilo calories per mole (k cal mol^-1)
or
kilo Joules per mole (kj mol^-1)

1 eV per atom = 23.06 kcal mol^-1
= 96.49 kj mol^-1.

→ Successive I.Es.
IE₃ > IE₂ > IE₁
where M (g) + IE₁ → M⁺ (g) + e^– (g)
M⁺ (g) + IE₂ → M²⁺ (g) + e^– (g)
M²⁺ (g) + IE₃ → M³⁺ (g) + e^– (g)

→ Variation of IE across a period: It generally increases from left to right in a period.

→ Variation of IE within a group: It generally decreases from top to bottom within a group.

→ Electron Gain Enthalpy of an element may be defined as the energy released when a neutral isolated gaseous atom accepts an extra electron from outside.
X(g) + e^– → X^– (g); ΔH = Δ_egH

→ Variation across a period: In general, it becomes more and more negative from left to right in a period.

→ Variation within a group: In general, it becomes less negative as we move down a group.

→ Atomic Radius: The average distance from the centre of the nucleus to the outermost shell containing electrons.

They are of three types:

1. Covalent radius
2. Vander Waal’s radius
3. Metallic radius

→ Variation across a period: In general it decreases in a period with an increase in atomic number from left to right.

→ Variation within a group: It increases with the increase in atomic number from top to bottom within a group.

→ Ionic Radius: It is defined as the effective distance from the centre of the nucleus of the ion up to which it exerts Its influence on the electronic cloud.

→ Variation within a group: The ionic radius increases as we move down a group.

The size of a cation is always less than its corresponding atom
Na⁺ < Na
Mg²⁺ < Mg

The size of an anion is always larger than its corresponding atom
Cl^– > Cl
O^2- > o

→ Isoelectronic Ions or species: Ions of different elements which have the same number of electrons but the different magnitude of the nuclear charge are called Isoelectronic ions.
Na⁺, F^–, Mg²⁺ etc. are iso electronic ions.

The ionic radii of isoelectronic ions decrease with the increase in nuclear charge.

→ Trends in groups and periods: Electronegativity. values for the representative elements increase along period and decrease down the group.

Summary of the Trends in the Periodic Properties of Elements in the Periodic Table

→ Valency: The electrons present in the outermost shell of an atom are called valence electrons and the number of these electrons determine the valence or the valency of the atom. It is because of this reason that the outermost shell is also called the valence shell of the atom and the orbitals present in the valence shell are called valence orbitals.

→ Variation along a period: As the no. of electrons increases from 1 to 8 in representative elements across a period, the valency first increases from 1 to 4 and then decreases to zero in the case of noble gases.

→ Variation within a group: As the no. of electrons remain the same within a group, therefore, all the elements in a group exhibit the same valency.

The resemblance of properties of Li with Mg (which is diagonally situated); Be with Al and B with Si is called Diagonal relationship.

It is due to similar polarising power.

By going through these CBSE Class 11 Chemistry Notes Chapter 2 Structure of Atoms, students can recall all the concepts quickly.

Structure of Atoms Notes Class 11 Chemistry Chapter 2

Sub-Atomic Particles: Dalton’s Atomic Theory regarded the atom as the ultimate particle of matter. It explained satisfactorily various laws of chemical combination like the law of conservation of mass, the law of constant composition, and the law of multiple proportions. However, it failed to explain the existence of sub-atomic particles which were later discovered like electrons and proton.

Discovery of Electron: Michael Faraday suggested the particular nature of electricity. When he passed electricity through a solution of an electrolyte, chemical reactions occurred at the electrodes with liberation and deposition of matter at the electrodes.

Michael Faraday discovered the sub-atomic particles like electrons from his well-known experiments in partially evacuated glass tubes called cathode ray discharge tubes. The cathode ray tube is made of glass containing two thin pieces of metal, called electrodes, sealed in it.

At very low pressure and at high voltage, current starts flowing through a stream of particles from cathode to anode. These were called cathode rays or cathode ray particles

Characteristics of Cathode rays:

1. The cathode rays start from the cathode and move towards the anode.
2. These rays travel in straight lines.
3. Cathode rays are made up of material particles.
4. On applying an electric field, these rays are deflected towards the positive plate. This shows that cathode rays carry a negative charge. These negatively charged particles are Electrons.
5. Cathode rays produce a heating effect.
6. They produce X-rays when they strike against the surface of hard metals like tungsten, molybdenum, etc.
7. They produce green fluorescence when they stride zinc sulfide.
8. They affect the photographic plates.
9. They possess a penetrating effect.
10. They possess the same charge/mass ratio.

\(\frac{\text { Charge }}{\text { Mass }}=\frac{e^{-}}{m}\) = 1.76 × 10⁸ coulombs/g Mass m
Charge = e^– = 1.60 × 10^-19 coulombs or 4.8 × 10^-10 esu

Thus the mass of electron m
= \(\frac{e}{e / m}=\frac{1.60 \times 10^{-19}}{1.76 \times 10^{8}}\)
= 9.11 × 10^-28 g
= 9.11 × 10^-31 kg
Thus, it is concluded that electrons are the basic constituent of all atoms.

The amount of deviation of the particles from their path in the presence of an electrical or magnetic field depends upon

• The magnitude of the negative charge on the particle, the greater the magnitude of the charge on the particle, the greater is the deflection.
• The mass of the particle-lighter the particle, the greater is the deflection.
• The strength of the electrical or magnetic field.

The deflection of electrons from their original path increases with the increase in the voltage or strength of the magnetic field.

Thus electron can be defined as the fundamental particle which carries one unit negative charge and has a mass nearly equal to \(\frac{1}{1837}\)th of that of the hydrogen atom.

Discovery of Protons and Newtons: Anode rays or Canal rays: If a perforated cathode is used in the discharge tube experiment, it is found that certain type of radiations also travels from anode to cathode.

Production of Anode rays or Positive rays

Thus anode rays are not emitted from the anode but are produced in the space between the anode and cathode.

Properties of Positive rays/canal rays:

1. The anode-rays originate in the region between two electrodes in the discharge tube.
2. These rays are made of material particles.
3. These rays are positively charged.
4. These rays produce heat when striking against a surface.
5. The magnitude of the charge on anode-rays varies from particle to particle depending on the number of electrons lost by an atom or molecule.
6. The mass of positive particles which constitute these rays depend upon the nature of the gas in the tube.
7. The charge/mass (e/m) ratio of anode-rays is not constant but depends upon the nature of gas in the tube. The value of e/m is greatest for the lightest gas, hydrogen.

The electric charge on the lightest positively charged particle from hydrogen gas was found to be exactly equal in magnitude but opposite in sign to that of the electron. This lightest positively charged particle from hydrogen gas was named a proton. The mass of a proton is almost 1836 times that of the electron.

When hydrogen gas is taken inside the tube
Charge on these particles = 1.6 × 10^-19 coulomb
\(\frac{\text { Charge }}{\text { mass }}\) = 958 × 10⁴ coulombs/g for each particle
∴ mass on each particle = \(\frac{1.6 \times 10^{-19}}{9.58 \times 10^{4}}\) = 1.67 × 10^-24 g

This mass is nearly the same as that of hydrogen atom.

Therefore, a Proton may be defined as the fundamental particle which carries one unit positive charge and has a mass nearly equal to that of the hydrogen atom.

Chadwick in 1932 discovered the 3rd sub-atomic neutral particle and named it Neutron. He bombarded a thin sheet of beryllium by a-particles to discover neutrons. Neutron is a neutral particle carrying no charge and has a mass slightly greater than that of proton/

Thomson Model of Atom:
J.J. Thomson proposed that an atom is a sphere (radius approximately 10-10 m) of positive electricity and electrons are embedded into like the seeds of watermelon. An important figure of this model is that the mass of the atom is uniformly distributed over the atom.

Thomson model of the atom

Later on, this model was rejected as Sphere electrons are mobile. Thomson model of the atom

Rutherford’s Nuclear Model of Atom: Rutherford bombarded very thin gold foil with a-particles.

The observations of this a-particle scattering experiment were:

1. Most of the a-particles passed through the gold foil undeflected.
2. A small fraction of the a-particles was deflected through small angles.
3. A very few a-particles (~ 1 in 20,000) bounced back, that is, were deflected by nearly 180°.

Conclusions:

1. Atom is hollow from within. There is empty space within the atom as most of the a-particles passed undeflected.
2. A few positively charged a-particles were deflected. These must have been deflected by some positively charged body present within the atom. This positively charged body is very small as compared to the size of the atom.
3. Calculations by Rutherford showed that the radius of this positive center called Nucleus is only 10^-15 m as compared to the radius of the atom which is about 10^-10 m.

Rutherford’s scattering experiments

On the basis of the above observations and conclusion, Rutherford proposed the nuclear model of the atom.
1. The positive charge and most of the mass of the atom were densely concentrated in an extremely small region. This very small portion of the atom was called the nucleus by Rutherford.

Scattering of a-particles by
(a) a single atom (b) a group of atoms

2. The nucleus is surrounded by electrons that move around the nucleus at a very high speed in circular paths called orbits. Thus, Rutherford’s model of the atom is similar to the solar system in which the nucleus is like the sun and moving electrons are like revolving planets.

3. Electrons and the nucleus are held together by electrostatic forces of attraction.

Atomic Number and Mass Number: Atomic Number (Z) is the number of protons present in the nucleus.
As an atom is electrically neutral, the no. of protons in the nucleus is equal to the number of electrons moving outside it.
No. of protons in hydrogen (Z) = 1
= no. of electrons in a neutral atom

No. of protons in sodium (Z) = 11
= no. of electrons in a neutral atom

While the positive charge of the nucleus is due to protons, the mass of the nucleus, due to both protons and neutrons. As both protons and neutrons are present in the nucleus, they are collectively called Nucleons.

The total no. of nucleons is termed as the Mass number (A) = No. of protons (Z) + No. of neutrons (n)
∴ No. of neutrons n = A – Z

→ Isobars and Isotopes: The composition of any atom of symbol, X can be represented by _Z^AX.

→ Isobars are defined as the atoms of different elements with the same mass number but a different atomic number, e.g., ₆¹⁴C and ₇¹⁴N

→ Isotopes are the atoms of the same element with the same atomic number but different mass numbers. Protium (₁¹H), deuterium (₁²D), and tritium (₁³T) are the isotopes of hydrogen.

Similarly, ₁₇³⁵Cl and ₁₇³⁷Cl are the isotopes of chlorine.

The chemical properties of atoms are controlled by the number of electrons which are determined by the no. of protons in the nucleus. No. of neutrons present in the nucleus have very little effect on the chemical properties of an element. Thus all the isotopes of a given element show the same chemical behavior.

→ Drawbacks of Rutherford Model of Atom:
1. According to Maxwell, charged particles when moving, dissipates energy in the form of electromagnetic radiations.
Slowly, the distance between the moving electron from the nucleus decreases. Calculations show that it should take an electron only 10^-8 to spiral into the nucleus.

But this does not happen. Thus Rutherford’s model cannot explain the stability of an atom.

2. Another serious drawback of the Rutherford model is that it says nothing about the electronic structure of atoms, i.e., how the electrons are distributed around the nucleus and what are the energies of these electrons.

→ Developments leading to Bohr’s Model of Atom: Neils Bohr improved upon the model of the atom as proposed by Rutherford.

Two developments played a major role in the formulation of Bohr’s model of the atom.

1. Electromagnetic radiations possess both wave-like and particle-like properties.
2. Quantization of electronic energy levels in atoms.

→ Wave Nature of Electromagnetic Radiation: Maxwell was the first to suggest that charged bodies moving under acceleration, produce alternating electrical and magnetic fields. These fields are transmitted in the form of waves called electromagnetic waves or electromagnetic radiations.

Properties associated with electromagnetic wave motion:

1. Electric and magnetic fields are perpendicular to each other and both are perpendicular to the direction of propagation of the wave.
2. These waves do not require medium and can move in a vacuum.
3. There are many types of electromagnetic radiations that differ from one another in wavelength (or frequency). They constitute electromagnetic spectrum (shown below). A visible part of the spectrum (around 10¹⁵ Hz) is only a small part of it.
4. Different kinds of units are used to represent electromagnetic radiation.
   SI unit for frequency (v -nu) is hertz (Hz, s^-1).

It is defined as the number of waves that pass through a given point in space in one second.
SI unit for wavelength (λ) should be a meter.
(a) Wavelength (λ): It is the distance between two consecutive points which are in the same phase along the direction of propagation. Depending upon the magnitude, the wavelength is expressed either in cm, micron, millimicron, Angstrom unit, or in nanometer.
1 Angstrom (Å) = 10^-8 cm = 10^-10 m
1 micron (g) = 10^-4 cm = 10^-6 m.
1 nanometer = 10^-9 m

(b) Frequency (v): It is defined as the number of wavelengths travelled in one second. Therefore,
v = \(\frac{\text { Velocity of the radiation }}{\text { Wavelength of the radiation }}=\frac{c}{\lambda}\)

The frequency is expressed in cycles per second or in Hertz (Hz) units.
1 Hz = 1 cycle/s

(c) Wave number (\(\bar{v}\)): It is defined as the number of wavelengths which can be accommodated in one cm length along the direction of propagation. Therefore,
Wave number (\(\bar{v}\)) = \(\frac{\text { Frequency of the radiation }(v)}{\text { Velocity of the radiation }(c)}=\frac{v}{c}\)

The wave number is generally expressed in the units of cm^-1, although it is not the SI unit.
Frequency = Velocity × wave number
or
v = c\(\bar{v}\)

Relationship between velocity, wavelength, and frequency of wave:
c = V × λ
where c = velocity, v = frequency, λ = wavelength

Electromagnetic spectrum: The different types of electromagnetic radiations differ only in their wavelengths and have frequencies.

The wavelengths increase in the following order.
Cosmic rays < γ-rays < X-rays < Ultra-violet rays < Visible rays < Infrared < Microwaves < Radio waves

(a) The spectrum of electromagnetic radiation

(b) Visible spectrum: The visible spectrum is onlv a small part of the entire spectrum

In a vacuum, all types of electromagnetic radiations, regardless of wavelength, travel at the same speed, i.e., 3.0 × 10⁸ ms^-1
This is called the speed of light and is given the symbol ‘c’.

Particle Nature of Electromagnetic Radiation: Planck’s Quantum Theory
The wave nature of electromagnetic radiation could explain experimental phenomena such as diffraction and interference. However, the experimental observations such as the emission of, radiation from a hot body, and the photoelectric effect could not be explained in terms of the wave nature of light.

→ Black body radiation: All hot bodies emit electromagnetic radiation. At high temperatures, a part of these radiations lies in the visible region of the spectrum With a further increase in the temperature of the body, the proportion of the higher frequency radiation increases. An ideal body that emits and absorbs radiations of all frequencies is called a black body.

Max Planck found that the characteristics of black body radiation could be accounted for by proposing that each electromagnetic oscillator, viz., an atom or a molecule, can emit or absorb only a certain discrete quantity of energy. This limitation of the energy of an object to discrete values is called the quantization of energy. According to Planck, the energy of an oscillator of frequency v is restricted to an integral multiple of the quantity, hv, where h is called the Planck’s constant.

→ Plank gave the name quantum to the smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation. The energy (E) of a quantum of radiation is proportional to its frequency (v) and is expressed as
E = h v

h is called Planck’s constant and has the value 6.626 × 10^-34 Js.
Thus, according to Planck
E = n h v
where n = 0,1, 2 , h = 6.626 × 10^-34 Js

The smallest amount of energy (n = 1) is then given by
E = h v

The energy to h v is called a quantum of energy that can be emitted or absorbed in the form of electromagnetic radiation.

→ The energy of Electromagnetic Radiation: All electromagnetic radiations are associated with a certain amount of energy.

According to Einstein

1.The radiation energy is emitted or absorbed in the form of small packets of energy. Each such packet of energy is called a quantum or photon. Each quantum has a certain discrete amount of energy associated with it.

2. Energy associated with a quantum or photon (e) is proportional to the frequency (v) of the radiation
Then E ∝ v
or
E = hv

where h is a constant called Planck’s constant. This constant (h) has value of 6.626 × 10^-34 Joule second (Js) or 3.99 × 10^-13 kJs mol^-1
The above relation may be written as ε = \(\frac{h c}{\lambda}\)

3. The energy associated with Avogadro’s number (N) of quanta is called an Einstein of energy (E). Thus, the Einstein of energy associated with the radiation of frequency v is. E = N_A hv

Photoelectric Effect: When a beam of light of suitable wavelength falls on a clean metal plate (such as cesium) in a vacuum, electrons are emitted from the surface of the metal plate. This phenomenon involving the emission of electrons from the surface of a metal by the action of light is known as the photoelectric effect. The electrons so emitted are called photoelectrons.

Photoelectric effect

The three important facts about the photo-electric effect observed are
1. The electrons are ejected only if the radiation striking the surface of the metal has at least a certain minimum frequency called threshold frequency (v_o). If the frequency is less than v_o, no electrons are ejected.
This value (v_o) is called Threshold Frequency. The minimum energy required to eject the electron (hv_o) is called the work function.

2. The velocity (and hence the kinetic energy) of the electron ejected depends upon the frequency of the incident radiation and is independent of its intensity.

3. The number of photoelectrons ejected is proportional to the intensity of incident radiation.

The above observations cannot be explained by the Electromagnetic wave theory. According to this theory, since radiations are continuous, therefore it should be possible to accumulate energy on the surface of the metal, irrespective of its frequency and thus radiations of all frequencies should be able to eject electrons.

Similarly, according to this theory, the energy of the electrons ejected should depend upon the lire intensity of the incident radiation.

If the striking photon of light has energy = hv and the minimum energy required to eject the electron is hv_o then the difference of energy (hv – hv_o) is transferred as the kinetic energy of the photoelectron
\(\frac{1}{2}\)hv – hv_o = h(v – v_o)

where m = mass of the electron and v is the velocity of the ejected electron.

Dual Behaviour of Electromagnetic Radiation: The particle nature of light can explain the black body radiation and photoelectric effect satisfactorily but cannot explain the known wave behavior of light like the phenomenon of interference and diffraction. Therefore, light possesses dual behavior either as a wave or as a stream of particles.

When radiation interacts with matter, it displays particle-like properties. When it propagates, it displays wave-like properties like diffraction and interference. Some microscopic particles like electrons also exhibit this wave-particle duality.

→ Evidence for the Quantized Electronic Energy Levels: Atomic Spectra: Atoms give discontinuous or line spectra. The spectrum given by atoms consists of a series of bright lines or bands separated from each other by a dark space. Each line in the spectrum corresponds to a specific wavelength.

There are two types of atomic spectra

1. Atomic emission spectra,
2. Atomic absorption spectra

1. Atomic emission spectra: A series of bright lines, separated from each other by dark spaces, produced by the excited atoms is called atomic emission spectra.

Each line in the emission spectrum corresponds to a specific wavelength. Therefore, each element gives a unique pattern of lines in the spectrum. No two elements give the same pattern of lines in their spectra.

2. Atomic absorption spectra: When a sample of atomic vapors is placed in the -path of white light from an arc lamp, it absorbs the light of certain characteristic wavelengths, and the light of other wavelengths gets transmitted. This produces a series of dark lines on a white background.

The spectrum of Hydrogen Atom: The spectrum of a hydrogen atom can be obtained by passing an electric discharge through the gas taken in the discharge tube under pressure. The spectrum consists of a large number of lines appearing in different regions of wavelengths. The lines in different regions were grouped into five different series of lines, each being named after the name of its discoverer.

These are the Lyman series. Balmer series, Paschen series, Brackett series and Pfund series. Lyman series appear in the ultraviolet region, Balmer series appear in the visible region while the other three series lie in the infrared region.

A simple relationship between the wavelengths of different lines can be given as
\(\frac{1}{λ}\) = \(\bar{v}\)(in cm^-1)
= R(\(\frac{1}{n_{2}^{2}}-\frac{1}{n_{1}^{2}}\))

where n₁ and n₂ are integers, such that n₁ > n₂. R is a constant, now called the Rydberg constant. The value of R is 109678 cm^-1. This expression is found to be valid for all the lines in the hydrogen spectrum and is also known as Rydberg equation.

For a given spectrum series, n₂ remains constant while n1 varies from line to line in the same series. For example, for Lyman series n₂ = 1 and = 2, 3, 4, 5 and for Balmer series n₂ = 2 and n₁ = 3, 4, 5

…. All the five series, the regions in which lines appear and the values of n₁ and n₂ are given below:


Emission or atomic spectrum of hydrogen

Of all the elements, the hydrogen atom has the simplest line spectrum.

Bohr’s Model For Hydrogen Atom Postulates:
1. The electron in the hydrogen atom can move around the. the nucleus in a circular path of fixed radius and energy. These paths are called orbits, stationary states, or allowed energy states.

2. The energy of an electron in the orbit does not change with time. However, it jumps from a lower energy level to a higher energy level where the requisite amount of energy is supplied to it and jumps from a higher orbit to a lower orbit with the release of energy.
ΔE = E₂ – E₁
where ΔE = change in energy, E₂ = energy of the electron in the higher orbit, E₁ = energy of the electron in the lower orbit.

3. The frequency of the radiation absorbed or emitted is given by
v = \(\frac{\Delta \mathrm{E}}{h}=\frac{\mathrm{E}_{2}-\mathrm{E}_{1}}{h}\)

4. The angular momentum of an electron in a given stationary state can be expressed as
mvr = \(\frac{n h}{2 \pi}\); n = 1, 2,3 2n
Thus an electron can move only in those orbits for which its angular momentum is an integral multiple of \(\frac{h}{2 \pi}\) (Quantization of angular momentum).
That is why only certain fixed orbits are allowed.

(a) The stationary states for electrons are numbered n = 1, 2, 3… . They are called Principal quantum numbers.
(b) the radii of stationary states are expressed as
r_n = n²a₀
where a_o = 52.9 pm

Thus the radius of the first orbit called Bohr radius is 52.9 pm (as n = 1).

(c) Energy of the electron in a given orbit
E_n = – R_H\(\left[\frac{1}{n^{2}}\right]\) where n = 1, 2, 3, ……….
R_H is called Rydberg Constant and its value is 2.18 × 10^-18 J. The energy of the lowest state, also called the ground state is
E₁ = – 2.18 × 10-18(\(\frac{1}{1^{2}}\)) = – 2.18 × 10^-18 J
For n = 2
E₂ = – 2.18 × 10-18(\(\frac{1}{2^{2}}\)) = – 0.545 × 10^-18 J

Significance of the negative sign before the electronic energy E_n: The energy of the electron in a hydrogen atom has a negative sign for all possible orbits. A free-electron at rest far away place from the nucleus has energy = 0, i.e., E_∞ = 0. As the electron gets closer to the nucleus (n decreases) En becomes larger in absolute value and more and more negative. Thus the most negative energy given by n = 1 corresponds to the most stable orbit.

(d) Bohr’s theory can also be applied to ions containing only one ‘ electron like hydrogen. For example He⁺, Li²⁺, Be³⁺ and so on. For them
E_n = – 2.18 × 10^-18(\(\frac{\mathrm{Z}^{2}}{n^{2}}\)) J and radii
r_n = \(\frac{52.9\left(n^{2}\right)}{Z}\) pm
where Z = atomic number. It has a value of 2, 3 for helium and lithium respectively.

(e) Magnitude of the velocity of the electron increases with the increase in nuclear charge and decreases with the increase’ of principal quantum numbers.

→ Explanation of Line Spectrum of Hydrogen: The energy difference between the two orbits is given by
ΔE = E_f – E_i
E_f, E_i energies in final and initial orbits
ΔE = \(\left(\frac{-\mathrm{R}_{\mathrm{H}}}{n_{f}^{2}}\right)-\left(\frac{\mathrm{R}_{\mathrm{H}}}{n_{i}^{2}}\right)\)

n_f, n_i are final and initial orbits

In the case of the absorption spectrum, n_f > n_i energy is absorbed.
In the case of emission spectrum n_i > n_f; ΔE is negative and energy is released.

Advantages of Bohr’s Model:

1. It explains the stability of the atom. An electron can not lose energy as long as it stays in a particular orbit.
2. It explains the line spectrum of hydrogen.

Different series in the hydrogen spectrum

Drawbacks of Bohr’s Model: Bohr’s model of atom suffers from the following weaknesses or limitations.
1. Inability to explain line spectra of multi-electron atoms: Bohr’s theory was successful in explaining the line spectra of the hydrogen atom and hydrogen-like particles, containing a single electron only. However, it failed to explain the line spectra of multi-electron atoms.

When spectroscopes with better resolving powers were used, it was found that even in the case of hydrogen spectrum, each line was split up into a number of closely spaced lines (called fine structure) which could not be explained by Bohr’s model of the atom.

2. Inability to explain Zeeman effect (splitting of lines in the magnetic field and stark effect (splitting of lines in the electric field)

3. Unable to explain the three-dimensional model of the atom. Bohr’s model gives a flat model of the atom with electrons moving in circular paths in one plane.

4. It does not explain the shapes of molecules.

5. It fails to explain de Broglie’s concept of the dual nature of matter and Heisenberg’s uncertainty principle.

Towards Quantum Mechanical Model of the Atom:
1. Dual Behaviour Matter: de-Broglie suggested that matter and hence electron-like radiations have a dual character – wave and particle. In other words, matter also possesses particles as well as Wave characters. This concept of the dual character of matter gave birth to the wave mechanical theory of matter according to which, the electrons, protons, and even atom when in motion possess all wave properties. Mathematically, de Broglie view may be written as below:
λ = \(\frac{h}{m v}\) …(1)

The equation (1) is known as de Broglie equation, m = mass of the particle, v = velocity of the particle, h = Planck’s constant, λ is the wavelength.

Since h is constant, its value is 6.6256 × 10^-34 Js
∴ λ ∝ \(\frac{1}{m v}\)
or
λ ∝ \(\frac{1}{\text { Momentum }}\)
(mv = momentum of a photon) … (2)

Equation (2) is known as de Broglie’s relationship which may be stated as the momentum of a particle in motion is inversely proportional to the wavelength of the waves associated with it.

2. Heisenberg’s Uncertainty Principle: One of the important consequences of the dual nature of an electron is the Uncertainty Principle, developed by Heisenberg. According to the Uncertainty Principle, it is impossible to determine simultaneously at any given moment both the position and momentum (velocity) of an electron with accuracy.

Mathematically, if Δx and Δp are the uncertainties in the position and momentum respectively, then
ΔxΔp ≥ \(\frac{h}{4 \pi}\)

One can see from this equation that if Ap increases, the Ax decreases and vice-versa. Since, Δp = m. Δv, hence the above equation can be written as
Δx × Δv >\(\frac{h}{4 \pi m}\)

Significance of Uncertainty Principle: One of the important implications of the Heisenburg Uncertainty Principle is that it rules out the existence of definite paths or trajectories of electrons and other similar particles.

The effect of the Heisenburg Uncertainty Principle is significant only for the motion of microscopic objects and is negligible for two macroscopic objects.

In dealing with milligram-sized or heavier objects, the value of Δv Δx is extremely small and insignificant and the associated uncertainties are hard of any real consequence. Therefore the precise statements of the position and momentum of electrons have to be replaced by the statements of probability, that the electron has at a given position and momentum. This is what happens in the quantum mechanical model of the atom.

→ Reasons for the failure of the Bohr Model: In the Bohr model, an electron is regarded as a charged particle moving in well-defined circular orbits about the nucleus. The wave character of the electron is not considered.

Bohr’s model of the hydrogen atom, therefore, not only ignores the dual behavior of matter but also contradicts Heisenburg’s Uncertainty Principle.

→ Quantum Mechanical Model of Atom: Quantum mechanics was developed independently by Heisenburg and Schrodinger.

Schrodinger equation is Ĥ φ = Eφ where Ĥ is a mathematical operator called Hamiltonian, E is the total energy of the system and φ is the wave function.

Important features of the quantum mechanical model of the atom:

1. The energy of the electrons in atoms is quantized.
2. The existence of quantized electronic energy levels is allowed solutions of the Schrodinger Wave Equation.
3. Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously. Therefore, only the probability of finding an electron at different points is required.
4. An atomic orbital is the wave function \p for an electron in an atom.
5. The probability of finding an electron at a point within an atom is proportional to the square of the orbital wave function, i.e., |φ|2 at that point. |φ|2 is called probability density and is always positive. From the value of | \p |2 at different points within an atom it is possible to predict the region around the nucleus where the electron will most likely be found.

Orbitals and Quantum Numbers:
→ Atomic Orbital: it is defined as the 3-dimensional region of space around the nucleus where the probability of finding an electron is maximum.

→ Quantum Numbers: The state of an electron in an atom is described by its location with respect to the nucleus and by its energy. Thus, the energy and angular momentum of an electron is quantized, i.e., an electron in an atom can have only certain permissible values of energy and angular momentum. These permissible states of an electron in an atom called Orbitals are identified by a set of four numbers. These numbers are called Quantum Numbers.

The various quantum numbers are
(a) Principal quantum numbers are denoted by n.
(b) Azimuthal or angular momentum quantum number denoted by l.
(c) Magnetic quantum number denoted by m.
(d) Spin quantum number denoted by s.

(a) Principal quantum number (n): This quantum number determines the main energy level or shell in which the electron in an atom is present and also the energy associated with it. In addition, it also determines the average distance of the electron from the nucleus in a particular shell. Starting from the nucleus, the energy shells are denoted as K, L, M, N, … etc., or as 1, 2, 3, 4, … etc: The maximum number of electrons that a shell can accommodate is 2n². Thus, K-shell (n = 1) can have a maximum of two electrons. L- shell (n = 2) can have eight electrons and similarly, eighteen electrons can be accommodated in M-shell (n = 3).

(b) Azimuthal or subsidiary or angular quantum number (l): This, the quantum number determines the angular momentum of the electron. This is denoted by l. The values of l give principal energy- shell in which an electron belongs. It can have positive integer values from zero to (n – 1) where n is the principal quantum number.
That is l = 0, 1,2, 3, …. (n – 1).

(c) Magnetic quantum number: This quantum number describes the behavior of an electron in a magnetic field. The values of ‘m’ are linked to that of l. For a given value of l, the possible values of m vary from -l to 0 and 0 to + l. Thus, the total values of m are (2l + 1). The orbitals are also named after the sub-shell in which these are present. The number of orbitals in different sub-shells are given:

(d) Spin quantum number: This quantum number describes the spin orientation of the .electron. It is designated by ‘s’. Since the electron can spin in only two ways-clockwise or anti-clockwise and, therefore, the spin quantum number can take only two values: + 1/2 or – 1/2. These two values are normally represented by two arrows pointing in the opposite direction i.e.↑ and ↓.

Shapes of atomic orbitals:
1. Shapes of s-orbitals: For s-orbitals, l = 0, hence the orbital angular momentum of an s-orbital is zero. As a result, the distribution of electron density is symmetrical around the nucleus and the probability of finding an electron for a given distance is the same at all angles. As the distribution of electron density is symmetrical, therefore, the most suitable figure to represent an s-orbital is a sphere.

(a) The probability of finding an electron is maximum near the nucleus and decreases with distance. In the case of 2s electrons, the probability is again maximum near the nucleus and then decreases to zero and increases again and then decreases as the distance from the nucleus increases. The intermediate region (a spherical shell) where the probability of finding an electron cloud is zero is called a Nodal surface/node. In general, any n orbital has (n – 1) nodes.

Shapes of is, 2s, and 3s orbitals

(b) The size and energy of the s-orbital increases as the principal quantum number n increases, i.e., size and energy of s-orbital increases in the order 1s < 2s < 3s ……

2. Shape of p-orbitals: For p-orbitals l = 1, so angular momentum of an electron in 2p orbital
= \(\sqrt{l(l+1)} \frac{h}{2 \pi}=\sqrt{2} \frac{h}{2 \pi}\)

As a result, the distribution of electron density around the nucleus is. not spherical. The probability diagram for a p-orbital is dumbbell shape. Such a diagram consists of a distorted sphere of high probability one on each side of the nucleus, concentrated along with N in a particular direction.

Shapes of p-orbital

Different orientatios of p-orbitais

Now, since the electron with l = 1 can have three values for the magnetic quantum number (m), i.e., m = – 1, 0 and + 1, hence there are three p-orbitals. All three 2p-orbitals have the same shape, but their directions are different. The directions are perpendicular to each other. Since these directions can be chosen as the x, y, z axes, hence the p-orbitals along these axes are labeled as p_x, p_y, and p_z respectively. The three p-orbitals of a particular energy level have equal energies and are called degenerate orbitals. 2p has no node, 3p has one 4p has two nodes, and so on. In general, no. of nodes in any orbital = (n – l – 1).

3. Shape of d-orbitals: For d-orbital, 1 = 2. Therefore, the angular momentum of -an electron in d orbitals is not zero. As a result, the d orbitals do not show spherical symmetry. For l = 2, the magnetic quantum number (m) should have five different values i.e., m = – 2, – 1, 0, 1, + 2. Accordingly, there are five different space orientations for d orbitals. These are designated as

The five d-orbitals

4. Energies of orbitals: In atoms, electrons can have only certain permissible energies. These permissible states of electrons are called energy levels.

In hydrogen and hydrogen-like atoms, all the orbitals having the same principal quantum number have the same energy. Thus, 2s and 2p orbitals have equal energies, 3s, 3p, and orbitals have equal energies, and 4s, 4p, and 4f orbitals have equal energies as shown above.

Energy level diagram for the few electronic shells of the hydrogen atom

The atoms containing two or more electrons are called multielectron atoms. In these atoms:
(a) Different orbitals having the same principal quantum number (n) may have different energies.
(b) For a particular main energy level, the orbital having a higher value of the azimuthal quantum number (l) has higher energy. For example, the energy of 2p orbital (l = 1) is higher than that of the 2s (l = 0) orbital, general, energies of the orbitals belonging to the same main energy level follow the order
s < p < d < f

Energy level diagram for the few electronic shells of a multi-electron atom

(c) When n > 3, the same orbitals belonging to a lower main energy level may have higher energy than some orbitals belonging to the higher main energy. For example, in the case of multi-electron atoms, the energy of 3d orbitals is higher than the energy of 4s orbitals.

(d) In multielectron atoms, the energy of any orbital is governed by both the principal quantum number (n) and azimuthal quantum number (l):

• The orbital having leaver (n + l) value has lower energy.
• For the orbitals having equal value of (n + 1), the orbital having lower value of n has lower energy. For example.
  4s orbital has n + l = 4 + 0 = 4 and
  3d orbital has n + l = 3 + 2 = 5.

Since, (n + l) value for 4s orbital is lower than that for 3d, hence 4s orbital has lower energy than 3d.

5. Filling of orbitals in atoms:
Aufbau principle: In the ground state of the atoms, the orbitals are filled in order of their increasing energies. In other words, electrons first occupy the lowest-energy orbital available to them and enter into higher energy orbitals only after the lower energy orbitals are filled.

The order in which the energies of the orbitals increase and hence the order in which orbitals are filled is as follows:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s …….

“n + l” Rule: The lower the value of (n + l) for an orbital, the lower is its energy, and hence earlier it will be filled. If two orbitals have the same value of (n + l), the orbital with the lower value of n will have lower energy. Hence it will be filled first.

Order of Filling Energy Levels (Aufbau Principle)

→ Pauli Exclusion Principle
No two electrons in an atom can have the same set of four quantum numbers.
OR
Only two electrons may exist in the same orbital and these electrons must have opposite spin.

Hund’s rule of maximum multiplicity: According to this rule, electron pairing will not take place in orbitals of the same energy (same subshell) until each orbital is singly filled. This principle is very (important in guiding the filling of p, d, and f orbitals, which have more than one kind of orbitals. For example, we know that there are three p orbitals. (p_x, p_y, and p_z) of the p-subshell in a principal energy level. According-” to Hund’s rule, each o.f the three p orbitals must get one electron of parallel spin before any one of them receives the second electron of opposite spin.

The electronic configuration of some atoms are given below:

After calcium, 3d subshell starts getting filled. The electronic configurations of elements from scandium (Z = 21) to zinc (Z = 30) are given below:

Total number of exchanges = 3+ 2 + l= 6
The number of exchanges that can take place in d5 configuration is as follows:

Gallium (Ga) Z = 31 to Krypton (Kr) Z = 36 (Electronic Configuration)
With Gallium (Ga) onwards, 4p orbitals get filled up as:

Important points to remember:

1. Mass No. (A) = Sum of protons and neutrons.
2. Atomic No. (Z) = No. of protons in the nucleus.
3. No. of neutrons = A – Z.
4. Nucleons are the particles (n + p) present in the nucleus.
5. Max. No. of electrons in a shell that can be present in an atom is given by 2n² where n = no. of the orbit.
6. An s-subshell can contain 2, a p-can contains 6, a d-can contain 10, and an f-subshell can contain 14 electrons, s-subshell has only one orbital; p-can has 3, d has 5; subshell has 7 orbitals.
7. Each orbital can maximum contains two electrons.
8. To form a cation from a neutral atom, electrons are removed equal to the no. of positive charges on the cation, while to form an anion from a neutral atom, electrons are added to the no. of negative charges on an anion.

Table Electronic Configurations of the Elements:

Elements with exceptional electronic configurations


Elements with exceptional electronic configurations.

→ Elements with atomic number 112 amid above have been reported but not yet frilly a the indicated and min med.

→ Electron: It is the fundamental particle that carries one unit negative charge and has a mass nearly equal to \(\frac{1}{1837}\) hydrogen atom.

→ Proton: A proton may be defined as that fundamental particle that carries one unit of positive charge and has a mass nearly equal to that of the hydrogen atom.

→ Neutron: A neutron may be defined as the fundamental particle which carries no charge but has a mass nearly equal to that of a hydrogen atom or proton.

→ Cathode rays: Cathode rays are a stream of electrons.

→ Electrons: Electrons are universal constituents of matter.

→ Mass Number (A): Sum of protons and neutrons.

→ Atomic Number (Z): Number of protons in the nucleus of an atom.

→ Nucleons: Sum of protons and neutrons.

→ Isotopes: Atoms of the same element having the same atomic number, but different mass numbers are called Isotopes.

→ Isobars: Atoms of different elements which have the same mass number, but a different atomic number are Isobars.

→ Isotones: Such atoms of different elements which contain the same number of neutrons are called Isotones.

The wavelength (λ) of a wave is the distance between any two consecutive crests or troughs.
1 Å = 10^-8 cm = 10^-10 m
1 nm = 10^-9 m, 1 pm = 10^-12 m

→ Frequency (v): It is the number of waves passing through a point in space in one second. Its unit is Hertz (Hz).
1 Hz = 1 cycle per second (cps)

→ Velocity (c): The velocity of a wave is defined as the linear distance traveled by the wave in one second. Its unit is cm per second or meters per second.

→ Amplitude (a): It is the height of the crest or depth of the trough of a wave It is expressed in units of length.

→ Wavenumber: It is defined as the number of waves present in one cm length. It is also defined as the reciprocal of the wavelength
\(\bar{v}\) = \(\frac{1}{λ}\)

Relationship between velocity, wavelength, and frequency of a wave
c = v × λ

→ Electromagnetic spectrum: When electromagnetic radiations of different wavelengths are arranged in order of their increasing wavelengths or decreasing frequencies, the complete spectrum obtained is called Electromagnetic Spectrum,

Cosmic rays < y-rays < X-rays < UV rays < visible < Infrared < Microwaves < radiowaves

→ Photon: Each packet of energy is called quantum. In the case of light, such a quantum is called Photon.

→ Black Body Radiation: If the substance being heated is a black body (which is a perfect absorber and perfect radiator of energy) the radiation emitted is called blackbody radiation.

→ Zeeman Effect: Splitting of spectral lines in the magnetic field.

→ Stark Effect: Splitting of spectral lines in the electric field.

→ Probability.: It is the best possible description of a situation that cannot be exactly described.

→ Orbit: It, is a well-defined circular path around the nucleus with . a fixed energy in which the electrons revolve.

→ Orbital: The three-dimensional region of space around the nucleus where there is a maximum probability of finding an electron.

→ Quantum Numbers may be defined as a set of four numbers that give complete information about the electron in an atom, i.e., energy, orbital occupied, size, shape, and orientation of that orbital, and the direction of electron spin.

Some Important Formulae:
→ c = v × λ
c = velocity;
λ = wavelength,
v = Frequency

→ E = hv
h = Planck’s coristt. = 6.625 × 10^-34 J sec
E = Energy of a photon

→ \(\bar{v}\) = \(\frac{1}{λ}\)
\(\bar{v}\) = wavenumber .
Charge on 1 electron = – 1
Change on 1 proton = 1 +
Charge on 1 neutron = 0
Mass of one electron = 9.1 × 10^-31 kg
Mass of a proton = 1.67 × 10^-27 kg .
Mass of neutron = 1.67 × 10^-27 kg
One unit charge = 4.8 × 10^-10 e.s.u.
= 1.6 × 10^-19 coulomb

Work of R.A. Millikan ,
Charge on one electron = 1.6 × 10^-19 coulomb
e/m for electron = 1.76 × 10⁸

∴ Mass of an electron = \(\frac{e}{e / m}=\frac{1.60 \times 10^{-19}}{1.76 \times 10^{8}}\)
= 9.11 × 10^-28 g

If X is an atom of an element

Mass of 1 Mole of electron
. = 9.11 × 10^-28 × 6.022 × 10²³ g = 0.55 mg

→ Photoelectric Effect: The phenomenon of the emission of electrons from the surface of certain metals (usually potassium, cesium, rubidium). When they are exposed to a team of light with certain minimum frequency called threshold frequency.
hv = hv₀ + \(\frac{1}{2}\) mv²

K.E. imparted to the ejected electron .
= \(\frac{1}{2}\) mv² = hv – hv₀

→ Line spectrum of hydrogen
\(\bar{v}\) = 109677(\(\frac{1}{2^{2}}-\frac{1}{n^{2}}\)) cm^-1
where n > 3, i.e. n = 3, 4, 5, ….
The value 109677 cm-1 is called Rydburg Constant.

→ de Broglie Equation
λ = \(\frac{h}{m \times v}=\frac{h}{p}\)
where p = momentum of the particle.

→ Heisenburg’s Uncertainty Principle

It is impossible to determine simultaneously both the position as well as momentum (or velocity) of a moving particle like an electron with absolute accuracy.

→ Pauli Exclusion Principle: No two electrons in an atom can have the same set of four quantum numbers.
Or
Only two electrons may exist in the same orbital and these electrons must have opposite spin.

→ The maximum number of electrons in the shell with principal quantum number n is equal to 2n².

→ Hund’s Rule of Maximum Multiplicity: Pairing of electrons in the orbitals belonging to the same subshell (p, d, or f) does not take place until each orbital belonging to that subshell has got one electron each, i.e., it is singly occupied.

→ Schrodinger Wave Equation: It is applicable to the wave nature of electrons.
Ĥ φ = E φ
where Ĥ is a mathematical operator called Hamiltonian operator.
or
\(\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}+\frac{\partial^{2} \psi}{\partial z^{2}}+\frac{8 \pi^{2} m}{h^{2}}\)(E – V)φ = 0

where φ is the amplitude of the wave, x, y, z are space coordinates E is the total energy of the electron, V is its potential energy m is the mass of the electron.

By going through these CBSE Class 11 Chemistry Notes Chapter 1 Some Basic Concepts of Chemistry, students can recall all the concepts quickly.

Some Basic Concepts of Chemistry Notes Class 11 Chemistry Chapter 1

Importance of Chemistry: Chemistry plays a central role in science and is often intertwined with branches of science like Physics, Biology, Geology, etc. Chemistry also plays an important role in meeting human needs for food, health care products, etc.

→ Chemistry deals with the composition, structure, and properties of matter. To understand Chemistry, we have to study the basic constituents of matter Atoms & Molecules and their relationship with mass. Chemistry is basically, about chemical transformations.

→ Different manifestations of Chemistry include fertilizers, alkalies, acids, salts, dyes, polymers, drugs, soaps, detergents, metals, alloys, and other inorganic and organic chemicals. Daily new drugs, dyes, polymers, etc. are finding their way from the laboratory to industry. Many life-saving drugs like Cisplatin and Taxol are proving effective in cancer therapy and AZT [Azidothymidine] in helping Aids victims.

Nature of Matter: Anything which has mass and occupies space is called matter. Matter can exist in three physical states-solids, liquids, and gases.

→ Solids: Solids have definite volume and definite shape.

→ Liquids: Liquids have a definite volume, but no definite shape. They take the shape of the container in which they are put.

→ Gases: Gases have neither definite volume nor definite shape. These three forms are interconvertible.

Matter can be classified as mixtures and pure substances. Mixtures can be both homogeneous as well as heterogeneous. Milk, air are examples of homogeneous mixtures. They are uniform throughout. If they are not having a uniform composition, they are a heterogeneous mixture. Iron and sand is an example of a heterogeneous mixture.

Elements like Cu, Ag, and compounds like Nad, AgNO, constitute pure substances. Elements consist of only one type of particle. When two or more elements combine, they form compounds. The smallest part of an element is an Atom whereas the smallest particle of a compound is a Molecule. Thus, copper is an element composed of Cu atoms whereas sodium chloride is a compound composed of Na⁺Cl^– molecules.

Properties of Matter and their Measurement: Properties can be classified into two categories:

1. Physical properties and
2. Chemical properties.

→ Physical properties: Physical properties are those which can be observed or measured without changing the identity or composition of the substance. Some examples of physical properties are color, odor, melting point, boiling point density, etc.

The measurement or observation of chemical properties requires a chemical change to occur. Examples of chemical properties are aridity, basicity, combustibility.

Base Physical Quantities and their Units:

Definitions of SI Base Units:


In SI, large and small quantities are expressed by using an appropriate prefix with the base units.

S.I. Prefixes:

Mass of a substance is the amount of matter present in it while weight is the force exerted by gravity on an object. The mass of a substance is constant whereas its weight may vary from one place to another due to change in gravity.
The SI unit of mass is a kilogram However, its fraction gram (1 kg = 1000 g), is used in laboratories due to the smaller amounts of chemicals used in chemical reactions.

Volume has the units of (length)³. So in the SI system, the volume has units of m³. But again, in Chemistry laboratories, the smallest volumes are used. Hence volume is often denoted by cm³ or dm³ units. A common unit, liter (L) which is not a SI unit, is used for the measurement of the volume of liquids.
1 L = 1000 mL, 1000 cm³ = 1 dm³

→ Density: Density of a substance is its amount of mass per unit volume.
∴ SI unit of density = \(\frac{\text { SI unit of mass }}{\text { SI unit of volume }}\)
= \(\frac{\mathrm{kg}}{\mathrm{m}^{3}}\) = kg m^-3
This unit is very large.

∴ Density is usually expressed is g cm^-3.

→ Temperature: SI unit of temperature is kelvin (K)
K = °C + 273.15
where °C is degree Celsius.

It is interesting to note that temperatures below 0°C (i.e., negative values) are possible on the Celsius scale but, in the Kelvin scale, the negative temperature is not possible.

In addition to Kelvin (K – SI unit), there are two more scales to measure temperature.

1. Celsius scale (°C)
2. Fahrenheit scale (°F)
   °F = \(\frac{9}{5}\)(°C) + 32

Uncertainty in Measurement: Many a time in the study of Chemistry, one has to deal with experimental data as well as theoretical calculations. There are meaningful ways to handle the numbers conveniently and present the data in a realistic way with certainly to the extent possible.

→ Scientific Notation: We can write 232.508 as 2.32508 × 10² in scientific notation. Similarly, 0.00016 can be written as 1.6 × 10^-4.

→ Multiplication and Division
Multiplication: (5.6 × 10⁵) × (6.9 × 10⁸) = (5.6 × 6.9)(10⁵ + 8)
= 5.6 × 6.9 × 10¹³
= 38.64 × 10¹³

Division:
\(\frac{2.7 \times 10^{-3}}{5.5 \times 10^{4}}\) = (2.7 ÷ 5.5)(10^-3-4)
= 0.4909 × 10^-7

→ Addition and Subtraction
Addition: 6.65 × 104 + 8.95 × 10³
= 6.65 × 10⁴ + 0.895 × 10⁴
= (6.65 + 0.895) × 10⁴
= 7.545 × 10⁴

Subtraction:2.5 × 10^-2 – 4.8 × 10^-3
= 2.5 × 10^-2 – 0.48 × 10^-2
= (2.5-0.48)10^-2
= 2.02 × 10^-2

→ Significant Figures: All experimental measurements have some degree of uncertainty associated with them. Precision and accuracy are often referred to while we talk about measurement.

→ Precision: Precision refers to the closeness of various measurements for the same quantity. However, accuracy is the agreement of a particular value to the true value of the result.

→ Significant figures: Significant figures are meaningful digits that are known with certainty.

→ Dimensional Analysis: Often in calculations, We have to convert units from one system to another. The method used to accomplish this is called the factor label method or unit factor method or dimensional analysis.

→ Laws of Chemical Combination: The combination of elements to form compounds is governed by the following five basic laws.

1. Law of Conservation of Mass
2. Law of Definite Proportions
3. Law of Multiple Proportions
4. Gay Lussac’s Law of Gaseous Volumes
5. Avogadro’s Law

1. Law of conservation of mass: In all physical and chemical changes, the total mass of the reactants is equal to that of the products.
Or
Matter can neither be created nor destroyed.

2. Law of definite proportions or Law of constant composition: The law states “A chemical compound always consists of the same elements combined together in the same fixed proportion by weight”.

3. Law of multiple proportions: When two elements combine to form two or more than two compounds, then the weights of the elements which combine with the fixed weight of the other, bear a simple ratio to one another.

4. Gay-Lussac’s Law of Gaseous Volumes: It states “When gases react together, they always do so in volumes which bear a simple ratio to one another and to the volumes of the products if gaseous, provided all measurements of volumes are done under similar conditions of temperature and pressure”.

5. Avogadro’s Hypothesis Or Law: Instates, “Equal volumes of all gases under similar conditions of temperature and pressure contain an equal number of molecules”.

Dalton’s Atomic Theory: The main postulates of this theory are:

1. Matter consists of indivisible atoms.
2. All the atoms of a given element have identical properties including identical mass. Atoms of different elements differ in mass.
3. Compounds are formed when atoms of different elements combine in a fixed ratio.
4. Chemical reactions involve the reorganization of atoms. These are neither created nor destroyed in a chemical reaction.

The main advantage of Dalton’s theory was that it could explain the laws of chemical combination.

Atomic and Molecular Masses:
1. Atomic Mass: The atomic mass of an element is the number of times an atom of that element is heavier than an atom of carbon taken as 12.

→ Atomic Mass Unit,(AMU) or u: One atomic mass unit (AMU) or u is equal to \(\frac{1}{12}\)th the mass of an atom of carbon – 12 isotopes.

1 amu = 1.66056 × 10^-24 g
Mass of an atom of hydrogen = 1.6736 × 10^-24 g

Thus, in terms of amu,
the mass of hydrogen atom = \(\frac{1.6736 \times 10^{-24} \mathrm{~g}}{1.66056 \times 10^{-24} \mathrm{~g}}\)
= 1.0078 amu = 1.0080 amu

Similarly, the mass of oxygen – 16(16O) atom would be 15.995 amu

Today, ‘amu’ has been replaced by u which is known as unified mass.

→ Average Atomic Mass: From different isotopes of an element based on their relative abundance, the average atomic mass of an element can be calculated.

For example, there are three isotopes of C – (¹²C, ¹³C, ¹⁴C) with their relative abundance (%) – 98.892, 1.108, and 2 × 10^-10 with their atomic mass (AMU) as 12, 13.00335, and 14.00317 respectively.
The average atomic mass of carbon will be
=.(0.98892)(12 u) + (0.01108)(13.00335 u) + (2 × 10^-12)(14.00317 u)
= 12.011 u.

→ Molecular Mass: Molecular mass is the sum of atomic masses of the elements present in a molecule.

Molecular mass of water (H₂O)
= 2 × atomic mass of hydrogen + 1 × atomic mass of oxygen = 2(1.008 u) + 16.00 u = 18.02 u,

Molecular mass of ethane (C₂H₆) will be = 2 × (12,011 u) + 6 × (1 008 u)
= 24.022 u + 6.048 u = 30 070 u

→ Formula Mass: The formula mass of NaCl which is composed of Na⁺ and Cl^– ions in a three-dimensional structure can be calculated
= Atomic mass of sodium + Atomic mass of chlorine
= 23.00 u + 35.5 u = 56.5 u.

Mole Concept and Molar Masses: In the SI system, mole (symbol, mol) was introduced as the base quantity for the amount of a substance.

→ Substance One Mole is the amount of a substance that contains as many particles or entities as there are atoms in exactly 12 g (or 0. 012 kg) of the 12C Isotope.

1 Mole = 6.0221367 × 10²³ atoms
The number of entities in 1 mol is also called Avogadro Constant and denoted by N_A.

Therefore, 6:022 × 10²³ entities (atoms, molecules, or any other particles) constitute one mole of that particular substance.
∴ 1 Mol of oxygen atoms = 6.022 × 10²³ atoms of oxygen.

Similarly, 1 Mol of ammonia molecules
= 6.022 × 10²³ molecules of ammonia
where n maybe 1, 2, 3,…..

In the SI system, Mole (symbol, mol) was introduced as the seventh base quantity for the amount of a substance.

One mole is the amount of a substance that contains as many particles or entities as there are atoms in exactly 12g (or 0.012 kg) of the UC isotope.

Stoichiometry and Stoichiometric Calculations: Stoichiometry deals with the calculation of masses and volumes of the reactants and products involved in a chemical reaction.

Let us consider the information available for the combustion of methane from its balanced chemical equation
CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(g)

Here methane and dioxygen are called reactants and carbon dioxide and water are called products. The letter (g) stands for gases. The coefficient 2 for O₂ and H₂O are called stoichiometric coefficients. Similarly, the coefficient for CH₄ and CO₂ is one in each case.

They represent the number of molecules (and moles as well taking part in the reaction or formed in the reaction).
(a) One mole of CH₄(g) reacts with two moles of O₂(g) to give one mole of CO₂(g) and two moles of H₂O(g).
(b) One molecule of CH₄(g) reacts with 2 molecules of O₂(g) to give one molecule of CO₂(g) and 2 molecules of H₂O(g).
(c) 22.4 L of CH₄(g) reacts with 44.8 L of O₂(g) at STP to give 22.4 L of CO₂(g) and 44,8 L of H₂O (g).
(d) 16 g of CH₄(g) reacts with 64 g of O₂(g) to give 44 g of CO₂(g) and 36 g of H₂O(g)

From above
mass ⇌ moles ⇌ no. of molecules
\(\frac{\text { Mass }}{\text { Volume }}\) = Density

→ Limiting Reagent: The reacting substance which gets used up first in the reaction is called the limiting reagent. This is because the amount of limiting reagent limits the amount of the product formed. A part of the other reactants which are present in amounts greater than the stoichiometric amounts is left behind as unconsumed reagents.

→ Reactions in Solutions: The concentration of a solution or the amount of substance present in its given volume can be expressed in any of the following ways:

1. Mass percent or weight percent (w/w%)
2. Mole fraction
3. Molarity
4. Molality

Stoichiometry of Reactions in Solutions:
1. Mass percentage or percent by mass: It is defined as the mass of solute in gram per 100 g of the solution. For example, a 10% solution of sodium chloride means that 10 g of NaCl is present in 100 g of the solution.

Mass % of the solute = \(\frac{\text { Mass of solute }}{\text { Mass of solution }}\) × 100
Both, the mass of the solute and that of the solution must be expressed in the same mass units. viz, both in grams or both in
kilograms, etc.

2. Mole Fraction (X): The mole fraction of any component of a solution is defined as the ratio of the number of moles of that component to the total number of moles of all the components of the solution. Thus if a solution contains A moles of A and n5 moles of B, then.

If the mole fraction of one component in a binary solution is known, that of the other can be determined.
i.e. X_B = 1 – X_A.

3. Molarity (M): The molarity of a solution is defined as the number of moles of solute dissolved per dm3 (or liter, L) of the solution. Molarity of any solution depends upon temperature. So, the molarity of any solution is specified for a given temperature.

Mathematically, molarity is defined as
Molarity of solution = \(\frac{\text { No. of moles of the solute }}{\text { Volume of the solution in litres (or in } \mathrm{dm}^{3} \text { ) }}=\frac{n \mathrm{~mol}}{\mathrm{VL}}\)

where n is the number of moles of the solute.
V is the volume of the solution in liters (or dm³).

Since, the number of moles of any substance is related to its mass and the molar mass,
No. of moles of solute = \(\frac{\text { Mass of the solute }}{\text { Molar mass of the solute }}\)

The molarity of a solution then can also be expressed as:
Molarity of the solution = \(\frac{\text { Mass of the solute }}{\text { Molar mass of the solute } \times \text { Volume of the solution in litres }}\)

So, W grams of a substance having molar mass M, dissolved in sufficient solvent, so as to make the total volume of V liter of the substance, the molarity (M) of the solution is given by
Molarity = \(\frac{\mathrm{Wg}}{\mathrm{Mg} \mathrm{mol}^{-1} \times \mathrm{V} \text { litre }}=\frac{\mathrm{W}}{\mathrm{M} \times \mathrm{V}}\) mol/L

4. MoLdity (m): The molality of a solution is defined as the number of moles of solute per kg of the solvent. If a solution is prepared by dissolving n moles of a solute in W kg of the solvent, then.
Molality, (m) = \(\frac{\text { No. of moles of solute }}{\text { Mass of the solvent in } \mathrm{kg} \mathrm{mol}^{-1}}\)

= \(\frac{n_{\text {solute }}}{W_{\text {solvent }} \text { kg }}=\frac{n_{\text {solute }}}{W_{\text {solvent }}}\)mol kg^-1
where n_solute = \(\frac{\text { Mass of the solute }}{\text { Molar mass of the solute }}\)

It is to be noted that molality of a solution does not change with temperature since mass remains unaffected with temperature.

→ Element: It consists of only one type of particles. These particles may be atoms or molecules. Sodium, copper, silver, hydrogen, oxygen etc. are some examples of elements.

→ Compound: When two or more atoms of different elements combine in a fixed proportion, the molecules of a compound is obtained.

→ Atomic mass unit (amu): It is defined as a mass exactly equal to one twelfth the mass of one carbon-12.
1 amu = 1.66056 × 10^-24 g
Nowadays’ amu’ has been replaced by u which is known as unified mass.

→ Mole: One mole is the amount of a substance that contains as many particles or entities as there are atoms in exactly 12 g {or 0.012 kg) of the 12C isotope.

→ Avogadro constant: The number of entities in 1 mol is called the Avogadro constant. It is denoted by N_A and is = 6.022 × 10²³.

→ Molar mass: The mass of one mole of a substance in grams is called its molar mass.

→ Empirical Formula represents the simplest whole-number ratio of various atoms present in a compound.

→ Molecular Formula: It shows the exact number of different types of atoms present in a molecule of a compound.

→ Mass percent:
Mass per cent = \(\frac{\text { Mass of solute }}{\text { Mass of solution }}\) × 100

→ Mole Fraction:
Mole fraction of a component = \(\frac{\text { No. of moles of the component }}{\text { Total no. of moles of solution }}\)

→ Molarity:
Molarity(M) = \(\frac{\text { No. of moles of the solute }}{\text { Volume of solution in litres }}\)

→ Molality
Molality (m) = \(\frac{\text { No. of moles of solute }}{\text { Mass of solvent in } \mathrm{kg}}\)

→ There are different laws which govern the combination of elements to form compounds.
They are mentioned below:

1. Law of conservation of mass.
2. Law of Definite Proportions.
3. Law of multiple proportions.
4. Gay Lussac’s Law of gaseous Volumes.
5. Avogadro Law.

Note: These laws have been defined earlier in the book.
These Laws led to Dalton’s Atomic Theory which states that atoms are building blocks of matter.