CBSE Notes

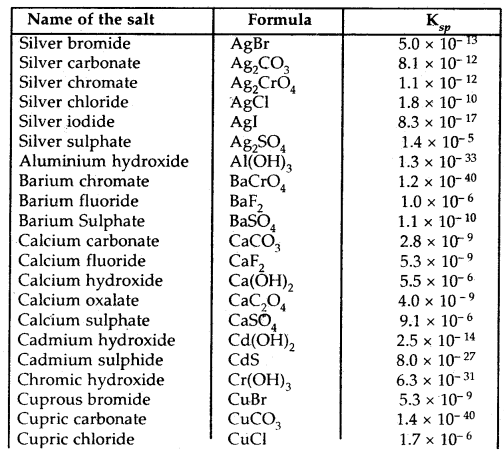
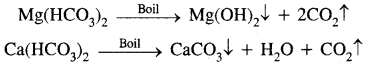By going through these CBSE Class 11 Chemistry Notes Chapter 10 The s-Block Elements, students can recall all the concepts quickly.

The s-Block Elements Notes Class 11 Chemistry Chapter 10

→ Gp. 1 Elements: Alkaline metals Electronic configuration, Atomic & Ionic radii Ionization enthalpy, hydration enthalpy.

→ Physical & Chemical properties.

→ Uses of Alkali metals.

→ General characteristics of the compounds of alkali metals-halides, salts of oxo-acids.

→ Anomalous properties of Lithium Points of difference between Li & other alkali metals

→ Points of Similarities between Lithium & Magnesium.

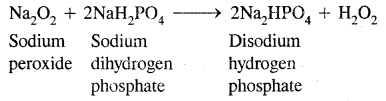
→ Important compounds of Sodium: Sodium carbonate, sodium chloride, sodium hydroxide & sodium hydrogen carbonates.

→ Biological importance of sodium & potassium

→ Gp. 2 Elements: Alkaline Earth metals

→ electronic configuration, Atomic & Ionic radii, Ionization enthalpy, hydration enthalpy

→ Physical & chemical properties & use of alkaline earth metals.

→ General characteristics of compounds of alkaline earth metals- oxides & hydroxides.

→ Halides, salts of oxo-acids & carbonates.

→ Anomalous behaviour of Beryllium-Diagonal relationship between Beryllium & Aluminium.

→ Some important compounds of calcium: Calcium oxide, calcium hydroxide & calcium carbonate, calcium sulphate & cement.

→ Biological importance of Mg & ca.

→ S-block Elements: Group-1 (Alkali metals) & Group-2 (Alkaline earth metals) Their oxides & hydroxides are alkaline in nature.

→ Ionization Enthalpy: Decreases down the group.

→ Atomic & Ionic sizes: Increases down the group.

→ Diagonal Relationship: Li in group-1 & Be in group-2 shows similarities in properties to the second member of the next group. Such similarities are termed a diagonal relationship.

→ Castner-Kellner process: Sodium hydroxides are manufactured by this process.

→ Solvay process: Sodium carbonate is prepared by this process.

→ Plaster of Paris: CaSO₄. \(\frac{1}{2}\) H₂O

→ Portland cement: It is an important constructional material. It is manufactured by heating a pulverised mixture of limestone & clay in a rotatory kiln.

→ Importance of Sodium, Potassium, Magnesium & Calcium: Monovalent Na, K ion & divalent Mg, Ca ions are found in large proportions in Biological fluids. These ions perform important biological functions such as maintenance of unbalance & nerve impulse conduction.

“The s-block, elements are called lighter metals because of their low density.

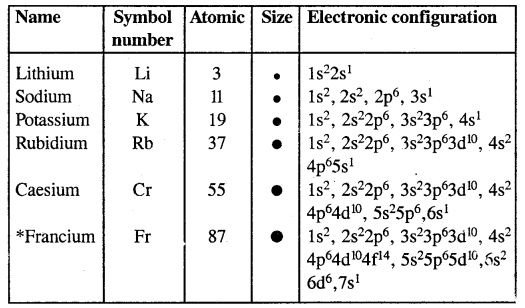
There are two groups (1 and 2) that belong to the s-block. In these two groups of elements, the last electron enters the s-subshell of the valence shell of their atoms. They are all highly reactive metals. The elements of group 1 are called alkali metals and consist up of elements: lithium, sodium, potassium, rubidium caesium and francium. These are so-called because these metals in reaction with water form hydroxides which are strongly alkaline in nature. Their general electronic configuration is ns type.

The elements of Group 2 include beryllium, magnesium calcium, strontium, barium and radium. These elements (except beryllium) are commonly known as alkaline earth metals. These are so .called because their oxides and hydroxides are alkaline in nature and these metal oxides are found in the earth’s crust. Their general electronic configuration is ns type.

Electronic Configuration Of Alkali Metals:

Francium is radioactive. Its largest-lived isotope 223 Fr has a half-life of only 21 minutes.

1. General characteristics of the alkali metals
(j) All the alkali metals have one valence electron ns1. This loosely held s-electron makes them the most electropositive metals which readily give M+ ions. Hence they are never found in a free state.
M → M+ + e-

Atomic and Ionic Radii
They have the largest sizes in a particular period in the periodic table. With the increase in atomic number, the atom becomes larger.

The monovalent ions (M⁺) are smaller than the parent atom, e.g.
Na⁺ → Na
K⁺ → K and so on

The atomic radii and ionic radii of alkali metals increase on moving down the group.
Li < Na < K < Rb < Cs and similarly
Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺

Ionisation Enthalpies
Due to large sizes, the ionisation enthalpies of alkali metals are considerably low and decrease down the group from Li so Cs, because the effect of increasing size outweighs the increasing unclear charge.

Hydration Energy: The hydration enthalpies of alkali metal ions decrease with an increase in ionic sizes.
Li⁺ > Na⁺ > K⁺ > Rb⁺ > Cs⁺
Li⁺ ion has a maximum degree of hydration and for this reason, lithium salts are mostly hydrated e.g. LiCl.2H₂O.

Physical Properties:
1. Physical Appearance: Alkali metals are silvery-white, soft and light metals.

2. Density: Because of their large size, these elements have low densities, which increases down the group from Li to Cs. However, potassium is lighter than sodium.

3. Melting points & boiling points: The melting and boiling points of the alkali metals are low indicating weak metallic bonding.

4. Flame colouration: The alkali metals and their salts impart characteristic colour to an oxidizing flame.” This is due to energy imparted to the loosely bound electron as a result of which it gets excited and jumps to higher energy levels. When the excited electron comes back to the ground state, there is the emission of radiation in the visible region.

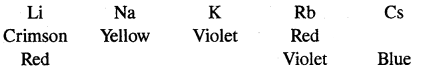
Alkali metals can therefore be detected by their flame tests.

Chemical Properties Of Alkali Metals:
The alkali metals are highly reactive due to their large size and low ionisation enthalpy and reactivity increases down the group.
1. Reactivity towards air: The alkali metals tarnish in dry air due to the formation of an oxide which in turn reacts with moisture to form hydroxides. They burn vigorously in oxygen forming oxides. Li forms monoxide, sodium forms peroxide, the other metals form superoxides.
2Li + O₂ → 2LiO (Oxide)
2Na + O₂ → Na₂O₂ (peroxide)
M + O₂ → MO₂ (superoxide)
[M = K, Rb, Cs]

Lithium (Li) shows exceptional behaviour in reacting with the nitrogen of air directly to form die nitride Li₃N as well.
6Li + N₂ → 2Li₃N (from the air)

Due to extreme reactivity, these metals are kept in kerosene oil.

2. Reactivity towards water:
2M + 2H₂O → 2M⁺ + 2OH^– + H₂↑
M = an alkali metal

Li reacts less vigorously with water. Other metals of the group react explosively with water. Reactivity increases down the group which is due to an increase in the electropositive character.

3. Reactivity towards hydrogen: Alkali metals react with hydrogen at about 673 K [Lithium at 1073 K] to form ionic hydrides which have high melting solids.
2M + H₂ → 2M⁺H^–

They also react with proton donors such as alcohol, gaseous ammonia and alkynes.
2C₂H₅OH + 2M → 2C₂H₅OM + H₂↑
CH = CH + Na → CH ≡ C^–Na⁺ + \(\frac{1}{2}\)H₂(g)

4. Reactivity towards halogens: The alkali metals react readily with halogens to form ionic halides M⁺X^–. However, lithium halide is somewhat covalent because of polarisation (The distortion of the electron cloud of the anion by the cation is called polarisation)
2M + X₂ → 2M⁺X^– Metallic (halide)

5. Solubility in liquid ammonia: All alkali metals are soluble in liquid ammonia. Dilute alkali metal-ammonia solution is blue in colour. With increasing concentration of metal in ammonia the blue colour starts changing to that of metallic copper after which a further amount of metal does not dissolve.

6. Reducing property (oxidation potentials): The tendency of an element to lose an electron is measured by its standard oxidation potential (E°), the more the value of E° of an element stronger will be its reducing character.
Since alkali metals have high values of E° these are powerful reducing agents and further lithium having the highest value is the strongest of them.

However, among the alkali metals, lithium although, has the highest ionization energy, yet is the strongest reducing agent. The greater reducing power of lithium is due to its larger heat of hydration which in turn is due to its small size.

7. Formation of alloys: The alkali metals form alloys amongst themselves as well as with other metals. The alkali metals dissolve readily in mercury forming amalgams. The process is highly exothermic.

General Characteristics Of The Compounds Of Alkali Metals:
(a) Oxides: Alkali metals when burnt in the air form oxides. The nature of oxides depends upon the nature of the alkali metal.

Under ordinary conditions, lithium forms the monoxide (Li₂O), sodium forms the peroxide (Na₂O₂) and the other alkali metals form mainly superoxides (MO₂) along with a small number of peroxides.

The increasing stability of the peroxide or superoxide, as the size of the metal ion increases, is due to the stabilization of large anions by larger cations through lattice energy effects. These oxides are easily hydrolysed by water to form the hydroxides according to the following reactions:
M₂O + H₂O → 2M⁺ + 2OH^–
M₂O₂ + 2H₂O → 2M⁺ + 2OH^– + O₂
2MO₂ + 2H₂O → 2M⁺ + 2OH^– + H₂O₂ + O₂

The oxides and the peroxides are colourless, but the superoxides are yellow or orange coloured. The superoxides are also paramagnetic. Sodium peroxide is widely used as an oxidizing agent in inorganic chemistry.

(b) Hydroxides: Alkali metal hydroxides, MOH are prepared, by dissolving the corresponding oxide in water. Their solubility in the water further increases as we move down the group due to a decrease in lattice energy.

Properties:

1. These are white crystalline solid, highly soluble in water and alcohols. Their solubility in the water further increases as we move down the group due to a decrease in lattice energy.
2. Since alkali metals are highly electropositive, their hydroxides form the strongest bases known. They dissolve in water with the evolution of much heat to give a strongly alkaline solution.
3. They melt without decomposition and are good conductors of electricity in the fused state.
4. These are stable to heat and do not lose water even at red heat. The thermal stability increases on moving from Li to Cs. However, they sublime at about 400°C and the vapours mainly consists of dimers. (MOH)₂.

(c) Halides: Alkali metal halides arc prepared by the direct combination of the element, M and halogens. They are normally represented by the formula MX and Cs and Rb, being of large size, also form Polyhalides, i.e. Csl₃

Properties:

1. All alkali halides except lithium fluoride are freely soluble in water (LiF is soluble in non-polar solvents).
2. They have high melting and boiling points.
3. Solubility of halides of alkaline metals: The solubility of alkali metal halides show a gradation. For example
   
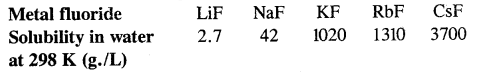
4. They are good conductors of electricity infused state.
5. They have an ionic crystal structure. However, lithium halides have a partly covalent character due to polarising power of Li+ ions.

(d) Carbonates and bicarbonates: All alkali metals from carbonates of the type M₂CO₃. Due to the high electropositive nature of the alkali metals, their carbonates (and also the bicarbonates) are highly stable to heat (however, lithium carbonate decomposes easily by heat. Further, as the electropositive character increases in moving down the group, the stability of carbonates (and bicarbonates) increases in the same order.

Both carbonates and bicarbonates are quite soluble in water and their solubility increases as we move down the group from Li to Cs. Since carbonates are salts of a weak acid (carbonic acid H₂CO₃), they are hydrolysed in water to give a basic solution.
2M⁺ + CO₃^– + H – OH = 2M⁺ + HCO₃^2- + OH^–

Since the alkali metals are highly electropositive, these are the only elements that form stable solid carbonates. However, lithium due to its less electropositive nature does not form solid bicarbonate.

(e) Hydrides: Alkaline metals form hydrides of the type M⁺N^–. The presence of hydrogen as an anion in alkali metal hydrides is evidenced by the fact that on electrolysis hydrogen is liberated at the anode. The hydrides are not very stable. They react with water liberating hydrogen
LiH + H₂O → LiOH + H₂

These hydrides are, therefore, used as reducing agents. Lithium aluminium hydride, LiAlH₄ is even a stronger reducing agent and is used in organic chemistry.

2. Anomalous properties of Lithium:
1. Points of difference between lithium and other Alkali Metals:
(a) Lithium is much harder, its m.p. and b.p. are higher than the other alkali metals.

(b) Lithium is the least reacting but the strongest reducing agent among all the alkali metals. On combustion in air, it forms mainly monoxide Li₂O and the nitride, Li₃N, unlike other alkali metals.

(c) LiCl is deliquescent and crystallizes as a hydrate, LiCl.2H₂O whereas other alkali metal chlorides do not form hydrates. Lithium bicarbonate is not obtained in solid form while all other elements of this group form solid bicarbonate. Lithium unlike other alkali metals forms no acetylide on reaction with ethane.

(d) Lithium nitrate when heated gives lithium oxide Li₂O whereas other alkali metal nitrates decompose to give the corresponding nitrite.
4LiNO₃ → 2Li₂O + 4NO₂ + O₂
4NaNO₃ → 2NaNO₂ + O₂

(e) LiF and Li₂O are comparatively much less soluble in water than the corresponding compounds of other alkali metals.

2. Points of similarities between Lithium and Magnesium
(a) Both lithium and magnesium are harder and lighter than other elements in their respective groups.
(b) Both Li and Mg react slowly with cold water. Their oxides and hydroxides are much less soluble and their hydroxides decompose on heating.
2LiOH → Li₂O + H₂O
Mg(OH)₂ → MgO + H₂O

(c) Both form nitrides by direct combination with N₂.
6Li + N₂ → 2Li₃N
3Mg + N₂ → Mg₃N₂

(d) Their oxides do not combine with an excess of O₂ to give peroxide or superoxide.

(e) The carbonates of both decompose on heating to give oxide and CO₂.

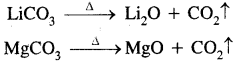
Solid bicarbonates are not formed by lithium and magnesium.

(f) Both LiCl and MgCL are soluble in ethanol.

(g) Both lithium perchlorate LiClO₄ and magnesium perchlorate Mg(ClO₄)₂ are extremely soluble in ethanol.

(h) Both LiCl and MgCl₂ are deliquescent and crystallise from aqueous solution as hydrates, LiCl.2H₂O and MgCl₂.8H₂O.

Some Important Compounds Of Sodium:
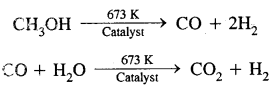
1. Sodium carbonate (washing soda) Na₂CO₃.10H₂O: Sodium carbonate is generally prepared by the Solvay process. In this process, the advantage is taken of the low solubility of sodium bicarbonate whereby it gets precipitated in the reaction of brine solution (sodium chloride) with ammonium bicarbonate. The latter is prepared by passing CO₂ to a concentrated solution of sodium chloride saturated with ammonia.

Ammonium carbonate first formed changes to ammonium bicarbonate.
1. 2NH₃ + H₂O + CO₂ → (NH₄)₂ CO₃
2. (NH₄)₂CO₃ + H₂O + CO₂ → 2NH4HCO₃
3. NH₄HCO₃ + NaCl → NH₄Cl + NaHCO₃

Sodium bicarbonate crystal separates. These are heated to give sodium carbonate.

In this process, NH₃ is recovered when the solution containing NH₄Cl is treated with Ca(OH)₂ Calcium chloride is obtained as a by-product.

5. 2NH₄Cl + Ca(OH)₂ → 2NH₃ + CaCl₂ + H₂O

Properties of sodium carbonate

1. It is a white crystalline solid which exists as decahydrate, Na₂CO₃10H₂O.
2. It is readily soluble in water.
3. On heating, the decahydrate loses its water of crystallisation to form monohydrate. Above 373 K, the monohydrate becomes completely anhydrous and changes to a white powder called soda ash.
   
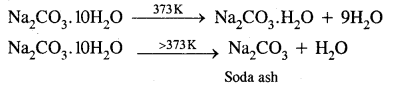
4. It gets hydrolysed by water to form an alkaline solution
   CO₃^2- + H₂O → HCO₃^– + OH^–

Uses of sodium carbonate

1. It is used in water-softening, laundering and cleaning.
2. It is used in the manufacture of glass, soap, borax and caustic soda.
3. It is used in paper, paint and textile industries.
4. It is an important laboratory reagent both in qualitative and quantitative analysis.

Sodium Chloride NaCl:
Crude sodium chloride present in seawater (2.7 to 2.9% salt) is generally obtained by evaporation. It contains Na₂SO₄ CaSO₄, CaCl₂ and MgCl₂ as impurities. CaCl₂ and MgCl, are undesirable impurities because they are deliquescent (absorb moisture easily from the atmosphere).

To obtain pure NaCl, the crude salt is dissolved in a minimum amount of water and filtered to remove insoluble impurities. The solution is then saturated with hydrogen chloride gas. Crystals of pure sodium chloride separate out. CaCl₂, and MgCl₂, being more soluble than NaCl remain in the solution.

Sodium chloride melts at 1081 K. It has a solubility of 36.Ogin 100g of water at 273K. The solubility does not increase appreciably with an increase in temperature.

Sodium Hydroxide (Caustic Soda) NaOH:
It is manufactured from the electrolysis of brine solution (an aqueous solution of NaCl) by Castner-Kellner cell. A mercury cathode and carbon anode are used.
Na⁺Cl^– (aq) → Na⁺(aq) + Cl^– (aq)
At cathode

At anode
Cl^– → \(\frac{1}{2}\) Cl₂ + e^–

The amalgam on treatment with water gives sodium hydroxide and H₂ gas.
2Na-amalgam + 2H₂O → 2NaOH + 2Hg + H₂

Properties

1. It is a white translucent solid.
2. Its M.Pt. is 591 K.
3. It gives a strongly alkaline solution in water.
4. Its crystals are deliquescent.
5. NaOH solution formed at the surface reacts with CO₂ from the atmosphere to form a crystal of Na₂CO₃.
   2NaOH + CO₂ → Na₂CO₃ + H₂O

Uses of sodium hydroxide:

1. It is used in the manufacture of sodium metal, soap, rayon, paper, dyes and drugs.
2. It is used in petroleum refining.
3. Sodium hydroxide is used for mercerizing cotton to make cloth unshrinkable.
4. It is used as a reagent in the laboratory.

Sodium Bicarbonate (Baking Soda) NaHCO₃:
Preparation
Na₂CO₃ + H₂O + CO₂ → 2NaHCO₃

Uses:

• Sodium bicarbonate is a mild antiseptic for skin infections.
• It is used in fire-extinguishers.
• It is known as baking soda because it decomposes on heating to generate bubbles of CO₂ (leaving holes in cakes or pastries and making them light and fluffy).

Biological Role Of Sodium & Potassium:
K+ ions and Na+ ions are present in the red blood cells. A 70 kg weighing man contains about 90g of Na and 170gof K. Sodium ions are found primarily on the outside of cells, is located in the blood plasma and in the interstitial fluid which surrounds the cells. These ions participate in the transmission of nerve signals in regulating the flow of water across cell membranes and in the transport of sugars and amino acids into cells.

Sodium and potassium which are chemically so alike, differ quantitatively in their ability to penetrate cell membranes, in their transport mechanisms and their efficiency to activate enzymes. Thus potassium ions are the most abundant cations within cell fluids, where they activate many enzymes, participate in the oxidation of glucose to produce ATP and with sodium, are responsible for the transmission of nerve; signals.

The ionic gradients of Na+ and K+ demonstrate that a discriminatory mechanism, called the sodium-potassium pump operate across the cell membranes which consumes more than one-third of the ATP used by a resting animal- about 15 kg per 21 h in a resting human.

Group-2 Elements: Alkaline Earth Metals: The group 2 elements comprise beryllium (Be), magnesium (Mg), calcium (Ca), strontium (Sr), Barium (Ba) and radium (Ra). They follow alkali metals in the periodic table. These (except Beryllium) are known as alkaline earth metals.
1. Atomic properties:
(a) Electronic configuration:

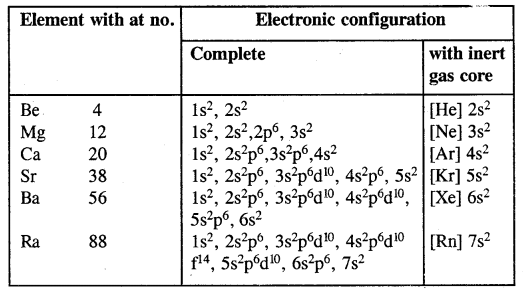
(b) Atomic and ionic sizes: The atomic and ionic radii of the alkaline earth metals are smaller than those of the alkaline metals in the corresponding periods. This is due to the increased nuclear charge in these elements.

(c) Ionization Enthalpies: The first ionization enthalpies of the alkaline earth metals are higher than those of Group 1 metals. The second ionization enthalpies of the alkaline earth metals are smaller than those of the corresponding alkali metals.

2. Physical properties of the alkaline earth metals:
(a) Physical appearance: These metals in general are silvery-white, lustrous and relatively soft, but harder than the alkali metals. Beryllium and magnesium appear to be somewhat greyish.

(b) Melting and boiling points: The fairly higher melting and boiling points of the alkaline earth metals compared to those of the corresponding alkali metals and attributed to their smaller sizes and presence of two valence electrons. The trend is, however, not systematic.

(c) Flame colour: Chlorides of alkaline earth metals, except that of Be and Mg, produce the characteristic colour of flame due to easy excitation of electrons to higher energy levels. Beryllium and magnesium atoms due to their small size, bind their electrons more strongly, i.e., their ionisation energies are high. Hence these possess high excitation energy and not excited by the energy of the flame to a higher energy state with a result no colour is produced in the flame.

(d) Electrical and thermal conductivities: These properties are characteristics of typical metals.

3. Chemical Reactivity:
(a) Action of air: Their less reactivity than the alkali metals is evident by the fact that they are only slowly oxidised on exposure to air. However, when burnt in the air, they form ionic oxides of the type MO, except Ba and Ra which give peroxides. Thus, the tendency of the metal to form higher oxides like peroxide increases on moving down the group. On ignition powdered Be burns to give BeO & Be₃N₂. Mg also burns with dazzling brilliance to give MgO and Mg₃N₂.

(b) Action of water: These metals react slowly with water liberating hydrogen and forming metal hydroxides, e.g.
Ca + 2H₂O → Ca(OH)₂ + H₂
The reaction with water becomes increasingly vigorous on moving down the group.
Ba > Sr > Ca > Mg > Be (Reactivity with water)

The inertness of Be and Mg towards water is due to the formation of a protective thin layer of hydroxide on the surface of the metals.

(c) Action of hydrogen: All these elements, except beryllium, combine with hydrogen to form hydrides MH₂, BeH₂ is prepared indirectly.
2BeCl₂ + LiAlH₄ → 2BeH₂ + LiCl + AlCl₃

(d) Action of halogens: All these elements combine with halogens at elevated temperatures forming halides, MX₂. Beryllium halides are covalent, while the rest are ionic. The solubility of halides (except fluoride) decreases on moving down the group.

(e) Action with nitrogen: All these elements burn in nitrogen forming nitrides, M3N2 which react with water to liberate ammonia.
3Ca + N₂ → Ca₃N₂
Ca₃N₂ + 6H₂O → 3Ca(OH)₂ + 2NH₃
The ease of formation of nitrides decreases on moving down the group.

(f) Action with acids: On account of their high oxidation potentials, they readily liberate hydrogen from dilute acids. For example.
Mg + 2HCl → MgCl₂ + H₂

The reactivity of alkaline earth metals increases on moving down the group. This is due to an increase in electropositive character from Be to Ba. Thus beryllium reacts very slowly, Mg reacts very rapidly while Ca, Sr and Ba react explosively.

(g) Formation of amalgam and alloys: They form an amalgam with mercury and alloys with other metals.

(h) Complex formation: Beryllium, due to its small size, forms a number of stable complexes, e.g., [BeF₃]^–, [BeF₄]^2-, [Be(H₂O)]²⁺ etc.

(i) Reducing Character: They are strong reducing agents, Their reducing power is less than the corresponding alkali metals.

(j) Solubility in liquid ammonia: Alkaline earth metals dissolve in liquid ammonia giving coloured solutions. When the metal- ammonia solutions are evaporated, Hexammoniates M(NH3)6 are formed. The tendency for the formation of ammoniates decreases with an increase in the size of the metal atom, i.e., on moving down the group.
M + (x + y) NH₃ → M(NH₃)²⁺ + 2e^– (NH₃)y

4. General characteristics of compounds of the alkaline earth metals:
(a) Oxides and Hydroxides: The alkaline earth metal oxides, MO are prepared either by heating the metal in oxygen or better by calcination of carbonates.

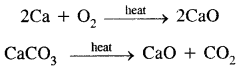
These are extremely stable, white crystalline solids. Except for BeO, all the alkaline earth oxides are ionic, in which doubly charged ions are packed in a NaCl-type of lattice leading to their high crystal lattice energy and hence high stability. However, beryllium oxide is covalent due to its small size and relatively large charge on the beryllium ion. The high melting point of BeO is due to its polymeric nature.

The heavier metal oxides react with water to form soluble hydroxides which are strong bases.
MO + H₂O → M(OH)₂ + heat [where M = Ca²⁺, Ba²⁺ or Sr²⁺)

The solubility of hydroxides of alkaline earth metals in water increases on moving down the group. This is due to the fact that with the increase in the size of the cation (down a group), the lattice energy- decreases more than the decrease in hydration energy.

Halides:
They are obtained:

1. by heating the metal with halogens at high temperature or
2. by treating, metal carbonates with dilute halogen acids.

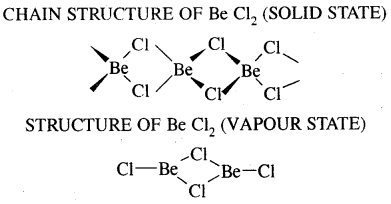
Beryllium halides are covalent compounds due to their small size and relatively high charge of Be²⁺ ion causing high polarising power. Due to the covalent bonding beryllium chloride, shows the following anomalous characteristics.

1. It has low melting and boiling points.
2. It does not conduct electricity in the fused state.
3. It is soluble in organic solvents such as ether.
4. It is hygroscopic and fumes in the air due to hydrolysis
   BaCl₂ + 2H₂O → Be(OH)₂ + 2HCl(g)
5. It is electron-deficient and behaves as Lewis acid.
   

The chlorides, fluorides, bromides and iodides of other alkaline earth metals are ionic solids and thus possess the following characteristics.

1. The melting and boiling points are high.
2. They conduct electricity in the molten state. Further, since the ionic character of the halides increases on moving down the group, the melting point and conductivity increase in the group from Mgd₂ to BaCl₂.
3. They are “hygroscopic and readily form hydrates, e.g., MgCl₂.6H₂O, CaCl₂.2H₂O, BaCl₂.2H₂O.
4. The halides (except fluorides) of the alkaline earth metals are soluble in water and their solubility decreases with an increasing atomic number of the metal due to a decrease in the hydration energy with the increasing size of the metal ion.

(c) Carbonates: The carbonates are invariable insoluble and therefore occur as solid rock materials in nature. However, the carbonates dissolve in water in the presence of carbon dioxide to give bicarbonates.

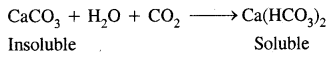
Most beryllium salts of strong oxo-acids crystallize as soluble hydrates. Beryllium carbonate is prone to hydrolysis and can be precipitated only in an atmosphere of carbon dioxide. The carbonates of magnesium and the other alkaline earth metals are all sparingly soluble in water, their thermal stability increases with increasing cationic size. Calcium carbonate finds use in the Solvay process for the manufacture of sodium carbonate in glassmaking and in cement manufacture.

(d) Sulphates: These can be prepared by dissolving the metal oxide in H₂SO₄.
MgO + H₂SO₄ → MgSO₄ + H₂O

The solubility of the sulphates of the alkaline earth metals decreases regularly on moving down the group. Thus beryllium sulphate is highly soluble in water, while barium and radium sulphates are practically insoluble.
The insolubility of barium sulphate is used for detecting an obstruction in the digestive system by the technique commonly known as barium meal.

The presence of BaSO₄ in the stomach helps in getting X-ray pictures because of the great scattering power of heavy Ba²⁺ ions. Barium sulphate is also used as a white pigment.

(e) Nitrates: The nitrates are made by the dissolution of the carbonates in dilute nitric acid. Magnesium nitrate crystallizes with six molecules of water. Barium nitrate crystallizes as an anhydrous salt. All of them decompose on heating giving the oxide.
2M(NO₃)₂ → 2MO + 4NO₂ + O₂ (M = Be, Mg, Ca, Sr or Ba)

Strontium and barium nitrates are used in pyrotechnics for giving red and green flames.

Anomalous behaviour of Beryllium
The anomalous behaviour of beryllium is mainly died to its very small size and partly due to its high electronegativity. These two factors increase the polarising power [Ionic charge/ (ionic radii)²] of Be²⁺ ions to such extent that it becomes significantly equal to the polarising power of Al³⁺ ions.

Hence the two elements resemble (diagonal relationship) very much.
1. Both of them have the same value of electronegativity (1.5).

2. The standard oxidation potential of Be and Al are of the same order (Be = 1.69 V, Al = 1.7 V)

3. In nature both occur together in beryl, 3BeO, Al₂O₃, 6SiO₂.

4. Due to its small size, beryllium has a high charge density and therefore, exhibits a strong tendency to form covalent compounds. Aluminium too has a strong tendency to form covalent compounds. Thus salts of both beryllium and aluminium have low m.p. are soluble in organic solvents and get hydrolysed by water.

Beryllium does show some tendency to form covalent compounds but other alkaline earth metals do not form covalent compounds.

5. Unlike other alkaline earth metals but like aluminium, beryllium is not easily affected by dry air.

6. Both (Be and Al) do not decompose water even on boiling; because of their weak electropositive character. Other alkaline earth » metals decompose even cold water evolving hydrogen.

7. Beryllium, like aluminium, reacts very slowly with dilute – mineral acids liberating hydrogen.
Be + 2HCl → BeCl₂ + H₂
2Al + 6HCl → 2AlCl₃ + 3H₂
Other alkaline earth metals react very readily with dilute acids.

8. The chlorides of both beryllium and aluminium have bridged chloride structures in the vapour phase.

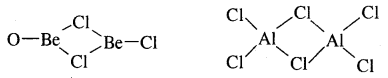
9. Salts of these, metals form hydrated ions e.g., [Be(OH₂)₄]³⁺ and [Al(OH₂)₆]³⁺ in aqueous solutions.

10. Beryllium and aluminium both react with caustic alkalies to form beryllate and aluminate respectively. Other alkaline earth metals do not react with caustic alkalies.

Some Important Compounds Of Calcium:
1. Calcium oxide (Quick lime), CaO: Preparation: By heating limestone at 1273 K

(a) The reaction is reversible and thus in order to assure the complete decomposition of CaCO₃, carbon dioxide formed must be swept away by a current of air.

(b) Temperature should not be too high, because, at high temperature, clay (present as an impurity in limestone) will react with lime to form fusible silicates.

Properties:
1. Calcium oxide is a white amorphous substance.

2. When heated in an oxy-hydrogen flame, it gives an intense white light called limelight.

3. Action of water: On adding water, it gives a hissing sound and forms calcium hydroxide commonly known as slaked lime. The reaction is exothermic and known as slaking of lime.
CaO + H₂O → Ca(OH)₂ ΔH = – 64.5 kJ/mol

4. It reacts with SiO₂ and P₂O₅ at high temperature forming calcium silicate, CaSiO₃ and calcium phosphate; Ca₃(PO₄)₂ respectively
6CaO + 3P₂O₅ → 2Ca₃(PO₄)₂

5. With moist chlorine it forms bleaching powder, Ca(OCl)₂. With moist CO₂ it forms CaCO₃ and with moist SO₂ it forms CaSO₃ and with moist HCl gas, it forms CaCl₂. None of these gases will react when perfectly dried.

6. When heated with carbon at 2000°C, it forms calcium Carbide.

Uses of calcium oxide:
(a) It is used as a drying agent as such or as soda lime.
(b) Large quantities of quick-lime are used in the production of slaked lime.
(c) As a constituent of mortar, it is used on a very large scale in building constructions.

2. Calcium Hydroxide (Slaked lime), Ca(OH)₂:
Preparation:

1. By treating lime (quick lime) with water
   Ca O + H₂O → Ca(OH)₂
2. By the action of caustic alkalies on a soluble calcium salt.

Properties:
(a) It is a white amorphous powder, only sparingly soluble in water. Its solubility decreases with the increase in temperature.

(b) When dried and heated to redness, it loses a molecule of water and converted into calcium oxide (lime).

(c) Action of CO₂: Lime water is frequently used for the detection of C0₂ gas. C0₂ gas turns lime water milky due to the formation of CaC0₃.
Ca(OH)₂ + CO₂ → CaC0₃(s) + H₂O
However, the precipitate disappears on prolonged treatment with C0₂ because of the conversion of CaS0₃ (insoluble) to calcium bicarbonate (soluble).

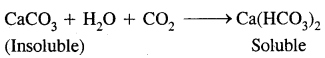
The above solution, if heated again gives turbidity. This is due to the decomposition of calcium bicarbonate to calcium carbonate,

(d) Milk of lime reacts with chlorine to form hypochlorite, a constituent of bleaching powder
2Ca(OH)₂ + 2Cl₂ → CaCl₂ + Ca(ClO)₂ + 2H₂O

Uses of calcium hydroxide: Calcium hydroxide finds various uses:
(a) For absorbing acid gases
(b) For preparing ammonia from ammonium chloride
(c) In the production of mortar, a building material
(d) In glassmaking, tanning industry, for the preparation of bleaching powder and for purification of sugar.
(e) It is also used as a disinfectant
(f) As lime water in laboratories.

3. Plaster of Paris, CaSO₄. \(\frac{1}{2}\) H₂O
Preparation:
It is obtained when gypsum, CaSO₄.2H₂O is heated to 393 K
2(CaSO₄.2H₂O) → 2CaSO₄.H₂O + 3H₂O

Properties:
1. It is a white powder.

2. It has a very remarkable property of setting into a hard mass on wetting with water. So, when water is added to Plaster of Paris, it sets into a hard mass in about half an hour. The setting of Plaster of Paris is due to its hydration to form crystals of gypsum which set to form a hard solid mass.

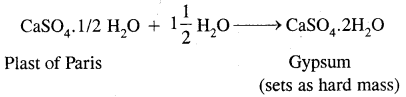
The setting of plaster of Paris is accompanied by a slight expansion in volume due to which it is used in making castes for statues, toys, etc.

Uses of Plaster of Paris:
(a) It finds extensive use in surgical bandages, in casting and moulding.
(b) It is also employed in dentistry, in ornamental work and for taking castes of statues and busts.

Properties:
(a) It is a white powder and exists in two crystalline forms: Calcite and aragonite.
(b) It is insoluble in water but dissolves in the presence of CO2 due to the formation of calcium bicarbonate.
CaCO3 + H2O + CO2 → Ca(HCO3)2

Uses:
(a) Limestone is used:

• for the manufacture of the lime, element, washing soda and glass and
• as a flux, since CaO obtained from its decomposition combines with silica to form calcium silicate, CaSiO₃.

(b) Marble is used:

• for building purposes and
• in the laboratory for the production of CO₂ gas.

(c) Chalk is used:

• in paints (white ash) and distempers and
• in the production of CO₂ in the laboratory.

(d) Precipitated chalk is used:

• in toothpaste and powders
• in medicine for indigestion
• in adhesives and in cosmetic powders and
• to de-acidify wines.

4. Portland cement: It is made by heating a mixture of limestone (or chalk, shells etc.) with alumina silicates in carefully controlled amounts so as to give the approximate composition CaO 70%, SiO₂ 20%, Al₂O₃ 5%, FeCO₃ 3%. The new minerals are ground to pass 300-mesh sieves and then heated in a rotary kiln to 1773 K to give sintered clinker. This is ground to 325 mesh sieve and mixed with 2-5% gypsum. An average-sized kiln can produce 1000-2000 tonnes of cement per day.

When mixed with water, the setting of cement takes place. Chemically, it is the hydration of the molecules of the constitutions and their rearrangement.

The adhesion of other particles to each other and to the embedded aggregates is responsible for the strength of the cement which is due, ultimately, to the formation of Si-O-Si-O bonds.

The purposes of adding gypsum are only to slow down the process of setting the cement so that it gets sufficiently hardened.

Concrete: It is a mixture of cement, sand, gravel (small pieces of stone) and the appropriate amount of water. When the cement concrete is filled in and around a wire-netting or skeleton of iron rods and allowed to set, the resulting structure is known as reinforced concrete (RCC).

Uses of cement: It is used in concrete and reinforces concrete, in plastering and in the construction of bridges, dams and buildings.

Biological Importance Of Magnesium & Calcium:
An adult body contains about 25g of Magnesium and 1200 g of calcium as compared with only 5g of iron and 0.06g of copper. The daily requirement in the human body has been estimated to be 200-300 mg.

All enzymes that utilize ATP in phosphate transfer require magnesium as the cofactor.

The main pigment for the absorption of light in plants for photosynthesis is green coloured chlorophyll which contains magnesium.

About 99% of body calcium is present in bones and teeth. It also plays important roles in neuromuscular function, interneuronal transmission, cell membrane integrity and blood coagulation. The calcium concentration in plasma is regulated at about 100 mg L^-1. It is maintained by two hormones.

Calcitonin and parathyroid hormone. Bone is not an inert and unchanging substance but is continuously being solubilized and redeposited to the extent of 400 mg per day in man. All the calcium passes through the plasma.

By going through these CBSE Class 11 Chemistry Notes Chapter 9 Hydrogen, students can recall all the concepts quickly.

Hydrogen Notes Class 11 Chemistry Chapter 9

→ Hydrogen: Hydrogen is the lightest atom with only one electron. Loss of this electron results in an elementary particle, the proton.

→ Isotopes of hydrogen: Protium (¹₁H), Deuterium (D or ²₁H) & Tritium (T or ³₁H). Tritium is radioactive.

→ Water-Gas Shift Reaction: Dihydrogen is obtained on an industrial scale by this reaction.

→ Bond dissociation Enthalpy: Bond dissociation enthalpy of dihydrogen is (435.88 KJ mol^-1) is highest for a single bond between two atoms of any elements.

→ Hydrides: Dihydrogen combines with almost all the elements under appropriate conditions to form hydrides. Three types of hydrides as Ionic or saline, covalent or molecular hydrides & metallic or non-stoichiometric hydrides.

→ Hydrogen Economy: The basic principle of a hydrogen economy is the transportation & storage of energy in the form of liquid or gaseous dihydrogen. In fact, it has promising potential for use as a non-polluting fuel of the near future.

→ Water: It is of great chemical & biological significance. Water molecule is highly polar in nature due to its bent structure. This property leads to hydrogen bonding which is maximum in ice & least in water vapor. Its property to dissolve many salts, particularly in large quantity makes it hard & hazardous for industrial use.

Temporary & permanent hardness can be removed by the use of, zeolites & synthetic ion exchangers.

→ Heavy water: D₂O is manufactured by the electrolysis of normal water. It is essentially used as a moderator in nuclear reactors.

→ Hydrogen peroxide: H₂O₂ has an interesting non-polar Structure & widely used as an industrial bleach & in pharmaceutical & pollution control treatment of industrial & domestic effluents.

→ Dihydrogen: Isotopes -Protium, Deuterium & Tritium, No. of neutrons-NIL, One, & Two Tritium is radioactive

→ Water-Gas: Mixture of CO & H₂.

→ Synthesis Gas or Syn Gas: When water gas is used for the synthesis of methanol & a no. of hydrocarbons. It is also called synthesis gas or syngas.

→ Coal Gasification: The process of producing syngas from coal is called coal gasification.

→ Uses of dihydrogen: In ammonia synthesis & in nitrogenous fertilizers & for preparing Vanaspati Ghee, manufacturing of organic chemical, particularly methanol; HCl & hydrides. Used as rocket fuel in space research. It does not produce any pollution & releases greater energy per unit mass of fuel in comparison to Gasoline & other fuels.

→ Hydrides: Three types of hydrides:

1. Ionic or Saline
2. Covalent or molecular
3. metallic or interstitial

→ Molecular hydrides:

1. Electron deficient
2. Electron precise
3. Electron rich

→ Water: Colourless & tasteless liquid. The unusual properties of water in the condensed phase (liquid & solid states) are due to the presence of extensive hydrogen bonding between water molecules.
Str. of the water molecule

→ Hard & Soft Water: The presence of Magnesium & Calcium salts in the form of hydrogen bicarbonates chloride & sulfate in water make water hard. Hard water does not give lather with soap. Water-free from soluble salts of calcium & magnesium is called Soft Water. It gives lather with soap easily.

→ Removal of Hardness of Water: Temporary hardness by boiling of water & by dark’s method. Permanent hardness by treatment with washing soda, Calgon’s method, ion exchange method & synthetic resins method.

→ Hydrogen-peroxide: Hydrogen peroxide is an important chemical used in the pollution control treatment of domestic & industrial effluents.

→ Storage of H₂O₂: H₂O₂ decomposes slowly on exposure to light. In presence of metal surfaces or traces of alkali (present in glass- containers), the following reaction is catalyzed.
2H₂O₂ (l) → 2H₂O(l) + O₂(g)

It is, therefore, stored in wax-lined glass or plastic vessels in dark. Urea can be added as a stabilizer. It is kept away from dust because dust can induce explosive decomposition of the compound.

→ Uses of H₂O₂:

1. As a hair bleach & a mild disinfectant. It is sold in the market as Perhydrol.
2. In manufacturing chemicals that are used in high-quality detergents.
3. In the synthesis of hydroquinone, tartaric acid & incertain food products & in pharmaceuticals (cephalosporin), etc.
4. It is also used in environmentally green chemistry.

→ Heavy Water: D₂O uses as a moderator in nuclear reactors & can be prepared by exhaustive electrolysis of water.

→ Hydrogen Economy: Hydrogen economy is an alternative. The basic principle of a hydrogen economy is the transportation & storage of energy in the form of liquid or gaseous dihydrogen. Nowadays, it is also used in fuel cells for the generation of electric power. Position of Hydrogen in the periodic table

Hydrogen is the first element in the periodic table. Its atom has only one proton and one electron. In the elemental form, it exists as H₂ and is called dihydrogen. The electronic configuration of hydrogen is Is1. Alkali metals have an electronic configuration of ns¹ which is similar. On the other hand like halogens (electronic configuration ns²np⁵, of 17th group) it is short by one electron than the corresponding noble gas configuration of He-1s². Hydrogen thus resembles both alkali metals as well as halogens.

But hydrogen also differs from alkali metals and halogens in some other respects. Thus it is unique in its behavior and is, therefore, best placed separately in the periodic table.

Occurrence of Dihydrogen (H₂):
It is the most abundant element in the universe (70% of the total mass of the universe) and is the principal element in the solar atmosphere. However, due to its light nature, it is much less abundant (0.15% by mass) in the earth’s atmosphere. In the combined form, it constitutes 15.4% of the earth’s crust and the oceans. In the combined form, besides in water, it occurs in plants, and animal tissues, carbohydrates, proteins, hydrides including hydrocarbons.

Isotopes of Hydrogen:
Hydrogen has three isotopes: protium ¹₁H, deuterium, ²₁H or D, and tritium, ³₁H or T.

They differ from one another in the number of neutrons. Ordinary hydrogen, protium has no neutrons, deuterium has one and tritium has two neutrons in the nucleus.

Tritium is radioactive and is present as 1 atom per 10¹⁸ atoms of protium. ²₁H or D is also known as heavy hydrogen.

Table: Physical properties of Dihydrogen and Dideuterium

Preparation of Dihydrogen

Laboratory Preparation of Dihydrogen H₂
(a) By the action of acids on metals: Metals (like Li. Na, Ba, Mg, Al, Zn, Fe, etc.) placed above hydrogen in the electrochemical series; when reacted with acids like HCl or dil. H₂SO₄ evolves hydrogen gas. Reaction with Li, K, Na, Ba, and Ca is violent while reaction with Zn, Fe, Al, and Mg is smooth.
Zn + H₂SO₄ → ZnSO₄ + H₂ (lab. method)
Fe + 2HCl → FeCl₂ + H₂

(b) By the action of alkalies on amphoteric metals Zn, Al, Pb, Sn, As, Sb, etc.)
Zn + 2NaOH → Na₂ZnO₂ (Sodium zincate ) + H₂
2Al + 2NaOH + 2H₂O → 2NaAlO₂ (Sodium aluminate) + 3H₂
Sn + 2KOH + H₂O → K₂SnO₃ (Potassium stannate) + 2H₂

(c) By the action of water on active metals (metals placed above electrochemical series)
1. Active metals like Na, K react at room temperature.
2Na + 2H₂O (cold) → 2NaOH + H₂ (violent)
Ca + 2H₂O (cold) → Ca(OH)₂ + H₂ (smooth)

2. Less active metals like Zn, Mg, Al liberate hydrogen only on heating.
Mg + 2H₂O (hot) → Mg(OH)₂ + H₂

3. Metals like Fe, Co, Ni, Sn can react only by passing steam.
3Fe (red hot) + 4H₂O (steam) → Fe₃O₄ + 4H₂

(d) By the action of water on a metal hydride:
LiH + H₂O → LiOH + H₂
CaH₂ + 2H₂O → Ca(OH)₂ + 2H₂

Commercial production of Dihydrogen: The commonly used processes are:

Electrolysis of acidified water, using platinum electrodes, is employed for the bulk preparation of dihydrogen.

(a) Hydrogen of high purity (> 99.95%) is obtained by electrolysis warm aqueous barium hydroxide between nickel electrodes.

(b) Reaction of steam on hydrocarbons or coke at high temperatures in the presence of catalyst yields hydrogen gas.


CO is converted to CO₂ bypassing the gas’s steam over an iron oxide or cobalt oxide catalyst at 673K resulting in the generation of more H₂.

This is called the water-gas shift reaction.

(c) Relatively smaller quantities of dihydrogen (1-17 m³ h^-1) are obtained by passing a 1.1 molar mixture of vaporized methanol and water over a “base-metal chromite” type catalyst at 673 K. The mixture of hydrogen and carbon monoxide obtained is made to react with steam to give CO₂ and more hydrogen.

(d) It is also produced as a by-product of the brine electrolysis process for the manufacture of chlorine and sodium hydroxide. Presently-77% of the industrial hydrogen produced is from petrochemicals, 18% from coal, 4% from the electrolysis of aqueous solution, and 1 % from other sources.

Properties of Dihydrogen:
(a) Physical Properties:

1. Hydrogen is colorless, odorless, and tasteless gas.
2. It is the lightest element and also the lightest gas.
3. It is sparingly soluble in water.
4. Its critical temperature is very low (-236.9°C) at or below which can be liquefied by the application of suitable pressure. At -258.8°C it can be liquefied.
5. Its molecule is diatomic, indicated by the ratio of its specific heats at constant pressure and constant volume (C_p/C_v = 1.40).
6. It is adsorbed (occluded) by certain metals like Fe, Au, Pt, and Pd.

(b) Chemical properties:
1. Dihydrogen H₂ combines with halogens (X₂) to give hydrogen halides (HX). While the reaction with fluorine takes place even in the dark, with iodine a catalyst is required.
H₂(g) + X₂(g) → 2HX(g) (X = F, Cl, Br, I)

2. With dioxygen, dihydrogen forms water. The reaction is strongly exothermic
2H₂(g) + O₂(g) → 2H₂O(1) ΔH° = -285.8 kJ mol^-1

3. Reaction with dinitrogen it forms ammonia (NH₃)

ΔH° = -92.6 kJ mol^-1

4. Reaction with metals: With many metals, it combines at high temperatures to yield the corresponding hydrides.
H₂(g) + 2M(g) → 2MH(s)
Where M is an alkali metal

5. Reaction with metal ions and metal oxides: It reduces
some metal ions in aqueous solution and oxides of metals (less active than iron) into corresponding metals.
H₂(g) + Pd²⁺ (aq) → Pd(s) + 2H⁺(aq)
H₂(g) + Cu²⁺ (aq) → Cu(s) + 2H⁺(aq)
in general: YH₂(g) + MxOy(s) → xM(s) + yH₂O(l)

Reaction with organic compounds: It reacts with many organic compounds in presence of catalysts to give useful hydrogenated products of commercial importance. For example;

1. Hydrogenation of vegetable oils using nickel as catalyst gives edible fats (margarine and vanaspati ghee)
2. Hydroformylation of olefins yields aldehydes which further undergo reduction to give alcohol.
   H₂ + CO + RCH = CH₂ → RCH₂CH₂CHO
   H₂ + RCH₂CH₂CHO → RCH₂CH₂CH₂OH

1. The largest single use of dihydrogen is in the synthesis of ammonia which is used in the manufacture of nitric acid and nitrogenous fertilizers.

2. Dihydrogen is used in the manufacture of vanaspati fat by the hydrogenation of polyunsaturated vegetable oils like soybean, cotton seeds, etc.

3. It is used in the manufacture of bulk organic chemicals, particularly methanol.

4. It is widely used for the manufacture of metal hydrides.

5. It is used for the preparation of hydrogen chloride, a highly useful chemical.

6. In metallurgical processes, it is used to reduce heavy metal oxides to metals.

7. Atomic hydrogen and oxy-hydrogen torches find a use for cutting and welding purposes. Atomic hydrogen atoms (produced by dissociation of dihydrogen with the help of an electric arc) are allowed to recombine on the surface to be welded to generate a temperature of 4000 K.

8. It is used as rocket fuel in space research.

9. Dihydrogen is used in fuel cells for generating electrical energy. It has many advantages over conventional fossil fuels and electric power. It does not produce any pollution and releases greater energy per unit mass of fuel in comparison to gasoline and other fuels.

Hydrides:
Dihydrogen under certain reaction conditions combines with almost all elements except noble gases to form binary compounds called hydrides expressed as EH [like MgH₂] or EmHn (like B₂H₆).

They are of 3 types:

1. Ionic or Saline or Salt-Like Hydrides
2. Covalent or Molecular Hydrides
3. Metallic or Non-Stoichiometric Hydrides

1. Ionic or Saline or Salt-Like Hydrides: Lighter metal hydrides like LiH, BeH, and MgH, have significant covalent character. Ionic hydrides like K⁺H. Na⁺H are crystalline, non-volatile, and non-conducting in solid-state. However, their melts conduct electricity and in electrolysis liberate dihydrogen gas at the anode which confirms the existence of H⁺ ions

They are generally formed by s-block elements which are highly electropositive in character. These hydrides are Stoichiometric. Saline hydrides react violently with water producing dihydrogen gas.
NaH(s) + H₂O(aq) → NaOH(aq) + H₂(g)

Lithium hydride is rather unreactive at a moderate temperature with O₂ or Cl₂. It is, therefore, used in the synthesis of other useful hydrides, e.g.
8 LiH + Al₂Cl₆ → 2LiAlH₄ + 6 LiCl
2 LiH + B₂H₆ → 2LiBH₄

2. Molecular hydrides/[Covalent Hydrides]: These are formed by elements of highly electronegative elements (viz non-metals) which share electron(s) with hydrogen. In most cases, bonds are covalent in character, although in some cases (eg HF) bond is partly ionic in character. These have molecular lattices. The molecules are held together by weak van der Waal’s forces. These hydrides are soft, have low m.p. and b.p. They have low electrical conductivity.
The stability decreases progressively down a group, e.g.
NH₃ > PH₃ > AsH₃ > SbH₃ > BiH₃

In a period the stability increases with increasing electronegativity of the element forming the hydride.
e.g., CH₄ < NH₃ < H₂O < HF

These become increasingly acidic in character on moving from left to right along a given row in the periodic table. Thus, while NH₃ is a weak base, H₂O is neutral and HF is acidic. Similarly, in the next row, while PH₃ is a weak base, H₂S is a weak acid and HCl is highly acidic.

These are used as reducing agents.
Molecular hydrides are further classified according to the relative numbers of electrons and bonds in their Lewis structure into:

1. Electron-deficient,
2. Electron-precise, and
3. Electron-rich hydrides.

An electron-deficient hydride, as the name suggests, has too few electrons for writing its conventional Lewis structure. Diborane (B₂H₆) is an example. In fact, all elements of group 13 will form electron-deficient compounds. They act as Lewis acids i.e., electron acceptors.

Electron-precise compounds have the required number of electrons to write their conventional Lewis structures. All elements of group 14 form such compounds (e.g., CH₄) which are tetrahedral in geometry.

Electron-rich hydrides have excess electrons which are present as lone pairs. Elements of groups 15-17 form such compounds. (NH₃ has 1-one pair, H₂O-2, and HF-3 lone pairs). They will behave as Lewis bases i.e., electron donors. The presence of lone pairs on highly electronegative atoms like N, O, and F in hydrides results in hydrogen bond formation between the molecules. This leads to the association of molecules.

3. Metallic or non-stoichiometric (or Interstitial) Hydrides:
These are formed by many (d-block or f-block elements. However, metals of groups 7, 8, and 9 do not form hydrides. These hydrides conduct heat and electricity. They are non-stoichiometric. Hydrogen atoms occupy interstitial places in the lattices of metals. They are reducing’ agents and give out hydrogen easily. Hydrogen in them is present in atomic form.

Water:
A major part of all living organisms is made up of water. The human body has about 85 % and some plants have as much as 95 % water. It is a crucial compound for the survival of all life forms.

Physical properties of water:
It is a tasteless and colorless liquid.
The molecular mass of H₂O is = 18.0151 g mol^-1
Melting point = 273.0 K
Boiling point = 373.0 K
enthalpy of formation = – 285.9 kJ mol^-1
Enthalpy of fusion = 6.01 kJ mol⁺
Enthalpy of vaporisation (373 K) = 40.66 kJ mol^-1
Density (at 298 K) = 1.00 g cm^–3.

The unusual properties of water in the condensed phase (liquid and solid states) are due to the presence of extensive hydrogen bonding between water molecules. It boils at a higher temperature than H₂S or H₂Se only because of hydrogen bonding.

Structure of Water:
In the gas phase, water is a bent molecule with a bond angle of 104.5° and an O-H bond length of 95.7 pm as shown in Fig (a). It is a highly polar molecule, (Fig.(b)). Its orbital overlap picture is shown in Fig. (c) In the liquid phase water molecules are associated together by hydrogen bonds.

(a) The bent structure of water;
(b) the water molecule as a dipole and
(C) the orbital overlap picture In water molecule.

Structure of Ice:
Ice has a highly ordered three-dimensional hydrogen-bonded structure as shown in Fig. Examination of ice crystals with x-rays shows that each oxygen atom is surrounded tetrahedrally by four other oxygen atoms at a distance of 276 pm.

The structure of Ice

Hydrogen bonding gives the ice a rather open type structure with wide holes. These holes can hold some other molecules of appropriate size interstitially.

Chemical Properties Of Water:
1. Amphoteric Nature: It has the ability to act as an acid as well as a base, i.e., it behaves as an amphoteric substance. In the Bronsted sense, it acts as an acid with NH₃ and a base with H₂S.
H₂O(l) + NH₃(aq) ⇌ NH⁺₄ (aq) + OH^–(aq)
H₂O(l) + H₂S(aq) ⇌ H₃O⁺ (aq) + HS^– (aq)

The auto-protolysis (self-ionization) of water takes place as follows:

2. Reduction Reaction:
2H₂O(l) + 2Na(s) → 2NaOH(aq) + H₂(g)

3. Oxidation Reaction:
2F₂(g) + 2H₂O(aq) → 4H⁺(aq) + 4F^–(aq) + O₂

4. Hydrolysis Reaction:
P₄O₁₀(s) + 6H₂O(l) → 4H₃PO₄(aq)
SiCl₄(l) + 2H₂O(l) → SiO₂(s) + 4HCl(aq)
N^3-(s) + 3H₂O(l) → NH₃(g) + 3OH^–(aq)

5. Hydrates Formation: From aqueous solutions, many salts can be crystallized as hydrated salts.

1. Coordinated water e.g. [Cr(H₂O)6]³⁺ 3Cl^–
2. Interstitial water e.g. BaCl₂.2H₂O.
3. Hydrogen bonded water e.g., [Cu(H₂O)₄]²⁺ SO₄ H₂O in CuSO₄. 5H₂O.

Hard and Soft Water:
The presence of calcium and magnesium salts in the form of hydrogen carbonate, chloride, and sulfate in water makes water Hard. Hard Water does not give lather with soap. Water-free from soluble salts of calcium and magnesium is called Soft Water. It gives lather with soap easily.

Hard water forms scum/precipitate with soap.

Disadvantages of using hard water

1. It is unsuitable for laundry.
2. It is harmful to boilers due to the deposition of salts as a scale on the walls of boilers. This reduces the efficiency of boilers.

There are two types of hardness:
(A) Temporary Hardness: It is due to the presence of the bicarbonates of calcium and magnesium, viz., Ca(HCO₃)₂ and Mg(HCO₃)₂

Temporary hardness can be removed by
1. Boiling

These precipitates are removed by filtration. The filtrate obtained is soft water.

2. Clark’s method: Lime water is added to hard water in Clark’s process to remove the precipitates of CaCO₃ formed.
Ca(HCO₃)₂ + Ca(OH)₂ → 2CaCO₃↓ + 2H₂O
Mg(HCO₃)₂ + 2Ca(OH)₂ → 2CaCO₃↓ + Mg(OH)₂↓ + 2H₂O

(B) Permanent Hardness: It is due to the presence of soluble salts of Mg and Ca in the form of chlorides and sulfates:
MgCl₂, CaCl₂, MgSO₄, CaSO₄. It can be removed by the following methods:
1. Treatment with washing soda (Na₂CO₃)
MCl₂ + Na₂CO₃ → 4 MCO₃↓ + 2NaCl
MSO₄ + Na₂CO₃ → MCO₃↓ + Na₂SO₄
M = Mg, Ca.

2. Calgon’s Method: Sodium hexametaphosphate Na6P60lg is commercially called Calgon. When added to hard water, the following reactions take place.
Na₆P₆O₁₈ → 2Na⁺ + Na₄P₆O₁₈^2-[M = Mg, Ca]
M²⁺ + Na₄P₆ O₁₈^2- → [Na₂MP₆O₁₈]^2-
The complex anion is not harmful.

3. Permutit Method: Permutit is an artificial zeolite- chemically it is sodium orthosilicate (Na₂Al₂Si₂O₈. xH₂O). Permutit removes cations like Ca²⁺, Mg^2+, and Fe²⁺ and releases an equivalent number of Na⁺ ions. For simplicity, it can be written as Na Z. When added to water the following reaction takes place
2NaZ + M²⁺(aq) → MZ₂(s) + 2Na⁺(aq); M = Mg, Ca

Permutit/zeolite is said to be exhausted when all the sodium in it is used up. It is regenerated when treating it with an aqueous sodium chloride solution.
MZ₂(S) + 2NaCl(aq) → 2NaZ + MCl₂(aq)

4. By the use of ion exchange resins (synthetic resins): This method removes all cations and anions present in water by means of ion-exchange resins. Water is first passed through cation exchange resins (giant organic molecules with-SO₃H or —COOH groups), which remove the cations like Na⁺, Ca²⁺, Mg²⁺ and others by exchange with H⁺. The resulting water is now passed through anion exchange resins (giant organic molecules with — NH₂ group) which remove the anions like Cl^–, SO₄^– and NO₃ by exchange with OH^–.

Hydrogen Peroxide (H₂O₂):
It is an important chemical used in the pollution control treatment of domestic and industrial effluents.

Preparation:
1. By the reaction of sulphuric acid or phosphoric acid on hydrated barium peroxide (BaO₂).
(a) BaO₂.8H₂O + H₂SO4 → BaSO₄(g) + H₂O₂ + 8H₂O

Anhydrous barium peroxide does not react readily with sulphuric
acid because a coating of insoluble barium sulfate is formed on its surface which stops further action of the acid. Hence hydrated barium peroxide, BaO2,.8H2O must be used.

(b) 3BaO₂ + 2H₃PO₄ → Ba₃(PO4)₂ + 3H₂O₂
Ba₃(PO₄)₂ + 3H₂SO₄ → 2BaSO₄(s) + 2H₃PO₄

Treatment with phosphoric acid is preferred to H₂SO₄ because soluble impurities like barium persulphate (from BaO₂.8H₂O+ H₂SO4) tend to decompose H₂O₂ while H₃PO₄ acts as a preservative (negative catalyst for H₂O₂). Moreover, excess barium peroxide should be avoided as it tends to decompose H₂O₂.
BaO₂ + H₂O₂ → BaO + H₂O + O₂

In both cases, BaSO₄ is removed by filtration and hence more or less a fuse H₂O₂ solution is obtained by this method.
1. By adding the calculated quantity of sodium peroxide to a 20 % ice-cold sulphuric acid solution (Merck’s process):
Na₂O₂ + H₂SO₄ → Na₂SO₄ + H₂O₂

Sodium sulfate is removed by cooling when crystals of Na₂SO₄ 10H₂O separate out.
In this method, sulphuric acid can be replaced by NaH₂PO₄

Manufacture of Hydrogen peroxide:
1. By electrolysis of 50 % sulphuric acid to give Perdisulphuric acid (H₂S₂O₈) which on distillation yields 30% solution of hydrogen peroxide.
2H₂SO₄ → 2H+ + 2HSO₄^–

At cathode (Cu coil):
2H+ + 2e^– → 2H + H₂ ↑

At anode (Pt)
2HSO₄^– → 2HSO₄ + 2e^–
2HSO₄ → H₂S₂O₈ (Persulphuric acid)
H₂S₂O₈ + 2H₂O → 2H₂SO₄ + H₂O₂

Alternatively, electrolysis may be done with ammonium hydrogen sulfate (ammonium sulfate + H₂SO₄).
(NH₄)₂SO₄ + H₂SO₄ → 2NH₄HSO₄
NH₄HSO₄ → H⁺ + NH₄SO₄

At cathode 2H⁺ + 2e^– → H₂
At anode 2NH₄SO₄ → (NH4)₂S₂O₈ + 2e^–

The ammonium persulphate formed is removed and quickly distilled with dil. H₂SO₄ under reduced pressure to give hydrogen peroxide.

2. By the auto-oxidation of 2-ethyl anthraquinone: In this process, the air is passed through a 10% solution of 2-ethyl anthraquinone in a mixture of benzene and higher alcohol.

The resulting 2-ethyl anthraquinone is then reduced by hydrogen in presence of palladium as a catalyst. Thus the continuity of the process is maintained and the process needs only H₂, atmosphere 0_2, and water as the major raw materials.

Physical Properties of hydrogen peroxide:

1. Pure hydrogen peroxide is a pale blue syrupy liquid.
2. It is an unstable liquid and decomposes into water and oxygen either on standing or on heating.
3. Hydrogen peroxide is diamagnetic.
4. In the pure state, its dielectric constant is 93.7 which increases with dilution.
5. It is more highly associated with hydrogen bonding than water.
6. Pure hydrogen peroxide is weakly acidic in nature while its aqueous solution is neutral.

Chemical properties:
It acts as an oxidizing as well as a reducing agent in both acidic and alkaline media. Simple reactions are described below.
1. Oxidising action in acidic medium
2Fe²⁺(aq) + 2H⁺(aq) + H₂O₂(aq) → 2Fe³⁺(ag) + 2H₂O(l)
PbS(s) + 4H₂O₂(aq) → PbSO₄(s) + 4H₂O(l)

2. Reducing action in acidic medium
2MnO₄ + 6H⁺ + 5H₂O₂ → 2Mn²⁺ + 8H₂O + 5O₂
HOCl + H₂O₂ → H₃O⁺ + Cl^– + O₂

3. Oxidising action in basic medium
2Fe²⁺ + H₂O₂ → 2Fe³⁺ + 2OH^–
Mn²⁺ + H₂O₂ → Mn⁴⁺ + 2OH^–

4. Reducing action in basic medium
I₂ + H₂O₂ + 2OH^– → 2I^– + 2H₂O + O₂
2MnO₄^– + 3H₂O₂ → 2MnO₂ + 3O₂ + 2H₂O + 2OH^–

Storage of H₂O₂
H₂O₂ decomposes slowly on exposure to light.
2H₂O₂(l) → 2H₂O(l) + O₂(g)

In the presence of metal surfaces or traces of alkali (present in glass containers), the above reaction is catalyzed. It is, therefore, stored in wax-lined glass or plastic vessels in dark. Urea can be added as a stabilizer. It is kept away from dust because dust can induce explosive decomposition of a compound.

Structure of H₂O₂
Hydrogen peroxide molecule has a non-polar structure. The molecular dimensions in the gas phase and chemical phase are shown in Fig.

(a) H₂O₂ structure (gas phase) Dihedral angle 111.5° (b) H,0, (so, id phase at 110 K. The dihedral angle is reduced to 90.2°.

Uses Of Hydrogen Peroxide:

1. In daily life, it is used as hair bleach and as a mild disinfectant. As an antiseptic, it is sold in the market as per hydro.
2. It is used to manufacture chemicals like sodium perborate and per-carbonate, which are used in high-quality detergents.
3. It is used in the synthesis of hydroquinone, tartaric acid, and certain food products and Pharmaceuticals (cephalosporin), etc.
4. It is employed in the industries as a bleaching agent for textiles, paper pulp, leather, oils, fats, etc.
5. Nowadays it is also used in Environmental (Green) Chemistry. For example, in pollution control treatment of domestic and industrial effluents, oxidation of cyanides, restoration of aerobic conditions to sewage wastes.

Heavy Water (D₂O):
It is extensively used as a moderator in nuclear reactors and in exchange reactions for the study of reaction mechanisms. It was first prepared by Urey by the exhaustive electrolysis of water.

It is used for the preparation of other deuterium compounds. For example,

Volume Strength Of Hydrogen Peroxide:
H₂O₂ is miscible with water in all proportions and forms a hydrate H₂O₂.H₂O (mp 221 K). A 30% solution of H₂O₂ is marketed as “100 Volume” hydrogen peroxide. It means that one milliliter of 30% H₂O₂ solution will give 100V of oxygen at STP. Commercially, it is marketed as 10V. It means it contains 3% H₂O₂.

Problem:
Calculate the strength of a 10 volume solution of hydrogen peroxide.
Answer:
10 volume solution of H₂O₂ means that 1L of this H₂O₂ will give 10L of oxygen at STP
2H₂O₂ (l) → O₂(g) + H₂O(l)
2 × 34 = 68g 22.4 L at STP
22.4 L of 02 at STP is produced from H₂O₂ = 68g

10 L of O₂ at STP is produced from H₂O₂ = \(\frac{68 \times 10}{22.4}\)g
= 30.36g
Therefore, the strength of H₂O₂ in 10 volume H₂O₂ = 30.36g L^-1.

Dihydrogen as a Fuel:
It releases large quantities of heat on combustion. On mass for mass basis H₂(g) can release, more energy than petrol (about three times). Moreover, pollutants in the combustion of dihydrogen will be less than petrol. The only pollutant will be oxides of dinitrogen (due to the presence of dinitrogen as an impurity with dihydrogen).

This, of course, can be minimized by injecting a small amount of water into the cylinder to lower the temperature so that reaction between dinitrogen and dioxygen may not take place.

However, the mass of the containers in which dihydrogen will be kept must be taken into consideration, A cylinder of compressed dihydrogen weighs about 30 times as much as a tank of petrol containing the same amount of energy. Also, dihydrogen gas is converted into a liquid state by cooling to 20K.

This would require expensive insulated tanks. Tanks of metal alloy like NaNi₅, Ti-TiH₂, Mg-MgH₂, etc. are in use of storage of dihydrogen in small quantities. These limitations have prompted researchers to search for alternative techniques to use dihydrogen in an efficient way.

In this view Hydrogen Economy is an alternative. The basic principle of a hydrogen economy is the transportation and storage of energy in the form of liquid or gaseous dihydrogen. The advantage of a hydrogen economy is that energy is transmitted in the form of dihydrogen and not as electric power.

It is for the first time in the history of India that a pilot project using dihydrogen as fuel was launched in Oct 2005 for running automobiles. Initially, 5 % dihydrogen has been mixed in CNG for use in four-wheeler vehicles. The percentage of dihydrogen would be gradually increased to reach the optimum level. Nowadays, it is also used in fuel cells for the generation of electric power.

By going through these CBSE Class 11 Chemistry Notes Chapter 8 Redox Reactions, students can recall all the concepts quickly.

Redox Reactions Notes Class 11 Chemistry Chapter 8

→ Reactions taking place in an electrochemical cell are redox reactions in nature.

→ In an electrochemical cell loss of free energy appears as electrical energy.

→ The reaction in an electrochemical cell is spontaneous in nature.

→ A salt bridge maintains the electrical neutrality of the two electrolytes in their half cells.

→ The e.m.f. of an electrochemical cell is E°_cathode — E°_anode cathode anode

→ According to the electronic concept, the loss of electron is oxidation, and the gain of the electron is reduced.

→ The oxidation number of free elements homo atomic molecules and also of the neutral molecule is zero.

→ Electrolysis is the migration of the ions of the electrolyte towards the oppositely charged electrode when the current is passed.

→ In an electrolytic cell, the redox reaction is non-spontaneous in nature.

→ The chemical energy of the redox reaction occurring in the galvanic cell is converted into electrical energy.

→ Electrons flow from anode to cathode in the external circuit while current flow from cathode to anode.

→ 95600 c of charge represents one Faraday.

→ Oxidation: Oxidation is a process in which an atom or ion loses an electron(s).

→ Reduction: Reduction is a process in which an atom or ion gains an electron(s).

→ Oxidizing agent: (Oxidant) is a species that can readily accept one or more electrons.

→ Reducing agent: (Reductant) is a species that readily lose one or more electrons.

→ Redox Reaction: Redox reaction is a chemical reaction in which oxidation and reduction occur simultaneously.

→ Electrochemical cell: Electrochemical cell is a device in which oxidation and reduction half-reactions are carried indirectly and the loss of chemical energy during the reaction appears as electrical energy.

→ Electrolytic cell: Electrolytic cell is a device in which electrical energy is supplied from an external source to bring about a chemical reaction.

→ Anode: Anode is an electrode where the electrons are released or where oxidation takes place.

→ Cathode: A cathode is an electrode where the electrons are accepted or where reduction takes place.

→ Half cell: A half cell is a portion of an electrochemical cell in which either oxidation or reduction takes place.

→ Standard hydrogen electrode: Standard hydrogen electrode is an electrode that is used to calculate the reduction potential of another electrode. Its own reduction potential is taken as zero.

→ Standard reduction potential: Standard reduction potential of an electrode is its reduction potential as compared to that of a standard hydrogen electrode which is taken as zero.

→ Salt bridge: Salt bridge is an inverted U-shaped glass tube that contains a suitable electrolyte and connects the two-half cells in an electrochemical cell.

→ E.m.f. of a cell: E.m.f. of a cell is the difference between the reduction potential of electrodes when the cell is not sending the current.

→ Potential difference: Potential difference is the difference of potential between two electrodes when the cell is sending currents.

→ Electro-chemical series: Electrochemical series is the series obtained by arranging the electrode in order of increasing standard reduction potential values.

→ Electrolyte: Electrolyte is a substance that is capable of conducting electricity either in a molten state or when dissolved in an aqueous solution.

→ Electrolysis: Electrolysis is the process of the decomposition of an electrolyte on passing electric current.

→ Oxidation Number: The oxidation number of an element is the residual charge which its atom appears to have when all other atoms present in its combination are removed as ions.

→ Disproportionation Reaction: In this reaction, an element in one oxidation state is simultaneously oxidized and reduced.

→ Redox couple: A redox couple consists of the oxidized and reduced forms of the same substance taking part in an oxidation and reduction half-reaction.

By going through these CBSE Class 11 Chemistry Notes Chapter 7 Equilibrium, students can recall all the concepts quickly.

Equilibrium Notes Class 11 Chemistry Chapter 7

Chemical equilibria are important in numerous biological and environmental processes. For example, equilibria involving O₂ molecules and the protein hemoglobin play a crucial role in the transport and delivery of O₂ from our lungs to our muscles. Similarly, equilibria involving CO molecules and hemoglobin account for the toxicity of CO.

In the case of evaporation of water in a closed vessel, the no, of molecules leaving the surface of water equals the no. of molecules of H₂O returning to liquid state from the vapor state. This is an equilibrium state. However, this equilibrium state is not static. It is Dynamic equilibrium. Thus at equilibrium, the rate of evaporation is equal to the rate of condensation. It may be represented by
H₂O (l) ⇌ H₂O (vap)

The mixture of reactants and products in the equilibrium state is called an equilibrium mixture.

The state of chemical equilibrium in a chemical reaction may be classified into three groups characterized by the extent to which the reactions proceed.

1. The reactions proceed nearly to completion and only negligible concentrations of the reactants are left.
2. The reactions in which only some amount of products are formed and most of the reactants remain unchanged at equilibrium stage.
3. The reactions in which concentrations of the reactants and products are comparable when the system is at equilibrium.

Equilibrium in Physical processes
1. Solid-Liquid Equilibrium: For example
ice ⇌ water
i.e. H₂O(s) ⇌ H₂O(l)
At equilibrium, rate of melting = rate of freezing.

The temperature at which the solid and liquid forms of any substance coexist is called the melting point.
2. Liquid-Vapour Equilibrium: For example
H₂O(l) ⇌ H₂O(g)
At equilibrium: rate of evaporation = rate of condensation.

3. Equilibrium involving dissolution of solids of gases in liquids: Different solids dissolve in any solvent to different extents. Certain solids dissolve more, while many others dissolve less.

The maximum mass (in grams) of a solute which can be dissolved in 100 g of a solvent at any temperature and pressure is called its solubility at that temperature and pressure,
(a) Solids in liquids: When a small quantity of sugar is added to some water (say 100 mL) it gets dissolved. When a little more sugar is added, it also gets dissolved. If the addition of sugar is continued, then a stage comes when no more sugar dissolves, and the added sugar settles down.

The solution at this stage contains the maximum amount of sugar the solution can have at that temperature. This solution is called a saturated solution of sugar. In a saturated solution
Sugar (s) N ⇌ Sugar (aq)
of sugar in contact with solid sugar, a dynamic equilibrium is established. At the equilibrium state, the number of sugar molecules going into the solution from the solid sugar is equal to the number of molecules precipitating out from the solution at a given temperature. Thus at equilibrium.

Rate of dissolution of solid sugar = Rate of precipitation of sugar from the solution.

(b) Gases in Liquids: Gases dissolve in liquids. The solubility of a gas in any liquid depends upon.

• nature of the gas and that of the liquid.
• the temperature of the liquid
• pressure of the gas over the surface of the solution.

The effect of pressure on the solubility of a gas in a liquid is described by Henry’s Law.

Henry law states that,
“At a certain temperature, the mass of a gas which dissolves in a definite volume of a liquid is proportional to the pressure of the gas over the solution.”

If p is the pressure of the gas over the solution, m is the mass of the gas dissolved in one unit volume of the liquid.
Then, according to Henry’s law
m ∝ p
or
m = kp
where k is the proportionality- constantly called Henry’s Law constant.

4. General Characteristics of Equilibria involving Physical Processes:
It has been noted that
(a) for liquid-vapor equilibrium, the vapor pressure is constant at t given temperature.
(b) for solid-liquid equilibrium, there is only one temperature (melting point) at 1 atm at which the two phases can coexist. If there is no exchange of heat with the surroundings, the mass of the two phases remains constant.
(c) for dissolution of solids in liquids the solubility is constant at a given temperature.
(d) for dissolution of gases in liquids, the concentration of a gas in a liquid is proportional to the pressure (concentration)! of the gas over the liquid.

Table: Some Features of Physical Equilibria

For the physical processes discussed above following characteristics are common to the system of equilibrium.

1. Equilibrium is possible only in a closed system at a given temperature.
2. Both the opposing processes occur at the same rate and there is a dynamic but stable condition. ,
3. All measurable properties of the system remain constant.
4. When equilibrium is attained for a physical process, it is characterized by the constant value of one of its parameters at a given temperature.
5. The magnitude of such quantities at any stage indicates the extent to which the physical process has proceeded before reaching equilibrium.

Equilibrium in Chemical Processes-Dynamic Equilibrium
Similar to physical systems, chemical reactions also attain a state of equilibrium. These reactions can proceed both in the forward direction as well as backward direction. When rates in both directions become equal, the concentrations of reactants and products remain constant. This is the stage of chemical equilibrium.

Let there be a reversible reaction
A + B ⇌ C + D
With time, concentrations of A and B decrease, and those of C and D increase. This leads to a decrease in the rate of forwarding direction and increases in the rate of backward direction. When both the rates become equal, the system reaches a state of equilibrium.

Characteristic of Chemical Equilibrium:

1. The equilibrium state is reached only if the process is carried out in a closed vessel.
2. It is dynamic equilibrium, i.e., at this stage the reaction, although appears to be stopped, actually takes place in both directions with the same speed.
3. An equilibrium state can be approached from both sides.
4. At equilibrium state/composition of the reactants and products remain constant.

3. Law of Chemical Equilibrium and Equilibrium Constant: Goldberg and Waage proposed that for a general reversible reaction
A + B ⇌ C + D

the following Equilibrium equation holds:
KC = \(\frac{[\mathrm{C}] \times[\mathrm{D}]}{[\mathrm{A}] \times[\mathrm{B}]}\)
where Kc is called equilibrium constant and the expression on the right side is called equilibrium constant expression.

The above equation is also called the Law of Mass Action because concentration was earlier referred to as active mass.

→ Law of mass action: It states that under a given set of conditions, the rate of a chemical reaction is directly proportional to the product of the concentration (active mass) of the reacting substances.
Active mass (Molar concentration) = \(\frac{\text { No. of moles }}{\text { Vol. in litres }}\)

The active mass of a gas or liquid means its molar concentration, while the active mass of a solid is always taken as unity, irrespective of the quantity.

The Law of mass action is applicable only to reversible reactions.
Let us consider a general reversible reaction
aA + bB ⇌ cC + dD
The rate of forwarding reaction = K_f [A]^a[B]^b
Similarly, the rate of backward reaction = K_f [C]^c[D]^d
where and K_f and K_b be the respective rate constants.

Since at equilibrium, the rate of both reactions are equal
K_f[A]^a[B]^b = K_f[C]^c[D]^d
\(\frac{\mathrm{K}_{f}}{\mathrm{~K}_{b}}=\frac{\left[\mathrm { C } \left[^{c}[\mathrm{D}]^{d}\right.\right.}{[\mathrm{A}]^{a}[\mathrm{~B}]^{b}}\)
or
K = \(\frac{[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{d}}{[\mathrm{~A}]^{a}[\mathrm{~B}]^{b}}\)
where K is.called equilibrium constant.

Characteristics of the equilibrium constant:
1. Its value is independent
(a) of the original concentration of the reactants.
(b) of volume.
(c) of the presence of inert materials.
(e) of the direction from which equilibrium is attained.
(f) of the nature and number of steps in the reaction as long as stoichiometry is not changed.

2. It has a definite value at a given temperature and changes with temperature.

For a reversible reaction at equilibrium; the ratio of the product of concentrations of the products to the product of concentrations of the reactants when each concentration term is raised to a power equal to the corresponding stoichiometric coefficient in the balanced chemical equation at a constant temperature is constant. This constant is called the Equilibrium Constant.

For a homogeneous chemical reaction aA + bB ⇌ cD + dD
when concentrations of reactants and products are expressed in moles per liter units represented by [ A], |B], [Cl, [D] (their active masses), the equilibrium constant is written as K_C and is given by
K_C = \(\frac{[C]^{c} \times[D]^{d}}{[A]^{a} \times[B]^{b}}\)

Further, if the reaction is a homogeneous gas-phase reaction then the molar concentration of a substance is directly proportional to K_p
K_p = K_c × (RT)^Δn
If Δn = 1,then K_p = K_c × RT

(c) If Δn < 0, i.e. when the no. of moles of reactants is more than that of products or when the reaction proceeds with a decrease in the no. of moles

→ Units of Equilibrium Constant: The unit of K depends upon the number of moles of reactants and products involved in the reaction.
1. When a total number of moles of products is equal to the number of moles of reactants, K has no units. For example.
N₂ (g) + O₂ (g) ⇌ 2NO (g)
K = \(\frac{[\mathrm{NO}(\mathrm{g})]^{2}}{\left[\mathrm{~N}_{2}(\mathrm{~g})\right]\left[\mathrm{O}_{2}(\mathrm{~g})\right]}\)

= \(\frac{[\mathrm{mol} / \mathrm{L}]^{2}}{[\mathrm{~mol} / \mathrm{L}][\mathrm{mol} / \mathrm{L}]}\) = no units.

2. When/ the total number of moles of products is different than the total number of moles of reactants. In such reactions, K has units. For example,
N₂ (g) + 3H₂ (g) ⇌ 2NH₃ (g)

Value of K_p for Some reactions

→ Homogeneous Equilibrium: A reversible reaction in which all the reactants and products at equilibrium are in the same phase is called a homogeneous equilibrium.
(a) In the gas phase

(b) In the liquid phase: Here, all the reactants and products are liquids that are miscible in one another. They may take place in an open or closed vessel.
CH₃COOH (l) + C₂H₅OH (l) ⇌ CH₃COOC₂H₅ (l) + H₂O (l)
KC = \(\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}(\mathrm{l})\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}(1)\right]}\)

(c) In the solution phase: Here the reactants and products are present in a solution. The choice of the solvent depends upon the nature of the reaction.
I₂ (aq) + r^– (aq) ⇌ I₃ (aq)
iodine iodine ion tri iodide ion
2H₂O (l) ⇌ H₃⁺O (aq) + OH^– (aq)
Fe³⁺ (aq) + SCN^– (aq) ⇌ [Fe(SCN)]²⁺ (aq)

Heterogeneous Equilibrium: A reversible reaction involving equilibrium between various chemical species present in two or more phases is said to be a heterogeneous chemical equilibrium. It may be noted here that all solids constitute separate phases.
Examples:

and [CaO] are both constants.

Here CaCO₃ and CaO are in solid phases and CO₂ is in the gaseous phase; [CaCO₃] = 1 and [CaO] = 1
(b) 3Fe (s) + 4H₂O (g) ⇌ Fe₃O₄ (s) + 4H₂ (g)

where PH₂ and PH₂O are the partial pressures of H₂ (g) and H₂O (g) at eqbm.

(c) Pb²⁺ (aq) + CrO₂^4- (aq) ⇌ PbCrO₄ (s)

(d) 2Hg (s)+ O₂ (g) ⇌ 2HgO (s)

(e) for the reaction
Ni (s) + 4CO (g) ⇌ Ni(CO)₄ (g)
K_C = \(\frac{\left[\mathrm{Ni}(\mathrm{CO})_{4}\right]}{[\mathrm{CO}]^{4}}\)

(f) Ag₂O (s) + 2HNO₃ (aq) ⇌ 2AgNO₃ (aq) + H₂O (l)
K_C = \(\frac{\left[\mathrm{Ag} \mathrm{NO}_{3}\right]^{2}}{\left[\mathrm{H} \mathrm{NO}_{3}\right]^{2}}\)

Applications of Equilibrium constants:
1. Predicting the direction and extent of reaction from the magnitude of the equilibrium constant: The magnitude of the equilibrium constant K of a reaction indicates how far a reaction can go and in which direction.

For example aA + bB ⇌ cC + dD is given by
K = [C]^c × [D]^d /[A]^a[B]^b
where all concentrations are at equilibrium. It is dear that the larger the value of K, the greater will be the equilibrium concentration of- the components on the R.H.S. of the reaction (products) relative to those on the L.H.S. (reactants).

Thus the value of K provides information about the extent and direction of the reaction.
(a) When K > > 1: When the value of K is very high such as; 10⁷ – 10¹⁵ or more, the reactions proceed to almost completion. In such reactions, almost the whole of the reacting substances gets converted into products.

(b) When K > 1: When the value of K is greater than one (but not too large), the reaction in the forward direction is favored more than the reaction in the backward direction. In such cases, the equilibrium concentration of products is higher than that of the reactants.

(c) When K = 1: When the value of K is equal to one, both the direction of the reaction are almost equally favored. In such cases the equilibrium concentrations of reactants and products are comparable.

(d) When K < 1: When the value of K is smaller than one, the reaction in the backward direction is favored. In such cases, the equilibrium concentrations of reactants will be much higher than the concentration of the products.

2. Calculating Equilibrium Concentrations: Once the value of the equilibrium constant for a reaction is known, we can use it to calculate the concentration of a substance (reactant or product) in the equilibrium mixture.

Relationship between Equilibrium Constant K, Reaction Quotient Q, and Gibbs Energy G

The value of K_C for a reaction does not depend upon the rate of the reaction. It is directly related to the thermodynamics of the reaction and in particular to the change in Gibbs energy, ΔG. If,

1. ΔG is negative, the reaction is spontaneous and proceeds in the forwarding direction. ’
2. ΔG is positive, the reaction is non-spontaneous. Instead, the products of the forward reaction shall be converted to the reactants, as ΔG will have a negative value for the reverse direction.
3. ΔG is 0, the reaction has achieved equilibrium, at this point, there is no longer any free energy left to drive the reaction.

Mathematically
ΔG = ΔG° + RT InQ, where G° is standard Gibbs energy
At equilibrium, when ΔG = 0 and Q = K_C, the above equation becomes
ΔG = ΔG° + RT InK = 0
or ΔG° = – RT InK.
InK = – ΔG°/RT

Taking antilog
K = e^-ΔG°/RT … (1)

Hence using the equation (1), the reaction spontaneity can be interpreted in terms of the value of ΔG°
1. If ΔG° < 0, then – ΔG/RT is positive and e^-ΔG°/RT > 1 making K > 1. It implies a reaction in the forward direction or a spontaneous reaction.

2. If ΔG° > 0, then – ΔG°/RT is negative and e^-ΔG°/RT < 1, that is K < 1 which implies a non-spontaneous reaction or a reaction which proceeds in the forward direction to such a small degree that only a very minute quantity of product is formed.

Factors affecting Equilibria:
1. Let Chatelier’s principle: “Whenever a system in equilibrium is subjected to a change in temperature,, pressure or composition, the equilibrium shifts in a direction so as to undo the effect of the change applied”.

2. Effect of concentration change: If a system is at equilibrium and the concentration of one of the species involved in the reaction is increased then the system will readjust so as decrease the concentration of that species. Thus/if the concentration of substance involved in the equilibrium is increased, the increased concentration, Similarly, if the concentration of some substances is decreased, the reaction will proceed so as to make up the loss in the concentration.

Let us consider the-reaction
aA + bB ⇌ cC + dD

At equilibrium, the concentration of A, B, C, and D are constant. If to this reaction at equilibrium, a small amount of the substance A is added, then according to Le Chatelier’s principle, the equilibrium shifts in a direction so as to undo the effect of the increased concentration of A. That is, the reaction proceeds in the d.rection so as to decrease the concentration of A.

This can be done only by making more A react with B to form more products. That is, an increase in the concentration of A (or any reactant) will shift the equilibrium towards the right, (products side). On the other hand, when the concentration of C (or any other product) is increased, the reaction will shift towards the left (reactant side).

Thus, in general, an increase in the concentration of any of the substances on one side of the equilibrium shifts the equilibrium to produce more of the substances on the other side of it.

3. Effect of Pressure Change: Change of pressure has no significant effect on the following equilibria:
(a) The equilibria involving only solids are not affected by a change of pressure because there is virtually no change in volume due to a change in pressure.

(b) The equilibria involving liquids and/or gases where the number of moles before and after the attainment of equilibrium remains the same, i.e., when Δn = 0, also are not affected by a change of pressure. When the pressure on a reaction involving gases (where Δn ≠ 0) is changed, the equilibrium will shift in a direction so as to undo the effect of change in pressure. For example, an increase in pressure will cause a decrease in volume.

So, an increase of pressure on a gaseous system will shift the equilibrium in a direction of a decrease in volume, and vice versa. Therefore, in a reaction which proceeds with a decrease in volume (Δn = -ve), the equilibrium will shift in the forward direction by increasing pressure.

On the other, hand, in a reaction which proceeds with an increase – in volume (Δn = +ve), the equilibrium will shift towards the right by decreasing the pressure.

4. Effect of Temperature Change: According to the Le Chatelier principle when the temperature of a system at equilibrium is increased, i.e., the heat is supplied to the system, the system should move in a direction so that the added heat is absorbed. So, an increase in the temperature of a chemical system at equilibrium favors the reaction that proceeds with the absorption of heat, i.e., an endothermic reaction is favored.

On the other hand, if the temperature of the system is decreased under constant pressure and volume conditions, the equilibrium – will shift in such a way so as to produce some heat. Thus, a decrease in the temperature of a system at equilibrium favors the reaction which proceeds with the evolution of heat, i.e., an exothermic reaction is favored.

For example, the reaction
N₂ (g) + 3H₂ (g) ⇌ 2NH₃ (g); ΔH = – 93.6 kj is exothermic in the forward direction and endothermic in the backward direction.

Let the temperature of the system at equilibrium be increased. Then, according to Le Chatelier’s principle, the equilibrium will shift in a direction heat is absorbed, i.e., in the endothermic direction. Therefore, on increasing temperature, the reaction will shift towards the left (reactant side). Thus, an increase in the temperature of this reaction will result in the formation of a lesser amount of ammonia.

On the other hand, a decrease in the temperature of this system will favor the endothermic direction of the equilibrium. Thus, when the temperature of this system is lowered, the equilibrium will shift in the forward direction, i.e., more ammonia will be produced.

5. Effect of a Catalyst: Catalyst has no effect on the equilibrium concentrations of the reactants and products. In fact, a catalyst accelerates the forward and the backward reactions to the same extent and therefore, simply helps’1 in the. attainment of the equilibrium state faster.

Inert gas added keeping the pressure of the system constant: In this gas, the addition of an inert gas increases the volume of the system, which in turn, causes the equilibrium position of the system to move in the direction of a large number of gaseous molecules. Thus, we will have

→ Inert gas added keeping the volume of the system constant: Addition of inert gas into a system at equilibrium under constant volume causes

1. an increase in the pressure of the system
2. an increase in the total number of moles in the system.

The total pressure of a system is therefore given by
P_total V = n_total RT
or
\(\frac{n_{\text {total }}}{P_{\text {total }}}=\frac{V}{R T}\)

Under constant-volume at any temperature, the ratio total/Ptotal remains constant even on the addition of inert gas. As a result, there is no change in any of the variables and the amounts of the substances at equilibrium remain unaffected by the addition of inert gas, i.e., the equilibrium position of the reaction remains unaffected.

Concentration Quotient or Reaction Quotient and predicting the direction of reaction:
For the reaction aA + bB ⇌ cC + dD at any stage of the reaction, other than the stage of chemical equilibrium, concentration ratio [C]^c[D]^d / [A]^a[B]^b is called concentration quotient or reaction quotient.

It is usually represented by Q_c or Q. Thus concentration quotient Q_c = [C]^c × [D]^d/[A]^a[B]^b

1. If Q = K, the reaction is in equilibrium.
2. If Q > K, Q will tend to decrease so as to become equal to K. As a result the reaction will proceed in the Backward direction.
3. If Q < K, Q will tend to increase. As a result, the reaction will proceed in the forward direction.

Consider the gaseous reaction of H2 and I2,
H₂ (g) + I₂ (g) ⇌ 2HI (g) K_c = 57.0 at 700 K.

Suppose we have molar concentrations
[H₂]_t = 0.10 M, [I₂]_t = 0.2 M and [HI]_t = 0.40 M.
(the subscript t on the concentration symbols means that the concentrations were measured at some arbitrary time t, not necessarily at equilibrium).

Thus, the reaction quotient; Qt at this stage of the reaction is given by,
Q_t = [HI]^t₂/|H₂]_t[I₂]_t = (0.40)²/(0.10) × (0.20) = 8.0.

Now, in this case, Q_c(8.0), does not equal K_c (57.0), so the mixture of H₂ (g), I₂ (g), and HI (g) is most at equilibrium; that is, more H₂ (g) and I₂ (g) will react to form more HI (g) and their concentrations will decrease till Q_c = K_c.

Predicting the direction of the reaction

The reaction quotient, Q_f is useful, we can predict the direction of reaction by comparing the values of Q_c and K_c
Thus, we can make the following generalizations concerning the direction of the reaction:

• If Q_r < K_t. net reaction goes from left to right.
• If Q_r > K_c, the net reaction goes from right to left.
• If Q_r = K_f, no net reaction occurs.

Problem (1)
The value of ΔG° for the phosphorylation of glucose in glycolysis is 13.8 kJ/mol. Find the value of at 298 K?
Solution: ΔG° = 13.8 kJ/mol = 13.8 × 103 J/mol
Also, ΔG° = – RT InK_c.

Hence, InK_c = – 13.8 × 10³ J/mol/8.31 Jmol^-1 × 298 K
InK_c = – 5.569
K_c = e – 5.569
K_c = 3.81 × 10^-3

Problem (2)
Hydrolysis of sucrose gives,
Sucrose + H₂O ⇌ Glucose + Fructose
Equilibrium constant K_c for the reaction is 2 × 1013 at 300 K. Calculate ΔG° at 300 K?
Answer:
ΔG° = – RT ln K_f
ΔG° = – 8.314 J mol^-1 K^-1 × 300 K × In (2 × 10¹³)
ΔG° = – 7.64 × 10⁴ J mol^-1

→ Ionic Equilibrium: There are substances that conduct electricity in their molten states or in the form of their aqueous solutions. These are called electrolytes. On the other hand, there are substances that do not conduct electricity in the molten states or in the form of their aqueous solutions and these are called non-electrolytes.

→ Strong and Weak Electrolytes: Depending upon the extent of ionization, the electrolytes may be divided into two classes: strong electrolytes and weak electrolytes.
1. Strong electrolytes: The substance which ionizes almost completely into ions in an aqueous solution are called strong electrolytes.

For example, HCl, H₂SO₄ HNO₃ NaOH, KOH, NaCl, KNO₃, etc. are strong electrolytes.
HCl + H₂O → H₃O+ + Cl^–
HNO₃ + H₂O → H₃O⁺ + NO₃^–

(ii) Weak electrolytes: The substances which ionize to a small extent in an aqueous solution are called weak electrolytes. For example, CH₃COOH, NH₄OH, (NH₄)₂ CO₃, HCN, etc. are weak electrolytes.
CH₃COOH + H₂O ⇌ H₃O+ + CH₃COO^–
NH₃ + H₂O ⇌ NH₄⁺ + OH^–

Ionization of weak electrolytes: Weak electrolytes are only partially ionized and a dynamic equilibrium is established between the ions and the unionized molecules. The equilibrium which is established between the unionized molecules and the ions in the solution of weak electrolytes is called ionic equilibrium,

The fraction of the total number of molecules of an electrolyte which \ ionizes into ions is called the degree of ionization or degree of dissociation.

It is denoted by the symbol an (alpha).
Degree of ionisation,
α = \(\frac{\text { Number of molecules of the electrolyte which ionise }}{\text { Total number of molecules of the electrolyte }}\)

Dissociation or Ionisation Constant for Weak Electrolytes: Consider a weak electrolyte CH3COOH in equilibrium with its ions when dissolved in water as
CH₃COOH (aq) + H₂O (l) ⇌ CH₃COO^– (aq) + H₃O⁺ (aq)

The equilibrium constant K, is
K_a = \(\frac{c \alpha^{2}}{1-\alpha}\)

Since the degree of dissociation of a weak acid is very small as compared to 1, then 1 – α may be taken approximately equal to 1.
K = cα²
α = \(\)\sqrt{\frac{\mathrm{K}_{a}}{c}} ∴ [H₃O⁺] = ca = \(\sqrt{\mathrm{K}_{a} c}\)

Thus, knowing the ionisation the ionisation constant K_a, degree of ionisation can be calculated.

Similarly, for a weak base, if the ionisation constant is K_b, c is the concentration and α is the degree of ionisation, then
K_b = \(\frac{c \alpha^{2}}{1-\alpha}\)
or
α = \(\sqrt{\frac{K_{b}}{c}}\)(1 – α) ≈ 1

Acids, Eases and Salts:
1. Arrhenius Acids and Bases: Arrhenius defined acids as substances that produce hydrogen ions in water and bases that produce hydroxyl ions. Thus, according to the Arrhenius concept, hydrogen chloride, acetic acid, and sulphuric acid, are acids because all these compounds give free H⁺ ions in an aqueous solution.
HCl (g) + H₂O (excess) ⇌ H⁺ (aq) + Cl^– (aq)
H₂SO₄ + H₂O (excess) ⇌ 2H⁺ (aq) + SO₂^-4 (aq)
CH₃COOH + H₂O (excess) ⇌ H⁺ (aq) + CH₃COO^– (aq)

The compounds such as NaOH and NH4OH are bases because these compounds give free OH- ions in aqueous solutions.
NaOH + H₂O (excess) ⇌ Na⁺ (aq) + OH^– (aq)
NH₄OH + H₂O (excess) ⇌ NH₄⁺ (aq) + OH^– (aq)

Ionization of Acids and Bases
→ The Bronsted-Lowry Acids and Bases: Any hydrogen-containing species (a molecule, a cation, or an anion) which is capable of donating one or more protons to any other substance is called an acid.

Any species (molecule, cation, or anion) which is capable of accepting one or more protons from acid is called a base.
Thus, according to the Bronsted-Lowry concept, an acid is a proton donor, and. a base is a proton acceptor.

Let us consider the dissolution of hydrogen chloride (HCl) in water described by the reaction
HCl (aq) + H₂O (1) ⇌ H₃O⁺ (aq) + Cl^– (aq)

In this reaction, HCl donates its one proton to become Cl^– and H₂O accepts one proton to become H₃O⁺. Thus, HCl is a Bronsted acid and H₂O is a Bronsted base.

Every acid must form a base on donating its proton and every base must form an acid on accepting a proton.

Conjugate Acid-Base Pairs: Consider the reaction between an acid and a base

In this reaction, HCl donates a proton (acts as an acid) and forms Cl^– ion which has a tendency to accept a proton (can act as a base). Similarly, NH₃ accepts a proton and acts as a base but it forms an NH₄⁺ ion which has a tendency to behave as an acid. In other words, an acid donates a proton .and becomes a base and a base accepts a proton and becomes an acid.

The base formed from acid is referred to as the conjugate base of the acid. Similarly’ the acid formed from a base is called the conjugate acid of the base. Thus, in the above example, Cl^– is the conjugate base of acid HCl arid NH₄⁺ is the conjugate acid of the base NH₃.

The pairs of acids and bases are formed from each other by the gain or loss of a proton are called conjugate acid-base pairs.

Thus, each acid-base reaction involves two pairs of conjugate acids and bases. These are labeled as 1 and 2 as shown below:

It may be noted that the conjugate base of a strong acid is a weak base and the conjugate base of a weak acid is a strong base. Strong acids like HCl, HNO₃ have weak bases like Cl^– and NO₃ and vice versa.

Lewis’s concept of Acids and Bases: G.N. Lewis (1923) proposed a more general and broader concept of acids and bases. According to this concept, an acid is a substance (molecule or ion) that can accept a pair of electrons while a base is a substance (molecule or ion) that can donate a pair of electrons. Some examples of Lewis acids and bases are

Lewis bases

1. Neutral species having at least one lone pair of electrons, e.g. NH₃, -NH₂, ROH
2. Negatively charged ions e.g., CN^–, Cl^–, OH^–.

Lewis acids

1. Molecules in which the central atom has incomplete octet e.g., AlCl₃, BF₃, FeCl₃, etc,
2. Simple cations act as Lewis acids, e.g., Ag⁺, H⁺, etc.
3. Molecules having empty d-orbitals in the central atom, e.g., SiF₄, SnCl₄, PF₅.
4. Molecules in which atoms of dissimilar electronegativities are joined by multiple bonds, e.g., CO₂, SO₂, etc.

The acid-base reaction may be written as:


Problem. Classify the following species into Lewis acids and Lewis bases and show how these act as such:

Answer:
This ion acts as a Lewis base as it can donate any one of its four electron pairs.

(b) OH^–
Answer:
OH^– is a lewis base as it can donate an electron lone pair.

(c) H⁺
Answer:
H⁺ A proton is a lewis acid as it can accept a lone pair of electrons from bases like OH^– and F^– ions.

(d) BCl₃^–
Answer:
BCl₃^– acts as a lewis acid as it can accept a lone pair from species like ammonia or amine molecules.

Ionization of water-ionic product of water
Water is a weak electrolyte and it undergoes self ionization as
H₂O + H₂O ⇌ H₃O⁺ + OH^–

Applying the law of chemical equilibrium
K = \(\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_{2} \mathrm{O}\right]^{2}}\)

Since the dissociation of water takes place to a small extent, the concentration of the undissociated water is nearly constant. Therefore,
K = \(\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\text {Constant }}\)
K × Constant = [H₃O⁺][OH^–]
or
K_w = [H₃O⁺][OH^–]

where is a constant and is known as ionic product of water. Its value is constant at a particular temperature. At 298 K, the value of K_w is 1.008 × 10^-14mol2 L^-2. That is,
K_w = [H₃O+][OH-] = 1.008 × 10^-14 at 298 K

It is quite evident that the concentrations of H3O+ and OH- ions are equal in pure water so that
[H₃O⁺] = [OH^–] = 1.0 × 10^-7 mol L^-1

It may be remembered that
if [H₃O⁺] = [OH^–]: the solution is neutral
[H₃O⁺] > [OH^–]: the solution is acidic
[H₃O⁺] < [OH^–]: the solution is basic.

In a basic or acidic solution, the concentration of H3O+ or OH- may be calculated as
[H₃O⁺] = \(\frac{\mathrm{K}_{w}}{\left[\mathrm{OH}^{-}\right]}\)[OH~] = \(\frac{\mathrm{K}_{w}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\)

pH scale
The pH of a solution may be defined as the negative logarithm of the H₃O⁺ ion concentration in moles per liter. Mathematically, it may be expressed as
pH = – log [H₃O⁺]
or
log [H₃O⁺]

For neutral solution, pH = – log [1.0 × 10^-7] = 7
In a similar way, by substituting different values of [H₃O⁺] in the above relation, it can be seen that

• For acidic solution pH <7
• For basic solution pH >7
• For neutral solution pH = 7

To express the acidic or basic character of a solution, a scale has been proposed from pH 1 to 14. This scale is known as the pH scale.

It may be noted that solutions having pH between 0 to 2 are strongly acidic, those with pH between 2 to 4 are moderately acidic while the others having pH between 4 to 7 are weakly acidic. Similarly, the solutions having pH values between 7 to 10 are weakly basic, those having pH 10 to 12 are moderately basic whereas the others which haying a pH range between 12 to 14 are strongly basic.

p^OH scale Like p^H, p^OH may be defined as
p^OH = – log [OH^–]

At 298K p^H + p^OH = pK° = – logK_w = – log 10^-14
∴ p^H + p^OH= 14

At 298 K, Ionic product of water =1.0 × 10^-14
[precisely = 1.08 × 10^-14 mol² L^-2]

The value of K_w goes on increasing as the temperature increases.

It is because with the increase in temperature, the degree of ionization of water into H⁺ ions and OH^– ions increases.
But since pH = – log [H⁺]
∴ the p^H of water decreases with an increase in temperature.

The ionization of Bases
The bases in their aqueous solutions furnish OH^– (hydroxyl) ions.
For example
NaOH + H₂O (excess) → Na⁺ (aq) + OH^– (aq)
NH₃ + H₂O (excess) ⇌ NH₄OH (aq) ⇌ NH₄⁺ (aq) + OH^– (aq)

Strong bases like NaOH and KOH are completely dissociated into their constituent ions in dilute solutions.

Weak Bases like NH₄OH, AgOH are ionized in an aqueous solution to a small extent only. The ionization of a base is characterized by an equilibrium constant called base dissociation constant (K_b), for example for a base like MOH
MOH + H₂O (excess) ⇌ M⁺ (aq) + OH^– (aq)
K_b = \(\frac{\left[\mathrm{M}^{+}(\mathrm{aq})\right] \times\left[\mathrm{OH}^{-}(\mathrm{aq})\right]}{[\mathrm{M}(\mathrm{OH})]}\)

If n moles of a base is dissolved in V liters of the solution and a is the degree of dissociation of the base, then the amounts of various species at equilibrium present are

• No. of moles of MOH = n(1 – α)
• No. of moles of OH^– = nα
• No. of moles of M⁺ = nα

The corresponding concentrations in moles per litre are
[MOH] = n(1 – α)/V mol L^-1 = C(1 – α) mol L^-1
[OH^–] = nα/V mol L^-1 = Cα mol L^-1
[M⁺] = na/V mol^-1 = Cα mol L^-1.

Thus, the ionisation constant of the base is given by
K_b = \(\frac{\left[\mathrm{M}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{MOH}]}=\frac{\mathrm{C} \alpha \cdot \mathrm{C} \alpha}{\mathrm{C}(1-\alpha)}=\frac{\mathrm{C} \alpha^{2}}{(1-\alpha)}\)

where C is the molar concentration of the base in solution.
If α is small (i.e., the base is fairly weak) then a can be ignored in comparison to 1. Then
K_b = Cα²
or
α = \(\sqrt{\frac{\mathrm{K}_{b}}{\mathrm{C}}}=\sqrt{\mathrm{K}_{b} \mathrm{~V}}\) ……..(1)

where V is the volume of the solution in liters containing one mole of the base MOH. From equation (1), it is apparent that the degree of ionization of the base increases with dilution.

The hydroxide ion concentration in the solution is given by,
[OH] = Cα = C × \(\sqrt{\frac{\mathrm{K}_{b}}{\mathrm{C}}}=\sqrt{\mathrm{K}_{b} \mathrm{C}}\).

→ Di and Polybasic Acids and Di-and Polyacidic Bases: Some of the acids like oxalic acid, sulphuric acid, and phosphoric acids have more than one ionizable proton per molecule of the acid. Such acids are known as polybasic or polyprotic acids. The ionization reactions for example of a dibasic acid H₂X, are represented by the equations:
H₂X (aq) ⇌ H⁺ (aq) + HX^– (aq)
HX^– (aq) ⇌ H⁺(aq) + X₂^–(aq)

And the corresponding equilibrium constants are given below:
K_a1 = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{HX}^{-}\right]}{\left[\mathrm{H}_{2} \mathrm{X}\right]}\) and
K_a2 = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{2-}\right]}{\left[\mathrm{HX}^{-}\right]}\)

Here K_a1 and K_a2 are called the first and second ionization constants respectively of the acid H₂X. Similarly for tribasic acid like H₃PO₄ we have three ionization constants.

Similarly, expressions can be written for di and poly acidic bases

Table: The ionization constants of some common polyprotic acids (298 K)

→ Common ion effect in the ionization of Acids and Bases: The products of ionization of acid are hydrogen ions and the corresponding anion. If any one of the products is added to the acid solution then the acid is ionized to a lesser extent in agreement with Le Chatelier’s principle. Let us consider the example of acetic acid whose dissociation may be represented by its dissociation equilibria.
HAc (aq) ⇌ H⁺ (aq) + Ac^– (Aq) .
K_a = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{A} c^{-}\right]}{[\mathrm{HAc}]}\)

If hydrogen ion is provided from any other source, it will combine with the acetate ion and reduce the degree of ionization of acetic acid. Similar will be the effect when the anion is added to the equilibrium mixture from an external source.

Hydrolysis of salts and the pH of their solutions: Salt hydrolysis describes the interaction of water and the cation/anion or both of a salt. The pH of the solution gets affected by this interaction. The cations (e.g., Na⁺, Rb⁺, Ca²⁺, Ba²⁺, etc.) of the strong Bases and, Anions (e.e. Cl^–, Br^–, I^–, NO₃^– etc.) of strong acids do not hydrolyze and therefore the solutions of salts formed by strong acids and bases are neutral i.e., their pH is 7. On the other hand, the solutions of salts formed from strong bases and weak acids are alkaline i.e., their pH is greater than 7. While the solutions of strong acids and weak bases are acidic i.e., their pH is less than 7.

→ The salts of strong bases and weak acids: Consider the solution of salts like MX formed by a strong base MOH and a weak acid HX. The salt is a strong electrolyte and is completely dissociated into M⁺ and X^– ions.
MX (s) + H₂O (l) → M⁺ (aq) + X^– (aq)

If the concentration of the salt is ‘C‘, then the concentration of M⁺ and X^– is also C. M⁺ is the cation of a strong base and therefore it remains as such but the anion X^– reacts with a water molecule to give unionized acid. This process is known as hydrolysis.
X^– (aq) + H₂O (l) ⇌ HX (aq) + OH^– (aq)

If ‘h’ is the degree of hydrolysis indicating the extent to which the anion is hydrolyzed and C is the concentration of MX or X^–, and further assuming that the concentration of water remains constant, the equilibrium constant for the reaction called the hydrolysis constant, K_h is given by the equation
K_h = \(\frac{[\mathrm{HX}]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{X}^{-}\right]}\)

Multiplying the numerator and the denominator of the right-hand side of the above equation by [H⁺], we obtain
K_h = \(\frac{[\mathrm{HX}]\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{X}^{-}\right]\left[\mathrm{H}^{+}\right]}=\frac{\mathrm{K}_{w}}{\mathrm{~K}_{a}}\)

If ‘C’ is the concentration of the salt in the solution and ‘h’ is the degree of hydrolysis, then after the equilibrium is established the concentration of various species in the solutions are given by the equations:
[X^–] = C(1 -h) and [OH^–] = [HX] = Ch

We then have the quadratic equation

→ The salts of strong acids and weak bases: The salt MX formed by a strong acid HX and a weak base MOH when dissolved in water dissociated into cations M⁺ and anions X^–. The cation undergoes hydrolysis represented by the reaction

If ‘C is the concentration of the salt in the solution, h is its degree of hydrolysis, then equilibrium concentrations of various species are given by the equation.
[MOH] = [H⁺] = Ch and [M⁺] = C(1 – h)
K_h = Hydrolysis constt. = \(\frac{\mathrm{K}_{w}}{\mathrm{~K}_{b}}\)
= \(\frac{(C h)^{2}}{C(1-h)}=\frac{C h^{2}}{1-h}\)

If h = degree of hydrolysis is small
1 -h ≈ 1
∴ K_h = Ch²

pH = \(\frac{1}{2}\)[p^K_w – p^K_b – log C]

At 298 K, the equation becomes
pH = 7 – \(\frac{1}{2}\)[p^K_b + logC]

→ The salts of weak bases and weak acids: Consider a salt MX formed by the weak base MOH and the weak acid MX. The salt in the aqueous solution is completely dissociated into the ions and both of these now ionize in water by the reaction
M⁺ (aq) + X^– (aq) + H₂O (l) ⇌ MOH (aq) + HX (aq)

Assuming that in dilute solution the concentration of water remains constant, the hydrolysis constant is given by the equation:
K_h = \(\frac{[\mathrm{MOH}][\mathrm{HX}]}{\left[\mathrm{M}^{+}\right]\left[\mathrm{X}^{-}\right]}\)

Multiplying the right hand side both in the numerator and the denominator by [H+][OH_], we get
K_h = \(\frac{[\mathrm{MOH}][\mathrm{HX}]}{\left[\mathrm{M}^{+}\right]\left[\mathrm{OH}^{-}\right]} \cdot \frac{[\mathrm{HX}]}{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right]}\) × [H+][OH-]

= \(\frac{K_{a}}{\left(K_{b} \times K_{a}\right)}\)

If ‘C’ the concentration of the salt and ‘h’ the degree of hydrolysis, then at equilibrium, the concentrations of various species are given by the relations
[MOH] = [HX] = Ch and [M⁺] = [X-] = C(1 – h) and
we have now
K_b = \(\frac{(\mathrm{C}) n^{2}}{\left[\mathrm{C}(1-h)^{2}\right]}=\frac{h}{(1-h)^{2}}\)
or
\(\frac{h}{1-h}\) = (K_h)^1/2

The concentration of the hydrogen ion can be calculated using the equation for the ionization constant of the acid, HX
K_a = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right]}{[\mathrm{HX}]}\)

If K_h is small then ‘h’ is also small and we have h = K1/2 and (1 – h) = 1 and we have
pH = p^K_a – log (h) = p^K_a – [(log (K^_b)^1/2]
= \(\frac{1}{2}\)[p^K_w + p^K_a – p^K_b]
and at 298 K, we have pH = 7 + \(\frac{1}{2}\)(p^K_a – p^K_b).

→ Problem: The p^K_a of acetic acid and p^K_b of ammonium hydroxide are respectively 4.76 and 4.75. Calculate the pH of ammonium acetate solution.
Answer:
pH = 7 + \(\frac{1}{2}\)(p^K_a – p^K_b) = 7 + \(\frac{1}{2}\)(7.46 – 4.75)
= 7 + \(\frac{1}{2}\)(0.01) = 7.005.

→ Buffer Solutions: Many-body fluids e.g. blood and urine have definite pH and any deviation in their pH indicates malfunctioning of the body. The control of pH is very important in chemical and biochemical processes.

The solutions which resist change in their pH on dilution or on the addition of a small amount of acid or base are called buffer solutions.

Solubility Equilibria of Sparingly Soluble Salts The solubility of a substance depends on a number of factors. They are the lattice enthalpy of the salt and the solvation enthalpy of the ion. For salt to dissolve in a solvent the strong forces of attraction between the ions (lattice energy) must be overcome by the ion solvent its solvation enthalpy must be greater than its lattice enthalpy. On the basis of their solubility, the salts can be classified into 3 categories.

Solubility Product Constant
Whenever a sparingly soluble ionic substance like AgCl, AgBr, Agl, BaSO₄, PbCrO₄, etc. is placed in a polar solvent like water, it dissolves to a very limited extent to produce ions in the solution. After a little while, an equilibrium between the solid phase and the ions in the solution is established. For example, for an ionic substance AB, the equilibrium is

Since the concentration of the solid substances, AB at any temperature is constant, hence the above equilibrium (between ions and solid substance) can be described by a new constant K.
K_sp = [A⁺(aq)][B^–(aq)]

K_sp is called the solubility product constant or simply as solubility product of the salt concerned

K_sp for a salt of the type AB₂: For a sparingly soluble ionic salt of type AB₂, the dissolution leads to the equilibrium AB₂ (S) + H₂O (excess) ⇌ [A²⁺ (aq) + 2B^– (aq)]
K_sp = [A²⁺ (aq)][B^– (aq)]²

→ K_sp for a salt of the type A_mB_n: For a salt of the type A_mB_n (s), dissolution leads to dissociation according to the reaction.
A_mB_n (s) + H₂O (excess) ⇌ mA^p+ (aq) + nB^q- (aq)
where m^p+ = n^q-

The solubility product constant for the salt AmBn is then expressed as ‘
K_sp = [A^p+ (aq)]m [B^q- (aq)]n

Thus, the solubility product constant (Ksp) of a sparingly soluble salt is defined as the product of the molar concentrations of the ions in its saturated solution each raised to the power equal to the stoichiometric coefficient of the species in the balanced chemical equation.

Common ion effect on the solubility of ionic salts: A shift in the position of the equilibrium involving molecular and ionic forms of an electrolyte, by adding a strong electrolyte having one ion common to it is called common ion effect.

The solubility of a sparingly soluble salt decreases when a highly soluble salt having one ion common to the sparingly soluble salt is added to the solution due to the common ion effect. For example,

The solubility of AgCl (sparingly soluble salt) in water decreases when a small amount of KCl or NaCl is added to the solution. This is because KCl or NaCl dissociate completely in solution to produce more Cl^– ions.
KCl → K⁺ + Cl_^–

This increase in the concentration of Cl^– ion shifts the equilibrium.
AgCl (s) ⇌ Ag⁺(aq) + Cl^–(aq)

towards left. This causes more precipitation of AgCl (s). As a result, the solubility of AgCl in the solution decreases.

Table: The solubility product constants, K_sp of some common ionic salts at 298 K


→ Equilibrium: It represents the state of a process in which the properties like the temperature, pressure, and concentration of the system do not show any change with the passage of time.

→ Equilibrium Mixture: The mixture of reactants and products in the equilibrium state is called an Equilibrium mixture.

Henry’s Law: The mass of a gas dissolved in a given mass of a solvent at any temperature is directly proportional to the pressure of the gas above the solvent.
i.e., m ∝ p
or
m = kp
where k is a constant of proportionality and is called Henry’s Constant. Its value depends upon the nature of the gas, the nature of the liquid, and the temperature.

Dynamic Equilibrium in Chemical Reactions The chemical reactions reach a state of dynamic equilibrium in which the rates of forward and reverse reactions are equal and there is no net change in composition.

Law of Chemical Equilibrium and Equilibrium Constant At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentrations of the reactants raised to their individual stoichiometric coefficients has a constant value. This constant value is called the Equilibrium Constant.

The equilibrium constant for a general reaction
a A + bB ⇌ cD + dD
is expressed by KC = \(\frac{[\mathrm{C}]^{c} \times[\mathrm{D}]^{d}}{[\mathrm{~A}]^{a} \times[\mathrm{B}]^{b}}\).
where [A], [B], [C], [D] are the equilibrium concentrations of the reactants and products.

If the equilibrium constant for the reaction
H₂ (g) + I₂ (g) ⇌ 2HI (g) is K_c = [HI]²/[H₂][I₂]

the equilibrium constant for the reverse reaction
2HI (g) ⇌ H₂ (g) + I₂ (g) at the same temp, is
K_c = [H₂][I₂]/[HI]² = \(\frac{1}{x}=\frac{1}{\mathrm{~K}_{\mathrm{C}}}\)

Thus K_C = \(\frac{1}{\mathrm{~K}_{\mathrm{C}}}\)

→ Homogeneous Equilibrium: When the reactants and products of a chemical reaction are in the same state, the system is said to have a homogeneous equilibrium.

→ Heterogeneous Equilibrium: Equilibrium in a system having more than one phase is called heterogeneous equilibrium.

Predicting the direction of the reaction For a general reaction
aA + bB ⇌ cD + dD
Q_c = [C]^c × [D]^d/[A]^a × [B]^b then

• If Q_c > K_c, the reaction will proceed in the direction of reactants (reverse reaction).
• If Q_c < K_c, the reaction will proceed in the direction of the products (forward reaction).
• If Q_c = K_c, the reaction mixture is already in equilibrium.

That is, no net reaction occurs.
Relationship between Equilibrium Constant K, Reaction Quotient Q, and Gibbs Energy G

• If ΔG is negative, the reaction is spontaneous and proceeds in the forward direction.
• If ΔG is positive, the reaction is non-spontaneous.
• If ΔG = 0, the reaction has achieved equilibrium.

Mathematically,
ΔG – ΔG° + RT InQ.
where G° is standard Gibbs energy.
At equilibrium, when ΔG = 0 and Q = K_c

The above equation becomes
ΔG = ΔG° + RT InK .
ΔG° = – RT InK.
InK = – ΔG°/RT

Taking antilogs
K = e^{-ΔG /RT}

Thus if ΔG° < 0 then – ΔG°/RT is positive and e^{-ΔG /RT} > 1 making K > 1 which implies a spontaneous reaction.

If ΔG° > 0; then – ΔG°/RT is negative and e-ΔG /RT < 1, that is Kc < 1, which implies a non-spontaneous reaction.

For a general reaction
aA + bB ⇌ cD + dD

If p_A, p_B p_C and p_D indicate their partial pressures and [A], [B], [C] and [D] indicate their molar concentrations,

where Δn = (number of moles of gaseous products) – (number of moles of gaseous reactants) in the balanced chemical equation.

→ Le-Chatelier’s Principle: When a system in equilibrium is subjected to a change of temperature, pressure, or concentration the equilibrium shifts in a direction so as to undo the effect of the change applied.

This is applicable to all chemical and physical equilibria.

Arrhenius Concept of Acids and Bases.
→ Acids: are hydrogen-containing substances that dissociate in water to give hydrogen ions H⁺ (aq).

→ Bases: Bases are substances that produce hydroxyl ions OH^– (aq) on dissociation in water.

Bronsted-Lowry Concept of Acids and Bases
→ Acid: Acid is a substance that is capable of donating a hydrogen – ion H⁺. It is a Proton-donor.

→ Base: It is a substance that is capable of accepting a hydrogen ion H⁺. It is a Proton-acceptor.

Conjugate Acid-base Pair: The acid-base pair which differs only by one proton is called a conjugate acid-base pair.
HCl is an acid whose conjugate base is Cl^–.
NH₃ is a base whose conjugate acid is NH₄⁺.
OH^– is called the conjugate base of an acid H₂O.

If Bronsted acid is a strong acid, then its conjugate base is a weak base and vice-versa,

Lewis Concept of Acids and Bases
→ Acid: It is species which accepts electron pair.

→ Base: It is a species that donates an electron pair.

Thus in the reaction
BF₃ + :NH₃ ⇌ BF3 :NH₃
BF₃ is an acid and: NH₃ is a base.

The Ionisation Constant of Water and its Ionic Product
K_w which is = [H⁺] × [OH^–] is called an Ionic product of water

At 298 K, concentration to H⁺ = 1.0 × 10^-7 M
∴ Concentration of [OH-] is also = 1.0 × 10^-7 M
K_w = [H⁺] × [OH^–] = [H₃O⁺] × [OH-]
= 1.0 × 10^-14M²

The value of Ka is temperature-dependent.
Acidic substance [H₃O⁺] > [OH^–]
Neutral substance [H₃O⁺] = [OH^–]
Basic substance [H₃P⁺] < [OH^–]

The pH scale
PH = – log a_H⁺
where a_H⁺ is hydrogen ion activity

Hence pH of pure water = – log [10^-7] = 7.
Acidic solution has pH < 7.
Basic solution has pH > 7
Pure water or Neutral solution has pH = 7
K_w = [H₃O⁺] × [OH^–] – 10^-14
– log K_w = – log {[H₃O⁺] × OH^–]} = – log 10^-14
– log K_w = – log [H₃O⁺] – log [OH^–] = – log 10^-14
or
p^K_w = p^H + p^OH = 14

→ p^H meter: It is a device that measures the p^H-dependent electrical potential of the test solution within 0.001 precission

Ionization constants of weak acids
For a weak acid HX

HX (aq) + H₂O (I) ⇌ H₃O⁺ (aq) + X^– (aq)
K_a = [H₃O⁺][X^–]/[HX]
where K_a is called the dissociation or ionization constant of acid HX.

At a given temperature, the value of K_a is a measure of the strength of the acid HX. K_a is a dimensionless quantity.
Ionization of weak bases:
For a weak base MOH
MOH (aq) ⇌ M⁺ (aq) + OH^– (aq)
K_b = [M⁺] × [OH^–]/[MOH] is called base ionisation constant.

The value of K_b is a measure of the strength of a base.
K_a + K_b = K_w for a conjugate acid-base pair
or
p^K_a + p^K_b = p^K_w = 14 at 298 K

Note 1. For a polybasic acid, if K_a1, K_a2… are successive dissociation constants, then
K_a1 > K_a2 >K_a3

Similarly, H₂ S is a stronger acid than H₂O.

Note 3. In HA, H-A bond polarity becomes the deciding factor for determining the acid strength. As the electronegativity of A increases, the strength of the acid also increases.

→ Common-Ion Effect: The suppression of the degree of dissociation of a weak acid or a weak base on the addition of a common ion is called Common-Ion Effect.

Thus the degree of dissociation of a weak base NH₄OH is suppressed on the addition of common ion NH₄⁺ by adding NH₄Cl which is a strong base.

Hydrolysis of Salts

1. Salts of strong acids and strong bases like NaCl, KCl, NaNO₃ KNO₃/ K₂SO₄, Na₂SO₄ do not undergo hydrolysis. Their solutions in water are neutral.
2. Salts of strong acids and weak bases like NH₄Cl, CuSO₄ yield acidic solutions in water.
3. Salts of weak acids and strong bases on hydrolysis like CH₃COONa, Na₂CO₃ yield basic solutions in water.
4. Salts of weak acids and weak bases undergo hydrolysis.
   e.g. CH₃COONH₄. Their acidic or basic nature depends upon the comparative strength of the acid/base.

Buffer Solutions: The solution which resists a change in pH value on dilution or with the addition of small amounts of acid or alkali is called Buffer solutions.

By going through these CBSE Class 11 Chemistry Notes Chapter 6 Thermodynamics, students can recall all the concepts quickly.

Thermodynamics Notes Class 11 Chemistry Chapter 6

Thermodynamic Terms: The laws of thermodynamics deal with energy changes at a macroscopic system involving a large number of molecules rather than a microscopic system containing a few molecules

→ System: The part of the universe which is under thermodynamic study/scrutiny is called a system.

→ Surroundings: The remaining part of the universe with which the system can exchange both matter and energy is called the surrounding. System and surrounding taken together constitute the universe.
The universe = The system + the surroundings.

Types of System
1. Open System: An open system is one in which there is an exchange of matter and energy between the system and surroundings, e.g., a reaction occurring in a test tube.

2. Closed System: A closed system is one in which there is only a transfer of energy and not matter with the surroundings, e.g., the presence of reactants in a closed vessel.

3. Isolated System: An isolated system is one in which no exchange of energy and matter is possible between the system and the surroundings. The presence of reactants in a thermos flask is an example of an isolated system.

→ The State of the System: When the properties of a system like its pressure, volume, temperature, and composition are specified quantitatively, it is said to have stated. If any of these observable (measurable) properties undergo a change, the system is said to have another state.

→ State Variables: Such properties of the system, by changing any one of which, the system changes its state, are called State Variables.

→ State Function: A physical quantity is said to be a state function if its value depends upon the initial state and final state of the system and not the path followed by the system. Internal energy, enthalpy, free energy, entropy are all state functions. Heat and work are not state functions, because they depend upon the path followed.

→ Extensive Properties: Extensive properties of a system are those properties that depend upon the amount of substance contained in the system. Mass, volume, heat capacity, internal energy, enthalpy, Gibbs free energy are all extensive properties.

→ Intensive Properties: Intensive properties of a system are those which are independent of the quantity of matter contained in the system. They depend upon only the nature of the substance. Temperature, pressure, viscosity, density, surface tension, refractive index, specific heat, freezing point, boiling point are all intensive properties.

There are four types of thermodynamic processes:

1. Isothermal Process: A process in which temperature remains constant.
2. Adiabatic Process: A process in which no heat exchange takes place,(i.e., q = 0) between the system and surroundings.
3. Isochoric Process: A process in which volume remains constant.
4. Isobaric Process: A process in which pressure remains constant.

→ Internal Energy ‘U’: Its absolute value cannot be determined.
The energy stored within a substance (or system) is called its internal energy. It is a state function.
ΔU denotes a change in internal energy.
ΔU = U₂ – U₁ = U_p – U_r
The internal energy of an ideal gas depends upon only its temperature.

Hence in an isothermal process involving an ideal gas ΔU = 0.

→ Reversible Process: When a process is carried out infinitesimally slowly so that it can be retraced at each step of the change, it is called a reversible process. In such a process system and surroundings are always in equilibrium. .

→ Irreversible Process: A process that is carried out so rapidly that the system does not get a chance to attain equilibrium It cannot be retracted to each step of the change. A reversible process may take infinite time for completion, whereas an irreversible process takes a finite time for completion.

• If w_reversible = work obtained in a reversible process
• If w_irreversible = work obtained in a reversible process is maximum.

→ Cyclic process: If a system after having undergone a series of changes returns back to its initial state, the process is called a cyclic process. The path of such a process is called a cycle.
In cyclic process ΔU = 0.

→ The first law of thermodynamics: States: “Energy can neither be created nor destroyed. However, it can be transformed from one form into another.”

In other words, the first law of thermodynamics can be stated as
“The total energy of the universe (system + surroundings) remains constant”.

The mathematical formulation of the first law of thermodynamics: Let us consider a system in its initial state having internal energy. U₁ If heat equal to q is supplied to the system, and work equal to w is done on the system, then the internal energy of the system is the final state (U₂) is given by
U₂ = U₁ + q + w
U₂ – U₁ = q + w
ΔU = q + w
or change in internal energy = Heat given to the system + work done on the syštem.

This relationship between internal energy, work, and heat is the mathematical statement of the first law of thermodynamics.

Applications: Heat, Work, and Internal Energy:
(a) Heat: The energy exchange between a system ad the surroundings when their temperatures are different is commonly known as heat.

If a system is at a temperature higher than the temperature of its surroundings, then it loses temperatures are different is commonly known as heat.

If a system is at a temperature higher than the temperature of its surroundings, then it loses heat energy to the surroundings. This transfer of heat lowers the temperature of the system and raises the temperature of the surroundings

(b) Work (w): Work is said to be done if the point of application of a force moves through a certain distance. For example, if a gas, enclosed in a cylinder fitted with an airtight piston has higher pressure than the external pressure, then the piston will move outwards. The piston continues to move until the pressure inside and outside are equal. In this, the gas inside the cylinder is pushing the piston outwards. Thus, the gas (system) is doing work.

(c) Internal Energy: the total energy contained in a system is called its internal energy or intrinsic energy. This is denoted by a symbol E or U.

The internal energy of a system depends upon the state of the system and not upon how the system attains that state. The internal energy thus is a state function.

Each substance or system possesses a definite amount of internal energy under a given set of conditions. For example, the internal energy of a system in state A be U_A and in state B, it is U_B. Then, change in the internal energy (ΔU) of the system is going from state A to B is
ΔU = U_final – U_initial = U_B – U_A = w_ad.
wad is positive when work is done on the system. wad is negative if the work is done by the system.

This change in the internal energy depends only upon the initial and the final state and not on how this change is brought about.

Heat capacity and specific heat capacity:
1. Heat capacity: The heat capacity (C) of a sample of a substance is defined as the quantity of heat energy required to raise its temperature by 1 K (or 1°C). From this definition, we can write
Q = C. Δt
where Q is the quantity of heat given to the sample, At is the rise in the temperature of the substance. The unit of heat capacity is Joules per degree Celsius (J/°C or J°C^-1) or Joules per Kelvin (J/K or JK^-1).

2. Specific heat capacity: The specific heat capacity of a substance is equal to the quantity of heat required to raise the temperature of 1 unit mass of capacity of the substance by 1 °C, or 1 K.
S.I. unit of specific heat is joules per kilogram per degree (J/Kg°CorJ/kg.K).

3. Molar heat capacity: The molar heat capacity (c_m) of a substance is defined as the quantity of heat required to raise the temperature of one mole of a substance by 1 K or (or 1°C). Thus

Molar heat capacity = Specific heat capacity × Molar mass
c_m = C × M
The unit of molar heat capacity is J mol^-1 K^-1.

There are two types of Heat Capacities.
1. Heat capacity at a constant volume (C_v): The heat supplied to a system to raise its temperature through 1°C keeping the volume of the system constant is called heat capacity at constant volume.

2. Heat capacity at constant pressure (C_p): The heat supplied to a system to raise its temperature through 1°C keeping external pressure constant is called heat capacity at constant pressure.
C_v = \(\frac{d \mathrm{E}}{d \mathrm{~T}}\)
C_p = \(\frac{d \mathrm{H}}{d \mathrm{~T}}\)

Relationship between (C_p) and (C_v) C_p – C_v = R

→ Enthalpy (H): The sum of internal energy (E) and the product of pressure and volume is called enthalpy.
H = E + PV
P = Pressure,
V = Volume like E, Enthalpy is also a state function.

Its absolute value like E cannot be determined.
Nor is there any necessity for it. What is required is ΔH:
Change in enthalpy.

The value of ΔE and ΔH can be measured with the help of a Bomb Calorimeter. Calorimetry is the technique to measure energy changes associated with chemical or physical processes.
ΔH = H_products – H_reactants

The enthalpy change of a reaction: (ΔrH) is equal to the heat absorbed or evolved during a reaction at constant temperature and pressure.

∴ ΔH = q_p where q_p: Heat absorbed or evolved at constant pressure.
ΔH = ΔE + P ΔV … (1)

When there is no change in volume (i.e. ΔV = 0)
ΔE = q_v where q_v = Heat change at constant volume.

Equation (1) becomes
q_P = q_v + PΔV
q_P = q_v + Δn_gRT
where Δn_g is the change in the no. of gaseous moles of the products minus that of the reactants.

Sign Convention for Heat and Work

• Heat absorbed by the system = q positive
• The heat evolved by the system = q negative
• Work done on the system = w positive
• Work done by the system = w negative

Enthalpies or Heats of Reactions (Δ_rH):
The enthalpy change (amount of heat evolved or absorbed) during a chemical reaction, the moles of reactants and products being the same as indicated by the balanced chemical equation is called Enthalpy of the reaction (Δ_rH).

Exothermic Reaction: These are the reactions in which heat is evolved. Here sum of heat contents of the reactants (H_R) > Sum of heat contents of the products (H_p).
or
H_R > H_p .
or
ΔH = H_p – H_R < 0
or
ΔH < 0
or
ΔH is negative

Examples of exothermic reactions:

1. C(s) + O₂(g) → CO₂(g) + 393.5 kJ
2. H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(1) + 285.8 kJ
3. N₂(g) + 3H₂(g) → 2NH₃(g) + 92.4 kJ

or in terms of ΔH

1. C(s) + O₂(g) → CO₂(g); ΔH = – 393.5 kJ
2. H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); ΔH = – 285.8 kJ
3. N₂(g) + 3H₂(g) → 2NH₃(g); ΔH = – 92.4 kJ

→ Endothermic Reactions: These reactions which proceed with an absorption of heat are called endothermic reactions.
In endothermic reactions sum of the enthalpies of the product > Sum of the enthalpies of reactants
or
ΣH_p > ΣH_R
or
ΔH = H_p – H_R > 0
or
ΔH >0
or
ΔH is positive

Examples of endothermic reactions

1. N₂(g) + O₂(g) → 2NO(g) – 180.7 kJ
2. C(s) + H₂O(g) → CO(g) + H₂(g) – 131.4 kJ
3. C(s) + 2S → CS₂(g) – 92.4 kJ

or writing the above thermochemical equation in terms of AH

1. N₂(g) + O₂(g) → 2NO(g); ΔH = + 180.7 kJ
2. C(s) + H₂O(g) → CO(g) + H₂(g); ΔH = + 131.4 kJ
3. C(s) + 2S → CS₂(g); ΔH = + 92.4 kJ

→ Thermochemical Equation: When a balanced chemical equation not only indicates the quantities of different reactants and products but also indicates the amount of heat evolved or absorbed, it is called a thermochemical equation.
thus N₂(g) + O₂(g) → 2NO(g); ΔH = + 180.7 kJ is a thermochemical equation

Factors on which the heat of the reaction depends

• Quantities of the reactants involved.
• The physical state of the reactants and products.
• Allotropic modifications
• The concentration of the solutions.
• Temperature
• Conditions of constant pressure or constant volume.

→ Standard Enthalpy Change: A substance in its most stable form at 25°C or 298 K under one atmospheric pressure is said to be in its standard form.

The enthalpy change of reaction when all the reactants and products are in their standard states i.e., at 25°C or 298 K and under a pressure of one bar is called standard enthalpy change.

It is usually represented by Δ_rH° or Δ_rH²⁹⁸.

Common Types of Enthalpy or Heat Changes
Enthalpy or Heat of formation: The enthalpy of formation is the enthalpy change when one mole a of the compound is formed from its elements. It is deno’.ed by ΔH_f.

For example, enthalpies of formation of carbon dioxide and methane (CH₄) may be expressed as
C(s) + O₂(g) → CO₂(g); ΔH = ΔH_f=- 395 kJ
C(s) + 2H₂(g) → CH₄(g); ΔH = ΔH_f = -74.8 kJ

If all the species of the chemical reactions are in their standard state, (i.e.. at 298 K and one atmospheric pressure) the enthalpy of formation is called standard enthalpy of formation, expressed as ΔH_f.

The enthalpy of every element in its standard state is arbitrarily assumed to be zero.

Thus, the enthalpy change accompanying the formation of one mole of a compound from its elements, all the substances being in their standard states (1 atm pressure and 298 K) is called standard enthalpy of formation.

The enthalpies of the formation of different substances can be used to calculate the enthalpy change of the reaction.

Standard enthalpies of
ΔH_f° = formation of all products
or
Standard enthalpies of formation of all reactants
Δ_fH° = ΣΔH_f° (products) – ΣΔH_f° (reactants)

→ Eptnalpy or Heat of combustion: The enthalpy change when 1 mole of a substance is completely burnt in excess of oxygen or air is called enthalpy of combustion. It is expressed as Δ_cH°
For example,
CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(l); Δ_fH° = – 890.3 kJ
C₆H₆(l) + \(\frac{15}{2}\) O₂(g) → 6CO₂(g) + 3H₂O(l); Δ_fH° = – 3268 kJ

→ Enthalpy or Heat of solution: The enthalpy change when one mole of a substance is dissolved in a specified quantity of a solvent at a given temperature is called enthalpy of solution.
NH₄NO₃(s) + H₂O(1) → NH₄+ NO₃^– (aq. 1.o m); ΔH = 26.0 kJ

To avoid the amount of solvent, the heat of the solution is usually defined as an infinitely dilute solution. Thus, the heat of solution at infinity dilution is the heat change when one mole of a substance is dissolved in such a large quantity of solvent so that further dilution does not give any further heat change.
NaCl(s) + aq → NaCl(aq); ΔH = 5.0 kJ

→ Enthalpy or Heat of neutralization: The heat change when one gram equivalent of an acid is completely neutralized by a base or vice versa in dilute solution, is called heat of neutralization.
For example,
1. Neutralisation of HCl with NaOH
HCl(aq) + NaOH(aq) → NaCI(aq) + H₂O(l); ΔH = – 57.1 kJ

2. Neutralisation of CH3COOH with NaOH
CH₃COOH(aq) + NaOH(aq) → CH₃COONa + H₂O(l); ΔH = – 55.9 kj.

→ Calorific Values of Foods and Fuels: Different fuels and foods produce different amounts of heat on combustion. They are usually expressed in terms of their calorific value. “The calorific value of a fuel or food is the amount of heat in calories (or joules) produced from the complete combustion of 1 gram of the fuel or the food.
e.g., C₆H₁₂O₆(S) + 6O₂(g) → 6CO₂(g) + 6H₂O(g) + 2840 kJ mol^-1
1 Mole = 180 g.
∴ Calorific value of glucose = \(\frac{2840}{180}\) = 15.78 kJ g^-1.

→ Measurement of Enthalpy of Combustion: At constant volume (q_v or q_v = AE) is done in a Bomb calorimeter. The known weight of the compound whose enthalpy of combustion is to determined is burnt in oxygen in a bomb calorimeter
M
ΔE = Q × Δf × \(\frac{M}{m}\)
where Q = Heat capacity of the calorimeter
Δt = rise in temperature of water in the calorimeter
m = mass of the substance taken
M = Molecular mass of the substance

Enthalpy Changes during Phase Transitions
1. Enthalpy of Fusion: It is the heat change accompanying the transformation of one mole of a solid substance into its liquid form at its melting point.
H₂O(S) (ice) → H₂O(l) (water); ΔH_fus = + 60 kJ mol^-1

2. Enthalpy of vaporization: It is the heat change accompanying the conversion of 1 mole of a liquid into its gaseous state at its boiling point.
H₂O(l) (water) → H₂O(g) (steam); Δ_vap H° = + 407 kJ mol^-1

3. Enthalpy of sublimation: It is the heat change that takes place when 1 mol of a solid changes directly into its vapor phase at a given temperature below its melting point.
I₂(s) → I₂(g); Δ_sub H° = + 62.39 kJ mol^-1
ΔH_sublimation = ΔH_fusion + ΔH_vaporisation

Hess’s Law of Constant Heat Summation
“The total amount of heat evolved or absorbed in a reaction is the same whether the reaction takes place in a single step or in a number of steps, provided the temperature is kept constant.
C(s) + O₂(g) → CO₂(g); ΔH = – 393.5 kJ mol^-1

It can be made to proceed in two steps

1. C(s) + \(\frac{1}{2}\)O₂(g) → CO(g); ΔH₁ = – 110.5 kJ mol^-1
2. CO(g) + \(\frac{1}{2}\)O₂(g) → CO₂(g); ΔH₂ = – 283.0 kJ mol^-1

Thus, the.total heat evolved in steps (1) and (2) is
ΔH₁ + ΔH₂ = – 110.5 + (- 283.0) = – 393.5 kJ mol^-1
which is the same when the reaction takes place directly in a single step.

From the above
Heat change is going from A → D via I route = Q
Heat change in going from A → B → C → D via route II = q₁ + q₂ + q₃
∴ Q = q₁ + q₂ + by Hess’s Law.

It is a corollary from the 1st Law of Thermodynamics.

Applications of Hess’s Law:

1. It helps to calculate the enthalpies of the formation of many compounds which cannot be determined experimentally.
2. It helps to calculate the enthalpy of allotropic transformations.
3. It helps to calculate the enthalpies of hydration.
4. It helps to calculate the enthalpies of different reactions.

→ Bond Enthalpy or Bond Energy: It is defined as the amount of energy required to dissociate one mole of bonds presents between the atoms in the gaseous molecules.
H₂(g) + 436 kJ mol^-1 → 2 H(g)
For diatomic molecules like H₂, bond energy is its bond dissociation energy.

→ Spontaneous Process: A process that can take place of its own or has an urge or tendency to take place is called a spontaneous process. It is simply a process that is feasible.
1. Examples of processes that take place by themselves

1. Dissolution of common salt in water
2. Evaporation of water in an open vessel
3. The flow of water downhill
4. The flow of heat from the hot end to the cold end.

2. Example of processes that take place on initiation

1. Lighting a candle (initiation by ignition)
2. Heating of CaCO₃ to give CaO and CO₂.

→ Non-Spontaneous Process: A process that can neither take place of its own nor on initiation is called a non-spontaneous process.

Examples of non-spontaneous processes.

1. The lighting of a candle (initiation by ignition)
2. Heating of CaCO₃ to give CaO and CO₂.

→ Non-Spontaneous Process: A process that can neither takes place of its own nor on initiation is called a non-spontaneous process.

Examples of non-spontaneous processes.

1. The flow of water uphill.
2. The flow of heat from a cold body to a hot body.

→ The Driving Force for a Spontaneous Process: The force which is responsible for the spontaneity of a process is called the driving force. It is based upon.

1. The tendency towards minimum energy: To acquire maximum stability the system tends to acquire minimum energy.
2. The tendency towards maximum randomness: When a system proceeds from a state of orderliness to disorderliness as the mixing up of two gases, it tries to have maximum randomness or disorder. An increase in disorder leads to the spontaneity of a process.

→ Entropy: It is a measure of disorder or randomness of the system. Like internal energy, enthalpy, entropy is also a state function and it is an extensive property. ΔS is called a change of entropy.
ΔS = S₂ – S₁ = ΣS_products – ΣS_reactants
= \(\frac{q_{\text {reversible }}}{\mathrm{T}}\) under isothermal conditions.

Thus Entropy change (ΔS) during a process is defined as the amount of heat (q) absorbed isothermally and reversible divided by the absolute temperature (T) at which the heat is absorbed.

→ Units of Entropy: As ΔS = \(\frac{q}{T}\) = jK^-1 mol^-1 (S.I. unit)
= Calories K^-1 mol^-1 (C.G.S. unit)

Entropy Change During Phase Transformations
1. Entropy of fusion (ΔS_fusion): The entropy of fusion is the change in entropy when 1 mole of a solid substance changes into its liquid form at its melting point.

Mathematically, ΔS_fus = S_liq – S_solid = \(\frac{\Delta \mathrm{H}_{\text {fusion }}}{\mathrm{T}_{m}}\)
where T_m = Melting point of the solid (K)
ΔH_fusion = Enthalpy of fusion per mole.

2. Entropy of Vaporization: It is defined as the entropy change when 1 mole of a liquid changes into its vapor at its boiling point.
Mathematically, ΔSvap = Svap – Sliq = \(\frac{\Delta \mathrm{H}_{\text {vap}}}{\mathrm{T}_{b}}\)
where, ΔH_vap = Enthalpy of vaporisation per mole
ΔS_vap = entropy of vaporisation
S_vap = Molar entropy of vapour
S_liq = Molar entropy of liquid
T_b = Boiling point of the liquid in Kelvin

3. Entropy as a state function: Let us examine entropy as a state function. Consider a cylinder containing a gas and is fitted with a frictionless and weightless piston which is in contact with a large heaf reservoir.

During isothermal and reversible expansion of the gas from volume V₁ to V₂, the substance will absorb heat, q at temperature T
∴ Change in entropy of the system ΔS_sys = \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}\)

Since an equivalent amount of heat will be lost by the reservoir, change in entropy of reservoir will be ΔS_res = \(\frac{-q_{\mathrm{rev}}}{\mathrm{T}}\)

Total change in entropy
ΔS_t = ΔS_sys + ΔS_res
= \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}+\left(\frac{-q_{\mathrm{rev}}}{\mathrm{T}}\right)\) = 0

If we compress the gas isothermally from a volume V₂ to V₁, heat given by the system is, – q_rev
ΔS_sys = \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}\)
and ΔS_res = \(\frac{-q_{\mathrm{rev}}}{\mathrm{T}}\)

Total change in entropy
ΔS₁ + ΔS₂ = 0

At the end of the cycle, the entropy of the system is the same as it had initially. Therefore, entropy is a state function.

The total entropy change (AStota]) system and surrounding of a spontaneous process is given by
ΔS_total = ΔS_system + ΔS_surr > 0 When a system is in equilibrium, the entropy is maximum, and the change in the entropy, ΔS = 0.

We can say that entropy for a spontaneous process increases till it reaches maximum but at equilibrium change in entropy is zero. Since entropy is state property, we can calculate the change in – entropy of a reversible process by
ΔS_sys = \(\frac{q_{\text {sys rev}}}{\mathrm{T}}\)

We find that both for reversible and irreversible expansion for an ideal gas, under isothermal conditions, ΔU = 0, but ΔStotal i.e., ΔS_sys + ΔS_surr is not zero for an irreversible process. Thus ΔH does not discriminate between reversible and irreversible processes, whereas ΔS does.

→ Gibbs energy and spontaneity: We have seen that for a system, it is the total entropy change, ΔStotal which decides the spontaneity of the process But most of the chemical reactions fall into the category of either closed systems or open systems. Therefore, for most of the chemical reactions, there are changes in both enthalpy and entropy. It is clear that neither decrease in enthalpy nor an increase in entropy alone can determine the direction of spontaneous change for these systems.

For this purpose, we define a new thermodynamic function the Gibbs energy or Gibbs function, G, as
G = H -TS
Gibbs function, G is an extensive property and a state function.

The change in Gibbs energy for the system, ΔGsys can be written as
ΔG_sys. = ΔH_sys – TΔS_sys – S_sysΔT

At constant temperature,
ΔT = 0 ΔG_sys = ΔH_sys – TΔS

Usually the subscript ‘system’ is dropped and we simply write this equation as
ΔG = ΔH – TΔS

Thus, Gibbs energy change = enthalpy change – temperature x entropy change, and is referred to as the Gibbs equation, one of the most important equations in chemistry. Here, we have considered both terms together for spontaneity: energy (in terms of ΔH) and entropy (ΔS, a measure of disorder) Dimensionally if we analyzed, we find that ΔG has units of energy because, both ΔH and the TΔS are energy terms (Since TΔS = (K) J/(K mol) = J/mol or J mol^-1).

Now let us consider how ΔG is related to reaction spontaneity.
We know, ΔS_total = ΔS_sys + ΔS_surr

If the system is in thermal equilibrium with the surroundings, then the temperature of the surrounding is the same as that of the system.

Therefore, an increase in entropy of the surrounding is equal to a decrease in the entropy of the system.
Therefore, entropy change of surroundings,
ΔS_sur = – \(\frac{\Delta \mathrm{H}_{\text {surr}}}{\mathrm{T}}\) = – \(\frac{\Delta \mathrm{H}_{\text {sys}}}{\mathrm{T}}\)

ΔS_sur = ΔS_sys + (- \(\frac{\Delta \mathrm{H}_{\text {sys}}}{\mathrm{T}}\))

Rearranging the above equation:
TΔS_total = TΔS_sys -ΔH_sys

For spontaneous process,
ΔS_total > 0, so TΔS_sys – ΔH_sys > 0

Using the equation, the above equation can be written as
ΔG = ΔH – TΔS < 0

ΔH_sys is the enthalpy change of a reaction, TΔS_sys is the energy that is not available to do useful work. So ΔG is the net energy available to do useful work and is thus a measure of the ‘free energy. For this reason, it is also known as the free energy of the reaction.

ΔG gives a criterion of spontaneity at constant pressure and temperature.

• If ΔG is negative (< 0), the process is spontaneous.
• If ΔG is positive (> 0), the process is nonspontaneous.

Note. If a reaction has a positive enthalpy change and positive entropy change, it can be spontaneous when TΔS is large enough to outweigh ΔH.

This can happen in two ways;
(a) The positive entropy change of the system can be ‘small’ in which case T must be large.
(b) The positive entropy change of the system can be ‘large’, in which case T may be small. The former is one of the reasons why reactions are often carried out at high temperatures.

→ Gibbs Energy Change and Equilibrium: “We have seen how a knowledge of the sign and magnitude of the free energy change of a chemical reaction allows:

1. Prediction of the spontaneity of the chemical reaction.
2. Prediction of*the useful work that could be extracted from it.

So far we have considered free energy changes in irreversible reactions. Let us now examine the free energy changes in reversible reactions.

‘Reversible’ under strict thermodynamic sense is a special way of carrying out a process such that the system is at all times in perfect equilibrium with its surroundings. When applied to a chemical reaction, the term ‘reversible’ indicates that a given reaction can proceed in either direction simultaneously, so that dynamic directions should proceed with a decrease in free energy, which seems impossible.

Therefore, we say that at equilibrium total free energy of the system is a minimum. If it is not, the system would spontaneously change to the configuration of lower free energy.

So, the criterion for equilibrium
A + B ⇌ C + D; is
Δ_rG = 0

Free energy is an extensive property and its value for a given substance will depend on the concentration of the substance. So we have to set its value at an equilibrium concentration as we set temperature and pressure. If the concentrations vary from the equilibrium values, Gibbs energy will also change, we can write
Δ_rG = Δ_rG° + RT ln Q … (1)

Here, ΔrG° is the difference in standard Gibbs energies of formation of the products and reactants, both in their standard, states. Similarly, Δ_rG is the Gibbs energy change at a definite, fixed composition of the reaction mixture. Q is the reaction quotient. R- Gas constant = 8.314 JK^-1 mol^-1. If the species are gases, these concentrations are expressed in partial pressure, and the reaction quotient will be Q_p and if species are in solution, the reaction quotient will be expressed in terms of molar concentration as Q.

At equilibrium, Q = K called equilibrium constant, and Δ_rG = 0,
0 = Δ_rG° + RT ln K
or
Δ_rG° = – 2.303 RT log K

We also know that
Δ_rG° = Δ_rH° – TΔ_rS° = – RT ln K …(2)

For strongly endothermic reactions, the value of ArH° may be large and positive. In such a case, the value of K will be much smaller than 1 and the reaction is unlikely to form much product. In the case of exothermic reactions, Δ_rH° is large and negative, and Δ_rG° is likely to be a large and negative tool. In such cases, K will be much larger than 1. We may expect strongly exothermic reactions to having a large K and hence can go to near completion. Δ_rG° also depends upon

Δ_rS°, if the changes in the entropy of reaction are also taken into account, the value of K or extent of chemical reaction will also be affected, depending upon whether Δ_rS° is positive or negative.

Using equation (2)

1. It is possible to obtain an estimate of ΔG° from the measurement of ΔH° and ΔS° and then calculate K at any temperature for economic yields of the products.
2. If K is measured directly in the laboratory, the value of ΔG° at any other temperature can be calculated.

Effect of Temperature on Spontaneity of Reactions

The terms low temperature and high temperature are relative. For a particular reaction, the high temperature could even mean room temperature.

→ System: That part of the universe in which observations are made surroundings. The remaining part of the universe with which the system can exchange both matter and energy is called the surroundings.

There are three types of system:

1. Open system
2. Closed system
3. Isolated system.

→ The state of the system: When the properties of a system like its pressure, volume, temperature, and composition are specified quantitatively, it is said to have a state.

→ State functions or state variables: The average measurable properties like temperature (T), volume (V), pressure (P), and amount (n) of the system are called state functions because their values depend only on the state of the system and not on how it is reached.

Internal Energy: The total energy stored in a system is called its internal energy (U). It may be chemical, electrical, mechanical, or any other type of energy.
(a) Work: It is a form of energy. Work is said to be done if the point of application of a force moves through a certain distance.

Adiabatic process: It is a process in which there is no transfer of heat between the system and surroundings.

Adiabatic system: The system that does not allow the exchange of heat between itself and its surroundings through its boundary is called an adiabatic system.

(b) Heat: The change of internal energy of a system by transfer of heat from the surroundings to the system or vice-versa without the expenditure of work is called heat (q).

Note:

1. q is positive when heat is transferred from the surroundings to the system.
2. Similarly, w is positive when work is done on the system, w is negative when work is done by the system.

First Law of Thermodynamics:
The energy of an isolated system is constant.
or
Energy can neither be created nor destroyed.

Mathematically, the first law of thermodynamics is
ΔU = q + w
where ΔU is the change of internal energy.

q is the heat absorbed/evolved and iv is the work done
Work done on gas

= – p_exΔV, where p_ex is the external pressure and ΔV is the change in volume from initial volume V_i to final volume V_f.

→ Reversible process: A process is reversible if it is brought about in such a way that it could at any moment, be reversed by an infinitesimal chance. It proceeds infinitely slowly by a series of 1 equilibrium states such that the system and surroundings are always in equilibrium with each other.

→ Irreversible process: A process or change which is brought, about so rapidly that the system does not get a chance to attain equilibrium. It cannot be retraced at each step of the change.

Under reversible conditions

where a pint is the internal pressure of the system. Since dp × dV is very small, we can write

Writing as (the pressure of the gas inside) p and for n moles of an ideal gas
pV = nRT
p = \(\frac{nRT}{V}\)

∴ Under isothermal conditions (i.e., at constant temperature)

If the gas expands in a vacuum (p_ext = 0), it is called the free expansion of the gas.
w_rev = 0

No work is said to be done during free expansion of a gas whether the process is reversible or irreversible.
Isothermal and free expansion of an ideal gas T = Constant (Isothermal expansion). In vacuum p_ext = 0
∴ w = 0, q = 0
∴ from ΔU = q + w
ΔU = 0
1. For isothermal irreversible change
q = – w = P_ext(V_f – V_i)

2. For isothermal reversible change
q = – w = nRT ln \(\frac{\mathrm{V}_{f}}{\mathrm{~V}_{i}}\)
= 2.303 nRT log \(\frac{\mathrm{V}_{f}}{\mathrm{~V}_{i}}\)

3. For adiabatic change, q = 0
ΔU = w ad

Enthalpy: Sum of internal energy U and the product of pressure and volume (PV) is called enthalpy (H)
Mathematically H = U + pV

Enthalpy change (ΔH) can be written as
ΔH = ΔU + pΔV ………..(1)
ΔH = q_p

Thus enthalpy change is the heat absorbed by the system at constant pressure.

• ΔH is negative for exothermic reactions
• ΔH is positive for endothermic reactions

At constant volume
ΔH = ΔU – q_v

Thus internal energy change is the heat change at constant volume.
pΔV = Δn_g RT
where Δng refers to the number of moles of gaseous products minus the number of moles of gaseous reactants.
Substituting the value of pΔV from (2) to (1)
ΔH = ΔU + Δn_gRT

→ Extensive Property: An extensive property is one whose value depends on the quantity or size of matter present in the system. For example, mass, volume, internal energy, enthalpy/heat capacity, etc. are extensive properties.

→ Intensive Property: The property which does not depend on the quantity or size of matter present in the system is called Intensive property. For example, temperature, density, pressure is intensive properties.

Heat Capacity (C): It is defined as the quantity of heat energy required to raise the temperature of a substance by 1 K (or 1°C).
q = C × ΔT
where ΔT is the. temperature change
At constant volume the heat capacity C is denoted by C_v
At constant pressure the heat capacity C is denoted by C_p

The relationship between C_p and C_v for an ideal gas
q_v = C_vΔT = ΔU …….(3)
q_p = C_pΔT = ΔH ………(4)

For 1 mole of an ideal gas
ΔH = ΔU + Δ(pV)
= ΔU + Δ(RT) [As pV = RT for 1 mole]
or
ΔH = ΔU + RΔT …….(5)

For equations (3) and (4), equation (5) becomes
C_pΔT = C_vΔT + RΔT
C_p = C_v + R
C_p – C_v = R

Measurement of ΔU and ΔH is done with the help of Calorimeter: Calorimetry is an experimental technique to measure energy changes associated with chemical or physical processes.

The instrument used for it is called a calorimeter.

Enthalpy change Δ_rH of a reaction.
Δ_rH = (Sum of enthalpies of products) – (sum of enthalpies of reactants)

Here symbol X(sigma) is used for summation and ai and b{ are the stoichiometric coefficients of the products and reactants respectively in the balanced chemical equation.

Standard enthalpy of reactions: the standard enthalpy of reaction is the enthalpy change for a reaction where all the participating substances are in their standard states.

The standard state of a substance at a specified temperature is its pure form at 1 bar.
Standard enthalpy change is denoted by ΔH°.

Standard enthalpy of fusion or Molar enthalpy of fusion Δ_fusH°: The enthalpy change that accompanies melting of one mole of a solid substance in the standard state is called standard enthalpy of fusion or molar enthalpy of fusion Δ_fus H°.
H₂O(S) → H₂O(l); Δ_fusH° = 6.00 kJ mol^-1

→ Standard or Molar enthalpy of Vaporization (Δ_vap H°): It is the amount of heat required to vaporize one mole of a liquid at constant. temperature and under standard pressure (1 bar).
H₂O(l) → H₂O(g); Δ_vapH° = 40.79 kJ mol^-1

→ Standard enthalpy of sublimation (Δ_subH°): It is the enthalpy change when one mole of a solid substance sublimes at a constant temperature and under standard pressure (1 bar).

Solid CO₂ or dry ice sublimes at 195 K with Δ_subH° = 25.2 kJ mol^-1

→ Standard enthalpy of formation: The standard enthalpy change for the formation of one mole of a compound from its elements in their most stable states of aggregation (also known as reference states) is called Standard Molar Enthalpy of Formation (Δ_rH°).
H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); Δ_fH° = – 285,8 kJ mol^-1

→ Thermochemical equation: A balanced chemical equation together with the value of its Δ_rH is called a thermochemical equation.
C₂H₅OH(l) + 3O₂(g) → 2CO₂(g) + 3H₂O(l); Δ_rH° = – 1367 kJ mol^-1

Hess’s Law of Constant Heat
If a reaction takes place in several steps, then its standard reaction enthalpy is the sum of the standard enthalpies of the intermediate reactions into whiter the overall reaction may be divided at the same temperature.
Or
The enthalpy change for a reaction is the same whether it occurs in one step or through a series of steps at the same, temperature.
Standard enthalpy of combustion: It is defined as the enthalpy change when one mole of a substance in its standard state is burnt completely in excess of oxygen or air. (Symbol: Δ_CH°).

→ Enthalpy of atomization (Δ_aH°): It is the enthalpy change on breaking one mole of bonds completely to obtain atoms in the gas phase.
CH₄(g) → C(g) + 4H(g); Δ_aH° = 1665 kJ mol^-1

Bond Enthalpy (Δbond H°): Two different terms are used
1. Bond dissociation enthalpy: It is the change in enthalpy when one mole of covalent bonds of a gaseous covalent compound is broken to form products in the gas phase.
Cl₂(g) → 2Cl(g); Δ_Cl-Cl H° = 242 kJ mol^-1

It is for diatomic molecules like H₂, Cl₂, O₂ in gas phase.
For polyatomic molecules the term used is the mean bond enthalpy. Consider the reaction:
CH₄(g) → C(g) + 4H(g); Δ_aH° = 1665 kJ mol^-1,
Δ_C-H° = (Δ_aH°) = \(\frac{1}{4}\)(1665 kJ mol^-1)
= 416 kJ mol^-1

Thus the mean C-H bond enthalpy in methane is 416 kJ mol^-1.
→ Enthalpy of Solution (Δ_Sol H°): It is the enthalpy change when one mole of it dissolves in a specified amount of solvent.

→ Enthalpy of Solution at infinite dilution: It is the enthalpy change observed on dissolving the substance in an infinite amount of the solvent when the interactions between the ions (or solute molecules) are negligible.

→ Lattice Enthalpy: The lattice enthalpy of an ionic compound is the enthalpy change that occurs when one mole of an ionic compound dissociates into its ions in a gaseous state.
Na⁺Cl^–(g) → Na+(g) + Cb(g); Δ_latticeH° = + 788 kJ mol^-1

→ Bom-Haber Cycle: It is used to determine the lattice enthalpies. Let us calculate the lattice enthalpy of Na+Cl-(s) by the following steps given below:

1. Na(s) → Na(g); Δ_subH° = 108.4 kJ mol^-1
2. Na(g) → Na⁺(g) + e^–(g); Δ_iH° = 496 kJ mol^-1
3. Cl₂(g) → Cl(g); Δ_bondH° – 121 kJ mol^-1
4. Cl(g) + e^–(g) → Cl^–(g); Δ H° = – 348.6 kJ mol^-1
5. Na+(g) + Cl^–(g) → Na⁺Cl^–(s); Δ_latticeH° = U

Heat of formation of.NaCl(s) is foirnd to be 411.2 kJ mol^-1
Na(s) + \(\frac{1}{2}\) Cl₂(g) → NaCl(s); Δ_FH° = – 411.2 kJ mol^-1

Applying Hess’s Law
-411.2 = 108.4 + 121 + 496 – 348.6 + U
or U = – 788 kJ

Thus, lattice energy for NaCl(s) has a large negative value. This explains why the compound NaCl(s) is highly stable.

→ Spontaneous Process: A spontaneous process is an irreversible process and may only be reversed by some external agency.

A decrease in enthalpy is one of the contributing factors for the spontaneity of a process, but it is not true for all cases.

→ Entropy: It is a measure of disorder or randomness of the system like internal energy (U) and enthalpy (H), entropy (S) is a state function.
Change in entropy ΔS = S₂ – S₁
= ΣS_Products – ΣS_reactants
ΔS is related with q and T for a reversible reaction as
ΔS = \(\frac{q_{rev}}{T}\)

For a spontaneous process: The total entropy change (ΔS_total) for the system and surroundings is > 0, i.e.,
ΔS_total = ΔS_system + ΔS_surf > 0

For a system in equilibrium, the entropy is maximum and change in entropy, ΔS = 0

→ Important Note: For both reversible and irreversible expansion of an ideal gas under isothermal conditions (T = constant) ΔU – 0, but ΔS_total, i.e., ΔS_sys+ ΔS_surr is 0 for a reversible process, but not zero for an irreversible process. Thus ΔU does not discriminate between reversible and irreversible processes whereas ΔS does.

→ Gibbs Energy (or Gibbs function): Gibbs energy (G) is an extensive property and it is a state function.
It is the thermodynamic quantity of a system, the decrease in whose value during a process is equal to the maximum possible useful work that can be obtained from the system.

Mathematically G = H – TS
where H is the heat content, T is the absolute temperature and S is the entropy of the system
ΔG = ΔH – TΔS
where ΔG is the change in Gibbs energy, ΔH is the enthalpy change, ΔS is the change in entropy. The above equation is called Gibbs-Helmholtz Equation.
-ΔG = W_{non-expansion} = W_useful
or
– ΔG = W_max

1. If ΔG is negative, the process will be spontaneous.
2. If ΔG = 0, the process is in. equilibrium.
3. If ΔG is positive, the direct process is non-spontaneous; the reverse process may be spontaneous.

Standard Gibbs energy change is related to the equilibrium constant by
Δ_rG° = – RT ln K, where K is equilibrium constant
or
Δ_rG° = – 2.303 RT log K.