CBSE Class 9

On this page, you will find Circles Class 9 Notes Maths Chapter 11 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 11 Circles will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 11 Notes Circles

Circles Class 9 Notes Understanding the Lesson

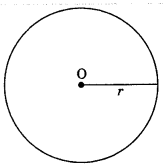
Circle is the collection of all points in a plane, which are equidistant from a fixed point in the plane. The fixed point is called the centre O and the given distance is called the radius r of the circle.

Concentric circles: Circles having same centre and different radii are called concentric circles.

Arc: A continuous piece of a circle is called an arc of the circle.

Chord: A line segment joining any two points on a circle is called the chord of the circle.

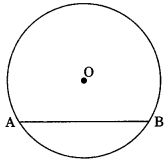
Diameter: A chord passing through the centre of a circle is called the diameter of the circle.

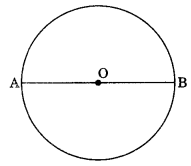
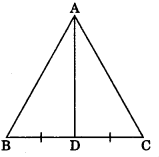
• Semicircle: A diameter of a circle divides it into two equal parts which are arc. Each of these two arcs is called semicircle.
• Angle of semicircle is right angle.
• If two arcs are equal, then their corresponding, chords are also equal.

Theorem 10.1: Equal chords of a circle subtend equal angle at the centre of the circle.
Theorem 10.2: If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
Theorem 10.3: The perpendicular drawn from centre to the chord of circle bisects the chord.

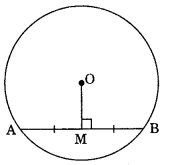
Theorem 10.4: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord. Theorem 10.5: There is one and only one circle passing through three non-collinear points.
Theorem 10.6: Equal chords of circle are equidistant from centre.

Theorem 10.7: Chords equidistant from the centre of a circle are equal in length.

• If two circles intersect in two points, then the line through the centres is perpendicular to the common chord.

Theorem 10.8: The angle subtended by an arc at the centre of circle is twice the angle subtended at remaining part of circumference.
Theorem 10.9: Any two angles in the same segment of the circle are equal.
Theorem 10.10: If a line segment joining two points subtends equal angles at two other points on the same side of the line containing the line segment, the four points lie on a circle (i.e., they are concyclic).

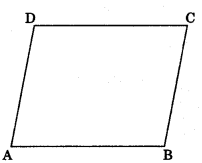
Cyclic Quadrilateral: If all the vertices of a quadrilateral lie on the circumference of circle, then quadrilateral is called cyclic.

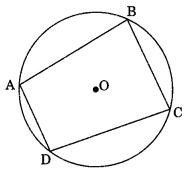
Theorem 10.11: In a cyclic quadrilateral the sum of opposite angles is 180°.
Theorem 10.12: In a quadrilateral if the sum of opposite angles is 180°, then quadrilateral is cyclic.

• The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

On this page, you will find Areas of Parallelograms and Triangles Class 9 Notes Maths Chapter 10 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 10 Areas of Parallelograms and Triangles will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 9 Notes Areas of Parallelograms and Triangles

Areas of Parallelograms and Triangles Class 9 Notes Understanding the Lesson

1. Area of a parallelogram = base x height
= DC x AE

2. Area of a triangle = \(\frac{1}{2}\)base x height
\(\frac{1}{2}\) BC x AD

3. Area of a trapezium = x (Sum of parallel sides) x Distance between them
\(\frac{1}{2}\) (AB + DC) x AE

4. Area of a rhombus =\(\frac{1}{2}\) \(\frac{1}{2}\) x product of diagonals A B
\(\frac{1}{2}\) x AC x BD

5. Two figures are said to be on the same base and between the same parallels, if they have a common side (base) and the vertices (or the vertex) opposite to the common base of each figure He on a line parallel to the base.

Theorem 9.1: Parallelograms on the same base and between the same parallels are equal in area.
ar(ABCD) = ar(EFCD)

Theorem 9.2: Triangles on the same base and between the same parallels are equal in area.
ar(ΔABC) = ar(ΔPBC)

Theorem 9.3: Two triangles having the same base and equal areas lie between the same parallels.
If a triangle and a parallelogram are on the same base and between the same parallels, then

(i) Area of triangle = \(\frac{1}{2}\) x area of the parallelogram
ar(ΔPDC) = \(\frac{1}{2}\) ar(||gmABCD)

(ii) A diagonal of parallelogram divides it into two triangles of equal areas.
ar(ΔABD) = ar(ΔBCD)

(iii) If each diagonal of a quadrilateral separates it into two triangles of equal area, then the quadrilateral is a parallelogram.

(iv) A median AD of a ΔABC divides it into two triangles of equal areas.
ar(ΔABD) = ar(ΔACD)

On this page, you will find Quadrilaterals Class 9 Notes Maths Chapter 9 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 9 Quadrilaterals will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 9 Notes Quadrilaterals

Quadrilaterals Class 9 Notes Understanding the Lesson

Quadrilateral
A plane figure bounded by four line segments is called quadrilateral.

Properties:

• It has four sides.
• It has four vertices or comers.
• It has two diagonals.
• The sum of four interior angles is equal to 360°.

In quadrilateral ABCD, AB, BC, CD and DA are sides; AC and BD are diagonals and
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

Types of Quadrilaterals
1. Parallelogram: A quadrilateral whose each pair of opposite sides are parallel.

• AB || DC
• AD || BC

2. Rectangle: A parallelogram whose one angle is 90°. Diagonals are equal.

3. Rhombus: A parallelogram whose adjacent sides are equal.
Note: Diagonal bisect each other at 90°.

4. Square: A rectangle whose adjacent sides are equal (four sides are equal). Diagonal bisect each other at 90°.

5. Trapezium: A quadrilateral whose one pair of opposite sides are parallel. AB || DC

6. Kite: It has two pair of adjacent sides that are equal in length but opposite sides are unequal.

Note:

• One of the diagonal bisects the other at right angle.
• One pair of opposite angles are equal.

Properties of a Parallelogram

• Opposite sides are equal.
  e.g., AB = DC and AD = BC
• Consecutive angles are supplementary.
  e.g., ∠A + ∠D = 180°
• Diagonals of parallelogram bisect each other.
• Diagonal divide it into two congruent triangles. A B

Theorem 8.1: A diagonal of a parallelogram divides it into two congruent triangles.
Theorem 8,2: In a parallelogram, opposite sides are equal.
Theorem 8.3: If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Theorem 8.4: In a parallelogram, opposite angles are equal.
Theorem 8.5: If in a quadrilateral, each pair of opposite angles of a quadrilateral is equal then it is a parallelogram.
Theorem 8.6: The diagonals of a parallelogram bisect each other.
Theorem 8.7: If the diagonals of quadrilateral bisect each other, then it is a parallelogram.
Theorem 8.8: A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.

Mid-point Theorem
Theorem 8.9: The line segment joining the mid-points of two sides of a triangle is parallel to the third.
Given: A triangle ABC, E and F are mid-points of sides AB and AC respectively.
i.e., AE = EB and AF = FC
To Prove:
(i) EF || BC
(ii) EF = \(\frac{1}{2}\) BC
Construction: Draw a line through C parallel to AB and extend EF which intersect at D.

Proof: (i) In AAEF and ACDF,
AF = CF (F is the mid-point of AC)
∠AFE = ∠CFD (Vertically opposite angles)
∠EAF = ∠DCF (Alternate interior angles)
∴ ΔAEF = ΔCDF (by ASA congruency)
∴ AE = CD (by CPCT)
and BE = CD (AE = BE)
EF = FD (by CPCT);
Hence, BCDE is a parallelogram.
ED || BC )
∴ EF || BC

(ii) BCDE is a parallelogram.
DE = BC
EF + FD = BC
2EF = BC
EF=\(\frac{1}{2}\)BC

Converse of Mid-Point Theorem

Theorem 8.10: The line drawn through the mid-point of one side of a triangle, parallel to another side  bisects the third side. ‘
Given: ΔABC in which E is the mid point of AB.
EF || BC
To Prove: AF = FC
Construction: Draw CD || AB and extend EF which intersect at D.
Proof: EF || BC
∴ ED || BC
AB || CD
⇒ BE || CD
∴ BCDE is a parallelogram.

Now in ΔAEF and ΔCDF, ∠AFE = ∠CFD (Vertically opposite angles)
∠EAF = ∠DCF (Alternate interior angles)
AE = CD (BE = AE opposite side of a parallelogram and BE = CD
∴ AAEF ≅ ACDF (by AAS congruency)
Hence AF = FC (by CPCT)

On this page, you will find Linear Equations in Two Variables Class 9 Notes Maths Chapter 8 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 8 Linear Equations in Two Variables will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 8 Notes Linear Equations in Two Variables

Linear Equations in Two Variables Class 9 Notes Understanding the Lesson

1. Equation: An equation is a mathematical statement that two things are equal. It consists of two expressions one on each side of an equals sign. For example,7x + 9 = 0

2. An equation in a statement of an equality containing one or more variables.
7x + 3y = 10

3. Linear equation in one variable: A linear equation or first degree equation, in the single variable x is an equation that can be written in the form ax + b = 0 where a, and b are equal numbers, when a≠0.
Examples:

• 2x+3=0
• 3y + 4 = \(\frac{y}{3}\)
• 7x-\(\frac{9}{2}\) =0
• 3x -7y = 73

These equations are solved by applying the properties of real numbers and properties of equality.

4. Solution of a linear equation: The value of the variable which when substituted in place of variable makes both sides of the given equation equal, is called the solution of given equation. These values of variables is also known as root of the equation.
Example:
3x + 4y – 5
Let x – 3, and y = -1
Putting x- 3 and y = -1 in the given equation 3 x 3 + 4 x (-1) = 5
⇒ 9 – 4 = 5
⇒ 5 = 5
∴ LHS = RHS
Hence (3, -1) is a solution of given equation.

5. Linear equation in two variables: A linear equation in two variables is a first degree equation which can be written in the form ax + by + c – 0 and a, b both are non-zero real number. Where a, b and c are real numbers.
Examples:

• 3x + 2y – 9 = 0
• 7x – 4y + 6 = 0

6. Graph of a Linear Equation in two Variables
Graph of a linear equation in two variables is a straight line.

Steps of graphing a line

• If the equation is not in slope intercept form, i.e., y = mx + c, then write the equation in such form.
• Plot they intercept at (0, 6).
• Plot two or three more points by counting the rise and run from the y intercepts.

While solving the equation we should put the following points in our mind.                         •

• We should add or subtract the same number on both the sides of the equation.
• We should multiply or divide by the same non-zero real number on both sides of the equation.

Note:

• A linear equation in one variable has only one solution.
• A linear equation in two variables has infinitely many solutions.

(a) If the slope is positive, count upward for the rise and to the right for the run (also down and left)
Example;    y = \(\frac{2}{3}\) x + 1

(b) If the slope is negative, count downward for the rise and to the right for the run (also up and left)                  Example:    y =\(\frac{2}{3} \)x + 1

7. Draw a line through the points and place arrows on the ends. Extend the line to cover the whole grid (not just connect the two points)

Note:

• The graph of every first degree equation in two variables is a straight line.
• Equation of x-axis is y = 0 (:Hi) Equation of y-axis is x = 0
• The graph of x = a is a straight line parallel to y-axis.
• The graph of y = b is a straight line parallel to x-axis.
• Graph of the equation y = mx (i.e., has no intercepts) is a straight line passing through origin.
  Every point which lies on the graph of the linear equation in two variables is a solution of linear equation.
• Graph of linear equation in one variable
• If given equation is in variable x only then its value represented graphically is on x-axis.
• If the given equation is in variable y only then its value represented graphically is on y-axis.

8. Graph of linear equation in one variable

• If given equation is in variable x only then its value represented graphically is on x-axis.
• If the given equation is in variable y only then its value represented graphically is on y-axis.

For example, 2x = 5 ⇒ x=\(\frac{5}{2}\)
Representation: In one variable,

In Cartesian plane or in two variables,

Draw a line through \(x=\frac{5}{2}\) parallel to y-axis. In such representation, the equation has many solutions.

On this page, you will find Heron’s Formula Class 9 Notes Maths Chapter 7 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 7 Heron’s Formula will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 7 Notes Heron’s Formula

Heron’s Formula Class 9 Notes Understanding the Lesson

1. Area of triangle with base ‘b’ and altitude ‘h’ is
Area = \(\frac{1}{2}\)(b x h)

2. Area of an isosceles triangle with equal sides ‘a’ each and third side b is
Area \(=\frac{b}{4} \sqrt{4 a^{2}-b^{2}}\)

3. Area of an equilateral triangle with side ‘a’ each is
Area=\(\frac{\sqrt{3}}{4} a^{2}\)

4. Area of a triangle by Heron’s formula when sides a, b and c are given is
Area = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Where s = semi-perimeter = \frac{a+b+c}{2}

5. Area of rhombus
Area= \(\frac{1}{2} d_{1} \times d_{2}\)
where d₁ and d₂ are the lengths of its diagonals.

6. Area of trapezium
Area=\(\frac{1}{2}\) (a+b) h
where a and b are parallel sides and h is distance between two parallel sides.