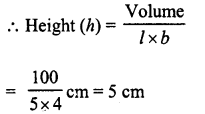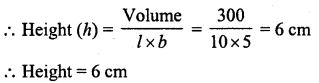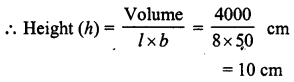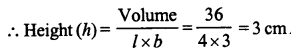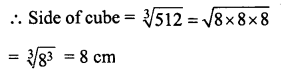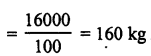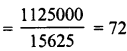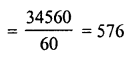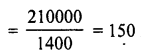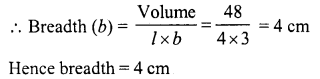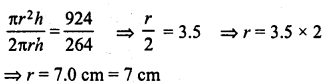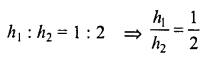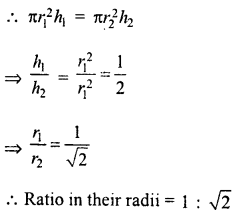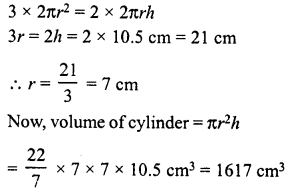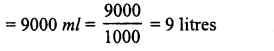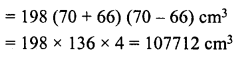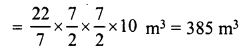CBSE Class 8

RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4

Question 1.
Find the volume in cubic metres (cu.m) of each of the cuboids whose dimensions are :
(i) length = 12 cm, breadth = 10 m, height = 4.5 m
(ii) length = 4 m, breadth = 2.5 m, height = 50 cm
(iii) length = 10 m, breadth = 25 dm, height = 25 cm.
Solution:
(i) Length of cuboid (l) = 12 m
Breadth (b) = 10m
and height (h) = 4.5 m
∴Volume = l x b x h = 12 x 10 x 4.5 m³
= 540 m³
(ii) Length of cuboid (l) = 4 m
Breadth (b) = 2.5m
Height (h) = 50 cm = 0.5 m
∴ Volume = l x b x h = 4 x 2.5 x 0.5 = 5 m³
(iii) Length of cuboid (l) = 10 m
Breadth (b) = 25 dm = 2.5 m
Height (h) = 25 cm 0.25 m
∴ Volume = l x b x h = 10 x 2.5 x 0.25 m³ = 6.25 m³

Question 2.
Find the volume in cubic decimetre of each of the cubes whose side is
(i) 1.5 m
(it) 75 cm
(iii) 2 dm 5 cm
Solution:
(i) Side of cube (a) = 1.5 m
∴ Volume = a³ = (1.5)³ m³
= 1.5 x 1.5 x 1.5 m³ = 3.375 m³
= 3.375 x 1000 = 3375 dm³
(ii) Side of cube (a) = 75 cm = 7.5 dm
∴ Volume = a³ = (7.5)3 dm³
= 421.875 dm³
(iii) Side of cube (a) = 2 dm 5 cm = 2.5 dm
∴ Volume = (a)³ = (2.5)³ dm³
= 15.625 dm³

Question 3.
How much clay is dug out in digging a well measuring 3m by 2m by 5m?
Solution:
Length of well (l) = 3m
breadth (b) = 2 m
and height (depth) (h) = 5 m
Volume of earth dug out = l x b x h = 3 x 2 x 5 = 30m³

Question 4.
What will be the height of a cuboid of volume 168 m³, if the area of its base is 28 m² ?
Solution:
Volume of a cuboid = 168 m³
Area of its base l.e., l x b = 28 m³

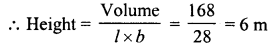
Question 5.
A tank is 8 m long, 6 m broad and 2 m high. How much water can it contain ?
Solution:
Length of tank (l) = 8 m
Breadth (b) = 6 m
Height (h) = 2 m
∴ Volume of water in the tank = l x b x h = 8 x 6 x 2 = 96 m³
= 96 x 1000 = 96000litres (∵1m³ = 1000litre)

Question 6.
The capacity of a certain cuboidal tank is 50000 litres of water. Find the breadth of the tank if its height and length are 10 m and 2.5 m respectively.
Solution:
Capacity of water in the tank = 50000 litres
∴ Volume of water = 50000 x \(\frac { 1 }{ 1000 }\) = 50 m³ (1000 l = 1 m³)
Height of tank (h)= 10 m
and length (l) = 2.5 m
Volume 50

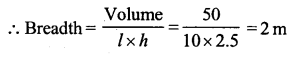
Question 7.
A rectangular diesel tanker is 2 m long, 2 m wide and 40 cm deep. How many litres of diesel can it hold ?
Solution:
Length of tanker (l) = 2 m
Breadth (b) = 2m
Depth (h) = 40 cm = 0.4 m
∴ Volume = l x bx h = 2 x 2 x 0.4=1.6m³
Quantity of diesel = 1.6 x 1000 litres (1 m³= 1000 l)
= 1600 litres

Question 8.
The length, breadth and height of a room are 5 m, 4.5 m and 3 m, respectively. Find the volume of the air it contains.
Solution:
Length of room (l) = 5 m
Breadth (6) = 4.5 m
and height (h) = 3 m
∴ Volume of air it contains
= l x b x h = 5 x 4.5 x 3 m³
= 67.5 m³

Question 9.
A water tank is 3 m long, 2 m broad and 1 m deep. How many litres of water can it hold ?
Solution:
Length of tank (l) = 3 m
Breadth (b) = 2 m
and depth (h) = 1 m
∴ Volume of tank = l x b x h
= 3 x 2 x 1 = 6 m³
∴ Quantity of water it can contains
= 6 x 1000 litres = 6000 litres (1 m³= 1000 litres)

Question 10.
How many planks each of which is 3 m long, 15 cm broad and 5 cm thick can be prepared from a wooden block 6 m long, 75 cm broad and 45 cm thick ?
Solution:
Length of wooden block (l) = 6 m
Width (b) = 75 cm = 0.75 m
Thickness (h) = 45 cm = 0.45 m
∴ Volume = l x b x h = 6 x 0.75 x 0.45 m³
Length of plank (l) = 3 m
Breadth (b) = 15 cm = 0.15 m
Thickness (h) = 5 cm = 0.05 m
∴ Volume = 3 x 0.15 x 0.05 m³
Number of planks

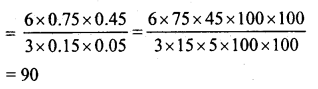
Question 11.
How many bricks each of size 25 cm x 10 cm x 8 cm will be required to build a wall 5 m long, 3 m high and 16 cm thick assuming that the volume of sand and cement used in the construction is negligible ?
Solution:
Size of one brick = 25 cm x 10 cm x 8 cm
∴ Volume of one brick = 25 x 10 x 8 cm³

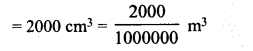
Length of wall (l) = 5 m
Width (b) = 0.16 m
Height (h) = 3 m
∴ Volume of wall = l x b x h
= 5 x 0.16 x 3 m³ = 2.4 m³
∴ Number of bricks required

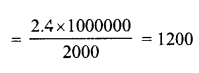
Question 12.
A village, having a population of 4000 requires 150 litres water per head per day. It has a tank which is 20 m long, 15 m broad and 6 m high. For how many days the water of this tank will last ?
Solution:
Total population of a village = 4000
Water required for each person for one day = 150 litres
∴ Water required for 4000 persons for one day = 150 x 4000 = 600000 litres
Length of tank (l) = 20 m
Breadth (b) = 15 m
Height (h) = 6 m
∴ Volume of tank = l x b x h = 20 x 15 x 6 m³ = 1800 m³
Capacity of water in the tank = 1800 x 1000 l= 1800000l (1 m³ = 1000 l)
∴ Number of days, the water will last

Question 13.
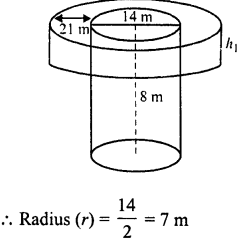
A rectangular field is 70 m long and 60 m broad. A well of dimensions 14 m x 8 m x 6 m is dug outside the field and the earth dugout from this well is spread evenly on the field. How much will the earth level rise ?
Solution:
Length of well (l) = 14 m
Breadth (A) = 8m
Depth (A) = 6m
∴ Volume of earth dugout = l x bx h
= 14 x 8 x 6 = 672 m³ Length of field = 70 m
and breadth = 60 m
Let h be the height of earth spread over
Then 70 x 60 x h = 672
⇒ h = \(\frac { 672 }{ 70×60 }\) = 0.16m
∴ Height of earth = 0.16 m = 16 cm

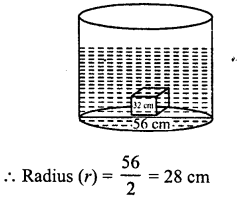
Question 14.
A swimming pool is 250 m long and 130 m wide. 3250 cubic metres of water is pumped into it. Find the rise in the level of water.
Solution:
Volume of water = 3250 m³
Length of pool (l) = 250 m
Breadth (b)= 130 m
∴ Height of water level

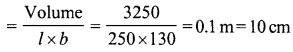
Question 15.
A beam 5 m long and 40 cm wide contains 0.6 cubic metres of wood. How thick is the beam?
Solution:
Volume of wood of the beam = 0.6 m³ = 600000
Length of beam (l) = 5 m = 500 cm
Breadth (b) = 40 cm

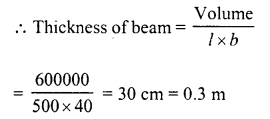
Question 16.
The rainfall on a certain day was 6 cm. How many litres of water fell on 3 hectares of field on that day ?
Solution:
Area of the field = 3 hectares
= 3 x 10000 square metres
= 30000 square metres
Height of rainfall = 6 cm = m³

Question 17.
An 8 m long cuboidal beam of wood when sliced produces four thousand 1 cm cubes and there is no wastage of wood in this process. If one edge of the beam is 0.5 m, find the third edge.
Solution:
Length of cuboidal beam (l) = 8 m = 800 cm
Number of cubical sliced = 4000
Edge of each cube = 1 cm
Volume of beam = 4000 (1)³ cm³ = 4000 cm³
One edge of the beam = 0.5 m = 50 cm.

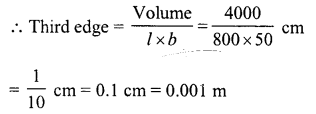
Question 18.
The dimensions of a metal block are 2.25 m by 1.5 m by 27 cm. It is melted and recast into cubes, each of the side 45 cm. How many cubes are formed ?
Solution:
Dimensions of metal block = 2.25 m x 1.5 m x 27 cm
∴ Volume = 2.25 x 1.5 x 0.27 m³
= 225 x 150 x 27 cm³ = 911250 cm³
Side of each cube (a) = 45 cm
∴ Volume of one cube = a³ = (45)³ cm³ = 91125 cm³
∴ Number of cubes = \(\frac { 911250 }{ 91125 }\) = 10

Question 19.
A solid rectangular piece of iron measures 6 m by 6 cm by 2 cm. Find the weight of this piece if 1 cm3 of iron weighs 8 gm.
Solution:
Dimensions of a piece of rectangular iron = 6m x 6cm x 2cm
∴ Volume = 600 x 6 x 2 cm³ = 7200 cm³
Weight of 1 cm³ = 8 gm
∴ Total weight of the piece = 7200 x 8 gm
= 57600 gm = \(\frac { 57600 }{ 1000 }\) kg = 57.6 kg

Question 20.
Fill in the blanks in each of the following so as to make the statement true :
(i) 1 m³ = ……… cm³
(ii) 1 litre = …….. cubic decimetre
(iii) 1 kl = …… m³
(iv) The volume of a cube of side 8 cm is …….. .
(v) The volume of wooden cuboid of length 10 cm and breadth 8 cm is 4000 cm3. The height of the cuboid is …….. cm
(vi) 1 cu.dm = …….. cu.mm
(vii) 1 cu.km = ……cu.m
(viii) 1 litre =…….. cu.cm
(ix) 1 ml = ……… cu.cm
(x) 1 kl = ……… cu.dm = ……. cu.cm.
Solution:
(i) 1 m³ = 1000000 or 10⁶ cm³
(ii) 1 litre = 1 cubic decimetre
(iii) 1 kl = 1 m³
(iv) The volume of a cube of side 8 cm is 512 cm³ (V = a³ = 8 x 8 x 8 = 512 cm³)
(v) The volume of a wooden cuboid of length 10 cm and breadth 8 cm is 4000 cm³. The height of the cuboid is 50 cm

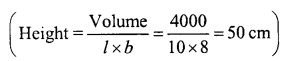
(vi) 1 cu.dm = 1000000 cu mm = 10⁶ cu.mm
(vii) 1 cu.km = 1000 x 1000 x 1000 cu.m = 109 cu.m
(viii) 1 litre = 1000 cu.cm = 10³ cu.cm
(ix) 1 ml = 1 cu.cm
(x) 1 kl = 1000 cu.dm = 100 x 100 x 100 cu.cm = 10⁶ cu.cm

Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 21 Mensuration II (Volumes and Surface Areas of a Cubiod and a Cube) Ex 21.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4

Question 1.
Find the volume of a cuboid whose
(i) length = 12 cm, breadth = 8 cm, height = 6 cm
(ii) length = 1.2 m, breadth = 30 cm, height = 15 cm
(iii) length = 15 cm, breadth = 2.5 dm, height = 8 cm

Solution:
In a cuboid,
(i) Length (l) = 12 cm
Breadth (b) = 8 cm
Height (h) = 6 cm
∴ Volume = Ibh = 12 x 8 x 6 cm³ = 576 cm³
(ii) Length (l) = 1.2 m = 120 cm
breadth (6) = 30 cm
Height (h) = 15 cm
∴ Volume = Ibh = 120 x 30 x 15 cm³ = 54000 cm³
(iii) Length (l) = 15 cm
Breadth (b) = 2.5 dm = 25 cm
Height (h) = 8 cm
∴ Volume = Ibh
= 15 x 25 x 8 cm³ = 3000 cm²

Question 2.
Find the volume of the cube whose side is
(i) 4 cm
(ii) 8 cm
(iii) 1.5 dm
(iv) 1.2 m
(v) 25 mm.
Solution:
(i) Side of a cube (a) = 4 cm
∴ Volume = a3 = (4)³ cm³ = 4 x 4 x 4 = 64 cm³

(ii) Side of cube (a) = 8 cm
∴ Volume = a3 = (8)³ 4 cm
= 8 x 8 x 8 cm³ = 512 cm³
(iii) Side of cube (a) = 1.5 dm = 15 cm
∴ Volume = a³ = (1.5)3 dm² = (15)³ cm³
= 15 x 15 x 15 = 3375 cm³
(iv) Side of cube (a) = 1.2 m = 120 cm
∴ Volume = a³ = (120)³ cm³
= 120 x 120 x 120 = 1728000 cm³
(v) Side of cube (a) = 25 mm = 2.5 cm.
∴ Volume = a³ = (2.5)³ cm³
= 2.5 x 2.5 x 2.5 cm³ = 15.625 cm³

Question 3.
Find the height of a cuboid of volume 100 cm3 whose length and breadth are 5 cm and 4 cm respectively.
Solution:
Volume of a cuboid =100 cm³
Length (1) = 5 cm
and breadth (b) = 4 cm

Question 4.
A cuboidal vessel is 10 cm long and 5 cm wide, how high it must be made to hold 300 cm3 of a liquid ?
Solution:
Volume of the liquid in the vessel = 300 cm³
Length (l)= 10 cm
Breadth (b) = 5 cm

Question 5.
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 litres of milk ?
Solution:
Capacity of milk = 4 litres
∴ Volume of the container = 4 x 1000 cm³ = 4000 cm³
Length (l) = 8 cm
Width (b) = 50 cm

Question 6.
A cuboidal wooden block contains 36 cm³ wood. If it be 4 cm long and 3 cm wide, find its height.
Solution:
Volume of wooden cuboid block = 36 cm³
Length (l) = 4 cm
Breadth (b) = 3 cm

Question 7.
What will happen to the volume of a cube, if its edge is (i) halved (ii) trebled ?
Solution:
Let side of original cube = a cm
∴ Volume = a³ cm³
(i) In first case,

(ii) In second case, when side (edge) is trebled, then side = 3a
∴ Volume = (3a)³ = 27a³
∴ It will be 27 times

Question 8.
What will happen to the volume of a cuboid if its (i) Length is doubled, height is same and breadth is halved ? (ii) Length is doubled, height is doubled and breadth is same ?
Solution:
Let l, b and h be the length, breadth and height of the given cuboid respectively.
∴ Volume = lbh.
(i) Length is doubled = 21

∴ The volume will be the same.
(ii) Length is doubled = 21
breadth is same = b height is doubled = 2h
∴ Volume = 2l x b x 2h = 4 lbh
∴ Volume will be 4 times

Question 9.
Three cuboids of dimensions 5 cm x 6 cm x 7 cm, 4 cm x 7 cm * 8 cm and 2 cm x 3 cm x 13 cm are melted and a cube is made. Find the side of cube.
Solution:
Dimensions of first cuboid = 5 cm x 6 cm x 7 cm
∴ Volume = 5 x 6 x 7 = 210 cm³
Dimensions of second cuboid = 4 cm x 7 cm x 8 cm
∴ Volume = 4x 7 x 8 = 224 cm³
Dimensions of third cuboid = 2 cm x 3 cm x 13 cm
∴ Volume = 2 x 3 x 13 = 78 cm³
Total volume of three cubes = 210 + 224 + 78 cm3 = 512 cm³
∴ Volume of cube = 512 cm³

Question 10.
Find the weight of solid rectangular iron piece of size 50 cm x 40 cm x 10 cm, if 1 cm3 of iron weighs 8 gm.
Solution:
Dimension of cuboidal iron piece = 50 cm x 40 cm x 10 cm
∴ Volume = 50 x 40 x 10 = 20000 cm³
Weight of 1 cm³ = 8 gm
∴ Total weight of piece = 20000 x 8 gm

Question 11.
How many wooden cubical blocks of side 25 cm can be cut from a log of wood of size 3 m by 75 cm by 50 cm, assuming that there is no wastage ?
Solution:
Length of log (l) = 3 m = 300 cm.
Breadth (b) = 75 cm
and height (h) = 50 cm
∴ Volume of log = lbh = 300 x 75 x 50 cm3 = 1125000 cm³
Side of cubical block = 25 cm
∴ Volume of one block = a² = 25 x 25 x 25 cm3 = 15625 cm³
∴ Number of blocks to be cut out

Question 12.
A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it, beads of volume 1.5 cm² each are to be made. Find the number of beads that can be made from the block ?
Solution:
Length of block (l) = 9 cm
Breadth (b) = 4 cm
and height (h) = 3.5 cm
∴ Volume = l x b x h = 9 x 4 x 3.5 cm³ = 126 cm³
Volume of one bead = 1.5 cm³
∴ Number of beads = \(\frac { 126 }{ 105 }\) = 84

Question 13.
Find the number of cuboidal boxes measuring 2 cm by 3 cm by 10 cm which can be stored in a carton whose dimensions are 40 cm, 36 cm and 24 cm.
Solution:
Length of cuboidal box (l) = 2 cm
breadth (b) = 3 cm
and height (h) = 10 cm
∴ Volume = lx b x h = 2 x 3 x 10 = 60 cm³
Volume of carton = 40 x 36 x 24 cm³
= 34560 cm³
∴ Number of boxes to be height in the carton

Question 14.
A cuboidal block of solid iron has dimensions 50 cm, 45 cm and 34 cm. How many cuboids of size 5 cm by 3 cm by 2 cm can be obtained from the block ? Assume cutting causes no wastage.
Solution:
Dimensions of block = 50 cm, 45 cm, 34 cm
∴ Volume = 50 x 45 x 34 = 76500 cm³
Size of cuboid = 5 cm x 3 cm x 2 cm
∴ Volume of cuboid =  5 x 3 x 2 = 30 cm³

Question 15.
A cube A has side thrice as long as that of cube B ? What is the ratio of the volume of cube A to that of cube B ?
Solution:
Let side of cube B = a
Then Volume = a³
and side of cube A = 3a
Volume = (3a)³ = 3a x 3a x 2a = 27a³
∴ Ratio of volume’s A and B = 27a³ : a³
= 27 : 1

Question 16.
An ice-cream brick measures 20 cm by 10 cm by 7 cm. How many such bricks can be stored in a deep fridge whose inner dimensions are 100 cm by 50 cm by 42 cm ?
Solution:
Dimensions of ice cream brick = 20 cm x 10 cm x 7 cm
∴ Volume = 20 x 10 x 7 cm³ = 1400 cm³
Dimensions of inner of fridge = 100 cm x 50 cm x 42 cm = 210000 cm³
∴ Number of bricks to be kept in the fridge

Question 17.
Suppose that there are two cubes, having edges 2 cm and 4 cm, respectively. Find the volume V₁ and V₂ of the cubes and compare them.
Solution:
Side of first cube (a) = 2 cm
∴ Volume (V₁) = a³ = (2) = 8 cm³
Similarly side of second cube = 4 cm
and volume (V₂) = (4)³ = 64 cm³
Now V₂ = 64 cm³ = 8 x 8 cm³
= 8 x V₁
⇒ V₂ = 8V₁

Question 18.
A tea-packet measures 10 cm x 6 cm x 4 cm.How many such tea-packets can be placed in a cardboard box of dimensions 50 cm x 30 cm x 0.2 m ?
Solution:
Dimensions of tea-packet = 10cm x 6cm x 4 cm
∴ Volume =10 x 6 x 4 = 240 cm³
Dimensions of box = 50 cm x 30 cm x 0.2 m
= 50 cm x30 cm x20 cm
∴ Volume = 50 x 30 x 20 = 30000 cm³
∴ Number of tea-packets to be kept = \(\frac { 30000 }{ 240 }\)

Question 19.
The weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
Solution:
Dimensions of a metal block = 5 cm x 4 cm x 3 cm = 5 x 4 x 3 = 60 cm³
Dimensions of a second block = 15 cm x 8 cm x 3 cm = 15 x 8 x 3 = 360 cm³
But weight of first block = 1 kg
∴ Weight of second block
= \(\frac { 1 }{ 16 }\) x 360 = 6 kg

Question 20.
How many soap cakes can be placed in a box of size 56 cm x 0.4 m x 0.25 m, it the size of soap cake is 7 cm x 5 cm x 2.5 cm ?
Solution:
Size of box = 56 cm x 0.4 m x 0.25 m = 56 cm x 40 cm x 25 cm
∴ Volume = 56 x 40 x 25 cm³ = 56000 cm³
Size of a soap cake = 7 cm x 5 cm x 2.5 cm
∴ Volume = 7 x 5 x 2.5 cm³ = 87.5 cm³
∴ Number of cakes to be kept in the box
= \(\frac { 56000 }{ 87.5 }\) = 640

Question 21.
The volume of a cuboid box is 48 cm3. If its height and length are 3 cm and 4 cm respectively, find its breadth.
Solution:
Volume of cuboid box = 48 cm³
Length (l) = 4 cm
Height = (h) = 3 cm

Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 22 Mensuration III (Surface Area and Volume of a Right Circular Cylinder) Ex 22.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1
• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Question 1.
Find the volume of a cuboid whose
(i) r = 3.5 cm, h = 40 cm
(ii) r = 2.8 m, h = 15 m
Solution:
(i) Radius (r) = 3.5 cm
Height (h) = 40 cm
Volume of cylinder = πr²h

Question 2.
Find the volume of a cylinder, if the diameter (d) of its base and its altitude (h) are:
(i) d= 21 cm, h = 10 cm
(ii) d = 7 m, h = 24 m.
Solution:
(i) Diameter (d) = 21 cm

Question 3.
The area of the base of a right circular cylinder is 616 cm3 and its height is 25 cm. Find the volume of the cylinder.
Solution:
Base area of cylinder = 616 cm²
Height (h) = 25 cm.
∴ Volume = Area of base x height
= 616 x 25 cm³ = 15400 cm³

Question 4.
The circumference of the base of a cylinder is 88 cm and its height is 15 cm. Find the volume of the cylinder.
Solution:
Circumference of the base of cylinder = 88 cm
Let r be the radius

Question 5.
A hollow cylindrical pipe is 21 dm long. Its outer and inner diameters are 10 cm and 6 cm respectively. Find the volume of the copper used in making the pipe.
Solution:
Length (Height) of hollow cylindrical pipe = 21 dm = 210 cm
Inner diameter = 6 cm
Outer diameter = 10 cm

Question 6.
Find the (i) curved surface area (ii) total surface area and (iii) volume of a right circular cylinder whose height is 15 cm and the radius of the base is 7 cm
Solution:
Radius of the cylider (r) = 7 cm
and height (h) = 15 cm
(i) Curved surface area = 2πrh

Question 7.
The diameter of the base of a right circular cylinder is 42 cm and its height is 10 cm. Find the volume of the cylinder.
Solution:
Diameter of the base of cylinder = 42 cm

Question 8.
Find the volume of a cylinder, the diameter of whose base is 7 cm and height being 60 cm. Also, find the capacity of the cylinder in litres.
Solution:
Diameter of cylinder = 7 cm

Question 9.
A rectangular strip 25 cm x 7 cm is rotated about the longer side. Find the volume of the solid, thus generated.
Solution:
Size of rectangular strip = 25 cm x 7 cm
By rotating, about the longer side, we find a right circular cylinder,
then the radius of cylinder (r) = 7 cm

Question 10.
A rectangular sheet of paper 44 cm x 20 cm, is rolled along its length to form a cylinder. Find the volume of the cylinder so formed.
Solution:
Size of sheet of paper = 44 cm x 20 cm
By rolling along length, a cylinder is formed in which circumference of its base = 20 cm
and height (h) = 44 cm

Question 11.
The volume and the curved surface area of a cylinder are 1650 cm3 and 660 cm2 respectively. Find the radius and height of the cylinder.
Solution:
Volume of cylinder = 1650 cm³
and curved surface area = 660 cm²
Let r be the radius and h be the height of the cylinder, then

Question 12.
The radii of two cylinders are in the ratio 2 :3 and their heights are in the ratio 5 : 3. Calculate the ratio of their volumes.
Solution:
Ratio in radii = 2:3
and in heights = 5:3
Let r₁,h₁ and r₂, h₂ are the radii and heights of two cylinders respectively.

Question 13.
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1 : 2. Find the volume of the cylinder, if its total surface area is 616 cm².
Solution:
Ratio in curved surface are and total surface area =1 : 2
Let r be the radius and h be the height.
Then 2πrh : 2πr (h + r)= 1 : 2

Question 14.
The curved surface area of a cylinder is 1320 cm2 and its base has diameter 21 cm. Find the volume of the cylinder.
Solution:
Curved surface area of a cylinder = 1320 cm²
Diameter of base = 21 cm

Question 15.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. Find the total surface area of the cylinder, if its volume is 1617 cm³.
Solution:
Ratio between radius and height of a cylinder = 2:3
Volume = 1617 cm³
Let r be the radius and A be the height of the cylinder, then

Question 16.
The curved surface area of a cylindrical pillar is 264 m² and its volume is 924 m³. Find the diameter and the height of the pillar.
Solution:
Let r be the radius and A be the height of the cylinder, then
2πrh = 264 …(i)
and πr2h= 924 …(ii)
Dividing (ii) by (i),

Question 17.
Two circular cylinders of equal volumes have their heights in the ratio 1 : 2. Find the ratio of their radii.
Solution:
Volumes of two cylinders are equal.
Let r1, r2 are the radii and h₁, h₂ are their heights, then

Now, volume of first cylinder = πr₁²h₁
and Volume of second cylinder = πr₂²h₂
Their volumes are equal

Question 18.
The height of a right circular cylinder is 10.5 m. Three times the sum of the areas of its two circular faces is twice the area of the curved surface. Find the volume of the cylinder.
Solution:
Height of cylinder (A) = 10.5 m.
Let r be the radius, then
Sum of areas of two circular faces = 2π²
and curved surface area = 2πrh
According to the condition,

Question 19.
How many cubic metres of earth must be dug-out to sink a well 21 m deep and 6 m diameter ?
Solution:
Diameter of well = 6 m

Question 20.
The trunk of a tree is cylindrical and its circumference is 176 cm. If the length of the trunk is 3 m, find the volume of the timber that can be obtained from the trunk.
Solution:
Circumference of cylindrical trunk = 176 cm

Question 21.
A well is dug 20 m deep and it has a diameter of 7 m. The earth which is so dug out is spread out on a rectangular plot 22 m long and 14 m broad, what is the height of the platform so formed ?
Solution:
Diameter of the well = 7 m
∴ Radius (r) = \(\frac { 7 }{ 2 }\) m
Depth (h) = 20 m
= Volume of earth dug out = πr²h

Question 22.
A well with 14 m diameter is dug 8 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 14 m

Question 23.
A cylindrical container with diameter of base 56 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 32 cm x 22 cm x 14 cm. Find the rise in the level of the water when the solid is completely submerged.
Solution:
Diameter of the base of a cylindrical container = 56 cm

Dimensions of the rectangular solid = 32 cm x 22 cm x 14 cm
∴ Volume of solid = 32 x 22 x 14 cm³ = 9856 cm³
∴Volume of water rose up = 9856 cm³
Let h be the height of water, then πr²h = 9856

Question 24.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways Le., either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinders thus formed.
Solution:
Size of paper = 30 cm and 18 cm.

(i) By rolling length wise,
The circumference of base = 30 cm

Question 25.
The rain which falls on a roof 18 m long and 16.5 m wide is allowed to be stored in a cylindrical tank 8 m in diameter. If it rains 10 cm on a day, what is the rise of water level in the tank due to it.
Solution:
Length of roof (l) = 18 m
Breadth (b) = 16.5 m
Height of water on the roof = 10 cm
∴ Volume of water collected

Question 26.
A Piece of ductile metal is in the form of a cylinder of diameter 1 cm and length 5 cm. It is drawnout into a wire of diameter 1 mm. What will be the length of the wire so formed ?
Solution:
Diameter of ductile metal = 1 cm
and length (h) = 5 cm
and radius (r) = \(\frac { 1 }{ 2 }\) cm

Question 27.
Find the length of 13.2 kg of copper wire of diameter 4 mm when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Weight of wire = 13.2 kg
Diameter of wire = 4 mm

Question 28.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:
Volume of brass = 2.2 cu.dm
= 2.2 x 10 x 10 x 10 = 2200 cm²
Diameter of wire = 0.25 cm

Question 29.
The difference between inside and outside surfaces of a cylindrical tube 14 cm long is 88 sq. cm. If the volume of the tube is 176 cubic cm, find the inner and outer radii of the tube.
Solution:
Let r and R be the radii of inner and outer surfaces of a cylindrical tube,

Question 30.
Water flows out through a circular pipe whose internal diameter is 2 cm, at the rate of 6 metres per second into a cylindrical tank, the radius of whose base is 60 cm. Find the rise in the level of water in 30 minutes.
Solution:
Diameter of pipe = 2 cm
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm = 0.01 m
Length of flow of water in 1 second = 6 m Length of flow in 30 minutes = 6 x 30 x 60 m = 10800 m
∴ Volume of water = πr²h

Question 31.
A cylindrical tube, open at both ends, is to made of metal. The internal diameter of the tube is 10.4 cm and its length is 25 cm. The thickness of the metal tube is 8 mm everywhere. Calculate the volume of the metal.
Solution:
Length of metal tube (h) = 25 cm
Internal diameter = 10.4 cm
∴ Internal radius (r) = \(\frac { 10.4 }{ 2 }\) = 5.2 cm
Thickness of metal = 8 mm = 0.8 cm
∴ Outer radius = 5.2 + 0.8 = 6 cm
Now volume of the metal

Question 32.
From a tap of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in one hour.
Solution:
Inner radius of pipe (r) = 0.75 cm
Rate of water flow = 7 m per second
∴ Length of water flow in 1 hour (h)
= 7 x 3600 m = 25200 m
∴ Volume of water in 1 hour

Question 33.
A cylindrical water tank of diameter 1. 4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled ?
Solution:
Diameter of cylindrical tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) = 0.7 m
Height (h) = 2.1m.

Question 34.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways Le. either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinder thus formed.
Solution:
In first case,
By rolling the paper along its length,
the circumference of the base = 30 cm
and height (h) = 18 cm

Note: See Q.No. 24 this exercise

Question 35.
How many litres of water flow out of a pipe having an area of cross-section of 5 cm2 in one minute, if the speed of water in the pipe is 30 cm/sec ?
Solution:
Speed of water = 30 cm/sec
∴ Water flow in 1 minute = 30 cm x 60 = 1800 cm
Area of cross-section = 5 cm²
∴ Volume of water = 1800 x 5 = 9000 cm³
Capacity of water in litres = 9000 x l ml

Question 36.
A solid cylinder has a total surface area of 231 cm². Its curved surface area is \(\frac { 2 }{ 3 }\) of the total surface area. Find the volume of the cylinder.
Solution:
Total surface area of a solid cylinder = 231 cm²
Curved surface area = \(\frac { 2 }{ 3 }\) of 231 cm² = 2 x 77 = 154 cm²
and area of two circular faces = 231-154 = 77 cm²
Let r be the radius, then

Question 37.
Find the cost of sinking a tubewell 280 m deep, having diameter 3 m at the rate of Rs 3.60 per cubic metre. Find also the cost of cementing its inner curved surface at Rs 2.50 per square metre.
Solution:
Diameter of well = 3 m
∴ Radius (r) = \(\frac { 3 }{ 2 }\) m
and depth (h) = 280 m
(i) Volume of earth dug out = πr²h

Rate of sinking the well = Rs 3.60 per m³
∴ Total cost of sinking = Rs 1980 x 3.60 = Rs 7,128
(ii) Inner curved surface area = 2πrh

Rate of cementing = Rs 2.50 per m²
∴ Total cost of cementing = Rs 2.50 x 2640
= Rs 6,600

Question 38.
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Note : See Q.No. 27 of this exercise

Question 39.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:
Note: See Q.No. 28 of this exercise.

Question 40.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 10 m

Question 41.
A hollow garden roller, 63 cm wide with a girth of 440 cm, is made of 4 cm thick iron. Find the volume of the iron.
Solution:
Width of roller (h) = 63 cm.

Outer circumference of roller = 440 cm

Question 42.
What length of a solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of length 16 cm, external diameter 20 cm and thickness 2.5 mm ?
Solution:
Length of hollow cylinder (h) = 16 cm
External diameter = 20 cm
∴ External radius (R) = \(\frac { 20 }{ 2 }\) = 10 cm
Thickness of iron = 2.5 mm
∴ Internal radius (r) = 10 – 0.25 = 9.75 cm
∴ Volume of iron = πh (R² – r²)

Question 43.
In the middle of rectangular field measuring 30 m x 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
Solution:
Diameter of well = 7 m
∴ Radius (r) = \(\frac { 7 }{ 2 }\) m
Depth (h) = 10 m.
∴ Volume of earth dug out = πr²h

Hope given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 26 Data Handling IV (probability) Ex 26.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 26 Data Handling IV (probability) Ex 26.1

Question 1.
The probability that it will rain to morrow is 0.85. What is the probability that it will not rain tomorrow ?
Solution:
Total number of possible events = 1
∴ P (\(\bar { A }\) ) = 0.85
∴ P (\(\bar { A }\) ) = 1-0.85 = 0.15

Question 2.
A die is thrown. Find the probability of getting (i) a prime number (ii) 2 or 4 (iii) a multiple of 2 or 3.
Solution:
Total number of possible events = 6 (1 to 6)
(i) Let A be the favourable occurrence which are prime number i.e., 2,3,5
∴ P(A) = \(\frac { 3 }{ 6 }\) = \(\frac { 1 }{ 2 }\)
(ii) Let B be the favourable occurrence which are 2 or 4
∴ P(B) = \(\frac { 2 }{ 6 }\) = \(\frac { 1 }{ 3 }\)
(iii) Let C be the favourable occurrence which are multiple of 2 or 3 i.e., 2, 3, 4, 6.
∴ P(C) = \(\frac { 4 }{ 6 }\) = \(\frac { 2 }{ 3 }\)

Question 3.
In a simultaneous throw of a pair of dice, find the probability of getting:
(i) 8 as the sum
(ii) a doublet
(iii) a doublet, of prime numbers
(iv) a doublet of odd numbers
(v) a sum greater than 9
(vi) an even number on first
(vii) an even number on one and a multiple of 3 on the other
(viii) neither 9 nor 11 as the sum of the numbers on the faces
(ix) a sum less than 6
(x) a sum less than 7
(xi) a sum more than 7
(xii) at least once
(xiii) a number other than 5 on any dice.
Solution:
By throwing of a pair of dice, total number of possible events = 6 × 6 = 36
(i) Let A be the occurrence of favourable events whose sum is 8 i.e. (2,6), (3,5), (4,4), (5,3) , (6,2) which are 5
∴ P(A) = \(\frac { 5 }{ 36 }\)
(ii) Let B be the occurrence of favourable events which are doublets i.e. (1, 1), (2, 2), (3, 3), (4,4), (5, 5) and (6, 6).
∴ P(B) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)
(iii) Let C be the occurrence of favourable events which are doublet of prime numbers which are (2, 2), (3,3), (5, 5)
∴ P(C) = \(\frac { 3 }{ 36 }\) = \(\frac { 1 }{ 12 }\)
(iv) Let D be the occurrence of favourable events which are doublets of odd numbers which are (1, 1), (3, 3) and (5, 5)
∴ P(D) = \(\frac { 3 }{ 36 }\) = \(\frac { 1 }{ 12 }\)
(v) Let E be the occurrence of favourable events whose sum is greater than 8 i.e, (3,6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6) which are 6 in numbers
∴ P(E) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)
(vi) Let F be the occurrence of favourable events in which is an even number is on first i.e (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1),(4,2), (4,3) (4,4), (4,5), (4,6), (6,1), (6,2), (6, 3), (6,4 ), (6, 5), (6,6) which are 18 in numbers.
∴ P(F) = \(\frac { 18 }{ 36 }\) = \(\frac { 1 }{ 2 }\)
(vii) Let G be the occurrence of favourable events in which an even number on the one and a multiple of 3 on the other which are (2,3), (2,6), (4, 3), (4, 6), (6, 3), (6, 6), (3, 2), (3, 4), (3, 6), (6,2), (6,4) = which are 11th number
∴ P(G) = \(\frac { 11 }{ 36 }\)
(viii) Let H be the occurrence of favourable events in which neither 9 or 11 as the sum of the numbers on the faces which are (1,1), (1,2), (1,3) , (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2,4) , (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3,5) , (4, 1), (4, 2), (4, 3), (4, 4), (4, 6), (5, 1), (5,2), (5,3), (5,5), (6,1), (6,2), (6,4), (6,6) which are 30
∴ P(H) = \(\frac { 30 }{ 36 }\) = \(\frac { 5 }{ 6 }\)
(ix) Let I be the occurrence of favourable events, such that a sum less than 6, which are (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4,1) which are 10
∴ P(I) = \(\frac { 10 }{ 36 }\) = \(\frac { 5 }{ 18 }\)
(x) Let J be the occurrence of favourable events such that a sum is less than 7, which are
(1.1) , (1,2), (1,3), (1,4), (1,5), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (5.1) which are 15
∴ P(J) = \(\frac { 15 }{ 36 }\) = \(\frac { 5 }{ 6 }\)
(xi) Let K be the occurrence of favourable events such that the sum is more than 7, which are (2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) which 15
∴ P(K) = \(\frac { 15 }{ 36 }\) = \(\frac { 5 }{ 12 }\)
(xii) Let L be the occurrence of favourable events such that at least P (L) one is black card
∴ P(L) = \(\frac { 26 }{ 52 }\) = \(\frac { 1 }{ 2 }\)
(xiii) Let M is the occurrence of favourable events such that a number other than 5 on any dice which can be (1,1), (1,2), (1,3), (1,4), (1,6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 6), (3,1), (3,2), (3, 3), (3,4), (3,6), (4,1), (4, 2), (4, 3), (4,4), (4,6), (6, 1), (6,2), (6, 3), (6,4), (6, 6) which are 25
∴ P(M) = \(\frac { 25 }{ 36 }\)

Question 4.
Three coins are tossed together. Find the probability of getting:
(i) exactly two heads
(ii) at least two heads
(iii) at least one head and one tail
(iv) no tails
Solution:
Total number of events tossed by 3 coins each having one head and one tail = 2x2x2 = 8
(i) Let A be the occurrence of favourable events which is exactly two heads, which can be 3 in number which are HTH, HHT, THH.
∴ P(A) = \(\frac { 3 }{ 8 }\)
(ii) Let B be the occurrence of favourable events which is at least two heads, which will be 4 which are HHT, HTH, THH, and HHH.
∴ P(B) = \(\frac { 4 }{ 8 }\) = \(\frac { 1 }{ 2 }\)
(iii) Let C be the occurrence 6f favourable events which is at least one head and one tail which are 6 which can be HHT, HTH, THH, TTH, THT, HTT
∴ P(C) = \(\frac { 6 }{ 8 }\) = \(\frac { 3 }{ 4 }\)
(iv) Let D be the occurrence of favourable events in which there is no tail which is only 1 (HHH)
∴ P(D) = \(\frac { 1 }{ 8 }\)

Question 5.
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is:
(i) a black king
(ii) either a black card or a king
(iii) black and a king
(iv) a jack, queen or a king
(v) neither a heart nor a king
(vi) spade or an ace
(vii) neither an ace nor a king
(viii) neither a red card nor a queen
(ix) other than an ace
(x) a ten
(xi) a spade
(xii) a black card
(xiii) the seven of clubs
(xiv) jack
(xv) the ace of spades
(xvi) a queen
(xvii) a heart
(xviii) a red card
Solution:
A pack of cards have 52 cards, 26 black and 26 red and four kinds each of 13 cards from 2 to 10, one ace, one jack, one queen and one king.
∴ Total number of possible events = 52
(i) Let A be the occurrence of favourable events which is a black king which are 2.
∴ P(A) = \(\frac { 2 }{ 52 }\) = \(\frac { 1 }{ 26 }\)
(ii) Let B be the occurrence of favourable events such that it is either a black card or a king.
Total = number of black cards = 26 + 2 red kings = 28
∴ P(B) = \(\frac { 28 }{ 52 }\) = \(\frac { 7 }{ 13 }\)
(iii) Let C be the occurrence of favourable events such that it is black and a king which can be 2.
∴ P(C) = \(\frac { 2 }{ 52 }\) = \(\frac { 1 }{ 26 }\)
(iv) Let D be the occurrence of favourable events such that it is a jack, queen or a king which will be4 + 4 + 4 = 12
∴ P(D) = \(\frac { 12 }{ 52 }\) = \(\frac { 3 }{ 13 }\)
(v) Let E be the occurrence of favourable events such that it is neither a heart nor a king.
∴ Number of favourable event will be 13 x 3 -3 = 39 – 3 = 36
∴ P(E) = \(\frac { 36 }{ 52 }\) = \(\frac { 9 }{ 13 }\)
(vi) Let F be the occurrence of favourable events such that it is a spade or an ace.
∴ Number of events = 13 + 3 = 16
∴ P(F) = \(\frac { 16 }{ 52 }\) = \(\frac { 4 }{ 13 }\)
(vii) Let G be the occurrence of favourable events such that it neither an ace nor a king.
∴Number of events = 52 – 4 – 4 = 44
∴ P(G) = \(\frac { 44 }{ 52 }\) = \(\frac { 11 }{ 13 }\)
(viii) Let H be the occurrence of favourable events such that it is neither a red card nor a queen.
∴Number of events = 26 – 2 = 24,
∴ P(H) = \(\frac { 24 }{ 52 }\) = \(\frac { 6 }{ 13 }\)
(ix) Let 1 be the occurrence of favourable events such that it is other than an ace.
∴ Number of events = 52 – 4 = 48
∴ P(I) = \(\frac { 48 }{ 52 }\) = \(\frac { 12 }{ 13 }\)
(x) Let J be the occurrence of favourable event such that it is ten
∴ Number of events = 4
∴ P(J) = \(\frac { 4 }{ 52 }\) = \(\frac { 1 }{ 13 }\)
(xi) Let K be the occurrence of favourable event such that it is a spade.
∴ Number of events =13
∴ P(K) = \(\frac { 13 }{ 52 }\) = \(\frac { 1 }{ 4 }\)
(xii) Let L be the occurrence of favourable event such that it is a black card.
∴ Number of events = 26
∴ P(L) = \(\frac { 26 }{ 52 }\) = \(\frac { 1 }{ 2 }\)
(xiii) Let M be the occurrence of favourable event such that it is the seven of clubs.
∴ Number of events = 1
∴ P(M) = \(\frac { 1 }{ 52 }\)
(xiv) Let N be the occurrence of favourable event such that it is a jack.
∴ Number of events = 1
∴ P(N) = \(\frac { 4 }{ 52 }\) = \(\frac { 1 }{ 13 }\)
(xv) Let O be the occurrence of favourable event such that it is an ace of spades.
∴ Number of events = 1
∴ P(O) = \(\frac { 1 }{ 52 }\)
(xvi) Let Q be the occurrence of favourable event such that it is a queen.
∴ VNumber of events = 4
∴ P(P) = \(\frac { 4 }{ 52 }\) = \(\frac { 1 }{ 13 }\)
(xvii) Let R be the occurrence of favourable event such that it is a heart card.
∴ Number of events =13
∴ P(P) = \(\frac { 13 }{ 52 }\) = \(\frac { 1 }{ 4 }\)
(xviii) Let S be the occurrence of favourable event such that it is a red card
∴ Number of events = 26
∴ P(P) = \(\frac { 26 }{ 52 }\) = \(\frac { 1 }{ 2 }\)

Question 6.
An urn contains 10 red and 8 white balls. One ball is drawn at random. Find the probability that the ball drawn is white.
Solution:
Number of possible events = 10 + 8 = 18
Let A be the occurrence of favourable event such that it is a white ball.
∴ Number of events = 8
∴ P(A) = \(\frac { 8 }{ 18 }\) = \(\frac { 4 }{ 9 }\)

Question 7.
A bag contains 3 red balls, 5 black balls and 4 white balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) white ? (ii) red ? (iii) black ? (iv) not red ?
Solution:
Number of possible events = 3 + 5 + 4 = 12 balls
(i) Let A be the favourable event such that it is a white ball.
∴ P(A) = \(\frac { 4 }{ 12 }\) = \(\frac { 1 }{ 3 }\)
(ii) Let B be the favourable event such that it is a red ball.
∴ P(B) = \(\frac { 3 }{ 12 }\) = \(\frac { 1 }{ 4 }\)
(iii) Let C be the favourable event such that it is a black ball.
∴ P(C) = \(\frac { 5 }{ 12 }\)
(iv) Let D be the favourable event such that it is not red.
∴ Number of favourable events = 5 + 4 = 9
∴ P(D) = \(\frac { 9 }{ 12 }\) = \(\frac { 3 }{ 4 }\)

Question 8.
What is the probability that a number selected from the numbers 1,2,3,…………, 15 is a multiple of 4 ?
Solution:
Number of possible events =15
Let A be the favourable event such that it is a multiple of 4 which are 4, 8, 12
∴ P(A) = \(\frac { 3 }{ 15 }\) = \(\frac { 1 }{ 5 }\)

Question 9.
A bag contains 6 red, 8 black and 4 white balls. A ball is drawn at random. What is the probability that ball drawn is not black ?
Solution:
Number of possible events = 6 + 8 + 4 = 18 balls
Let A be the favourable event such that it is not a black
∴ Number of favourable events = 6 + 4=10
∴ P(A) = \(\frac { 10 }{ 18 }\) = \(\frac { 5 }{ 9 }\)

Question 10.
A bag contains 5 white and 7 red balls. One ball is drawn at random, what is the probability that ball drawn is white ?
Solution:
Number of possible events = 5 + 7 = 12
Let A be the favourable event such that it is a while which are 5.
∴ P(A) = \(\frac { 5 }{ 12 }\)

Question 11.
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is (i) white (if) red (iii) not black (iv) red or white.
Solution:
Number of possible events = 4 + 5 + 6 = 15
(i) Let A be the favourable events such that it is a white.
∴ P(A) = \(\frac { 6 }{ 15 }\) = \(\frac { 2 }{ 5 }\)
(ii) Let B be the favourable event such that it is a red
∴ P(B) = \(\frac { 4 }{ 15 }\)
(iii) Let C be the favourable event such that it is not black.
∴ Number of favourable events = 4 + 6=10
∴ P(C) = \(\frac { 10 }{ 15 }\) = \(\frac { 2 }{ 3 }\)

Question 12.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is: (i) red (ii) black.
Solution:
Number of possible events = 3 + 5 = 8
(i) Let A be the favourable events such that it is red.
∴ P(A) = \(\frac { 3 }{ 8 }\)
(ii) Let B be the favourable event such that it is black.
∴ P(B) = \(\frac { 5 }{ 8 }\)

Question 13.
A bag contains 5 red marbles, 8 white marbles, 4 green marbles. What is the probability that if one marble is taken out of the bag at random, it will be
(i) red
(ii) white
(iii) not green.
Solution:
Total number of possible events = 5 + 8+4=17
(i) Let A be the favourable event such that it is red.
∴ P(A) = \(\frac { 5 }{ 7 }\)
(ii) Let B be the favourable event such that it is white
Then P (B) = \(\frac { 8 }{ 7 }\)
(iii) Let C be the favourable event such that it is not green.
∴ Number of favourable events = 5 + 8 = 13
∴ P(C) = \(\frac { 13 }{ 17 }\)

Question 14.
If you put 21 consonants and 5 vowels in a bag. What would carry greater probability ? Getting a consonant or a vowel ? Find each probability.
Solution:
Total number of possible events = 21 + 5 = 26
(i) Probability of getting a consonant is greater as to number is greater than the other.
(ii) Let A be the favourable event such that it is a consonant.
∴ P(A) = \(\frac { 21 }{ 26 }\)
(iii) Let B be the favourable event such that it is a vowel.
∴ P(B) = \(\frac { 5 }{ 26 }\)

Question 15.
If we have 15 boys and 5 girls in a class which carries a higher probability ? Getting a copy belonging to a boy or a girl ? Can you give it a value ?
Solution:
Number of possible outcome (events) = 15 + 5 = 20
∵ The number of boys is greater than the girls
∴ The possibility of getting a copy belonging to a boy is greater.
Let A be the favourable outcome (event) then
P(A) = \(\frac { 15 }{ 20 }\) = \(\frac { 3 }{ 4 }\)

Question 16.
If you have a collection of 6 pairs of white socks and 3 pairs of black socks. What is the probability that a pair you pick without looking is (i) white ? (if) black ?
Solution:
Total number of possible outcomes =6+3=9
(i) Let A be the favourable outcome which is white pair.
∴ P(A) = \(\frac { 6 }{ 9 }\) = \(\frac { 2 }{ 3 }\)
(ii) Let B be the favourable outcome which is a black pair.
∴ P(B) = \(\frac { 3 }{ 9 }\) = \(\frac { 1 }{ 3 }\)

Question 17.
If you have a spinning wheel with 3 green sectors, 1-blue sector and 1-red sector, what is the probability of getting a green sector ? Is it the maximum ?
Solution:
Total number of possible outcomes = 3 + 1 + 1 =5
Let A be the favourable outcome which is green sector
∴ P(A) = \(\frac { 3 }{ 5 }\)
∴ Number of green sectors is greater.
∴ It’s probability is greater.

Question 18.
When two dice are rolled :
(i) List the outcomes for the event that the total is odd.
(ii) Find probability of getting an odd total.
(iii) List the outcomes for the event that total is less than 5.
(iv) Find the probability for getting a total less than 5.
Solution:
∵ Every dice has 6 number from 1 to 6.
∴ Total outcomes = 6 x 6 = 36.
(i) List of outcomes for event then the total is odd will be (1,2), (1,4), (1,6), (2,1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6,1), (6, 3), (6, 5)
(ii) Probability of getting an odd total
Let A be the favourable outcomes which are
P(A) = \(\frac { 18 }{ 36 }\) = \(\frac { 1 }{ 2 }\)
(iii) List of outcomes for the event that total is less than 5 are (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2,1), which are 6.
(iv) Probability of getting a total less than 5 Let B be the favourable outcome,
Then P (B) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)

Hope given RD Sharma Class 8 Solutions Chapter 26 Data Handling IV (probability) Ex 26.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 27 Introduction to Graphs Ex 27.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 27 Introduction to Graphs Ex 27.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 27 Introduction to Graphs Ex 27.1
• RD Sharma Class 8 Solutions Chapter 27 Introduction to Graphs Ex 27.2

Question 1.
The following table shows the number of patients discharged from a hospital with HIV diagnosis in different years :

Represent this information by a graph.
Solution:
Represent years along x-axis and number of patients along y-axis. Now, plot the points (2002, 150), (2003, 170), (2004, 195), (2005, 225) and (2006, 230) on the graph and join them in order. We get the required graph as shown on the graph.

Question 2.
The following table shows the amount of rice grown by a farmer in different years :

Plot a graph to illustrate this information.
Solution:
We represent years along x-axis and rice (in quintals) along y-axis. Now we plot the points (2000,200), (2001, 180), (2002,240), (2003,260), (2004,250), (2005,200) and (2006,270) on the graph and join them in order as shown on the graph.

Question 3.
The following table gives the information regarding the number of persons employed to a piece of work and time taken to complete the work:

Plot a graph of this information.
Solution:
We represent number of person along x-axis and time taken in day along y-axis. Now plot the points (2,12), (4,6), (6,4) and (8, 3) on the graph and join them in order as shown on the graph.

Question 4.
The following table gives the information regarding length of a side of a square and its area :

Draw a graph to illustrate this information.
Solution:
We represent length of a side (in cm) along x-axis and Area of square (in cm2) along the y-axis. Now plot the points (1,1), (2, 4), (3, 9), (4, 16) and (5, 25) on the graph and join them in order. We get the required graph as shown on the graph.

Question 5.
The following table shows the sales of a commodity during the years 2000 to 2006.

Draw a graph of this information.
Solution:
We represent years on x-axis and sales (in lakh rupees) along y-axis. Now plot the points
(2000, 1.5), (2001, 1.8), (2002, 2.4), (2003, 3.2), (2004, 5.4), (2005, 7.8) and (2006, 8.6) on the graph and join them in order we get the required graph as shown.

Question 6.
Draw the temperature-time graph in each of the following cases :

Solution:
(i) We represent time along x-axis and temperature (in °F) alongy-axis. Now plot the points (7:00, 100), (9:00, 101), (11:00, 104), (13:00, 102), (15:00, 100), (17:00, 99), (19:00, 100) and (21:00, 98) on the graph and join them in order to get the required graph as shown on the graph.


(ii) We represent time along x-axis and temperature (in °F) along j-axis. Now plot the points (8:00, 100), (i0:00, 101), (12:00, 104), (14:00, 103), (16:00, 99), (18:00,98), (20:00,100) on the graph and join them in order to get the required graph as shown on the graph.

Question 7.
Draw the velocity-time graph from the following data :

Solution:
We represent time (in hours) along x- axis and speed (in km/hr) along y-axis. Now plot the points (7:00,30), (8:00,45), (9:00,60), (10:00, 50), (11:00, 70), (12:00, 50), (13:00, 40) and (14:00,45) on the graph and join them in order to get the required graph as shown.

Question 8.
The runs scored by a cricket team in first 15 overs are given below :

Draw the graph representing the above data in two different ways as a graph and as a bar chart.
Solution:
We represent overs along.t-axis and runs along v-axis. Now plot the points (1,2), (II, 1), (III, 4), (IV, 2), (V, 6), (VI, 8), (VII, 10), (VIII, 21), (IX, 5), (X, 8), (XI, 3), (XII, 2), (XIII, 6), (XIV, 8), (XV, 12) on the graph and join them to get the graph, as shown bar graph of the given data is given below:

Question 9.
The runs scored by two teams A and B in first 10 overs are given below :

Draw a graph depicting the data, making the graphs on the same axes in each case in two different ways as a graph and as a bar chart.
Solution:
We represent overs along x-axis and runs scored by team A and team B with different types of lines along y-axis.
Plot the points for team A : (I, 2), (II, 1), (III,8), (IV, 9), (V, 4), (VI, 5), (VII, 6), (VIII, 10), (IX, 6) and (X, 2)
and for team B, the points will be : (I, 5), (II, 6), (III, 2), (IV, 10), (V, 5), (VI, 6), (VII, 3), (VIII, 4), (IX, 8), (X, 10).
Then join them in order to get the required graph for team A and team B as shown.
Note : For team A ………
for team B …………

Hope given RD Sharma Class 8 Solutions Chapter 27 Introduction to Graphs Ex 27.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.