NCERT Solutions for Class 8 Science Chapter 1 Crop Production and Management are part of NCERT Solutions for Class 8 Science. Here we have given NCERT Solutions for Class 8 Science Chapter 1 Crop Production and Management.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Science |
| Chapter | Chapter 1 |
| Chapter Name | Crop Production and Management |
| Number of Questions Solved | 11 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Science Chapter 1 Crop Production and Management
NCERT TEXTBOOK EXERCISES
Question 1.
Select the correct word from the following list and fill in the blanks, float, water, crop, nutrients, preparation
(a) The same kind of plants grown and cultivated on a large scale at a place is called __________.
Answer:
Crop
(b) The first step before growing crops is ___________ of the soil.
Answer:
Preparation
(c) Damaged seeds would ___________ on top of water.
Answer:
Float
(d) For growing a crop, sufficient sunlight, __________ and __________ from the soil are essential.
Answer:
water
Nutrients
Question 2.
Match items in column A with those in column B.
| Column A | Column B |
| (i) Kharif crops | (a) Food for cattle |
| (ii) Rabi crops | (b) Urea and super phosphate |
| (iii) Chemical fertilisers | (c) Animal excreta, cow dung, urine and plant waste |
| (iv) Organic manure | (d) Wheat, gram, pea |
| (e) Paddy and maize |
Answer.
| Column A | Column B |
| (i) Kharif crops | (e) Paddy and maize |
| (ii) Rabi crops | (d) Wheat, gram, pea |
| (iii) Chemical fertilisers | (b) Urea and superphosphate |
| (iv) Organic manure | (c) Animal excreta, cow dung, urine, and plant waste |
Question 3.
Give two examples of each:
- Kharif crop
- Rabi crop
Answer.
- Paddy, maize
- Wheat, gram.
Question 4.
Write a paragraph in your own words on each of the following:
- Preparation of soil
- Sowing
- Weeding
- Threshing
Answer.
(1) Preparation of soil: It is the first step before growing a crop. One of the most important tasks in agriculture is to turn the soil and loosen it. This allows the roots to penetrate deep in the soil. The process of loosening and turning of soil is called tilling or ploughing which is done by a plough. Ploughs are made of wood or iron. The ploughed fields may have big pieces of soil called crumbs. These crumbs are broken and the field is levelled for sowing and for irrigation.
(2) Sowing: It is the process of putting seeds in the soil. For this purpose, good quality seeds are selected which are clean, healthy, of good variety, and give a high yield. Seeds are sown with the help of a traditional funnel-shaped tool or a seed drill. An appropriate distance between the seeds is also important to avoid overcrowding.
(3) Weeding: In a crop field many other undesirable plants may grow naturally along with the crop. These are called weeds. Weeds should be removed to protect the crops. The process of removal of weeds is called weeding. Weeding is necessary because weeds compete with the cultivated plants for space, light, water, and nutrients. Some weeds are poisonous for animals and human beings. Tilling before sowing of crops helps in uprooting and killing of weeds, which may then dry up and get mixed with the soil. The weeds must be removed before they produce flowers and seeds. They are removed either manually or by using weedicides.
(4) Threshing: After harvesting, the crops are threshed for removing grain seeds from the chaff. This is carried out with the help of a thresher or a machine called ‘combine’ which is in fact a combined harvester and thresher.
Question 5.
Explain how fertilisers are different from manure.
Answer.
| Fertilisers | Manure |
1. Fertilisers are chemicals which are rich in a particular nutrient like nitrogen, phosphorus, and potassium. 2. Excessive use of fertilisers destroys soil fertility. | 1. Manures are decomposed organic matter obtained from plant or animal wastes. 2. The use of manures improves soil texture as well as its water-holding capacity. |
Question 6.
What is irrigation? Describe two methods of irrigation which conserve water.
Answer.
The supply of water to crops at different intervals is called irrigation. The two methods of irrigation in which water is conserved are the sprinkler system and the drip system.
(1) Sprinkler system: This system is mostly used on uneven lands where water is available in smaller quantities. In this system, perpendicular pipes having rotating nozzles on the top are joined to the main pipeline at regular intervals. When water is allowed to flow through the main pipe under pressure with the help of a pump, it escapes from the rotating nozzles. It is sprinkled on the crop as if it is raining. It is very useful for sandy soil.
(2) Drip system: In this system, the water falls drop by drop just at the position of the roots. So, it is called a drip system. It is the best technique for watering fruit plants, gardens, trees, etc. This system consists of the main pipe to which lateral pipes are joined. The specially prepared nozzles are attached to these lateral pipes. The nozzles are grounded just near the roots of the plants. It provides water drop by drop to plants. Water is not wasted at all. So, it is a boon in regions where the availability of water is poor.
Question 7.
If wheat is sown in the Kharif season, what would happen? Discuss.
Answer.
The best season for the wheat crops is from November/December to March/April. If it is sown in the Kharif season its production will be decreased considerably.
Question 8.
Explain how soil gets affected by the continuous plantation of crops in a field.
Answer.
The continuous growing of crops makes the soil deficient in certain nutrients. To avoid this, the following practices should be facilitated:
- Crop rotation
- Manuring the soil
- Leaving field fallow
Question 9.
What are weeds? How can we control them?
Answer.
The undesirable plants in the field that grow naturally are called weeds. Weeds must be removed, otherwise, our own crop plants may not get sufficient water, nutrients, space, and light. So, they are removed either by manual method or by using weedicides.
The manual removal includes physical removal of weeds by uprooting or cutting them close to the ground from time to time. This is done with the help of a khurpi or a harrow. By using weedicides also, we can remove weeds. These weedicides damage only weeds and do not harm crops, e.g., 2, 4-D.
Question 10.
Arrange the following boxes in proper order to make a flow chart of sugarcane crop production.
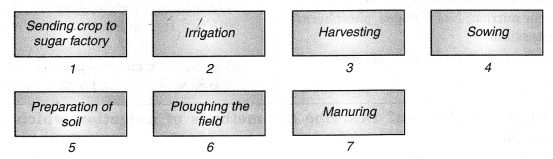
Answer.
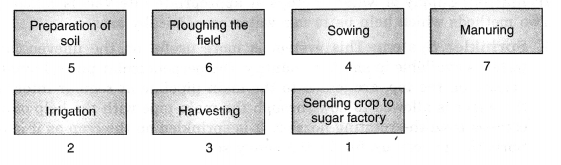
Question 11.
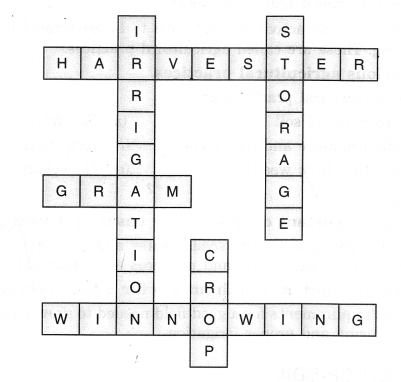
Complete the following word puzzle with the help of clues below.
Down
1. Providing water to the crops.
2. Keeping crop grains for a long time under proper conditions.
5. Certain plants of the same kind grown on a large scale.
Across
3. A machine used for cutting the matured crop.
4. A rabi crop that is also one of the pulses.
6. A process of separating the grain from the chaff.
Answer.
We hope the NCERT Solutions for Class 8 Science Chapter 1 Crop Production and Management help you. If you have any query regarding NCERT Solutions for Class 8 Science Chapter 1 Crop Production and Management, drop a comment below and we will get back to you at the earliest.