RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
Other Exercises
- RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
- RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
- RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
- RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
- RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
- RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
- RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7
Question 1.
Write the following squares of bionomials as trinomials :
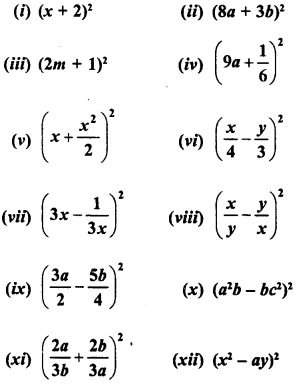
Solution:
Using the formulas
(a + b)2 = a2 + 2ab + b2 and (a – b)2 = a2 – 2ab + b2
(i) (a + 2)2 = (a)2 + 2 x a x 2 + (2)2
{(a + b)2 = a2 + 2ab + b2}
= a2 + 4a + 4
(ii) (8a + 3b)2 = (8a)2 + 2 x 8a * 3b + (3b)2 = 642 + 48ab + 9 b2
(iii) (2m+ 1)2 = (2m)2 + 2 x 2m x1 + (1)2
= 4m2 + 4m + 1
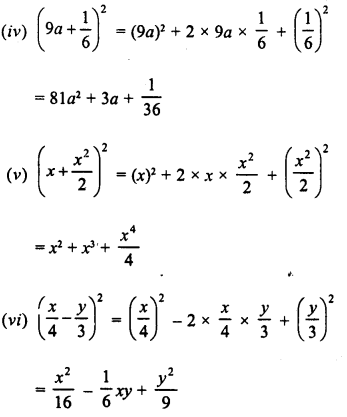
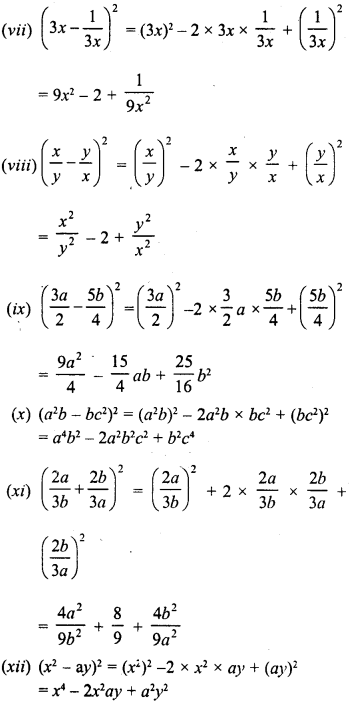
Question 2.
Find the product of the following binomials :
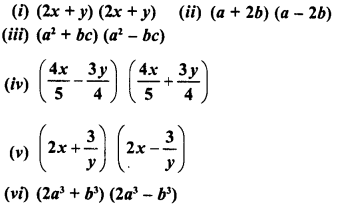
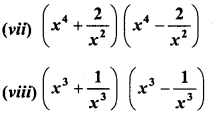
Solution:
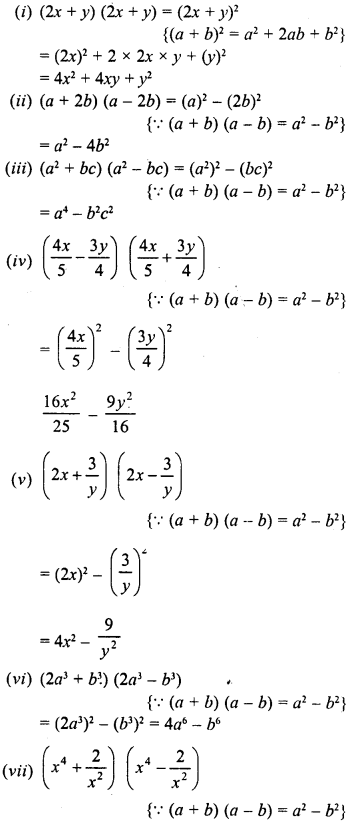
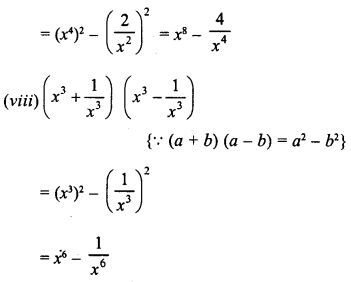
Question 3.
Using the formula for squaring a binomial, evaluate the following :
(i) (102)2
(ii) (99)2
(iii) (1001)2
(iv) (999)2
(v) (703)2
Solution:
(i) (102)2 = (100 + 2)2
= (100)2 + 2 x 100 x 2 + (2)2
{(a + b)2 = a2 + 2ab + b2}
= 10000 + 400 + 4 = 10404
(ii) (99)2 = (100 – 1)2
= (100)2 – 2 x 100 X 1 +(1)2
{(a – b)2 = a2 – 2ab + b2}
= 10000 -200+1
= 10001 -200 =9801
(iii) (1001 )2 = (1000 + 1)2
{(a + b)2 = a2 + 2ab + b2}
= (1000)2 + 2 x 1000 x 1 + (1)2
= 1000000 + 2000 + 1 = 1002001
(iv) (999)2 = (1000 – 1)2
{(a – b)2 = a2 – 2ab + b2}
= (1000)2 – 2 x 1000 x 1 + (1)2
= 1000000 – 2000 + 1
= 1000001 -2000 = 998001
Question 4.
Simplify the following using the formula:
(a – b) (a + b) = a2 – b2 :
(i) (82)2 (18)2
(ii) (467)2 (33)2
(iii) (79)2 (69)2
(iv) 197 x 203
(v) 113 x 87
(vi) 95 x 105
(vii) 1.8 x 2.2
(viii) 9.8 x 10.2
Solution:
(i) (82)2 – (18)2 = (82 + 18) (82 – 18)
{(a + b)(a- b) = a2 – b2} = 100 x 64 = 6400
(ii) (467)2 – (33)2 = (467 + 33) (467 – 33)
= 500 x 434 = 217000
(ii) (79)2 – (69)2 = (79 + 69) (79 – 69)
148 x 10= 1480
(iv) 197 x 203 = (200 – 3) (200 + 3)
= (200)2 – (3)2
= 40000-9 = 39991
(v) 113 x 87 = (100 + 13) (100- 13)
= (100)2 – (13)2
= 10000- 169 = 9831
(vi) 95 x 105 = (100 – 5) (100 + 5)
= (100)2 – (5)2
= 10000 – 25 = 9975
(vii) 8 x 2.2 = (2.0 – 0.2) (2.0 + 0.2)
= (2.0)2 – (0.2)2
= 4.00 – 0.04 = 3.96
(viii)9.8 x 10.2 = (10.0 – 0.2) (10.0 + 0.2)
(10.0)2 – (0.2)2
= 100.00 – 0.04 = 99.96
Question 5.
Simplify the following using the identities :
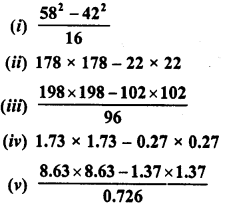
Solution:
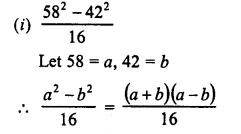
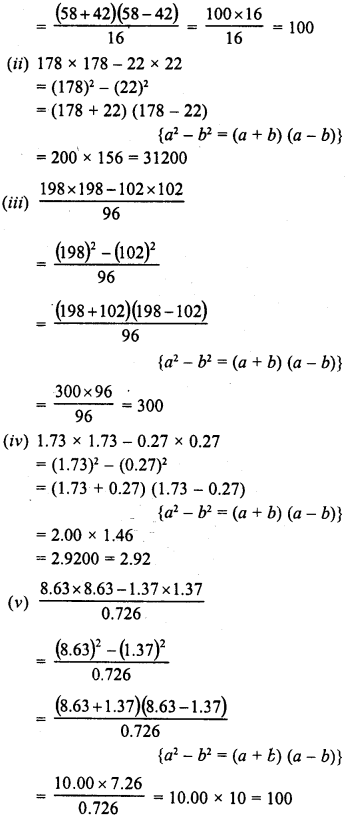
Question 6.
Find the value of x, if
(i) 4x = (52)2 – (48)2
(ii) 14x = (47)2 – (33)2
(iii) 5x = (50)2 – (40)2
Solution:
(i) 4x = (52)2 – (48)2
⇒ 4x = (52 + 48) (52 – 48)
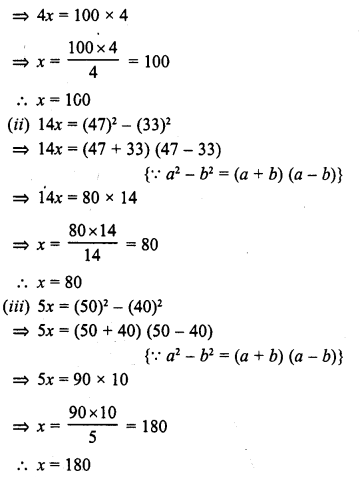
Question 7.
If x + \(\frac { 1 }{ x }\)= 20, find the value of x2+ \(\frac { 1 }{ { x }^{ 2 } }\)
Solution:
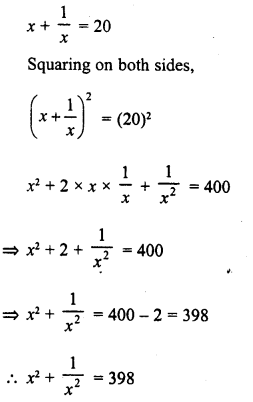
Question 8.
If x – \(\frac { 1 }{ x }\) = 3, find the values of x2 + \(\frac { 1 }{ { x }^{ 2 } }\) and x4 + \(\frac { 1 }{ { x }^{ 4 } }\)
Solution:
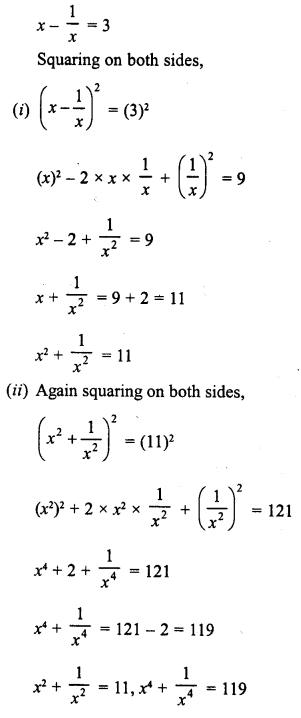
Question 9.
If x2 – \(\frac { 1 }{ { x }^{ 2 } }\)= 18, find the values of x+ \(\frac { 1 }{ x }\) and x– \(\frac { 1 }{ x }\)
Solution:

Question 10.
Ifx+y = 4 and xy = 2, find the value of x2+y2.
Solution:
x + y = 4
Squaring on both sides,
(x + y)2 = (4)2
⇒ x2 +y2 + 2xy = 16
⇒ x2+y2 + 2 x 2 = 16 (∵ xy = 2)
⇒ x2 + y2 + 4 = 16
⇒ x2+y2 = 16 – 4= 12 ‘
∴ x2+y2 = 12
Question 11.
If x-y = 7 and xy = 9, find the value of x2+y2.
Solution:
x-y = 7
Squaring on both sides,
(x-y)2 = (7)2
⇒ x2+y2-2xy = 49
⇒ x2 + y2 – 2 x 9 = 49 (∵ xy = 9)
⇒ x2 +y2 – 18 = 49
⇒ x2 + y2 = 49 + 18 = 67
∴ x2+y2 = 67
Question 12.
If 3x + 5y = 11 and xy = 2, find the value of 9x2 + 25y2
Solution:
3 x + 5y = 11, xy = 2
Squaring on both sides,
(3x + 5y)2 = (11)2
⇒ (3x)2 + (5y)2 + 2 x 3x x 5y = 121
⇒ 9x2 + 25y2 + 30 x 7 = 121
⇒ 9x2 + 25y2+ 30 x 2 = 121 (∵ xy = 2)
⇒ 9x2 + 25y2 + 60 = 121
⇒ 9x2 + 25y2 = 121 – 60 = 61
∴ 9x2 + 25y2 = 61
Question 13.
Find the values of the following expressions :
(i)16x2 + 24x + 9, when X’ = \(\frac { 7 }{ 45 }\)
(ii) 64x2 + 81y2 + 144xy when x = 11 and y = \(\frac { 4 }{ 3 }\)
(iii) 81x2 + 16y2-72xy, whenx= \(\frac { 2 }{ 3 }\) andy= \(\frac { 3 }{ 4 }\)
Solution:
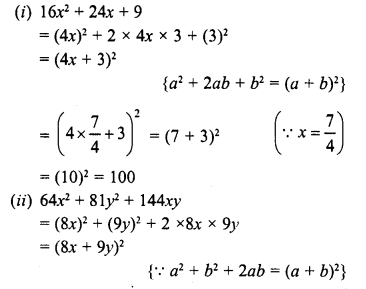
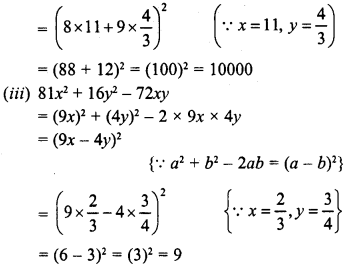
Question 14.
If x + \(\frac { 1 }{ x }\) = 9, find the values of x4 + \(\frac { 1 }{ { x }^{ 4 } }\).
Solution:
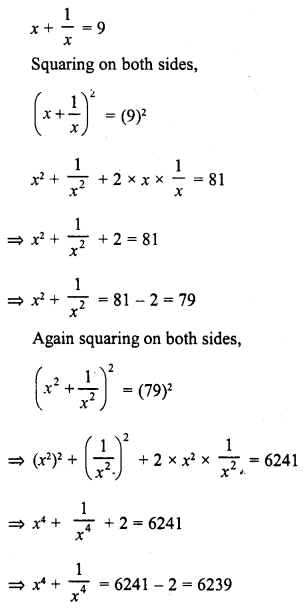
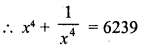
Question 15.
If x + \(\frac { 1 }{ x }\) = 12, find the values of x– \(\frac { 1 }{ x }\).
Solution:
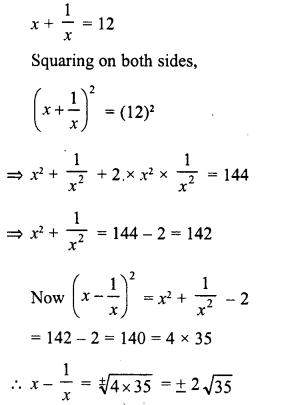
Question 16.
If 2x + 3y = 14 and 2x – 3y = 2, find the value of xy.
Solution:
2x + 3y = 14, 2x – 3y= 2
We know that
(a + b)2 – (a – b)2 = 4ab
∴ (2x + 3y)2 – (2x – 3y)2 = 4 x 2x x 3y = 24xy
⇒ (14)2 – (2)2 = 24xy
⇒ 24xj= 196-4= 192
⇒ xy = \(\frac { 192 }{ 24 }\) = 8
∴ xy = 8
Question 17.
If x2 + y2 = 29 and xy = 2, find the value of
(i) x+y
(ii) x-y
(iii) x4 +y4
Solution:
x2 + y2 = 29, xy = 2
(i) (x + y)2 = x2 + y2 + 2xy
= 29 + 2×2 = 29+ 4 = 33
∴ x + y= ±√33
(ii) (x – y)2 = x2 + y2 – 2xy
= 29- 2×2 = 29- 4 = 25
∴ x-y= ±√25= ±5
(iii) x2 + y2 = 29
Squaring on both sides,
(x2 + y2)2 = (29)2
⇒ (x2)2 + (y2)2 + 2x2y2 = 841
⇒ x4 +y + 2 (xy)2 = 841
⇒ x4 + y + 2 (2)2 = 841 (∵ xy = 2)
⇒ x4 + y + 2×4 = 841
⇒ x4 + y + 8 = 841
⇒ x4 + y = 841 – 8 = 833
∴ x4 +y = 833
Question 18.
What must be added to each of the following expressions to make it a whole square ?’
(i) 4x2 – 12x + 7
(ii) 4x2 – 20x + 20
Solution:
(i) 4x2 – 12x + 7 = (2x)2 – 2x 2x x 3 + 7
In order to complete the square,
we have to add 32 – 7 = 9 – 7 = 2
∴ (2x)2 – 2 x 2x x 3 + (3)2
= (2x-3)2
∴ Number to be added = 2
(ii) 4x2 – 20x + 20
⇒ (2x)2 – 2 x 2x x 5 + 20
In order to complete the square,
we have to add (5)2 – 20 = 25 – 20 = 5
∴ (2x)2 – 2 x 2x x 5 + (5)2
= (2x – 5)2
∴ Number to be added = 5
Question 19.
Simplify :
(i) (x-y) (x + y) (x2 + y2) (x4 + y4)
(ii) (2x – 1) (2x + 1) (4x2 + 1) (16x4 + 1)
(iii) (7m – 8m)2 + (7m + 8m)2
(iv) (2.5p -5q)2 – (1.5p – 2.5q)2
(v) (m2 – n2m)2 + 2m3n2
Solution:
(i) (x – y) (x + y) (x2 + y2) (x4 +y)
= (x2 – y2) (x2 + y) (x4 + y4)
= [(x2)2 – (y2)2] (x4+y4)
= (x4-y4) (x4+y4)
= (x4)2 – (y4)2 = x8 – y8
(ii) (2x – 1) (2x + 1) (4x2 + 1) (16x4 + 1)
= [(2x)2 – (1)2] (4x2 + 1) (16x4 + 1)
= (4x2 – 1) (4x2 + 1) (16x4 + 1)
= [(4x2)2-(1)2] (16x4+ 1)
= (16x4-1) (16x4+ 1)
= (16x4)2– (1)2 = 256x8 – 1
(iii) (7m – 8m)2 + (7m + 8n)2
= (7m)2 + (8n)2 – 2 x 7m x 8n + (7m)2 + (8n)2 + 2 x 7m x 8n
= 49m2 + 64m2 – 112mn + 49m2 + 64m2 + 112mn
= 98 m2 + 128n2
(iv) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
= (2.5p)2 + (1.5q)2 – 2 x 2.5p x 1.5q
= [(1.5p)2 + (1.5q)2 – 2 x 1.5 p x 2.5q]
= (6.25p2 + 2.25q2 – 7.5 pq) – (2.25p2 + 6.25q2-7.5pq)
= 6.25p2 + 2.25q2 – 7.5pq – 2.25p2 – 6.25q2 + 7.5pq
= 6.25p2 – 2.25p2 + 2.25g2 – 6.25q2
= 4.00P2 – 4.00q2
= 4p2 – 4q2 = 4 (p2 – q2)
(v) (m2 – n2m)2 + 2m3M2
= (m2)2 + (n2m)2 -2 x m2 x n2m + 2;m3m2
= m4 + n4m2 – 2m3n2 + 2m3n2
= m4 + n4m2 = m4 + m2n4
Question 20.
Show that :
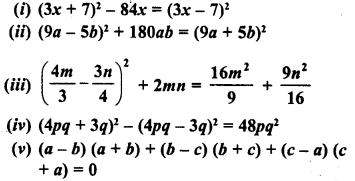
Solution:
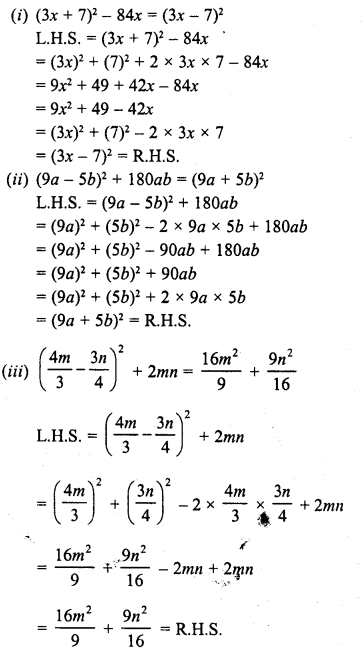
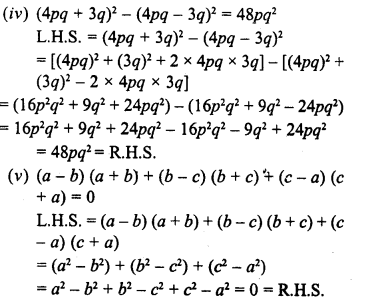
Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.