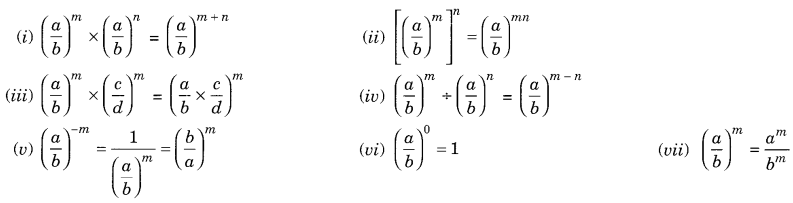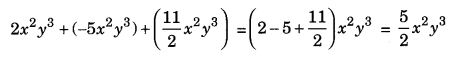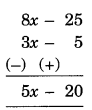CBSE Class 8

On this page, you will find Exponents and Powers Class 8 Notes Maths Chapter 12 Pdf free download. CBSE NCERT Class 8 Maths Notes Chapter 12 Exponents and Powers will seemingly help them to revise the important concepts in less time.

CBSE Class 8 Maths Chapter 12 Notes Exponents and Powers

Exponents and Powers Class 8 Notes Conceptual Facts

• A numeral (a)ⁿ is called an exponential expression where a is called base and n the exponent or power.
  aⁿ = a x a x a x a……… x a (n times)
• A negative rational number raised to an even power is always positive, \(\text { e.g. },\left(-\frac{1}{2}\right)^{4}=\frac{1}{16}\)
• A negative rational number raised to an odd power is always negative, i.e., \(=\left(-\frac{1}{2}\right)^{3}=-\frac{1}{8}\)

Laws of exponents:

On this page, you will find Mensuration Class 8 Notes Maths Chapter 11 Pdf free download. CBSE NCERT Class 8 Maths Notes Chapter 11 Mensuration will seemingly help them to revise the important concepts in less time.

CBSE Class 8 Maths Chapter 11 Notes Mensuration

Mensuration Class 8 Notes Conceptual Facts

1. Area of rectangle
A = Length x Breadth
= a x b sq. units

2. Area of square
A = (side)²
= a² sq. units

3. Area of triangle
A = \(\frac{1}{2}\) x b x h sq.units

4. Area of equilateral triangle
A = \(\frac{\sqrt{3}}{4} a^{2}\) sq.units

5. Area of parallelogram
A = b x h sq. units

6. Area of Circle
A = πr² sq. units

7. Area of trapezium
A = \(\frac{1}{2}\)(a + b) x h sq. units

8. Area of general quadrilateral
A = Area of ΔABC + area of ΔACD
= \(\frac{1}{2}\) (a + b) x AC sq. units

9. Area of rhombus
A = \(\frac{1}{2}\) (d₁ x d₂) sq. units

10. Surface area of cube
A = 6a² sq. units

11. Surface area of cuboid
A = 2 [ab + bc + ca] sq. units

12. Surface area of cylinder
A = 2πrh sq. units

13. Volume of cube V = a³ units

14. Volume of cuboid V = a x b x c cu. units

15. Volume of cylinder V = πr²h

On this page, you will find Visualising Solid Shapes Class 8 Notes Maths Chapter 10 Pdf free download. CBSE NCERT Class 8 Maths Notes Chapter 10 Visualising Solid Shapes will seemingly help them to revise the important concepts in less time.

CBSE Class 8 Maths Chapter 10 Notes Visualising Solid Shapes

Visualising Solid Shapes Class 8 Notes Conceptual Facts

3-D figures: Any shape which occupies space and has three dimensions, i.e., length, breadth and heights is called 3-D solid or a figure.

Parts of a solid objects:

• Face
• Vertex
• Edge

Types of Solids:

(i) Prism:

(ii) Pyramids:

(iii) Other Solid

Euler’s Formula:
Number of faces + Number of vertices – Number of edges = 2

On this page, you will find Algebraic Expressions and Identities Class 8 Notes Maths Chapter 9 Pdf free download. CBSE NCERT Class 8 Maths Notes Chapter 9 Algebraic Expressions and Identities will seemingly help them to revise the important concepts in less time.

CBSE Class 8 Maths Chapter 9 Notes Algebraic Expressions and Identities

Algebraic Expressions and Identities Class 8 Notes Conceptual Facts

1. Algebraic Expression: A combination of numbers which includes literal number connected by the
symbols +, -, x and + is called an algebraic expression.

For example: 5x, 8x -3, 2x + 3y, \(\frac{3}{4}\)x² 4xyz are some algebraic expressions.
Here. 5, 8, 3, 2. and 4 are constants and the literal numbers are x, y and z.

The different parts of the expression are called terms.
5x, 8x, 2x, 3y, \(\frac{3 x^{2}}{4}\) etc., are all the terms.

2. Coefficient: A coefficient is a multiplicative factor in some term of a polynomial. It is usually a number,
but may be only expression along.

For example in 7x² – 3xy + y + 3. The first three terms respectively have coefficient 7, -3 and 3 is a
constant in given polynomial.

3. Monomial: The expression having only one term is called monomial.
For example: 3x, 8xy, 6×2, 11xyz, etc.

4. Binomial: The expression containing two terms is called binomial.
Forexample: 2x +y,x +y, 3xy-5z, \(\frac{1}{2}\) xy + 5, etc.

5. Trinomial: The expression containing three terms is called trinomial.
For example: x + 2y + 3, xy – z +\(\frac{1}{2}\) , \(\frac{1}{2}\) x²+ 2x + 5, etc.

6. Polynomial: Algebraic expression containing one or more terms with non-zero coefficient is called a
polynomial.
For example: 2+3x, x+y+3z-5, \(\frac{1}{2}\) x²+yz -5, etc.

7. Like and Unlike Terms: Algebraic expressions having same combination of literal numbers are called
like terms.
For example: 4xy, -5xy, –\(\frac{17}{3}\) xy, are like terms.

8. Algebraic expressions having different combinations of literal numbers are called unlike terms.
For example: (xy, yz, zx), (2x², – 5xy², 7xyz), (3, – 5x, 7yz) etc.

9. Degree of Algebraic Expression: Highest power of the variable of an algebraic expression is called its degree.
For example: Degree of 3x² – 7x + 5 is 2.

Addition or Subtraction of two or more polynomials:

• Collect the like terms together.
• Find the sum or difference of the numerical coefficients of these terms.

For example:
(i) Add: 2x²y³, -5x²y³ + \(\frac{11}{2}\)x²y^z
Answer:

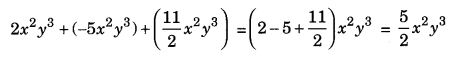
(ii) Subtract: (3x – 5) from (8x – 25)
Answer:

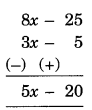
[Arrange the terms columnwise and change the sign of and add]

Multiplication Rule of Signs:
(+x) x (+y) = (+xy)
(+x) x (-y) = (-xy)
(-x) x (y) = (-xy)
(-x) x (-y) = (+xy)

On this page, you will find Comparing Quantities Class 8 Notes Maths Chapter 8 Pdf free download. CBSE NCERT Class 8 Maths Notes Chapter 8 Comparing Quantities will seemingly help them to revise the important concepts in less time.

CBSE Class 8 Maths Chapter 8 Notes Comparing Quantities

Comparing Quantities Class 8 Notes Conceptual Facts

1. In every hundred or per hundred is called as percent. For example: 30% means 30 in every hundred.
To change a percentage to a fraction:
40% \(\frac{40}{100}\)=0.4 , 125% = \(\frac{125}{100}\)=1.25

2. Percentage increase and decrease
Increase 240 by 10% = 240 + \(\frac{10}{100}\) x 240 = 240 + 24 = 264
Decrease 180 by 18% = 180 – \(\frac{18}{100}\) x 180 = 180 – 32.4 = 147.6

3. Profit and Loss
Profit = SP – CP,Loss= CP – SP

4. Profit and Loss are always calculated on CP.

5. Marked Price: The printed or the tagged price of an article is known as marked price or MP.

6. Discount: The deduction allowed on the market price is called Discount. It is generally given in percent.

7. Net Price: The selling price after the discount to an article is called its Net Price.

SP = MP – Discount
\(\mathrm{MP}=\left(\frac{100 \times \mathrm{SP}}{100-\mathrm{Discount} \%}\right)\)

8. Sales Tax: Sales tax is a tax levied by the Government on the selling price of an article at a rate given by the Government.

9. Value Added Tax (VAT): VAT is an extra tax which is levied and collected by State Government in lieu of State Tax.

10. Simple Interest:
\(\mathrm{SI}=\frac{\text { Principal } \times \text { Rate } \times \text { Time }}{100}\)

11. Compound Interest: Cl = Amount – Principal
\(\mathrm{CI}=\mathrm{P}\left(1+\frac{r}{100}\right)^{n}-\mathrm{P}\)

Amount = \(\mathrm{P}\left(1+\frac{r}{100}\right)^{n}\) where n represent time in years.

12. Conversion of Period:

• If interest is calculated half-yearly or semi-annually, then ‘r’ is halved and T is doubled.
• If interest is calculated quarterly, then V’ is one-fourth and T is four times.