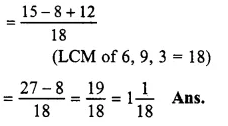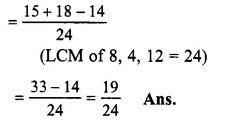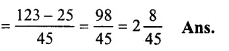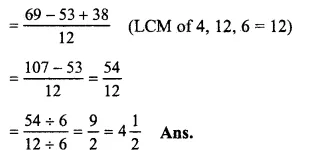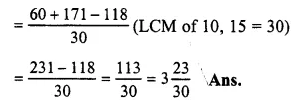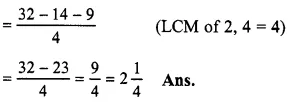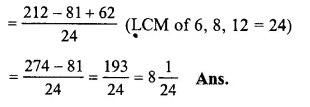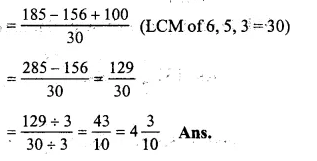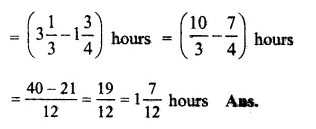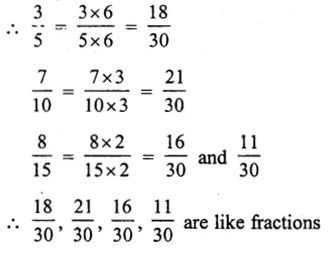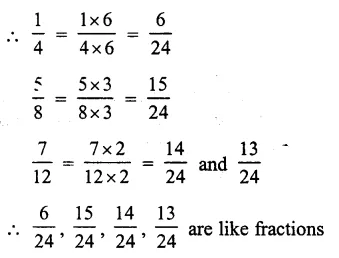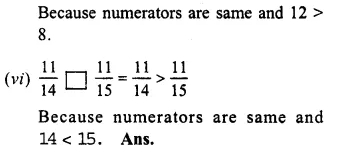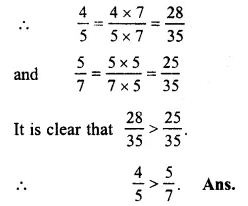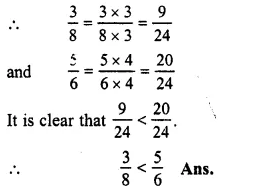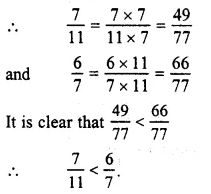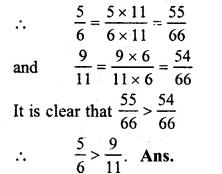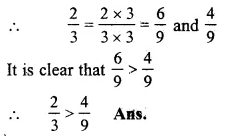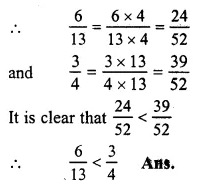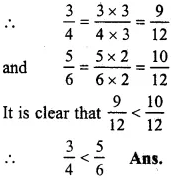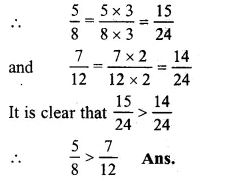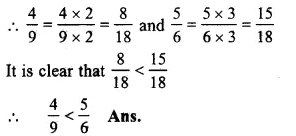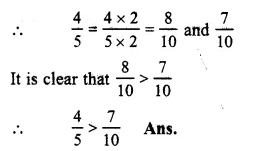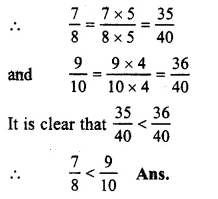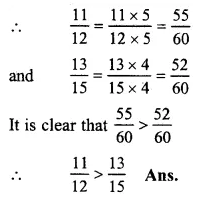CBSE Class 6

RS Aggarwal Class 6 Solutions Chapter 18 Circles Ex 18

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 18 Circles Ex 18

Question 1.
Solution:
Method :

Take a point O on the paper as shown in the figure. With the help of the rular, open out compasses in such a way that the distance between the metal point and pencil point is 4 cm. Take the compasses in the same position and put its metal point at O and draw the circle.
Remove the compasses and again open out the compasses in such a way that the distance between the metal point and pencil point is 5.3 cm. Taking O as the centre, draw another circle. Again remove the compasses and similarly draw the third circle with radius 6.2 cm. Then the required circles are as shown in the figure which have radius OA = 4 cm., OB = 5.3 cm. and OC = 6.2 cm.

Question 2.
Solution:
Method : Take a point C on the paper. With the help of the rular, open out the compasses in such a way that the distance between its metal point and pencil point is 4.5 cm. Take the compasses in the same position and put its metal point at C and draw the circle. Mark points P, Q and R as shown in the figure as required.

Question 3.
Solution:
Method : Take a point O on the paper. With the help of the rular, open out the compasses in such a way that the distance between the metal point and pencil point is 4 cm. Take the compasses in the same position and put the metal point at O and draw the circle.

Take A and B any points on the circle and join AB. ThenAB is the chord of the circle. Mark points X and Y on the circle as shown. Then arc AXB and arc AYB are the required minor and major arcs respectively.

Question 4.
Solution:
(i) False
(ii) True
(iii) False
(iv) False
(v) True.

Question 5.
Solution:
Steps of construction :
(i) With centre O and radius 3.7 cm, draw a circle.
(ii) Take a point A on the circumference of the circle.
(iii) Join OA.
(iv) At O, draw another radius OB such that ∠AOB = 72° with the help of protractor. Then sector AOB is the required one.

Question 6.
Solution:
(i) > (ii) < (iii) > (iv) >. Ans.

Question 7.
Solution:
(i) Passes through
(ii) at the centre, on the circle
(iii) chord
(iv) arc
(v) sector.

Hope given RS Aggarwal Solutions Class 6 Chapter 18 Circles Ex 18 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 17 Quadrilaterals Ex 17B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17B

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17A
• RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17B

Objective questions
Mark against the correct answer in each of the following :

Question 1.
Solution:
(c) ∵ Sum of angles of a quadrilateral is 360°.

Question 2.
Solution:
Sum of 4 angles of a quadrilateral = 360° and three angles of a quadrilateral are 80°, 70° and 120°
∵ Fourth angle = 360° – (80° + 70° + 120°)
= 360° – 270° – 90° (c)

Question 3.
Solution:
Sum of angles of a quadrilateral = 360°
The ratio in there four angles is 3 : 4 : 5 : 6

Question 4.
Solution:
(d) Y Quadrilateral having one pair of parallel sides is a trapezium.

Question 5.
Solution:
(d) ∵ Quadrilateral having opposite sides parallel is called a parallelogram.

Question 6.
Solution:
(b) ∵ A trapezium having nonparallel sides equal is called an isosceles trapezium.

Question 7.
Solution:
(b) ∵ Diagonals of a rhombus bisect each other at right angles.

Question 8.
Solution:
(b) ∵ A square has four equal sides and also diagonals are equal.

Question 9.
Solution:
A quadrilateral having two pairs of equal adjacent sides but unequal opposite angles is called a kite. (c)

Question 10.
Solution:
A regular quadrilateral is a quadrilateral having equal sides and equal angles which is a square. (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5F

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Find the difference:

Question 1.
Solution:
\(\frac { 5 }{ 8 } -\frac { 1 }{ 8 } \)
= \(\\ \frac { 5-1 }{ 8 } \)
= \(\frac { 4 }{ 8 } \)
= \(\frac { 4\div 4 }{ 8\div 4 } \)
= \(\frac { 1 }{ 2 } \)

Question 2.
Solution:
\(\frac { 7 }{ 12 } -\frac { 5 }{ 12 } \)

Question 3.
Solution:
\(4\frac { 3 }{ 7 } -2\frac { 4 }{ 7 } \)
= \(\frac { 31 }{ 7 } -\frac { 18 }{ 7 } \)

Question 4.
Solution:
\(\frac { 5 }{ 6 } -\frac { 4 }{ 9 } \)

Question 5.
Solution:
\(\frac { 1 }{ 2 } -\frac { 3 }{ 8 } \)

Question 6.
Solution:
\(\frac { 5 }{ 8 } -\frac { 7 }{ 12 } \)

Question 7.
Solution:
\(2\frac { 7 }{ 9 } -1\frac { 8 }{ 15 } \)
= \(\frac { 25 }{ 9 } -\frac { 23 }{ 15 } \)
(changing into improper fractions)

Question 8.
Solution:
\(3\frac { 5 }{ 8 } -2\frac { 5 }{ 12 } \)
= \(\frac { 29 }{ 8 } -\frac { 29 }{ 12 } \)

Question 9.
Solution:
\(2\frac { 3 }{ 10 } -1\frac { 7 }{ 15 } \)
= \(\frac { 23 }{ 10 } -\frac { 22 }{ 15 } \)

Question 10.
Solution:
\(6\frac { 2 }{ 3 } -3\frac { 3 }{ 4 } \)
= \(\frac { 20 }{ 3 } -\frac { 15 }{ 4 } \)

Question 11.
Solution:
\(7-5\frac { 2 }{ 3 } \)
= \(\frac { 7 }{ 1 } -\frac { 17 }{ 3 } \)
(changing into improper fractions)

Question 12.
Solution:
\(10-6\frac { 3 }{ 8 } \)
= \(\frac { 10 }{ 1 } -\frac { 51 }{ 8 } \)
(changing into improper fractions)

Simpilify

Question 13.
Solution:
\(\frac { 5 }{ 6 } -\frac { 4 }{ 9 } +\frac { 2 }{ 3 } \)

Question 14.
Solution:
\(\frac { 5 }{ 8 } +\frac { 3 }{ 4 } -\frac { 7 }{ 12 } \)

Question 15.
Solution:
\(2+\frac { 11 }{ 15 } -\frac { 5 }{ 9 } \)
= \(\frac { 90+33-25 }{ 45 } \)
(LCM of 15 and 9 = 45)

Question 16.
Solution:
\(5\frac { 3 }{ 4 } -4\frac { 5 }{ 12 } +3\frac { 1 }{ 6 } \)
= \(\frac { 23 }{ 4 } -\frac { 53 }{ 12 } +\frac { 19 }{ 6 } \)
(changing into improper fractions)

Question 17.
Solution:
\(2+5\frac { 7 }{ 10 } -3\frac { 14 }{ 15 } \)
= \(\frac { 2 }{ 1 } +\frac { 57 }{ 10 } -\frac { 59 }{ 15 } \)
(changing into improper fractions)

Question 18.
Solution:
\(8-3\frac { 1 }{ 2 } -2\frac { 1 }{ 4 } \)
= \(\frac { 8 }{ 1 } -\frac { 7 }{ 2 } -\frac { 9 }{ 4 } \)
(changing into improper fractions)

Question 19.
Solution:
\(8\frac { 5 }{ 6 } -3\frac { 3 }{ 8 } +2\frac { 7 }{ 12 } \)
= \(\frac { 53 }{ 6 } -\frac { 27 }{ 8 } +\frac { 31 }{ 12 } \)
(changing into improper fractions)

Question 20.
Solution:
\(6\frac { 1 }{ 6 } -5\frac { 1 }{ 5 } +3\frac { 1 }{ 3 } \)
= \(\frac { 37 }{ 6 } -\frac { 26 }{ 5 } +\frac { 10 }{ 3 } \)
(changing into improper fractions)

Question 21.
Solution:
\(3+1\frac { 1 }{ 5 } +\frac { 2 }{ 3 } -\frac { 7 }{ 15 } \)
= \(\frac { 3 }{ 1 } +\frac { 6 }{ 5 } +\frac { 2 }{ 3 } -\frac { 7 }{ 15 } \)

Question 22.
Solution:
By subtracting \(9 \frac { 2 }{ 3 } \) from 19, we get the required number

Question 23.
Solution:
By subtracting \(6 \frac { 7 }{ 15 } \) from \(8 \frac { 1 }{ 5 } \) we get the required number

Question 24.
Solution:
Sum of \(3 \frac { 5 }{ 9 } \) and \(3 \frac { 1 }{ 3 } \)
= \(\frac { 32 }{ 9 } +\frac { 10 }{ 3 } \)

Question 25.
Solution:
\(\\ \frac { 3 }{ 4 } \), \(\\ \frac { 5 }{ 7 } \)

Question 26.
Solution:
Milk bought by Mrs. Soni = \(7 \frac { 1 }{ 2 } \) litres
and milk consumed by here = \(5 \frac { 3 }{ 4 } \) litres

Question 27.
Solution:
Total time of film show = \(3 \frac { 1 }{ 3 } \) hours
Total spent on advertisement = \(1 \frac { 3 }{ 4 } \) hours
Duration of the film

Question 28.
Solution:
On a day, rickshaw pullar earned

Question 29.
Solution:
Total length of wire =\(2 \frac { 3 }{ 4 } \)-metres
Length of one piece = \(\\ \frac { 5 }{ 8 } \) metre
Length of the other piece

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Find the sum :

Question 1.
Solution:
\(\frac { 5 }{ 8 } +\frac { 1 }{ 8 } \)

Question 2.
Solution:
\(\frac { 4 }{ 9 } +\frac { 8 }{ 9 } \)

Question 3.
Solution:
\(1\frac { 3 }{ 5 } +2\frac { 4 }{ 5 } \)
\(\frac { 8 }{ 5 } +\frac { 14 }{ 5 } \)

Question 4.
Solution:
\(\frac { 2 }{ 5 } +\frac { 5 }{ 6 } \)
= \(\\ \frac { 4+15 }{ 18 } \) (LCM of 9 and 6 = 18)
= \(\\ \frac { 19 }{ 18 } \)
= \(1 \frac { 1 }{ 18 } \)

Question 5.
Solution:
\(\frac { 7 }{ 12 } +\frac { 9 }{ 16 } \)

Question 6.
Solution:
\(\frac { 4 }{ 15 } +\frac { 17 }{ 20 } \)

Question 7.
Solution:
\(2\frac { 3 }{ 4 } +5\frac { 5 }{ 6 } \)
= \(\frac { 11 }{ 4 } +\frac { 35 }{ 6 } \)

Question 8.
Solution:
\(3\frac { 1 }{ 8 } +1\frac { 5 }{ 12 } \)
= \(\frac { 25 }{ 8 } +\frac { 17 }{ 12 } \)

Question 9.
Solution:
\(2\frac { 7 }{ 10 } +3\frac { 8 }{ 15 } \)
= \(\frac { 27 }{ 10 } +\frac { 53 }{ 15 } \)

Question 10.
Solution:
\(3\frac { 2 }{ 3 } +1\frac { 5 }{ 6 } +2 \)
\(\frac { 11 }{ 3 } +\frac { 11 }{ 6 } +\frac { 2 }{ 1 } \)

Question 11.
Solution:
\(3+1\frac { 4 }{ 15 } +1\frac { 3 }{ 20 } \)
=\(\frac { 3 }{ 1 } +\frac { 19 }{ 15 } +\frac { 23 }{ 20 } \)

Question 12.
Solution:
\( 3\frac { 1 }{ 3 } +4\frac { 1 }{ 4 } +6\frac { 1 }{ 6 } \)
\(\frac { 10 }{ 3 } +\frac { 17 }{ 4 } +\frac { 37 }{ 6 } \)
(changing into improper fractions)

Question 13.
Solution:
\(\frac { 2 }{ 3 } +3\frac { 1 }{ 6 } +4\frac { 2 }{ 9 } +2\frac { 5 }{ 18 } \)
\(\frac { 2 }{ 3 } +\frac { 19 }{ 6 } +\frac { 38 }{ 9 } +\frac { 41 }{ 18 } \)

Question 14.
Solution:
\(2\frac { 1 }{ 3 } +1\frac { 1 }{ 4 } +2\frac { 5 }{ 6 } +3\frac { 7 }{ 12 } \)

Question 15.
Solution:
\(2+\frac { 3 }{ 4 } +1\frac { 5 }{ 6 } +3\frac { 7 }{ 16 } \)
\(\frac { 2 }{ 1 } +\frac { 3 }{ 4 } +\frac { 13 }{ 8 } +\frac { 55 }{ 16 } \)

Question 16.
Solution:
Cost of a pencil = Rs. \(3 \frac { 2 }{ 5 } \)
Cost of an eraser = Rs.\(2 \frac { 7 }{ 10 } \)

Question 17.
Solution:
Length of cloth for kurta = \(4 \frac { 1 }{ 2 } \) metres
Length of cloth for pyjamas = \(2 \frac { 2 }{ 3 } \) metres

Question 18.
Solution:
Distance travelled by Rickshaw = \(4 \frac { 3 }{ 4 } \) km
Distance travelled on foot = \(1 \frac { 1 }{ 2 } \) km

Question 19.
Solution:
Weight of empty cylinder = \(16 \frac { 4 }{ 5 } \) kg
Weight of gas filled in it = \(14 \frac { 2 }{ 3 } \) kg
Total. weight of cylinder with gas

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Question 1.
Solution:
(i) Like fraction : Fractions having the same denominators are called like fractions. For examples:
\(\frac { 2 }{ 11 } ,\frac { 3 }{ 11 } ,\frac { 4 }{ 11 } ,\frac { 5 }{ 11 } ,\frac { 8 }{ 11 } \)
(ii) Unlike fraction : Fraction having the different denominators, are called unlike fractions. For examples:
\(\frac { 1 }{ 3 } ,\frac { 4 }{ 7 } ,\frac { 5 }{ 9 } ,\frac { 3 }{ 8 } ,\frac { 7 }{ 11 } \)

Question 2.
Solution:
We know that like fractions have same denominator
Now \(\frac { 3 }{ 5 } ,\frac { 7 }{ 10 } ,\frac { 8 }{ 15 } ,\frac { 11 }{ 30 } \)
LCM of 5, 10, 15 and 30 = 30

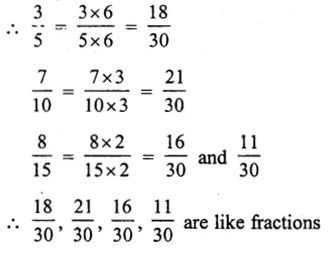
Question 3.
Solution:
We know that like fraction have same denominators
\(\frac { 1 }{ 4 } ,\frac { 5 }{ 8 } ,\frac { 7 }{ 12 } ,\frac { 13 }{ 24 } \)
LCM of 4, 8, 12, 24 = 24

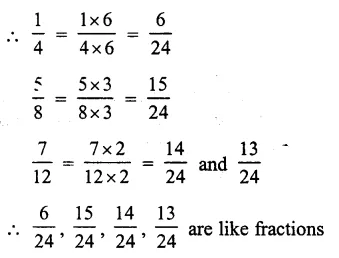
Question 4.
Solution:

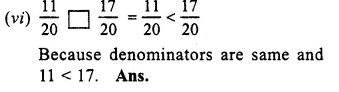
Question 5.
Solution:

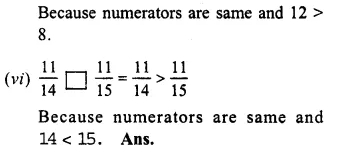
Compare the fractions given below :

Question 6.
Solution:
\(\frac { 4 }{ 5 } and\frac { 5 }{ 7 } \)
LCM of 5 and 7 = 35

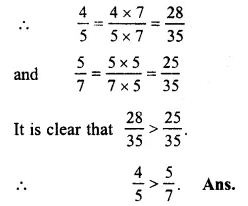
Question 7.
Solution:
\(\frac { 3 }{ 8 } and\frac { 5 }{ 6 } \)
LCM of 8 and 6 = 24

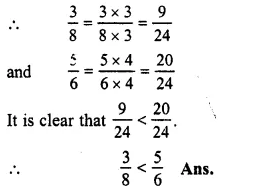
Question 8.
Solution:
\(\frac { 7 }{ 11 } and\frac { 6 }{ 7 } \)
LCM of 11 and 7 = 77

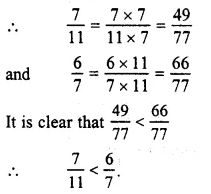
Question 9.
Solution:
\(\frac { 5 }{ 6 } and\frac { 9 }{ 11 } \)
LCM of 6 and 11 = 66

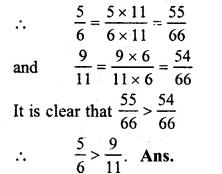
Question 10.
Solution:
\(\frac { 2 }{ 3 } and\frac { 4 }{ 9 } \)
LCM of 3 and 9 = 9

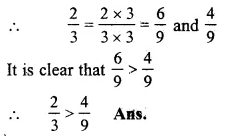
Question 11.
Solution:
\(\frac { 6 }{ 13 } and\frac { 3 }{ 4 } \)
LCM of 13 and 4 = 52

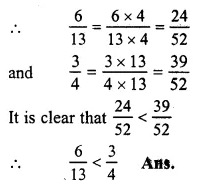
Question 12.
Solution:
\(\frac { 3 }{ 4 } and\frac { 5 }{ 6 } \)
LCM of 4 and 6 = 12

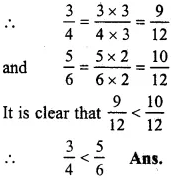
Question 13.
Solution:
\(\frac { 5 }{ 8 } and\frac { 7 }{ 12 } \)
LCM of 8 and 12 = 24

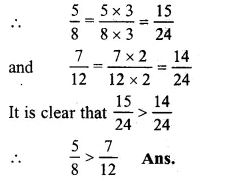
Question 14.
Solution:
\(\frac { 4 }{ 9 } and\frac { 5 }{ 6 } \)
LCM of 9 and 6 = 18

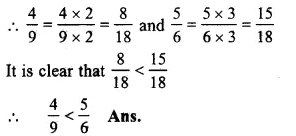
Question 15.
Solution:
\(\frac { 4 }{ 5 } and\frac { 7 }{ 10 } \)
LCM of 5 and 10 = 10

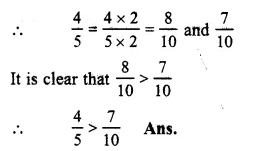
Question 16.
Solution:
\(\frac { 7 }{ 8 } and\frac { 9 }{ 10 } \)
LCM of 8 and 10 = 40

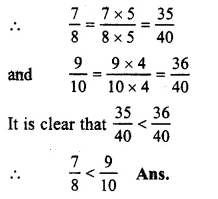
Question 17.
Solution:
\(\frac { 11 }{ 12 } and\frac { 13 }{ 15 } \)
LCM of 12 and 15 = 60

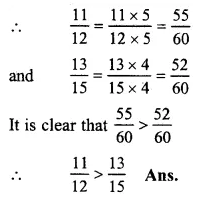
Question 18.
Solution:
\(\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,\frac { 5 }{ 6 } and\frac { 7 }{ 8 } \)
LCM of 2, 4, 6 and 8 = 24

Question 19.
Solution:
\(\frac { 2 }{ 3 } ,\frac { 5 }{ 6 } ,\frac { 7 }{ 9 } and\frac { 11 }{ 18 } \)
LCM of 3, 6, 9 and 18 = 18

Question 20.
Solution:
\(\frac { 2 }{ 5 } ,\frac { 7 }{ 10 } ,\frac { 11 }{ 15 } and\frac { 17 }{ 30 } \)
LCM of 5, 10, 15 and 30 = 30

Question 21.
Solution:
\(\frac { 3 }{ 4 } ,\frac { 7 }{ 8 } ,\frac { 11 }{ 16 } and\frac { 23 }{ 32 } \)
LCM of 4, 8, 16 and 32 = 32

Arrange the following fractions in the descending order :

Question 22.
Solution:
\(\frac { 3 }{ 4 } ,\frac { 5 }{ 8 } ,\frac { 11 }{ 12 } and\frac { 17 }{ 24 } \)
LCM of 4, 8, 12 and 24 = 24

Question 23.
Solution:
\(\frac { 7 }{ 9 } ,\frac { 5 }{ 12 } ,\frac { 11 }{ 18 } and\frac { 17 }{ 36 } \)
LCM of 9, 12, 18 and 36 = 36

Question 24.
Solution:
\(\frac { 2 }{ 3 } ,\frac { 3 }{ 5 } ,\frac { 7 }{ 10 } and\frac { 8 }{ 15 } \)
LCM of 3, 5, 10 and 15 = 30

Question 25.
Solution:
\(\frac { 5 }{ 7 } ,\frac { 9 }{ 14 } ,\frac { 17 }{ 21 } and\frac { 31 }{ 42 } \)
LCM of 7, 14, 21 and 42 = 42

Question 26.
Solution:
∴ the numerators are equal
∴ The fraction having small denominator is greater than the fraction having large denominator
∴ In descending order, we can write
\(\frac { 1 }{ 12 } ,\frac { 1 }{ 23 } ,\frac { 1 }{ 7 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 17 } ,\frac { 1 }{ 50 } \)

Question 27.
Solution:
Here, the numerators of all fractions are equal
∴ The fraction having small denominator is greater than the fraction having large denominator
Now in descending order is
\(\frac { 3 }{ 4 } ,\frac { 3 }{ 5 } ,\frac { 3 }{ 7 } ,\frac { 3 }{ 11 } ,\frac { 3 }{ 13 } ,\frac { 3 }{ 17 } \)

Question 28.
Solution:
Lalita read 30 pages of a book containing 100 pages
She read \(\\ \frac { 30 }{ 100 } \) = \(\\ \frac { 3 }{ 10 } \) part of the book and Sarita read \(\\ \frac { 2 }{ 5 } \) of the book
Now in \(\\ \frac { 3 }{ 10 } \) and \(\\ \frac { 2 }{ 5 } \), LCM of 10, 5 = 10
\(\\ \frac { 3 }{ 10 } \) = \(\\ \frac { 3 }{ 10 } \)
\(\\ \frac { 2 }{ 5 } \) = \(\\ \frac { 2\times 2 }{ 5\times 2 } \) = \(\\ \frac { 4 }{ 10 } \)
From above, Sarita read more
as \(\\ \frac { 4 }{ 10 } \) or \(\frac { 2 }{ 5 } >\frac { 3 }{ 10 } \)

Question 29.
Solution:
Rafiq exercised for \(\\ \frac { 2 }{ 3 } \) hour and Rohit exercised for \(\\ \frac { 3 }{ 4 } \) hour
In \(\\ \frac { 2 }{ 3 } \) and \(\\ \frac { 3 }{ 4 } \), LCM of 3 and 4 = 12
\(\\ \frac { 2 }{ 3 } \) = \(\\ \frac { 2\times 4 }{ 3\times 4 } \) = \(\\ \frac { 8 }{ 12 } \)
\(\\ \frac { 3 }{ 4 } \) = \(\\ \frac { 3\times 3 }{ 4\times 3 } \) = \(\\ \frac { 9 }{ 12 } \)
\(\frac { 9 }{ 12 } >\frac { 8 }{ 12 } \)
=> \(\frac { 3 }{ 4 } >\frac { 2 }{ 3 } \)
∴ Rohit exercised more time

Question 30.
Solution:
In VI A, 20 student passed out of 25 or \(\\ \frac { 20 }{ 25 } \) or \(\\ \frac { 4 }{ 5 } \) students passed
But in VI B, 24 out of 30 passed 24 or \(\\ \frac { 24 }{ 30 } \) or \(\\ \frac { 4 }{ 5 } \) students passed
Now \(\\ \frac { 4 }{ 5 } \) = \(\\ \frac { 4 }{ 5 } \)
∴ Both sections gave same result

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.