CBSE Class 12

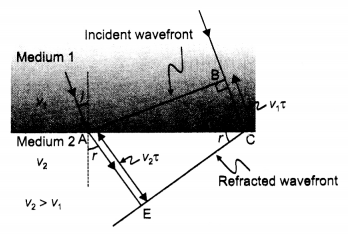
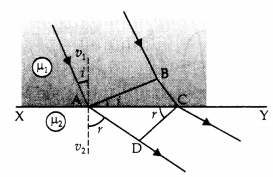
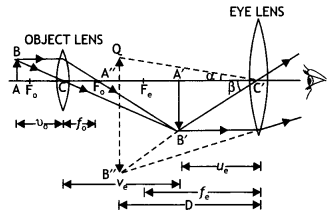
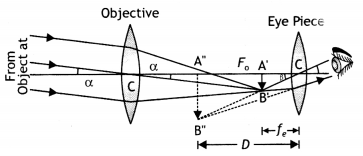
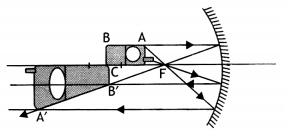
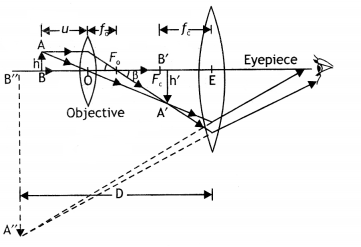
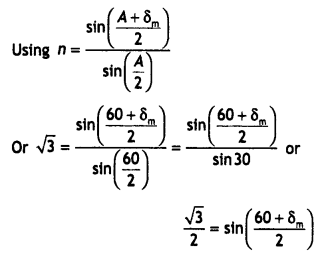
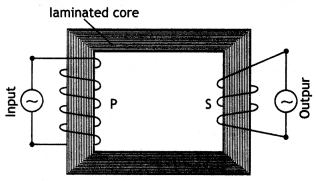
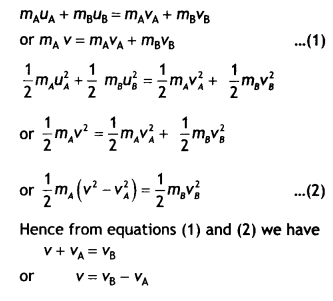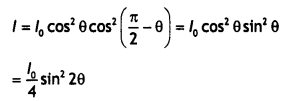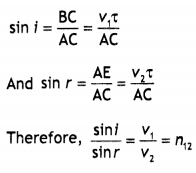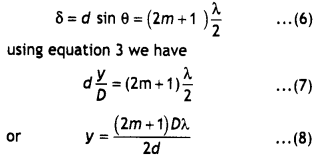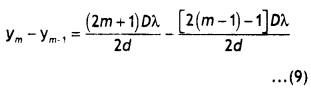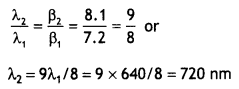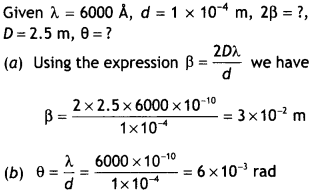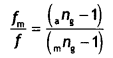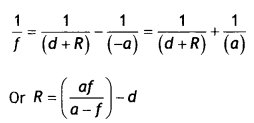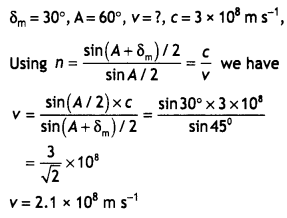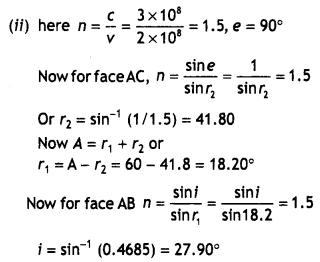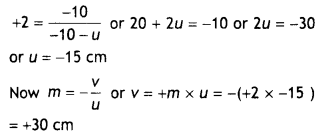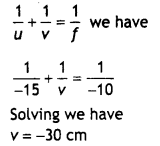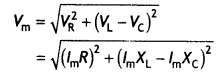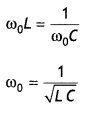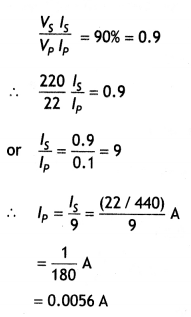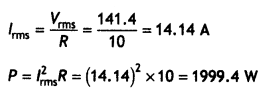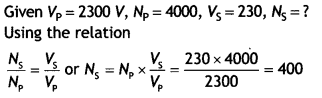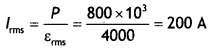Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 11 Dual Nature of Radiation and Matter. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 11 Important Extra Questions Dual Nature of Radiation and Matter

Dual Nature of Radiation and Matter Important Extra Questions Very Short Answer Type

Question 1.
If the maximum kinetic energy of electrons emitted by photocell is 4 eV, what is the stopping potential?
Answer:
The stopping potential is 4 V.

Question 2.
Two metals A and B have a work function 4 eV and 10 eV respectively. Which metal has a higher threshold wavelength?
Answer:
The threshold wavelength is inversely proportional to the work function. Therefore metal A has a higher threshold wavelength.

Question 3.
Ultraviolet light is incident on two photo-sensitive materials having work functions W₁ and W₂ (W₁ > W₂). In which case will the kinetic energy of the emitted electrons be greater? Why?
Answer:
The kinetic energy of the emitted photoelectrons is given by 1/2 mv² = hv – W; therefore the lesser the work function for a given frequency, the more is the kinetic energy of the emitted photoelectrons. Since W₂ < W₁, kinetic energy will be more for the metal having work function W₂.

Question 4.
Does the threshold frequency depend on the intensity of light?
Answer:
No, it does not.

Question 5.
Name the experiment which establishes the wave nature of a particle.
Answer:
Davison-Germer experiment.

Question 6.
Mention one physical process for the release of electrons from a metal surface.
Answer:
Photoelectric effect.

Question 7.
Name a phenomenon that illustrates the particle nature of light.
Answer:
Photoelectric effect.

Question 8.
Define the work function for a given metallic surface.
Answer:
The minimum amount of energy required to just eject an electron from a given metal surface is called the work function for that metal surface.

Question 9.
What is the value of stopping potential between the cathode and anode of a photocell, if the maximum kinetic energy of the electrons emitted is 5 eV?
Answer:
Stopping potential = 5 V.

Question 10.
Define the term ‘stopping potential’ in relation to the photoelectric effect. (CBSE AI 2011)
Answer:
It is the negative potential of the collector plate for which no photoelectron reaches the collector plate.

Question 11.
Write the relationship of de-Broglie wavelength associated with a particle of mass m in terms of its kinetic energy E. (CBSE Delhi 2011C)
Answer:
The required relation is λ = \(\frac{h}{\sqrt{2 m E}}\)

Question 12.
State de-Broglie hypothesis. (CBSE Delhi 2012)
Answer:
It states that moving particles should possess a wave nature.

Question 13.
Define the term “threshold frequency”, in the context of photoelectric emission. (CBSE Delhi 2019)
Answer:
It is the minimum frequency of incident radiation (light) that can cause photoemission from a given photosensitive surface.
Or
Define the term “Intensity” in the photon picture of electromagnetic radiation. (CBSE Delhi 2019)
Answer:
It is defined as the number of energy quanta (photons) per unit area per unit time.

Question 14.
Write the expression for the de-Broglie wavelength associated with a charged particle having charge ‘q’ and mass ‘m’, when it is accelerated by a potential V. (CBSE AI 2013)
Answer:
The expression is λ = \(\frac{h}{\sqrt{2 m q V}}\)

Question 15.
Define the intensity of radiation on the basis of the photon picture of light. Write its SI unit. (CBSE AI 2014)
Answer:
The intensity of radiation is defined as the number of energy quanta per unit area per unit time. It is measured in W m-2.

Question 16.
Name the phenomenon which shows the quantum nature of electromagnetic radiation. (CBSE Al 2017)
Answer:
Photoelectric effect.

Question 17.
If the distance between the source of light and the cathode of a photocell is doubled how does it affect the stopping potential applied to the photocell? (CBSE Delhi 2017C)
Answer:
No effect.

Question 18.
Draw graphs showing the variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity. (CBSE AI 2018)
Answer:
The graphs are as shown.

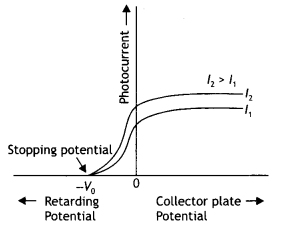
Question 19.
An electron is accelerated through a potential difference V. Write the expression for its final speed if it was initially at rest. (CBSE AI Delhi 2018C)
Answer:
Using eV = \(\frac{1}{2}\)mv² or v = \(\sqrt{\frac{2 e V}{m}}\)

Question 20.
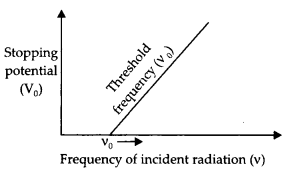
Write the name given to the frequency v0, in the following graph (showing the variation of stopping potential (V_o) with the frequency (v) of the incident radiation) for a given photosensitive material. Also name the constant, for that photosensitive material, obtained by multiplying v_c with Planck’s constant.

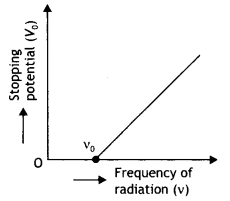
Answer:
The constant obtained by multiplying v0 with Planck’s constant is called the work function of the material. This frequency is called the threshold frequency.

Question 21.
Electrons are emitted from a photosensitive surface when it is illuminated by green light but electron emission does not take place by yellow light. Will the electrons are emitted when the surface is illuminated by
(a) red light
Answer:
No electron will be emitted when illuminated by a red light.

(b) blue light?
Answer:
Electron emission takes place with blue light.

Question 22.
The frequency (v) of incident radiation is greater than the threshold frequency v0 in a photocell. How will the stopping potential vary if frequency (v) is increased keeping other factors constant?
Answer:
On increasing the frequency v of the incident light, the value of stopping potential also increases.

Question 23.
How much time is taken by a photoelectron to come out of a metal surface, when the light of wavelength less than threshold wavelength λ_o is incident on it?
Answer:
It is an instantaneous process. The time required is of the order of a nanosecond (10^-9 s).

Question 24.
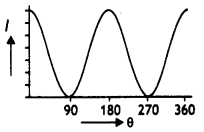
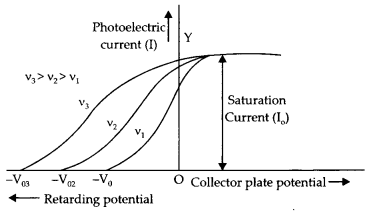
The given graphs show the variation of photoelectric current (l) with the applied voltage (V) for two different materials and for two different intensities of the incident radiations. Identify the pairs of curves that correspond to different materials but the same intensity of incident radiations.

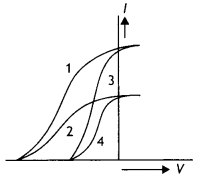
Answer:
Pairs 1 – 2 and pairs 3 – 4

Question 25.
Red light, however bright, cannot cause the emission of electrons from a clean zinc surface. But even weak ultraviolet radiations can do so. Why?
Answer:
This is because the threshold frequency of the given metal is greater than the frequency of red light.

Question 26.
If the intensity of incident radiation on metal is doubled, what happens to the kinetic energy of electrons emitted?
Answer:
The kinetic energy of emitted electrons remains unchanged.

Question 27.
If the intensity of the incident radiation in a photocell is increased, how does the stopping potential vary?
Answer:
Stopping potential remains unaffected.

Question 28.
The work function of aluminium is 4.2 eV. If two photons each of energy 2.5 eV are incident on a surface, will the emission of photoelectron take place?
Answer:
No, emission of photoelectron will not take place.

Question 29.
A photon and an electron have the same de-Broglie wavelength. Which is moving faster?
Answer:
Photon is moving faster with a speed c = 3 × 10⁸ ms^-1. An electron must have a velocity less than the speed of light.

Question 30.
Does the ‘stopping potential’ in photoelectric emission depend upon
(i) the intensity of the incident radiation in a photocell
Answer:
No

(ii) the frequency of the incident radiation?
Answer:
Yes.

Question 31.
The de-Broglie wavelengths, associated with a proton and a neutron, are found to be equal. Which of the two has a higher value for kinetic energy?
Answer:
Proton.

Question 32.
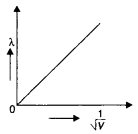
The figure shows a plot of \(\frac{1}{\sqrt{V}}\) where V is the accelerating potential vs the de-Broglie wavelength λ in case of two particles having the same charge q but different masses m₁ and m₂. Which line A or B represents the particle of greater mass? (CBSE AI 2013C)

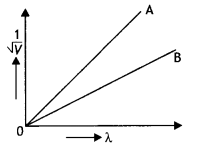
Answer:
Particle A

Question 33.
Do X-rays exhibit the phenomenon of the photoelectric effect?
Answer:
Yes, they do exhibit the phenomenon of the photoelectric effect.

Question 34.
Draw a graph showing the variation of de-Broglie wavelength with the momentum of an electron. (CBSE AI 2019)
Answer:
The graph is shown below.

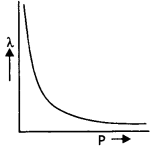
Question 35.
The work function of two metals A and B are 2 eV and 5 eV respectively. Which of these is suitable for a photoelectric cell using visible tight?
Answer:
Metal A having a lower work function of 2 eV is suitable for use with visible light.

Question 36.
Estimate the frequency associated with a Photon of energy 2 eV. (CBSE Delhi 2019C)
Answer:
Since E = hv

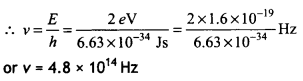
Question 37.
For a given photosensitive material and with a source of the constant frequency of incident radiation, how does the photocurrent vary with the intensity of incident light? (CBSE AI 2011C)
Answer:
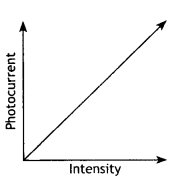
The photoelectric current increases linearly with the intensity of light.

Question 38.
Draw a graph showing the variation of the de-Broglie wavelength of an electron as a function of its kinetic energy. (CBSE Delhi 2015C)
Answer:
The graph is as shown.

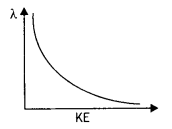
Question 39.
(a) In the explanation of the photoelectric effect, we assume one photon of frequency v collides with an electron and transfers its energy. This leads to the equation for the maximum energy E_max of the emitted electron as E_max = hv – Φ_o where Φ_o is the work function of the metal. If an electron absorbs 2 photons (each of frequency v), what will be the maximum energy for the emitted electron?
Answer:
Emax = 2hv – Φ

(b) Why is this fact (two photons absorption) not taken into consideration in our discussion of the stopping potential? (NCERT Exemplar)
Answer:
The probability of absorbing 2 photons by the same electron is very low. Hence ’ such emissions will be negligible.

Question 40.
Do all the electrons that absorb a photon comes out as photoelectrons? (NCERT Exemplar)
Answer:
No, most electrons get scattered into the metal. Only a few come out of the surface of the metal.

Dual Nature of Radiation and Matter Important Extra Questions Short Answer Type

Question 1.
An a-particle and a proton of the same kinetic energy are in turn allowed to pass through a magnetic field B, acting normal to the direction of motion of the particles. Calculate the ratio of radii of the circular paths described by them. (CBSE Delhi 2019)
Answer:
Given q_α = 2e, q_p = e, K_α = K_p, mα = 4m_p, r_α/r_p = ?
Using the expression
r = \(\frac{\sqrt{2 m K}}{q B}\) we have

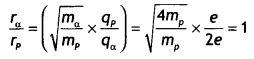
Question 2.
How will the photoelectric current change on decreasing the wavelength of incident radiation for a given photosensitive material?
Answer:
Photoelectric current is independent of the wavelength of the incident radiation. Therefore there will be no change in the photoelectric current.

Question 3.
Estimate the ratio of the wavelengths associated with the electron orbiting around the nucleus in the ground and first excited states of a hydrogen atom. (CBSE Delhi 2019C)
Answer:
Since De Brogue’s hypothesis is related to
Bohr’s atomic model as

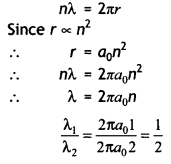
Question 4.
Show graphically how the stopping potential for a given photosensitive surface varies with the frequency of the incident radiation.
Answer:
The required graph is as shown

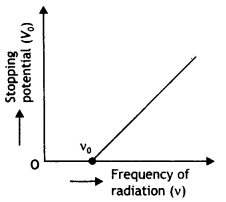
Question 5.
the de-Broglie wavelength associated with an electron accelerated through a potential difference V is λ. What will be its wavelength when accelerating potential is increased to 4 V?
Answer:
The de-BrogLie wavelength is inversely proportional to the square root of potential, therefore = \(\frac{\lambda_{2}}{\lambda_{1}}=\frac{\sqrt{V}}{\sqrt{4 V}}=\frac{1}{2}\) . Thus wavelength
wilt become half of its previous value.

Question 6.
Plot a graph showing the variation of de Brogue wavelength (λ) associated with a charged particle of mass m, versus \(\frac{1}{\sqrt{V}}\) where V is the potential difference through which the particle is accelerated. How does this graph give us information regarding the magnitude of the charge of the particle? (CBSE Dethi 2019)
Answer:
The plot is as shown.


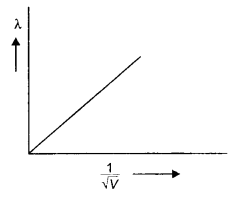
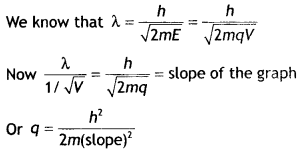
Question 7.
X-rays of wavelength ‘λ’ fall on a photosensitive surface, emitting electrons. Assuming that the work function of the surface can be neglected, prove that the de-Broghe wavelength of the electrons emitted will be \(\sqrt{\frac{h \lambda}{2 m c}}\)
Answer:
The energy possessed by X-rays of wavelength λ is given by E=hc / λ.
Consider an electron of mass charge e to be accelerated the potential difference of V volts the velocity gained by it.

Then kinetic energy of electron is
E = \(\frac{1}{2} m v^{2}\) = eV
or
v = \(\sqrt{\frac{2 \mathrm{eV}}{\mathrm{m}}}=\sqrt{\frac{2 E}{m}}\)

If λ is the de-Broglie wavelength associated with an electron, then

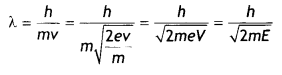
Substituting for e, we have

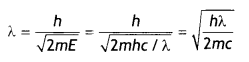
Question 8.
Explain with the help of Einstein’s photoelectric equation any two observed features in the photoelectric effect. cannot be explained by the wave theory. (CBSE Delhi 2019)
Answer:
According to Einstein’s equation, we have
\(\frac{1}{2} m v_{\max }^{2}\) = h(v – vo)

Two features
(a) Maximum energy is directly proportional to the frequency
(b) Existence of threshold frequency Explanation of two features:

1. The energy of the photon is directly proportional to the frequency
2. No photoelectric emission is possible if hv < hv_o

Question 9.
Why is the wave theory of electromagnetic radiation not able to explain the photoelectric effect? How does the photon picture resolve this problem? (CBSE Delhi 2019)
Answer:
According to the wave theory, the more intense a beam, more is the kinetic energy it will impart to the photoelectron. This does not agree with the experimental observations (max K.E. of the emitted photoelectron is independent of intensity) on the photoelectric effect. Also according to the wave theory photoemission can occur at all frequencies.

The photon picture resolves this problem by saying that light in interaction with matter behaves as if it is made of quanta or packets of energy, each of energy hv. This picture enables us to get a correct explanation of all the observed experimental features of the photoelectric effect.

Question 10.
(a) Define the terms,
(i) threshold frequency and
(ii) stopping potential in the photoelectric effect.
(b) Plot a graph of photocurrent versus anode potential for radiation of frequency v and intensities l₁ and l₂. (l₁ < l₂). (CBSE Delhi 2019)
Answer:
(a) Threshold frequency: It is the frequency of the incident radiation below which photoelectric effect does not take place.
Stopping potential: It is the minimum negative (retarding) potential, given to the anode (collector plate) for which the photocurrent stops or becomes zero.

(b) The plot is as shown.

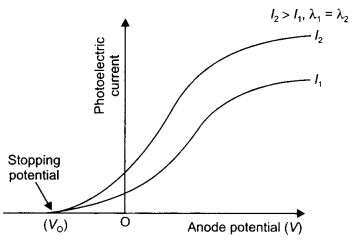
Question 11.
A proton and a particle are accelerated through the same potential difference. Which one of the two has
(i) greater de-Broglie wavelength, and
(ii) less kinetic energy? Justify your answer. (CBSE AI 2016)
Answer:
(i) We know that λ = \(\frac{h}{\sqrt{2 m q V}}\), therefore
we have

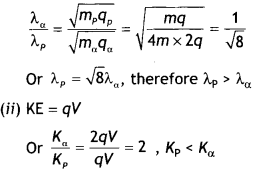
Question 12.
Plot a graph showing the variation of de-Broglie wavelength λ versus \(\frac{1}{\sqrt{V}}\) where V is the accelerating potential for two particles A and B carrying the same charge but masses m1 m2 (m1 > m2). Which one of the two represents a particle of smaller mass and why? (CBSE Delhi 2016)
Answer:
The graph is as shown.

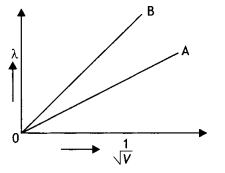
we know that λ = \(\frac{h}{\sqrt{2 m q V}}\)

In graphs, charge of both particles is the same, but the slope of graph B is more. It means that mass of particle B is less (since slope ∝ \(\frac{1}{\sqrt{m}}\)

Question 13.
For a photosensitive surface, the threshold wavelength is λo. Does photoemission occur if the wavelength λ of the incident radiation is
(i) more than λ_o and
(ii) less than λ_o? Justify your answer.
Answer:
The photoelectric effect occurs and hence photoelectrons are ejected when the wavelength of the incident radiation is lesser than the threshold wavelength.
(i) When λ > λ_o, photoemission does not take place.
(ii) When λ < λ_o, photoemission takes place.

Question 14.
Two monochromatic radiations of frequencies v₁ and v₂ (v₁ > v₂) and having the same intensity is, in turn, an incident on a photosensitive surface to cause photoelectric emission. Explain, giving a reason, in which case (i) more number of electrons will be emitted and (ii) maximum kinetic energy of the emitted photoelectrons will be more. (CBSE Delhi 2014C)
Answer:
The number of photoelectrons emitted depends upon the intensity of radiation and the kinetic energy of photoelectrons depends upon the frequency of radiation, therefore

1. The same number of electrons will be emitted.
2. Photoelectrons will have more kinetic energy for radiation of frequency v₁.

Question 15.
A proton and an a-particle are accelerated, using the same potential difference. How are the de-Broglie wavelengths λP and λα related to each other? (NCERT Exemplar)
Answer:

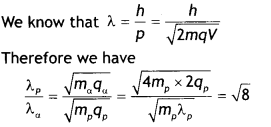
Question 16.
There are materials that absorb photons of shorter wavelength and emit photons of longer wavelength. Can there be stable substances that absorb photons of larger wavelength and emit light of shorter wavelength? (NCERT Exemplar)
Answer:
In the first case energy given out is less than the energy supplied. In the second case, the material has to supply energy as the emitted photon has more energy. This cannot happen for stable substances.

Question 17.
Two monochromatic beams A and B of equal intensity l hit a screen. The number of photons hitting the screen by beam A is twice that by beam B. Then what inference can you make about their frequencies? (NCERT Exemplar)
Answer:

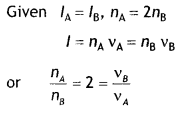
The frequency of beam B is twice that of beam A.

Question 18.
Two particles A and B of de Broglie wavelengths λ₁ and λ₂ combine to form a particle C. The process conserves momentum. Find the de Broglie wavelength of the particle C. (The motion is one dimensional.) (NCERJExemplar)
Answer:
The motion is one dimension, therefore
(i) If the particles move in the same direction

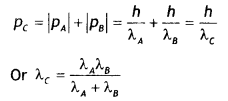
(ii) If the particles move in the opposite direction

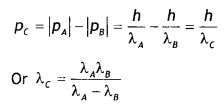
Question 19.
Find the frequency of light that ejects electrons from a metal surface, fully stopped by a retarding potential of 3.3 V. If photoelectric emission begins in this metal at a frequency of 8 × 10¹⁴ Hz, calculate the work function (in eV) for this metal.
Or
Monochromatic light of frequency 6.0 × 10¹⁴ Hz is produced by a laser. The power emitted is 2.0 × 10^-3W. Calculate the (i) energy of a photon in the light beam and (ii) the number of photons emitted on an average by the source. (CBSE Delhi 2018C)
Answer:
We have

Dual Nature of Radiation and Matter Important Extra Questions Long Answer Type

Question 1.
What is the photoelectric effect? Write Einstein’s photoelectric equation and use it to explain (a) independence of maximum energy of emitted photoelectrons from the intensity of incident light and
(b) existence of a threshold frequency for the emission of photoelectrons.
Answer:
The election of photoelectrons from a metal surface when Light of suitabLe frequency is incident on it is catted photoelectric effect.

Einstein’s equation of photoelectric effect is \(\frac{1}{2}\)mv² = hv – ω₀
(a) In accordance with Einstein’s equation, the kinetic energy of the photoelectrons is independent of the intensity of the incident radiation.
(b) In accordance with Einstein’s equation, the kinetic energy will be positive and hence photoelectrons will be ejected if v > v₀. Thus below a certain frequency called threshold frequency, photoelectrons are not ejected from a metal surface (if v < v₀).

Question 2.
An electron of mass m and charge q is accelerated from rest through a potential difference of V. Obtain the expression for the de-Broglie wavelength associated with it. If electrons and protons are moving with the same kinetic energy, which one of them will have a larger de-Broglie wavelength associated with it? Give reason.
Answer:
Consider an electron of mass m and charge e to be accelerated through a potential difference of V volts. Let v be the velocity gained by it. Then kinetic energy of the electron is

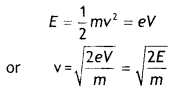
If λ is the de-Broglie wavelength associated with an electron, then

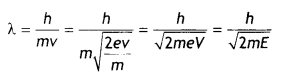
Since de-Broglie wavelength is inversely proportional to the square root of mass, the lesser the mass, the more is the de- Broglie wavelength. Since the mass of an electron is lesser than that of the proton, the electron has a greater de-Broglie wavelength than a proton.

Question 3.
Sketch the graphs showing the variation of stopping potential with the frequency of incident radiations for two photosensitive materials A and B having threshold frequencies v₀ > v’₀ respectively.
(a) Which of the two metals A or B has a higher work function?
(b) What information do you get from the slope of the graphs?
(c) What does the value of the intercept of graph ‘A’ on the potential axis represent?
Answer:
The graphs are as shown below.

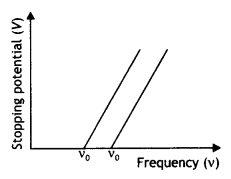
(a) The work function is directly proportional to the threshold frequency. The threshold frequency of metal A is greater than that of metal B; therefore A has a greater work function than B.
(b) The slope of the graphs gives the value of Planck’s constant.
(c) The intercept on the potential axis is negative (-W₀/e) w.r.t. stopping potential, i.e. Work function = e × magnitude of the intercept on the potential axis. We may infer it to give the voltage which, when applied with opposite polarity to the stopping voltage, will just pull out electrons from the metallic atom’s outermost orbit.

Question 4.
When a given photosensitive material is irradiated with light of frequency v, the maximum speed of the emitted photoelectrons equals Vmax. The graph shown in the figure gives a plot of V²max varying with frequency v.

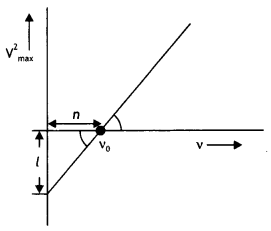
Obtain an expression for
(a) Planck’s constant, and
Answer:
By Einstein’s photoelectric equation we have

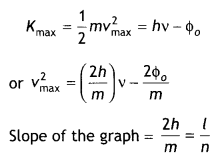
(b) The work function of the given photosensitive material in terms of the parameters T, ‘n’ and the mass ‘m’ of the electron.
Answer:
The intercept on V²_max axis is = \(\frac{2 \phi_{o}}{m}\) = l
Therefore, work function Φ₀ = \(\frac{ml}{2}\)

(c) How is threshold frequency determined from the plot? (CBSE AI 2019)
Answer:
The threshold frequency is the intercept on the v axis i.e. v₀ = n

Question 5.
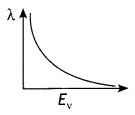
X-rays fall on a photosensitive surface to cause photoelectric emission. Assuming that the work function of the surface can be neglected, find the relation between the de-Broglie wavelength (λ) of the electrons emitted to the energy (E_v) of the incident photons. Draw the nature of the graph for λ as a function of E_v. (CBSE Delhi 2014C)
Answer:
Consider an electron of mass m and charge e to be accelerated through a potential difference of V volt. Let v be the velocity gained by it. Then kinetic energy of the electron is

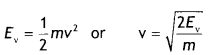
If λ is the de-Broglie wavelength associated with an electron, then
λ = \(\frac{h}{m v}=\frac{h}{\sqrt{2 m E_{v}}}\)

The nature of the graph is as shown.

Question 6.
Light of intensity ‘l’ and frequency ‘v’ is incident on a photosensitive surface and causes photoelectric emission. What will be the effect on anode current when
(a) the intensity of light is gradually increased,
(b) the frequency of incident radiation is increased and
(c) the anode potential is increased?
In each case, all other factors remain the same. Explain giving justification in each case. (CBSE AI 2015)
Answer:
(a) Anode current will increase with the increase of intensity as the more the intensity of light, the more is the number of photons and hence more number of photoelectrons are ejected.
(b) No effect as the frequency of light affects the maximum K.E. of the emitted photoelectrons.
(c) Anode current will increase with anode potential as more anode potential will accelerate the more electrons till it attains a saturation value and gets them collected at the anode at a faster rate.

Question 7.
The graphs, drawn here, are for the phenomenon of the photoelectric effect.


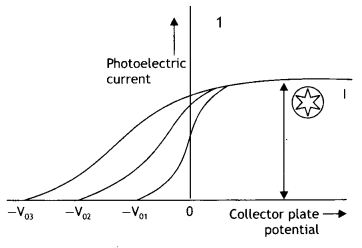
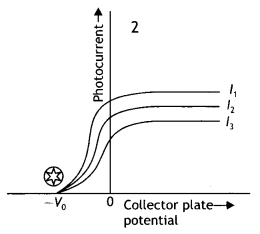
(a) Identify which of the two characteristics (intensity/frequency) of incident light is being kept constant in each case.
Answer:
Graph 1: Intensity, Graph 2: Frequency

(b) Name the quantity, corresponding to themark, in each case.
Answer:
Graph 1: Saturation current, Graph 2: stopping potential

(c) Justify the existence of a ‘threshold frequency’ for a given photosensitive surface. (CBSE Delhi 2016C)
Answer:
The electrons require minimum energy to set themselves free. This is called the work function. As the energy of the photon depends upon its frequency, the photons must possess a minimum frequency so that their energy becomes equal to or greater than the work function. This is called threshold frequency and is given by v₀ = \(\frac{\omega_{0}}{h}\)

Question 8.
Draw a graph showing the variation of de-Broglie wavelength λ of a particle of charge q and mass, with the accelerating potential V. An alpha particle and a proton have the same de-Broglie wavelength equal to 1 Å. Explain with calculations, which of the two has more kinetic energy. (CBSE Delhi 2017C)
Answer:
The graph is as shown.
The de-Broglie wavelength of a particle is given by the expression λ = \(\frac{h}{\sqrt{2 m q V}}\)

Since the alpha particle and the proton have the same de- Broglie wavelength, we have

\(\frac{h}{\sqrt{2 m_{a} E_{\alpha}}}=\frac{h}{\sqrt{2 m_{p} E_{p}}}\)

Therefore proton has a greater value of de-Broglie wavelength.
Now kinetic energy is given by the expression
\(\frac{E_{a}}{E_{p}}=\frac{m_{p}}{m_{\alpha}}=\frac{m}{4 m}=\frac{1}{4}\)

Thus proton has more kinetic energy.

Question 9.
(a) Plot a graph showing the variation of photoelectric current with collector plate potential for different frequencies but of the same intensity of incident radiation.
Answer:
The graph between current I and plate potential.

(b) Green and blue light of the same intensity are incident separately on the same photosensitive surface. If both of these cause photoelectric emission, which one will emit photoelectrons
(i) having greater kinetic energy and
Answer:
The blue light will emit photoelectrons having greater kinetic energy because the frequency and hence energy (E = hv) of blue light is more than the frequency and hence the energy of green light.

(ii) producing larger photocurrent? Justify your answer. (CBSE 2019C)
Answer:
Photoelectric current will be nearly the same for the blue and green light because the intensity of saturation current is independent of the frequency of incident light.

Question 10.
Radiation of frequency 10¹⁵ Hz is incident on two photosensitive surfaces P and Q. The following observations were recorded:
(a) Surface P: No photoemission occurs.
(b) Surface Q: Photoemission occurs but photoelectrons have zero kinetic energy. Based on Einstein’s photoelectric equation, explain the two observations.
Answer:
Einstein photoelectric equation is h(v – v₀) = \(\frac{1}{2}\) mv²
(a) As in the case of surface P no photoemission takes place, we conclude that threshold frequency for P has a value greater than the frequency 10¹⁵ Hz of the given radiation.
(b) In the case of surface Q photoemission takes place but the kinetic energy of photoelectrons means that this radiation just overcomes the work function of the metal. In other words, the frequency 10¹⁵ Hz, of this radiation is equal to the threshold frequency.

Question 11.
When the light of frequency v₁ is incident on a photosensitive surface, the stopping potential is V₁ If the frequency of incident radiation becomes v₁/2, the stopping potential changes to V₂. Find out the expression for the threshold frequency for the surface in terms of V₁ and V₂.
If the frequency of incident radiation is doubled, will the maximum kinetic energy of the photoelectrons also be doubled? Give reason. (CBSE AI 2019)
Answer:
By Einstein’s photoelectric equation.
eV₁ = hv₁ – hv₀ …(i).
and

If the frequency is doubled, the maximum kinetic energy will not be doubled.
K_max = hv – hv₀
K_new = 2hv – hv₀ = hv + K_max

Question 12.
(a) Define the terms
(i) threshold frequency and
Answer:
Threshold frequency (v₀) is the minimum value of frequency of incident radiations below which the photoelectric emission stops, altogether.

(ii) stopping potential in the context of the photoelectric effect.
Answer:
Stopping potential is the value of retarding potential at which the photoelectric current becomes zero for the given frequency of incident radiations.

(b) Draw a graph showing the variation of stopping potential (V₀) with frequency (v) of incident radiation for a given photosensitive material. (CBSE 2019C)
Answer:
The graph between v and V₀

Question 13.
State Einsteins photoelectric equation explaining the symbols used.

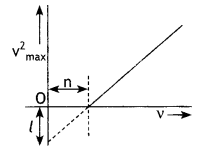
Light of frequency y is incident on a photosensitive surface. A graph of the square of the maximum speed of the electrons (v²_max) vs. y is obtained as shown in the figure. Using Einstein’s photoelectric equation, obtain expressions for (i) Planck’s constant and (ii) the work function of the given photosensitive material in terms of parameters l, n and mass of the electron m. (CBSE Delhi 2018C)
Answer:
Einstein’s photoelectric equation is
hv = hv₀ (= ω₀) = \(\frac{1}{2}\)mv2max
v = frequency of incident Light
ω₀ = threshold frequency of photosensitive A material.
ω₀ = work function.
\(\frac{1}{2}\)mv2max = max. the kinetic energy of the emitted photoelectrons

(Also accept if the student writes)
hv = ω₀ + eV_s
ω₀ = Work function of photosensitive material
V_s = stopping potential)

From Einstein’s photoelectronic equation,
we have

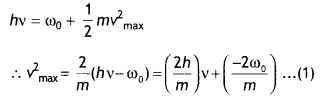
(i) Slope of the given graph = \(\frac{l}{n}\)
∴ \(\frac{2 h}{m}=\frac{l}{n}\)
or
h = \(\frac{m l}{2 n}\)

(ii) Intercept on the y-axis = – l
From equation (1)
– l = \(\frac{-2 \omega_{0}}{m}\) ⇒ ω₀ = \(\frac{ml}{2}\)

Question 14.
(a) In the photoelectric effect, do all the electrons that absorb a photon comes out as photoelectrons irrespective of their location? Explain.
Answer:
No, it is not necessary that if the energy supplied to an electron is more than the work function, it will come out. The electron after receiving energy may lose energy to the metal due to collisions with the atoms of the metal. Therefore, most electrons get scattered into the metal. Only a few electrons near the surface may come out of the surface of the metal for whom the incident energy is greater than the work function of the metal.

(b) A source of light, of frequency greater than the threshold frequency, is placed at a distance be ‘d’ from the cathode of a photocell. The stopping potential is found to be V. If the distance of the light source is reduced to d/n (where n > 1), explains the changes that are likely to be observed in the (a) photoelectric current and (b) stopping potential. (CBSE Sample Paper 2018-19)
Answer:

1. On reducing the distance, intensity increases. Photoelectric current increases with the increase in intensity.
2. Stopping potential is independent of intensity and therefore remains unchanged.

Question 15.
Explain the laws of the photoelectric effect on the basis of Einstein’s photoelectric equation.
Answer:
The laws of the photoelectric effect can be explained on the basis of Einstein’s photoelectric equation, i.e.
\(\frac{1}{2}\)mv² = h (v – v₀)
(a) From the equation we find that the kinetic energy will be positive and hence photoelectrons will be emitted if v > v₀, i.e. the incident frequency is greater than the threshold frequency.

(b) It is clear from the expression that the kinetic energy of the emitted photoelectrons varies linearly with the frequency of the incident radiation.

(c) According to Einstein highly energetic radiation has a high frequency and an intense beam of radiation has more photons. Therefore when a high-intensity beam of radiation is incident on the metal surface, a large number of photoelectrons are emitted as the photoelectric effect is a one-one phenomenon, i.e. one photon can eject one photoelectron. Thus the more the intensity of the incident radiation, the more is the photoelectric current.

(d) As soon as a photon is an incident on a metal surface it is immediately absorbed by an electron, which sets itself free and comes out of the metal surface. The time lag is being negligible. Thus the photoelectric effect is instantaneous.

Question 16.
Define the terms threshold frequency and stopping potential in relation to the phenomenon of the photoelectric effect. How is the photoelectric current affected on increasing the
(i) frequency and
(ii) the intensity of the incident radiations and why?
Answer:
Stopping potential (V₀): The negative potential of the plate at which no photoelectrons reach is called the stopping potential or the cut-off potential.

Threshold frequency (v₀): The minimum frequency of the incident radiation, which can eject photoelectrons from a material, is known as the threshold frequency or cut-off frequency of the material.

1. When the frequency has increased the energy absorbed by a single electron on collision with a photon also increases. E= hv, h is Planck’s constant. This raises the kinetic energy of the emitted photoelectrons but has no effect on current as the number of electrons being liberated remains the same.
2. When the intensity of the incident radiation is increased, the number of photons crossing a unit area per second increases. These photons liberate more electrons and hence current increases.

Question 17.
Write Einstein’s photoelectric equation and mention which important features in the photoelectric effect can be explained with the help of this equation.
The maximum kinetic energy of the photoelectrons gets doubled when the wavelength of light incident on the surface changes from λ₁ to λ₂. Derive the expressions for the threshold wavelength λ₀ and work function for the metal surface. (CBSE Delhi 2015)
Answer:
Einstein’s equation is
E_max = hv – ω or \(\frac{1}{2}\)mv²max = hv – ω

Here m is the mass of the photoelectron and v_max is maximum velocity.
(a) In accordance with Einstein’s equation, the kinetic energy of the photoelectrons is independent of the intensity of the incident radiation.
(b) In accordance with Einstein’s equation, the kinetic energy will be positive and hence photoelectrons will be ejected if v > v_o. Thus below a certain frequency called the threshold frequency, photoelectrons are not ejected from a metal surface.
Given E₁ = E, E₂ = 2E,
By Einstein’s equation we have

Question 18.
Point out two distinct features observed experimentally in the photoelectric effect which cannot be explained on the basis of the wave theory of light. State how the ‘photon picture’ of light provides an explanation of these features. (CBSE AI 2016C)
Answer:
The two features are

1. The intensity of light determines the photoelectric current and
2. Existence of threshold frequency.

According to the wave picture of light, the free electrons at the surface of the metal (over which the beam of radiation falls) absorb the radiant energy continuously. The greater the intensity of radiation, the greater is the amplitude of electric and magnetic fields. Consequently, the greater the intensity, the greater should be the energy absorbed by each electron. In this picture, the maximum kinetic energy of the photoelectrons on the surface is then expected to increase with the increase in intensity.

Also, no matter what the frequency of radiation is, a sufficiently intense beam of radiation (over sufficient time) should be able to impart enough energy to the electrons so that they exceed the minimum energy needed to escape from the metal surface. A threshold frequency, therefore, should not exist, which is against the observations. Thus the photoelectric effect cannot be explained on the basis of the wave nature of light

Question 19.
Using photon picture of light, show how Einstein’s photoelectric equation can be established. Write two features of the photoelectric effect that cannot be explained by the wave theory. (CBSE AI 2017)
Answer:
According to Einstein, the emission of a photoelectron is the interaction of quanta of light with a single electron. The photon is completely absorbed by the electron. The electron, which absorbs the photon, utilises this energy to set itself free. An amount of energy equal to the work function (ω) is required by the electron to set itself free. The remaining energy hv – ω (if hv > ω) is available to the electron as its maximum kinetic energy. Thus according to Einstein, we have

Here m is the mass of the photoelectron and v_max is maximum velocity. Actually, most of the electrons possess kinetic energy less than the maximum kinetic energy because they lose a part of their energy due to collisions with the atoms on their way out from inside the metal. Thus electrons with different kinetic energy are emitted.

Now the work function is given by ω = hv_o, therefore the above equation becomes
\(\frac{1}{2}\)mv²_max = hv – hv_o = h(v – v_o)

(a) Dependence of kinetic energy on the frequency of the incident radiation.
(b) Existence of threshold frequency.

Question 20.
(a) How does one explain the emission of electrons from a photosensitive surface with the help of Einstein’s photoelectric equation?
(b) The work function of the following metals is given: Na = 2.75 eV, K = 2.3 eV, Mo = 4.17eV and Ni = 5.15 eV. Which of these metals will not cause photoelectric emission for radiation of wavelength 3300 Å from a laser source placed 1 m away from these metals? What happens if the laser source is brought nearer and placed 50 cm away? (CBSE Delhi 2017)
Answer:
(a) According to Einstein’s equation we have
\(\frac{1}{2}\)mv² = h (v – v_o)

If the frequency of the incident radiation is above the threshold frequency (v_o), the KE of the photo¬electrons will be positive and hence will be emitted.

Let us calculate the energy possessed by the photon of wavelength 3300 Å.

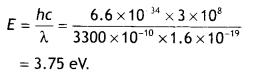
As the energy of the incident photon is less than the work functions of Mo and Ni, so the metals Mo and Ni will not give photoelectric emission.

If the laser is brought closer, the intensity of radiation increases. This does not affect the result regarding Mo and Ni, but the photoelectric current will increase for Na and K with the increase in intensity.

Question 21.
When a monochromatic yellow coloured light beam is incident on a given photosensitive surface, photoelectrons are not ejected, while the same surface gives photoelectrons when exposed to the green coloured monochromatic beam. What will happen if the same surface is exposed to (i) violet and (ii) red coloured monochromatic beam of light? Justify your answer.
Answer:
Photoelectrons are ejected from a metal surface if the frequency of incident radiation is greater than the threshold frequency of that metal.

Since yellow light does not eject photoelectrons while green light does, the threshold frequency of the given metal is greater than the frequency of yellow light.
(a) Violet light has a greater frequency than yellow light, therefore when violet light is incident on the metal surface photoelectrons will be ejected.
(b) Red light has a smaller frequency than yellow light; therefore when the red light is incident on the metal surface, photoelectrons will not be ejected.

Question 22.
(a) Why photoelectric effect cannot be explained on the basis of the wave nature of light? Give reasons.
Answer:
According to the wave picture of light, the free electrons at the surface of the metal (over which the beam of radiation falls) absorb the radiant energy continuously. The greater the intensity of radiation, the greater is the amplitude of electric and magnetic fields.

Consequently, the greater the intensity, the greater should be the energy absorbed by each electron. In this theory, the maximum kinetic energy of the photoelectrons on the surface is then expected to increase with the increase in intensity.

Also, no matter what the frequency of radiation is, a sufficiently intense beam of radiation (over sufficient time) should be able to impart enough energy to the electrons so that they exceed the minimum energy needed to escape from the metal surface. A threshold frequency, therefore, should not exist, which is against the observations. Thus the photoelectric effect cannot be explained on the basis of the wave nature of light.

(b) Write the basic features of the photon picture of electromagnetic radiation on which Einstein’s photoelectric equation is based. (CBSE Delhi 2013)
Answer:
The basic features are

1. Radiation energy is built up of discrete units.
2. An electron absorbs the quanta of energy.

Question 23.
Obtain the expression for the wavelength of the de-Broglie wave associated with an electron accelerated from rest through a potential difference V.
The two lines A and B as shown in the graph plot the de-Broglie wavelength A. as a function of 1/\(\sqrt{V}\) (V is the accelerating potential) for two particles having the same charge. Which of the two represents the particle of heavier mass?

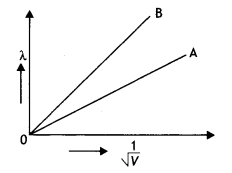
Answer:
Consider an electron of mass m and charge e to be accelerated through a potential difference of V volts. Let v be the velocity gained by it. Then kinetic energy of an electron is

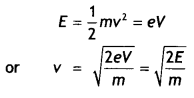
If λ is the de-Broglie wavelength associated with an electron, then

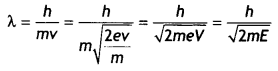
In graphs, the charge of both particLes is the same, but the slope of graph A is Less. It means that mass of particle A is more (since slope = \(\frac{h}{\sqrt{2 m E}}\)).

Question 24.
The given graphs show the variation of the stopping potential Vs with the frequency (v) of the incident radiations for two different photosensitive materials M1 and M2.

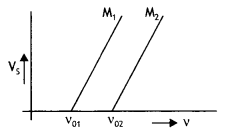
(i) What are the values of work functions for M₁ and M₂?
(ii) The values of the stopping potential for M₁ and M₂ for a frequency (v₃) of the incident radiations greater than v_o2 are V₁ and V₂ respectively. Show that the slope of the lines equals \(\frac{V_{1}-V_{2}}{v_{02}-v_{01}}\)
Answer:
(i) The values of work functions for M₁ and M₂ are ω₁ = hv_o1 and ω₂ = hv_o2.
(ii) The slope of the graphs is given by the variation of quantity along the Y-axis ‘ to the variation in quantity on the X-axis.

Now for M₁

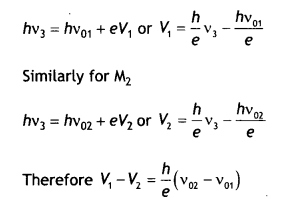
Therefore slope of the graphs is
\(\frac{h}{e}=\frac{V_{1}-V_{2}}{v_{02}-v_{01}}\)

Question 25.
Why are de-Broglie waves associated with a moving football not visible?
The wavelength of a photon and the de-Broglie wavelength of an electron have the same value. Show that energy of the photon is \(\frac{2λmc}{h}\) times the kinetic energy of the electron, where m, c and h have their usual meanings.
Answer:
(i) The de-Broglie wavelength of moving particles is given by the expression
λ = \(\frac{h}{mv}\). For a football the mass is large, hence the wavelength is extremely small and hence is not visible.

(ii) Now energy of a photon of wavelength λ. is E = hv = \(\frac{hc}{λ}\) ….(1)
and kinetic energy of an electron is Ke = \(\frac{1}{2}\)mv²

If de-Broglie wavelength (A) of electron be,
λ = \(\frac{h}{mv}\)
or
v = \(\frac{h}{mλ}\)

Therefore kinetic energy of electron will be

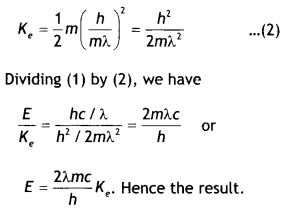
Numerical Problems:

Question 1.
What is the de Brogue wavelength associated with an electron, accelerated through a potential difference of 100 volts? (NCERT)
Answer:
Accelerating potential V = 100 V. The de-Broglie wavelength λ is
λ = \(\frac{1.227}{\sqrt{V}}\)nm = \(\frac{1.227}{\sqrt{100}}\) = 0.123 nm
The de-Broglie wavelength associated with an electron in this case is of the order of X-ray wavetengths.

Question 2.
In an experiment on the photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be 4.12 × 10^-15 V s. Calculate the value of Planck’s constant. (NCERT)
Answer:
Given slope = 4.12 × 10^-15 V s, h = 1

The slope of the voltage versus frequency graph gives the value of h/e, therefore we have
h = Slope × e = 4.12 × 10^-15 × 1.6 × 10^-19
Or
h = 6.59 × 10^-34 J s

Question 3.
The threshold frequency for a certain metal is 3.3 × 10¹⁴ Hz. If the light of frequency 8.2 × 10¹⁴ Hz is incident on the metal, predict the cut-off voltage for the photoelectric emission. (NCERT)
Answer:
Given v_o = 3.3 × 10¹⁴ Hz, v = 8.2 × 10¹⁴ Hz, V_o = ?

Using the relation h (v – v_o) = eV0 we have h(v – v_o)

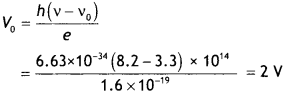
Question 4.
The work function for a certain metal is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wavelength 330 nm? (NCERT)
Answer:
Given ω_o = 4.2 eV
The energy possessed by the incident radiation of wavelength 330 nm is
E = \(\frac{h c}{\lambda}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{330 \times 10^{-9} \times 1.6 \times 10^{-19}}\) = 3.8 eV

Since this energy is less than the work function of the metal, no photoelectric emission will take place.

Question 5.
Light of frequency 7.21 × 10¹⁴ Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 × 10 m s^-1 are ejected from the surface. What is the threshold frequency for the photoemission of electrons? (NCERT)
Answer:
Given v = 7.21 × 10¹⁴ Hz, v = 6.0 × 10 m s^-1, v_o = ?
Using the relation h (v – v_o) = \(\frac{1}{2}\)mv² We have

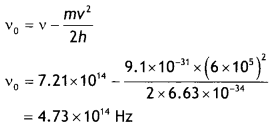
Question 6.
Calculate the (a) momentum and (b) de Broglie wavelength of the electrons accelerated through a potential difference of 56 V. (NCERT)
Answer:
Given V = 56 V, p = ?, λ = ?
Using the relation

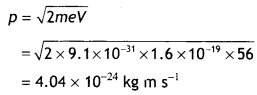
The de-Broglie wavelength is given by
λ = \(\frac{h}{p}=\frac{6.63 \times 10^{-34}}{4.04 \times 10^{-24}}\) = 0.164 nm

Question 7.
A particle is moving three times as fast as an electron. The ratio of the de-Broglie wavelength of the particle to that of the electron is 1.813 × 10^-4. Calculate the particle’s mass and identify the particle. (NCERT)
Answer:
Givenv = 3v_e, λ/λ_e = 1.813 × 10^-4
We know that λ = \(\frac{h}{p}=\frac{h}{m v}\)

therefore we have
m = me\(\frac{\lambda_{e} v_{e}}{\lambda v}=\frac{9.11 \times 10^{-31}}{1.813 \times 10^{-4} \times 3}\)

Solving we have m = 1.675 × 10^-27 kg
This is the mass of a proton or a neutron.

Question 8.
Using the graph shown in the figure for stopping potential v/s incident frequency of photons, calculate Planck’s constant. (CBSE Delhi 2015C)

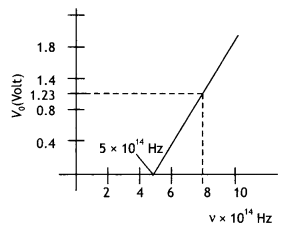
Answer:
By Einstein’s equation we have eV_o = h(v – v_o)

Therefore slope of the graph is \(\frac{V_{0}}{v}=\frac{h}{e}\). Now slope of graph is

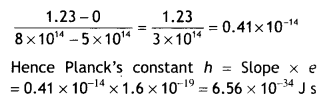
Question 9.
If the light of wavelength 412.5 nm is incident on each of the metals given below, which ones will show photoelectric emission and why? (CBSE AI Delhi 2018)

Answer:
The energy of a photon of the given light is,

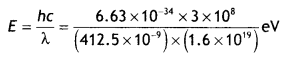
E = 3.01 eV. Thus, metals having a work function less than the energy of a photon of falling light will show the photoelectric effect So, Na and K will show the photoelectric effect.

Question 10.
Two metals A and B have work functions 2 eV and 5 eV respectively. Which metal will emit electrons, when irradiated with light of wavelength 400 nm and why?
Answer:
The energy possessed by radiation of wavelength 400 nm is E = hv = hc/λ or

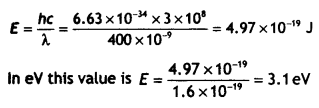
Since this energy is more than the work function of metal A, metal A will emit electrons.

Question 11.
Calculate the maximum kinetic energy of electrons emitted from a photosensitive surface of work function 3.2 eV, for the incident radiation of wavelength 300 nm.
Answer:

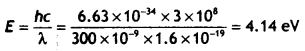
Therefore the kinetic energy of the emitted photoelectrons is
K.E_max = hv – hv_o = 4.14 – 3.2 = 0.94 ev

Question 12.
The work function, for a given photosensitive surface, equals 2.5 eV. When the light of frequency y falls on this surface, the emitted photoelectron is completely stopped by applying a retarding potential of 4.1 V. What is the value of y?
Answer:

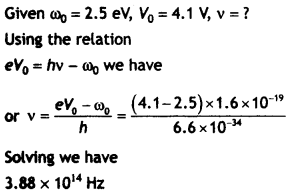
Question 13.
A nucleus of mass M Initially at rest splits into two fragments of masses M’/3 and 2M’/3 (M > M’). Find the ratio of de-Broglie wavelengths of the two fragments.
Answer:
By the principle of conservation of momentum

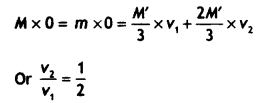
The ratio of de-Broglie wavelength is

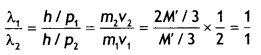
Question 14.
An electron microscope uses electrons accelerated by a voltage of 50 kV. Determine the de-Broglie wavelength associated with the electrons. Taking other factors, such as numerical aperture etc. to be the same, how does the resolving power of an electron microscope compare with that of an optical microscope which uses yellow light? (CBSE AI 2014)
Answer:
Given V = 50 kV, λ = ?
Using the expression λ = \(\frac{1.227}{\sqrt{V}}\) nm we have
λ = \(\frac{1.227}{\sqrt{50 \times 10^{3}}}\) nm = 5.48 × 10^-12 m

Wavelength of yellow light λy = 5.9 × 10^-7 m

Now RP ∝ \(\frac{1}{λ}\)

Therefore we have

Question 15.
A proton and a deuteron are accelerated through the same accelerating potential. Which one of the two has
(a) the greater value of de-Broghe wavelength associated with it and
Answer:
(a) The de-Broglie wavelength is given by the expression λ = \(\frac{h}{\sqrt{2 m q V}}\). Since potential is same, we have

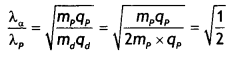
Or
λ_p = \(\sqrt{2} \lambda_{a}\)

Thus proton has a greater value of de-Broglie wavelength.

(b) less momentum? Give reasons to justify your answer. (CBSE Delhi 2014)
Answer:
Now p = h/λ.

As the wavelength of a proton is more than that of a deuteron, the momentum of a proton is lesser than that of a deuteron. Hence, the momentum of the proton is less.

Question 16.
(a) Monochromatic light of frequency 6.0 × 10¹⁴ Hz is produced by a laser. The power emitted is 2.0 × 10^-3 W. Estimate the number of photons emitted per second on an average by the source.
Answer:
Each photon has energy
E = hv = (6.63 × 10^-34) × (6.0 × 10¹⁴)
= 3.98 × 10^-19 J

If N is the number of photons emitted by the source per second, the power P transmitted in the beam equals N times the energy per photon E so that P = NE, then
N = \(\frac{P}{E}=\frac{2.0 \times 10^{-3}}{3.98 \times 10^{-19}}\)
= 5.0 × 10¹⁵ photons per second.

(b) Draw a plot showing the variation of photoelectric current versus the intensity of incident radiation on a given photosensitive surface. (CBSE Delhi 2014)
Answer:
With the increase of intensity of radiations, photocurrent increase.

Question 17.
An electron is revolving around the nucleus with a constant speed of 2.2 × 10⁸ m s^-1. Find the de Broglie wavelength associated with it. (CBSE AI 2014C)
Answer:
Given v= 2.2 × 10⁸ m s^-1, λ = ?
Using the expression

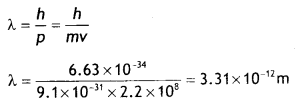
Question 18.
Given the ground state energy E0 = – 13.6eV and Bohr radius αo = 0.53 Å. Find out how the de Broglie wavelength associated with the electron orbiting in the ground state would change when it jumps into the first excited state. (CBSE AI 2015)
Answer:
The de-Broglie wavelength is given by 2πr_n = nλ

In ground state, n = 1 and r0 = 0.53 Å, therefore λ_o = 2 × 3.14 × 0.53 = 3.33 Å
In first excited state, n = 2 and
r₁ = 4 × 0.53 Å = 2.12 Å,

therefore λ₁ = (2 × 3.14 × 2.12)/2 = 6.66 Å
Therefore λ₁ – λ_o = 6.66 – 3.33 = 3.33 Å

In other words, the de-Broglie wavelength becomes double.

Question 19.
A proton and an a-particle have the same de-Broglie wavelength. Determine the ratio of (i) their accelerating potentials and (ii) their speeds. (CBSE Delhi 2015)
Answer:
(i) The de Broglie wavelength is given by λ = \(\frac{h}{\sqrt{2 m q V}}\). Since the de-Broglie waveLength is the same (or proton and alpha particle, we have

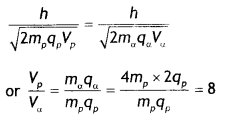
(ii) The de-Broglie wavelength is given by λ = \(\frac{h}{mv}\). Since the de-Broglie wavelength is the same (or proton and alpha particle, we have

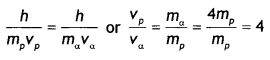
Question 20.
The work function (ω_o), of a metal X, equals 3 × 10^-19 J. Calculate the number (N) of photons, of light of wavelength 26.52 nm, whose total energy equals W. (CBSE Delhi 2016C)
Answer:
Given ωo_o = 3 × 10^-19 J, N = ?, λ = 26.52 nm = 26.52 × 10^-9 m
The energy possessed by one photon

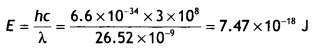
Therefore the number of photons

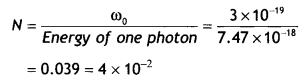
Question 21.
The KE of a beam of electrons accelerated through a potential V, equals the energy of a photon of wavelength 5460 nm. Find the de Broglie wavelength associated with this beam of electrons. (CBSE AI 2016C)
Answer:
The de-Broglie wavelength is given by

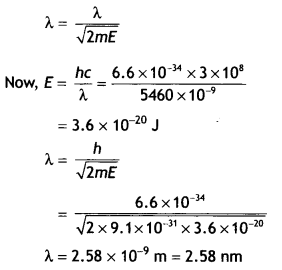
Question 22.
Calculate the kinetic energy of an electron having de Broglie wavelength of 1 A. (CBSE AI 2017C)
Answer:
Using the relation

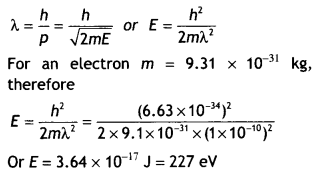
Question 23.
Find the frequency of light that ejects electrons from a metal surface, fully stopped by a retarding potential of 3.3 V. If photoelectric emission begins in this metal at a frequency of 8 × 10¹⁴ Hz, calculate the work function (in eV) for this metal. (CBSE AI 2018C)
Answer:
The work function is given by ω0 = hv0

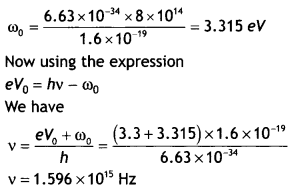
Question 24.
Monochromatic light of frequency 6.0 × 10¹⁴ Hz is produced by a laser. The power emitted is 2.0 × 10^-3 W. Calculate the (i) energy of a photon in the light beam and
Answer:
Each photon has an energy
E = hv = (6.63 × 10^-34)(6.0 × 10¹⁴)
= 3.98 × 10^-19 J

(ii) a number of photons emitted on an average by the source. (CBSE AI 2018C)
Answer:
If N is the number of photons emitted by the source per second, the power P transmitted in the beam equals N times the energy per photon E so that P = NE. Then
N = \(\frac{P}{E}=\frac{2.0 \times 10^{-3}}{3.98 \times 10^{-19}}\)
= 5.0 × 10¹⁵ photons per second.

Question 25.
The following table gives the values of work function for a few photosensitive metals.

If each of these metals is exposed to radiations of wavelength 300 nm, which of them will not emit photoelectrons and why?
Answer:
The energy of the radiation is
E = \(\frac{h c}{\lambda}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{300 \times 10^{-9} \times 1.6 \times 10^{-19}}\) = 4.14 eV

This energy is greater than the work functions of Na and K and lesser than the work function of Mo. Hence Mo will not emit photoelectrons.

Question 26.
The work function of caesium is 2.14 eV. Find
(i) the threshold frequency for caesium, and
Answer:
For the cut-off or threshold frequency the energy hv₀ of the incident radiation must be equal to work function Φ₀ so that
v₀ = \(\frac{\phi_{0}}{h}=\frac{2.14 \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}}\)
= 5.16 × 10¹⁴ Hz
Thus, for frequencies less than this threshold frequency, no photoelectrons are ejected.

(ii) the wavelength of the incident light if the photocurrent is brought to zero by a stopping potential of 0.60 V. (NCERT)
Answer:
Photocurrent reduces to zero when the maximum kinetic energy of the emitted photoelectrons equals the potential energy eV₀ by the retarding potential V₀.
Einstein’s Photoelectric equation is eV₀ = hv – ω₀ = \(\frac{hc}{λ}\) – ω₀

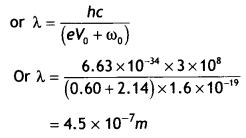
Question 27.
An electron, an a-particle, and a proton have the same kinetic energy. Which of these particles has the shortest de-Broglie wavelength? (NCERT)
Answer:
For a particle, de-Broglie wavelength λ = h/p
Kinetic energy, K = p2/2m.
Then, λ = \(\frac{h}{\sqrt{2 m K}}\)

For the same kinetic energy K, the de-Broglie wavelength associated with the particle is inversely proportional to the square root of their masses. A proton (¹₁H) is 1836 times massive than an electron and a particle (²₄He) four times that of a proton. Hence, a-particle has the shortest de-Broglie wavelength.

Question 28.
A particle is moving three times as fast as an electron. The ratio of the de Broglie wavelength of the particle to that of the electron is 1.813 × 10^-4. Calculate the particle’s mass and identify the particle. (NCERT)
Answer:
the de-Broglie wavelength of a moving particle, having mass m and velocity v
λ = \(\frac{h}{p}=\frac{h}{m v}\)

Mass, m = h/λv
For an electron, mass me = h/λ_e ve
Now, we have v/ve = 3 and λ/λ_e = 1.813 × 10^-4

Then the mass of the particle

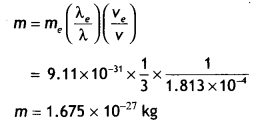
Thus, the particle with this mass could be a proton or a neutron.

Question 29.
What are the (a) momentum, (b) speed, and (c) de Brogue wavelength of an electron with the kinetic energy of 120 eV? (NCERT)
Answer:
Given E = 120 eV, p =?, v =?, λ =?
Using the relation

Question 30.
Consider a metal exposed to the light of wavelength 600 nm. The maximum energy of the electron doubles when the light of wavelength 400 nm is used. Find the work function in eV. (NCERT Exemplar)
Answer:
Given λ₁ = 600 nm, E₁ = E, λ₂ = 400 nm,
E₂ = 2E, Φ =?
Now E_max = hv — Φ

According to the question (hc = 1230 eVnm)

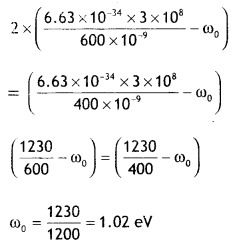
Question 31.
A student performs an experiment on the photoelectric effect, using two materials A and B. A plot of vis given In the figure.
(a) Which material A or B has a higher work function?
(b) Given the electric charge of an electron = 1.6 × 10^-19 C, find the value of h obtained from the experiment for both A and B. Comment on whether it is consistent with Einstein’s theory. (NCERT Exemplar)

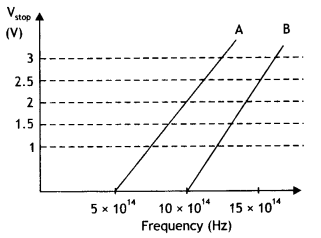
Answer:
(a) The higher the stopping potential, the higher is the work function. The stopping potential of B ís higher than that of A, therefore the work function of B is higher than that of A.

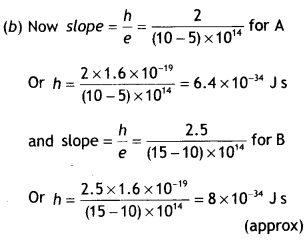
Question 32.
A particle A with a mass m_A is moving with a velocity y and hits a particle B (mass m_B) at rest (one-dimensional motion). Find the change in the de-Broglie wavelength of particle A. Treat the collision as elastic. (NCERT Exemplar)
Answer:
Given U_A = V, U_B = 0
Since the collision is elastic, momentum and kinetic energy wiLt be conserved.

Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 10 Wave Optics. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 10 Important Extra Questions Wave Optics

Wave Optics Important Extra Questions Very Short Answer Type

Question 1.
Sketch the refracted wavefront emerging from convex tens, If a plane wavefront is an incident normally on it.
Answer:
The figure is as shown.

Question 2.
How would you explain the propagation of light on the basis of Huygen’s wave theory?
Answer:
To explain the propagation of light we have to draw a wavefront at a later instant when a wavefront at an earlier instant is known. This can be drawn by the use of Huygen’s principle.

Question 3.
Draw the shape of the reflected wavefront when a plane wavefront is an incident on a concave mirror.
Answer:
The reflected wavefront is as shown.

Question 4.
Draw the shape of the refracted wavefront when a plane wavefront is an incident on a prism.
Answer:
The shape of the wavefront is as shown.

Question 5.
Draw the type of wavefront that corresponds to a beam of light diverging from a point source.
Answer:
The wavefront formed by the light coming from a very far off source is a plane and for a beam of light diverging from a point, a wavefront is a number of concentric circles.

Question 6.
Draw the type of wavefront that corresponds to a beam of light coming from a very far off source.
Answer:
The wavefront is as shown.

Question 7.
Name two phenomena that establish the wave nature of light.
Answer:
Interference and diffraction of light.

Question 8.
State the conditions which must be satisfied for two light sources to be coherent.
Answer:
(a) Two sources must emit light of the same wavelength (or frequency).
(b) The two light sources must be either in-phase or have a constant phase difference.

Question 9.
Draw an intensity distribution graph for diffraction due to a single-slit.
Answer:
The intensity distribution for a single-slit diffraction pattern is as shown.

Question 10.
Name one device for producing plane polarised light. Draw the graph showing the variation of intensity of polarised light transmitted by an analyser.
Answer:
Nicol prism can be used to produce plane polarised light. The graph is as shown.

Question 11.
State Huygens’ principle of diffraction of light. (CBSE AI 2011C)
Answer:
Huygens principle states that
(a) Each point on a wavefront is a source of secondary waves which travel out with the same velocity as the original waves.
(b) The new wavefront is given by the forward locus of the secondary wavelets.

Question 12.
In what way is a plane polarised tight different from an unpolarised light? (CBSE AI 2012C)
Answer:
Plane polarized light vibrates 1n only one plane.

Question 13.
Which of the following waves can be polarised: (i) Heatwaves (ii) Sound waves? Give a reason to support your answer. (CBSE Delhi 2013)
Answer:
Heatwaves are transverse In nature.

Question 14.
Define the term ‘wavefront’. (CBSE AI 2014C)
Answer:
It Is defined as the locus of all points In a medium vibrating in the same phase.

Question 15.
Define the term ‘coherent sources’ which are required to produce interference pattern in Young’s double-slit experiment. (CBSE Delhi 2014C)
Answer:
Two sources that are In phase or have a constant phase difference are called coherent sources.

Question 16.
What change would you expect if the whole of Young’s double-slit apparatus were dipped into the water?
Answer:
The wavelength λ, of light In water, is less than that in air. Since the fringe width β is directly proportional to the wavelength of light, therefore, the fringe width will decrease.

Question 17.
When light travels from a rarer to a denser medium, it loses some speed. Does the reduction in speed Imply a reduction in the energy carried by the light wave?
Answer:
No, the energy carried by a wave depends upon the amplitude of the wave and not on Its speed of propagation.

Question 18.
If one of the slits say S₁, is covered then what changes occur in the Intensity of light at the centre of the screen?
Answer:
The intensity 1s decreased four times because l ∝ 4a² where a is the amplitude of each wave.

Question 19.
How does the angular separation between fringes in a single-slit diffraction experiment change when the distance of separation between the slit and screen is doubled? (CBSE AI 2012)
Answer:
No change.

Question 20.
What is the effect on the interference fringes in Young’s double-slit experiment If the separation between the screen and slits Is Increased?
Answer:
The fringe width Increases.

Question 21.
How does the Intensity of the central maximum change If the width of the slit Is halved in a single-slit diffraction experiment?
Answer:
The width of the central maxima is doubled and the intensity is reduced to one-fourth of Its original value.

Question 22.
The polarising angle of a medium Is 60°, what is the refractive index of the medium? (CBSE Delhi 2019)
Answer:
Using the expression
μ = tan i_p = tan 60° = 1.732.

Question 23.
In the wave picture of light intensity of light is determined by the square of the amplitude of the wave. What determines the intensity of light in the photon picture of light?
Answer:
For a given frequency intensity of light in the photon, the picture is determined by the number of photons crossing a unit area per unit time.

Question 24.
How does the Intensity of the central maximum change if the width of the slit is halved in the single-slit diffraction experiment?
Answer:
The width of the central maximum is doubled and the intensity is reduced to one-fourth of its original value.

Question 25.
What would happen If the path difference between the interfering beams that is S₂P – S₁P became very large?
Answer:
If the path difference becomes very large it may exceed the coherent length. Thus the coherence of the waves reaching P is lost and no interference takes place.

Question 26.
In Young’s double-slit experiment, what would happen to the intensity of the maxima and the minima if the size of the hole illuminating the two coherent holes were gradually Increased?
Answer:
The fringe width will decrease and finally, there will be general illumination on the screen.

Question 27.
What is the Brewster angle for air to glass transition? (Refractive index of glass =1.5.) (NCERT)
Answer:
Given μ = 1.5, i_P = ?
Using the relation μ = tan i_P we have
l_p = tan^-1 (1.5) = 56.3°

Question 28.
Is Huygen’s principle valid for longitudinal sound waves? (NCERT Exemplar)
Answer:
Yes

Question 29.
Consider a point at the focal point of a convergent lens. Another convergent lens of the short focal length is placed on the other side. What is the nature of the wavefronts emerging from the final image? (NCERT Exemplar)
Answer:
Spherical.

Question 30.
What is the shape of the wavefront on earth for sunlight? (NCERTExemplar)
Answer:
Spherical with a huge radius as compared to the earth’s radius so that it is almost a plane.

Question 31.
Draw a graph showing the intensity distribution of fringes due to diffraction at a single-slit. (CBSE 2018C)
Answer:

Wave Optics Important Extra Questions Short Answer Type

Question 1.
How can one distinguish between an unpolarised and linearly polarised light beam using polaroid? (CBSE Delhi 2019)
Answer:
The two lights will be allowed to pass through a polariser. When the polarizer is rotated in the path of these two light beams, the intensity of light remains the same in all the orientations of the polariser, then the light is unpolarised. But if the intensity of light varies from maximum to minimum then the light beam is a polarised light beam.

Question 2.
What is meant by plane polarised light? What type of waves shows the property of polarisation? Describe a method of producing a beam of plane polarised light?
Answer:

1. The light that has its vibrations restricted in only one plane is called plane polarised light.
2. Transverse waves show the phenomenon of polarization.
3. Light is allowed to pass through a polaroid. The polaroid absorbs those vibrations which are not parallel to its axis and allows only those vibrations to pass which are parallel to its axis.

Question 3.
Write the Important characteristic features by which the Interference can be distinguished from the observed diffraction pattern. (CBSE AI 2015)
Answer:
(a) In the interference pattern the bright fringes are of the same width, whereas in the diffraction pattern they are not of the same width.
(b) In interference all bright fringes are equally bright while in diffraction they are not equally bright.

Question 4.
State Brewster’s law. The value of Brewster’s angle for the transparent medium is different for the light of different colours. Give reason. (CBSE Delhi 2016)
Answer:
When the reflected ray and the refracted ray are perpendicular then μ = tani_p where i_p is the polarising angle or Brewster angle.

Brewster’s angle depends upon the refractive index of the two media in contact. The refractive index in turn depends upon the wavelength of light used (different colours) hence Brewster’s angle is different for different colours.

Question 5.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids.
Answer:
Let l_o be the intensity of polarised light after passing through the first polarizer P₁. Then the intensity of light after passing through the second polarizer P2 will be l = l_ocos 2θ, where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be
l = l_o cos² θ cos² (90° – θ) = l_o cos² θ sin² θ = (l_o /4)sin² 2θ

Therefore, the transmitted intensity will be maximum when θ = π/4

Question 6.
Is energy conserved in interference? Explain.
Answer:
Yes, energy is conserved in interference. Energy from the dark fringes is accumulated in the bright fringes. If we take
l = 4a²cos²\(\frac{\phi}{2}\), then intensity at bright points is l_max = 4a² and intensity at the minima l_min = 0. Hence average intensity in the pattern of the fringes produced due to interference is given by
Ī = \(\frac{I_{\max }+I_{\min }}{2}=\frac{4 a^{2}+0}{2}\) = 2a²

But if there is no interference then total intensity at every point on the screen will be l = a² + a² = 2a², which is the same as the average intensity in the interference pattern.

Question 7.
An incident beam of light of intensity lo is made to fall on a polaroid A. Another polaroid B is so oriented with respect to A that there is no light emerging out of B. A third polaroid C is now introduced midway between A and B and is so oriented that its axis bisects the angle between the axes of A and B. What is the intensity of light now between (i) A and C (ii) C and B? Give reasons for your answers.
Answer:
Polaroids A and B are oriented at an angle of 90°, so no light is emerging out of B. On placing polaroid C between A and B such that its axis bisects the angle between axes of A and B, then the angle between axes of polaroids A and B is 45° and that of C and B also 45°.
(a) Intensity of light on passing through Polaroid A or between A and C is l₁ = \(\frac{l_{0}}{2}\)
(b) On passing through polaroid C, intensity of light between C and B becomes
l₂ = l₁ cos² θ = \(\frac{l_{0}}{2}\) × cos² 45° = \(\frac{l_{0}}{4}\)

Question 8.
One of the slits of Young’s double-slit experiment is covered with a semi¬transparent paper so that it transmits lesser light. What will be the effect on the interference pattern?
Answer:
There will be an interference pattern whose fringe width is the same as that of the original. But there will be a decrease in the contrast between the maxima and the minima, i.e. the maxima will become less bright and the minima will become brighter.

Question 9.
Light from a sodium lamp is passed through two polaroid sheets P₁ and P₂ kept one after the other. Keeping P₁, fixed, P₂ is rotated so that its ‘pass axis can be at different angles, θ, with respect to the pass-axis of P₁.
An experimentalist records the following data for the intensity of light coming out of P₂ as a function of the angle θ.

I = Intensity of beam falling on P₁
(a) One of these observations is not in agreement with the expected theoretical variation of I, identify this observation and write the correct expression.
(b) Define the Brewster angle and write the expression for It in terms of the refractive index of the medium.
Answer:
(a) The observation \(\frac{1}{\sqrt{2}}\) is not correct. It should be 1/2.
(b) It is the angle of incidence at which the refracted and the reflected rays are perpendicular to each other. It is related to the refractive index as tan i_p = μ

Question 10.
How will the interference pattern in Young’s double-slit experiment get affected, when
(a) distance between the slits S₁, and S₂ reduced and
(b) the entire set-up is immersed in water? Justify your answer in each case. (CBSE Delhi 2011C)
Answer:
We know that fringe width β of the dark or bright fringes is given by β = \(\frac{D \lambda}{d}\) where d is the distance between the slits.
(a) When the distance between the slits, i. e. d is reduced then p will increase. The interference pattern will thus become broader.
(b) When the entire set up is immersed in water, the pattern will become narrow due to the decrease in the wavelength of light. The new wavelength λ’ = λ/n, hence β’= β/n

Question 11.
Discuss the intensity of transmitted light when a Polaroid sheet is rotated between two crossed polaroids? (NCERT)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁. Then the intensity of light after passing through the second polarizer P₂ will be l = l_o cos² θ

where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be

Therefore, the transmitted intensity will be maximum when θ = π/4

Question 12.
A Polaroid (I) is placed In front of a monochromatic source. Another Polaroid (II) is placed in front of this Polaroid (I) and rotated till no light passes. A third Polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II)? Explain. (NCERT Exemplar)
Answer:
Only in the special case when the pass axis of (III) is parallel to fill or (II) there shall be no light emerging. In all other cases, there shall be light emerging because the pass axis of (II) is no longer perpendicular to the pass axis of (III).

Question 13.
(a) Good quality sunglasses made of polaroids are preferred over ordinary coloured glasses. Explain why.
(CBSE AI2019)
Answer:
Polaroid sunglasses are preferred over coloured sunglasses because they reduce the intensity of light.

(b) How is plane polarised light defined?
Answer:
Plane polarised light: Light in which vibrations of electric field vector are restricted to one plane containing the direction of propagation.

(c) A beam of plane polarised light is passed through a polaroid. Show graphically, a variation of the intensity of the transmitted light with the angle of rotation of the Polaroid.
Answer:
The graphical variation is as shown.

Wave Optics Important Extra Questions Long Answer Type

Question 1.
Define the term wavefront. Using Huygen’s wave theory, verify the law of reflection.
Or
Define the term, “refractive index” of a medium. Verify Snell’s law of refraction when a plane wavefront is propagating from a denser to a rarer medium. (CBSE Delhi 2019)
Answer:
The wavefront is a locus of points that oscillate in the same phase.

Consider a plane wavefront AB incident obliquely on a plane reflecting surface MM^–. Let us consider the situation when one end A of was front strikes the mirror at an angle i but the other end B has still to cover distance BC. The time required for this will be t = BC/c.

According to Huygen’s principle, point A starts emitting secondary wavelets and in time t, these will cover a distance c t = BC and spread. Hence, with point A as centre and BC as radius, draw a circular arc. Draw tangent CD on this arc from point C. Obviously, the CD is the reflected wavefront inclined at an angle ‘r’. As incident wavefront and reflected wavefront, both are in the plane of the paper, the 1^st law of reflection is proved.

To prove the second law of reflection, consider ΔABC and ΔADC. BC = AD (by construction),
∠ABC = ∠ADC = 90° and AC is common.

Therefore, the two triangles are congruent and, hence, ∠BAC = ∠DCA or ∠i = ∠r, i.e.the angle of reflection is equal to the angle of incidence, which is the second law of reflection.
Or
The refractive index of medium 2, w.r.t. medium 1 equals the ratio of the sine of the angle of incidence (in medium 1) to the sine of the angle of refraction (in medium 2), The diagram is as shown.

From the diagram

Question 2.
(a) Sketch the refracted wavefront for the incident plane wavefront of the light from a distant object passing through a convex lens.
Answer:

(b) Using Huygens’s principle, verify the laws of refraction when light from a denser medium is incident on a rarer medium.
Answer:
Refraction from denser to the rarer medium: Let XY be plane refracting surface separating two media of refractive index μ₁ and μ₂ (μ₁ > μ₂)

Let a plane wavefront AB incident at an angle i. According to Huygen’s principle, each point on the wavefront becomes a source of secondary wavelets and

Time is taken by wavelets from B to C = Time taken by wavelets from A to D


(c) For yellow light of wavelength 590 nm incident on a glass slab, the refractive index of glass Is 1.5. Estimate the speed and wavelength of yellow light Inside the glass slab. (CBSE 2019C)
Answer:
Given λ = 590 nm, μ = 1.5
Velocity of light inside glass slab.
∴ v = \(\frac{C}{\mu}=\frac{3 \times 10^{8}}{1.5}\) = 2 × 10⁸ ms^-1

Wavelength of yellow light inside the glass slab.
λ₁ = \(\frac{\lambda}{\mu}=\frac{290}{1.5}\) = 393.33 nm

Question 3.
(a) State the postulates of Huygen’s wave theory.
Answer:
The postulates are
All points on a given wavefront are taken as point sources for the production of spherical secondary waves, called wavelets, which propagate outward with speed characteristic of waves in that medium.

(b) Draw the type of wavefront that corresponds to a beam of light (i) coming from a very far off the source and (ii) diverging from a point source.
Answer:
After some time has elapsed, the new position of the wavefront is the surface tangent to the wavelets or the envelope of the wavelets in the forward direction.


Question 4.
What is meant by the diffraction of light? Obtain an expression for the first minimum of diffraction.
Answer:
The divergence of light from its initial line of travel when it passes through an opening or an obstacle is called diffraction or the phenomenon of bending of light around the sharp corners and spreading into the regions of the geometrical shadow is called diffraction.

Consider that a monochromatic source of light S, emitting light waves of wavelength λ, is placed at the principal focus of the convex lens L₁. A parallel beam of light, i.e. a plane wavefront, gets incident on a narrow slit AB of width ‘a’ as shown in the figure.

The diffraction pattern is obtained on a screen Lying at a distance D from the slit and at the focal plane of the convex lens L₂.

Consider a point P on the screen at which wavelets travelLing in a direction making angle O with CO are brought to focus by the lens. The wavelets from different parts of the slit do not reach point P in phase, although they are initially in phase. It is because they cover unequal distances in reaching point R The waveLets from points A and B will have a path difference equal to BN.

From the right angLed ANB, we have
BN = AB sin θ or BN = a sin θ …(1)

Suppose that the point P on the screen is at such a distance from the centre of the screen that BN = λ. and the angle θ = θ₁.

Then, equation 1 gives
λ = a sin θ₁ or sin θ₁ = \(\frac{λ}{a}\)

Such a point one screen will be the position of the first secondary minimum.

Question 5.
Describe an experiment to show that light waves are transverse in nature.
Answer:
Light is a transverse wave. This can be shown with the help of this simple experiment. The figure shows an unpolarized light beam incident on the first polarising sheet, called the polariser where the transmission axis is indicated by the straight line on the polariser.

The polariser can be a thin sheet of tourmaline (a complex boro-silicate). The Light, which is passing through this sheet, is polarised vertically as shown, where the transmitted electric vector is E_o. A second polarising sheet called the analyser intercepts this beam with its transmission axis at an angle θ to the axis of the polariser. As the axis of the analyser is rotated slowly, the intensity of Light received beyond It goes on decreasing.

When the transmitting axis of the analyser becomes perpendicular to the transmission axis of the polariser, no beam is obtained beyond the analyser. This means that the anaLyser has further polarised the beam coming from the polariser. Since only transverse waves can be polarised, therefore, this shows that light waves are transverse In nature.

Question 6.
Derive an expression for the width of the central maxima for diffraction of light at a single-slit. How does this width change with an increase in the width of the slit?
Answer:
The width of the central maxima for diffraction of light at a single-slit is the distance from the 1st diffraction minima on one side of the central maxima to the 1st diffraction minima on another side of the central maxima.

If a be the width of slit then for 1st diffraction minima, we have
sin θ = ± λ
or
sin θ = θ = ± \(\frac{λ}{a}\)

Angular width of central maxima
= 2θ = ± \(\frac{2λ}{a}\)

If D be the distance between the slit and the screen, then linear width ‘x’ of the central maxima is given by
x = d × 2θ = D × \(\frac{2λ}{a}\) = \(\frac{2Dλ}{a}\)

As the width (a) of the slit is increased, the linear width of central maxima goes on decreasing because x ∝ \(\frac{1}{a}\)

Question 7.
(a) Sketchthegraphshowingthevariation of the intensity of transmitted light on the angle of rotation between a polarizer and an analyser.
Answer:
The graph is as shown below

(b) A ray of light is incident at an angle of incidence i_p on the surface of separation between air and a medium of refractive index µ, such that the angle between the reflected and refracted ray is 90°. Obtain the relation between i_p and µ.
Answer:
Suppose an unpolarised light beam is an incident on a surface as shown in the figure below. The beam can be described by two electric field components, one parallel to the surface (the dots) and the other perpendicular to the first and to the direction of propagation (the arrows). It is found that the parallel components reflect more strongly than the other component, this results in a partially polarised beam. Furthermore, the refracted ray is also partially polarized.

Now suppose the angle of incidence, i is varied until the angle between the reflected and the refracted beam is 90°. At this particular angle of incidence, the reflected beam is completely polarised with its electric vector parallel to the surface, while the refracted beam is partially polarised. The angle of incidence at which this occurs is called the polarising angle i_p.

An expression can be obtained relating the polarising angle to the index of refraction n, of the reflecting surface. From the figure, we see that at the polarising angle
i_p + 90° + r = 180°
or
r = 90° – i_p.

Using Snell’s law we have n = \(\frac{\sin i}{\sin r}=\frac{\sin i_{p}}{\sin r}\)

Now sin r = sin (90° – i_p) = cos i_p, therefore the above expression becomes
n = \(\frac{\sin i_{p}}{\cos i_{p}}\) = tan ip

Question 8.
Describe Young’s double-slit experiment to produce an interference pattern due to a monochromatic source of light. Deduce the expression for the fringe width. (CBSE Delhi 2011)
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r1 and r2 are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,
y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe
y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,
y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, a width of the bright fringe is

From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

Question 9.
(a) Explain, with the help of a diagram, how plane polarised light Is obtained by scattering.
Answer:
It is found that when unpolarised sunlight is incident on a small dust particle or air molecules it is scattered in all directions. The light scattered in a direction perpendicular to the incident light is found to be completely polarised.

The electric vector of incident light has components both in the plane of the paper as well as perpendicular to the plane of the paper. The electrons under the influence of the electric vector acquire motion in both directions. However, radiation scattered by the molecules in perpendicular direction contains only components represented by dots (.), i.e. polarised perpendicular to the plane of the paper.

(b) Between two polaroids placed In crossed position a third Polaroid is introduced. The axis of the third Polaroid makes an angle of 30° with the axis of the first polaroid. Find the intensity of transmitted light from the system assuming / to be the intensity of polarised light obtained from the first polaroid. (CBSE A! 2011C)
Answer:
Let l_o be the intensity of light passing through the first polaroid.

The intensity of light passing through the middle polaroid whose axes are inclined at 30° to the first polaroid by Malus law is
l’ = l_o cos² 30° = l_o × 3/4 = 3l_o/4

The intensity of light passing through the system is, therefore, (for the second crystal θ = 60°)
l” = l’cos² 60° = 3l_o/4 × 1 /4
or
l” = 3l_o/16

Question 10.
(a) Why are coherent sources necessary to produce a sustained interference pattern?
Answer:
Interference will be sustained if there is a constant phase difference between the two interfering waves. This is possible if the two waves are coherent.

(b) In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference Is λ, is K units. Find out the intensity of light at a point where the path difference is λ/3. (CBSE Delhi 2012)
Answer:
Intensity at any point on the screen
l = l₁ + l₂ + 2\(\sqrt{1_{1}1_{2}}\) cos Φ

Let l0 be the intensity of either source, then l₁= l₂ = l_o
When p = λ, Φ = 2π

Question 11.
Use Huygen’s principle to explain the formation of the diffraction pattern due to a single-slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band? (CBSE Delhi 2012)
Answer:
(a) The arrangement is shown below in the figure.

When a plane wavefront WW’ falls on a single-slit AB, each point on the unblocked portion ADB of wavefront sends out secondary, wavelets in all the directions. For secondary waves meeting at point O, the path difference between waves is zero and hence the secondary waves reinforce each other giving rise to the central maximum at the symmetrical point O.

Consider secondary waves travelling in a direction making an angle θ with DO and reaching the screen at point P. Obviously, path difference between the extreme secondary waves reaching point P from A and B.
= BC = AB sin θ = a sin θ.

If this path difference a sin θ = λ, then point P will be minimum Intensity. In this situation, wavefront may be supposed to consist of two equal halves AD and BD and for every point on AD, there will be a corresponding point on DB having a path difference λ/2. Consequently, they nullify the effect of each other and point P behaves as the first secondary minimum. In general, if path difference a sin θ = nλ where n = 1, 2, 3, …. then we have secondary minima corresponding to that angle of diffraction θ_n.

However, if for some point P₁ on the screen secondary waves BP₁ and AP₁ differ In path by 3λ/2 then point P₁ will be the position of the first secondary maxima. Because in this situation, wavefront AB may be divided into three equal parts such that path difference between corresponding points on the first and second will be λ/2 and they will nullify. But secondary waves from the third part remain as such and give rise to the first secondary maxima, whose Intensity will be much less than that of central maxima.

In general, if path difference a sin θ = (2n + 1)θ/2, where n = 1, 2, 3, …… then we have nth secondary maxima corresponding to these angles.

The width of the central maxima is the distance between the first secondary minima on either side of the centre of the screen. The width of the central maxima is twice the angle θ subtended by the first minima on either side of the central maxima. Now sin θ = \(\frac{\lambda}{a}\). Since θ is small a therefore it can be replaced by tan θ, hence sin θ = \(\frac{\lambda}{a}=\frac{y}{L} or y = [latex]\frac{L \lambda}{\mathrm{a}}\).

This gives the distance of the first secondary minima on both sides of the centre of the screen. Therefore, the width of the central maxima is 2y, hence
2y = \(\frac{2L \lambda}{\mathrm{a}}\)

(b) The size reduces by half according to the relation: size = X/d. Intensity becomes twice the original intensity.

Question 12.
(a) Using the phenomenon of polarization, show how the transverse nature of light can be demonstrated.
Answer:
Light is a transverse wave. This can be shown with the help of this simple experiment. The figure shows an unpolarized light beam incident on the first polarising sheet, called the polariser where the transmission axis is indicated by the straight line on the polariser.

The polariser can be a thin sheet of tourmaline (a complex boro-silicate). The Light, which is passing through this sheet, is polarised vertically as shown, where the transmitted electric vector is E_o. A second polarising sheet called the analyser intercepts this beam with its transmission axis at an angle θ to the axis of the polariser. As the axis of the analyser is rotated slowly, the intensity of Light received beyond It goes on decreasing.

When the transmitting axis of the analyser becomes perpendicular to the transmission axis of the polariser, no beam is obtained beyond the analyser. This means that the anaLyser has further polarised the beam coming from the polariser. Since only transverse waves can be polarised, therefore, this shows that light waves are transverse in nature.

(b) Two polaroids P₁ and P₂ are placed with their pass axes perpendicular to each other. Unpolarised light of intensity l0 is Incident on P₁. A third polaroid P₃ is kept in between P₁ and P₂ such that its pass axis makes an angle of 30° with that of P₁. Determine the intensity of light transmitted through P₁ P₂ and P₃. (CBSE AI 2014)
Answer:
The intensity of light passing through P₁ is half of the light falling on it. Therefore, the light coming out of P₁ is l0_o/2 Now light coming out of P₃ is

and light coming out of polariser P₂ is

Question 13.
What does a Polaroid consist of? Show using a simple Polaroid that light waves are transverse in nature. The intensity of light coming out of a Polaroid does not change irrespective of the orientation of the pass axis of the polaroid. Explain why. (CBSE AI 2015)
Answer:
A polaroid consists of long-chain molecules aligned in a particular direction.

Let the light from an ordinary source (like a sodium lamps pass through a polaroid sheet P₁ it is observed that its intensity is reduced by half. Now, let an identical piece of polaroid P₂ be placed before P₁ As expected, the light from the lamp is reduced in intensity on passing through P₂2 alone. But now rotating P₁ has a dramatic effect on the light coming from P₂. In one position, the intensity transmitted by P₂ followed by P₁ is nearly zero. When turned by 90° from this position, P₁ transmits nearly the full intensity emerging from P₂ shown in the figure.

Since only transverse waves can be polarised, therefore, this experiment shows that light waves are transverse in nature. The electric vectors (associated with the propagating light wave) along the direction of the aligned molecules get absorbed. Thus, if an unpolarized light wave is an incident on such a polaroid then the light wave will get linearly polarized with the electric vector oscillating along a direction perpendicular to the aligned molecules; this direction is known as the pass-axis of the Polaroid.

Thus, if the light from an ordinary source (like a sodium lamp) passes through a polaroid sheet P it is observed that its intensity is reduced by half. Rotating P has no effect on the transmitted beam and transmitted intensity remains constant as there is always an electric vector that oscillates in a direction perpendicular to the direction of the aligned molecules.

Question 14.
Find an expression for intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. In which position of the polaroid sheet will the transmitted Intensity be maximum? (CBSE Delhi 2015)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁. Then the intensity of light after passing through the second polarizer P₂ will be
l = l_o cos² θ

where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be

The transmitted intensity will be maximum when 2θ = π/2 or θ = π/4

Question 15.
Distinguish between unpolarised and linearly polarised light. Describe with the help of a diagram how unpolarised light gets linearly polarised by scattering. (CBSE Delhi 2015)
Answer:
The two lights will be allowed to pass through a polariser. When the polarizer is rotated in the path of these two light beams, the intensity of light remains the same in all the orientations of the polariser, then the light is unpolarised. But if the intensity of light varies from maximum to minimum then the light beam is a polarised light beam.

It is found that when unpolarised sunlight is incident on a small dust particle or air molecules it is scattered in all directions. The light scattered in a direction perpendicular to the incident light is found to be completely polarised.

The electric vector of incident light has components both in the plane of the paper as well as perpendicular to the plane of the paper. The electrons under the influence of the electric vector acquire motion in both directions. However, radiation scattered by the molecules in perpendicular direction contains only components represented by dots (.), i.e. polarised perpendicular to the plane of the paper.

Question 16.
(a) Explain how a diffraction pattern is formed due to interference of secondary wavelets of light waves from a slit.
Answer:
(a) Diffraction at single slit: Consider monochromatic plane wavefront WW’ incident on the slit AB as shown in Fig. Imagine the slit to be divided into a large number of very narrow strips of equal width parallel to the slit. When the wavefront reaches the slit, each narrow strip parallel to the slit can be considered to be a source of Huygen’s secondary wavelets.

Central Maxima. Let us first consider the effect of all the wavelets at point O. All wavelets cover the same distance and reach 0 in the same phase. The wavelets superimpose constructively and give maximum intensity at O.

Position of secondary minima. Consider the intensity at a point P at an angle θ with the original direction.
Draw AL ⊥ BP.
In ΔABL


or
sin θ = \(\frac{λ}{a}\)

For second minima, BL = 2A
or a sin θ = 2λ

Similarly, for nth minima a sin θ = nλ
or sin θ = \(\frac{nλ}{a}\) , where n = 1, 2, ……

Position of secondary maxima: If path difference BL = \(\frac{3λ}{2}\), then slit AB can be divided into three equal parts and the path difference between wavelets from corresponding points in the first two parts will be \(\frac{λ}{2}\) and hence cancels each other’s effect and produces destructive Interference and the third path will produce its maxima at P called first secondary maxima.

Similarly, if BL = \(\frac{5λ}{2}\), we get second secondary maxima and so on.

For nth maxima
a sin θ = (2n + 1)\(\frac{λ}{a}\)
or
sin θ = \(\frac{(2 n+1) \lambda}{2 a}\)

Thus we find that the intensity of the central fringe is maximum whereas that of other fringes fall off rapidly in either direction from the centre of the fringe pattern.

(b) Sodium light consists of two wavelengths, 5900 Å and 5960 Å. If a slit of width 2 × 10^-4 m is Illuminated by sodium light, find the separation between the first secondary maxima of the diffraction pattern of the two wavelengths on a screen placed 1.5m away. (CBSE 2019C)
Answer:
The separation between the first secondary maxima of the diffraction pattern of two wavelengths is:

Question 17.
(a) Derive Snell’s law on the basis of Huygen’s wave theory when light Is travelling from a denser to a rarer medium.
Answer:
The ray diagram is as shown.


(b) Draw the sketches to differentiate between plane wavefront and spherical wavefront. (CBSE AI 2016)
Answer:
Spherical wavefront and plane wavefront

Question 18.
The figure drawn here shows the geometry of path differences for diffraction by a single-slit of width a.

Give appropriate ‘reasoning’ to explain why the intensity of light is
(a) Maximum at the central point C on the screen.
(b) (Nearly) zero for point P on the screen when θ = λ / a.
Hence write an expression for the total linear width of the central maxima on a screen kept at a distance D from the plane of the slit. (CBSE Delhi 2016C)
Answer:
(a) At central point C, the angle is zero, all path differences are zero. Hence all the parts of the slit contribute to the same phase. This gives the maximum intensity at point C.
(b)

From figure
NP – LP = NQ= a sin θ = aθ When θ = λ/a

Then path difference NP – LP = aθ = λ.
Hence MP – LP = NP – MP = λ/2

It implies that the contribution from corresponding points in two halves of the slit has a phase difference of π. Therefore, contributions from two halves cancel each other in pairs, resulting in a zero net intensity at point P on the screen. Half angular width of central maxima = λ/a Half linear width = λD/a

Linear width of central maxima = 2λD/a

Question 19.
Two polaroids, P₁ and P₂, are ‘set-up’ so that their ‘pass axis is ‘crossed’ with respect to each other. AQ third Polaroid, P₃ is now introduced between these two so that its ‘pass axis makes an angle with the ‘pass axis of P_1. A beam of unpolarized light, of Intensity I, Is Incident on P₁ If the Intensity of light that gets transmitted through this combination of three polaroids, Is I’, find the ratio \(\left(\frac{I^{\prime}}{I}\right)\) when θ equals: (i) 30°, (ii) 45° (CBSE Delhi 2016C)
Answer:
The diagram is as shown.

The intensity of unpolarized light is given as l.
It becomes half after passing through Polaroid P₁ (l/2)
Using Malus law for the intensity of light passing through P3 we have
l₁ = \(\left(\frac{l}{2}\right)\) cos²θ

This intensity l₁ is Incident on P₂, hence the intensity of light coming out of P₂ will be

Question 20.
What is the effect on the Interference pattern observed In Young’s double-slit experiment In the following cases:
(a) Screen is moved away from the plane of the slits,
(b) Separation between the slits is Increased and
(c) Widths of the slits are doubled. Give the reason for your answer.
Answer:
The fringe width is given by the expression
β = \(\frac{Dλ}{d}\)

(a) When D Is Increased, the fringe width Increases.
(b) When d 1s Increased the fringe width decreases.
(c) If the width w of the slits Is changed then Interference occurs only If \(\frac{1}{w}\) > \(\frac{1}{d}\) remains satisfied, where d is the distance between the slits.

Question 21.
Two slits In Young’s double-slit experiment are illuminated by two different lamps emitting light? Will you observe the Interference pattern? Justify your answer. Find the ratio of Intensities at two points on a screen In Young’s double-slit experiment, when waves from two slits have a path difference of (i) 0 and (ii) λ/4.
Answer:
The two sources act as Independent sources of light and hence can never be coherent. In a light, source light is produced by billions of atoms under proper excitation condition and each atom acts independently of the other atoms. Thus there Is no coherence ‘ between these two Independent sources hence no interference.

The phase difference corresponding to the two paths are Φ = 0 and Φ = π/2

Now intensity at the screen when the phase difference is Φ = 0 is
l_A = l₁ +l₂ + 2\(\sqrt{l_{1} l_{2}}\)cos Φ
or
l_A = l + l + 2\(\sqrt{l l}\)cos Φ = 4l

Now intensity at the screen when the phase difference is Φ = 90° Is
l_B = l₁ +l₂ + 2\(\sqrt{l_{1} l_{2}}\)cos Φ
or
l_B = l + l + 2\(\sqrt{l l}\)cos 90° = 2l
Therefore, ratio of intensities is
\(\frac{l_{A}}{l_{B}}=\frac{4l}{2l}\) = 2

Question 22.
(a) In a single-slit diffraction pattern, how does the angular width of the central maximum vary, when
(i) the aperture of the slit Is Increased?
(ii) distance between the slit and the screen is decreased?
Justify your answer In each case.
Answer:
The angular width of the central maxima in a single-slit diffraction pattern is given by 2θ = \(\frac{2λ}{a}\) where λ is the wavelength of light and ‘a’ the slit width.
(i) When the aperture of the slit is increased the angular width decreases.
(ii) When the distance between the slit and the screen is decreased, the angular width will remain the same but the linear width will increase.

(b) How Is the diffraction pattern different from the interference pattern obtained In Young’s double¬slit experiment? (CBSE Delhi 2011C)
Answer:
The difference is shown in the table:

Question 23.
(a) Can two independent monochromatic light sources be used to obtain a steady interference pattern? Justify your answer. (CBSE 2019C)
Answer:
No, because the phase difference between the light waves from two independent sources keeps on changing continuously and for a steady interference pattern, the phase difference between the waves should remain constant with time. Hence two independent monochromatic light sources cannot produce a steady interference pattern.

(b) In Young’s double-slit experiment, explain the formation of interference fringes and obtain an expression for the fringe width.
Answer:
Interference of light

Let S₁, S₂ be the two fine slits illuminated by a monochromatic source S of wavelength λ.

The intensity of light at any point P on the screen at a distance D from the slit depends upon the path difference between S₂P and S₁P.
∴ Path difference = S₂P – S₁P
= (S₂A + AP) – S₁P

Path difference = S₂A = d sin θ
Since θ is small, sin θ can be replaced by tan θ.
∴ Path difference = d tan θ = d\(\frac{y}{D}\)

Constructive interference [Bright Fringes]. For bright fringes, the path difference should be equal to integral multiple of A.
∴ \(\frac{dy}{D}\) = nλ
or
y = n\(\frac{λD}{d}\)

For nth fringe, let us write y as y_n
so y_n = n\(\frac{λD}{d}\)

The spacing between two consecutive bright fringes is equal to the width of a dark fringe.
∴ Width of the dark fringe.
β = y_n – y_n-1 = \(\frac{nλD}{d}\) – (n – 1)\(\frac{λD}{d}\) = \(\frac{λD}{d}\) …(i)

Destructive interference. [Dark Fringes].
For dark fringes, the path difference should be an odd multiple of λ/2.
∴ \(\frac{d}{D}\)y = (2n + 1)λ/2
or
y’ = \(\frac{D}{d}\)(2n + 1)\(\frac{λ}{2}\) = \(\frac{(2 n+1) \lambda D}{2 d}\)

For nth fringe, writing y as yn, we get
y’_n = \(\frac{(2 n+1) \lambda D}{2 d}\).

The spacing between two consecutive dark fringes is equal to the width of a bright fringe.
∴ Width of the bright fringe.

From Eqs. (i) and (ii), we find that dark and bright fringes are of same width given by
β = \(\frac{λD}{d}\).

(c) In an interference experiment using monochromatic light of wavelength A, the intensity of light of point, where the path difference is X, on the screen is K units. Find out the Intensity of light at a point when path difference is λ/4. (CBSE 2019C)
Answer:
The intensity of light on the screen where the waves meet having phase difference Φ is:


Question 24.
(a) Two monochromatic waves emanating from two coherent sources have the displacements represented by y₁ = a cos ωt and y₂ = a cos (ωt + Φ), where Φ is the phase difference between the two displacements. Show that the resultant intensity at a point due to their superposition is given by l = 4l_o cos² Φ/2, where l_o = a².
Answer:
Let the displacements of the waves from the sources S₁ and S₂ at a point on the screen at any time t be given by y₁ = a cos ωt and y₂ = a cos (ωt + Φ), where Φ is the constant phase difference between the two waves. By the superposition principle, the resultant displacement at point P is given by

Thus the amplitude of the resultant displacement is A = 2a cos (Φ/2)

Therefore the intensity at that point is
l = A² = 4a² cos² \(\frac{Φ}{2}\)

(b) Hence obtain the conditions for constructive and destructive interference. (CBSE AI 2014C)
Answer:
Bright fringes: For bright fringes I = max, therefore Φ = 0° or cos Φ = +1
or
Φ = 2 n π
Dark fringes: For dark fringes l = 0,
therefore Φ = π or cos Φ = -1
or
Φ = (2n + 1) π

Question 25.
A parallel beam of monochromatic light falls normally on a narrow slit of width ‘a’ to produce a diffraction pattern on the screen placed parallel to the plane of the slit. Use Huygens’ principle to explain that
(a) the central bright maxima is twice as wide as the other maxima.
Answer:
The width of the central maxima is the distance between the first secondary minima on either side of the centre of the screen. The width of the central maxima is twice the angle 6 subtended by the first minima on either side of the central maxima.

Now sin θ = \(\frac{λ}{a}\). Since θ is small there, a fore it can be replaced by tan 0, hence
tan θ = \(\frac{λ}{a}\) = \(\frac{y}{L}\)
or
y = \(\frac{Lλ}{a}\). This gives the distance of the first secondary min¬ima on both sides of the centre of the screen. Therefore, the width of the central maxima is 2y, hence
2y = \(\frac{2Lλ}{a}\)

(b) the Intensity falls as we move to successive maxima away from the centre on either side. (CBSE Delhi 2014C)
Answer:
The maxima in diffraction pattern are formed at (n +1 /2) λ/a, with n = 2, 3, etc. These become weaker with increasing n, since only one third, one- fifth, one-seventh, etc., of the slit contributes in these cases.

Question 26.
Answer the following questions:
(a) In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
Answer:

(b) Light of wavelength 5000 A propagating 1n air gets partly reflected from the surface of the water. How will the wavelengths and frequencies of the reflected and refracted light be affected? (CBSE Delhi 2015)
Answer:
No change in the wavelength and frequency of reflected light. In the case of refracted light, there is no change in frequency but the wavelength becomes 1/1.33 times the original wavelength.

Question 27.
(a) Good quality sun-glasses made of polaroids are preferred over ordinary coloured glasses. Justify your answer,
Answer:
A Polaroid sun-glass limits the light entering the eye, thus providing a soothing effect.

(b) Two polaroids and P₂ are placed In crossed positions. A third Polaroid P₃ is kept between P₁ and P₂ such that the pass axis of P₃ is parallel to that of P₁. How would the Intensity of light l₂ transmitted through P₂ vary as P₃ Is rotated? Draw a plot of Intensity l₂ Vs the angle ‘θ’, between pass axes of P₁ and P₃. (CBSE AI 2015C)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁ Then the intensity of light after passing through the second polarizer P₃ will be
l = l_o cos² θ
where θ is the angle between pass axes of P₁ and P₃. Since P₁ and P₂ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – θ).

Hence the intensity of light emerging from P2 will be

Therefore, the transmitted intensity will be maximum when θ = π/4

For graph

Question 28.
In a single-slit diffraction pattern, how does the angular width of central maximum change, when
(a) slit width is decreased,
(b) distance between the slit and screen is increased, and
(c) light of smaller visible wavelength is used? Justify your answer in each case.
Answer:
We know that the angular width of the central maximum of the diffraction pattern of a single-slit is given by
w = \(\frac{2Dλ}{a}\).

(a) If slit width ‘a’ is decreased, the angular width will increase because
x ∝ \(\frac{1}{a}\)

(b) Increase in distance between the slit and the screen does not affect the angular width of diffraction maxima. However, linear width of the maxima
w = \(\frac{2Dλ}{a}\) will increase.

(c) If the light of a smaller visible wavelength is used, the angular width is decreased because x ∝ λ.

Question 29.
Light, from a sodium lamp, is passed through two polaroid sheets P₁ and P₂ kept one after the other. Keeping P₁ fixed, P₂ is rotated so that its ‘pass axis can be at different angles, θ, with respect to the pass-axis of P₁
An experimentalist records the following data for the Intensity of light coming out of P₂ as a function of the angle θ.

(a) l_o = Intensity of beam falling on P₁ One of these observations is not in agreement with the expected theoretical variation of l, Identify this observation and write the correct expression.
Answer:
The observation \(\frac{l_{0}}{2 \sqrt{2}}\) is not correct. It should be l_o/4.

(b) Define the Brewster angle and write the expression for it in terms of the refractive index of the medium.
Answer:
It is the angle of incidence at which the refracted and the reflected rays are perpendicular to each other. It is related to the refractive index as tan i_p = n

Question 30.
(a) Light, from a monochromatic source, is made to fall on a single-slit of variable width. An experimentalist records the following data for the linear width of the principal maxima ‘ on a screen kept at a distance of 1 m from the plane of the slit.

Use any two observations from this data to estimate the value of the wavelength of light used.
Answer:
The width of the central maxima is given by the expression β = \(\frac{2Lλ}{a}\)
or
λ₁ = \(\frac{βa}{2L}\)

Using the values of the first observation we have
λ₁ = \(\frac{6 \times 10^{-3} \times 0.1 \times 10^{-3}}{2 \times 1}\) = 0.3 × 10^-6

Using the values of the second observation we have
λ₁ = \frac{3 \times 10^{-3} \times 0.2 \times 10^{-3}}{2 \times 1} = 0.3 × 10^-6

Thus the wavelength of light used is λ = 0.3 × 10^-6 m

(b) Show that the Brewster angle iB for a given pair of transparent media is related to their critical angle ic through the relation i_c = sin^-1 (ωt i_B)
Answer:
We know that

Question 31.
For a single-slit of width, “a” the first minimum of the interference pattern of monochromatic light of wavelength λ occurs at an angle of λ/a. At the same angle λ/a, we get a maximum for two narrow slits separated by a distance ‘a’. Explain. (CBSE Delhi 2014)
Answer:
The path difference between two secondary wavelets is given by nλ = a sin θ. Since θ is a very small sin θ = 0. So, for the first-order diffraction n = 1, the angle is λ/a. Now we know that θ must be very small θ = 0 (nearly) because of which the diffraction pattern is minimum.

Now for interference case, for two interfering waves of intensity l1 and l2 we must have two slits separated by a distance. We have the resultant intensity,
l = l₁ + l₂ + 2\(\sqrt{l_{1} l_{2}}\) cos θ

Since θ = 0° (nearly) corresponding to angle λ/a so cos θ = 1 (nearly)
So,
l = l₁ + l₂ + 2\(\sqrt{l_{1} l_{2}}\) cos θ
l = l₁ + l₂ + 2\(\sqrt{l_{1} l_{2}}\)

We see the resultant intensity is the sum of the two intensities, so there is a maxima corresponding to the angle λ/a.

This is why, at the same angle of λ/a, we get a maximum for two narrow slits separated by a distance “a”.

Question 32.
Show using a proper diagram of how unpolarised light can be linearly polarized by reflection from a transparent glass surface. (CBSE AI 2018, Delhi 2018)
Answer:
An ordinary beam of light, on reflection from a transparent medium, becomes partially polarised. The degree of polarisation increases as the angle of incidence is increased. At a particular value of the angle of incidence, the reflected beam becomes completely polarised. This angle of incidence is called the polarising angle (i_p).

Question 33.
Answer the following questions:
(a) In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
Answer:
The size reduces by half according to the relation: size = λ/d. Intensity increases fourfold.

(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment?
Answer:
The intensity of interference fringes in a double-slit arrangement is modulated by the diffraction pattern of each slit.

(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
Answer:
Waves diffracted from the edge of the circular obstacle interfere constructively at the centre of the shadow producing a bright spot.

(d) Two students are separated by a 7 m partition wall in a room 10 m high. If both light and sound waves can bend around obstacles, how is it that the students are unable to see each other even though they can converse easily? (NCERT)
Answer:
For diffraction or bending of waves by obstacles/apertures by a large angle, the size of the latter should be comparable to the wavelength. If the size of the obstacle/aperture is much too large compared to the wavelength, diffraction is by a small angle. Here the size is of the order of a few metres. The wavelength of light is about 5 × 10^-7 m, while sound waves of, say, 1 kHz frequency have a wavelength of about 0.3 m. Thus, sound waves can bend around the partition while light waves cannot.

Question 34.
(a) When an unpolarized light of intensity l0 is passed through a polaroid, what is the intensity of the linearly polarised light? Does it depend on the orientation of the polaroid? Explain your answer.
Answer:
(a) The intensity of the linearly polarised light would be l_o/2.
No, it does not depend on the orientation.
Explanation: The polaroid will let the component of the unpolarized light, parallel to its pass axis, to pass through it irrespective of its orientation.

(b) A plane polarised beam of light is passed through a polaroid. Show graphically the variation of the intensity of the transmitted light with an angle of rotation of the polaroid incomplete one rotation. (CBSE Delhi 2018C)
Answer:
We have l = l_o cos² θ
∴ The graph is as shown below

Question 35.
(a) If one of two identical slits producing interference in Young’s experiment is covered with glass so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the Interference pattern.
Answer:
As intensity is directly proportional to the square of the amplitude.


(b) What kind of fringes do you expect to observe if white light is used Instead of monochromatic light?
Answer:
The central fringe will be white and the remaining will be coloured fringes of different width in the VIBGYOR sequence.

Question 36.
Find an expression for intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. In which position of the polaroid sheet will the transmitted intensity be maximum? (CBSE Delhi 2015)
Answer:
Let l0 be the intensity of polarised light after passing through the first polarizer P₁ Then the intensity of light after passing through the second polarizer P₂ will be
l = l_o cos² θ
where 0 is the angle between pass axes of P₁ and P₂. Since P₁ and P₃ are crossed the angle between the pass axes of P₂ and P3 will be (π/2 – θ). Hence the intensity of light emerging from P₃ will be

The transmitted intensity will be maximum when 2θ = π/2 or θ = π/4

Question 37.
Derive the expression for the fringe width In Young’s double-slit experiment.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r₁ and r₂ are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o0 = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,

y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe

y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,

y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, a width of the bright fringe is

From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

Question 38.
(a) Using Huygens’ principle, draw a diagram to show the propagation of a wave-front originating from a monochromatic point source.
Answer:

(b) Describe diffraction of light due to a single-slit. Explain the formation of a pattern of fringes obtained on the screen and plot showing a variation of intensity with path difference in single-slit diffraction.
Answer:
Let us discuss the nature of the Fraunhofer diffraction pattern produced by a single-slit. Let us examine the waves coming from the various portions of the slit, as shown in the figure. According to Huygens principle, each portion of the slit acts as a source of waves. Hence, light from one portion of the slit can interfere with the light of another portion, and the resultant intensity on the screen will depend on the direction of θ. The secondary waves coming from the different parts of the slit interfere to produce either maxima or minima, thereby giving rise to a diffraction pattern.

For the diagram

2y = \(\frac{2Lλ}{a}\)

Question 39.
What is the effect on the interference fringes in Young’s double-slit experiment due to each of the following operations:
(a) the screen is moved away from the plane of the slits;
Answer:
The angular separation of the fringes remains constant (= λ/d). The actual separation of the fringes increases in proportion to the distance of the screen from the plane of the slits

(b) the (monochromatic) source is replaced by another (monochromatic) source of shorter wavelength;
Answer:
The separation of the fringes (and also angular separation) decreases.

(c) the separation between the two slits is Increased
Answer:
The separation of the fringes (and also angular separation) decreases.

(d) the source slit is moved closer to the double-slit plane;
Answer:
Let s be the size of the source and S its distance from the plane of the two slits. For interference, fringes to be seen the
condition \(\frac{s}{S}<\frac{\lambda}{d}\) should be satisfied otherwise interference patterns produced by different parts of the source overlap and no fringes are seen. Thus as S decreases (i.e. the source slit is brought closer), the interference pattern gets less and less sharp and when the source is brought too close for this condition to be valid the fringes – disappear. Till this happens, the fringe separation remains fixed.

(e) the width of the source slit is Increased;
Answer:
Same as in (d). As the source slit width increases fringe pattern gets less and less sharp. When the source slit is so wide that the condition \(\frac{s}{S}<\frac{\lambda}{d}\) is not satisfied the interference pattern disappears.

(f) the monochromatic source is replaced by a source of white light? (In each operation take all parameters other than the one specified to remain unchanged.)
Answer:
The interference patterns due to different component colours of white light overlap (incoherently). The central bright fringes for different colours are in the same position. Therefore, the central fringe is white. For a point P for which S₂P – S₁P= λ_b /2, where (λ_b = 400 nm) represents the wavelength for the blue colour, the blue component will be absent and the fringe will appear red in colour. Slightly farther away from where S₂Q – S₁Q = λ_b = λ_r/2 where λ_r (800 nm) is the wavelength for the red colour, the fringe will be predominantly blue. Thus, the fringe closest on either side of the central white fringe is red and the farthest will appear blue. After a few fringes, no clear fringe pattern is seen.

Question 40.
What is the diffraction of light? Draw a graph showing the variation of intensity with the angle in a single-slit diffraction experiment. Write one feature which distinguishes the observed pattern from the double-slit interference pattern. How would the diffraction pattern of a single-slit be affected when:
(i) the width of the slit is decreased?
(ii) the monochromatic source of light is replaced by a source of white light?
Answer:
Diffraction is the bending of light around obstacles or openings. It is a consequence of the wave nature of light. For diffraction to take place the obstacle should be of the order of the wavelength of light.

The intensity distribution for the single-slit diffraction pattern is as shown.

The intensity of all bright fringes is the same in Young’s interference pattern, but in diffraction, the intensity of bright fringes falls off on both sides of the central fringe.
We know that the angular width of the central maximum of the diffraction pattern of a single-slit is given by = \(\frac{2Dλ}{a}\)
(i) If slit width ‘a’ is decreased, the angular width will increase because
x ∝ \(\frac{1}{a}\)

(ii) When monochromatic light is replaced by white light, all the seven wavelengths form their own diffraction pattern, so coloured fringes are formed. The first few fringes are visible but due to overlapping the clarity of fringes decreases as the order increases.

Question 41.
(a) Define a wavefront. Using Huygens’ geometrical construction, explain with the help of a diagram how the plane wavefront travels from the instant t₁ to t₂ in the air.
Answer:
(a) Wavefront: It is the locus of the medium or points of a medium that is in the same phase of disturbance
First, consider a plane wave moving through free space as shown in the figure. At t = 0, the wavefront is indicated by the plane labelled AA’. In Huygens’s construction, each point on this wavefront is considered a point source. For clarity, only a few points on AA’ are shown. With these points as sources for the wavelets, we draw circles each of radius cΔt, where c is the speed of light in free space and Δt is the time of propagation from one wavefront to the next. The surface drawn tangent to these wavelets is the plane BB’, (Wavefront at a later time t). Here A₁ A₂ = B₁ B₂ = C₁C₂ = C_τ

(b) A plane wavefront is incident on a convex lens. Explain, with the help of the diagram, the shape of the refracted wavefront formed. (CBSE AI 2019)
Answer:
Spherical wavefront

Question 42.
(a) In Young’s double-slit experiment, derive the condition for
(i) constructive Interference and
(ii) destructive Interference at a point on the screen.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a wavelength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r₁ and r₂ are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,

y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe

y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,

y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, the width of the bright fringe is

From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

(b) A beam of light consisting of two wavelengths, 800 nm and 600 nm, is used to obtain the interference fringes in Young’s double-slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide. (CBSE Al 2012)
Answer:
Let at a distance y from central maxima the bright fringes due to wavelengths l1 and l2 coincide first time. For this to happen, nl₁ = (n + 1)l₂, where n is an integer.
or
\(\frac{n+1}{n}=\frac{\lambda_{1}}{\lambda_{2}}=\frac{800 \times 10^{-9}}{600 \times 10^{-9}}=\frac{4}{3}\) solving for n we have n = 3

It means that at distance nth (3^th) maxima for wavelength λ₁ is just coinciding with (n + 1)^th (4^th) maxima for wavelength l₂

Question 43.
(a) How does an unpolarized light incident on a Polaroid get polarised? Describe briefly, with the help of a necessary diagram, the polarisation of light by reflection from a transparent medium.
(b) Two polaroids ‘A’ and ‘B’ are kept in a crossed position. How should a third Polaroid ‘C’ be placed between them so that the intensity of polarised light transmitted by Polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A? (CBSE AI 2012)
Answer:
(a) The polariser allows only those vibrations of light to pass which are parallel to the pass axis of the polariser and blocks the remaining vibrations. Thus the light vibrations are restricted to only one plane.

Suppose an unpolarised light beam is an incident on a surface as shown in (figure a). The beam can be described by two electric field components, one parallel to the surface (the dots) and the other perpendicular to the first and to the direction of propagation (the arrows). It is found that the parallel components reflect more strongly than the other component, this results in a partially polarised beam. Furthermore, the refracted ray is also partially. polarised. Now suppose the angle of incidence 6, is varied until the angle between the reflected and the refracted beam is 90° (fig b). At this particular angle of incidence, the reflected beam is completely polarised with its electric vector parallel to the surface, while the refracted beam is partially polarised.

(b) Let l0 be the intensity of unpolarized light incident on Polaroid A. Then l_o/2 will be the intensity of polarised light after passing through the first polariser A. Then the intensity of light after passing through second polariser B will be l = (l_o/2)cos²θ

where θ is the angle between pass axes of A and B. Since A and B are crossed the angle between the pass axes of B and C will be (π/2 – θ). Hence the intensity of light emerging from C will be

Therefore, we have
\(\frac{l_{0}}{8}=\frac{l_{0}}{8}\) sin² 2θ or sin 2θ = 1 or 2θ = 90°
i.e. θ = π/4

Therefore, the transmitted intensity will be maximum when θ = π/4

Question 44.
(a) Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young’s double-slit experiment.
(b) In the diffraction due to a single slit experiment, the aperture of the slit is 3 mm. If monochromatic light of wavelength 620 nm is incident normally on the slit, calculate the separation between the first order minima and the 3^rd order maxima on one side of the screen. The distance between the slit and the screen is 1.5 m. (CBSE Delhi 2019)
Answer:
(a) (i) Interference pattern has a number of equally spaced bright and dark bands, while the diffraction pattern has a central bright maximum which is twice as wide as the other maxima.

(ii) In interference pattern, the intensity of all bright fringes is the same, while in diffraction pattern intensity of bright fringes goes on decreasing with the increasing order of the maxima.

Let the displacements of the waves from the sources S₁ and S₂ at a point P on the screen at any time t be given by y₁ = a cos cot and y₂ = a cos (ωt + Φ), where Φ is the constant phase difference between the two waves.

By the superposition principle, the resultant displacement at point P is given by

Thus the amplitude of the resultant displacement is
A = 2a cos (Φ/2) …(4)

Therefore the intensity at that point is
l = A² = 4a² cos²\(\frac{Φ}{2}\) …(5)

(b) Given a = 3mm = 3 × 10^-3m, λ = 620nm = 620 × 10^-9 m, D = 1.5 m Distance of first-order minima from centre of the central maxima = X_D1 = λ_D/a

Distance of third order maxima from centre of the central maxima X_D3 = 7λ_D/2a

Distance between first order minima and third order maxima = X_D3 – X_D1

Question 45.
(a) In Young’s double-slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence deduce the expression for the fringe width.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S_D1 and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S2 and S1 at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r1 and r2 are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. Therefore, the condition for dark fringes, or destructive interference, at P is given by

This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,

y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe

y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,

y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, the width of the bright fringe is

From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

(b) Show that the fringe pattern on the screen is actually a superposition of single-slit diffraction from each slit.
Answer:
It is a broader diffraction peak in which there appear several fringes of smaller width due to the double-slit interference pattern. This is shown below:

(c) What should be the width of each slit to obtain 10 maxima of the double-slit pattern within the central maximum of the single-slit pattern, for the green light of wavelength 500 nm, if the separation between two slits is 1 mm? (CBSE AI 2015)
Answer:
Given 10 b = width of central maxima in diffraction pattern λ = 500 nm, d= 1 mm,
Now 10\(\frac{Dλ}{d}\) = \(\frac{Dλ}{a}\)
or
a = \(\frac{d}{5}=\frac{1}{5}\) = 0.2 mm

Question 46.
(a) Define a wavefront. How is it different from a ray?
Answer:
A wavefront is defined as the locus of all adjacent points at which the phase of vibration of a physical quantity associated with the wave is the same.

It is in two dimensions while a ray is in one dimension.

(b) Depict the shape of a wavefront in each of the following cases.
(i) Light diverging from a point source,
Answer:

(ii) Light emerging out of a convex lens when a point source is placed at its focus.
Answer:

(c) Using Huygen’s construction of secondary wavelets, draw a diagram showing the passage of a plane wavefront from a denser into a rarer medium. (CBSE AI 2015C)
Answer:
The diagram is as shown

Question 47.
(a) Why does unpolarised light from a source show a variation in intensity when viewed through a Polaroid which is rotated? Show with the help of a diagram how unpolarised light from sun got linearly polarised by scattering.
(b) Three identical Polaroid sheets P1, P2 and P3 are oriented so that the pass axis of P2 and P3 are inclined at angles of 60° and 90° respectively with the pass axis of P1. A monochromatic source S of unpolarised light of intensity l0 is kept in front of the polaroid sheet P! as shown in the figure. Determine the intensities of light as observed by the observer at O when Polaroid P3 is rotated with respect to P2 at angles θ = 30° and 60°. (CBSE AI 2016)

Answer:
(a) When light passes through a Polaroid it absorbs all vibrations which are not parallel to its pass axis.
It is found that when unpolarised sunlight is incident on a small dust particle or air molecules it is scattered in all directions. The light scattered in a direction perpendicular to the incident light is found to be completely polarised.

The electric vector of incident light has components both in the plane of the paper as well as perpendicular to the plane of the paper. The electrons under the influence of the electric vector acquire motion in both directions. However, radiation scattered by the molecules in perpendicular direction contains only components represented by dots (.), i.e. polarised perpendicular to the plane of the paper.

(b) Let l0 be the intensity of light before passing P₁ Intensity of light coming out of P₁ will be l_o/2.

Then the intensity of light after passing through second poloroid (analyser) is
l₂ = \(\frac{l_{0}}{2}\)cos²60° = \(\frac{l_{0}}{8}\)

When P₃ is rotated with respect to P₂ at an angle of 30°, then angle be¬tween the pass axis of P₂ and P₃ will be θ = 30°+ 30° = 60°.
Hence l3 = l2 cos²60° = \(\frac{l_{0}}{8} \times \frac{1}{4}=\frac{l_{0}}{32}\)
or
θ = 30° – 30° = 0°

Therefore, l₃ = l₂ cos² 0° = l₂ = l_o/8
When P₃ is rotated with respect to P₂ at an angle of 60°, then the angle between the pass axis of P₂ and P₃ will be
θ = 30° + 60° = 90°

Question 48.
(a) Derive an expression for path difference in Young’s double-slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
Answer:
Consider a point P on the viewing screen; the screen is Located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance d as shown in the figure. Let us assume that the source of tight is monochromatic having a waveLength X. Under these conditions, the waves emerging from S and S have the same frequency and amplitude and are In phase.

If δ is the path difference between the waves from slits S₂ and S₁ at point P then
δ = r₂ – r₁ = d sin θ …(1)

where it is assumed that r₁ and r₂ are parallel, which is approximately true because D is much greater than d.

If this path difference is either zero or some Integral multiple of the wavelength, the waves are in phase at P and constructive Interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
δ = d sin θ = m λ …(2)

Here m is called the order number. In order to find the position of maxima measured vertically from O to P, i.e. y we assume that D >> d, that is, the distance from the slits to the screen is much larger than the distance between the two slits. (In practice D = 1 m and d = a few millimetre) Under these conditions, θ is small, and so the approximation sin θ ≈ tan θ. Therefore, from triangle POQ in the figure, we find that
sin θ = tan θ = \(\frac{Y}{D}\) …(3)

Substituting this in equation (2) we have
d \(\frac{Y}{D}\) = m λ …(2)

rewriting the above equation we have
y = \(\frac{mDλ}{d}\) …(4)
This gives the distance of the mth maxima from the centre 0 of the screen. For m = 0, 1, 2, 3, 4, ……. the values of y are
y_o = 0 …….. position of the central bright fringe

y₁ = \(\frac{Dλ}{d}\) ……. position of the first bright fringe

y₂ = \(\frac{2Dλ}{d}\) ……. position of the second bright fringe

y_m = \(\frac{mDλ}{d}\) …….position of the mth bright fringe

The spacing between any two bright fringes gives the width of a dark fringe. Therefore,

This gives the width of the dark fringe. Similarly, when the path difference is an odd multiple of λ/2, the waves arriving at P will be 180° out of phase and will give rise to destructive interference. There¬fore, the condition for dark fringes, or de¬structive interference, at P is given by

This gives the distance of the mth minima from the centre O of the screen. For m is equal to 0, 1, 2, 3, ……. we have
y’_o = \(\frac{Dλ}{2d}\), ……. position of the first dark fringe,
y’₁ = \(\frac{3Dλ}{2d}\) ……. position of the second dark fringe
y’₂ = \(\frac{5Dλ}{2d}\) ……. position of the third dark fringe and,
y’_m = \(\frac{(2 m+1) D \lambda}{2 d}\) ……. position of the mth dark fringe

Now the spacing between two consecutive dark fringes gives the width of the bright fringe, therefore, the width of the bright fringe is

From equations 5 and 9 we find that the fringe width of the bright and the dark fringe is the same, therefore, the fringe width is given by
β = \(\frac{Dλ}{d}\) …(10)

(b) The Intensity at the central maxima in Young’s double-slit experiment is l0. Find out the intensity at a point where the path difference is λ/6, λ/4 and λ/3. (CBSE AI 2016)
Answer:
Let l be the intensity of light coming out of each slit. Since waves at the central maxima are in phase, therefore, we have

Question 49.
(a) Define a wavefront. Using Huygens’ Principle, verify the laws of reflection at a plane surface.
Answer:
The wavefront is a locus of points that oscillate in the same phase.

Consider a plane wavefront AB incident obliquely on a plane reflecting surface MM^–. Let us consider the situation when one end A of wavefront strikes the mirror at an angle i but the other end B has still to cover distance BC. The time required for this will be t = BC/c.

According to Huygen’s principle, point A starts emitting secondary wavelets and in time t, these will cover a distance c t = BC and spread. Hence, with point A as centre and BC as radius, draw a circular arc. Draw tangent CD on this arc from point C. Obviously, the CD is the reflected wavefront inclined at an angle ‘r’. As incident wavefront and reflected wavefront, both are in the plane of the paper, the 1^st law of reflection is proved.

To prove the second law of reflection, consider ΔABC and ΔADC. BC = AD (by construction),
∠ABC = ∠ADC = 90° and AC is common.

Therefore, the two triangles are congruent and, hence, ∠BAC = ∠DCA or ∠i = ∠r, i.e.the angle of reflection is equal to the angle of incidence, which is the second law of reflection.
Or
The refractive index of medium 2, w.r.t. medium 1 equals the ratio of the sine of the angle of incidence (in medium 1) to the sine of the angle of refraction (in medium 2), The diagram is as shown.

From the diagram

(b) In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band? Explain.
Answer:
Size of central maxima reduces to half, (Size of central maxima = 2λD/d) Intensity increases.
This is because the amount of light, entering the slit, has increased and the area, over which it falls, decreases.

(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the obstacle. Explain why. (CBSE AI 2018, Delhi 2018)
Answer:
This is because of the diffraction of light. Light gets diffracted by the tiny circular obstacle and reaches the centre of the shadow of the obstacle.
β = \(\frac{Dλ}{d}\).

(i) When D is decreased, the fringe width decreases.
(ii) When d is Increased, the fringe width decreases.

Question 50.
The following figure shows an experiment set up similar to Young’s double-slit experiment to observe interference of light.

Here SS₂ – SS₁ = λ/4
Write the condition of (i) constructive,
(ii) destructive Interference at any point P in terms of path difference Δ = S₂P – S₁P.

Does the central fringe observed in the above set up tie above or below O? Give reason in support of your answer.
Yellow light of wavelength 6000°A produces fringes of width 08 mm in Young’s double-slit experiment. What will be the fringe width if the light source is replaced by another monochromatic source of wavelength 7500° A and separation between the slits is doubled?
Answer:
Given SS₂ – SS₁ = λ/4
Now path difference between the two waves from slits S₁ and S₂ on reaching point P on screen is

(a) For constructive interference at point P both difference Δx = nλ.
Therefore

where n = 0, 1, 2, 3, …

(b) For destructive interference at point P path difference

For central bright fringe, putting n = 0 in equation (1), we get
\(\frac{y d}{D}=-\frac{\lambda}{4}\)
or
y = – \(\frac{\lambda D}{4 d}\)

The -ve sign indicates that the central bright fringe will be observed below centre O of the screen, at distance below it.
Given λ₁ = 6000°A, β₁ = 0.8 mm,
λ₂ = 7500°A, β₂ = ?, d₂ = 2d₁

Using the expression
β = \(\frac{Dλ}{d}\) we have
\(\frac{\beta_{2}}{\beta_{1}}=\frac{\lambda_{2} d_{1}}{\lambda_{1} d_{2}}=\frac{7500}{6000} \times \frac{d_{1}}{2 d_{1}}\)

Solving we have β₂ = 0.5 mm

Question 51.
(a) There are two sets of apparatus of Young’s double-slit experiment. Inset A, the phase difference between the two waves emanating from the slits does not change with time, whereas in set B, the phase difference between the two waves from the slits changes rapidly with time. What difference will be observed in the pattern obtained on the screen in the two setups?
(b) Deduce the expression for the resultant intensity in both the above- mentioned setups (A and B), assuming that the waves emanating from the two slits have the same amplitude A and same wavelength λ.
Or
(a) The two polaroids, in a given setup, are kept ‘crossed’ with respect to each other. A third polaroid, now put in between these two polaroids, can be rotated. Find an expression for the dependence of the intensity of light I, transmitted by the system, on the angle between the pass axis of the first and the third polaroid. Draw a graph showing the dependence of l on θ.
(b) When an unpolarized light is an incident on a plane glass surface, find the expression for the angle of incidence so that the reflected and refracted light rays are perpendicular to each other. What is the state of polarization, of reflected and refracted light, under this condition?
Answer:
(a) Set A: Stable interference pattern, the positions of maxima and minima, does not change with time.
Set B: Positions of maxima and minima will change rapidly with time and an average uniform intensity distribution will be observed on the screen.

(b) Let the displacements of the waves from the sources S1 and S2 at a point on the screen at any time t be given by y₁ = a cos ωt and y₂ = a cos (ωt + Φ), where Φ is the constant phase difference between the two waves. By the superposition principle, the resultant displacement at point P is given by

Thus the amplitude of the resultant displacement is A = 2a cos (Φ/2)

Therefore, the intensity at that point is l = A² = 4a² cos²\(\frac{Φ}{2}\) – 4l_o cos²\(\frac{Φ}{2}\)
Since Φ = 0, l.e. there is no phase difference, hence l = 4 l_o

Inset B, the intensity will be given by the average intensity
l = 4l_o\(\left(\cos ^{2} \frac{\phi}{2}\right)\) = 2l_o
Or
(a) Let P₁ and P₂ be the two crossed Polaroids and P₃ be the polaroid kept between the two. Let l_o, be the intensity of polarised light after passing through the first Polaroid P₁. Then the Intensity of light after passing through the second Polaroid P₂ will be,
l = l_o cos² θ
where θ is the angle between pass axes of P₁ and P₂. Since P₁ and P₂ are crossed the angle between the pass axes of P₂ and P₃ will be (π/2 – 0). Hence the intensity of light emerging from P2₂ will be

The transmitted intensity will be maximum when π = π/4. The graph is as shown

(b) The ray diagram is as shown.

When light Is incident at a certain angle called Brewster angle, the reflected beam is completely polarised with its electric vector parallel to the surface, while the refracted beam is partially polarised. The angle of incidence at which this occurs is called the polarising angle i_B.

From figure we see that at the polaris-ing angle
i_B + 90° + r = 180°
or
r = 90° – i_B.

Using Snell’s law we have
μ = \(\frac{\sin i_{\mathrm{B}}}{\sin r}\)

Now sin r = (90° – i_B), therefore the above expression becomes

Nature of polarisation: Reflected light and linearly polarised

Numerical Problems:
Formulae for solving numerical problems

• Fringe width is given by β = \(\frac{Dλ}{d}\)
• Brewster’s Law: μ = \(\frac{\sin \theta_{p}}{\cos \theta_{p}}\) = tan θ_p
• Intensity of light coming out of a polariser l = l_o cos² θ
• If l₁ and l₂ are the intensities of light emitted by the two sources, w₁ and w₂ be the widths of the two slits, a₁ and a₂ be the amplitudes of the waves from the two slits then,
  \(\frac{l_{1}}{l_{2}}=\frac{w_{1}}{w_{2}}=\frac{a_{1}^{2}}{a_{2}^{2}}\)
• lf l_max and lmin be the intensities of light at the maxima and the minima the
  \(\frac{l_{\max }}{l_{\min }}=\frac{\left(a_{1}+a_{2}\right)^{2}}{\left(a_{1}-a_{2}\right)^{2}}\)

Question 1.
Laser light of wavelength 630 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 7.2 mm. Calculate the wavelength of another source of laser light that produces interference fringes separated by 8.1 mm using the same pair of slits. (CBSE Al 2011C)
Answer:
Given λ₁ = 630 nm, β₁ = 7.2 mm, β₂ = 8.1 mm, λ₂ =?

We know that β = \(\frac{Dλ}{d}\), for the same value of D and d we have β₂ ∝ λ,
Therefore, we have

Question 2.
What is the speed of light in a denser medium of polarising angle 30°? (CBSE Delhi 2019)
Answer:

Question 3.
Laser light of wavelength 640 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 7.2 mm. Calculate the wavelength of another source of light that produces interference fringes separated by 8.1 mm using the same arrangement. Also, find the minimum value of the order (n) of the bright fringe of the shorter wavelength which coincides with that of the longer wavelength. (CBSE AI 2012C)
Answer:
Given λ₁ = 640 nm, λ₂ = ?, b₁ = 7.2 mm and b₂ = 8.1 mm

Using the expression β = \(\frac{Dλ}{a}\) we have

Now n fringes of shorter wavelength will coincide with (n – 1) fringes of Longer wavelength
n₁λ₁ = n₂λ₂
or
n × 640 = (n – 1) × 720
Solving for n we have n =9

Question 4.
Yellow light (λ = 6000 Å) illuminates a single-slit of width 1 × 10 m. Calculate
(a) the distance between the two dark tines on either side of the central maximum, when the diffraction pattern is viewed on a screen kept 1.5 m away from the slit;
(b) the angular spread of the first diffraction minimum. (CBSE AI 2012C)
Answer:

Question 5.
Find the ratio of Intensities of two points P and Q on the screen in Young’s double-slit experiment when the waves from sources S₁ and S₂ have a phase difference of (i) π/3 and (11) π/2.
Answer:
Intensity at the screen when the phase difference is Φ = π/3 is

Now intensity at the screen when the phase difference is Φ = 90° is

Therefore, ratio of intensities is
\(\frac{l_{p}}{l_{Q}}=\frac{3l}{2l}=\frac{3}{2}\)

Question 6.
In young’s double-slit experiment, two sifts are separated by 3 mm distance and illuminated by the light of wavelength 480 nm. The screen is at 2 m from the plane of the slits. Calculate the separation between the 8th bright fringe and the 3N dark fringes observed with respect to the central bright fringe.
Answer:
Using the formuLa

Question 7.
Two coherent sources have Intensities In the ratio 25: 16. Find the ratio of the Intensities of maxima to minima, after the interference of light occurs.
Answer:
In the given problem

Question 8.
The ratio of intensities of maxima and minima in an interference pattern is found to be 25: 9. Calculate the ratio of light intensities of the sources producing this pattern.
Answer:
Given

Question 9.
In Young’s double-slit experiment using the light of wavelength 400 nm, Interference fringes of width X are obtained. Th. the wavelength of light is Increased to 600 nm and the separation between the slits Is halved. If on. wants the observed fringe width on the screen to b. the same in the two cases, find the ratio of the distance between the screen and the plan. of the Interfering sources In the two arrangements.
Answer:
Let D₁ be the distance between the screen and the sources when a tight of wavelength 400 nm Is used.

β = \(\frac{Dλ}{a}\)
or
X = \(\frac{D_{1} \times 400 \times 10^{-9}}{d}\) …(i)

Let D₂ be the distance between the screen and the sources to obtain the same fringe width, when light of wavelength 600 nm is used. Then,
X = \(\frac{D_{2} \times 600 \times 10^{-9}}{d}\) ….(ii)

From the equations (i) and (ii), we have
\(\frac{D_{1}}{D_{2}}=\frac{600 \times 10^{-9}}{400 \times 10^{-9}}\) = 1.5

Question 10.
In Young’s slit experiment, Interference fringes are observed on a screen, kept at D from the slits. If the screen Is moved towards the slits by 5 × 10^-2 m, the change in fringe width Is found to be 3 × 10^-5 m. If the separation between the slits is 10-3 m, calculate the wavelength of the light used.
Answer:
Given ΔD = 5 × 10^-2-2 m, Δβ = 3 × 10^-5-5 m, d = 10^-3 m,

Using the relation β = \(\frac{Dλ}{a}\) we have for the two cases
β₁ = \(\frac{D_{1} \lambda}{d}\) and
β₂ = \(\frac{D_{2} \lambda}{d}\) subtracting we have
β₁ – β₂ = \(\frac{λ}{d}\)(D1 – D2)
or

Question 11.
A slit of width ‘a’ is illuminated by monochromatic light of wavelength 700 nm at Normal Incidence. Calculate the value of ‘a’ for the position of
(a) the first minimum at an angle of diffraction of 30°.
(b) first maximum at an angle of diffraction of 30°.
Answer:
Given X = 700 nm = 7 × 10^-7 m

Question 12.
Estimate the angular separation between . first order maximum and third order minimum of the diffraction pattern due to a single-slit of width 1 mm, when light of wavelength 600 nm is incident normal on it. (CBSE AI 2015C)
Answer:
Given d = 1 mm = 10^-3 m,
λ = 600 nm = 6 × 10^-7 m,
For first order maxima
d sin θ = n λ
or
sin θ = \(\frac{n \lambda}{d}=\frac{6 \times 10^{-7}}{10^{-3}}\) = 6 × 10^-4
or
θ_max = 1.047°
Now for minima we have
d sin θ = (2n+1 )\(\frac{λ}{2}\)

For third-order minima we have n = 3
Therefore we have

sin θ = (2 × 3 + 1)\(\frac{λ}{2d}\) = \(\frac{7λ}{2d}\)
= \(\frac{7 \times 6 \times 10^{-7}}{2 \times 10^{-3}}\)
= 21 × 10^-4
or
θ_min = 6.397°

Therefore, angular separation is
θ_min – θ_max = 6.397 – 1.047 = 5.35°

Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 9 Ray Optics and Optical Instruments. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 9 Important Extra Questions Ray Optics and Optical Instruments

Ray Optics and Optical Instruments Important Extra Questions Very Short Answer Type

Question 1.
When light undergoes refraction at the surface of separation of two media, what happens to its frequency/wavelength?
Answer:
There is no change in its frequency, but its wavelength changes.

Question 2.
Define the refractive index.
Answer:
The Refractive index of a medium is defined as the ratio of the speed of light in a vacuum to the speed of light in the given medium.

Question 3.
What is the distance between the objective and eyepiece of an astronomical telescope in its normal adjustment?
Answer:
Distance between objective and eyepiece of telescope = f_o + f_e

Question 4.
Name the phenomenon responsible for the reddish appearance of the sun at sunrise and sunset.
Answer:
Atmospheric refraction.

Question 5.
What are the two main considerations that have to be kept in mind while designing the ‘objective’ of an astronomical telescope?
Answer:
Two main considerations are

1. Large light gathering power
2. Higher resolution (or resolving power)

Question 6.
Under what condition does a biconvex lens of glass having a certain refractive index act as a plane glass sheet when immersed in a liquid? (CBSE Delhi 2012)
Answer:
When the refractive index of the liquid is equal to the refractive index of a glass of which the lens is made.

Question 7.
Write the relationship between the angle of incidence ‘i’, angle of prism ‘A’ and angle of minimum deviation for a triangular prism. (CBSE Delhi 2013)
Answer:
2i = A + δ_m

Question 8.
Why can’t we see clearly through the fog? Name the phenomenon responsible for it. (CBSE Al 2016)
Answer:
Because it scatters light. Scattering of light.

Question 9.
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light? Give reason. (CBSE AI 2017)
Answer:
It decreases as δ_m ∝ \(\frac{1}{λ}\)

Question 10.
The objective lenses of two telescopes have the same apertures but their focal lengths are in the ratio 1: 2. Compare the resolving powers of the two telescopes. (CBSE AI 2017C)
Answer:
Same as resolving power does not depend upon the focal length of lenses.

Question 11.
An object is kept in front of a concave lens. What is the nature of the image formed? (CBSE Delhi 2017C)
Answer:
Virtual and erect.

Question 12.
The refractive index of the material of a concave lens is n₁. It is immersed in a medium of refractive index n₂. A parallel beam of tight is incident on the lens. Trace the path of the emergent rays when n₂ > n₁.
Answer:
The path of rays is as shown

Question 13.
A convex lens made of glass of refractive index μ_L is immersed in a medium of refractive index μ_m. How will the lens behave when μ_L < μ_m?
Answer:
The lens will continue to behave as a convex lens.

Question 14.
The image of an object formed by a lens on the screen is not in sharp focus. Suggest a method to get clear focusing of the image on the screen without disturbing the position of the object, the lens or the screen.
Answer:
Limit the field of view of the lens by using a blackened glass having a small circular hole in the middle.

Question 15.
In the figure given below, the path of a parallel beam of light passing through a convex lens of refractive index ng kept in a medium of refractive index nm is shown. Is (i) n_g = n_m or (ii) n_g > n_m, or (iii) n_g < n_m?

Answer:
As the rays of light do not suffer any deviation, therefore n_g = n_m.

Question 16.
In the figure path of a parallel beam of light passing through a convex lens of refractive index ng kept in a medium of refractive index, nm is shown. Is (i) n_g = n_m or (ii) n_g > n_m, or (iii) n_g < n_m?

Answer:
As the rays of light diverge, therefore n_g < n_m.

Question 17.
The refractive index of the material of a concave lens is μ₁. It is immersed in a medium of refractive index μ₂. A parallel beam of light is incident on the lens. Trace the path of emergent rays when μ₂ < μ₁.
Answer:
The path of rays is as shown below.

Question 18.
Suppose that the lower half of the concave mirror’s reflecting surface is covered with an opaque (non-reflective) material. What effect will this have on the image of an object placed in front of the mirror?
Answer:
The image of the whole object will be formed. However, as the area of the reflecting surface has been reduced the intensity of the image will below (in this case, half).

Question 19.
For the same value of angle of incidence, the angles of refraction in three media A, B and C are 15°, 25° and 35° respectively. In which medium would the velocity of light be minimum? (CBSE Al 2012)
Answer:
Medium A.

Question 20.
When red light passing through a convex lens is replaced by the light of blue colour, how will the focal length of the lens change? (CBSE AI 2013C)
Answer:
It will decrease.

Question 21.
A biconvex lens made of a transparent material of refractive index 1.25 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason. (CBSE AI 2014)
Answer:
The diverging lens as its focal length will become negative.

Question 22.
A concave lens of refractive index 1.5 is immersed in a medium of refractive index 1.65. What is the nature of the lens? (CBSE Delhi 2015)
Answer:
It will behave as a convex lens.

Question 23.
Why can’t we see clearly through a fog? Name the phenomenon responsible for it. (CBSE AI 2016)
Answer:
Because it scatters light. Scattering of light.

Question 24.
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light? Give reason. (CBSE AI 2017)
Answer:
It decreases as δ_m ∝ \(\frac{1}{λ}\)

Question 25.
The objective lenses of two telescopes have the same apertures but their focal lengths are in the ratio 1: 2. Compare the resolving powers of the two telescopes. (CBSE AI 2017C)
Answer:
Same as resolving power does not depend upon the focal length of lenses.

Question 26.
An object is kept in front of a concave lens. What is the nature of the image formed? (CBSE Delhi 2017C)
Answer:
Virtual and erect.

Question 27.
A convex lens is held in water. What change, if any, do you expect In its focal length?
Answer:
Focal Length of the given Lens increases in accordance with tens maker’s formula
\(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

This is because _wμ_{g a}μ_g

Question 28.
Violet light is incident on a converging lens of focal length f. State with reason, how the focal length of the lens will change 1f the violet light is replaced by a red light.
Answer:
As μ_r < μ_v hence in accordance with the relation
\(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) focal Length of Lens for red colour will be more.

Question 29.
What is the minimum value of the refractive index of the prism shown in the figure below?

Answer:
μ = \(\frac{1}{\sin i_{c}}=\frac{1}{\sin 45^{\circ}}=\frac{1}{\sqrt{2}}\)

Question 30.
How does the resolving power of a telescope change on decreasing the aperture of its objective lens? Justify your answer.
Answer:
As the resolving power of a telescope is \(\frac{D}{1.22λ}\) hence on decreasing the aperture of its objective lens, the resolving power of the telescope decreases in the same ratio.

Question 31.
What will happen to a ray of light incident normally on the interface of air and glass?
Answer:
It will pass un-deviated into the glass.

Question 32.
What is the speed of light in glass having a refractive index of 1.5?
Answer:
Speed of light in glass v = c/n = 3 × 10⁸ / 1.5 = 2 × 10⁸ m s^-1

Question 32.
Light of wavelength 600 nm in air enters a medium of refractive index 1.5. What will be its frequency in the medium?
Answer:
Frequency does not change when light moves from one medium into another. Therefore frequency of light
v = \(\frac{c}{\lambda}=\frac{3 \times 10^{8}}{600 \times 10^{-9}}\) = 5 × 10¹⁴ Hz

Question 34.
How does the focal length of a convex lens change if monochromatic red light Is used instead of monochromatic blue
light?
Answer:
Focal Length increases, i.e. f_r > f_v.

Question 35.
Two thin lenses of power + 5 D and – 3 D are in contact. What Is the focal length of the combination?
Answer:
Here P = P₁ + P₂ = + 5 – 3 = + 2 D
Hence f = 1/P = ½ m = + 50 cm.

Question 36.
Use the maker’s formula to write an expression for the (relative) refractive index, μ, of the material in terms of its focal length, f and the radii of curvature, r₁ and r₂, of Its two surfaces.
Answer:
The formula is \(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{r_{1}}-\frac{1}{r_{2}}\right)\)

Question 37.
Two thin lenses of power – 4 D and 2 D are placed in contact coaxially. Find the focal length of the combination. (CBSE Ai 2012C)
Answer:
Total power P = – 4 + 2 = – 2 D
Now f = 1/P = 1/ -2 = – 0.5 m

Question 38.
A convex lens is placed In contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens? (CBSE Delhi 2014)
Answer:
20 cm

Question 39.
The focal length of a biconvex lens is equal to the radius of curvature of either face. What is the refractive index of the material of the lens? (CBSEAI 2015)
Answer:
1.5
Using \(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

Given R₁ = R

Question 40.
An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the ens are reversed? (NCERT Exemplar)
Answer:
No, the reversibility of the Lens does not change the lens formula.

Ray Optics and Optical Instruments Important Extra Questions Short Answer Type

Question 1.
The aperture of the objective lens of an astronomical telescope is doubled. How does it affect
(i) the resolving power of the telescope and
(ii) the intensity of the image? (CBSE Sample Paper 2018-19)
Answer:
The resolving power of a telescope is given by the expression \(\frac{D}{1.22λ}\).

(i) When the aperture of the objective lens is increased, the resolving power of the telescope increases in the same ratio.
(ii) The intensity of the image is given by the expression β ∝ D₂, thus when the aperture is doubled, the intensity of the image becomes four times.

Question 2.
How does the resolving power of a compound microscope change on (a) decreasing the wavelength of light used, and (b) decreasing the diameter of the objective lens?
Answer:
The resolving power of a microscope is given by the expression RP = \(\frac{2 n \sin \theta}{\lambda}\)

(a) If the wavelength of the incident tight is decreased, the resolving power of the microscope increases.
(b)There is no effect of the decrease in the diameter of the objective on the resolving power of the microscope.

Question 3.
The layered lens shown in the figure is made of two kinds of glass. How many and what kinds of images will be produced by this lens with a point source placed on the optic axis? Neglect the reflection of light at the boundaries between the layers.

Answer:
Two images will be formed as the lens may be thought of, as two separate lenses of different focal lengths. The images will be surrounded by bright halos.

Question 4.
Monochromatic light is refracted from air into a glass of refractive index n. Find the ratio of wavelengths of the incident and refracted light.
Answer:
Using the relation λ₁n₁ = λ₂n₂ we have
\(\frac{\lambda_{1}}{\lambda_{2}}\) = n

Question 5.
Draw a labelled ray diagram to show the image formation in a compound microscope.
Answer:
The labelled diagram is as shown.

Question 6.
A ray of light while travelling from a denser to a rarer medium undergoes total internal reflection. Derive the expression for the critical angle in terms of the speed of light in the two media.
Answer:
Snell’s law can be used to find the critical angle. Now Snell’s law, when the ray moves from denser medium ‘b’ to rarer medium ‘a’, is given by


Now we know that n = \(\frac{c}{v}\) , substituting in the above relation we have
\(\frac{c}{v}=\frac{1}{\sin i_{c}}\) or sin i_c = \(\frac{v}{c}\)

Question 7.
Draw a labelled diagram for a refracting type astronomical telescope. How will its magnifying power be affected by increasing for its eyepiece (a) the focal length and (,b) the aperture? Justify your answer. Write two drawbacks of refracting type telescopes. (CBSE Sample Paper 2018-19)
Answer:
The labelled diagram of the telescope is as shown in the figure.

(a) The magnifying power of a telescope is given by M = \(\frac{f_{0}}{f_{\mathrm{e}}}\). If the focal length of the eyepiece is increased, it will decrease the magnifying power of the telescope.

(b) Magnifying power does not depend upon the aperture of the eyepiece. Therefore there is no change in the magnifying power if the aperture of the eyepiece is increased.

Drawbacks:

• Large-sized lenses are heavy and difficult to support.
• Large-sized lenses suffer from chromatic and spherical aberration.

Question 8.
Draw a labelled ray diagram of a Newtonian type reflecting telescope. Write any one advantage over refracting type telescope.
Answer:
The labelled diagram is shown below.

Due to the large aperture of the mirror as compared to a lens the image formed is much brighter than that formed by a refracting type telescope.

Question 9.
A right-angle crown glass prism with a critical angle of 41° is placed between the object PQ in two positions as shown in figures (a) and (b). Trace the path of rays from P and Q passing through the prisms in the two cases.

Answer:
The path of rays is as shown.


Question 10.
Write two conditions necessary for total internal reflection to take place.
Answer:
(a) The incident ray should travel from the denser to the rarer medium.
(b) The angle of incidence, in the denser medium, should be greater than the critical angle for the given pair of media.

Question 11.
(a) Explain the working of a compound microscope with the help of a labelled diagram.
Answer:
A compound microscope is an instrument used to see highly magnified images of tiny objects.

Working:
Let a tiny object AB be placed in front of the objective lens at a distance more than F₀. Its real and enlarged image is formed at A ‘ B ‘. The image A’ B’ acts as an object for the eyepiece and forms the final image at A” B “,

i.e. at a distance D, the least distance of distinct vision.

(b) Write the considerations that you keep in mind while choosing lenses to be used as eyepiece and objective in a compound microscope. (CBSE 2019C)
Answer:
The objective and eyepiece should have a short focal length for large magnification.

Question 12.
Explain the working of a refracting telescope with the help of a labelled diagram. What are the main limitations of this type of telescope and how are these overcome in a reflecting telescope? (CBSE 2019C)
Answer:
Refracting telescope

Working:
When the rays of light are made to incident on the objective from a distant object, the objective forms the real and inverted image at its focal plane. The lens is so adjusted that the final image is formed at least distance of distinct vision or at infinity.

Limitations:

• Large-sized lenses are needed which are expensive.
• Large-sized lenses suffer from spherical aberration and distortions.

Reflecting telescope (To overcome limitations):

• Reflecting telescopes are free from chromatic aberration and spherical aberration is very small.
• They are less heavy and easier to support.

Question 13.
Explain why the colour of the sky is blue.
Answer:
As sunlight travels through the earth’s atmosphere, it gets scattered (changes its direction) by the atmospheric particles. Light of shorter wavelengths is scattered much more than light of longer wavelengths. (The amount of scattering is inversely proportional to the fourth power of the wavelength. This is known as Rayleigh scattering.)

Hence, the bluish colour predominates in a clear sky, since blue has a shorter wavelength than red and is scattered much more strongly. In fact, violet gets scattered even more than blue, having a shorter wavelength. But since our eyes are more sensitive to blue than violet, we see the sky blue.

Question 14.
Why does the sun look reddish during sunrise and sunset?
Answer:
At sunset or sunrise, the sun’s rays have to pass through a larger distance in the atmosphere (Figure). Most of the blue and other shorter wavelengths are removed by scattering. The least scattered light reaching our eyes, therefore, the sun looks reddish. This explains the reddish appearance of the sun near the horizon.

Question 15.
What are the two ways of adjusting the position of the eyepiece while observing the final image in a compound microscope? Which of these is usually preferred and why?
Answer:
The two ways
(a) Final image formed at least distance of distinct vision.
(b) Final image formed at infinity.

The second one is usually preferred as it helps the observer to observe the final image with his/her eye in a relaxed position.

Question 16.
Write the relation between the angle of incidence (i), the angle of emergence (e), the angle of the prism (A) and the angle of deviation (δ) for rays undergoing refraction through a prism. What is the relation between ‘i’ and ‘e’ for rays undergoing minimum deviation? Using this relation obtain an expression for the refractive index (μ) of the material of the prism in terms of ‘A’ and angle of minimum deviation.
Answer:
The relation is i + e = A + δ_m
In the minimum deviation position ∠i = ∠e
In the minimum deviation position we have A = r₁ + r₂ = r + r = 2r
or
r = A / 2
and i + i = A + δ_m
or
2i = A + δ_m
or
i = \(\frac{A+\delta_{m}}{2}\)

substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)

Question 17.
Draw a ray diagram showing the formation of the image by a concave mirror of an object placed beyond its centre of curvature. If the lower half of the mirror’s reflecting surface is covered, what effect will it have on the image? (CBSE AI 2011C)
Answer:
The required ray diagram is shown below.

When the lower half of the mirror’s reflecting surface is covered, the intensity of the image will be reduced.

Question 18.
An object AB is kept in front of a concave mirror as shown in the figure.

(a) Complete the ray diagram showing the image formation of the object.
(b) How will the position and intensity of the image be affected if the lower half of the mirror’s reflecting surface is painted black? (CBSE AI 2012)
Answer:
The completed ray diagram is as shown.

No change in the position of the image, but the intensity will decrease.

Question 19.
Draw a ray diagram to show the formation of the image by an astronomical telescope when the final image is formed at the near point. Answer the following, giving reasons
(a) Why the objective has a larger focal length and a larger aperture than the eyepiece?
(b) What would be the effect on the resolving power of the telescope if its objective lens is immersed in a transparent medium of the higher refractive index? (CBSE AI 2012C)
Answer:
The ray diagram is as shown.

(a) The objective lens has a large focal length and large aperture for large magnification and resolving power.
(b) The resolving power will increase as the wavelength of light used will decrease.

Question 20.
Two convex lenses of the same focal length but of aperture A₁ and A, (A, < A₁), are used as the objective lenses in two astronomical telescopes having identical eyepieces. What is the ratio of their resolving power? Which telescope will you prefer and why? Give reason. (CBSE Delhi 2011)
Answer:
The resolving power is directly proportional to the aperture. Therefore the ratio of their resolving power is RP = \(\frac{A_{1}}{A}\).

Since A₁ > A therefore we will prefer the telescope with aperture A1 as it will gather a larger amount of light than the telescope of aperture A.

Question 21.
Which two of the following lens L₁ L₂ and L₃ will you select as objective and eyepiece for constructing the best possible (a) telescope and (b) microscope. Give a reason to support your answer. (CBSE Delhi 2015C)

Answer:
(a) For telescope

• Objective lens L₂: Because it has a large focal length and large aperture
• Eye lens L₃: Because it has a small focal length and small aperture

(b) For Microscope

• Objective lens L₃: Because it has a small aperture and small focal length
• Eye lens L₃: because it has a large aperture and large focal length

Question 22.
Draw a ray diagram to show how a right-angled isosceles prism may be used to bend the path of light by 90°.
Write the necessary condition in terms of the refractive index of the material of this prism for the ray to bend by 90°. (CBSE Delhi 2016C)
Answer:
The ray diagram is as shown.

The angle of incidence in the denser medium should be greater than the critical angle for the given pair of media, i.e.

Question 23.
The image of a candle is formed by a convex lens on a screen. The lower half of the lens is painted black to make it completely opaque. Draw the ray diagram to show the image formation. How will this image be different from the one obtained when the lens is not painted black?
Answer:
The ray diagram depicting the image is shown

The image formed will be less bright as compared to that when half of the lens is not painted black. This is because every part of the lens forms the image. When the lower half is blackened, light from this portion will be blocked, hence the intensity of light in the image will be less.

Question 24.
A magician during a show makes a glass lens with n = 1.47 disappear in a trough of liquid. What is the refractive index of the liquid? Could the liquid be water?
Answer:
The refractive index of the liquid must be equal to 1.47 in order to make the lens disappear. This means n₁ = n₂. This gives 1 /f = 0 or f = ∞. The lens in the liquid will act as a plain sheet of glass. No, the liquid is not water, it could be glycerine.

Question 25.
Explain with reason, how the resolving power of an astronomical telescope will change, when
(a) frequency of the incident light on the objective lens is increased,
(b) the focal length of the objective lens is increased, and
(c) the aperture of the objective lens is halved?
Answer:
Resolving power of a telescope = \(\frac{D}{1.22 \lambda}\) hence
(a) on increasing the frequency of incident light, wavelength X decreases and consequently resolving power is increased.
(b) increase in focal length of the objective lens will have no effect on the resolving power, and
(c) if the aperture of the objective lens is halved, then resolving power is also halved.

Question 26.
Explain with reason, how the resolving power of a compound microscope will change when
(a) frequency of the incident light on the objective lens is increased,
(b) the focal length of the objective lens is increased, and
(c) the aperture of the objective lens is increased.
Answer:
Resolving power of a compound microscope RP = \(\frac{2 \mu \sin \theta}{\lambda}\), hence
(a) on increasing the frequency of incident light, its wavelength X decreases and consequently resolving power increases.
(b) on increasing the focal length of the objective lens, the value of sine and hence resolving power decreases.
(c) on increasing the aperture of the objective lens, the value of sin 0 and hence resolving power increases.

Question 27.
A convex lens of the focal length is kept in contact with a concave lens of focal length f₂. Find the focal length of the combination. (CBSE AI 2013)
Answer:
For a convex lens +f₁ and for a concave lens – f₂, using the expression
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
or

Question 28.
(a) The relation between the angle of incidence ‘i’ and the corresponding angle of deviation (δ), for a certain optical device, is represented by the graph shown in the figure. Identify this device. Draw a ray diagram for this device and use it for obtaining an expression for the refractive index of the material of this device in terms of an angle characteristic of the device and the angle, marked as δ_m, in the graph. (CBSE Al 2016C)

Answer:
(a) The device is a prism.
The relation is i + e = A + δ_m
In the minimum deviation position ∠i = ∠e
In the minimum deviation position we have A = r₁ + r₂ = r + r = 2r
or
r = A / 2
and i + i = A + δ_m
or
2i = A + δ_m
or
i = \(\frac{A+\delta_{m}}{2}\)

substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)

(b) The diagram is as shown.

Ray Optics and Optical Instruments Important Extra Questions Long Answer Type

Question 1.
Draw a labelled ray diagram to show the image formation in a refracting type astronomical telescope. Obtain an expression for the angular magnifying power and the length of the tube of an astronomical telescope in its ‘normal adjustment’ position. Why should the diameter of the objective of a telescope be large?
Answer:
A labelled diagram of the telescope is shown in the figure.

The object subtends an angle at the objective and would subtend essentially the same angle at the unaided eye. Also, since the observers’ eye is placed just to the right of the focal point f’₂, the angle subtended at the eye by the final image is very nearly equal to the angle β.

Therefore, M = \(\frac{\beta}{\alpha}=\frac{\tan \beta}{\tan \alpha}\) …(1)

From right triangles ABC and ABC’ as shown in figure, we have
tan α = \(\frac{\mathrm{AB}}{\mathrm{CB}}=\frac{-h}{f_{0}}\) and
tan β = \(\frac{\mathrm{AB}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{-h}{f_{\mathrm{e}}}\)

substituting the above two equations in equation (1), we have
M = \(\frac{\beta}{\alpha}=\frac{-h^{\prime}}{f_{e}} \times \frac{f_{0}}{-h^{\prime}}=\frac{f_{0}}{f_{e}}\)

The length of the telescope is the distance between the two lenses which is L = f_o + f_e The diameter of the objective of a telescope should be large so that it can collect more light and image of distant objects is formed clear.

Question 2.
Draw a ray diagram to show the formation of an erect image of an object kept in front of a concave mirror. Hence deduce the mirror formula. (CBSE 2019C)
Answer:
An object AB is placed between P and F. The course of rays for obtaining erect image A₁B₁ of object AB is shown in the figure.

Draw DG ⊥ on the principal axis.
Triangles DGF and A₁ B₁C are similar

Since Point G is close to P, so GF = PF

Multiplying and dividing both sides by uvf, we get
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)

Question 3.
(a) Define the term power of a lens. Write its SI units.
Answer:
The power of a lens is the reciprocal of its focal length in the metre.
i.e. P = \(\frac{1}{f(\text { in } m)}\)

S.I. unit of power of a lens is dioptre (D).

(b) Derive the expression for the power of two thin lenses placed coaxially in contact with each other. (CBSE 2019C)
Answer:
Power of two thin lenses in contact. Consider an object O placed at a distance u on the principal axis of the lens A. Rays of light starting from O forms, the image at I₁
∴ \(\frac{1}{v_{1}}-\frac{1}{u}=\frac{1}{f_{1}}\) …(1)

Place lens B in contact with A. The image I₁ will serve as a virtual object and forms a real image I.
∴ Again apply lens formula
\(-\frac{1}{v_{1}}+\frac{1}{v}=\frac{1}{f_{2}}\) …(2)

Adding (1) and (2), we have

where f is the focal length of the combination

From (3), \(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)

The total power of the lens combination is given by
P = P₁ + P₂

Question 4.
A biconvex lens of refractive index μ1 focal length ‘f and radius of curvature R is immersed in a liquid of refractive index μ₂. For (i) μ₂ > μ₁, and (ii) μ₂ < μ₁, draw the ray diagrams in the two cases when a beam of light coming parallel to the principal axis is incident on the lens. Also, find the focal length of the lens in terms of the original focal length and the refractive index of the glass of the lens and that of the medium. (CBSE AI 2013C)
Answer:

(b) Given: As the lens is equiconvex therefore R₁ = R₂ = R, _aμ_g = μ₁; _aμ₁ = μ₂ f_a = f, f_L = ?

Using the expression

Question 5.
Write the conditions for observing a rainbow. Show, by drawing suitable diagrams, how one understands the formation of a rainbow. (CBSE AI 2014C)
Answer:
The conditions for observing a rainbow are that the sun should be shining in one part of the sky (say near the western horizon) while it is raining in the opposite part of the sky (say the eastern horizon). An observer can therefore see a rainbow only when his back is towards the sun.

Sunlight is first refracted as it enters a raindrop, which causes the different wavelengths (colours) of white light to separate. The longer wavelength of light (red) is bent the least while the shorter wavelength (violet) are bent the most. Next, these component rays strike the inner surface of the water drop and get internally reflected if the angle between the refracted ray and normal to the drop surface is greater than the critical angle (48°, in this case).

The reflected light is refracted again as it comes out of the drop as shown in the figure. It is found that the violet light, emerges at an angle of 40° related to the incoming sunlight and red light emerges at an angle of 42°. For other colours, angles lie in between these two values.

Question 6.
Explain the basic differences between the construction and working of a telescope and a microscope. (CBSE AI 2015)
Answer:
(a) In a telescope the objective has a large aperture and a large focal length, while in a microscope both the aperture and focal length of the objects are small (f_e > f_o). In a telescope, the eyepiece has a small aperture as compared to the objective, while in a microscope the eyepiece has a bigger aperture than the objective (f_e < f_o).

(b) A telescope increases the angle the object subtends at the eye thereby increasing its clarity by bringing it closer, while a microscope actually magnifies the object or a telescope magnifies distant objects, while a microscope magnifies nearby objects.

Question 7.
Why does white light disperse when passed through a glass prism?
Using the lens maker’s formula show how the focal length of a given lens depends upon the wavelength of light incident on it. (CBSE Delhi 2015C)
Answer:
It is because a glass prism offers a different refractive index to different wavelengths of light.
Lens maker’s formula is \(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\).

The refractive index depends upon wavelength as n ∝ \(\frac{1}{λ}\), therefore f ∝ λ.

Hence the focal length of a lens increases with the increase in the wavelength of light.

Question 8.
A thin converging lens has a focal length f in air. If it is completely immersed in a liquid, briefly explain, how the focal length of the lens will vary?
Answer:
The focal length of a converging lens is given by
\(\frac{1}{f}\) = (_an_g – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
where ang = refractive index of Lens with respect to air.

And In a given liquid medium the focal Length of the Lens is given by
\(\frac{1}{f_{m}}\) = (_mn_g – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

Therefore the ratio of the totaL focal Length is

(a) If _mn_g < _an_g then f is +ve and has a value greater than f, i.e. focal length of the lens increases when immersed in a given liquid medium.

(b) If _mn_g >_an_g, then f is -ve, i.e. the lens will begin to behave as a diverging lens.

Question 9.
When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency. Explain why?
Answer:
Reflection and refraction arise through the interaction of incident light with the atomic constituents of matter. Atoms may be viewed as oscillators that take up the frequency of the external agency (light) causing forced oscillations. The frequency of light emitted by a charged oscillator equals its frequency of oscillation. Thus the frequency of scattered light equals the frequency of incident light.

Question 10.
The image of an object formed by the combination of a convex lens (of focal length f) and a convex mirror (of the radius of curvature R), set up as shown is observed to coincide with the object. Redraw this diagram to mark on it the position of the centre of curvature of the mirror. Obtain the expression for R in terms of the distances marked as ‘a’ and ‘d’ and focal length f of the convex lens. (CBSE Delhi 2016C)

Answer:
The final image, formed by the combination, is coinciding with the object itself. This implies that the rays, from the object, are retracing their path, after refraction from the tens and reflection from the mirror. The (refracted) rays are, therefore, fatling normally on the mirror. It follows that the rays A B, and A’ B’, when produced, are meeting at the centre of curvature C of the mirror. Hence C is the centre of curvature of the mirror.

From the figure, we then see that for the convex lens we have

u = – a and v = + (d + R). If f is the focal length of the lens, we have


Question 11.
Define the magnifying power of a compound microscope when the final image is formed at infinity. Why must both the objective and the eyepiece of a compound microscope have short focal lengths? Explain. (CBSE Delhi 2017)
Answer:
It is defined as the ratio of the angle subtended on the eye by the final image when it lies at infinity to the angle subtended on the eye by the object when it lies at the least distance of distinct vision from the eye or the near point of the eye. The magnifying power of a microscope is given by
M = M_e × M_o = \(\frac{L}{f_{0}} \times\left(1+\frac{D}{f_{e}}\right)\)

Since it depends inversely on the focal lengths of the objective and the eyepiece, therefore both have to be small to get a large magnification.

Question 12.
(a) Draw a ray diagram for the formation of the image by a compound microscope.
Answer:
The ray diagram is as shown.

(b) You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct a compound microscope?

Answer:
The objective should have a short focal length and large aperture while the eyepiece should have a short focal length and small aperture. Thus for objective lens L₃ should be used and for eyepiece lens, L₂ should be used.

(c) Define the resolving power of a microscope and write one factor on which it depends. (CBSE AI 2017)
Answer:
The resolving power of a microscope is given by the expression
RP = \(\frac{2 \mu \sin \theta}{1.22 \lambda}=\frac{2 \mu v \sin \theta}{1.22 c}\)

It depends upon the wavelength/ frequency of the incident light.

Question 13.
Draw a labelled ray diagram of an astronomical telescope in the near point adjustment position. (CBSE Delhi 2019)
A giant refracting telescope at an observatory has an objective lens of focal length 15 m and an eyepiece of focal length 1.0 cm. If this telescope is used to view the Moon, find the diameter of the image of the Moon formed by the objective lens. The diameter of the Moon is 3.48 × 10⁶ m, and the radius of the lunar orbit is 3.8 × 10⁸ m.
Answer:
A Labelled ray diagram is as shown.

Given f_o = 15 m, f_e = 1.0 cm = 0.01 m, M = ? D_m = 3.48 × 10⁶ m, r = 3.8 × 10⁸ m,
Using M = \(\frac{f_{0}}{f_{e}}=\frac{15}{0.01}\) = 1500

The angle subtended by the moon at the objective of the telescope

Question 14.
(a) Amobilephoneliesalongtheprincipal axis of a concave mirror. Show with the help of a suitable diagram the formation of its image. Explain why magnification is not uniform.
Answer:
The image of the mobile phone formed by the concave mirror is shown in the below figure.

The part of the mobile phone that is at C will form an image of the same size only at C. In the figure, we can see that B’C = BC. The part of the mobile phone that lies between C and F will form an enlarged image beyond C as shown in the figure. It can be observed that the magnification of each part of the mobile phone cannot be uniform on account of different locations. That is why the image formed is not uniform.

(b) Suppose the lower half of the concave mirrors reflecting surface is covered with an opaque material. What effect this will have on the image of the object. Explain. (CBSE Delhi 2014)
Answer:
The intensity of the image will decrease while the whole image will be for.

Question 15.
(a) Draw a labelled ray diagram of a compound microscope, when the final image forms at the least distance of distinct vision.
(b) Why is its objective of short focal length and of short aperture compared to its eyepiece? Explain.
(c) The focal length of the objective is 4 cm while that of the eyepiece is 10 cm. The object is placed at a distance of 6 cm from the objective lens.
(i) Calculate the magnifying power of the compound microscope, if its final image is formed at the near point.
(ii) Also calculate the length of the compound microscope. (CBSE AI 2019)
Or
(a) With the help of a labelled ray diagram, explain the construction and working of a Cassegrain reflecting telescope.
(b) An amateur astronomer wishes to estimate roughly the size of the sun using his crude telescope consisting of an objective lens of focal length 200 cm and an eyepiece of focal length 10 cm. By adjusting the distance of the eyepiece from the objective, he obtains an image of the sun on a screen 40 cm behind the eyepiece. The diameter of the sun’s image is measured to be 6-0 cm. Estimate the sun’s size, given that the average earth-sun distance is 1.5 × 10¹¹ m.
Answer:
(a) The diagram is as shown.

(b) The magnifying power of compound microscope m = m₀ × m_e = \(\frac{L}{f_{o}}\left(1+\frac{D}{f_{e}}\right)\)

To have high magnifying power and high resolution, the focal length of the objective and its aperture should be short.

The focal length of the eyepiece is comparatively greater than the objective so an image formed by the objective lens may form within the focal length of the eyepiece and the final magnified image may be formed.

Aperture is short for higher resolution,

(c) Given u_o = – 6 cm
For objective lens we have

(i) For magnifying power of compound microscope we have
m = \(\frac{v_{o}}{u_{o}}\left(1+\frac{D}{f_{e}}\right)=\frac{12}{6}\left(1+\frac{25}{10}\right)\) = 7

(ii) Length of the compound microscope L = v₀ + u_e = 12 + 7.14 = 19.14 cm
Or
(a) Cassegrain reflecting telescope consists of a large concave (primary) parabolic mirror having a hole in its centre. There is a small convex (secondary) mirror near the focus of the concave mirror. The eyepiece is placed near the hole of the concave mirror. The parallel rays from a distant object are reflected by the large concave mirror. These rays fall on the convex mirror which reflects these rays outside the hole. The final magnified image is formed at infinity.

The diagram is as shown.

(b)

Magnification produced by the eye piece is
me = \(\frac{v_{e}}{u_{e}}=\frac{40}{40 / 3}\) = 3

Diameter of the image formed by the objective is
D = 6/3 = 2 cm

If D is the diameter of the sun then the angle subtended by it on the objective will be
α = \(\frac{D}{1.5 \times 10^{11}}\) rad

Now, angle subtended by the image at the objective = angle subtended by the sun
α = \(\frac{\text { size of image }}{f_{0}}=\frac{2}{200}=\frac{1}{100}\) rad

Therefore,
\(\frac{D}{1.5 \times 10^{11}}=\frac{1}{100}\)
D = 1.5 × 10⁹

Question 16.
A convex lens is placed in contact with a plane mirror. An axial point object, at a distance of 20 cm from this combination, has its image coinciding with itself. What is the focal length of the convex lens?
Answer:
Figure (a) shows a convex lens L in contact with a plane mirror M. P is the point object, kept in front of this combination at a distance of 20 cm, from it. Since the image of the object is coinciding with the object itself, the rays from the object, after refraction from the lens, should fall normally on the mirror M, so that they retrace their path and form an image coinciding with the object itself.

This will be so, if the incident rays from P form a parallel beam perpendicular to M, after refraction from the lens. For clarity, M has been shown at a finite distance from L, in figure (b). For lens L, since the rays from P form a parallel beam after refraction, P must be at the focus of the lens. Hence the focal length of the lens is 20 cm.


Question 17.
A convex lens and a convex mirror (of the radius of curvature 20 cm) are placed co-axially with the convex mirror placed at a distance of 30 cm from the lens. For a point object, at a distance of 25 cm from the lens, the final image, due to this combination, coincides with the object itself. What is the focal length of the convex lens?
Answer:
The ray diagram is as shown.

The final image, formed by the combination, is coinciding with the object itself. This implies that the rays, from the object, are retracing their path, after refraction from the lens and reflection from the mirror. The (refracted) rays are, therefore, falling normally on the mirror. It follows that the rays A B, and A’ B’, when produced, are meeting at the centre of curvature C of the mirror. Hence O₂C = 20 cm, the radius of curvature of the mirror. From the figure, we then see that for the convex lens u = – 25 cm and v = + (30 + 20) cm = + 50 cm. If f is the focal length of the lens, we have
\(\frac{1}{50}-\frac{1}{(-25)}=\frac{1}{f}\)
or
f = 16.67 cm

Question 18.
Derive a relation between focal length, image distance and object distance for a
concave mirror.
Answer:
Consider a concave mirror of small aperture, image distance and object distance for a Figure below shows two rays of light leaving the tip of the object. One of these rays passes through the centre of curvature C of the mirror, hitting the mirror head-on and reflecting back on itself. The second ray BP strikes the mirror at its pole P and reflects as shown obeying the laws of reflection. The image of the tip of the arrow is located at the point where these two rays intersect. Thus the image is formed between the focus and centre of curvature.

Consider the two right-angled triangles BAP and B’A’P

Now from triangle BAP using trigonometry, we have
tan θ = \(\frac{AB}{PA}\) …(1)

Therefore equation (7) becomes
\(\frac{\mathrm{PA}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PA}-\mathrm{PC}}{\mathrm{PC}-\mathrm{PA}^{\prime}}\)

By Cartesian sign conventions we have PA = -u, PA’ = -v and PC = – R, substituting in equation (8), we have

simplifying we have 2uv = vR + uR dividing both sides by uvR we have
\(\frac{1}{u}+\frac{1}{v}=\frac{2}{R}\) …(11)

but R = 2 f, where f is the focal length of the mirror. Therefore the above equation
reduces to \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
which is the required mirror formula.

Question 19.
With the help of a suitable ray diagram, derive a relation between the object distance (u) image distance v and radius of curvature (R) for a convex spherical surface, when a ray of light travels from rarer to denser medium. (CBSE Delhi 2011C)
Answer:
Let a convex spherical surface XPY separate a rarer medium of refractive index (n₁) from a denser medium of refractive (n2). The real image of object 0 is formed by refraction from the convex spherical surface of radius of curvature R. The angle α β γ are shown in the figure.

Let ∠AOP = α, ∠AIP = β and ∠ACP = γ.

From point A, drop AN perpendicular to the principal axis of the spherical refracting surface. From triangle AOC, we have
i = α + γ

Since the aperture of the spherical refracting surface is small, point A will be close to point P and hence angles α, β and γ will be small. As such, these angles may be replaced by their tangents.

Therefore, equation (1) may be written as
i = tanα + tanγ …(2)

From right angled triangles ΔALO and ΔALC, we have

tan α = \(\frac{AL}{LO}\) and tan γ = \(\frac{AL}{LC}\)

Substituting for tan α and tan γ in equation (2), we have

i = \(\frac{AL}{LO}\) + \(\frac{AL}{LC}\) …(3)

Again, as aperture of the refracting surface is small, point L will be close to point P, the pole of the refracting surface.
Therefore,
LO ≈ PO and LC ≈ PC

Therefore, equation (3) becomes
i = \(\frac{AL}{PO}\) + \(\frac{AL}{PC}\) …(4)

Now, from triangle ΔACI, γ = r + β
or
r = γ— β

Since angles γ and β are small, we have
r = tan γ— tan β …(5)

From right angled triangles ΔALC and ΔALI,
we have
tan γ = \(\frac{A L}{L C} \approx \frac{A L}{P C}\) and tan β = \(\frac{A L}{L I} \approx \frac{A L}{P I}\)

Substituting for tan β and tan γ in equation (5) we have
r = \(\frac{\mathrm{AL}}{\mathrm{PC}}-\frac{\mathrm{AL}}{\mathrm{PI}}\) …(6)

Now by Snell’s Law at point A we have
n₁ sin i = n₂ sin r

Since angles are small, therefore the above relation becomes
n₁ i = n₂ r …(7)

Substituting the values of i and r from equations (4) and (6) we have

Applying new Cartesian sign conventions:
PO = – u (a distance of the object is against incident Light)

PI = + v (distance of image Is along incident Light)
PC = + R (a distance of the centre of curvature is along with incident Light) we have

The above equation connects u, V and R to the absolute refractive indices of the material of the refracting surface and that of the rarer medium.

Question 20.
A ray of light Is an Incident on one face of a glass prism and emerges out from the other face. Trace the path of the ray and derive an expression for the refractive index of the glass prism. Also, plot a graph between the Angle of incidence and angle of deviation. (CBSE Delhi 201 IC)
Answer:
The graph is as shown

Consider a cross-section XYZ of a prism as shown in the figure. Let A be the angle of the prism. A ray PQ of monochromatic light is incident on face XY of the prism at an angle i. The ray is called the incident ray and the angle is called the angle of incidence. This ray is refracted towards the normal NQE and travels in the prism along QR. This ray is called the refracted ray at the face XY.

Let r₁ be the angle of refraction at this surface. The refracted ray QR is incident at an angle r₂ on the surface XZ. The ray QR again suffers refraction and emerges out of face XZ at an angle e along with RS. The ray is called the emergent ray and the angle e is called the angle of emergence. When the ray SR is extended backwards it meets the extended ray PQ at point D such that δ is the angle of deviation of the ray.

As seen from figure we have in triangle QDR that ∠DQR = i – r₁ and
∠DRQ = e – r₂. Therefore from triangle QDR we have
δ = ∠DQR + ∠DRQ = (i – r₁) + (e – r₂)
or
δ = (i + e) – (r₁ + r₂) …(1)

Now from the quadrilateral XQER, we have
A + E = 180° …(2)

In triangle QER we have r₁ + r₂ + e – 180° …(3)

From equations (2) and (3) we have
A = r₁ + r₂ …(4)

Substituting in equation (1) we have
δ = i + e – A
or
i + e = A + δ … (5)

The deviation produced by a prism depends upon (i) the angle of incidence (ii) the angle of prism and (Hi) the refractive index of the material of the prism. It is found that as the angle of incidence changes, the angle of deviation also changes.

A graph between the angle of incidence and the angle of deviation is shown in the figure above. As the angle of incidence increases, the angle of deviation first decreases becomes a minimum for a particular angle of incidence and then increases. The minimum value of the angle of deviation is called the angle of minimum deviation. It is denoted by δ_m. In this position the ray of light passes symmetrically through the prism, i.e. the refracted ray QR is parallel to the base of the prism. In this position, the angle of incidence is equal to the angle of emergence, i.e. i = e. Also in this position, the angle of refraction at the faces of the prism are equal, i.e. r₁ = r₂.

Substituting these values in equations (4) and (5) we have
A = r₁ + r₂ = r + r = 2r
or
r = A/2 …(6)
and i + i = A + δm
or
2i = A + δm
or
i = \(\frac{A+\delta_{m}}{2}\) …(7)

substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)

Question 21.
(a) Draw a ray diagram showing the image formation by a compound microscope. Obtain an expression for total magnification when the image is formed at infinity.
Answer:
The ray diagram is as shown.


(b) How does the resolving power of a compound microscope get affected, when
(i) the focal length of the objective is decreased.
(ii) the wavelength of light is increased? Give reasons to justify your answer. (CBSE AI 2015C)
Answer:
The resolving power of a microscope is given by the expression RP = \(\frac{2 n \sin \theta}{\lambda}\)
(i) There is no effect of the increase in the focal length of the objective on the resolving power of the microscope.
(ii) If the wavelength of the incident light is increased, the resolving power of the microscope also decreases.

Question 22.
An optical instrument uses eye-lens of power 12.5 0 and an object lens of power 50 D and has a tube length of 20 cm. Name the optical instrument and calculate its magnifying power, if it forms the final image at infinity. (CBSE Delhi 2017C)
Answer:
It is a compound microscope.
The ray diagram is as shown.

Let m_o and me be the magnifications produced by the objective lens and eye lens respectively, the total magnifying power of the microscope
M = m_o x m_e

Now m_o = – \(\frac{v_{0}}{u_{0}}\)

Also, the magnifying power of the eyepiece when the final image is formed at infinity
m_e = \(\frac{D}{f_{e}}\)

Thus magnifying power of the microscope is
M = \(\frac{-v_{0}}{u_{0}} \times \frac{D}{f_{e}}\)

As a first approximation, u_e ≈ f_e and v_e ≈ L = distance between objective and eyepiece (or length of microscope tube), then we have
M = \(\frac{-L}{f_{0}} \times \frac{D}{f_{e}}\)

Question 23.
Use the mirror equation to show that
(i) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Answer:
By mirror formula we have \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Therefore \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) and for concave mirror u and f both are having negative sign, i.e. f < 0 and u < 0.

It means that v > 2f, having a negative sign. Thus, the image is real and lies beyond 2f.

(ii) a convex mirror always produces a virtual image independent of the location of the object.
Answer:
(Ii) For a convex mirror \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) but f is positive and u is negative, i.e. f >0 but u < 0.

Therefore, it is self-evident from the above relation that irrespective of the value of u, the value of v is aLways +ve. It means that the Imaged formed by the convex mirror is always virtual independent of the location of the object.

(iii) an object placed between the pole and the focus of a concave mirror produces a virtual and enlarged image. (CBSE AI 2011)
Answer:
As for a concave mirror f and u, both are negative, hence

It means that for an object placed between the pole and principal focus of a concave mirror the image formed (as v is +ve) is virtual and magnification

m = \(\frac{1}{O}=\frac{|v|}{|u|}\) > 1, i.e. the image is an enlarged image.

Question 24.
(i) Obtain Lens makers formula using the expression \(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{\left(n_{2}-n_{1}\right)}{R}\), here the ray of light propagating from a rarer medium of refractive index (n₁) to a denser medium of refractive index (n₂) is incident on the convex side of spherical refracting surface of radius of curvature R.
(ii) Draw a ray diagram to show the image formation by a concave mirror when the object is kept between its focus and the pole. Using this diagram, derive the magnification formula for the Image formed. (CBSE DelhI 2011)
Answer:
(i) The course of rays through the Lens Is as shown. For refraction at the spherical surface XP₁Y, we have


Consider the second surface XP₂Y. Actually, the materiaL of the Lens does not extend beyond XP₁Y. Therefore, before the refracted ray from A₁ could meet the principal axis, it will suffer refraction at point A₂ on the second face XP₂Y and the Lightray will finally meet the principal axial. Such that l is the final image. Thus point lies the real Image of the virtual object I. Hence for refraction at the surface XP₂Y we have

The above equation becomes

But n₂/n₁ = n, the absolute refractive index of the material of the lens, therefore the above equation takes the form
\(\frac{1}{v}-\frac{1}{u}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

But by lens formula we have \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
Therefore, from the above two equations we have
\(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) …(7)

This is the Lens maker’s equation or formula.

(ii) The ray diagram is as shown

Now from triangle BAP we have
tan θ = \(\frac{AB}{PA}\) …(1)

Also from triangle B’A’P, we have A’B’
tan θ = \(\frac{A^{\prime} B^{\prime}}{P A^{\prime}}\) …(2)

Comparing equations (1) and (2), we have

By Cartesian sign convention AB = h, A’B’ = h’, PA = – u and PA’= v . Substituting in equations (3) we have

But \(\frac{h^{\prime}}{h}\) = m ( Linear magnification),
therefore
m = – \(\frac{\text { image distance }}{\text { object distance }}\)

Question 25.
(a) Two thin convex lenses L₁ and L₂ of focal lengths f₁ and f₂ respectively, are placed coaxially in contact. An object is placed at a point beyond the focus of lens L₁. Draw a ray diagram to show the image formation by the combination and hence derive the expression for the focal length of the combined system.
Answer:
Consider two lenses A and B of focal length f₁ and f₂ placed in contact with each other. Let the object be placed at a point O beyond the focus of the first lens L₁ as shown.

The first lens L₁ produces an image at l₁ Since image l₂ is real, it serves as a virtual object for the second lens L₂, producing the final image at l. Since the lenses are thin, we assume the optical centres of the lenses to be coincident. Let this central point be denoted by P.

For the image formed by the first lens L₁, we get
\(\frac{1}{v_{1}}-\frac{1}{u}=\frac{1}{f_{1}}\) …(i)

For the image formed by the second lens L₂, we get
\(\frac{1}{v}-\frac{1}{v_{1}}=\frac{1}{f_{2}}\) …(ii)

Adding equations (i) and (ii) we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\) …(iii)

If the two lens-system is regarded as equivalent to a single lens of focal length f, we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) …(iv)

Therefore from equations (iii) and (iv) we get
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)

(b) A ray PQ incident on the face AB of a prism ABC, as shown in the figure, emerges from the face AC such that AQ = AR.

Draw the ray diagram showing the passage of the ray through the prism. If the angle of the prism is 60° and the refractive index of the material of the prism is \(\sqrt{3}\), determine the values of angle of incidence and angle of deviation. (CBSE AI 2015)
Answer:
The ray diagram is as shown

The prism, in this situation, is in the minimum deviation position, therefore we have
r = \(\frac{A}{2}=\frac{60}{2}\) = 30°

Hence n = \(\frac{\sin i}{\sin r}=\frac{\sin i}{\sin 30^{\circ}}\) = \(\sqrt{3}\)

This gives, i = 60°
Hence from
i = \(\frac{A+\delta_{m}}{2}\) we have
δ_m = 2i – A = 2 × 60° – 60° = 60°

Question 26.
(a) Plot a graph to show the variation of the angle of deviation as a function of the angle of incidence for light passing through a prism. Derive an expression for the refractive index of the prism in terms of angle of minimum deviation and angle of prism.
(b) What is the dispersion of light? What is its cause?
(c) A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in the figure. What must be the minimum value of the refractive index of glass? Give relevant calculations. (CBSE Delhi 2016)

Answer:

For a prism we have
i + e = A + δ …(1)

From the graph between the angle of incidence and the angle of deviation it follows that as the angle of incidence increases, the angle of deviation first decreases becomes a minimum for a particular angle of incidence and then again increases. The minimum value of the angle of deviation is called the angle of minimum deviation. It is denoted by 5m. In this position the ray of light passes symmetrically through the prism, i.e. the refracted ray QR is parallel to the base of. the prism. In this position, the angle of incidence is equal to the angle of emergence, i.e. i = e. Also in this position, the angle of refraction at the faces of the prism are equal, i.e. r₁ = r₂. Substituting these values in equations (4) and (5) we have
A = r₁ + r₂ = r + r = 2r
or
r = A/2 …(2)
and
i + i = A + δ_m
or
2i = A + δ_m
or
i = \(\frac{A+\delta_{m}}{2}\) …(3)

Substituting for i and r in the expression for Snell’s law we have a speed of light in a vacuum

(b) The phenomenon of splitting a ray of white tight into its constituent colours (wavelengths) is catted dispersion.
Cause: It is because different wavelengths travel at different speeds In a medium other than vacuum.

(C) The diagram of the path of rays through the prism is as shown.
Here θ = 45° > i_c

Now n = \(\frac{1}{\sin i_{c}}=\frac{1}{\sin 45^{\circ}}=\frac{1}{1 / \sqrt{2}}=\sqrt{2}\)
Therefore n > \(\sqrt{2}\)

Numerical Problems :

Formulae for solving numerical problems

• When Light travels from an optically denser medium to an optically rarer medium It bends away from the normal.
• When light travels from an optically rarer medium to an optically denser medium It bends towards from the normal. speed of Light in vacuum
• μ = \(\frac{\text { speed of light in vacuum }}{\text { speed of light in the medium }}\)
• μ = \(\frac{1}{\sin \theta_{c}}\)
• In minimum deviation position A = 2r or
  
• Lens maker’s formula
  \(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
• MagnifyIng power of a compound microscope
  M = M_e × M_o = \(\frac{L}{f_{0}} \times\left(1+\frac{D}{f_{e}}\right)\)

Question 1.
A convex lens made up of a glass of refractive index 1.5 is dipped, In turn, In
(a) a medium of refractive index 1.65,
Answer:
When dipped in the medium of refractive index 1.65, it will behave as a concave lens and when dipped in the medium of refractive index 1.33, it will behave as a convex lens.

(b) a medium of refractive index 1.33.
(i) Will it behave as a converging or a diverging lens in the two cases?
Answer:
Its focal length in another medium is given by

Thus f_m = -5.5 f_a, i.e. focal length increases and becomes negative.

(ii) How will Its focal length change In the two media? (CBSE AI 2011)
Answer:
Similarly

Thus f_m = 3.3 f_a, i.e. focal length increases.

Question 2.
A compound microscope uses an objective lens of focal length 4 cm and an eyepiece lens of focal length 10 cm. An object is placed at 6 cm from the objective lens. Calculate the magnifying power of the compound microscope. Also, calculate the length of the microscope. (CBSE Al 2011)
Answer:
f_o = 4 cm, f_e = 10 cm, u_o = – 6 cm, M = ?, L = ?
Using

Hence angular magnification


Question 3.
A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece lens of focal length 1 cm is used, find the angular magnification of the telescope.
If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.42 × 10⁶ m and the radius of the lunar orbit is 3.8 × 10⁸ m. (CBSE AI 2011, Delhi 2015)
Answer:
Given f_o = 15 m, f_e = 1.0 cm = 0.01 m, M = ?
Dm = 3.48 × 10⁶ m, r = 3.8 × 10⁸ m,

Using M = \(\frac{f_{0}}{f_{\mathrm{e}}}=\frac{15}{0.01}\) = 1500

The angle subtended by the moon at the objective of the telescope

Question 4.
A beam of light converges at a point P. A concave lens of focal length 16 cm is placed in the path of this beam 12 cm from P. Draw a ray diagram and find the location of the point at which the beam would now converge. (CBSE Delhi 2011C)
Answer:
The ray diagram is shown in the figure. In the absence of the concave lens the beam converges at point P. When the concave lens is introduced, the incident beam of light is diverged and now comes to focus at point Q. Thus for the concave lens P serves as a virtual object giving rise to a real Image at Q.

Here u = + 12 cm, f = – 16 cm, v = ?, Now for a lens

Hence v = 48 cm
i. e. the point at which the beam is focused is 48 cm from the lens.

Question 5.
Two convex lenses of focal length 20 cm and 1 cm constitute a telescope. The telescope is focused on a point that is 1 m away from the objective. Calculate the magnification produced and the length of the tube, if the final image Is formed at a distance of 25 cm from the eyepiece. (CBSE Delhi 2011 C)
Answer:
Given f_o = 2o cm, f_e = 1 cm, u = – 100 cm, M =?, y =?

Fora lens \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
or
\(\frac{1}{v}-\frac{1}{-100}=\frac{1}{20}\)
or
v = 25cm

Since the eye lens forms the image of the virtual object at the distance of distinct vision for the eye lens
v = – 25 cm, f_e = 1 cm,

Now \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
or
\(\frac{1}{-25}-\frac{1}{u}\) = 1
or
u = – \(\frac{25}{26}\)cm

Now magnification produced by the object lens
m_o = \(\frac{v}{u}=-\frac{25}{100}=-\frac{1}{4}\)

Magnification produced by the eye Lens
m_e = \(\frac{v}{u}=\frac{-25}{-25}\) × 26 = 26

Hence total magnification
M = m_o × m_e = -1 /4 × 26 = – 6.5

Question 6.
(a) Under what conditions are the phenomenon of total internal reflection of light observed? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
(b) Three lenses of focal lengths +10 cm, -10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination. (CBSE Delhi 2019 C)

Answer:
(a) (i) Light travels from a denser medium to a rarer medium.
(ii) Angle of Incidence in the denser medium is more than the critical angle for a given pair of media.
For the grazing incidence n sin i_C = l sin 90°
n = \(\frac{1}{\sin i_{c}}\)

(b) For convex lens f = + 10 cm

Object distance for concave lens u₂ = 15 – 5 = 10 cm

For third lens
\(\frac{1}{f_{3}}=\frac{1}{v_{3}}-\frac{1}{\infty}\) ⇒ v₃ = 30 cm

Question 7.
A ray of light incident on an equilateral glass prism (μ_g = \(\sqrt{3}\)) moves parallel to the baseline of the prism inside it. Find the angle of Incidence for this ray. (CBSE Delhi 2012)
Answer:
Given A = 60°, μ_g = \(\sqrt{3}\), i = ?

Using the expression μ = \(\frac{\sin i}{\sin A / 2}\)
or

Question 8.
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays ‘1’ and ‘2’ are respectively 1.35 and 1.45. Trace the path of these rays after entering through the prism. (CBSE AI 2014)

Answer:
The critical angle for the two rays is

This shows that the angle of Incidence for ray ‘2’ Is greater than the critical angle. Hence it suffers total internal reflection, white ray ‘1’ does not. Hence the path of rays is as shown.

Question 9.
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept at 15 cm from each other. A point object lies 60 cm in front of the convex lens. Draw a ray diagram to show the formation of the image by the combination. Determine the nature and position of the image formed. (CBSE AI 2014)
Answer:
The ray diagram is as shown.

For the convex lens, we have
u₁ = – 60 cm, f = + 20 cm, v = ?

Using lens formula we have

Had there been only the Lens, the image would have been formed at Q₁, which acts as a virtual object for the convex mirror.
Therefore u₂ = OQ₁ – OO’ = 30 – 15 = 15 cm

Using mirror formuLa we have
\(\frac{1}{v_{2}}+\frac{1}{u_{2}}=\frac{2}{R}\)
or
\(\frac{1}{v_{2}}+\frac{1}{u_{15}}=\frac{2}{20}\)

Solving for v₂ we have
v₂ = 30cm

Hence the final image is formed at (Point Q) a distance of 30 cm behind the mirror.

Question 10.
A ray PQ is an incident normally on the face AB of a triangular prism refracting angle of 60°, made of a transparent material of refractive index 2 / \(\sqrt{3}\), as shown in the figure. Trace the path of the ray as it passes through the prism. Also, calculate the angle of emergence and angle deviation. (CBSE Delhi 2014C)

Answer:
Critical angle for glass
µ = \(\frac{1}{\sin i_{c}}\)
or
sin i_c = \(\frac{1}{\mu}=\frac{\sqrt{3}}{2}\)= 0.866
or
i_c = 60°

Now the ray is incident at an angle of 60° which is equal to the critical angle, therefore the ray graces the other edge of the prism

Therefore the angle of emergence is = 90°
Hence δ = 30°

This is as shown.

Question 11.
An object Is placed 15 cm In front of a convex lens of focal length 10 cm. Find the nature and position of the image formed. Where should a concave mirror of radius of curvature 20 cm be placed so that the final image is formed at the position of the object itself? (CBSE AI 2015)
Answer:
Given u = -15 cm, f = + 10 cm, v = ?
For lens we have

Nature of image-real, magnified Final image formed will be at the object itself only if the image formed by the lens is at the position of the centre of curvature of the mirror
∴ Distance of mirror from lens, D = 30 + R = 30 + 20 cm = 50 cm

Question 12.
Define the critical angle for a pair of media. A point source of monochromatic light ‘S’ is kept at the centre of the bottom of a cylinder with the radius of 15 cm. The cylinder contains water (refractive index 4/3) to a height of 7.0 cm. Draw the ray diagram and calculate the area of the water surface through which the light emerges in the air. (CBSE Delhi 2015C)
Answer:
It the angle of incidence in the denser medium for which the angle of refraction in the rare medium is 90°.
Given h = 7 cm, A = πr² = ?, μ = 4/3 = 1.33

Due to total internal reflection light from the bulb will not come out of the entire surface of the water as shown.

The angle of the cone through which tight will spread out is twice the critical angle.

Therefore the radius of the circular patch will be
Using the relation r= \(\frac{h}{\sqrt{\mu^{2}-1}}\) we have
r = \(\frac{7}{\sqrt{(1.33)^{2}-1}}\) = 7.98 cm

Therefore area of the surface of water through which light comes out
A = πr² = 3.14 × (7.98)² = 199.95 cm²

Question 13.
A ray PQ incident on the refracting face BA Is refracted in the prism BAC as shown In the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive Index of the material of prism is \(\sqrt{3}\), calculate angle θ. (CBSE AI 2016)

Answer:
Here As AQ = AR, therefore QR is parallel to BC, hence prism is in minimum deviation position
A = 60°, θ = δ_m = ?, n = \(\sqrt{3}\)

Solving θ = 60°

Question 14.
(i) A ray of light incident on face AB of an equilateral glass prism shows a minimum deviation of 30°. Calculate the speed of light through the prism.

(ii) Find the angle of incidence at face AB so that the emergent ray grazes along with the face AC. (CBSE Delhi 2017)
Answer:
(i) Given


Question 15.
A small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index p up to a height h. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut off light from the bulb. (CBSE Sample Paper 2018-19)
Answer:
Let d be the diameter of the disc. The bulb shall be invisible if the incident rays from the bulb at 0 to the surface at d/2 are at the critical angle.
Let l be the angle of incidence
Then sin i = \(\frac{1}{μ}\) = tan i.
Now

Question 16.
A ray of light is incident on a glass prism of refractive index μ and refracting angle A. If it just suffers total internal reflection at the other face, obtain an expression relating to the angle of incidence, angle of prism and critical angle.
Answer:
For a ray to just suffer total internal reflection at the second face of the prism r₂ = i_c
Now A = r₁ + i_c, therefore r₁ = A – i_c

Now by Snells Law, we have

or
μ = \(\frac{\sin i}{\sin \left(A-1_{c}\right)}=\frac{1}{\sin i_{c}}\)

Question 17.
(a) Define, the refractive index of a medium.
(b) In the following ray diagram, calculate the speed of light In the liquid of unknown refractive index. (CBSE AI 2017C)

Answer:
(a) It is defined as the ratio of the speed of light in a vacuum to the speed of light in the given medium.
(b) The speed of Light can be found by using the formula
\(\frac{v}{c}=\frac{\sin 1}{\sin r}\)
or
v = \(\frac{\sin i}{\sin r}\) × c

From the diagram, we find that

Question 18.
A concave lens made of material of refractive index n₁ is kept In a medium of refractive index n2. A parallel beam of light is incident on the lens. Complete the path of the rays of light emerging from the concave lens If (i) n₁ > n₂ (ii) n₁ < n₂ and (iii) n₁ n₂
Answer:
The path of rays in the three cases is as shown.

Question 19.
A convex ten made of a material of refractive index n₁ is kept in a medium of refractive index n₂. A parallel beam of light is incident on the lens. Complete the path of rays of light emerging from the convex lens if (i) n₁ > n₂, (ii) n₁ = n₂, and (iii) n₁ < n₂.
Answer:
The path of the rays in the three cases is as shown.

Question 20.
Write the Lens Maker’s formula and use it to obtain the range of values of μ (the refractive index of the material of the lens) for which the focal length of an equi-convex lens, kept in air, would have a greater magnitude than that of the radius of curvature of its two surface. (CBSE Delhi 2016C)
Answer:
Lens maker’s formula is given by
\(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)

For equiconvex Lens we have R₁ = + R and
R₂ = – R
Therefore we have
\(\frac{1}{f}\) = (n – 1)\(\frac{2}{R}\)

For f to be greater than R
2(n – 1) < 1
2n – 2 < 1
2n < 3
n < 1.5
Hence range is 1.0< n < 1.5

Question 21.
A ray of light passing from the air through an equilateral glass prism undergoes minimum deviation when the angle of Incidence is 3/4th of the angle of the prism. Calculate the sp..d of light In the prism. (CBSE AI 2017)
Answer:
Given A = 60°, i = 3/4 × 60 = 45°,
c = 3 × 10⁸ m s^-1,

Now δ_m = 2i – A
= 90 – 60 = 30°

Using the formula

Question 22.
Calculate the value of the angle of Incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of the prism is \(\sqrt{2}\). (CBSE 2017C)
Answer:
The diagram is as shown.


Question 23.
How is the working of a telescope different from that of a microscope?
The focal lengths of the objective and eyepiece of a microscope are 1.25 cm and 5 cm respectively. Find the position of the object relative to the objective in order to obtain an angular magnification of 30 in normal adjustment. (CBSE Delhi 2012)
Answer:
A microscope increases the size of the object whereas a telescope brings the object closer for better vision.
Given f_o = 1.25 cm, f_e = 5 cm, M = 30 cm, u = l
In normal adjustment final image is formed at infinity, therefore we have

Question 24.
(a) Draw a labelled ray diagram showing the image formation of a distant object by a refracting telescope. Deduce the expression for its magnifying power when the final image is formed at infinity.
(b) The sum of focal lengths of the two lenses of a refracting telescope is 105 cm. The focal length of one lens is 20 times that of the other. Determine the total magnification of the telescope when the final image is formed at infinity. (CBSE AI 2014C)
Answer:
(a) For the diagram

From right triangles ABC and ABC’ as shown in figure, we have
tan α = \(\frac{\mathrm{AB}}{\mathrm{CB}}=\frac{-h}{f_{0}}\) and
tan β = \(\frac{\mathrm{AB}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{-h}{f_{\mathrm{e}}}\)

From the above we have we have
M = \(\frac{\beta}{\alpha}=\frac{-h}{f_{e}} \times \frac{f_{0}}{-h}=\frac{f_{0}}{f_{e}}\)

(b) L = 105 cm, f_o = 20f_e,

Now L = f_o + f_e = 21f_e
Or
fe = 105/21 = 5 cm
Hence f_o = 20 × f_e 20 × 5 = 100 cm
Hence M = f_o/f_e = 100/ 5 = 20

Question 25.
(a) Explain with reason, how the power of a diverging lens changes when
(i) it is kept in a medium of refractive index greater than that of the lens.
(ii) Incident red light is replaced by violet light.
(b) Three lenses L₁, L₂, and L₃ each of focal length 30 cm are placed coaxially as shown in the figure. An object is held at 60 cm from the optic centre of L₁. The final image is formed at the focus of L₃. Calculate the separation between (i) L₁ and L₂ and (ii) L₂ and L₃ (CBSE AI 2017C)

Answer:
(a) (i) The power of is given by the expression P = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) medium changes the power of the lens decreases as its focal length increases.
(ii) We know that f ∝ X, therefore a decrease in the wavelength from red to violet decreases the focal length and increases the power of the lens.

(b) Given f₁ = f₂ = f₃ = 30 cm
For lens L1, u₁ = 60 cm = 2f₁, therefore the image will be formed at If on the other side of the lens L₁.

Since the final image for lens L₃ is formed at the focus, therefore the rays of light falling on lens L₃ should come from infinity. This is possible if the image of L₁ lies at the focus of L₂.

Thus distance L₁L₂ = 60 + 30 = 90 cm

Also, distance L₂L₃ can have any value as the rays between L₂ and L₃ will be parallel.

Question 26.
Calculate the radius of curvature of an equi-concave lens of refractive Index 1.5, when It Is kept In a medium of refractive index 1.4, to have a power of -5 D?
OR
An equilateral glass prism has a refractive Index of 1.6 In the air. Calculate the angle of minimum deviation of the prism, when kept In a medium of refractive Index \(\frac{4 \sqrt{2}}{5}\). (CBSE Delhi 2019)
Answer:
Given n_L = 1.5, n_M = 1.4, P = -5 D
Focal length f \(\frac{1}{P}=\frac{1}{-5}=\frac{-100}{5}\) = 20 cm

Using the lens makers formula and putting
R₁ = – R and
R₂ = +R

Solving for R, we get
R = 20/7 = 2.86cm
or
Given A = 60, n = 1.6, δm =?,n_M = \(\frac{4 \sqrt{2}}{5}\)

Using the prism formula

Question 27.
A ray of light passes through an equilateral glass prism, such that the angle of Incidence Is equal to the angle of emergence. If the angle of emergence is v times the angle of the prism, calculate the refractive index of the glass prism.
Answer:
Given the angle of prism A = 60°,
the angle of incidence i = angle of emergence ‘e’ and under this condition angle of deviation is minimum.

Question 28.
The magnifying power of an astronomical telescope In the normal adjustment position is 100. The distance between the objective and the eyepiece is 101 cm. Calculate the focal length of the objective and the eyepiece.
Answer:

Question 29.
A double convex lens made of glass of refractive Index 1.5 has both radii of curvature of magnItude 20 cm. An object 2 cm high is placed at 10 cm from the lens. Find the position, nature and size of the image.
Answer:
Given n = 1.5 and for a double convex Lens R₁ = + 20 cm and R₂ = – 20 cm

Now size of the object O = + 2 cm and u = – 1o cm

The image ¡s virtual and erect.

Question 30.
Three rays of light-red (R), green (G) and blue (B) are Incident on the face AB of a right-angled prism ABC. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively. Trace the path of the rays through the prism. How will the situation change if these rays were incident normally on one of the faces of an equilateral prism?

Answer:
The course of rays through the prism is as shown below.
Critical angle for a light ray is given by
sin i_c = \(\frac{1}{n}\)
or
i_c = sin^-1\(\left(\frac{1}{n}\right)\)

Now critical angle for red ray (R)
i_R = sin^-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.39}\right)\) = 46°

Critical angle for green ray (G)
i_G = sin^-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.44}\right)\) = 44°

and Cnticat angLe for bLue ray (B)
i_B = sin^-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.47}\right)\) = 42°52′

Thus the angle of incidence for blue and green rays inside the prism will be greater than the critical angle for these two colours. Therefore blue and green rays undergo total internal reflection. The angle of incidence for red colour is smaller than its critical angle; therefore it does not undergo total internal reflection. This is depicted in the figure below.

For an equilateral prism, the light rays pass through the prism suffering deviation. The angle of deviation δ = (n – 1) A. Hence, the deviation for red coloured ray will be the least and that for blue ray maximum. Paths of rays are shown in the figure below.

Question 31.
You are given three lenses of powers 0.5 D, 4 D, 10 D. State, with reason, which two lenses will you select for constructing a good astronomical telescope.
Calculate the resolving power of this telescope, assuming the diameter of the objective lens to be 6 cm and the wavelength of light used to be 540 nm.
Answer:
The focal lengths of the three lenses are
f₁ = 1 /P₁ = 1 / 0.5 = 2 m = 200 cm,
f₂ = 1 /P₂ = 1 / 4 = 0.25 m = 25 cm,
f₃ = 1 /P₃ = 1 /10 = 0. 1 m = 10 cm,

For an astronomical telescope, the objective should have a large focal length and the eyepiece should have a small focal length. Therefore for the objective, we will use the lenses of power 0.5 D and for the eyepiece the lens of power 10 D.

Given D = 6 cm = 0.06 m, λ = 540 nm = 540 × 10^-9 m

Now resolving power
R.P. = \(\frac{D}{1.22 \lambda}=\frac{0.06}{1.22 \times 540 \times 10^{-9}}\) = 91074.6

Question 32.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different positions separated by 20 cm. Calculate the focal length of the lens.
OR
A convex lens of focal length 20 cm and a concave lens of focal length 15 cm are kept 30 cm apart with their principal axes coincident. When an object is placed 30 cm in front of the convex lens, calculate the position of the final image formed by the combination. Would this result change if the object were placed 30 cm In front of the concave tens? Give reason. (CBSE AI 2019)
Answer:
The image of an object can be obtained at two different positions of a convex lens for a fixed value of the distance between the object and the screen if values of u and v are interchanged in these two positions. This situation is as shown below.

Here x + 20 + x = 90 cm or x = 35cm
Therefore, u = -35 cm, v = + 55 cm, f = ?

or

For image formed by a convex Lens
f₁ = + 20 cm, u = – 30 cm

Therefore, u for concave Lens = 60 – 30 = + 30 cm and f₂ = – 15 cm

Now for concave lens

No, the result will not change as per the principle of reversibility.

Question 33.
For an equilateral glass prism, the minimum angle of deviation, for a parallel beam of monochromatic Incident light, is measured to be 30°. What is the refractive index of the glass used for making this prism?
If this prism were to be placed in a medium of refractive Index 1.414, how would a ray of light incident on one of its refracting faces pass through it? Draw the ray diagram for the same.
Answer:
Given A = 60°, δ_m = 30°, μ = ?
Using the relation

When this prism is placed in a medium of refractive index 1.414, it will behave like a plane glass piece as both the prism and the medium have the same refractive index.

The ray diagram is as shown.

Question 34.
Find the position of the image formed by the lens shown in the figure.

Another lens is placed in contact with this lens to shift the image further away from the lens. What is the nature of the second lens?
Answer:
f = + 10 cm, u = – 30 cm, v =?
Using the lens equation we have

The second lens Is concave.

Question 35.
A beam of light of wavelength 400 nm is incident normally on a right-angled prism as shown. It is observed that the light just grazes along with the surface AC after falling on it. Given that the refractive index of the material of the prism varies with the wavelength as per the relation
μ = 1.2 + \(\frac{b}{\lambda^{2}}\) calculate the value of b and the refractive index of the prism material for a wavelength λ = 500 nm. [(Given θ = Sin^-1 (0.625)]

Answer:
The figure can be redrawn as shown below.

By symmetry angle, θ will be the critical angle.
Therefore
μ = \(\frac{1}{\sin \theta}=\frac{1}{0.625}\) = 1.6

Now the value of the constant b is obtained as follows:
μ_A = 1.2 + \(\frac{b}{\lambda^{2}}\)
or
1.6 = 1.2 + \(\frac{b}{(400)^{2}}\)

Solving for b we have b = 64000 nm²
Now for a wavelength λ = 500 nm the refractive index of the material of the prism is
μ = 1.2 + \(\frac{(64000)^{2}}{(500)^{2}}\) = 1.456

Question 36.
A convex lens, of focal length 20 cm, has a point object placed on its principal axis at a distance of 40 cm from It. A plane mirror Is placed 30 cm behind the convex lens. Locate the position of the image formed by this combination.
Answer:
We first consider the effect of the lens. For the Lens, we have

u = – 40 cm and f = + 20 cm
Using the lens formula, we get
\(\frac{1}{v}-\frac{1}{(-40)}=\frac{1}{20}\)
or
v = + 40 cm

Had there been the lens only the image would have been formed at Q₁. The plane mirror M is at a distance of 30 cm from the lens L. We can, therefore, think of a Q₁ as a virtual object, located at a distance of 10 cm, behind the plane mirror M. The plane mirror, therefore, forms a real image (of this virtual object Q₁) at Q₁, 10 cm in front of it. This is shown in the figure.

Question 37.
(i) Calculate the distance of an object of height h from a concave mirror of radius of curvature 20 cm, so as to obtain a real image of magnification 2. Find the location of the image also.
(ii) Using the mirror formula, explain why does a convex mirror always produce a virtual image. (CBSE Delhi 2016) Answer:
Given R = – 20 cm or f = – 10 cm, m = + 2 (real image), u = ?, v = ?
Using the relation m = \(\frac{f}{f-u}\) we have

(b) For a convex mirror \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\) but f is positive and u is negative i.e., f > 0 but u < 0.
Therefore, it is self-evident from the above relation that irrespective of the value of u, the value of v is always +ve. It means that the image formed by a convex mirror is always virtual Independent of the location of the object.

Question 38.
A convex lens of focal length 20 cm and a concave mirror of focal length 10 cm are placed co-axially 50 cm apart from each other. An incident beam parallel to its principal axis is incident on the convex lens. Locate the position of the (final) image formed due to this combination.
Answer:
The incident beam, on lens L_, is parallel to its principal axis. Hence the lens forms an image Q₁ at its focal point, i.e. at a distance OQ₁ (= 20 cm) from the lens. This image, Q₁, now acts as a real object for the concave mirror. For the mirror, we then have: u = – 30 cm, and f = – 10 cm,

Hence using the mirror formula, we get
\(\frac{1}{v}+\frac{1}{(-30)}=\frac{1}{(-10)}\)
or
v = – 15 cm

The lens-mirror combination, therefore, forms a real image Q at a distance of 15 cm from M. The ray diagram is as shown in

Question 39.
A convex lens of focal length 25 cm and a concave mirror of radius of curvature 20 cm are placed coaxially 40 cm apart from each other. An incident beam parallel to the principal axis is incident on the convex lens. Find the position and nature of the image formed by the combination. (CBSE Al 2016)
Answer:
The image of the object is formed at the focus of the convex lens, i.e. 25 cm. This image acts as an object for the concave mirror and ties at a distance (40 – 25) = 15 cm from the mirror.

Hence for the mirror
u = – 15 cm, v =? f = R/2 = 20/2 = 10 cm

Using mirror formula we have

The image is formed in front of the mirror.

Question 40.
(i) A screen is placed at a distance of 100 cm from an object. The image of the object is formed on the screen by a convex lens for two different locations of the lens separated by 20 cm. Calculate the focal length of the lens used.
(ii) A converging lens is kept coaxially in contact with a diverging lens both the lenses being of equal focal length. What is the focal length of the combination? (CBSE AI 2016)
Answer:
(i) Given u + v= 100 or v= 100 – u
Using lens formula From lens first \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) we have

Or
f = 24 cm

(ii) f = infinity. \(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{-f_{2}}\) = 0

Question 41.
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. By rotating the prism, the angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light. The refracting angle of the prism is 60°. (NCERT)
Answer:
Given δ_m = 40°, aμg = ?, _aμ_w = 1.33, A = 60°

Solving for δ_m we have δ_m = 100°

Question 42.
A beam of light converges to a point P. A lens is placed in the path of the convergent beams 12 cm from P. At what point does the beam converge if the lens is
(i) a convex lens of focal length 20 cm,
Answer:
(i) Here u = 12 cm, f = + 20 cm and v = ?
Using the formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) we have
\(\frac{1}{v}=\frac{1}{12}+\frac{1}{20}=\frac{3+5}{60}=\frac{8}{60}\)
or
v = 7.5 cm

(ii) a concave lens of focal length 16 cm? (NCERT)
Answer:
Here u = 12 cm, f = – 16 cm and v =?
Using the formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)we have
\(\frac{1}{v}=\frac{1}{12}+\frac{1}{-16}=\frac{-3+4}{48}=\frac{1}{48}\)
or
v = 48 cm

Question 43.
A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (i) the least distance of distinct vision (25 cm), (ii) infinity? What is the magnifying power of the microscope in each case? (NCERT)
Answer:
Given f0 = 2.0 cm, fe = 6.25 cm, L = 15 cm, u0 = ?,

Now applying Lens formula for objective Lens we have \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u} \text { or } \frac{1}{u_{0}}=\frac{1}{v_{0}}-\frac{1}{f_{0}}\)

Question 44.
A small telescope has an objective lens of a focal length of 144 cm and an eyepiece of a focal length of 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece? (NCERT)
Answer:
Given f_o = 144 cm, f_e = 6.0 cm, M = ?,
L = f_o + f_e = ?

Using the formula M = \(\frac{f_{0}}{f_{e}}=\frac{144}{6}\) = 24 and
L = f_o + f_e = 144 + 6 = 150 cm

Question 45.
(a) A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope?
(b) If this telescope Is used to view the moon, what is the diameter of the Image of the moon formed by the objective lens? The diameter of the moon is 3.48 × 10⁶ m, and the radius of lunar orbit Is 3.8 × 10⁸ m. (NCERT)
Answer:
Given f_o = 15 m, f_e = 1.0 cm = 0.01 m, M = ?
D_m = 3.48 × 10⁶ m, r = 3.8 × 10⁸m,
(a) Using M = \(\frac{f_{0}}{f_{e}}=\frac{15}{0.01}\) = 1500
(b) AngLe subtended by moon at the objective of the teLescope
α = \(\frac{D_{m}}{r}=\frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}\)

Therefore angLe subtended by the image
β = M × α = 1500 × \(\frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}\)

If I be the Linear size of the image then

Question 46.
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524. (NCERT)
Answer:
Given A = 60°, i = ?, μ = 1.524
For a ray to just suffer total internal reflection at the second face of the prism r₂ = i_c
Now sin ic = \(\frac{1}{\mu}=\frac{1}{1.524}\) = 0.6562
or
i_c = 41°

Now A = r₁ + r₂, therefore r₁ = A – r2
r₁ = 60 – 41 = 19°

Now by Snell’s law we have
μ = \(\frac{\sin i}{\sin r_{1}}\)
or
sin i = μ × sinr₁ = 1.524 × sin 19°
or
i = 29.75° = 30°

Question 47.
A small telescope has an objective lens of a focal length of 140 cm and an eyepiece of a focal length of 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when
(a) the telescope is in normal adjustment (i.e. when the final image is at infinity.
Answer:
Given f_o = 140 cm, f_e = 5.0 cm, M = ?
For normal adjustment we have
M = \(\frac{f_{0}}{f_{e}}=\frac{140}{5}\) = 28

(b) the final image is formed at the least distance of distinct vision (25 cm) (NCERT)
Answer:
When the final image is formed at the least distance of distinct vision we have
M = \(\frac{f_{0}}{f_{e}}\left(1+\frac{f_{e}}{D}\right)=\frac{140}{5}\left(1+\frac{5}{25}\right)\) = 33.6

Question 48.
(a) The refractive index of glass is 1.5. What is the speed of light In a glass? (Speed of light in a vacuum is 3.0 × 10⁸ ms^-11 )
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
(a) Given μ = 1.5, c = 3.0 × 10⁸ m s^-1
v = \(\frac{c}{\mu}=\frac{3 \times 10^{8}}{1.5}\) = 2.0 × 10⁸ ms^-1

(b) No. The refractive index, and hence the speed of light in a medium, depends on wavelength. When no particular wavelength or colour of light is specified, we may take the given refractive index to refer to yellow colour or mean light. Now we know violet colour deviates more than red in a glass prism, i.e. μ_v > μ_R. Therefore, the violet component of white light travels slower than the red component.

Question 49.
Three immiscible liquids of densities d₁ > d₂ > d₃ and refractive indices μ₁ > μ₂ > μ₃ are put in a beaker. The height of each liquid column is d₃. A dot is made at the bottom of the beaker. For near-normal vision, find the apparent depth of the dot. (NCERT Exemplar)
Answer:
The situation is as shown.

Let the apparent depth be O₁ for the object as seen from μ2, then
Apparent depth = real depth/μ
O₁ = \(\frac{h / 3}{\mu_{1} / \mu_{2}}=\frac{\mu_{2} h}{3 \mu_{1}}\)

If seen from O₃ the apparent depth O₂ is
Apparent depth = real depth/μ
O₂ = \(\frac{\left(h / 3+O_{1}\right)}{\mu_{2} / \mu_{3}}=\frac{\mu_{3}}{\mu_{2}}\left(\frac{h}{3}+\frac{\mu_{2}}{\mu_{1}} \frac{h}{3}\right)\)

Seen from outside the apparent height is
Apparent depth = real depth/μ

Question 50.
For a glass prism (μ = \(\sqrt{3}\)) the angle of minimum deviation Is equal to the angle of the prism. Find the angle of the prism. (NCERT Exemplar)
Answer:

Question 51.
In many experimental set-ups, the source and screen are fixed at a distance say D and the lens Is movable. Show that there are two positions for the lens for which an image Is formed on the screen. Find the distance between these points and the ratio of the Image sizes for these two points. (NCERT Exemplar)
Answer:
The situation is shown.

If there was no cut then the object would have been at a height of 0.5 cm from the principal axis OO’. Consider the image for this case by lens formuLa we have
\(\frac{1}{v}=\frac{1}{u}+\frac{1}{f}=\frac{1}{-50}+\frac{1}{25}=\frac{1}{50}\)
Or
v = 50 cm
Hence magnification of the image is.
m = \(\frac{v}{u}=\frac{-50}{50}\) = -1

Thus the image would have been formed at 50 cm from the pole and 0.5 cm below the principal axis. Hence with respect to the X-axis passing through the edge of the cut lens, the co-ordinates of the image are (50 cm, -1 cm)

Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 8 Electromagnetic Waves. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 8 Important Extra Questions Electromagnetic Waves

Electromagnetic Waves Important Extra Questions Very Short Answer Type

Question 1.
Name the part of the electromagnetic spectrum which has the longest wavelength and write its one use. (CBSE 2019C)
Answer:

• In the electromagnetic spectrum, long radio waves have the longest wavelength.
• Radio waves are used in communication systems.

Question 2.
The small ozone layer on the top of the stratosphere is crucial for human survival. Why?
Answer:
The ozone layer absorbs the ultraviolet rays, emitted by the sun, which are harmful to the living tissues of human beings.

Question 3.
Name the part of the electromagnetic spectrum which is used in the “greenhouse” to keep plants warm.
Answer:
Infrared rays.

Question 4.
How are radio waves produced? (CBSE AI 2011)
Answer:
They are produced by rapid acceleration and decelerations of electrons in aerials.

Question 5.
How are X-rays produced? (CBSE Al 2011)
Answer:
By the transition of inner-shell electrons.

Question 6.
How are microwaves produced? (CBSE AI 2011)
Answer:
By using a magnetron.

Question 7.
A plane electromagnetic wave travels in a vacuum along the z-direction. What can you say about the direction of electric and magnetic field vectors? (CBSE Delhi 2011)
Answer:
The electric and magnetic field vectors will be along the x and y directions.

Question 8.
What is the frequency of electromagnetic waves produced by the oscillating charge of frequency v? (CBSE Delhi 2011C)
Answer:
The frequency of electromagnetic waves produced by the oscillating charge of frequency v is also v.

Question 9.
What are the directions of electric and magnetic field vectors relative to each other and relative to the direction of propagation of electromagnetic waves? (CBSE AI 2012)
Answer:
The three are mutually perpendicular to one other.

Question 10.
Welders wear special goggles or face masks with glass windows to protect their eyes from electromagnetic radiation. Name the radiations and write the range of their frequency. (CBSE Al 2013)
Answer:
UV radiations, 10¹⁵ to 10¹⁷ Hz

Question 11.
To which part of the electromagnetic spectrum does a wave of frequency 5 × 10¹⁹ Hz belong? (CBSEAI 2014)
Answer:
X – rays

Question 12.
The available frequency AC source is connected to a capacitor. Will the displacement current change if the frequency of the AC source is decreased? (CBSE Al 2015C)
Answer:
No

Question 13.
Why microwaves are considered suitable for radar systems used in aircraft navigation? (CBSE Delhi 2016)
Answer:
They have a small wavelength and travel along a straight line with deflecting.

Question 14.
Do electromagnetic waves carry energy and momentum? (CBSE AI 2017)
Answer:
Yes.

Question 15.
How is the speed of em-waves in vacuum – determined by the electric and magnetic field? (CBSE Delhi 2017)
Answer:
c = \(\frac{E_{0}}{B_{0}}\)

Question 16.
Why is skywave propagation of signals restricted to a frequency of 30 MHz? (CBSE Al 2017 C)
Answer:
The atmosphere is transparent to frequencies higher than 30 MHz.

Question 17.
Name the electromagnetic radiations used for
(a) water purification
Answer:
UV radiation

(b) eye surgery. (CBSEAI 2018, Delhi 2018)
Answer:
Visible light

Question 18.
Write the range of frequencies of electromagnetic waves which propagate through sky wave mode. (CBSE Al 2018 C)
Answer:
A few MHz up to 30 to 40 MHz.

Question 19.
Optical and radio telescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth. Why?
Answer:
This is because of the fact that X-rays are absorbed by the atmosphere, whereas light and radio waves penetrate through it.

Question 20.
A charged particle oscillates about its mean equilibrium position with a frequency of 10⁹ Hz. What is the frequency of the electromagnetic wave produced by the oscillator?
Answer:
Same as that of the oscillating charged particle, i. e. 10⁹ Hz.

Question 21.
Why are infrared radiations referred to as heat waves also? Name the radiations which are next to these radiations in the electromagnetic spectrum having
(a) Shorter wavelength and
(b) Longer wavelength.
Answer:
This is because they produce a heating effect.
(a) Visible light and
(b) Microwaves.

Question 22.
What physical quantity are the same for X-rays of wavelength 10^-10 m, the red light of wavelength 680 nm, and radio waves of wavelength 500 m?
Answer:
Since all of them are electromagnetic waves, their speed in a vacuum will be the same, i.e. 3 × 10⁸ m s^-1.

Question 23.
A charged particle oscillates about its mean equilibrium position with a frequency of 10⁹ Hz. What is the frequency of the electromagnetic waves produced by the oscillator?
Answer:
The frequency of the electromagnetic waves produced by the oscillator is the same as its frequency of vibration, i.e. 10⁹ Hz.

Question 24.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in a vacuum is B₀ = 510 nT. What is the amplitude of the electric field part of the wave?
Answer:
Given B₀ = 510 nT = 510 × 10^-9 T, E₀ = ?

Using the relation E₀ = c × B₀, we have
E₀ = 3 × 108 × 510 × 10^-9 = 153 N C^-1

Question 25.
Why does a microwave oven heat up a food item containing water molecules most efficiently?
Answer:
It is because the frequency of the microwave matches the resonant frequency of water molecules. This makes the molecules vibrate with maximum amplitude thereby producing heat.

Question 26.
Name the most energetic electromagnetic radiation and write its frequency range. (CBSE AI 2019 C)
Answer:
The most energetic radiations are Gamma Rays Frequency range of gamma rays is: 10¹⁸ Hz to 10²³ Hz
Or
Name the electromagnetic radiations used in eye surgery or to kill germs in water purifiers. Write its frequency, range.
Answer:

1. Radiations used for eye surgery or to kill germs are Ultraviolet Rays.
2. The frequency range of ultraviolet rays: 10⁵ Hz to 10¹⁷ Hz.

Electromagnetic Waves Important Extra Questions Short Answer Type

Question 1.
Radio waves and gamma rays both are transverse in nature and electromagnetic in character and have the same speed in a vacuum. In what respect are they different?
Answer:
The radio waves have an atomic origin, while gamma rays have a nuclear origin. Further owing to their very small wavelength, gamma rays are highly penetrating in comparison to radio waves.

Question 2.
Show that the average energy density of the electric field equals the average density of the magnetic field.
Answer:
The average density of the electric field is given by
U_e = \(\frac{1}{2}\)ε₀E² and the average energy density of the magnetic field is given by U_B = \(\frac{B^{2}}{2 \mu_{0}}\).

But B = \(\frac{E}{c}\) and c = \(\frac{1}{\sqrt{\mu_{0} \varepsilon_{0}}}\) , hence the above equation becomes U_B = \(\frac{B^{2}}{2 \mu_{0}}=\frac{E^{2}}{2 \mu_{0} c^{2}}\)

U_B = \(\frac{E^{2}}{2 \mu_{0} \times \frac{1}{\mu_{0} \varepsilon_{0}}}=\frac{1}{2} \varepsilon_{0} E^{2}\). Hence the result.

Question 3.
State four properties of electromagnetic waves.
Answer:
(a) They do not require any material medium to travel.
(b) They are transverse in nature, i.e. electric and magnetic fields are perpendicular to each other and also to the direction of the propagation of the wave.
(c) The energy of the wave is divided equally amongst the electric and the magnetic field.
(d) They travel, in free space, with a velocity of 3 × 10⁸ m s^-1.

Question 4.
Electromagnetic radiations with wavelength
(a) λ₁ are used to kill germs in water purifiers.
(b) λ₂ are used in TV communication systems.
(c) λ₃ plays an important role in maintaining the earth’s warmth.
Name the part of the electromagnetic spectrum to which these radiations belong. Arrange these wavelengths in decreasing order of their magnitude.
Answer:
(a) λ₁ – Ultraviolet radiations.
(b) λ₂ – Microwaves
(c) λ₃ – Infrared rays
Their order is λ₁ < λ₃ < λ₂.

Question 5.
Name the constituent radiation of the electromagnetic spectrum which
(a) is used in satellite communication.
Answer:
Microwaves.

(b) is used for studying crystal structure.
Answer:
X-rays

(c) is similar to the radiations emitted during the decay of a radioactive nucleus.
Answer:
Gamma rays

(d) is absorbed from sunlight by the ozone layer.
Answer:
UV rays

(e) produces an intense heating effect.
Answer:
Infrared rays

(f) has its wavelength range between 390 nm and 770 nm.
Answer:
Visible light.

Question 6.
Name the radiations of the electromagnetic spectrum which are used in
(a) warfare to look through the haze.
Answer:
Infrared rays

(b) radar and geostationary satellites
Answer:
Microwaves.

(c) studying the structure and properties of atoms and molecules.
Answer:
Gamma rays.

Question 7.
Why are microwaves used in RADAR?
Answer:
Microwaves are electromagnetic waves of very short wavelength. Such waves are used in RADAR due to the reason that they can travel in a particular direction in the form of a beam without being deflected.

Question 8.
Electromagnetic waves with wavelength
(a) λ₁ are used to treat muscular strain.
(b) λ₂ are used by an FM radio station for broadcasting.
(c) λ₃ are used to detect fractures in bones.
(d) λ₄ are absorbed by the ozone layer of the atmosphere.
Identify and name the part of the electromagnetic spectrum to which these radiations belong. Arrange
these wavelengths in decreasing order of magnitude.
Answer:
(a) Infrared radiations are used to treat muscular strain.
(b) Radio and microwave radiations are used for FM transmission.
(c) X-rays are used to detect fractures in bones.
(d) Ultraviolet radiation is absorbed by the ozone layer of the atmosphere.
The decreasing order of their wavelength is
λ₂ > λ₁ > λ₄ > λ₃.

Question 9.
(a) Draw a graph of a linearly polarised em wave propagating in the Z-direction showing the directions of the oscillating electric and magnetic fields.
Answer:
Graph of linearly polarised em wave propagating in the Z-axis.

(b) Write the relations (i) between the speed of light and the amplitudes of electric and magnetic fields, (ii) for the speed of em wave in terms of a permittivity e0, and magnetic permeability p0, of the medium. (CBSE 2019C)
Answer:
(i) Relation between speed of light and amplitudes of electric and magnetic field c = \(\frac{E_{0}}{B_{0}}\)

(ii) Speed of light in terms of ε₀ and μ0,
c = \(\frac{1}{\sqrt{\mu_{0} \varepsilon_{0}}}\)

Question 10.
Arrange the following electromagnetic waves in the order of their increasing wavelength:
(a) Gamma rays
(b) Microwaves
(c) X-rays
(d) Radio waves
How are infrared waves produced? What role does infrared radiation play in
(a) maintaining the Earth’s warmth and
(b) physical therapy? (CBSE Al 2015)
Answer:
Gamma(γ) rays, X-rays, Microwaves, Radio waves:
Infrared rays are produced by hot bodies/ vibration of atoms and molecules Infrared rays: (a) Maintain the earth’s warmth through the greenhouse effect, (b) produce heat

Question 11.
Name the parts of the electromagnetic spectrum which is
(a) suitable for radar systems used in aircraft navigation.
Answer:
Microwave: They are produced by oscillating circuits.

(b) used to treat muscular strain.
Answer:
Infrared rays: They are produced by the vibration of atoms and molecules.

(c) used as a diagnostic tool in medicine. Write in brief, how these waves can be produced. (CBSE Delhi 2015)
Answer:
X-rays: They are produced by bombarding high atomic number targets with electrons.

Question 12.
An e.m wave Y₁ has a wavelength of 1 cm while another e.m wave, Y₂ has a frequency of 10¹⁵ Hz. Name these two types of waves and write one useful application for each. (CBSE AI 2016 C)
Answer:
Y₁ – Microwaves and
Y₂ – Ultraviolet waves.

• Microwaves: used for communication.
• Ultraviolet waves: used for sterilization.

Question 13.
Identify the electromagnetic waves whose wavelengths vary as
(a) 10^-12 m < λ < 10^-8 m
Answer:
X – rays: a study of crystal structure

(b) 10^-3 m < λ < 10^-1 m. Write one of their uses. (CBSE Al 2017)
Answer:
Microwaves: radar and communication

Question 14.
Name the type of e.m waves having a wavelength range of 0.1 m to 1 mm. How are these waves generated? Write their two uses. (CBSE Al 2017 C)
Answer:

• Microwaves: These are generated with the help of special vacuum tubes (called klystrons, magnetrons, and Gunn diodes).
• Uses: Cooking, radar, and communication

Question 15.
(a) Give one use of electromagnetic radiations obtained in nuclear disintegrations.
Answer:
Treating cancer.

(b) Give one example each to illustrate the situation where there is
(i) displacement current but no conduction current and
Answer:
Between the plates of a capacitor

(ii) only conduction current but no displacement current.(CBSE Al 2018 C)
Answer:
Outside the plates of a capacitor

Question 16.
Scientists predict that a global nuclear war on the earth will be followed by a severe nuclear winter, with devastating effects on the earth. What is the basis of this prediction?
Answer:
The explosions will produce so much dust, which will cover the whole atmosphere, thereby blocking the sun’s rays from reaching the earth. This will cause the setting in of a long winter, which is called nuclear winter.

Question 17.
If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now?
Answer:
Due to the Greenhouse effect, the temperature of the earth’s surface is raised in the presence of the atmosphere. In the absence of the atmosphere, the heat received by the earth during the day is completely lost during the night. Hence the average surface temperature will be lower than the preset temperature.

Question 18.
A capacitor of capacitance ‘C is being charged by connecting it across a dc source along with an ammeter. Will the ammeter show a momentary deflection during the process of charging? If so, how would you explain this momentary deflection and the resulting continuity of current in the circuit? Write the expression for the current inside the capacitor. (CBSE AI 2012)
Answer:
Yes, this is due to the rate of change of electric flux inside the capacitor due to the production of displacement current. The expression for the current inside the capacitor is l_D = ε_o \(\frac{d \phi_{E}}{d t}\)

Question 19.
Define displacement current. What role does it play while charging a capacitor by dc source? Is the value of displacement current the same as that of the conduction current? Explain. (CBSE AI 2019)
Answer:

• Displacement current is the current due to the change of electric flux.
• It provides continuity of current in circuits containing capacitors.
• Yes, the value of displacement current is equal to the conduction current.
• l_d = ε_o \(\frac{d \phi_{e}}{d t}\)

Question 20.
Why is the orientation of the portable radio with respect to the broadcasting station important? (NCERT Exemplar)
Answer:
This is because the electromagnetic waves are plane polarised; hence the receiving antenna should be parallel to the electric/magnetic part of the wave.

Question 21.
(a) Give one use of electromagnetic radiations obtained in nuclear disintegrations.
Answer:
used to destroy cancer cells

(b) Give one example each to illustrate the situation where there is
(i) displacement current but no conduction current and
Answer:
The region, between the plates of a capacitor, connected to a time-varying voltage source, has a displacement current but no conduction current.

(ii) only conduction current but no displacement current. (CBSE Delhi 2018C)
Answer:
The wires, connected to the plates of a capacitor, joined to a time-varying or steady voltage source, carry a conduction current but no displacement current. (Alternatively, A circuit, having no capacitor in it, and carrying a current has conduction current but no displacement current.)

Electromagnetic Waves Important Extra Questions Long Answer Type

Question 1.
Answer the following:
(a) Name the em waves which are used for the treatment of certain forms of cancer. Write their frequency range.
Answer:
Gamma rays.
Frequency range > 3 × 10²⁰ Hz

(b) Thin ozone layer on top of the stratosphere is crucial for human survival. Why?
Answer:
The thin ozone layer on top of the stratosphere is crucial for human survival because it absorbs most of the ultraviolet rays coming from the sun. If the ozone layer had not been there, then ultraviolet rays would have entered the earth and caused danger to the survival of the human race.

(c) An em wave exerts pressure on the surface on which it is incident. Justify. (CBSE Delhi 2014)
Answer:
An em wave carries a linear momentum with it. The linear momentum carried by a portion of a wave having energy U is given by p = U/c.

Thus, if the wave incident on a material surface is completely absorbed, it delivers energy U and momentum p = U/c to the surface. If the wave is totally reflected, the momentum delivered is p = 2U/c because the momentum of the wave changes from p to – p. Therefore, it follows that an em wave incident on a surface exerts a force and hence a pressure on the surface.

Question 2.
Answer the following questions:
(a) Why is the thin ozone layer at the top of the stratosphere crucial for human survival? Identify to which part of the electromagnetic spectrum does this radiation belongs and write one important application of the radiation.
Answer:
The thin ozone layer on top of the stratosphere is crucial for human survival because it absorbs most of the ultraviolet rays coming from the sun. If the ozone layer had not been there, then ultraviolet rays would have entered the earth and caused danger to the survival of the human race. This radiation is UV radiation. It is used in sterilization.

(b) Why are infrared waves referred to as heat rays? How are they produced? What role do they play in maintaining the earth’s warmth through the greenhouse effect? (CBSE Delhi 2015C)
Answer:
Infrared radiations heat up the material on which they fall, hence they are also called heat rays. They are produced by the vibration of atoms and molecules. After falling on the earth, they are reflected back into the earth’s atmosphere. The earth’s atmosphere does not allow these radiations to pass through as such they heat up the earth’s atmosphere.

Question 3.
How are electromagnetic waves produced? What is the source of energy of these waves? Write mathematical expressions for electric and magnetic fields of an electromagnetic wave propagating along the z-axis. Write any two important properties of electromagnetic waves. (CBSE AI 2016)
Answer:
Electromagnetic waves are produced by accelerated charges which produce an oscillating electric field and magnetic field (which regenerate each other).

• Source of the Energy: Energy of the accelerated charge or the source that accelerates the charges.
• Expression: E_x = E_o sin (kz – ωt) and B_y = B_o sin (kz – ωt)
  (a) They are transverse in nature.
  (b) They don’t require a medium to propagate.

Question 4.
How are em waves produced by oscillating charges?
Draw a sketch of linearly polarised em waves propagating in the Z-direction. Indicate the directions of the oscillating electric and magnetic fields. (CBSE Delhi 2016)
Answer:
(a) An oscillating charge produces an oscillating electric field in space, which produces an oscillating magnetic field. The oscillating electric and magnetic fields regenerate each other, and this results in the production of em waves in space.
(b) See Figure.

Question 5.
Write Maxwell’s generalization of Ampere’s Circuital Law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is i = ε_o\(\frac{d \phi_{E}}{d t}\) where ΦE is the electric flux produced during charging of the capacitor plates. (CBSE Delhi 2016)
Answer:
The generalized form of Maxwell ampere law is
\(\oint \vec{B} \cdot \overrightarrow{d l}\)= μ_o(l + l_D) where l_D = ε_o\(\frac{d \phi_{E}}{d t}=\frac{d q}{d t}\)

The electric flux Φ between the plates of the parallel plate capacitor through which a time-dependent current flow is given by:
Φ_E = E A, but E = σ/ε_o
Therefore we have

Question 6.
(a) Why are Infrared waves often called heatwaves? Explain.
Answer:
Infrared waves have frequencies lower than those of visibLe Light; they have the ability to vibrate not only the electrons but the entire atoms or molecules of a body. This vibration increases the internal energy and temperature of the body. That is why infrared waves are often called heat waves.

(b) What do you understand by the statement, “Electromagnetic waves transport momentum”? (CBSE AI, Delhi 2018)
Answer:
If we consider a plane perpendicular to the direction of propagation of the electromagnetic wave, then electric charges present on the plane will be set and sustained in motion by the electric and magnetic fields of the electromagnetic wave. The charges present on the surface thus acquire energy and momentum from the waves. This just illustrates the fact that an electromagnetic wave (like other waves) transfers energy and momentum.

Question 7.
(a) When the oscillating electric and magnetic fields are along the x- and y-direction respectively
(i) point out the direction of propagation of the electromagnetic wave,
Answer:
Z-axis

(ii) express the velocity of propagation in terms of the amplitudes of the oscillating electric and magnetic fields.
Answer:
c = E_o / B_o

(b) How do you show that the em wave carries energy and momentum? (CBSE A! 2013C)
Answer:
Consider a plane perpendicular to the direction of propagation of the electromagnetic wave. If there are, on this plane, electric charges, they will be set and sustained in motion by the electric and magnetic fields of the electromagnetic wave. The charges thus acquire energy and momentum from the waves. This illustrates the fact that an electromagnetic wave carries energy and momentum.

Question 8.
Answer the following questions:
(a) Show, by giving a simple example, how em waves carry energy and momentum.
Answer:
Consider a plane perpendicular to the direction of propagation of the electromagnetic wave. If there are, on this plane, electric charges, they will be set and sustained in motion by the electric and magnetic fields of the electromagnetic wave. The charges thus acquire energy and momentum from the waves. This just illustrates the fact that an electromagnetic wave (like other waves) carries energy and momentum.

(b) How are microwaves produced? Why is it necessary in microwave ovens to select the frequency of microwaves to match the resonance frequency of water molecules?
Answer:
Microwaves (short-wavelength radio waves), with frequencies in the gigahertz (GHz) range, are produced by special vacuum tubes (called klystrons, magnetrons, and Gunn diodes). In such ovens, the frequency of the microwaves is selected to match the resonant frequency of water molecules so that energy from the waves is transferred efficiently to the kinetic energy of the molecules. This raises the temperature of any food containing water.

(c) Write two important uses of infrared waves. (CBSE Delhi 2014C)
Answer:
Remote control of electronic devices, heating

Question 9.
A parallel plate capacitor is being charged by a time-varying current. Explain briefly how Ampere’s circuital law is generalized to incorporate the effect due to the displacement current. (CBSE AI 2011)
Answer:
Consider the curve C bounding two surfaces S₁ and S₂. For the bound surface S1; the current passes through it, as such, we can write Ampere’s circuital law as
\(\oint_{s_{1}} \vec{\phi} \cdot \vec{d}\) = μ_ol …(1)

If however, we choose the bound surface S2 that passes through the plates of the capacitor and is not pierced by a current-carrying conductor, then Ampere’s circuital law is written as
\(\oint_{s_{2}} \vec{\phi} \cdot \vec{d}\) = 0 ….(2)

The above two equations contradict each other. To resolve this contradiction, Maxwell showed that this inconsistency is due to the assumed discontinuity of the current. According to Maxwell a current called displacement current “flows” between the plates of the capacitor, where there is no conduction current.

Therefore Ampere’s circuital law takes the generalised expression \(\oint \vec{B} \cdot d \vec{l}\) = μ_o (l + l_D),

here l is the conduction current and lD is the displacement current given by
l_D = ε_o \(\frac{d \phi_{E}}{d t}=\frac{d q}{d t}\).

Outside the plates of the capacitor, conduction current flows and displacement current is zero, whereas inside the plates of the capacitor, displacement current exists and there is no conduction current.

Question 10.
(a) Identify the part of the electromagnetic spectrum used in (i) radar and (ii) eye surgery. Write their frequency range.
Answer:
Microwaves:
Frequency range (10¹⁰ to 10¹² Hz) Ultraviolet rays:
Frequency range (10¹⁵ to 10¹⁷ Hz)

(b) Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field. (CBSE Delhi 2019)
Answer:
The average density of the electric field is
u_E = \(\frac{1}{2}\)εo E²

Question 11.
Answer the following questions:
(a) Long-distance radio broadcasts use short-wave bands. Why?
Answer:
The long-distance radio broadcast is not possible using long or medium wave bands because these waves, traveling as ground waves, can cover a maximum distance of 200 km. When used as sky waves, the short waves pass through the lower portion of the atmosphere but are reflected back from the ionosphere. In this way, short waves can travel very large distances and can even travel around the earth.

(b) It is necessary to use satellites for long-distance TV transmission. Why?
Answer:
TV waves have a frequency range of 47 MHz to 940 MHz. These frequencies are not reflected by the ionosphere. As space waves, they can cover a distance of 50-60 km only. Therefore, for long-distance TV transmission, we make use of satellites that reflect the TV signal wave back towards the earth.

(c) Optical and radio telescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth. Why?
Answer:
In optical and radio-telescopes we use visible light and radio waves, respectively, which can pass through the atmosphere. Hence, such telescopes are built on the ground. However, X-rays have extremely small wavelengths and are absorbed by the atmosphere. Hence, X-ray astronomy is not possible from ground stations. X-ray astronomy is possible only from satellites orbiting the earth at a height of 500 km or more.

(d) The small ozone layer on top of the stratosphere is crucial for human survival. Why?
Answer:
The thin ozone layer on top of the stratosphere is crucial for human survival because it absorbs most of the ultraviolet rays coming from the sun. If the ozone layer had not been there, then ultraviolet rays would have entered the earth and caused danger to the survival of the human race.

(e) If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now?
Answer:
If the earth did not have an atmosphere, then its average surface temperature would be lesser than what it is now because in that case greenhouse effect will be absent.

(f) Some scientists have predicted that a global nuclear war on the earth would be followed by a severe nuclear winter’ with a devastating effect on life on the earth. What might be the basis of this prediction?
Answer:
The prediction is based on the assumption that the large dust clouds produced by global nuclear war would perhaps cover a substantial part of the sky and solar radiations will not be able to reach the earth. It may cause a severe winter on the earth with a devastating effect on life on the earth.

Numerical Problems

Question 1.
The frequency values v₁ and v₂, for two spectral lines of the e.m. spectrum are found to be 5 × 10²⁰ Hz and 2.5 × 10¹¹ Hz respectively. Find the ratio, λ₁/λ₂ of their wavelengths.
Answer:

Question 2.
In a plane electromagnetic wave, the electric field oscillates with a frequency of 2 × 10¹⁰ Hz and an amplitude of 40 VM.
(i) What is the wavelength of the wave and
(ii) what is the energy density due to the field?
Answer:

Question 3.
A plane electromagnetic wave of frequency 25 MHz travels In free space along the x-direction. At a particular point In space and time, the electric vector is \(\vec{E}\) = 6.3 Vm^-1 ĵ. Calculate \(\vec{B}\) at this point. (NCERT)
Answer:
The magnitude of B and E are related as c = \(\frac{E}{B}\), therefore B = \(\frac{E}{c}=\frac{6.3}{3 \times 10^{8}}\) = 2.1 × 10^-8. This field is along the z-axis, i.e. perpendicular to both the propagation of the wave and the electric field.

Question 4.
The magnetic field in a plane electromagnetic wave Is given by B = 2 × sin (0.5 × 10^-3 x + 1.5 × 10¹¹ t) T
(a) What are the wavelength and frequency of the wave?
Answer:
(a) Comparing the given equation with the equation

(b) Write an expression for the electric field. (NCERT)
Answer:
E_o = cB_o = 2 × 10⁷ × 3 × 10⁸ = 60 Vm^-1

The electric field component is perpendicular to the direction of propagation and the direction of the magnetic field. Therefore, the electric field component aLong the z-axis is obtained as
E_z = 60 sin(0.5 × 10^{3 ×} + 1.5 × 10¹¹ t)Vm^-1

Question 5.
A radio can tune In to any station in the 7.5 MHz to 12 MHz bands. What is the corresponding wavelength band? (NCERT)
Answer:

Thus the wavelength band is 40 m to 25m.

Question 6.
Suppose that the electric field amplitude of an electromagnetic wave E₀ = 120 N C^-1 and that Its frequency is v = 50.0 MHz. (a) Determine, B0, ω k, and λ. (b) Find expressions for E and B. (NCERT)
Answer:


Question 7.
In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0 × 10¹⁰ Hz and amplitude 48 V m^-1.
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the E field equals the average energy density of the 8 fields. [c = 3 × 10⁸ms^-1.] (NCERT)
Answer:

(c) The average density of electric field is
given by U_e = \(\frac{1}{2}\)ε₀E² and the average energy density of the magnetic field is given by U_B = \(\frac{B^{2}}{2 \mu_{0}}\). But B = \(\frac{E}{c}\) and C = \(\frac{1}{\sqrt{\mu_{0} \varepsilon_{0}}}\) , hence the above equation becomes UB = \(\frac{B^{2}}{2 \mu_{0}}=\frac{E^{2}}{2 \mu_{0} c^{2}}\),

Question 8.
Suppose that the electric field part of an electromagnetic wave in a vacuum is
E = {(3.1 NC^-1>)cos(1.8 rad m^-1)y + (5.4 × 106 rad s^-1)t}î
(a) What is the direction of propagation?
(b) What is the wavelength?
(c) What is the frequency v?
(d) What is the amplitude of the magnetic field part of the wave?
(e) Write an expression for the magnetic field part of the wave. (NCERT)
Answer:
The electric field is of the form

(e) Expression for magnetic field part of the wave
\(\vec{B}\) = B_o cos (ky + ωt) k̂
or
\(\vec{E}\) = {(10.3 n T)cos[(1.8 rad m^-1)y + (5.4 × 10⁶ rad s^-1)t} î

Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 7 Alternating Current. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.

Class 12 Physics Chapter 7 Important Extra Questions Alternating Current

Alternating Current Important Extra Questions Very Short Answer Type

Question 1.
The instantaneous current flowing from an ac source is l = 5 sin 314 t. What is the rms value of current?
Answer:
The rms value of current is \(\frac{5}{\sqrt{2}}\).

Question 2.
The instantaneous emf of an ac source is given by E = 300 sin 314 t. What is the rms value of emf?
Answer:
The rms value of voltage is \(\frac{300}{\sqrt{2}}\)

Question 3.
Give the phase difference between the applied ac voltage and the current in an LCR circuit at resonance.
Answer:
The applied ac voltage and the current in an LCR circuit at resonance are in phase.
Hence phase difference = 0.

Question 4.
What is the phase difference between the voltage across the inductor and the capacitor in an LCR circuit?
Answer:
The phase difference is 180°.

Question 5.
What is the power factor of an LCR series circuit at resonance?
Answer:
The power factor is one.

Question 6.
In India, the domestic power supply is at 220 V, 50 Hz, while in the USA it is 110 V, 50 Hz. Give one advantage and one disadvantage of 220 V supply over 110 V supply.
Answer:
Advantage: less power loses
Disadvantage: more fatal.

Question 7.
Define the term ‘wattles current’. (CBSE Delhi 2011)
Answer:
It is the current at which no power is consumed.

Question 8.
In a series LCR circuit, V_L = V_C ≠ V_R. What is the value of the power factor? (CBSE AI 2015)
Answer:
One.

Question 9.
Define capacitor reactance. Write its SI units. (CBSE Delhi 2015)
Answer:
It is the opposition offered to the flow of current by a capacitor. It is measured in ohm.

Question 10.
Define quality factor in series LCR circuit. What is its SI unit? (CBSE Delhi 2016)
Answer:
The quality factor is defined as the ratio of the voltage developed across the capacitor or inductor to the applied voltage. It does not have any unit.

Question 11.
A choke and a bulb are in series to a dc source. The bulb shines brightly. How does its brightness change when an iron core is inserted inside the choke coil?
Answer:
There is no change in the final brightness as the inductive reactance is zero for dc.

Question 12.
A solenoid with an iron core and a bulb are connected to a dc source. How does the brightness of the bulb change, when the iron core is removed from the solenoid?
Answer:
There Is no change In the finaL brightness as the inductive reactance is zero for dc.

Question 13.
In a serles LCR circult, the voltage across an inductor, capacitor and a resistor are 20 V, 20 V and 40 V, respectively. What Is the phase difference between the applied voltage and the current In the circuit?
Answer:
WhenV_L = V_C, then the circuit is in series resonance, therefore both current and voltage are in phase.

Question 14.
Why Is there no power consumption In an Ideal inductor connected to an ac source?
Answer:
This is because current and voltage across an ideal inductor are out of phase by 900.
Hence P = V_RMS I_RMS cos 90° = O

Question 15.
Can a choke be replaced by a capacitor of suitable capacitance?
Answer:
Yes, because even then the power consumed will be zero.

Question 16.
Find the inductance of the Inductor that would have a reactance of 50 ohm when used with an ac source of frequency 25/π kHz.
Answer:
Using X_L = 2 πf L or L = \(\frac{X_{L}}{2 \pi f}\), therefore
L = \(\frac{50 \times \pi}{2 \pi \times 25}\) = 1 H

Question 17.
The figure gIven below shows the variation of an alternating emf with time. What Is the average value of the emf for the shaded part of the graph?

Answer:
Average or mean value of ac over half cycle or in time T/2 is
E_m = 2E_o/π = 0.637 E_o = 0.637 × 314
or Em = 200 V.

Question 18.
What is the power dissipated in an ac circuit in which the voltage and current are given by V = 230 sin(ωt + π/2) and l = 10 sin ωt.
Answer:
Since the phase difference between the voltage and current is π/2, therefore power consumed = V_rms l_rms cos π/2 = 0

Question 19.
When a lamp is connected to an alternating voltage supply, it lights with the same brightness as when compared to a 12 V dc battery. What Is the peak value of alternating voltage?
Answer:
The peak value is V = 12 × \(\sqrt{2}\) = 16.97 V

Question 20.
Why is the use of a.c. voltage preferred over d.c. voltage? Give two reasons. (CBSEAI 2014)
Answer:

1. Can be increased or decreased easily.
2. Can easiLy be converted into dc.

Question 21.
Can the Instantaneous power output of an ac source ever be negative? Can the average power output be negative?
Answer:
Yes, No.

Alternating Current Important Extra Questions Short Answer Type

Question 1.
State the phase relationship between the current flowing and the voltage applied in an ac circuit for (i) a pure resistor (ii) a pure inductor.
Answer:

1. Electric current and voltage applied in a pure resistor are in same phase, i.e. Φ = 0°
2. Applied voltage leads electric current flowing through pure-inductor in an ac circuit by phase angle of π/2.

Question 2.
A light bulb is in turn connected in a series (a) across an LR circuit, (b) across an RC circuit, with an ac source. Explain, giving the necessary mathematical formula, the effect on the brightness of the bulb in case (a) and (b), when the frequency of the ac source is increased. (CBSE 2019C)
Answer:
(a) The current in LR circuit is given by
l = \(\frac{V}{\sqrt{R^{2}+\omega^{2} L^{2}}}\)

When the frequency of ac source ω increases, l decreases, and hence brightness decreases.

(b) The current in RC circuit is given by
l = \(\frac{V}{\sqrt{R^{2}+\frac{1}{\omega^{2} C^{2}}}}\)

When the frequency of ac source ω increases, l increases, and hence brightness increases.

Question 3.
An air-core solenoid is connected to an ac source and a bulb. If an iron core is inserted in the solenoid, how does the brightness of the bulb change? Give reasons for your answer.
Answer:
Insertion of an iron core in the solenoid increases its inductance. This in turn increases the value of inductive reactance. This decreases the current and hence the brightness of the bulb.

Question 4.
A bulb and a capacitor are connected in series to an ac source of variable frequency. How will the brightness of the bulb change on increasing the frequency of the ac source? Give reason.
Answer:
When the frequency of the ac is increased, it will decrease the impedance of the circuit as Z = \(\sqrt{R^{2}+(1 / 2 \pi f C)^{2}}\). As a result, the current and hence the brightness of the bulb will increase.

Question 5.
An ideal inductor is in turn put across 220 V, 50 Hz, and 220 V, 100 Hz supplies. Will the current flowing through it in the two cases be the same or different?
Answer:
The current through the inductor is given by l = \(\frac{V}{X_{L}}=\frac{V}{2 \pi f L}\). The current is inversely proportional to the frequency of applied ac.

Since the frequency is different therefore the current will also be different.

Question 6.
State the condition under which the phenomenon of resonance occurs in a series LCR circuit, Plot a graph showing the variation of current with a frequency of ac source in a series LCR circuit.
Answer:
The phenomenon occurs when the inductive reactance becomes equal to the capacitive reactance., i.e. X_L – X_C
⇒ ω L = \(\frac{1}{ωC}\)
⇒ ω = \(\frac{1}{\sqrt{L C}}\)

The graph is as shown below.

Question 7.
Give two advantages and two disadvantages of ac over dc.
Answer:
Advantages of ac:
(a) The generation and transmission of ac are more economical than dc.
(b) The alternating voltage may be easily stepped up or down as per need by using suitable transformers.

Disadvantages of ac:
(a) It is more fatal than dc.
(b) It cannot be used for electrolysis.

Question 8.
In a series, LCR circuit connected to an ac source of variable frequency and voltage v = v_m sin ωt, draw a plot showing the variation of current (l) with angular frequency (ω) for two different values of resistance R₁ and R₂ (R₁ > R₂). Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced? Define the Q-factor of the circuit and give its significance. (CBSE Delhi 2013C)
Answer:
The plot is as shown.

Resonance occurs in an LCR circuit when
X_L = X_C.
The smaller the value of R sharper is the resonance. Therefore the curve will be sharper for R₂. It determines the sharpness of the resonance. The larger the value of Qsharper is the resonance.

Question 9.
You are given three circuit elements X, Y, and Z. When the element X is connected across an a.c. source of a given voltage, the current and the voltage are in the same phase. When the element Y is connected in series with X across the source, voltage is ahead of the current in phase by π/2. But the current is ahead of the voltage in phase by π/2 when Z is connected in series with X across the source. Identify the circuit elements X, Y, and Z. When all the three elements are connected in series across the same source, determine the impedance of the circuit. Draw a plot of the current versus the frequency of the applied source and mention the significance of this plot. (CBSE AI 2015)
Answer:
X-Resistor, Y-Inductor, Z-Capacitor For expression of the impedance of LCR circuit see X is a resistor
Y is a capacitor
Z is an inductor

Consider the impedance triangle
Z = \(\sqrt{R^{2}+\left(X_{t}-X_{C}\right)^{2}}\)

The plot is as shown.

Significance, at ω = ω₀ (resonance frequency) current, is maximum.

Question 10.
Given three elements X, Y, and Z to be connected across an ac source. With the only X connected across the ac source, voltage and current are found to be in the same phase. With only element Y in the circuit, the voltage lags behind the current in phase by π/2, while with the element Z in the circuit, the voltage leads the current in phase by π/2
(a) Identify the elements X, Y, and Z.
Answer:
X is resistor
Y is a capacitor
Z is an inductor

Consider the impedance triangle
Z = \(\sqrt{R^{2}+\left(X_{t}-X_{C}\right)^{2}}\)

(b) When all these elements are connected in series across the same source,
(i) determine the power factor,
Answer:
Power factor = cos Φ = R/Z
= \(\frac{R}{\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}}\)

(ii) find out the condition when the circuit is in resonant state. (CBSE AI 2019)
Answer:
Circuit will be in resonance when X_L – X_C = 0

Question 11.
A coil with an air core and an electric bulb are connected in series across a 220 V 50 Hz ac source. The bulb glows with some brightness. How will the glow of the bulb be affected by introducing a capacitor in series with the circuit? Justify your answer.
Answer:
The impedance of an LR circuit is given by the expression
Z = \(\sqrt{R^{2}+X_{L}^{2}}\) and

the impedance of a series LCR circuit is given by the expression
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\).

Now current flowing through the two circuits is given by V
l = \(\frac{V}{Z}\).

Since Z decreases when a capacitor is connected to an LR circuit therefore there is an increase in current through the circuit. This increases the brightness of the bulb.

Question 12.
In the given circuit, inductor L and resistor R have identical resistance. Two similar electric lamps B1 and B2 are connected as shown. When switch S is closed,
(i) which one of the lamps lights earlier,
(ii) will the lamps be equally bright after some time? Justify your answer.

Answer:
(i) Lamp B₂ connected with the resistor will light up first. This is because the current through the inductor will grow before attaining maximum value.
(ii) When the current through the inductor becomes maximum, after some time, both the lamps will be equally bright.

Question 13.
Figure (a), (b), and (c) show three ac circuits in which equal currents are flowing. If the frequency of emf be increased, how will the current be affected in these circuits? Give the reason for your answer.

Answer:
There will be no change in the current in figure (b) as the resistance of the resistor does not depend upon the frequency of the applied ac.

The reactance of the inductor in figure (a) is given by X_L = 2πf L. An increase in frequency increases the value of inductive reactance. This decreases the current through the circuit.

The reactance of the capacitor in figure (c) is given by X_C = \(\frac{1}{\omega C}=\frac{1}{2 \pi f C}\). An increase in frequency decreases the value of capacitive reactance. This increases the current through the circuit.

Question 14.
An alternating voltage of frequency f is applied across a series LCR circuit. Let f_r be the resonance frequency for the circuit. Will the current in the circuit lag, lead, or remain in phase with the applied voltage when (i) f > f_r (ii) f < f_r Explain your answer in each case.
Answer:
(i) When f > f_r, then the circuit behaves as an inductive circuit. Thus emf leads current. This is because the inductive reactance is given by the expression X_L = 2πfL. At high-frequency X_L will be more.

(ii) When f < f_r> then the circuit behaves as a capacitive circuit. Thus emf lags current. This is because the capacitive reactance is given by the expression X_C = \(\frac{1}{2 \pi f C}\). This value is more at low 2πfC frequency.

Question 15.
For a series LCR circuit, connected to a sinusoidal ac voltage source, identify the graph that corresponds to ω > \(\frac{1}{\sqrt{L C}}\). Give reason.

Answer:
When ω > \(\frac{1}{\sqrt{L C}}\), the circuit behaves as an inductive circuit. In an inductive circuit, emf leads current. This is depicted in the graph (a).

Question 16.
Draw the graphs showing the variations of (a) inductive reactance and (b) capacitive reactance, with the frequency of applied voltage in the ac circuit. How do the values of (a) inductive, and (b) capacitive reactance change, when the frequency of applied voltage is tripled?
Answer:
The graphs are as shown below.

(a) The inductive reactance is given by the expression X_L = 2πfL. Therefore if the frequency is tripled then the value of X_L also gets tripled.
(b) The capacitive reactance is given by the expression X_C = \(\frac{1}{2 \pi f C}\). Therefore if the frequency is tripled then the value of X_C becomes one-third of its previous value.

Question 17.
Can the voltage drop across the inductor or the capacitor in a series LCR circuit be greater than the applied voltage of the ac source? Justify your answer.
Answer:
Yes, the voltage drop across the inductor or the capacitor in a series LCR circuit be greater than the applied voltage of the ac source. It is because the applied voltage is equal to the algebraic sum (as obtained by the use of a phasor diagram) of V_R, V_L, and V_C, i.e.
V = l\(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)

whereas V_L = l X_L and V_C = l X_C.
Thus, it is self-evident that V_L or V_C may be greater than V.

Question 18.
Mention the factors on which the resonant frequency of a series LCR circuit depends. Plot a graph showing the variation of the impedance of a series LCR circuit with the frequency of the applied ac source.
Answer:
In a series LCR circuit, the resonant frequency depends on the value of inductance L and capacitance C present in the circuit.
The graph showing the variation of impedance Z of a series LCR circuit with the frequency f of the applied ac source is shown below.

Question 19.
A lamp is connected in series with a capacitor. Predict your observations for dc and ac connections. What happens in each case if the capacitance of the capacitor is reduced? (NCERT)
Answer:
When a dc source is connected to a capacitor, the capacitor gets charged and after charging no current flows in the circuit and the lamp will not glow. There will be no change even if C is reduced. With ac source, the capacitor offers capacitive reactance (1/ω_C), and the current flows in the circuit. Consequently, the lamp will shine. Reducing C will increase reactance and the lamp will shine less brightly than before.

Question 20.
A light bulb and an open coil inductor are connected to an ac source through a key as shown in the figure.

The switch is closed and after some time, an iron rod is inserted into the interior of the inductor. The glow of the light bulb (a) increases; (b) decreases (c) is unchanged as the iron rod is inserted. Give your answer with reasons. (NCERT)
Answer:
As the iron rod is inserted, the magnetic field inside the coil magnetizes the iron rod thereby increasing the magnetic field inside it. Hence, the inductance of the coil increases. Consequently, the inductive reactance of the coil increases. As a result, a larger fraction of the applied ac voltage appears across the inductor, leaving less voltage across the bulb. Therefore, the glow of the light bulb decreases.

Question 21.
Draw the effective equivalent circuit of the circuit shown in the figure at very high frequencies and find the effective impedance. (NCERT Exemplar)

Answer:
At high frequency, the capacitive reactance is small while the inductive reactance is large. Therefore the capacitive reactance can be neglected while no current will flow through the inductors. Therefore the equivalent reactance of the circuit is Z = R₁ + R₃ and hence the circuit becomes

Question 22.
Study the circuits (a) and (b) shown in the figure and answer the following questions.

(a) Under which conditions would the rms currents in the two circuits be the same?
Answer:
This will happen when the impedance of both the circuits is the same, i.e. R. This is possible when circuit (b) is in resonance.

(b) Can the rms current in circuit (b) be larger than that in (a)? (NCERT Exemplar)
Answer:
No, because in circuit (b)
l_rms = \(\frac{V_{\text {rms }}}{Z}=\frac{V_{\text {rms }}}{\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}}\), Z cannot be less than R.

Question 23.
How does the sign of the phase angle Φ, by which the supply voltage leads the current in an LCR series circuit, change as the supply frequency is gradually increased from very low to very high values? (NCERT Exemplar)
Answer:
The phase angle for an LCR circuit is given by the expression
tan Φ = \(\frac{R}{Z}=\frac{X_{L}-X_{C}}{R}=\frac{2 \pi f L-1 / 2 \pi f C}{R}\)

At low frequencies X_L < X_C and at high frequencies X_L > X_C Therefore Φ changes from negative to zero and to positive; zero at the resonant frequency.

Question 24.
A device ‘X’ is connected to an ac source. The variation of voltage, current, and power in one complete cycle is shown in the figure.
(a) Which curve shows power consumption over a full cycle?
(b) What is the average power consumption over a cycle?
(c) Identify the device ‘X’. (NCERT Exemplar)

Answer:
(a) A
(b) Zero
(c) L or C or LC

Question 25.
Both alternating current and direct current are measured in amperes. But how is the ampere defined for an alternating current? (NCERT Exemplar)
Answer:
An ac current changes direction with the source frequency and the charge flow would average to zero. Thus, the ac ampere must be defined in terms of some property that is independent of the direction of the current. Joule’s heating effect is such property and hence it is used to define misvalue of ac.

Question 26.
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit In which resistance, capacitance, and inductance have values of 10 0, 1 μF, and 1 H, respectively.
Find (i) the peak voltage across the inductor at resonance
(ii) the quality factor of the circuit. (CBSE Sample Paper 2018-19)
Answer:
Given V_m = 10V, R = 1o Ω, L = 1 H, C = 1 μF,
V_L = ?, Q = ?

Q= ω_r L/R = (10³ × 1)/10 = 100

Question 27.
Draw a labeled diagram of a step-down transformer. State its working principle Write one main cause of energy loss in this device and the method used for reducing it.
Answer:
The labeled diagram is as shown.

It works on the principle of mutual induction i.e., whenever magnetic flux linked with a coil changes an emf is induced in the neighboring coil.

One main cause of loss of energy is heat produced due to the production of eddy currents. This can be reduced by laminating the iron core.

Alternating Current Important Extra Questions Long Answer Type

Question 1.
Prove mathematically that the average power over a complete cycle of alternating current through an Ideal inductor is zero.
Answer:
Let the instantaneous value of voltage and current in the ac circuit containing a pure inductor are
V = V_m sin ωt and
l = l_m sin (ωt – π/2) = – l_m cos ωt
where π/2 is the phase angle by which voltage Leads currently when ac flows through an inductor. Suppose the voltage and current remain constant for a small-time dt. Therefore, the electrical energy consumed in the small-time dt is
dW = V l dt

The total electrical energy consumed in one time period of ac is given by

Therefore, the total electrical energy consumed in an ac circuit by a pure inductor is W = 0

Now average power is defined as the ratio of the total electrical energy consumed over the entire cycle to the time period of the cycle, therefore
P_av = \(\frac{W}{T}\) = 0

Hence, the average power consumed in an ac circuit by a pure inductor is P_av = 0
Thus a pure inductor does not consume any power when ac flows through it. Whatever energy is used in building up current is returned back during the decay of current.

Question 2.
Draw the phasor diagram of a series LCR connected across an ac source V= V_o sin ωt. Hence, derive the expression for the impedance of the circuit. Obtain the conditions for the phase angle under which the current is
(i) maximum and
(ii) minimum. (CBSE AI 2019)
Answer:
The voltages across the various elements are drawn as shown in the figure below.

From the diagram, we observe that the vector sum of the voltage amplitudes V_R, V_L, and V_C equals a phasor whose length is the maximum applied voltage V_m, where the phasor Vm makes an angle φ with the current phasor lm. Since the voltage phasors, V_L and V_C are in opposite direction, therefore, a difference phasor (V_L – V_C) is drawn which is perpendicular to the phasor V_R. Adding vectorially we have


where X_L = ω L and X_C = 1 / ω C, therefore, we can express the maximum current as
l_m = \(\frac{V_{\mathrm{m}}}{\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{\mathrm{C}}\right)^{2}}}\)

The impedance Z of the circuit is defined as Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{C}\right)^{2}}\)

For maximum lm, Z should be minimum (Z = R) or X_C = X_L = 0 and Φ = 0

For (l_m)min Φ → 90° (|X_C – X_L| >> R) Z → ∞

Question 3.
(a) The graphs (i) and (ii) represent the variation of the opposition offered by the circuit element to the flow of alternating current with a frequency of the applied emf. identify the circuit element corresponding to each graph.


(b) Write the expression for the impedance offered by the series combinations of the above two elements connected across the ac source. Which will be ahead in phase in this circuit, voltage or current? (CBSE AI 2011C)
Answer:
(a) In figure (i) the opposition to the flow of current does not depend upon frequency, the circuit element is a resistor.

In figure (ii) the opposition increases with frequency, the current element is an inductor.

(b) When the resistor R and the inductance L are connected in series across an ac source, the impedance Z of the circuit is given by
Z = \(\sqrt{R^{2}+X_{L}^{2}}\), where X_L is the inductive reactance.

In an L – R circuit, the voltage is ahead of the current.

Question 4.
An Inductor L of inductance XL is connected in series with bulb B and an ac source. How would the brightness of the bulb change when
(a) the number of turns In the Inductor Is reduced,
(b) an Iron rod Is Inserted Into the Inductor and
(c) a capacitor of reactance X_C = X_L
Is Inserted in series In the circuit. Justify your answer In each case. (CBSE Delhi 2015)
Answer:
(a) When the number of turns of the inductor reduced it decreases the inductance of the inductor as (L ∝ n²) where n is the number of turns. This in turn decreases the inductive reactance X_L which increases the current in the circuit and hence the brightness of the bulb decreases.
(b) When an iron rod is inserted in the inductor, it increases the inductive reactance, which in turn decreases the current and hence the brightness of the bulb.
(c) When X_L = X_C, the circuit acts as a resistive circuit, i.e. the impedance becomes minimum and maximum current flows. This makes the bulb glow more brightly.

Question 5.
An inductor L of reactance X_L is connected in series with a bulb B to an ac source as shown in the figure below. Briefly explain how the brightness of the bulb changes, when
(a) number of turns of the inductor Is reduced? and
(b) a capacitor of reactance X_C = X_L is included in series in the same circuit?

Answer:
If R is the resistance of the bulb, then the total impedance of the circuit is Z = \(\sqrt{R^{2}+X_{L}^{2}}\) and the corresponding current is l = V l Z.
(a) If the number of turns of the inductor is reduced then its inductance L and consequently there is a decrease in the reactance. This leads to a decrease in the impedance of the circuit. As a result the current flowing through the circuit increases. This increases the brightness of the bulb.

(b) When a capacitor of reactance X_C = X_L is included in the circuit, then the new impedance becomes Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\) = R. Thus the impedance has its minimum value. This increases the current through the circuit, which results in an increase in the brightness of the bulb.

Question 6.
A capacitor, ‘C’ a variable resistor ‘R’, and a bulb ‘B’ are connected in series to the ac mains in the circuit as shown. The bulb glows with some brightness. How will the glow of the bulb change if (a) a dielectric slab is introduced between the plates of the capacitor, keeping resistance R to be the same (b) the resistance R is increased keeping the same capacitance? (CBSE Delhi 2014)

Answer:
(a) As the dielectric slab is introduced between the plates of the capacitor, its capacitance will increase. Hence, the potential drop across the capacitor will decrease (V = Q/C). As a result, the potential drop across the bulb will increase (since both are connected in series). So, its brightness will increase.
(b) As the resistance (R) is increased, the potential drop across the resistor will increase. As a result, the potential drop across the bulb will decrease (since both are connected in series). So, its brightness will decrease.

Question 7.
What is meant by impedance? Give its unit. Using a phasors diagram or otherwise derive the expression for the Impedance of an ac circuit containing L, C, and R in series. Find the expression for the resonant frequency.
Answer:
It is the opposition offered by LR or CR or LCR circuit to the flow of ac. It is measured in ohm.

For derivation of Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)

The impedance Z of the circuit is defined as
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\)

The graph is shown.

The current through an LCR circuit is given by the expression l_v = \(\frac{E_{v}}{Z}\)

where Z is the impedance. Substituting the value of Z in the above equation we have
l_v = \(\frac{E_{v}}{\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}}\)

Because the impedance depends on the frequency of the source, we see that the current in the LCR circuit will depend upon frequency. The current, therefore, reaches its maximum value when the impedance is minimum. This happens when X_L = X_C, corresponding to Z = R. The frequency ω at which this occurs is called resonant angular frequency. To find ω0, we use the condition X_L = X_C, from which we get

But ω_o = 2 πf_o, where f_o is called resonance frequency. Therefore, the above equation becomes f_o = \(\frac{1}{2 \pi} \frac{1}{\sqrt{L C}}\)

Question 8.
Explain the term ‘inductive reactance’. Show graphically the variation of an inductive reactance with the frequency of the applied alternating voltage.
An ac voltage E = E_o sin ωt is applied across a pure inductor of inductance L. Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of π/2.
Answer:
It is the opposition offered to the flow of current by a pure inductor.

Consider an ac circuit consisting of a pure Inductor connected to the terminaLs of an ac source. Let the Instantaneous value of the ac source be
V = V_m sin ωt ….(1)

Let V_L be the instantaneous voltage drop across the inductor, then Kirchoff’s loop rule when applied to the circuit gives V + V_L = 0
or
V – L\(\frac{di}{dt}\) = 0 …(2)

since V_L = – L\(\frac{di}{dt}\)
Using equations (1) and (2) we have

Integrating the above equation we have

where \(\frac{V_{m}}{\omega L}\) = l_m , ω_L = 2πfL has the dimensions of resistance and is called the inductive reactance of the circuit. Using the trigonometric identity cos ωt = – sin (ωt – π/2) in equation (6) we have
l_L =l_m sin (ωt – π/2) …(7)
Comparing equation (1) with equation (7) we see that the current lags voltage by π/2 radian or 90°.

Question 9.
Explain the term ‘capacitive reactance’. Show graphically the variation of a capacitive reactance with the frequency of the applied alternating voltage.
An ac voltage E=E_o sin cot is applied across a pure capacitor of capacitance C. Show mathematically that the current flowing through it leads the applied voltage by a phase angle of π/2.
Answer:
It is the opposition offered to the flow of current by a pure capacitor.
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = V_m sin ωt …(1)

Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – V_C = 0
V = V_C = Vm Sin ωt …(2)

But from the definition of capacitance, V_C = Q / C or Q= V_CC. Substituting for V_C we have
Q = C V_m sin ωt …(3)

Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CV_m sin ωt = ω C V_m cos ωt …(4)

But dQ/dt = lc, therefore the above equation becomes,
l_C = ω C V_m cos ωt = l_m cos ωt …(5)
where
l_m = \(\frac{v_{m}}{\frac{1}{\omega C}}\)

Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCV_m = l_m.

Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
l_C = l_m sin (ωt + π/2) …..(6)

Comparing this expression with equation (1)

we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.

The graph of variation of X_C with f is as shown.

Question 10.
Derive an expression for the impedance of a series LCR circuit connected to an ac supply of variable frequency. Plot a graph showing a variation of current with the frequency of the applied voltage. Explain briefly how the phenomenon of resonance in the circuit can be used in the tuning mechanism of a radio or a TV set. (CBSE Delhi 2011)
Answer:
The voltages across the various elements are drawn as shown in the figure below.

From the diagram, we observe that the vector sum of the voltage amplitudes V_R, V_L, and V_C equals a phasor whose length is the maximum applied voltage V_m, where the phasor V_m makes an angle Φ with the current phasor lm. Since the voltage phasors, V_L and V_C are in opposite directions, a different phasor (V_L – V_C) is drawn which is perpendicular to the phasor V_R.

Adding vectorially, we have
V_m = \(\sqrt{V_{R}^{2}+\left(V_{L}-V_{c}\right)^{2}}\)
= \(\sqrt{\left(l_{m} R\right)^{2}+\left(l_{m} X_{L}-l_{m} X_{c}\right)^{2}}\) …(1)
or
V_m = lm\(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\) …(2)

where X_L = ω L and X_C = 1/ω C, therefore we can express the maximum current as
l_m = \(\frac{V_{m}}{\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}}\) …(3)

∴ l_m = \(\frac{V_{m}}{Z}\)

The impedance Z of the circuit is defined as
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\)

The graph is shown.

The graph is as shown.

The antenna of a radio accepts signals from many broadcasting stations. The signals picked up in the antenna act as a source in the tuning circuit of the radio, so the circuit can be driven at many frequencies. But to hear one particular radio station, we tune the radio. In tuning, we vary the capacitance of a capacitor in the tuning circuit such that the resonant frequency of the circuit becomes nearly equal to the frequency of the radio signal received. When this happens, the amplitude of the current with the frequency of the signal of the particular radio station in the circuit is maximum and that particular radio station is tuned in.

Question 11.
A device ‘X’ is connected to an ac source V = V_o sin ωt. The variation of voltage, current, and power in one cycle is shown in the following graph.

(a) Identify the device ‘X’.
Answer:
Capacitor

(b) Which of the curves A, B, and C represent the voltage, current, and power consumed in the circuit? Justify your answer.
Answer:
A: Power, B: Voltage, and C: Current.

(c) How does its impedance vary with the frequency of the ac source? Show graphically.
Answer:
For a capacitor, Impedance is given by X_C = 1 /ω_C = 1 /2πf_C. This is shown graphically as

(d) Obtain an expression for the current in the circuit and its phase relation with ac voltage. (CBSE AI 2017)
Answer:
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = V_o sin ωt …(1)

Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – V_C = 0
or
V = V_C = V_o sin ωt …(2)

But from the definition of capacitance,
V_C = Q / C
or
Q= V_C C.

Substituting for Vc we have
Q = CV_o sin ωt …(3)

Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\) CV_o sin ω t = ω C V_o cos ω t …(4)

But dQ/dt = i_c, therefore the above equation becomes,
i_c = ω C V_o cos ω t = l_o cos ω t …(5)

Here the term 1/ωc has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCV_m = l_m. Using the trigonometric identity cos ω t = sin (ω t + π/2) equation (5) can be written as
i_c = l_o sin (ω t + π/2) …(6)

Comparing this expression with equation (1) we see that the current is 90° (π/2 ) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.

Question 12.
A device X is connected across an ac source of voltage V = V_o sin ωt. The current through X is given as l = l_o sin (ωt + π/2).
(a) Identify the device X and write the expression for Its reactance.
(b) Draw graphs showing the variation of voltage and current with time over one cycle of ac, for X.
(c) How does the reactance of device X vary with the frequency of the ac? Show this variation graphically.
(d) Draw the phasor diagram for the device X. (CBSE AI 2018, Delhi 2018)
Answer:
(a) X: capacitor
Reactance X_C = 1 / ω_C = 1 / 2πf_C

(b) The graphs area as shown.

(c) Reactance of the capacitor varies in inverse proportion to the frequency. Therefore, the graph is as shown.

(d) The phasor diagram is as shown.

Question 13.
A resistor of 200 Ω and a capacitor of 15.0 μF is connected In series to a 220 V, 50 Hz ac source, (a) Calculate the current in the circuit; (b) Calculate the voltage (rms) across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltage? If yes, resolve the paradox. (NCERT, CBSE Delhi 2004)
Answer:
Given R = 200 Ω, C= 15.0 μF = 15.0 × 10^-6 F, V = 220 V, f = 50 Hz
(a) In order to calculate the current, we need the impedance of the

Therefore the current in the circuit is
l = \(\frac{V}{Z}=\frac{220}{291.5}\) = 0.7555 A

(b) Since the current is the same throughout the circuit we have
V_R = I_R = 0.755 × 200 = 151 V
V_C = lX_C = 0.755 × 212.3 = 160.3 V

The algebraic sum of the two voltages VR and Vc is 311.3 V which is more than the source voltage of 220 V. How to resolve this paradox? As you have learned in the text, the two voltages are not in the same phase. Therefore, they cannot be added like ordinary numbers. The two voltages are out of phase by ninety degrees. Therefore, the total of these voltages must be obtained using the Pythagorean theorem;
V = \(\sqrt{V_{R}^{2}+V_{C}^{2}}\) = 220 V

Thus if the phase difference between two voltages is properly taken into account, the total voltage across the resistor and the capacitor is equal to the voltage of the source.

Question 14.
Explain why the reactance offered by an inductor increases with the increasing frequency of an alternating voltage.
(NCERT Exemplar)
Answer:
An inductor opposes the flow of current through it by developing a back emf according to Lenz’s law. The induced voltage has a polarity so as to maintain the current at its present value. If the current is decreasing, the polarity of the induced emf will be so as to increase the current and vice versa. Since the induced emf is proportional to the rate of change of current, it will provide greater reactance to the flow of current if the rate of change is faster, i.e. if the frequency is higher. The reactance of an Inductor, therefore, is proportional to the frequency, being given by ω_L.

Question 15.
(a) Prove that an Ideal capacitor in an ac circuit does not dissipate power.
Answer:
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = V_m sin ωt …(1)

Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – V_C = 0
V = V_C = V_m Sin ωt …(2)

But from the definition of capacitance, V_C = Q / C or Q= V_CC. Substituting for Vc we have
Q = C V_m sin ωt …(3)

Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CV_m sin ωt = ω C V_m cos ωt …(4)

But dQ/dt = lc, therefore the above equation becomes,
l_C = ω C V_m cos ωt = l_m cos ωt …(5)
where
l_m = \(\frac{v_{m}}{\frac{1}{\omega C}}\)

Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCV_m = l_m.

Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
l_C = l_m sin (ωt + π/2) …..(6)

Comparing this expression with equation (1)

we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.

The graph of variation of X_C with f is as shown.

Power in capacitive circuit P = E_v l_v cos Φ. In pure captor 0 = 90° phase difference between voltage and current is π/2.
So power consumed in pure capdtor P_av = E_v l_v cos 90° = 0.

(b) An ideal inductor of 200 mH, capacitor of 400 μF, and a resistor of 10 Ω are connected In series to an ac source of 50 V and variable frequency. Calculate
(i)the angular frequency at which maximum power dissipation occurs in the circuit and the corresponding value of effective current and
(ii) the value of Q factor in the circuit. (CBSE AI 2017C)
Answer:

Question 16.
(a) What is the principle of transformer?
(b) Explain how laminating the core of a transformer helps to reduce eddy current losses in it.
(c) Why the primary and secondary coils of a transformer are preferably wound on the same core?
Or
Show that In the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the Inductor Is constant In time. (CBSE Sample Paper 2018-19)
Answer:
(a) It works on the principle of mutual induction.
(b) In order to reduce the eddy current loss, the resistance of the core should be Increased. In a transformer, the core Is made up of thin sheets of steel, each lamination being insulated from others by a thin layer of varnish. As the laminations are thin, they will have relatively high resistance.
(c) This is done to maximize the sharing of magnetic flux and also so that magnetic flux per turn should become the same in both the primary and secondary coils.
Or
Let at any instant t, q be the charge on the capacitor and ‘l’ be the current through the inductor
q (t) = q₀ cos ωt
i (t) = – q₀ ω sin ωt
Energy stored in the capacitor at time t is
U_E = \(\frac{1}{2} \frac{q^{2}}{c}=\frac{1}{2} \frac{q_{0}^{2}}{C}\) cos² ωt

Energy stored in the inductor at time t is

This sum is constant in time as q₀ and C, both are time-independent.

Question 17.
Explain why the reactance provided by a capacitor to an alternating current decreases with increasing frequency. (NCERT Exemplar)
Answer:
A capacitor does not allow the flow of direct current through it as the resistance across the gap is infinite. When an alternating voltage is applied across the capacitor plates, the plates are alternately charged and discharged. The current through the capacitor is a result of this changing voltage (or charge). Thus, a capacitor will pass more current through it if the voltage is changing at a faster rate, i.e. if the frequency of the supply is higher. This implies that the reactance offered by a capacitor is less with increasing frequency; it is given by 1 /ω_C.

Question 18.
(a) With the help of a labeled diagram, describe briefly the underlying principle and working of a step-up transformer.
(b) Write any two sources of energy loss in a transformer.
(c) A step-up transformer converts a low input voltage into a high output voltage. Does it violate the law of conservation of energy? Explain. (CBSE Delhi 2011)
Answer:
(a) The diagram is as shown.

It works on the principle of mutual induction i.e., whenever magnetic flux linked with a coil changes an emf is induced in the neighboring coil. In a step-up transformer, the number of turns in the secondary is more than that in the primary.

The ac source causes an alternating current in the primary, which sets up an alternating flux in the core; this induces an emf in each winding of the secondary, in accordance with Faraday’s law. The induced emf in the secondary gives rise to an alternating current in the secondary, and this delivers energy to the device to which the secondary is connected.

For step up : N_s> > N_p
\(\frac{\varepsilon_{s}}{\varepsilon_{p}}=\frac{N_{s}}{N_{p}}\) and \(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\)

(b) Two major sources of energy loss in this device are:

1. Heat produced due to production of eddy currents.
2. Copper loss: heat produced in the copper coils

(c) No, a transformer does not change the power. Thus if a voltage increases current gets decreased such that the energy and power remain the same.

Question 19.
(a) Explain with the help of a labeled diagram, principle, and working of a transformer. Deduce the expression for its working formula.
Answer:
For diagram as shown.

• Principle: A transformer works on the basis of mutual induction.
• Working: In a 100% efficient transformer

ε_s l_s = ε_p l_p where l and l_p, are the secondary and primary currents, therefore we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) ….(1)

Now a 1oo % efficient transformer
we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}} \frac{\frac{d \phi}{d t}}{\frac{d \phi}{d t}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}\) …(2)

Therefore form (1) and (2) we have
\(\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) = k

Efficiency of transformer = \(\frac{V_{s} I_{s}}{V_{p} I_{p}}\).

(b) Name any four causes of energy loss in an actual transformer. (CBSEAI 2013C)
Answer:

1. Copper loss
2. Iron loss
3. Flux loss
4. Hysteresis loss

Question 20.
(a) Draw a schematic sketch of an ac generator describing its basic elements. State briefly its working principle. Show a plot of the variation of (i) Magnetic flux and alternating emf versus time generated by a loop of wire rotating in a magnetic field,
Answer:
A schematic sketch is as shown.

Working principle: Electromagnetic induction.

The graphs are as shown.

(b) Why is a choke coil needed in the use of fluorescent tubes with ac mains? (CBSE Delhi 2014)
Answer:
It is used to regulate current with minimum loss of energy.

Question 21.
(a) Draw a labeled diagram of the AC generator. Derive the expression for the instantaneous value of the emf induced in the coil.
Answer:
It is based on the principle of electromagnetic induction. When a coil is rotated about an axis perpendicular to the direction of the uniform magnetic field, an induced emf is produced across it.

Working: The working of the ac generator can be understood with the help of the various positions of the armature as shown in the figure below.


Suppose at time t = 0, the plane of the loop is perpendicular to B. As the loop rotates from position t = 0 to position t T/2, the Induced emf changes from zero to maximum value and then becomes zero again as shown in the diagram For angles 0° and 1800 the instantaneous rate of magnetic flux is zero, hence induced emf Is zero.

As the Loop moves from position t = T/2 to position t = T, the emf again changes from zero to the maximum value and then again becomes zero. But this time it reverses Its direction. For angles 90° and 270° maximum magnetic flux are linked with the coil hence the emf is a maximum. Thus the output of the ac generator varies sinusoidally with time. The Induced emf does not depend upon the shape of the Loop but depends only upon the area of the loop.

The emf generated Is given by the expression ε = nBAω Sin ωt, where ω is the speed of rotation of the coil

(b) A circular coil of cross-sectional area 200 cm² and 20 turns is rotated about the vertical diameter with an angular speed of 50 rad s^-1 in a uniform magnetic field of magnitude 3.O × 10^-2 T. Calculate the maximum value of the current in the coil. (CBSE Delhi 2017)
Answer:
Given A = 200 cm², ω = 50 rad s^-1, n = 20
S = 3 × 10^-2 T, ε_o = ?,

Using the relation ε0 = nBAω
= 20 × 3 × 10^-2 × 200 × 10^-4 × 50 = 0.6 V

Question 22.
Draw a labeled diagram of a step-up transformer. Obtain the ratio of secondary to primary voltage in terms of the number of turns and currents in the two coils.
A power transmission line feeds input power at 2200 V to a step-down transformer with its primary windings having 3000 turns. Find the number of turns in the secondary to get the power output at 220 V. (CBSE Delhi 2017)
Answer:
(a) The diagram is as shown.

It works on the principle of mutual induction i.e., whenever magnetic flux linked with a coil changes an emf is induced in the neighboring coil. In a step-up transformer, the number of turns in the secondary is more than that in the primary.

The ac source causes an alternating current in the primary, which sets up an alternating flux in the core; this induces an emf in each winding of the secondary, in accordance with Faraday’s law. The induced emf in the secondary gives rise to an alternating current in the secondary, and this delivers energy to the device to which the secondary is connected.

For step up : N_s > N_p
\(\frac{\varepsilon_{s}}{\varepsilon_{p}}=\frac{N_{s}}{N_{p}}\) and \(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\).

Principle – It works on the principle of electromagnetic induction. When the current in one circuit changes, an induced current is set up in the neighboring circuit.

(b) N_s = ?, N_p = 3000
E_p = 2200 V, E_s = 220 V

Since, E_s/E_p = N_s/N_p
220/2200 = N_s/3000
N_s = 300

Question 23.
(a) State the principle of working of a transformer.
Answer:
It works on the principle of mutual inductance i.e. whenever the magnetic flux Linked in a coil changes an induced emf Is produced in the neighboring coil.

(b) Define the efficiency of a transformer.
Answer:
It is the ratio of the output power to the input power.

(c) State any two factors that reduce the efficiency of a transformer.
Answer:
Copper Loss, flux Loss

(d) Calculate the current drawn by the primary of a 90% efficient transformer which steps down 220 V to 22 V If the output resistance Is 440 Ω. (CBSFAI 2018 C)
Answer:
Given η = 90%, V_p = 22OV, V_s = 22V, R_o = 440 W
Now l_s = V_s/R = 22/440 = 0.05 A

Also η = \(\frac{P_{0}}{P_{1}}=\frac{V_{s} l_{s}}{V_{p} l_{p}}\) , therefore we have

\(\frac{90}{100}=\frac{22 \times 0.05}{220 \times l_{\mathrm{p}}}\)
or
l_p = 0.0056 A

Question 24.
Draw an arrangement for winding of primary and secondary coil In a transformer with two coils on a separate limb of the core.
State the underlying principle of a transformer. Deduce the expression for the ratio of secondary voltage to the primary voltage In terms of the ratio of the number of turns of the primary and secondary winding. For an ideal transformer, obtain the ratio of primary and secondary currents In terms of the ratio al the voltages in the secondary and primary voltages. Write any two reasons for the energy losses which occur In actual transformers, (CBSE Dei hi 2016C)
Answer:
Principle: When an alternating voltage is applied to the primary, the resulting current produces an alternating magnetic flux which Links the secondary and Induces an emf in it.

Induced emf, or voltage, in the secondary, with ‘N_s‘ number of turns,
ε_s = – N_s \(\frac{d \phi}{d t}\)

Back emf In the primary with Np turns,
ε_p = – N_p \(\frac{d \phi}{d t}\)

Since ε_s = V_s and ε_p = V_p
Therefore we have
\(\frac{V_{p}}{V_{s}}=\frac{N_{p}}{N_{s}}\)

For an ideal transformer,
Input power = output power
Therefore
l_pV_p = l_sV_s
Or
\(\frac{V_{p}}{V_{s}}=\frac{l_{s}}{l_{p}}\)

(a) Heat energy Loss.
(b) Humming effect Loss.

Question 25.
A pure inductor is connected across an ac source. Show mathematically that the current in it lags behind the applied emf by a phase angle of π/2. What is its inductive reactance? Draw a graph showing the variation of an inductive reactance with the frequency of the ac source.
Answer:
Consider an ac circuit consisting of a pure Inductor connected to the terminaLs of an ac source. Let the Instantaneous value of the ac source be
V = V_m sin ωt ….(1)

Let V_L be the instantaneous voltage drop across the inductor, then Kirchoff’s loop rule when applied to the circuit gives V + V_L = 0
or
V – L\(\frac{di}{dt}\) = 0 …(2)

since V_L = – L\(\frac{di}{dt}\)
Using equations (1) and (2) we have

Integrating the above equation we have

where \(\frac{V_{m}}{\omega L}\) = l_m , ω_L = 2πfL has the dimensions of resistance and is called the inductive reactance of the circuit. Using the trigonometric identity cos ωt = – sin (ωt – π/2) in equation (6) we have
l_L =l_m sin (ωt – π/2) …(7)
Comparing equation (1) with equation (7) we see that the current lags voltage by π/2 radian or 90°.

Question 26.
An alternating emf Is applied across a capacitor. Show mathematically that the current leads the emf by a phase angle π/2, What Is its capacitive reactance? Draw a graph showing the variation of a capacitive reactance with the frequency of the ac source.

Answer:
Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = V_m sin ωt …(1)

Let Vc be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – V_C = 0
V = V_C = V_m Sin ωt …(2)

But from the definition of capacitance, V_C = Q / C or Q= V_CC. Substituting for V_C we have
Q = C V_m sin ωt …(3)

Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CV_m sin ωt = ω C V_m cos ωt …(4)

But dQ/dt = l_C, therefore the above equation becomes,
l_C = ω C V_m cos ωt = l_m cos ωt …(5)
where
lm = \(\frac{v_{m}}{\frac{1}{\omega C}}\)

Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCVm = lm.

Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
l_C = l_m sin (ωt + π/2) …..(6)

Comparing this expression with equation (1)

we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, currently leads emf by 90°.

The graph of variation of X_C with f is as shown.

Question 27.
(a) In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with the frequency of the ac source.
Answer:
The voltages across the various elements are drawn as shown in the figure below.

From the diagram, we observe that the vector sum of the voltage amplitudes V_R, V_L, and V_C equals a phasor whose length is the maximum applied voltage Vm, where the phasor Vm makes an angle Φ with the current phasor lm. Since the voltage phasors, V_Land V_C is in opposite directions, a different phasor (V_L – V_C) is drawn which is perpendicular to the phasor V_R.

Adding vectorially, we have
V_m = \(\sqrt{V_{R}^{2}+\left(V_{L}-V_{c}\right)^{2}}\)
= \(\sqrt{\left(l_{m} R\right)^{2}+\left(l_{m} X_{L}-l_{m} X_{c}\right)^{2}}\) …(1)
or
V_m = l_m\(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\) …(2)

where X_L = ω L and X_C = 1/ω C, therefore we can express the maximum current as
l_m = \(\frac{V_{m}}{\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}}\) …(3)

∴ l_m = \(\frac{V_{m}}{Z}\)

The impedance Z of the circuit is defined as
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{c}\right)^{2}}\)

The graph is shown.

(b) What is the phase difference between the voltages across the inductor and the capacitor at resonance in the LCR circuit?
Answer:
The phase difference between the voltage across the inductor and the capacitor at resonance is 180°.

(c) When an inductor is connected to a 200V dc voltage, a current of 1A flows through it. When the same inductor is connected to a 200V, 50 Hz ac source, only 0.5A current flows. Explain why? Also, calculate the self-inductance of the inductor. (CBSE Delhi 2019)
Answer:
Inductor will offer an additional impedance to ac due to its self-inductance.

Now R = \(\frac{V_{\text {rms }}}{l_{\text {rms }}}=\frac{200}{1}\) = 200 Ω

The impedance of the inductor
Z = \(\frac{V_{\mathrm{rms}}}{l_{\mathrm{rms}}}=\frac{200}{0.5}\) = 400 Ω

Now Z = \(\sqrt{R^{2}+X_{L}^{2}}\) , therefore
X_L² = Z² – R²
X_L = \(\left(\sqrt{(400)^{2}-(200)^{2}}\right)\) = 346.4 Ω

Hence inductance (L) is
L = \(\frac{X_{L}}{\omega}=\frac{346.4}{2 \times 3.14 \times 50}\) = 6.2 H

Question 28.
(a) Obtain the expression for the average power dissipated in a series LCR circuit driven by an ac source of voltage V = V_m sin ωt supplying the current i = i_m sin (ωt + Φ).
Answer:
Average Power dissipated in a series LCR circuit
Given V = V_m sin tot
And l = i_m sin (ωt + Φ)
Instantaneous Power
P = Vi

(b) Define the terms:
(i) Wattless current, and
Answer:
Wattles’s current: If the average power consumed due to the flow of current in a circuit is zero, the current is said to be wattless.

(ii) Q – a factor of LCR circuit.
Answer:
Q-factor of an LCR Circuit: Q-factor of the LCR circuit is the ratio of the potential difference across inductance (or capacitance) at resonance to the applied voltage.

Question 29.
Distinguish between the terms reactance and impedance of an ac circuit. Prove that an ideal capacitor connected to an ac source does not dissipate power.

Consider an ac circuit consisting of a capacitor connected to an ac source. Let the instantaneous value of emf be
V = V_m sin ωt …(1)

Let V_C be the instantaneous voltage drop across the capacitor, then by Kirchoff’s loop rule,
V – V_C = 0
V = V_C = V_m Sin ωt …(2)

But from the definition of capacitance, V_C = Q / C or Q= V_CC. Substituting for Vc we have
Q = C V_m sin ωt …(3)

Differentiating equation (3) with respect to time we have,
\(\frac{d Q}{d t}=\frac{d}{d t}\)CV_m sin ωt = ω C V_m cos ωt …(4)

But dQ/dt = lc, therefore the above equation becomes,
l_C = ω C V_m cos ωt = l_m cos ωt …(5)
where
lm = \(\frac{v_{m}}{\frac{1}{\omega C}}\)

Here the term \({\frac{1}{\omega C}}\) has the dimensions of resistance and is called the capacitive reactance of the circuit and ωCVm = lm.

Using the trigonometric identity cos ωt = sin (ωt + π/2), equation (5) can be written as
l_C = l_m sin (ωt + π/2) …..(6)

Comparing this expression with equation (1)

we see that the current is 90° (π/2) out of phase with the voltage across the capacitor. In other words, current leads emf by 90°.

The graph of variation of Xc with f is as shown.

Question 30.
Define the term root mean square (rms) value of ac. Derive the relation between rms value and the peak value of ac.
Answer:
It is that value of steady current (dc) which when passed through a resistor in a given time produces the same heat as is produced by the ac. when passed through the same resistor for the same time. It is abbreviated as rms value of current. It is denoted by l_rms.

Consider an ac source. Let the instantaneous value of current be represented by the equation
i = l_m sin ωt

Let this current pass through a resistor of resistance R. Therefore in a small-time dt, the amount of heat produced in the resistor is
dH = i² R dt

The total amount of heat produced in one complete cycle of ac is given by

Let l_rms be the virtual value of ac, then the amount of heat produced in the same resistor of resistance R, in the same time T is
H = l_rms²RT …(2)

Therefore from equations (1) and (2) we have
l_rms = \(\frac{l_{m}}{\sqrt{2}}\) = 0.707 lm

Question 31.
(a) Prove that the current flowing through an Ideal Inductor connected across a.c. source lags the voltage In phase by nil.
Answer:
(a) Consider an ac circuit consisting of a pure inductor connected to the terminals of an ac source. Let the instantaneous value of the ac source be
V = V_m sin ω t …(1)

Let V_L be the instantaneous voltage drop across the inductor, then Kirchoff’s loop rule when applied to the circuit gives V + V_L = 0
or
V – L\(\frac{di}{dt}\) = 0 …(2)

since V_L = – L \(\frac{di}{dt}\)

Using equations (1) and (2) we have
L\(\frac{di}{dt}\) = V_m sin ω t …(3)
or
di = \(\frac{V_{m}}{L}\) sin ω t dt …(4)

Integrating the above equation we have

C = 0, over a period of cycle

\(\frac{V_{\mathrm{m}}}{\omega L}\) = l_m, ω_L = 2πfL has the dimensions of resistance and is called the inductive reactance of the circuit. Using the trigonometric identity
cos ω t = – sin (ωt – π/2) in equation (6) we have
l_L = l_m sin (ωt – π/2) …(7)

Comparing equation (1) with equation (7) clearly shows that the current lags voltage by π/2 radian or 90°.

(b) An inductor of self-inductance 100 mH and a bulb are connected in series with a.c. source of rms voltage 10 V, 50 Hz. It is found that the effective voltage of the circuit leads the current in phase by π/4. Calculate the resistance of the bulb used and average power dissipated in the circuit, if a current of 1 A flows in the circuit. (CBSE Delhi 2017C)
Answer:
(b) V= 10 V, f = 50 Hz, l = 1.0 A, Φ = π/4, R = ?, L = 100mH = 0.1 H
Now Z = V/l = 10/1.0 = 10 ohm

Also Z = \(\sqrt{R^{2}+X_{L}^{2}}\) = 10
Now cos Φ = \(\frac{R}{Z}\)
or
Therefore, R = cos Φ × Z
Or
R = cos π/4 × 10 = 7 ohm

Power dissipated
P_av = l_rms V_rms cos Φ = \(\frac{V_{m}^{2}}{Z}\) × cos Φ
0r
P_av = \(\frac{(10)^{2}}{10}\) × 0.707 = 7.07 W

Question 32.
(a) Draw graphs showing the variations of inductive reactance and capacitive reactance with the frequency of the applied ac source.
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c) An alternating voltage of 220 V is applied across a device X, a current of 0.25 A flows, which lag behind the applied voltage In phase by \(\frac{π}{2}\) radian. If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y. (CBSEAI 2018C)
Or
(a) State the principle of working of a transformer.
(b) Define the efficiency of a transformer.
(c) State any two factors that reduce the efficiency of a transformer.
(d) Calculate the current drawn by the primary of a 90% efficient transformer which steps down 220 V to 22 V, if the output resistance is 440 Ω.
Answer:
(a) The two graphs are as shown.

(b) (The current leads the voltage by an angle 0 where 0 < θ < \(\frac{π}{2}\).) The required phasor diagram is as shown.
Here θ = tan^-1 \(\frac{1}{ωCR}\)

(c) In device X:
Current lags behind the voltage by \(\frac{π}{2}\)
∴ X is an inductor.

In device Y:
Current is in phase with the applied voltage
∴ X is a resistor.

We are given that 0.25 = \(\frac{220}{X_{L}}\)
or
X_L = \(\frac{220}{0.25}\) Ω = 880 Ω

Also 0.25 = 0.25 = \(\frac{220}{X_{R}}\)

∴ X_R = \(\frac{220}{0.25}\) Ω = 880 Ω

For the series combination of X and Y, Equivalent impedance
= \(\sqrt{X_{L}^{2}+X_{R}^{2}}\) = (880\(\sqrt{2}\) Ω

∴ Current flowing = \(\frac{220}{880 \sqrt{2}}\) A = 0.177 A
Or
(a) A transformer works on the principle of mutual induction. (Alternatively, an emf is induced in the secondary coil when the magnetic flux linked with it changes with time due to changing magnetic flux linked with the primary coil).

(b) The efficiency of a transformer equals the ratio of the output power to the input power.
Efficiency = \(\frac{\text { output power }}{\text { input power }}\)
or
Efficiency = \(\frac{V_{S} I_{S}}{V_{P} I_{p}}\)
(c)

• Eddy current Losses
• route heat Losses
• hysteresis Losses
• magnetic flux leakage Losses

We have

Question 33.
(a) Draw a schematic diagram of a step-up transformer. Explain its working principle. Assuming the transformer to be 100% efficient, obtain the relation for
(i) the current in the secondary in terms of the current in the primary, and
(ii) the number of turns in the primary and secondary windings.
(b) Mention two Important energy losses in actual transformers and state how these can be minimized. (CBSE Delhi 2011C)
Answer:
(a) For diagram as shown.

• Principle: A transformer works on the basis of mutual induction.
• Working: In a 100% efficient transformer

ε_s l_s = ε_p l_p where l and l_p are the secondary and primary currents, therefore we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) ….(1)

Now a 1oo % efficient transformer
we have
\(\frac{\varepsilon_{\mathrm{s}}}{\varepsilon_{\mathrm{p}}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}} \frac{\frac{d \phi}{d t}}{\frac{d \phi}{d t}}=\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}\) …(2)

Therefore form (1) and (2) we have
\(\frac{N_{\mathrm{s}}}{N_{\mathrm{p}}}=\frac{l_{\mathrm{p}}}{l_{\mathrm{s}}}\) = k

Efficiency of transformer = \(\frac{V_{s} I_{s}}{V_{p} I_{p}}\)

(b) The two important energy losses in actual transformers are:

1. Iron losses in the core of the transformer.
2. Loss of energy in the primary and secondary due to Joule heating. The iron losses due to eddy currents are minimized by laminating the iron core.

Question 34.
(a) Draw the diagram of a device that is used to decrease high ac voltage into a low ac voltage and state its working principle. Write four sources of energy loss in this device.
Answer:
The labeled diagram is as shown.

It works on the principle of mutual induction, i.e. whenever magnetic flux linked with a coil changes, an emf is induced in the neighboring coil.

The possible causes of energy losses in transformers are:

• Flux leakage
• Copper loss
• Eddy currents
• Hysteresis loss

(b) A small town with a demand of 1200kW of electric power at 220 V is situated 20 km away from an electric plant generating power at 440V. The resistance of the two wirelines carrying power is 0.5 Ω per km. The town gets the power from the line through a 4000 – 220V step-down transformer at a sub-station in the town. Estimate the line power loss in the form of heat. (CBSE Delhi 2019)
Answer:
Total resistance of the line = length × resistance per unit length = 40 km × 0.5 = 20 Ω

Current flowing in the line l = P/V
= 1200 × 10³ /4000 = 300 A

Power loss = l²R = (300)² × 20 = 1800 kW

Question 35.
(a) State the principle of an ac generator and explain its working with the help of a labeled diagram. Obtain the expression for the emf induced in a coil having N turns each of cross-sectional area A, rotating with a constant angular speed ‘co’ in a magnetic field B, directed perpendicular to the axis of rotation.
Answer:
For principle and diagram


Suppose at time t = 0, the plane of the loop is perpendicular to B. As the loop rotates from position t = 0 to position t T/2, the Induced emf changes from zero to maximum value and then becomes zero again as shown in the diagram For angles 0° and 1800 the instantaneous rate of magnetic flux is zero, hence induced emf Is zero. As the Loop moves from position t = T/2 to position t = T, the emf again changes from zero to the maximum value and then again becomes zero. But this time it reverses Its direction. For angles 90° and 270° maximum magnetic flux are linked with the coil hence the emf is a maximum. Thus the output of the ac generator varies sinusoidally with time. The Induced emf does not depend upon the shape of the Loop but depends only upon the area of the loop.

The emf generated Is given by the expression ε = nBAω Sin ωt, where ω is the speed of rotation of the coiL.

(b) An airplane is flying horizontally from west to east with a velocity of 900 km h^-1. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth’s magnetic field is 5 × 10^-4 T and the angle of dip is 30°. (CBSEAI 2018, Delhi 2018)
Answer:
Potential difference developed between the ends of the wings
ε = BLv

Given Velocity V = 900 km h^-1 = 250 m s^-1
Wing span (L₁) = 20 m

Vertical component of Earth’s magnetic field
B_v = BH tan δ = 5 × 10-4 (tan 30°) T

∴ Potential difference
= 5 × 10^-4 (tan 30°) × 20 × 250 = 1.44 V

Question 36.
Explain, with the help of a diagram, the principle and working of an ac generator. Write the expression for the emf generated in the coil in terms of its speed of rotation.
Answer:
It is based on the principle of electromagnetic induction. When a coil is rotated about an axis perpendicular to the direction of a uniform magnetic field, an induced emf is produced across it.

Working: The working of the ac generator can be understood with the help of the various positions of the armature as shown in figure below.


Suppose at time t = 0, the plane of the loop is perpendicular to B. As the loop rotates from position t = 0 to position t T/2, the Induced emf changes from zero to maximum value and then becomes zero again as shown in the diagram For angles 0° and 1800 the instantaneous rate of magnetic flux is zero, hence induced emf Is zero. As the Loop moves from position t = T/2 to position t = T, the emf again changes from zero to a maximum value and then again becomes zero. But this time it reverses Its direction. For angles 90° and 270° maximum magnetic flux are linked with the coil hence the emf is a maximum. Thus the output of the ac generator varies sinusoidally with time. The Induced emf does not depend upon the shape of the Loop but depends only upon the area of the loop.

The emf generated Is given by the expression ε = nBAω Sin ωt, where ω is the speed of rotation of the coiL.

Numerical Problems:
Formulae for solving numerical problems

• Capacitive reactance X_C = \(\frac{1}{\omega C}=\frac{1}{2 \pi f C}\)
• Inductive reactance X_L = ω_L = 2πfL
• When ac flows through an LR circuit then,
  Z = \(\sqrt{R^{2}+X_{L}^{2}}\) and tan Φ = \(\frac{X_{L}}{R}=\frac{\omega L}{R}\)
• When ac flows through a CR circuit then,
  Z = \(\sqrt{R^{2}+X_{C}^{2}}\) and tan Φ = \(\frac{X_{c}}{R}=\frac{1}{\omega C R}\)
• For a senes LCR circuit driven by voltage V = V_m sin ωt, the current is given by
  l = l_m sin (ωt + Φ) where
  l_m = \(\frac{V_{m}}{\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}}\)
• The impedance of this circuit is given by
  Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
  \(\frac{V_{s}}{V_{p}}=\frac{N_{s}}{N_{p}}=\frac{I_{p}}{I_{s}}\) = k.

Question 1.
The figure shows how the reactance of an Inductor varies with frequency. (a) Calculate the value of the Inductance of the Inductor using Information given In the graph. (b) If this Inductor is connected In senes to a resistor of 8 ohms, find what would be the impedance at 300 Hz.

Answer:
(a) We know that X_L = 2πfL or L = \(\frac{X_{L}}{2 \pi f}\).
Now slope of the graph is
\(\frac{X_{L}}{f}=\frac{8-6}{400-300}=\frac{2}{100}\) = 0.02

Therefore L is L = \(\frac{X_{L}}{2 \pi f}=\frac{0.02}{2 \times 3.14}\) = 0.0032 H

(b) NowR = 8 ohm, f = 300 Hz, Z = ?
Now Z = \(\sqrt{R^{2}+X_{L}^{2}}\) . Therefore we have
Z = \(\sqrt{R^{2}+X_{L}^{2}}\) = \(\sqrt{(8)^{2}+(6)^{2}}\) = 10 Ω

Question 2.
A 25.0 μF capacitor, a 0.10-henry Inductor, and a 25.0-ohm resistor are connected in series with an ac source whose emf is E= 310 s. In 314 t (i) what is the frequency of the .mf? (ii) Calculate (a) the reactance of the circuit (b) the Impedance of the circuit and (C) the current in the circuit.
Answer:
Given C = 25.0 μF, L = 0.10 henry, R = 25.0 ohm, E_o = 310V,
Comparing with the equation E = E_o sin ωt,
we have
(i) ω = 314 or f = 50 Hz

Question 3.
A sinusoidal voltage V = 200 sin 314 t Is applied to a resistor of 10 ohms. Calculate (i) rms value of current (ii) rms value of voltage and (iii) power dissipated as heat in watt.
Answer:
V_o = 200 V, ω = 314 rads^-1 , V_rms = ?, l_rms = ?, P = ?

Question 4.
Find the inductance of the inductor used in series with a bulb of resistance 10 ohms connected to an ac source of 80 V, 50 Hz. The power factor of the circuit is 0.5. Also, calculate the power dissipation in the circuit.
Answer:
Given R = 10 ohm, V = 80 Hz, f = 50 Hz, cos Φ = 0.5 , L = ?, P = ?
Using the formula
cos Φ = \(\frac{R}{\sqrt{R^{2}+X_{L}^{2}}}\)
or
0.25(R² + X²) = R²
Or
O.25X_L² = O.75R²
or
X_L = 17.32 ohm

Now using X_L = 2πfL we have
L = \(\frac{X_{L}}{2 \pi f}=\frac{17.32}{2 \times 3.14 \times 50}\) = 0.055 H

Now Z = \(\sqrt{R^{2}+X_{L}^{2}}\)
= \(\sqrt{(10)^{2}+(17.32)^{2}}\) = 20 Ω

Now P_av = l_rms V_rms cos Φ = \(\frac{V_{m}^{2}}{Z}\) × cos Φ
or
Pav = \(\frac{(80)^{2}}{2 \times 20}\) × 0.5 = 160 W

Question 5.
When an alternating voltage of 220 V is applied across a device X, a current of 0.5 A flows through the circuit and Is in phase with the applied voltage. When the same voltage is applied across a device Y, the same current again flows through it, but it leads the voltage by π/2. If element ‘X’ is a pure resistor of 100 ohms,
(a) name the circuit element ‘Y’ and
Answer:
The element Y is a capacitor.

(b) calculate the rms value of current, if rms value of voltage is 141 V.
Answer:
The value of Xc is obtained as below

X_C = \(\frac{V}{I}=\frac{220}{0.5}\) = 440 ohm

Therefore impedance of the circuit
Z = \(\sqrt{R^{2}+X_{C}^{2}}=\sqrt{(100)^{2}+(440)^{2}}\) = 451.2 ohm

Therefore rms value of current V 141
l = \(\frac{V_{r m s}}{Z}=\frac{141}{451.2}\) = 0.3125 A

Question 6.
When an alternating voltage of 220 V is applied across a device X, a current of 0. 5 A flows through the circuit and is in phase with the applied voltage. When the same voltage is applied across a device V, the same current again flows through it, but it lags the voltage by π/2.
(a) Name the devices X and Y.
Answer:
The element X is a resistor and Y is an inductor.

(b) Calculate the current flowing through the circuit when the same voltage is applied across the series combination of the two devices X and Y.
Answer:
Now both R and XL are the same and are given by
R = X_L = \(\frac{220}{0.5}\) = 440 ohm

Hence impedance of the circuit
Z = \(\sqrt{R^{2}+X_{L}^{2}}\)
= \(\sqrt{(440)^{2}+(440)^{2}}\)
= 622.2 ohm

Therefore current flowing through the circuit is
l = \(\frac{V}{Z}\) = \(\frac{220}{622.2}\) = 0.353 A

Question 7.
A 15.0 μF capacitor Is connected to a 220 V, 50 Hz source. Find the capacitive reactance and the current (rms and peak) In the circuit. If the frequency Is doubled, what happens to the capacitive reactance and the current?
Answer:
Given C= 15.0 μF= 15 × 10^-6 F, V= 220 V,
f = 50 HZ, X_C = ? l_m = ?

The capacitive reactance is

Now l_rms = \(\frac{V_{r m s}}{X_{c}}=\frac{220}{212}\) = 1.04 A

Peak value of current
l_m = \(\sqrt{2}\) × lrms = 1.4.1 × 1.04 = 1.47 A

This current oscillates between + 1.47A and – 1.47 A, and is ahead of the voltage by π/2.

If the frequency is doubled, the capacitive reactance is halved and consequently, the current is doubled.

Question 8.
A sinusoidal voltage of peak value 283 V and frequency 50 Hz is applied to a series LCR circuit in which R = 3 Ω, L = 25.48 mH and C = 796 μF. Find
(a) the impedance of the circuit;
(b) the phase difference between the voltage across the source and the current;
(c) the power dissipated in the circuit; and
(d) the power factor.
Answer:
Given V_m = 283 V, f = 50 Hz, R = 3 Ω
L = 25.48 mH, and C = 796 μF.
(a) To find the impedance of the circuit, we first calculate XL and Xc
X_L = 2πfL = 2 × 3.14 × 50 × 25.48 × 10^-3 = 8 Ω
X_C = \(\frac{1}{2πfC}\)
= \(\frac{1}{2 \times 3.14 \times 50 \times 796 \times 10^{-6}}\) = 4 Ω

Therefore impedance of the circuit is
Z = \(\sqrt{R^{2}+\left(X_{\mathrm{L}}-X_{C}\right)^{2}}\)
= \(\sqrt{3^{2}+(8-4)^{2}}\)
= 5 Ω

(b) Phase difference
Φ = tan^-1\(\frac{X_{L}-X_{c}}{R}\) = tan-1 \(\frac{8-4}{3}\) = 53.1°
Since Φ is positive therefore voltage leads current by the above phase.

(c) The power dissipated in the circuit is
P = \(\frac{V_{\mathrm{rms}}^{2}}{Z}=\frac{V_{\mathrm{m}}^{2}}{2 \mathrm{Z}}=\frac{(283)^{2}}{2 \times 5}\) = 8008.9 W
(d) power factor = cos Φ = cos 53.1° = 0.6

Question 9.
A capacitor and a resistor are connected in series with an ac source. If the potential difference across the C, R is 120 V and 90 V respectively, and if rms current of the circuit is 3 A, calculate the (i) impedance and (ii) power factor of the circuit.
Answer:
Given V_C = 120 V, V_R = 90 V, f = 3 A. and R = 90/3 = 30 ohm ,

Effective voltage in the circuit
V = \(\sqrt{V_{C}^{2}+V_{R}^{2}}=\sqrt{(120)^{2}+(90)^{2}}\)= 150 V .
(i) Therefore impedance of the circuit
Z = \(\frac{V}{l}=\frac{150}{3}\) = 50 Ω.

(ii) Now power factor of the circuit is
cos Φ = \(\frac{R}{Z}=\frac{30}{50}\) = 0.6

Question 10.
An inductor 200 mH, a capacitor C, and a resistor 10 ohm are connected in series with 100 V, 50 Hz ac source. If the current and the voltage are in phase with each other, calculate the capacitance of the capacitor.
Answer:
When current and voltage are in phase then X_L = X_C

Question 11.
An ac voltage of 100V, 50 Hz is connected across a 20-ohm resistor and 2 mH inductors in series.
Calculate (i) impedance of the circuit, and
(ii) rms current in the circuit. (NCERT)
Answer:
Given, V = 100 V, f = 50 Hz, R = 20 ohm, L = 2 mH = 2 × 10^-3 H, Z = ?, lrms = ?
Using the relation
(a) Z = \(\sqrt{(R)^{2}+\left(X_{L}\right)^{2}}=\sqrt{(R)^{2}+(2 \pi f L)^{2}}\)
Z = \(\sqrt{(20)^{2}+\left(2 \times 3.14 \times 50 \times 2 \times 10^{-3}\right)^{2}}\)
Z = 20 ohm
(b) lrms= V/Z= 100/20 = 5 A

Question 12.
A light bulb is rated at 100 W for a 220 V supply. Find (a) the resistance of the. bulb; (b) the peak voltage of the source; and (c) the rms current through the bulb. (NCERT)
Answer:
(a) We are given P = 100 W and V = 220 V.
The resistance of the bulb is
R = \(\frac{V^{2}}{P}=\frac{(220)^{2}}{100}\) = 484 Ω

(b) The peak voltage of the source is
Vm = \(\sqrt{2}\)V = \(\sqrt{2}\) × 220 = 311V

(c) Since P = I V, therefore l = P/V= 100/220 = 0.45 A

Question 13.
A pure Inductor of 25.0 mH is connected to a source of 220 V. Find the inductive reactance and rms current in the circuit if the frequency of the source is 50 Hz. (NCERT)
Answer:
The inductive reactance,
X_L = 2 πf L = 2 × 3.14 × 50 × 25 × 10^-3 Ω
= 7.85 ohm

The rms current in the circuit is
l = \(\frac{V}{X_{L}}=\frac{220}{7.85}\) = 28 A

Question 14.
A 100 Ω resistor is connected to a 220 V, 50 Hz ac supply.
(a) What is the rms value of current in the circuit?
(b) What is the net power consumed over a full cycle? (NCERT)
Answer :
Given u_rms = 220 V, f = 50 Hz, l_rms = ?, P = ?
(a) lrms = \(\frac{V_{\mathrm{rms}}}{R}=\frac{220}{100}\) = 2.2 A

(b) Power consumed over one cycle of ac P = V_rms × l_rms = 220 × 2.2 = 484 W

Question 15.
(a) The peak voltage of an ac supply is 300 V. What is the rms voltage?
(b) The rms value of current in an ac circuit is 10 A. What is the peak current? (NCERT)
Answer:
(a) V_m = 300V, V_rms =?

Using Vrms = \(\frac{V_{\mathrm{m}}}{\sqrt{2}}=\frac{300}{\sqrt{2}}\) = 212.16 V

(b) Using
l_m = l_rms × V₂ = 10 × \(\sqrt{2}\) = 14.14 A

Question 16.
A 44 mH inductor is connected to 220 V, 50 Hz ac supply. Determine the rms value of the current in the circuit. (NCERT)
Answer:
Given L = 44 mH = 44 × 10^-3 H, V_rms = 220 V, f = 50Hz,l_rms = ?
Using the relation
l_rms = \(\frac{V_{\text {rms }}}{x_{L}}=\frac{V_{\text {rms }}}{2 \pi f L}=\frac{220}{2 \times 3.14 \times 50 \times 44 \times 10^{-3}}\)
= 15.9 A

Question 17.
A coil of inductance 0.50 H and resistance 100 Ω is connected to a 240 V, 50 Hz ac supply, (a) What is the maximum current in the coil? (b) What Is the time lag between the voltage maximum and the current maximum? (NCERT)
Answer:
Given L = 0.5 H, R = 100 Ω, V_rms = 240 V,
f= 50 Hz, ω = 2πf= 2 × 3.14 × 50 = 314 s^-1 l_m = ?
(a) Now
Z = \(\sqrt{R^{2}+X_{L}^{2}}=\sqrt{(100)^{2}+(0.5 \times 314)^{2}}\)
Z = 186.1 Ω

Therefore
l_m = \(\frac{V_{m}}{Z}=\frac{\sqrt{2} \times V_{\mathrm{rms}}}{Z}=\frac{\sqrt{2} \times 240}{186.1}\)
l_m = 1.82 A

(b) Let Φ be the phase angle by which current lags emf, then
tan Φ = \(\frac{X_{L}}{R}=\frac{0.5 \times 314}{100}\) = 1.571
Φ = 57.5° or Φ = 57.5 × π/180 rad

Therefore timw lag
t = \(\frac{\phi T}{2 \pi}=\frac{57.5 \times \pi}{180 \times 2 \pi \times 50}\) = 3.194 × 10^-3 s

Question 18.
A coil of 0.01-henry Inductance and 1-ohm resistance is connected to 200 volts, 50 Hz ac supply. Find the Impedance of the circuit and time lag between max alternating voltage and current. (NCERT Exemplar)
Answer:
Given L = 0.01 henry, R = 1 ohm,
V_rms = 200V, f = 50Hz, Z = ?, t = ?
We know that
X_L = 2πfL = 2 × 3.14 × 50 × 0.01 = 3.14 ohm
Now
Z = \(\sqrt{R^{2}+X_{\mathrm{L}}^{2}}=\sqrt{(3.14)^{2}+(1)^{2}}\) = 3.3 Ω
Also tan Φ = \(\frac{X_{L}}{R}=\frac{3.14}{1}\)= 3.14
Or
Φ = tan^-1 (3.14)
Or
Φ = 72° or 72 × π/180 rad
Now time lag Δt is
Δt = \(\frac{\phi}{\omega}=\frac{72 \times \pi}{180 \times 2 \pi \times 50}=\frac{1}{250}\) s

Question 19.
An electrical device draws 2 kW power from AC mains (voltage 223 V (rms) = V50,000 V). The current differs (lags) in phase by Φ (tan Φ = – 3/4) as compared to voltage.
Find (i)R,
(ii) X_C – X_L
(iii) lm
Another device has twice the values for R, X_C, X_L. How are the answers affected? (NCERT Exemplar)
Answer:
Given P = 2 kW = 2000 W, V_rms = 223
= \(\sqrt{50,000}\) V, tan Φ = – 3/4, R = ?,X_C – X_L = ?, l_m = ?

(i)
Solving for R we have
R = 20 ohm

(ii) Also X_C – X_L = (-3/4) R = – 15 Ω
Hence lrms =\(\frac{V}{Z}=\frac{223}{25}\) = 9 A
(iii) l_m = \(\sqrt{2}\) × lrms = 1.414 × 9 = 12.6 A

If R, X_C, X_L, are all doubled, tan Φ does not change. Therefore as Z is doubled, the current becomes halved.

Question 20.
An alternating voltage given by V = 140 sin 314 t is connected across a pure resistor of 50 Ω. Find
(a) the frequency of the source.
(b) the rms current through the resistor. (CBSEAI 2012)
Answer:
R = 50 Ω, f = ?, l_rms = ?, V_m = 140 V
Comparing with V = V_m sin 2πft,
we have
2πft = 314 t
or
f = 50 Hz
lrms = \(\frac{V_{r m s}}{R}=\frac{140}{50 \sqrt{2}}\) = 1.98 A

Question 21.
The figure shows a series LCR circuit with L = 5.0 H, C = 80 μF, R = 40 Ω connected to a variable frequency 240 V source. Calculate

(a) The angular frequency of the source drives the circuit at resonance.
(b) The current at the resonating frequency.
(C) The rms potential drops across the capacitor at resonance. (CBSE Delhi 2012)
Answer:
Given L= 5.0 H, C= 80 μF , R = 40 Ω, Vrms = 240 V ω_o = ?, l_rms = ?, V_C = ?
(a)Angutar frequency at resonance
ω0 = \(\sqrt{\frac{1}{L C}}=\sqrt{\frac{1}{5 \times 80 \times 10^{-6}}}\) = 50 s^-1

(b)At resonance Z = R = 4O Ω
Now lrms = \(\frac{V_{\mathrm{rms}}}{\mathrm{Z}}=\frac{240}{40}\) = 6 A

(C) V_C = l_rms × X_C = 6 (50 × 80 × 10^-6) = 1500 V

Question 22.
The figure shows a series LCR circuit connected to a variable frequency 200 V source with L = 50 mH, C = 80 μF and R = 40 Ω.
Determine
(a) the source frequency which derives the circuit in resonance;
(b) the quality factor (Q) of the circuit. (CBSEAI 2014C)

Answer:
(a) Given V = 200 V, L = 50 mH, C = 80 μF, R = 40 Ω
Source frequency at resonance

Question 23.
When an alternating voltage of 220 V is applied across a device X, a current of 0.5 A flows through the circuit and is in phase with the applied voltage. When the same voltage is applied across another device Y, the same current again flows through it, but it leads the voltage by π/2 rattan.
(a) Name the devices X and Y.
(b) Calculate the current flowing In the circuit when the same voltage Is applied across the series combination of the two devices X and Y.
Answer:
(a) The two devices are resistor and capacitor, respectively.

(b) Given l = 0.5 A, V = 220 V, X_L = ?, R = ? , l = ?
Now X_C and R are equal and are given by
X_C = R = \(\frac{220}{0.5}\) = 440 Ω

Hence impedance of the circuit
Z = \(\sqrt{R^{2}+X_{C}^{2}}=\sqrt{2(440)^{2}}\) = 622.25 Ω

Therefore current through the combination is
l = \(\frac{V}{Z}=\frac{220}{622.25}\) = 0.354 A

Question 24.
In the following circuit, calculate (a) the capacitance of the capacitor, if the power factor of the circuit is unity, (b) the Q-factor of this circuit. What is the significance of the Q-factor in a.c. circuit? Given the angular frequency of the a.c. source to be 100 s^-1. Calculate the average power dissipated in the circuit. (CBSE Delhi 2017C)

Answer:
(a) when the power factor is unity the circuit is in resonance, therefore, we have

Quality factor determines the sharpness of tuning at resonance. More the Q factor more the sharpness.

Question 25.
The figure below shows how the reactance of a capacitor varies with frequency.

(a) Use the Information on the graph to calculate the value of capacity of the capacitor.
(b) An inductor of inductance L has the same reactance as the capacitor at 100 Hz. Find the value of L.
(c) Using the same axes, draw a graph of reactance against frequency for the inductor.
(d) If this capacitor and inductor were connected in series to a resistor of 10 Ω, what would be the impedance of the combination at 300 Hz?
Answer:
(a) From the graph we find that for a frequency of 100 Hz the capacitive reactance is 6 ohm, therefore

(b) Now given X_L = X_C at 100 Hz, therefore X_L = 6 ohm

(c) The X_L – f graph is as shown below.

(d) For a frequency of 300 Hz, X_L = 18 ohm and X_C = 2 ohm. If resistance is 10 ohm then the impedance of the combination is

Question 26.
The given graphs (i) and (ii) represent the variation of the opposition offered by the circuit element to the flow of alternating current, with the frequency of the applied emf. Identify the circuit element corresponding to each graph.

A circuit is set up by connecting L= 100 mH, C = 5 μf and R =100 Ω in series. An alternating emf of (150 \(\sqrt{2}\)) volt, (500/π) Hz is applied across this series combination. Calculate the impedance of the circuit. What is the average power dissipated in (a) the resistor, (b) the capacitor, (c) the inductor, and (d) the complete circuit?
Answer:
(a) Resistor and (b) Inductor
Given L = 100 mH = 0.1 H, C = 5μF = 5 × 10^-6F, R=100 Ω,

Average power dissipated in
(a) the resistor P = l²R = (1.5)² × 100 = 225 W
(b) power in inductor is zero.
(c) power in capacitor is zero.
(d) the complete circuit is same as that in a resistor.

Question 27.
The output voltage of an ideal transformer, connected to a 240 V ac mains, is 24 V. When this transformer is used to light a bulb with rating 24 V, 24 W, calculate the current in the primary coil of the circuit.
Answer:

Question 28.
An ac generator consists of a coil of 50 turns and an area of 2.5 m² rotating at an angular speed of 60 rads^-1 in a uniform magnetic field B = 0.2 tesla, between the two fixed pole pieces. The resistance of the circuit including that of the coil is 500 ohm (a) Calculate the maximum current drawn from the generator. (b) What is the flux when the current is zero and (c) Would the generator work if the coil were stationary and instead the pole pieces rotated together with the same speed as above? Give a reason for your answer.
Answer:
Given n = 50, A = 2.5 m², ω = 60 rads^-1, B = 0.2 T, R = 500 ohm, l₀ = ?
(a) The maximum induced emf produced in the coil is
ε₀ = nBAω = 50 × 0.2 × 2.5 × 60 = 1500 V

Therefore maximum current in the circuit is
l₀ = \(\frac{\varepsilon_{0}}{R}=\frac{1500}{500}\) = 3 A

(b) The flux in this case is maximum and is given by Φ = nBA = 50 × 0.2 × 2.5 = 25 Wb

(c) Yes, for a generator to work there should be relative motion between the magnet and the coil.

Question 29.
The primary coil of an ideal step-up transformer has 100 turns and the transformation ratio is also 100. The input voltage and the powers are 220 V and 1100 W respectively. Calculate:
(a) number of turns in the secondary
(b) the current In the primary
(C) the voltage across the secondary
(d) the current in the secondary
(e) power in the secondary
Answer:
Here, N = 100, Transformation ratio = 100
V_p = 220 V, P_p = 1100W
(a) Number of turns in the secondary
N_s = N_p × Transformation ratio
= 100 × 100 = 10,000

(b) Current in the primary
l_p = \(\frac{P_{p}}{V_{p}}=\frac{1100}{220}\) = 5 A

(C) Voltage across the secondary V_s = V_p × transformation ratio
= 220 × 1oo = 22000 V

(d) Current in the secondary
l_s = \(\frac{V_{p} l_{p}}{V_{s}}=\frac{220 \times 5}{22000}\) = 0.05 A

(e) Power in the secondary = power in the primary (ideal transformer) = 1100 W

Question 30.
Calculate the current drawn by the primary of a transformer which steps down 200 V to 20 V to operate a device of resistance 20 Q. Assume the efficiency of the transformer to be 80 %.
Answer:

Question 31.
The primary of a transformer has 200 turns and the secondary has 1000 turns. If the power output from the transformer at 1000 V is 9 kW, calculate
(a) The primary voltage and
(b) The heat loss in the primary coil if the resistance of the primary is 0.2 Ω and the efficiency of the transformer is 90%.
Answer:

Question 32.
A power transmission line feeds input power at 2300 V to a step-down transformer with its primary windings having 4000 turns. What should be the number of turns in the secondary In order to get output power at 230 V? (NCERT)
Answer:

Question 33.
A small town with a demand of 800 kW of electric power at 220 V situated 15 km away from an electric plant generating power at 440 V The resistance of the two wirelines carrying power is 0.5 Ω per km. The town gets power from the line through a 4000 – 220 V step-down transformer at a sub-station in the town.
(a) Estimate the line power loss in the form of heat.
(b) How much power must the plant supply, assuming their negligible power loss due to leakage?
(c) Characterise the step-up transformer at the plant. (NCERT)
Answer:
Electric power required P = 800 kW = 800 × 10³ W
Voltage required V0 = 220 V

Distance of the power station
d = 15km = 15 × 10³m

Resistance per kilometre = 0.5 ohm per km
Total resistance R = 0.5 × 2 × 15 = 15 ohm

Input voltage V_i = 440 V

Primary voltage of transformer ε_p = 4000 V
Secondary voltage of transformer ε_s = 220 V
(a) Rms value of current in the two wire line

Therefore power loss along the line
= l^2_rmsR = (200)² × 15 = 600 kW

(b) Assuming negligible loss due to leakage Total power supply = power demand of town + power loss along the line
P = 800 kW + 600 kW = 1400 kW

(c) Voltage drop on the line = 200 × 15 = 3000 V
Hence voltage at the generation station
V= 4000 + 3000 = 7000 V

Therefore the step-up transformer at the plant is 440 V – 7000 V.

Question 34.
A 60 W load is connected to the secondary of a transformer whose primary draws line voltage. If a current of 0.54 A flows in the load, what is the current in the primary coil? Comment on the type of transformer being used. (NCERT Exemplar)
Answer:
Given P_s = 60 W, l_s = 0.54 A
We know that P=V I, therefore we have V_s = P_s/l_s = 60 /0.54 = 110 V

Therefore the transformer is a step-down transformer, whose transformation ratio is 1/2
Therefore
l_p = 1/2 × l_s = 1/2 × 0.54 = 0.27 A