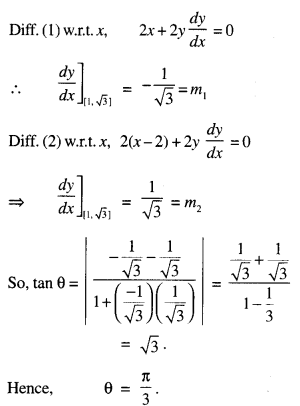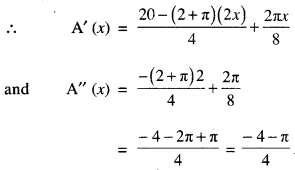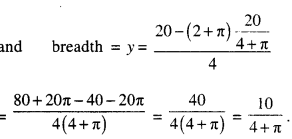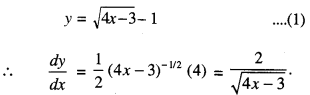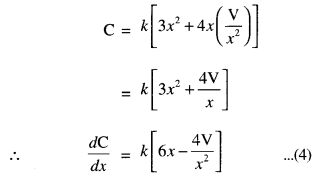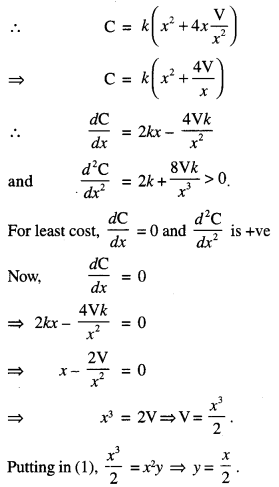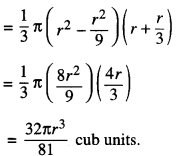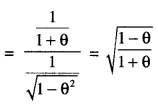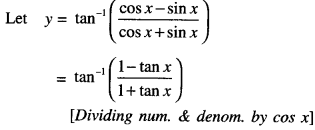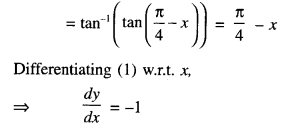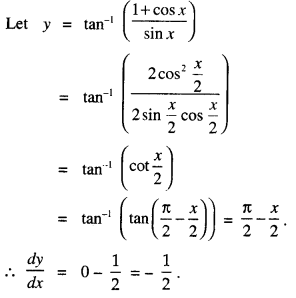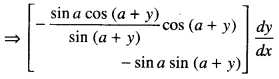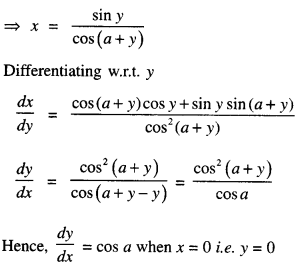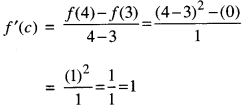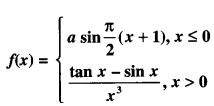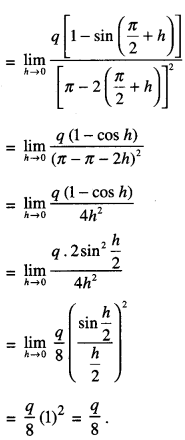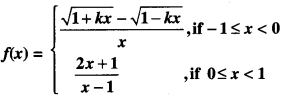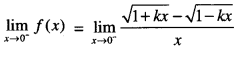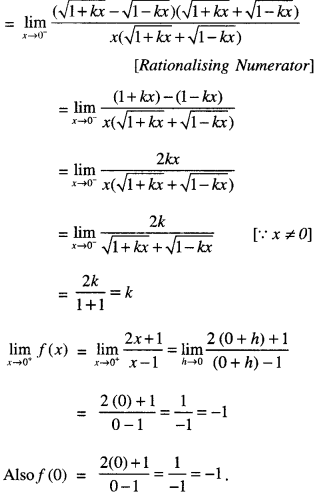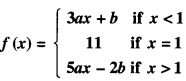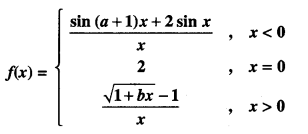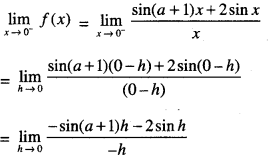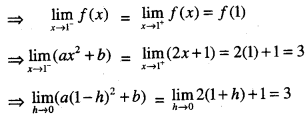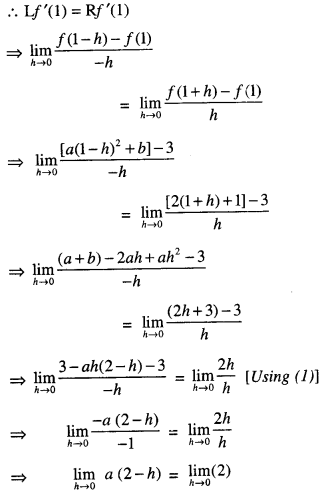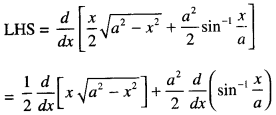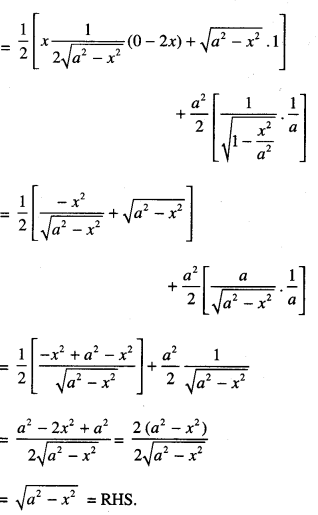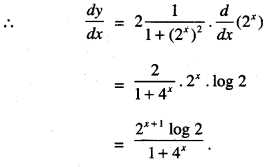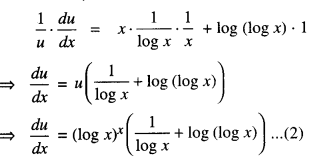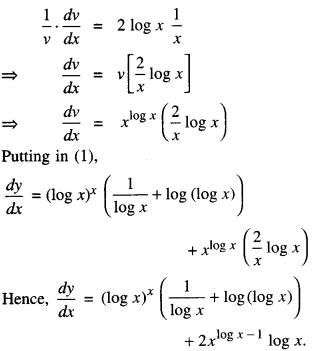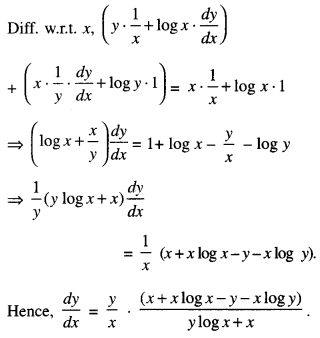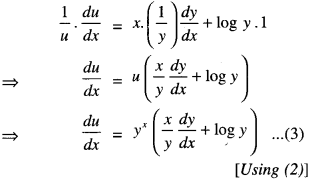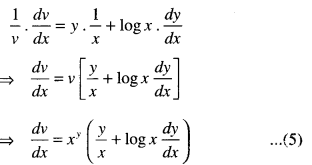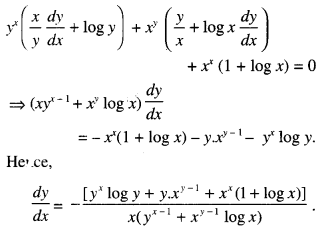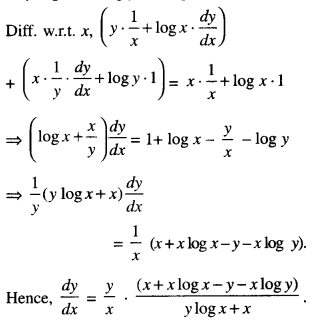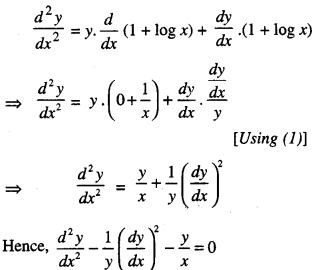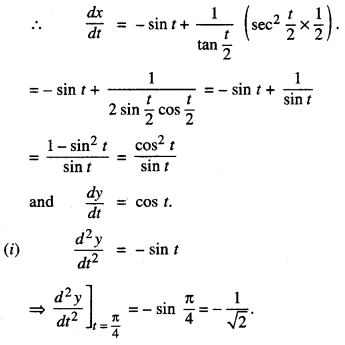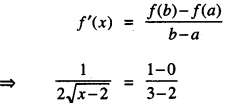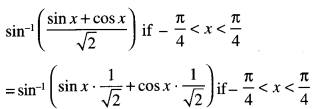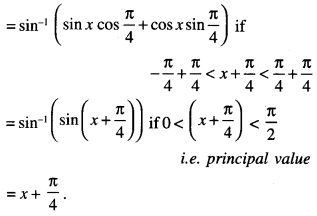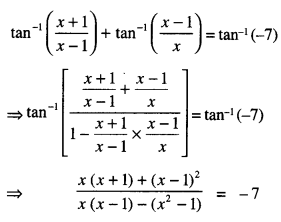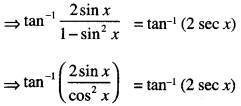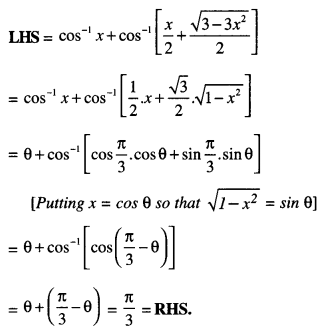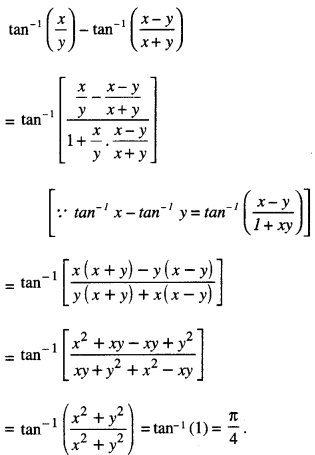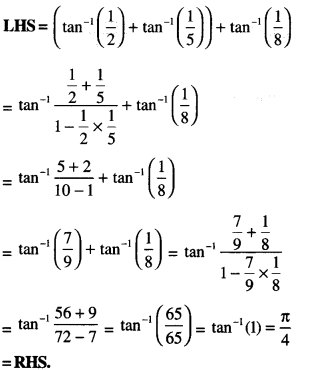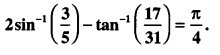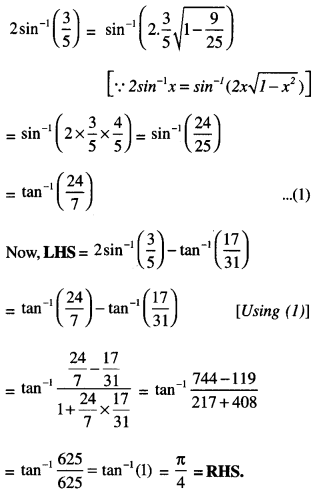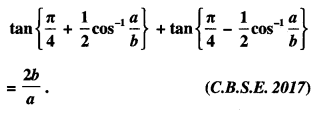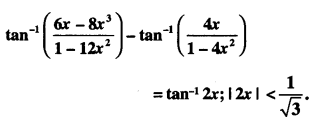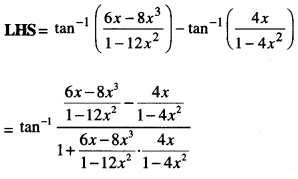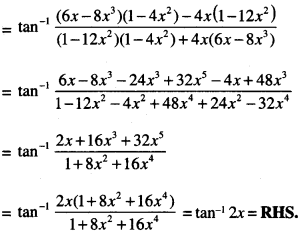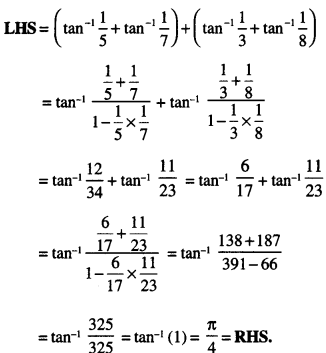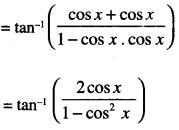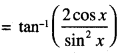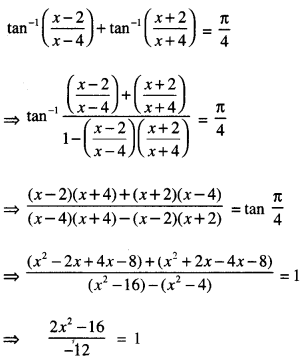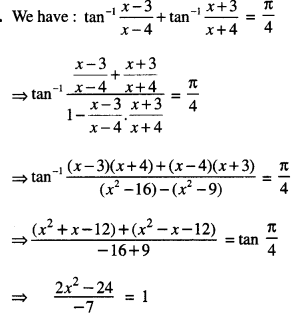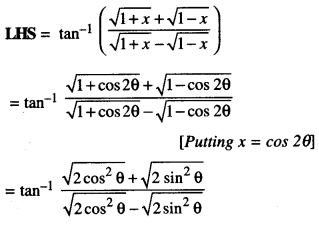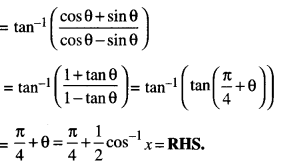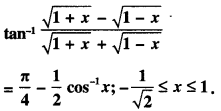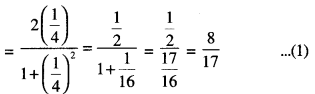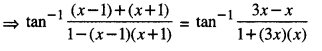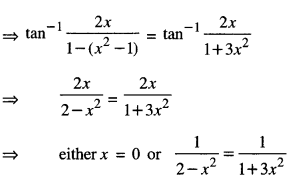CBSE Class 12

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 7 Integrals. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 7 Important Extra Questions Integrals

Integrals Important Extra Questions Very Short Answer Type

Question 1.
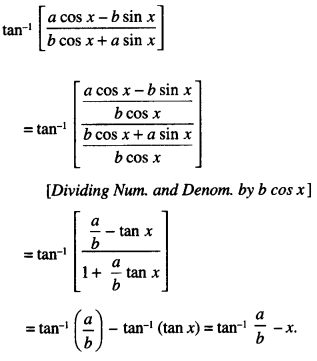
Find \(\int \frac{3+3 \cos x}{x+\sin x} d x\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int \frac{3+3 \cos x}{x+\sin x} d x\) = 3 log lx + sin xl + c.
[∵ Num. = \(\frac{d}{d x}\) denom.]

Question 2.
Find : ∫(cos² 2x – sin² 2x)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = ∫cos 4x dx = \(\frac{\sin 4 x}{4}\)+ c.

Question 3.
Find : ∫ \(\frac{d x}{\sqrt{5-4 x-2 x^{2}}}\)   (C.B.S.E. Outside Delhi 2019)
Solution:

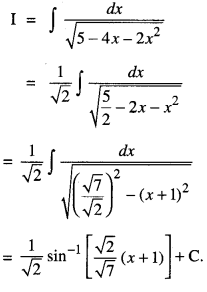
Question 4.
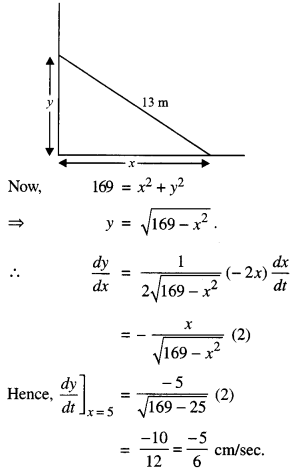
Evaluate ∫ \(\frac{x^{3}-1}{x^{2}}\) dx (N.C.E.R.T. C.B.S.E. 2010C)
Solution:

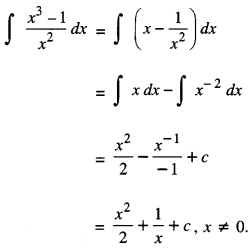
Question 5.
Find : \(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin x \cos x} d x\) (A.I.C.B.S.E. 2017)
Solution:

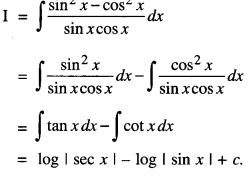
Question 6.
Write the value of \(\int \frac{d x}{x^{2}+16}\)
Solution:

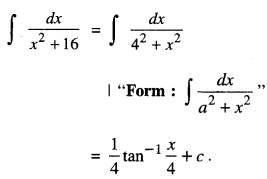
Question 7.
Evaluate: ∫ (x³ + 1)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int_{-2}^{2} x^{3} d x+\int_{-2}^{2} 1 \cdot d x\) = I₁
⇒ 0 + \([x]_{-2}^{2}\) [∵ I₁ is an odd function] = 2 – (-2) = 4.
⇒ 2 – (-2) = 4.

Question 8.
Evaluate: \(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx. (C.B.S.E. 2014)
Solution:
\(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx
\(\int_{0}^{\pi / 2}\)e^x (-cos x + sinx)dx
|“Form: ∫e^x (f(x) + f'(x) dx”
= \(\left[e^{x}(-\cos x)\right]_{0}^{\pi / 2}\)
= -e ^π/2cos\(\frac{\pi}{2}\) + e⁰ cos 0
= -e ^π/2 (0) + (1) (1)
= -0 + 1 = 1

Question 9.
Evaluate: \(\int_{0}^{2} \sqrt{4-x^{2}} d x\). (A.I.C.B.S.E. 2014)
Solution:

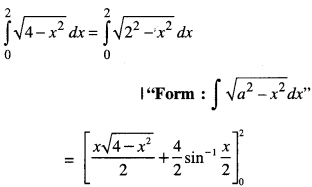
= [0 + 2 sin^-1(1)] – [0 + 0]
= 2sin^-1(1)= 2(π/2) = π

Question 10.
Evaluate : If f(x) = \(\int_{0}^{x}\) t sin t dt, then write the value of f’ (x). (A.I. C.B.S.E. 2014)
Solution:
We have : f(x) = \(\int_{0}^{x}\) t sin t dt.
f'(x) = x sin x. \(\frac{d }{d x}\) (x) – 0
[Property XII ; Leibnitz’s Rule]
= x sin x . (1)
= x sin x.

Question 11.
Prove that: \(\int_{0}^{2a}\) f(x)dx = \(\int_{0}^{2a}\) f(2a-x)dx. o o
Solution:
Put x = 2a – t so that dx = – dt.
When x = 0, t – 2a. When x = 2a, t – 0.
\(\int_{0}^{2a}\) f(x)dx = \(\int_{2a}^{0}\) f(2a-t)(-dt)
=\(\int_{2a}^{0}\) f{2a-t)dt = \(\int_{0}^{2a}\) f(2a-t)dt o
[Property II]
= \(\int_{0}^{2a}\) (2a – x) dx, [Property I]
which is true.

Integrals Important Extra Questions Short Answer Type

Question 1.
Evaluate :
\(\int \frac{\cos 2 x+2 \sin ^{2} x}{\cos ^{2} x} d x\) (C.B.S.E)
Solution:

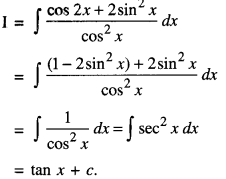
Question 2.
Find : \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Solution:
I = \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Put tan x = t so that sec² x dx = dt.
∴ I = \(\int \frac{d t}{\sqrt{t^{2}+2^{2}}}\)
= log |t + \(\sqrt{t^{2}+4}\)| + C
= log |tan x + \(\sqrt{tan^{2}+4}\)| + C

Question 3.
Find : \(\int \sqrt{1-\sin 2 x} d x, \frac{\pi}{4}<x<\frac{\pi}{2}\)
Solution:

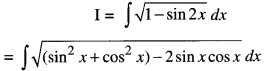
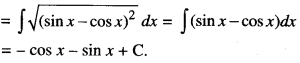
Question 4.
Find ∫sinx . log cos x dx (C.B.S.E 2019 C)
Solution:
∫sinx . log cos x dx
Put cox x = t
so that – sin x dx = dt
i.e., sin x dx = – dt.
∴ I = -∫log t.1dt
= -[ log t.t – ∫ 1/t. t dt ]
[Integrating by parts]
= – [t log t – t] + C = f(1 – log t) + C
= cos x (1 – log (cos x)) + C.

Question 5.
Find : \(\int \frac{\left(x^{2}+\sin ^{2} x\right) \sec ^{2} x}{1+x^{2}} d x\) (CBSE Sample Paper 2018-19)
Solution:

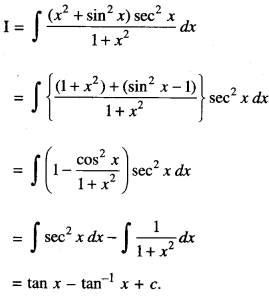
Question 6.
Evaluate \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\) (CBSE Sample Paper 2018-19)
Solution:
I = \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\)

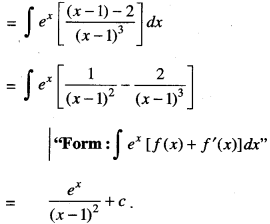
Question 7.
Find ∫sin^-1 (2x)dx
Solution:

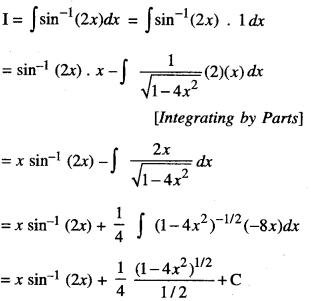
Question 8.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx.
Solution:
Here, f(x)=( 1-x²) sin x cos² x.
f(x) = (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 9.
Evaluate : \(\int_{-1}^{2} \frac{|x|}{x} d x\) dx.
Solution:

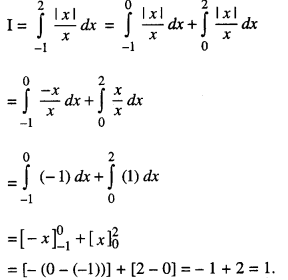
Question 10.
Find \(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)   (C.B.S.E. 2018 C)
Solution:
\(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)
= 3∫sce² x dx – 5∫sec x tan x dx
= 3tan x – 5sec x + C

Question 11.
Find :
\(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:
Let I = \(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)
Put tan³ x = t
so that 3 tan² x sec² x dx = dt
i.e tan² x sec²x dx = \(\frac{d t}{3}\)

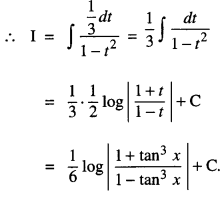
Question 12.
Find : ∫ sin x .log cos x dx.   (CBSE 2019C)
Solution:
I = ∫ sin x .log cos x dx.
Put cos x = t
i.e. sinx dx = -dt
∴ I = – ∫log t.1 dt
= -[logt.t – ∫1/t . t. dt]
[Integrating by parts]
= – [t log t – t] + C
= t(1 – log t) + C
= cos x (1 – log (cos JC)) + C.

Question 13.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx   (C.B.S.E. 2019 (Delhi))
Solution:
Here, f(x) = (1 – x²) sin x cos² x
∴ f(-x) – (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 14.
Evaluate \(\int_{-1}^{2} \frac{|x|}{x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

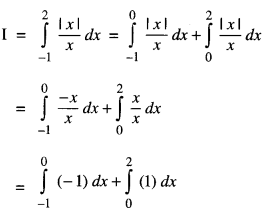
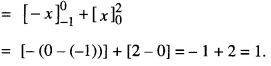
Question 15.
Find : \(\int_{-\pi / 4}^{0} \frac{1+\tan x}{1-\tan x} d x\)
Solution:

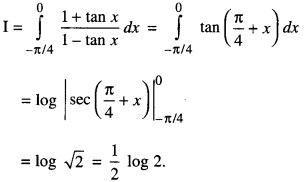
Integrals Important Extra Questions Long Answer Type 1

Question 1.
Evaluate : \(\int \frac{\sin ^{6} x+\cos ^{6} x}{\sin ^{2} x \cos ^{2} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

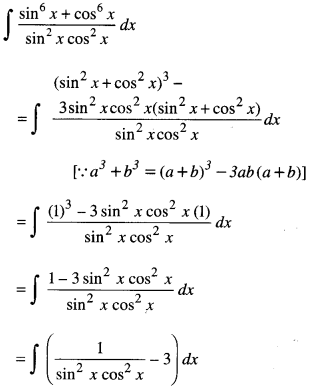
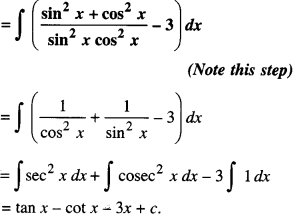
Question 2.
Integrate the function \(\frac{\cos (x+a)}{\sin (x+b)}\) w.r.t. x. (C.B.S.E. 2019 (Delhi))
Solution:

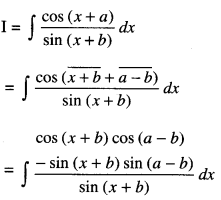
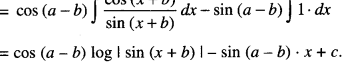
Question 3.
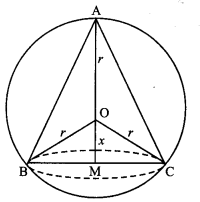
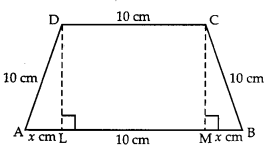
Evaluate : ∫ x² tan^-1 x dx. (C.B.S.E. (F) 2012)
Solution:

Question 4.
Find : ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx (N.C.E.R.T.; A.I.C.B.S.E. 2010 C)
Solution:
Let ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx
= ∫ log(log x)dx + ∫\(\frac{1}{(\log x)^{2}}\) dx …… (1)
Let I = I₁ + I₂
Now I₁ = ∫ log (log x) dx
=∫ log (log x) 1 dx
= log (log x).x – ∫ \(\frac{1}{\log x \cdot x}\)x.dx
(Integrating by parts)
= xlog(logx) – ∫ \(\frac{1}{\log x}\)dx ……….. (2)
Let I₁ = I₃ + I₄

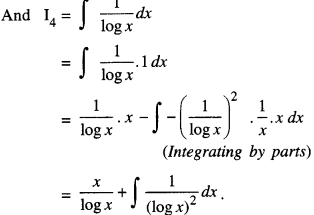
Putting in (2),
I₁ = x log (x) – \(\frac{x}{\log x}-\int \frac{1}{(\log x)^{2}}\) dx
Putting in (1),
I = x log (log x)

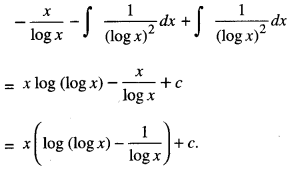
Question 5.
Integrate : ∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx   (N.C.E.R.T.)
Solution:
∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx
[From ∫ e^xf(x) + f'(x) ]dx”]
= ∫ e^x tan^-1 x dx +∫ e^x \(\frac{1}{1+x^{2}}\) ) dx
= ∫ tan^-1 x. e^x dx +∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
= tan^-1 x. e^x – ∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
+∫ \(\frac{1}{1+x^{2}}\) ) e^xdx
(integrating first integral by parts)
= e^x tan^-1x + c.

Question 6.
Integrate : \(\int e^{x}\left(\frac{x^{2}+1}{(x+1)^{2}}\right) d x\) (N.C.E.R.T)
Solution:

Question 7.
Find \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\) (C.B.S.E. 2018)
Solution:
Let i = \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\)
Put sin x = t so that cos x dx = dt.

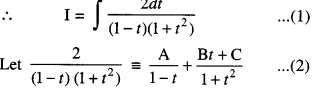
⇒ 2 ≡ A(1 + t²) + (Bt + C) (1 – t)
2 ≡ (A – B)t² + (B – C)t + (A + C).
Comparing coeffs. of t²,
A-B = 0
⇒ A = B
Comparing coeffs. of t,
0 = B – C
⇒ B = C.
Comparing constant terms,
2 = A + C.
Thus, A = B = C = 1.
∴ From (2),
\(\frac{2}{(1-t)\left(1+t^{2}\right)}=\frac{1}{1-t}+\frac{t+1}{t^{2}+1}\)
∴ From (1)

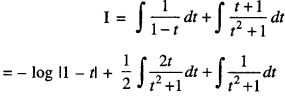
= – log |1 — t| + \(\frac { 1 }{ 2 }\) log |t² + 1| + tan^-1 t + c
= – log |1 — t| + \(\frac { 1 }{ 2 }\) log (t² + 1) + tan^-1t + c
[∵ t² ≥ 0 ⇒ t² + 1 > 0 ∴ |t² + |1 = t² + 1]
= – log |1 – sin x| + \(\frac { 1 }{ 2 }\) log (sin² x + 1) + tan^-1 (sin x) + c
= – log (1 – sin x) + \(\frac { 1 }{ 2 }\) log (1 + sin²x)
+ tan^-1 |sin x| + c.
[∵’ 1 – sin x ≥ 0 |1 – sin x| = 1 – sin x]

Question 8.
Find : \(\int \frac{3 x+5}{x^{2}+3 x-18} d x\) (C.B.S.E. 2019)
Solution:
Let 3x + 5 = A(2x + 3) + B.
Comparing,
2A = 3, 3A + B = 5

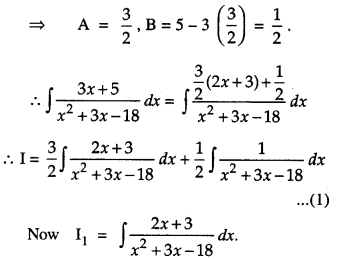
Put x2 + 3x – 18 – t
so that (2x + 3 )dx = dt.
∴ I₁ = \(\int \frac{d t}{t}\) = log |t|
= log + | x² + 3x – 18 |

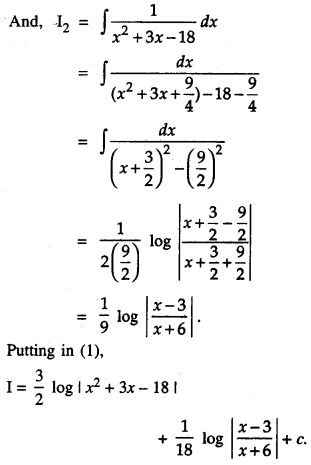
Question 9.
Find: \(\int \frac{\cos x}{(1+\sin x)(2+\sin x)} d x\) 2019C)
Solution:

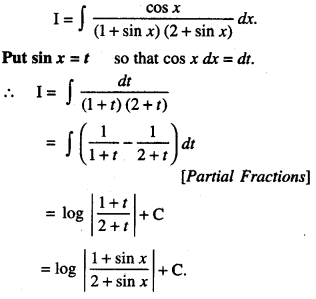
Question 10.
Find: \(\int \frac{x^{4}+1}{2\left(x^{2}+1\right)^{2}} d x\) (C.B.S.E. Sample Paper 2018-19)
Solution:

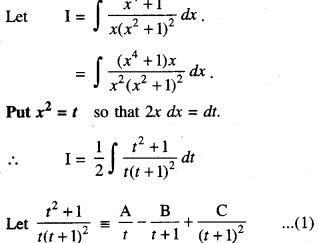
⇒ t² + 1 ≡ A(t + 1)² + Bdt + 1) + Ct …(2)
Comparing coeffs. of like terms, we get :
A = 1, B = 0 and C = – 2.
Putting in (1),

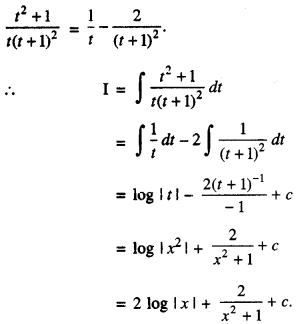
Question 11.
Evaluate : \(\int \frac{x+2}{\sqrt{x^{2}+5 x+6}} d x\) (A.I.C.B.S.E. 2014)
Solution:

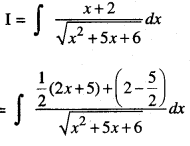
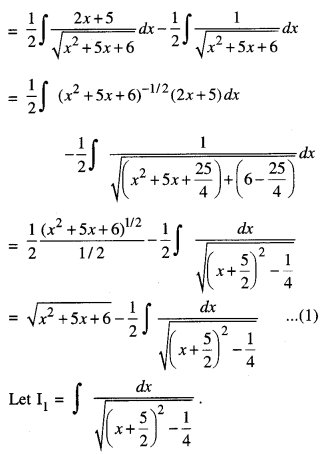
Question 12.
Evaluate : \(\int \frac{2 x+5}{\sqrt{7-6 x-x^{2}}} d x\)
Solution:

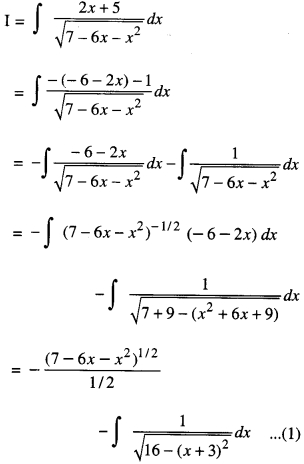
Question 13.
Evaluate : \(\int \frac{d x}{5+4 \cos x}\)
Solution:
I = \(\int \frac{d x}{5+4 \cos x}\)
Put cos x = \(\frac{1-t^{2}}{1+t^{2}}\)
where t = tan \(\frac { x }{ 2 }\) so that dt = \(\frac { 1 }{ 2 }\) sec² \(\frac { x }{ 2 }\) dx
i.e dt = \(\frac { 1 }{ 2 }\)( 1+ tan²\(\frac { x }{ 2 }\))dx
i.e. dt = \(\frac { 1 }{ 2 }\) (1 + t2) dx i.e. dx = \(\frac{2 d t}{1+t^{2}}\)

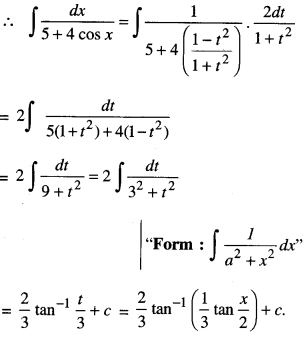
Question 14.
Evaluate : \(\int \frac{d x}{x\left(x^{3}+1\right)}\) (A.I. C.B.S.E 2013)
Solution:
I = \(\int \frac{d x}{x\left(x^{3}+1\right)}=\int \frac{x^{2} d x}{x^{3}\left(x^{3}+1\right)}\)
[Multiplying numerator and denominator by x²]
Put x³ = t so that 3x² dx = dt
i.e , x² dx = \(\frac { 1 }{ 3 }\) dt

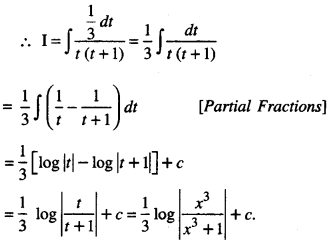
Question 15.
Evaluate : \(\int_{0}^{2} e^{x} d x\) as the limit of a sum. (N.C.E.R.T.)
Solution:
Here f(x) = e^x ; a = 0, b = 2.
∴ f(a) -f(0) = e° = 1
f(a + h) =f(0 + h) = e^h
f(a + 2h) =f(0 + 2h) = e^2h, …….,

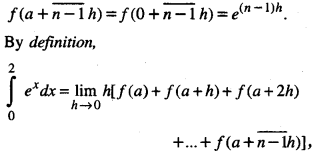
where nh = b – a = 2 – 0 = 2
= \(\lim _{h \rightarrow 0}\) h[1 + e^h +e^2h +… + e^(n-1)hh]
= \(\lim _{h \rightarrow 0} h \frac{1 \cdot\left(e^{n h}-1\right)}{e^{h}-1}\)

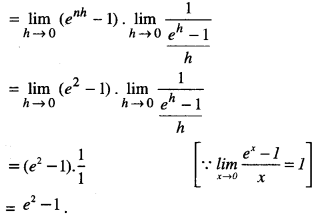
Question 16.
Evaluate: \(\int_{-1}^{2}\) (e^3x + 7x – 5)dx as a limit of sums. (A.I.C.B.S.E. 2015)
Solution:
Here f(x) = e^3x + 7x – 5 ; a = – 1, b = 2.
f (a) = f(- 1) = e^-3 – 7 – 5 = e^-3 – 12
f (a + h) = f(-1 + h)
= e^-3(-1 + h) + 1 (-1 + h)-5

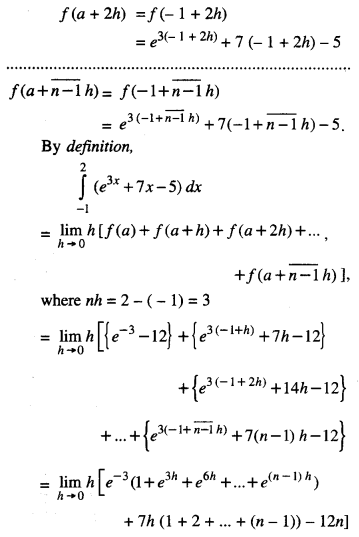
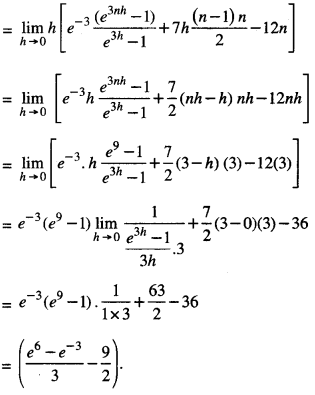
Question 17.
Evaluate: \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\). (N.C.E.R.T.)
Solution:
Let I = \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\)
Put x⁵ = t so that 5x⁴ dx = dt.
When x = – 1, t = – 1. When x = 1, t= 1.

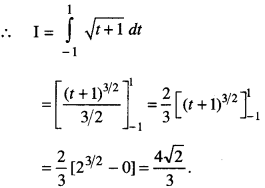
Question 18.
Prove that:
\(\int_{0}^{a} f(x)=\int_{0}^{a} f(a-x) d x\) , hence evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E 2019C)
Solution:
(i) Put x = a – y so that dx = -dy.
When x = 0, y = a. When x = a, y = 0.
∴ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – y)(-dy)
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f{a-x)dx.

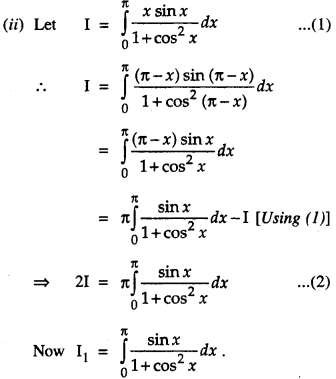
Put cos x = t
so that – sin x dx = dt
i.e. sin x dx = -dt.
When x = 0, t – cos 0=1.
When x = π, t – cos π = -1.

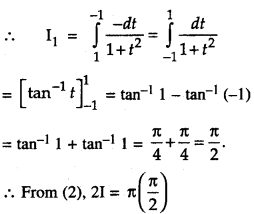
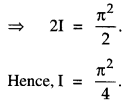
Question 19.
Evaluate : \(\int_{-1}^{2}\) |x³ – x | dx   (N.C.E.R.T.; C.B.S.E. 2016; A.I.C.B.S.E. 2012)
Solution:

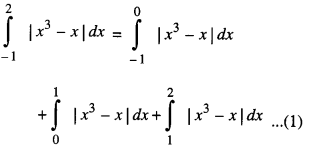
On [- 1, 0], x³ – x ≥ 0
⇒ | x³ – x | = x³ – x;
On [0, 1], x³ – x ≤ 0
⇒ | x³ – x | = -(x³ – x) = x – x³
On [1, 2], x³ – x > 0
⇒ | x³ – x | = x³ – x

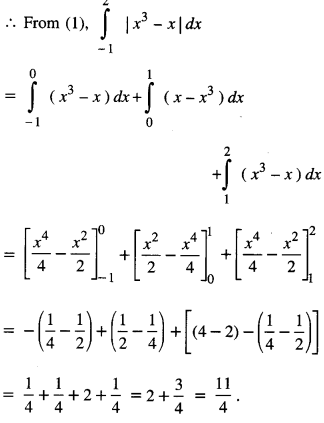
Question 20.
Solve the differential equation:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx.
Solution:
The given differential equation is:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx

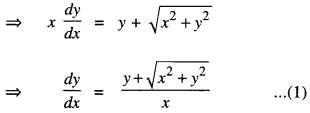
Put y = vx, so that \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
∴(1) becomes:



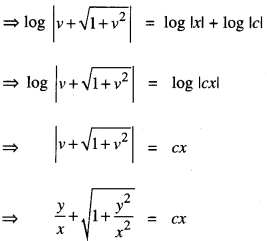
Which is the reqd. solution.

Question 21.
Evaluate : \(\int_{-1}^{1} \frac{x+|x|+1}{x^{2}+2|x|+1} d x\) (CB.S.E. Sample Paper 2018 – 19)
Solution:

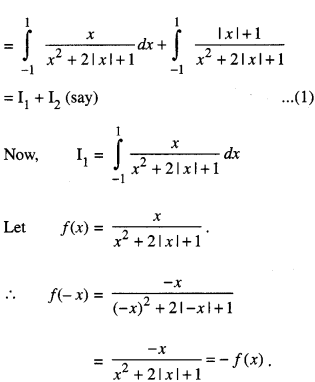
Thus f(-x) = -f(x)
⇒ f(x) is an odd function
∴ I₁ = 0 …… (2)


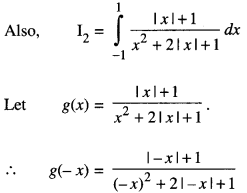
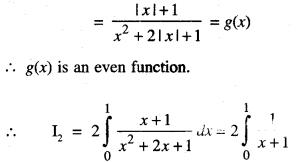
= 2 [log |x + 1|]\(\text { ] }_{0}^{1}\)
= 2 [log 2 – log 1]
= 2 [log 2-0]
= 2 log 2 …(3)
∴ From (1), (2) and (3), we get:
I = 2 log 2.

Question 22.
Find : \(\int \frac{4}{(x-2)\left(x^{2}+4\right)} d x\) (C.B.S.E. 2018 C)
Solution:
\(\frac{4}{(x-2)\left(x^{2}+4\right)} \equiv \frac{\mathrm{A}}{x-2}+\frac{\mathrm{B} x+\mathrm{C}}{x^{2}+4}\)
4 ≡ A(x² + 4) + (Bx + C)(x-2)
By comparison,
A = \(\frac { 1 }{ 2 }\), B = –\(\frac { 1 }{ 2 }\)
and C = 1.

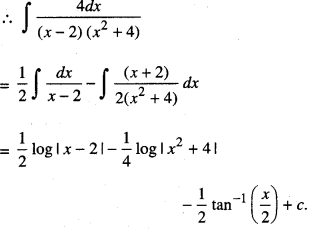
Integrals Important Extra Questions Long Answer Type 2

Question 1.
Evaluate : \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Solution:
Let I = \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Put tan^-1 x = t i.e, x = tan t
So that \(\frac{1}{1+x^{2}} d x\) = dt

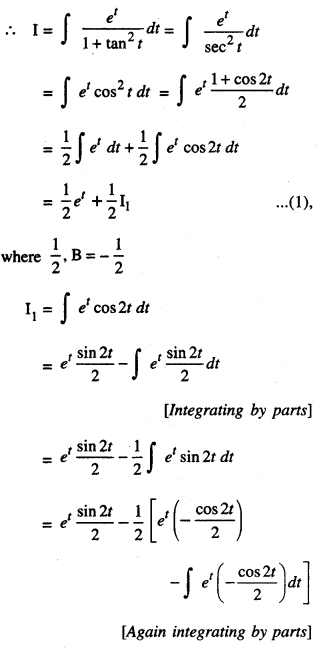
Question 2.
Integrate : \(\int \frac{x^{3}+x}{x^{4}-9} d x\)
Solution:

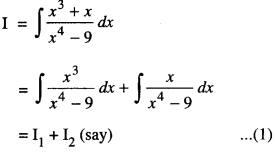
Now I₁ = \(\int \frac{x^{3}}{x^{4}-9} d x\)
Put x⁴ – 9 = t so that 4x³ dx – dt
i.e x³dx = \(\frac{d t}{4}\)

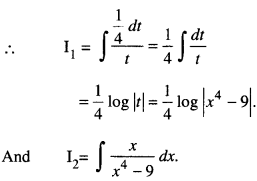
Put x² = u so that 2x dx = du
i.e, xdx = \(\frac{1}{2}\) du
Putting the values of Ij and I2 in (1), we get:

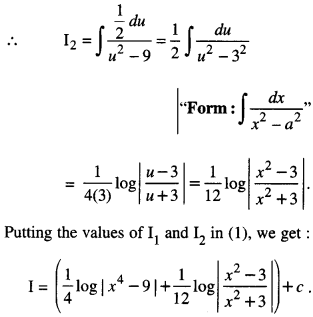
Question 3.
Find : \(\int \frac{\cos \theta}{\left(4+\sin ^{2} \theta\right)\left(5-4 \cos ^{2} \theta\right)} d \theta\) (A.I.C.B.S.E. 2017)
Solution:

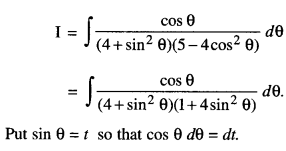
Question 4.
Evaluate : \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Solution:
I = \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Put sin² x = t so that 2 sin x cos x dx = dt
i.e. sin 2x dx = dt.

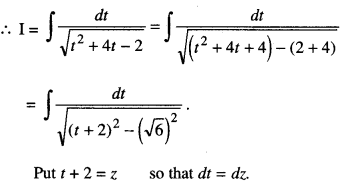
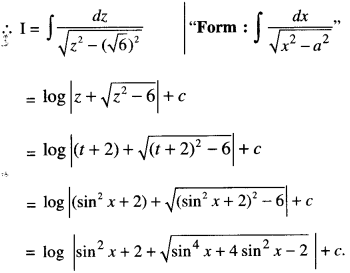
Question 5.
Evaluate : \(\int \frac{x^{2}-1}{x^{4}+1} d x\)
Solution:

Question 6.
Evaluate: \(\int(\sqrt{\tan x}+\sqrt{\cot x}) d x\) (N.C.E.R.T.; A.I.C.B.S.E. 2014; C.B.S.E. 2010S)
Solution:

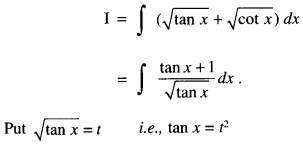
so that sec2 x dx = 2t dt
i.e., (1 + tan² x) dx = 2t dt
⇒ (1 + f) dx = 21 dt

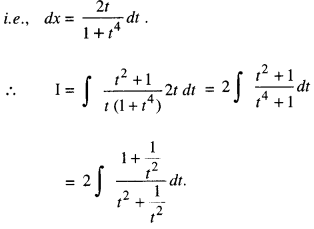
[Dividing Num.. & Denom. by t²]
Put t – \(\frac { 1 }{ t }\)= y so that (1 + \(\frac{1}{t^{2}}\) )dt = dy
Also t² – 2 + \(\frac{1}{t^{2}}\) = y²
t² + \(\frac{1}{t^{2}}\) = y² + 2

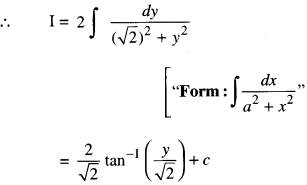
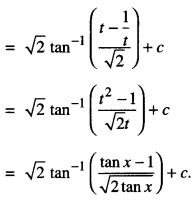
Question 7.
Evaluate \(\int_{0}^{\pi / 2} \frac{x+\sin x}{1+\cos x} d x\) (A.I.C.B.S.E. 2011)
Solution:


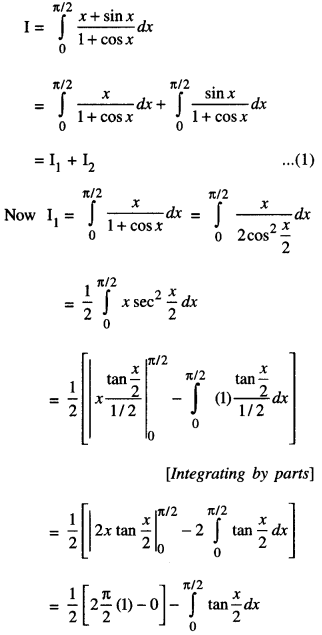
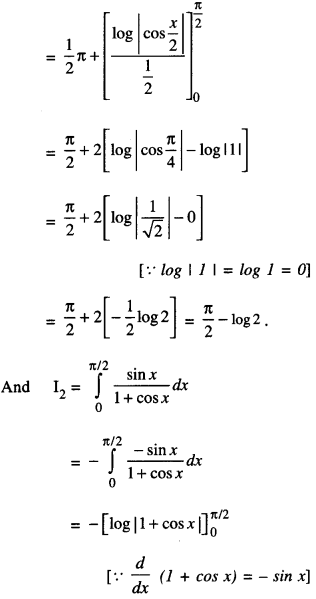
= – [log|1+0|] – [log|1+1|]
= – [0-log2] = log 2
[log|1| = log I = 0]
From (1), I = (\(\frac{\pi}{2}\)– log 2) + log 2 = \(\frac{\pi}{2}\)

Question 8.
Evaluate :
\(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\) (C.B.S.E. 2016)
Solution:
Let I = \(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\)
Put \(\frac{\pi}{4}\) + x = t
x = t – \(\frac{\pi}{4}\) so that dx = dt
when x = 0, t = \(\frac{\pi}{4}\)
when x = π, t = \(\frac{5\pi}{4}\)

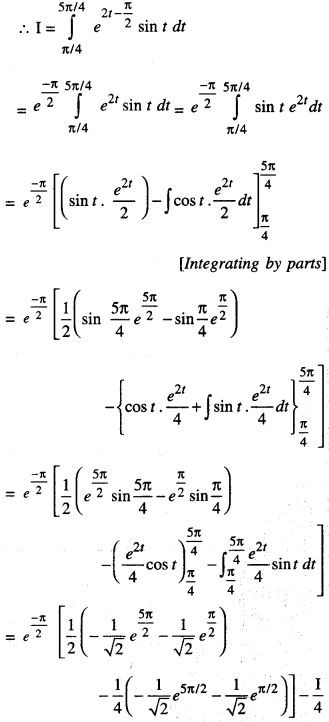
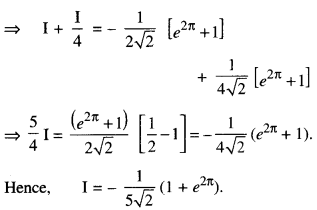
Question 9.
Evaluate : \(\int_{1}^{3}\) (x² + 3x + e^x )dx, as the limit of the sum. (C.B.S.E. 2018)
Solution:
Let f (x) = x² + 3x + e^x
f(x) = f(1)
= 1² + 3(1) + e¹ = 4 + e
f(a + h) = f(1 + h.)
= (1+h)² + 3(1+h) + e^1+h
= 4 + 5 h + h² + e^1+h
f(a + 2h) = f(1 + 2h)
= (1 +2h)² + 3(1 +2h) + e^1+2h
= 4 + 10h+ 4h² + e^1+2h

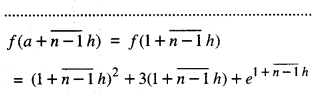
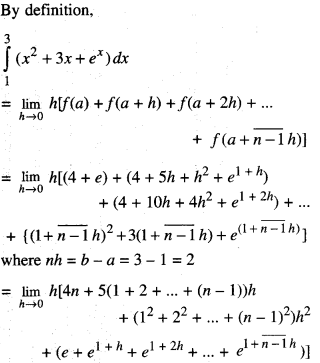
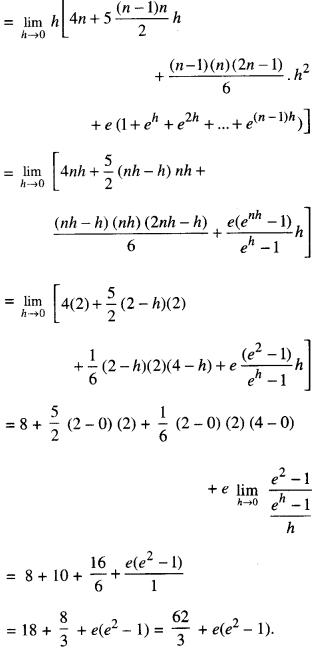
Question 10.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x}{\sin x+\cos x} d x\)
Solution:

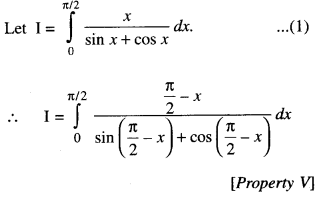
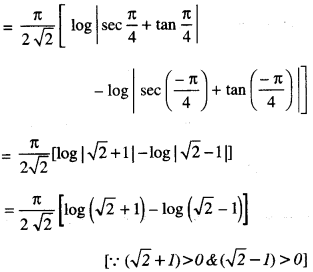
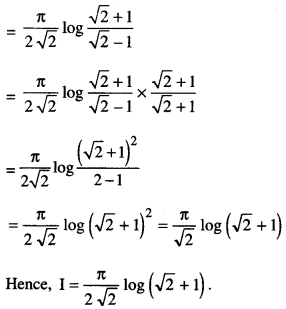
Question 11.
Evaluate : \(\int_{0}^{\pi / 2} \frac{\cos ^{2} x}{\cos ^{2} x+4 \sin ^{2} x} d x\)
Solution:


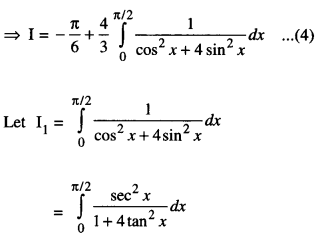
[Dividing Num. and Denom. by cos² x]
Put tan x = t so that sec² x dx = dt.
When x = \(\frac{\pi}{2}\), t = tan \(\frac{\pi}{2}\) → ∞

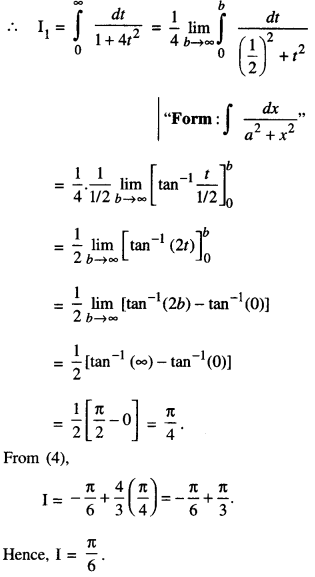
Question 12.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2017; A.I.C.B.S.E. 2013, 12)
Solution:

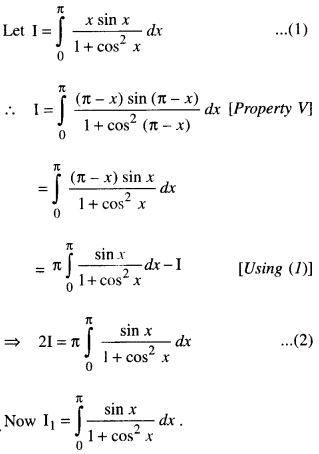
Put cos x = t so that – sin x dx = dt
i.e. sin x dx = – dt.
When x = 0, t = cos 0 = 1.
When x = π, t = cos π = – 1.

Question 13.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2018)
Solution:

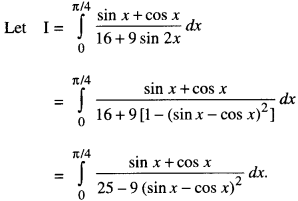
Put sin x – cos x = t
so that (cos x + sin x) dx = dt.
When x = 0, t = 0 – 1 = -1.

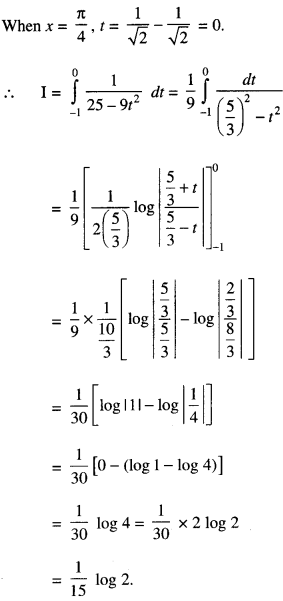
Question 14.
Evaluate \(\int_{0}^{3 / 2}|x \sin \pi x| d x\) (C.B.S.E. 2017)
Solution:

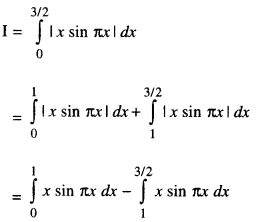
In (0, 1), x sin πx is +ve
⇒ | x sin πx | = x sin πx.
In (0, 3/2), x sin πx is +ve
⇒ | x sin πx | = -x sin πx.

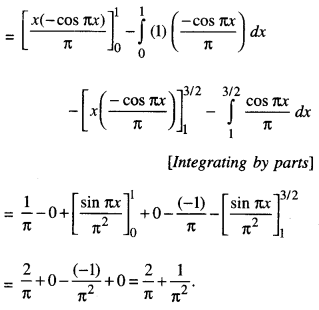
Question 15.
\(\int_{0}^{4}\) |x| + |x-2| + |x-4|)dx (C.B.S.E. 2013)
Solution:
By definition,

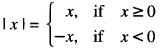
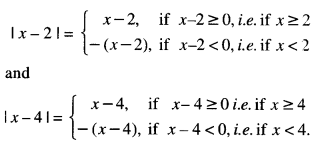
Now, \(\int_{0}^{4}\) (| x | + | x – 2| + | x – 4|) dx
= \(\int_{0}^{4}\) (|x| + |x-2| + |x-4|)dx
\(\int_{0}^{4}\) (| x | + | x – 2| + |x – 4| ) dx
= \(\int_{0}^{4}\) [x + (x-2)}-(x-4)]dx
= \(\int_{0}^{4}\) [(-x +6) dx + = \(\int_{0}^{4}\) (x+2)dx

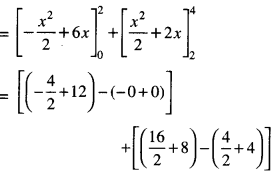
= 10 +(16-6)= 10+10 = 20.

Question 16.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x \sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x\) (C.B.S.E. 2018 C)
Solution:


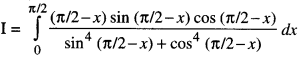
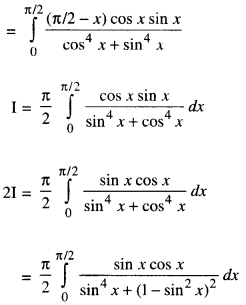
Let sin² x = t
⇒ sin x cos x dx = 1/2 dt
For x-0,t = sin² 0 = 0
and for x = π/2, t = sin² π/2 = 1

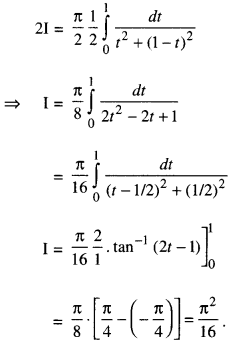
Question 17.
Evaluate : \(\int_{1}^{3}\)(3x² + 2x + 1)dx as the limit ofa sum. (C.B.S.E. 2018 C)
Solution:
a = 1, b = 3
and h = 2/n
nh = 2
\(\int_{1}^{3}\)(3x² + 2x + 1)dx
\(\lim _{h \rightarrow 0}\)
= lim h\f(l) +/(1 + h) +/(1 + 2h) + …
= \(\lim _{h \rightarrow 0}\) h[f(1) +f(1 + h) +f(1 + 2h) + …+ f(1 + (n — 1)h)]
= \(\lim _{h \rightarrow 0}\) h[(6+ {3(1 +h)² + 2(1 + h)+ 1} + (3(1 + 2h)² + 2(1 + 2h) + 1) + … + {3(1 +(n – 1)h)² + 2(1 +(n – 1)h)+ 1)]
= \(\lim _{h \rightarrow 0}\) h[6+ {3(1 + h² + 2h) + 2(1 +h) + 1) + {3(1 +4h² + 4h) } + 2(1 +2h)+ 1}+… + {3(1 + (n – 1)² h² + 2(n – 1)h) + 2(1 +(n—1)h)+(l +(n – 1)h}

= \(\lim _{h \rightarrow 0}\) h[(6) + (6 + 8h + 3h²) + (6 + 16h + 12h²) + … + [(6 + 3(n – 1)² h² + 8 (n —1)h}]

= \(\lim _{h \rightarrow 0}\)[6n+8h(1 + 2 +…+(n – 1))
+3h² {(1² + 2² + …+(n – 1)²}]

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 6 Applications of Derivatives. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 6 Important Extra Questions Applications of Derivatives

Applications of Derivatives Important Extra Questions Very Short Answer Type

Question 1.
For the curve y = 5x- 2x³, if increases at the rate of 2 units/sec., find the rate of change of the slope of the curve when x = 3. (C.B.S.E. 2017)
Solution:
The given curve is y = 5x – 2x³
∴ \(\frac{d y}{d x}\) = 5 – 6x²
i.e. m = 5 – 6x²,
where ‘m’ is the slope.
∴ \(\frac{d m}{d t}\) = —12x\(\frac{d x}{d t}\) =-12x(2) = -24x
∴ \(\left.\frac{d m}{d t}\right]_{x=3}\)= -24(3) = -72.
Hence, the rate of the change of the slope = -72.

Question 2.
Without using the derivative, show that the function f(x) = 7x – 3 is a strictly increasing function in R. (N.C.E.R.T.)
Solution:
Let x₁ and x₂∈ R.
Now x₁ > x₂
⇒ 7x₁ > 7x₂
⇒ 7x₁ – 3 > 7x₂ – 3
⇒ f(x₁) > f(x₂).
Hence, ‘f ’ is strictly increasing function in R.

Question 3.
Show that function:
f(x) = 4x³ – 18×2 – 27x – 7 is always increasing in R. (C.B.S.E. 2017)
Solution:
We have :f(x) = 4x³ – 18×2 – 27x – 7
∴ f(x) = 12x² – 36x + 27 = 12(x² – 3x) + 27
= 12(x² – 3x + 9/4) + 27 – 27
= 12(x – 3/2)²∀ x∈ R.
Hence, f(x) is always increasing in R.

Question 4.
Find the slope of the tangent to the curve:
x = at²,y = 2at at t = 2.
Solution:
The given curve is x – at², y = 2at.
∴ \(\frac{d x}{d t}\) = 2at
\(\frac{d x}{d t}\)= 2a
∴ \(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}=\frac{2 a}{2 a t}=\)
Hence, slope of the tangent at t = 2 is: \(\left.\frac{d y}{d x}\right]_{t=2}=\frac{1}{2}\)

Question 5.
Find the maximum and minimum values, if any, of the following functions without using derivatives:
(i) f(x) = (2x-1)² + 3
(ii) f(x)= 16x² – 16x + 28
(iii) f(x) = -|x+ 1| + 3
(iv) f(x) = sin 2x + 5
(v) f(x) = sin (sin x).
Solution:
(i) We have :
f(x) = (2x – 1)² + 3.
Here D_f = R.
Now f(x) ≥ 3.
[∵ (2x – 1)² ≥ 0 for all x ∈ R]
However, maximum value does not exist.
[∵ f(x) can be made as large as we please]

(ii) We have :
f(x) = 16x² – 16x + 28.
Here D_f = R.
Now f(x) = 16 (x² – x + \(\frac{1}{4}\) + 24
= (16(x – \(\frac{1}{2}\) )² + 24
⇒ f(x) ≥ 24.
[∵ 16(x – \(\frac{1}{2}\) )² ≥ 0 for all x ∈ R
Hence, the minimum value is 24.
However, maximum value does not exist.
[ ∵ f(x) can be made as large as we please]

(iii) We have :
f(x) = – 1x + 11 + 3
⇒ f(x) ≤ 3.
[ ∵ -|x + 1| ≤ 0]
Hence, the maximum value = 3.
However, the minimum value does not exist.
[∵ f(x) can be made as small as we please]

(iv) We have :
f(x) = sin2x + 5.
Since – 1 ≤ sin 2x ≤ 1 for all x ∈ R,
– 1+5 ≤ sin2x + 5 ≤ 1+5 for all x∈ R
⇒ 4 ≤ sin2x + 5 ≤ 6 for all x ∈ R
⇒ 4 ≤ f(x) ≤ 6 for all x ∈ R.
Hence, the maximum value = 6 and minimum value = 4.

(v) We have :
f(x) = sin (sin x).
We know that – 1 ≤ sin x ≤ 1 for all x ∈ R
⇒ sin(-1) ≤ sin(sinx) ≤ sin 1 for all x ∈ R
⇒ – sin 1 ≤ f(x) ≤ sin 1.
Hence, maximum value = sin 1 and minimum value = -sin 1.

Question 6.
A particle moves along the curve x² = 2y. At what point, ordinate increases at die same rate as abscissa increases? (C.B.S.E. Sample Paper 2019-20)
Sol. The given curve is x² = 2y …(1)
Diff.w.r.t.t, 2x\(\frac{d x}{d t}\) = 2 \(\frac{d y}{d t}\)
⇒ 2x\(\frac{d x}{d t}\) = 2 \(\frac{d x}{d t}\)
∵ \(\frac{d y}{d t}=\frac{d x}{d t}\) given
From(1), 1 = 2y ⇒ y = \(\frac{1}{2}\)
Hence, the reqd. point is (1, \(\frac{1}{2}\) )

Applications of Derivatives Important Extra Questions Long Answer Type 1

Question 1.
A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall? (C.B.S.E. Outside Delhi 2019)
Solution:
Here, \(\frac{d x}{d t}\) = 2 cm/sec.

Hence, the height is decreasing at the rate of 5/6 cm/sec.

Question 2.
Find the angle of intersection of the curves x² + y² = 4 and (x – 2)² + y²= 4, at the point in the first quadrant (C.B.S.E. 2018 C)
Solution:
The given curves are :
x² + y² = 4 ………….(1)
(x – 2)² + y² = 4 ………….. (2)

From (2),
y = 4 – (x – 2)²
Putting in (1),
x² + 4-(x-2)² = 4
⇒ x² – (x – 2)² = 0
⇒ (x + x-2)(x-x + 2) = 0
⇒ (2x – 2)(2) = 0
⇒ x = 1.
Putting in (1),
1 + y² = 4
⇒ y = √3
∴ Point of intersection = (1, √3 )

Question 3.
Find the intervals in which the function: f(x) = – 2x³ – 9x² – 12x + 1 is (i) Strictly increasing
(ii) Strictly decreasing. (C.B.S.E. 2018 C)
Solution:
Given function is:
f(x) = – 2x³ – 9x² – 12x + 1.
Diff. w.r.t. x,
f'(x) = -6x² – 18x – 12
= -6(x + 1) (x + 2).

Now, f'(x) – 0
⇒ x = -2, x = -1
⇒ Intervals are (-∞ – 2), (-2, -1) and (-1, ∞).
Getting f’ (x) > 0 in (-2, -1)
and f'(x) < 0 in (-∞, -2) u (-1, ∞)
⇒ f(x) is strictly increasing in (-2, -1) and strictly decreasing in (-∞, 2) u (-1, ∞).

Question 4.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 metres. Find the dimensions of the window to admit maximum light through the whole opening. (C.B.S.E. 2018 C)
Solution:
Let ‘x’ and ‘y’ be the length and breadth of the rectangle ABCD.
Radius of the semi-circle = \(\frac { x }{ 2 }\) .
Circumference of the semi-circle = \(\frac{\pi x}{2}\)

For Max ./Min. of A (x), A’ (x) = 0
\(\frac{20-(2+\pi)(2 x)}{4}+\frac{2 \pi x}{8}=0\)
20-(2 + π)(2x) + πx = 0
20 + x(π – 4 – 2π) = 0
20 – x(4 + π) = 0
x = \(\frac{20}{4+\pi}\)

And radius of semi-circle = \(\frac{10}{4+\pi}\)

Question 5.
The length ‘x’ of a rectangle is decreasing at the rate of 3 cm/m and width ‘y’ is increasing at the rate of 2 cm/m. When x = 10 cm and y = 6 cm, find the rate of change of:
(a) the perimeter and
(b) the area of the rectangle. (N. C.E.R.T.)
Solution:
We have: \(\frac{d x}{d t}\) = -3 cm/m …(1)
and \(\frac{d y}{d t}\) = 2 cm/m …(2)

a) Perimeter, p = 2x + 2y.
∴ \(\frac{d p}{d t}=2 \frac{d x}{d t}+2 \frac{d y}{d t}\)
= 2(-3) + 2(2)
[Using (1) and (2)]
= – 6 + 4 = -2.
Hence \(\left.\frac{d p}{d t}\right]_{x=10 \atop y=6}\) = -2cm/m.

(b) Area, A = xy.
∴ \(\frac{d \mathrm{~A}}{d t}=x \frac{d y}{d t}+y \frac{d x}{d t}\) = x(2) + y(-3)
[Using (1) and (2)]
Hence \(\left.\frac{d p}{d t}\right]_{x=10 \atop y=6}\) = 10(2) + 6(-3)
= 20-18
= 2cm²/m.

Question 6.
A stone is dropped into a quiet lake and waves move in circles at a speed of 4 cm per second. At the instant when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing ? (N.C.E.R.T.)
Solution:
Let ‘r’ be the radius of the circular wave.
Then A = π r², where A is the enclosed area at time t.
Differentiating w.r.t. t, we have:
\(\frac{d \mathrm{~A}}{d t}=2 \pi r \frac{d r}{d t}=2 \pi r(4)\) [∵ \(\frac{d r}{d t}\) = 4cm/s]
= 8πr.
When r = 10cm, \(\frac{d A}{d t}\)= 8K (10) = 80π cm²/s.
Hence, the enclosed area is increasing at the rate of 80π cm²/s.. when r = 10 cm.

Question 7.
Find the intervals in which the function f(x) is (i) strictly increasing (ii) strictly decreasing:
f(x) = x³ – 12x² + 36x + 17. (C.B.S.E. 2009 C)
Solution:
We have :
f(x) = x³ – 12x² + 36x + 17 – 12x² + 36x + 17.
∴ f'{x) = 3x² – 24x + 36.

(i) For f(x) to be strictly increasing function of x: f'(x) > 0
⇒ 3x² – 24x + 36 > 0
⇒ x² – 8x+ 12 > 0
⇒ (x – 2) (x – 6) > 0
⇒ x < 2 or x > 6.
Hence, f(x) is increasing in the interval (-∞ 2) ∪ (6, ∞).

(ii) For f (x) to be strictly decreasing function of x:
f'(x) <0 ⇒  3x² – 24x + 36 < 0 ⇒ x² – 8x + 12 < 0 ⇒ (x – 2) (x – 6) < 0 ⇒ 2 < x < 6.
Hence, f(x) is decreasing in the interval (2,6).

Question 8.
Find the intervals in which the function :
f(x) = 3x⁴ – 4x³ – 12x² + 5 is:
(a) strictly increasing
(b) strictly decreasing. (C.B.S.E. 2014)
Solution:
We have: f(x) = 3x⁴ – 4x³ – 12x² + 5.
∴ f'(x) = 12x³ – 12x² – 24x
= 12x(x² – x – 2)
= 12x(x – 2)(x + 1).
When x < – 1.
f”(x) = 12 (-ve) (-ve) (-ve) = -ve.
Thus f(x) is strictly decreasing.
When -1 < x < 0.
f'(x) = 12(-ve)(-ve)(+ve) = +ve.
Thus f(x) is strictly increasing.

When 0 < x < 2. f'(x) = 12(+ve)(-ve)(+ve)=-ve. Thus f(x) is strictly decreasing. When x > 2.
f'(x) – 12(+ve)(+ve)(+ve) = +ve.
Thus f(x) is strictly increasing.
Combining,/(x) is
0a) strictly increasing in (-1,0) u (2, ∞) and
(b) strictly decreasing in (-∞, -1) u (0,2).

Question 9.
Find the point at which the tangent to the curve
y = \(\sqrt{4 x-3}\) 1 has its slope \(\frac{2}{3}\) (N.C.E.R.T.)
Solution:
The given curve is :

By the question,
slope = \(\frac{2}{3}\)
\(\frac{2}{\sqrt{4 x-3}}=\frac{2}{3}\)
⇒ \(\sqrt{4 x-3}\) = 3.
Squaring, 4x – 3 = 9
⇒ 4x = 12
⇒ x = 3.
Putting in (1),
y = \(\sqrt{4(3)-3}=\sqrt{9}-1\)
= 3-1 = 2.
Hence, the reqd. point is (3,2).

Question 10.
Find the equations of all lines having slope 2 and being tangents to the curve:
\(y+\frac{2}{x-3}=0\) (N.C.E.R.T)
Solution:
The given curve is y + \(y+\frac{2}{x-3}=0\) = 0
y = \(-\frac{2}{x-3}\)
∴ \(\frac{d y}{d x}=\frac{2}{(x-3)^{2}}\)
By the question, \(\frac{2}{(x-3)^{2}}\) = 2
⇒ (x-3)² = 1
x – 3 = ± 1
⇒ x = 2, 4.

When x = 2, then from (1),
y = \(\frac{-2}{2-3}=\frac{-2}{-1}\)
= 2.
When x = 4, then from (1),
y = \(\frac{-2}{4-3}=\frac{-2}{1}\) = 2

Thus there are two tangents to the given curve with slope 2 and passing through (2, 2) and (4,-2).
∴ The equation of the tangent through (2,2) is: y-2 = 2(x-2)
⇒ y-2x + 2 = 0
and the equation of the tangent through (4,-2) is:
y-(-2) = 2(x-4)
⇒ y-2x+ 10 = 0.

Question 11.
Find the equation of the tangent to the curve y = \(\sqrt{3 x-2}\) which is parallel to the line 4x – 2y + 5 = 0. Also, write the equation of normal to the curve at the point of contact.
(C.B.S.E. 2019)
Solution:
(i) The given curve is y = \(\sqrt{3 x-2}\) …(1)
∴ Slope of the tangent, \(\frac{d y}{d x}=\frac{3}{2 \sqrt{3 x-2}}\)
Slope of the given line 4x – 2y + 5 = 0 is \(-\frac{4}{-2}\) = 2
Since the tangent is parellel to (2)
∴ \(\frac{3}{2 \sqrt{3 x-2}}\) = 2 (∵ m₁ = m₂)
3 = 4\(\sqrt{3 x-2}\)
9 = 16(3x – 2)
= 48x = 41
x = \(\frac{41}{48}\)

⇒ 6(4y-3) = 48x-41
⇒ 48x-24y = 23.

(ii) Slope of normal x Slope of tangent = – 1
⇒ Slope of normal = – 1/2
∴ The equation of the normal is :
\(y-\frac{3}{4}=-\frac{1}{2}\left(x-\frac{41}{48}\right)\)

Question 12.
Find the equations of the tangent and the normal to the curve 16x² + 9y² = 145 at the point (x₁, x₂ where x₁ = 2 and y₁ > 0. (C.B.S.E. 2018)
Solution:
The given curve is :
16x² + 9y² = 145 …(1)
Since (x_1s, y₁,) lies on (1),
.-. 16x²+9y] = 145
⇒ 16(2)² + 9y₁² = 145
⇒ 9y₁² = 145-64
⇒ 9y₁² = 81
⇒ y₁² =9
y₁ = 3 [∵ y₁ > 0]
Thus, the point is (2, 3).
Diff (1) w.r.t x ,

(i) The equation of tangent is :
y – 3 = \(\frac{-32}{27}\) (x-2)
⇒ 27y – 81 = -32x + 64
⇒ 32x + 27y = 145

(ii) The equation of normal is :
y – 3 = \(\frac{27}{32}\)(x – 2)
⇒ 32y – 96 = 27x – 54
⇒ 27x – 32y + 42 =0.

Question 13.
Find the equations ofthe tangent and normal to the curve given by:
x = a sin³ θ, y = a cos³θ at a point, where θ = \(\frac{\pi}{4}\) (1C.B.S.E. 2014)
Solution:
The given curve is:
x = a sin³ θ, y = a cos³θ

∴ Slope of the tangent at θ = \(\frac{\pi}{4}\)

and slope of the normal = 1.
When θ = \(\frac{\pi}{4}\), then from (1),

∴ The equations of the tangent and normal to (1) at θ = \(\frac{\pi}{4}\) are :

Question 14.
Find the equation of the tangent to the curve
ay² = x³ at the point (am², am³) (C.B.S.E. 2019 C)
Solution:
The given curve is ay² = x³
y = a^-1/23/2

∴ The equation of the tangent is:
y – y’ = \(\frac{d y}{d x}\) (x – x’)
y – am³ = \(\frac{3 m}{2}\)(x – am²)
2y – 2 am³ = 3 mx – 3 am³
3mx – 2y = am³.

Question 15.
Find the equation of the tangent to the curve x² + 3y = 3, which is parallel to the line y – 4x + 5 = 0. (C.B.S.E. 2009 C)
Solution:
The given curve is x² + 3y = 3
y = \(\frac{1}{3}\) (3 – x²
∴ \(\frac{d y}{d x}=\frac{1}{3}(0-2 x)=-\frac{2}{3} x\)
which is the slope of the tangent.
But the tangent is parallel to the line
y – 4x + 5 = 0, whose slope is 4.
Thus \(-\frac{2}{3}\)x = 4 [∵ m₁ = m₂]
⇒ x = -6.
From(l), y = \(\frac{1}{3}\) (3 – 36) = -11.
Thus the point of contact is (- 6, – 11).
The equation of the tangent is :
y + 11 = 4(x + 6)
⇒ y + 11 = 4x + 24
⇒ 4x – y+ 13 = 0.

Question 16.
Find the equations of the normal to the curve y = 4x³ – 3x + 5, which are perpendicular to the line 9x – y + 5 = 0.
(C.B.S.E. Sample Paper 2018-19)
Solution:
The given curve is :
y = 4x² – 3x + 5.
Let the required normal be at (x₁ y₁,).
Slope of the tangent = \(\frac{d y}{d x}\) = 12x² – 3.
m₁ = slope of the normal

and m₂ = Slope of the line = 9.
Since, the normal is perpendicular to the lines
m₁ m₂ = -1
\(\frac{-1}{12 x_{1}^{2}-3} \times 9\) = -1
12x₁² = 9
x₁² = 1
x₁ = ±1.

When x₁ = 1, then y₁ = 4-3 + 5 = 6.
When x₁ = -1, then y₁ = -4 + 3 + 5 = 4.
Thus the points are (1, 6) and (-1,4).
∴ The equations of the normal are :
y – 6 = \(-\frac { 1 }{ 9 }\) (x-1) i.e.,x + 9y = 55
and y – 4= \(-\frac { 1 }{ 9 }\) (x+ 1) i.e.,x + 9y = 35.

Question 17.
Using differentials, find the approximate value of \(\sqrt[3]{0.026}\) , upto three places of decimals.
Solution:
Let y = f(x) = x^1/3
Take x = 0.027,
x + Δx = 0.026
Δx = 0.026 – 0.027 = -0.001.
x = 0.027,
y = \(\sqrt[3]{0 \cdot 027}\) =0.3.
Let dx = Δx = -0.001.

Question 18.
If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area. (N.C.E.R.T.; A.I.C.B.S.E. 2011)
Solution:
Let ‘r’ be the radius of the sphere and Ar be the error in measuring the radius.
Then r = 9m and Δr = 0.03 m.
Now S, the surface area of the sphere is given by:
S = 4πr²
∴ \(\left(\frac{d S}{d r}\right)\) = 8πr
Now dS = \(\left(\frac{d S}{d r}\right)\)Δr = (8πr)Δr
= (8π)(9))(0.03) = 2.16πm²
Hence, the approximate error in calculating the surface area is 2.16πm²

Question 19.
Find the absolute maximum and the absolute minimum value of the function given by:
f(x) = sin²x – cos x, x ∈ [0, π]. (A.I.C.B.S.E. 2015)
Solution:
We have :
f(x) = sin²x – cos x.
∴ f'(x) – 2 sin x cos x + sin x
= sinx(2cosx+ 1).
Now f'(x) 0
⇒ sin x (2 cos x + 1) = 0
⇒ sin x = 0 or cosx = \(-\frac{1}{2}\)
x = 0, π or x = \(\frac{2 \pi}{3}\)
Now f(0) = 0 – 1 = -1

Hence, absolute maximum value is \(\frac{5}{4}\) and absolute minimum values is – 1.

Question 20.
Find all the points of local maxima and local minima of the function ‘f’ given by: f(x) = 2x³ – 6x² + 6x + 5. (N.C.E.R.T.)
We have: f(x) = 2x³ – 6x² + 6x + 5.
f'(x) = 6x² – 12x + 6 = 6(x – 1)².
f”(x) = 12 (x – 1).
Now f'(x) = 0 gives x = 1.
Also, f”(1) = 0.
Thus x = 1 is neither a point of maxima nor of minima
Now f” (x) = 12.
And f'”(x)]_x=1 = 1 = 12 ≠ 0.
Hence, x = 1 is a point of inflexion.

Applications of Derivatives Important Extra Questions Long Answer Type 2

Question 1.
Water is leaking from a conical funnel at the rate of 5 cm Vs. If the radius of the base of funnel is 5 cm and height 10 cm, find the rate at which the water level is dropping when it is 2.5 cm from the top.
Solution:
Here 5 cm is the radius and 10 cm is the height of the conical funnel.
Let ‘r’ be the radius of the base and ‘h’ the height at any stage.

∴ V, volume of water in conical funnel
= \(\frac{1}{3}\) πr²h …………. (1)
Now Δs OBC and OED are similar

∴ From (1), V, volume of water in conical funnel

When the water level is 2.5 cm from the top, then
h = 10 – 2.5 = 7.5 cm.

Hence, the rate at which the water level is 16 .
dropping is \(\frac{16}{45 \pi}\) cm/s.

Question 2.
A man is moving away from a tower 41.6 m high at the rate of 2 m/s. Find the rate at which the angle of elevation of the top of tower is changing when he is at a distance of 30 m from the foot of the tower. Assume that the eye level of the man is 1.6 m from the ground.
Solution:
Let AB (= 41.6 m) be the tower.
Let the man be at a distance of ‘x’ metres from the tower AB at any time t. If ‘0’ be the angle of elevation at time t, then :

⇒ tan θ = \(\frac { 40 }{ x }\)
⇒ x = 40 cot θ …………. (1)
\(\frac{d x}{d t}\) = -40 cosec² θ. \(\frac{d \theta}{d t}\)
⇒ 2 = -40 cosec².θ\(\frac{d \theta}{d t}\) [∵ \(\frac{d x}{d t}\) = 2(given) ]

When x = 30, then from (1),
30 = 40 cot θ
⇒ cot θ = \(\frac{3}{4}\)
so that cosec² θ = 1+ cot\frac{3}{4} = 1 + \(\frac{9}{16}=\frac{25}{16}\)
Putting in (2),

Hence, the angle of elevation of the top of the
tower is reducing at the rate of \(\frac{4}{125}\) radians/s.

Question 3.
Find the intervals in which:
f(x) = sin 3x – cos 3r, 0 < x < π, is strictly increasing or strictly decreasing. (C.B.S.E. 2016)
Solution:
We have : f'(x) = sin 3x – cos 3x.
f'(x) = 3 cos 3x + 3 sin 3x.
Now f(‘x) = 0
⇒ 3 cos 3x + 3 sin 3x = 0
⇒ cos 3x = – sin 3x
⇒ tan 3x = – 1

⇒ f is strictly decreasing.
In \(\left(0, \frac{\pi}{4}\right), f^{\prime}(x)\) < 0 f is strictly increasing. ⇒ f is strictly decreasing. In \(\left(\frac{7 \pi}{12}, \frac{11 \pi}{12}\right)\)f'(x) >0
⇒ f is strictly increasing.
In \(\left(\frac{11 \pi}{12}, \pi\right)\), f'(x) < 0
⇒ f is strictly decreasing.
Hence, ‘f’ is strictly increasing in

Question 4.
Show that the equation of normal at any point ‘t’ on the curve:
x = 3 cos t – cos³t and y = 3 sin t – sin³t is : 4(y cos³ t-x sin³t) = 3 sin 4t. (C.B.S.E. 2016)
Solution:
The given curve is :
x = 3 cos t – cos³t and y = 3 sin t – sin³t.
\(\) = -3 sin t – 3 cos²t (- sin t)
= -3 sin t (1- cos²t)
= -3 sin t sin² t
= -3 sin³t
and \(\frac{d y}{d t}\) = 3 cos t – 3 sin²t cos t
= 3 cos t (1- sin²t)
= 3 cos t cos² t = 3 cos² t.
= \(\frac{3 \cos ^{3} t}{-3 \sin ^{3} t}=-\frac{\cos ^{3} t}{\sin ^{3} t}\)
∴ Slope of normal = \(\frac{\sin ^{3} t}{\cos ^{3} t}\)
∴ The equation of the normal at ‘t’ is: y – (3 sin t – sin³ t)
= \(\frac{\sin ^{3} t}{\cos ^{3} t}\)(x – 3 cos t + cos³ t)
⇒ y cos³ t – 3 sin t cos³ t + sin³ t cos³ t
⇒ x sin³ t – 3 cos t sin³ t + sin³ t cos³ t
⇒ y cos³ t – x sin³t
= 3 sin t cos t (cos³t – sin³t)
⇒ y cos³ t – x sin³ t = \(\frac{3 \sin 2 t \cos 2 t}{2}\)
⇒ y cos³ t – x sin³ t = \(\frac{3}{4}\) sin 4t
⇒ 4(y cos³ t – x sin³ t) = 3 sin 4t, which is true.

Question 5.
A cuboidal shaped godown with square base is to be constructed. Three times as much cost per square metre is incurred for constructing the roof as compared to the walls. Find the dimensions of the godown if it is to enclose a given volume and minimize the cost of constructing the roof and the walls.
(C.B.S.E. Sample Paper 2018-19 C)
Solution:
Let the length and breadth of the base = x and the height of the godown = y.
If C be the cost of construction and V, the volume.
∴ C = k[3x² + 4xy] …(1),
where k > 0 is constant of proportionality
⇒ x2y = V (constant) …(2)
⇒ y = \(\frac{\mathrm{V}}{x^{2}}\) …………. (3)
Putting the value of y from (3) in (1), we get:

Question 6.
A given quantity of metal is to be cast into a solid half circular cylinder (i.e., with rectangular base and semi-circular ends). Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its circular ends is π: (π + 2). (C.B.S.E. Sample Paper 2019-20)
Solution:
Let ‘r’ be the radius and ‘h’, the height of the cylinder.
∴ V = Volume of half cylinder = \(\frac { 1 }{ 2 }\) πr²h …….(1)

Total surface area, S = S₁ (Surface area of semi¬circular ends) + S₂ (Curved surface of half cylinder) + S₃ (Surface area of rectangular base having height h and width 2r)
( \(\frac { 1 }{ 2 }\)πr² \(\frac { 1 }{ 2 }\)πr²) + \(\frac { 1 }{ 2 }\)(2πrh) + 2rh
= πr² + πrh + 2rh
= πr² + (π + 2)r\(\frac{2 \mathrm{~V}}{\pi r^{2}}\)
[Using (1)]
∴ S = πr² + \(\frac{2 \mathrm{~V}}{\pi r}\) (π+2) ……. (2)
∴ \(\frac{d \mathrm{~S}}{d r}=2 \pi r-\frac{2 \mathrm{~V}}{\pi r^{2}}(\pi+2)\)

= 2π + 4π = 6π
which is +ve
∴ S is minimum when π²r³ = V(π + 2)
π²r³ = \(\frac { 1 }{ 2 }\)πr²(π + 2)
\(\frac{h}{2 r}=\frac{\pi}{\pi+2}\)
Hence, h:2r = π: {π + 2), which is true.

Question 7.
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If the building of tank costs ₹70 per sq. metre for the base and ₹45 per sq. metre for the sides, what is the cost of least expensive tank? (C.B.S.E. 2019)
Solution:
Let ‘x’ and ‘y’ be the length and breadth respetively of the tank.
And depth of the tank = 2 m.
∴ Volume of the tank = 2xy.

By the question,
2xy = 8
⇒ xy = 4 …(1)
Nowarea of the base = xy
and area of the sides = 2 (x + y) (2) = 4 (x + y)
∴ Cost of construction
= ₹(70xy+ 45 (4(x + y)) …(2)
= ₹(70xy+ 1800 + y))
∴ C, the cost of construction
= 70 (4) +180( x + \(\frac{4}{x}\)) [Using (1)]
= 280 + 180 ( x + \(\frac{4}{x}\))
∴ \(\frac{d \mathrm{C}}{d x}=180\left(1-\frac{4}{x^{2}}\right)=180\left(\frac{x^{2}-4}{x^{2}}\right)\)

For max ./min.,
\(\frac{d \mathrm{C}}{d x}\) = 0
x² – 4 = 0
x = ±2.
x = 2. [∵ Length can’t be -ve]

From(1), y = \(\frac{4}{2},\) = 2.
Thus the tank is a cube of side 2 m.
∴ Least cost of construction
= ₹[280 + 180(2 + \(\frac{4}{2},\) )] [From (3)]
= ₹ (280 + 720) = ₹1000. [From (3)]

Question 8.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quanity of water. Show that the cost of the material will be least when the depth of the tank is half of its width. (C.B.S.E. 2018)
Solution:
Let ‘x’ be the side of the square base and V the depth of the tank.
Now, V = x²y …(1)
Now S, surface area = x² + 4xy
∴ C, cost is proportional to surface area = k(x² + 4xy)

Hence, the cost of material least when depth is half of its width.

Question 9.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius ‘r’ is \(\frac { 4r }{ 2 }\). Also find the maximum volume of the cone.
(C.B.S.E. 2019 (Delhi))
Solution:
(i) Let ‘x’ be the distance of the base BC from the centre O of the sphere.

∴ Height of the cone = AM = r + x
andradius of the base = BM = \(\sqrt{r^{2}-x^{2}}\).
∴ V, the volume of the cone
= \(\frac{1}{3}\)π(r² – x2)(r+x).
∴ \(\frac{d \mathrm{~V}}{d x}\)= \(\frac{1}{3}\)π(r² – x²) + \(\frac{1}{3}\)π( – 2x)(r + x)
= \(\frac{\pi}{3}\)(r + x)(r – x – 2x)
= \(\frac{\pi}{3}\)(r + x)(r – 3x)
and \(\frac{d^{2} V}{d x^{2}}\) = \(\frac{\pi}{3}\)(r + x)( – 3) + \(\frac{\pi}{3}\)(1) (r – 3x)
= \(\frac{\pi}{3}\)( – 3r – 3x + r – 3x)
= \(\frac{\pi}{3}\)( – 2r – 6x).
For V to be max, \(\frac{d \mathrm{~V}}{d x}\) = 0 and \(\frac{d^{2} \mathrm{~V}}{d x^{2}}\) < 0
Now \(\frac{d \mathrm{~V}}{d x}\) = 0 gives :
\(\frac{\pi}{3}\) (r + x )(r – 3x) = 0
⇒ x = -r, \(\frac{r}{3}\)
but x ≠ -r
x = \(\frac{r}{3}\)
Also \(\left.\frac{d^{2} \mathrm{~V}}{d x^{2}}\right]_{x=\frac{r}{3}}=\frac{\pi}{3}(-2 r-2 r)=-\frac{4}{3} \pi r\)
Which is -ve
Hence, V is max. when x = \(\frac{r}{3}\) i.e., when altitude
r +x = r + \(\frac{r}{3}\) = \(\frac{4r}{3}\)

(ii) Maximum volume of the cone

Question 10.
If the lengths ofthree sides ofa trapezium other than base are equal to 10 cm, then find the area of the trapezium when it is maximum. (N.C.E.R.T.; A.I.C.B.S.E. 2010)
Solution:

Let ABCD be the trapezium such that:
AD = BC = CD = 10 cm.
Draw DL and CM perpendiculars on AB.
Let AL = x cm.
Now ΔALD ≅ Δ BMC.
∴ MB = AL = x cm.
Also LM = 10 cm.
And DL = CM = \(\sqrt{100-x^{2}}\)
Let ‘A’ be the area of the trapezium.
Then A (x) = 1/2 (10 + (10 + 2x)) \(\sqrt{100-x^{2}}\)
[Area of Trap. = \(\frac{1}{2}\) (sum of II sides) {height))
= \(\frac{1}{2}\)(2x + 20) \(\sqrt{100-x^{2}}\)
= (x + 10) \(\sqrt{100-x^{2}}\) ………(1)
A'(x) = (x + 10)

Now A'(0) = 0
⇒ -2x² – 10A+ 100 = 0
⇒ x² + 5x – 50 = 0
= (x+ 10) (x-5) = 0
=» x = -10,5.
But x ≠ – 10.
[ ∵ x, being the distance, can’t be – ve]
Thus A = 5 cm.
And

Thus A (A) is maximum when x = 5.
Hence, A (5) = (5 +10) \(\sqrt{100-25}\)
[Using (1)]
= 15√75 = 75√3 cm².

Question 11.
A metal box with a square base and vertical sides is to contain 1024 cm³. The material for the top and bottom costs₹ 5 per cm² and the material for the sides costs ₹ 2.50 per cm² Find the least cost of the box. (C.B.S.E 2017)
Solution:
Let ‘x’ cm be the side of square base and ‘y’ cm the height.
∴ volume of the box = x x x x y = x²y.
By the question,
x²y = 1024 …(1)
Now the cost, C = 5(x²) + \(\frac { 5 }{ 2 }\) (4xy)
= 5x²+ 10xy
= 5x² + 10x (\(\frac{1024}{x^{2}}\)) …………(2) [Using (1)]

Now for least cost, \(\frac{d \mathrm{C}}{d x}\) = 0
⇒ 10x – \(\frac{10240}{x^{2}}\) = 0
⇒x³ = (1024)^1/3
⇒ x = (1024)^1/3
And \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) > 0 for x = (1024)^1/3
Hence, least cost =5 (1024)^2/3 + \(\frac{10240}{(1024)^{1 / 3}}\)
= 5(1024)^2/3 + 10(1024)^2/3
= ₹ 15(1024)^2/3

Question 12.
Show that the height of the cylinder, open at the top, of given surface area and greatest volume is equal to the radius of its base. (C.B.S.E. 2010, 2019 C)
Solution:
Let ‘r’ and ‘h’ be the radius and height respectively of the cylinder.
∴ S, the surface area = πr² + 2πrh
h = \(\frac{\mathrm{S}-\pi r^{2}}{2 \pi r}\) …………(1)
And V, the volume = πr²h
i.e. V = πr² \(\left(\frac{\mathrm{S}-\pi r^{2}}{2 \pi r}\right)\) [Using(1)]
V = \(\frac{r}{2}\) (S – πr²)
V = \(\frac{1}{2}\)(Sr – πr³)
∴ \(\frac{d \mathrm{~V}}{d r}\) = \(\frac{r}{2}\) (S – 3πr²) …….. (2)
and \(\frac{d^{2} \mathrm{~V}}{d r^{2}}=-\frac{3 \pi}{2}\) (2r) = -3 πr ………(3)
For greatest volume , \(\frac{d \mathrm{~V}}{d r}\) = 0 and \(\frac{d^{2} \mathrm{~V}}{d r^{2}}\) < 0
Now \(\frac{d \mathrm{~V}}{d r}\) = 0
= \(\frac{r}{2}\) (S – 3πr²) = 0
S = 3πr²

Hence, height = radius of the base.

Question 13.
An Apache helicopter of enemy is flying along the curve given by: y = x² + 7.
A soldier, placed at (3,7), wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.
(NCERT; C.B.S.E. 2019 C)
Solution:
Let P (x, x² + 7) be the position of the helicopter at any instant.
Also A is (3,7).

Let f(x) = (x – 3)² + x⁴.
f'(x) = 2(x-3) + 4x³ = 4x³ + 2x – 6
= 2(2x³ + x – 3) = 2(x – 1)(2x² + 2x + 3).
Now f'(x) = 0
x – 1 = 0, or 2x² + 2x+3 = 0
⇒ x = 1.
[∵ Roots of 2x² + 2x + 3 = 0 are not real] Thus, there is only one point x = 1.
And f(1) = (1 -3)²+ 14 = 4 + 1 = 5.
∴ Distance between soldier and helicopter is √5
Now √5 is either max. value or min. value.
Since \(\sqrt{f(0)}=\sqrt{(0-3)^{2}+(0)^{4}}=3>\sqrt{5}\)
⇒ √5 is min. value of \(\sqrt{f(x)}\).
Hence, √5 is the reqd. minimum distance between the soldier and the helicopter.

Question 14.
Show that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle. (C.B.S.E. Sample Paper 2019-20)
Solution:
Let O be the centre and V, the radius of the circle in which AABC is inscribed.

For maximum area, the vertex A should be at a maximum distance from the base BC
⇒ A must lie on the diameter, which is perp. to BC
⇒ ΔABC is isosceles.
Let ∠BAC = θ. Then ∠BOC = 2θ
⇒ DOC = θ.
Now BC = 2DC = 2OC sin θ = 2rsine…(1)
and AD = AO + OD = AO + OC cos θ
= r + r cos θ = r (1 + cos θ) …(2)
If ‘A’ be the area of the triangle, then:
A = \(\frac { 1 }{ 2 }\) (BC) (AD) = \(\frac { 1 }{ 2 }\) (2r sin θ) r (1 + cos θ)
[Using (1) & (2)]
⇒ A = r² (sin θ + sin θ cos θ).
= r²(cos θ + cos² θ – sin² θ)
= r² (cos²θ + cos θ) = r² (2cos² θ -1 + cos θ)
= r² (2cos ²θ + cos θ – 1) …………. (3)
and \(\frac{d^{2} \mathrm{~A}}{d \theta^{2}}\) = r²(4cox θ sin θ – sin θ) ……(4)
For ‘A’ to be maximum \(\frac{d \mathrm{~A}}{d \theta}\) = 0 and \(\frac{d^{2} \mathrm{~A}}{d \theta^{2}}\) < 0
Now, \(\frac{d \mathrm{~A}}{d \theta}\) = 0
⇒ r² (2 cos² θ + cos θ – 1) = 0
⇒ 2 cos² θ + cos θ – 1 = 0
⇒ (2 cos θ -1) (cos θ + 1) = 0

Thus, A is maximum when θ = \(\frac{\pi}{3}\)
But ΔABC is isosceles.
Hence, for maximum area, triangle is equilateral.

Question 15.
Find the point on the circle x² + y² = 80, which is nearest to the point (1,2). (C.B.S.E. 2019)
Solution:
Let P (√80 cos θ, √80 sin θ)
i.e. (4√5 cosθ, 4√5 sin θ) be a point on the circle x² + y² = 80.
And, A(1, 2) is the given point.
|AP| = \(\sqrt{(4 \sqrt{5} \cos \theta-1)^{2}+(4 \sqrt{5} \sin \theta-2)^{2}}\) ………….. (1)
AP is least⇒ AP² is least
D = AP² = (4√5cos θ – 1)
(4√5 sinθ – 2)² …………. (2)
\(\frac{d D}{d \theta}\)= 2(4√5 cos θ – 1)(- 4√5sin θ)
+ 2 (4θ5sin θ – 2)(4θ5cos θ)
= – 160 sin θ cos θ + 8√5 sin θ + 160 sin θ cos θ – 16√5 cos θ ………… (3)
= 8√5 (sin θ-2 cos θ) ………… (3)
and \(\frac{d^{2} \mathrm{D}}{d \theta^{2}}\) = 8√5 (cos θ + 2 sin θ) …(4)
Now \(\frac{d \mathrm{D}}{d \theta}\) = 0
⇒ 8√5(sin θ – 2 cos θ) = 0
⇒ sin θ – 2 cos θ = 0 tan θ = 2

Thus, D is least when tan θ = 2
Hence, from (1), least distance

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 5 Continuity and Differentiability. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 5 Important Extra Questions Continuity and Differentiability

Continuity and Differentiability Important Extra Questions Very Short Answer Type

Question 1.
If y = log (cos e^x), then find \(\frac{d y}{d x}\) (Delhi 2019)
Solution:
We have :y = log (cos e^x)
∴ \(\frac{d y}{d x}=\frac{1}{\cos e^{x}}\left(-\sin e^{x}\right) \cdot e^{x}\)
= – e^x tan e^x

Question 2.
Differentiate cos {sin (x)²} w.r.t. x. (Outside Delhi 2019)
Solution:
Let y = cos {sin (x)²}.
∴ \(\frac{d y}{d x}\)= – sin {sin (x)²}. \(\frac{d y}{d x}\){sin (x)²}
= – sin {sin (x)²}. cos(x)² \(\frac{d y}{d x}\) (x²)
= – sin {sin (x)²}. cos(x)²2x
= -2x cos(x)² sin {sin(x)²}.

Question 3.
Differentiate sin²(x²) w.r.t. x².   (C.B.S.E. Sample Paper 2018-19)
Solution:
Let y = sin²(x²).
∴ \(\frac{d y}{d x}\) = 2 sin (x²) cos (x²) = sin (2x²).

Question 4.
Find \(\frac{d y}{d x}\), if y + siny = cos or.
Solution:
We have: y + sin y = cos x.
Differentiating w.r,t. x, we get:
\(\frac{d y}{d x}\) + cos y. \(\frac{d y}{d x}\) = – sin x
(1 + cos y)\(\frac{d y}{d x}\) = -sin x
Hence, \(\frac{d y}{d x}\) = \(-\frac{\sin x}{1+\cos y}\)
where y ≠ (2n + 1)π, n ∈ Z.

Question 5.
If y = \(\sin ^{-1}\left(6 x \sqrt{1-9 x^{2}}\right),-\frac{1}{3 \sqrt{2}}<x<\frac{1}{3 \sqrt{2}}\) then find \(\frac{d y}{d x}\). (C.B.S.E. 2017)
Solution:
Here y = sin^-1\(\left(6 x \sqrt{1-9 x^{2}}\right)\)
Put 3x = sin θ.
y = sin^-1 (2 sin θ cos θ)
= sin^-1 (sin 2θ) = 2θ
= 2 sin^-1 3x
\(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^{2}}}\)

Question 6.
Is it true that x = e^logx for all real x? (N.C.E.R.T.)
Solution:
The given equation is x = e^logx
This is not true for non-positive real numbers.
[ ∵ Domain of log function is R+]
Now, let y = e^logx
If y > 0, taking logs.,
log y = log (e^logx) = log x.log e
= log x . 1 = log x
⇒ y = x.
Hence, x = e^logx is true only for positive values of x.

Question 7.
Differentiate the following w.r.t. x : 3^{x + 2}. (N.C.E.R.T.)
Solution:
Let y = 3^{x + 2}.
\(\frac{d y}{d x}\) = 3^{x + 2}.log3. \(\frac{d}{d x}\)(x + 2)
= 3^{x + 2} .log3.(1 + 0)
= 3^{x + 2}. log 3 = log 3 (3^{x + 2}).

Question 8.
Differentiate log (1 + θ) w.r.t. sin^-1θ.
Solution:
Let y = log (1 + θ) and u = sin^-1θ.

Question 9.
If y = x^x , find \(\frac{d y}{d x}\).
Solution:
Here y = x^x …(1)
Taking logs., log y = log x^x
⇒ log y = x log x.
Differentiating w.r.t. x, we get:
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x \(\frac{1}{x}\) + logx.(1)
= 1 + log x.
Hence, \(\frac{d y}{d x}\) = y (1 + log x) dx
= x^x (1 + log x). [Using (1)]

Question 10.
If y = \(\sqrt{2^{x}+\sqrt{2^{x}+\sqrt{2^{x}+\ldots \ldots+0 \infty}}}\) then prove that: (2y – 1)\(\frac{d y}{d x}\) = 2^x log 2.
Solution:
The given series can be written as :
y = \(\sqrt{2^{x}+y}\)
Squaring, y² = 2^x + y
⇒ y² – y = 2^x.
Diff. w.r.t. x, (2y -1)\(\frac{d y}{d x}\) = 2^x log 2.

Question 11.
Discuss the applicability of Rolle’s Theorem for the function f(x) = (x- 1)^2/5 in the interval [0, 3].
Solution:
Since f(x) is a polynomial in x,
∴ it is continuous in [0, 3].
And f'(x) = \(\frac { 2 }{ 5 }\)(x-1) ^-3/5 = \(\frac{2}{5} \cdot \frac{1}{(x-1)^{3 / 5}}\)
which does not exist at x = 1
⇒ f(x) is not derivable in (0, 3).
Hence, Rolle’s theorem is not applicable.

Continuity and Differentiability Important Extra Questions Short Answer Type

Question 1.
Discuss the continuity of the function : f(x) = |x| at x = 0. (N.C.E.R.T.)
Solution:

Hence ‘f’ is continuous at x = 0.

Question 2.
If f(x) = x + 1, find \(\frac{d}{d x}\)(fof)(x). (C.B.S.E. 2019)
Solution:
We have : f(x) = x + 1 …(1)
∴ fof(x) = f (f(x)) =f(x)+ 1
= (x + 1) + 1 = x + 2.
∴ \(\frac{d}{d x}\)(fof)(x).) = \(\frac{d}{d x}\)(x + 2) = 1 + 0 = 1.

Question 3.
Differentiate \(\tan ^{-1}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\) with respect to x. (C.B.S.E. 2018 C)
Solution:

Question 4.
Differentiate: tan^-1 \(\left(\frac{1+\cos x}{\sin x}\right)\) with respect to x. (C.B.S.E. 2018)
Solution:

Question 5.
Write the integrating factor of the differential equation :
(tan^-1 y – x) dy = (1 + y²) dx. (C.B.S.E. 2019 (Outside Delhi))
Solution:
The given differential equation is :
(tan^-1 y – x) dy = (1 + y²) dx
⇒ \(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) Linear Equation
∴ I.F = \(e^{\int \frac{1}{1+y^{2}} d x}=e^{\tan ^{-1} y}\)

Question 6.
Find \(\frac{d y}{d x}\) if y = sin^-1\(\left[\frac{5 x+12 \sqrt{1-x^{2}}}{13}\right]\) (A.I.C.B.S.E. 2016)
Solution:

Question 7.
Find \(\frac{d y}{d x}\) if y = \(\sin ^{-1}\left[\frac{6 x-4 \sqrt{1-4 x^{2}}}{5}\right]\) (A.I.C.B.S.E. 2016)
Solution:

Question 8.
If y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ , prove that \(\frac{d y}{d x}=\frac{n y}{\sqrt{x^{2}+a^{2}}}\)
Solution:
y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ ……… (1)

Question 9.
The total cost C(x) associated with the production of ‘x’ units of an item is given by C(x) = 0.005x³ – 0.02x² + 30x + 5000.
Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of the total cost at any level of output. (C.B.S.E. 2018)
Solution:
We have: 0.005x³ – 0.02x² + 30x + 5000
∴ Marginal cost,
C'(x) = (0.005)(3x²) – 0.02(2x) + 30.
Hence,C'(3) = (0.005) (3×9)- (0.02) (6) + 30
= 0.135-0.12 + 30
= 30.135 – 0.12
= 30.02 units nearly

Question 10.
If (x² + y²)² = xy, find \(\frac{d y}{d x}\). (C.B.S.E. 2018)
Solution:
We have : (x² + y²)² = xy
Diff. w.r.t. x,
2(x² + y²)\(\frac{d}{d x}\)(x²+ y²) = x\(\frac{d y}{d x}\) + y(1)
2(x² + y²) [2x +2y\(\frac{d y}{d x}\) ] = x\(\frac{d y}{d x}\) + y
4x(x² + y²) – y = \(\frac{d y}{d x}\) [x – 4y(x² + y²)]
Hence \(\frac{d y}{d x}=\frac{4 x^{3}+4 x y^{2}-y}{x-4 y x^{2}-4 y^{3}}\)

Question 11.
Fing \(\frac{d y}{d x}\) if x^2/3 + y^2/3 = a^2/3 (N.C.E.R.T)
Solution:
The given equation is
if x^2/3 + y^2/3 = a^2/3
Its parametric equations are :
x = a cos³ θ,
y = a sin³ θ
[x^2/3 + y^2/3 = a^2/3 (cos²θ + sin²θ) = a^2/3(I) = a^2/3]

Question 12.
Find the value of \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{4}\), if:
x = ae^θ (sin θ – cos θ)
and y = ae^θ (sin θ + cos θ). (A.I.C.B.S.E. 2014)
Solution:
We have : x= ae^θ (sin θ – cos θ)
and y= ae^θ(sin θ + cos θ).
\(\frac{d x}{d \theta}\) = ae^θ (cos θ + sin θ) + ae^θ(sin θ – cos θ)
= 2ae^θsin θ
and \(\frac{d y}{d \theta}\) = ae^θ (cos θ – sin θ) + ae^θ(sinθ + cosθ)
= 2ae^θ cos θ

Question 13.
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ), find \(\frac{d y}{d x}\) where θ = \(\frac{\pi}{3}\) (C.B.S.E 2018)
Solution:
We have :
x = a(2θ – sin 2θ)
and y = a(1 – cos 2θ).
∴ \(\frac{d x}{d \theta}\) = a(2 – 2 cos 2θ)
and \(\frac{d y}{d \theta}\) = a(0 + 2 sin 2θ) = 2a sin 2θ.

Question 14.
Find f’ (x), if f(x) = (sin x)^{sin x} for all 0 < x < π. (N.C.E.R.T.)
Solution:
We have :
f(x) = (sin x)^{sin x} …(1)
Taking logs., log f(x) = log (sin x)^{sin x}
⇒ log f(x) = sin x log (sin x).
Diff. w.r.t. x,

= cos x (1 + log sin x)
⇒ f’ (x) = f(x) cos x (1 + log sin x).
Hence ,f'(x) = (sin x)^{sin x}cos x (1 + log sin x).
[Using (i)]

Question 15.
If x¹⁶ y⁹ = (x² + y)¹⁷, prove that \(\frac{d y}{d x}=\frac{2 y}{x}\) (C.B.S.E. (F) 2012)
Solution:
We have :
x¹⁶ y⁹ = (x² + y)¹⁷.
Taking logs.,
log (x¹⁶ y⁹) = log (x² + y)¹⁷
⇒ 16 log x + 9 log y = 17 log (x² + y).
Diff. w.r.t. x,

Question 16.
If y = ae^2x + be^-x, then show that \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y=0\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
Here,
y = ae^2x + be^-x ……… (1)
∴ \(\frac{d y}{d x}\) = 2ae^2x – be^-x …….. (2)
And \(\frac{d^{2} y}{d x^{2}}\) = 4ae^2x + be^-x ……….. (3)
Now, \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y\)
= [4ae^2x + be^-x] – [2ae^2x – be^-x] – 2[ae^2x + be^-x] [Using (1), (2) & (3)]
= 4ae^2x + be^-x – 2ae^2x + be^-x – 2ae^2x – 2be^2x = 0.

Question 17.
If y = log(1 + 2t² + t⁴), x = tan^-1t, find \(\frac{d^{2} y}{d x^{2}}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
We have : y = log(1 + 2t² + t⁴)
⇒ y = log (1 + t²)²
⇒ y = 21og (1 + t²).

Question 18.
If x sin (a + y) + sin a cos (a + y) = 0, then prove that: \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\) (A.I.C.B.S.E. 2013)
Solution:
We have :
x sin (a + y) + sin a cos (a + y) = 0 …(1)
⇒ x = \(-\frac{\sin a \cos (a+y)}{\sin (a+y)}\) …..(2)
Diff (1) w.r.t x,
x cos (a + y)(0+\(\frac{d y}{d x}\) ) + sin (a + y). 1 + sina(-sin(a+y))(0+\(\frac{d y}{d x}\)) = 0
(xcos(a + y) – sin a sin (a + y)] \(\frac{d y}{d x}\) = – sin (a + y)

⇒ – sin (a + y) [Using (2)]
⇒ -sin a[cos²(a+y)+sin²(a+y)] \(\frac{d y}{d x}\) = -sin² (a+y)
⇒ -sin a(1) \(\frac{d y}{d x}\) = = -sin² (a+y)
Hence \(\frac{d y}{d x}\) = \(\frac{\sin ^{2}(a+y)}{\sin a}\)
Which is true.

Question 19.
If sin y = x cos (a + y), then show that \(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\cos a}\) Also, show that \(\frac{d y}{d x}\) = cos a, when x = 0. (C.B.S.E. 2018C)
Solution:
Given, sin y = x cos (a + y)

Question 20.
Find the value of ‘c’ in Rolle’s Theorem for the function f (x) = x³ – 3x in [-√3, 0]. (A.1.C.B.S.E. 2017)
Solution:
We have : f(x) = x³ – 3x.
(i) f(x) is continuous in [-√3, 0].
[∵ f(x) is a polynomial in x]

(ii) f'(x) = 3x² – 3 …(1)
∴ f'(x) exists for each x in (-√3,0)

(iii) f(-√3) = (-√3)3 – 3(-√3)
= -3√3 + 3√3 = 0
f(0) = 0 – 0 = 0.
∴ f(-√3) =f(0).
Thus all the conditions of Rolle’s Theorem are satisified.
∴ There exists at least one number ‘c’ between – √3 and 0 such that f'(c) = 0.

But f'(c) = 3c² – 3. [Putting x – c in (1)
∴ f'(c) = 0
3c² – 3 = 0
c² = 1
c = ± 1.
c = – 1 ∈ (-√3,0).
Hence, Rolle’s Theorem is verified and c = – 1.

Question 21.
Find a point on the parabola y = (x – 3)², where the tangent is parallel to the chord joining (3, 0) and (4,1).
Solution:
We have : y = f(x) = (x – 3)².
We discuss the applicability of L.M.V. Theorem in [3, 4],
(i) fix) is continuous in [3, 4],
[ ∵ f(x) is a polynomial]

(ii) f'(x) = 2(x – 3), which exists for all x ∈ (3,4).
∴ f(x) is derivable in (3, 4).
Thus both the conditions of Lagrange’s Mean Value Theorem are satisfied.
∴ There exists at least one number c ∈ (3, 4) such that

⇒ 2(c – 3) = 1
⇒ 2c = 1
⇒ c = \(\frac{7}{2}\) ∈ (3, 4).
When x = \(\frac{7}{2}\), then y = (\(\frac{7}{2}\) – 3)² = 1/4
Hence, the required point is ( \(\frac{7}{2}, \frac{1}{4}\) )

Continuity and Differentiability Important Extra Questions Long Answer Type 1

Question 1.
Find the value of ‘a’ for which the function ‘f’ defined as :

is continuous at x =0 (CBSE 2011)
Solution:


Also f(0) = a sin π/2 (0+1)
= a sin π/2 = a(1) = a
For continuity,
\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a = 1/2 = a
Hence, a = 1/2

Question 2.
Find the values of ‘p’ and ‘q’ for which :

is continuous at x = 2 (CBSE 2016)
Solution:


Also f(\(\frac{\pi}{2},\)) = p
For continuity \(\lim _{x \rightarrow \frac{\pi^{-}}{2}} f(x)=\lim _{x \rightarrow \frac{\pi^{*}}{2}} f(x)\)
= f(\(\frac{\pi}{2},\))
⇒ \(\frac{1}{2}=\frac{q}{8}\) = p
Hence p = 1/2 and q = 4

Question 3.
Find the value of ‘k’ for which

is continuous at x = 0 (A.I.C.B.S.E. 2013)
Solution:


For continuity \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ k = -1 = -1
Hence k = -1

Question 4.
For what values of ‘a’ and ‘b\ the function ‘f’ defined as :

is continuous at x = 1. (CBSE 2011)
Solution:
\(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}\) (3ax +b)
= \(\lim _{h \rightarrow 0}\) (3a (1-h) + b]
= 3a(1 – 0) + b
= 3a + b
\(\lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{+}}(5 a x-2 b)\)
= \(\lim _{h \rightarrow 0}\) [5a (1+h) – 2b]
= 5a (1+0) – 2b
= 5a – 2b
Also f(1) = 11
Since ‘f’ is continuous at x = 1,
∴ \(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}} f(x)\)= f(1)
⇒ 3a + b = 5a – 2b = 11.
From first and third,
3a + b = 11 …………… (1)
From last two,
5a – 2b = 11 …………… (2)
Multiplying (1) by 2,
6a + 2b = 22 ………….. (3)
Adding (2) and (3),
11a = 33
⇒ a = 3.
Putting in (1),
3(3) + b = 11
⇒ b = 11 – 9 = 2.
Hence, a = 3 and b = 2.

Question 5.
If f(x) , defined by the following is continuous at x = 0, find the values of a, b, and c.

(A.I.C.B.S.E 2011)
Solution:


Also f(0) = 2
Since f(x) is continuous at x = 0,
∴ \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a + 3 = b/2 = 2
Hence,a = -1 and b = 4.

Question 6.
Find ‘a’ and ‘b’, if the function given by :
f(x) = \(\left\{\begin{array}{ll}
a x^{2}+b, & \text { if } x<1 \\ 2 x+1, & \text { if } x \geq 1 \end{array}\right.\) is differentiable at x = 1. (C.B.S.E. Sample Paper 2018)
Solution:
Since ‘f’ is derivable at x = 1, ∴ ‘f’ is continuous at x = 1 im 33 => a + b = 2 + 1 = 3
⇒ a + b = 3 …………. (1)
Again since ‘f is differentiable at x = 1


2a = 2
Putting in (1),
1 + b = 3
⇒ b = 3 – 1
⇒ b = 2.
Hence, a = 1 and b = 2.

Question 7.
Prove that: \(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]\) = \(\sqrt{a^{2}-x^{2}}\)
(C.B.S.E. (F) 2011)
Solution:

Question 8.
Differentiate \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\) w.r.t x (N.C.E.R.T)
Solution:
Let y = \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\)
= \(\sin ^{-1}\left(\frac{2.2^{x}}{1+\left(2^{x}\right)^{2}}\right)\)
Put 2^x = tan θ
so that θ = tan^-1(2^x) ………… (1)
Then y = \(\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 (sin 2θ)
= 2θ = 2tan^-1(2^x).
[Using (1)]

Question 9.
If log (x² + y²) = 2 tan^-1 [ y/x] show that : \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (C.B.S.E. 2019)
Solution:

Question 10.
If y = tan^-1\(\left(\frac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)\), x² ≤ 1, then find \(\frac{d y}{d x}\)
We have : log (x2 + y2) = 2 tan-1 (A.I.C.B.S.E. 2015)
Solution:

Question 11.
Differentiate the following with respect to x = sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\) (A.I.C.B.S.E. 2013)
Solution:
= sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\)
= sin^-1\(\left(\frac{2.2^{x} \cdot 3^{x}}{1+(6)^{2 x}}\right)\)
= sin^-1\(\left(\frac{2.6^{x}}{1+(6)^{2 x}}\right)\)
Put 6^x = tan θ
So that θ = tan^-1(6^x) …………(1)
Then y = sin^-1( \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\) )
= sin^-1(sin 2θ)
= 2θ = 2tan^-1(6^x) [Using (1)]

Question 12.
Differentiate : tan^-1\(\left[\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}\right]\) w.r.t cos^-1 x² (C.B.S.E. Outside Delhi 2019)
Solution:

Question 13.
If x^y – y^x = a^b, find \(\frac{d y}{d x}\). (Delhi 2019)
Solution:
We have : x^y – y^x = a^b
Putting x^y = u and y^x = v, we get:
u – v = a^b
so that, \(\frac{d u}{d x}-\frac{d v}{d x}\) =0 ………….(1)
Now, u = x^y
Taking logs.,
log u = log x^y
⇒ log u = y log x.
Diff. w.r.t. x,

And, v = y^x
Taking logs., log v = log y^x
⇒ log v = x log y.

Question 14.
If y = (log x)^x + x^logx, find \(\frac{d y}{d x}\) (C.B.S.E. 2019)
Solution:
Let y = (log x)^x + x^logx = u + v,
where u = (log x)^x and v = x^logx
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……….(1)
Now, u = (log x)^x
so that log u = x log (log x).
Diff. w.r.t. x,

Again, v = x^logx
so that log v = log x. log x = (logx)²
Diff w.r.t x,

Question 15.
If \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\) then prove that \(\frac{d y}{d x}=\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\) (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\)
Putting x = sin A and y = sin B, we get:
\(\sqrt{1-\sin ^{2} \mathrm{~A}}+\sqrt{1-\sin ^{2} \mathbf{B}}=a\)= a (sin A – sin B) ⇒ cos A + cos B = a (sin A – sin B)

Question 16.
If x = a sec³ θ and y = a tan³θ, find \(\frac{d^{2} y}{d x^{2}}\)
Solution:
Given : x = a sec³ θ
y = a tan³θ

Question 17.
Find \(\frac{d y}{d x}\), if x^y. y^x = x^x. (C.B.S.E 2018C)
Solution:
We have: x^y y^x = x^x.
Taking logs.,log x^y y^x = log x^x
⇒ y log x + x log y=x log x

Question 18.
Find \(\frac{d y}{d x}\) if y^x + x^y + x^x = a^b (N.C.E.R.T. A.I.C.B.S.E.2015)
Solution:
We have: y^x + x^y + x^x
Putting y^x = u. x^y = v and x^x = w, we get:
u + y + w = a^b
Diff. w.r.t. x, \(\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}\) = 0 …………… (1)
Now u = y^x ………….(2)
Taking logs., log u = log y^x
log u = x log y.
Diff. w.r.t. x,

And v = x^y
Taking logs., log v = log x^y
log v = y log x.
Diff. w.r.t. x,

[using (4)]
Lastly w = x^x
Taking logs.,
log w = xlog x
∴ \(\frac{d w}{d x}\) = x (1+log x) …………. (7)
From (1) , using (3), (5) and (7), we get:

Question 19.
If y = e^{tan-1 x}, prove that:\(\left(1+x^{2}\right) \frac{d^{2} y}{d x^{2}}+(2 x-1) \frac{d y}{d x}=0\)
(C.B.S.E. 2018C)
Solution:
Given: y = e^tan-1x,
Differentiating w.r.t. x
\(\frac{d y}{d x}=e^{\ln ^{-1} x}\left(\frac{1}{1+x^{2}}\right)=\frac{y}{1+x^{2}}\)
Agian differentiating w.r.t. x
(1 + x²)\(\frac{d y}{d x}\) = y
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + 2x \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + (2x – 1) \(\frac{d y}{d x}\) = 0

Question 20.
If x cos (a + y) = cos y, then prove that:
\(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\)
Hence show that :
sin a \(\frac{d^{2} y}{d x^{2}}\) + sin 2(a + y)\(\frac{d y}{d x}\) = 0
Solution:
We have : x cos (a + y) = cos y …………(1)
x = \(\frac{\cos y}{\cos (a+y)}\) …………..(2)
Diff. (I) w.r.t. x,
-x sin (a + y) (0 + \(\frac{d y}{d x}\) ) + cos (a + y) .1
⇒ -sin y.\(\frac{d y}{d x}\)
⇒ (xsin(a+y) – siny)\(\frac{d y}{d x}\) = cos(a +y)
⇒ (\(\frac{\cos y}{\cos (a+y)}\) sin (a+y) – sin y)\(\frac{d y}{d x}\)
⇒ cos (a + y) [Using (2)]
(sin (a + y) cos y – cos (a + y) sin y)\(\frac{d y}{d x}\)
⇒ cos² (a + y)
⇒ sin (a + y – y) \(\frac{d y}{d x}\) = cos²(a+y)
\(\frac{d y}{d x}\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\)
which is true.

Question 21.
If y = (sin^-1 x)², prove that:
\(\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-2=0\) (C.B.S.E. 2019)
Solution:
We have y = (sin^-1 x)²
∴ y₁ = 2(sin^-1 x). \(\frac{1}{\sqrt{1-x^{2}}}\)
⇒ \(\sqrt{1-x^{2}} \cdot y_{1}\) = 2(sin^-1 x).
Squaring, (1 – x²) y₁² = 4(sin^-1 x)²
⇒ (1 – x²) y₁² = 4y [Using (1)]
Diff. w.r.t x,
(1 – x²) 2y₁y₂ + (-2x) y₁² = 4y₁
⇒ (1 – x²) y₂ – xy₁ = 2 [Dividing by 2y₁ ]
Hence, (1-x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) – 2 = 0.

Question 22.
If y = cos (m cos^-1 x), show that
(a – x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) + m²y = 0 (C.B.S.E. Sample Paper 2018-2019)
Solution:
We have :

Question 23.
If y = sin (sin x), prove that
\(\frac{d^{2} y}{d x^{2}}\) + tanx \(\frac{d y}{d x}\) + y cos²x = 0. (C.B.S.E. 2018)
Solution:
We have :
y = sin (sin x)
∴ \(\frac{d y}{d x}\) = cos (sin x) . cos x ……(2)
and \(\frac{d^{2} y}{d x^{2}}\) = cos (sin x) (- sin x) + cos x [- sin (sin x). cos x]
= – sin x cos (sin x) – cos²x sin (sin x) …(3)
:. LHS = \(\frac{d^{2} y}{d x^{2}}\) + tan x \(\frac{d y}{d x}\) + y cos² x
⇒ – sin x cos (sin x) – cos² x sin (sin x) + tan x cos (sin x).cos x + sin (sin x) cos² x
[Using (1). (2) and (3)]
⇒ – sin x cos (sin x) – cos² x sin (sin x) + sin x cos (sin x) + cos² x sin (sin x)
⇒ – sin x cos (sin x) + sin x cos (sin x)
= 0 = RHS.

Question 24.
If x = sin t, y = sin pt, prove that:
(1 – x²)\(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) + p²y = 0
(Outside Delhi 2019)
Solution:
We have : x = sin t
and y = sin pt.
\(\frac{d y}{d x}\) = cos t
and \(\frac{d y}{d x}\) = p cos pt

which is true.

Question 25.
Find \(\frac{d y}{d x}\), if x^y.y^x = x^x. (C.B.S.E. 2019 C)
Solution:
We have: x^y.y^x = x^x
Taking logs., logx^y y^x = log x^x
⇒ y log x + x log y = x log x

Question 26.
If y = x^x, prove that
\(\frac{d^{2} y}{d x^{2}}-\frac{1}{y}\left(\frac{d y}{d x}\right)^{2}-\frac{y}{x}=0\) (C.B.S.E. 2016,14)
Solution:
We have : y = x^x.
Taking logs.,
log y = x log x.
Duff. w.r.t. x,
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x. \(\frac{1}{y}\) + log x.1
\(\frac{d y}{d x}\) = y(1+1ogx) ………….(1)
Again duff. w.r.t. x,

Question 27.
If x = a (cos 2θ + 2θ sin 2θ) andy = a (sin 2θ – 2θ cos 2θ), find \(\frac{d^{2} y}{d x^{2}}\) at θ = \(\frac{\pi}{8}\)
(C.B.S.E. Sample Paper 2019-20)
Solution:
We have: x – a (cos 2θ + 2θ sin 2θ)
∴ \(\frac{d x}{d \theta}\) = a (- 2 sin 2θ + 2 sin 2θ + 4θ cos 2θ).
⇒ \(\frac{d x}{d \theta}\) = 4aθ cos 2θ ………..(1)
And y = a (sin 2θ – 2θ cos 2θ).
∴ \(\frac{d y}{d \theta}\) = a (2 cos 2θ + 4θ sin 2θ – 2 cos 2θ)
\(\frac{d y}{d \theta}\) = 4aθsin 2θ ………….. (2)

Question 28.
If x = cos t + log tan (t/2) y = sin t , then find the values of \(\frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\) at t = \(\frac{\pi}{4}\)
(C.B.S.E. 2019 Delhi Set-II)
Solution:
We have x = cos t log tan (t/2) and
y = sin t

Question 29.
If y = a cos (log x) + b sin (log x), show that:
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\) (C.B.S.E. 2019C)
Solution:
We have:
y = a cos (log x) + b sin (log x) …..(1)
\(\frac{d y}{d x}\) = – a sin (log x) \(\frac{1}{x}\) + b cos (log x) \(\frac{1}{x}\)
x\(\frac{d y}{d x}\) = -asin (log x) + b cos (log x).
Again diff. w.r.t.x., \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot 1\)
= – a cos (log x) . \(\frac{1}{x}\) – b sin (log x) . \(\frac{1}{x}\)
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\)
= – [a cos (log x) + b sin (log x)]
= -y. [Using (1)]
Hence, \(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\)

Question 30.
Use Lagrange’s Theorem to determine a point P on the curve f(x) = \(\sqrt{x-2}\), defined in the interval [2, 3], where the tangent is parallel to the chord joining the end points on the curve.
Solution:
We have y = f(x) = \(\sqrt{x-2}\) …….(1)
∴ f'(x) = \(\frac{1}{2 \sqrt{x-2}}\)
now f(a) = f(2) = \(\sqrt{2-2}=\sqrt{0}\) = 0
and f(b) = f(3) = \(\sqrt{3-2}=\sqrt{1}\) = 1.
By Lagrange’s Theorem, we have :

⇒ \(\frac{1}{4(x-2)}\) = 1 [Squaring both
⇒ 1 = 4x – 8
⇒ 4x = 9
⇒ x = \(\frac{9}{4}\) ∈ (2, 3).
Putting in (1), y = \(\sqrt{\frac{9}{4}-2}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)
Hence, ( \(\frac{9}{4}, \frac{1}{2}\) ) is the reqd. point.

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 3 Matrices. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 3 Important Extra Questions Matrices

Matrices Important Extra Questions Short Answer Type

Question 1.
Write the element a₂₃ of a 3 x 3 matrix A = [a_ij] whose elements atj are given by : \(\frac{|i-j|}{2}\)
Solution:
We have [a_ij] = \(\frac{|i-j|}{2}\)
∴ a₂₃ = \(\frac{|2-3|}{2}=\frac{|-1|}{2}=\frac{1}{2}\)

Question 2.
For what value of x is
\(\left[\begin{array}{lll}
1 & 2 & 1
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]=0\) ? (C.B.S.E. 2019(C))
Answer:
We have
\(\left[\begin{array}{lll}
1 & 2 & 1
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]=0\)

[1 + 4 + 1 2 + 0 + 0 0 + 2 + 2] \(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
[6 2 4 ]\(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
⇒ [0 + 4 + 4x] =0
⇒ [4 + 4x] = [0]
⇒ 4 + 4x = 0.
Hence, x = -1.

Question 3.
Find a matrix A such that 2A – 3B + 5C = 0,
Where B = \(\left[\begin{array}{ccc}
-2 & 2 & 0 \\
3 & 1 & 4
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
2 & 0 & -2 \\
7 & 1 & 6
\end{array}\right]\)
Solution:
Here, 2A – 3B + 5C = 0
⇒ 2A = 3B – 5C

Question 4.
If A = \(\left(\begin{array}{l}
\cos \alpha-\sin \alpha \\
\sin \alpha-\cos \alpha
\end{array}\right)\) , then for what value of ‘α’ is A an identity matrix? (C.B.S.E. 2010)
Solution:
Here A = \(\left(\begin{array}{l}
\cos \alpha-\sin \alpha \\
\sin \alpha-\cos \alpha
\end{array}\right)\)
Now A = I = \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) when
cos α = 1 and sin α = 0.
Hence, α = 0.

Question 5.
Find the values of x, y, z and t, if:
\(2\left[\begin{array}{ll}
x & z \\
y & t
\end{array}\right]+3\left[\begin{array}{rr}
1 & -1 \\
0 & 2
\end{array}\right]=3\left[\begin{array}{ll}
3 & 5 \\
4 & 6
\end{array}\right]\)
Solution:
We have :

⇒ 2x + 3 = 9 …………. (1)
2z – 3 = 15 …………. (2)
2y = 12 …………. (3)
2t + 6 = 18 …………. (4)

From (1), ⇒ 2x = 9 – 3
⇒ 2x = 6
⇒ x = 3.

From (3) 2y = 12
⇒ y = 6.

From (2), ⇒ 2z – 3 = 15
⇒ 2z = 18
⇒ z = 9.

From (4), 2t + 6 = 18
⇒ 2t = 12
⇒ t = 6.
Hence, x = 3,y = 6, z = 9 and t = 6.

Question 6.
If A = \(\left[\begin{array}{rrr}
2 & 0 & 1 \\
2 & 1 & 3 \\
1 & -1 & 0
\end{array}\right]\), then find (A² – 5A). (CBSE 2019)
Solution:
We have A = \(\left[\begin{array}{rrr}
2 & 0 & 1 \\
2 & 1 & 3 \\
1 & -1 & 0
\end{array}\right]\)
Then A² = AA

Question 7.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\) and I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) , find k so that A² = 5A + b kI (C.B.S.E. Sample Paper 2018-2019)
Solution:

⇒ 8 = 15 + k and 3 = 10 + k
⇒ k = -1 and k = -7.
Hence, k – -7.

Question 8.
If A and B are symmetric matrices, such that AB and BA are both defined, then prove that AB – BA is a skew symmetric matrix. (A.I.C.B.S.E. 2019)
Solution:
Since A and B are symmetric matrices,
∴ A’ = A and B’ = B …(1)
Now,(AB – BA)’= (AB)’ – (BA)’
= B’A’ – A’B’
= BA – AB [Using (1)]
= – (AB – BA).
Hence, AB – BA is a skew-symmetric matrix.

Question 9.
For the matrix A = \(\left[\begin{array}{ll}
2 & 3 \\
5 & 7
\end{array}\right]\) find (A + A’) and show that it is a symmetric matrix. (A.I.C.B.S.E. 2019)
Solution:

Now (A + A’)’ = \(\left[\begin{array}{cc}
4 & 8 \\
8 & 14
\end{array}\right]\) = (A + A’)
Hence (A + A’) is symmetric

Question 10.
If the matrix A = \(\left[\begin{array}{ccc}
0 & a & -3 \\
2 & 0 & -1 \\
b & 1 & 0
\end{array}\right]\) is skew symmetric, find the values of ‘a’ and ‘b’: (C.B.S.E. 2018)
Solution:

Comparing, 2 = -a ⇒ a = -2
and – 3 = -b ⇒ b = 3.
Hence, a = -2 and b = 3.

Matrices Important Extra Questions Long Answer Type 1

Question 1.
Find the values of a, b, c and d from the following equation :
\(\left[\begin{array}{cc}
2 a+b & a-2 b \\
5 c-d & 4 c+3 d
\end{array}\right]=\left[\begin{array}{cc}
4 & -3 \\
11 & 24
\end{array}\right]\) (N.C.E.R.T)
Solution:
We have
\(\left[\begin{array}{cc}
2 a+b & a-2 b \\
5 c-d & 4 c+3 d
\end{array}\right]=\left[\begin{array}{cc}
4 & -3 \\
11 & 24
\end{array}\right]\)
Comparing the corresponding elements of two given matrices, we get:
2a + b = 4 …(1)
a-2b = – 3 …(2)
5c-d = 11 …(3)
4c + 3d = 24 …(4)
Solving (1) and (2):
From (1),
b = 4 – 2a …(5)
Putting in (2), a – 2 (4 – 2a) = – 3
⇒ a – 8 + 4a = -3
⇒ 5a = 5
⇒ a = 1.
Putting in (5),
b = 4 – 2(1) = 4 – 2 = 2.
Solving (3) and (4):
From (3),
d = 5c- 11 …(6)
Putting in (4),
4c+ 3 (5c- 11) = 24
⇒ 4c + 15c – 33 = 24
⇒ 19c = 57
⇒ c = 3.
Putting in (6),
d = 5 (3) – 11 = 15 – 11 = 4.
Hence, a = 1, b = 2, c = 3 and d = 4.

Question 2.
If \(\left[\begin{array}{rrr}
9 & -1 & 4 \\
-2 & 1 & 3
\end{array}\right]\) = A + \(\left[\begin{array}{rrr}
1 & 2 & -1 \\
0 & 4 & 9
\end{array}\right]\) then find the matrix A. (C.B.S.E. 2013)
Solution:

Comparing:
9 = a₁₁ + 1 – 1 = a₁₂ + 2,
4 = 1₁₃ – 1, -2 = a₂₁
1 = a₂₂ + 4, and 3 = a₂₃ + 9
a₁₁ = 8, a₁₂ = – 3,
a₁₃ = 5, a₂₁ = -2
a₂₂ = – 3, and a₂₃ = – 6.
Hence, A = \(\left[\begin{array}{rrr}
8 & -3 & 5 \\
-2 & -3 & -6
\end{array}\right]\)

Question 3.
If A = \(=\left[\begin{array}{rr}
2 & 2 \\
-3 & 1 \\
4 & 0
\end{array}\right]\) B = \(\left[\begin{array}{ll}
6 & 2 \\
1 & 3 \\
0 & 4
\end{array}\right]\)find the matrix C such that A + B + C is a zero matrix.
Solution:

Comparing :
8 + c₁₁ = 0 ⇒ c₁₁ = -8,
4 + C₁₂ = 0 ⇒ C₁₂ = -4,
– 2 + C₂₁ = 0 ⇒ C₂₁ = 2
4 + C₂₂ = 0 ⇒ C₂₂ =- 4,
4 + c₃₁ = 0 ⇒ C₃₁ = -4
and 4 + c₃₂ = 0 ⇒ C₃₂ = -4.
Hence, C = \(\left[\begin{array}{rr}
-8 & -4 \\
2 & -4 \\
-4 & -4
\end{array}\right]\)

Question 4.
If A = \(\left[\begin{array}{rr}
8 & 0 \\
4 & -2 \\
3 & 6
\end{array}\right]\) B = \(\left[\begin{array}{rr}
2 & -2 \\
4 & 2 \\
-5 & 1
\end{array}\right]\) then find the matrix ‘X’, of order 3 x 2, such that 2A + 3X = 5B. (N.C.E.R.T.)
Solution:
We have : 2A + 3X = 5B
⇒ 2A + 3X-2A = 5B-2A
⇒ 2A-2A + 3X = 5B-2A
⇒ (2A – 2A) + 3X = 5B – 2A
⇒ O + 3X = 5B – 2A
[ ∵ – 2A is the inverse of2A]
⇒ 3X = 5B – 2A.
[ ∵ O is the additive identity]
Hence, X = \(\frac{1}{3}\)(5B – 2A)

Question 5.
If A is a square matrix such that A2 = A, then write the value of 7A – (I + A)3, where I is an identity matrix. (A.I.C.B.S.E. 2014)
Solution:
(I + A)² = (I + A) (I + A)
= II + IA + AI + AA
= I + A + A + A²
= I + 2A + A [∵ A² = A]
= I + 3A …(1)
∴ (I + A)³ = (I + A)² (I + A)
= (I + 3A) (I + A) [Using (1)]
= II + IA + 3AI + 3AA
= I + A + 3A + 3A²
= I + A + 3A + 3A [∵ A² = A]
= I + 7 A …(2)
Hence, 7A – (I + A)³ = 7A – (I + 7A)
[Using (2)]
= -I.

Question 6.
Compute the indicated product:
\(\left[\begin{array}{lll}
2 & 3 & 4 \\
3 & 4 & 5 \\
4 & 5 & 6
\end{array}\right]\left[\begin{array}{rrr}
1 & -3 & 5 \\
0 & 2 & 4 \\
3 & 0 & 5
\end{array}\right]\) (NCERT)
Solution:

Number of columns of A = Number of rows of B = 3.
Thus AB is defined and is a 3 x 3 matrix.


Question 7.
IF A = \(\), show that A² – 6A² + 7A + 2I = 0   (N.C.E.R.T)
Solution:

Question 8.
Prove the following by the principle of Mathematical Induction:
If A = \(\left[\begin{array}{ll}
3 & -4 \\
1 & -1
\end{array}\right]\)
than An = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\) (N.C.E.R.T)
Solution:
Set I. When n = 1

Thus the result is true when n = 1.
Step II. Let us assume that the result is true for any natural number m, where 1 ≤ m ≤ n

Thus the result is true when n = m+ 1.
Hence, by Mathematical Induction, the required result is true for all n ∈ N.

Question 9.
If A = \(\left[\begin{array}{r}
-2 \\
4 \\
5
\end{array}\right]\), B = [1 3 -6], then verify that (AB)’ = B’A’ (N.C.E.R.T.)
Solution:
We have :
A = \(\left[\begin{array}{r}
-2 \\
4 \\
5
\end{array}\right]\), B = [1 3 -6]

From (1) and (2), (AB)’ = B’A’
which verifies the result.

Question 10.
By using elementary transformations, find the inverse of the matrix A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
(N.C.E.R.T.)
Solution:
(By Elementary Row Transformations)
We know A = I₂A

Matrices Important Extra Questions Long Answer Type 2

Question 1.
Two farmers Ram Kishan and Gurucharan Singh cultivate only three varieties of rice namely Basmati, Permal and Naura. The sale (in ?) of these varieties of rice by both the farmers in the month of September and October are given by the following matrices A and B :

Find :
(i) What were combined sales in September and October for each farmer in each variety?
(ii) What was the change in sales from September to October?
(iii) If both farmers receive 2% profit on gross sales, compute the profit for each farmer and for each variety in October. (N.C.E.R.T.)
Solution:
(i) Combined sales in September and October :

(ii) Change in sales from September to October:

(iii) 2% of B = \(\frac{2}{100}\) x B = 0.02 B

Hence, Ram Kishan receives ₹ 100, ₹ 200 and ₹ 120 as profit and Gurucharan Singh receives ₹ 400, ₹200 and ₹ 200 in each variety of rice in the month of October.

Question 2.
Three schools A, B and C organised a mela for collecting funds for helping the rehabilitation of flood victims. They sold handmade fans, mats and plates from recycled meterial at a cost of ₹25, ₹100 and ₹50 each. The number of articles sold are given below :

Find the funds collected by each school separately by selling the above articles. Also, find the total fund collected for the purpose.
(C.B.S.E. 2015)
Solution:
Quantity matrix, A = \(\left[\begin{array}{lll}
40 & 25 & 35 \\
50 & 40 & 50 \\
20 & 30 & 40
\end{array}\right]\)
Cost Matrix B = [laatex]\left[\begin{array}{c}
25 \\
100 \\
50
\end{array}\right][/latex]
Total fund = Quantity matrix x Cost matrix

Fund collected by school A = ₹5,250
Fund collected by school B = ₹7,750
Fund collected by school C = ₹5,500 and total fund collected = 5250 + 7750 + 5500
= ₹18,500.

Question 3.
If A = \(\left(\begin{array}{rr}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right)\), find α satisfing 0 < α < when A + A^T = √2I₂
Where A^T is transpose of A. (A.I.C.B.S.E. 2016)
Solution:

Question 4.
If \(\left(\begin{array}{cc}
a+b & 2 \\
5 & b
\end{array}\right)\) = \(\left(\begin{array}{ll}
6 & 5 \\
2 & 2
\end{array}\right)^{\prime}\) (C.B.S.E. 2010C)
Solution:

Comparing:
a + b – 6 ………….. (1)
and b = 2 ………….(2)
Putting the value of b from (2) in (1),
a + 2 = 6.
Hence, a = 4.

Question 5.
Express the matrix A as the sum of a symmetric and a skew-symmetric matrix, where :
A = \(\left[\begin{array}{rrr}
3 & -2 & -4 \\
3 & -2 & -5 \\
-1 & 1 & 2
\end{array}\right]\) (A.I.C.B.S.E. 2010)
Solution:
We have

Question 6.
Find the inverse of the following matrix, using elementary operations :
A = \(\left[\begin{array}{ccc}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right]\)  (C.B.S.E. 2019)
Solution:
We know that A + I₃A\

Question 7.
Find the inverse of the following matrix, using elementary transformation:
\(\left[\begin{array}{rrr}
2 & -1 & 3 \\
-5 & 3 & 1 \\
-3 & 2 & 3
\end{array}\right]\)  (C.B.S.E. Sample Paper 2017-18)
Solution:
We know that A = IA

Question 8.
If A = \(\left[\begin{array}{rrr}
2 & 1 & 1 \\
1 & 0 & 1 \\
0 & 2 & -1
\end{array}\right]\) , find the inverse of A, using elementary row transformations and hence solve the following equation:
XA = [1 0 1 ] (C.B.S.E. Sample Paper 2017-18)
Solution:
(i) We know that A = I₃ A

Here, x = 0, y = 1, z = 0

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 2 Inverse Trigonometric Functions. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 2 Important Extra Questions Inverse Trigonometric Functions

Inverse Trigonometric Functions Important Extra Questions Very Short Answer Type

Question 1.
Find the principal value of sin^-1 ( \(\frac { 1 }{ 2 }\) )
Solution:
\(\sin ^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{6} \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
Hence, the principal value of sin^-1 ( \(\frac { 1 }{ 2 }\) ) is \(\frac{\pi}{6}\)

Question 2.
What is the principal value of:
cos^-1 (cos \(\frac{2 \pi}{3}\) + sin^-1 (sin \(\frac{2 \pi}{3}\) ) ?
Solution:

Question 3.
Find the principal value of:
tan^-1 (√3)- sec^-1 (-2). (A.I.C.B.S.E. 2012)
Solution:

Question 4.
Evaluate : tan ^-1 ( 2 cos (2 sin^-1 ( \(\frac{1}{2}\) )))
Solution:

Question 5.
Find the value of tan^-1(√3) – cot^-1(-√3). (C.B.S.E. 2018)
Solution:
tan^-1(√3) – cot^-1(—√3)
\(=\frac{\pi}{3}-\left(\pi-\frac{\pi}{6}\right)=-\frac{\pi}{2}\)

Question 6.
If sin^-1 ( \(\frac { 1 }{ 3 }\) ) + cos^-1 x = \(\frac{\pi}{2}\), then find x.(C.B.S.E. 2010C)
Solution:
sin^-1 ( \(\frac { 1 }{ 3 }\) ) + cos^-1 x = \(\frac{\pi}{2}\)
⇒ x = 1/3
[sin^-1 x + cos^-1 x = \(\frac{\pi}{2}\)

Question 7.
If sec^-1 (2) + cosec^-1 (y) = \(\frac{\pi}{2}\) , then find y.
Solution:
sec^-1 (2) + cosec^-1 (y) = \(\frac{\pi}{2}\)
⇒ y = 2 [∵ sec^-1 x + cosec^-1 x= \(\frac{\pi}{2}\) ]

Question 8.
Write the value of sin [ \(\frac{\pi}{3}\) – sin ^-1 ( \(\frac { -1 }{ 2 }\) ) ]
Solution:
sin [ \(\frac{\pi}{3}\) – sin^-1 ( \(\frac { -1 }{ 2 }\) ) ]
= sin [ \(\frac{\pi}{3}\) + sin^-1 ( \(\frac { 1 }{ 2 }\) ) ]
[∵ sin^-1 (-x) = -sin^-1x]
= sin ( \(\frac{\pi}{3}+\frac{\pi}{6}\) ) = sin \(\frac{\pi}{2}\) = 1

Question 9.
Prove the following:

Solution:

Question 10.
If tan^-1 x + tan^-1y = \(\frac{\pi}{4}\) , xy < 1, then write the value of the x + y + xy (A.I.C.B.S.E. 2014)
Solution:
We have tan^-1 x + tan^-1y = \(\frac{\pi}{4}\)

Hence x + y + xy = 1.

Question 11.
Prove that: 3 sin^-1 x = sin^-1(3x – 4x²);
x ∈ [\(\frac { -1 }{ 2 }\) , \(\frac { 1 }{ 2 }\)] (C.B.S.E 2018)
Solution:
To prove: 3 sin^-1 x = sin^-1(3x – 4x²)
Put sin^-1 x = θ
so that x = sin θ.
RHS = sin^-1 (3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3θ) = 3θ = 3 sin^-1x = LHS.

Inverse Trigonometric Functions Important Extra Questions Short Answer Type

Question 1.
Express sin^-1 ( \(\frac{\sin x+\cos x}{\sqrt{2}}\) )
Where \(-\frac{\pi}{4}\) < x < \(\frac{\pi}{4}\), in the simples form.
Solution:

Question 2.
Prove that :
\(\cos ^{-1} \frac{12}{13}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{56}{65}\)   (A.I.C.B.S.E. 2019; C.B.S.E. 2010)
Solution:

Question 3.
Prove that :
sin ^-1 \(\frac{8}{17}\) + cos ^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{36}{77}\) (A.I.C.B.S.E. 2019)
Solution:
L.H.S = sin^-1 \(\frac{8}{17}\) + cos^-1 \(\frac{4}{5}\)
= tan^-1 \(\frac{8}{15}\) + tan^-1\(\frac{3}{4}\)

= R.H.S

Question 4.
Solve the following equation:
\(\tan ^{-1}\left(\frac{x+1}{x-1}\right)+\tan ^{-1}\left(\frac{x-1}{x}\right)=\tan ^{-1}(-7)\) (A.I.C.B.S.E. 2019; C)
Solution:

⇒ 2x² – 8x + 8 = 0
⇒ x² – 4x + 4 = 0
⇒ (x – 2)² = 0.
Hence, x = 2.

Question 5.
Solve the following equation:
2 tan^-1(sin x) = tan^-1 (2 sec x), x ≠ \(\frac{\pi}{2}\)   (C.B.S.E. (F) 2012)
Solution:
2 tan^-1(sinx) = tan^-1 (2 secx)

⇒ tan ^-1 (2sec x tan x) = tan^-1 (2sec x)
⇒ 2 sec x tan x = 2 sec x
tan x = 1 [∵ sec x ≠ 0 ]
Hence, x= \(\frac{\pi}{2}\)

Question 6.
Solve the following equation
cos (tan^-1 x) = sin ( cot ^-1\(\frac { 3 }{ 4 }\) )
(A.I.C.B.S.E. 2013)
Solution:
We have:
cos (tan^-1 x) = sin ( cot ^-1\(\frac { 3 }{ 4 }\) )
cos (tan^-1 x) = sin ( sin ^-1\(\frac { 4 }{ 5 }\) )
cos (tan^-1 x) = \(\frac { 4 }{ 5 }\)
tan^-1 x = cos^-1\(\frac { 4 }{ 5 }\)
⇒ tan^-1 x = tan ^-1\(\frac { 3 }{ 4 }\)
Hence x = \(\frac { 3 }{ 4 }\)

Question 7.
Prove that
3cos^-1 x = cos^-1 (4x³ – 3x), x ∈ [ \(\frac { 1 }{ 2 }\) , 1 ]
Solution:
Put x = cos θ in RHS
As 1/2 ≤ x ≤ 1
RHS = cos^-1 (4cos³ θ – 3cos θ),
= cos^-1 (cos 3θ) = 3θ = 3cos^-1 x = L.H.S

Inverse Trigonometric Functions Important Extra Questions Long Answer Type 1

Question 1.
prove that \(\frac { 1 }{ 2 }\) ≤ x ≤ 1, then
\(\cos ^{-1} x+\cos ^{-1}\left[\frac{x}{2}+\frac{\sqrt{3}-3 x^{2}}{2}\right]=\frac{\pi}{3}\) (CBSE. Sample paper 2017 – 18)
Solution:

Question 2.
Find the value of :
\(\tan ^{-1}\left(\frac{x}{y}\right)-\tan ^{-1}\left(\frac{x-y}{x+y}\right)\)
Solution:

Question 3.
Prove that :
tan ^-1( \(\frac{1}{2}\) ) + tan ^-1 ( \(\frac{1}{5}\) ) + tan ^-1( \(\frac{1}{8}\) ) = \(\frac{\pi}{4}\) (C.B.S.E. 2013: A.I.C.B.S.E. 2011)
Solution:

Question 4.

Solution:

Question 5.

Solution:
Put cos ^-1 (a/b) = θ so that cos θ = a/b.

Question 6.

Solution:

Question 7.

( A.I.C.B.S.E. 2016)
Solution:

Question 8.
\(\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}\) (C.B.S.E. 2016)
Solution:

Question 9.
Solve for x : 2 tan^-1 (cos x ) = tan^-1(2 cosec x). (C.B.S.E. 2016)
Solution:
2 tan^-1 (cos x ) = tan^-1 (cos x) + tan^-1 (cos x)


= tan^-1 (2cot x cosec x) …(1)
Now 2 tan^-1(cos x) = tan^-1(2 cosec x)
⇒ tan^-1(2 cot x cosec x) = tan^-1 (2cosec x)
[Using (1)]
⇒ 2 cot x cosec x = 2 cosec x
⇒ cotx cosecx = cosec x
⇒  sin x = tan x sin x
⇒either sin x = 0 or tan x = 1.
Hence, x = nπ ∀ n ∈ Z or x
= πm + \(\frac{\pi}{4}\) ∀ m ∈ Z

Question 10.
If tan^-1 \(\left(\frac{x-2}{x-4}\right)\) + tan^-1 \(\left(\frac{x+2}{x+4}\right)\) = \(\frac{\pi}{4}\) find the value of ‘x’   (A.I.C.B.S.E. 2014)
Solution:
We have

⇒ 2x² – 16 = -12
⇒ 2x² = 16 – 12
⇒ 2x² = 4
⇒ x² = 2
Hence x = ±√2

Question 11.
If tan^-1 \(\left(\frac{x-3}{x-4}\right)\) + tan^-1 \(\left(\frac{x+3}{x+4}\right)\) = \(\frac{\pi}{4}\) find the value of ‘x’ (A.I.C.B.S.E. 2017)
Solution:

⇒ 2x² – 24 = -7
⇒ 2x² = 17
⇒ 2x² = 4
⇒ x² = 17/2
Hence x = \(\pm \sqrt{\frac{17}{2}}\)

Question 12.
Prove that : \(\tan ^{-1} \sqrt{x}=\frac{1}{2} \cos ^{-1}\left(\frac{1-x}{1+x}\right)\)
x∈ [0,1] (C.B.S.E. 2019C)
Solution:
Let tan ^-1 √x = θ
So that √x = tan θ i.e. x = tan²θ

Question 13.
Solve for x : tan ^-1 (2x) + tan ^-1 (3x) = \(\frac{\pi}{4}\) (C.B.S.E. 2019)
Solution:
The given equation is
tan ^-1 (2x) + tan ^-1 (3x) = \(\frac{\pi}{4}\) …. (1)

⇒ 5x = 1 – 6x²
⇒ 6x² + 5x – 1 = 0
⇒ x = -1 or x = \(\frac{1}{6}\)
Hence, x = \(\frac{1}{6}\)
[∵ x = -1 does not satisfy (1)]

Question 14.
Solve : tan^-1 4x + tan^-1 6x = \(\frac{\pi}{4}\) (C.B.S.E. 2019)
Solution:
We have tan^-1 4x + tan^-1 6x = \(\frac{\pi}{4}\)

⇒ 10x = 1 – 24x²
⇒ 24x² + 10x – 1 = 0
⇒ 24x²+ 12x – 2x – 1 = 0
⇒ 12x(2x + 1) – 1 (2x + 1) = 0
⇒ (2x+1)(12x – 1) = 0
⇒ 2x + 1 = 0 or 12x – 1 = 0
x = \(-\frac{1}{2}\) or x = \(\frac{1}{2}\).
Hence, x = \(-\frac{1}{2}\) or \(\frac{1}{12}\)
As x = \(-\frac{1}{2}\) does not satisfy the given equation.
Hence x = \(-\frac{1}{12}\)

Question 15.
If (tan^-1 x )² + (cot^-1 x )² = \(\frac{5 \pi^{2}}{8}\) , then find ‘x’ (C.B.S.E. 2015)
Solution:
We have
(tan^-1 x )² + (cot^-1 x )² = \(\frac{5 \pi^{2}}{8}\)
Put tan^-1 x = t so that cot^-1x = \(\frac{\pi}{2}\) – t
∴ (1) become : t² + (\(\frac{\pi}{2}\) – t)² = \(\frac{5 \pi^{2}}{8}\)

When tan^-1x = \(\frac{3 \pi}{4}\)
then x = tan \(\frac{3 \pi}{4}\) = -1.
When tan^-1 x = \(-\frac{\pi}{4}\),
then x = tan(\(-\frac{\pi}{4}\)) = -1.
Hence, x = -1.

Question 16.
Write : tan ^-1\(\frac{1}{\sqrt{x^{2}-1}}\) , |x| > 1 in the simplest form.
Solution:
Put x = sec θ

Question 17.
Prove that

(C.B.S.E. 2012)
Solution:

Question 18.
Prove that :
tan^-1x + tan^-1 \(\frac{2 x}{1-x^{2}}\) = tan ^-1\(\frac{3 x-x^{3}}{1-3 x^{2}}\) (N.C.E.R.T
Solution:
Put x = tan θ so that θ = tan ^-1 x

= 3θ = 3 tan^-1x = tan^-1x + 2tan^-1x
= tan^-1x + tan^-1\(\frac{2 x}{1-x^{2}}\)
= L.H.S.

Question 19.
Simplify : tan^-1 [ \(\left[\frac{a \cos x-b \sin x}{b \cos x+a \sin x}\right]\)]
If \(\frac{a}{b}\) tan x > -1    (N.C.E.R.T)
Solution:

Question 20.
Prove that tan ^-1 [ \(\frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}\) ]
= \(\frac{\pi}{4}+\frac{1}{2}\) cos^-1 x ; \(-\frac{1}{\sqrt{2}}\) ≤ x ≤ 1. (C.B.S.E. 2019C)
Solution:

Question 21.
Show that

(N.C.E.R.T.A.I. CBSE 2014)
Solution:

Question 22.
cos[tan^-1{sin (cot^-1x)}] = \(\sqrt{\frac{1+x^{2}}{2+x^{2}}}\)
(A.I. C.B.S.E. 2010)
Solution:
Put cot^-1 = θ so that x = cot θ
∴ sin θ = \(\frac{1}{\sqrt{1+x^{2}}}\)

Question 23.
Find the value of sin (2 tan^-1 1/4) + cos (tan^-1 2√2)   (C.B.S.E. Sample Paper 2018 – 2019)
Solution:
Put tan^-1 1/4 = θ so that θ = 1/4
Now, sin 2θ = \(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\)

To evaluate cos(tan^-1 2√2) :
Put tan^-12√2 = Φ
So that tan Φ = 2√2
cos Φ = 1/3
Hence, sin (2tan^-1(1/4)) + cos (tan^-12√2)
= sin 2θ + cos Φ = \(\frac{8}{17}+\frac{1}{3}=\frac{41}{51}\)
[Using (1) and (2)]

Question 24.
Solve for x:
tan^-1(x – 1) + tan^-1x + tan^-1(x + 1) = tan^-1(3x).    (A.I.C.B.S.E. 2016)
The given equation is:
tan^-1(x —1) + tan^-1(x) + tan^-1(x + 1) = tan^-13x
tan^-1(x— 1)+tan^-1(x+ 1) = tan^-13x – tan^-1


⇒ 1 + 3x² = 2 – x²
⇒ 4x² = 1
⇒ x² = 1/4
⇒ x = \(\pm \frac{1}{2}\)
Hence, x = 0, \(\pm \frac{1}{2}\)