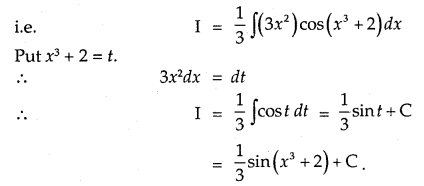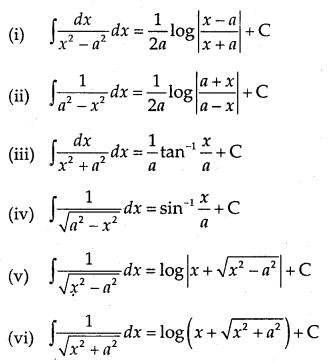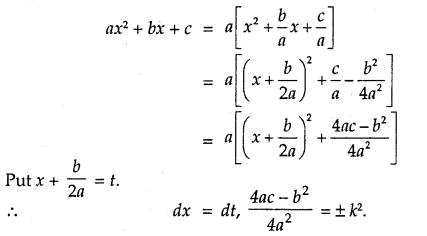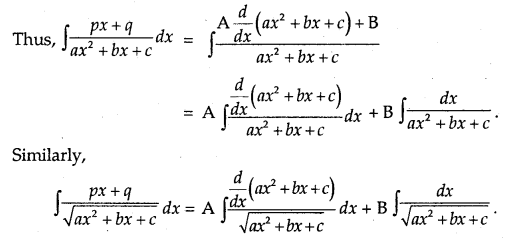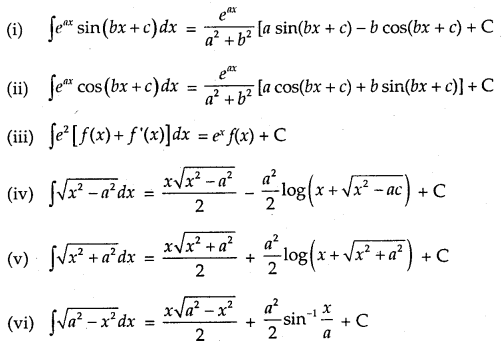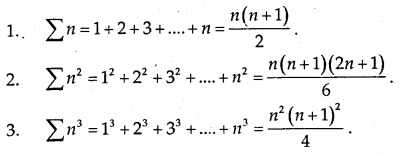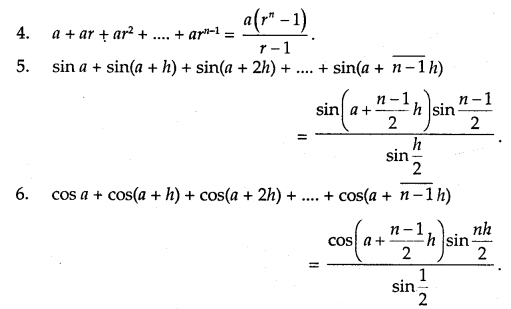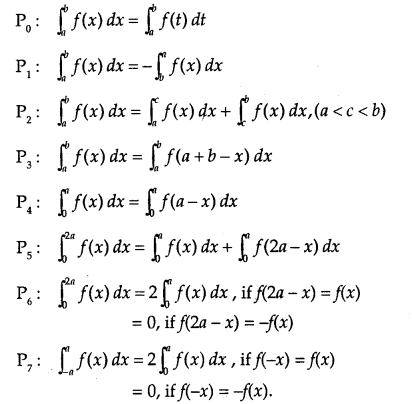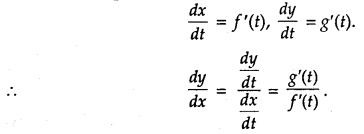CBSE Class 12

By going through these CBSE Class 12 Maths Notes Chapter 9 Differential Equations, students can recall all the concepts quickly.

Differential Equations Notes Class 12 Maths Chapter 9

Differential Equations:
An equation involving the derivative (derivatives) of the dependent variable with respect to the independent variable (variables) is called a differential equation.
e.g. x\(\frac{d y}{d x}\) + y = 0, 2 \(\frac{d^{2} y}{d x^{2}}\) + y³ = 0 are the differential equation

Ordinary Differential Equation:
A differential equation involving derivatives of the dependent variables with respect to only one independent variable is said to be an ordinary differential equation.

Partial Differential Equation:
A differential equation involving derivatives with respect to more than one independent variable is known as a partial differential equation.

Notation: Derivatives may also be written as
\(\frac{d y}{d x}\) = y’, \(\frac{d^{2} y}{d x^{2}}\) = y”, \(\frac{d^{3} y}{d x^{3}}\) = y”’,…………

Order of Differential Equation:
The order of the highest order derivative of the dependent variable with respect to independent variable involved in the differential equation is called the order of the differential equation e.g.
\(\frac{d y}{d x}\) and \(\frac{d^{2} y}{d x^{2}}\) + \(\frac{d y}{d x}\)+ y = k involve derivatives whose highest orders are 1 and 2 respectively.

∴ \(\frac{d y}{d x}\) + y = c is of order 1 and \(\frac{d^{2} y}{d x^{2}}\) + \(\frac{d y}{d x}\) + c y = x is of order 2.
∴ \(\frac{d y}{d x}\) + y = c is order 1 an \(\frac{d^{2} y}{d x^{2}}\) + \(\frac{d y}{d x}\) + c y = x is of order 2.

Degree of differential equation:
When a differential equation is a polynomial equation in derivatives, the highest power (positive integral index) of the highest order derivative is known as the degree of the differential equation e.g.
1. In \(\left(\frac{d y}{d x}\right)^{2}\) + \(\frac{d y}{d x}\) + y = c, the highest order derivative is \(\frac{d y}{d x}\), its positive integral power is 2. Its degree is 2.

2. In \(\frac{d^{3} y}{d x^{3}}\) + \(\frac{d^{2} y}{d x^{2}}\) + \(\frac{d y}{d x}\) + 4 = 0, the highest order derivative is \(\frac{d^{3} y}{d x^{3}}\). Its positive integral power is 1.
∴ Its degree is one.

Solution of differential equation:
The solution of a differential equation is a function y = f(x) which satisfies the given differential equation. It is known as its solution.

General solution (primitive):
The solution which contains as many arbitrary constants as the order of the differential equation is said to be the general solution (primitive) of the differential equation.

Particular solution:
The solution obtained from the general solution by giving particular values to the arbitrary constants is called a particular solution of the differential equation.

Formation of differential equation:
To form a differential equation, we proceed as follows:

1. Write the given equation.
2. Differentiate w.r.t. x successively as many times as the number of arbitrary constants involved in the given equation.
3. Eliminate the arbitrary constants.

The resulting equation is the required differential equation e.g.
(a) The equation y = mx has one arbitrary constant m.

∴ Differentiating, we get \(\frac{d y}{d x}\) = m.
Eliminating m, y = \(\left(\frac{d y}{d x}\right)\)x is the required differential equation.

(b) Consider the family of curves
y = a cos (x + b) …………(1)
Here, a and b are the arbitrary constants.
Now, \(\frac{d y}{d x}\) = – a sin (x + b) …….(2)
and \(\frac{d^{2} y}{d x^{2}}\) = – a cos (x + b) ……(3)

Eliminating a and b using (1) and (3), we get
\(\frac{d^{2} y}{d x^{2}}\) = – y
or
\(\frac{d^{2} y}{d x^{2}}\) + y = 0, which is the required differential equation.

Methods of Solving First Order, First Degree Differential Equations:
1. Variables are Separable
When the equation may be expressed as \(\frac{d y}{d x}\) = h(y) g(x), then we can write it as \(\frac{d y}{h(y)}\) = g(x) dx.
Intergrating, we get the solution as ∫\(\frac{d y}{h(y)}\) = ∫g(x) dx + C.

2. Homogeneous Differential Equation
Let us write the differential equation as \(\frac{d y}{d x}\) = f(x, y).
Replacing x by λ, x, and y by λy, we get f(λx, λy)= λn f(x, y).
Then the differential equation is homogeneous of degree n.

To solve such an equation
\(\frac{d y}{d x}\) = f(x,y),put y = v x
or
\(\frac{d y}{d x}\) = v + x\(\frac{d y}{d x}\)

We get v + x \(\frac{d v}{d x}\) = f(v)
or
x\(\frac{d v}{d x}\) = f(v) – v

∴ Solution is ∫\(\frac{d v}{f(v)-v}\) = ∫\(\frac{d x}{x}\) + C.

3. Linear Differential Equation
(a) The linear differential equation is of the form \(\frac{d y}{d x}\) + Py = Q, where P and Q are the functions of x.

This is a first-order, first-degree differential equation. To solve the equation, we find the integrating factor
I.F. = e^{∫p dx}.

Then, the solution is
ye^{∫p dx} = ∫Qe^{∫p dx} dx + C.

(b) When the equation is of the form \(\frac{d x}{d y}\) + Px = Q,
where P and Q are the functions of y, then
I.F. = e^{∫p dy}
∴ Solution is
x e^{∫p dy} = ∫Qe^{∫p dy} dy + C.

DEFFRENTIAL EQUATION
Definition. An equation f(x, y, \(\frac{d y}{d x}, \frac{d^{2} y}{d x^{2}}, \ldots \frac{d^{n} y}{d x^{n}}\)) = 0, which expresses a relation between dependent and independent variables and their derivatives of any order, is called a differential equation.

2. FORMATION OF DIFFERENTIAL EQUATIONS
Here we differentiate the given equation as many times as the number of arbitrary constants and then eliminate the arbitrary constants from them.

3. SOLUTION OF DIFFERENTIAL EQUATION
It is a relation between the variables involved such that this relation and the differential co-efficients obtained therefrom satisfy the given differential equation.

4. SOLUTION OF DIFFERENT FORMS OF DIFFERENTIAL EQUATIONS
(i) If the equation is :
\(\frac{d y}{d x}\) = f(x), then y = ∫ f(x)dx + c.

(ii) Variables Separable. If the equation is:
\(\frac{d y}{d x}\) = f(x)g(y), then: \(\int \frac{d y}{g(y)}\) = ∫ f(x) + c.

(iii) Reducible to Variables Seperable.
If the equation is \(\frac{d y}{d x}\) = f(ax + by + c), then put ax + by + c= z. dx

(iv) Homogeneous Equation.
If the equation is \(\frac{d y}{d x}=\frac{f(x, y)}{g(x, y)}\), where f(x, y), g(x, y) are homogeneous functions of the degree in x and v. then put y = vx.

(v) Linear Equation.
If the equation is \(\frac{d y}{d x}\) + Px = Q where P, Q are constants or functions of x, then ye^∫Pdx = ∫Qe^∫Pdx dx + c, where e^∫Pdx is the integrating factor (I.F.).

By going through these CBSE Class 12 Maths Notes Chapter 8 Application of Integrals, students can recall all the concepts quickly.

Application of Integrals Notes Class 12 Maths Chapter 8

Area under Simple curves:
1. Let us find the area bounded by the curve y = f(x), x-axis, and the ordinates x = a and x – b. Consider the area under the curve as composed of a large number of thin vertical stripes.

Let there be an arbitrary strip of height y and width dx.
Area of elementary strip dA = y dx, where y = f(x).

Total area A of the region between x-axis, ordinates x – a, x = b and the curve y = f(x)
= sum of areas of elementary thin strips across the region PQML.
A = ∫_a^b dA = ∫_a^b ydx = ∫_a^b f(x) dx.

2. The area A of the region bounded by the curve x = g(y), y-axis, and the lines
y = c and y = d is given by
A = ∫_c^d x dy

3. If the curve under consideration lies below x-axis, then f(x) < 0 from x = a to x = b. So, the area bounded by the curve y = f(x) and the ordinates x = a, x = b and x-axis is negative. But the numerical value of the area is to be taken into consideration.
Then, area = |∫_a^b f(x)dx|.

4. It may also happen that some portion of the curve is above the x-axis and some portion is below the x-axis as shown in the figure. Let A₁ be the area below the x-axis and A₂ be the area above the x-axis. Therefore, area A bounded by the curve y = f(x), x-axis and the ordinates x = a and x = b is given by
A = |A₁| + A₂.

Area between two curves:
1. Let the two curves by y = f(x) and y = g(x), as shown in the figure. Suppose these curve intersect at x = a and x = b.
Consider the elementary strip of height y where y = f(x) – g(x), with width dx.
∴ dA = y dx.
⇒ A = ∫_a^b (f(x) – g(x))dx
= ∫_a^b f(x) dx – ∫_a^b g(x) dx.
= Area bounded by the curve y = f(x) – Area bounded by the curve y = g(x), where f(x) > g(x).

2. If the two curves y = f(x) and y = g(x) intersect at x-a,x – c and x = b such that a < c < b, then:

If f(x) > g(x) in [a, c] and f(x) < g(x) in [c, b], then the area of the regions bounded curve
= Area of the region PAQCP + Area of the region QDRBQ
= ∫_a^c f(x) – g(x)) dx + ∫_c^b (g(x) – f(x)) dx.

1. Area Under Simple Curves
(i) Area of the region bounded by the curve y = f (x), x-axis and the linesx = a and x = b(b > a) is given by the formula:
Area = \(\int_{a}^{b}\) ydy = \(\int_{a}^{b}\) f(x) dy.

2. Area of the region bounded by the curve x = g(x),  y-axis and the lines y = c,y = d is given by the formula:
Area = \(\int_{c}^{d}\) xdy = \(\int_{c}^{d}\) g(y) dy.

2. Area Between two Curves
(i) Area of the region enclosed between two curves y = f (x), y = g (x) and the lines x = a, x = b is
\(\int_{a}^{b}\) [f(x) -g(x)] dx, where f(x) ≥ g (x) in [a, b],

(ii) Iff (x) ≥ g (x) in [a, c] and f(x) ≤ g (x) in [c, b], a < c < b, then we write the area as:
Area = \(\int_{a}^{c}\) [f(x) – g(x)] dx + \(\int_{c}^{b}\) [g(x) – f(x)] dx.

By going through these CBSE Class 12 Maths Notes Chapter 7 Integrals, students can recall all the concepts quickly.

Integrals Notes Class 12 Maths Chapter 7

→ Integration is the inverse process of differentiation. If we are given the derivative of a function and we have to find the function whose derivative is given, the process of finding the primitive or the original function is called the integration or anti-differentation.

Let \(\frac{d}{d x}\)[F(x) + c] = F ‘(x) = f(x)
⇒ F(x) + c is the antiderivative or integal of f(x). This may be written as ∫f(x)dx = F(x) + c,
where c is an arbitrary constant called constant of integration.
∫f(x) dx is called indefinite integral.

Properties of Indefinite Integral.

1. The processes of differentiation and integration are inverse processes of each other, i.e.,
   \(\frac{d}{d x}\)∫f(x) dx = f(x).
2. Indefinite integrals with the same derivatives belong to the same family of curves and so they are equivalent, i.e.,
   in ∫f(x) dx = F(x) + c, [F(x) + c] denotes the same family of indefinite integrals of f(x).
3. ∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x) dx.
4. ∫k f(x) dx = k ∫f(x) dx, where k is real number.
5. If k₁, k₂,………… k_n are the real numbers, then ∫[k₁ f₁(x)+ k₂ f₂(x) +………..+ k_nf_n(x)] dx = k₁∫f₁(x)dx +k₂ ∫f₂(x) dx + +k_n∫f_n(x)dx.

→ We know the formulae for the derivatives of many functions. Corresponding integrals are given below:

Geometrical Interpretation of Indefinite Integral:
∫f(x) dx = F(x) + C = y (say).
y = F(x) + C represents a family of curves. By giving different values to C, we get different members of family. These members can be obtained by shifting any of the curves parallel to itself.

Comparison between Differentiation and Integration:

Integration by Substitution:
Let I = ∫f(x) dx. This integral can be transformed into another form by changing the independent variable x to t by putting x=g(t).
∴ \(\frac{dx}{dt} \) = g'(t) or dx = g'(t) dt
∴ I = ∫f[g(t)]g'(t) dt

Note: While making a substitution, it should be kept in mind that the f[g(t)] is in the form of some standard formula, whereas g'(t) is a factor, along with f[g(t)] e.g.
Consider the integral I = ∫x² cos(x³ + 2)dx
If we put x³ + 2 = t, its derivative 3x² is a factor and cos t can easily be integrated.

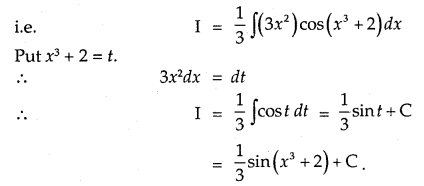
Some Results:

1. ∫tan x = log|sec x| + C
2. ∫cot x = log|sin x| + C
3. ∫sec x = log|sec x + tan x| + C
4. ∫cosec x dx = log|cosec x – cot x| + C

→ Use of Trigonometric Identities:
Use following trigonometric identities for integrating the functions such as sin2x.cos2x, sin3x, cos3x, sin x cos x, etc.

1. sin² x = \(\frac{1-\cos 2 x}{2}\), cos2 x = \(\frac{1+\cos 2 x}{2}\)
2. sin³ x = \(\frac{3 \sin x-\sin 3 x}{4}\), cos2 x = \(\frac{3 \cos x+\cos 3 x}{4}\)
3. 2sinA cosB = sin(A + B) + sin(A – B)
   2cosA sinB = sin(A + B) – sin(A – B)
   2cosA cosB = cos(A + B) + cos(A – B)
   2sinA sinB = cos(A – B) – cos(A + B)

Some more Integrals:

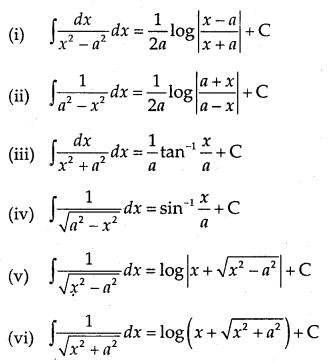
→ How to integrate when the integral has ax² + bx + c or \(\sqrt{a x^{2}+b x+c}\) in the denominator?

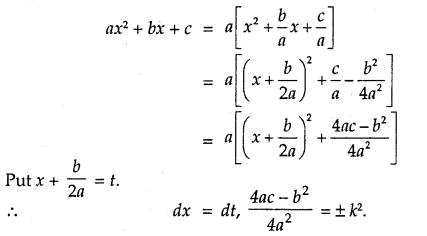
So, ax² + bx + c changes to t² ± k².
Thus, \(\frac{1}{a x^{2}+b x+c}\) converts into the form \(\frac{1}{t^{2} \pm k^{2}}\) and
\(\frac{1}{\sqrt{a x^{2}+b x+c}}\) converts into the form \(\frac{1}{\sqrt{t^{2} \pm \dot{k}^{2}}}\).

→ To find the integration of type ∫\(\frac{p x+q}{a x^{2}+b x+c}\) dx or ∫\(\frac{p x+q}{\sqrt{a x^{2}+b x+c}}\) dx:
Put px + q = A\(\frac{d}{d x} \)(ax² + bx + c) + B

Compare the two sides and find the value of A and B.

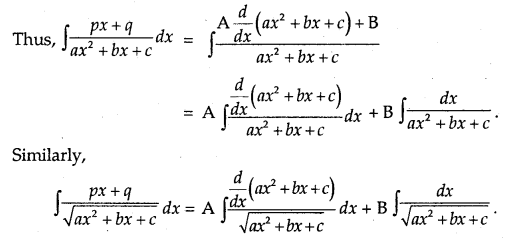
Partial Fractions of Rational Functions.
(a) Let \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) be a rational function, where P(x) and Q(x) are
polynomials, where Q(x) ≠ 0.

1. If degree of P(x) is less than degree of Q(x), then \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) called a proper rational function.
2. If degree of P(x) is greater than the degree of Q(x), then \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) is known as an improper rational function.

This can be expressed in the form f(x) + \(\frac{\mathrm{P}_{1}(x)}{\mathrm{Q}(x)}\) by dividing P(x) by Q(x), so that degree of P1(x) is less than the degree of Q(x).

(b) 1. Let \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) be a proper rational function. Find the factors of Q(x). Let these factors be linear.
P(x)
Suppose Q(x) = (x + a)(x + b)(x + c), Then, \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) is written as
\(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}=\frac{\mathrm{A}}{x+a}+\frac{\mathrm{B}}{x+b}+\frac{\mathrm{C}}{x+c}\)
or
P(x) = A(x + b)(x + c) + B(x + a)(x + e) + C(x+a)(x+ b)

It is an identity which is true for all values of x ∈ R.
To find A,put x =-a.
To find B, put x = – b.
To find C, put x = – c.
Thus, the fractions so obtained on the R.H.S. are the partial fractions. e.g.
Let us find the partial fraction of \(\frac{1}{(x-1)(x-2)}\)

∴ \(\frac{1}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\)
1 = A(x – 2) + B(x – 1)
Put x = 1, 1 = A(1 – 2) = – A
∴ A = -1

Put x = 2, 1 = B(2 – 1) = B
∴ B = 1

2. Let the linear factor(s) be repeated. Q(x) = (x + a)(x + b)2.
Then,
\(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}=\frac{\mathrm{A}}{x+a}+\frac{\mathrm{B}}{x+b}+\frac{\mathrm{C}}{(x+b)^{2}}\)
Also, P(x) = A(x + b)2 + B(x + n)(x + b) + C(x + a)

3. Suppose one of the factors of Q(x) be quadratic.
Let Q(x) = (x + a)(x² + bx + c). Then,
\(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}=\frac{\mathrm{A}}{x+a}+\frac{\mathrm{B} x+\mathrm{C}}{x^{2}+b x+c}\)
Also, P(x) A(x² + b + c) ÷ (x + a)(Bx + c)
Put x = – a, value of A is obtained.
Put x =0, 1, -1, etc., and obtain equations involving A, B, C.

Substitute the value of A in these equations. Then, solve them to find the values of B and C.
OR
Compare the co-efficients of x², x and constant. Solve the equations so obtained e.g.: Let us find the partial fractions of
\(\frac{1}{(x-1)\left(x^{2}+1\right)}\)
\(\frac{1}{(x-1)\left(x^{2}+1\right)}=\frac{A}{x-1}+\frac{B x+C}{x^{2}+1}\)
∴ 1 = A(x² + 1) + (x – 1)(Bx + C)
1 = A(x² + 1) + B(x² – x) + C(x – 1)
Put x=1, I =A(1 + 1) = 2A
∴ A = \(\frac{1}{2}\).

Comparing the coefficients of x², we get
O = A + B
∴ B = -A = – \(\frac{1}{2}\)

Comparing the coefficients of x, we get
O = -B + C
∴ C = B = –\(\frac{1}{2}\).
∴ \(\frac{1}{(x-1)\left(x^{2}+1\right)}=\frac{1}{2(x-1)}-\frac{x+1}{2\left(x^{2}+1\right)}\).

Note: It is obvious that by converting the rational function into partial fractions, we can easily integrate the given rational function.

Integration by Parts
Let u and v be the functions of x, then
∫uv dx = u∫v dx – ∫u'[∫vdx]dx
= u × Integral of v – Integral of (derivative of u × Integral of v]

Note: Out of two functions, which function is to be considered as first. Usually, we proceed as follows:
∫xⁿ f(x) dx xⁿ = u is First function.
∫(Inverse trig, function) × f(x) dx

Inverse trig. function = u is First function.
∫(log x)f(x) dx, Take log x = u as first function.

Some Integrals:

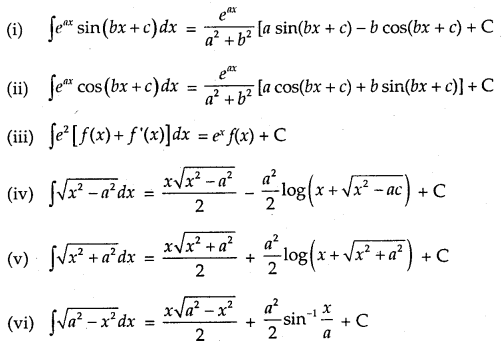
Definite Integral as the Limit of Sum
Definite integral as a limit of a sum is defined as

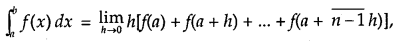
where h = \(\frac{b-a}{n}\). As h → 0, n → ∞.

Note: Some useful series to find the definite integral as the limit of the sum.


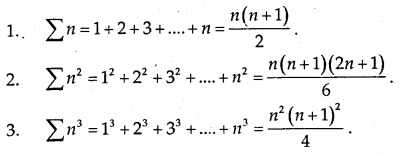
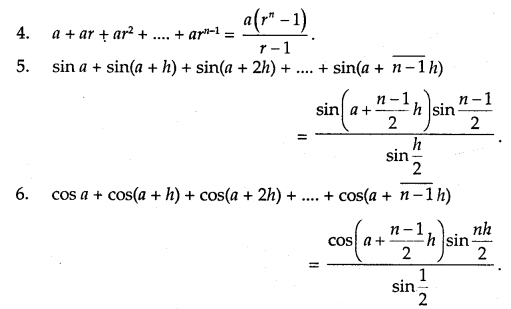
Area Function:
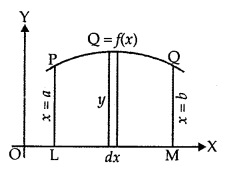
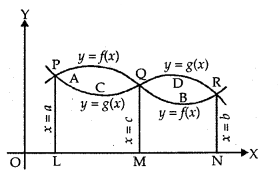
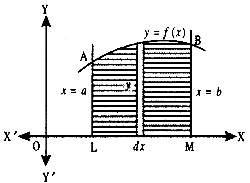
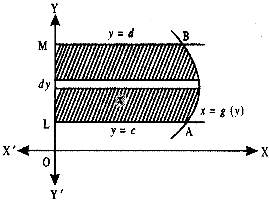
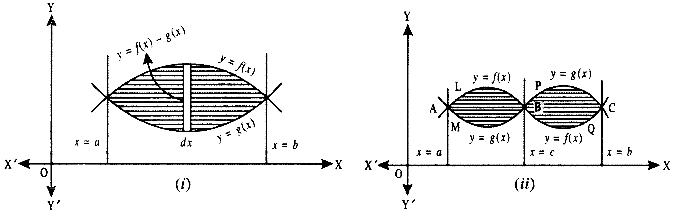
∫_a^bf(x) dx is defined as the area of the region bounded by the curve y = f(x), a ≤ x ≤ b,the x-axis and the ordinates x = a and x = b. Let x be a given point in [a, b]. Then,

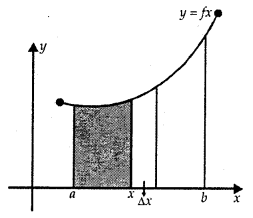
∫_a^b f(x) dx represents the area of the shaded region. It is as shmmed that f(x) > 0 for x ∈ [a, b].
This function is denoted by A(x) which is known as area function. i.e.,
A(x) = ∫_a^x f(x) dx.

→ First Fundamental Theorem of Integral Calculus
Let f be a continuous function on the closed interval [a, b] and let A(x) be the area function. Then, A'(x) =f(x) for all x E [a, b].

→ Second Fundamental Theorem of Integral Calculus
Let f be a continuous function defined on closed interval [a, b] and F be antiderivative of f Then,
∫a b f(x) = [F(x)]ba = F(b) — F(a).

→ Evaluation of Definite Integral by Substitution

1. To evaluate ∫a b f(x) dx, let the substitution be x = g(t) such that dx = g'(t) dt.
2. Let t = t₁ at x = a, t = t₂ at x = b.

The new limits are t1 to t.
∴ ∫ab f(x) dx = ∫_t1 ^t₂ f[g(t)g'(t) dt
= F(t₂) – F(t₁), where
∫f[g(t)]g'(t) dt = F(t).

Properties of Definite Integrals:

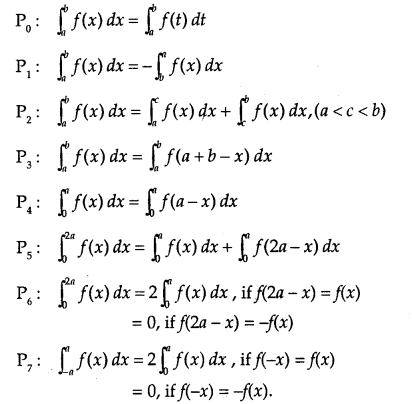
1. DEFINITION
If \(\frac{d}{d x}\) f(x) = F(x), then ∫F(x) dx = f(x) + c, where ‘c’ is a constant of integration.

2. STANDARD RESULTS

(i). Power Rule. ∫ xⁿ dx = \(\frac{x^{n+1}}{n+1}\) + c, provided n ≠ – 1
(ii) ∫ \(\frac{1}{x}\) dx = log |x| + c, x ≠ 0
(iii) ∫a^xdx = \(\frac{a^{x}}{\log a}\) + c, a > 0, a ≠ 1 for all x ∈ R
(iv) ∫ e^x dx = e^x + c ∀ x ∈ R
(v) ∫ sin x dx= -cosx+c ∀ x ∈ R
(vi) ∫ cos x dx = sin x + c ∀ x ∈ R
(vii) ∫ sec² xdx = tan x + c, x ≠ an odd multiple of \(\frac{\pi}{2}\)
(viii) ∫ cosec² x = – cot x + c, x ≠ an even multiple of \(\frac{\pi}{2}\)
(ix) ∫ sec x tan x dx = sec x + c, x ≠ an odd multiple of \(\frac{\pi}{2}\)
(x) ∫ cosec x cot x dx = – cosec x + c,x ≠ an even multiple of \(\frac{\pi}{2}\)
(xi) ∫ tan x dx – – log | cos x | + c = log |sec x| + c, x ≠ x an odd multiple of \(\frac{\pi}{2}\)
(xii) ∫ cot x dx = log |sin x| + c, x ≠ an even multiple of \(\frac{\pi}{2}\)
(xiii) ∫ sec x dx = log |sec x + tan x| + c, x ≠ an odd multiple of \(\frac{\pi}{2}\)
(xiv) ∫ cosec x dx =  log |cosec x – cot x| + c, x ≠ an even multiple of \(\frac{\pi}{2}\).

3. FUNDAMENTAL THEOREMS

(i) ∫ a f(x) dx = a ∫ f(x)dx, where ‘a ’ is any real constant
(ii) ∫ [f₁(x) ± f₂(x)]dx = ∫ f₁(x)dx ± ∫ f₂(x)dx
(iii) \(\frac{d}{d x}\)[∫f(x)dx] = f(x)
(iv) ∫\(\frac{f^{\prime}(x)}{f(x)}\)dx = log |f(x)| + c
(v) ∫ f(x))ⁿ f'(x)dx = (\(\frac{(f(x))^{n+1}}{n+1}\) + c, n ≠ -1
(vi) ∫ \(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx = sin^-1\(\frac{x}{a}\) + c
(vii) ∫ \(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx = \(\frac{1}{a} \tan ^{-1} \frac{x}{a}\) + c
(viii) ∫ \(\frac{1}{\sqrt{a^{2}+x^{2}}}\)dx = log|x + \(\sqrt{a^{2}+x^{2}}\)|+ c
(ix) ∫ \(\frac{d x}{\sqrt{x^{2}-a^{2}}}\) = log|x + \(\sqrt{x^{2}-a^{2}}\) |+ c
(x) ∫ \(\sqrt{a^{2}-x^{2}} d x=\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}+c\)
(xi) ∫ \(\sqrt{a^{2}+x^{2}} d x=\frac{x}{2} \sqrt{a^{2}+x^{2}}+\frac{a^{2}}{2} \log \left|x+\sqrt{a^{2}+x^{2}}\right|+c\)
(xii) ∫ \(\sqrt{x^{2}-a^{2}} d x=\frac{x}{2} \sqrt{x^{2}-a^{2}}-\frac{a^{2}}{2} \log \left|x+\sqrt{x^{2}-a^{2}}\right|+c\)
(xiii) ∫ \(\frac{1}{a^{2}-x^{2}}\)dx = \(\frac{1}{2 a} \log \left|\frac{a+x}{a-x}\right|\)+ c
(xiv) ∫ \(\frac{1}{x^{2}-a^{2}}\)dx = \(\frac{1}{2 a} \log \left|\frac{x-a}{x+a}\right|\)+ c

4. IMPORTANT RULES

(i) Rule to integrate ∫ sin^m x cosⁿ x dx.
(a) If the index of sin x is a positive odd integer, put cos x = t.
(b) If the index of cos x is a positive odd integer, put sin x = t.

(ii) Rule to integrate : \(\int \frac{1}{a \sin ^{2} x+b \cos ^{2} x} d x, \int \frac{1}{a+b \cos ^{2} x} d x\) ; etc.
a sin x + b cos x J a + b cos x
(a) Divide the numerator and denominator by cos²x
(b) Replace sec²x, if any, in the denominator by 1 + tan²x
(c) Put tan x = t so that sec²x dx = dt.

(iii) Integration of Parts.
Integral of the product of two functions = First function x Integral of second – Integral [(diff. coeff. of first) x (integral of second)].

(iv) Rule to integrate \(\int \frac{1}{\text { linear } \sqrt{\text { linear }}} d x\) or \(\int \frac{1}{\text { quadratic } \sqrt{\text { linear }}} d x\) Put \(\sqrt{\text { linear }}=t\)

(v) Rule of integrate \(\int \frac{1}{\text { linear } \sqrt{\text { quadratic }}} d x\) Put linear = \(\frac { 1 }{ t }\)

(vi) Rule to integrate \(\int \frac{x d x}{\text { (Pure Quad.) } \sqrt{\text { Pure Quad }}}\). Put \(\sqrt{\text { Pure Quad }}\) = t

(vii) Rule to integrate \(\int \frac{d x}{\text { (Pure Quad.) } \sqrt{\text { Pure Quad }}}\) Put x = \(\frac{1}{t}\) and \(\sqrt{\text { Pure Quad }}\) = u.

5. Integral As The Limit of a sum

\(\int_{a}^{b}\) f(x)dx = \(\lim _{h \rightarrow 0}\) h[f(a)+f(a + h)+f(a + 2h)+… + f(a + \(\overline{n-1}\)h)], where h = \(\frac{b-a}{n}\).

6. FUNDAMENTAL THEOREM OF INTEGRAL CALCULUS

\(\int_{a}^{b}\)f(x) dx = F(b) – F(a), where ∫ f(x) dx = F(x).

7. PROPERTIES OF DEFINITE INTEGRALS

I. \(\int_{a}^{b}\) f(x)dx = \(\int_{a}^{b}\) f(t) dt

II. \(\int_{a}^{b}\) f(x)dx = –\(\int_{a}^{a}\)f(x)dx. Particular case: \(\int_{a}^{a}\)f(x)dx = 0

III. \(\int_{a}^{b}\) f(x)dx = \(\int_{a}^{b}\) f(a + b – x)dx.

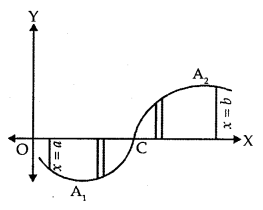
IV. \(\int_{a}^{b}\) f(x)dx = \(\int_{a}^{c}\)f(x)dx + f(x)dx = \(\int_{c}^{b}\) f(x)dx, where a < b < c

V. \(\int_{0}^{a}\) f(x)dx = \(\int_{a}^{b}\) f(a – x)dx

VI. \(\int_{-a}^{a}\) f(x)dx = 0 if f(-x) = -f(x)
= 2\(\int_{0}^{a}\) f(x)dx if f(-x) = f(x)

VII. \(\int_{0}^{2a}\) f(x)dx = \(\int_{0}^{a}\) f(x)dx =\(\int_{0}^{a}\) f(2a – x)dx

VIII. \(\int_{0}^{2a}\) f(x)dx = 2\(\int_{0}^{a}\) f(x) dx
= 0

f(2a-x)dx = f(x)
if (2a – x) = f(x)

By going through these CBSE Class 12 Maths Notes Chapter 6 Application of Derivatives, students can recall all the concepts quickly.

Application of Derivatives Notes Class 12 Maths Chapter 6

Rate of change of Quantities: Let y =f(x) be a function. If the change in one quantity y varies with another quantity x, then \(\frac{d y}{d x}\) = f ‘ (x) denotes the rate of change of y with respect to x. At x = x₀\(\left.\frac{d y}{d x}\right]_{x=x_{0}}\), or f'(x) represents the rate of change of y w.r.t. x at x = x₀.

Let I will be the open interval contained in the domain of real-valued function f.

Increasing Function: f is said to be increasing function on I, if x₁ < x₂ on I, then f(x₁) ≤ f(x₂) for all x₁, x₂ ∈ I.

Strictly Increasing Function: f is said to be strictly increasing on I if x₁ < x₂ in I ⇒ f(x1) < f(x₂) for all x₁, x₂ ∈ I.

Decreasing Function: f is said to be decreasing function on I, if x₁ < x₂ in I, then f(x₁) ≥ f(x₂) for all x₁, x₂ ∈ I.

Strictly Decreasing Function: f is said to be strictly decreasing function on I, if x₁ < x₂ in I ⇒ f(x₁) > f(x₂) for all x₁, x₂ ∈ I.

Increasing and Decreasing Functions at x₀:
Let x₀ be a point in the domain of definition of a real valued function f and there exists an open interval I = (x₀ – h, x₀ + h) containing x0 such that

1. f is increasing at x₀, if x₁ < x₂ in I ⇒ f(x₁) ≤ f(x₂).
2. f is strictly increasing at x₀, if x₁ < x₂ in I ⇒ f(x₁) < f(x₂).
3. f is decreasing at x₀, if x₁ < x₂ in I ⇒ f(x₁) ≥ f(x₂).
4. f is strictly decreasing at x₀, if x₁ < x₂ ⇒ f(x₁) >f(x₂).

Test: Increasing/decreasing/constant Functions:
Let f be continuous on [a, b] and differentiable in an open interval (a, b), then

1. f is increasing on [a, b], if f ‘(x) > 0 for each x ∈ (a, b).
2. f is decreasing on [a, b], if f ‘(x) < 0 for each x ∈ (a, b).
3. f is constant on [a, b], if f ‘(x) = 0 for each x ∈ (a, b).

→ Tangent to a curve: Let y = f(x) be the equation of a curve. The equation of the tangent at (x₀, y₀) is y – y₀ = m(x – x₀),
where m = slope of the tangent
= \(\left.\frac{d y}{d x}\right]_{\left(x_{0}, y_{0}\right)}\) = f ‘(x₀).

→ Normal to the curve: Let y = f(x) be the equation of a curve.
Equation of the normal is
y – y₀ = – \(\frac{1}{m}\)(x – x₀)
or
x – x₀ + m(y – y₀) = 0,
where m = slope of the tangent
= \(\left.\frac{d y}{d x}\right]_{\left(x_{0}, y_{0}\right)}\) = f ‘(x₀)

It may be noted that, slope of normal
= – \(\frac{1}{m}=\frac{-1}{f^{\prime}\left(x_{0}\right)}\).

→ Particular case of tangent: Let m = tan θ. If θ = 0, then m = 0.
Equation of tangent is y – y₀ = 0, i.e., y = y₀.
If θ = \(\frac{π}{2}\), m is not defined.
∴ (x – x₀) = \(\frac{1}{m}\) (y – y₀).
when θ = \(\frac{π}{2}\), then cot \(\frac{π}{2}\) = 0.

∴ Equation of tangent is x – x₀ = 0 or x = x₀.

→ Approximation: Let f: D → R, D⊂R such that y = f(x) and Δy is the increment in y corresponding to increment Δx in x, where Δy = f(x + Δx) – f(x).
Now,

1. the differential of x denoted by dx is defined by dx = Δx
2. The differential of y, denoted by dy, is defined by
   dy = f ‘(x)dx
   or
   dy = (\(\frac{dy}{dx}\))Δx

Maximum value, Minimum Value, Extreme Value:
Let f be a function defined in the interval I. Then,
1. Maximum Value:
If there exists a point x = c in I such that f(c) > f(x), for all x ∈ I, then/is maximum in I. Point c is known as a point of the maximum value in I.

2. Minimum Value:
If there exists a point x = c in I such that f(c) ≤ f(x), for all x ∈ I, then/is minimum in I. Point c is called as a point of the minimum value in I.

3. Extreme Value:
If there exists a point x = c in I such that f(c) is either a maximum value or a minimum value in I, then f is having an extreme value in I. Point c is said to be an extreme point.

Local Maxima and Minima:
Let f be a real-valued function and x = c be an interior point in the domain of f, then
(a) Local Maxima: c is a point of local maxima, if there is an h > 0, such that f(c) ≥ f(x) for all x ∈ (c – h, c + h).
The value f(c) is called the local maximum value of f.

(b) Local Minimum: c is a point of local minimum, if there is an h > 0, such that f(c) ≤ f(x) for all x ∈ (c – h, c + h).
The value of f(c) is known as the local minimum value of f.

Geometrically if x = c is a point of local maxima of f, then f is increasing (f ‘(x) > 0) in the interval (c – h, c) and decreasing (f ‘(x) < 0) in the interval (c, c + h)

This implies f ‘(c) = 0.

Test of Maxima and Minima:
1. Let f be a function on an open interval I and c ∈ I will be any point. If f has local maxima or local minima at x = c, then either f ‘(c) = 0 or f is not differentiable at c.

Let f be continuous at a critical point c in it.

2. If f ‘(x) changes sign from positive to negative as x increases through c, i.e.,

1. (i) f ‘(x) > 0 at every point in (c – h, c) and
2. (ii) f ‘(x) < 0 at every point in (c, c + h), where h is sufficiently small, then there is a point of local maxima.

3. If f ‘(x) changes sign from negative to positive as x increases through c, i.e.,

1. f(x) < 0 at every point in (c – h, c) and
2. f ‘(x) > 0 at every point in (c, c + h), where It is sufficiently small, then c is a point of local minima.

4. If f ‘(x) does not change significantly as x increase through c, then c is neither a point of local maxima nor a point of local minima. Such a point is called point of inflection.

Second Derivative Test of Maxima and Minima:
Let f be a function defined on an interval I and c ∈ I and f be differentiable at c. Then,

1. Maxima: x = c is a local maxima, if f'(c) = 0 and f “(c) < 0.
2. Minima: x = c is a local minima, iff'(c) = 0 and f “(c) > 0. Here, f(c) is the local minimum value off.
3. Point of Inflection: If f ‘(c) = 0 and f “(c) = 0, then test fails. Then, we apply the first derivative test as x increases through c.

Maximum and Minimum Values in a Closed Interval:
Consider the function f(x) = x+ 3, x ∈ [0,1]. Here f ‘(c) ≠ 0. It has neither maxima nor minima. But f(0) = 3. This is the absolute minimum or global minimum or least value.

Further, f(1) = 4. This is the absolute maximum or global maximum or greatest value.
Further, consider f be any other continuous function having local maxima and minima.

Absolute Maxima and Minima:
Let f be a continuous YA function on an interval I = [a, b].
Then, f has the absolute maximum value and/attains it at least once in I. Similarly,f has the absolute minimum value and attains at least once in I.

At x = b, there is a minimum.
At x = c, there is a maxima.
At x = a, f(a) is the greatest value or absolute maximum value.
– At x = d,f(d) is the least value or absolute minimum value.

To find absolute maximum value or absolute minimum value:

1. Find all the critical points viz. where f ‘ (x) = 0 or f is not differentiable.
2. Consider the endpoints also.
3. Calculate the values of the function at all the points found in steps (1) and (2).
4. Identify the maximum and minimum values out of the values calculated in step 3. These are absolute maximum and absolute minimum values.

1. DERIVATIVEASARATEMEASURE
f'(x) is the rate measure of fix) w.r.t. x.

2. INCREASING AND DECREASING FUNCTIONS

(i) A function f(x) is said to be increasing function of x
if x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂)
or x₁ ≥ x₂ ⇒ f(x₁) ≥ f(x₂)

(ii) A function f(x) is said to be a strictly increasing function of x
if x₁ < x₂ ⇒ f(x₁) < f(x₂)
or x₁ > x₂ ⇒ f(x₁) > f(x₂)

(iii) A function f(x) is said to be a decreasing function of x,
if x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂)
or x₁ ≥ x₂ ⇒ f(x₁) ≤ f(x₂)

(iv) A function f(x) is said to be a strictly decreasing function of x,
if x₁ < x₂ ⇒ f(x₁) > f(x₂)
or x₁ > x₂ ⇒ f(x₁) < f(x₂)

(v) Monotone Function. A function is said to be monotone if it is either increasing or decreasing.

3. TANGENTSANDNORMALS

(i) lf y = f(x), then the slope of the tangent at P (x = c) is \(\left.\frac{d y}{d x}\right]_{x=c}\)

(ii) Equation of the normal at P(x’, y’) to the curve y = f(x) is y – y’ =\(\left(\frac{d y}{d x}\right)_{\mathrm{P}}\) (x – x’)

(iii) Equation of the normal at P(x’, y’) to the curve y = f(x) is y – y’= \(-\frac{1}{\left(\frac{d y}{d x}\right)_{\mathrm{P}}}\) (x – x’)

4. MAXIMA AND MINIMA

(i) Method to find absolute max. and min., values in a given interval.
(a) Find all points when \(\frac{d y}{d x}\) =0.
(b) Take end points of the interval.
(c) At all these points, calculate values of y.
(d) Take the maximum and minimum values out of these values.

(ii) If f(a) is an extreme value of f(x), then f'(a) = 0.

(iii) Local Maximum and Minimum values.
(a) First Derivative Test GUIDE-LINES:
Let y=f(x).
Step (i) Put \(\frac{d y}{d x}\) = 0. Solve it for getting x = a, b, c,… dx

Step (ii) Select x = a.
Study the sign of \(\frac{d y}{d x}\) when (I) x < a slightly dx (II) x > a slightly.
(a) If the former is + ve and latter is -ve, then f(x) is max. at x = a.
(b) If the former is – ve and latter is +ve, then f(x) is min. at x = a.

Step (iii) Putting those values of x for which f(x) is max. or min. and get the corresponding max. or min. values of f(x).

(b) Second Derivative Test GUIDE-LINES:
Step (i) Put y = f(x) and find \(\frac{d y}{d x}\) i.e., f(x).

Step (ii) Put \(\frac{d y}{d x}\) = 0 i.e. f'(x) = 0 and solve it for x giving 😡 = a, b, c,…

Step (iii) Select x = a. Find \(\frac{d^{2} y}{d x^{2}}\) i.e. f”(x) at x = a.

(I) If \(\left.\frac{d^{2} y}{d x^{2}}\right]_{x=a}\) i. e. f”(a) is -ve, then x = a gives the max. value.
(II) If \(\left.\frac{d^{2} y}{d x^{2}}\right]_{x=a}\)i.e. f”(a) is +ve, then x = a gives the min. value.
Similarly for x = b, c,…

By going through these CBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability, students can recall all the concepts quickly.

Continuity and Differentiability Notes Class 12 Maths Chapter 5

Continuity (Definition): if f be a real-valued function on a subset of real numbers and let c be a point in its domain, then f is a continuous function at e, if

Obviously, if the left-hand limit and right-hand limit and value of the function at x = c exist and are equal to each other, i.e., if

then f is continuous at x = c.

Algebra of continuous functions:
Let f and g be two real functions, continuous at x = c, then

1. Sum of two functions is continuous at x = c, i.e., (f + g) (x), defined as f(x) + g(x), is continuous at x = c.
2. Difference of two functions is continuous at x = c, i.e., (f – g) (x), defined as f(x) – g(x), is continuous at x = c.
3. Product of two functions is continuous at x = c, i.e., (f g) (x), defined as f(x) . g(x) is continuous at x = c.
4. Quotient of two functions is continuous at x = c, (provided it is defined at x = c), i.e.,
   (\(\frac{f}{g}\))(x), defined as \(\frac{f(x)}{g(x)}\) [g(x) ≠ 0], is continuous at x = c.

However, if f(x) = λ, then
(a) λ.g, defined ty .g(x), is also continuous at x = c.
(b) Similr1y, if \(\frac{λ}{g}\) is defined as \(\frac{λ}{g}\) (x) = \(\frac{λ}{g(x)}\) , then \(\frac{λ}{g}\) is also continuous at x = c.

→ Differentiability: The concept of differentiability has been introduced in the lower class. Let us recall some important results.

→ Differentiability (Definition): Let f be a real function and c is a point in its domain. The derivative of f at c is defined as

Every differentiable function is continuous.

→ Algebra of Derivatives: Let u and v be two functions of x.

1. (u ± v)’ = u’ ± v’
2. (uv)’ = u’v + uv’
3. \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}\), where v ≠ 0.

→ Derivative of Composite Function: Let t be a real valued function which is a composite of two functions u and v, i.e., f = vou. Put u(x) = t and f= v(t).
∴ \(\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}\)

→ Chain Rule: Let/be a real valued function which is a composite fimction of u, v and w, i.e., f(wov)ou.
Put u(x) = t, v(t) = s and f = w(s). Then,
\(\frac{d f}{d x}=\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x}\).

→ Derivatives of Inverse Trigonometric Functions:

Implicit Functions: An equation in form f(x, y) = 0, in which y is not expressible in terms of x, is called an implicit function of x and y.

Both sides of the equations are differentiated termwise. Then, from this equation, \(\frac{d y}{d x}\) is obtained. It may be noted that when a function of y occurs, then differentiate it w.r.t. y and multiply it by \(\frac{d y}{d x}\).

e.g., To find \(\frac{d y}{d x}\) from cos² y + sin xy = 1, we differentiate it as

Exponential Functions:

The exponential function, with positive base b > 1, is the function y = b^x.

1. The graph of y = 10^x is shown in the figure.
2. Domain = R
3. Range = R⁺
4. The point (0,1) always lies on the graph.
5. It is an increasing function, i.e., as we move from left to right, the graph rises above.
6. As x → – ∞, y → 0.
7. \(\frac{d}{dx}\) (a^x) = a^x log, a, \(\frac{d}{dx}\) e^x = e^x.

Logarithmic Functions:
Let b> 1 be a real number. b^x = a may be written as log_b a = x.

1. The graph of y = log₁₀ x is shown in the figure.
2. Domain = R⁺, Range = R.
3. It is an increasing function.
4. As x → 0, y → ∞.
5. The function y = e^x and y = log_e x are the mirror images of each other in the line y = x.
6. \(\frac{d}{dx}\) (loga x) = \(\frac{1}{x}\) l0ga e, \(\frac{d}{dx}\) loge x = \(\frac{1}{x}\)

→ Other properties of Logarithm are:

1. log_b pq = log_b p + log_b q
2. log_b \(\frac{p}{q}\) = log_a p – log_a q
3. log_b px = x log_b p – log_b q
4. log_a b = \(\frac{\log _{a} p}{\log _{b} p}\)

→ Logarithmic Differentiation:
Whenever the functions are given in the form

1. y = [u(x)]v(x) and
2. y = \(\frac{u(x) \times v(x)}{w(x)}\)

take log of both sides. Simplify and differentiate, e.g.,
Let y = (cos x)sin x, log y = sin x log cos x

Differentiating, \(\frac{1}{y}\) \(\frac{dy}{dx}\) = cos x log Cos x + sin x . – \(\frac{sin x}{cos x}\)
∴ \(\frac{dy}{dx}\) = (cos x)^{sin y} [cos x log cosx – sin x tan x].

→ Derivatives of Functions in Parametric Form: Let the given equations be x = f(t) and y = g(t), where t is the parameter. Then,

→ Second Order Derivative:
Let y = f(x), then \(\frac{dy}{dx}\) =f ‘(x).
If f ‘(x) is differentiable, then it is again differentiated.

Rolle’s Theorem:
Let f: [a, b] → R be continuous on closed interval [a, b] and differentiable on open interval (a, b) such that f(a) = f(b), where a and b are real numbers, then there exists some c ∈ (a, b) such that f ‘(c) = 0.

From the figure, we observe that f(a) = f(b). There exists a point c₁ ∈ (a, b) such that f ‘ (c) = 0, i.e., tangent at c1 is parallel to x-axis. Similarly, f(b) = f(c) → f ‘ (c₂) = 0.

→ Mean Value Theorem: Let f: [a, b] → R be a continuous function on the closed interval [a, b] and differentiable in the open interval (a, b). Then, there exists some c ∈ (a, b) such that
f ‘ (c) = \(\frac{f(b)-f(a)}{b-a}\)

Now, we know that \(\frac{f(b)-f(a)}{b-a}\) is the slope of secant drawn between A[a,f(a)] and B[b,f(b)]. We t k know that the slope of the line joining (x_1, y₁) and (x₂, y₂) is \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

The theorem states that there is a point c ∈ (a, b), where f ‘(c) is equal to the slope of AB.

In other words, there exists a point c ∈ (a, b) such that tangent at x = c is parallel to AB.

1. CONTINUITY
(i) Left Continuity. A function ‘f ’ is left-continuous at x = c if \(\lim _{x \rightarrow c^{-}}\) f (x) = f(c).

(ii) Right Continuity. A function ‘f ’ is right-continuous at x = c if \(\lim _{x \rightarrow c^{+}}\) f (x) = f(c).

(iii) Continuity at a point. A function ‘ f ’ is continuous at x = c if
\(\lim _{x \rightarrow c^{-}}\) (x) = \(\lim _{x \rightarrow c^{+}}\) f(x) = f(c).

2. (i) Polynominal functions
(ii) Rational functions
(iii) Exponential functions
(iv) Trigonometric functions are all continuous at each point of their respective domain.

3. DIFFERENTIABILITY
(i) Left Derivative. A function ‘f ’ is said to possess left derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c-h)-f(c)}{-h}\) exists finitely.

(ii) Right Derivative. A function ‘f ’ is said to possess right derivative at x = c if
\(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.
(iii) Derivative. A function is said to possess derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.

4. CONTINUITY AND DERIVABILITY
A real valued function is finitely derivable at any point of its domain, it is necessarily continuous at that point. The converse is not true.

5. STANDARD RESULTS

(i) \(\frac{d}{d x}\) (xⁿ) = nx^n-1 ∀ x ∈ R
(ii) \(\frac{d}{d x}\) ((ax + b)n = n(ax + b)^{n – 1} . a ∀ x ∈ R
(iii) \(\frac{d}{d x}(|x|)=\frac{x}{|x|}\), x ≠ 0

6. GENERAL THEOREMS
(i) The derivative of a constant is zero.
(ii) An additive constant vanishes on differentiation i.e. if f(x) = g(x) + c, where ‘c’ is any constant, then f'(x) = g'(x).
(iii) If f(x) = ag(x), then f'(x) = ag'(x), where ‘a’ is a scalar.
(iv) If f(x) = g(x) + h(x), then f'(x) = g'(x) + h'(x).

Extension.
If f(x) = a₁f₁ ± a₂f₂ ……. ± a_nf_n(x), then :
f'(x) = a₁f₁‘(x) ± a₂f₂‘(x) ± ……. ± a_nf_n‘(x)

(v) If f(x) = \(\frac{g(x)}{h(x)}\), then f'(x) = g(x)h'(x) + g'(x)h(x)
(vi) If f(x) = \(\frac{g(x)}{h(x)}\), then f ‘(x) = \(\frac{h(x) g^{\prime}(x)-g(x) h^{\prime}(x)}{(h(x))^{2}}\), h(x) ≠ 0.
(vii) If f(x) = \(\frac{1}{h(x)}\), then f'(x) = \(-\frac{h(x)}{[h(x)]^{2}}\), h'(x) ≠ 0

7. IMPORTANT RESULTS

(i) (a) \(\frac{d}{d x}\) (sinx) = cos x and \(\frac{d}{d x}\) (cos x) = – sin x ∀ x ∈ R
(b) \(\frac{d}{d x}\) (tan x) = sec² x and \(\frac{d}{d x}\) (sec x) = sec x tan x ∀ x ∈ R except odd multiples of \(\frac{\pi}{2}\)
(c) \(\frac{d}{d x}\)(cot x) = – cosec² x and \(\frac{d}{d x}\) (cosec x) = -cosec x cot x ∀ x ∈ R except even multiple of \(\frac{\pi}{2}\)

(ii)
(a) \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(b) \(\frac{d}{d x}\)(cos^-1x) = \(-\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(c) \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^{2}}\) ∀ x ∈ R
(d) \(\frac{d}{d x}\)(cot^-1x) = \(-\frac{1}{1+x^{2}}\) ∀ x ∈ R
(e) \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{|x| \sqrt{x^{2}-1}}\) x > 1 or x < -1
(f) \(\frac{d}{d x}\)cosec^-1x) = \(-\frac{1}{|x| \sqrt{x^{2}-1}}\), x > 1 or x < -1

(iii) (a) \(\frac{d}{d x}\) (a^x) = a^x log_e a, a > 0
(b) \(\frac{d}{d x}\)(e^x) = e^x
(c) \(\frac{d}{d x}\)(log_a x) = \(\frac{1}{x}\) log_a e, x > 0
(d) \(\frac{d}{d x}\) (log x) = \(\frac{1}{x}\), x>0.

8. CHAIN RULE
\(\frac{d}{d x}\) (f(g(x)) = f'(g(x)).g'(x)

9. PARAMETRIC EQUATIONS
\(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}\), \(\frac{d x}{d t}\) ≠ 0
Or \(\frac{d y}{d x}=\frac{d y}{d t} \times \frac{d t}{d x}\)

10.MORE RESULTS

(i) \(\frac{d y}{d x}=\frac{1}{\frac{d x}{d y}}\)
(ii) \(\frac{d y}{d x} \times \frac{d x}{d y}=1\)

11. ROLLE’S THEOREM
If a function f(x) is :

(i) continuous in [a, b]
(ii) derivable in (a, b)
(iii) f (a) = f (b), then there exists at least one point ‘c’ in (a, b) such that f’ (c) = 0.

12. LAGRANGE’S MEAN VALUE THEROEM (LMV THEOREM OR MV THEOREM)
If a function f(x) is :
(i) continuous in [a, b]
(ii) derivable in (a, b), then there exists at least one point ‘c’ in (a, b) such that \(\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)\)