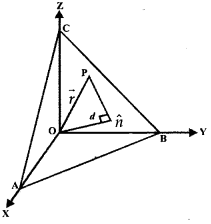
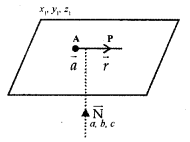
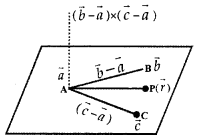
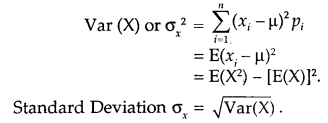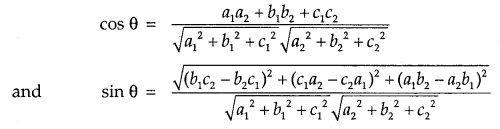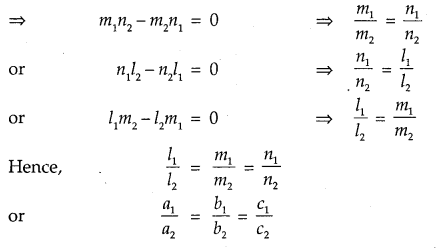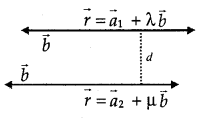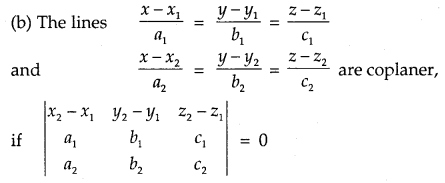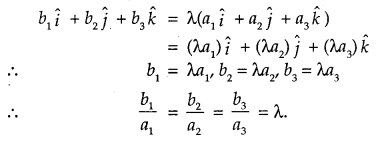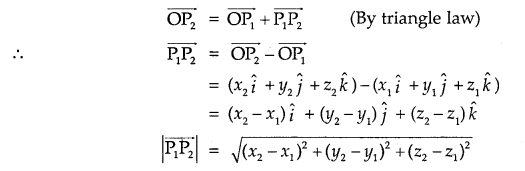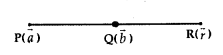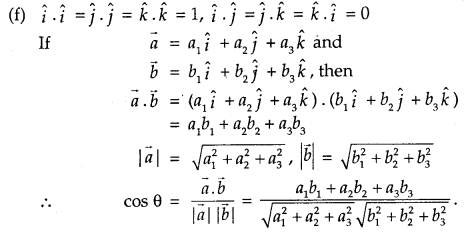By going through these CBSE Class 12 Maths Notes Chapter 10 Vector Algebra, students can recall all the concepts quickly.
Vector Algebra Notes Class 12 Maths Chapter 10
Some Basic Concepts:
1. Vector (Definition): A quantity that has magnitude, as well as direction, is called a vector.
\(\overrightarrow{\mathrm{AB}}\) is a directed line segment.

It is a vector \(\overrightarrow{\mathrm{AB}}\) and its direction is from A to B.
→ Initial Points: The point A wherefrom the vector \(\overrightarrow{\mathrm{AB}}\) starts is known as the initial point.
→ Terminal point: Point B, where it ends is said to be the terminal point.
→ Magnitude: The distance between initial point and terminal point of a vector is the magnitude (or length) of the vector \(\overrightarrow{\mathrm{AB}}\) . It is denoted by |\(\overrightarrow{\mathrm{AB}}\)| or |\(\overrightarrow{\mathrm{a}}\)| or simply as a.
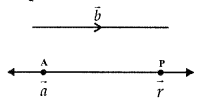
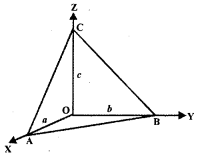
2. Position Vector: Consider a point F(x, y, z) in space. The vector \(\overrightarrow{\mathrm{OP}}\) with an initial point as origin O and terminal point P, is called the position vector of P. It may be denoted by \(\overrightarrow{\mathrm{p}}\).
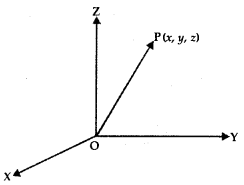
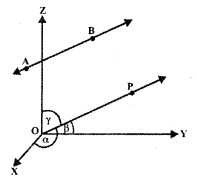
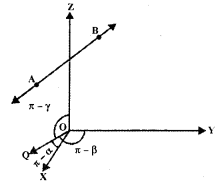
3. Direction Cosines: Let OX, OY, OZ be the coordinates axes and F(x, y, z) be any point in the space. Let OP makes angles α, β, γ with coordinates axes OX, OY, OZ respectively.
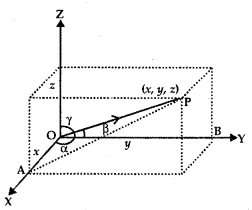
The angles α, β, γ are known as direction angles. The cosine of these angles, i.e., cos α, cos β, cos γ is called direction cosines of line OP. These direction cosines are denoted by Z, m, n, i.e., Z = cos α, m = cos β, and n = cos γ.
4. Relation between l, m, n, and Direction Ratios: The perpendiculars PA, PB, PC are drawn on coordinate axes OX, OY, OZ respectively. Let OP = r,
In ΔOAP, ∠A = 90°, cos α = \(\frac{x}{r}\) = l ∴ x = Ir
In ΔABP, ∠B = 90°, cos β = \(\frac{y}{r}\) = m ∴ y = mr
In ΔOCP, ∠C = 90°, cos γ = \(\frac{z}{r}\) = n ∴ z = nr
Thus, the coordinates of P may be expressed as (lr, mr, nr).
Also, OP2 = x2 + y2 + z2 = r2 = (lr)2 + (mr)2 + (nr)2
⇒ l2 + m2 + n2 = 1.
When l, m, n are multiplied by a scalar k, we get the direction ratios, i.e., lk, mk, nk are the direction ratios of OA.
Types of vectors:
1. Zero Vector or Null Vector: A vector whose initial and terminal points coincide is known as zero vector (\(\overrightarrow{0}\)).
2. Unit Vector: A vector whose magnitude is unity is said to be a unit vector. It is denoted as â, so that | â | = 1.
3. Co-initial Vectors: Two or more vectors having the same initial point are called co-initial vectors.
4. Collinear Vectors: If two or more vectors are parallel to the same line, such vectors are known as collinear vectors.
5. Equal Vectors: If two vectors \(\vec{a}\) and \(\vec{b}\) have the same magnitude and direction, regardless of the positions of their initial points, such vectors are said to be equal, i.e., \(\vec{a}\) = \(\vec{b}\) .
6. Negative of a Vector: A vector whose magnitude is the same as that of a given vector (say \(\overrightarrow{\mathrm{AB}}\)), but the direction is opposite to that of it, is known as negative of vector \(\overrightarrow{\mathrm{AB}}\). i.e., \(\overrightarrow{\mathrm{BA}}\) = – \(\overrightarrow{\mathrm{AB}}\).
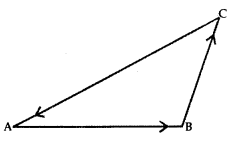
6. Sum of Vectors:
1. Sum of Vectors \(\vec{a}\) and \(\vec{b}\):
Let the vectors \(\vec{a}\) and \(\vec{b}\) be so positioned that initial point of one coincides with terminal point of the other i.e., let \(\vec{a}\) = \(\overrightarrow{\mathrm{AB}}\) and \(\vec{b}\) = \(\overrightarrow{\mathrm{BA}}\) .
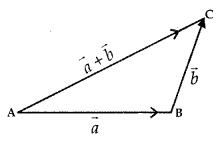
Then, the vector \(\vec{a}+\vec{b}\) is represented by the third side of ΔABC
i. e.,
\(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overline{\mathrm{AC}}\) ……..(1)
or
\(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AB}}=\overline{\mathrm{BC}}\)
and
\(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{BC}}=\overline{\mathrm{AB}}\)
This is known as the triangle law of addition.
Further, \(\overrightarrow{\mathrm{AC}}\) = – \(\overrightarrow{\mathrm{CA}}\)
So, (1) may be written as
\(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}\) = – \(\overrightarrow{\mathrm{CA}}\)
∴ \(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}\) = \(\overrightarrow{0}\)
When sides of a triangle ABC are taken in order, i.e., initial and terminal points coincides, then
\(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}\) = \(\overrightarrow{0}\)
2. Parallelogram law of Addition:
If the two vectors \(\vec{a}\) and \(\vec{b}\) are represented by the two adjacent sides OA and OB of a parallelogram OACB, then their sum \(\vec{a}\) + \(\vec{b}\) is represented in magnitude and direction by the diagonal OC of the parallelogram through their common point O.
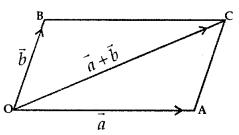
i.e., \(\overline{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OC}}\)
Properties of Vector Addition:
Property 1: For two vectors \(\vec{a}\) and \(\vec{b}\), the sum is commutative i.e.,
\(\vec{a}+\vec{b}\) = \(\vec{b}+\vec{a}\)
Property 2: For three vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) the sum of vectors is associative,- i.e.,
\((\vec{a}+\vec{b})+\vec{c}\) =\(\vec{a}+(\vec{b}+\vec{c})\)
7. Multiplication of a vector by a scalar:
Let \(\vec{a}\) be the given vector and λ be a scalar.
Product of λ and \(\vec{a}\) = λ\(\vec{a}\).
(i) When λ is +ve, \(\vec{a}\) and λ \(\vec{a}\) have the same sense of direction.
(ii) When λ is -ve, \(\vec{a}\) and λ\(\vec{a}\) are of the opposite directions.
Also, |λ\(\vec{a}\)| = |λ| |\(\vec{a}\)|
→ Additive Inverse of Vector \(\vec{a}\)
If there exists a vector – \(\vec{a}\) such that
\(\vec{a}\) + (- \(\vec{a}\)) = \(\vec{a}\) – \(\vec{a}\) = \(\vec{0}\), then – \(\vec{a}\) is called the additive inverse of \(\vec{a}\).
→ Unit Vector \(\vec{a}\)
Let λ = \(\frac{1}{|\vec{a}|}\) . So, | λ\(\vec{a}\)| = |λ| |\(\vec{a}\)|
= \(\frac{1}{|\vec{a}|}\) × |\(\vec{a}\)| = 1
∴ \(\frac{1}{|\vec{a}|}\) × |\(\vec{a}\)| = a, where |\(\vec{a}\)| ≠ 0 and \(\vec{a}\) is the unit vector.
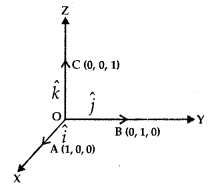
8. Components of Vector:
Let us take the points A(1, 0, 0), B(0,1, 0) and 0(0, 0,1) on the co-ordinate axes OX, OY and OZ respectively.
Obviously |\(\overrightarrow{\mathrm{OA}}\)| = 1, |\(\overrightarrow{\mathrm{OB}}\)| = 1 and |\(\overrightarrow{\mathrm{OC}}\)| = 1.
Vectors \(\overrightarrow{\mathrm{OA}}\), \(\overrightarrow{\mathrm{OB}}\) and \(\overrightarrow{\mathrm{OC}}\) each having magnitude 1 are known as unit vectors. They are denoted by î, ĵ and k̂ respectively.
Consider the vector \(\overrightarrow{\mathrm{OP}}\), where P is the point (x, y, z). Now, OQ, OR, OS are the projections of OP on co-ordinates axes.
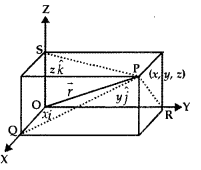
∴ OQ = x, OR = y, OS = z
\(\overrightarrow{\mathrm{OQ}}\) = xî, \(\overrightarrow{\mathrm{OR}}\) =yĵ, \(\overrightarrow{\mathrm{OS}}\) = zk̂.
⇒ \(\overrightarrow{\mathrm{OP}}\) – xî + yĵ +zk̂.
Also, |\(\overrightarrow{\mathrm{OP}}\)| = \(\sqrt{x^{2}+y^{2}+z^{2}}\) = |\(\vec{r}\)|
x, y, z are called the scalar components and xî, yĵ, and zk̂ are the vector components of vector \(\overrightarrow{\mathrm{OP}}\)
Some properties:
Let \(\vec{a}\) =a1î + a2ĵ + a3k̂ and \(\vec{b}\) =b1î +b2ĵ +b3k̂
1. \(\vec{a}\) + \(\vec{b}\) =(a1 î + a2ĵ + a3k̂) + (b1 î +b2ĵ +b3k̂)
⇒ (a1 + b1)î + (a2 + b2)ĵ + (a3 + b3)k̂
2. \(\vec{a}\) – \(\vec{b}\) or (a1î + a2ĵ +a3k̂) = (b1î + b2ĵ + b3k̂)
3. λ\(\vec{a}\) = λ(a1î + a2ĵ + a3k̂)
⇒ (λa1)î + (λa2)ĵ+ (λa3)k̂
4. \(\vec{a}\) and \(\vec{b}\) are collinear, if and only if there exists a non-zero scalar X such that \(\vec{b}\) = λ\(\vec{a}\), i.e.,
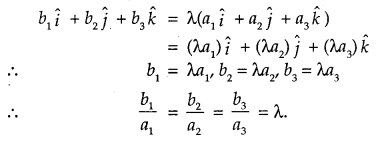
9. Vector joining two points:
Let P1(x1, y1, z1) and P2(x2, y2, z2) be the two points. Then, the vector joining the points P1 and P2 is \(\overline{\mathrm{P}_{1} \mathrm{P}_{2}}\)
Join P1 and P2 with O.
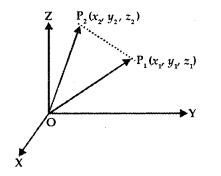
Now,
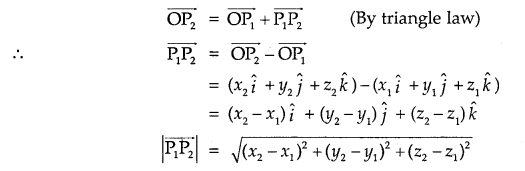
10. Dividing a line segment in a given ratio:
1. A line segment PQ is divided by a point R in the ratio m: n internally.
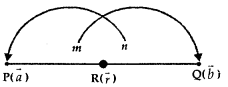
i.e., \(\frac{\mathrm{PR}}{\mathrm{RQ}}=\frac{m}{n}\)
If \(\vec{a}\) and \(\vec{b}\) are the position vectors of P and Q then the position vector \(\vec{r}\) of R is given by
\(\vec{r}\) = \(\frac{m \vec{b}+n \vec{a}}{m+n}\)
2. When R divides PQ externally,
\(\frac{\mathrm{PR}}{\mathrm{RQ}}=\frac{m}{n}\)
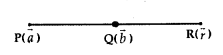
Replacing n by -n,
\(\vec{r}\) = \(\frac{m \vec{b}-n \vec{a}}{m-n}\)
Product of two vectors (Dot Product)
1. Scalar (or Dot) Product:
Scalar product of two vectors \(\vec{a}\) and \(\vec{b}\) is defined as \(\vec{a}\) . \(\vec{b}\) = | \(\vec{a}\) | \(\vec{b}\) | cos 0, where 0 is the angle between a and b (0,< θ < π).
2. From definition we derive:
(a) \(\vec{a}\).\(\vec{b}\) is a scalar quantity.
(b) When θ = 0, \(\vec{a}\).\(\vec{b}\) = |\(\vec{a}\)| |\(\vec{a}\).\(\vec{b}\)|.
Also, \(\vec{a}\). \(\vec{a}\) = |\(\vec{a}\)|2 = |\(\vec{a}\)|.
(c) When θ = \(\frac{π}{2}\)
⇒ When \(\vec{a}\) ⊥ \(\vec{a}\), \(\vec{a}\). \(\vec{b}\) = 0.
(d) When either \(\vec{a}\) = 0 or \(\vec{b}\) = 0, \(\vec{a}\). \(\vec{b}\) = 0.
(e) cos θ = \(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\)
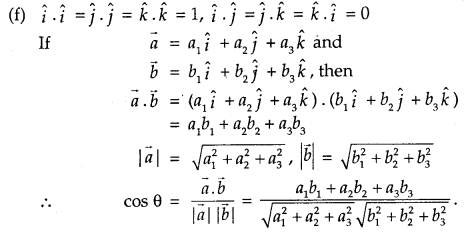
3. Properties of scalar Product
(a) Scalar product is commutative, i.e.,
\(\vec{a}\) . \(\vec{b}\) = \(\vec{b}\).\(\vec{a}\)
(b) If a is scalar, then
(α \(\vec{a}\) ). \(\vec{b}\) = α(\(\vec{a}\).\(\vec{b}\)) – \(\vec{a}\). (α\(\vec{b}\))
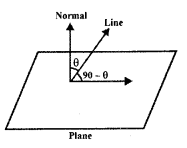
11. Projection of vector along a directed line:
Let the vector \(\overrightarrow{\mathrm{AB}}\) makes ar angle θ with directed line l.
Projection of AB on l = |\(\overrightarrow{\mathrm{AB}}\)| cos θ = \(\overrightarrow{\mathrm{AC}}\) = \(\overrightarrow{\mathrm{P}}\).
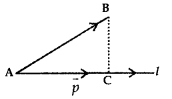
The vector is \(\overrightarrow{\mathrm{P}}\) is called the projection vector. Its magnitude is
|\(\overrightarrow{\mathrm{P}}\)|, which is known as projection of vector \(\overrightarrow{\mathrm{AB}}\).
The angle θ between \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{AC}}\) is given by
cos θ = \(\frac{\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}}{|\overline{\mathrm{AB}}||\overline{\mathrm{AC}}|}\)
Now, projection AC = \(\overrightarrow{\mathrm{AB}}\) cos θ = cos θ \(\frac{\overline{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}}{|\mathrm{AC}|}\)
= \(\overrightarrow{\mathrm{AB}}\).(\(\frac{\overrightarrow{\mathrm{AC}}}{|\overrightarrow{\mathrm{AC}}|}\))
If, \(\overrightarrow{\mathrm{AB}}\) = \(\vec{a}\) and \(\overrightarrow{\mathrm{AC}}\) = \(\vec{p}\), then
AC = \(\vec{a}\)(\(\frac{\vec{p}}{|\vec{p}|}\)) = \(\vec{a}\).\(\vec{p}\)
Thus, the projection of \(\vec{a}\) on \(\vec{b}\)
= \(\vec{a}\)(\(\frac{\vec{b}}{|\vec{b}|}\)) = \(\vec{a}\).\(\vec{b}\).
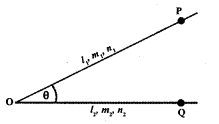
Note: If α, β, γ are the direction angles of the vector
\(\vec{a}\) = (a1î + a2ĵ + a3k̂), the direction cosines of a are given as
cos α = \(\frac{\vec{a} \cdot \hat{i}}{|\vec{a}||\hat{i}|}=\frac{a_{1}}{|\vec{a}|}\)
cos β = \(\frac{a_{2}}{|\vec{a}|}\)
cos γ = \(\frac{a_{3}}{|\vec{a}|}\)
12. Vector Product of two vectors:
1. Definition: The vector product of two non-zero vectors \(\vec{a}\) and \(\vec{b}\), denoted by \(\vec{a}\) × \(\vec{b}\) is defined as
\(\vec{a}\) × \(\vec{b}\) = |\(\vec{a}\) ||\(\vec{b}\) |sin θ.n̂
where θ is the angle between \(\vec{a}\) and \(\vec{b}\), 0 ≤ θ ≤ π. Unit vector n̂ is perpendicular to both vectors \(\vec{a}\) and \(\vec{b}\), such that \(\vec{a}\), \(\vec{b}\) and n̂ form a right handed system.
2. Note:
(a) \(\vec{a}\) × \(\vec{b}\) = | \(\vec{a}\) | | \(\vec{b}\) | sin θ. n̂
- If \(\vec{a}\) = 0 or \(\vec{b}\) = 0, \(\vec{a}\) × \(\vec{a}\) = \(\vec{0}\)
- \(\vec{a}\) || \(\vec{b}\), \(\vec{a}\) × \(\vec{b}\) = 0
(b) \(\vec{a}\) × \(\vec{b}\) = – \(\vec{b}\) × \(\vec{a}\)
\(\vec{a}\) × \(\vec{b}\) ≠ \(\vec{b}\) × \(\vec{a}\)
⇒ vector product is not commutative.
(c) When θ = \(\frac{π}{2}\), \(\vec{a}\) × \(\vec{b}\) = |\(\vec{a}\)| × |\(\vec{b}\)| × n̂
or
| \(\vec{a}\) × \(\vec{b}\) | = |\(\vec{a}\)||\(\vec{b}\)|
(d) î × î = ĵ × ĵ = k̂ × k̂ = 0
and î × ĵ = k̂, ĵ × k̂ = ĵ, k̂ × î = ĵ.
⇒ĵ × î = – k̂, k̂ × ĵ = -î , î × k̂ = – ĵ.
(e) sin θ = \(\frac{|\vec{a} \times \vec{b}|}{|\vec{a}||\vec{b}|}\)
(f) If \(\vec{a}\) and \(\vec{b}\) represent adjacent sides of a parallelogram, then its area |\(\vec{a}\) × \(\vec{b}\)|.
(g) If \(\vec{a}\) and \(\vec{b}\) represent adjacent sides of a triangle, then its area = \(\frac{1}{2}\) |\(\vec{a}\) × \(\vec{b}\)|
(h) Distributive Property
\(\vec{a}\) × (\(\vec{b}\) + \(\vec{c}\)) = \(\vec{a}\) × \(\vec{b}\) + \(\vec{b}\) x× \(\vec{c}\)
1. Let α be a scalar, then
α(\(\vec{a}\) × \(\vec{b}\)) = (α\(\vec{a}\)) × \(\vec{b}\) = \(\vec{a}\) × (α\(\vec{b}\))
2. \(\vec{a}\) = (a1 î + a2 ĵ + a3 k̂) and
\(\vec{b}\) = (b1 î + b2 ĵ + b3 k̂), then
\(\vec{a}\) × \(\vec{a}\) = \(\left|\begin{array}{lll}
\hat{i} & \hat{j} & \hat{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|\)
1. PROPERTIES OF \TXHORS UNDER ADDITION
(i) Commutative Law. \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
(ii) Associative Law, \(\vec{a}+(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+\vec{c}\)
(iii) Additive Identity. \(\vec{a}+\overrightarrow{0}=\vec{a}=\overrightarrow{0}+\vec{a}\)
(iv) Additive Inverse. \(\vec{a}+(-\vec{a})=\overrightarrow{0}=(-\vec{a})+\vec{a}\)
2. \(\vec{AB}\) = (POSITION VECTOR OF B)-(POSITION VECTOR OF A).
3. SCALAR PRODUCT
(i) Def. The scalar product of \(\vec{a}\) and \(\vec{b}\) is defined as \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\), where ‘θ’ is the angle between \(\vec{a}\) and \(\vec{b}\)
(ii) Condition of Perpendicularity. If \(\vec{a}\) and \(\vec{b}\) are perpendicular, then \(\vec{a} \cdot \vec{b}\) = 0.
(iii) If \(\hat{i}, \hat{j}, \hat{k}\) are unit vectors, which are perpendicular to each other, then :
\(\hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0\) and \(\hat{i}^{2}=\hat{j}^{2}=\hat{k^{2}}\)
(iv) Properties:
(a) CommutativeLaw. \(\vec{a}\cdot \vec{b}=\vec{b} \cdot \vec{a}\)
(b) Associative Law, does not hold.
(c) Distributive Laws, \(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\) and \((\vec{b}+\vec{c}) =\vec{b} \cdot \vec{a}+\vec{c} \cdot \vec{a}\)
(d) \((m\vec{a}) \cdot \vec{b}=m(\vec{a} \cdot \vec{b})=\vec{a} \cdot(m \vec{b})\), m being a scalar.
(e) \(\vec{a} \cdot \vec{a}=a^{2}\)
4. VECTOR PRODUCT
(i) Definition. The vector product of \(\vec{a}\) and \(\vec{b}\) is given by: \({a} \times \vec{b}=|\vec{a} \| \vec{b}| \sin \theta \hat{n}\) , where ‘θ’ the angle between \(\vec{a}\) and \(\vec{b}\) and \(\hat{n}\) is a unit vector perpendicular to the plane of \(\vec{a}\) and \(\vec{b}\) .
(ii) When two vectors are parallel, then \(\vec{a} \times \vec{b}=\overrightarrow{0}\)
(iii) If \(\hat{i}, \hat{j}, \hat{k}\) are unit vectors, which are perpendicular to each other, then :
\(\hat{i} \times \hat{j}=\hat{k}=-\hat{j} \times \hat{i} ; \text { etc. } \hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{0}\)
(iv) Properties :
(a) Commutative Law does not hold.
(b) \((m \vec{a}) \times \vec{b}=m(\vec{a} \times \vec{b})=\vec{a} \times(m b)\), m being a scalar.
(c) If \(\vec{a}=a_{1} \hat{i}+a_{2} \hat{j}+a_{3} \hat{k}, \vec{b}=b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k}\), then \(\vec{a} \times \vec{b}\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|\)
(d) Distributive Law. \(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)
5. SCALAR TRIPLE PRODUCT
(i) Def. If \(\vec{a}, \vec{b}, \vec{c}\) are three vectors, then the scalar product of \(\vec{a} \times \vec{b}\) with \(\vec{c}\) is called scalar triple product
(ii) Properties:
(a) Condition for three vectors to be coplanar. If \(\vec{a}, \vec{b}, \vec{c}\) are all coplanar vectors, then \(\left[\begin{array}{lll}
\rightarrow & \rightarrow & \rightarrow \\
a & b & c
\end{array}\right]\) = 0
(b) If any two of the three vectors \(\vec{a}, \vec{b}, \vec{c}\) are equal, then \([\vec{a} \vec{b} \vec{c}]\) = 0
(c) If any two of the three vectors \(\vec{a}, \vec{b}, \vec{c}\) are parallel, then \(\left[\begin{array}{ccc}
\rightarrow & \rightarrow & \rightarrow \\
a & b & c
\end{array}\right]\) = 0
(d) In the scalar triple product, the position of dot and cross can be interchanged at pleasure provided the cyclic order of the vectors is maintained.
(e) In the scalar triple product, the change in the cyclic order of die vectors changes the sign of the product.