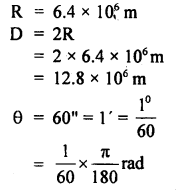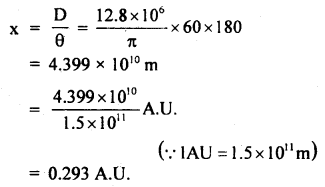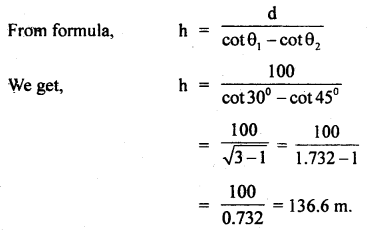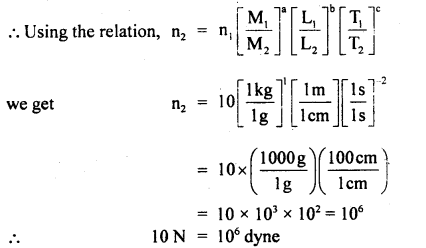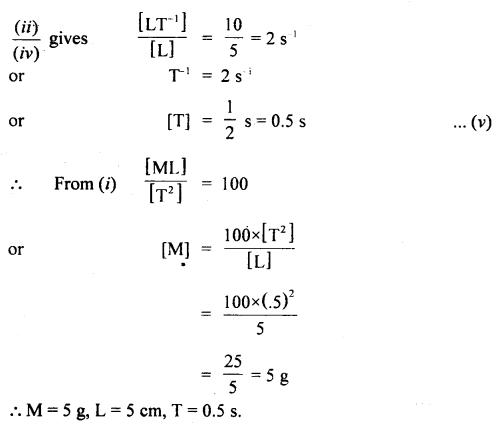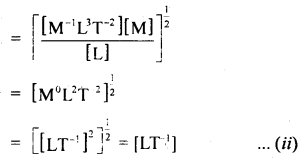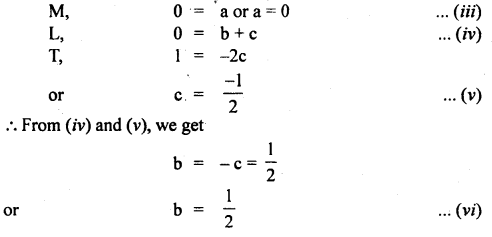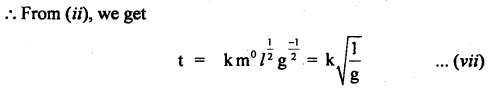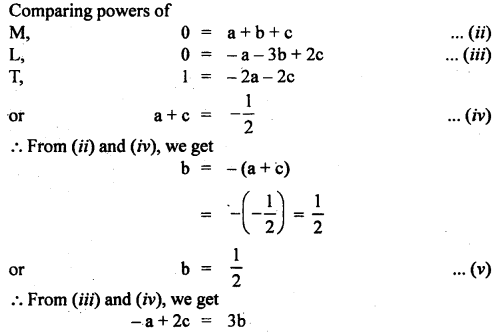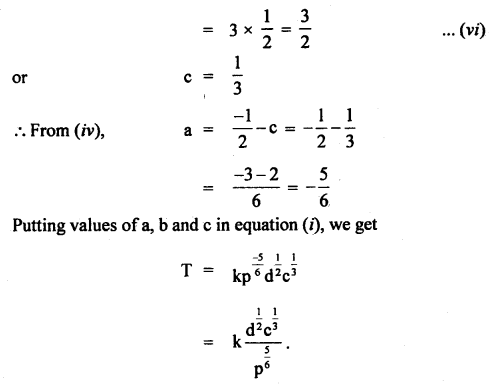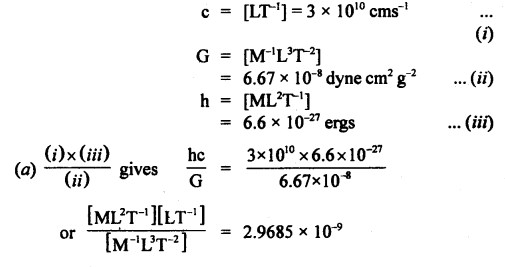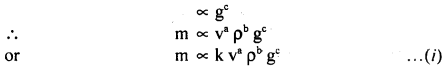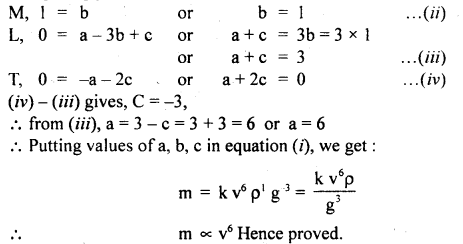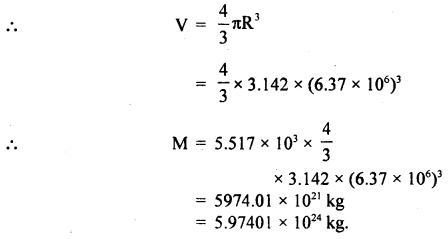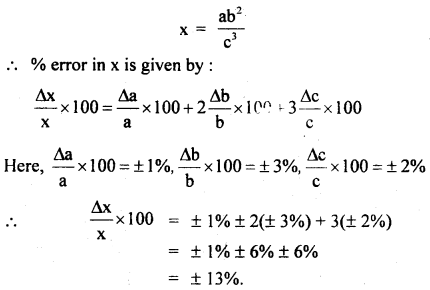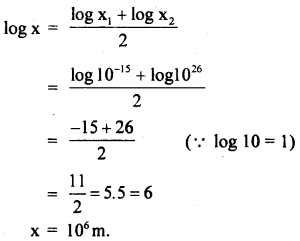CBSE Class 11

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 4 Motion in a Plane. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 4 Important Extra Questions Motion in a Plane

Motion in a Plane Important Extra Questions Very Short Answer Type

Question 1.
Under what condition |a + b| = |a| + |b| holds good?
Answer:
When a and b act in the same direction i. e. when 0 = 0 between • them, then |a + b|=|a| + |b|.

Question 2.
Under what condition |a – b| = |a| – |b| holds good?
Answer:
The condition |a – b|=|a| – |b| holds goods when a and b act in the opposite direction.

Question 3.
The sum and difference of the two vectors are equal in magnitude
i. e. |a + b|=|a – b|. What conclusion do you draw from this?
Answer:
The two vectors are equal in magnitude and are perpendicular to each other.

Question 4.
What is the angle between \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\) and \(\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{A}}\)?
Answer:
The given vectors act along two parallel lines in opposite directions i.e. they are anti-parallel, so the angle between them is 180°.

Question 5.
What is the minimum number of coplanar vectors of different magnitudes which can give zero resultant?
Answer:
3, If three vectors can be represented completely by the three sides of a triangle taken in the same order, then their resultant is zero.

Question 6.
When a – b = a + b condition holds good than what can you say about b?
Answer:
For a – b = a + b condition to hold good, b must be a null vector.

Question 7.
What is the magnitude of the component of the 9î – 9ĵ + 19k̂ vector along the x-axis?
Answer:
9.

Question 8.
Can displacement vector be added to force vector?
Answer:
No.

Question 9.
What is the effect on the dimensions of a vector if it is multiplied by a non-dimensional scalar?
Answer:
There is no effect on the dimensions of a vector if it is multiplied by a non-dimensional scalar.

Question 10.
(a) What is the angle between î + ĵ and î vectors?
Answer:
45°

(h) What is the angle between î – ĵ and the x-axis?
Answer:
45°

(c) What is the angle between î + ĵ and î – ĵ?
Answer:
90°

Question 11.
What is the dot product of 2î + 4ĵ + 5k̂ and 3î + 2ĵ + k̂?
Answer:
19.

Question 12.
What must be the value of ‘a’ in 2î + 2ĵ – ak̂ so that it is perpendicular to 5î + 7ĵ – 3k̂?
Answer:
8.

Question 13.
Is finite rotation a vector quantity? Why?
Answer:
No. This is because the addition of two finite rotations does not obey commutative law.

Question 14.
Is infinitesimally small rotation a vector quantity? Why?
Answer:
Yes. This is because the addition of two infinitesimally small rotations obeys commutative law.

Question 15.
(a) Can the resultant of two vectors of different magnitudes be zero?
Answer:
No

(b) Can the magnitude of the rectangular component of a vector be greater than the magnitude of the vector itself?
Answer:
No.

Question 16.
A quantity has both magnitude and direction. Is it necessarily a vector? Why? Give an example.
Answer:
No. The given quantity will be a vector only if it obeys the laws of vector addition. Electric current.

Question 17.
In a vector equation, all the quantities are of similar nature but their directions are different. Does it mean that the vector equation is necessarily incorrect? Electric current.
Answer:
No. In a vector equation, the vectors need not be in the same direction.

Question 18.
Why vectors cannot be added algebraically?
Answer:
The vectors cannot be added algebraically because they possess both magnitude and direction.

Question 19.
Fifty vectors each of magnitude 10 units are completely represented by the sides of a polygon in the same order. What will be the resultant?
Answer:
Their resultant will be zero. This is because the vector sum of all the vectors represented by the sides of a closed polygon taken in the same order- is zero.

Question 20.
What will be the angle between \(\vec{A}\) and \(\vec{B}\) if \(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}=\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{A}}\)?
Answer:
The angle between A and B may be of any value if A + B = B + A.

Question 21.
How will you prove that the given vectors are neither parallel nor perpendicular?
Answer:
The given vectors will neither be parallel nor perpendicular if neither their cross product nor their dot product is zero.

Question 22.
How will you prove that the two vectors are parallel?
Answer:
If their cross product is zero, then the two vectors are said to be parallel.

Question 23.
How will you prove that two vectors are perpendicular?
Answer:
Two vectors will be perpendicular to each other if their dot product is zero.

Question 24.
(a) What is the minimum possible resultant of two forces 2N and 1N?
Answer:
1N

(b) What is the maximum possible resultant of two forces 2N and 1N?
Answer:
3N.

Question 25.
Is P² a scalar or a vector? Justify your answer.
Answer:
P2 is scalar because it is the dot product of P and P.

Question 26.
Is it necessary to mention the direction of a vector having zero magnitudes? Why?
Answer:
No. A vector having zero magnitudes is called a null vector. In this case, there is no sense of direction as the null vector is represented by a point.

Question 27.
Can a vector vary with time? Give example.
Answer:
Yes. For example, when an object moves, its position vector continuously changes with time.

Question 28.
Define a projectile.
Answer:
It is defined as an object thrown with some initial velocity moves under the effect of gravity alone.

Question 29.
Define trajectory.
Answer:
It is defined as the path followed by the projectile during its flight.

Question 30.
Define maximum height attained by a projectile.
Answer:
It is defined as the maximum vertical distance traveled by the projectile during its journey.

Question 31.
Define the horizontal range of the projectile.
Answer:
It is defined as the maximum horizontal distance between the point of projection and the point in the horizontal plane where the projectile hits it back after the journey.

Question 32.
At what angle a ball must be thrown to get maximum horizontal range?
Answer:
It must be thrown at an angle of 45° to the horizontal.

Question 33.
At what point in its trajectory does a projectile have its minimum velocity?
Answer:
At the highest point of the trajectory, a projectile has its minimum velocity.

Question 34.
How much is the velocity of the projectile at its highest point along the vertical direction?
Answer:
It is zero.

Question 35.
When a projectile is fired at an angle with the horizontal, then which of the components of its velocity remains constant throughout the trajectory?
Answer:
The horizontal component of its velocity remains constant throughout the trajectory.

Question 36.
At what point of the trajectory of a ball thrown upward is the acceleration perpendicular to the velocity?
Answer:
The acceleration is perpendicular to the velocity at the highest point of the trajectory.

Question 37.
A bob of mass 0.1 kg hung from the ceiling of a room by a string 2m long is set into oscillation. The speed of the bob at its mean position is 1 ms-1. What is the trajectory of the bob if its string is cut when the bob is: (a) at one of its extreme position (b) at its mean position.
Answer:
(a) straight line,
(b) parabolic path.

Question 38.
A cannon on a level plane is aimed at an angle P above the horizontal and a shell is fired with a muzzle speed v towards a vertical cliff a distance x away. At what height y from the bottom, the shell would hit the cliff?
Answer:
y = x tan β – \(\frac{\mathrm{gx}^{2}}{2 \mathrm{v}^{2} \cos ^{2} \beta}\)

Question 39.
A body is projected so that it has maximum range R. What is .the maximum height reached during the flight?
Answer:
Maximum height is \(\frac{1}{4}\) of maximum range i.e. h = \(\frac{R}{4}\).

Question 40.
A bullet x is fired from a gun when the angle of elevation of the gun is 30°. Another bullet y is fired from the gun at an angle of elevation 60°. Tell which of the two bullets would have a greater horizontal range?
Answer:
Both will have the same range.

Question 41.
A particle moves in a plane with uniform acceleration ¡n a direction different from its initial velocity. What is the nature of the path followed by it?
Answer:
It is a parabolic path in nature.

Question 42.
A projectile of mass m is fired with initial velocity u at angle 6 with the horizontal. What is the change in momentum as it rises to the highest point of the trajectory?
Answer:
Change in momentum = Force × time = mg × \(\frac{\mathrm{u} \sin \theta}{\mathrm{g}}\) = mu sinθ

Question 43.
Name the five physical quantities which change during the motion of an oblique projectile.
Answer:
Five physical quantities are velocity, the vertical component of velocity, momentum, kinetic energy, potential energy.

Question 44.
Name the two quantities which would be reduced if air resistance is taken into account in the study of the motion of the oblique projectile which quantity would be increased?
Answer:
The quantities which are reduced:

1. maximum height
2. horizontal range.

The angle at which the projectile hits the ground would be increased.

Question 45.
At which point of the trajectory of the projectile, the speed is maximum?
Answer:
The speed is maximum at two points which are:

1. The point from where the projectile is thrown.
2. The point where the projectile returns back to the plane of projection.

Question 46.
What is the condition for the following formula to be valid?
Average velocity = \(\)\frac{\text { Initial velocity + final velocity }}{2}
Answer:
It is valid only if acceleration is constant.

Question 47.
A body travels with uniform acceleration ai for time t, and with uniform acceleration a2 for time t2. What is the average acceleration?
Answer:
aaverage = \(\frac{a_{1} t_{1}+a_{2} t_{2}}{t_{1}+t_{2}}\).

Question 48.
Even when rain is falling vertically downwards the front screen of a moving car gets wet. On the other hand, the back screen remains dry. Why?
Answer:
The rain strikes the car in the direction of the relative velocity of the rain with respect to the car.

Question 49.
Can a body have a constant velocity and still have a varying speed?
Answer:
No. If the velocity of a body is constant then its speed cannot vary.

Question 50.
(a) What are the units of angular speed?
Answer:
Units of angular speed are radian/second (rad s-1]).

(b) What is the relation between time period (T) and frequency (v)?
Answer:
T= \(\frac{1}{v}\)

Question 51.
(a) Give an example of a body moving with uniform speed but having a variable velocity and an acceleration that remains constant in magnitude but changes in direction.
Answer:
A body having uniform circular motion.

(b) What is the direction of a centripetal acceleration with reference to the position vector of a particle moving in a circular path?
Answer:
It is always along the position vector but directed towards the center of the circle.

Motion in a Plane Important Extra Questions Short Answer Type

Question 1.
Name two quantities that are the largest when the maximum height attained by the projectile is largest.
Answer:
Time of flight and the vertical component of velocity are the two quantities that are the largest when the maximum height attained by the projectile is the largest.

Question 2.
A stone dropped from the window of a stationary railway carriage takes 2 seconds to reach the ground. At what time the stone will reach the ground when the carriage is moving with
(a) the constant velocity of 80kmh^-1
(b) constant acceleration of 2ms^-2?
Answer:
The time taken by the freely falling stone to reach the ground is given by
t = \(\sqrt{\frac{2 h}{g}}\)

In both cases, the stone will fall through the same height as it is falling when the railway carriage is stationary. Hence the stone will reach the ground after 2 seconds.

Question 3.
Can a particle accelerate when its speed is constant? Explain.
Answer:
Yes. A particle can be accelerated if its velocity changes. A particle having uniform circular motion has constant speed but its direction of motion changes continuously. Due to this, there is a change in velocity and hence the particle is moving with variable velocity. Thus particle is accelerating.

Question 4.
(a) Is circular motion possible at a constant speed or at constant velocity? Explain.
Answer:
Circular motion is possible at a constant speed because, in a circular motion, the magnitude of the velocity i.e. speed remains constant while the direction of motion changes continuously.

(b) Define frequency and time period.
Answer:
Frequency is defined as the number of rotations completed by a body in one second and the time period is defined as the time taken by an object to complete one rotation.

Question 5.
When the component of a vector A along the direction of vector B is zero, what can you conclude about the two vectors?
Answer:
The two vectors A and B are perpendicular to each other.
Explanation: Let θ = angle between the two vectors A and B component of vector A along the direction of B is obtained by resolving A i.e. A cos θ.

Now according to the statement
A cos θ = 0
or
cos θ = 0 = cos 90°
θ = 90°
i.e. A ⊥ B

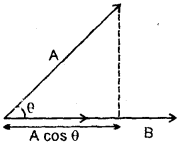
Hence proved.

Question 6.
Comment on the statement whether it is true or false “Displacement vector is fundamentally a position vector.’’ Why?
Answer:
The given statement is true. The displacement vector gives the position of a point just like the position vector. The only difference between the displacement and the position vector is that the displacement vector gives the position of a point with reference to a point other than the origin, while the position vector gives the position of a point with reference to the origin. Since the choice of origin is quite arbitrary, so the given statement.

Question 7.
Does the nature of a vector changes when it is multiplied by a scalar?
Answer:
The nature of a vector may or may not be changed when it is multiplied.

For example, when a vector is multiplied by a pure number like 1, 2, 3,…. etc., then the nature of the vector does not change. On the other hand, when a vector is multiplied by a scalar physical quantity, then the nature of the vector changes.

For example, when acceleration (vector) is multiplied by a mass (scalar) of a body, then it gives force (a vector quantity) whose nature is different than acceleration.

Question 8.
Can the walk of a man be an example of the resolution of vectors? Explain.
Answer:
Yes, when a man walks, he pushes the ground with his foot. In return, an equal and opposite reaction acts on his foot. The reaction is resolved into two components: horizontal and vertical components. The horizontal component of the reaction helps the man to move forward while the vertical component balances the weight of the man.

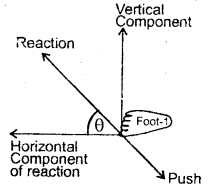
Question 9.
Explain under what conditions, the resultant of two vectors will be equal to either of them.
Answer:
The resultant of two vectors will be equal to either of them if:

1. The two vectors are of the same magnitude.
2. The two vectors are inclined to each other at 120°.

Explanation: Let x be the magnitude of each of the two vectors say P and Q. If 9 = angle between P and Q, then the magnitude of their resultant vector (R) is given by the relation

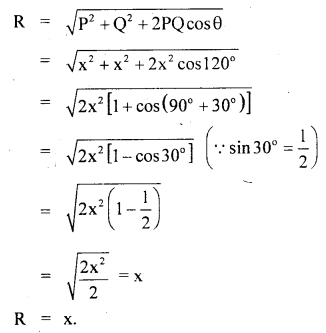
Question 10.
Why the magnitude of the rectangular components of a vector can’t be greater than the magnitude of the vector itself?
Answer:
The magnitude of rectangular components of a vector itself cannot be greater than the magnitude of the vector itself because the rectangular components of a vector A are A_x = A cos θ and A_y = A sin 9. As sin θ and cos θ both are ≤ 1, so both A_x and A_y cannot be greater than A.

Question 11.
Can a flight of a bird be an example of the composition of vectors? Explain.
Answer:
Yes, the flight of a bird can be an example of the composition of vector i.e. addition of vectors as is shown in the figure here. As it flies, it strikes the air with its wings W, W along with WO. So, according to Newton’s third law of motion, airstrikes the wings in opposite directions with the same force in reaction represented by OA and OB. Thus according to the parallelogram law of vectors, the resultant of OA and OB is OC. This resultant upward force OC is responsible for the flight of the bird.

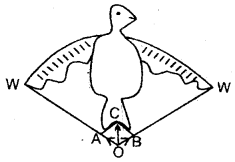
Question 12.
Can commutative law be applied to vector subtraction?
Answer:
Let P and Q be the two vectors.
∴ As P – Q ≠ Q – P, so commutative law is not applied to vector subtraction.

Question 13.
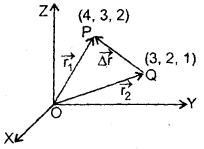
Write down the vector whose head is at (4, 3, 2) and whose tail is at (3, 2, 1).
Answer:
Let r, and r2 be the position vectors of the points P (4, 3, 2) and Q (3, 2, 1) respectively
∴ r₁ = 4î + 3ĵ + 2k̂
and r₂ = 3î + 2ĵ + 1k̂

Let QP = Δr be the required vector
Now applying triangle law of vector addition of ΔOQP, we get
r₂ + Δr = r₁
or
Δr = r₁ – r₂
= (4î + 3ĵ + 2k̂) – (3î + 2ĵ + 1k̂)
= (î + ĵ + k̂ ).

Question 14.
If A.B = A.C, is it safe to conclude that B = C?
Answer:
Let θ₁, θ₂ be the angler between A and B, B and C respectively


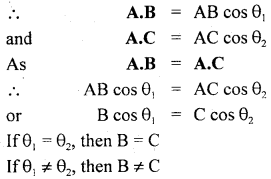
So we conclude that it is not safe to conclude that B = C until θ₁ = θ₂.

Question 15.
Define Tensor. Give example.
Answer:
It is defined as a physical quantity that has no direction but has different values in different directions. It is neither a vector nor a scalar, e.g. moment of Inertia has no direction but its values are different in different directions. Hence moment of inertia is neither a scalar nor a vector but a tensor. Other examples of the tensor are refractive index, stress, strain, density.

Question 16.
How does a sling work?
Answer:
It works on the principle of parallelogram law of vectors. A rubber sling is attached to the two ends of a sling. The stone to be thrown is held at point O. When the rubber string is pulled, the tensions are produced along with OA and OB. When the string is released, the stone moves under the effect of resultant force OC.

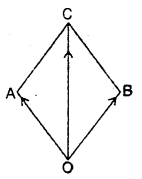
Question 17.
Why does a tennis ball bounce higher on hills than in plains?
Answer:
We know that the maximum height of a projectile is given by the relation

where θ = angle of projection
and u = initial velocity of projection.

From (i), we see that the maximum height is inversely proportional to the acceleration due to gravity (g). So smaller the g, greater shall be the maximum height. Since the value of g is lesser on the hills than on the plains, so a tennis ball will bounce more on hills than on plains.

Question 18.
Two particles are moving with equal and opposite velocities in such a way that they are always at a constant distance apart. Calculate the time after which the particles return to their initial positions.
Answer:
Clearly, the two particles are at the two ends of the diameter of a circular path. It is further clear that each particle will return to its initial position after describing one circle.

If t = required time, then
t = \(\frac{2 \pi r}{v}=\frac{\pi d}{v}\)
where v = speed of particles.
r = radius of the circular track,
d = constant distance between particles.
= diameter of the circular path = 2r.

Question 19.
A ball P is projected directly towards a second ball Q. The horizontal distance x of the second ball is lesser than the horizontal range R of the first ball. The second ball is released from the rest at the instant the first is projected, will the two balls collide.
Answer:
Yes, the initial elevation of 2nd ball = x tan θ
During time t, the second ball covers a distance = \(\frac{1}{2}\) gt2

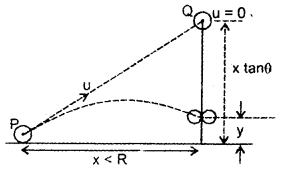
If y = elevation at the instant of collision, then

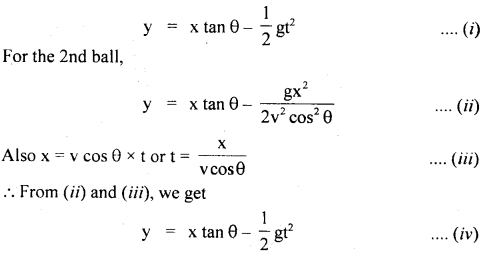
Thus from (i) and (iv), it is clear that both the balls attain the same elevation at time t. So that two must collide, whatever may be the initial velocity of the first ball.

Question 20.
Which one of the following is greater?
(a) The angular velocity of the hour hand of a watch.
(b) The angular velocity of the Earth around its own axis. Why?
Answer:
The angular velocity of the hour hand of a watch.is greater than the angular velocity of the earth around its own axis.

Explanation: We know that the angular velocity (w) of an object has
Time period (T) is given by
ω = \(\frac{2 \pi}{\mathrm{T}}\) ….(i)
(a) T for hour hand of a watch is 12h

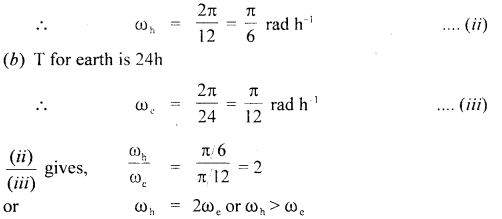
Thus clearly angular velocity of the hour hand is more than the angular velocity of the earth around its own axis because of the T_earth > T_{hour hands}.

Question 21.
A bomber in the horizontal flight drops a bomb when it is just above the target. Explain whether the bomb hits the target or misses it?
Answer:
The bomb will miss the target. This is due to the fact that at the time of dropping, the bomb possesses a horizontal speed equal to the speed of the bomber. So bomb will drop and hit the ground some distance away (= horizontal speed of bomber x time) from the place of dropping.

Question 22.
(a) What is the direction of the area of the vector?
Answer:
It acts perpendicular to the plane containing the area i.e. it acts normal to the surface area.

(b) What are the characteristics of the motion of an Earth satellite revolving around it in a fixed orbit?
Answer:
The satellite motion in a fixed orbit is characterized by the following factors:

1. The Earth’s gravitational pull at the height is equal to the centripetal force at that height.
2. The angular velocity of the satellite about the Earth’s center remains constant.
3. The linear speed of the satellite is also constant.

Question 23.
A ball is thrown horizontally and at the same time, another ball is dropped from the top of a tower with the same velocity.
(i) Will both the balls hit the ground with the same velocity?
Answer:
When the balls hit the ground, their vertical velocities are equal. However, the horizontal velocities will be different. Hence the resultant velocities of the two balls are different, so the balls would hit the ground with different velocities.

(ii) Will both the balls reach the ground at the same time?
Answer:
Both the balls would reach the ground at the same time because their initial vertical velocities, acceleration, and distances covered are all equal.

Question 24.
Three balls thrown at different angles reach the same maximum height (fig. given), then answer the following:

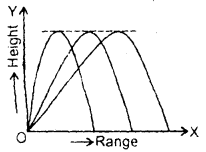
(a) Are the vertical components of the initial velocity the same for all the balls? If not, which one has the least vertical velocity component?
Answer:
Since maximum height is directly proportional to the vertical component of initial velocity hence the vertical components of velocity in the three cases are the same as the maximum height attained is the same.

(b) Will they all have the same time of flight?
Answer:
Yes, all will have same time of flight T = \(\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\) as sin θ is same for all.

(c) Which one has the greatest horizontal velocity component?
Answer:
The projectile having maximum range has the greatest horizontal component of the initial velocity.

Question 25.
When a car is driven too fast around a curve it skids outward. How would a passenger sitting inside explain the car’s motion? How would an observer standing by the roadside explain the event?
Answer:
The passenger inside the car is in the reference frame of the car so he experiences centrifugal force \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) acting on the car. So to remain in a circular path force should be larger as it is proportional to v₁₂.

An observer on the roadside finds that the centripetal force \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) acting on the car becomes inadequate with an increase in v. Since again v₂ r and r is insufficient so the car skids.

Question 26.
Show that the horizontal range of projectile for two angles of projection α and β is same when α + β = 90°.
Answer:
The horizontal ranges for two angles of projections are

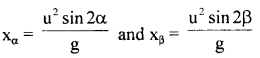
assuming that projection velocity is the same in both cases

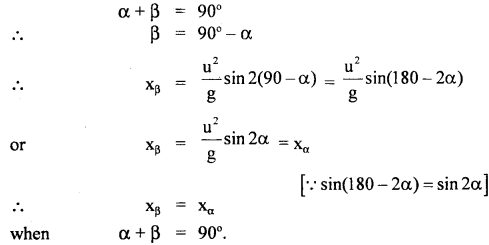
Question 27.
Why is it easier to pull a lawn roller than to push it? Explain.
Answer:
(a) Consider the case of the pull of roller as shown in Fig. (a):
Here the force of pull (F) has two components:
(i) F cos θ which moves the roller horizontally.
(ii) F sin θ which acts vertically upward and opposite to the weight (mg) of the roller.
∴ Net weight of the roller = mg – F sin θ ….(i)

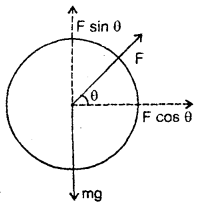
(b) Case of the push of roller: In this case, the components of F are:
(i) F cos θ which helps to move the roller horizontally.
(ii) F sin θ which acts vertically downward in the direction of the weight (mg) of the roller.
∴ Net weight of the roller = mg + F sin θ ….(ii)

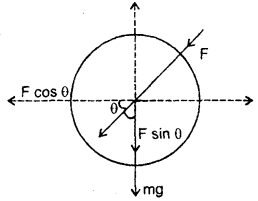
Now from equations (i) and (ii), it is clear that the net weight (i.e. apparent weight) of the roller becomes greater in the case of pushing than in the case of pulling. But due to friction, the force required to move a body is directly proportional to the effective weight of the body. So a smaller force is required to move the roller in case of pulling than in case of pushing. Hence it is easier to pull than to push a lawn roller.

Question 28.
(a) Is the maximum height attained by a projectile largest when the maximum range is maximum?
Answer:
No. the angle for the maximum horizontal range is 45° but for the maximum height the largest range is 41°:

(b) A body in uniform horizontal circular motion possesses variable velocity. Does it mean that the kinetic energy of the body is also variable?
Answer:
No, since the magnitude of velocity in uniform motion is constant, hence the kinetic energy will also not change.

(c) Why vector cannot be added algebraically?
Answer:
The algebraic sum does not take into account the direction of a physical quantity. It adds only magnitudes, hence it is not suitable for vector sum.

Question 29.
(a) How can a vector be tripled?
Answer:
By multiplying the vector by number 3 (a scalar) or by adding two more similar vectors i.e. vectors of the same magnitude and direction to the given vector.

(b) State Triangle law of vector addition.
Answer:
It states that if two vectors are represented completely (i.e. both in magnitude and direction) by the two sides of a triangle taken in the same order then their resultant is represented completely by the third side of the triangle taken in the opposite order.

Question 30.
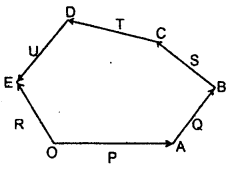
State polygon law of vector addition. Show it graphically.
Answer:
It states that if a number of vectors are represented completely by the sides of a polygon taken in the same order, then their resultant is represented completely by its closing side taken in the opposite order. If P, Q, S, T, and U be the vectors represented completely by the sides OA, AB, BC, CD, and DE of the polygon taken in the same order, then their resultant (R) is represented by OE taken in opposite order s.t.
R = P + Q + S + T + U

Question 31.
Define null vector. What are its properties? What is its physical significance?
Answer:
It is defined as a vector having zero magnitudes and acting in an arbitrary direction. It is denoted by O.
Properties of null vector:

1. The addition or subtraction of zero vector from a given vector is again the same vector.
   i.e. A + O = A
   A – O = A
2. The multiplication of zero vector by a non-zero real number is again the zero vector
   i.e. n.O = O
3. If n₁ A = n2B where n₁ and n₂ are non-zero real numbers, then the relation will hold good
   if A = B = O
   i.e. both A and B are null vectors.

The physical significance of null vector: It is useful in describing the physical situation involving vector quantities.
e.g. A – A = O
0 × A = O.

Motion in a Plane Important Extra Questions Long Answer Type

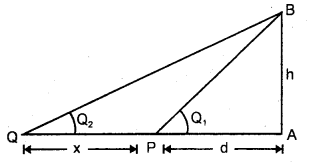
Question 1.
Discuss the problem of a swimmer who wants to cross the river in the shortest time.
Answer:
Let v_s and v_r be the velocities of swimmer and river respectively.
Let v = resultant velocity of v_s and v_r

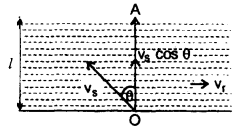
1. Let the swimmer begins to swim at an angle θ with the line OA where OA is ⊥ to the flow of the river.
If t = time taken to cross the river, then
t = \(\frac{l}{v_{s} \cos \theta}\) …(i)

where l = breadth of the river
For t to be minimum, cos 0 should be maximum.
i.e. cos θ = 1

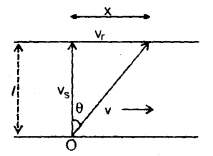
This is possible if θ = 0
Thus, we conclude that the swimmer should swim in a direction perpendicular to the direction of the flow of the river.

2. v = \(\sqrt{v_{s}^{2}+v_{r}^{2}}\)
where v\(\vec{v}\) is the resultant velocity of v_s and v_r.

3. tan θ = \(\frac{v_{\mathrm{r}}}{\mathrm{v}_{\mathrm{s}}}=\frac{\mathrm{x}}{l}\)
or
x = l\(\frac{\mathbf{v}_{\mathrm{r}}}{\mathbf{V}_{\mathrm{s}}}\)

4. t = \(\frac{l}{\mathrm{~V}_{\mathrm{s}}}\)

Question 2.
State and prove parallelogram law of vector addition. Discuss some special cases.
Answer:
It states that if two vectors can be represented completely (i.e. both in magnitude and direction) by the two adjacent sides of a parallelogram drawn from a point then their resultant is represented completely by its diagonal drawn from the same point.

Proof: Let P and Q be the two vectors represented completely by the adjacent sides OA and OB of the parallelogram OACB s.t.
\(\overrightarrow{\mathrm{OA}}\) = P, \(\overrightarrow{\mathrm{OB}}\) = Q
or
| \(\overrightarrow{\mathrm{OA}}\) | = |P|, | \(\overrightarrow{\mathrm{OB}}\) | = |Q|

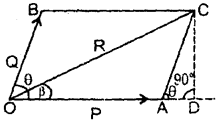
θ = angle between them = ∠AOB

If R be their resultant, then it will be represented completely by the diagonal OC through point O s.t. OC = R
The magnitude of R: Draw CD ⊥ to OA produced,


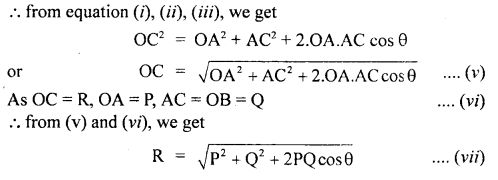
eqn. (vii) gives the magnitude of R.

The direction of R: Let β be the angle made by R with P
∴ in rt. ∠d ΔODC,

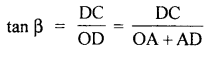
Special cases: (a) When two vectors are acting in the same direction:
Then θ = 0°

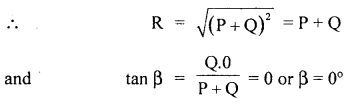
Thus, the magnitude of the resultant vector is equal to the sum of the magnitudes of the two vectors acting in the same direction, and their resultant acts in the direction of P and Q.

(b) When two vectors act in the opposite directions:
Then θ = 180°

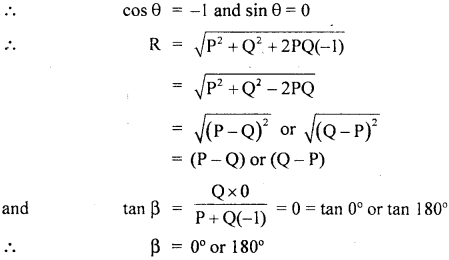
Thus, the magnitude of the resultant of two vectors acting in the opposite direction is equal to the difference of the magnitude of two vectors and it acts in the direction of the bigger vector.

(c) If θ = 90° i.e. if P ⊥ Q,
then cos 90° = 0
and
sin 90° = 1

R = \(\sqrt{P^{2}+Q^{2}}\)
and
tan β = \(\frac{O}{P}\).

Question 3.
Derive the relation between linear velocity and angular velocity. Also, deduce its direction.
Answer:
Let R be the radius of the circular path of center O on which an object is moving with uniform angular velocity co. Let v = its linear velocity. Let the object move from point P at time t to point Q at time t + Δt. If r and r + Δr be its position vectors at point P and Q respectively, then


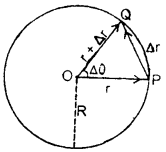
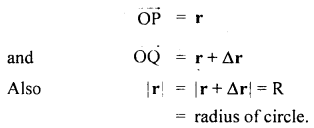
∴ Linear displacement of the particle from P to Q in small time interval Δt = Δr.
Let Δθ = its angular displacement
∴ ω = \(\frac{Δθ}{Δt}\)
or
Δθ = ωΔt ….(1)

Also we know that Δθ = \(\frac{\widehat{\mathrm{PQ}}}{\mathrm{R}}\) …(2)

∴ from (1) and (2), we get

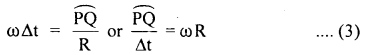
Now when Δt → 0, then from eqn. (1) Δθ → 0
so arc PQ = \(\widehat{\mathrm{PQ}}\) = chord PQ

Thus eqn. (3) reduces to

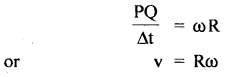
where v = \(\frac{PQ}{Δt}\) is the linear velocity of the object.

Direction of velocity vector: In isosceles ΔOPQ,

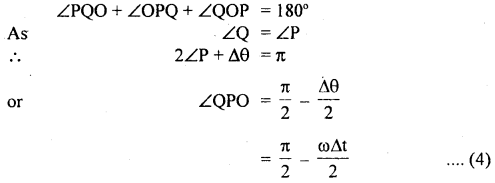
when Δt → 0, ∠QPO → \(\frac{π}{2}\)
i.e. \(\overrightarrow{\mathrm{OP}}\) tends to become ⊥ to \(\overrightarrow{\mathrm{OP}}\)
or
\(\overrightarrow{\mathrm{OP}}\) tends to lie along the tangent at P. Hence velocity vector at P is directed along the tangent to the circle in the direction of motion.

Question 4.
What do you understand by the rectangular resolution of a vector? Resolve it into its two rectangular components.
Answer:
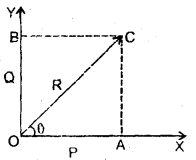
It is defined as the process of splitting a given vector into two or three-component vectors at right angles to each other. The component vectors are called rectangular components of the given vector. Let R be the given vector acting in the X – Y plane at an angle θ with the x-axis. Let \(\overrightarrow{\mathrm{OC}}\) = R. From point C, draw perpendiculars CA and CB on X and Y axes respectively. If P and Q be the rectangular components of R along the X and Y axis respectively, then

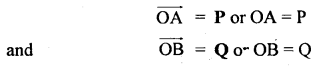
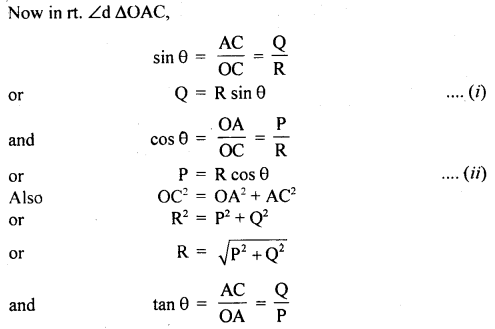
Also according to the triangle law of vector addition,
R = P + Q
= Pî + Qĵ
or
R= (R cosθ)î+ (R sinθ)ĵ
Thus if A_x and A_y be the two rectangular components of A along the X and Y axes respectively.
Then A = A_x + A_y
A = A_xî + A_yĵ

Note: Similarly in three dimensions,
A = A_xî +A_yĵ + A_zk̂

Position vector in two and three dimensions can be expressed as:
r = xî + yĵ
and
r = xî + yĵ + zk̂ .

Question 5.
Define centripetal acceleration and derive its expression. Also, deduce its direction.
Answer:
Centripetal acceleration: It is defined as the acceleration which always acts towards the center along the radius of the circular path.
“Centripetal” comes from a Greek term that means “centre¬seeking”.

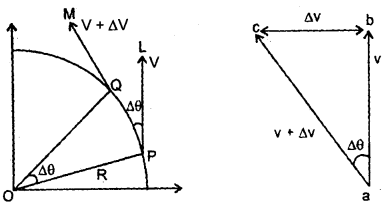
The expression for centripetal acceleration: Let a body be moving wi^h constant angular velocity 0) and constant speed v in a circular path of radius R and center O.

Let the body be at points P and Q at time t and t + Δt respectively.
Also, let Δθ = ∠POQ be the angular displacement in a small-time inverted Δt, thus

If v and v + Δv be the velocity vectors of the body at points P and Q acting along PL and QM respectively. As the body is moving with uniform speed, so lengths PL and PM are equal i.e. PL = PM. The change in velocity Δv from P to Q is due to the change in the direction of the velocity vector.

Hence the magnitude of the acceleration of the body is given by

From point ‘a’ draw \(\overrightarrow{\mathrm{ab}}\) parallel and equal to \(\overrightarrow{\mathrm{PL}}\) and \(\overrightarrow{\mathrm{ac}}\) parallel and equal to \(\overrightarrow{\mathrm{QM}}\), thus

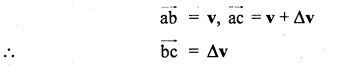
Clearly, the angle between ab and ac is Δθ. As Δt is quite small so
b and c lie on very close to each other, thus be can be taken to be an arc \(\widehat{\mathrm{bc}}\) of a circle of radius ab = |v|.

Also when Δt → 0, then L.H.S. of Eqn. (4) represents acceleration. Thus Eqn. (4) can be written as


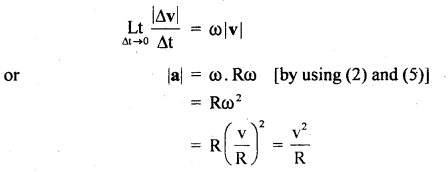
eqn. (6) gives the magnitude of the acceleration produced in the body.

The direction of acceleration: Acceleration always acts in the direction of Δv which acts from b to c. When Δt is decreased, Δθ also decreases. If Δt → 0, then Δθ → 0, so Δv tends to be perpendicular to ab. As ab ∥ PL, so Δv tends to act perpendicular to PL i.e. along PO i.e. along the radius towards the center of the circular path.

Since v and R are always constant, so the magnitude of centripetal acceleration is also constant. But the direction changes pointing always towards the center. So centripetal acceleration is not a constant vector.

Question 6.
A body is projected with some initial velocity making an angle θ with the horizontal. Show that its path is a parabola. Find the maximum height attained, time for maximum height, horizontal range, maximum horizontal range, and the time of flight.
Answer:
Let the body be projected with velocity u inclined at angle θ with the horizontal. The horizontal and vertical components of velocity and acceleration are
U_x, a_x, and U_y, a_y where
u_x = u cos θ, U_y = u sin θ, a_x = 0, a_y = -g
where g is the acceleration due to gravity.

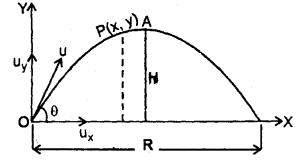
The coordinates of O are (0, 0). Considering horizontal motion, The position of the body after time t has coordinates (x, y) where
x (t) = X_o + u_x t + 1/2 a_x × t²

Substituting for various factors
x(t) = 0 + u cos θ . t + 0
x(t) = u cos θ t

Equation of trajectory:
Substituting for t from eq. (1) in eq. (2), we get

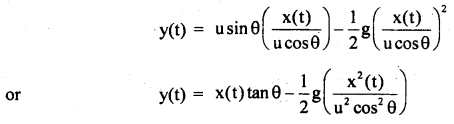
This is an equation of a parabola. Thus, the path of a projectile is a parabola.

Maximum height attained: At the maximum height, the vertical componènt of velocity becomes O (zero). Now using the equation of motion

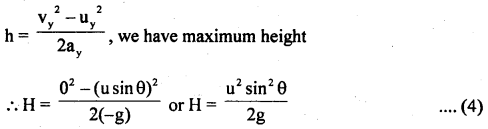
Time for maximum height: Using equation of motion, v = u + at or v_y = Uy + a_y t, we have

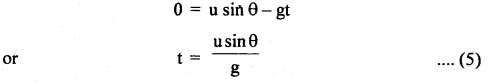
Horizontal range: Let the horizontal range be R. Since there is no acceleration in the horizontal direction, so
x = x(0) + u_xt + \(\frac{1}{2}\)a_x t²
Here x(0) = 0, u_x = u cos θ, a_x = 0, and t is the total time of flight which is twice the time for maximum height because the body takes the same time in rising to and falling from the highest point.

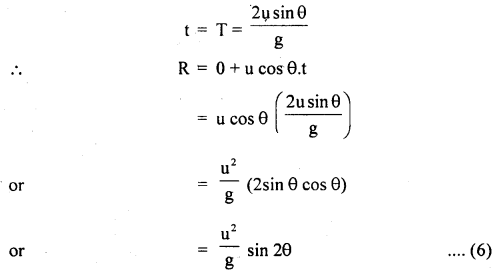
Maximum horizontal range: For R to be maximum, sin 2θ in Eqn. (6) must be maximum i.e. sin 2θ = 1,

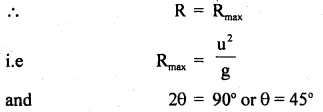
Thus, for R to be maximum, 0 must be 45°. It is independent of the mass of the body.

Time of flight of the projectile: The projectile after completing its flight returns back to the same horizontal level from which it was projected. Therefore, the vertical displacement in the whole flight is zero. Considering vertical motion.


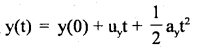
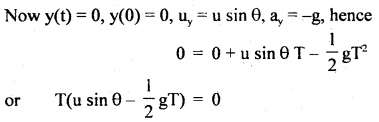
Therefore, either T = 0 or u sin θ – \(\frac{1}{2}\) g T = 0
T = 0 corresponds to the initial (starting) position,

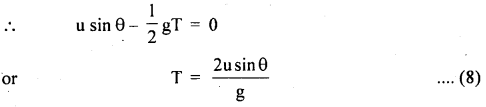
Equation (8) gives the total time of flight This is twice the time for maximum height.

Question 7.
A projectile is projected at an angle a with the vertical with initial velocity u. Find the maximum height attained, time of flight, and the horizontal range.

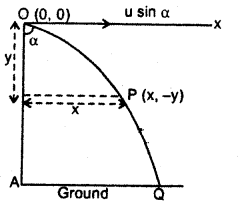
Answer:
Let the particle be projected from O with velocity u. The magnitude of horizontal and vertical components of the velocity are u sinα and u cosα respectively. Coordinates of O are (0, 0).

Maximum height: Consider the vertical motion. The initial speed Uy = u cosα and final speed v_y = 0, acceleration ay = – g, then using the
equation of motion s = \(\frac{v^{2}-u^{2}}{2 a}\) we have

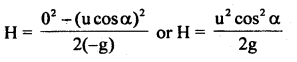
Time of flight: It is the total time taken by the projectile in going from O to A. The vertical displacement = 0. Considering vertical motion and using the equation of motion

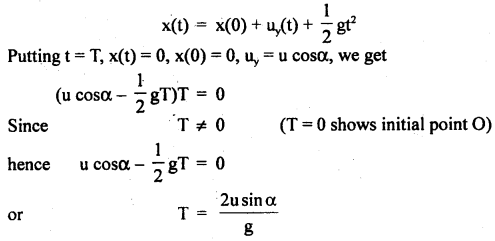
Horizontal range: Considering horizontal motion u_x = u sinα,
a_x = 0,
∴ using equation of motion

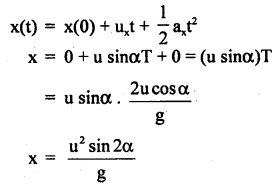
Numerical Problems:

Question 1.
What is the angle between the following pair of vectors?
A = î + ĵ + k̂,B = – 2î – 2ĵ – 2k̂
Answer:
We know that
A.B = AB cos θ

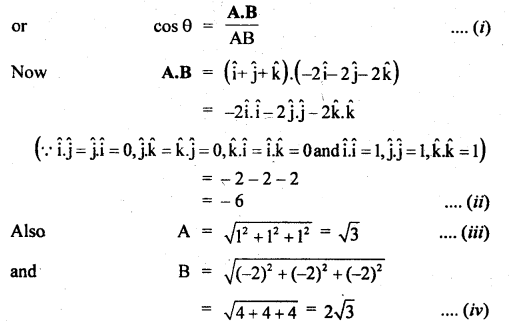
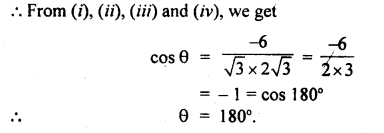
Question 2.
Prove that 2î – 3ĵ – k̂ and – 6î + 9ĵ + 3k̂ are parallel.
Answer:
Let A = 2î – 3ĵ – k̂
and B = – 6î + 9ĵ + 3k̂

These two vectors will be parallel if their cross-product is zero.
i.e. if A × B = 0


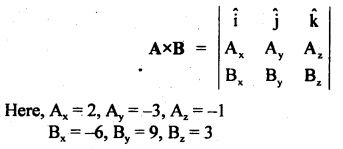
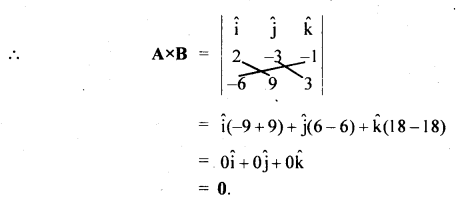
Hence proved.

Question 3.
Calculate the area of the triangle determined by two vectors
A = 3î + 4ĵ and B = – 3î + 7ĵ
Answer:
We know that area of a triangle is given by

Question 4.
A man wants to cross the river to an exactly opposite point on the other bank. If he can row his boat with twice the velocity of the current, then at what angle to the current, he must keep the boat pointed.
Answer:

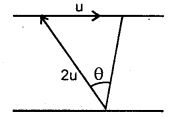
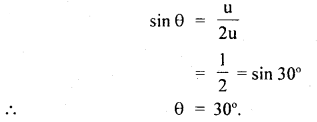
Question 5.
A body is acted upon by the following, velocities:
(i) 7 ms^-1 due to E,
(ii) 10 ms^-1 due S,
(iii) 5\(\sqrt{2}\) ms^-1 due N.E.
Find the magnitude and direction of the resultant velocity.

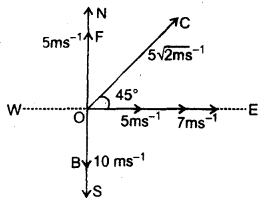
Answer:
Let OA, OB and OC represent the velocities given in the statement i.e.
OA = 7 ms^-1
OB = 10 ms^-1
and OC = 5\(\sqrt{2}\) ms^-1
To find their resultant velocity, resolve OC into two rectangular components along east and north.

Hence resultant velocity along east = 7 + 5 = 12 ms^-1 and resultant velocity along south = OB – OF = 10 – 5 = 5 ms^-1.

If R be the resultant velocity, then the magnitude of R is obtained by applying the parallelogram law of vector addition as

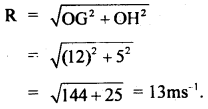
When OG = 12ms^-1 and OH 5ms^-1.

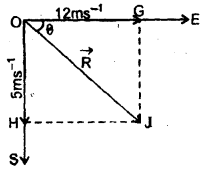
The direction of R: Let θ be the angle made by R with the east.
∴ in rt. ∠d ΔOGI,

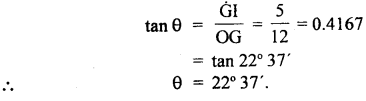
Question 6.
If \(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}=\overrightarrow{\mathbf{C}}\), prove that C = (A² + B² + 2AB cosθ)^1/2 where θ ¡s the angle between \(\overrightarrow{\mathbf{A}}\) and \(\overrightarrow{\mathbf{B}}\).
Answer:

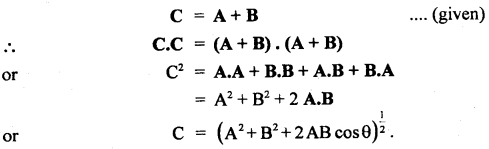
Question 7.
Determine the value of k so that the vectors \(\overrightarrow{\mathbf{A}}\) = 6î + kĵ – 4k̂ and \(\overrightarrow{\mathbf{B}}\) = 3î + 4ĵ + 5k̂ are perpendicular.
Answer:

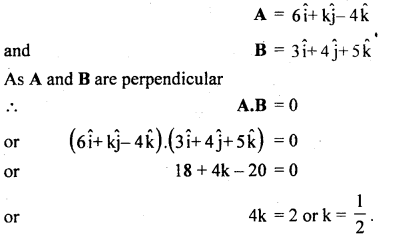
Question 8.
Determine a unit vector which is perpendicular to both \(\overrightarrow{\mathbf{A}}\) = 2î + ĵ + k̂ and \(\overrightarrow{\mathbf{B}}\) = î – ĵ + 2k̂
Answer:
Let n̂ be the unit vector perpendicular to both A and B.
Also, Let C be the vector that acts along n̂
∴ By definition of the cross product,

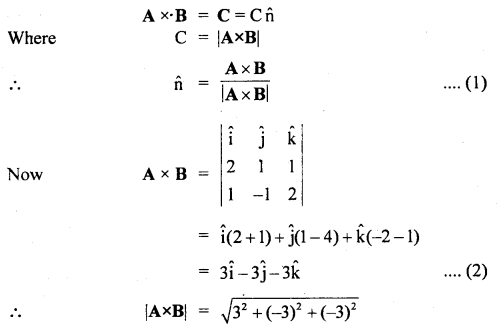
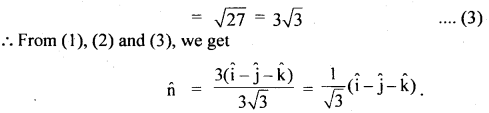
Question 9.
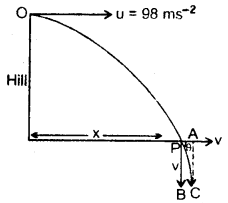
A projectile is fired horizontally with a velocity of 98 ms^-1 from the top of a hill 490 m high. Find:
(i) the velocity with which it strikes the ground.
(ii) the time is taken to reach the ground.
(iii) the distance of the target from the hill.
Answer:

(i) h = 490 m, a = g = 9.8 ms²
U_y = initial velocity along the y-axis at the top of the tower = 0

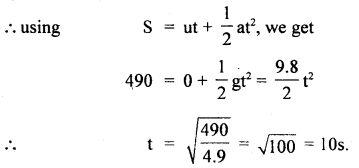
(ii) Let v be the velocity along the y-axis with which the projectile hits the ground.

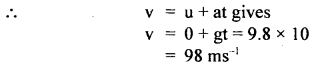
If V be the resultant velocity of hitting the ground

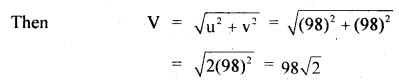
Let θ be the angle made by V with the horizontal

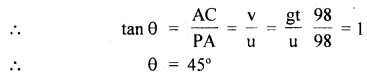
(iii) Let x, be the distance of the target from the hill.
∴ x = horizontal distance covered with u in a time t.
ut = 98 × 10 = 980 m.

Question 10.
A boy stands at 78.4 m from a building and throws a ball which just enters a window 39.2 m above the ground. Calculate the velocity of the projection of the ball.
Answer:
Let the boy standing at A throw a ball with initial velocity u.
θ = angle of the projection made with the horizontal.

As the boy is at 78.4 m from the building and the ball just enters above the ground.

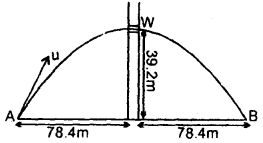
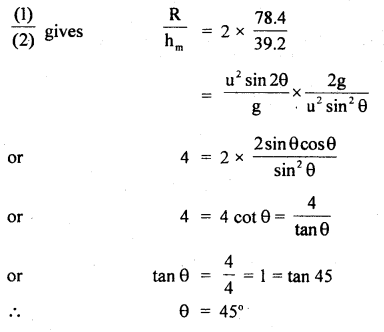
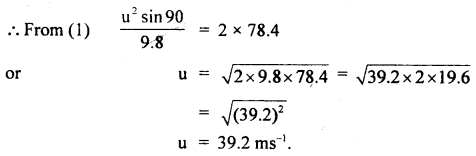
Question 11.
The equation of trajectory of an oblique projectile is
y = \(\sqrt{3}\)x – \(\frac{1}{2}\)gx²
What is the initial velocity in ms’ and the angle of projection of the projectile in degree?
Answer:
Comparing the given equation with the standard equation of the trajectory of an oblique projectile.

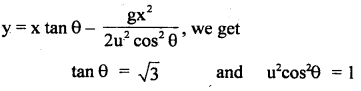
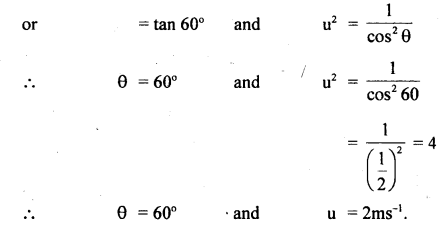
Question 12.
Two particles located at a point begin to move with velocities 4 ms^-1 and 1 ms^-1 horizontally in opposite directions. Determine the time when their velocity vectors become perpendicular. Assuming that the motion takes place in a uniform gravitational field of strength g.
Answer:
Let v₁ and v₂ be the velocities of first and 2nd particles respectively after a time t.
∴ v₁ = 4î – gt ĵ
v₂ = – î – gt ĵ
For v₁ and v₂ to be ⊥ to each other, then their dot product must be zero.

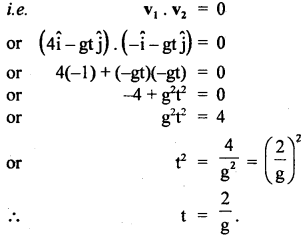
Question 13.
In the previous question, determine the distance between particles at t = \(\frac{2}{g}\).
Answer:
The separation between the particles is to take place only along the horizontal.
∴ the separation between the particles
= relative speed of the particles along horizontal × time

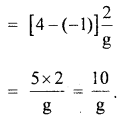
Question 14.
The maximum range of a projectile is range. What is the angle of projection for the actual range?
Answer:
We know that the horizontal range of a projectile is given by
R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\) …(i)

Where u = initial velocity of projection
θ = angle of projection with horizontal

Also, we know that the maximum horizontal range (Rmax) is given by

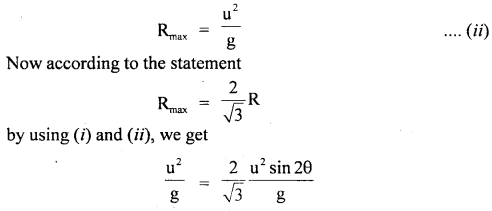
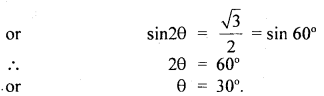
Question 15.
A body is projected with a velocity of 40 ms^-1. After two seconds, it crosses a verticle pole of 20.4 m. Find the angle of projection and the horizontal range.
Answer:
Here, u = 40 ms^-1
height of verticle pole, h = 20.4 m
t = 2 seconds

Let us take vertical motion

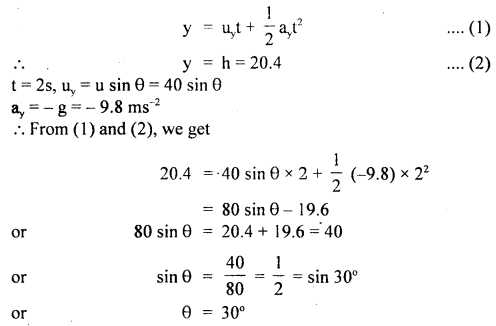
∴ The horizontal range is given by the relation,

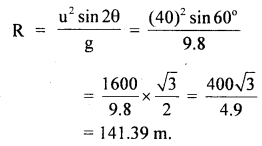
Question 16.
The greatest and the least resultant of two forces acting at a point are 29 N and 5 N respectively. If each force is increased by 3 N, find the resultant of two new forces when acting at a point at an angle of 90° with each other.
Answer:
Let A and B be the two forces.
∴ Greatest Resultant = A + B = 29 N ….(1)
least Resultant = A – B = 5 N ….(2)

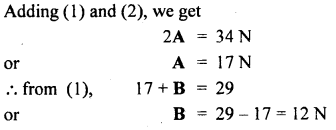
Let A and B be the new forces such that
A’ = A + 3 = 17 + 3 = 20N and
B’ = B + 3 = 12 + 3 = 15 N

Here, θ = angle between A’ and B’ = 90°
Let R be the resultant of A’ and B’.
∴ according to parallelogram law of vector addition

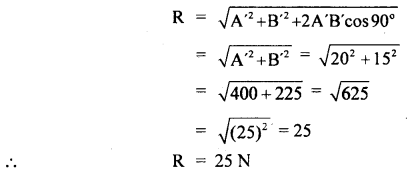
The direction of R:
Let β be the angle made by R with A’

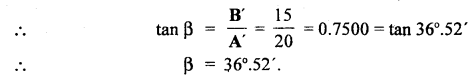
Question 17.
An aircraft is trying to fly due north at a speed of 100 ms^-1 but is subjected to a crosswind blowing from west to east at 50 ms^-1. What is the actual velocity of the aircraft relative to the surface of the earth?
Answer:
Let V_a and V_w be the velocities of aircraft and wind respectively.
∴ V_a = 100 ms^-1 along N direction
V_w = 50 ms^-1 along E direction

If V be the resultant velocity of the aircraft, then these may be represented as in the figure given below. So the magnitude of V is given by,


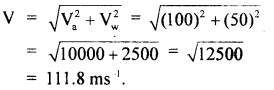
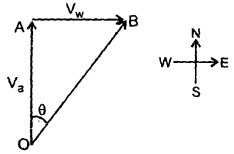
Let ∠AOB = θ be the angle which the resultant makes with the north direction.

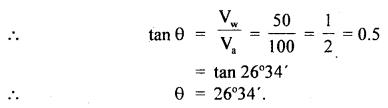
Question 18.
Calculate the total linear acceleration of a particle moving in a circle of radius 0.4 m at the instant when its angular velocity is 2 rad s^-1 and angular acceleration is 5 rad s^-2.
Answer:
Since the particle possesses angular acceleration, so its total linear acceleration (a) is the vector sum of the tangential acceleration (a,) and the centripetal acceleration (ac). a₁ and a_c, are at right angles to each other.
a = \(\sqrt{a_{t}^{2}+a_{c}^{2}}\) …. (1)

Now r = radius of the circular path = 0.4 m
ω = angular velocity of the particle = 2 rad s^-1
α = angular acceleration = 5 rad s^-2


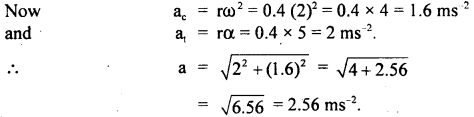
Let θ = angle made by a with a,

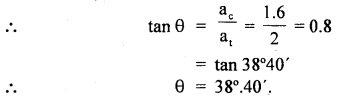
Question 19.
Calculate the greatest number of rotations per minute which can be given to a body of mass 500 gms tied to a string of length 1.5 m, if the string can withstand a maximum tension of 40 N.
Answer:
Here, m = mass of body = 500 gms = 0.5 kg
r = radius of circle = 1.5 m
F_c = Centripetal force = 40 N
Now we know that

Hence the body can be given 70 rotations per minute without breaking the string.

Question 20.
An airplane flies 400 km west from city A to city B then 300 km north-east to city C and finally 100 km north to city D. How far is it from city A to city D? In what direction must the airplane go to return directly to the city A from city D?
Answer:
Given, AB = 400 km
BC = 300 km
CD = 100 km
AD =?

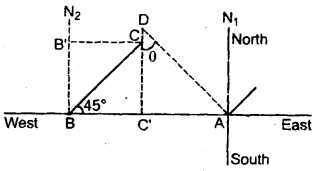
Let N₁, N₂ represent north directions.
∠ABC = 45°
Draw CC’ ⊥ AB, And CB’ ⊥ BN₂
Now in ΔBC’ C

From AAC’D, AD is given by

Question 21.
Which of the following quantities are independent of the choice of the orientation of the coordinates axes:
a + b, 3a_x + 2b_y, [a + b – c], angle between b and c, a?
Answer:
a + b, |a + b – c|, angle between b and c, a are the quantities that are independent of the choice of the orientation of the coordinate axes.

But the value of 3a_x + 2b_y depends on the orientation of the axes.

Question 22.
A machine gun is mounted on the top of a tower 100 m high. At what angle should the gun be inclined to cover a maximum range of firing on the ground below? The muzzle speed of the bullet is 150 ms^-1. (take g = 10 ms^-2)
Answer:
Here, u = 150 ms^-1
h = 100 m
g = 10 ms^-2

Let R = horizontal range of the projectile.
If t = time during which the bullet covers, horizontal range R = time during which the bullet falls through a height h (= 100 m).
Let θ = angle of projection with horizontal, then
u_x = u cos θ = 150 cos θ = horizontal component of speed of the projection,
u_y = 150 sin θ = vertical component of the speed of projection.

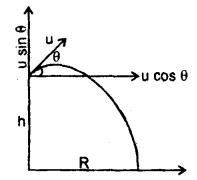
Considering the upward motion positive, then using the equation


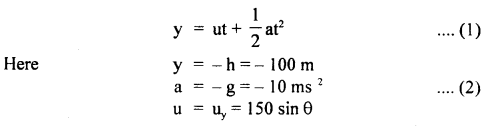
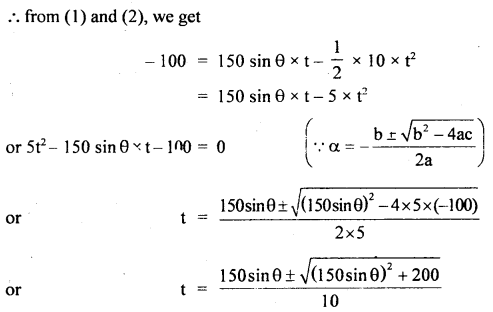
∴ The horizontal range covered by the (using positive sign only) projectile is given by
x = u_x × t

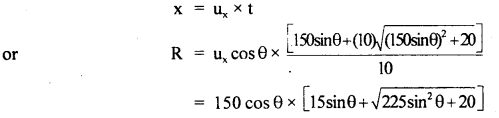
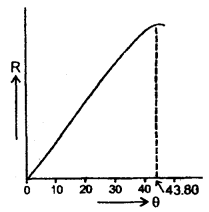
To maximize this function graphically, a graph between R and θ by taking arbitrary values of θ is plotted. We find from the graph that R is maximum for θ = 43.8°.

Question 23.
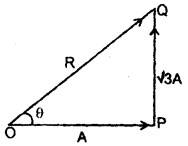
Two vectors of magnitude A and \(\sqrt{3}\) A are perpendicular to each other. What is the angle which their resultant makes with A?
Answer:
Let θ = angle made by R (resultant of A and \(\sqrt{3}\) A) with A
∴ In ΔOPQ

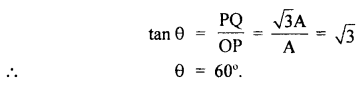
Question 24.
If |a + b| = |a – b|, then find the angle between a and b using properties of the dot product of vectors.
Answer:
Here, |a + b| = |a – b| …. (i) given
Squaring on both sides of eqn. (i), we get

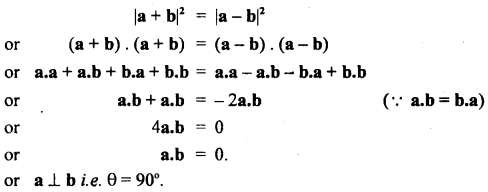
Question 25.
The express cross product of two vectors in cartesian coordinates.
Answer:
Let A and B be the two vectors s.t.


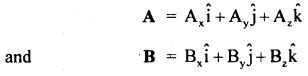
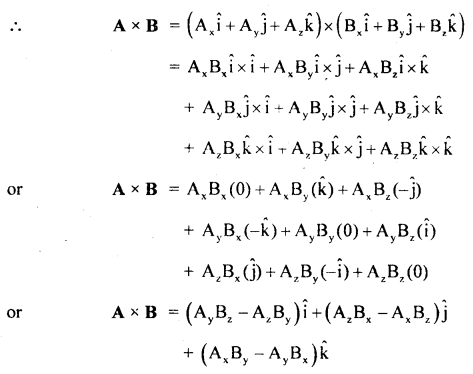
It can be written in a determinant form as

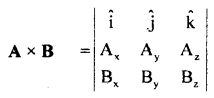
Value-Based Type:

Question 1.
Two friends Raman and Madhav arc playing on the bank of a river. They are throwing stones in the river. Raman is a student of the science stream whereas Madhav from the commerce stream. Every time Raman throws the stone far away than Madhav. Madhav was surprised and could not understand the reason. Finally, Raman explained the fact that it is relating to physics.
(i) What values are shown here by Roman?
Answer:
Intelligence, social, cooperative, and willing to share his knowledge,

(ii) Which concept is being used here?
Answer:
Horizontal range of a projectile

(iii) What is the minimum angle to get the maximum horizontal range?
Answer:
We know that: Maximum range: R = \(\frac{u^{2} \sin 2 \theta}{\mathrm{g}}\)

For maximum range
Sin 2θ = maximum value
i.e sin 2θ =1
⇒ sin 2θ = sin 90°
⇒ 2θ = 90° or θ =45°
Hence, if the body is projected at an angle of 45°, it will cause maximum horizontal range.

Question 2.
Himanshu and Shika are the two students of class XI. Himanshu fired a bullet at an angle of 30° with the horizontal which hits the ground 3 km away. Shika told that I could hit a bird that is 4 km away by adjusting its angle of projection. Himanshu immediately betted, He told if you can I would give you Its. 1000 otherwise you have to pay the same to me. Himanshu was sure that you can never hit that bird. However, killing a bird is not good for the environment. Assume the muzzle speed to be fixed, and neglect air resistance.
(i) Is betting a good practice?
Answer:
No

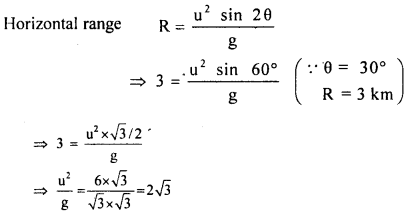
(ii) How Himanshu is sure that the bullet could not hit the target?
Answer:
Max horizonatal range = \(\frac{\mathrm{u}^{2}}{\mathrm{~g}}\) [∵ muzzle velocityin fixed]
ie R_max = \(\frac{\mathrm{u}^{2}}{\mathrm{~g}}\) = 2\(\sqrt{3}\) = 3.464 km g
So, the bullet can not hit the target which is 4 km away.

(iii) Which values are depicted in the above question?
Answer:
Values depicted are:
(a) Concern for environment and living creature
(b) Avoid betting
(c) Intelligent

Question 3.
Rain is falling vertically with a speed of 35 m s^-1. A girl of class XI rides a bicycle with a speed of 12 m s^-1 in the east to west direction. She could not understand that in which direction she should half her umbrella. When she came back to her home she asked her mother who was a physics teacher in a reputed school. She explained as under:
(i) Which value is displayed by the girl?
Answer:
Willing to know the scientific reason, curiosity

(ii) What justification was given by her mother?
Answer:
V_f = The velocity of rain
V_b = The velocity of bicycle
Both these velocities are with respect to the ground.
The velocity of rain relative to the velocity of the bicycle is given by
V_rb = V_r – V_b

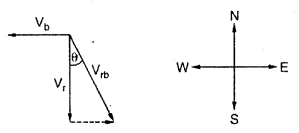
This relative velocity vector as shown above makes an angle θ with the vertical.
It is given by:

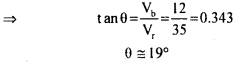
∴ The girl should hold her umbrella at an angle of about 19° with the vertical towards the west.

Question 4.
Sita a student of class XI was suffering from malaria. The area is full of mosquitoes. She was not having a mosquito net. Her friend Geeta has an extranet. She gave it to Sita. Also, she took Gita to Doctor, got her medicines. After a week Sita became normal.
(a) Comment upon the qualities of Sita.
Answer:
Sita has a caring attitude, and concern for others.

(b) The mosquito net over a 7 m × 4 m bed is 3 m high. The net has a hole at one corner of the bed through which a mosquito enters the net. It files and Sita at the diagonally opposite upper corner of the net
(i) Find the magnitude of the displacement of the mosquito
Answer:
We know that
A = \(\sqrt{\left(A_{x}\right)^{2}+\left(A_{y}\right)^{2}+\left(A_{x}\right)^{2}}=\sqrt{7^{2}+4^{2}+3^{2}}\)
= \(\sqrt{74}\) m

(ii) Taking the hole as the origin, the length of the bed as the X-axis, its width as the Y-axis and vertically up as the Z-axis, write the components of the displacement vector.
Answer:
The components of the vector are 7 m, 4 m, and 3 m

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 2 Units and Measurements Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 2 Important Extra Questions Units and Measurements

Units and Measurements Important Extra Questions Very Short Answer Type

Question 1.
If the size of the atom were enlarged to the tip of the sharp pin, how large would the height of Mount Everest be?
Answer:
10¹⁰ m.

Question 2.
What does the LASER mean?
Answer:
It stands for Light Amplification by Stimulated Emission of Radiation.

Question 3.
If the Universe were shrunk to the size of the Earth, how large would the Earth be on this scale?
Answer:
1o^-11 m (size of an atom.).

Question 4.
A research worker takes 100 careful readings in an experiment. If he repeats the same experiment by taking 400 readings, then by what factor will the probable error be reduced?
Answer:
By a factor of 4.

Question 5.
What is the number of significant figures in 0.06070?
Answer:
4.

Question 6.
Which of the following reading is most accurate?
(a) 7000m,
(b) 7 × 10² m,
(c) 7 × 10³ m
Answer:
(a) i.e. 7000 m.

Question 7.
The density of a cube is calculated by measuring the length of one side and its mass. If the maximum errors in the measurement of mass and length are 3% and 2% respectively, then what is the maximum possible error in the measurement of density?
Answer:
3% + 3 × 2% = 9%.

Question 8.
The mass of a body as measured by two students is given as 1.2 kg and 1.23 kg. Which of the two is more accurate and why?
Answer:
The second measurement is more accurate as it has been made to the second decimal point.

Question 9.
Do the inertial and gravitational masses of ordinary objects differ in magnitude?
Answer:
No.

Question 10.
Are S.I. units Coherent? Why?
Answer:
Yes, because all the derived units in this system can be obtained by multiplying or dividing a certain set of basic units.

Question 11.
Do A.U. And Å represents the same magnitudes of distance?
Answer:
No, 1 A.U. = 1.496 × 10¹¹ m and 1 Å = 10¹⁰ m.

Question 12.
What does SONAR stand for?
Answer:
It stands for Sound Navigation and Ranging.

Question 13.
What is the atomic mass unit (a.m.u.)?
Answer:
It is defined as \(\frac{1}{12}\)th of the mass of one 6C12 atom
i.e. 1 a.m.u. = \(\frac{1}{12} \times \frac{12}{6.023 \times 10^{23}}\) = 1.66 × 10^-27 kg

Question 14.
Which is the most accurate clock?
Answer:
Cesium atomic clock.

Question 15.
Write the S.I. units of the following physical quantities:
(a) Luminous intensity
Answer:
Candela (cd)

(b) Temperature
Answer:
Kelvin (K)

(c) Electric current
Answer:
Ampere (A)

(d) Amount of substance
Answer:
Mole (mol)

(e) Plane angle
Answer:
Radian (rd)

(f) Solid angle
Answer:
Steradian (sr)

(g) Pressure.
Answer:
Nm-2 = pascal (pa).

Question 16.
What is the difference between mN, Nm, and nm?
Answer:

• mN means.milli-newton, 1 mN = 10^-3N.
• Nm means newton-meter, 1 Nm = 1 J
• nm means namometer, 1 nm = 10^-9 m.

Question 17.
If x = a + bt + ct² where x is in meter and t in seconds, what is the unit of c?
Answer:
The unit on the left-hand side is a meter so the units of ct² should also be a meter. Since t² has units of s², so the unit of c is ms^-2

Question 18.
Will the dimensions of a physical quantity be the same, whatever be the units in which it is measured? Why?
Answer:
Yes, the dimensions don’t depend on the system of units chosen.

Question 19.
Write the dimensions of:
(i) gravitational constant
Answer:
[M^-1 L³ T²]

(ii) Plank’s constant
Answer:
[M L² T^-1]

(iii) torque
Answer:
[M L² T²]

(iv) surface tension
Answer:
[M L⁰ T^-2]

(v) angular momentum.
Answer:
[M L² T^-1]

Question 20.
Name at least two physical quantities each having dimensions:
(a) [M L^-1 T^-2]
Answer:
Pressure and stress,

(b) [M L² T^-1]
Answer:
Plank’s constant and angular momentum.

Question 21.
State the principle of homogeneity of dimensions?
Answer:
It states that the dimensions of each term on both sides of an equation are the same.

Question 22.
Which are the main types of errors in a physical measurement?
Answer:
Main errors are systematic error, random error, gross error, relative error, and percentage error.

Question 23.
Which one is large, the number of microseconds in a second or the number of seconds in a year?
The number of seconds in a year = 10⁷s and the number of microseconds in a second = 10⁶μs. So the number of seconds in a year is larger than microseconds in a second.

Question 24.
Do significant figures change if the physical quantity is measured in different systems of units?
Answer:
No, significant figures don’t depend on the system of units. e.s. 250 g = 2.50 × 10^-1 kg.
Both have 3 significant figures.

Question 25.
Suggest a distance corresponding to each of the following order of length:
(a) 10^-4 m
Answer:
Size of the atomic nucleus

(b) 10^-9 m
Answer:
Size of the oil molecule

(c) 10⁴ m
Answer:
Height of Mount Everest

(d) 10⁷ m
Answer:
Radius of Earth

(e) 10⁹ m.
Answer:
The radius of Sun.

Question 26.
What do you understand by the following?
(a) Century
Answer:
It is the largést unit of time, 1 century = 100 years.

(b) Shake
Answer:
It is the smallest unit of time, 1 shake = 10^-8s.

(c) Lunar month
Answer:
It is the time taken by the moon to complete one revolution around the Earth, 1 lunar month = 27.3 days.

(d) Leap year
Answer:
A year that is divisible by four and in which the month of February is of 29 days is called a leap year.

(e) Tropical year.
Answer:
The year in which the total solar eclipse takes place is called a tropical year.

Question 27.
What is the role of power (index) of a measurable in the formula used for calculation of a quantity in regard to the error in the quantity as determined in the given experiment?
Answer:
The error in the quantity becomes power times the error,
i.e. if x = p^a q^b. Then
\(\frac{\Delta x}{x}=a \frac{\Delta p}{p}+b \frac{\Delta q}{q}\)

Question 28.
How will you find the size of a liquid molecule?
Answer:
Using the formula, t = \(\frac{\mathrm{nV}}{500 \mathrm{~A}}\) we can find the size of the liquid molecule.
where V = volume of liquid (say oleic acid),
n = no. of drops in the solution of \(\frac{1}{500}\) concentration
A = area of the film of oleic acid left
t = thickness of the film.

Question 29.
What do you mean by the term measurement?
Answer:
Measurement means the comparison of a physical quantity with its unit to find out how many times the unit is contained in the given physical quantity.

Question 30.
Sort out the incorrect representation of units and write them
(i) m/sec
Answer:
ms^-1

(ii) Newton
Answer:
newton

(iii) kelvin
Answer:
kelvin

(iv) m.m.
Answer:
mm

(v) Jk^-1
Answer:
JK^-1

(vi) kg/m³
Answer:
kgm^-3

(vii) wH
Answer:
Wh

(viii) gms^-2
Answer:
gs2

(ix) length = 5M
Answer:
length = 5 m

(x) B = 4g (B = magnetic field intensity).
Answer:
B = 4G

Question 31.
Define light year.
Answer:
It is defined as the distance traveled by light in one year.
1 L.Y. (ly) = 3 × 10⁸ ms^-1 × 365 × 24 × 60 × 60s ≈ 9.46 × 10¹⁵ m.

Question 32.
Define Astronomical distance.
Answer:
It is defined as the distance between the Earth and Sun.
1 A.U. = 1.496 × 10¹¹ m~ 1.5 × 10¹¹ m.

Question 33.
What is the limit of
(i) accuracy
Answer:
The least count of the measuring instrument is the limit of accuracy with which a physical quantity can be measured.

(ii) error?
Answer:
The error in measurement is taken equal to half the least count.

Question 34.
What do you mean by ‘Order of magnitude’?
Answer:
Order of magnitude is defined as the approximation to the nearest power of 10 used to express the magnitude of a physical quantity under consideration, e.g.

1. The order of magnitude of the time interval of 1.2 × 10^-6 s is -6.
2. The order of magnitude of the distance of 4.5 × 10⁶ is +6.

Question 35.
Find the order of magnitude of a light-year.
Answer:
I light year = 9.46 × 10¹⁵ m ≈ 10¹⁶m
∴ The order of magnitude of light-year is +16.

Question 36.
Derive the dimensional formula of:
(a) Angular velocity
Answer:
Angular velocity = \(\frac{\text { Angle }}{\text { Time }}=\frac{1}{\mathrm{~T}}\) = [M⁰ L⁰ T^-1]

(b) Angular momentum
Answer:
Angular momentum = momentot inertia × Angular velocity
= mass x (radius of rotalion)² (Time)^-1
= [M L² T^-1].

Question 37.
Derive the dimensional formula of:
(a) Impulse
Answer:
Impulse = Force x Time
= [M L T^-2][T]
= [M L² T^-1].

(b) Surface energy
Answer:
Surfäce energy = \(\frac{\text { Energy }}{\text { Surface area }}\)
= \(\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{\left[\mathrm{L}^{2}\right]}\)
= [M L⁰ T^-2].

Question 38.
Derive the dimensional formula of
(a) Specific gravity
Answer:
Specific gravity = \(\frac{\text { Density of substance }}{\text { Density of water at } 4^{\circ} \mathrm{C}}\)
= \(\frac{\left[\mathrm{ML}^{3} \mathrm{~T}^{0}\right]}{\left[\mathrm{ML}^{-3} \mathrm{~T}^{0}\right]}\)
= [M⁰ L⁰ T⁰]

(b) Coefficient of viscosity .
Answer:
Coefficient of viscosity = \(\frac{\text { Force } \times \text { Distance }}{\text { Area } \times \text { velocity }}\)
= \(\frac{\left[\mathrm{MLT}^{-2}\right][\mathrm{L}]}{\left[\mathrm{L}^{2}\right]\left[\mathrm{LT}^{-1}\right]}\)
= [M L^-1 T^-1]

Question 39.
Derive the dimensional formula of:
(a) Universal gas constant
Answer:
Universal gas constant = \(\frac{\text { Pressure } \times \text { Volume }}{\text { Temperature }}\)
= \(\frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\left[\mathrm{L}^{3}\right]}{[\mathrm{K}]}\)
= [M L²  T² K^-1]

(b) Specific heat.
Answer:
Specific heat = \(\frac{\text { Heat }}{\text { Mass } \times \text { Temperature }}\)
= \(\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{[\mathrm{MK}]}\)
= [M⁰ L² T^-2 K^-1].

Question 40.
Derive the dimensional formula of:
(a) Coefficient of elasticity
Answer:
Coefficient of elasticity = \(\frac{\text { Stress }}{\text { Strain }}\)
= \(\frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]}{\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]}\)
= [M L^-1 T^-2]

(B) Boltzmann’s constant
Answer:
Boltzmann’s constant = \(\frac{\text { Energy }}{\text { Temperature }}\)
= \(\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{[\mathrm{K}]}\)
= [M L² T^-2 K^-1]

Question 41.
Define dimensions of a physical quantity.
Answer:
They are defined as the powers to which the fundamental units of mass, length, and time have to be raised to obtain its units, e.g. derived unit of area is [M⁰ L² T⁰]. Thus its dimensions are 1 zero in mass, 2 in length, and zero in time.

Question 42.
Define the dimensional formula of a physical quantity.
Answer:
It is defined as an expression that shows which of the fundamental units and with what powers appear into the derived unit of a physical quantity.
e.g. dimensional formula of force is [M¹ L¹ T²].

Question 43.
Define dimensional equation of a physical quantity.
Answer:
It is defined as the equation obtained by equating the symbol of a physical quantity with its dimensional formula, e.g. [F] = [M L T^-2] is the dimensional equation of force.

Question 44.
Define one kilogram.
Answer:
It is the mass of platinum-iridium cylinder (90% Pt + 10% Ir) having its diameter equal to its height (both equal to 3.9 cm) kept in the International Bureau of Weights and Measures of Sevres near Paris.

Question 45.
Define one second.
Answer:
It is defined as the time interval occupied by 9, 192, 631, 770 vibrations corresponding to the transition between two hyperfine levels of cesium -133 (Cs¹³³) atom in the ground state.

Question 46.
Define one ampere.
Answer:
It is defined as that constant current which when flowing through two parallel, straight conductors of the infinite length of negligible cross-section held one meter apart in a vacuum produces a force of 2 × 10^-7 N/m between them.

Question 47.
Define Kelvin.
Answer:
It is defined as \(\frac{1}{273.16}\) fraction of the thermodynamic temperature at the triple point of water.

Question 48.
Define radian.
Answer:
It is defined as the angle made at the center of a circle by an arc of length equal to the radius of the circle.

Question 49.
Define steradian.
Answer:
It is defined as the solid angle made at the center of a sphere by an area cut from its surface whose area is equal to the square of the radius of the sphere.

Question 50.
Define one mole.
Answer:
It is defined as the amount of substance that contains the same number of elementary units {i.e. atoms) as there are atoms in 0.012 kg of carbon-12.

Question 51.
Define standard meter.
Answer:
It is defined to be equal to exactly 1650763.73 wavelengths of orange-red light emitted in vacuum by krypton-86 atom i.e. kr⁸⁶.
i. e. 1 metre = 16,50,763.73 wavelengths.
Or
It is also defined as the distance traveled by light in \(\frac{1}{299792458}\) second.

Here 299792458 ms^-1 is the exact value of the velocity of light.

For all practical purposes, c = 2.9 × 10⁸ ms^-1 = 3.0 × 10⁸ ms^-1.

Units and Measurements Important Extra Questions Short Answer Type

Question 1.
If the size of a nucleus is scaled up to the tip of a sharp pin, what roughly is the size of an atom?
Answer:
The size of a nucleus is in the range of 10^-15 m to 10^-14 m. The tip of a sharp pain may be taken to be in the range of 1o^-5 m to 10^-4 m. Thus we are scaling up the size of the nucleus by a factor of 10^-5/10^-15 = 10¹⁰. An atom roughly of size 10^-10 m will be scaled up to a rough size of 10^-10 × 10¹⁰ = 1 m. Thusanucleus in an átom is as small in size as the tip of a sharp pin placed at the center of a sphere of radius about a meter.

Question 2.
(a) What do you mean by physical quantity?
Answer:
It is defined as a quantity that can be measured, e.g. mass, length, time, etc.

(b) What do you understand by:
(i) Fundamental physical quantities?
Answer:
They are defined as those quantities which cannot be expressed in terms of other quantities and are independent of each other, e.g. mass, length, time.

(ii) Derived physical quantities?
Answer:
They are defined as the quantities which can be expressed in terms of fundamental quantities, e.g. velocity, acceleration, density, pressure, etc.

Question 3.
(a) Define the unit of a physical quantity.
Answer:
It is defined as the reference standard used to measure a physical quantity.

(b) Define:
(i) Fundamental units.
Answer:
They are defined as the units of fundamental quantities. They are independent of each other and are expressed by writing the letter of the fundamental quantity in a parenthesis.
e.g. Fundamental units of mass, length and time are [M], [L], [T] respectively.

(ii) Derived units.
Answer:
They are defined as those units which can be derived from fundamental units. They are expressed by writing the symbol of a derived quantity in a parenthesis.
e.g. D.U. of velocity = [u]
acceleration = [a]
pressure = [P]
work = [W] and so on.

Question 4.
Define one Candela.
Answer:
It is defined as the luminous intensity in a perpendicular direction of a surface of \(\frac{1}{600,000}\) square meter area of a black body at a temperature of freezing platinum (1773°C) under a pressure of 101,325 N/m².

It is the S.I. unit of luminous intensity.

Question 5.
What is the advantage of choosing wavelength of light radiation as standard of length?
Answer:

1. It can be easily made available in any standard laboratory as Krypton is available everywhere.
2. It is well defined and does not change with temperature, time, place or pressure, etc.
3. It is invariable.
4. It increases the accuracy of the measurement of length (1 part in 10⁹).

Question 6.
Which type of phenomenon can be used as a measure of time? Give two examples of it.
Answer:
Any phenomenon that repeats itself regularly at equal intervals of time can be used to measure time.

The examples are:

1. Rotation of earth – the time interval for one complete rotation is called a day.
2. Oscillations of a pendulum.

Question 7.
Find the number of times the heart of a human being beats in 10 years. Assume that the heartbeats once in 0.8s.
Answer:
In 0.8 s, the human heart makes one beat.

∴ In 1 s, the human heart makes = \(\frac{1}{0.8}=\frac{10}{8}\) beats.

∴ In 10 years, the human heart makes
= \(\frac{10}{8}\) × 365 × 24 × 60 × 60 beats.
= 3.942 × 10⁸ beats.

Question 8.
Why it is not possible to establish a physical relation involving more than three variables using the method of dimensions?
Answer:
The dimensional analysis fails to derive a relation involving more than three unknown variables. The reason is that there will be more than three unknown factors in that case whose values cannot be determined from the three relations which we get by comparing the powers of M, L, and T.

Question 9.
What is the difference between accurate and precise measurement?
Answer:
A given measurement is said to be accurate in relation to other similar measurements if the error involved in it is least.

A given measurement is said to be precise in relation to other similar measurements if it is taken with an instrument with the minimum least count.

Question 10.
Pick up the most accurate and most precise measurement out of (a) 50.0 m, (b) s.oe m, (e) 5.00 cm, (f) 5.00 mm.
Answer:
The following table gives the relative error in count of the given measurement:

Clearly, the first measurement is most accurate because the relative error in it is minimum. The fourth measurement is most precise because it is taken with an instrument having the minimum least count among the v given measurements.

Question 11.
Define one parsec.
Answer:
It is defined as the distance at which an arc of length equal to y one astronomical unit subtends an angle of one second at a point.


Note: 1 L.Y. = 6.3 × 10⁴ A.U.
1 parsec = 3.26 L.Y.

Question 12.
Define annual parallax.
Answer:
It is defined as the angle (θ) subtended by the basis at the object (0). It is also called the parallactic angle.

∴ Parallactic angle = \(\frac{\text { Length of arc }}{\text { Radius }}\)
Or
θ = \(\frac{b}{s}\)

∴ s = \(\frac{b}{θ}\)

The parallax method is used to measure the distance of stars.
Here, b = basis = E₁E₂ distance where E₁ and E₂ are the two observation points on earth. θ = angle made by the star at point O. To find θ, let us observe the star 0’ simultaneously and let Φ₁ and Φ₂ be the angles made at E₁ and E₂.
∴ θ = Φ₁ + Φ₂
∴ s = \(\frac{b}{\phi_{1}+\phi_{2}}\)

Question 13.
Give Avogadro’s method to measure distances of the order of 10^-10 m.
Answer:
It is the indirect method of measuring the distances of the order of 10-10 m which is the size of an atom i.e. small distances. An atom is a tiny sphere. When such atoms lie packed in any substance; empty spaces are left in between. According to Avogadro’s hypothesis, the volume of all atoms in one gram of substance is \(\frac{2}{3}\) of the volume occupied by one gram of the substance.

i.e. V’ = \(\frac{2}{3}\)V ….(i)
Where V = actual volume of one gram mass.
V’ = volume occupied by atoms in I gram mass.
ρ = density of the substance.
∴ V = \(\frac{1}{ρ}\) …(ii)

Let m = atomic weight of the substance.
N = Avogadro’s number

∴Number of atoms in I gram of the substance = \(\frac{N}{M}\)
If r be the radius of each atom, then
V’ = no. of atoms in I gram x volume of each atom
Or
V’ = \(\frac{N}{M}\) x \(\frac{4}{3}\) 4πr3 …. (iii)

∴ From (i), (ii), and (iii), we get

Thus, r the radius of an atom can be calculated from equation (iv).

Question 14.
What arè the characteristics of a standard unit?
Answer:
The characteristics of a standard unit are as follows:

1. It should be well defined.
2. It should be of the proper size.
3. It should be easily accessible.
4. It should be reproducible in all places.
5. It should not change with time, place, and physical conditions such as pressure, tèmperature, etc.
6. It should be widely accepted.

Question 15.
What are the advantages of the S.I. system?
Answer:
Following are the main advantages of the S.I. system over other systems of units i.e. (C.G.S, FPS, and MKS).
1. It is a coherent system of units i.e. a system based on a certain set of fundamental units from which all derived units are obtained by multiplication or division without introducing numerical factors i.e. units of a given quantity are related to one another by the power of 10. So the conversions are easy.

2. S.I. is a rational system of units as it assigns only one unit to a particular physical quantity e.g. Joule is the S.I. unit for all types of energies while MKS units of mechanical energy, heat energy, and electrical energy are Joule, calorie, and watt-hour respectively.

3. It is an absolute system of units: There are no gravitational units on the system. The use of factor ‘g’ is thus eliminated.

4. It is a metric system i.e. the multiples and submultiples of units are expressed as powers of 10.

Question 16.
Point out the measurable likely to create the maximum error in the following experimental measurement.
Young’s modulus ‘Y’ of the material of the beam is calculated using the relation Y = mgl³/4bd³δ
When w = mg, δ = depression, I, b, d = length, breadth, thickness.
Answer:

Thus clearly m, l, b, d and 8 introduce the maximum error in the measurement of Y.

Question 17.
Classify the physical quantities on basis of their dimensional formula.
Answer:
They are divided into the following four categories:
1. Dimensional variables: They are defined as the physical quantities which possess dimensions and have variable values e.g. Area, velocity, force, etc.

2. Non-dimensional variables: They are defined as the physical quantities which have no dimensions but have variable values, e.g. Angle, specific gravity, strain, sin0, cos0 (i.e. trigonometric functions).

3. Dimensional constants: They are defined as the physical quantities which have both dimensions and constant values, e.g. Plank’s constant, speed of light in vacuum, gravitational constant.

4. Dimensionless constants: They are defined as the physical quantities which do not have dimensions but have constant values, e.g. n, e, pure numbers 1, 2, 3, …… etc.

Question 18.
What are the limitations of dimensional analysis?
Answer:
Following are the limitations of dimensional analysis:

1. Dimensionless constants involved in the physical relationship can not be determined.
2. It fails to derive the relations involving plus or minus signs like s = ut + \(\frac{1}{2}\)at²,
   v = u + at,
   v² — u² = 2as etc.
3. It fails to derive a relation involving more than three physical quantities.
4. This method does not help to derive the relations containing exponential and trigonometrical functions.
5. This method gives no information on whether a quantity is a scalar or vector.
6. It does not tell about the physical correctness of a relation.

Question 19.
Define significant figures. State the rules for determining the number of significant figures in a given measurement.
Answer:
They are defined as the number of digits up to which we are sure about their accuracy. In other words, they are defined as those digits that are known correctly in an experimental observation plus one more digit that is uncertain.

Following are the rules for determining significant figures:

1. All non-zero digits are significant.
2. All zeros occurring between non-zero digits are significant.
3. All zeros to the right of the last non-zero digit are not significant.
4. All zeros to the right of a decimal point and to the left of a non¬zero digit are not significant, e.g. 0.000879 has (3) significant figures.
5. All zeros to the right of a decimal point and to the right of a non-zero digit are significant, e.g. 0.2370 contains (4) sig-fig.
6. All zeros to the right of a non-zero digit and to the left of an expressed decimal are significant, e.g. 21900. has (5) sig-fig.

Question 20.
Mankind has existed for about 10⁶ years whereas the s. the universe is about 1010 years old. If the age of the universe is taken to be one day, how many seconds has mankind existed?
Answer:
Since

Mankind has existed for 8.64s on the new chosen scale.

Question 21.
State and explain the rule for finding the maximum possible error in a result.
Answer:
The maximum possible error is found in different ways in different types of results as follows:
(a) When the result involves the sum of two quantities,
i. e. if x = p + q
then, maximum possible error = maximum absolute error in first quality + maximum absolute error in the second quality. i.e. Δx = Δp + Δq

(b) When the result involves the difference of the quantities
i.e. if x = p – q
then, maximum possible error in x = maximum absolute error in p + maximum possible error in q
i.e. Δx = Δp + Δq

(c) When the result involves the multiplication of two quantities i.e. x = pq; then maximum relative error in x is given by
\(\frac{\Delta x}{x}=\frac{\Delta p}{p}+\frac{\Delta q}{q}\)

(d) When the result involves the quotient of tw«j observed quantities i.e. when x = p/q, then Maximum relative error in x is given by
\(\frac{\Delta x}{x}=\frac{\Delta p}{p}+\frac{\Delta q}{q}\)

(e) When the result involves some power oFa physical quantity, i.e. when x = pa qb, then maximum absolute e> u r in x is given by
\(\frac{\Delta x}{x}=a \frac{\Delta p}{p}+b \frac{\Delta q}{q}\)

i.e. maximum possible relative error in x = power × relative . error in p + power × relative error in q.

Thus the error is always additive in nature and maximum, permissible error is equal to the sum of maximum possible error in the i. individual quantities of that quantity.

Question 22.
How do you represent very large and very small physical y quantities? Write the prefixes, multiple, submultiple, and their symbols in a tabular form.
Answer:
The very long and very small quantities are written in powers of 10. The prefixes are tabled below:

Question 23.
Explain the importance of reference frames in measurements.
Answer:
(a) All measurements are made with reference to a point or portion i.e., a frame of reference.
(b) The number of time units contained in a physical quantity gets changed with a change in the reference frame.
(c) The same physical quantity may have different values in different reference frames.

Question 24.
Briefly describe the various techniques to measure time.
Answer:
The various techniques to measure time are:
(a) The synchronous motor run on a.c. of frequency 50 hertz is used to measure time as its rotation provides a time scale.

(b) Electronic oscillations: The semiconductor oscillators produce high-frequency oscillations i.e. of a very small time period. These oscillations thus can be used to measure the small time intervals.

(c) Quartz-crystal clocks: These clocks work on the piezoelectric effect. The oscillations so produced can be used to measure time intervals.

(d) Atomic clock: These are usually Cs-133 atom clocks whose electrons make a definite number of repeated jumps between two energy levels. These are very precise and are used to define second, so time can be measured.

(e) Decay of elementary particles: The study of decay can provide a scale for the measurement of very small intervals of time as unstable elementary particles decay between 10^-16 to 10^-24 seconds.

(f) Radioactive dating: Very long intervals of time can be measured by comparing them with the techniques of radioactive dating. The half-life period of decay of carbon is a standard time frame to determine the age of fossils etc.

Question 25.
Explain the rules for finding significant figures in the sum, difference, product, and quotients of true numbers.
Answer:
The rules for counting significant figures in algebraic operations are given below:
1. Addition and Subtraction: The sum or the difference of two numbers has significant figures only in those places where these are in the least precise amongst the given number. For example, if we subtract 45.7 from 46.9267 the result is 1.2267. But it should be written only 1.2 because the least precise of the two numbers is 45.7 and there is only one digit after the decimal.

Similarly in the sum of numbers 4205, 112.39, 77.93, and 213.2532, the correct result is 824.0 to the significant figures. So, in addition, or subtraction the same number of the decimal. places are retained in the result as are present in the number with the minimum amount of decimal places.

2. Multiplication and Division: The product or quotient of two numbers does not have more significant figures than are present in the least precise of the given numbers. e.g. in the product of two quantities 0.025 with 40, we get 1.000 but the answer is to be written as 1.0 because there are two significant figures in 40 the least of the two numbers. Similarly in a quotient when we divide 16.775 by 2.5, we get 6.71. The result of the significant figure will be 6.7.

Question 26.
Is it possible for an equation to be dimensionally correct still to be wrong? If so indicate the number of ways in which this might happen.
Answer:
It is possible that an equation may be dimensionally correct but physically it is wrong. For example the displacement of a particle moving with velocity u and acceleration ‘a’ after time t is given by
s = ut + 1/2at²

However, s = 1/2at² is dimensionally correct, as [L] = [LT²][T²]² shows dimensions on LHS = dimensions on RHS. Therefore, in certain circumstances, an equation may be dimensionally correct but actually, it is not physically correct. This happens especially in equations involving the sum and difference of two or more terms and in functions involving trigonometric functions. For example, the displacement y maybe y = a where a is the amplitude. This is dimensionally correct but does not give the full picture of the physical phenomenon.

The correct equation is

y = a sin wt or y = a sin \(\frac{2 \pi}{\lambda}\) (vt + x) etc.

Question 27.
Show that bigger is the unit smaller is the numerical value of physical quantity and vice-versa.
Answer:
In any system of unit, the following relations hold good
n₁u₁ = n₂u₂

Where n₁ and n₂ are the numerical values, u₁ and u₂ represent the unit of a physical quantity. This relation is based on the simple thing that the magnitude of a physical quantity remains the same in different systems of units.
Thus nu = constant or n ∝ \(\frac{1}{u}\)

If larger the n smaller will be the unit (u) and smaller the numerical value (n) Larger will be u. E.g. if the length of a rod l be 1 m in the S.I. system. Then it is 100 cm in the C.G.S. system i.e.

l = 1 m = 100 cm. Here clearly 1 < 100 and m > cm. Hence proved.

Question 28.
The difference in the order of magnitude of the longest and shortest distances and most massive and least massive objects are quite different. Write the same and compare them.
Answer:
The size of the nucleus is of the order 10^-15 m and the intergalactic distance is of the order of 10²² m. So, the ratio between the longest and the shortest distance is:
\(\frac{10^{22} \mathrm{~m}}{10^{-15} \mathrm{~m}}\) = 10³⁷

The smallest mass is the mass of an electron of the order of 10^-30 kg and the longest mass is the mass of the galaxy of the order of 10⁴² kg. So, the ratio of maximum to minimum mass is
\(\frac{10^{42} \mathrm{~kg}}{10^{-30} \mathrm{~kg}}\) = 10⁷²

Now the ratio between the mass ratio and distance ratio is
\(\frac{10^{72}}{10^{37}}\) = 10³⁵

The ratio betwe< n minimum mass and minimum distance is
\(\frac{10^{-30} \mathrm{~kg}}{10^{-15} \mathrm{~m}}\) = 10^-15

The ratio between maximum mass and minimum distance is
\(\frac{10^{42} \mathrm{~kg}}{10^{22} \mathrm{~m}}\) = 10²⁰

Question 29.
Define the terms
(i) mean absolute error
Answer:
The arithmetic means of all the absolute errors is known as mean absolute error.

(ii) relative error and
Answer:
The relative error is the ratio of mean absolute error to the mean or true value of the quantity measured.
Relative error = \(\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}}\)

(iii) percentage error.
Answer:
Percentage error is the relative error expressed in percent
Percentage error = \(\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}}\) × 100

Question 30.
State the rules applied in rounding off measurements.
Answer:
While rounding off measurements, the following rules are applied:
1. If the digit to be dropped is smaller than 5, then the preceding digit should be left unchanged.
e.g. 7.93 is rounded off to 7.9.

2. If the digit to be dropped is greater than 5, then the preceding digit should be raised by 1.
e.g. 17.26 is rounded off to 17.3.

3. If the digit to be dropped in 5 followed by digits other than zero, then the preceding digit should be raised by 1.
e.g. 7.351 on being rounded off to first decimal becomes 7.4.

4. If the digit to be dropped in 5 or 5 followed by zeros, then the preceding digits are not changed if it is even.
e.g. (a) 3.45 on being rounded off becomes 3.4.
(b) 3.450 on being rounded off becomes 3.4.

5. If the digit to be dropped in 5 or 5 followed by zeros, then the preceding digit is raised by one if it is odd.
e.g. (a) 3.35 on being rounded off becomes 3.4.
(b) 3.50 on being rounded off becomes 3.4.

Note: Rules (iv) are based on the convention that the number is to be rounded off to the nearest even number.

Units and Measurements Important Extra Questions Long Answer Type

Question 1.
State the rules for writing the units of physical quantities in the S.I. system.
Answer:
While writing the units of physical quantities following rules are followed with S.L units:
(1) The S.l. units are written in the form of symbols after the number i.e., number of time, the unit is contained in the physical quantity so that physical quantity = nu

With symbols, certain rules are laid down:

• Units in symbols are never written in plural i.e., meters is only m and not ms, years is y.
• The units based on the name of the scientists are written beginning with small letters and with capital letters in symbolic form viz, weber (Wb), newton (N), etc.
• No full stop is used at the end of the symbol.
• Symbols of units not based on the name of scientists are written as small letters viz. kilogram (kg), second (s), etc.

(2) Bigger and smaller number of units are represented with symbols corresponding to the power of 10 viz. 10⁶ is mega (M), 10¹² is Tera (T), 10^-3 is milli (m), 10^-9 is nano (n), etc.

(3) All units are written in numerator viz. kg/m³ is kg m, Nm²c².

(4) The units are written within parenthesis in graphs below the corresponding taxes viz. (ms^-1) and (s) in the velocity-time graph.

(5) Units of a similar physical quantity can be added or subtracted.

Question 2.
Explain the Triangular method.
Answer:
It is used to measure the distance of an accessible or inaccessible hill or a tower by measuring the angle which the object makes at point P (say)

Let x = distancy of point P from the foot of tower = PA .
∴ h = x tan θ

It is also used to measure the distance of an inaccessible object eg. a tree on the other bank of a river.

Let h = height of the inaccessible object.
Let θ₁, θ₂ = be the angle made at P and Q by the object.
Let PA = d, PQ = x.

∴ In ΔPAB and ΔQAB,

Question 3.
What are the uses of dimensional analysis? Explain each of them.
Answer:
Dimensional analysis is used for:
(a) checking the dimensional correctness of the given physical equation or relation.
(b) converting one system of units to another system.
(c) deriving the relationship between various physical quantities.

(a) checking of the dimensional correctness of a physical relationship is done by using the principle of homogeneity of dimensions. If the dimensions of M, L, T of each term on R.H.S. are equal to the dimensions of M, L, T of each term on L.H.S., then the given- physical relation is dimensionally correct, otherwise wrong.

(b) conversion: It is based on the fact that the magnitude of a physical quantity remains the same whatever may be the system of units, i.e. n₁u₁ = n₂u₂.

are the units of M, L, T in the first and second system of units of a physical quantity having dimensions of M, L, T, and a, b, c respectively.

Thus if fundamental units of both systems, dimensions of the quantity, and its numerical value n₁ in one system, are known then we can easily calculate n₂ in another system.

(c) Derivation of a relationship between various physical quantities is based on the principle of homogeneity of dimensions.

Following are the steps used:

1. We must Know the physical quantities (say p, q, r) upon which a physical quantity say x depends.
2. We must know the dimensions of p, q, r say a, b, c respectively.
3. 
4. Now, write the dimensions of each physical quantity on both sides of the equation
5. and compare the powers of M, L, T to find a, b, c. Putting values of a, b, c in the equation
6. we get the required relation.

Numerical Problems:

Question 1.
The average distance from Earth to the Sun is 1.49 × 10¹¹ m. Find out the value of 1 percent in m.
Answer:
According to the definition of parsec,

Question 2.
The parallax of a heavenly body measured from two points: diametrically opposite on the Earth’s equator is 60 seconds. If the radius of the Earth is 6.4 × 10⁶ m, determine the distance of the heavenly body from the center of Earth. Convert this distance in AU.
Answer:
Here

∴ The distance of the heavenly body from Earth is given by

Question 3.
Find the height of a rock mountain if on moving 100 m towards the rock in the horizontal direction through the base of
the rock, the angle of elevation of itš top increases from 300 to 45°.
Answer:
Here d = 100 m, θ₁ = 30°, θ₂ = 45°, h =?

Question 4.
Find the number of air molecules in a room of volume 12 m³. Given 1 mole of air at N.T.P. occupies a volume of 22.4 liters.
Answer:
No. of atoms in I mole of air = N
= 6.023 × 10²³

∴ Also at N.T.P., 1 mole of air occupies 22.4 liters of volume
= 22.4 × 10^-3 m³

∴ No. of molectiles ir 22.4 × 10^-3 m³ volume = 6.023 × 10²³
∴ No. of molecules in 12 m³ volume = \(\frac{6.023 \times 10^{23}}{22.4 \times 10^{-3}}\) × 12
= 3.23 × 10²⁶

Question 5.
(a) Convert ION into dyne using dimensional analysis.
Answer:
Newton (N) and dyne are the S.I. and C.G.S. units of force having dimensional formula [MLT^-2]
∴ a = 1, b = 1, c = – 2

S.I. system
n₁ = 10
M₁ = 1 kg
L₁ = 1 m
T₁ = 1 s

C.G.S. system.
n₂ = ?
m₂ = 1 g
L₂= 1 cm
T₂ = 1 s

(b) Find the units of length, mass, and time of the unit of force, velocity, and energy are 100 dynes, 10 cms^-1, and 500 erg respectively.
Answer:

Question 6.
Check the dimensional correctnesïof the relation
V = \(\sqrt{\frac{2 G M}{R}}\)
Answer:
It is done using the principle of homogeneity of dimensions i.e. if the dimensions of each term of both sides of the equation are the same, Then it is dimensionally correct.
Now dimensions of V = [LT^-1].
G = [M^-1 L³ T²]
M = [M]
R = [L]

∴ Dimensions of L.H.S. = [V] = [LT^-1] …(f)
Dimensions of R.H.S = \(\sqrt{\frac{G M}{R}}\)

Now from equations (i) and (ii), it is clear that the dimensions of L.H.S = R.H.S, so the given relation is dimensionally correct.

Question 7.
Suppose that the oscillatións of a simple pendulum depend on
(i) mass of the bob (m),
(ii) length of the string (1),
(iii) acceleration due to gravity (g) and (iv) angular displacement
(iv) Dimensionally show which of the above factors here an influence upon the period and in what way?
Answer:
Let t ∝ m^a l^b g^c θ^d
or t = k’ m^a l^b g^c q^d ….(i)
here k’ is a dimensionless constant.

Since q is dimensionless, hence equation (i) reduces to
t = K m^a l^b g^c …(ii)

where K. = k¹.θ^d is another dimensionless constant.
Now writing the dimensional formula of each physical quantity on both sides of equation (ii), we get
[M⁰ L⁰ T^-1] = [M]^a [L]^b [LT²]^c = [M^a L^b-c T^-2c]

Comparing dimensions of


Thus from equation (vii), we see that the period of the pendulum is directly proportional to the square root of the length of string, and inversely proportional to the square root of acceleration due to gravity and is independent of the mass of the bob.

Question 8.
Given that the period T of oscillation of a gas bubble from an explosion underwater depends on P, d, and E, where the symbols are pressure, density, and total energy of the explosion. Find dimensionally a relation for T.
Answer:
Let T ∝p^a d^b E^c
or
T = k p^a d^b E^c …(i)
where k is a dimensionless constant.

Writing dimensional formula of each physical quantity on both sides of equation (i), we get

Question 9.
If the velocity of light c, the constant of gravitation G, and Plank’s constant h be chosen as fundamental units, find the value of a gram, a centimeter, and a second in terms of new units of mass, length, and time respectively.
Given c = 3 × 10¹⁰ cms^-1
G = 6.67 × 10^-8 dyne cm² g^-2
h = 6.6 × 10^-27 ergs.
Answer:

Question 10.
Assuming that the mass m of the largest stone that can be moved by a flowing river depends on the velocity y density p and acceleratión due to gravity g. Show that m varies as the sixth power of the velocity of flow.
Answer:
Let, m ∝ v^a
m ∝ρ^bb

where k is a dimensionless constant.

Writing dimensions of each physical quantity on both sides of equation (i), we get
[M¹ L⁰ T⁰] = [LT^-1] [ML^-3]^b [LT^-2]^c
[M^b L ^a-3b+2c T^-a-2c]

Comparing powers of:

Question 11.
The radius of Earth is 6.37 × 106 m and its average density is 5.517 × 10³ kg m^-3. Calculate the mass of Earth to correct significant figures.
Answer:
M = pV
Here, R = 6.37 × 10⁶ m,
ρ = 5.517 × 10³ kg m³

Here R has 3 significant figures and the density has four. Thus the final result should be rounded off to 3 significant figures.

Hence, M = 5.97 × 10²⁴ kg.

Question 12.
The length, breadth, and thickness of a block of metal were measured with the help of Vernier Callipers. The measurements are:
l = (5.250 ± 0.001) cm
b = (3.450 ± 0.001) cm,
t = (1.740 ± 0.001) cm.
Find the percentage error in the volume of the block.
Answer:
The volume of the block is given by:
V = lbt

∴ The relative percentage error in V is given by:

Question 13.
An experiment measures quantities a, b, c, and x is calculated from the relation:
x = ab²/c³
The percentage errors in a, b, c are ± 1%, ± 3%, and ± 2% respectively what is the % error in x?
Answer:

Question 14.
The radius of the proton is about 10^-9 microns and the radius of the universe is about 10²⁸ cm. Name a physical object whose size is approximately halfway between these two extremes on the logarithmic scale.
Answer:
Radius of proton, x₁ = 10^-9 microns = 10^-9 × 10⁶m .
= 10^-15m

Radius of universe, x₂ = 10²⁸ cm = 10²⁶m.

If x be the size halfway between these two extremes on the logarithmic scale is:

Since 10⁶m is the order of the size of the Earth. So the physical object is Earth.

Question 15.
The velocity v (cms^-1) of a particle is given in terms of time t (s) by the equation y = at + \(\frac{b}{t+c}\). What are the dimensions of a, b and c?
Answer:
v = at + \(\frac{b}{t+c}\).

L.H.S. is velocity, so according to principle of homogeneity t, of dimensions, at and must have the dimensions of \(\frac{b}{t+c}\) velocity.

Question 16.
The young’s modulus (Y) of a material is given by the relation Y = \(\frac{\mathbf{M g L}}{\pi \mathbf{r}^{2} \boldsymbol{l}}\). If the percentage error in W(= mg), L, r and l are 0.5%, 1%, 3% and 4% respectively, what is the percentage error in Y? If the calculated value of Y is 18.79 × 10¹¹ dyne cm^-2, to what value should we round off the result?
Answer:
The total percentage error in Y is given by:

Since Y = 18.79 × 10¹¹ dyne cm^-2, it can be rounded off to
Y = 19 × 10¹¹ dyne cm^-2

The total percentage error in this result is:
\(\frac{19 \times 11.5}{100}\) = 2.2

So, the result of Y can be quoted as (19 ± 2.2) × 10¹¹ dyne cm^-2

Question 17.
The refractive index as measured by relation:
μ = \(\frac{\text { real depth }}{\text { apparent depth }}\) was found to have values 1.29, 1.33, 1.34, 1.35, 1.32, 1.36, 1.30, 1.33.
Find the mean value of μ, the mean value of the absolute error, the relative error, and the percentage error.
Answer:
Mean value of μ

Question 18.
Derive the dimensions of a/b in the relation:
F = a\(\sqrt{x}\) + bt²
where F is the force, x is the distance and t is the time.
Answer:
Here, F= a\(\sqrt{x}\) + bt² …(i)

According to the principle of homogeneity of dimensions, a \(\sqrt{x}\) and bt² should have dimensions of F.

Question 19.
Calculate the number of seconds in a:
(i) day
(ii) year
and express them in orders of magnitude.
Answer:
(i) No.of seconds in a day = 24 × 60 × 60s
= 86400s
= 8.64 × 104s
= 0.864 × 105s
∴ order of magnitude = 5

(ii) No.of seconds in a year = 365 days
= 365 × 0.864 × 105s
= 315360 × 105s
= 31536 × 107s
∴ order of magnitude = 7.

Question 20.
A stone is lying in a fluid stream. The force F acting on it depends on the density of the fluid δ, the velocity of flow v, and the maximum area of cross-section A perpendicular to the direction of flow. Find the relation between the force F and the velocity v.
Answer:
Let, F ∝ ρ^a
∝ v^b
∝ A^c
or
F ∝ p^a v^b A^c
or
F = k p^a v^b A^c …(i)

Now writing the dimensional formula of each physical quantity on both sides of equation (i), we get:
[MLT^-2] = [ML^-3]^a [LT^-1]^b [L²]^c
= [M^a L^-3a+b+2c T^-b] …(ii)

Comparing dimensions of M, L, T on both sides of equation (ii), we get:

Question 21.
If we suppose the velocity of light (c), acceleration due to gravity (g), and pressure (p) as the fundamental units, then And the dimensional formula of mass in this system of units.
Answer:

Question 22.
The density p of a piece of metal of a mass m of and volume V is given by the formula, ρ = m/V.
If, m = 325.32 ± 0.0lg
V = 136.41 ± 0.01 cm³.
Find the percentage error in p:
Answer:
Here, m = 325.32g, Δm = 0.01 g
V = 136.41 cm³, ΔV = 0.01 cm³

Question 23.
The specific resistance σ of a circular wire of radius r cm, resistance R Ω and and length L is given by:
σ = \(\frac{\pi r^{2} R}{L}\)
If, r = 0.20 ± 0.02 cm
R = 20 ± 1Ω
L = 80 ± 0.01 cm, then find the % error in σ.
Answer:
% error in σ is given by:

Question 24.
If S² = a t⁴, where S is in meters, t in second, then find the unit of a.
Answer:
Here, S² = a t⁴
According to the principal of homogeneity of dimensions,
at⁴ = m²
∴ a = \(\frac{\mathrm{m}^{2}}{\mathrm{t}^{4}}\) = m² s^-4

Question 25.
Calculate the value of 600m. + 600mm with due regard to the significant digits.
Answer:
Here, because there is no significant digit after the decimal point in 600m, so 600m + 600mm.
= 600m + 600 × 10^-3m
= 600m + 0.600m
= 600.6m = 601m.

Value-Based Type:

Question 1.
The teacher of class XI asked Madan and Prathiva to find the distance of the moon from the Earth. Pratibha said it is impossible to find. But Madan was excited to know. He observed the moon from two diametrically opposite points A and B on Earth. The angle q subtended at the moon by the two directions of observation is 1°54′. Given the diameter of the Earth to be about (1.276 × 10⁷ m).
(i) Which values arc depicted by Madan?
Answer:
The values depicted by Madan are :
(a) Curiosity
(b) Sincerity
(c) Willing to know and implement the scientific ideas.

(ii) Which mathematical concept is used in the above problem?
Answer:
Parallax method

(iii) Compute the distance of the moon from the Earth?
Answer:

We have

Question 2.
Muesli went to London to his uncle who is a doctor over there. He found that the currency is quite different from India. He could not understand the pound and how it is converted into rupees. He asked an English man that how far is central London from here.

He replied that it is about 20 miles. Mukesh was again confused as he never used these units in India. When his uncle came back from his clinic he curiously inquired all about it. His uncle told him about the unit system used in England. He explained that here F.P.S system is used.

It means distance is measured in the foot, Mass in the pound, and time in seconds. But in India, it is an MKS system.
(i) What values are depicted by Mukesh?
Answer:
(a) Curiosity
(b) Willing to know
(c) Intelligence

(ii) How many types of unit systems are there?
Answer:
The unit system is:
(a) CGS (centimeter, gram and second) system
(b) FPS (foot, pound and second) system
(c) MKS (meter, kilogram, and second) system

Question 3.
Two friends Sachin and Dinesh are confused as a book with many printing errors contains four different formulas of the displacement ‘y’ of a particle undergoing a certain periodic motion.
(a) y=asin 2πt/T
(b) y = asinvt

[a = Maximum displacement of the particle,
v = Speed of the particle, T = time-period of motion]

Sachin told that he has no idea whereas Dinesh ruled out the wrong formulas on dimensional grounds.
(i) which values are displayed by Dinesh?
Answer:
the values displayed by Dinesh are:
(a) Sincerity
(b) Curiosity
(c) application of knowledge

(ii) which one of the above is correct? Give justification to support your answer.
Answer:


L.H.S = R.H.S ; Hence the equation is correct.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 1 Physical World. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 1 Important Extra Questions Physical World

Physical World Important Extra Questions Very Short Answer Type

Question 1.
Name that branch of science that deals with the study of Earth.
Answer:
Geology.

Question 2.
Name that branch of science that deals with the study of stars.
Answer:
Astronomy.

Question 3.
Name the scientist and the country of his origin whose field of work was elasticity.
Answer:
Robert Hook, England.

Question 4.
The word “Physics” comes from a Greek word. Name the word.
Answer:
The word is ‘fuses meaning ‘Nature’.

Question 5.
The word science has come from a Latin verb. Name the verb.
Answer:
The name of the Latin verb is ‘Scientia’.

Question 6.
What is the meaning of the verb ‘Scientia’?
Answer:
To ‘know’

Question 7.
Name the scientist and the country of his origin who received the Nobel Prize for his work on molecular spectra.
Answer:
C.V. Raman, India.

Question 8.
What is the most incomprehensible thing about the world?
Answer:
It is comprehensible.

Question 9.
Name a great scientist who gave the following comment on science.
“Science is not just a collection of laws, a catalog of unrelated facts. It is a creation of the human mind, with its freely invented ideas and concepts.”
Answer:
Albert Einstein.

Question 10.
Which famous philosopher gave the following comments on science?
“We know very little and yet it is astonishing that we know so much, and still more astonishing that so little knowledge of science can give so much power.”
Answer:
Bertrand Russel.

Question 11.
Who discovered the electron?
Answer:
J.J. Thomson.

Question 12.
Who discovered neutron?
Answer:
James Chadwick.

Question 13.
Who gave the general theory of relativity?
Answer:
Albert Einstein.

Question 14.
Who proposed the wave theory of light?
Answer:
Huygen.

Question 15.
Name four physics devices widely used in medical diagnosis.
Answer:

1. X-rays,
2. Ultrasound,
3. Stethoscope,
4. Microscope.

Question 16.
Name Indian-born scientist who received Nobel Prize for his discoveries in astronomy.
Answer:
S. Chandra Shekhar.

Question 17.
Metaphysics is a science that is concerned with what?
Answer:
Supernatural .events.

Question 18.
Which science is considered to be the mother of all sciences?
Answer:
Physics.

Question 19.
Name the discovery made by S.N. Bose.
Answer:
Bose-Einstein Statistics.

Question 20.
Name the scientist and the country of his origin whose field of work was ‘cosmic rays’.
Answer:
Hess, Austria.

Question 21.
What are the meaning of the Sanskrit word ‘Vijnan’ and the Arabic word ‘Ilm’?
Answer:
Knowledge.

Question 22.
Name the Sanskrit equivalent word of Physics.
Answer:
Bhautiki.

Question 23.
Name the field of Physics in which India was a leading country in the sixties.
Answer:
Cosmic rays.

Question 24.
Who discovered X-rays?
Answer:
W. Roentgen.

Question 25.
Which electronic media can help in eradicating illiteracy in India?
Answer:
Television.

Question 26.
Name the technology based on the amplification of light by population inversion?
Answer:
Laser.

Question 27.
Who discovered nuclear forces?
Answer:
H. Yukawa.

Question 28.
To which country he belonged?
Answer:
japan.

Question 29.
Who discovered Radium?
Answer:
Pierre Curie and Marie Curie.

Question 30.
Name the discovery made by W. Roentgen.
Answer:
X-rays.

Question 31.
What has been said by P.A.M. Dirac regarding physics in relation to society?
Answer:
P.A.M. Dirac said, “It is more important to have beauty in the equations of physics than to have them agree with experiments.”

Question 32.
What did Issac Newton say to measure the degree of impact of science on society?
Answer:
He said “Nature is pleased with simplicity, and affects not the pomp of superfluous causes.

Question 33.
What Neils Bohr said regarding science in relation to society?
Answer:
He said “The task of science is both to extend the range of our experience and to reduce it to order.

Question 34.
Name a few Indian physicists who have made significant contributions in the field of physics.
Answer:
C.V. Raifiaq, S. Chandra Shekhar, S.N. Bose, Homi J. Bhabha, and Meghnath Saha.

Question 35.
Name the scientific principle on which airplane works.
Answer:
Bernoulli’s theorem.

Question 36.
Name the scientific principle on which radio and T.V. works.
Answer:
Propagation of electromagnetic waves.

Question 37.
Name the scientific principle upon which laser works.
Answer:
Amplification by a process called population inversion.

Question 38.
Name the technology which works on the scientific principle “Newton’s second and third laws of motion”.
Answer:
Rocket propulsion.

Question 39.
Name the forces which are of nuclear origin.
Answer:
Strong forces.

Question 40.
What is Physics?
Answer:
It is that branch of science which deals with nature and natural phenomena.
Or
It is that branch of physical science that is to seek out and understands the basic laws of nature upon which all physical phenomena depend. It has brought to us deeper and deeper levels of understanding nature.

Question 41.
What is Science?
Answer:
It is defined as the systematic study of physical phenomena.

Question 42.
What are Biological Sciences? Give three examples.
Answer:
Those sciences which deal with living things are called Biological Sciences, e.g. Zoology, Botany, Ornithology.

Question 43.
What are Physical Sciences? Give a few examples.
Answer:
They ate defined as the sciences which deal with non-living things,
e.g. Physics, Chemistry, Astronomy, Astrology, Geology, Geography, Oceanology.

Question 44.
Define Theory.
Answer:
It is defined as the behavior of physical systems explained in terms of a set of a minimum number of laws.

Question 45.
What do you understand by the term scientific method?
Answer:
The systematic observations, logical reasoning, model-making, and theoretical prediction form the scientific method.

Question 46.
Name the scientific principle on which electric generator works.
Answer:
Electromagnetic induction (E.M.I.).

Question 47.
Name the technology which works on the scientific principle ‘Nuclear Fission’.
Answer:
Nuclear Reactor.

Question 48.
Name the technology which works on the scientific principle “Digital logic of electronic circuits”.
Answer:
Calculators and computers.

Question 49.
Name the scientific principle upon which the working of cyclotron defends.
Answer:
The motion of charged particles under electric and magnetic fields.

Question 50.
Name the. scientist and his country who discovered wireless1 telegraphy.
Answer:
G. Marconi, Italy.

Physical World Important Extra Questions Short Answer Type

Question 1.
Differentiate between Biological and Physical sciences?
Answer:

Question 2.
What is the relation between Physics and Technology?
Answer:
Broadly speaking, physics and technology both constitute science. Physics is the heart and technology is the body of science.

The application of the principles of physics for practical purposes becomes technology, e.g.

1. Airplanes fly on the basis of Bernoulli’s theorem.
2. Rockets propulsion is based on Newton’s second and third laws of motion.
3. The generation of pow%r from the nuclear reactor is based on the phenomenon of controlled nuclear fission.
4. Lasers are based on the population inversion of electrons and so on. Thus, we can say that to some extent technology is applied to Physics.

Question 3.
What is the relation between Physics and society?
Answer:
Most of the development made in Physics has a direct impact on society, e.g.

1. Exploration of new sources of energy is of great importance to society.
2. Rapid means of transport are no less important for society.
3. society has-been enriched due to the advances in electronics, lasers, and computers.
4. The development of T.V., radio, satellites, telephone, the telegraph has revolutionized the means of communications which have a direct impact on society and so on.

Question 4.
Is Science on speaking terms with humanities?
Answer:
Yes, there is a deep relation between the development of humanity on account of science. Many socio-economic, political, and ethical problems are being tackled and solved by science. Science has greatly helped in developing art and culture. Many musical instruments have been developed due to the theories in Physics. The steam engine is inseparable from the industrial revolution which had a great impact on human civilization.

Question 5.
What is the relation between Physics and Technology?
Answer:
The interplay between physics and technology is the basic to the progress of science which is ever dynamic. Laws in waves and oscillation opened several technological fields which include telescopy, ultrasounds, microscopy, X-rays, and laser. Powerhouses, big cranes, healing devices, etc. work on the principle of electromagnetism. Atomic energy and nuclear weapons are on account of fission. Similarly, Radar, television, the internet, etc. are all based on simple laws of physics. So until there is no theory i.e. physics, there can be no experiment i.e. technology. Hence both are deeply related.

Question 6.
Is Physics more of a philosophy or more of a mathematical science?
Answer:
Physics is not a purely abstract science devoid of philosophy. Physicists are natural philosophers and Einstein is an example to quote. So Philosophy has provided the backbone to Physics.

Question 7.
Define Biophysics.
Answer:
It is defined as the understanding of biological processes based upon the principles of Physics. For example, spectroscopic techniques are used to study the constitution of biological molecules and disorders in them. Laws of thermodynamics are used to explain various biological activities of predators and also the activities of molecules.

Hence the application of Physics to bioscience is now well known to all of us.

Question 8.
Define Technology?
Answer:
It is defined as the study of newer techniques of producing machines, gadgets, etc. by using scientific discoveries and advancements. It is largely dependent on Physics.

Question 9.
Has imagination any role in Physics?
Answer:
One of the definitions of Physics says that “It is the science-based on imagination and intuition which can be tested experimentally and mathematically.” Thus, imagination has a great role in the development of physics. Schrodinger, De-Broglie, Heisenberg, and most of the other scientists who were physicists were great imaginers.

Question 10.
Name a few aspects of your daily life in which you rely on the simplicity of nature.
Answer:
Laws of Physics represent the nature in simplest form. We face nature in many ways in our daily life. For example, we work, walk, write, talk and stand on our feet, and so on. The natural way of taking bath, chewing food, etc. can easily be understood in terms of simple laws of science. Even though actions like swimming, running, and playing may be complex but the underlying laws of nature are quite simple such as Newton’s laws, friction, etc.

Question 11.
The physicists think at a level far higher than a normal individual. Explain.
Answer:
For everyone to become a leader in his field, he has to think for a higher level than an ordinary person. This is more so for the case of physicists as the technological development meant for uplifting the living condition of mankind is highly dependent on the farsightedness of the physicists in particular. He must think at a level that is philosophical and mathematically quantifying so that they can visualize the requirement of people is quite advance.

Question 12.
Name a few wartime and maritime applications of Physics.
Answer:
(a) Wartime: The wartime applications are Bombs, nuclear weapons, jet fighter bombers, missiles, ships, radar, sonar, wireless communications, transportation, and electronics.

(b) Maritime: The maritime application of physics is Navigation of ships, tankers, airplanes, T.V., radio, and music system, etc.

Question 13.
Name five Indian scientists and the field of their work.
Answer:
Following are the five Indian Scientists and the field of their work:

Question 14.
Who invented:
(i) Computer
Answer:
Charles Babbage

(ii) Transistor,
Answer:
J. Bardeen

(iii) Electric bulb and Telegraphy,
Answer:
A. Edison

(iv) Radar,
Answer:
Appleton

(v) Wireless telegraphy,
Answer:
Marconi

(vi) Telephone.
Answer:
Graham Bell.

Question 15.
Name the theories given by the following:
(i) Neil Bohr
Answer:
Theory of atomic structure

(ii) Lawrence,
Answer:
Cyclotron

(iii) Henry Becquerel,
Answer:
Natural radioactivity

(iv) Galileo,
Answer:
Principle of Inertia

(v) Bragg,
Answer:
Crystal structure by X- rays

(vi) Abdus Salam,
Answer:
Unified Field Theory

(vii) Millikan.
Answer:
Charge on an electron.

Question 16.
Give the nationality of the following scientists:
(i) Van der Waals,
Answer:
Dutch

(ii) Curie,
Answer:
French

(iii) Yukawa,
Answer:
Japanese

(iv) Galileo,
Answer:
Italian

(v) Michelson,
Answer:
U.S.A. (American)

(vi) Heisenberg,
Answer:
German

(vii) Archimedes,
Answer:
Greek

(viii) Maxwell,
Answer:
Scottish

(ix) Cavendish,
Answer:
English

(x) Hubble.
Answer:
Austrian.

Question 17.
List the Various gadgets you use in your house.
Answer:
The following are the gadgets commonly used in our house:

1. Pressure Cooker
2. Electric light
3. Tube light
4. Electric fan
5. Water cooler
6. Refrigerator
7. Washing machine
8. Gas stove
9. Electric iron
10. Mixi
11. Geyser
12. Electric motor.

Question 18.
Write the physical principle upon which the working of the gadgets mentioned in the above question is based.
Answer:
These are based on the following physical principles:

1. The boiling point rises with the increase in pressure.
2. Light is produced when the current is passed through a given resistor.
3. Light is emitted when an electric discharge is passed through the gas.
4. A rotating magnetic field is produced on passing current which notates the motor.
5. Due to evaporation of water, cooling in the air which is being forced out by the fan is produced.
6. On absorbing heat from the surroundings, compressed volatile liquid on sudden expansion causes cooling.
7. Current produces a rotating magnetic field that operates the motor.
8. Heat is produced due to the burning of L.P.G.
9. It works on the principle of heating effect of electric current.
10. Torque is produced on the coil due to the electric current passed through it, hence it rotates.
11. Current shows the heating effect when passed through the conductor.
12. It rotates due to the torque produced on the coil on passing an electric current through it.

Question 19.
Name one Scientist each from the following countries who have won Nobel Prize.
(a) Japan
Answer:
H. Yukawa

(b) England
Answer:
Janies Chadwick

(c) India
Answer:
C.V. Raman

(d) The U.S.A.
Answer:
K. Feynman

(e) Germany.
Answer:
Max. Plank.

Question 20.
How Darwin showed that scientific themes are at once simple even though phenomena in nature may be complex.
Answer:
Darwin found a simple basis for the origin of species and descent of man which is “Living things change producing descendants with different characteristics in a process that has been going on for as long as there has been life” by taking a large number of observations on the theory of evolution while onboard ship.

Question 21.
Illustrate by an example the beauty of a Scientific Theory.
Answer:
The theory proposed by Darwin was opposed by the church and now we have new discoveries such as selfish genes and punctuated equilibria but Darwin’s basic theory still holds. This is the beauty of Davin’s theory of evolution.

Question 22.
In science sometimes we observed certain phenomena experimentally but are unable to give a logical equation or theory for that sometimes, it also happens that we have a scientific theory supported by’ mathematical formulation yet are unable to test it immediately. Site one such example.
Answer:
Einstein worked to establish a relation between the energy and mass of the body. He was of the view that these are the two sides of the same coin or two facts of the same physical quantity. He succeeded when he gave his mass-energy equation E = mc². But its experimental verification came 40 years later in 1945 when the atomic bomb was exploded over Japan.

Question 23.
Why do we call physics an exact science? What is the aim of science?
Answer:
Physics is called exact science because it is based on the measurement of fundamental quantities.
The main aim of science is to find the truth behind the various processes taking place in the universe.

Question 24.
How science has helped in solving the food problem in several countries?
Answer:
Science has helped in solving food problem in the following ways:
(a) It has given improved and new agricultural implements.
(b) Science has improved the quality of seeds by genetic engineering.
(c) High-yielding hybrid varieties of grains have been developed. Some easily reaping varieties have also been developed and grown.
(d) Use of pesticides and insecticides has saved crops from being destroyed by insects and pests.
(e) Some new types of crops are also developed and are being developed to meet the requirement of society.

Question 25.
What is a scientific temperament and scientific way of doing things?
Answer:
A mindset molded in a particular set of thinking called the scientific way is known as scientific temperament. It is not only based on logic, facts but on reliable observations. The ultimate test of truth in science is experimental verification.

A scientific way of doing things involves the following steps:
(a) Identifying the problem or aim.
(b) Collecting all relevant information or data related to the problem.
(c) Hypothesising or proposing a possible theory.
(d) Taking experimental observation yielding consistent results.
(e) Predicting or making statements.

Question 26.
What is the scope of Physics?
Answer:
The scope of Physics is very wide i.e. the domain of Physics covers a very wide variety of natural phenomena.

For example, the range of distances we study in Physics varies from 10¹⁴ m (size of the nucleus) to 10²⁵ m (size of the universe).

Similarly, the range of masses included in the study of Physics varies from 10^-30 kg (mass of an electron) to 10⁵⁵ kg (mass of the universe). Also, the range of time i.e. time intervals of events we come across in the study of Physics varies from 10²² seconds (time taken by light to cross a nuclear distance) to 10^-8 seconds (lifetime of the sun).

Thus we see that the scope of Physics is really very wide. It includes; optics, electricity waves, and oscillations, heat and thermodynamics, magnetism, atomic and nuclear physics, computers, and electronics.

Question 27.
Physics is an exciting subject! Comment.
Answer:
The study of Physics is exciting in many ways, e g.:

1. Journey to the moon with controls from the grounds.
2. Lasers and their ever-increasing applications.
3. Live transmission of events thousands of kilometers away on the T: V.
4. The speed and memory of the fifth generation of computers.
5. Study of various types of forces in nature.
6. Technological advances in health science.
7. The use of robots is quite exciting.
8. Telephone calls over long distances and so on. Thus, Physics is exciting not only to the scientist but also to a layman, children, women, etc. The musical instruments, toy guns, toy trains, etc. all are constructed using simple principles of physics like collision, potential energy, and vibration, etc. Today the situation is that even our thought process and social values are affected by Physics. Thus, it is quite amazing.

Question 28.
Write a short note on the origin and development of Physics.
Answer:
Physics as a science took roots from the days of Copernicus, i. e., nearly four centuries ago when it was not well understood and it was considered as a part of philosophy, i.e., knowledge. Later on, with the development of knowledge about nature and its various activities, the knowledge was divided into physical and biological sciences.

Some important developments like Newton’s law of gravitation, ideas about light were developed in the 18th century. The 19th century saw some of the great discoveries in Physics and at the end f the century i.e. 1889, the electromagnetic theory was developed, Fouriuatun of Einstein’s and Plank’s ideas were laid down apart from laying the basis for the industrial revolution. Physics progressed very fast in the first quarter of the 20th century.

Atomic structure, the theory of relativity, quantum theory, nuclear physics, basics of laser theory and most of the other developments took place in this period. Then came transistors, semiconductors, television, radar, and few important discoveries during World War II.

Further development in quantum mechanics, thin-film technology, computers, lasers was developed from 1950 onward. Today we have no theoretical development beyond quantum mechanics. A unified theory is not being tried yet. This is the present status with achievements in applied fields.

Question 29.
Explain the role of science in the entertainment industry.
Answer:
Progress in science especially in physics and technology has enriched no other field as the field of entertainment. We see scientific toys like robots for children and merry-go-rounds of all sorts in amusement and entertainment parks which are not only highly entertaining but also test the endurance of an individual.

These are based on the laws of forces and the critical stages are those when a man is pitted against gravity. T.V. has invaded a large number of houses as a source of entertainment and so are the music blaring CD players. Computers have become another source of individual indoor entertainment. The use of laser beams in music and drama shows and disco dances is highly rewarding.

With the improvement in physics and technology, circus entertainment to have changed with the application of science. Thus, we conclude that the role of science and technology in the entertainment industry has increased tremendously.

Question 30.
Give some of the uses and applications of artificial satellites.
Answer:
The following are the fields where satellites are being used –
(a) Remote sensing
(b) Communication
(c) Spying
(d) Weather forecasting

(a) Remote sensing: In remote sensing, infrared photography s used from a high altitude. The technique has improved a lot and the resolution has gone down to about 5m in an area. This technique has helped in mineral and oil exploration. It has also helped in the study of forest living and crop patterns.

(b) Communication: In the field of communication, satellites have brought revolution during the last 20 years. Now new items are flashed all around the globe. Cricket matches can be seen anywhere on the globe which is played in one small part of a country. Internet, E-mail, etc. have brought people much more closer and the world has become a unified entity.

(c) Spying: In spying also use IR technology.

(d) Weather forecasting: Weather forecasting has become more reliable with the use of satellites. The rains, cyclones can now be predicted with greater accuracy 36 hours in advance or even earlier. The movement of glaciers, the position of ice and snow deposition, and the resulting flow of water in rivers is known well in advance.

Physical World Important Extra Questions Long Answer Type

Question 1.
How Physics is related to other sciences?
Answer:
Physics is so important to a branch of science that without the knowledge of Physics, other branches of science cannot make any progress.

This can be seen from the following:
(a) Physics in relation to Mathematics: The theories and concepts of Physics lead to the development of various mathematical tools like differential equations, equations of motion, etc.

(b) Physics in n .ation to Chemistry: The concept of iñteraction between various particles leads to understanding the bonding and the chemical structure of a substance. The concept of X-ray diffraction and radioactivity has helped to distinguish between the various solids and to modify the periodic table.

(c) Physics in relation to Biology: The concept of pressure and its measurement has helped us to know the blood pressure of a human being, which in turn is helpful to know the working of the heart. The discovery of X-rays has made it possible to diagnose the various diseases in the body and fracture in bones.

The optical and electron microscopes are helpful in the studies of various organisms. Skin diseases and cancer can be cured with the help of high-energy radiation like x-rays, ultraviolet rays.

(d) Physics in relation to Geology: The internal structure of various rocks can be known with the study of the crystal structure. The age of rocks and fossils can be known easily with the help of radioactivity i.e. with the help of carbon dating.

(e) Physics in relation to Astronomy: Optical telescope has made it possible to study the motion of various planets and satellites in our solar system.

The radio telescope has helped to study the structure of our galaxy and to discover pulsars and quasars (heavenly bodies having star-like structures). Pulsars are rapidly rotating neutron stars. Doppler’s effect predicted the expansion of the universe. Kepler’s laws are responsible to understand the nature of the orbits of the planets around the sun.

(f) Physics in the relation to Meteorology: The variation of pressure with temperature leads to the forecast of the weather.

(g) Physics in relation to Seismology: The movement of the earth’s crust and the types of waves produced help us in studying the earthquake and its effect.

Question 2.
Write a short note on origin and Fundamental forces in nature.
Answer:
These are the following four basic forces in nature:
(a) Gravitational forces
(b) Electromagnetic forces
(c) Weak forces
(d) Strong force or nuclear forces.

Some of the important features of these forces are discussed below:
(a) Gravitational forces: These are the forces of attraction between any two bodies in the universe due to their masses separated by a definite distance. These are governed by Newton’s law of gravitation given by
F = G \(\frac{m_{1} m_{2}}{r^{2}}\)

where m₁, m₂ are the masses of two bodies
r = distance between them
G = universal gravitational constant
= 6.67 × 10^-11 Nm²kg^-2

Characteristics of gravitational forces:

1. They are always attractive. They are never repulsive. They exist between macroscopic as well as microscopic bodies.
2. They are the weakest forces in nature.
3. They are central forces in nature i.e. they set along the line joining the centers of two bodies.
4. They are conservative forces.
5. They obey inverse square law i.e. F ∝\(\frac{1}{r^{2}}\) they vary inversely as the square of the distance between the two bodies.
6. They are long-range forces i.e. gravitational forces between any two bodies exist even when their distance of separation is quite large.
7. The field particles of gravitational forces are called gravitons. The concept of the exchange of field particles between two bodies explains how the two bodies interact from a distance.

(b) Electromagnetic forces: They include the electrostatic and magnetic forces. The electrostatic forces are the forces between two static charges while magnetic forces are the forces between two magnetic poles. The moving charges give rise to the magnetic force. The combined action of these forces is called electromagnetic forces.

Characteristics of electromagnetic forces:

1. These forces are both attractive as well as repulsive.
2. They are central forces in nature.
3. They obey inverse square law.
4. They are conservative forces in nature.
5. These forces are due to the exchange of particles known as photons which carry no charge and have zero rest mass.
6. They are 10³⁶ times stronger as compared to gravitational forces and 10¹¹ times stronger than weak forces.

(c) Strong forces: They are the forces of nuclear origin. The particles inside the nucleus are charged particles (protons) and neutral particles (neutrons) which are bonded to each other by a strong interaction called nuclear force or strong force. Hence they may be defined as the forces binding the nucleons (protons and neutrons) together in a nucleus. They are responsible for the stability of the atomic nucleus.

They are of three types:

1. n-n forces are the forces of attraction between two neutrons.
2. p-p forces are the forces of attraction between two protons.
3. n-p forces are the forces of attraction between a proton and a neutron.

Characteristics of Nuclear forces:

1. They are basically attractive in nature and become repulsive when the distance between nucleons is less than O.S fermi.
2. They obey inverse square law.
   (a) and
   (b) types are the forces that we encounter in the macroscopic world while
   (c) and
   (d) types are the forces that we encountered in the microscopic world.

(c) Weak forces: They are defined as the interactions which take, place between elementary particles during radioactive decay of a radioactive substance. In P-decay, the nucleus changes into a proton, an electron, and a particle called anti-neutrino (which is uncharged). The interaction between the electron and the anti-neutrino is known as weak interaction or weak force.

Characteristics of Weak forces:

• They are 1025 times stronger than the gravitational forces.
• They exist between leptons and leptons, leptons and mesons. etc.

Question 3.
Distinguish between the studies in the fields of science, engineering, and technology. Give an outline of the two or three industrial revolutions brought about by advancements in technology over the last twenty-five years or so.
Answer:
Science is concerned with the unfolding of the basic aspects of nature. It formulates simple laws and finds the rhythm in nature, materials, and energy. Using basic principles of science, the ways to use them for the production of different kinds of articles is called technology, i.e., it is the application of science.

The execution of the application of technology in engineering. The production of articles using machines and implements in engineering. This involves the design, development, and manufacturing of articles.

The most notable technology development in the last 25 years is in the field of information technology, computers, and electronic media. The revolution in information technology has opened up fields on the internet, satellite linking of information systems and services other peripheral developments in the industry.

Computers have changed the face of society and made life easy in several fields. It has improved work efficiency in many segments of the industry and public life. Computers have touched the lives of children playing video games and adults alike. It has helped big organizations like railways, banks, and financial institutions like the insurance sector.

India has become one of the biggest centers of software exports and a big foreign exchange earner. Advance scientific research and industrial designing are being done by computers. TV has entered most Indian houses and community centers-courtesy revolution in electronic media.

The younger generation is mad after the stereo music with CD facilities. The transistors and tape recorders are left far behind. Electronic media has changed the face of the entertainment industry as well as information dissemination. Quick transmission of news, views, and comments are accepted as natural ones by listeners and viewers.

Value-Based Type:

Question 1.
A debate was organized by a school on woman’s innate nature, capacity, and intelligence. The arguments given by the two groups were as under:
Team A: Nature makes little difference in men and women in their anatomy and feeling. So, women are not on par with men. Hence, she is inferior to men in spheres of activity like sports, scaling of mountains like the Himalayas, etc.
Team B: The students of team ‘B’ have demolished this view using scientific arguments, and by quoting examples of great women, in science and other spheres; and persuade yourself and others that, give equal opportunity, women are on par with men.
Now, Answer these questions:
(i) Which values are displayed by team ‘B’?
Answer:
The values displayed by team B are:
(a) Gender equality.
(b) Justice and support to women.
(c) Equal opportunities to women.

(ii) Do you think team B was correct? Give proper justification with examples.
Answer:
Yes, there is no difference in the capacity of women and men as far as working capacity, intelligence, decision making is concerned. It is a biological fact that the development of the human brain does not depend upon sex but on nutrition contents and heredity. If equal opportunities are afforded to both men and women, then the female mind will be as efficient as the male mind.

The list of successful women from various fields is as under Kalpana Chawala, Madame Curie, Indira Gandhi, Mother Teresa, Margaret Thatcher, etc.

Question 2.
Two friends of class XI Mohan and Raghav were discussing the role of physics in society. Mohan Said to Raghav that physics does not have any impact on our society. Since he was a student of Arts Stream. But Mohan who is a science student explained that physics and Society are directly linked because whatever is discovered in physics, it immediately affects society.

The latest technology has played an important role in the fields of communication such as radios, computers, TVs, mobile phones and connects the people with each other. Nuclear energy has brought a profound change in the thinking and living style of human beings.
(i) Which values are displayed here by Mohan?
Answer:
The values displayed by Mohan are :
(a) Intelligence
(b) Awareness
(c) Logical

(ii) Give some discoveries which have really affected society more.
Answer:
(a) Theory of relativity
(b) X-ray
(c) Radioactivity
(d) Photoelectric effect
(e) Steam engine (based on laws of thermodynamics)
(f) Computer (Based on Digital logic)
(g) Super Conductivity
(h) Radio and TVs.

Question 3.
India has had a long and unbroken tradition of great Scholarship in mathematic, astronomy, linguistics, logic, and ethics. Yet, in parallel with this, several superstitious and obscurantist attitudes and practices flourished in our society and unfortunately continue even today-among many educated people too.

A student of Class XI gave an idea to overcome this evil of our society by using scientific explanations through mass media, radio television, and newspapers.
(i) Which values are displayed by the student?
Answer:
(a) Awareness
(b) Scientific and logical ideas
(c) Concern for the upliftment of our society to eradicate the evils of society.
(d) Intelligence, Sharp mind.

(ii) How will you use your knowledge of science to develop strategies to counter these attitudes?
Solution:
Educating the common man is the only way to get rid of superstitions and obscurantist attitudes. The mass media like newspapers, magazines, radio, television, etc. Can play a vital role. School and college curriculum can be suitably developed so that there is an emphasis on these topics. Teachers can play an important role to organize the seminar and motivate them.

Question 4.
A seminar was organized to know the views of students on whether the particular application is good, bad or something that cannot be so clearly categorized:
(a) Prenatal sex determination.
(b) Development of nuclear weapons.
(c) Mass vaccination
(d) Cloning
(e) Purification of water for drinking.

Now, answers these questions:
(i) Which values arc depicted here?
Answer:
To create awareness through group activities, to develop problem-solving ability, scientific knowledge can be put to good or bad use, depending on the user.

(ii) Do you think such type of group activities are important in day-to-day life?
Answer:
Yes.

(iii) Give justification for each of the above topics from (a-e):
Answer:
(a) Bad, it leads to the practice of abortion in the case of the female fetus.
(b) Bad, because nuclear weapons may cause mass destruc¬tion of mankind.
(c) Good, because it helped to eradicate the disease.
(d) Bad, because it can destroy the normal family life.
(e) Good, because it will help to improve good health of the citizens.

Important Questions for Class 11 Biology Chapter Wise with Answers Pdf Download 2020-21: Here we are providing CBSE Important Extra Questions for Class 11 Biology Chapter Wise State Board Pdf download in Hindi and English Medium. Students can get Class 11 Biology NCERT Solutions, Biology Class 11 Important Extra Questions and Answers designed by subject expert teachers.

CBSE Class 11th Biology Important Extra Questions and Answers Chapter Wise Pdf

1. The Living World Biology Class 11 Important Questions
2. Biological Classification Class 11 Biology Important Questions
3. Plant Kingdom Class 11 Biology Chapter Wise Questions
4. Animal Kingdom Question Bank Biology Class XI
5. Morphology of Flowering Plants Biology Important Questions
6. Anatomy of Flowering Plants Class 11 Important Questions
7. Structural Organisation in Animals Important Questions
8. Cell: The Unit of Life Class 11 Important Questions
9. Biomolecules 11th Std Biology Important Questions
10. Cell Cycle and Cell Division Class 11 Important Questions
11. Transport in Plants Class 11 Important Questions
12. Mineral Nutrition Class 11 NCERT Biology Important Questions
13. Photosynthesis in Higher Plants Class 11 Important Questions
14. Respiration in Plants Biology Important Questions for Class 11
15. Plant Growth and Development Class 11 Important Questions
16. Digestion and Absorption Biology Questions and Answers for Class 11
17. Breathing and Exchange of Gases Class 11 Important Questions
18. Body Fluids and Circulation Class 11 Important Questions
19. Excretory Products and their Elimination Class 11 Important Questions
20. Locomotion and Movement Class 11 Important Questions
21. Neural Control and Coordination Class 11 Important Questions
22. Chemical Coordination and Integration Class 11 Important Questions

We hope the given CBSE Important Questions of Biology Class 11 Chapter Wise Pdf download in Hindi and English Medium will help you. If you have any queries regarding NCERT Class 11 Biology Extra Important Questions and Answers, drop a comment below and we will get back to you at the earliest.

CBSE Class 11 Chemistry Chapter Wise Important Questions with Answers Pdf Download 2020-21: Here we are providing CBSE Important Extra Questions for Class 11 Chemistry Chapter Wise Pdf download State Board in Hindi and English Medium. Students can get Class 11 Chemistry NCERT Solutions, Chemistry Class 11 Important Extra Questions and Answers designed by subject expert teachers.

Class 11th Chemistry Important Extra Questions with Answers Chapter Wise Pdf

1. Some Basic Concepts of Chemistry Class 11 Important Questions
2. Structure of Atom Chemistry Class 11 Chapter Wise Questions
3. Classification of Elements and Periodicity in Properties Important Questions
4. Chemical Bonding and Molecular Structure Important Questions
5. States of Matter Chemistry Class 11 Important Questions
6. Thermodynamics Class 11 Chemistry Important Questions
7. Equilibrium Important Questions for Class 11 Chemistry
8. Redox Reactions Chemistry Questions and Answers for Class 11
9. Hydrogen Class 11 Important Questions
10. The s-Block Elements Class 11 Important Questions
11. The p-Block Elements Class 11 Important Questions
12. Organic Chemistry: Some Basic Principles and Techniques Class 11 Important Questions
13. Hydrocarbons Class 11 Important Questions
14. Environmental Chemistry 11th Chemistry Important Questions

We hope the given CBSE Important Questions of Chemistry Class 11 Chapter Wise Pdf download in Hindi and English Medium will help you. If you have any queries regarding NCERT Class 11 Chemistry Extra Important Questions and Answers, drop a comment below and we will get back to you at the earliest.