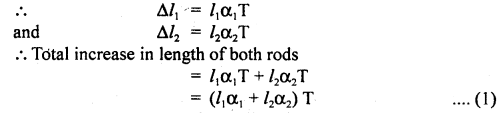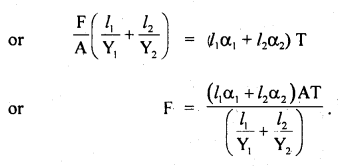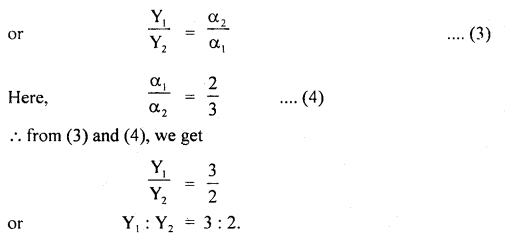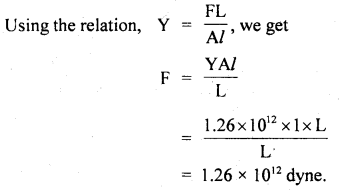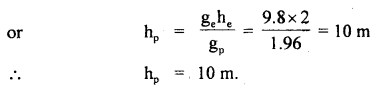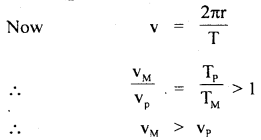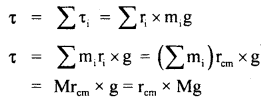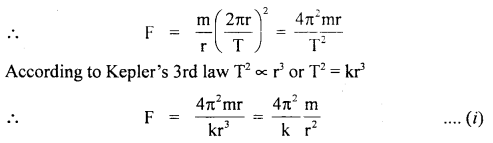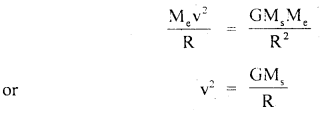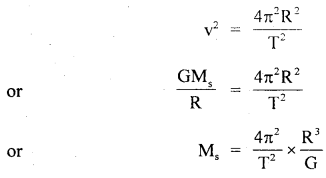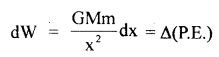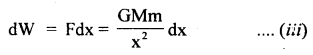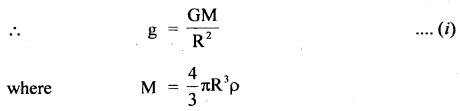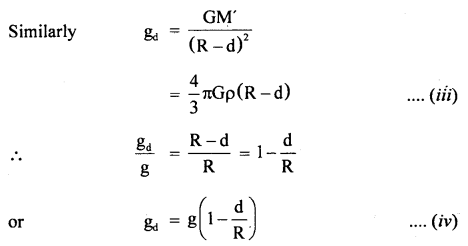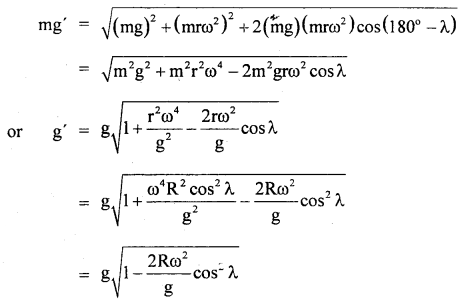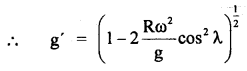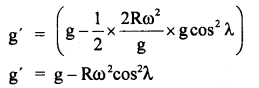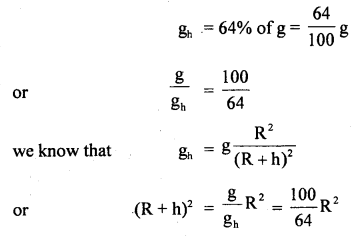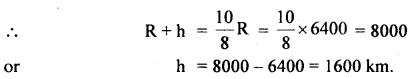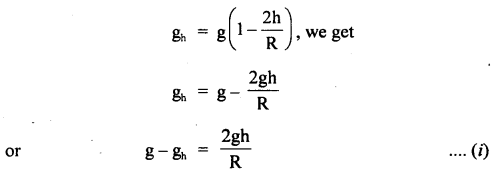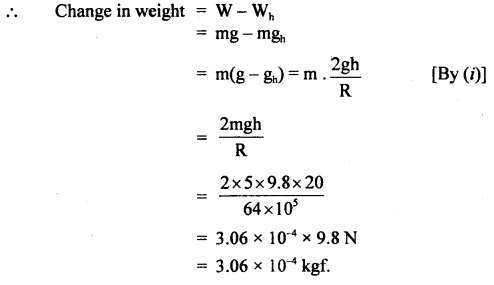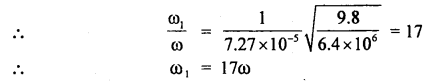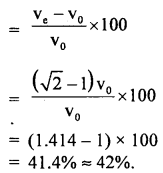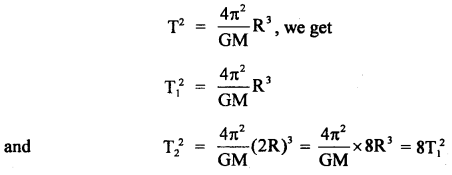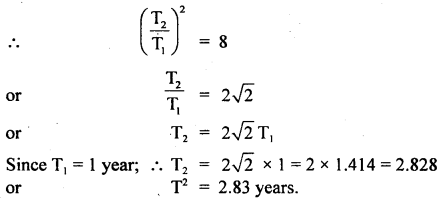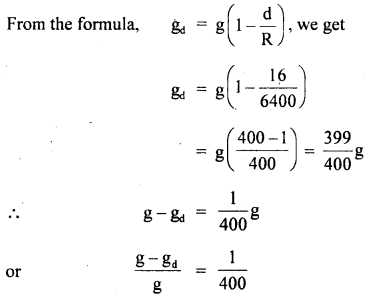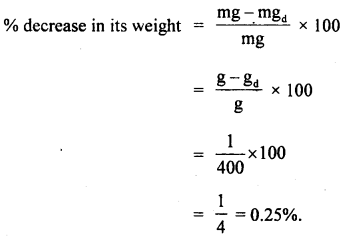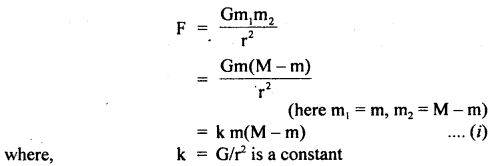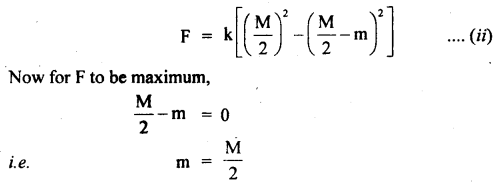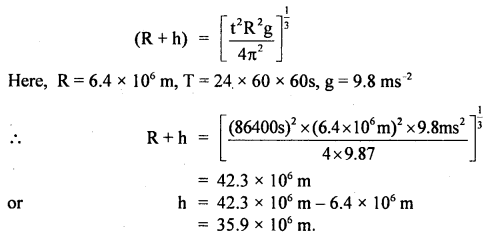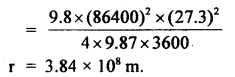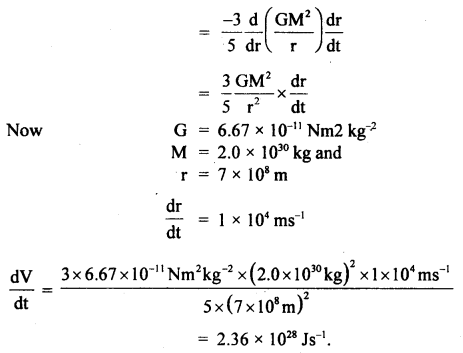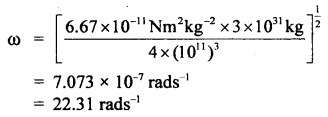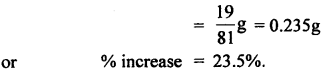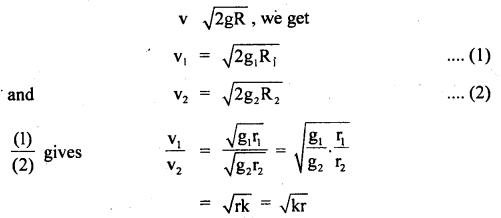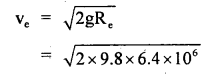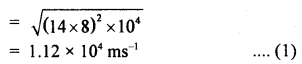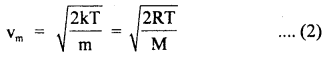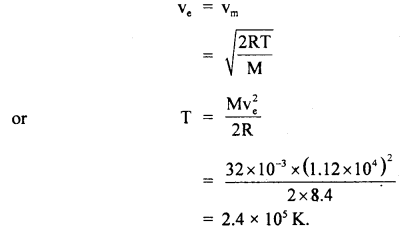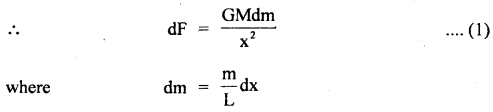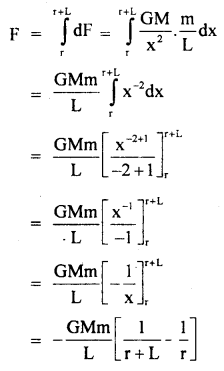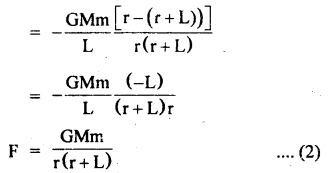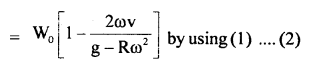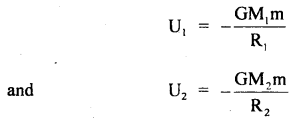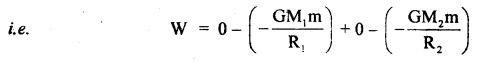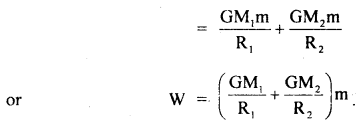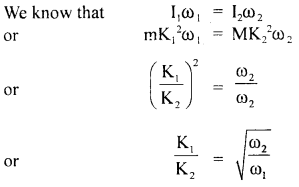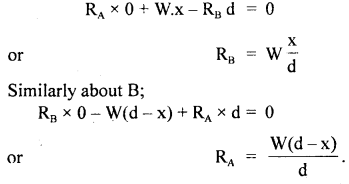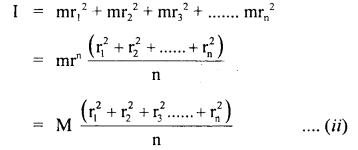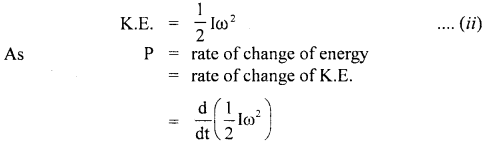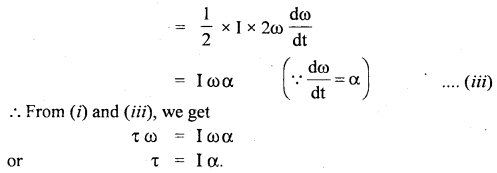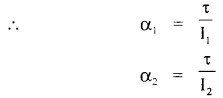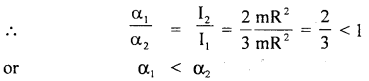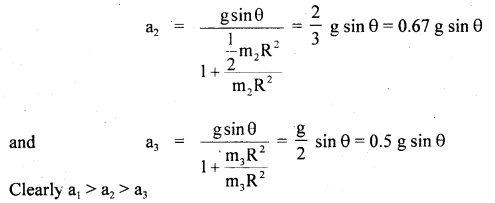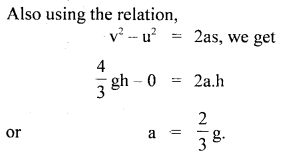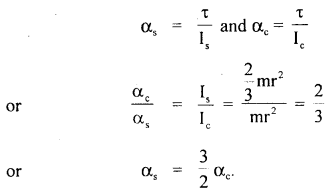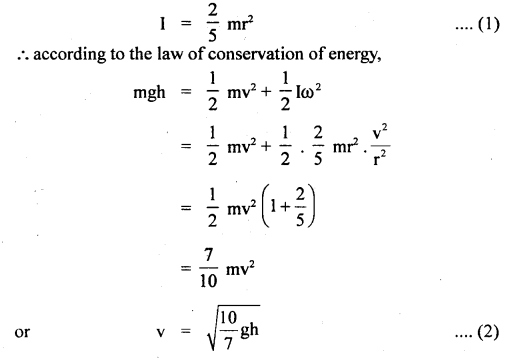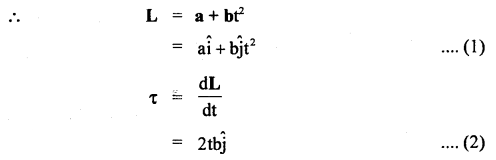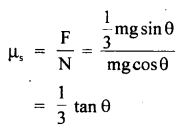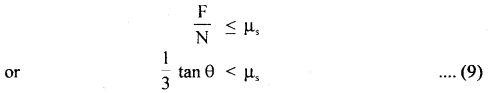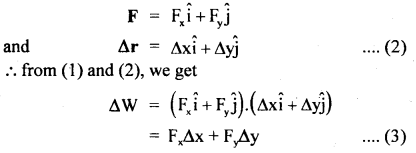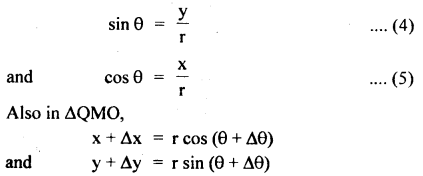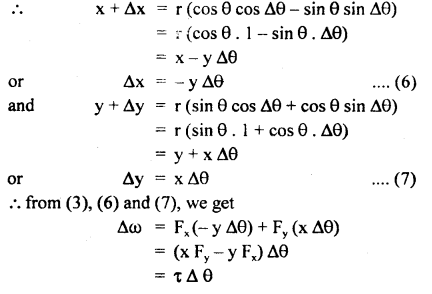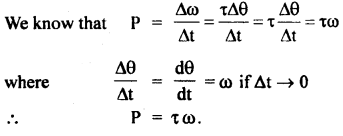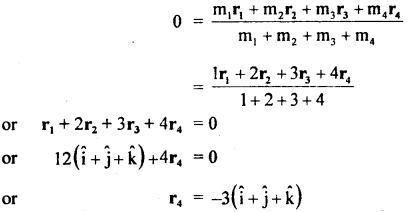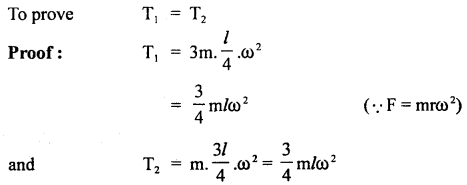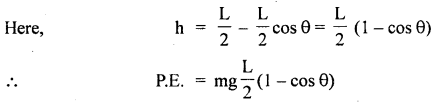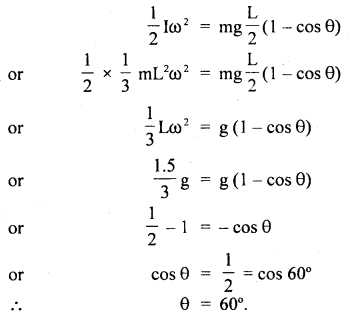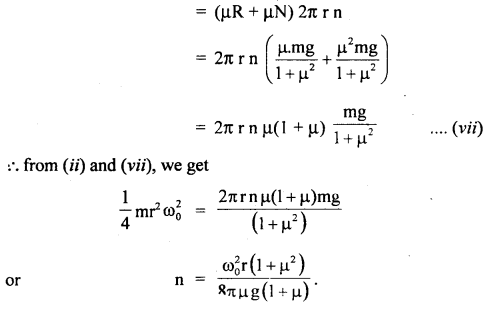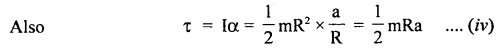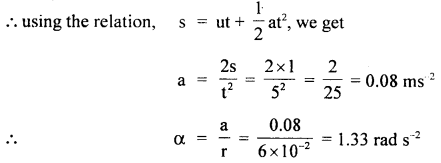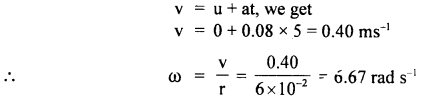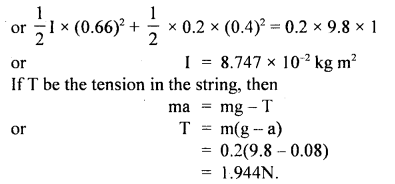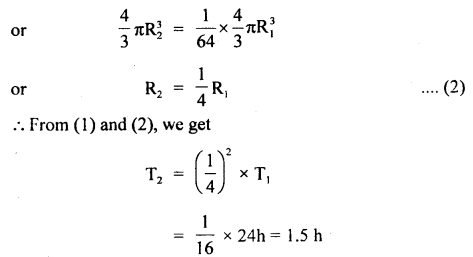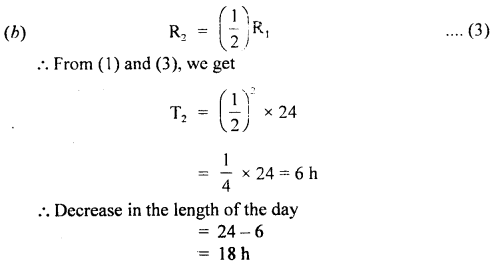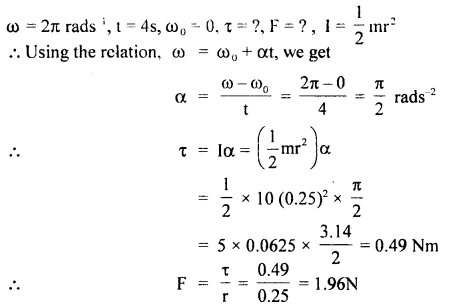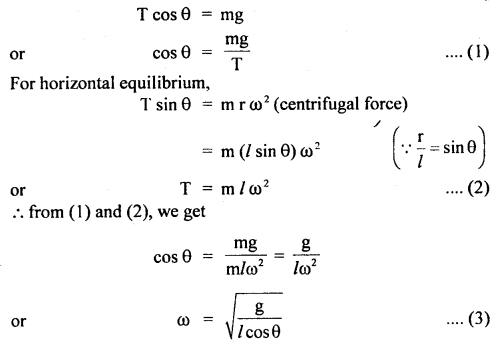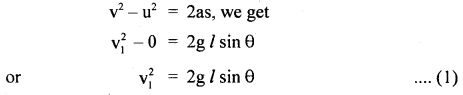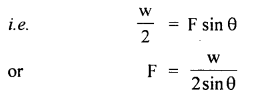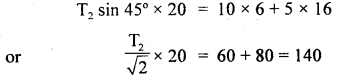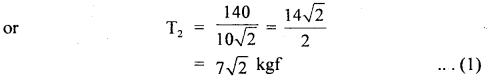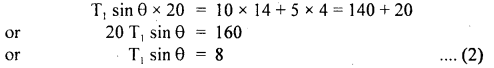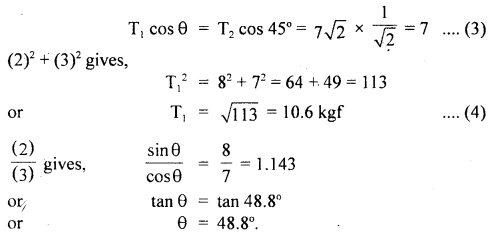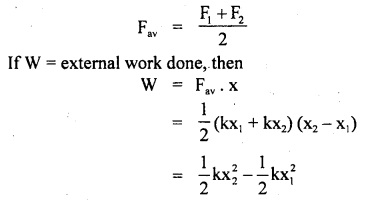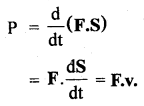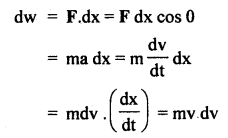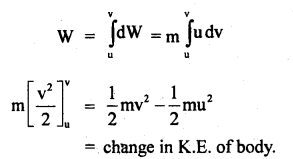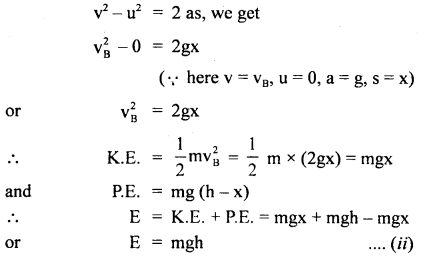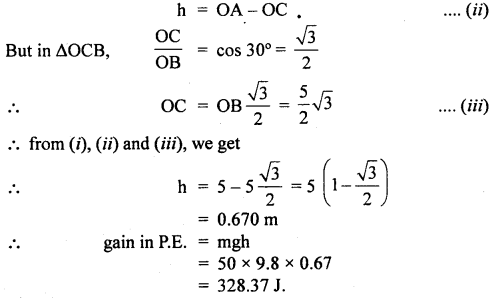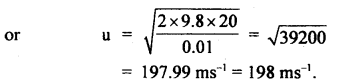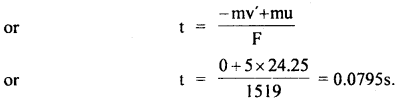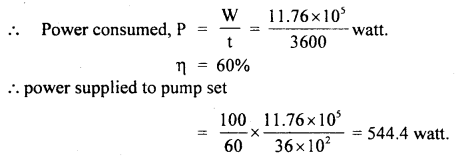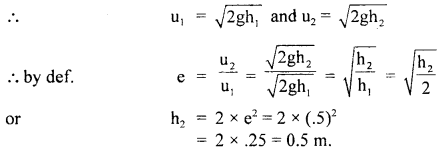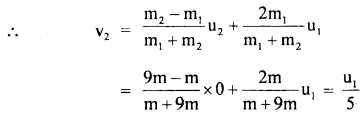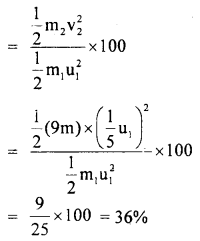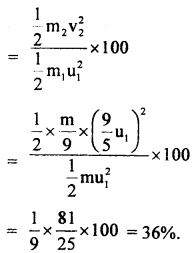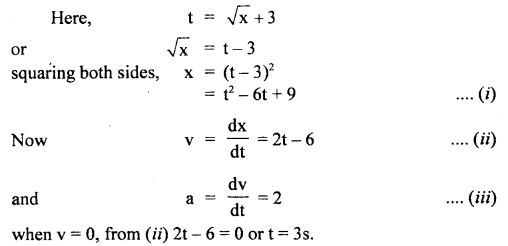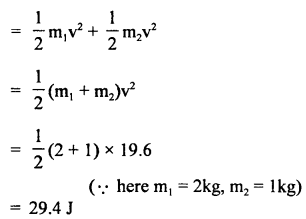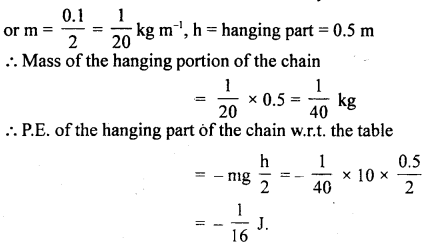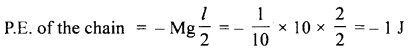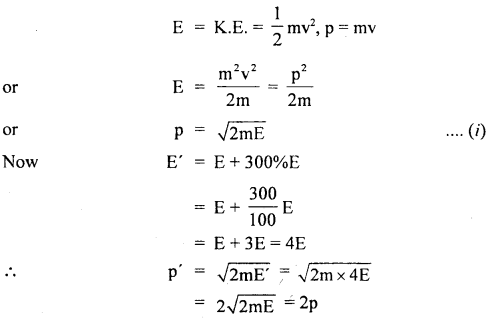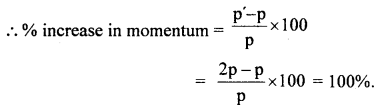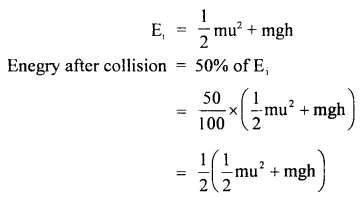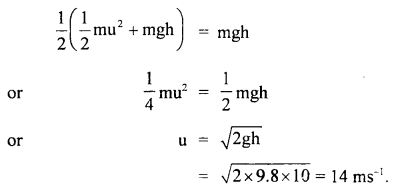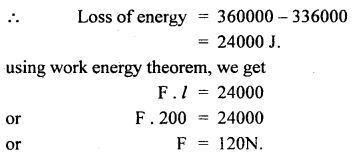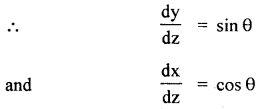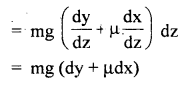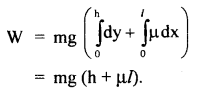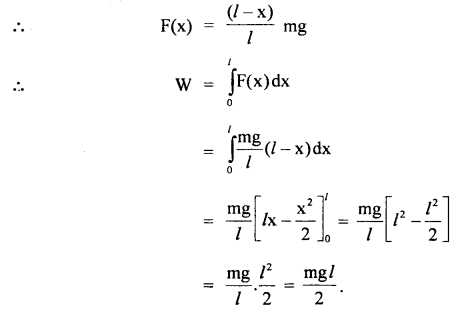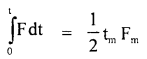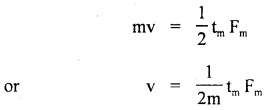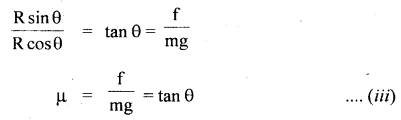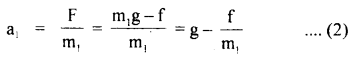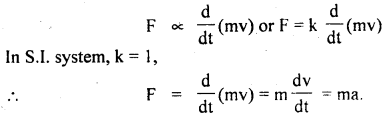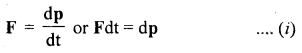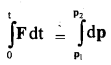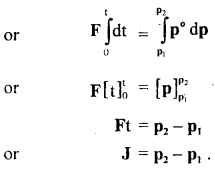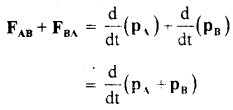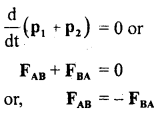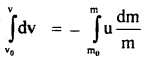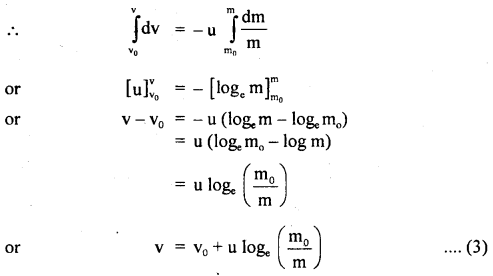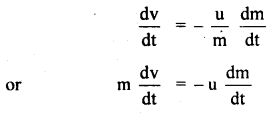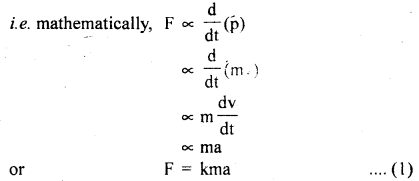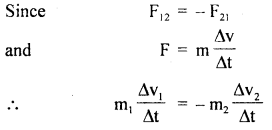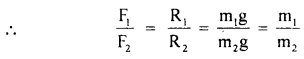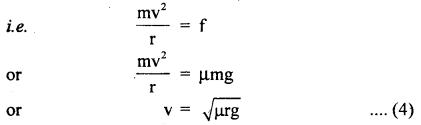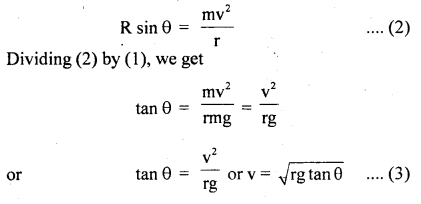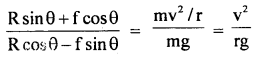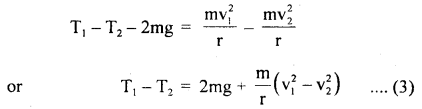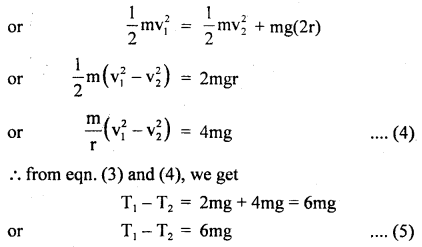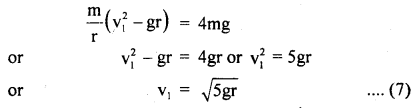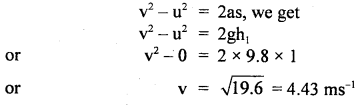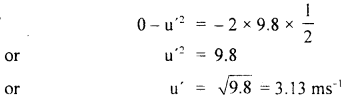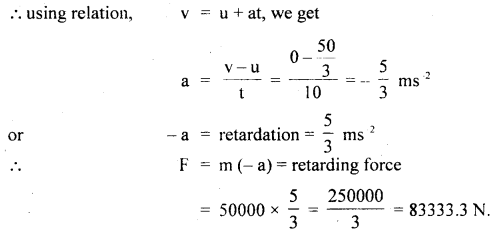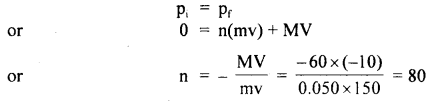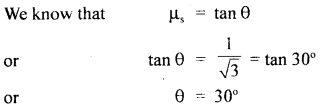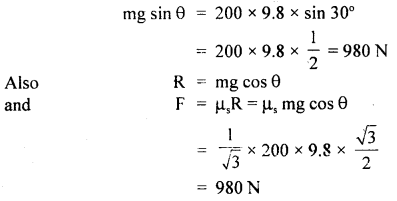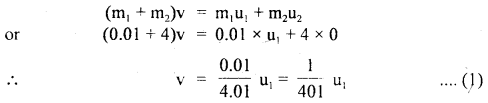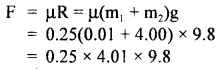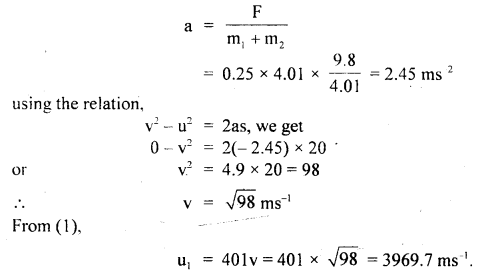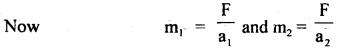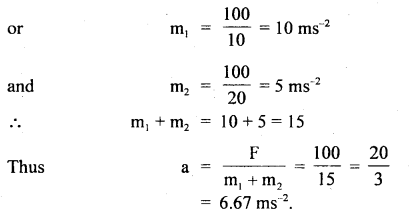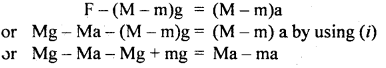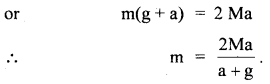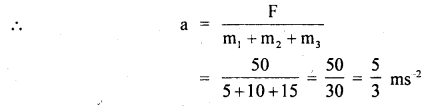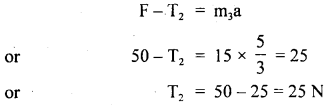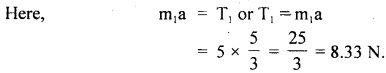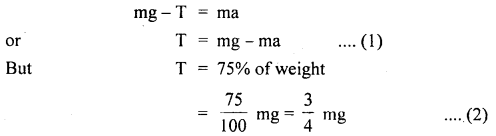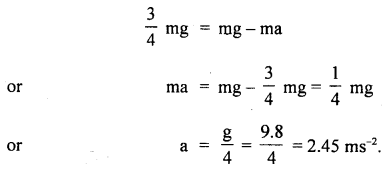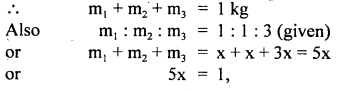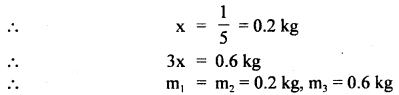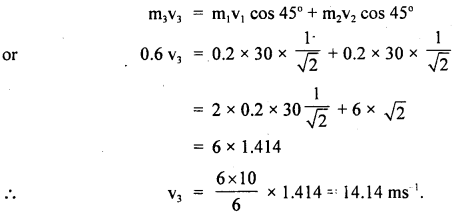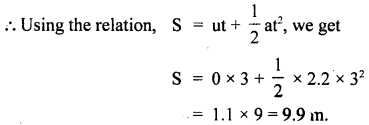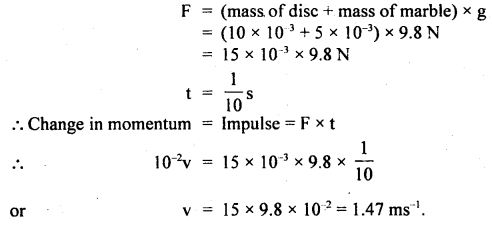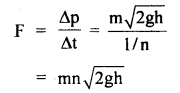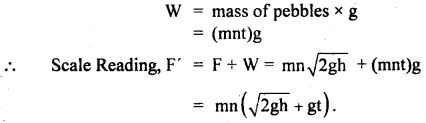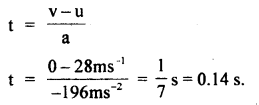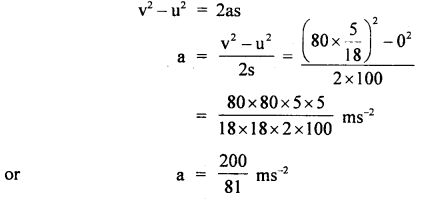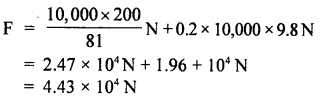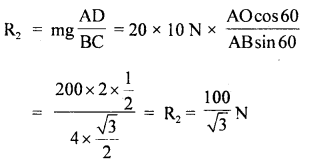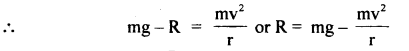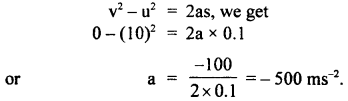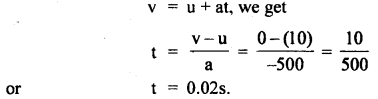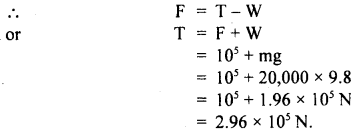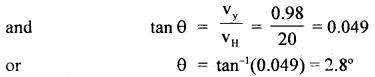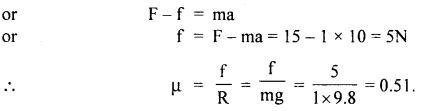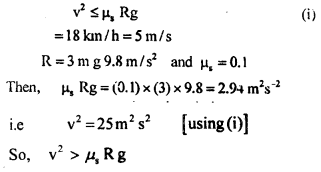CBSE Class 11

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 9 Mechanical Properties of Solids. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 9 Important Extra Questions Mechanical Properties of Solids

Mechanical Properties of Solids Important Extra Questions Very Short Answer Type

Question 1.
Give an example of pure shear.
Answer:
The twisting of a cylinder produces pure shear.

Question 2.
What is an elastomer?
Answer:
It is a substance that can be elastically stretched to large values t of strain.

Question 3.
What is breaking stress?
Answer:
It is defined as the ratio of maximum load to which the wire is < subjected to the original cross-sectional area.

Question 4.
What is the:
(a) value of modulus of rigidity of a liquid?
Answer:
zero.

(b) order of strain within the elastic limit?
Answer:
10^-3 cm per cm = 10^-3 cm/cm.

Question 5.
A wire is stretched to double its length. What is the value of longitudinal strain?
Answer:
Unity.

Question 6.
Mention a situation where the restoring force is not equal and opposite to the applied force.
Answer:
This happens when the body is deformed beyond the elastic limit.

Question 7.
What is a Cantilever?
Answer:
It is a beam loaded at one end and free at the other end.

Question 8.
A wire is suspended from a roof but no weight is attached to the wire. Is the wire under stress?
Answer:
Yes, the weight of the wire itself acts as the deforming force.

Question 9.
Why strain has no units?
Answer:
As it is the ratio of two similar quantities.

Question 10.
What is Poisson’s ratio?
Answer:
It is the ratio of lateral strain to linear strain.

Question 11.
What is the:
(a) the bulk modulus of a perfectly rigid body?
Answer:
infinite.

(b) value of Y for a perfectly rigid body?
Answer:
infinite.

(c) bulk modulus for an incompressible liquid?
Answer:
infinite.

Question 12.
Why does spring balance shows wrong readings after they have been used for a long time?
Answer:
Because of elastic fatigue.

Question 13.
Name three physical properties which can have different values in different directions.
Answer:
Thermal conductivity, compressibility, and electrical conductivity.

Question 14.
What will happen to the potential energy if a wire is
(a) compressed,
(b) stretched?
Answer:
In both cases, the potential energy of the wire increases as work has to be done on the wire.

Question 15.
Which of the two materials (see figure here) would you choose for a car tire? Why?

Answer:
Rubber (A) would be used to avoid excessive heating of the car tire.

Question 16.
How are depression and load interrelated in the case of a beam
(a) having rectangular cross-section and loaded in the middle?
Answer:
δ = \(\frac{\mathrm{W} l^{3}}{4 \mathrm{bd}^{3} \mathrm{Y}}\)

(b) having circular cross-section and loaded in the middle?
Answer:
δ = \(\frac{\mathrm{W} l^{3}}{12 \mathrm{Y} \pi \mathrm{r}^{4}}\)

Question 17.
Write copper, steel, glass, and rubber in the order of increasing coefficient of elasticity.
Answer:
Rubber, glass, copper, and steel.

Question 18.
How does Young’s modulus change with rising in temperature?
Answer:
Young’s modulus of a material decreases with rising in temperature.

Question 19.
The length of a wire is cut in half. What will be the effect on the increase in its length under a given load?
Answer:
An increase in length will be reduced to half as Δl ∝ l.

Question 20.
A wire is replaced by another wire of the same length and material but of twice diameter. What will be the effect on the:
(a) increase in its length under a given load?
Answer:
Increase in length will be reduced to one fourth as Δl ∝ \(\frac{1}{\mathrm{r}^{2}}\).

(b) maximum load which it can bear?
Answer:
The maximum bearable load becomes four times as breaking force ∝ area. (= πr²)

Question 21.
Sand does not possess any definite shape and volume, still, it is solid?
Answer:
Sand is a divided rock. It has all properties of solids and even its particles have indefinite volume like amorphous solids.

Question 22.
Name one material that is famous for a large elastic after effect.
Answer:
Glass.

Question 23.
Why some solids have high thermal and electrical conductivity?
Answer:
Because such solids have a large number of free electrons available in them (e.g. metals).

Question 24.
When a wire is bent back and forth, it becomes hot. Why?
Answer:
When a wire is bent back and forth, the deformations are beyond the elastic limit.

Question 25.
Two identical solid balls, one of ivory and the other of wet- clay are dropped from the same height on the floor. Which one will rise to a greater height after striking the floor and why?
Answer:
The ivory ball will rise to a greater height as compared to a clay ball because ivory is more elastic than wet clay.

Question 26.
Define ductile materials.
Answer:
They are defined as materials whose plastic range is relatively large.

Question 27.
Define brittle materials.
Answer:
They are defined as materials whose plastic range is relatively small.

Question 28.
Define elastic fatigue.
Answer:
It is defined as the loss of strength of the material caused due to repeated alternating strains to which the material is subjected.

Question 29.
Define elastic after effect.
Answer:
It is defined as the delay in regaining the original state by a body after the removal of the deforming force.

Question 30.
Define elasticity.
Answer:
It is the property of matter due to which it regains its original shape and size when the deforming forces have been removed.

Question 31.
Define hydrostatic stress.
Answer:
When a body is subjected to a uniform and equal force from all sides, then the corresponding stress is called hydrostatic stress.

Question 32.
Define plasticity.
Answer:
It is defined as the property of matter due to which it does not regain its original shape and size after the removal of deforming forces.

Question 33.
Define tangential or shearing stress.
Answer:
It is defined as the deforming force acting per unit area tangential to the surface.

Question 34.
Define deforming force.
Answer:
It is defined as the external force which when applied to a body changes its configuration (i.e. shape and size).

Question 35.
Define elastic limit.
Answer:
Maximum stress is called the elastic limit.

Question 36.
Define Young’s modulus.
Answer:
Within elastic limits, it is defined as the ratio of normal stress to longitudinal strain.

Question 37.
Define compressibility.
Answer:
It is defined as reciprocal of bulk modulus
i. e. compressibility = \(\frac{1}{\mathrm{~K}}=\frac{\Delta \mathrm{V}}{\mathrm{PV}}\)

Question 38.
Define modulus of rigidity.
Answer:
Within elastic limits, it is the ratio of tangential stress (T) to shear strain (θ)

Question 39.
What is the limitation of Hook’s law?
Answer:
It holds good when the wire is loaded within its elastic limit.

Question 40.
What are the factors on which the modulus of elasticity of material depends?
Answer:
Nature of the material and the manner of deforming the wire.

Question 41.
Name the property of a body that opposes its deformation?
Answer:
Elasticity.

Question 42.
Which of the three types of elasticity (Y, K, and t) is possessed by all the three states of the matter?
Answer:
The volume elasticity (K) is possessed by all three states of the matter.

Question 43.
Explain why liquids don’t possess rigidity?
Answer:
Liquids don’t possess rigidity because they have no shape of their own.

Question 44.
A wire of length L and cross-sectional area A is made of a material of Young’s modulus Y. If the wire is stretched by an amount x, then what is the work done?
Answer:

Question 45.
What is the importance of the stress-strain curve?
Answer:
Its slope gives the modulus of elasticity.

Question 46.
A bar is subjected to equal and opposite forces PQ is a plane ‘ making angle θ with the cross-section ‘a’ of the bar. Calculate the tensile stress on PQ.
Answer:

Area PQ = \(\frac{a}{\cos \theta}\)

Tensile stress = \(\frac{\mathrm{F} \cos \theta}{\mathrm{a} / \cos \theta}=\frac{\mathrm{F} \cos ^{2} \theta}{\mathrm{a}}\)

Question 47.
Calculate shearing stress on PQ in Fig.

Answer:
Shearing stress = \(\frac{F \sin \theta}{a / \cos \theta}=\frac{F}{a} \sin \theta \cos \theta=\frac{F}{2 a}(2 \sin \theta \cos \theta)\)
= \(\frac{F}{2a}\) sin 2θ

Question 48.
In a bar is subjected to equal and opposite forces PQ is a plane making angle θ with the cross-section ‘a’ of the bar. Calculate the tensile stress on PQ.when the tensile stress can be maximum?
Answer:
We know that, Tensile stress = \(\frac{\mathrm{F} \cos ^{2} \theta}{\mathrm{a}}\)
For tensile stress to be maximum, cos20 must be maximum – i.e. cos θ = 1 or θ = 0.

Question 49.
In Calculate shearing stress on PQ, when the shearing stress can be maximum?

Answer:Shearing stress = \(\frac{F}{2a}\) sin2θ
For shearing stress to be maximum, sin20 must be maximum

Question 50.
The length of a rod is doubled, under the action of a constant force. If the initial stress is S, then what will be the final stress?
Answer:
We know that stress = \(\frac{F}{A}\) . Also AL = constant for a given rod. When L is doubled, A becomes half, so stress becomes double.

Mechanical Properties of Solids Important Extra Questions Short Answer Type

Question 1.
What are the factors due to which three states of matter differ from one’s Other?
Answer:
Three states of-matter differ from each other due to the following two factors:
(a) The different magnitudes of tester atomic and intermolecular forces.
(b) The degree of random thermal motion of the atoms and molecules of a substance depends upon the temperature.

Question 2.
When we stretch a wire, we have to perform work Why? What happens to the energy given to the wire in this process?
Answer:
In a normal situation, the atoms of a solid are at the locations of minimum potential energy. When we stretch a wire, the work has to be done against interatomic forces. This work is stored in the wire in the form of elastic potential energy.

Question 3.
Why are the bridges declared unsafe after long use?
Answer:
A bridge during its use undergoes alternative strains a large number of times each day, depending upon the movement of vehicles on it. When a bridge is used for a long time it loses its elastic strength, due to which the number of strains in the bridge for given stress will become large and ultimately the bridge may collapse. Thus, !» to avoid this, the bridges are declared unsafe after long use.

Question 4.
Why are the springs made of steel and not of copper?
Answer:
Spring will be a better one if a large restoring force is set up in it on being deformed, which in turn depends upon the elasticity of the material of the spring. Since Young’s modulus of elasticity of steel is more than that of copper, hence steel is preferred in making the springs.

Question 5.
A heavy machine is to be installed in a factory. To absorb vibrations of the machine, a block of rubber is placed between the machinery and the floor. Which of the two rubbers (A) and (B) of Figure would you prefer to use for this purpose? Why?

Answer:
The area of this hysteresis loop measures the amount of heat energy dissipated by the material. Since the area of the loop B is more than that of A, therefore B can absorb more vibrations than that of Av Hence B is preferred.

Question 6.
Metal wires after being heavily loaded dop’\ regain their lengths completely explain why?
Answer:
A material regains its original Configuration (length, shape dr volume) only when the deforming force is within the elastic limit. Beyond the elastic limit, the bodies lose the property of elasticity and hence don’t completely regain the length of being heavily loaded.

Question 7.
Explain. Why spring balances show wrong readings after they have been, Used for a long time?
Answer:
When spring balances are used for a long time, they get fatigued. So the springs of such balances will take time to recover their original configuration. Hence the readings shown by such spring balances will be wrong.

Question 8.
Elasticity is said to be the internal property of matter. Explain.
Answer:
When a deforming force acts on a body, the atoms of the substances get displaced from their original positions. Due to this the configuration of the matter (substance) changes. The moment, the deforming force is removed, the atoms return to their original positions and hence the substance or matter regains its original configuration. Hence elasticity is said to be the internal property of matter.

Question 9.
Define tensor physical quantities. Give an example.
Answer:
They are defined as the physical quantities having different values in different directions e.g. stress.

Question 10.
Define compressional stress.
Answer:
It is defined as the restoring force developed per unit area of cross-section of a body when it is compressed i.e. when its length decreases under the action of deforming force.

Question 11.
Define longitudinal or tensile stress.
Answer:
It is defined as the restoring force developed per unit area of cross-section of a body when the length of the body increases in the direction of the deforming force.

Question 12.

and tell in which significant ways do these curves differ from the stress-strain curve.
Answer:

1. Hook’s law is not obeyed at all.
2. The elastic region is large here.
3. The material does not retrace the same curve while unloading.

Question 13.
Define restoring force.
Answer:
It is defined as the internal force which comes into play from within the body due to which it regains or tends to regain its original configuration.

For a perfectly elastic body restoring force = Deforming force.

Question 14.
Define longitudinal strain.
Answer:
It is defined as the ratio of change in length to the original length of an object when deformed by an external force

i.e. Longitudinal strain = \(\frac{l}{\mathrm{~L}}=\frac{\text { change in length }}{\text { original length }}\)

Question 15.
Define volumetric strain.
Answer:
It is defined as the ratio of change in volume per unit original volume of the body when deformed by an external force change in volume AV

i.e. Volumetric strain = \(\frac{\text { change in volume }}{\text { original volume }}=\frac{\Delta \mathrm{V}}{\mathrm{V}}\)

Question 16.
Define shear strain.
Answer:
It is defined as the ratio of the lateral displacement of a layer to its perpendicular distance from a fixed layer.

Aliter: It is defined as the angle through which a line originally perpendicular to the fixed face gets turned on applying tangential deforming force.

Question 17.
State Hook’s law.
Answer:
Hook’s law: States that within elastic limits, stress is directly proportional to the strain.
i. e. stress ∝ strain
or
\(\frac{\text { Stress }}{\text { Strain }}\) = constant = E.
where E is called coefficient or modulus of elasticity of the material.

Question 18.
Define bulk modulus.
Answer:
Within elastic limits, it is defined as the ratio of normal stress to volumetric strain.

Question 19.
On what factors does the value of the coefficient of elasticity depend? Why it is of it three types?
Answer:
Its value depends upon the:

1. nature of the material of the body.
2. the way in which the body is deformed.

It is of three types as strain is of three types.

Question 20.
Why a hard wire is broken by bending it repeatedly in opposite direction?
Answer:
It is because of the loss of strength of the material due to repeated alternating strains to which the wire is subjected.

Question 21.
When a cable is cut to half its original length, the maximum load it can withstand does not change. Why?
Answer:
The breaking stress is constant for a given material. Now breaking lord = breaking stress × area. When we cut the cable to half its length, its area of cross-section does not change. Hence there is no effect on the maximum load, the cable can support.

Question 22.
What causes restoring stress when a wire is stretched and when a body is compressed?
Answer:
When a wife is stretched, the restoring stress is caused by inter atomic-attraction and when a body is compressed, the restoring stress is caused by interatomic repulsion.

Question 23.
Are elastic restoring forces conservative?
Answer:
The elastic restoring forces are conservative when the loading and unloading curves coincide, but when these curves are different, the elastic restoring forces are non-conservative.

Question 24.
When a cable is cut to half its original length, how does this affect the elongation under the given load?
Answer:

Now as L is made \(\frac{L}{2}\) l will become \(\frac{L}{2}\), so elongation will become half of its value before cutting.

Question 25.
Why do solids have well-defined and reproducible external shapes?
Answer:
It is because, the atoms and molecules are arranged in a definite and regular way throughout the body of the solids, so they have well-defined and reproducible external shapes.

Question 26.
Why any metallic part of the machinery is never subjected to stress beyond the elastic limit of the material?
Answer:
If it is subjected beyond the elastic limit, then a permanent deformation will be set in that metallic part of the machine.

Question 27.
The braking force for a wire is F. What will be the breaking force for
(a) two parallel wires of the same size?
Answer:
When two wires of the same size are suspended in parallel, force F equal to the braking force for a wire will acton each wire if a force 2F is applied on the parallel combination.

(b) for a single wire of double the thickness?
Answer:

If the thickness is doubled, then the braking force will be four times the braking force.

Question 28.
Elasticity has a different meaning in Physics and in our daily life. Why?
Answer:
In daily life, a body is said to be more elastic if large deformation or strain is produced on subjecting the material to a given stress. But in Physics, it is exactly the opposite. A body is said to be more elastic if a small strain is produced on applying the given stress.

Question 29.
The length of a Wire is increased by 16 cm when a weight of 5 kg is hung. If all conditions are the same, what will be the increase in its length when the diameter is doubled?
Answer:
We know that,

when d = diameter of wire

∴ l ∝ \(\frac{1}{\mathrm{~d}^{2}}\)
Thus when d is doubled, l reduces to \(\frac{1}{4}\)th
i.e. l’= \(\frac{l}{4}=\frac{8}{4}\) = 2 cm. 4 4

Question 30.
When stress is equal to Young’s modulus of elasticity, then calculate the extension of a wire of length l.
Answer:
Here, L = original length of wire.
Let Δl = extension of wire = ?
Stress = Y (given)

Mechanical Properties of Solids Important Extra Questions Long Answer Type

Question 1.
(a) What are the factors affecting elasticity?
Answer:
The following factors affect the elasticity of a material:

1. Effect of hammering and rolling: It causes a decrease in the plasticity of the material due to break¬up of crystal grains into smaller units and hence – the elasticity of the material increases.
2. Effect of Annealing: Annealing results in the increases in the plasticity of the material due to, the formation of large crystal grains. Hence the elasticity of the material decreases.
3. Effect of the presence of impurities: The effect of the presence of impurities in a material can be both ways i.e. it can increase as well as decrease the elasticity r of the material. The type of effect depends upon the
   nature of the impurity present in the material.
4. Effect of temperature: The increase in the temperature of the material in most cases causes a decrease in the elasticity of the material. The elasticity of invar does not change with the change of temperature.

(b) Define Poisson’s ratio.
Answer:
Poisson’s Ratio (σ): Within elastic limits, it is defined; as the ratio of lateral strain (β) to the linear strain i.e.
σ = \(\frac{β}{α}\)

(c) Define breaking load.
Answer:
Breaking Load: It is defined as the product of the breaking stress and area of cross-section of the given object. It is also called maximum load a body (cable/ wire) can support

i.e. breaking load = Breaking stress × area of cross-section. It should be noted that breaking stress is a constant for the given material.

Question 2.
The length of a metallic wire is L₁ when tension is T₁ and L₂ when tension is T₂. Find the original length of the wire.
Answer:
Let L, A be the length and area of the cross-section of the wire.
Also, let l be the extension produced on applying a force F, then

where Y = Young’s modulus.
Now when F = T₁ and l = L₁ – L.

Numerical Problems:

Question 1.
A mass of 5 kg is hung from a copper wire of 1 mm diameter and 2 m in length. Calculate the extension produced. What should be the minimum diameter of the wire so that its elastic limit is not exceeded? Elastic limit for copper = 1.5 × 10⁹ dyne cm^-2, Y for copper = 1.1 × 10¹² dyne cm^-2.
Answer:


Let d₁ be the minimum diameter, then maximum stress

Question 2.
A cube of aluminum of each side 4 cm is subjected to a tangential (shearing) force. The top of the cube is sheared through 0.012 cm w.r.t. the bottom face.
Find (a) shearing strain,
(b) shearing stress,
(c) shearing force. Given η = 2.08 × 10¹¹ dyne cm^-2.
Answer:
Here,
length of each side, L = 4 cm
Lateral displacement, x = 0.012 cm ,
η = 2.08 × 10¹¹ dyne cm^-2.

Question 3.
The breaking stress of aluminum is 7.5 × 10⁸ dyne cm^-2. Find the greatest length of aluminum wire that can be hung vertically without breaking. The density of aluminum is 2.7 g cm^-3. Take g = 980 cm s^-2.
Answer:
Here, breaking stress = 7.5 × 10⁸ dyne cm^-2, ρ = 2.7 g cm^-3

Let l be the greatest length of the wire that can be hung vertically without breaking.
mass of wire, m = area of cross-section × length × density = a /ρ.
∴ Weight of wire, W = mg = a / ρ g.

This is equal to the maximum force that the wire can withstand.

Question 4.
Calculate the % increase in the length of a wire of diameter 2,5 unstretched by a force of 100 kg. Y for the wire = 12,5 × 10¹¹ dyne cm^-2.
Answer:

Question 5.
Compare the densities of water at the surface and bottom of a lake 1oo m deep, given that the compressibility is \(\frac{10^{3}}{22}\) per atm and 1 atm = 1.015 × 10⁵ Pa.
Answer:

Let V = Volume of 1 kg water at the surface.
V’ = Volume of 1 kg water at the bottom of lake 100 m deep
= V – ΔV, where ΔV = decrease in volume, increase in pressure, P = hρg = 100 × 10³ × 9.8 Nm²

If ρ_s and ρ_b be the densities of water at the surface and at the bottom of the lake respectively, then

Question 6.
A steel wire 2 mm in diameter is stretched between two clamps, when its temperature is 40° C. Calculate the tension in the wire, when its temperature falls to 30° C. Given, coefficient of linear
Answer:

If Δl be the change n length of the wire, then

Question 7.
When a weight W is hung from one end of a wire of length L (other end being fixed), the length of the wire increases by l fig. (a). If the wire is passed over a pulley and two weights W each is hung at the two ends fig. (b), what will be the total elongation in the wire?

Answer:
(a) Let Y = Young’s modulus of the material of the wire. If ‘a’ be its area of cross-section, then

(b) When the wire is passed over the pulley, let l’ be the increase in the length of each segment. Since \(\frac{L}{2}\) = length of each segment.

∴ Total increase in the length of the wire is given by
= l’ + l’ = 2l’ = 2 × \(\frac{l}{2}\) = l.

Question 8.
A uniform cylindrical wire is subjected to longitudinal tensile stress of 5 × 10⁷ Nm^-2. The Young’s Modulus of the material of the wire is 2 × 10¹¹ Nm^-2. The volume change in the wire is 0.02%. Calculate the fractional change in the radius of the wire.
Answer:

Question 9.
A wire loaded by the weight of density 7.6 g cm^-3 is found to measure 90 cm. On immersing the weight in water, the length decreases by 0.18 cm. Find the original length of the wire.
Answer:
Let L = original length of the wire =?
A = be its area of cross-section.
W = load attached to the wire.

Then Young’s Modulus of the wire is given by

Here, ΔL = 90 – L = Change in the length of wire.

Volume of weight attached,

∴ Mass of water displaced = V × density of water
= \(\frac{W}{7.6}\) × l = \(\frac{W}{7.6}\)

∴ Net weight after immersing in water ¡s
W’ = W – \(\frac{W}{7.6}\) = \(\frac{6.6}{7.6}\) W

Length of wire after immersing ¡n water
= 90 – 0.18 = 89.82 cm.

∴ Increase in length on immersing in water,

Question 10.
Two exactly similar wires of steel and copper are stretched by equal forces. If the total elongation is 1 cm, find by how much each wire is elongated. Given Y for steel = 20 × 10¹¹ dyne cm^-2, Y for copper = 12 × 10¹¹ dyne cm^-2.
Answer:
Let Δl_s and Δl_c be the elongation produced in steel and copper wires respectively.
L_s, L_c be their respective lengths,
L_s = L_c (∵ wires are similar)
Y_s = 20 × 10¹¹ dyne cm^-2
Y_c = 12 × 10¹¹ dyne cm^-2
Δl_s + Δl_c = 1 cm
A = area of cross-section of each wire.
F = equal force applied.

∴ Using the relation,

Dividing (ii) by (i), we get

Question 11.
A rubber rope of length 8 m is hung from the ceiling of a room. What is the increase in the length of the rope due to its own weight? Given Young’s modulus of elasticity of rubber is 5 × 10⁶ Nm^-2 and density of rubber = 1.5 × 10³ kg m^-3. Take g = 10 ms^-2.
Answer:
Here, ρ = 1.5 × 10³ kg m^-3
L = 8m
Y = 5 × 10⁶ Nm^-2

Let Mg and A be the weight and area of the cross-section of the rubber rope.
As weight acts at C. G. so effective length = \(\frac{L}{2}\)
∴ Mg = A L ρ g (∵ M is distributed over L)

Let ΔL = increase in the length of the rope =?

Question 12.
A sample of bone in the form of a cylinder of cross-sectional area 1.5 cm² is loaded on its upper end by a mass of 10 kg. By careful measurements with a traveling microscope, the length of the cylindrical sample is observed to decrease by 0.0065%. Calculate the value of Young’s Modulus for the specimen. Given g = 9.8 ms^-2.
Answer:

Question 13.
Estimate the maximum height of a mountain.
Answer:
The elastic behavior of the earth helps us to calculate the maximum height of mountains on earth.

Let h be the height of a mountain.
ρ = density of rocks of the mountain

∴ The pressure at the base of the mountain h ρ g = Stress
The elastic limit of a typical rock 3 × 10⁸ Nm^-2

The stress must be less than the elastic limits, otherwise, the rock-begins to sink.

It may be noted that the height of Mount Everest is nearly 9 km.

Question 14.
A uniform pressure P is exerted on all sides of a solid cube. It is heated through t°C in order to bring its volume back to the value it had before the application of pressure. Find the value of t.
Answer:
Let γ = coefficient of cubical expansion of the cube.
Let K be the bulk modulus of elasticity of its material.
V = initial volume.
P = pressure applied.
ΔV = Decrease in its volume.

where t = rise in its temperature so as to increase the volume by ΔV s.t. it is brought back to its initial volume.
∴ From (i) and (ii), we get

Question 15.
If K be the bulk modulus of a metal and a pressure P is applied uniformly on all its sides. If p be the density of metal, then find the fractional increase in its density.
Answer:
Let M = mass of metal
V = mass of volume
∴ ρ = \(\frac{M}{V}\) ….(i)

Let ΔV = Decrease in its volume when a pressure P is applied.
If ρ’ be its new density, then

Question 16.
The rubber cord catapult has a cross-sectional area of 1 mm² and a total unstretched length of 10 cm. It is stretched to 12 cm and then released through a projectile of the mass of 2 gm. Taking Y =5 × 10⁸ Nm^-2, find tension ¡n the cord and velocity of projection.
Answer:
Here, Y = 5 × 10⁸ Nm^-2
A = 1mm2 = 10^-6 m²
L = 10 cm = 0.1 m
Δl = 12 – 10 = 2cm = 0.02m
m = 2 × 10^-3 kg
T =?
V =?

This is converted into K.E. of the projectile.

Question 17.
What should be the greatest length of a steel wire which when fixed at one end can hang freely without breaking? Density (ρ) of steel = 7.8 g cm³, breaking stress for steel = 7.8 × 10⁹ dynes/cm².
Answer:
Here, breaking stress = 7.8 × 10⁹ dyne cm²
Le.t A = area of cross-section of the wire
ρ = 7.8 g cm^-3
g = 980 cms^-2

Let l = length required = ?
∴ V = volume of wire = lA

∴ Stretching force = weight of the wire = ρ V g
= ρlAg

∴Maximum stress = Breaking stress

Question 18.
A copper wire of negligible mass, area of cross-section 10^-6 m², and length 1 m are kept on a smooth horizontal table with one end fixed. A ball of mass 1 kg is attached to the other end. The wire and ball are rotating with an angular velocity of 20 rad s-1. If the elongation in the wire is 10^-3 m, then find Young’s modulus.
Answer:
Here, L = original length of the wire = 1 m
l = elongation length of the wire = 10^-3 m
A = area of cross-section of wire = 10^-6 m²
M = mass of ball attached to the wire = 1 kg
ω = angular velocity of rotation = 20 rad s^-1
Y = ?
Force on wire = centripetal force

Question 19.
If the angular velocity of the wire and the ball in the above question is increased to Loo rad s, then the wire breaks down. Calculate the breaking stress.
Answer:
As per above question M = 1 kg
L = 1m .
A = 10^-6 m²
Here, ω = angular velocity = 100 rad s^-1
Breaking stress = ?

Using the formula,

Question 20.
A wire of radius r stretched without tension along a straight line is tightly fixed at points A and B as shown in the figure. What is the tension in the wire when it is pulled into the shape XYZ?

Answer:
Let T = Tension in the wire = ?
r = radius of the wire
∴ A = area of cross-section of the wire = πr²
θ = ∠XYC = ∠ZYC
l = X C = CZ

If Δl be the extension of the wire, then

Question 21.
A wire of density 9 g cm^-3 is stretched between two clamps 100 cm apart, while subjected to an extension of 0.05 cm. What is the lowest frequency of transverse vibrations in the wire, assuming Y = 9 × 10¹¹ dyne/cm²?
Answer:
Here, ρ = density of wire = 9 g cm³
Y = 9 × 10¹¹ dyne/cm²
L = distance between two clamps = 100 cm
l = extension of wire = 0.05 cm

Let v = lowest frequency of transverse vibrations = ?
If F and A be the stretching force and area of the cross-section of the wire, then

Also, the lowest frequency or fundamental frequency of transverse vibrations is given by

where L’ = 100 + 0.05 = 100.05 cm
m = mass/length = Aρ = area × density

Question 22.
A steel wire with a cross-sectional area of 0.5 mm² is held between two fixed supports. If the tension in the wire is negligible and it is just taut at a temperature of 20°C. Determine the tension when the temperature falls to 0°C. Y = 21 × 10¹¹ dyne/cm² and coefficient of linear expansion is 12 × 10^-6 per degree centigrade. Assume distance between two supports. remains same.
Answer:
Here, let L = length of the wire
A = its area of cross-section = 0.5mm²
= 0.005 cm²
Y = 21 × 10¹¹ dyne/cm²

α = coefficient of linear expansion
= 12 × 10-6 °C^-1

Let T = tension in the wire = ?
If Δl be extension, then
Δl = α L Δt
where Δt = 20 – 0 = 20°C

This strain is tensile as the wire is kept taut and not allowed to contract.

∴ Tensile stress in the wire = Y × strain
= Y α Δt

∴ T = Tensile stress × A
= Y α Δt A
= 21 × 10¹¹ × 12 × 10^-6 × 20 × 0.005
= 25.2 × 10⁵ dyne.

Question 23.
Two rods of different metals having the same area of cross-section A are placed between the two fixed points and they have the parameters as l₁, α₁, Y_1, and l₂, α₂, Y₂ respectively where l stands for their lengths, a for coefficients of linear expansion. The temperature of both is increased by T°C. Find the force with which the rods act on each other.

Answer:
Due to the rise in temperature by T°C, let Δl₁ and Δl₂, be the increase in lengths of the two rods.

As the two fixed points don’t allow the length to increase, hence thermal stress \(\frac{F}{A}\) is developed.

∴ Decrease in length due to thermal stress = increase in length due to thermal linear expansion

Question 24.
Two rods of different materials having coefficients of linear expansion α₁ and α₂ and Young’s modulus Y₁ and Y₂ respectively are fixed between two massive points and are heated such that they undergo the same increase in temperature. There is no bending in rods of α₁: α₂ = 2: 3 and thermal stresses produced in two rods are equal. Calculate the ratio Y₁: Y₂.
Answer:
It is a common cause of thermal expansion and elastic compression.

For the same rise in temperature (Δt) and same stress,
Yα = constant
or
Y₁α₁ = Y₂α₂

Question 25.
What force is required to stretch a copper wire 1 cm² in cross¬section to double its length? Y for copper is 1.26 × 10¹² dyne cm^-2.
Answer:
Here, A = 1 cm²
Let L = length of the wire.

Also, Let L’ be the new length when a stretching force F is applied.
L’ = 2L
Then l = extension = L’ – L = 2L – L = L
F = ?
Y = 1.26 × 10¹² dyne cm^-2

Value-Based Type:

Question 1.
Raman and his friend Sbhan while going to the school on a motorcycle noticed that a bridge had collapsed. Immediately they went to their physics teacher and enquired about the reasons for falling off the bridge. After knowing the reasons that very interesting; they decided to pursue their career as civil engineers and vowed to construct 100% quality dams and bridges.
(a)Comment upon the values possessed by them.
Answer:
Sympathy, determination, and concern for society, honesty, and integrity.

(b) Name the property that helps in constructing bridges. Also, define the property.
Answer:
Elasticity: The property of the body to regain its original configuration (i .e length, volume, or shape) when the deforming force is removed, is called elasticity.

Question 2.
Ram and his friend Ramesh are the students of class XI. They are discussing “elastic fatigue”. Ram told that just as a tired person elastic body also relieved of the fatigue or regains its original degree of elasticity when allowed to rest for some time. Raman did not convince Ram. They went to solve this problem before their physics teacher.
(i) What values are displayed by Ram and Ramesh?
Answer:
The values displayed by them are:
(a) Curiosity
(b) Awareness
(c) Attitude to find the solution by discussion
(d) Interested in learning.

(ii) Whether Ram’s ideas and reasons were correct or not?
Answer:
Yes, Ram’s ideas and reasons were correct and were recommended by their teachers.

(iii) Why do spring balance shows wrong readings after they have been used for a long time?
Answer:
This is due to elastic fatigue.

Question 3.
Kamal read a topic in a newspaper that a bridge declared unsafe by the Government. The bridge was 2 km away from his house and he used to cross it almost daily. The condition of the bridge does not look so bad. However, it was built 60 years ago. The next day Kamal asked the reason for this question to his friends.
(i) What value is displayed by Kanal here?
Answer:
Values displayed are:
Curiosity, awareness, group discussion, and keenness to know the scientific reasons.

(ii) Why the bridge declared unsafe after long use?
Answer:
Due to the repeated stress and strain, the material used in the bridges loses elastic strength and ultimately may collapse. Hence, bridges are declared unsafe after long use.

Question 4.
Two friends Mohan and Dinesh arc discussing elasticity. Mohan told that steel is more elastic than rubber. Dinesh was surprised and asked his teacher the-Fcascm-Jachind it.
(i) What value is displayed by Dinesh?
Answer:
The values displayed by Dinesh are:
Curiosity, Interested in learning.

(ii) How his teacher explained it?
Answer:
Let the two pieces of wire, one of steal and the other of rubber having an equal length (L) and equal area of cross-section (A). Let each be stretched by equal force (F).

Then, Young’s modulus of steel and rubber are:

Hence, Steal is more elastic than rubber.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 8 Gravitation. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 8 Important Extra Questions Gravitation

Gravitation Important Extra Questions Very Short Answer Type

Question 1.
What velocity will you give to a donkey and what velocity to a monkey so that both escape the gravitational field of Earth?
Answer:
We will give them the same velocity as escape velocity is independent of the mass of the body.

Question 2.
How does Earth retain most of the atmosphere?
Answer:
Due to force of gravity.

Question 3.
Earth is continuously pulling the moon towards its center. Why does not then, the moon falls on the Earth?
Answer:
The gravitational force between the Earth and the moon provides the necessary centripetal force to the moon to move around the Earth. This centripetal force avoids the moon to fall onto the Earth.

Question 4.
Which is greater out of the following:
(a) The attraction of Earth for 5 kg of copper.
(b) The attraction of 5 kg copper for Earth?
Answer:
Same.

Question 5.
Where does a body weigh more – at the surface of Earth or in a mine?
Answer:
At the surface of Earth, a body weighs more.

Question 6.
How is it that we learn more about the shape of Earth by studying the motion of an artificial satellite than by studying the motion of the moon?
Answer:
This is because an artificial satellite is closer to the Earth than Moon.

Question 7.
If the Earth is regarded as a hollow sphere, then what is the weight of an object below the surface of Earth?
Answer:
Zero.

Question 8.
What is the formula for escape velocity in terms of g and R?
Answer:
Ve = \(\sqrt{2gR}\) .

Question 9.
What is the orbital period of revolution of an artificial satellite revolving in a geostationary orbit?
Answer:
It is 24 hours.

Question 10.
Can we determine the mass of a satellite by measuring its time period?
Answer:
Yes.

Question 11.
Is it possible to put a satellite into an orbit by firing it from a huge canon?
Answer:
Tins can be possible only if we can ignore air friction and technical difficulties.

Question 12.
What is the amount of work done in bringing a mass from the surface of Earth on one side to a point diametrically opposite on the other side? Why?
Answer:
The work done is zero. Because the gravitational potential difference is zero.

Question 13.
Name one factor on which the period of revolution of a planet around the Sun depends.
Answer:
Mean distance of the planet from the Sun.

Question 14.
The gravitational potential energy of a body of mass m is -10⁷ J. What is the energy required to project the body out of the gravitational field of Earth?
Answer:
10⁷ J.

Question 15.
Does the force of friction and other contact forces arise due to gravitational attraction? If not, what is the origin of these forces?
Answer:
No. The contact forces have an electrical origin.

Question 16.
Two satellites are at different heights. Which would have greater orbital velocity? Why?
Answer:
The satellite at the smaller height would have greater velocity.
This is because v₀ ∝ \(\frac{1}{\sqrt{\mathrm{r}}}\) .

Question 17.
How much energy is required by a satellite to keep it orbiting? Neglect air resistance? Why?
Answer:
No energy is required by a satellite to keep it orbiting. This is because the work done by the centripetal force is zero.

Question 18.
At noon the attractions of the Earth and Sun on a body on the surface of Earth are in opposite directions. But at midnight, they are in the same direction. Does a body weigh more at mid-night?
Answer:
No. The weight of the body is due to the Earth’s gravity only. What is the full form of the geostationary satellite APPLE? The full form of APPLE is the Ariane Passenger PayLoad Experiment.

Question 19.
What is geodesic?
Answer:
It is the shortest distance between any two points.

Question 20.
Why is G called a universal constant?
Answer:
G is called a universal constant because its value is the same everywhere.

Question 22.
Where does a body weigh more at the pole or at the equator?
Answer:
It weighs more at the pole.

Question 23.
What is the relation between orbital and escape velocity?
Answer:
v_e = \(\sqrt{2}\)v₀.

Question 24.
The weight of a body is 20N, What is the gravitational pull of the body on the Earth?
Answer:
20N.

Question 25.
Why Newton’s law of gravitation is said to be universal- law?
Answer:
It is called so because this law holds good irrespective of the nature of the interacting bodies at all places and at all times.

Question 26.
A particle is to be placed, in turn, outside four objects, each of mass m;
(a) a large uniform solid sphere,
(b) a large uniform spherical shell,
(c) a small uniform solid sphere,
(d) a small uniform shell.
In each situation, the distance between the particle and the center of the object is d. Rank the objects according to the magnitude of the gravitational force they apply on the particle, greatest first.
Answer:
They all apply the same gravitational force and hence all will tie.

Question 27.
Can we determine the mass of a satellite by measuring its time-period?
Answer:
No.

Question 28.
Does the gravitational force between two particles depends upon the medium between them?
Answer:
No, it does not depend upon the medium between the two particles.

Question 29.
Two artificial satellites of different masses are moving in the same orbit around the Earth. Can they have the same speed?
Answer:
Yes, they can have the same speed as orbital speed is independent of the mass of the satellite.

Question 30.
In an imaginary system, the central star has the same mass as our Sun but is much brighter so that only a planet twice the distance between Earth and the Sun can support life. Assuming biological evolution (including aging processes etc.) on that planet similar to ours, what would be the average life span of a ‘human’ on that planet in terms of its natural year? The average life span of a human on the Earth may be taken to be 70 years.
Answer:
25 planet years.

Question 31.
If the force of gravity acts on all bodies in proportion to their masses, then why does not a heavy body fall faster than a light body?
Answer:
Acceleration due to gravity is independent of the mass of the body.

Question 32.
What is the weight of a body in a geostationary satellite?
Answer:
The weight of a body is zero in a geostationary satellite.

Question 33.
A satellite does not need any fuel to circle around the Earth. Why?
Answer:
The gravitational force between satellite and Earth provides the centripetal force required by the satellite to move in a circular orbit.

Question 34.
What will be the effect on the weight of the bodies if Earth stops rotating about its axis?
Answer:
The weight of the bodies will increase.

Question 35.
Name the natural satellite of Earth.
Answer:
Moon.

Question 36.
Why a multi-stage rocket is required to launch a satellite?
Answer:
This is done to save fuel.

Question 37.
Mention one difference between g and G.
Answer:
The value of ‘G’ remains the same throughout the universe while the value of ‘g’ varies from place to place.

Question 38.
When an apple falls towards the Earth, the Earth moves up to meet the apple. Is the statement true? If yes, why is the Earth’s motion not noticeable?
Answer:
Yes, the statement is true. The acceleration of Earth is very small as compared to that of apple as the mass of Earth is very large.

Question 39.
Which of the following observations point to the equivalence of inertial and gravitational mass? Why?
(a) Two spheres of different masses dropped from the top of a long evacuated tube reach the bottom of the tube at the same time.
(b) The time period of a simple pendulum is independent of its mass.
(c) The gravitational force on a particle inside a hollow isolated sphere is zero.
(d) For a man in a closed cabin that is falling freely under gravity, gravity disappears.
(e) An astronaut inside a spaceship orbiting around the Earth feels weightless.
(f) Planets orbiting around the Sun obey Kepler’s Third Law.
(g) Gravitational force on a body due to the Earth is equal and opposite to the gravitational force on the Earth due to the body.
Answer:
As bodies are in motion in observations (a), (b), (d), (e), (f), thus, these point to the equivalence of inertial and gravitational masses.

Question 40.
How will the value of acceleration due to gravity be affected if the Earth begins to rotate at a speed greater than its present speed?
Answer:
Acceleration due to gravity will decrease if the angular speed of rotation of Earth increases.

Question 41.
How do we choose zero levels of gravitational potential energy?
Answer:
It corresponds to the infinite separation between two interacting masses.

Question 42.
Is it possible to put an artificial satellite in an orbit in such a way that it always remains visible directly over New Delhi? Why?
Answer:
It is not possible. This is because New Delhi is not in the equatorial plane.

Question 43.
A body is suspended with a spring balance attached to the ceiling of an elevator. The balance shows a reading of 5 divisions when the elevator is stationary. During the downward acceleration of the elevator, the balance shows zero reading. Do you think that the inertial mass and gravitational mass of the body are equal? Justify your answer.
Answer:
Yes, they will be equal. The two masses differ only when the velocity of the lift approaches the velocity of light.

Question 44.
Does a comet move faster at aphelion or perihelion?
Answer:
At the perihelion where it is close to Sun, the comet moves faster.

Question 45.
Due to some unforeseen event, the planet of the I0 satellites of Jupiter does not pass through the center of Jupiter. Will the orbit of I₀ be stable? Why?
Answer:
No. For a stable orbit, the plane of the orbit must pass through the center (equatorial plane) of the planet.

Question 46.
Is it appropriate to describe the condition of weightlessness as the condition of masslessness? Why?
Answer:
No. Weight and mass are different physical quantities. A body may have zero weight but never zero mass. So it is not appropriate to describe the condition of weightlessness as a condition of masslessness.

Question 47.
Define central force.
Answer:
It is defined as the force which is always directed along the position vector of the point of application of the force w.r.t. the fixed point i.e. away or towards a fixed point.

Question 48.
The angular momentum is always conserved in the motion under a central force. Name the two results that follow from this.
Answer:

1. The motion of a particle under the central force is always confined to a plane.
2. The position vector of the particle w.r.t. the center of force has a constant areal velocity i.e. the position vector sweeps out equal areas in equal times as the particle moves under the influence of the central force.

Question 49.
Why an astronaut has a sense of weightlessness in a satellite revolving around the Earth?
Answer:
For revolving around the Earth, the astronaut and the satellite require the centripetal force, and their weight is used up in providing the necessary centripetal force. So the astronaut feels weightlessness in space.

Question 50.
Why an astronaut in an orbiting spacecraft is not in zero-gravity although he is in a state of weightlessness?
Answer:
We know that acceleration due to gravity depends on the height, so there is some value of acceleration due to gravity at every point on the orbit of the spacecraft and his weight is used up in providing the necessary centripetal force for the orbital motion.

Gravitation Important Extra Questions Short Answer Type

Question 1.
Explain how the weight of the body varies en route from the Earth to the moon. Would its mass change?
Answer:
When a body is taken from Earth to the moon, then its weight slowly decreases to zero and then increases till it becomes \(\frac{1}{6}\)th of the weight of the body on the surface of the moon.

We know that mg_h = mg (1 – \(\frac{2 h}{R}\))

As h increases, g_h, and hence mg_h, decreases. When R = \(\frac{R}{2}\) the force of attraction of Earth is equal to the force of attraction of the moon.

Then g_h = 0, so mg becomes zero, and the value of g on the moon’s surface is \(\frac{1}{6}\)th of its value on the surface of Earth. Hence on increasing h beyond \(\frac{R}{2}\), mg starts increasing due to the gravity of the moon. f ts mass remains constant.

Question 2.
Among the known type of forces in nature, the gravitational force ¡s the weakest. Why then does ¡t play a dominant role in the motion of bodies on the terrestrial, astronomical, and cosmological scale?
Answer:
Electrical forces are stronger than gravitational forces for a given distance, but they can be attractive as well as repulsive, unlike gravitational force which is always attractive. As a consequence, the forces between massive neutral bodies are predominantly gravitational and hence play a dominant role at long distances. The strong nuclear forces dominate only over a range of distances of the order of 10^-14 m to 10^-15m.

Question 3.
Show that the average life span of humans on a planet in terms of its natural years is 25 planet years if the average span of life on Earth is taken to be 70 years.
Answer:
Take the distance between Earth and Sun twice the distance between Earth and planet. According to Kepler’s third law of planetary motion,

where T_e, T_R is the average life span on Earth and planet respectively.
R_g = distance between Earth and Sun.
R_p = distance between Earth and planet.
Here, R_e = 2R_p

Question 4.
Hydrogen escapes faster from the Earth than oxygen. Why?
Answer:
The thermal speed of hydrogen is much larger than oxygen. Therefore a large number of hydrogen molecules are able to acquire escape velocity than that of oxygen molecules. Hence hydrogen escapes faster from the Earth than oxygen.

Question 5.
In a spaceship moving in a gravity-free region, the astronaut will not be able to distinguish between up and down. Explain why?
Answer:
The upward and downward sense is due to the gravitational force of attraction between the body and the earth. In a spaceship, the gravitational force is counterbalanced by the centripetal force needed by the satellite to move around the Earth in a circular orbit. Hence in the absence of zero force, the astronaut will not be able to distinguish between up and down.

Question 6.
Why the space rockets are generally launched from west to east?
Answer:
Since the Earth revolves from west to east around the Sun, so when the rocket is launched from west to east, the relative velocity of the rocket = launching velocity of rocket + linear velocity of Earth. Thus the velocity of the rocket increases which helps it to rise without much consumption of the fuel. Also, the linear velocity of Earth is maximum in the equatorial plane.

Question 7.
Explain why the weight of a body becomes zero at the center of Earth.
Answer:
We know that the weight of a body at a place below Earth’s surface is given by
W = mg_d …. (i)
Where gd = acceleration due to gravity at a place at a depth ‘d’ below Earth’s surface and is given

From Eqn. (i) W = 0 at the center of Earth.
i.e., g decreased with depth and hence becomes zero at the center of Earth, so W = 0 at Earth’s center.

Question 8.
We cannot move even our little fingers without disturbing the whole universe. Explain why.
Answer:
According to Newton’s law of gravitation, every particle of this universe attracts every other particle with a force that is inversely proportional to the square of the distance between them. When we move our fingers, the distance between the particles changes, and hence the force of attraction changes which in turn disturbs the whole universe.

Question 9.
Explain why tennis ball bounces higher on hills than on plains.
Answer:
The value of acceleration due to gravity is lesser on hills than on the plains, so the weight of the tennis ball at hills is lesser than that on the plains and hence it re-bounces more. In other words, the force with which the Earth attracts the ball on hills will be lesser than that on the plains.

Question 10.
Why is the atmosphere comparatively rarer on some of the planets as compared to that on earth?
Answer:
The escape velocity of some of the planets is very small as compared to that on the surface of Earth. Most of these gases have their root mean square (r.m.s.) velocities more than the escape velocity on these planets and hence they have escaped from the surface of these planets and hence the atmosphere is rarer on some of the planets than on Earth.

Question 11.
Why moon has no atmosphere? Explain.
Answer:
An atmosphere means the presence of a mixture of a number of gases. The molecules of these gases are in the state of continuous random motion moving with different velocities. As the value of escape velocity On the surface of the moon is small (only 2.5 km s^-1), the molecules of gases with velocities greater than the escape velocity moved out of the atmosphere. As time passed, nearly all the molecules escaped from the moon’s atmosphere.

Question 12.
Under what conditions a satellite will be called geo-stationary?
Answer:
The following are the conditions to be fulfilled by a satellite to be geostationary:

1. The time period of the satellite around the Earth must be equal to the rotational period of the satellite i.e. 24 hours.
2. The direction of motion of the satellite must be the same as that of the Earth.
3. The height of the geostationary satellite must be about 36000 km.

Question 13.
What are the uses of Artificial Satellites?
Answer:
Following are some of the important uses of Artificial Satellites:

1. They are used as communication satellites to send messages to distant places.
2. They are used as weather satellites to forecast weather.
3. They are used to know the exact shape of Earth.
4. They are used to telecast T.V. programs to distant places.
5. They are used to explore the upper region of the atmosphere.

Question 14.
Under what condition, a rocket fired from Earth will launch an artificial satellite around Earth?
Answer:
Following are the basic conditions:

1. The rocket must take the satellite to a suitable height above the surface of Earth.
2. From the desired height, the satellite must be projected with a suitable velocity called orbital velocity.
3. In the orbital path of the satellite, the air resistance should be negligible so that its velocity does not decrease and it does not bum due to the heat produced.

Question 15.
The acceleration due to gravity on a planet is 1.96 ms^-2. If it is safe to jump from a height of 2m on the Earth, what will be the corresponding safe height on the planet?
Answer:
The safety of a person depends upon the momentum with which the person hits the planet. Since the mass of the person is constant therefore the maximum velocity (v) is the limiting factor.
In case of earth, v² = 2g_eh_e …. (i)
In case of planet, v² = 2g_ph_p …. (ii)
where h_e, h_p are safe heights of jumping from Earth and planet respectively,
Here, h_e = 2m; g_p = 1.96 ms^-2, ge = 9.8 ms^-2

∴ From (i) and (ii), we get
2g_e h_e = 2g_p h_p

Question 16.
Is it correct to state that we are living at the bottom of a gravitational well? Why?
Answer:
Yes. The gravitational force varies with distance from the center of Earth as shown in the fig. below. The graph clearly shows a minimum at a point on the surface of Earth. Thus, it is correct to state that we are living at the bottom of a gravitational well.

Question 17.
Prove that if two spheres of the same material, mass, and radius, are put in contact, the gravitational attraction between them is directly proportional to the fourth power of their radius.
Answer:
Let m = mass of each sphere.
R = radius of each sphere,
p = density of the material of the spheres.
∴ If F be the gravitational attraction between them, then according to Newton’s law of gravitation,


∴ From (1) and (2), we get

Question 18.
Prove that if the gravitational attraction of the Sun on the planets varies as nth power of the distance (of the planet from the Sun), then a year of the planet will be proportional to R^{(n + 1)/2}.
Answer:
Let m = mass of the planet
R = radius of its orbit around Sun
M = mass of the sun
V = orbital speed of the planet
Then,

Question 19.
The figure below shows four arrangements of three particles of equal masses:

(a) Rank the arrangements according to the magnitude of the net gravitational force on the particle labeled m, greatest first, and explain.
(b) In arrangement 2, in the direction of the net force closer to the line of length d or to the line of length D?
Answer:
(a) 1,2 and 4 tie, 3 (b) line d.
Explanation: (a) An arrangement (1), the forces exerted by both the particles are in the same direction. So these forces get add up to give maximum force. In arrangements (2) and (4), the angle between individual forces as well as the distances are the same. So the magnitudes of the net forces in (2) and (4) are the same and greater than in arrangement (3) and less than in (1).

In arrangement (3), the angle between the separate forces is maximum i.e. 180. So the net force is minimum.

(b) Due to the smaller distance, force is greater the net force always makes a smaller angle with the larger force as compared to the angle with a smaller force.

Question 20.
Why the atmosphere of Jupiter contains light gases (generally hydrogen) whereas the Earth’s atmosphere has little hydrogen gas?
Answer:
The escape velocity of Jupiter is much larger than the escape velocity of Earth. So to escape from the surface of Jupiter, a very large velocity is required. Since the thermal velocity of hydrogen gas molecules is lesser than the escape velocity of Jupiter, therefore hydrogen can’t escape from the surface of Jupiter.

Question 21.
Why does not an astronaut use a simple pendulum clock in a satellite revolving around the Earth?
Answer:
Acceleration due to gravity is zero inside a satellite therefore the time period of vibration of the simple pendulum
T = 2π \(\sqrt{\frac{l}{g}}\) will be infinity

So the pendulum will do not vibrate inside the satellite and hence the clock will not work. So astronaut does not use a simple pendulum clock in a satellite.

Question 22.
Show that Kepler’s Second law is the law of conservation of angular momentum.
Answer:
The second law states that the areal velocity is constant i.e. area covered by the radius vector is the same in equal intervals of time. If the velocity and radius at the time, t₁ is v₁ and r₁ while at another place these are v₂ and r₂ in the same time, then the area covered by the planet in these intervals are

This shows that the law leads to the conservation of angular momentum law.

Question 23.
Astronomical observations show that Mercury moves faster and Pluto slower, why is it so?
Answer:
Planets obey Kepler’s Third law of motion.

T_M = time of revolution of Mercury around Sun at distance R_M.
T_P = time of revolution of Pluto around Sun at distance R_P.


Pluto moves slower as compared to Mercury due to the reason that R_P > R_M.

Question 24.
Calculate the density of Earth.
Answer:
Let us assume the Earth to be a homogeneous sphere of radius R, density ρ, and mass M.

Question 25.
Find an expression for the torque on a body due to gravity. Show that this torque about the center of mass of a body is zero.
Answer:
Suppose a body is made up of a large number of particles of masses m₁, m₂, m₃, ….. etc. situated at r₁, r₂, r₃,… etc. positions from the center of mass of the body. Each particle is pulled by gravity with a force F = mg. Let this force on ith particle be f = mg. Since the position vector of this particle is r_1, hence the torque on this particle due to a national poll of the Earth is
τ_i = r_i × m_ig
Then total torque on the body

Then torque about the center of mass is eventually 0 as r_cm = 0 from the center of mass,
∴ τ = 0.

Question 26.
How do Kepler’s laws lead to Newton’s universal law of gravitation?
Answer:
Kepler’s laws are applicable to the motion of planets around the Sun. Almost all planets revolve around the Sun in nearly circular orbits.

Let m = mass of a planet.
M = mass of Sun.
r = radius of the circular orbit of the planet, around the Sun.
v = linear velocity of the planet in its orbit.
T = Time period of the planet.

The centripetal force required by the planet is.
F = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\)
But v = circumference of the orbit / period of revolution = \(\frac{2πr}{T}\)

This centripetal force is provided by the force of attraction between the Sun and the planet. According to Newton, the force of attraction between the planet and the Sun is mutual.

which is Newton’s law of gravitation.

Question 27.
Explain how the mass of the Sun can be determined by studying the motion of Earth around it.
Answer:
The Sun’s gravitational force provides the necessary centripetal force to the Earth for its revolution around the Sun in an orbit of radius r. Let the mass of Sun be M_s and that of Earth M_c. Thus centripetal force is then

where R = radius of orbit of Earth.
Let T = Time period of revolution of Earth around Sun, then

we know R, G, and T so the mass of the Sun can be found out by putting their values.

Question 28.
Derive an expression for the gravitational potential energy above the surface of Earth.
Answer:
Let the body of mass m be taken at a height h above the surface of Earth. At any instant of time t, it reaches at a distance x from the center of Earth. The work done in raising the body through dx is

Hence, the work done in taking the body from the surface of the Earth (x = R) to a height h above the earth’s surface (x = R + h) is given by


This work done is stored in the body in the form of gravitational
P.E. i.e. P.E. = W = mgh
P.E. above the surface of Earth = mgh.

Question 29.
What is the binding energy of the satellite?
Answer:
The minimum energy required to free a satellite from the gravitational attraction is called its binding energy. The binding energy is the negative value of the total energy of the satellite. Let a satellite of mass m be revolving around the earth of mass M and radius R.

∴ The total energy of satellite = P.E. + K.E.

Bindind energy of satellite = – (total energy of satellite)
\(\frac{GMm}{2R}\)

Question 30.
In a cavendish experiment, two spheres of mass 10 g each are suspended with a torsion rod of length 2m when two lead spheres of mass 10 mg each are brought near the suspended sphere as shown in the figure, the spheres are displaced through 2mm each. The torsional rod is deflected through an angle of 0.02 radian. Calculate the value of G if the torsional couple per unit twist of the suspension wire is 1.66 × 10^-4 Nm.

Answer:
Answer:
Force exerted by a bigger sphere on the small sphere is
F= \(\frac{GMm}{2R}\)
where r = separation between bigger and small spheres.
M = mass of the bigger sphere.
m = mass of the smaller sphere.

The force on the two sides produces torque and the suspension wire produces opposite torque = cθ = restoring couple produced.
where c = Torsional couple per unit twist.
θ = Twist

If l be the length of torsion rod, the deflecting couple
= Fl = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\) l

Since the rod is in equilibrium after the deflection
∴ deflecting couple = restoring couple

Gravitation Important Extra Questions Long Answer Type

Question 1.
(a) Derive the expression for the orbital velocity of an artificial Earth’s satellite. Also, derive its value for an orbit near Earth’s surface.
Answer:
Let m = mass of the satellite.
M, R = mass and radius of Earth.
h = height of the satellite above the surface of Earth.
r = radius of the robot of the satellite
= R + h.
v₀ = orbital velocity of the satellite.

The centripetal force \(\frac{\mathrm{mv}_{0}^{2}}{\mathrm{r}}\) required by the satellite to move in a circular orbit is proved by the gravitational force between satellite and the Earth.



If the satellite is close to the earth’s surface, then h ≈ 0

(b) Derive the expression for escape velocity of a body from the surface of Earth and show that it \(\sqrt{2}\) times the orbital velocity close to the surface of the Earth. Derive its value for Earth.
Answer:
Escape velocity is the minimum velocity with which a body is projected from Earth’s surface so as to just escape its gravitational pull or of any other planet. It is denoted by v_e.

Expression: Consider the earth to be a homogenous sphere of radius R, mass M, center O, and density p.
Let m = mass of the body projected from point A on the surface of Earth with v_el. v_e.

∴ K.E. of the body at point A = \(\frac{1}{2}\) mv_e² …(i)
Let it reaches a point P at a distance x from O. If F be the gravitational force of attraction on the body at P, then

F = \(\frac{\mathrm{GMm}}{\mathrm{x}^{2}}\) …(ii)

Let it further moves to Q by a distance dx.
If dW be the work done in moving from P to Q, then

If w be the total work done in moving the body from A to ∞,
Then

∴ According to the law of conservation of energy
K.E. = RE


Relation between v_e and v_o: Also we know that the orbital velocity around Earth close to its surface is given
by v₀ = \(\sqrt{gR}\)
and ve = \(\sqrt{2gR}\) = \(\sqrt{2}\) \(\sqrt{gR}\)
= \(\sqrt{2}\)v₀
Hence proved.

Question 2.
(a) Explain Newton’s law of gravitation.
Answer:
We know that Newton’s law of gravitation is expressed mathematically as:

where r̂ = unit vector along F
It was found that law is equally applicable anywhere in the universe between small and big objects like stars and galaxies. The value of G remains the same everywhere. (Some scientists have claimed that as the size of the object under consideration becomes big like a galaxy, the value of G also changes). Hence this law of Newton is also called Newton’s universal law of gravitation.

The force of attraction is called the force of gravitation or gravitational force. This force is only attractive and is never repulsive. The force is both ways i.e., particle 1 attracts particle 2 and so does particle 2 attracts particle 1.
Hence F₁₂ = – F₂₁.

The law is a direct outcome of the study of acceleration of bodies. Newton wondered how Moon revolves around the Earth or other planets revolve around the Sun. His calculations showed that the Moon is accelerated by the same amount as does any other object towards the Earth.

His famous narration of the apple falling from the tree and noticing every other object fall towards Earth led to the announcement of his famous law of gravitation about 50 years later in his book ‘Principia’.

Out of the known forces in nature, the Gravitational force is the weakest, yet it is the most apparent one as it acts for long distances and between objects which are visible to us. The law of gravitation has been used to determine the mass of heavenly bodies. It has been used to study the atmosphere of planets. Man-made satellites remain in the orbits due to gravitation.

(b) Define gravitational field intensity. Derive its expression at a point at a distance x from the center of Earth. How is it related to acceleration due to gravity?
Answer:
The gravitational field intensity at a point is defined as the force acting on a unit mass placed at that point in the field.

Thus, the gravitational field intensity is given by:
E = \(\frac{F}{m}\)
Now at distance x from the center of Earth, the gravitational force is

So, the intensity of the gravitational field at the surface of Earth is equal to the acceleration du&to gravity.

Question 3.
Discuss the variation of acceleration due to gravity with:
(a) Altitude or height
(b) Depth
(c) Latitude i.e. due to rotation of Earth.
Answer:
Let M, R be the mass and radius of the earth with center O.
g = acceleration due to gravity at a point
An on Earth’s surface.

(a) Variation of g with height: Let g_0h be the acceleration due to gravity at a point B at a height h above the earth’s surface

If h << R, then using Binomial Expansion, we get

Thus, from Eqn. (3), we conclude that acceleration due to gravity decreases with height.

(b) With depth: Let the Earth be a uniform sphere.

Let g_d = acceleration due to gravity at a depth d below earth’s surface i.e. at point B.

Let ρ = density of Earth of mass M.

Also, let M’ = mass of Earth at a depth d, then

From equation (iv), we see that acceleration due to gravity decreases with depth.
Special case: At the center of Earth, d = R
∴ g_d = 0

Hence an object at the center of Earth is in a state of weightlessness.

(c) Variation of g with latitude:
Let m = mass of a particle at a place P of latitude X.
ω = angular speed of Earth about axis NS.

As the earth rotates about the NS axis, the particle at P also rotates and describes a horizontal circle of radius r,
where r = PC = OP cos λ, = R cos λ

Let g’ be the acceleration due to gravity at P when the rotation of Earth is taken into account. Now due to the rotation of the earth, two forces that act on the particle at P are:

1. Its weight mg, acting along with PO.
2. Centrifugal force mroo2 along PO’.

∴ The angle between them = 180 – λ
∴ According to the parallelogram law of vector addition

[As \(\frac{\mathrm{R} \omega^{2}}{\mathrm{~g}}\) is very small (= \(\frac{1}{289}\))so its square and higher powers are neglected.]

Using binomial expansion, we get

⇒ g decreases with the rotation of the earth.

1. At poles, λ = 90°, ∴ g’ = g_p = g
2. At equator, λ = 0, g’ = g_e = g- Rω².

Clearly g_p > g_e.

Numerical Problems:

Question 1.
At what height from the surface of Earth will the value of g be reduced by 36% from the value at the surface? The radius of Earth, R = 6400 km.
Answer:
Let h be the height above the surface at which g reduces by 36% i.e. becomes 64% of that at the surface i.e.

Question 2.
A mass of 5 kg is weighed on a balance at the top of a tower 20 m high. The mass is then suspended from the pan of the balance by a fine wire 20 m long and is reweighed. Find the change in the weight, R = 6400 km.
Answer:
h = 20 m
m = mass = 5 kg
R = 6400 km = 64 × 10⁵m
g = 9.8 ms^-2

As h < R, so from relation,

Now weight at the foot of tower, W = mg
Now weight at the top of tower, W_h = mg_h

Question 3.
How much faster than its present rate should the Earth rotate about its axis in order that the weight of the body on the equator may be zero? What will be the duration of the day? The radius of Earth, R = 6400 km.
Answer:
We know that the value of ‘g’ at latitude λ is
g_λ = g – R ω² cos²λ
at equator λ = 0,
∴ cos 0 = 1
∴ g_λ = g – Rω²

Let ω₁ = new angular speed of rotation so that weight at equator becomes zero

in equation (1), we get

i.e. the Earth must rotate 17 times faster thair its present speed. Now the duration of the day 24 hours i.e. earth makes one rotation in 24 hours. When it rotates 17 times faster, it will make 17 rotations in 24 hours

∴ Time for 1 rotation (Duration of Day) = \(\frac{24}{17}\) = 1.412 hours.

Question 4.
Show the moon would escape if its speed were increased by 42%.
Answer:
Let M = mass of Earth.
m = mass of the moon,
r = radius of the circular orbit of the moon around the Earth.
v_o = orbital velocity of the moon.

The centripetal force needed by moon = Gravitational force between the Earth and moon

∴ % increase in the velocity of the moon

Question 5.
If the Earth has a mass 9 times and a radius twice of the planet Mars, calculate the minimum velocity required by a rocket to pull out of the gravitational force of Mars. Escape velocity on the surface of Earth is 11.2 km s^-1.
Answer:
Let Mm and be the mass and radius of Mars,
and M, R = mass and radius of Earth.

Also, let v and Vm be the escape velocities from Earth and Mars respectively.

Question 6.
What would be the duration of the year ¡f the distance between the Earth and the Sun gets doubled?
Answer:
Let T₁ = time period of Earth about the Sun when the distance between Sun and Earth is R and T₂ = time period of Earth about the Sun when the distance between Earth and Sun is 2R.

Now using the relation,

Question 7.
The period of the moon around Earth is 27.3 days and the radius of its orbit is 3.9 × 10⁵ km. Find the mass of Earth, G = 6.67 × 10^-11 Nm2 Kg^-2.
Answer:
T = time period = 27.3 days
= 27.3 × 24 × 60 × 60s.

r = radius of orbit
= 3.9 × 10⁵ km = 3.9 × 10⁸m.

G = 6.67 × 10^-11 N m2 kg^-2.
M = mass of Earth = ?

Let m, v be the mass and linear velocity of the moon. Then the centripetal force to the moon is provided by the force of attraction between Earth and the moon.

Question 8.
Find the percentage decrease in weight of a body when taken 16 km below the surface of Earth. Take the radius of Earth = 6400 km.
Answer:
Here, R = 6400 km, d = 16km

If m = mass of the body, then

Question 9.
A mass M is broken into two parts m and M – m. How are m and M related so that the force of gravitational attraction between the two parts is maximum?
Answer:
Let r = distance between two parts i.e. m and M – m
If F be the gravitational attraction between m and M – m, then from Newton’s law of gravitation,

eqn. (i) may be rewritten as:

∴ each piece has equal mass.

Aliter:
For F to be maximum,

Question 10.
A satellite orbits the Earth at a height of 500 km from its surface.
Calculate (i) K.E.
(ii) P.E.
(iii) Total energy.
Mass of satellite is 300 kg, mass of Earth is 6 × 10²⁴ kg, radius of Earth = 6.4 × 10⁶ m, G = 6.67 × 10^-11 Nm² kg^-2. Will your answer alter if the Earth were to shrink suddenly to half its size?
Answer:


If the earth shrinks suddenly to half its radius (R becomes R/2) but r = (R + h) remains unchanged, then the answer will not alter.

Question 11.
If a body is projected with a velocity v greater than ve (escape velocity from Earth’s surface), find its velocity in interstellar space.
Answer:
Let v’ be the velocity of the body of mass m in interstellar space where the gravitational field of Earth is zero; so the P.E. of the body is also zero.

∴ According to the law of conservation of energy,
we have, K.E. + RE. at the surface of Earth

Question 12.
What will be the acceleration due to gravity on the surface of the moon if its radius is 1/4th of the radius of Earth and its mass l/80th of the mass of Earth?
Answer:The value of acceleration due to gravity is g =\(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)

Question 13.
Consider an Earth satellite so positioned that it appears stationary to an observer on Earth and serves the purpose of a fixed relay station for intercontinental transmission of television and other communications. What should be the height at which the satellite should be positioned and what would be the direction of its motion? (Radius of Earth R = 6400 km.)
Answer:
Suppose the satellite is stationed at height h from the surface of the Earth, then

Question 14.
If the moon followed a circular orbit of radius r around the Earth with a uniform angular velocity co, so that ω²r² = gR², where R is the radius of the Earth and g the acceleration due to gravity. If r = 60R and the period of revolution of the moon around the Earth is 27.3 days. Find R.
Answer:

Question 15.
The mass of asteroid Ceres is approximately 7 × 10²⁰ kg and its diameter is 1100 km. What is the value of acceleration due to gravity at its surface? What would be the weight of an 80 kg astronaut on this asteroid?
Answer:
The radius of the asteroid Ceres,

∴ Weight of astronaut, W = mg = 80 × 0.15 ms^-2 = 12 N.

Question 16.
The mass of the Sun is 2 × 10³⁰ kg and its radius 7 × 10⁸ m. Calculate the rate of emission of radiation from it if its radius shrinks at the rate of 1 × 10⁴ ms^-1.
Answer:
The self-energy of the Sun, considering it spherical in shape, is given by

Question 17.
Two stars of mass 3 × 10³¹ kg each, in a double star, rotate about their common center of mass 10¹¹ m part
(i) Calculate their common angular speed.
Answer:
Let one-star move in a circular orbit of radius R, then gravitational pull provides the necessary centripetal force. Also, the distance between two stars = x, and they have equal mass then x = 2R.
Therefore,

Substituting the given values, we have

(ii) If a meteorite passes through its center of mass moving at right angles to the line joining the stars. In order to escape from the gravitational field of the double star what should be the speed of the meteorite?
Answer:
The meteorite can escape from the gravitational field if the sum of its K.E. and P.E. due to the two stars is greater than 0 i.e.

Question 18.
Neglecting the presence of other planets and satellites, calculate the binding energy of the Sun-Earth system. Mass of Earth ME = 6 × 10²⁴ kg, mass of Sun = 1.98 × 10³⁰ kg, Orbital radius of Earth R= 1.5 × 10¹¹ m.
Answer:
The binding energy is equal to the amount of energy spent in bringing the Earth-Sun system from infinity to the distance R. In other words, this is equal to the energy required to separate them to infinity hence it is equal to (P.E.)g

Question 19.
If the radius of the Earth decreases by 10%, the mass remaining unchanged, what will happen to the acceleration due to gravity?
Answer:
Here, let M, R be the mass and radius of the earth. If g be the acce. to due to gravity on earth’s surface, then

If g’ be the new value of acceleration.

Question 20.
The ratio of the radii of the planets P₁ and P₂ is k and the ratio of the acceleration due to gravity on them is r. Calculate the ratio of the escape velocities from them.
Answer:
Let r₁ and r₂ be the radii of the planet P₁ and P₂ respectively having respective accelerations due to gravity g_1, and g₂.

If v₁ and v₂ be the escape velocities from P₁ and P₂ respectively, then using the relation,

Question 21.
Calculate the temperature at which oxygen molecules can escape from the surface of Earth. Assume the radius of Earth as 6.4 × 10⁶ m and g = 9.8 ms^-2, the universal gas constant, R = 8.4 J mol^-1 k^-1.
Answer:
Here, R_e = radius of Earth = 6.4 × 10⁶ m
If a v_e be the escape velocity of oxygen molecules from Earth’s surface, then


According to the kinetic theory of gases, the most probable velocity of the molecules of a gas is given by,

where M = molecular weight of the gas = 32 × 10^-3 kg for O₂.
R = 8.4J mol^-1 k^-1
For the escape of the gas molecules,

Question 22.
Find the gravitational force of attraction on a uniform rod of length L and mass m due to uniform earth as shown in Fig. How the rod will behave if L << r.

Answer:
Let M, R be the mass and radius of earth respectively. As the earth is uniform, so its whole mass may be supposed to be concentrated at its center O.

Let dF be the force due to earth on the mass element dx at a distance x from O.

If F be the total force on the rod, then


Now if the rod is very small as compared to its distance from the earth i.e. if r >> L, then r + L ≈ r.

∴ From (2), we get F = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)
i.e. the rod behaves as a point mass lying at a distance r from the center of the earth.

Question 23.
Calculate the scale reading of a spring balance having a body suspended to it and is in a ship sailing along the equator with a speed v.
Answer:
Let m = mass of the body suspended
W₀ = scale reading of the spring balance when the ship is at rest

Let ω = angular speed of rotation of the Earth of radius R
∴ The value of g at equator is given by
g_θ = (g – Rω²)
∴ W₀ = mg_θ = m(g – rω²) ….(1)

when the ship sails from west to east with the speed v on Earth’s surface, then its angular speed \(\frac{v}{R}\) gets added to ω i.e. ω’ = ω + \(\frac{v}{R}\)


similarly if the ship sails from east to west, then the scale reading is given by

Question 24.
Calculate the minimum work done in bringing a spaceship of mass 1000 kg from the surface of Earth to the moon.
Answer:
Let M₁, M₁  = masses of earth and moon respectively.
R₁, R₂ = radius of earth and moon respectively,
m = mass of spaceship.

If U₁ and U₂ be the gravitational P.E. of the spaceship on Earth and the moon respectively, then

The total work (W) will have to be done on the spaceship first against the gravity of Earth and-then against the gravity of the moon through the zero-gravity region while going from the Earth to theme on.

Question 25.
Taking moon’s period of revolution about the Earth as 30 days, calculate its distance from the Earth;
G = 6.67 × 10^-11 Nm² Kg^-2, M = mass of Earth = 6 × 10²⁴ kg.
Answer:
Here, T = 30 days = 30 × 24 × 3600s
= 30 × 86400 s
G = 6.67 × 10¹¹ Nm²Kg^-2
M = 6 × 10²⁴ kg

Let m = mass of moon.
Let x = distance of moon from Earth = ?

Here, the force of attraction between moon and Earth provides the centripetal force to the moon i.e.

Value-Based Type:

Question 1.
Suresh was struggling to understand Kepler’s second law of planetary motion. Then his friend Raman who came to him explained how the planet moves around the sun obeying Kepler’s law of planetary motion.
(a) Comment upon the values of Raman.
Answer:
Raman shares his friends and wants to improve his knowledge in the subjects, has a concern towards his friends.

(b) State Kepler’s laws of planetary motion.
Answer:
Kepler’s 1st law of planetary motion: Every planet revolves around Sun in an elliptical orbit with Sun at one of its foci. BacondlawsThe radius vector joining the center of Sun and planet sweeps out equal areas in equal intervals of time i.e. areal velocity of the planet around the Sun always remains constant. Third law: The square of the time period T of revolution of a planet around the Sun is proportional to the cube of the semi-major axis R of its elliptical orbit i.e.
T2 ∝ R3

Question 2.
Suresh went to a picnic on a hill station. The teacher told all the students to weigh by weighing machine before going to the hill station. His weight was 56 Kg. When we reached the hill station along with his friends, our teacher again told us to find their weight using a weighing machine installed in front of a shopping mall. He found that his weight was lesser than 56 Kg i.e 52 Kg, He was surprised and asked the teacher the reason behind it. The teacher explained that the acceleration due to gravity decreases as we go up from the ground. Hence, your weight will be lesser than on the ground.
(i) What values of Suresh are displayed here?
Answer:
Awareness, intelligence, and logic.

(ii) Why does the teacher tell everyone to find their weight?
Answer:
The teacher wanted to explain the acceleration due to gravity through the demonstration method.

(iii) If a body is taken to a height equal to the radius of the earth from its surface, how will the weight of a body change?
Answer:
We know that:


Hence, the weight of the body will reduce to one-fourth of its original weight on the surface of the earth.

Question 3.
Two friends Jagat and Ram are discussing escape velocity, Jagat told that if a body is projected vertically upwards with escape velocity, it will cross the earth’s gravitational field and will never come back to the earth’s surface again. Ram was not convinced with Jagat. So, they went to ask their physics teacher about escape velocity. The teacher explained to him about escape velocity:
(i) What values are displayed by Jagat and Ram? Is Jagat’s definition was correct?
Answer:
Yes, Jagat’s definition was correct.
Values are: Curious to know, intelligent, co-operative, helping and sharing their ideas.

(ii) What is the value of escape velocity?
Answer:
We know that:
Ve= \(\sqrt{2 \mathrm{~g} \mathrm{R}_{\mathrm{E}}}\)
[ On substituting the values g and RE]
= 112 km / s
This is the value of escape speed, sometimes loosely called the escape velocity.

Question 4.
Abhinav and Ankit are in the same section of class 11. Ankit fell sick for two days. So, he could not attend the classes. In two days his physics teacher explained about “Earth Satellites” and “Weightlessness”. Abhinav explained these two topics to Ankit later on Sunday.
(i) Which values are displayed by Abhinav?
Answer:
The values displayed by Abhinav are:
Helping nature, Ability, and Willingness to explain, patience

(ii) Find an expression for the weight of a body at the center of the Earth.
Answer:
We know that the value of acceleration due to gravity at a depth “d” below the surface of the earth is given by at the center of the earth

∴ Weight of a body at the center of the earth mg’ = m × o = o
So, the body will be weightless.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 7 System of Particles and Rotational Motion. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 7 Important Extra Questions System of Particles and Rotational Motion

System of Particles and Rotational Motion Important Extra Questions Very Short Answer Type

Question 1.
Can the geometrical centre and C.M. of a body coincide? Give examples.
Answer:
Yes, C.M. and geometrical centre may coincide when the body has a uniform mass density, e.g. C.M. and geometrical centre are the same in case of a sphere, cube and cylinder etc.

Question 2.
How does the M.I. change with the speed of rotation?
Answer:
M.I. is not affected by the speed of rotation of the body.

Question 3.
Under what conditions, the torque due to an applied force is zero?
Answer:
We know that τ = rF sin θ. If θ = 0 or 180,
or
r = 0, then τ = 0, r = 0 means the applied force passes through the axis of rotation.

Question 4.
Is it correct to say that the C.M. of a system of n-particles is always given by average position vectors of the constituent particles? If not, when the statement is true?
Answer:
No, this statement is true when all the particles of the system are of the same mass.

Question 5.
A cat is able to land on her feet after a fall. Which principle of Physics is being used by her?
Answer:
Principle of conservation of angular momentum.

Question 6.
What is conserved when a planet revolves around a star?
Answer:
Angular momentum.

Question 7.
If no external torque acts on a body, will its angular velocity remain conserved?
Answer:
No, it is the angular momentum that will be conserved.

Question 8.
A body is rotating at a steady rate. Is a torque acting on the body?
Answer:
No, torque is required only for producing angular acceleration.

Question 9.
What is the other name for angular momentum?
Answer:
Moment of momentum.

Question 10.
Out of two spheres of equal masses, one rolls down a smooth inclined plane of height h and the other is falling freely through height h. In which case, the work done is more?
Answer:
The same work is done in both cases.

Question 11.
Many great rivers flow towards the equator. What effect does the sediment they carry to the sea have on the rotation of the Earth?
Answer:
This will increase the M.I. of the Earth about its own axis and hence the time of rotation of Earth will increase.

Question 12.
Can the mass of a body be considered concentrated at its centre of mass for purposes of computing its rotational inertia?
Answer:
No, the distribution of mass is extremely important in the calculation of M.I.

Question 13.
On what factors does the M.I. of a body depend?
Answer:
It depends on:

1. Position of the axis of rotation.
2. Way of distribution of mass about the axis of rotation.
3. Mass of the body.

Question 14.
Should there exist mass at the location of C.M. of a system? Give an example.
Answer:
No, e.g. the C.M. of a ring is at the centre where there is no mass.

Question 15.
Should the C.M. of a body necessarily, lie inside the body? Explain.
Answer:
No, it may lie outside the body. In the case of the semicircular ring, it is at the centre which is outside the ring.

Question 16.
What is the position vector of C.M. of two particles of equal masses?
Answer:
It is the average of the position vectors of the two particles.

Question 17.
If one of the particles is heavier than the other, to which side will their C.M. shift?
Answer:
It will shift closer to the heavier particle.

Question 18.
What is an isolated system?
Answer:
An isolated system is that on which no external force is acting.

Question 19.
Why do we prefer to use a wrench with a long arm?
Answer:
The turning effect of a force is τ = r × F. When the arm of the wrench is long, r is larger. So smaller force is required to produce the same turning effect.

Question 20.
What is the rotational analogue of mass and force?
Answer:
M.I. and torque are the respective rotational analogue.

Question 21.
Is the radius of the gyration of a body a constant quantity? Why?
Answer:
No. It depends upon the position of the axis of rotation and also on the distribution of mass of the body about this axis.

Question 22.
Two solid spheres of the same mass are made of metals of different densities. Which of them has a larger M.I. about a diameter?
Answer:
The sphere of metal with smaller density shall be bigger in size and hence it will have a larger M.I.

Question 23.
A solid cylinder is rolling without slipping on an inclined plane. What is the torque provided by the weight of the cylinder, about the C.M. of the cylinder?
Answer:
Zero, This is because the line of action of the weight passes through the C.M.

Question 24.
A solid cylinder is rolling without slipping on an inclined plane. What is the torque provided by the weight of the cylinder, about the C.M. of the cylinder?
(a) What is the torque provided by the normal reaction? Why?
Answer:
Zero as the line of action of the force passes through the C.M.

(b) Which force causes the cylinder to rotate about its C.M.?
Answer:
Force of friction

(c) Through which point the axis of rotation passes?
Answer:
Point of contact.

(d) What is the instantaneous velocity of the point of contact?
Answer:
Zero.

(e) What is the acceleration of the cylinder rolling down the inclined planed.
Answer:
a = \(\frac{2}{3}\) g sin θ

(f) What is the condition for rolling without slipping?
Answer:
\(\frac{1}{3}\)tan θ < μ_s.

Question 25.
Give an example of rigid body motion in which the centre of mass of the body is in motion.
Answer:
The motion of a cylinder rolling down an inclined plane is-the required example.

Question 26.
Give an example of rigid body motion in which the centre of mass of the body remains at rest.
Answer:
The motion of a point mass tied to a string and wound on a cylinder capable of rotating without friction about its own axis is the required example.

Question 27.
The angular speed of a body changes from to, of oo2 without applying a torque but due to changes in M.I. Find the ratio of the radii of gyration in the two cases.
Answer:

Question 28.
A disc is recast into a hollow and thin cylinder of the same radius. Which will have larger M.I.? Explain.
Answer:
M.I. of the cylinder will be larger because most of its mass is located away from the axis of rotation as compared to that of the disc.

Question 29.
Angular momentum of a system is conserved if its M.I. is changed. Is its angular K.E. also conserved?
Answer:
No, as I change, K.E. also changes and hence it does not remain conserved.

Question 30.
If a body is rotating, is it necessarily being acted upon by an external torque.
Answer:
No. Torque is required only for producing angular acceleration.

Question 31.
Can a torque be balanced by a single force?
Answer:
No.

Question 32.
To cut a tree, why we often make a cut on the side facing the direction in which we wish the tree to fall?
Answer:
It is done so that the weight of the tree applies torque about the cut and thus the tree falls in that direction.

Question 33.
About which axis the moment of inertia of a body is minimum?
Answer:
The moment of inertia of a body is minimum about the axis passing through the centre of mass of the body.

Question 34.
Is the moment of inertia a vector quantity?
Answer:
No, it is a scalar quantity.

Question 35.
What are the dimensions of a moment of inertia?
Answer:
The dimensions of the moment of inertia are one in mass, two in length and zero in time as its dimensional formula is [M L² T^o].

Question 36.
Can all magnitudes of angular displacement be treated as vectors?
Answer:
No, only infinitesimally small magnitudes of the angular displacement can be treated as vectors.

Question 37.
Can all magnitudes of angular velocity be treated as vectors?
Answer:
Yes, all magnitudes of instantaneous angular velocity can be treated as vectors, but it may not be possible to treat all magnitudes of average angular velocity as vectors.

Question 38.
Does the moment of inertia of a rigid body change with the speed of rotation?
Answer:
No, as it is independent of the speed of rotation of the body.

Question 39.
Can θ, ω and α be expressed in degrees instead of radians in the rotational kinematic equations?
Answer:
Yes, as it makes no difference whether we express them in radians or in degrees.

Question 40.
Does the radius of gyration depend on the angular speed of rotation of the body?
Answer:
No, it is independent of the angular speed of rotation of the body.

Question 41.
How does the ice skater or an acrobat takes the advantage of the law of conservation of the angular momentum?
Answer:
They do so by folding or extending their arms and legs and thus change their moment of inertia which causes a decrease or an increase in their speed of .pinning.

Question 42.
Why there are two propellers in the helicopter?
Answer:
The two propellors help in making the helicopter fly at the same level. If there is only one propeller in it, then it may begin to rotate in a direction opposite to that of the propeller so as to conserve the angular momentum.

Question 43.
A homogenous disc is revolving about its axis which is stationary? Is the disc possessing linear momentum? Why?
Answer:
No, it is zero as the momentum of one half of the disc is equal and opposite to that of the other half.

Question 44.
Does the disc in A homogenous disc is revolving about its axis which is stationary? Is the disc possessing linear momentum? Why possesses angular momentum?
Answer:
Yes, it possesses angular momentum.

Question 45.
No torque acts on a body. Should its angular velocity be conserved? Why?
Answer:
No, in absence of torque, angular momentum remains conserved and not the angular velocity.

Question 46.
A particle revolves uniformly along a circle (on a smooth horizontal table) by means of a string connected to it. Does its angular momentum changes from its initial value if the string is cut suddenly?
Answer:
No, the particle flies away tangentially, keeping angular momentum conserved as no external torque acts on the particle.

Question 47.
Is the angular momentum of a comet revolving around a massive star in a highly elliptical orbit constant over the entire orbit?
Answer:
Yes, the force acting on the comet is radial and hence there is no change in its angular momentum.

Question 48.
What is the significance of the C.M. of the system of particles?
Answer:
It helps us in describing the behaviour of a macroscopic body in terms of the laws developed for microscopic bodies.

Question 49.
Does the acceleration of a cylinder rolling down an inclined plane depend upon the mass of the cylinder?
Answer:
No.

Question 50.
When there is no external torque acting on a rotating body which of the following quantities can change?
(i) angular acceleration
(ii) angular momentum
(iii) angular speed.
Answer:
Both angular acceleration and angular momentum do not change, but the angular speed may change if the M.I. is allowed to change.

System of Particles and Rotational Motion Important Extra Questions Short Answer Type

Question 1.
What is the difference between the centre of gravity and C.M.?
Answer:
C.G.: It is the point where the whole of the weight of the body is supposed to be concentrated i.e. on this point, the resultant of the gravitational force on all the particles of the body acts.
C.M.: It is the point where the whole of the mass of the body may be supposed to be concentrated to describe its motion as a particle.

Question 2.
There are two spheres of the same mass and radius, one is solid and the other is hollow. Which of them has a larger moment of inertia about its diameter?
Answer:
The hollow sphere shall have greater M.I., as its entire mass is concentrated at the boundary of the sphere which is at maximum distance from the axis.

Question 3.
What shall be the effect on the length of the day if the polar ice caps of Earth melt?
Answer:
Melting of polar ice caps will produce water spread around the Earth going farther away from the axis of rotation that will increase the radius of gyration and hence M.I. In order to conserve angular momentum, the angular velocity ω shall decrease. So the length of the day (T = \(\frac{2 \pi}{\omega}\)) shall increase.

Question 4.
If only an external force can change the state of motion of the C.M. of a body, how does it happen that the internal force of brakes can bring a vehicle to rest?
Answer:
The internal force of brakes converts the rolling friction into sliding friction. When brakes are applied, wheels stop rotating. When they slide, the force of friction comes into play and stops the vehicle. It is an external force.

Question 5.
What do you understand by a rigid body?
Answer:
A rigid body is that in which the distance between all the constituting particles remains fixed under the influence of external force. A rigid body thus conserves its shape during its motion.

Question 6.
Distinguish between internal and external forces.
Answer:

1. The mutual forces between the particles of a system are called internal forces.
2. The forces exerted by some external source on the particles of the system are called external forces.

Question 7.
Two equal and opposite forces act on a rigid body. Under what conditions will the body (a) rotate, (Z>) not rotate?
Answer:
Two equal and opposite forces acting on a rigid body such that their lines of action don’t coincide constitute a couple. This couple produces a turning effect on the body. Hence the rigid body will rotate. If the two equal and opposite forces act in such a way that their lines of action coincide, then the body will not rotate.

Question 8.
(a) Why is it easier to balance a bicycle in motion?
Answer:
The rotating wheels of a bicycle possess angular momentum. In the absence of an external torque, neither the magnitude nor the direction of angular momentum can change. The direction of angular momentum is along the axis of the wheel. So the bicycle does not get tilted.

(b) Why spokes are fitted in the cycle wheel?
Answer:
The cycle wheel ¡s constructed in such a way so as to increase the M.I. of the wheel with minimum possible mass, which can be achieved by using spokes and the M.I. is increased to ensure the uniform speed.

Question 9.
A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The C.M. of the rod is at a distance x from A. Find the normal reactions at knife edges A and B.
Answer:
Let RA and RB be the normal reactions at points A and B respectively.

As the rod in is an equilibrium position, so the sum of moments of the forces about the knife edges must be equal to zero.

∴ Taking moments of forces about point A, we have

Question 10.
What are the essential features of angular momentum?
Answer:
Following are the essential features of angular momentum:

1. The angular momentum of a particle with respect to a point gives an idea of the strength of its rotational tendency about that point.
2. The magnitude of the angular momentum is defined in terms of mass and velocity of the particle and its distance from the reference point i. e. L = m v r.
3. The vector concept of the angular momentum is useful. Its direction is the axial direction given by the right-hand rule. The direction of L is ⊥ to the plane containing r and v.

Question 11.
(a) What is the physical significance of M.I.?
Answer:
The inability of a body to change its state of uniform rotation about an axis is called rotational inertia or M.I. of the body.
It plays the same roll in rotatory motion as is being played by the mass in translational motion i.e. it is a rotational analogue of mass.

(b) Define M.I. of a body rotating about an axis.
Answer:
M.I. of a body about a fixed axis of rotation is defined as the sum of the products of the masses and square of the perpendicular distances of various constituent particles from the axis of rotation.

Question 12.
Define the radius of gyration of a body rotating about an axis.
Answer:
It is defined as the ⊥ar distance of the point from the axis of rotation at which if the whole mass of the body is supposed to be concentrated then its M.I. about the given axis remains the same as with the actual distribution of mass. It is denoted by K.

Question 13.
Derive the expression for the radius of gyration.

Answer:
Let M = total mass of a rigid body rotating about ZZ’ axis.
Let it is made up of n particles each of mass m and situated at Tar
distances r₁, r₂, …. and rn from the axis of rotation.
∴ M = mn …. (i)

If I am its M.I. about ZZ’ axis,
Then by def. of M.I.,

Also by definition of K,
I = MK² ….(iii)
∴ from (ii) and (iii), we get

Question 14.
Show that in the absence of an external force the velocity of the C.M. of a system remains constant.
Answer:
Let us consider a body of mass m whose C.M. is moving with a velocity v and external force is zero. The equation of motion of the C.M. can be written as

i.e. in the absence of external force, the C.M. moves with a constant speed along a straight line. If R0 be the position vector of the C.M. at time t = 0, then the position vector of the C.M. after the time t is given by
R(t) = R₀ + vt.

Question 15.
Define Torque. What is its physical significance?
Answer:
It is defined as the turning effect of a force about the axis of rotation or it is the moment of a force about the axis of rotation.
i.e τ = Fd
where F = force applied on a body.
d is the ⊥ar distance of the line of action of the force from the axis of rotation.

Mathematically in vector form, τ may be expressed as
τ = r × F

i.e. it is the cross product of the position vector r and Force F

Note: d is called lever arm of the force
i.e. Torque = Force × lever arm

Question 16.
There is a stick half of which is wooden and half is of steel. It is pivoted at the wooden end and force is applied at the steel end at right angles to its length. Next, it is pivoted at the steel end and the same force is applied at the wooden end. In which case is the angular speed greater and why?
Answer:
We know that the greater the angular acceleration greater is the angular speed. Also α = \(\frac{τ}{I}\)
In the former case, M.I. is greater than in the latter case (steel being heavier than wood).

Thus angular acceleration in the 2nd case is greater than in the 1st case and hence the angular speed.

Question 17.
How would you distinguish between a hard-boiled egg and a raw egg each spinning on a tabletop?
Answer:
The raw egg will have greater M.I. as compared to the boiled egg because the mass of the raw egg tries to move away from the axis of rotation.

We know that α = \(\frac{τ}{I}\), so the angular acceleration is inversely proportional to the M.I. as the boiled egg will spin with greater speed than the raw egg.

Question 18.
Using the expression for power and K.E. of rotational motion, derive the relation τ = Iα.
Answer:
We know that power is given by
P = τ ω
Also, we know that,

Question 19.
Equal torques are applied on a hollow cylinder and hollow sphere, both having the same mass and radius. The cylinder rotates about its axis and the sphere rotates about its diameter. Which one will acquire greater speed and why?
Answer:
The speed of rotation depends upon the angular acceleration produced.

where α₁ and α₂ are angular accelerations of hollow-cylinder and hollow sphere respectively.

The sphere acquires greater speed than the cylinder as α is more for it and ω is directly proportional to α.

Question 20.
A thin wheel can stay upright on its rim for a considerable time when rolled with a considerable velocity, while it falls from its upright position with the slightest disturbance, when stationary. Explain.
Answer:
When the wheel is still and standing upright on the rim, the equilibrium is unstable. But when the wheel is rolling it possesses an angular momentum in the horizontal direction which is a conserved quantity of the motion. The angular momentum does not change unless the force of friction slows down the angular velocity.

Greater is the velocity, greater is the angular momentum and hence greater internal torque is needed to change the angular momentum. When the angular velocity tends to zero, the angular momentum also tends to zero, so even with little disturbance, the angular momentum can be changed.

Question 21.
Three homogeneous rigid bodies: a solid sphere, a solid cylinder and a hollow cylinder are placed at the top of an inclined plane. If they all are released from rest at the same elevation and roll without slipping, which one reaches the bottom first and which one reaches last?
Answer:
Let a₁, a₂, a₃ be their respective linear accelerations respectively.


∴ solid sphere will reach first and hollow cylinder reaches last.

Question 22.
Three uniform and thin rods each of mass m and length l are placed along the three co-ordinate axes with one end at the origin. Find the M.I. of the system about the x-axis.
Answer:
We know that the M.I. of’a rod about its end is given by
= \(\frac{\mathrm{m} l^{2}}{12}+\frac{\mathrm{m} l^{2}}{4}=\frac{\mathrm{m} l^{2}}{3}\)

The M.I. of two rods lying along y and z axes about x-axis will be
I_x = \(\frac{\mathrm{m} l^{2}}{3}+\frac{\mathrm{m} l^{2}}{3}=\frac{2 \mathrm{~m} l^{2}}{3}\)

Question 23.
A mass m is supported by a massless string wound round a uniform cylinder of mass m and radius r. Find with what acceleration will it fall when released from rest?
Answer:
Let it falls through a height h on releasing.

According to the law of conservation of energy,

Question 24.
The speed of the inner layers of the whirlwind in a tornado is alarmingly high. Explain why?
Answer:
The inner layers of the whirlwind in a tornado are close to the axis of rotation. It means the M.I. of the air molecules of inner layers is small. Hence according to the law of conservation of angular momentum, co of the inner layers of the whirlwind in a tornado is very high.

Question 25.
State the two theorems of the moment of inertia. Give an example of the application of each.
Answer:
There are two theorems of the moment of inertia of a body namely,
(a) the theorem of perpendicular axes and
(b) the theorem of parallel axes.

(a) Theorem of perpendicular axes: It states that the moment of inertia of a body about an axis passing through a point in the body is equal to the sum of the moment of inertia about two mutually perpendicular axes lying in a plane perpendicular to the given axis and passing through the chosen point.
i.e. I_z = I_x + I_y.

(b) Theorem of parallel axes: It states that the moment of inertia of a body about an axis is equal to the sum of the moment of inertia of the body about an axis parallel to the given axis and passing through its centre of mass plus the product of mass and the square of the distance between the two axes
i.e. I = I_c + mh².

Question 26.
Why cannot a single force balance the torque?
Answer:
The effect of torque is to produce the angular acceleration and its effect is entirely different than that of the force which causes linear acceleration. Thus a single force cannot balance the torque.

Question 27.
Equal torques are applied on a cylinder and a sphere, both having the same mass and radius. The cylinder rotates about its axis and the sphere rotates about one of its diameters. Which one will acquire greater speed and why?
Answer:
The speed of rotation acquired will depend upon the angular acceleration produced and is given by
α = \(\frac{τ}{I}\)

where τ = is the torque, I am the moment of inertia,
As τ is the same in both the cases, so

Thus, the sphere acquires greater speed than the cylinder as α_s > α_c.

Question 28.
Explain why small angular displacements are treated as vectors?
Answer:
Let a particle undergoing pure rotational motion describes a circular path as shown here.

Let r = radius of its path in XY plane (say).
Let its position changes from P to Q in time At so that radial line OP describes an ∠POQ = Δθ.
Δθ is called angular displacement of the particle.

We know that Δθ = \(\frac{\text { Length of arc } \mathrm{PQ}}{\text { Radius of the circle }(=\mathrm{r})}\)
or
arc PQ = (Δθ)r …. (1)

If Δθ is very small, then Δθ → 0, so arc PQ ≅ chord PQ i.e. the particle may be assumed to be displaced along the chord PQ. In that case, the displacement vector of the particle P is given by
PQ = Δr(say)
i.e. arc PQ = |Δr| ……(2)

The position vector of the particle at P may be written as:
OP = r
Also OQ = r
∴ |OP| = |OQ| = r

∴ from (1) and (2), we get
|Δr| = (Δθ) | r | ….(3)

If we represent Δθ as a vector along the axis of rotation, then from (2), we get
Δr = Δθ × r.

Question 29.
The same solid sphere is made to roll down from the same height on two inclined planes having different angles of inclination. In which case will it take less time to reach the bottom?
Answer:
Let L be the length of the inclined planes having angels of inclination θ1, and θ2 respectively from which the ball begins to slide down

Let r = radius of the sphere.
m = mass of the sphere.
v = speed with which the sphere will reach the bottom,

let ω = \(\frac{v}{r}\) be its angular speed.
If I be a M.I. of the sphere, then

this show that in both cases, the sphere will reach the bottom with the same velocity. Let t be the time taken to reach the ground
∴ using v = u + at, we get
v = a . t
or
t = \(\frac{v}{a}\) …. (3)
Also for an inclined plane,
a = g sin θ
or
a ∝ sin θ …..(4)

From (3) and (4), we get
t ∝ \(\frac{v}{sin θ}\)
or
t ∝ \(\frac{1}{sin θ}\) as v is same in both the cases. sm0
i.e. t will be less for the inclined plane with a larger angle of inclination.

Question 30.
The angular momentum of a particle relative to certain I points Ovaries with time as L = a + bt² where a and b are constant vectors with a ⊥ b. Find the force moment \(\vec{τ}\) relative to the point O acting on the particle when the angle between the vectors \(\vec{τ}\) and L equal 45°.
Answer:
Here, let a and b act along X and Y axis respectively. L = a + bt² = aî + bĵt²

i.e. τ acts along Y-axis.
when L is at 45° with τ i.e. with Y-axis,

Question 31.
What are the important characteristics of C.M.?
Answer:

1. Its position remains unchanged in rotational motion about itself but changes in linear motion.
2. Its position is independent of the coordinate system chosen.
3. The sum of the moments of the masses of the system about the C.M. is zero.
4. Its position depends upon the shape of the body.
5. Its position depends upon the mass distribution of the body.
6. C.M. coincides with C.G. for a symmetrical body.
7. The C.M. of a circular ring lies outside the material body.
8. The C.M. of a circular disc lies within the material of the body.

System of Particles and Rotational Motion Important Extra Questions Long Answer Type

Question 1.
Discuss the rolling of a cylinder (without slipping) down a rough inclined plane and obtain an expression for the necessary coefficient of friction between the cylinder and the surface.
Answer:
Consider a solid cylinder of mass m, radius R and MJ. I rolling down an inclined plane without slipping as shown in the figure. The condition of rolling down without slipping means that at each instant of time, the point of contact P of the cylinder with the inclined plane is momentarily at rest and the cylinder is rotating about that as the axis.

Let θ = angle of inclination of the plane. The forces acting on the cylinder are:

1. The weight mg of the cylinder acting vertically downward.
2. The force of friction F between the cylinder and the surface of the inclined plane and acts opposite to the direction of motion.
3. The normal reaction N due to the inclined plane acting normally to the plane at the point of contact. The weight W of the cylinder can be resolved into two rectangular components:
   (a) mg cos θ along ⊥ to the inclined plane.
   (b) mg sin θ along the inclined plane and in the downward direction. It makes the body move downward.

Let a = linear acceleration produced in the cylinder,
Then according to Newton’s 2nd law of motion,
ma = mg sin θ – F …. (1)
and N = mg cos θ …. (2)

If α = angular acceleration of the cylinder about the axis of rotation, then
τ = I α …. (3)

Here, τ is provided by F i.e.
τ = F.R …. (4)

∴ from (3) and (4), we get



If μ_s be the coefficient of static friction between the cylinder and the surface,
Then

For rolling without slipping

equation (9) is the required condition for rolling without slipping i.e. \(\frac{1}{3}\) tan θ should be less than equal to μs i.e. the maximum allowed inclination of the plane with the horizontal is given by
θ_max = tan^-1 (3 μ_s)

Question 2.
Prove that
(a) Δω = τ Δθ
Answer:
Let F = force applied on a body moving in XY plane.
Δr = linear displacement produced in the body by the force F in moving from P to Q.
If Δω is the small work done by the force, then by definition of work.

ΔW = F . Δr ….(1)

In component form,

Let PN ⊥ on X-axis & PON = θ
∴ in rt ∠d ΔPNO,

As Δθ is very small, i.e. Δθ → 0, cos Δθ → 1 and sin Δθ → Δθ

(b) P = τ ω.
Answer:

Numerical Problems:

Question 1.
Three particles of masses 1g, 2g and 3g have their centre of mass at the point (2,2,2). What must be the position of the fourth particle of mass 4g so that the combined centre of mass may be at the point (O, O, O).
Answer:
Let r₁, r₂, r₃ are the position vectors of the three mass particles w.r.t. origin. Then their centre of mass is given by

If r’ be the position vector of the new C.M. then
r’ =0
and r₄ be the position vector of the fourth particle from the origin, then

∴ the new particle should be at (- 3, – 3, – 3).

Question 2.
Two balls of masses 3m and m are separated by a distance of l.
(a) Find the position of the C.M.
(b) If these two balls are attached to a vertical axis by means of two threads whose combined length is l and rotated in a horizontal plane with uniform angular velocity ω about an axis of rotation passing through C.M. Prove that the tensions in the two strings will become equal.
Answer:
Here, m₁ = 3m, m₂ = m; AB = l
(a) Let x = distance of the C.M. from the ball A of mass 3m
∴ l – x = distance of the C.M. from the ball B.

∴ From the definition of C.M.
3m . x = m (l – x)
or
x = \(\frac{l}{4}\)

(b) Let T₁ and T₂ be the tensions in the strings connecting 3m and m to the axis through C.M. respectively and rotating in a horizontal plane with angular velocity coω.
∴ radii of their circular paths = \(\frac{l}{4}\) and \(\frac{3l}{4}\) respectively.

Hence proved.

Question 3.
Calculate the M.I. about a transverse axis through the centre of a disc whose radius is 20 cm. Its density is 9g cm^-3 and its thickness is 7 cm.
Answer:
Here, R = 20 cm, t = thickness = 7 cm density of material of disc,

Question 4.
A cylinder of mass 5 kg and radius 30 cm and free ω rotate about its axis, receives an angular impulse of 3 kg mV initially followed by a similar impulse after every 4s. What is the angular speed of the cylinder 30s after the initial impulse? The cylinder is at rest initially.
Answer:
Here, M = 5 kg
R = 30 cm = 0.3 m
ω = ? after 30s
I = M.I. of the cylinder about its axis
= \(\frac{1}{2}\)mR² = \(\frac{1}{2}\) × 5 × (0.3)²
= 0.225 kg m²

∴ The initial angular speed of the-cylinder, ω_o = 0
Initial angular momentum of the cylinder, L_o = Iω_o = 0
Initial impulse received by the cylinder, L’_o = 3 kg m² s^-1

The angular impulse received by the cylinder will produce a change in its angular momentum. If L is the angular momentum of the cylinder after the initial impulse, then
L’_o = L – L_o
or
L = L’_o + L_o = 3 + 0 = 3 kg m² s^-1

As the cylinder receives angular impulse after every 4s.
∴ Angular momentum of the cylinder after 4s = 3 + 3 = 6kg m² s^-1
Angular momentum of the cylinder after 8s = 3 × 2 + 3 = 9kg m² s^-1
Angular momentum of the cylinder after 12s = 3 × 3 + 3 = 12kg m² s^-1
Angular momentum of the cylinder after 28s = 3 × 7 + 3 = 24kg m² s^-1

Next angular impulse is to be received by the cylinder at t = 32s
∴ between 28s and 30s no impulse is received
∴ angular momentum of the cylinder after 30s = 24kg m² s^-1

If ω = angular speed of the cylinder after 30s, then

Question 5.
A cord is wound around the circumference of a wheel of diameter 0.3m. The axis of the wheel is horizontal. A mass of 0.5kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5m in 4s, what is the angular acceleration of the wheel? Also, find out the M.I. of the wheel.
Answer:
Here, mass attached, m = 0.5kg
radius of wheel, R = \(\frac{0.3}{2}\) = 0.15m
initial linear velocity of the mass attached, u = 0
Distance covered, s = 1.5m, t = 4s

let a = linear acce. of the mass after 4s

If τ = torque applied by the mass attached, then

Question 6.
One end of a uniform rod of mass m and length L is supported by a frictionless hinge which can withstand a tension of 1.75mg. The rod is free to rotate in a vertical plane. To what maximum angle should the rod be rotated from the vertical position so that when left, the hinge does not break?
Answer:
Let θ = maximum angle = ?
T = 1.75 mg
When the rod is in a vertical position, then the net force acting on the rod
F= 1.75mg – mg = 0.75mg
when the rod rotates, centripetal force,


When the rod is in the displaced position A, then K.E. of rotation is converted in RE.
∴ P.E. of the rod at displaced position = mg h

For rod I = \(\frac{1}{3}\) mL²

∴ According to the law of conservation of energy,

Question 7.
A uniform cylinder of radius r is rotating about its axis at the angular velocity ω_o. It is now placed into a corner as shown in the figure. The coefficient of friction between the wall and the cylinder as well as the ground and cylinder is μ. Then And the number of turns n, the cylinder completes before it stops?
Answer:
The forces acting on the system are shown in the figure.

Let m = mass of the cylinder
The initial K.E. = \(\frac{1}{2}\) Iω_o²

where I = M.I. of the cylinder about its axis of rotation.

work done by the frictional force before the cylinder comes to rest is

Question 8.
Two masses m₁ = 15kg, m₂ = 10kg are attached to the ends of a cord which passes over the pulley of an Atwood’s machine. The mass of the pulley is m = 10kg and its radius is R = 0.1m. Calculate the tension in the cord, the acceleration ‘a’ of the system and the number of revolutions made by the pulley at the end of 2s from start.
Answer:
Here, m₁ = 15kg, m₂ = 10kg and tensions are shown in the figure.
As the pulley has a finite mass m = 10kg, so the two tensions are not equal.

Let a = linear acceleration of the system,
∴ according to Newton’s law of gravitation,
m₁g – T₁ = m₁a …. (i)
and
T₂ – m₂g = m_o1a ….(ii)

Here tension in the cord exerts torques on the pulley assumed to be a solid disc.
∴ Torque on the pulley, τ = (T₁ – T₂)R …. (iii)
(in the clockwise direction)

Question 9.
A wheel of radius 6cm is mounted so as to rotate about a horizontal axis through its centre. A string of negligible mass wrapped around its circumference carries a mass of 0.2kg attached to its free end as shown in the figure. When it falls, the mass descends through one metre in 5s. Calculate the angular acceleration of the wheel, its M.I. and tension in the cord.
Answer:
Let a = acce. of the falling body.
Here, s = 1m
t = 5s
r = 6 cm = 6 × 10^-2 m
m = 0.2kg
u = 0


If v = velocity of the wheel after 5 s, then using the relation

P.E. lost by falling mass = mgh
Increase in translational KE. = \(\frac{1}{2}\)mv²
Increase in rotational K.E. = \(\frac{1}{2}\)Iω²
or
\(\frac{1}{2}\)Iω² + \(\frac{1}{2}\)mv² = mgh

Question 10.
A rod of length l, whose lower end is resting along the horizontal plane starts to topple from the vertical position. What is the velocity of the upper end when it hits the ground?
Answer:
Let m = mass of the rod
when the rod is in the vertical position, it possesses P.E. given by
P.E = mg (\(\frac{l}{2}\))
Here, h = \(\frac{l}{2}\) because C.G. of the rod is at a height \(\frac{l}{2}\) above the ground. When the rod topples, it gains K.E. of rotation.

Question 11.
A thin wire of length l and uniform linear mass density ρ is bent into a circular loop with a centre at O as shown in the figure. What is the moment of inertia of the loop about the axis XX’?

Answer:
Here, ρ = mass per unit length,
m = mass of the loop,
∴ m = ρl
R = radius of the ring or loop.
ID = M.I. of the ring about its diameter.
ID = \(\frac{1}{2}\)mR² = \(\frac{1}{2}\)ρlR²

Since XX’ is parallel to the diameter of the loop,
∴ According to the theorem of parallel axes, M.I. about XX’ is given by

Question 12.
A long horizontal rod has a bead that can slide along its length and initially placed at a distance l from one end A of the rod. The rod is set in angular motion about A with constant angular acre. α. If the coefficient of friction between the rod and the bead be μ and gravity is neglected, then find the time after which the bead starts slipping?
Answer:
Bead starts slipping if centripetal force = force of friction

Question 13.
Point masses m₁ and m₂ are placed at the opposite ends of a rigid rod of length l and negligible mass. The rod is to be set rotating about an axis ⊥ to it. Find the position on this rod through which the axis should pass in order that the work required to set the rod rotating with angular velocity ω0 should be minimum.
Answer:
Let the axis of rotation be at a distance x from m₁.
∴ the distance of the axis from m₂ = l – x
When the rod is set into rotation, the increase in the rotational K.E. is given by


According to the work-energy theorem,
work done = increase in rotational K.E.

Question 14.
An isolated particle of mass m is moving in a horizontal plane (x – y) along the X-axis at a certain height above the ground. It suddenly explodes into 2 fragments of masses \(\frac{m}{4}\) and \(\frac{3}{4}\) m. An
instant later, the smaller fragment is at y = + 15 cm. What is the position of the larger fragment at this instant?
Answer:
There is no motion along the y-axis as the isolated particle moves along the x-axis at a certain height. The C.M. will remain stationary along the y-axis even after the collision.

∴ larger fragment will be at – 5cm.

Question 15.
What would be the duration of the day if:
(a) Earth suddenly shrinks to \(\frac{1}{64}\) th of its original volume, mass remaining uncharged. (I of earth = \(\frac{2}{5}\) mR²)?
(b) Earth suddenly contracts to half of its present radius (without any central torque acting on it). By how much would the day be decreased?
Answer:
Let T₁ and ω₁, be the time period and angular velocity of revolution of Earth before contraction.
T₂, ω₂ = angular velocity after contraction.
I₁, I₂ = its M.I. before and after contraction.
R₁, R₂ radius of Earth before and after contraction.
Since no external torque acts, so

(a) Volume after contraction = \(\frac{1}{64}\) (volume before contraction)

Question 16.
The energy of 484J is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. Find the M.I. of the flywheel.
Answer:

Let I = M.I. of the flywheel

Question 17.
What constant torque must be applied to a disc of mass 10kg and diameter 50cm so that it acquires an angular velocity of 2π rads^-1 in 4s? The disc is initially at rest and rotates about an axis through the centre of the disc and in a plane ⊥ to the disc. Also, find the tangential force to be applied.
Answer:
Here, m = 10 kg, r = \(\frac{50}{2}\) = 25 cm = 0.25 m

Question 18.
On the application of constant torque, a wheel is turned from rest through an angle of 200 rads in 8s.
(a) What is its angular acceleration?
(b) If the same torque continues to act what will be the angular velocity of the wheel after 16s from start?
Answer:

Question 19.
A cat weighing lO kg is standing on a flatboat so that she is 20 m from the shore. She walks 8m on the boat towards the shore and then stops. The boat weighs 40 kg and we can assume that there is no friction between it and the water. How far is she from the shore at the end of this time?
Answer:
Here, initially, the C.M. of the cat-boat system is at the centre of the boat at x = 20m away from shore.

M = mass ofboat4O kg
m = mass of cat 10 kg
Taking mass moments about the shore.

Total initial mass moment = (M + m)x
= (40+ 10)20= 1000 kgm.

Let the final distance of the cat be x, from the shore, then C.M. of the boat will be at a distance (x₁ + 8)m from the shore.
Total final mass moment = mx₁ + M(x₁ + 8)
= 10x₁+ 40(x₁ + 8) = 50x₁ + 320

according to mass moment conservation,
1000 = 50 x₁ + 320
or
50x₁ = 1000 – 320 = 680
∴ x₁ = \(\frac{680}{50}\)
= 13.6m

Aliter: If the walking of a cat does not move the boat, then the distance of the cat from the shore would have been = 20 – 8 = 12 m.

But here, as no external force acts in this situation, so the C.M. of the boat-cat system must not move and it causes the boat to move behind. C.M. has shifted towards the shore due to the 8 m walk of cat to a position dividing the 8 m distance in the inverse ratio of its own and cat’s mass.

∴ Shift of C.M = \(\frac{8 \times 10}{40+10}=\frac{80}{50}\) = 1.6 m

Since the C.M. is not to shift, the boat must move behind by a distance 1.6 m
∴ distance of cat from the shore = 12 + 1.6= 13.6 m.

Question 20.
A stationary pulley carries a rope whose one end supports a ladder with a man and the other end carries a weight of mass M. The man climbs up a distance w.r.t the ladder and then stops. Find the displacement x of the centre of inertia of the system.

Answer:
Let m = mass of man
Here, M = mass attached to one end
l = distance by which the man climbs up w.r.t. ladder.

In the ladder-climbing process, the man is being away from the C.M.
∴ increase in the moment of the mass of man about C.M. = ml
= decrease of the moment about C.M.

It must be shared by the whole mass 2M of the system
If x be the shift in the C.M. in the same direction,
Then ml = 2Mx
or
x = \(\frac{\mathrm{ml}}{2 \mathrm{M}}\) in the same direction.

Question 21.
A small ball is suspended from a point O by a light thread of length l. Then the ball is drawn aside so that the thread deviates through an angle θ from the vertical and set in motion in a horizontal direction at right angles to the vertical plane in which the thread is located. What is the initial velocity that has to be given to the ball so that it could deviate by a maximum angle \(\frac{π}{2}\) during the motion?
Answer:
Let r be the radius of the circle in which the ball rotates.

T = tension in the thread,
θ = angle made by thread with vertical,
w = angular velocity of the ball in the circle,
l = length of thread,
mg = weight of the ball.

∴ T is resolved in two rectangular components.
∴ for vertical equilibrium,

Let v be the linear velocity required to start the motion of the ball and is given by
∴ v = l ω = l. \(\sqrt{\frac{\mathrm{g}}{l \cos \theta}}=\sqrt{\frac{\mathrm{g} l}{\cos \theta}}\)

During motion of the ball producing deviation of \(\frac{π}{2}\), velocity vector rotates by \(\frac{π}{2}\) causing a change in velocity = v\(\sqrt{2}\)

Let v₀ = initial imparted velocity then v0 must provide v\(\sqrt{2}\)
or
v_o = \(\sqrt{2}\)v
= \(\sqrt{2}\). \(\sqrt{\frac{\mathrm{g} l}{\cos \theta}}=\sqrt{\frac{2 \mathrm{~g} l}{\cos \theta}}\)

Question 22.
A solid cylinder
(i) slides
(ii) rolls from rest down an inclined plane.
Compare the velocities when the cylinder reaches the bottom of the plane.
Answer:
Let l = length of an inclined plane having an angle of inclination θ.
(i) When the cylinder slides down the plane,
a = g sin θ
Let v₁ = velocity with which it reaches the bottom
∴ using the relation,

(ii) When the cylinder rolls, then let v₂ be its velocity on reaching the bottom.
when r = radius of the cylinder, for a solid cylinder,

Question 23.
A flexible chain of weight W hangs between two fixed points A and B at the same level as shown here.
Find (i) force applied by a chain on each endpoint.
(ii) the tension in the chain at the lowest point.
Answer:
Let W = weight of the chain
∴ \(\frac{w}{2}\) = reaction at each endpoint A and B vertically upward

\(\frac{w}{2}\) balances downward
(i) Component F sin 0 of force F applied by a chain on each point

(ii) At lowest point C, the tension T is horizontal and equals the horizontal component of force F

Question 24.
The moment of inertia of a body about a given axis is 1.2 kg m². Initially, the body is at rest. In order to produce a rotational K.E. of 1500J, for how much duration, an acceleration of 25 rads^-2 must be applied about that axis.
Answer:

Question 25.
A thin bar XY of negligible weight is suspended by strings R and S shown in fig. The bar carries masses of 10 kg and 5 kg. Find the tensions in the strings and the angle θ if the system is in the static equilibrium.
Answer:
T₁, T₂ = ?
θ = ?

Taking moments about point X, we get


Again taking moment about point Y, we get

Also for horizontal equilibrium

Value-Based Type:

Question 1.
A physics teacher explained about conservation of Angular momentum in the class. After the completion of her explanation, she wants to test how far the students are able to understand the topic.
In the process. she selected two students to name Babita and Ram. Both could explain the topic with examples.
(a) What questions of them impress you?
Answer:
Both were doing a group study, discussing together they have given answers.

(b) A physics teacher sits on a stool that is free to rotate nearly without friction about a vertical axis her outstretched hands each hold a large, mass so that the rotational inertia is 12 kg m² by pulling her arms close to her body she is able to reduce her rotational inertia to 6 kg m2. If her student starts spinning at 0.5 rad/s, what is her speed after she draws her arms in?
Solution:
In the absence of external torque, her angular momentum stays constant so that

When her rotational inertia halves, her angular velocity doubles.

Question 2.
Radha found the wheel getting detached from her uncle’s car. She took it to the workshop and got it repaired. She informed her uncle, who is a mechanical engineer, about this matter.
(a) What according to you the values displayed by Radha?
Answer:
Radha takes care of things and has a concern for others. Prac deal with finding the solutions to problems.

(b) A thin wheel can stay up-right on its rim for a considerable length of time when rolled with considerable velocity, while it falls from its upright position at the slightest disturbance, when stationary, Explain.
Answer:
When the wheel is rolling, the angular momentum is conserved. However, due to the frictional force, it continues to decrease. Thus, the wheel can stay upright on its rim only for a certain interval of time. In the stationary position, the wheel falls due to unstable equilibrium.

Question 3.
Two friends Raman and Sohan are discussing the speed and rotation of a wheel. One of them said that it is due to ‘ rotational motion about a fixed axis. The next day Raman brought a problem which is as under:
“The angular speed of a motor wheel is increased from 1200 rpm to 3120 rpm in 16 seconds.”
(i) What values are displayed by Raman?
Answer:
Values displayed are:
(a) Curiosity.
(b) Keen observation of the surroundings.
(e) Keen to find a solution.

(ii) What is the angular acceleration, assuming the accelera¬tion to be uniform?
Answer:
Here, W_o = Initial angular speed (in rad/s)
W = Final angular speed (in rad/s)

Question 4.
A 10-year boy was sitting stationary at one end of a long trolly. The trolly is moving on a smooth horizontal floor at a definite speed. He was a naughty boy and enjoying it very much. Suddenly he stood up and ran about the trolly in any manner. He was surprised to see that trolly did not become unbalanced at all. He was curious to know the reason for it, he asked this question to his science teacher. The teacher explained to him about the centre of mass of the trolly and child together.
(i) what values of the boy are depicted here?
Answer:
Values depicted here in the above problem are:
Curiosity, awareness, willing to know the scientific reason, presence of mind.

(ii) What is the centre of mass of the body?
Answer:
For a system of particles, the centre of mass is defined as that point where the entire mass of the system is imagined to
be concentrated.

(iii) How did the teacher explain the reason?
Answer:
The teacher explained that the body of the boy and trolly is a single system and the forces involved are totally internal. Since there is no external force. So, there is no change in the momentum of the system and hence the velocity of the system remains unchanged when the child gets up and runs about on the trolly in any manner.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 6 Work, Energy and Power. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 6 Important Extra Questions Work, Energy and Power

Work, Energy and Power Important Extra Questions Very Short Answer Type

Question 1.
What is the source of the kinetic energy of the falling raindrops?
Answer:
It is the gravitational potential energy that is converted into kinetic energy.

Question 2.
A spring is stretched. Is the work done by the stretching force positive or negative?
Answer:
Positive because the force and the displacement are in the same direction.

Question 3.
What is the type of collision when?
(a) Does a negatively charged body collide with a positively charged body?
Answer:
Perfectlyjnelastic collision.

(b) Do macroscopic bodies collide?
Answer:
Inelastic collision.

(c) Do two quartz balls collide?
Answer:
Perfectly elastic collision.

Question 4.
(a) Give two examples of potential energy other than gravitational potential energy.
Answer:
Electrostatic P.E. and elastic P.E.

(b) Give an example of a device that converts chemical energy into electrical energy.
Answer:
Daniell cell.

(c) Heat energy is converted into which type of energy in a steam engine?
Answer:
Mechanical energy.

(d) Where is the speed of the swinging pendulum maximum?
Answer:
At the bottom of the swing.

(e) A heavy stone is lowered to the ground. Is the work done by the applied force positive or negative?
Answer:
Negative work.

Question 5.
What is the work done by the centripetal force? Why?
Answer:
Zero. This is because the centripetal is always perpendicular to the displacement.

Question 6.
(a) What is the work done by the tension in the string of simple pendulum?
Answer:
zero

(b) What is the work done by a porter against the force of gravity when he is carrying a load on his hand and walking on a horizontal platform?
Answer:
zero

(c) Name the force against which the porter in part (A) is doing some work.
Answer:
Frictional force.

Question 7.
When an arrow is shot, wherefrom the arrow will acquire its K.E.?
Answer:
It is the potential energy of the bent bow which is converted into K.E.

Question 8.
When is the exchange of energy maximum during an elastic collision?
Answer:
When two colliding bodies are of the same mass, there will be a maximum exchange of energy.

Question 9.
Does the work done in raising a load onto a platform depend upon how fast it is raised?
Answer:
The work done is independent of time.

Question 10.
Name the parameter which is a measure of the degree of elasticity of a body.
Answer:
Coefficient of restitution.

Question 11.
When a ball is thrown up, the magnitude of its momentum first decreases and then increases. Does this violate the conservation of momentum principle?
Answer:
No. This is because the momentum of the system (ball and air molecules) remains constant. When the momentum of the ball decreases, the momentum of air molecules in contact increases and vice-versa.

Question 12.
In a tug of war, one team is slowly giving way to the other. What work is being done and by whom?
Answer:
+ve. The winning team is performing work over the losing team.

Question 13.
A light and a heavy body have equal momentum. Which one of them has more K.E.?
Answer:
The lighter body has more K.E.

Question 14.
By using simple mechanical devices such as a lever, wedge, inclined plane, pulley, wheel, etc. we can do work even by applying small force. What makes it possible to do so?
Answer:
These mechanical devices multiply forces.

Question 15.
Two protons are brought closer. What is the effect on the potential energy of the system?
Answer:
Work is done to overcome the force of repulsion, so the potential energy of the system increases.

Question 16.
Where is the energy of a vertically projected body maximum?
Answer:
It is the same at all points. This is in accordance with the law of conservation of energy.

Question 17.
Out of a pair of identical springs of force constants, 240Nm^-1 one is compressed by 10 cm and the other is stretched by 10 cm. What is the difference in the potential energies stored in the two springs?
Answer:
The difference in potential energies is zero. This is because
E_p = \(\frac{1}{2}\) ky². In both cases, k and y² are the same.

Question 18.
What should be the angle between the force and the displacement for maximum and minimum work?
Answer:
For maximum work, θ = 0° and for minimum work θ = 90°.

Question 19.
Does the P.E. of a spring decreases/increase when it is compressed or stretched? Why?
Answer:
P.E. of a spring increases in both cases. This is because work is done by us in compression as well as in stretching the spring.

Question 20.
Can a body have momentum without energy?
Answer:
No, because for momentum, it must have some velocity and hence energy.

Question 21.
What type of energy is stored in the spring of the watch?
Answer:
Potential energy.

Question 22.
Can a body have energy without momentum?
Answer:
Yes, everybody has some internal energy due to the thermal agitation of the particles of the body. But the vector sum of linear momenta of the moving particles may be zero. It may have energy due to its position (P.E.) and thus momentum is zero.

Question 23.
In which motion, momentum changes but not the K.E.?
Answer:
In uniform circular motion.

Question 24.
Is the whole of K.E. lost in any perfectly inelastic collision?
Answer:
No, only as much K.E. is lost as is necessary for the conservation of linear momentum.

Question 25.
Can the P.E. of an object be negative?
Answer:
Yes, it can be negative when the forces involved are attractive.

Question 26.
The momentum of a body is increased by 50%. What is the percentage change in its K.E.?
Answer:
When the momentum is increased by 50%, velocity increases by
i.e. velocity becomes \(\frac{3}{2}\) times, so K.E. becomes \(\frac{9}{4}\) times
i.e. \(\frac{9}{4}\) × 100 = 225%. Hence increase in K.E. = 225 – 100 = 125%.

Question 27.
What is the work done by Earth’s gravitational force in keeping the moon in its orbit in a complete revolution?
Answer:
Zero, because gravitational force is a conservative force.

Question 28.
A spring is cut into two equal halves. How is the spring constant of each half affected?
Answer:
The Spring constant of each half becomes twice the spring constant of the original spring.

Question 29.
What happens to the energy of our watch which we wind once a day?
Answer:
The work done in winding the watch is stored as P.E. in the spring which is converted into K.E. of the moving parts of the watch.

Question 30.
Is collision possible even without actual contact of the colliding particles? Give example.
Answer:
Yes, such collision is called collision at a distance. The collision between subatomic particles (like proton and neutrons) are examples of such collisions.

Question 31.
A cake of mud is thrown on a wall where it sticks. What happens to its initial K.E.?
Answer:
A part of the K.E. is used in deforming the cake and the remaining part is converted into heat and sound energy.

Question 32.
Nuclear fission and .fusion reactions are the examples of conversion of mass into energy. Can we say that strictly speaking, mass is converted into energy even in an exothermic chemical reaction?
Answer:
Yes, mass is converted into energy in an exothermic chemical reaction also. But the mass change in a chemical reaction is about a million times less than in a nuclear reaction.

Question 33.
What type of energy is lost in doing work against friction?
Answer:
The kinetic energy is lost in doing work against the friction.

Question 34.
Define 1 Joule.
Answer:
A joule of work is said to be done when a force of 1 N displaces a body through 1 m.

Question 35.
Define an erg.
Answer:
An erg of work is equal to work done by a force of 1 dyne of displacing a body through one centimeter.

Question 36.
Derive the relation between 1 J and 1 erg.
Answer:
We know that 1 J = 1 N × 1 m = 1 Nm

Question 37.
What is the nature of the work done by the resistive force of air on a vibrating pendulum in bringing it to rest and why?
Answer:
Negative, because the air always opposes the displacement of the pendulum bob.

Question 38.
What is the work done on a body in moving it in a circular path with a constant speed? Why?
Answer:
Zero, because it is acted upon by centripetal force in a direction perpendicular to its motion.
i.e. W = FS cos 90° = 0.

Question 39.
A truck and car are moving with the same K.E. and are brought to rest by the application of brakes that provide equal retarding force. Which one will come to rest in a shorter distance? Why?
Answer:
Both of them come to rest at the same distance as
K.E. = F.S₁ = F.S₂
or
FS₁ cos 180 = F.S₂ cos 180
or
S₁ = S₂.

Question 40.
A conservative force does positive work on a body. What happens to the potential energy of the body? Give an example.
Answer:
It (P.E.) decreases.
e.g. a body falling freely under gravity.

Question 41.
A man rowing a boat upstream is at rest w.r.t. the shore. Is any work being done in this case? Why?
Answer:
Yes, as there is a relative displacement between the boat and the stream.

Question 42.
Why friction is a non-conservative force?
Answer:
It is because the work done against friction along a closed path is non-zero.

Question 43.
Does the work done in raising a load onto a platform depend upon how fast it is raised?
Answer:
No, work done does not depend upon the time taken in doing it.

Question 44.
On what factors, does the work done depend?
Answer:
It depends upon the applied force and the displacement of the body.

Question 45.
How will the kinetic energy of a body change if its momentum is tripled? Why?
Answer:
K.E. becomes nine (9) times its initial value as K.E. ∝ p².

Question 46.
Which physical quantity is conserved during both the elastic and inelastic collision?
Answer:
Linear momentum is conserved in both collisions.

Question 47.
What is the most common feature of all types of collisions?
Answer:
Linear momentum is conserved in all types of collisions.

Question 48.
Define variable force.
Answer:
It is defined as the force which either changes in magnitude or direction.

Question 49.
Give an example of variable force.
Answer:
When an object is falling towards the Earth, the gravitational force acting on it goes on changing, so it is a variable force.

Question 50.
Define an electron volt (eV).
Answer:
It is defined as the K.E. acquired by an electron when a potential difference of 1 volt is applied across it.

Work, Energy and Power Important Extra Questions Short Answer Type

Question 1.
An airplane’s velocity is doubled,
(a) What happens to its momentum? Is the law of conservation of momentum obeyed?
Answer:
The momentum of the airplane will be doubled. Yes, the law of conservation of momentum will also be obeyed
because the increase in momentum of the airplane is simultaneously accompanied by an increase in momentum of exhaust gases.

(b) What happens to its kinetic energy? Is the law of conservation of energy obeyed?
Answer:
K.E. becomes four times. Yes, the law of conservation of energy is obeyed with the increase in K.E. coming from the chemical energy of fuel i. e. from the burning of its fuel.

Question 2.
In a thermal station, coal is used for the generation of electricity. Mention how energy changes from one form to the other. before it is transformed into electrical energy?
Answer:
When coal is burnt, heat energy is produced which converts water into steam. This steam rotates the turbine and thus heat energy is converted into mechanical energy of rotation. The generator converts this mechanical energy into electrical energy.

Question 3.
Chemical, gravitational and nuclear energies are nothing but potential energies for different types of forces in nature. Explain this statement clearly with examples.
Answer:
A system of particles has potential energy when these particles are held a certain distance apart against some force. For example, chemical energy is due to the chemical bonding between the atoms. Gravitational energy arises when the objects are held at some distance against the gravitational attraction.

Nuclear energy arises due to the nuclear force acting between the nuclear particles.

Question 4.
What went wrong at the Soviet atomic power station at Chernobyl?
Answer:
In this reactor, graphite was used as a moderator. The fuel elements were cooled by water and steam was produced from within the reactor. Both water and the steam came in contact with hot graphite. Due to this hydrogen and carbon-monoxide (CO) were released. When they came in contact with air, there was a big explosion.

Question 5.
A man can jump higher on the moon than on Earth. With the same effort can a runner improve his timing for a 100 m race on the moon as compared to that on Earth?
Answer:
Man can jump higher on the moon because the acceleration due to gravity on the moon is less than that on the Earth. But acceleration due to gravity does not affect the horizontal motion. Hence the runner can’t improve his timing on the moon for the 100 m race.

Question 6.
How many MeV are there in a 1-watt hour?
Answer:
We know that 1 watt hour = 1 JS^-1 × 3600 s = 3600 J

Question 7.
What is Newton’s experimental law of impact?
Answer:
The ratio of the relative speed of separation after a collision to the relative speed of approach before the collision is always constant. This constant is known as the coefficient of restitution. It is denoted by e.
∴ e = \(\frac{\mathbf{V}_{2 \mathrm{f}}-\mathbf{v}_{1 \mathrm{f}}}{\mathbf{u}_{1 \mathrm{i}}-\mathbf{u}_{2 \mathrm{i}}}\)

where u_1i and u_2i, are the velocities of the bodies before collision and v_2f, v_1f are the velocities of the bodies after the collision.

Question 8.
Two masses one n times as heavy as the other have the same K.E. What is the ratio of their momenta?
Answer:

Question 9.
Two bodies A and B having masses m_A and m_B respectively have equal K.E. If p_A and p_B be their respective momenta, then prove that the ratio of momenta is equal to the square root of the ratio of respective masses. f_c.
Answer:
Let v_A and v_B be the velocities of A and B respectively.
Since their kinetic energies are equal,


Hence Proved

Question 10.
How fast-moving neutrons can be quickly slowed down by passing through heavy water?
Answer:
Heavy water (D₂O) contains deuterium atoms i.e. hydrogen nuclei. They have nearly the same mass as those of neutrons. So when neutrons strike against deuterium atoms, most of the K.E. of the former is transferred to the deuterium atoms i.e. K.E. is exchanged between them.

Question 11.
Will water at the foot of the waterfall be at a different temperature from that at the top? If yes, explain.
Answer:
Yes, when water reaches the ground, its gravitational potential energy is converted into kinetic energy which is further converted into heat energy. This raises the temperature of the water. So water at the foot of the waterfall is at a higher temperature as compared to the temperature of water at the top of the waterfall.

Question 12.
How is the kinetic energy of a particle related to the direction of motion of the particle? Can K.E. be negative?
Answer:
The kinetic energy of a particle is not related to the direction of motion of the particle. K.E. is always positive. It cannot be negative.

Question 13.
An automobile jack is employed to lift a heavyweight. The applied force is much smaller than the weight of the automobile. Can it be said that the work is done in less than the work done in? lifting the automobile directly through a height.
Answer:
No, in the case of the automobile jack, the work done is not calculated from the equation W = FS cos θ, but the work done is calculated from an equation (W = τ θ = FRθ) of rotational motion. In both cases, the same amount of work is done.

Question 14.
What would be the effect on the potential energy of the system of two electrons brought closer?
Answer:
Work has to be done to overcome the force of repulsion. This work done will be stored in the form of P.E. so, it increases the potential energy of the system.

Question 15.
Can the kinetic energy be increased without the application of an external force? If yes, give an example.
Answer:
Yes, this is possible. If work is done by the internal force, then K.E. will be increased. As an example, when a bomb explodes, the combined K.E. of all the fragments is greater than the initial K.E.

Question 16.
Mountain roads rarely go straight up the slope, but wind up gradually why?
Answer:
If roads were to go straight up, the slope (θ) would have been large, the frictional force (µmg cos θ) would be small. The wheels of the vehicle would slip. Also for going up a large slope, a greater power shall be required.

Question 17.
A truck and a car moving with the same K.E. are stopped by applying the same retarding force by means of brakes. Which one will stop at a smaller distance?
Answer:
Both will stop at the same distance which follows from the work-energy theorem.
K.E. = work done in stopping= retarding force × distance
As K.E. and force for both are equal, so the distance covered must be equal.

Question 18.
A truck and a car are moving with the same K.E. on a straight road. Their engines are simultaneously switched off. Which one will stop at a lesser distance?
Answer:
The vehicle stops when its K.E. is spent working against the force of friction between the tires and the road. This force of friction varies directly with the weight of the vehicle.

As K.E. = work done
= force of friction × distance
or
E = F × S
or
S = E/F.
Forgiven K.E., S, will be smaller where F is larger such as in the; case of a truck.

Question 19.
A man rowing a boat upstream is at rest w.r.t. the shore. Is any work being done in this case?
Answer:
No, because the man is applying the force and there is no relative motion between the boat and the shore.

Question 20.
A body is heated by giving Q an amount of heat energy. Will its mass increase or decrease or remain constant? If it increases or decreases, then by how much?
Answer:
The variation in mass depends on the nature of the body. For most solids, there is no variation in mass on heating. However, if the solid is volatile, heating will change the mass of the solid. Heating of solids, in general, bring about a change in state, and during this process, some loss of mass occurs due to evaporation.

Question 21.
A football kicked by a player leaves the ground and after traveling in the air reaches the ground and comes to stop at some other position on the ground. Identify the energy transformation in this process. Is the energy of the ball conserved?
Answer:
The kinetic energy imparted to the ball is converted into potential energy at the highest point and a small part remains kinetic. Then it is converted into kinetic energy when it hits the ground. This energy is used up in overcoming the friction against air and the ground. Due to the dissipation of energy in overcoming friction against air and ground, the kinetic energy of the ball is not conserved.

Question 22.
A child enjoys going high and high in a swing by pumping energy. Explain the large amplitude from the rest position using the work-energy idea.
Answer:
The child pumps energy to the swing at the appropriate time and place from his muscular work. In each swing friction at hinges and air, friction reduces the velocity which he compensates by providing energy to the swing at the appropriate time which partly increases the amplitude of the swing as well. So, periodic muscular work provides the energy to the swing.

Question 23.
How fast neutrons can be slowed down by heavy water? Where does the energy go?
Answer:
The fast neutrons collide with water molecules and transfer a good part of their kinetic energy to the water molecules. As a result, the kinetic energy and hence the speed of the neutrons is decreased i.e. they are slowed down. The energy received by the water molecules increases their speed and there is an increase in the thermal energy of the mass of water.

Question 24.
Show that the work done by an elastic force on a spring is stored as the potential energy of the spring.
Answer:
Consider an elastic spring that is extended or compressed. The force does not remain constant in this case. The elastic force Fel according to Newton’s Third law of motion is
F_el = – F_ext
when F_ext = external force applied
The Fel is always proportional to the compression or extension
i.e. F_el = – kx
∴ F_ext = kx
If F_av be the average force, then

If x₁ = O (choosing x₁ as origin), then x₂ = x
The work done by an elastic force is stored as potential energy in the spring and is given by
W = P.E. = \(\frac{1}{2}\) kx².

Question 23.
What ¡s transformation of energy? Give at least five exam pies.
Answer:
The change of energy from one form to another is known as energy transformation. For example:

1. Diesel on burning produces hot gases and heat which is transformed into mechanical energy and is used to run trains and motor vehicles or pumps.
2. Electric energy is transformed into light in a tube or bulb.
3. The electric energy is changed into heat in an oven or heater.
4. Light is converted into electricity with the help of a photovoltaic cell.
5. In a microphone, sound energy is converted into electrical energy.

Question 26.
Which of the following does work: the hammer or the nail, a cricket bat or a ball? Explain.
Answer:
Hammer does work on nails. The force is applied by a hammer on the nail (object) and moves it through some distance. A bat does work on the ball and pushes. Initially, the bowler does work on the ball which init turn exerts impulse on the bat. The bat reacts with the added force of the batsman and thus, the bat does work on the ball.

Question 27.
A particle of mass m is moving in a horizontal circle of radius r under a centripetal force equal to \(\frac{\mathbf{k}}{\mathbf{r}^{2}}\) where k is a constant. What is the total energy of the particle?
Answer:

Question 28.
What are the relations between
(a) kilowatt hour and kilocalorie?
Answer:


(b) metric horsepower and kilocalorie per hour?
Answer:

Question 29.
Prove that instantaneous power is given, by the dot product of force and velocity i.e. P = F.v.
Answer:
Let AW be the amount of work done in a small time interval Δt. If Pav be the average power, then

where F constant force producing a displacement S
∴ From (ii) and (iii), we get

Question 30.
Define spring constant or force constant. What is its S.I. unit?
Answer:
It is defined as the extension per unit displacement produced in the spring or wire.
According to Hook’s law, the extension is always directly proportional to the tension or force applied on a spring i.e.
F ∝ x
or
F = k x
or
k = \(\frac{F}{x}\)

where k is the force constant
S.I unit of k is Newton metre^-1 (Nm^-1).

Work, Energy and Power Important Extra Questions Long Answer Type

Question 1.
(a) State work-energy theorem or principle.
Answer:
It states that the work done on a body is equal to the change in its kinetic energy.
i.e. W = change in kinetic energy
Proof: Let m = mass of a body moving in a straight line with a constant initial velocity u.

Let F = force applied on it at point A to B so that its velocity is V at B.
If dx = small displacement from P to Q
and a = acceleration produced in the body, then
F = ma

If dw be the work done from P to Q, then

If W = total work done from A to B, then

(b) State and prove the law of conservation of energy.
Answer:
It states that energy can neither be created nor can be destroyed but it can be changed from one form of energy into another i.e. total energy = constant.

Proof: Let a body of mass m be lying at rest at point A at a height h above the ground. Let it be allowed to fall freely and reaches a point B after falling through a distance x and it finally hits the ground at point C. Let v and V be its velocities at points B and C respectively.
∴ AB = x and BC = h – x

At point A: u = 0
∴ K.E. = 0
P.E. = mgh

If E be the total energy of the body, then
E = K.E. + P.E. = 0 + mgh
or
E = mgh …. (i)

At point B: using the relation,

At point C: Here, v = v_c, a = g, s = h

Thus, from (i), (ii), and (iii), it is clear that total energy at points A, B, and C is the same. It is purely P.E. at A and purely K.E. at point C.

Numerical Problems:

Question 1.
An engine draws a train up an incline of 1 in 100 at the rate of 36 km h^-1. If the resistance due to friction is 5 kg wt per ton, calculate the power of the engine. Mass of train and engine is 100

Answer:
Here, m = 100 metric ton = 100 × 1000 kg
Total force of friction,
f1 = 100 × 5 = 500 kg wt
= 500 × 9.8 N = 4900 N
sin θ = \(\frac{1}{100}\)

Let f2 = Downward force on the train
= component of its weight acting in downward direction parallel to the inclined plane = mg sin θ
= 100 × 1000 × 9.8 × \(\frac{1}{100}\) = 9800 N

If F be the total force against which engine has to work, then

Question 2.
Calculate the work done and power of an engine that can maintain a speed of SO ms^-1 for a train of mass 3 × 106 kg on a rough level track for 5 km. The coefficient of friction is 0.05. Given g = 10 ms^-2.
Answer:
Here,

Question 3.
A 10 kg block slides without acceleration down a rough inclined plane making an angle of 20° with the horizontal. Calculate the work done over a distance of 1.2 m when the inclination of the plane is increased to 30°.
Answer:
Here, angle of sliding = 20°
μ = coefficient of friction
= tan 20° = 0.3647
S = 1.2 m

m = mass of block = 10 kg.

Let a = acceleration when the inclination is increased to 30° and F be the value of limiting friction then

Question 4.
A bullet of mass 0.03 kg moving with a speed of 400 ms^-1 penetrates 12 cms into a fixed block of wood. Calculate the average force exerted by the wood on the bullet.
Answer:
Here,
mass of bullet, m = 0.03 kg
initial K.E. = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 0.03 × (400)² = 2400 J
Final K.E. = \(\frac{1}{2}\)mv² = 0

∴ ΔK = Loss in kinetic energy = 2400 J
Let F = average force applied by block on bullet
S = 0.12 m

∴According to work energy principle
W = ΔK
or
FS = ΔK
or
F × 0.12 = 2400
or
F = 2 × 104 N

Question 5.
A boy of mass 50 kg sits in a swing suspended, by a rope 5 m long. A person pulls the swing to one side so that the rope makes an angle of 30° with the vertical. What is the gain in gravitational P.E. of the boy?
Answer:
Here, θ = 30°
OA = OB = 5 m …. (i)
m = 50 kg

Vertical height through which boy at B rises up is given by

Question 6.
(a) bullet of mass 20 g moving with a velocity of 500 ms^-1 strikes a tree and goes out from the other end. with a velocity of 400 ms^-1. Calculate the work done in passing through the tree.
Answer:
Here m = 0.02 kg
u = 500 ms^-1
v = 400 ms^-1
w = ?
from work energy theorem, work done loss in K.E.

(b) A bullet of mass 0.01 kg is fired horizontally into a 4 kg wooden block at rest on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet remains embedded in the block and the combination moves 20 m before coming to rest. With what speed did the bullet strike the block?
Answer:
Here S = 20 m
μ = 0.25
M = mass of block = 4 kg
m = mass of bullet = 0.01 kg

∴ R = normal reaction = Mg = 4 × 9.8
F = μR = 0.25 × 4 × 9.8 = 9.8 N
v = 0
u = ?
or
loss in KE. = work done by the force of friction against the block.

Question 7.
A stone of mass 5 kg falls from the top of a cliff 30 m high and buries itself one meter deep into the sand. Find the average resistance offered and time taken to penetrate into the sand.
Answer:
Here, m = 5 kg
h = 30 m
S = 1 m
∴ P.E. of stone = mgh = 5 × 9.8 × 30 = 1470 J

Let F = average force of resistance offered by the sand and F’ = net upward force.

Now momentum of stone before penetration
mu = mv = 5 × 24.25 (∵ here u = v)

Final momentum of stone when it becomes stationary (i.e. v’ = 0)
= mv’ = m(0) = 0
∴ Ft = – mv’ + mu

Question 8.
An automobile moving at a speed of 72 km h^-1 reaches the foot of a smooth incline when the engine is switched off. How much distance does the automobile go up the incline before coming to rest? Take angle of incline 30°, g = 9.8 ms^-2.
Answer:
Here, θ = 30°
Initial velocity of the automobile at point A when it is switched off = 72 kmh^-1
= 72 × \(\frac{5}{18}\) = 20 ms^-1

Let m = mass of automobile.
Initial K.E. of the automobile at A = \(\frac{1}{2}\) m(20)² = 200 m

F = mg sin θ = force opposing the motion of the automobile
= m × 9.8 sin 30° = (4.9m)N

Let it stop at B after travelling AB = S
∴ Final K.E. = 0
∴ change in K.E. = 200m – 0 = 200m J
∴ W = work done by the automobile
= FS = (mg sin θ) × S = 4.9 m × S

∴ According to work-energy theorem,
W = change in K.E.
or
4.9m S = 200m
or
S = \(\frac{200}{4.9}\) = 40.8m

Question 9.
A pump-set is used to lift water to a reservoir of 6000 liters capacity over an average height of 20m. If it takes 1 hour to All the reservoir completely, calculate the work done and the power supplied to the set if its efficiency is 60%, g = 9.8 ms^-2.
Answer:
Mass of 1 litre of water = 1 kg .
∴ m = 6000 kg
h = 20 m

∴ W = work done = P.E. = mgh
= 6000 × 9.8 × 20= 11.76 × 10s J
t = 1 h = 3600 s

Question 10.
A wooden ball is dropped from a height of 2 m. What is the height up to which the ball will rebound if the coefficient of restitution is 0.5?
Answer:
Here, e =0.5
Let the ball fall from a height h1 from point A and rebound to B at a height of h₂.
∴ h₁ = 2 m

∴ If u₁ be the velocity on reaching the ground = velocity of approach and u₂ = Velocity on leaving the ground = velocity of separation

Question 11.
What percentage of K.E. of a moving particle is transferred to the stationary particle of
(a) 9 times it’s mass
Answer:
Let m₁ = mass of moving particle = m
and m₂ = mass of stationary particle = 9 m
and their velocities are u₁ and u₂ = 0 (given)
v₂ = velocity of the stationary particle after the collision.

So, % of K.E. transferred to the stationary particle

(b) equal mass,
Answer:

(c) \(\frac{1}{9}\) th of its mass.
Answer:

Question 12.
Calculate the work done in raising a stone of mass 6 kg of specific gravity 2 immersed in water from a depth of 4 m to 1 m below the surface of the water. Take g = 10 ms^-2.
Answer:
Here, m = 6 kg
∴ weight of stone = 6 × 10 = 60 N
specific gravity of stone = 2
∴ d = density of stone
= 2 × lg cm^-3
= 2g cm^-3.

∴ volume of stone = \(\frac{\mathrm{m}}{\mathrm{d}}=\frac{6 \times 1000 \mathrm{~g}}{2 \mathrm{gcm}^{-3}}\) = 3000 cm3
= 3000 × 10^-6 m³
= 3 × 10^-3 m³
= volume of displaced water.

Weight of water displaced or upward thrust on the stone
= volume × density of water × g
= 3 × 10^-3 × 1000 × 10 = 30 N

∴ The net force acting on the stone = weight of stone – upward thrust on the stone
or F = 60 – 30 = 30 N
Distance through which stone is raised = (4 – 1 )m = 3m
∴ work done, W = FS = 30 × 3 = 90 J.

Question 13.
An antenna radiates energy for 24 hours at the rate of 1 kW. Calculate the equivalent mass for radiated energy.
Answer:

Question 14.
A particle moves from position r₁ = 3î + 2ĵ – 6k̂ to position r₂ = 14î + 13ĵ – 9k̂ under the action of a force (4î + ĵ + 3k̂)N. Calculate the work done.
Answer:
Here, F = (4î + ĵ + 3k̂)N
Displacement of the particle,

Question 15.
The displacement x of a particle moving in one dimension under the action of a constant force is related to the time by the equation t = \(\sqrt{x}\) + 3.
where x is in meters and t is in seconds.
Find (i) the displacement of the particle when its velocity is zero and
(ii) work is done by force in the first six seconds.
Answer:

Question 16.
A 1 kg mass on a floor is connected to a 2 kg mass by a string passing over a pulley as shown in the figure. Obtain the speed of the masses (after they are released) when the 2 kg mass just touches the floor. Show that the gain in kinetic energy of the system equals the loss in its potential energy. The 2 kg mass is initially at a height 3 m above the ground.
Answer:
Here, m₂ = 1kg
m₁ = 2kg
u = 0
h = 3m
The system is shown in the figure. According to Newton’s Second law of motion, the equation of motion for 2 kg mass is
mg – T = ma
or
2 × 9.8 – T = 2a …(i)


(Free body diagrams of m₁ and m₂)

Since both the masses are initially at rest, therefore initial K.E. of the system = 0
Final K.E. of the system

∴ Gain in K.E. = 29.4 – 0 = 29.4 J
Initially P.E. of the system = m₁gh₁ + m₂gh₂
= 2 × 9.8 × 3 + 1 × 9.8 × 0
= 58.8 J ( ∵ here h₂ = 0)

Finally, the 2 kg reaches the floor and mass 1 kg is at a height of 3m.
∴ Final P.E. of the system = m₁gh₁ + m₂gh₂
= m₁g × 0 + 1 × 9.8 × 3
= 29.4 J

∴ Loss of P.E. = 58.8 – 29.4
= 29.4 J
Thus Gain in K.E. = Loss of P.E. = 29.4 J.

Question 17.
A homogeneous and inextensible chain of length 2 m and mass 100 g lies on a smooth table, A small portion of the chain of length 0.5 m hangs from the table. Initially, the part of the chain lying on the table held and then released. Calculate the velocity with which the chain leaves the table, g = 10 ms’2.
Answer:
Mass of chain, M = 100 g = 0.1 kg
length of chain, l = 2 m

∴ Mass per unit length of the chain, m = \(\frac{M}{l}\)


Let v = velocity of the chain when it leaves the table.

Question 18.
The K.E. of a body increases by 300%. How much linear momentum of the body will increase?
Answer:

Question 19.
A ball falls under gravity from a height of 10m with an initial downward velocity of u. It collides with the ground, loses 50% of its energy in the collision, and then rises back to the same height. Find the initial velocity u.
Answer:
Here, u = initial velocity of the ball
h = its height

Let M = mass of the ball
∴ The total initial energy of the ball at height h,

The ball rises to height h due to this energy.
∴ P.E. of ball = mgh
∴ According to the law of conservation of energy

Question 20.
The heart of a man pumps 4-liter blood per minute at a pressure of 130 mm of mercury. If the density of mercury is 13.6 gm cm³, then calculate the power of the heart.
Answer:
Here, the height of the mercury column,

Question 21.
A body is allowed to fall from a height of 100 m. Find the increase in temperature of the body on reaching the ground if the whole of heat produced remains in the body. Given that the specific heat of the body = 0.2, J = 4.2 J cal^-1.
Answer:
Loss in P.E. of the body in falling through 100 m = m × 9.8 × 100 J = \(\frac{980 \mathrm{~m}}{4.2}\) (∵ P.E = mgh)

This loss is transformed into the heat state of the body = ms θ
where θ = rise in temperature.

Question 22.
A truck of mass 2000 kg has a velocity of 8 ms^-1 when it starts from a point to descend a slope 200 m long. The vertical height of the slope is 18 m and the truck arrives at the bottom with a velocity of 20 ms^-1. Calculate the resistance offered.
Take g = 10 ms^-2.

Answer:
Here, l = XY = length of slope.
= 200 m
OX = h = 18 m
Let u and v be the velocities of the .truck at points X and Y respectively.

Question 23.
A body of mass m slowly hauled up the hill by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force if the height of the hill is h, the length of its base is l, and the coefficient of friction is μ.

Answer:
Let PQ be the plane patch of the hill
dz = its length inclined at an angle θ with the horizontal

Force required to move the mass from P to Q
= mg sin θ + μmg cos θ

∴ Work done from P to Q = mg (sin θ + μcos θ).

∴ W = total work done in moving the mass m from A to B is given by

Question 24.
A chain of mass m and length l lying on a rough table starts sliding off the table all by itself till the hanging part equals n. Calculate the total work performed by the friction forces acting on the chain by the moment it slides off the table completely.
Answer:
Weight of suspended chain = n mg
weight of the part of the chain on the table = (1 – n) mg

Let μ = coefficient of friction of tabletop.
For sliding motion of the chain on the tabletop under the weight of’ the hanging chain,
μ(l – n) mg = n mg
or
μ = \(\frac{n}{1 – n}\) …(i)

The initial force of friction when the chain is pulled on the tabletop
= μ(1 – n)mg

Final force, when all the chain has been pulled = 0
mean friction = \(\frac{\mu(1-n) m g}{2}\)

Distance for which the chain is pulled = – (1 – n)l
∴ W = mean force × distance

Question 25.
A flexible chain of length l and mass m is slowly pulled up at a constant speed over the edge of a table by a force F(x) parallel to the edge of the tabletop. Calculate the work done by F(x).
Answer:
Here the force required to pull the chain over the table varies with distance.
It is equal to the weight of the fraction of the chain \(\frac{(l-\mathrm{x})}{l}\)still hanging over the edge.

Value-Based Type:

Question 1.
Rajesh and Rakesh are two friends who participated in a quiz contest. The teacher asked Ramesh to lift a 20 kg weight vertically upwards to a height of 10 m and Rekcsh asked to pull 20 kg of weight by a rope over a pulley from a depth of 10 m from a well. There was a prize for one who will do more work. Rajesh claimed that he has done more work than Rakesh because he has not used any kind of lever. The teacher told Rajesh that he has done zero work but Rakesh has done the work. Hence, the prizes were given to Rakesh
(i) Why the teacher told that Rajesh did not do any work? justify your answer.
Answer:

1. The teacher wanted to check the knowledge of physics and awareness in a playful manner.
   He used the demonstration method to create interest.
2. We know that:
   W = F d cos θ
   In the case of Rajesh:
   θ = 90° and cos 90°=o
   ∴ work done(w) =Fd × o = o
   Hence, no work was done.

Question 2.
Shikha is doing her Engineering from IIT Delhi. Her mother was also an Engineer who wanted to check the knowledge of her daughter. She asked a question as to under. “If we assume that the moon orbits around the earth is perfectly circular then the earth’s gravitational force does no work. Is it correct?”
She explained that the moon’s displacement is tangential Whereas the earth’s force is inwards and θ = \(\frac{π}{2}\)
So, W = F.d. cos \(\frac{π}{2}\) = o
(i) Which values are displayed by Shikha?
Answer:
Values displayed are:
Explanatory, intelligent, cooperative.

(ii) Why her mother asked such a question?
Answer:
Her mother wanted to test the knowledge and presence of mind of her daughter to ask such type of tricky questions.

Question 3.
Suraj went to Big Bazaar to purchase certain goods. There he has noticed an old lady struggling with her shopping. Immediately he showed her the lift and explained to her how it carries the load from one floor to the next. Even then the old lady was not convinced. Then Suraj took her in the lift and showed her how to operate it..That old lady was very happy.
(a) What values does Suraj possess?
Answer:
Suraj is sympathetic and also has the attitude of helping others. He has patience.

(b) An elevator can carry a maximum load if 1800 kg is mov¬ing up with a constant speed of 2 m/s, The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horsepower.
Answer:
The downward force on the elevator is
F = mg + F_f = (1800 × 10) + 4000 = 22000 N

The motor must supply enough power to balance this force.
Hence P = F.V = 22000 × 2 = 44000 = 59 hp

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 5 Laws of Motion. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 5 Important Extra Questions Laws of Motion

Laws of Motion Important Extra Questions Very Short Answer Type

Question 1.
(a) Why do we beat dusty blankets with a stick to remove dust particles?
Answer:
It is done due to inertia of rest.

(b) A stone when thrown on a glass window smashes the window pane to pieces. But a bullet fired from a gun passes through it making a hole. Why?
Answer:
This is due to the inertia of rest.

Question 2.
(a) If you jerk a piece of paper from under a book quick enough, the book will not move, why?
Answer:
It is due to the inertia of rest.

(b) Passengers sitting or standing in a moving bus fall in forward direction when the bus suddenly stops. Why?
Answer:
This is due to the inertia of motion.

Question 3.
(a) Why passengers are thrown outward when a bus in which they are travelling suddenly takes a turn around a circular road?
Answer:
This is due to the inertia of direction.

(b) Is any force required to move a body with constant velocity?
Answer:
No.

Question 4.
(a) Why a one rupee coin placed on a revolving table flies off tangentially?
Answer:
This is due to the inertia of direction.

(b) Why mud flies off tangentially to the wheel of a cycle?
Answer:
This is due to the inertia of direction.

Question 5.
(a) When the electric current is switched off, why the blades of a fan keep on moving for some time?
Answer:
This is due to the inertia of motion.

(b) Why the passengers fall backward when a bus starts moving suddenly?
Answer:
This is due to the inertia of rest.

Question 6.
(a) A body of mass m is moving on a horizontal table with constant velocity. What is the force on the table?
Answer:
mg i.e. equal to the weight of the body.

(b) Name a factor on which the inertia of a body depends.
Answer:
Mass.

Question 7.
(a) Rocket works on which principle of conservation?
Answer:
Law of conservation of linear momentum.

(b) Is the relation \(\overrightarrow{\mathbf{F}}=\mathbf{m} \overrightarrow{\mathbf{a}}\) applicable to the motion of a rocket?
Answer:
No.

Question 8.
(a) Will a person while firing a bullet from a gun experience a backward jerk? Why?
Answer:
Yes, it is due to the law of conservation of linear momentum.

(b) A bomb explodes in mid-air into two equal fragments. What is the relation between the directions of their motion? Answer:
The two fragments will fly off in two opposite directions.

Question 9.
(a) What happens to the acceleration of an object if the net force on it is doubled?
Answer:
As a = \(\frac{F}{m}\) i.e. a ∝ F, so acceleration will be doubled when m the force is doubled.

(b) An electron moving with a certain velocity collides against a stationary proton and sticks to it. Is the law of conservation of linear momentum true in this case?
Answer:
Yes, it is true.

Question 10.
(a) According to Newton’s third law of motion, every force is accompanied by an equal (in magnitude) and opposite (in direction) force called reaction, then how can a movement take place?
Answer:
As the action and reaction never act on the same body, so the motion is possible.

(b) You can move a brick easily by pushing it with your foot on a smooth floor, but, if you kick it, then your foot is hurt. Why?
Answer:
As Ft remains constant, so if t is reduced, then F will be increased and hence hurt our foot.

Question 11.
(a) Why does a swimmer push the water backward?
Answer:
So as to get forward push according to Newton’s third law of motion.

(b) Why does not a heavy gun kick so strongly as a light gun using the same bullets (i.e. cartridges)?
Answer:
The recoil speed of the gun is inversely proportional to its mass. So the recoil speed of the heavy gun is lesser than that of the light gun.

Question 12.
(a) Can a rocket operate in free space?
Answer:
Yes.

(b) In a game of tug of war, two opposing teams are pulling the rope with equal (in magnitude) but the opposite force of 1000 kg wt at each end of the rope. What is the tension in the rope if a condition of equilibrium exists?
Answer:
1000 kg wt.

Question 13.
(a) Which of Newton’s laws of motion is involved in rocket propulsion?
Answer:
Newton’s third law of motion.

(b) Action and reaction are equal in magnitude and opposite in direction, then why do not they cancel/balance each other?
Answer:
They don’t balance each other as they act on different bodies.

Question 14.
(a) A passenger sitting in a bus at rest pushes it from within. Will it move? Why?
Answer:
No, internal forces are unable to produce motion in a system.

(b) How would you explain the motion of a motorcyclist in a globe of death in a circus?
Answer:
It is a case of motion in a vertical circle.

Question 15.
Can a body in linear motion be in equilibrium? why?
Answer:
Yes, it will be in equilibrium if the vector sum of the forces acting upon the body is zero.

Question 16.
Is the law of conservation of momentum valid for a system consisting of more than two particles?
Answer:
Yes, the law of conservation of momentum is a general law that is applicable to all systems.

Question 17.
Which is greater out of the following
(i) The attraction of 1 kg lead for Earth,
(ii) the attraction of Earth for 1 kg of lead? Why?
Answer:
Both are equal, the forces of action and reaction are always equal and opposite in direction according to Newton’s third law of motion.

Question 18.
Mention the conditions for the maximum and minimum pull of a lift on a supporting cable.
Answer:

1. The pull of the cable is minimum (zero) when the lift is falling freely.
2. The pull of the cable is maximum when the lift is moving up with the same acceleration.

Question 19.
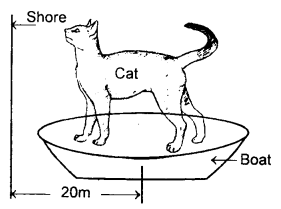
A man is at rest in the middle of a pond on perfectly frictionless ice. How can he get himself to the shore of the pond?
Answer:
He can get himself to the shore if he throws away his shirt or anything in his possession in a direction opposite to the desired direction of motion or by spitting in the forward direction or by blowing air from his mouth.

Question 20.
Suppose you are seated in a cabin that has no doors, no windows, etc., and is also soundproof. Shall it be possible to detect the uniform velocity with which this cabin is moving? Why?
Answer:
No, this is because when the cabin is. moving with uniform velocity, there will be no net unbalanced force.

Question 21.
(a) Why do we pull the rope downwards for climbing up?
Answer:
When we pull the rope downwards, an upward reaction helps us to rise up.

(b) Why is it easier to roll than to pull a barrel along a road?
Answer:
It is due to the fact that rolling friction is less than sliding friction.

Question 22.
(a) Why are the lubricants used in machines?
Answer:
Lubricants are used in machines so as to reduce friction.

(b) Friction is independent of the area, but brakes of a very small contact area are not used. Why?
Answer:
This is done so as to avoid wear and tear.

Question 23.
Mention a factor on which coefficient of friction depends.
Answer:
The coefficient of friction depends upon the nature of the surfaces in contact.

Question 24.
Carts with rubber tires are easier to ply than those with iron tires. Why?
Answer:
The coefficient of friction between the rubber tires and the road is lesser than the coefficient of friction between iron and steel.

Question 25.
Why are wheels made circular? Explain.
Answer:
Circular wheels roll without sliding on the road. Since rolling friction is less than sliding friction, so they move easily.

Question 26.
(a) What do you mean by dry friction?
Answer:
When both the bodies in contact are solids, then the force of friction is called dry friction.

(b) A soda water bottle is falling freely. Will the bubbles of the gas rise in the water of the bottle?
Answer:
A freely falling soda water bottle is in a state of weightlessness. Thus the bubbles of the gas will not rise in the water of the bottle rather they remain floating.

Question 27.
What do you mean by liquid or fluid or wet friction?
Answer:
It is defined as the friction which conies into play between a surface and a liquid or fluid.

Question 28.
“Friction is a self-adjusting force.” Is this statement correct?
Answer:
This statement is correct only so long as the friction is static friction. Up to the limiting friction, the force of friction is equal (in magnitude) and opposite to the applied force.

Question 29.
(a) Several forces act simultaneously on a body. In which direction will it move?
Answer:
It will move in the direction of the net force.

(b) Name the physical quantity which is a measure of inertia of a body?
Answer:
Inertial mass.

Question 30.
Can a force change only the direction of the velocity of an object keeping its magnitude constant?
Answer:
Yes, a force can only change the direction of the velocity of an object keeping its magnitude constant.

Question 31.
(a) Two objects having different masses have some momentum. Which one of them will move faster?
Answer:
The object with a smaller mass will move faster.

(b) A table is lying on the floor of a room. Is some force of friction acting on it?
Answer:
No.

Question 32.
(a) A book is lying on an inclined plane. Is some force of friction acting on the book?
Answer:
Yes

(b) Name the physical quantity which can be found from the area under the force-time graph.
Answer:
Impulse

(c) Will the body be in equilibrium under the action of three non-coplanar forces.
Answer:
No.

Question 33.
(a) Write the S.I. units of force, momentum, and impulse.
Answer:
S.I. unis of force, momentum, and impulse are newton (N), kg ms^-1, and Ns (Newton-second).

(b) Why should the hammer be heavier to push the nail deeper into the wooden blocks?
Answer:
It should be heavier so as to increase the impact of force i.e. more force applied for a shorter time.

Question 34.
(a) Why rockets are given conical shapes?
Answer:
The rockets are given conical shapes so as to reduce atmospheric friction.

(b) How does air friction affect the maximum height of a projectile?
Answer:
The maximum height of a projectile is reduced due to air friction.

Question 35.
(a) Explain why jet planes cannot move in air-free space but rockets can move?
Answer:
Jet planes use atmospheric oxygen to foil their fuel but rockets carry their own fuel and don’t depend on atmospheric oxygen.

(b) Is it correct to state that a body always moves in the direction of the net force acting on it?
Answer:
The statement is true only for bodies at rest before the application of force.

Question 36.
At which place on Earth, the centripetal force is maximum?
Answer:
The centripetal force is maximum at the equator.

Question 37.
What provides the centripetal force in the following cases?
(i) Electron revolving around the nucleus.
Answer:
It is provided by
The electrostatic force of attraction between the electron and the nucleus.

(ii) Earth revolving around the sun.
Answer:
The gravitational force of attraction between Earth and Sun.

(iii) Car taking a turn on a banked road.
Answer:
A component of the reaction of the road.

Question 38.
(a) What is the direction of the angular velocity of the minute hand of a wall-clock?
Answer:
The direction of the angular velocity of the minute hand of a wall- clock is perpendicular to the wall and directed inwards.

(b) What is the difference between ‘Newton’ and ‘newton’?
Answer:
Newton is the name of a scientist but newton is the S.l. unit of force named after the scientist Newton.

Question 39.
(a) Is it possible that a particle moving with a constant velocity may not have a constant speed?
Answer:
No.

(b) For uniform circular motion, does the direction of centripetal force depend on the sense of rotation {i.e. clockwise or anti-clockwise)?
Answer:
No. It is always radial irrespective of the sense of rotation.

Question 40.
Why chinaware crockery is wrapped in paper or straws?
Answer:
Paper or straw provides a cushion between th° pieces of crockery.
In case of any jerk (impulse), these will prolong the time of impact and reduce its effect, the crockery will thus be saved.

Question 41.
AH, vehicles are provided with springs and shockers, why?
Answer:
To reduce the impact of force on the vehicle as shockers and springs break the impact of force and increase the time of action of force thus reduce the impulse and save the vehicle from shock.

Question 42.
A body falls from a single-story building roof on a muddy floor and another boy falls from the same height on a stone, who is likely to survive out of them and why?
Answer:
The boy who falls on a muddy floor will survive due to the reduction of the impact of force by prolonging the time of reduction of force from maximum to zero.

Question 43.
What is the effect on the direction of centripetal force when the revolving body reverses its direction of motion?
Answer:
The centripetal force will be directed towards the center of the circle. This fact does not depend upon the sense of the rotation of the circle.

Question 44.
Is it correct to say that the banking of roads reduces the wear and tear of the tires of automobiles? If yes explain.
Answer:
Yes, if the road is not banked, then the necessary centripetal force will be provided by the force of friction between tires and the road. On the other hand; when the road is banked, a component of the normal reaction provides the necessary centripetal force, which reduces wear and tear.

Question 45.
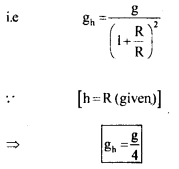
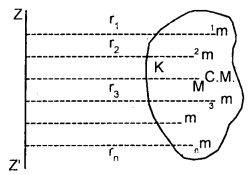
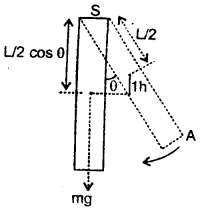
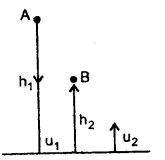
The linear velocity of a particle moving on the circumference of the circle is equal to the velocity acquired by a freely falling body through a distance equal to one-fourth the diameter of the circle. What is the centripetal acceleration of the particle moving along the circle?
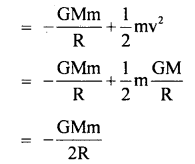
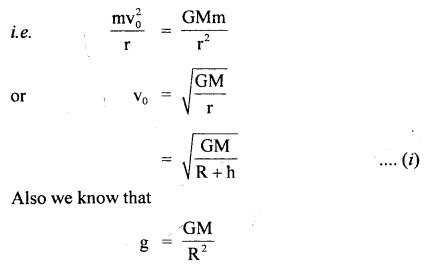
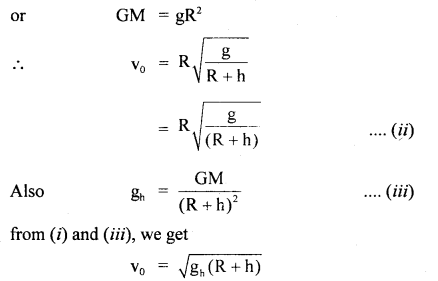
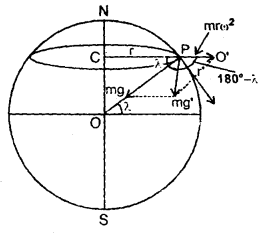
Answer:

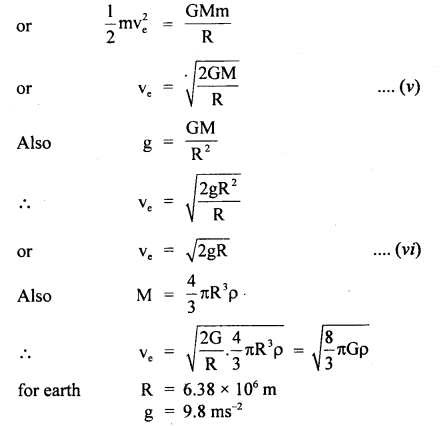
Question 46.
(a) A body is moving with uniform velocity. Can it be said to be in equilibrium? Why?
Answer:
Yes, it can be said to be in equilibrium when it moves with uniform velocity as no acceleration i.e. no net force acts on the body.

(b) Why Newton’s second law of motion is not applicable to the motion of a rocket?
Answer:
Newton’s second law i.e. F = ma is applicable only if the mass (m) of the body remains constant. In the case of the rocket, the mass continuously decreases and hence F = ma is not applicable.

Question 47.
(a) A thief jumps from the upper story of a house with a load on his back. What is the force of the load on his back when the thief is in the air?
Answer:
When the thief is in the air, he is in the state of free fall, and hence in the state of weightlessness. So the force of the load on his back is zero.

(b) When a body falls to the Earth, the Earth also moves up to meet it. But the motion of Earth is not noticeable. Why? Answer:
We know that acceleration is the ratio of the applied force to the mass of the body. As the mass of Earth is very large, so its acceleration is very small.

Question 48.
What are the different effects a force is capable of producing?
Answer:
Force can cause the following

1. Circular motion
2. Translatory motion
3. Deformations in the body on which it is applied.

Question 49.
A ball is thrown up at a speed of 36 ms-1 by a thrower. If the ball returns to the thrower with the same speed. Will, there be any change in:
(a) Momentum of the ball?
Answer:
There will be a change in the direction of the momentum of the ball.

(b) Magnitude of the momentum of the ball?
Answer:
There is no change in the magnitude of the momentum of the ball.

Question 50.
When a ball falls from a height its momentum increases. What causes the increase in the momentum of the ball?
Answer:
The gravitational force acting in the direction of motion increases the velocity and hence momentum of the ball.

Question 51.
When a high jumper leaves the ground, where does the force which accelerates the jumper upward comes from?
Answer:
The high jumper after taking a short run presses the ground hard, the ground, in turn, reacts on him and provides the necessary upward accelerating force to the jumper. Thus, the reaction of the ground on the jumper is the required force.

Question 52.
Name the forces which are in equilibrium in each of the following situations:
(a) a book resting on a table.
Answer:
The gravitational force on the book and a force of reaction of the table.

(b) a cork floating on water.
Answer:
The gravitational force on the cork and an upward thrust or buoyant force of water.

(c) a pendulum bob suspended from the ceiling with the help of a string.
Answer:
The gravitational force on the bob and the tension in the string.

Laws of Motion Important Extra Questions Short Answer Type

Question 1.
(a) A learner shooter fired a shot from his rifle and his shoulder got injured ¡n the process. What mistake did he commit?
Answer:
We know that a gun recoils i.e. moves back after firing. To avoid injury to the shoulder, the gun must he held tightly against the shoulder. The learner shooter might have not held it tightly against his shoulder and hence the gun must have injured his shoulder after firing.

(b) When the horse suddenly stops, the rider falls in the forward direction. Why? Explain it.
Answer:
When the horse suddenly stops, the rider falls in forwarding direction due to the inertia of motion.

Explanation: The lower portion of the rider comes to rest along with the horse while the upper portion of the rider continues to move forward. Hence, he falls forward.

Question 2.
(a) Newton’s first law of motion is the law of Inertia. Explain.
Answer:
According to Newton’s first law of motion, a body can’t change its state of rest or of uniform motion along a straight line unless an external force acts on it. It means that the natural tendency of the material body is to continue in the state of rest or that of uniform motion which is termed as inertia. Thus Newton’s first law is the law of inertia.

(b) What happens to a stone tied to the end of a string and whirled in a circle if the string suddenly breaks? Explain why?
Answer:
The stoneflies off tangentially to the circle along a straight line at the point where the string breaks. It is due to the inertia of direction. When the string breaks, the force acting on the stone ceases. In the absence of force, the stoneflies away in the direction of instantaneous velocity which is along the tangent to the circular path.

Question 3.
(a) An astronaut accidentally gets separated out of his small spaceship accelerating in inter-steller space at a constant rate of 100 ms^-2. What is the acceleration of the astronaut at the instant after he is outside the spaceship?
Answer:
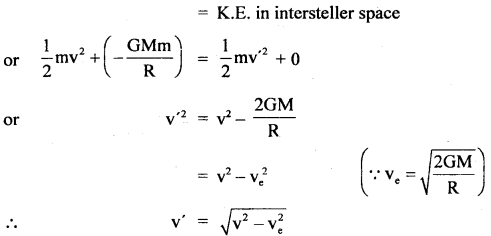
According to Newton’s first law of motion, the moment he is out of the spaceship, there is no external force on the astronaut, thus his acceleration is zero. Here we are assuming that he is out of the gravitational field of heavenly bodies i.e. there are no nearby stars to exert a gravitational force on him and the small spaceship exerts a negligible gravitational attraction on him.

(b) How is it that a stone dropped from a certain height falls much more rapidly as compared to a parachute under similar conditions?
Answer:
As the surface area of a parachute is much larger as compared to the surface area of a stone, so the air resistance, i. e. fluid friction in the case of the parachute is much larger than in the case of stone. Hence the parachute falls slowly.

Question 4.
(a) When a man jumps out of a boat, then it is pushed away. Why?
Answer:
This is due to Newton’s third law of motion. When the man jumps out of the boat, he applies a force on it in the backward direction, and in turn, the reaction of the boat on the man pushes him out of the boat.

(b) Explain how lubricants reduce friction?
Answer:
The lubricants spread as a thin layer between the two surfaces. The motion now is between the surface and the lubricant layer which changes the dry friction into wet friction. As wet friction is less than dry friction, hence lubricants reduce friction.

Question 5.
Two hoys on ice-skates hold a rope between them. One boy is much heavier than the other. The lightweight boy pulls on the rope. How will they move?
Answer:
The light-weight boy is doing the action on the heavy boy by pulling the rope. According to Newton’s third law, equal and opposite force (reaction) also acts on the light boy. As the mass of the boy pulling the rope is lesser, so the acceleration produced in him will be more. Thus both the boys move tow; rds each other and the lighter boy will move faster.

Question 6.
Explain why ball bearings are used in machinery?
Answer:
We know that rolling friction is much lesser than sliding friction, so we convert the sliding friction into rolling friction which is done using ball bearings that are placed in between the axle and the hub of the wheel. The ball bearings tend to roll around the axle as the wheel turns and as such the frictional force is reduced.

Question 7.
Why a horse has to apply more force to start a cart than to keep it moving? Explain.
Answer:
Static friction comes into play when the horse applies force to start the motion in the cart. On the other hand, kinetic friction comes into play when the cart is moving.

Also, we know that the static friction is greater than the kinetic friction, so the horse has to apply more force to start a cart than to keep it moving.

Question 8.
Sand is thrown on tracks or roads covered with snow. Explain why?
Answer:
When the roads (or tracks) are covered with snow, then there is a considerable reduction of frictional force between the tires of the vehicles and the road (or between the track and the wheels of the vehicle or train) which leads to the skidding of the vehicles (or trains). Thus, driving is not safe. When sand is thrown on the snow-covered roads (or tracks), then the force of friction increases, so safe driving is possible.

Question 9.
Explain why is it difficult to move a cycle along a road with its brakes on?
Answer:
When we move the cycle with its brakes on, then its wheels can only skid i.e. slide along the road as they can’t rotate. So the friction is sliding in nature. As the sliding friction is greater than fr,e rolling friction, therefore, it is difficult to move a cycle with its brakes on.

Question 10.
Explain how proper inflation of tires saves fuel?
Answer:
When the tires are properly inflated, the area of contact between the tires and the ground is reduced which in turn reduces the rolling friction. As a result of this, there is less dissipation of energy against friction. So the cover of the automobile/eater distance for the same quantity of fuel consumed. Hence proper inflation of tires leads to saving fuel.

Question 11.
Explain how the man at rest in the middle of a pond of perfectly frictionless ice comes out by blowing air or splitting etc.?
Answer:
By blowing air from b’s mouth in a forwarding direction, the man applies some force in that direction and hence imparts some momentum to the air blown out from his mouth. According to the law of conservation of linear momentum, an equal and opposite momentum will be imparted to his body. Since there is no force of friction and hence no energy is wasted. Finally, by doing the same action again and again he gets himself on the shore.

Question 12.
Give one argument in favor of the fact that frictional force is a non-conservative force.
Answer:
The direction of the frictional force is opposite to the direction of motion. When a body is moved, say from point A to B and then back to A, then work is required to be done both during forward and backward motion. So the network done in a round trip is not zero. Hence the frictional force is a non-conservative force.

Question 13.
Why is it more dangerous to fall on frozen ice than on fresh snow?
Answer:
The fresh snow is softer and frozen ice is harder. So the impulse caused by falling on fresh snow is much lesser than frozen snow. Thus, falling on frozen ice may cause serious injury or maybe fatal (the reaction will be much greater in this case).

Question 14.
(a) An astronaut in open space is away from his spaceship. How can he return to his ship?
Answer:
Using Newton’s third law of motion, he can reach his spaceship. He must throw objects with appropriate force opposite to the direction of the spaceship. The recoil will send him-to his spaceship.

(b) Why mudguards are used in vehicles?
Answer:
The mud stuck to the tires fly off tangentially to the tires due to the inertia of direction. The mudguards are i so placed that they come in the way of mud and it is stopped by them from spilling all over.

Question 15.
What is the difference between absolute and gravitational units of force?
Answer:
The absolute units of force don’t depend upon the value of acceleration due to gravity, so they remain the same throughout the universe. But the gravitational units of force depend upon the value of ‘g’ which is different at different places.

Question 16.
A disc of mass m is placed on a table. A stiff spring is attached to it and is vertical. To the other end of the spring is attached a disc of negligible mass. What minimum force should be applied to the upper disc to press the spring such that the lower disc is lifted off the table when the external force is suddenly removed?
Answer:
The minimum force should be mg. When a force mg is applied vertically downwards on the upper disc, the lower disc will be pressed against the floor with a force mg. The floor will exert an upward reaction mg. When the external force is suddenly removed, this reaction will just lift the lower disc.

Question 17.
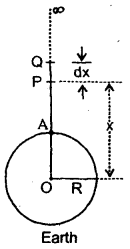
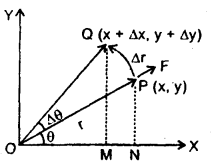
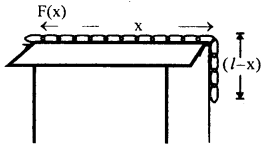
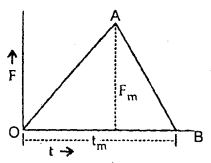
A force acting on a material particle of mass m first grows to a maximum value Fm and then decreases to zero. The force varies with time according to a linear law, and the total time of motion is t_m. What will be the velocity of the particle at the end of this time interval if the initial velocity is zero?
Answer:
In the given problem,

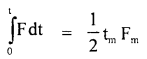
= area under F – t graph
= area of ΔOAB ..(1)

Also by definition of impulse, we know that

Where m = mass of the particle,
v = its velocity after time interval
i.e. after time tm

∴ From (1) and (2), we get

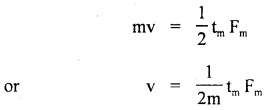
Question 18.
Sometimes we need to increase friction. Why? Given an example.
Answer:
Sometimes friction between two surfaces decreases to such an extent that it is difficult to move on that surface. So friction needs to be increased. For example, vehicles can’t move on a road covered with snow. In such cases, we have to throw sand on the road to increase the friction.

Question 19.
Vehicles stop applying brakes. Does this phenomenon violate the principle of conservation of momentum?
Answer:
The law of conservation of momentum is not violated by stopping vehicles from applying brakes. Some retarding force is being applied due to brakes and the vehicle comes to rest such that the total loss of its momentum is equal to the impulse of the applied force. Thus the law of conservation of momentum is not violated.

Question 20.
“Two surfaces if made extremely smooth, will have a very low value of friction between them.” Is the statement true? Justify your answer with two illustrations.
Answer:
The given statement is wrong. This is because the force of frictions increased when the surfaces in contact are made highly smooth.

Examples:

1. In factories, the conveyer belt is made smooth by rubbing it with wax or resin. The wheel over which the belt is to move is also made extremely smooth. Due to the increased force of friction between the belt and the wheel, slipping does not take place.
2. The wheels of the railway train and the surfaces of the railway tracks are also made very smooth.

Question 21.
Why force of friction increases when the two surfaces in contact are made extremely smooth i.e. polished beyond a certain limit?
Answer:
When the two surfaces in contact are made extremely smooth, then they come in intimate contact with each other. So the force of adhesion comes into play- Due to this force, the motion of one surface over the other surface becomes retarding and hence causes an increase in the friction.

Question 22.
(a) A small amount of water spread on a marble floor causes slipping. Why?
Answer:
Water fills the grooves in the floor and makes it more smooth thus reducing friction and it causes slipping.

(b) Why automobile tires have generally irregular projections over their surface?
Answer:
The automobile tires have generally irregular projections over their surface so as to

1. Increase friction.
2. Increase the grip with the ground and thus avoiding their skidding.

Question 23.
A body moving over the surface of another body suddenly comes to rest. What happens to friction between the two surfaces?
Answer:
The force of friction will be present only so long as there is relative motion between the two bodies and it automatically disappears as soon as the relative motion ceases.

Question 24.
Explain why one should take short steps rather than long steps while walking on ice?
Answer:
There is a danger of slipping if one walks on ice by taking long steps. This can be explained as –

Explanation: Let R represents the reaction offered by ice while walking on it.
Also, let mg = weight of the person walking on the ice.

Let f = force of friction between ice and the foot of the person walking on it.
Let θ = angle made by R with the vertical.

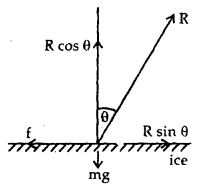
The rectangular components of R are shown in the figure. The vertical component i.e. R cos θ will balance the weight of the person and the horizontal component i.e. R sin θ will help the person to walk forward by balancing the f.
i. e. R cos θ = mg …(i)
and R sin θ = f …(ii)

Dividing (ii) by (i), we get

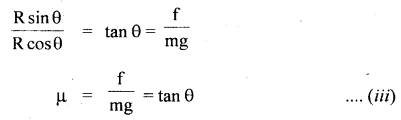
where μ = coefficient of friction and has a fixed value.

If steps are longer, then θ is more, so tan θ will be more. But as p. is fixed, so f is to be increased which is not possible, hence there is a danger of slipping in a long step.

Question 25.
Why a cricket player lowers his hands while catching a cricket ball?
Answer:
While taking a catch, a cricket player moves his hands backward. He has to apply retarding force to stop the moving ball in his hands. If he catches the ball abruptly, then he has to apply a large retarding force for a short time. So he gets hurt.

On the other hand, if he moves his hands backward then the player applies the force for a longer time to bring the ball to rest. In this case, he has to apply less retarding force and thus will not get hurt.

Thus to avoid injuries to his hands, he lowers his hands while catching a cricket ball.

Question 26.
Why are buffers provided between the bogies of a railway train?
Answer:
Buffers are provided between the bogies of a train to reduce shocks or jerks by reducing the impulse or impact of a force. Springs of buffers increase the time of contact in the collision of bogies and thus the force acting on the bogies will be small and hence the passengers sitting inside the train will feel fewer jerks.

Question 27.
It is more difficult to catch a cricket ball than to catch a tennis ball moving with the same velocity. Explain why?
Answer:
The mass of a cricket ball is greater than the mass of a tennis ball, so the change in momentum of the cricket ball is more than that of the tennis ball. Hence greater force is required to catch the cricket ball than that of the tennis ball.

Question 28.
(a) A body of mass 25 g is moving with a constant velocity of 5 ms’1 on a horizontal frictionless surface in a vacuum, what is the force acting on the body?
Answer:
F = ma, where a = acceleration of the body.
For constant velocity, a = 0, so F = 0.
Thus when a body moves with constant velocity then no force acts on it.

(b) A bird is sitting on the floor of a wire cage and the cage is in the hand of a boy. The bird starts flying in the cage. Will the boy experience any change in the weight of the cage? Why?
Answer:
Lighter. Since the cage is made of wire, the air inside the cage is not bound with the cage, rather it is in contact with the atmospheric air. Therefore the boy will not experience the weight of the bird when it flies in the cage. Thus the cage will appear lighter when the bird starts flying in the cage.

Question 29.
A woman stands on a spring scale on an elevator. In which case will the scale record the minimum reading and the maximum reading?
(i) elevator stationery,
Answer:
When the elevator is stationary, then reading of the scale = actual weight of woman = mg.

(ii) elevator cable breaks, free fall,
Answer:
When the elevator falls freely, it is the case of weightlessness.
∴ Reading of the scale = m(g – g) = 0 (∴ a = g)

(iii) elevator accelerating upward and
Answer:
When the elevator accelerates upwards, the reading of the scale = m(g + a), where a = acceleration of the elevator.

(iv) elevator accelerating downward.
Answer:
When the elevator accelerates downwards, then the reading of the scale = m(g – a).
Thus, the reading of the scale is minimum when the elevator falls freely and the reading of the scale is maximum when the elevator accelerates upwards.

Question 30.
Two bodies of different masses m₁ and m₂ are falling from the same height. If resistance offered by the air be the same for both the bodies, then will they reach the Earth simultaneously? Assume m₁ > m₂?
Answer:
Let f be the resistance offered by the air for both the bodies.
If F = Net force acting on the body of mass m, i.e. weight W₁ = m₁g,

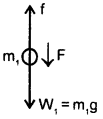
Then F = W₁ – f
= m₁g – f …(1)

If a₁ = acceleration produced in the body of mass m, then

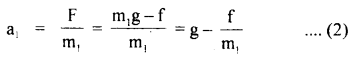
Similarly if a₂ be the acceleration produced in the body of mass m2,
then
a₂ = g – \(\frac{\mathrm{f}}{\mathrm{m}_{2}}\) ….(3)

Now as m₁ > m₂, so it is clear from equation (2) and (3) that
a₂ < a₁ or a₁ > a₂.

Thus, we conclude that the body having larger acceleration will reach earlier, so the body of larger mass will reach the earth earlier than the body of smaller mass.

Question 31.
How does air friction affect the maximum height of a projectile?
Answer:
The air friction reduces both vertical and horizontal components of velocity. The air friction depends on the volume of the body or the air displaced. So the height attained by the body in projectile motion is severely restricted by the air friction. The height reached is reduced compared to one which is attained in the absence of air.

Question 32.
Why is it difficult to climb a greasy pole or rope?
Answer:
For climbing any pole or rope, the climber presses the pole or rope with his feet which in turn pushes the feet and the person climbs up. But the man’s feet push the pole only if there is friction between the pole and the feet so that feet can hold on.

When grease is applied to the pole, the friction is sharply reduced and the foot cannot press it in the absence of friction. Thus, man does not get the reaction required to climb, hence it is difficult to climb a greasy pole or rope.

Question 33.
Does F = ma represent Newton’s second law of motion under all conditions? Give a reason for your answer.
Answer:
No, F = ma does not represent Newton’s second law of motion under all conditions. In fact the statement of Newton’s second law of motion relates force with a change in momentum of the body i. e.

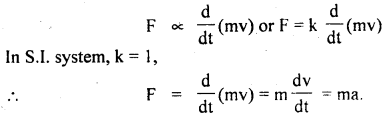
In a reference frame where the velocity of the body is too high i.e., it approaches the speed of light then mass does not remain the same. Thus, in that case,

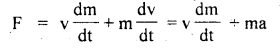
holds goods which are different from F = ma.

Question 34.
Several passengers are standing in a running bus, it is said to be dangerous. How will you justify the statement?
Answer:
There are three reasons for such situations to be dangerous –

1. Standing passengers raise the center of gravity of the bus and thus the bus comes in unstable equilibrium. This becomes dangerous.
2. A sudden brake applied by the driver will cause passengers to fall forward one over the other. Thus, they may be injured and there may be stamped.
3. If the bus is suddenly stopped, the passenger’s forward momentum may push it slightly ahead which may cause the accident in a congested traffic situation.

Question 35.
In a circus in the game of swing, the man falls on a net after leaving the swing but he is not injured, why?
Answer:
When the man falls on the net it is depressed where a man falls on it and thus the time of contact is increased. Due to this, the force of reaction on the man is reduced to a great extent. Because the increase in time reduces the impulse which is equal to the changes in momentum (FΔt = m Δv). So, F is quite less and the man is not injured by the net. In fact, F pushes him up once and again he falls on the net.

Question 36.
(a) A meteorite burns in the atmosphere before it reaches the Earth’s surface. What happens to its momentum?
Answer:
A meteorite while traveling towards earth shares its momentum with atmospheric particles and the remaining momentum is imparted to the Earth.

(b) By accident a person fell on a floating ice slab in a pond. He has nothing with him to get out and the ice slab is big enough so that he cannot put his hands or feet in the water. How can he save himself by coming out of the ice slab?
Answer:
The person should know how to generate a force so that the ice slab is thrown away opposite to the direction of the force along with. This, he can do by spitting forcefully or sneezing, etc. again and again till the slab reaches the shore of the lake from where he can get out from the slab by the same technique.

Question 37.
In pushing a box up an inclined plane, is it better to push horizontally or to push parallel to the inclined plane? Why?
Answer:
The box should be pushed by a force parallel to the plane. This will neither increase the reaction nor the force of friction. If the force is applied horizontally, only a component of the force will push the box up but the second component acting normally to the inclined plane will increase the reaction of the plane and thereby increase the force of friction. This will make the pushing of the box up the inclined harder.

Question 38.
Explain the role of friction in the case of bicycle brakes. What will happen if a few drops of oil are put on the rim?
Answer:
When the brakes are applied, the rubber padding creates

1. a normal force on the rim, and the brakes and
2. force of friction are created in the direction opposite to the rotation of the wheel.

Thus, brakes stop the rotation of the wheels and the cycle is stopped.

If a few drops of oil are put on the rim, the friction is reduced but brakes apply a force on the rim which increases the normal reaction and thereby the force of friction. No doubt that now bicycle will take a longer time to stop and a small amount of oil will be thrown out due to centrifugal force.

Question 39.
A man cannot run faster on the sandy ground but a snake can. Why?
Answer:
The greater friction of sandy ground stops the man from running faster but the snake gets support as its points of contact with the ground help in holding and pushing its body. The normal reaction of man is much more as compared to that of snake, that too is a factor in the relative force of friction acting on the two.

Laws of Motion Important Extra Questions Long Answer Type

Question 1.
(a) State and prove impulse-momentum Theorem.
Answer:
It states that the impulse of force on a body is equal to the change in momentum of the body.
i.e. J = F_t = P₂ – P₁

Proof: From Newton’s Second law of motion, we know that

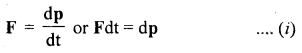
Let P₁ and P₂ be the linear momenta of the body at time t = 0 and t respectively.
∴ integrating equation (i) within these limits, we get


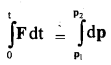
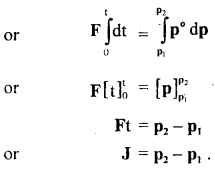
Hence proved.

(b) Prove that Newton’s Second law is the real law of motion.
Answer:
Proof: If we can show that Newton’s first and third laws are contained in the second law, then we can say that it is the real law of motion.
1. First law is contained in second law: According to Newton’s second law of motion,
F = ma …(i)
where m = mass of the body on which an external force F is applied and a = acceleration produced in it.

If F = 0, then from equation (1), we get
ma = 0, but as m ≠ 0
∴ a = 0

which means that there will be no acceleration in the body if no external force is applied. This shows that a body at rest will remain at rest and a body in uniform motion will continue to move along the same straight line in the absence of an external force. This is the statement of Newton’s first law of motion. Hence, the First law of motion is contained in the Second law of motion.

2. Third law is contained in second law: Consider an isolated system of two bodies A and B. Let them act and react internally.
Let FAB = force applied on body A by body B
and FBA = force applied on body B by body A

It \(\frac{\mathrm{d} \mathbf{p}_{\boldsymbol{A}}}{\mathrm{dt}}\) = rate of change of momentum of body A
and
\(\frac{\mathrm{d} \mathbf{p}_{\boldsymbol{B}}}{\mathrm{dt}}\) = rate of change of momentum of body B

Then according to Newton’s second law of motion,


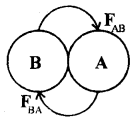
(2) and (3) gives

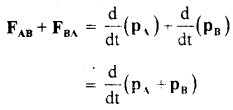
As no external force acts on the system (∵ it is isolated), therefore according to Newton’s second law of motion,

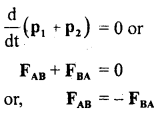
or
Action = – Reaction,
which means that action and reaction are equal and opposite. It is the statement of Newton’s 3rd law of motion. Thus 3rd law is contained in the second law of motion.

As both First and Third Law is contained in Second law, so Second law is the real law of motion.

Question 2.
Derive the general expression for the velocity of a rocket in flight and obtain the expression for the thrust acting on it.
Answer:
The working of a rocket is based upon the principle of conservation of momentum. Consider the flight of the rocket in outer space where no external forces act on it.
Let m_o = initial mass of rocket with fuel.
V_u = initial velocity of the rocket,
m = mass of the rocket at any instant t.
v = velocity of the rocket at that instant.
d_m = mass of the gases ejected by the rocket, in a small-time it.
u =H velocity of exhaust gases,
DV = increase in the velocity of the rocket in a time dt.

∴ Change in the momentum of exhaust gases = dm. u
Change in momentum of rocket = – (m – dm) dv.

A negative sign shows that the rocket is moving in a direction opposite to the motion of exhaust gases.

Applying the law of conservation of linear momentum,
dm.u = – (m – dm) dv …(1)

As dm being very small as compared to m, so it can be neglected, Thus, eqn. (1) reduces to
dm.u = – m dv
or
dv = – u \(\frac{dm}{m}\) …(2)

Instantaneous velocity of the rocket:
At t = 0, mass of rocket = m0, velocity of rocket = v_o.
At t = t, mass of rocket = m, velocity of rocket = v.

∴ Integrating Eqn. (1) within these limits, we get

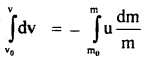
In actual practice, the velocity of exhaust gases nearly remains constant.

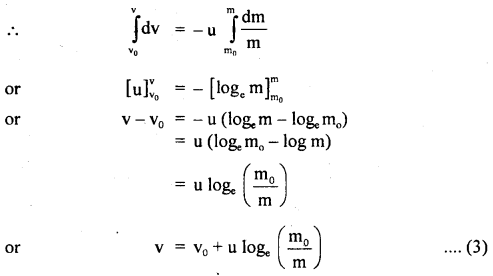
equation (3) gives the instantaneous velocity of the rocket. In general v_o = 0 at t = 0,

∴ Eqn. (3) reduces to

From Eqn. (4), we conclude that the velocity of the rocket at any instant depends upon:

1. speed (u) of the exhaust gases.
2. Log of the ratio of initial mass (m0) of the rocket to its mass (m) at that instant of time.

Upthrust on the rocket (F): It is the upward force exerted on the rocket by the expulsion of exhaust gases. It is obtained as follows:
Dividing Eqn. (2) by dt, we get


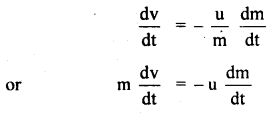
where F = ma is the instantaneous force (thrust).

From Eqn. (5), we conclude that the thrust (F) on the rocket at any instant is the product of the velocity of exhaust gases and the rate of combustion of fuel at that instant. Here negative sign shows that the thrust and velocity of exhaust gases are in opposite direction.

Question 3.
(a) Define inertia. What are its different types? Give examples.
Answer:
The tendency of bodies to remain in their state of rest or uniform motion along a straight line in the absence of an external force is called inertia.

Inertia is of the following three types:
1. The inertia of rest: When a body continues to lie at the same position with respect to its surrounding, it is said to possess inertia of rest. This situation may be changed only by the application of external force. For example, if a cot or sofa is lying in a particular place in the house, it will remain there even after days or years unless someone removes (by applying force) the same from its position. This is an example of the inertia of rest.

2. The inertia of motion: When a body is moved on a frictionless surface or a body is thrown in a vacuum, it will continue to move along its original path unless acted upon by an external force. In actual situations, air or floor etc. exert friction on the moving bodies so we are unable to visualize a force-free motion. This type of inertia when a body continues to move is called the inertia of direction.

3. In the above examples it is found that the direction of motion of the body or particle also does not change unless an external force acts on it. This tendency to preserve the direction of motion is called the inertia of direction.

(b) Explain Newton’s First law of motion. Why do we call it the law of inertia?
Answer:
According to the First law of motion, “Everybody continues to be in the state of rest or of uniform motion along a straight line until it is acted upon by an external force.”

It means that if a book lying on a table,-it will remain there for days or years together unless force is applied on it from outside to pick it.

Similarly, if a body is moving along a straight line with some speed, it will continue to do so until some external force is applied to it to change its direction of motion.

Thus First law tells us the following:

1. It tells us about the tendency of bodies to remain in the state of rest or of motion and the bodies by themselves can neither change the state of rest nor of uniform motion. This tendency is called inertia. To break the inertia of rest or motion or direction, we need an external force. Thus the definition of the first law matches with the definition of inertia and hence first law is called the law of inertia.
2. The first law of motion also provides the definition of another important physical quantity called force. Thus force is that agency which changes or tends to change the state of rest or of uniform motion of a body along a straight line.

(c) State Newton’s Second law of motion. How does it help to measure force? Also, state the units of force.
Answer:
It states that the time rate of change of momentum of a body is directly proportional to the force applied to it.

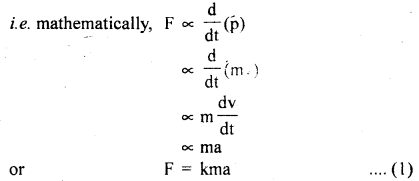
where a = \(\frac{dv}{dt}\) = acceleration produced in the body of mass m.
k = proportionality constant which depends on the system of units chosen to measure F, m, and a.

In the S.I. system, k = l,
∴ F = ma

The magnitude of the force is given by
F = ma …. (2)

Note: We have assumed that the magnitude of velocity is smaller and much less than the speed of light. Only under this condition Eqns. (1) and (2) hold good.

The definition of the Second law and its mathematical form is given in Eqn. (2) provide us a mean of measuring force.

One can easily find the change in velocity of a body in a certain interval of time. Both velocity and time can be easily measured. Thus by knowing the mass of the body one can determine both change in momentum as well as the acceleration of the body produced by an external force. If the force is increased, the rate of change of momentum is also found to increase. So also is the acceleration. Now with known values of m and we can find F.

Units of force: Force in S.I. units is measured in newton or N. From Eqn. (1) or (2) we can see that a newton of force is that fore? which produces 1 ms^-2 acceleration in the body of mass 1 kg.
1 newton = 1 kilogram × 1 metre/(second)²
or
1 N = 1 kg × 1 ms^-2 = 1 kg ms^-2

In CGS system force is measured in dyne
1 dyne = 1 gram × 1 cm/s2 = 1 g cm s^-2
Since 1 N = 1 kgm s^-2= 1000 g × 100 cm s^-2
= 10⁵ g cm s^-2 = 105 dyne
1 N = 10⁵ dyne
or
1 dyne = 10⁵ N

Gravitational Unit: If a falling mass of 1 kg is accelerated towards the Earth with 9.8 ms^-2, then the force generated is called 1 kg wt (1-kilogram weight) force. It is the S.I. gravitational unit of force.

We know that the earth accelerates the mass with g = 9.8 ms^-2
1 Kg wt = 9.8 N [1 kg × 9.8 ms 2 = 9.8 N]

C.G.S. gravitational unit is gf or g wt.
1 gf = 1g × 980 cms^-2
= 980 dyne

Question 4.
(a) State Newton’s Third law of motion. Discuss its consequences.
Answer:
Newton’s Third law of motion states that “to every action, there is always an equal and opposite reaction.”’
So, if a body 1 applies a force F₁₂ on body 2 (action), then body 2 also applies a force F₂] on body 1 but in opposite direction, then
F₂₁ = – F₁₂

In terms of magnitude
|F₂₁| = |-F₁₂|

It is very important to note that F₁₂ and F₂₁ though are equal in magnitude and opposite in direction yet act on different points or else no motion will be possible.

For example, hands pull up a chest expander (spring), and spring in turn exerts a force on the arms. A football when pressed reacts on the foot with the same force and so on. The most important consequence of the third law of motion is the law of conservation of linear momentum and its application in collision problems.

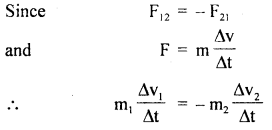
Here Δt is the time for which the bodies come in contact during impact. This is the same for the two bodies of masses m₁ and m₂ and having velocity changes Δv₁ and Δv₂ respectively. Therefore,
m₁ Δv₁ = – m₂ Δv₂
or
m₁ Δv₁ + m₂Δv₂ = 0

Let u₁, u₂ and v₁ and v₂ be initial and final velocities of the two masses before and after collision, then
m₁(v₁ – u₁) = – m₂(v₂ – u₂)
or
m₁u₁ +m₂u₂ = m₁v₁ + m₂v₂

Momentum before impact = momentum after impact
This is the law of conservation of momentum.

(b) State the law of conservation of linear momentum and illustrate it with examples.
Answer:
‘The linear momentum of an isolated system always remains the same provided no external force is applied on it.’ This is the law of conservation of linear momentum.

The linear momentum of a body = mass × velocity
p = mv
If a system has several bodies initially at rest then initial momentum = 0.
The final momentum = p₁ + p₂ + p₃ + ……

According to law of conservation of linear momentum
p₁ + p₂ + p₃ + …. = 0

Linear momentum is a vector quantity and is measured. in kg ms^-1or Ns.

For example, a gun and a bullet make a system in which both are initially at rest. When the bullet of mass m is
fired with muzzle velocity v, the gun of mass M gets a recoil velocity V. Since the initial linear momentum of the system is zero.
MV + mv = 0
or
MV = – mv

Thus gun moves in the opposite direction to that of the bullet.

(c) Define the terms – momentum and impulse. What are their units in the S.I. system?
Answer:
The total quantity of motion possessed by the body is called is momentum. Mathematically, it is equal to the product of the mass of the body and the velocity of the body.

In linear motion, this term is called linear momentum P.
It is a vector quantity.
p = mv
The units of linear momentum are kg ms-1 or NS in S.I. units.

Impulse: The action or impact of force is called the impulse of force. Mathematically, impulse J is equal to the product of the force F acting on the body and the time for which the force acts on it. Thus
J = F × t = Ft

J is a vector quantity and is measured in Ns or kg ms-1
The action of force or impulse is increased if the force acts for a smaller interval.

Question 5.
(a) State and explain the laws of friction.
Answer:
Following are the laws of friction:
1. The direction of the force of friction is always opposite to the direction of relative motion i.e. motion of the body over the surface of another body.

It can be seen easily that if a ball is rolled on the floor, it will be stopped after traveling through some distance if no other force is applied to it. This is because the force of friction that comes into play opposes the motion and slows down the ball which finally comes to rest.

2. The force of friction always acts tangentially along the surfaces of contact of the two bodies.

3. The magnitude of the limiting friction (F) is always directly proportional to the normal reaction (R) between the two surfaces i.e.
F ∝ R
or
F = μR

If we take two bodies of masses m₁ and m₂ s.t. m₁ > m₂. We apply forces F₁ and F₂ which just move these bodies on a surface. We find that F₁ > F₂. The body of mass m presses the surface by a force m₁g, and the surface exerts normal reaction R₁ on it equal to m1g. Thus F₁ ∝ R₁ or F ∝ m₁g.
Similarly F₂ ∝ R₂

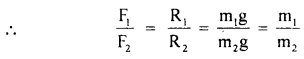
4. The force of friction depends on the nature of smoothness or the state of polishing of the surfaces in contact.

Let us have a wooden plank on which blocks of wood, copper, and glass of the same mass are placed. These are pulled by a spring balance. We find that spring balance shows different readings for just starting the motion.
Hence we conclude that friction depends on the nature of the surfaces in contact.

5. The force of friction is independent of the area of the surface of contact of two bodies as long as the normal reaction is constant.

The force applied to slide the body is the same but the contact area is different for the wooden block placed on a wooden plank.

(b) What are the advantages and disadvantages of friction.
Answer:
Advantages of friction:

1. It helps in walking, talking, writing, sleeping, etc.
2. The brakes of vehicles can’t work without friction.
3. Moving belts remain on the rim of wheels due to friction.
4. Adhesives work due to friction.
5. Cleaning with sandpaper is due to friction.
6. Nuts and bolts are held together due to friction.

Disadvantages of fraction:

1. A significant amount of energy of a moving object is wasted in the form of heat energy to overcome friction.
2. It causes a lot of wear and tear of the parts of machinery in contact, thus reducing their lifetime.
3. It restricts the speed of moving vehicles like buses, airplanes, trains, etc.
4. The efficiency of machines decreases due to the presence of a force of friction.
5. A machine gets burnt due to the force of friction between its different moving parts due to friction.

(c) What are various methods of reducing friction?
Answer:
Reduction of friction saves a lot of energy. The various methods of reducing friction are listed below:
1. Making the surfaces smooth by various methods such as:

• Polishing the surfaces and rubbing surfaces.
• Covering the surface with smooth materials such as metal foils or sun mica etc.
• Lubricating the surfaces by lubricating oils and other materials such as granite.

2. With the help of these above methods, the irregularities, grooves, etc. are filled up and the surface becomes smooth. For example in many machines grease is used to lower friction.

3. Streamlining the shape of bodies: The shape of bodies is made streamline to reduce friction. For example, the shape of high-speed buses, railway engines, ships, boats, airplanes, etc. is made of streamline to reduce fluid friction. It not only reduces friction but also helps in providing the pushing force.

4. Making changes to convert sliding into rolling friction: Since the rolling friction is much less than the sliding friction, several machine parts are designed in such a manner that they have rolling friction. For example, ball bearings are used in bicycle and machine shafts. The vehicles have wheels instead of sliding arrangements for the same reason.

Question 6.
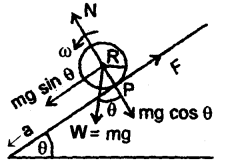
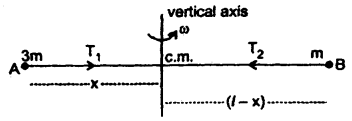
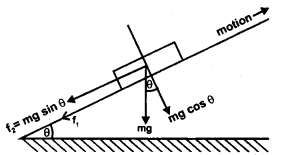
(a) Discuss the motion of a vehicle on a level road having a circular turn.
Answer:
Consider a vehicle (say a car) of mass m moving with a constant speed v on a circular level (flat) road of radius r. While taking the round, the tires of the car tend to leave the road and move away from the center of the curve. So the forces of friction f₁ and f₂ act inward on the two tires 1 and 2 respectively shown in fig. If R₁ and R₂ be the normal reactions of the ground on the tires, then
f₁ = μR₁ and
f₂ = μR₂

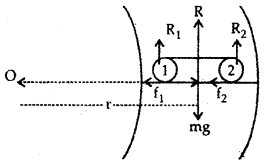
If f be the total force of friction, then
f = f₁ + f₂
= μ(R₁ + R₂) = μR ….(1)

where R = R₁ + R₂ is the total reaction of the ground on the car.
Also R = mg (weight of the car) …. (2)

∴ From (1) and (2), we get
f = μmg …. (3)

This total- force of friction provides the necessary centripetal force \(\frac{m v^{2}}{r}\) to the vehicle to move in the circular path.

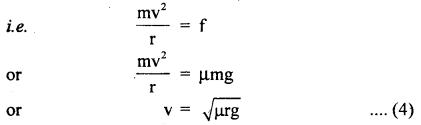
Equation (4) gives the maximum speed with which the vehicle can move on the given circular road without skidding.

If its speed becomes more than the speed given by (4), then the centripetal force needed by the car will not be provided by the force of friction and hence the vehicle will skid and go off the road.

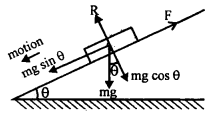
(b) What is the need for the banking of circular roads/tracks? Describe the motion of a car on a banked road.
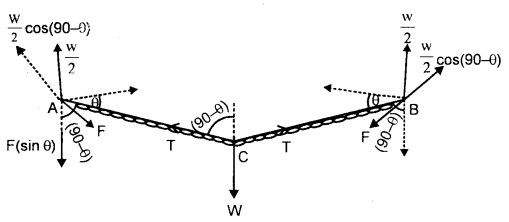
Answer:
We know that a vehicle cannot remain on a circular road if its speed is more than the speed given v = \(\sqrt{µrg}\). In such a case, the force of friction is not sufficient to provide the necessary centripetal force. The additionally required centripetal force is obtained by banking the circular road i.e. its outer edge is raised a little above the inner edge by a suitable angle θ with the horizontal. This process is called banking and the angle is called the angle of banking.

Case I:
The motion of the car without taking into account the force of friction between the tires of car and the road:
Let OX = horizontal line
m = mass of the car
V = its velocity
r = radius of the circular road.

The following force acts on the car:

1. Its weight mg acts vertically downwards.
2. The normal reaction of the road acts at an angle θ to the vertical.

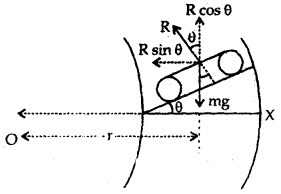
Let us resolve R into two rectangular components:
R cos θ which is equal and opposite to mg
i.e. R cos θ = mg …(1)
R sin θ which acts towards the centre of the circular path provides the necessary centripetal force \(\left(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\right)\) to the car i.e.

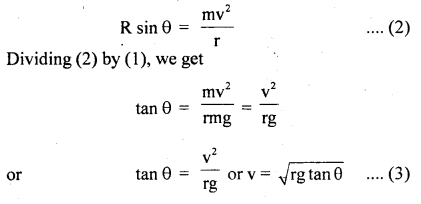
eqn. (3) gives the maximum safe speed of the car.

If it negotiates the curve on the banked road with a speed greater than that given by equation (3), then it will skid away.

Case II:
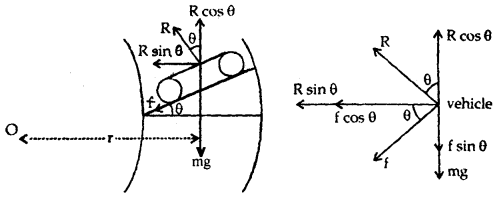
The motion of a car on a banked road taking into account the friction between the tires and the road.
The following forces act on the car:

1. Its weight mg acting vertically downwards.
2. Reaction R of the road acts at an angle θ to the verticle.
3. The force of friction between the tires and the road acts along the road inwardly.

Let us resolve f and R into rectangular components along with horizontal and vertical directions as shown in the figure.


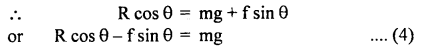
Necessary centripetal force required for motion around the circular path i.e.

R sin θ + f cos θ = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) ….(5)

Dividing (5) by (4), we get

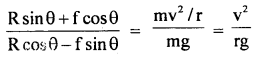
Dividing on L.H.S. by R cos θ in numerator and denominator, we get

Equation (6) gives the maximum speed for safely negotiating a curve on a banked road.

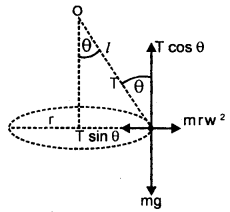
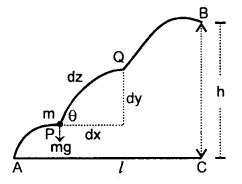
(c) Describe the motion of a body in a vertical circle.
Answer:
When a body moves in a vertical circle, its velocity decreases from lowest point L to highest point H. Then it again increases as it moves from H to L. The.reasOn is that gravity opposes the motion of the body as it rises and helps in motion as it falls. Thus, motion is not uniform. Let m = mass of a body tied to one end of a string of length r and is rotated in a vertical circle of center O. L, H are lowest and highest points respectively.

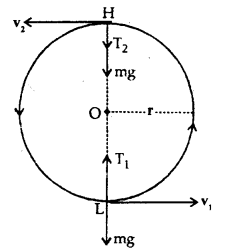
Let v₁ and v₂ be the velocities of the body at L and H respectively which act along the tangent to the circle. mg= weight of the body which acts vertically downward both at L and H.

Also, let T₁ and T₂ be the tensions in the string at L and H respectively and both act towards O. Thus, the net force at L towards O is T₁ – mg and provides the necessary centripetal force i.e.

Similarly, T₂ + mg at H provides the necessary centripetal force at H i.e.

Subtracting Egn. (2) from (1), we get

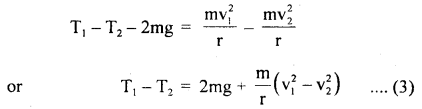
According to the law of conservation of energy,
Total energy at L = Total energy at H

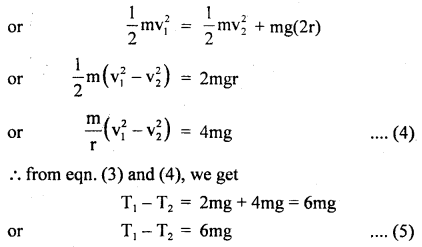
i. e. in a vertical circle, the difference in tensions at the lowest and highest points is six times the weight of the body.
For completing the vertical circle successfully, the string must remain tight even at H i.e. it should not slack at H.

For this, T₂ must be zero i.e. T₂ = 0.

∴ From eqn. (2), mg = \(\frac{\mathrm{mv}_{2}^{2}}{\mathrm{r}}\)
or
v₂ = \(\sqrt{gr}\) ….(6)

Eqn. (6) gives the minimum velocity of the body at the highest point i.e. v_min = (rg)^1/2

If v₂ < \(\sqrt{gr}\), then the string will slack at H and the vertical circle will not be completed.
From Eqn. (4) and (6), we get

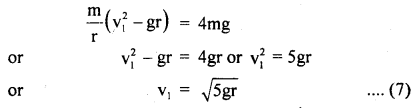
Equation (7) gives the minimum velocity of projection required at the lowest point L so that the body just completes the vertical circle successfully. This phenomenon is called looping the vertical loop.

Numerical Problems:

Question 1.
A machine gun placed horizontally in front of a target fires 600 bullets per minute into the target. The average mass of the bullet is 50 gm and the bullets are fired at a speed of 800 ms^-1. Calculate the average force applied to the target.
Answer:
Mass of each bullet, m = 50 gm = \(\frac{1}{20}\) kg.
v = velocity of each bullet = 800 ms^-1
No. of bullet fired, n = 600,
t = 60s,
average foce exerted on the target = fav = ?
∴ p₁ = initial momentum of each bullet
= mv = \(\frac{1}{20}\) × 800 = 40 kg ms^-1

∴ Total momentum of 600 bullets per min.,
P_i = nP₁
= 600 × 40 = 24000 kg ms^-1

As the bullets come to rest after striking the target,
∴p_f = final momentum of bullets = 0

Thus change in momentum ΔP = p_i – p_f = 24000 kg ms
But by definition,

Impulse = average force × time
= change in momentum
or
F_av × t = Δp

∴ F_av = \(\frac{\Delta \mathrm{p}}{\mathrm{t}}=\frac{24000}{60}\)

Question 2.
A rubber ball of mass 50 gm falls from a height of 1 m and rebounds to a height of 0.5 in. Finds the impulse and average force between the ball and the ground if the time for which they are in contact is 0.1 s.
Answer:
m = mass of ball = 50gm = \(\frac{50}{1000}=\frac{1}{20}\) kg, J =?. F =?

Case I:
u = initial velocity of ball = O
h₁ = height through which it falls 1m
y = final velocity of the ball =?
a = g = 9.8 ms^-2
∴ using the relation,

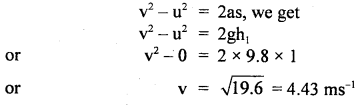
If p₁ be the momentum of the ball when it is about to reach the ground or before the impact,
then
p₁ = mv = \(\frac{1}{20}\) × 4.43 = 0.221 kg ms^-1

Case II: u’ initial velocity = velocity after rebounding = ?
v = final velocity = 0
S = h₁  = height up to which it rises = 0.5 m = \(\frac{1}{2}\) m
a = – g = – 9.8 ms^-2

∴ using equn. (i), we get

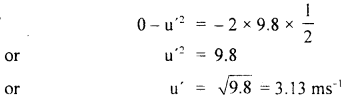
If p₁ = momentum of the ball after impact, then
p₂ = mu = \(\frac{1}{20}\) × 3.13 = 0.156 kg ms

∴ impulse is given by

Question 3.
A bus moving with a velocity of 60 kmh-1 has a weight of 50 tonnes. Calculate the force required to stop it in 10s.
Answer:
m = mass of bus = 50 tonnes = 50 × 1000 kg
u = initial velocity of bus = 60 kmh^-1 = 60 × \(\frac{5}{18}\) ms^-1 = \(\frac{50}{3}\) ms-1
v = final velocity of bus = 0
t = 10 s, a = ? and retarding force, F = ?

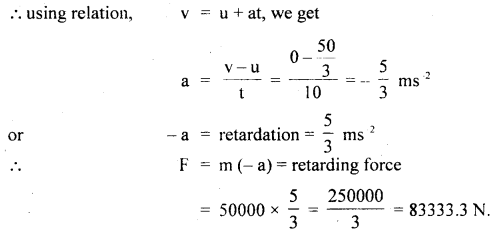
Question 4.
A hunter has a machine gun that can fire 50 g bullets with a velocity of 150 ms^-1. A 60 kg tiger springs at him with a velocity of 10 ms^-1. How many bullets must the hunter fire into the tiger so as to stop him in his track?
Answer:
m = mass of bullet = 50 gm = 0.050 kg
M = mass of tiger = 60 kg
v = velocity of bullet = 150 ms^-1
V = velocity of tiger = – 10 ms^-1
(∵ it is coming from opposite direction) .

Let n = no. of bullets fired per second at the tiger so as to stop it.
∴ p_i = 0 before firing …. (i)
p_f = n(mv) + MV …. (ii)

∴ According to the law of conservation of momentum,

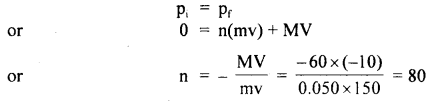
Question 5.
A mass of 200 kg rests on a rough inclined plane of angle 300. If the coefficient of limiting friction is \(\frac{1}{\sqrt{3}}\) find the greatest and the least forces in newton, acting parallel to the plane to keep the mass ¡n equilibrium.
Answer:
Here, m = mass of body = 200 kg
Let angle of inclination = θ
μ_s = coefficient of limiting friction = \(\frac{1}{\sqrt{3}}\)

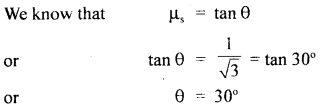
The rectangular components of mg are as shown in fig.

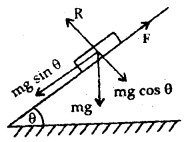
Here mg sin θ acts along the plane in the downward direction and is given by

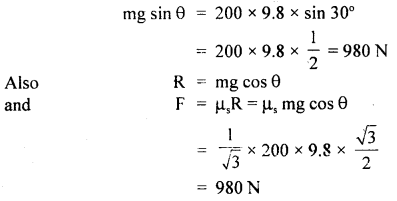
(i) the least forces in newton, acting parallel to the plane to keep the mass in equilibrium. given by
f₂₁ =mg sinθ – F = 980 – 9800 = 0

(ii) The greatest force to be applied to keep the mass in equilibrium is given by
f₂ = mg sin θ + F = 980 + 980 = 1960 N.

Question 6.
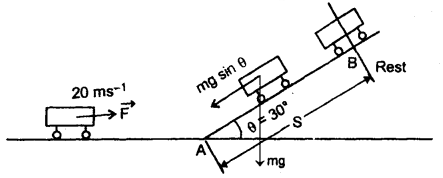
Find the force required to move a train of 2000 quintals up an incline of 1 in 50, with an acceleration of 2 ms^-2, the force of friction being 0.5 newtons per quintal.
Answer:
Here, m = 2000 quintals
= 2000 × 100 kg (v 1 quintal = 100 kg)
sin θ = \(\frac{1}{50}\) , acceleration, a = 2 ms^-2

F = force of friction
= 0.5 N per quintal
= 0.5 × 2000 = 1000 N

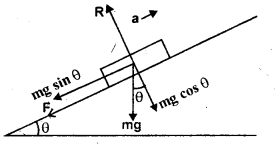
In moving up an inclined plane, force required against gravity
= mg sin 0
= 2000 × 100 × 9.8 × \(\frac{1}{50}\)
= 39200N.
Also if f = force required to produce acce. = 2 ms^-2.
Then f = ma = 200000 × 2 = 400000 N

∴Total force required = F + mg sin θ + f
= 1000 + 39200 + 400000 = 440200 N.

Question 7.
A bullet of mass 0.01 kg is fired horizontally into a 4 kg wooden block at rest on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet remains embedded in the block and the combination moves 20 m before coming to rest. With what speed did the bullet strike the block?
Answer:
Here, m₁ = mass of the bullet = 0.01 kg
m₂ = mass of the wooden block = 4 kg
μ₂ = coefficient of kinetic friction = 0.25
initial velocity ofblock, u₂ = 0, s = distance moved by combination=20 m

Let u₁ = initial velocity of the bullet
If v = velocity of the combination, then according to the principle of conservation of linear momentum,

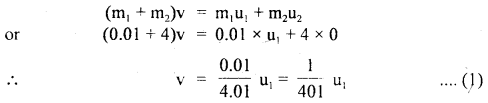
If F = kinetic force of friction,
Then

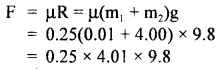
Then retardation ‘a’ produced is given by

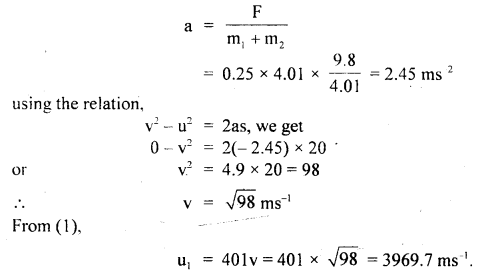
Question 8.
A force of 100 N gives a mass m₁ an acceleration of 10 ms^-2, and of 20 ms^-2 to a mass m₂. What acceleration would it give if both the masses are tied together?
Answer:
Let a = acceleration produced if m₁ and m₂ are tied together.
F = 100 N, Let a₁ and a₂ be the acceleration produced in m₁ and m₂ respectively.
∴ a₁ = 10 ms^-2, a₂ = 20 ms^-2 (given)

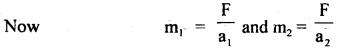
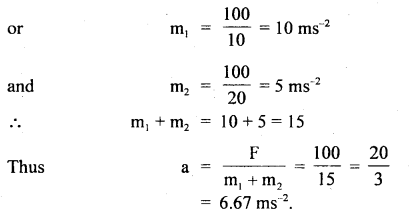
Question 9.
A balloon with mass M is descending down with an acceleration ‘a’ < g. What mass m of its contents must be removed so that it starts moving up with an acceleration ‘a’?
Answer:
Let F = retarding force acting on the balloon in the vertically upward direction.

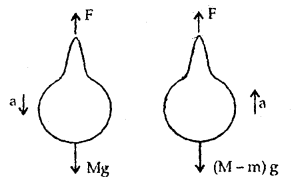
When the balloon is descending down with an acceleration ‘a’, then the net force acting on the balloon in the downward direction is given
by
Ma = Mg – F
or
F = Mg – Ma ….(i)
When the mass m is taken out of the balloon, then its weight is
= (M – m)g

Now as the balloon is moving upward with acceleration ‘a’, so the net force acting on the balloon in the upward direction is given by:

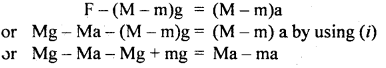
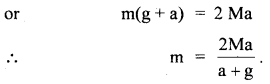
Question 10.
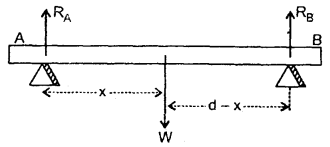
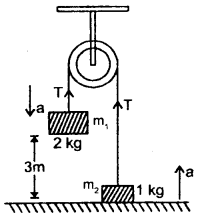
Three blocks are connected as shown below and are on a horizontal frictionless table. They are pulled to right with a force F = 50 N. If m₁ = 5 kg, m₂ = 10 kg and m₃ = 15 kg, find tensions T₃ and T₂.
Answer:
Here, F = 50 N, m₁ = 5 kg, m₂ = 10 kg m₃ = 15 kg.

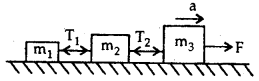
As the three blocks move with an acceleration ‘a’

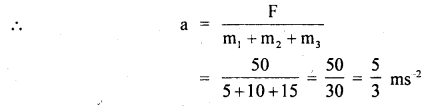
To determine T₂: Consider the free body diagram (1). Here F and T2 act towards the right and left respectively.

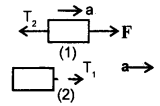
As the motion is towards the right side, so according to Newton’s Second law of motion:

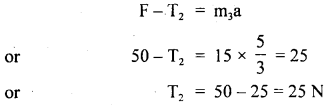
To determine T₃: Consider the free body diagram (2)

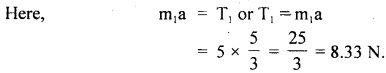
Question 11.
A monkey is descending from the branch of a tree with constant acceleration. If the breaking strength is 75% of the weight of the monkey, then find the maximum acceleration with which the monkey can slide down without breaking the branch.
Answer:
Let a = constant acceleration of the monkey descending from the branch of tree = T

∴ According to Newton’s Second law of motion,

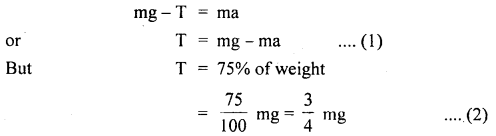
∴ from (1) and (2), we get

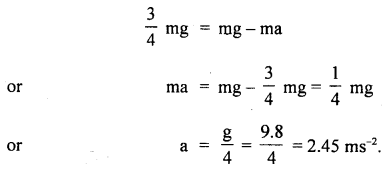
Question 12.
A body of mass 1 kg initially at rest explodes and breaks into three fragments of masses in the ratio 1:1:3. The two pieces of equal mass fly off perpendicular to each other with a speed of 30 ms^-1 each. What is the velocity of the heavier fragment?
Answer:
Let m₁, m₂, and m₃ be the masses of the three fragments


Also let v₂  and v₂ be the velocities of the two fragments. ..
∴ v₁ = v₂ = 30 ms^-1
If v₃ be the velocity of the heaviest fragment, then according to the law of conservation of linear momentum in the horizontal direction,

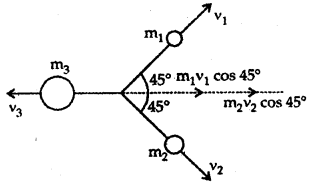
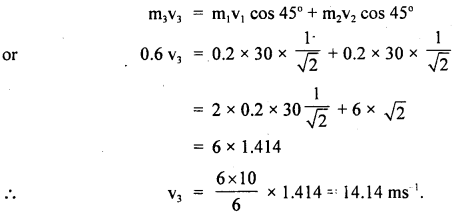
Question 13.
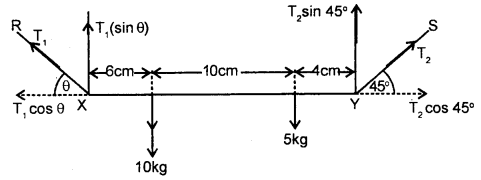
A mass of 4 kg is suspended by a rope of length 30 m from the ceiling. A force of 30 N in the horizontal direction is applied at the mid-point of the rope. What is the angle, the rope makes with the vertical in equilibrium? Take g = 10 ms^-2 and neglect the mass of the rope.
Answer:
OA = OB 1.5 m
Let ∠AOC = 0
F = horizontal force = 30 N
m = mass of the body = 4 kg
mg = 4 × 10 = 40 N

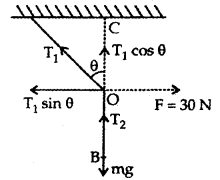
Let T₁ and T₂ be the tensions in parts OA and OB respectively, where O = midpoint of the rope
∴ T₂ = mg = 40 N
At point O, three forces T₂, T_1, and 30 N are acting.

Let us resolve T₁ into rectangular components.
Horizontal component of T₁ = T₁ sin θ
Vertical component of T₁ = T₁ cos θ
Now T₁ cos θ =40 ….(i)
and T₁ sin θ = 30 …. (ii)

Dividinig (ii) by (i), we get

tan θ = \(\frac{3}{4}\) = 0.75 = tan 36.87°
θ = 36.87°.

Question 14.
An elevator weighs 4000 kg. when the upward tension in the supporting cable is 48000 N, what is the upward acceleration? Starting from rest how far does it rise in 3s?
Answer:
Weight of elevator,
W = Mg = 4000 kgf = 4000 × 9.8 N
= 39200 N
mass of elevator, M = 4000 kg

F = Force on elevator in upward direction = upward tension in the cable = 48000 N.
If F’ = Net force on the elevator in the upward direction
Then F’ = F – W = 48000 – 39200 = 8800 N

If a = upward acceleration,
Then a = \(\frac{\mathrm{F}^{1}}{\mathrm{M}}=\frac{8800}{4000}=\frac{11}{5}\) = 2.2 ms^-2

Let S be the distance covered by the elevator in 3s. For upward motion, we have
u = 0,a = 2.2ms^-2, t = 3s

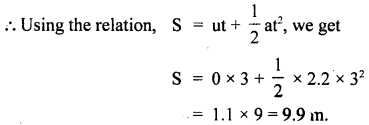
Question 15.
A disc of mass 10 gm is kept floating horizontally by throwing 10 marbles per second against-it from below. If the mass of each marble is 5 gm, calculate the velocity with which the marbles are striking the disc. Assume that the marbles strike the disc normally and rebound downward with the same speed.
Answer:
When each marble hits the disc, it produces an impulsive force and acts against the weight of the disc. This force keeps the disc floating for \(\frac{1}{10}\) s.

Let v = velocity with which each marble strikes the disc and rebounds downward.
Impulse imparted by each marble = charge in momentum
= mv – (- mv) = 2 mv

Since m = 5g = 5 × 10^-3 kg
∴ Impulse = 2 × 5 × 10^-3v
= 10^-2 v kg ms^-1.

Now average force between the disc and each marble = weight of the disc.
The resultant downward force produces the change in momentum.

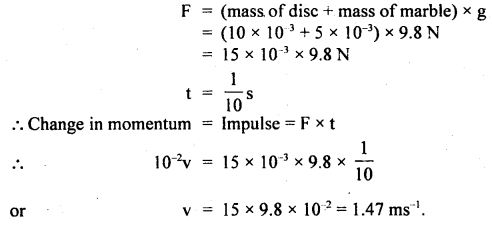
Question 16.
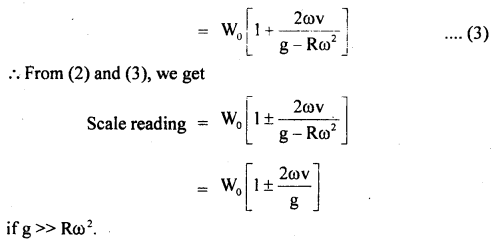
A box is placed on a horizontal measuring scale that reads zero when the box is empty. A stream of pebbles is then dropped in to the box from a height h above its bottom at the rate of n pebbles per second. Each pebble has a mass m. If the pebbles collide with the box such that they immediately come to rest after collision. Find the scale reading at time t after the bubble begins to fill the box.
Answer:
Let v = speed the pebble when it strikes the box.
Then using v₂ – u₂ = 2as, we get
v₂ – 0 = 2gh (∵ here a = g, S = h, u = 0)
or
v = \(\sqrt{2gh}\)

Mass of each pebble = m
Momentum of each pebble = mv = m \(\sqrt{2gh}\)
Each pebble comes to rest after colliding the box

∴ Change in momentum during each collision = m \(\sqrt{2gh}\)
Δt = Time for each colbsion = \(\frac{1}{n}\)s

Force exerted by pebbles on the box,

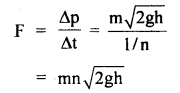
Weight of pebbles after time t is

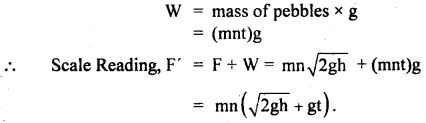
Question 17.
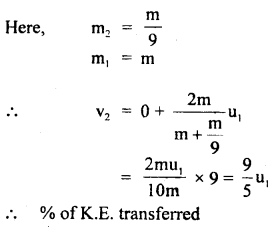
A stone of mass 5 kg falls from the top of a cliff 40 m high and buries itself 2 m deep in the sand. Find the average resistance offered by the sand and the time it takes to penetrate (g = 9.8 ms^-2).
Answer:
Let the acceleration of the stone in the sand be “a”.
The velocity it gains by falling through a height of 40 m is
v = \(\sqrt{2gh}\) = \(\sqrt{2 \times 9.8 \mathrm{~ms}^{-2} \times 40 \mathrm{~m}}\)
= 28 ms^-1 = u = initial velocity

When it buries in the sand its final velocity is zero so the acceleration
a = \(\frac{0^{2}-\left(28 \mathrm{~ms}^{-1}\right)^{2}}{2 \times 2 \mathrm{~m}}\) = -196 ms^-1

(i) The average resistance offered by the sand is
F = ma = 5 kg × 196 ms^-2 = 980 N

(ii) Let t be the time of penetration in the sand
using equation

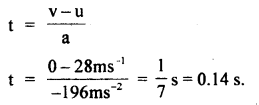
Question 18.
An airplane required a speed of 80 km h^-1 for takeoff on a 100 m long runway. The coefficient of friction between the tires of the plane and the runway is 0.2. Assuming that the plane accelerates uniformly, what is the force required by the engine to take off the plane? The mass of the airplane is 10,000 kg.
Answer:
Take off speed of plane, v = 80 km h^-1
Run-on the ground, s = 100 m
u = initial velocity = 0
Acceleration ‘a’ of the plane is obtained from

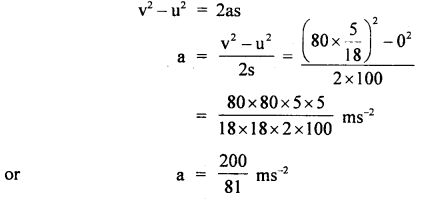
The force to produce this acceleration = ma= 10,000 × \(\frac{200}{81}\) N
Force needed to overcome friction = μm = μmg
= 0.2 × 10,000 × 9.8 N

The force required to be given to the engine is

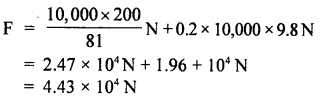
Question 19.
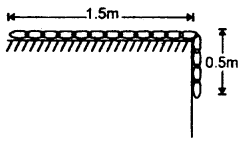
A 4 m long ladder of aluminum having 20 kg mass rests against a smooth wall making an angle of 30° with it. Find the coefficient of friction between the ladder and the ground so that ladder does not slip. Take g = 10 ms⁴.
Answer:
Let the ladder AB of length 4 m rest against smooth wall BC. The reaction of the ground is say R₁ and that of the wall on the ladder is R₂. The weight of the ladder acts at the midpoint O in a vertically downward direction (assuming the ladder to be uniform).

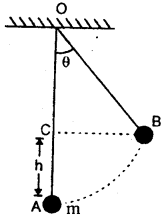
Let F be the force of friction.
Taking moments of mg and R₂ about A, we get
mg × AD = R₂ × BC

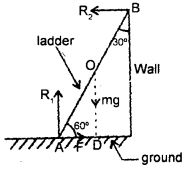
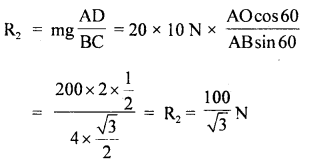
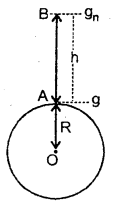
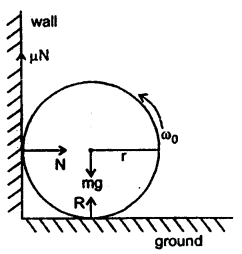
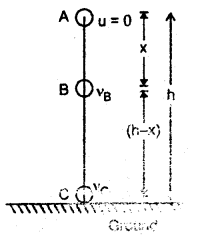
Question 20.
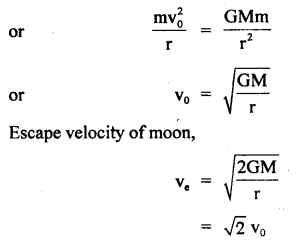
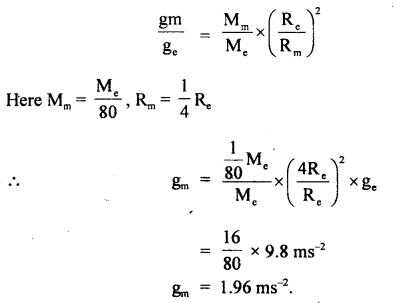
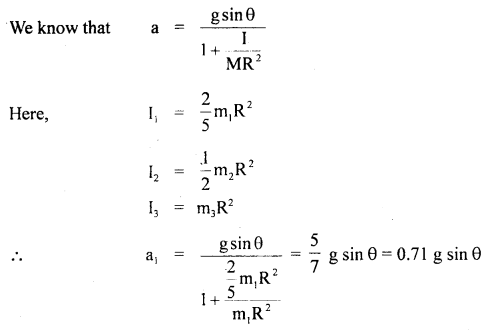
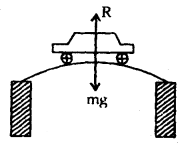
Prove that a motor car moving over a convex bridge is lighter than the same car resting on the same bridge.
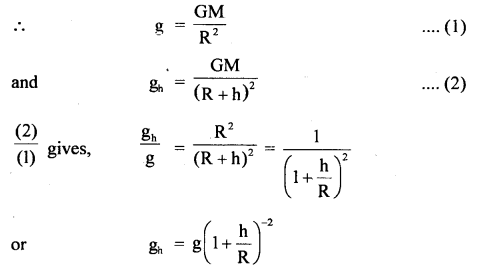
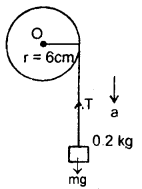
Answer:
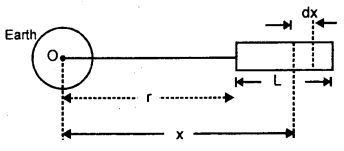
The motion of the motor car over the convex bridge is the motion along the segment of a circle. The centripetal force is provided by the difference of weight mg of the car and the normal reaction R of the bridge.

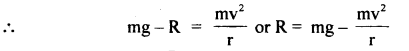
∴R = apparent weight of the moving car
Clearly R < mg i.e. the weight of the moving car is less than the weight of the stationary car.

Question 21.
A hammer weighing 1 kg moving with a speed of 10 ms^-1 strikes the head of a nail driving it 10 cm into a wall. Neglecting the mass of the nail, calculate:
(a) the acceleration during the impact.
(b) the time interval during the impact,
(c) the impulse.
Answer:
Here, the initial velocity of nail = velocity of the hammer
i. e. u = 10 ms^-1
Final velocity of nail, v = 0, m = mass of hammer = 1 kg
Distance covered, s = 10 cm = 0.1 m

Let t be the time interval for which impact lasts and let a be the acceleration produced =?
(а) Using the relation,

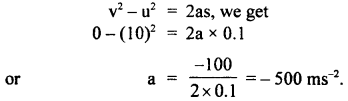
(b) Also using the relation,

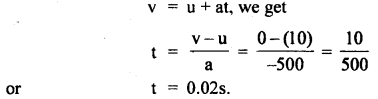
(c) Impulse
Ft = (ma)t
= 1 × (-500) × 0.02
= – 10 Ns.

Question 22.
A rocket with a lift of mass 20,000 kg is blasted upward with an initial acceleration of 5 ms². Calculate internal thrust of the blast
Answer:
Here, m = 20,000 kg
a = 5 ms^-1
∴ F = ma = 20,000 × 5N = 10⁵ N

Let T = upward of thrust and
W = weight of rocket.

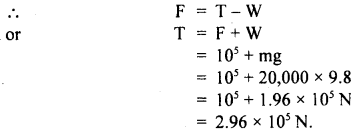
Question 23.
A car starts from rest and accelerates uniformly with 2ms2. At t = 10 s, a stone is dropped out of the window (1m high) of the car. What are the : (a)velocity, (b) acceleration of the stone at t = 10.ls. Neglect air resistance and take g = 9.8 ms².
Answer:
(a) Here, the stone will possess horizontal velocity due to the motion of the car and vertical downward velocity due to gravity.
Here u = 0, a = 2 ms^-2, t = 10s, g = 9.8 ms^-2

If v_H and v_y be its horiìontal and vertical velocities respectively, then using relation,
v = u + at, we get
v_H = u + at = 0 + 2 × 10 = 20 ms^-1
and
v_y = u + gt = 0 + 9.8 × 0.1 = 0.98 ms^-1

If \(\overrightarrow{\mathbf{v}}\) be its resultant velocity at < θ with horizontal direction, then


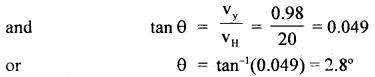
The vertical component of acceleration,
g = 9.8 ms^-2

Since the velocity is constant as no force acts on the stone at the time of dropping, so the horizontal component of acce. is zero.

If a’ be its acce. at 10.1 s, then
a’ = \(\sqrt{\mathrm{g}^{2}+0^{2}}\) = g = 9.8 ms^-2.

Question 24.
A stream of water flowing horizontally with a speed of 15 ms^-1 gushes out of a tube of cross-sectional area 10^-2 m² and hits at a vertical wall nearby. What is the force applied on the wall by the impact of water, assuming it does not rebound? The density of water is 1000 kg m^-3.
Answer:
Here, A = area of cross-section of tube
= 10^-2 m²
v = speed of water = 15 ms^-1
ρ = density of water = 103 kg m^-3

If V be the volume of water striking the wall per second, then
V = Av = 10^-2 × 15 = 0.15 m3 s^-1

Let m be the mass of water striking/sec.
∴ m = Vρ = 0.15 × 1000 = 150 kg s^-1

Let pi = initial momentum of water striking the wall s^-1,
∴ P_i = mv
= 150 × 15 = 2250 kg ms^-2

p_f = final momentum of water/sec = 0 as it does not rebound
∴ Δp = change in momentum/s = p_f – P_i
= 0 – 2250 = – 2250 kg ms^-2
or
F = 2250 N.

Question 25.
A body of mass 1 kg lies on a rough horizontal plane. A horizontal force of 15 N produces in the body an acceleration of 10 ms”2. Find the force of friction and coefficient of friction between the body and the table.
Answer:
Here, m = mass of body = 1 kg
F = force = 15 N
a = acceleration = 10 ms^-2

Let f be the force of friction and μ, be the coefficient of friction
∴ the net force on the body = F – f

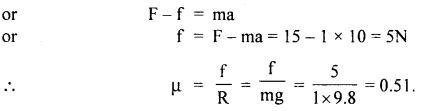
Value-Based Type:

Question 1.
Anil is a student of the science stream who lived on the first floor of a building. One day he and his grandfather were enjoying the holiday. Suddenly he observed that dense smokes are coming from his neighbor’s flat. People were crying and panic was there. There was a rush on the staircase. He was thinking about how he could save his grandfather. Suddenly an idea came to his mind. He took a turban cloth and suspended it on the ground and asked a person to hold the other end of the cloth tightly; Then he asked his grandfather to gently sit on the turban cloth. He was now able to comfortably reach the ground:
(i) What values and qualities displayed by Anil?
Answer:
The values displayed by Anil are Caring, Presence of mind, Courageous, and affection to elderly people.

(ii) Which concept is being used here?
Answer:
Motion on a Rough inclined plane

(iii) What will be the tension in the cloth inclined at an angle of 30° from horizontal when a person of mass 60 kg falls through it with an acceleration Of 2 m/s²
Answer:

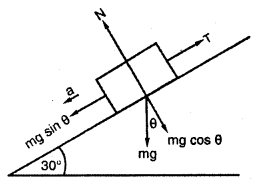
Here, m = 60 kg, θ = 30°, a = 2m/s2, g = 10 m/s²
∴ Tension T =mg sin θ – ma
= m(g sin θ – a)
= 60(10 × sin30°- 2)
= 60 × (10 × \(\frac{1}{2}\) – 2)
= 60 × 3 = 180N

Question 2.
Two friends Vipul and Mohan are cycling at 18 km/h on a level road. Vipul told that there is a sharp circular turn of the radius of 3 m. So, reduce your speed to avoid slipping. But Mohan was a careless boy and he did not follow his advice. Suddenly he slipped and felt the importance of his friend’s idea.
(i) Which values are depicted by Vipul?
Answer:
Cooperative, caring, awareness, and helping nature.

(ii) Explain why the cyclist Mohan slip while taking the turn?
[Take us = 0.1 ]
Answer:
If the speed is too large or if the turn is too sharp (i.e. of too small a radius) or both, the frictional force is not sufficient to provide the necessary centripetal force, and the cyclist slips. The condition for the cyclist not to slip is given by:

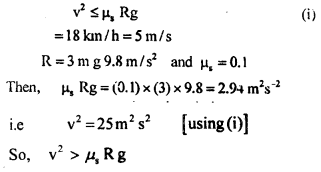
Hence, the condition is not obeyed. So, the cyclist will slip while taking the circular turn.

Question 3.
Mahesh was driving a car with his old grandfather. After some time when the destination was about to come, he did not apply the brakes. But he stopped the engine. Even then the car was running on the road for some time. His grandfather surprised and asked his grandson the reason for the car running without the engine on. Mahesh was a student of the science stream of class XI. He explained that it is due to the momentum of the car.
(i) Which values are displayed by Mahesh here?
Answer:
The values displayed by Mahesh are:
Intelligence, awareness, helping nature, and willingness to explain the scientific reason, (i.e explanation).

(ii) What is momentum and on which factors it depends?
Answer:
The momentum of a body is defined as the product of its mass and velocity.
i.e Momentum = mass × velocity
or
P = m × v
Momentum is directly proportional to mass as well as its velocity.
So, Momentum depends on the mass and the velocity of a moving body.

Question 4.
Suresh noticed a big Granite Rock in his locality. He thought that if they worked upon it they could earn money. He took permission from the Government, completed all the formalities. He broke the Rock using a bomb. The rock was made into slices. They established a Granite industry. Many of the people in the surroundings started to earn and live comfortably.
(a) What values of Suresh impress you?
Answer:
Suresh knows how to utilize the natural resources, has got concerned for others. Also, he knows how to complete all legal formalities before taking up any work.

(b) A bomb is thrown in a horizontal direction with a velocity of 50 m/s. It explodes into two parts of masses 6 kg and 3 kg. the heavier fragment continues to move in the hori¬zontal direction with a velocity of 80 m/s. Calculate the velocity of the lighter fragment.
Solution: r
According to low of conservation of momentum
Total momentum of fragments = Momentum of the Bob
m₁ v₁ + m₂ v₂ = M V
⇒ 6 × 80 + 3 × V₂ = 9 × 50
⇒ V₂ = -10 m/s.

Question 5.
Rakesh with an intention to win in the interschool sports practiced the high jump every day for about a month. He participated and won I position in the interschool sports.
(a) Comment upon the values Rakesh possesses.
Answer:
Rakesh has the determination, he plans and executes his plan accordingly.

(b) Why does an athlete run some steps before taking a jump?
Answer:
An Athlete runs some steps before taking a jump to gain some initial momentum, which helps him to jump more?
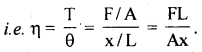
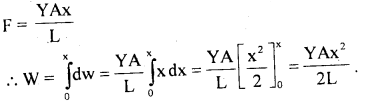
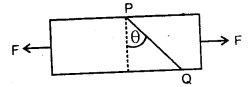
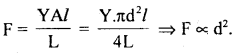
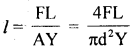
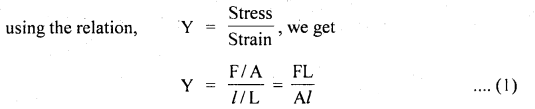
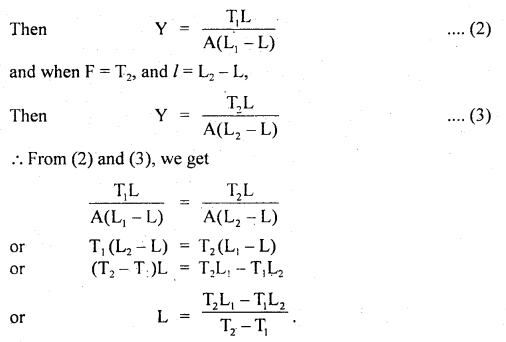
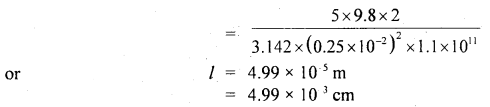
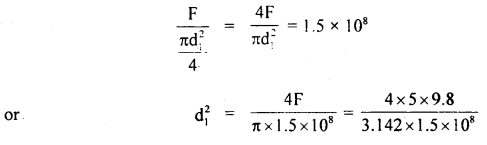
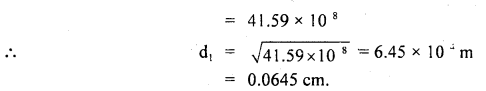
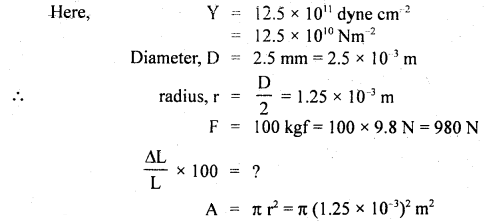
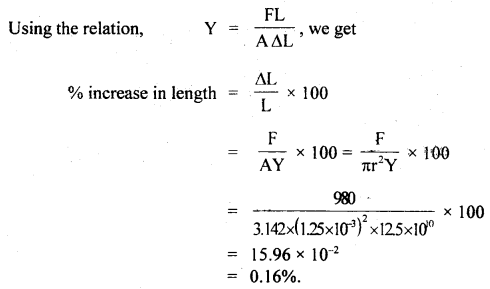
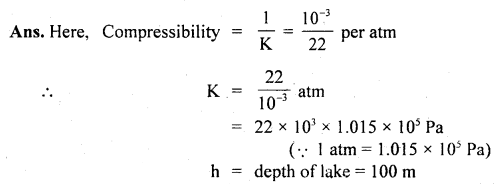
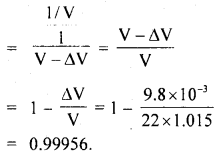
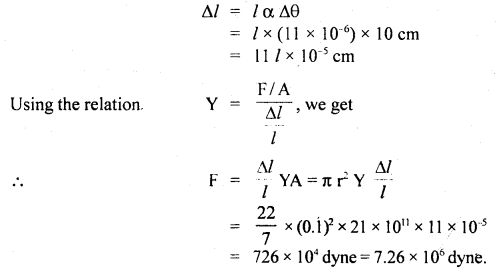
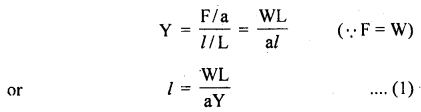
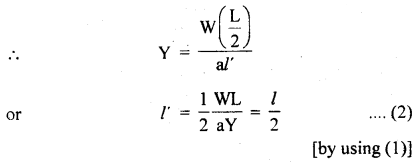
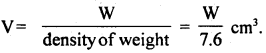
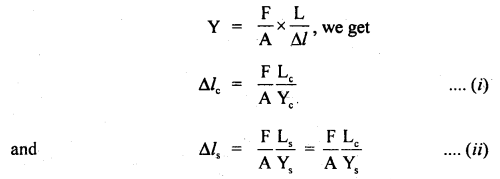
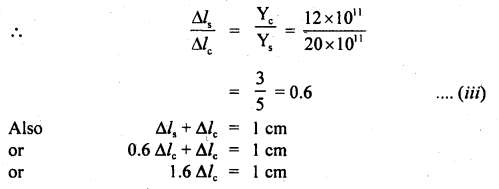
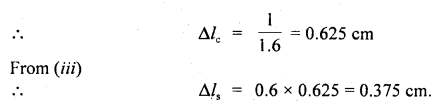
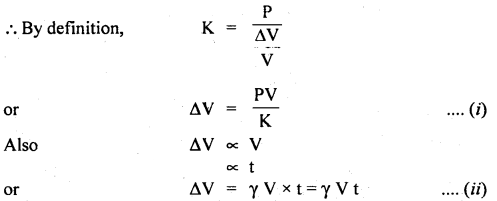
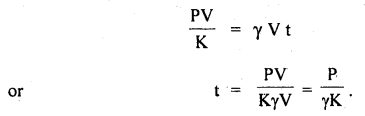
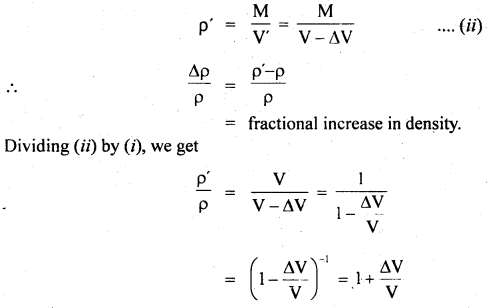
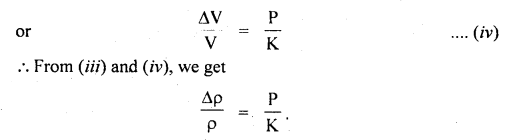
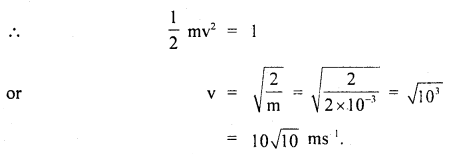
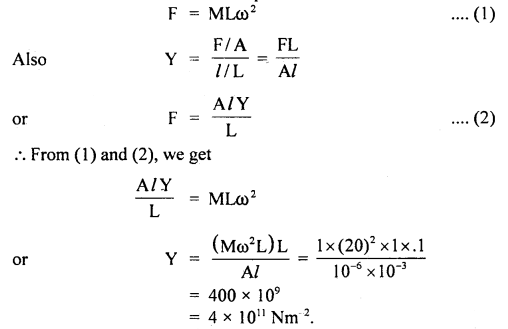
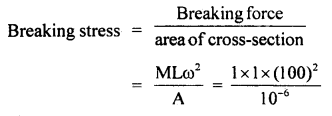
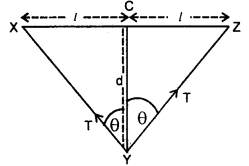
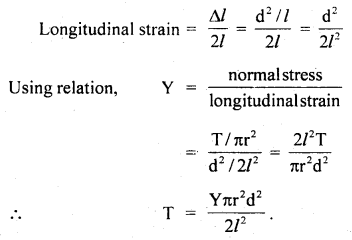
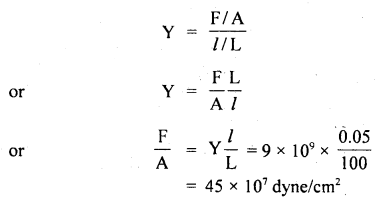
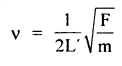
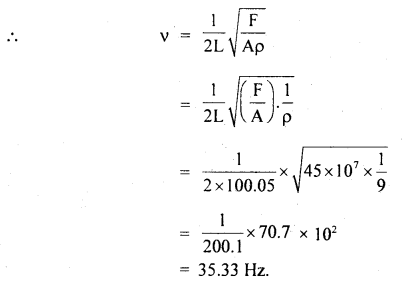