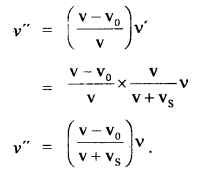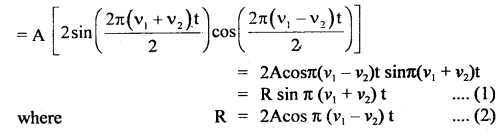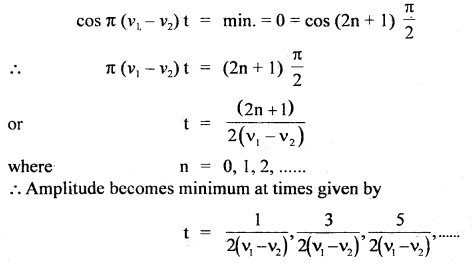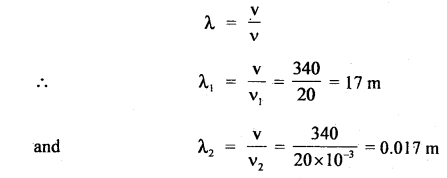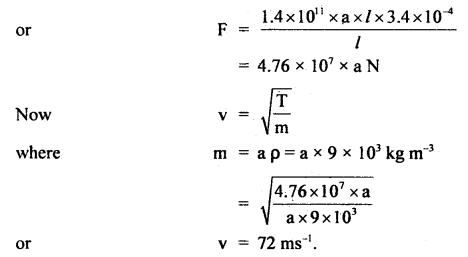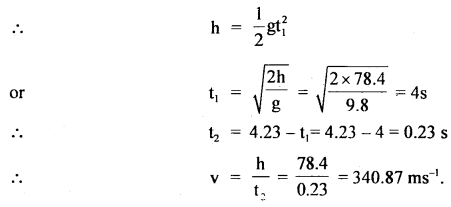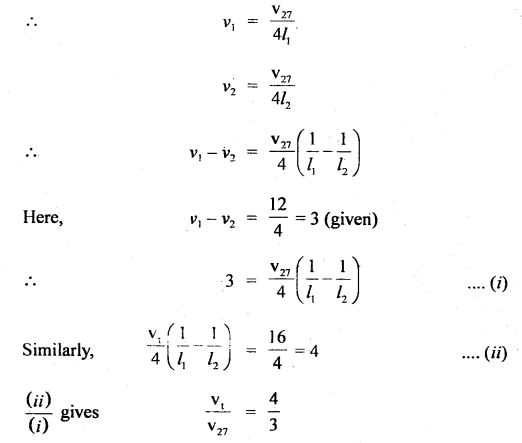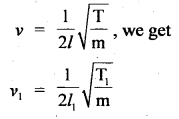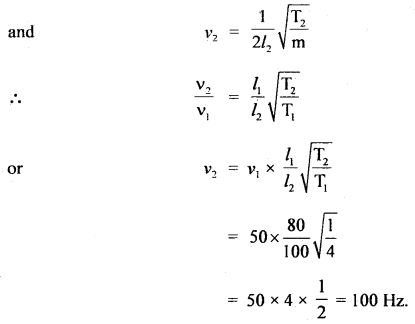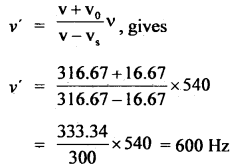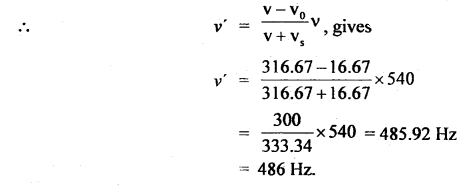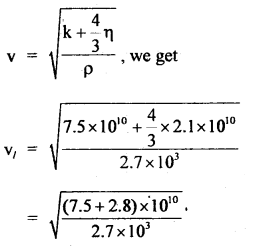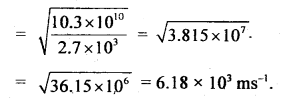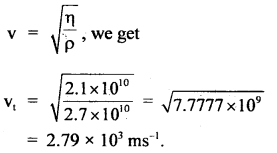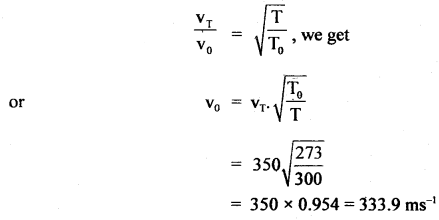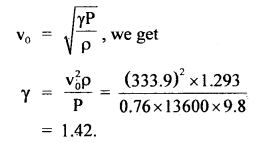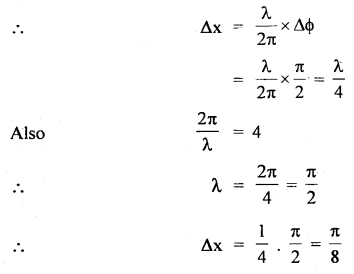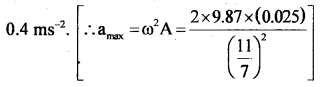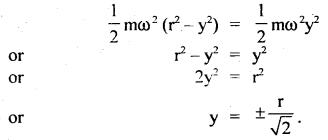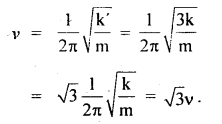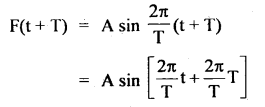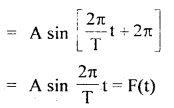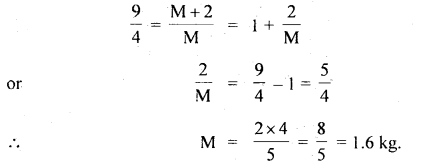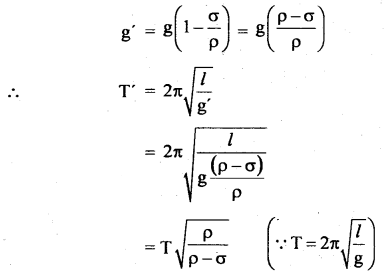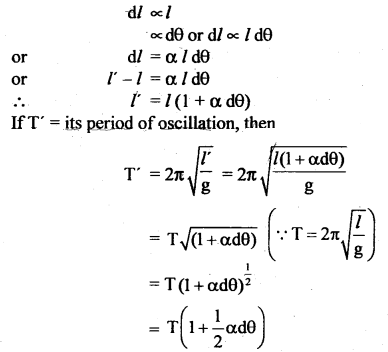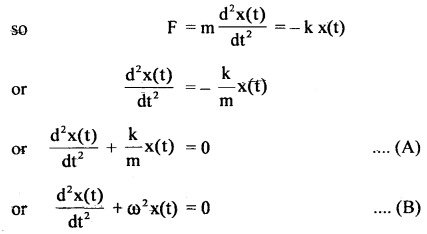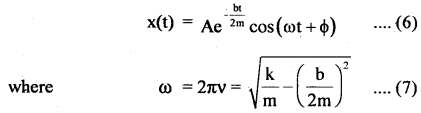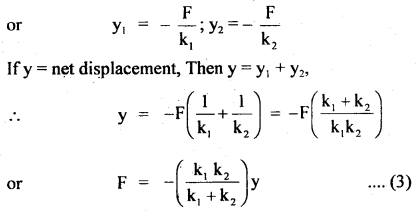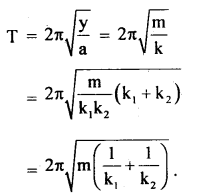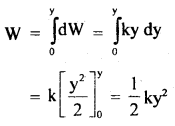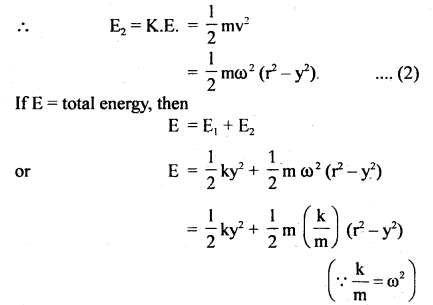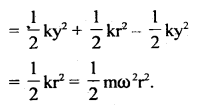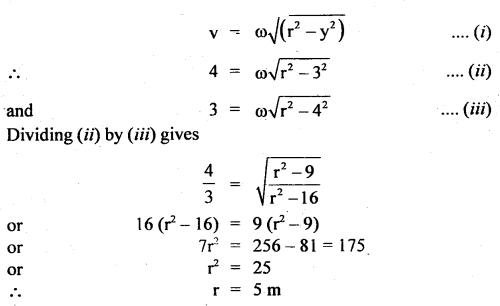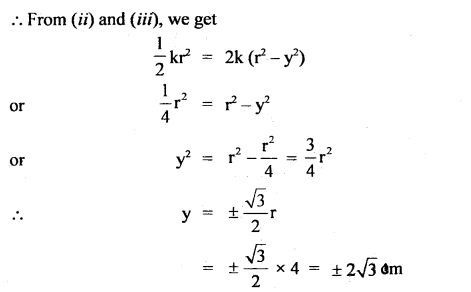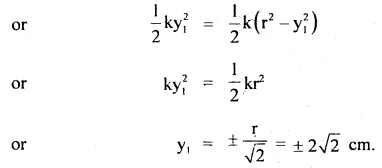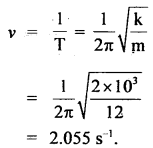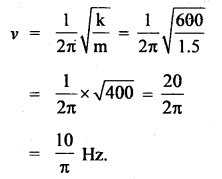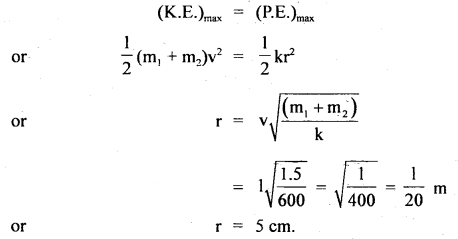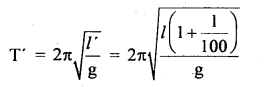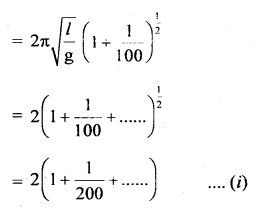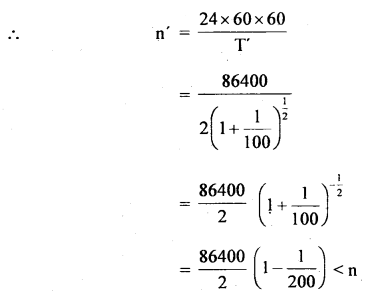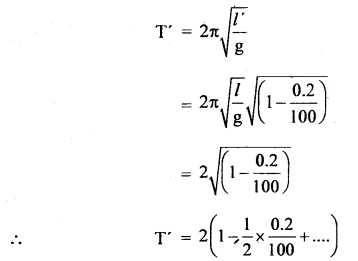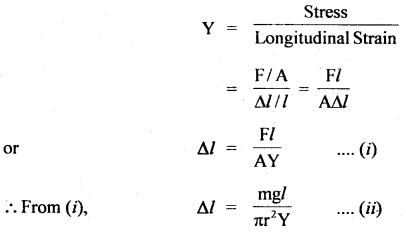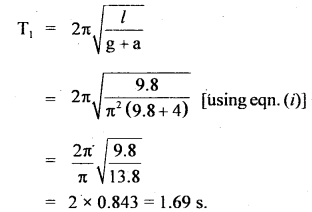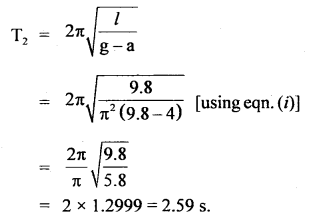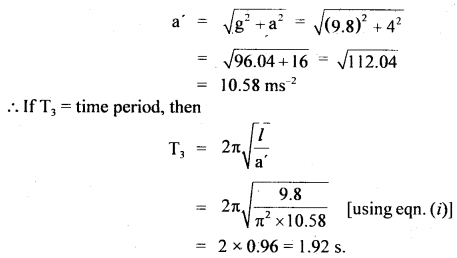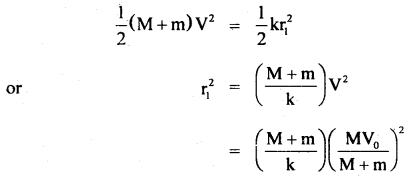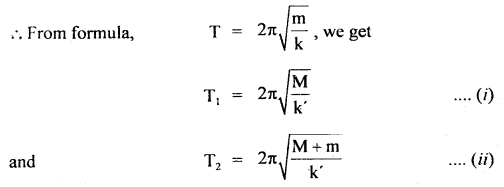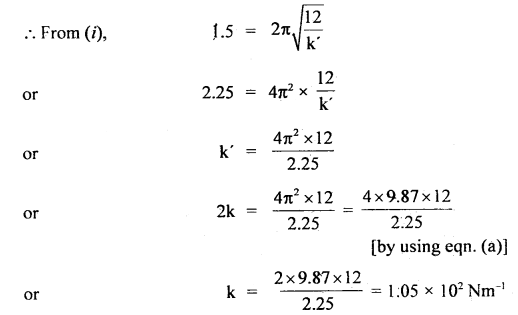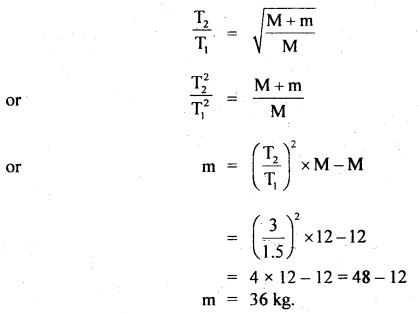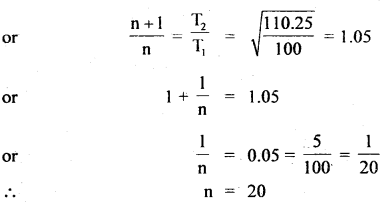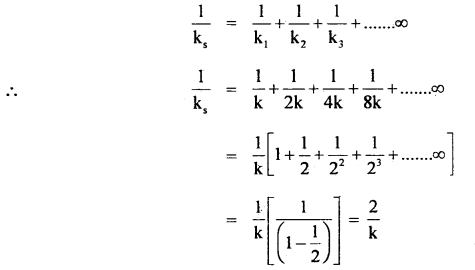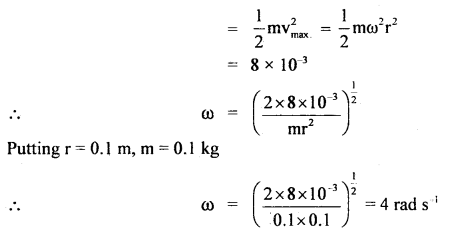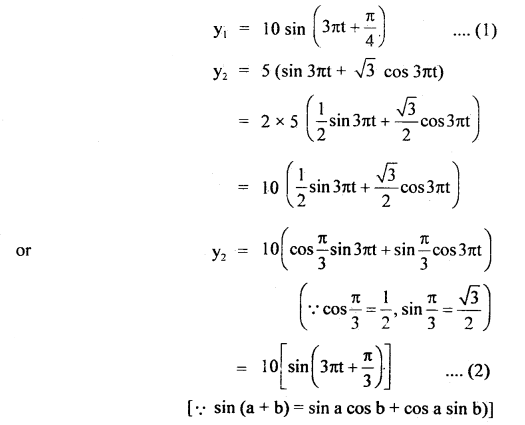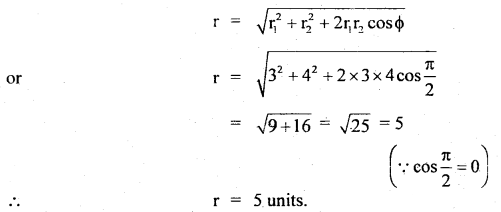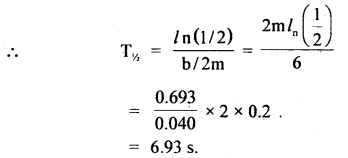CBSE Class 11

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 3 Plant Kingdom. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 3 Important Extra Questions Plant Kingdom

Plant Kingdom Important Extra Questions Very Short Answer Type

Question 1.
Define pyrenoid.
Answer:
Pyrenoid is a starch storing organelle present in green algae.

Question 2.
Define ramenta.
Answer:
The hair-like structure present on the younger stem, petiole, and rachis of mature leaves is known as ramenta.

Question 3.
What is the function of mucilage in aquatic plants?
Answer:
Mucilage protects the algae from epiphytic growth and the decaying effect of water.

Question 4.
How much water can Sphagnum absorb?
Answer:
Sphagnum can absorb water up to 18 times its weight.

Question 5.
What is the function of air vesicles in brown algae?
Answer:
The air vesicles in brown algae maintain buoyancy.

Question 6.
Why is Adiantum called a ‘walking fern’?
Answer:
Adiantum is known as ‘walking fern’ because the leaf tips come in contact with the soil, They strike adventitious roots and develop into a new plant.

Question 7.
Give one example of the monocarpic plant.
Answer:
Bamboo.

Question 8.
What are sori?
Answer:
They are groups of separation found in Dryopteris fern.

Question 9.
What are rhizoids?
Answer:
They are slender unicellular or multicellular hair-like structures that penetrate in the moist soil and absorb the water for the plants.

Question 10.
Which pigments are found in green algae?
Answer:
Chlorophyll ‘a’ and ‘b’ and ‘Beta’ carotene.

Question 11.
Define a fruit.
Answer:
Fruit is a developed ovary of the flower that encloses seeds and may be associated with other parts of the flower.

Question 12.
Name the group of vascular plants with naked seed.
Answer:
Gymnosperms.

Question 13.
Name the green algae used as food.
Answer:
Chlorella, Ulva.

Question 14.
Name the following:
(i) Photosynthetic pigments of brown algae
Answer:
Chlorophyll a and c and fucoxanthin,

(ii) Unicellular, biflagellate, pear-shaped green algae.
Answer:
Chlamydomonas,

Question 15.
What are coralloid roots?
Answer:
Coralloid roots are irregular, negatively geotropic,

Question 16.
What is triple fusion?
Answer:
The fusion of the diploid secondary nucleus and one male gamete is called triple fusion.

Question 17.
Define a seed.
Answer:
It is a ripened ovule and capable of forming a new plant.

Question 18.
Define a fruit.
Answer:
Fruit is a ripened ovary.

Question 19.
Give one example of a dicot seed and one of a monocot seed.
Answer:
Dicot: Gram, Monocot: Maize Grain.

Plant Kingdom Biology Important Extra Questions  Short Answer Type

Question 1.
Why are red algae able to survive in the deep-sea?
Answer:
Red algae contain phycoerythrin and phycocyanin pigments. Phycoerythrin is able to absorb the blue wavelengths of light and thus can photosynthesize. Since red algae can utilize blue and green rays they can live at greater depths.

Question 2.
What are the features that have led to the success and dominance of vascular plants?
Answer:

1. Development of deep penetrating roots to anchor the plant in soil and absorb water and minerals for the plants from the deeper layers of the soil.
2. Development of cutin as a waterproof layer on leaves to reduce transpiration.
3. Development of mechanical tissue to provide support.
4. Development of a well developed vascular system.

Question 3.
Define monopodial growth?
Answer:
When the main axis of the trunk rises straight from the base and reaches up to the tip, this type of growth is known as monopodial growth.

Question 4.
Why do marine algae have no mechanical tissue?
Answer:
Marine algae have no mechanical tissue because buoyancy holds them erect under the sea surface.^

Question 5.
Explain the different types of sexual reproduction in green algae.
Answer:
Sexual reproduction in green algae can be of three different types:

1. Isogamy: Both the fusing gametes are morphologically and physiologically similar.
2. Anisogamy: The fusing gametes are structurally similar but differ in size and behaviour.
3. Oogamy: The female gamete is bigger, food-laden and non-motile, whereas the male gamete is smaller, without food reserve and motile.

Question 6.
Why are seed plants considered the most successful land plants?
Answer:
Seed plant is considered as the most successful land plants because:

1. Fertilization is not water-dependent.
2. Seed enclosing the future embryo is well protected within the ovary.
3. The extensive root system for anchoring and absorption of water.
4. Well developed mechanical tissue
5. Formation of bark during secondary growth for protection.

Question 7.
Give one example of each
(i) Liverworts
Answer:
Riccia

(ii) Mosses
Answer:
Funaria

(iii) A pteridophyte having bipinnate leaves.
Answer:
Dryopteris

(iv) A pteridophyte having Unipinnate leaves.
Answer:
Adiantum caudatum

Question 8.
Give five distinguishing characteristics of red algae.
Answer:
Five distinguishing characteristics of red algae are:

1. Most of the red algae are marine.
2. The motile stage is absent in the life cycle.
3. The plant body varies from unicellular filamentous to parenchymatous form.
4. The cell wall possesses cellulose and hydrocolloids.
5. Photosynthetic pigments include chlorophyll a, carotenoids and phycobilins.

Question 9.
Discuss the development of seed habit.
Answer:
The development of seed habit takes place due to the

1. Development of heterospory.
2. The megasporangium developed an intelligent covering with a micropyle.
3. The development of female gametophyte takes place from functional-megaspore.
4. Development of pollen tube.
5. The fertilized ovule developed into a seed.

Question 10.
Draw a neat diagram of Chlamydomonas.
Answer:

Chlamydomonas

Question 11.
Draw a neat diagram of Spirogyra.
Answer:

Spirogyra

Question 12.
Describe the fern sporophyte.
Answer:
Fem sporophyte is differentiated into root, the stem is a rhizome with adventitious roots, the young part of the rhizome has ramenta. the leaves are bipinnately compound.

Question 13.
Distinguish between Antherida and Archaegonia.
Answer:

Question 14.
How do red algae differ from brown algae?
Answer:
Differences between red algae and brown algae:

Red algae

Porphyra or Polysiphonia

Question 15.
Distinguish the reproductive organs of gymnosperms and angiosperms.
Answer:

Question 16.
Mention the changes that take place when the fruit ripens.
Answer:

1. Starch is converted into sugar.
2. The production of various organic substances gives it a texture, taste and flavour.
3. The breakdown of chlorophyll leads to changes in the colour of the skin of the fruit.

Question 17.
What is the importance of seed?
Answer:

1. The seed contains the young embryo which develops into a new plant.
2. Seed can be dispersed and carried to faraway places without losing viability.
3. Seed is neither the beginning nor the end of life. It is a state of suspended animation.

Question 18.
Describe the important characteristics of gymnosperms.
Answer:
Characteristic features of gymnosperms:

1. Gymnosperms are evergreen woody, perennial plants.
2. Plants are heterosporous.
3. Reduction of gametophytic generation.
4. The enclosure of the female gametophyte by the megasporangium.
5. Ovules are exposed to receive pollen grains.
6. Gymnosperms possess exposed or naked seeds.
7. Polyembryony is a common occurrence.
8. Xylem lacks vessels and phloem lacks companion cells. Example Cycas, Pinus and Cedms.

Question 19.
Name two characters Used for the classification of dicotyledons in 3 sub-classes.
Answer:
Number and nature of floral whorls. Sub-classes are divided into series mainly on the position of the ovary with respect to other floral parts.

Question 20.
Explain briefly the alternation of generation in bryophytes.
Answer:
Alternation of generations: Moss plants are a gametophyte. Spore is the beginning of the gametophytic generation. It develops into protonema which rises to male and female gametes produced in them. Club-shaped antheridium bears biflagellate sperms or antherozoids. Flask-shaped archegonium encloses the female egg. a zygote is formed after the fertilization (syngamy) of male and female gametes with the help of water.

Repeated divisions of the zygote give rise to the embryo (2n) which soon develop into a sporophyte. The sporophyte of moss gets differentiated into three parts -foot, seta and capsule. Inside the capsule, single-celled spores are produced. After the dehiscences, they begin to germinate and give rise to the protonema to start the cycle again. Gametophytic generation al¬ternates the sporophytic generation.

Question 21.
Draw the haplontic life-cycle.
Answer:

Haplontic life-cycle

Question 22.
Draw the diplontic and haplo-diplontic cycles.
Answer:

Diplontic cycles

Haplo-diplontic cycles

Plant Kingdom Biology Important Extra Questions Long Answer Type

Question 1.
What are angiosperms? Give their characteristic features.
Answer:
Angiosperms are a group of flowering plants where seeds are embedded in the fruits.

They show the following characters:

1. The ovules/seeds are enclosed within the ovary, or we may say that after fertilization seeds are located in the fruit.
2. Male and female gametes i.e. pollen grains and egg nucleus are borne by the flowers.
3. During pollination pollen grains fall on the stigma, they develop on the stigma of the ovary and male gametes enter the egg nucleus through Onicropyh.
4. Male gametophyte is a three-celled structure when dehisced.
5. Embryosac or female gametophyte is eight celled when young and becomes seven celled at the time of fertilization.
6. There is double fertilization wherein one male gamete fuses with the egg nucleus to form a diploid zygote and another fuse with the secondary nucleus to form a triploid endosperm.
7. Xylem consists of tracheids, vessels fibres and parenchyma while phloem consists of sieve tubes, companion cells and phloem parenchyma and fibres. Xylem conducts water to the tip of tall trees and phloem is responsible for the translocation of food.

Question 2.
Write brief notes on:
(i) Green algae
Answer:
Green Algae: The Class (Chlorophyta: ‘GK’ choros = green: phyton = plant) has over 7,000 species. They are in several shapes and sizes. Some are unicellular and microscopic. Some are motile colonies like Volvox. Some, are multinucleated but unicellular i.e. coenocytic like cholera.

Volvox

Chlamydomonas

Chara

(ii) Brown algae
Answer:
Brown Algae: The Class (Phaeophyta: GK: pharos = brown: phyton = plant) has about 2,000 species, mostly marine. Some of, the world’s largest sea plants measuring 40-60 metres long. Brown algae occur chiefly in cooler seas. Some are filamentous. Brown algae like Laminaria are attached firmly to the rocks below by holdfasts.

Laminaria

Fucus

Dictyota

(iii) Club moss
Answer:
Club mass: It belongs to Lycopsida. In most parts of the world, Lycopodium is found. Sporangia’ are produced on mature leaves.

(iv) Horsetail
Answer:
Horsetail: Also called Sphenopsida. This group exists only Equisetuin. Because they look like the tail of a horse, so they are called horsetail. These plants are up to 1 metre in length. But some extinct species are of several metres. The root, stem and leaves are true.

(v) Sporophyll
Answer:
SporphyMs: They are special spore-bearing leaves and. produce sporangia in sori on their underside, where haploid spores are formed by meiosis. Spores germinate to form an independent, small gametophyte, the prothallus. This bears archegonia and antheridia. Male gamete from antheridia and swim in a film of water to egg cells in archegonia and fertilize them.

Question 3.
Discuss the development of seed habit.
Answer:
The seed plants have two kinds of sporangia. These sporangia are born on the sporophylls.

One type of sporangia are ovule or megasparangium. The other type of sporangia is the pollen sac or archegonium. The egg develops a pollen sac or microsporangium. The egg develops in the ovule from the megaspores. Many pollen grains are produced in the pollen sac.

The pollen grains are dispersed by the air! They reach the ovule. The male gamete and the female egg cell fuse together. The zygote is formed as a result of fertilization. Later on, the zygote forms the embryo. The seed is developed from the ovule. The development of seed habit in gymnosperm and angiosperm do not require liquid water during fertilization

Question 4.
What are the different lifestyles shown by Angiosperms?
Answer:

1. Hydrophytic plants are the plants that live in water or swampy places. Hydrophytes are categorised into, two groups:
   (a) Submerged plants like Hydrilla, Vallisneria, Utriculria and
   (b) Floating plant-like Nymphea, Wolffia and Pistia.
2. Xerophytic plants are those plants that live in the scarcity of water e.g. cactus.
3. Halophytes are a type of xerophytic plants that are present in saline conditions.
4. Insectivorous plants-A few angiosperms, though green and autotrophic trap insects to overcome the shortage of nitrogen. For example, pitcher plant, sundew, bladderwort.

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 2 Biological Classification. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 2 Important Extra Questions Biological Classification

Biological Classification Important Extra Questions Very Short Answer Type

Question 1.
What are imperfect fungi?
Answer:
Asexually reproducing fungi belonging to Deuteromycites are imperfect fungi

Question 2.
How many basidiospores are formed after Karyogamy and meiosis?
Answer:
4

Question 3.
What is plasmogamy?
Answer:
Fusion of protoplasms between two motile or non-motile gametes.

Question 4.
What do you mean by mycorrhiza?
Answer:
Mycorrhiza is a symbiotic association between fungi with roots of higher plants.

Question 5.
How does the spore of slime molds disperse?
Answer:
By air currents

Question 6.
Name the protein-rich layer found in Euglenoids.
Answer:
Pellicle.

Question 7.
Give an example of red dinoflagellates?
Answer:
Gonyaulax.

Question 8.
Who is known as ‘Producers of the oceans’?
Answer:
Diatoms

Question 9.
Name the organism responsible for algal bloom?
Answer:
Blue-green algae.

Question 10.
Who has discovered viroids?
Answer:
T.O. Diener.

Biological Classification Biology Important Extra Questions Short Answer Type

Question 1.
What are the slime molds?
Answer:
1. The slime molds are both plant and animal-like.

2. They are plant-like in the production of spores during reproduction and animal-like in the mode of nutrition and rheumatic organization.

3. Their rheumatic structure consists of an acellular, multinucleate mobile mass of protoplasm which lacks a good wall called plasmodium.

4. The reproductive stage consists of sporangia and spores formed after meiosis. The spores on germination produce either flagellated swarm cells or myxamoebae.

5. These divide mitotically, then behave as gametes and fuse in pairs to form a diploid zygote. The zygote nucleus divides mitotically but the nuclear division is not followed by cell wall formation so that all nuclei lie free in the cytoplasm.

6. The enlargement of the zygote into plasmodium takes place which moves freely on the substratum and feeds on bacteria, fungal and algal spores, and also absorbs nutrients directly from the substratum. The plas¬modium then settles on dry places and develops into sporangia. Therefore asexual stage is plant-like and the sexual stage is animal-like.

Question 2.
Write a short note on kingdom Plantae.

Kingdom Plantae
Answer:
1. Kingdom Plantae includes all autotrophic plants which are photosynthetic forms called green plants starting from simple algae, bryophytes, pteridophytes to gymnosperm and angiosperms.

2. The plant cell has a cell wall mainly made of cellulose and, eukaryotic structure with prominent chloroplasts. Some plants are heterophilic like insectivorous plants which feed on insects and flies e.g. Bladderwort and Venus flytrap.

(3) The life cycle has two phases-sporophytic and gametophytic which are diploid (2n) and haploid (n) respectively. That means zygote (2n) undergoes meiosis to form haploid (n) spores these spores germinate into a gametophyte, then these gametes (male and female) fuse to form a zygote (2n) again which gives rise to the sporophyte. This phenomenon is called the alternation of generation.

Question 3.
Write a short note on Mycoplasma.
Answer:

1. Discovered by E.Nocard and E.R. Roux (1998) mycoplasma is the smallest known aerobic prokaryotes without a cell wall.
2. They were isolated from cattle suffering from bovine pleuropneumonia and hence they were designated as PPLO (pleuropneumonia-like organisms)
3. They are found in different forms as a spheroid, thin, stellate called pleomorphic.
4. They occur in soil, sewage, human, and plants.

Question 4.
Write a short note on Kingdom Animalia.
Answer:

1. Kingdom Animalia includes all animals except the protozoan. The members are multicellular eukaryotes. The cell wall is absent cells, organized into tissue. They directly or indirectly depend on plants for food.
2. They digest their food in an internal cavity and store food reserves as glycogen or fat. They are heterotrophic and the mode of nutrition is holozoic nutrition. They act as decomposers and help in the recycling of minerals.
3. Kingdom Plantae includes the multicellular, photosynthetic eukaryotic forms.
4. They have well-established mechanisms for absorption and Kingdom Animalia includes all animals except the protozoans. They are multicellular eukaryotes and are holozoic. The cells lack walls.

Question 5.
Write a short note on Lichens.
Answer:
Lichens are a symbiotic association between algae and fungi. The algae component is known as phycobiont and the fungal component as mycobiont which are autotrophic and heterotrophic respectively. Algae prepare food for fungi and fungi provides shelter and absorbs mineral nutrient and water for its partner.

On the basis of the structure of thallus, lichens can be classified into three types

1. Crustose: forms a crust on the substrate which is not easily separated from the substrate e.g. Graphis
2. Foliose: forms the leafy lobed structure attached to the substrate with the help of rhizines easily separated from substrate eg. Parmelia.
3. Fruticose: forms shrubby, cylindrical, and branched thallus. They grow erect or hang from the substrate e.g. Usnea. Lichens are the pioneer colonizers of bare rocks. They also colonize tree trunks in temperate climatic regions.

Biological Classification Biology Important Extra Questions Long Answer Type

Question 1.
Describe the kingdom Monera.
Answer:
This kingdom comprises single-celled prokaryotic organisms like bacteria, filamentous actinomycetes, and photosynthetic blue-green algae of Cyanobacteria. The salient features are already given in Table 2.1 we will further discuss the following organisms briefly.

Bacteria: Bacteria are single-celled microscope true prokaryotic organisms which are almost omnipresent. They colonize soil, water, and air. These can survive

in extreme environmental conditions like high temperature, high salt concentration, in absence of oxygen (anaerobic) or in presence of oxygen (aerobic) in high acidic or alkaline pH, etc. (sometimes these are called Archaebacteria).

Some bacteria can be chemotrophs that derive energy from inorganic compounds in absence of oxygen e.g. methanogenic bacteria produce methane gas (CH₄) from CO₂ and H₂, some live by oxidizing hydrogen supplied eg. Thiothsix.

Some are parasites on plants and animals e.g. Xanthomonas citri and Vibrio Cholera; another form symbiotic association with plant roots e.g. Rhizobium.

The bacteria can be of various sizes and shape i.e. spherical or round, coccus (pi. cocci), rod-shaped and bacillus (pi. Bacilli), spiral-shaped spirillum (pi. Priscilla). Long and helical shaped called spirochetes. Many bacteria have one or more slender, long flagellum (pi. flagella) which helps them to move in the liquid substrate. Some bacteria form endospores under poor nutrient conditions.

Question 2.
Write the distinct characters of protozoa.
Answer:
1. Protozoa are single-celled heterotrophs or ‘first animal’. They can be free-living and parasitic members, mobile with flagellar movement, by pseudopodia, or by ciliary movements e.g. Euglena and Amoeba.

2. Cell wall is absent in some like Amoeba so they can change their shape. The Euglena is autotrophic because of the presence of chlorophyll it performs photosynthesis but in the absence of light, it becomes heterotropic and ingests other protists or food particles.

3. They reproduce asexually by binary fission but some reproduce sexually by fusion of gametes followed by meiosis. Another important member of protists is the malarial parasite, Plasmodium, causing the notorious disease malaria in man, carried by mosquitoes, it multiplies rapidly in the liver of humans and brings about the cyclic fever releasing toxins into the bloodstream of its host.

Photograph of Amoeba and Euglenas

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 1 The Living World. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 1 Important Extra Questions Living World

The Living World Important Extra Questions Very Short Answer Type

Question 1.
Name two organisms that do not reproduce?
Answer:
Mules, sterile worker bees.

Question 2.
Define ‘living’?
Answer:
Organisms exhibiting distinctive characters like growth, reproduction, etc. are called living.

Question 3.
Is regeneration a characteristic of living organisms?
Answer:
Yes, because fragmented organisms regain the lost part of the body.

Question 4.
What is biodiversity? or Define Biodiversity?
Answer:
The number and variety of organisms present on earth are referred to as biodiversity.

Question 5.
Name the International Authority who gives scientific name to the plants.
Answer:
International Code for Botanical Nomenclature (ICBN)

Question 6.
Write the scientific names of the following
(i) Mango
Answer:
Mangifera indica

(ii) Human
Answer:
Homo sapiens

(iii) Cat
Answer:
Felis Domestica

(iv) Tiger
Answer:
Panthera tigris.

Question 7.
What is taxonomy?
Answer:
Taxonomy is the science of classification that is grouping them on the basis of certain similarities.

Question 8.
How does taxonomy differ from systematics?
Answer:
Systematics is the study of the diversity of plants. The study of systematics leads to their taxonomic grouping.

Question 9.
What is a species?
Answer:
A population of identical individuals which can freely interbreed to produce fertile off-springs.

Question 10.
What is a taxon?
Answer:
A level of classification is called taxon e g., species, genus, family, etc. all are taxons.

The Living World Important Extra Questions Short Answer Type

Question 1.
How are zoological parks useful to biologists.
Answer:
Zoological parks are places where animals are maintained and allowed to breed in natural habitats.
(a) It gives information about endangered animals.
(b) Helps the biologists in developing hybrids with superior quality.
(c) Support the workers of biotechnology.

Question 2.
Write the universal rules of nomenclature.
Answer:

1. Biological names are generally in Latin and written in Italics. They are Latinised or derived from Latin irrespective of their origin.
2. the First word in a biological name represents the genus while the second component denotes a specific epithet.
3. Both the words in a Biological name when written in hand are separately underlined or printed in Italics to indicate their Latin origin.
4. First-world denoting genus starts with a capital letter while the specific epithet is written starting with a small word. It can be illustrated with the example of Mangifera indica.
5. The name of the author appears after a specific epithet i.e., the end of the biological name, and is written in the abbreviated form e.g. Mangifera indica (Linn). It indicates that species was first described by Linnaeus.

Question 3.
Explain about taxonomical aids/tools?
Answer:
Identification of organisms requires intensive laboratory and field studies. The information about an organism is collected and analyzed. The collection of actual specimens of plant species is essential and is a prime source of taxonomic studies.

These are also fundamental not only to study but also to training in systematics. It is used for the classification of an organism and the information gathered is also stored along with even the specimens. In some cases, the specimen is preserved for future studies.

Biologists have established certain procedures and techniques to store and preserve the information as well as the specimens. These techniques are, in fact, aids available for the identification and classification of organisms. The knowledge of these aids is quite helpful in biological studies. Some of these are explained to help to understand the usage of these aids.

Some of the taxonomical aids are

1. Herbarium,
2. Botanical Gardens
3. Museums
4. Zoological Parks
5. Keys.

Question 4.
“Consciousness is a defining property of living organisms.” Explain.
Answer:
Flora and fauna both respond to physical-chemical or biological environmental stimuli. Awareness of their surroundings makes organisms live. Mimosa pudiea respond to touch. Photoperiodic affects flowering in plants. Thus unicellular microscopic to multicellular huge organisms show the property of consciousness.

Question 5.
Reproduction can’t be an all-inclusive defining characteristic of living organisms? Illustrate the statement.
Answer:
In nature, there are many organisms that can’t reproduce. Mules, sterile worker bees are some examples of such organisms.

But the non-living object is strictly unable to reproduce.

Viruses are placed between living and non-living. They are crystallized like non-livings but replicate when enter inside living organisms.

The Living World Important Extra Questions Long Answer Type

Question 1.
Explain two defining characteristics of living organisms.
Answer:
Growth Unicellular and multicellular organisms increase their mass and number through cell-division. Non-livings increase their size by the accumulation of matter.
(a) Cell has protoplasm which is living matter. Cell before division increases their mass through replication of genetic matter. It is absent in non-livings.

(b) Metabolic Activity: Anabolic and catabolic reaction constantly occurs in living organisms, formation and conversion of biomolecules is metabolism.

‘In Vitro, such reactions can be maintained. In non-living, there is the absence of metabolism.

Question 2.
Explain the utility of systematics for classification.
Answer:
For classification, systematic studies have to carried out.

1. First, the organisms have to be described for all their morphological and other characteristics.
2. Based on its characteristic, it is seen whether it is similar (or different) to any known group or taxa-identification is carried out.
3. Based on its similar characteristic it is then placed in known taxa or the organism is classified. Sometimes organisms are very different from the ones already described anywhere in the world, then they are placed in a new group or ‘taxa’ and named.
4. Once the organism has been placed in the right taxa-the last step is nomenclature or naming. If the organism is already known-its the correct name is determined. If an organism is not described before-it is given a new name.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 15 Waves. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 15 Important Extra Questions Waves

Waves Important Extra Questions Very Short Answer Type

Question 1.
In a resonance tube, the second resonance does not occur exactly at three times the length at the first resonance. Why?
Answer:
This is due to the end correction.

Question 2.
What is the nature of ultrasonic waves and what is their frequency?
Answer:
Ultrasonic waves are longitudinal waves in nature and have frequencies greater than 20 k Hz.

Question 3.
Is the principle of superposition wave valid in the case of electromagnetic (e.m.) waves?
Answer:
Yes.

Question 4.
A rod is clamped at one end and it is hit by a hammer at the other end
(a) at a right angle to its length
(b) along the length.
What types of waves are produced in each case?
Answer:
(a) Transverse waves
(b) Longitudinal waves.

Question 5.
Why do not we hear beats if the frequency of ìwo sounds is widely different?
Answer:
The beats can’t be heard as separate due to the persistence of hearing if the difference in frequencies is more than 10 Hz.

Question 6.
What causes the rolling sound of thunder?
Answer:
The multiple reflections of the sound of lighting results in the rolling ’ sound of thunder.

Question 7.
A tuning fork produces resonance in a closed pipe. But the ‘ same tuning fork is unable to, produce resonance in an open organ pipe of equal length. Why?
Answer:
It is because the fundamental frequencies of open and closed organ pipes of the same length are different,

Question 8.
Thick and big curtains are preferred in a big hall. Why?
Answer:
To increase the absorption and decrease the reverberation time and hence making the sound uniform,

Question 9.
Why female voice is sweeter than that of a man?
Answer:
This is because the frequency of a lady’s voice is greater than that of a man’s voice.

Question 10.
The frequency of the fundamental note of a tube closed at one end is 200 Hz. What will be the frequency of the fundamental note of a similar tube of the same length but open at both ends?
Answer:
400 Hz.

Question 11.
A wave transmits energy. Can it transmit momentum?
Answer:
Yes.

Question 12.
By how much the wave velocity increases for 1°C rise of temperature?
Answer:
Wave velocity increases by 0.61 ms for 1°C rise of temperature.

Question 13.
Why the sound heard is more in carbon dioxide than in air?
Answer:
This is because the intensity of sound increases with the increase in the density of the medium.

Question 14.
What is the relation between path difference and phase difference?
Answer:
Phase difference = \(\frac{2π}{λ}\) × path difference.

Question 15.
Is it possible to have interference between the waves produced by two violins? Why?
Answer:
No. This is because the sounds produced will not have a constant, phase difference.

Question 16.
The windowpanes of houses sometimes get cracked due to some explosion at a large distance. Which waves are responsible for this?
Answer:
Shockwaves.

Question 17.
Why the velocity of sound is generally greater in solids than in gases?
Answer:
This is because \(\frac{E}{ρ}\) for solids is much greater than for gases.

Question 18.
An observer places his ear at the end of a long steel pipe. He can hear two sounds when a workman hammers the other end of the pipe. Why?
Answer:
This is because the sound is transmitted both through air and medium.

Question 19.
Why a stationary wave is so named?
Answer:
A stationary wave is so named because there is no net propagation of energy. .

Question 20.
How do we identify our friends from his voice while sitting in a dark room?
Answer:
The quality of sound helps us to identify the sound.

Question 21.
Why bells are made of metal and not of wood?
Answer:
This is because the wood has high damping.

Question 22.
What is the nature of light waves?
Answer:
Electromagnetic waves.

Question 23.
When a vibrating tuning fork is moved speedily towards a wall, beats are heard. Why?
Answer:
This is due to the difference in the frequency of the incident wave and the apparent frequency of the reflected wave.

Question 24.
The weight suspended from a sonometer wire is increased by a factor of 4. Will the frequency of the wire be increased exactly by a factor of 2? Justify your answer.
Answer:
No. There will be a slight increase in the length of the wire. So the frequency shall become slightly less than double.

Question 25.
Are sound waves in air longitudinal or transverse?
Answer:
Longitudinal.

Question 26.
Can you notice the Doppler effect if both the listener and the source of sound are moving with the same velocity in the same
direction? Why?
Answer:
No. This is because there is no relative motion between the source of sound and the listener.

Question 27.
If oil of density higher than that of water is used in place of water in a resonance tube, how does the frequency change?
Answer:
The frequency is governed by the air column and does not depend, upon the nature of the liquid. So frequency would not change.

Question 28.
Which property of the medium enables the transverse waves to pass through it?
Answer:
Modulus of rigidity.

Question 29.
In a thunderstorm why flash of light is seen earlier than the sound of thunder?
Answer:
The speed of light is much higher than the speed of sound waves.

Question 30.
What is the main difference between the brazing of a honeybee and the roaring of a lion?
Answer:
Brazing of honeybee is of high pitch and lion’s roar has high intensity.

Question 31.
If you set your watch by the sound of a distant siren, will it go fast or slow?
Answer:
It will go slow due to the low value of the speed of sound in the air.

Question 32.
What is a dispersive medium?
Answer:
A medium in which the wave velocity depends on the frequency of the wave is called a dispersive medium.

Question 33.
Will sound be louder at node or antinode in a stationary wave?
Answer:
It will be louder at node due to large pressure variation there as
ΔP = – strain × elasticity.

Question 34.
Even if a powerful thermonuclear explosion takes place on a planet, the sound is not heard on Earth. Why?
Answer:
The interplanetary space is devoid of continuous material. In the absence of a material, the medium sound is not heard on the earth.

Question 35.
In older days messages were conveyed to distant villages by beating of big drums. Why?
Answer:
It has a larger area and the intensity of sound (I) is directly proportional to the area of an oscillator (A) i.e. I ∝ A.

Question 36.
Which is the most basic property of the wave?
Answer:
Frequency is the basic property of the wave.

Question 37.
You can make waves in a pond by throwing a stone in it. What is the source of energy of the wave?
Answer:
The kinetic energy of the stone is the source of wave energy.

Question 38.
Why echoes are not heard in a small room?
Answer:
Because the minimum distance between the obstacle reflecting sound waves and the source of sound is less than 17 m in a small room, so echoes are not heard.

Question 39.
Name two properties that are common to all types of mechanical waves?
Answer:

1. They require a material medium for their propagation.
2. The medium itself does not move with the wave.

Question 40.
In sound, beats are heard when two independent sources are sounded together. Is it possible in the case of sources of light?
Answer:
No. This is because the phase difference between two independent sources of light is random.

Question 41.
Mention a condition when Doppler’s effect in sound is not applicable.
Answer:
When the velocity of the source or listener exceeds the velocity of sound.

Question 42.
What will be the velocity of sound in a perfectly rigid rod and why?
Answer:
Infinite because the value of Young’s modulus of elasticity is infinite for a perfectly rigid rod.

Question 43.
Sound is simultaneously produced at one end of two strings of the same length, one of rubber and the other of steel. In which string will the sound reach the other end earlier and why?
Answer:
In the case of steel-string as \(\frac{Y}{d}\) ratio is larger for steel than rubber.

Question 44.
Two persons cannot talk on the moon just as they do on the earth. Why?
Answer:
Due to the absence of air on the moon.

Question 45.
Graphs between the pressure P and the speed v in a gas are shown below. Explain with the reason which one is correct?

Answer:
(c) As the speed of sound (y) is independent of pressure, so y remains constant, hence (e) is correct.

Question 46.
Why the bells of colleges and temples are of large size?
Answer:
The larger the area of the source of sound more is the energy transmitted into the medium. Consequently, the intensity of sound is more and loud sound is heard.

Question 47.
State the limitations of Doppler’s effect.
Answer:
Doppler’s effect is applicable only when there is the relative velocity between the source and the listener and is less than the velocity of sound. The effect is not applicable if the relative velocity is greater than the velocity of sound i.e. if the source or observer moves with supersonic velocity.

Question 48.
Animals and human beings have two ears. What help do they render in listening sound from a distant source?
Answer:
The two ears receive sound in different phases, thus they help in locating the direction of the source of the sound. Turning of head and receiving sound in phase turns the direction.

Question 49.
An observer at a sea-coast observes waves reaching the coast. What type of waves does he observe? Why?
Answer:
Elliptical waves while the waves on the surface of the water are transverse, the waves just below the surface of the water are longitudinal. So the resultant waves are elliptical.

Question 50.
Why the reverberation time is larger for an empty hall than a crowded hall?
Answer:
It is due to the fact that the energy absorption in an empty hall is very small as compared to that of the crowded one.

Waves Important Extra Questions Short Answer Type

Question 1.
Here are the equations of three waves:
(a) y (x, t) = 2 sin (4x – 2t)
(b) y (x, t) = sin (3x – 4t)
(c) y (x, t) = 2 sin (3x – 3t).
Rank the waves according to their (A) wave speed and (B) maximum transverse speed, greatest first.
Answer:
(A) b, c, a.
Standard wave equation is y (x, t) = A sin (ωt – kx)
∴ (a) v_a = \(\frac{\omega}{k}=\frac{2}{4}=\frac{1}{2}\) unit = 0.5 unit.

(b) v_b = \(\frac{\omega}{k}=\frac{4}{3}\)unit = 1.33 unit.

(C) V_c = \(\frac{\omega}{k}=\frac{3}{3}\) = 1 unit.
clearly v_b > v_c > v_a, so order is b, c, a.

(b) Transverse speed (vt) = \(\frac{\mathrm{d} y}{\mathrm{dt}}\)
∴ |(v_t)_a| = 2 × 2 = 4
|(v_t)_b| = 4
|(v_t)_c| = 2 × 3 = 6

∴ clearly (c), (a) and (b) tie.

Question 2.
Which physical quantity is represented by the ratio of the intensity of wave and energy density? Why?
Answer:
Velocity.

Question 3.
When are the tones called harmonics?
Answer:
The tones are called harmonics if the frequencies of the fundamental tone and other overtones produced by a source of sound are in the harmonic series.

Question 4.
What will be the effect on the frequency of the sonometer wire if the load stretching the sonometer wire is immersed in water?
Answer:
Due to the upthrust due to buoyancy experienced by the load, the effective weight will decrease, so tension and hence frequency will decrease as v ∝ \(\sqrt{T}\).

Question 5.
An organ pipe is in resonance with a tuning fork. If the pressure of air in the pipe is increased by a factor of 139, then how should the length be changed for resonance?
Answer:
We know that the velocity of sound is independent of pressure, so there is no change in frequency and hence there is no need to change the length of the pipe.

Question 6.
Sound waves travel through longer distances during the night than during the day. Why?
Answer:
Earth’s atmosphere is warmer as compared to the surface of the earth at night. The temperature increases with altitude and thus the velocity of sound increases. It is a case of reflection from denser to rarer medium.

The sound waves get totally internally reflected.

Question 7.
Water is being continuously poured into a vessel. Can you estimate the height of the water level reached in the vessel simply by listening to the sound produced?
Answer:
Yes, the frequency of the sound produced by an air column is inversely proportional to the length of the air column. As the level of water in the vessel rises, the length of the air column in the vessel decreases, so the frequency of sound increases, and hence shrillness of sound increases.

From the shrillness of sound, we can have a rough estimate of the level of water in the vessel.

Question 8.
A sonometer wire resonates with a tuning fork. If the length of the wire between the bridges is made twice even then it can resonate with the same fork. Why?
Answer:
When the length of the wire is doubled, the fundamental frequency is halved and the wire vibrates in two segments so the sonometer wire will still resonate with the given tuning fork.

Question 9.
Doppler’s effect in sound is asymmetric. Explain.
Answer:
Sound waves require a material medium for their propagation.

The apparent frequency is different whether the source moves towards the stationary observer or an observer moves towards the stationary source. Thus the Doppler’s effect is said to be asymmetric. No such asymmetry occurs in light because apparent frequency remains the same in either the case whether the source or the listener moves.

Hence Doppler’s effect is said to be symmetric in light.

Question 10.
What is redshift?
Answer:
It is due to Doppler’s effect in the case of light waves. It is known that all stars are moving away from each other. So apparent frequency of light from a star as received by an observer on earth is less than the actual frequency. Since wavelength is inversely proportional to the frequency, the apparent wavelength of light from stars is more than the actual wavelength.

In other words, due to the Doppler effect, the wavelength of light shifts towards a longer end i.e. towards red color and so it is called redshift.

Question 11.
A sitar wife and a tabla when sounded together give 4 beats/ sec. What do we conclude from this? As the tabla membrane is tightened, the beat rate increases or decreases, explain.
Answer:
When sitar and tabla are sounded together, they give 4 seats/ sec. From this, we conclude that the frequencies of the two sounds differ by 4. If the frequency of tabla is greater than that of a sitar, then on tightening the tabla membrane, the frequency of tabla will further increase and hence the difference in frequencies will increase.

Thus beat rate will increase. If the frequency of tabla is less than that of sitar, then on tightening the tabla membrane, the frequency of tabla will increase and the difference in frequencies will decrease. So beat rate will decrease.

Question 12.
Explain why frequency is the most fundamental property of a wave.
Answer:
When a wave passes from one medium to another, its velocity and wavelength change but the frequency remains the same. Hence frequency is said to be the most fundamental property of a wave.

Question 13.
Sound is produced by vibratory motion, explain why then a vibrating pendulum does not produce sound?
Answer:
The sound which we can hear has a frequency from 20 Hz to 20,000 Hz.

The frequency of the vibrating pendulum does not lie within the audible range and hence it does not produce sound.

Question 14.
Explain why stringed instruments are provided with hollow boxes.
Answer:
The hollow boxes are set into forced vibrations along with the strings. The loudness is higher if the area of the vibrating body is more. So hollow boxes attached to increase the loudness of sound.

Question 15.
When we start filling an empty bucket with water, the pitch of sound produced goes on changing. Why?
Answer:
An empty bucket behaves as a closed organ pipe. The frequency of fundamental note produced by it is given by
v = \(\frac{v}{4l}\).

As the bucket starts filling, the length (l) of the resonating air column decreases, and hence frequency increases. Since the pitch of a sound depends upon the frequency. So it changes with the change in frequency.

Question 16.
Two loud-speakers have been installed in an open space to listen to a speech. When both are operational, a listener sitting at a .particular- place receives a very faint sound. Why? What will happen if one loud-speaker is kept off?
Answer:
When the distance between two loud-speakers from the position of listener is an odd multiple of \(\frac{λ}{2}\), then due to destructive interference between sound waves from two loud-speakers, a feeble sound is heard by the listener.

When one loud-speaker is kept off, no interference will take place and the listener will hear the full sound of the operating loud-speaker.

Question 17.
Why is the sound produced in the air not heard by a person deep inside the water?
Answer:
The velocity of sound in water is much lesser than the velocity of sound in air. So the sound waves are mostly reflected from the surface of the water. Only little refraction of sound from air to water takes place. Moreover, the refracted sound waves die off after traveling a small distance in the water. Hence no sound waves reach deep inside the water.

Question 18.
The reverberation time is larger for an empty hall than a crowded hall. Explain why?
Answer:
The sound prolongs for a longer time in an empty hall as it does not get absorbed. In the case of a crowded hall, the sound is absorbed by the audience. Hence reverberation time is less in the crowded hall.

Question 19.
If a balloon is filled with C0₂ gas, then how will it behave for sound as a lens? On filling it with hydrogen gas, what will happen?
Answer:
The speed of sound in CO₂ is less than in air (∴ v ∝ \(\frac{1}{\sqrt{\rho}}\)). So the balloon filled with CO₂ gas behaves as a concave lens.

When it is filled with hydrogen, the speed of sound in H2 gas becomes greater than in air. So it will behave as a convex lens.

Question 20.
Why on reflection from the rigid surface, the wave does not change type, and only phase change occurs, while on reflection from a smooth surface, type changes while phase does not change?
Answer:
When a compression strikes the rigid surface, the surface does not move but pushes the compression back as such. On the other hand, the direction of vibration of the particles of the medium is reversed. Thus the type of wave does not change while phase change occurs.

When a compression strikes the smooth surface (i.e. yielding surface), the compression continues to move forward with the surface. But due to refraction, a part of the wave moves backward. Thus type changes while phase does not change.

Question 21.
Explain why transverse elastic waves can’t propagate through a fluid?
Answer:
When a transverse elastic wave travels through a solid, a shearing strain develops which is supported by the elastic solid because of the development of a restoring force. Thus elastic waves can propagate through solids.

But a liquid or a gas (i.e. fluid) can’t support a shearing strain. So there will be no restoring forces when there are transverse displacements and so transverse vibrations are not possible.

Question 22.
Two strings of the same material and length under the same tension may vibrate with different fundamental frequencies. Why?
Answer:
The frequency of vibration of the string is given by

If ρ = density of the material of string.
l, r = its length and radius.
D = diameter = 2r, then

Hence the two strings may vibrate with different frequencies when they have different diameters.

Question 23.
Distinguish between transverse waves and longitudinal waves.
Answer:
Longitudinal waves:

1. Particles of the medium vibrate along the direction of propagation of the wave.
2. They travel in the form of alternate compressions and rare¬factions.
3. They can be formed in any medium i.e. solid, liquid, or gas.
4. When these waves propagate, there are pressure changes in ‘ the medium.
5. They can’t be polarised.

Transverse waves:

1. Particles of the medium vibrate, to the direction of propagation of the wave.
2. They travel in the form of alternate crests and troughs.
3. These can be formed in solids and on the surfaces of liquids only.
4. There are no pressure changes due to the propagation of these waves in the medium.
5. They can be polarised.

Question 24.
Distinguish between progressive waves and stationary waves.
Answer:
Progressive waves:

1. The disturbance travels onward. It is1 handed over from one particle to the next.
2. Energy is transported in the medium along with the propagation of waves.
3. Each particle of the medium executes S.H.M. with the same amplitude.
4. No particle of the medium is permanently at rest.
5. Changes in pressure and density are the same at all points of the medium.

Stationary waves:

1. The disturbance is confined to a particular region and there is no onward motion.
2. No energy is transported in the medium.
3. All the particles of the medium except at nodes execute S.H.M. with different amplitude.
4. The particles of the medium at nodes are at rest.
5. The changes of pressure and density are maximum at nodes and minimum at antinodes.

Question 25.
Distinguish between musical sound and noise.
Answer:
Musical sound:

1. It produces a pleasant effect on the ear.
2. It has a high frequency.
3. There are no sudden changes in the amplitude of the musical sound waves.
4. It is a desirable sound.

Noise:

1. It produces an unpleasant effect on the ear.
2. It has a low frequency.
3. There are sudden changes in the amplitude of noise waves.
4. It is an undesirable sound.

Question 26.
What are the characteristics of wave motion?
Answer:

1. Wave motion is a form of disturbance that travels in a medium due to repeated periodic motion of the particles of the medium.
2. The wave velocity is different from the particle velocity.
3. The vibrating particles of the medium possess both K.E. and P.E.
4. The particle velocity is different at different positions of its vibrations whereas wave velocity is constant throughout a given medium.
5. Waves can undergo reflection, refraction, diffraction, dispersion, and interference.

Question 27.
Show that for 1°C change in temperature, the velocity of sound changes by 0.61 ms-1.
Answer:
We know that v ∝ \(\sqrt{T}\) .
If v_t and v_o be the velocity of sound at T°C and 0°C respectively,

where α = \(\frac{\mathbf{v}_{\mathrm{t}}-\mathbf{v}_{0}}{\mathrm{t}}\) is called temp. coefficient of the velocity of sound.

Putting v_o = 332 ms^-1 at T0 i.e. 0°C, we get
α = \(\frac{332}{546}\) = 0.61 ms^-1 °C^-1

Question 28.
An electric bell is put in an evacuated room (a) near the center (b) close to the glass window, in which case the sound is heard (i) inside the room, (ii) out of the room.
Answer:

1. Sound is not heard in cases (a) and (b) inside the room as the medium is not there for the propagation of sound.
2. In case (a) sound cannot be heard outside for the reason given in (i) above.

In case (b) since the bell is very close to the window, the glass pane picks up its vibrations which are conveyed to the eardrum through the air outside the room. So, the sound can be heard in condition (b).

Question 29.
One of the primitive musical instrument is flute, yet produces good musical sound, how?
Answer:
The flute is an open organ pipe instrument having some holes which determine the wavelength and hence the frequency of sound. produced. By closing one or more holes, the length of the vibrating air column is changed and thus different harmonics are produced. The harmonic rich sound is a good musical sound.

Question 30.
Write basic conditions for the formation of stationary waves.
Answer:
The basic conditions for the formation of stationary waves are listed below:

1. The direct and reflected waves must be traveling along the same line.
2. For stationary wave formation, the superposing waves should either be longitudinal or transverse. A longitudinal and a transverse wave cannot superpose.
3. For the formation of stationary waves, there should not be any relative motion between the medium and oppositely traveling waves.
4. The amplitude and period of the superposing waves should be the same.

Question 31.
What is the difference between interference and stationary waves? In which phenomenon, out of the two, energy is not propagated? Why there is no energy at interference minimum?
Answer:
The superposition of two waves close to each other traveling in the same direction produces interference. The energy gets redistributed. It is minimum or zero at points of destructive interference and maximum at points of constructive interference. It is to be noted that the interference minima may not be points of zero energy unless •, the frequencies and amplitudes of the superposing waves are exactly equal.

The superposition of two similar waves (waves having the same amplitude and period) traveling in opposite direction produce stationary waves The nodes have no vibration of particles but antinodes have a maximum amplitude of vibration.

Question 32.
Write the applications of beats.
Answer:
Beats are used to:

1. Determine an unknown frequency by listening to the best frequency Δv. Then unknown frequency V’ = v ± Δv where v is known and it is close to the unknown frequency. The exact value of v’ is found by loading and filling the tuning fork of unknown frequency from which + or – sign is chosen.
2. Tune musical instruments by sounding them together and reducing beats number to zero.
3. Make a sound rich in musical effect by the deliberate introduction of beats between different musical instruments.
4. To produce very low-frequency pulses which otherwise cannot be produced. The beat frequency is the low-frequency sound.
5. Receive radio program by the superheterodyne method.
6. Detect harmful gases in mines.

Waves Important Extra Questions Long Answer Type

Question 1.
Derive expressions for apparent frequency when
(i) source is moving towards an observer at rest.
(ii) the observer is moving towards the source at rest.
(iii) both source and observer are in motion.
Answer:
Let S and O be the positions of. source and observer respectively.
υ = frequency of sound waves emitted by the source.
v = velocity of sound waves.

Case (i) Source (S) in motion and observer at rest: When S is at rest, it will emit waves in one second and these will occupy a space of length v in one second.
If λ = wavelength of these waves, then
λ = \(\frac{v}{υ}\) …(i)

Let vs = velocity of a source moving towards O at rest and let S reaches to S’ in one second. Thus the sound waves will be crowded in length (v – vs). So if λ’ be the new wavelength,
Then λ’ = \(\frac{v-v_{s}}{v}\)

if υ’ be the apparent frequency, then
υ’ = \(\frac{v}{\lambda^{\prime}}=\frac{v}{v-v_{s}}\)υ

∴ υ’ > v i.e. when S moves towards O, the apparent frequency of sound waves is greater than the actual frequency.

(ii) If the observer moves towards the source at rest:

Let v_o = velocity of an observer moving towards S at rest.
As the observer moves towards S at rest, so the velocity of sound waves w.r.t. the observer is v + v_o.

If υ’ = apparent frequency, then
υ’ = \(\frac{\mathbf{v}+\mathbf{v}_{0}}{\lambda}=\frac{\mathbf{v}+\mathbf{v}_{0}}{\mathbf{v}}\)υ
clearly v’ > υ.

(iii) If both S and O are moving
(a) towards each other: We know that when S moves towards stationary observer,

then υ’ = \(\frac{\mathbf{v}}{\mathbf{v}-\mathbf{v}_{\mathrm{s}}}\)

When O moves towards S, then
υ” = \(\left(\frac{v+v_{0}}{v}\right) v^{\prime}=\left(\frac{v+v_{0}}{v-v_{s}}\right) v\)

(b) If both S and O move in the direction of sound waves:
Then the apparent frequency is given by

υ” = \(\left(\frac{\mathbf{v}-\mathbf{v}_{0}}{\mathbf{v}-\mathbf{v}_{\mathrm{s}}}\right)\)υ

(c) When both S and O are moving away from each other:
When source moves away from O at rest, then apparent frequency is given by
υ’ = \(\frac{v}{v+v_{s}}\)υ

When the observer is also moving away from the source, the frequency v’ will change to v” and is given by

Question 2.
Give the analytical treatment of beats.
Answer:
Consider two simple harmonic progressive waves traveling simultaneously in the same direction and in the same medium. Let

• A be the amplitude of each wave.
• There is no initial phase difference between them.
• Let v₁ and v₂ be their frequencies.

If y₁ and y₂ be displacements of the two waves, then
y₁ = A sin 2π v₁ t and
y₂ = A sin 2π v₂ t

If y be the result and displacement at any instant, then
y = y₁ + y₂
= A (sin 2π v₁ t) + sin (2π v₂ t)

is the amplitude of the resultant displacement and depends upon t. The following cases arise.
(a) If R is maximum, then
cos π (v₁ – v₂) t = max. = ±1 = cos nπ
∴ π (v₁ – v₂) t = nπ
or
t = \(\frac{\mathrm{n}}{v_{1}-v_{2}}\) …(3)
where n = 0, 1, 2, …..

∴ Amplitude becomes maximum at times given by
t = \(0, \frac{1}{v_{1}-v_{2}}, \frac{2}{v_{1}-v_{2}}, \frac{3}{v_{1}-v_{2}}\)…..

∴ Time interval between two consecutive maxima is
= \(\frac{1}{v_{1}-v_{2}}\)

∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ – v₂
∴ no. of beasts formed per sec. = v₁ – v₂.

(b) If R is minimum, then

∴ Time interval between two consecutive minima is = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ – v₂
∴ no. of beasts formed per sec. = v₁ – v₂.
Hence the number of beats formed per second is equal to the difference between the frequencies of two component waves.

Question 3.
What conditions are necessary for the good acoustical properties of the building? How are they met?
Answer:
An acoustically good building is one in which the sound is heard clearly in every nook and corner, some conditions must be fulfilled.

These are:
(a) the building should have proper reverberation time, the reverberation time is given by Sabine’s formula which for a hall is
T = \(\frac{0.166 \mathrm{~V}}{\sum \alpha \mathrm{A}}\)
The reverberation time is adjusted by:

1. changing the volume (V): This can be changed little due to the size of the hall already fixed.
2. changing effective absorbing area: This can be done artificially by putting heavy curtains, paintings, providing open windows, wall coverings, etc.
3. providing sufficiently energetic sound: The sound should be sufficiently loud and intelligible at every point.
4. eliminating echo: Except for the desired one, echoes must be eliminated.
5. properly focussing the sound: The sound has to be properly focussed to avoid the source of silence and also unreliable focussing.
6. avoiding unique reinforcement: No single overtone should uniquely be reinforced then the total quality of the note will be affected.
7. avoiding extra noise: Extra noises including resonance within the building has to be avoided.
8. eliminating smooth curved surfaces: Smooth surfaces reflect sound sharply which may cause several problems.

To achieve these goals following steps need to be taken:
(a) Properly design the building to optimize its acoustic condition.
(b) Decorate selectively the building with paintings, floral designs, perforations.
(c) Use false perforated or cardboard ceilings, and perforated structures at the curved walls.
(d) Use carpets, upholster seats with holes in the bottom.
(e) Use carpets or mats etc. on floors.
(f) Heavy curtains, wall hangings, etc. should be used.
(g) Properly place the mike and loud-speakers in the hall.
(h) Avoid sharp corners in the hall and make the stage back parabolic with mike at its focus.

Numerical Problems:

Question 1.
How far does the sound travel in the air when a tuning fork of frequency 280 Hz makes 15 vibrations? Given the velocity of sound is 336 ms^-1.
Answer:
Velocity of sound, v = 336 ms^-1
frequency, v = 280 Hz

∴ Time of one complete vibration,
T = \(\frac{1}{v}=\frac{1}{280}\) s.
Time to complete 15 vibrations,
t = 15 T
= \(\frac{1}{280}\) × 15

If x be the distance covered in time t, then
x = v × t
= 336 × \(\frac{15}{280}\) = 18 m
x = 18 m.

Question 2.
Audible frequencies have a range of 20 Hz to 20 × 10³ Hz.
Express this range in terms of
(i) period T,
(ii) wavelength λ,
(iii) angular frequency CD.
Given the velocity of sound = 340 ms^-1.
Answer:
V = 340 ms^-1
Using v₁ = 20 Hz
v₂ = 20 × 10³ Hz
(i) T = \(\frac{1}{v}\), we get
T₁ = \(\frac{1}{20}\) = 0.005 s
and T₂ = \(\frac{1}{20}\) × 10³
= 0.00005 s = 5 × 10^-5 s.

(ii) we know that

∴ The wavelength range is 17 m to 0.0 17 m.

(iii) Angular frequency, ω = 2πv
∴ ω₁ = 2πv₁ = 2π × 20= 40π rads^-1
ω₂ = 2πv₂ = 2π × 20 × 10³
= 40π × 103 rad s^-1
∴ angular frequency range is 40π rad s^-1 to 40π × 10³ rad s^-1

Question 3.
A copper wire is held at the two ends by rigid supports. At 30°C, the wire is just taut with negligible tension. Find the speed of transverse waves in the wire at 10°C. α = 1.7 × 10^-5 °C^-1, λ = 1.4 × 10¹¹ Nm^-1 and ρ = 9 × 10³ kg m^-3
Answer:
When the temperature changes from 30°C to 10°C, then the change in length of the wire is
Δl = l ∝ Δt = l × 1.7 × 10^-5 × 20
= 3.4 × l × 10^-4 m

Here, ρ = 9 × 10³ kg m^-3
Y = 1.4 × 10¹¹ Nm^-2
Δt = 30 – 10 = 20°C
α = 1.7 × 10^-5 °C^-1

Now Y = \(\frac{\mathrm{F} / \mathrm{a}}{\mathrm{\Delta}l / \mathrm{l}}\)
or
F = Ya \(\frac{Δl}{l}\)
where a = area of cross section of the wire.

Question 4.
The speed of sound in hydrogen is 1270 ms^-1. What will be the speed in a mixture of oxygen and hydrogen mixed in a volume ratio of 1:4?
Answer:
Let V₁ and V₂ be the volumes of O₂ and H₂ respectively in the mixture.
ρ₁ and ρ₂ be their respective densities.

If m1 and m2 be the mass of oxygen and hydrogen respectively, then
m₁ = V₁ρ₁
and m₂ = V₂ρ₂

If ρ be the density of the mixture, then



Also, let v₁ = velocity of sound in the mixture
and v₂ = velocity of sound in the hydrogen
= 1270 ms^-1.

Question 5.
A tuning fork A of unknown frequency is sounded with a tuning fork B of frequency 288. Four beats are heard in one second. Tuning fork A is then loaded with a little wax and again sounded with fork B. Again 4 beats are heard in one second. What is the frequency of A?
Answer:
Since tuning fork A of known frequency say v gives 4 beats/ sec with B of frequency 288, so frequency of tuning fork A is given by
∴ v = 288 ± 4 = 284 or 292.
On loading A with wax, it again produces 4 beats/s with B of frequency 288.

If the frequency of A is 292, it means on loading A with wax, its frequency falls to 284 which can produce 4 beats/s with a B frequency of 288. So the frequency of A maybe 292.

If the frequency of A is 284, on loading it with wax, its frequency falls below 284 so that when it is sounded with B of frequency 288, it forms more than 4 beats/s which is not consistent with the given condition.

So the frequency of A can’t be 284. Hence the frequency of A = 292.

Question 6.
The first overtone of an open organ pipe beats with the first overtone of a closed organ pipe with a beat frequency of 2.2 Hz. The fundamental frequency of a closed organ pipe is 110 Hz. Find the lengths of the pipes. The velocity of sound in air = 330 ms^-1.
Answer:
Fundamental frequency of closed organ pipe is
v_c = \(\frac{\mathrm{v}}{4 \mathrm{~L}_{\mathrm{c}}}\)
L_c = length of closed pipe v
or
L_c = \(\frac{\mathrm{v}}{4 \mathrm{~v}_{\mathrm{c}}}\)

Here, ν_c = 110 Hz
v = 330 ms^-1

∴ L_c = \(\frac{330}{4 \times 110}\) = 0.75m = 75 cm. 0.4 × 110
Now frequency of first overtone of open pipe is
v₁ = \(\frac{\mathrm{v}}{\mathrm{L}_{0}}\)
where L_o = length of open pipe Frequency of first overtone of closed pipe is

Frequency of first overtone of closed pipe is
ν₂ = \(\frac{3 v}{4 L_{c}}=3\left(\frac{v}{4 L_{c}}\right)\)
= 3ν_c = 3 × 110 = 330 Hz

Question 7.
An open pipe is suddenly closed at one end with the result that the frequency of the 3rd harmonic of the closed pipe is found to be higher by loo Hz than the fundamental frequency of the open pipe. What is the fundamental frequency of open pipe?
Answer:
ν_o = \(\frac{v}{2L}\)
where ν0 = fundamental frequency of open pipe. The frequency of the third harmonic of closed pipe is

Question 8.
A set of 24 tuning forks is so arranged that each gives 4 beats per second with the previous one and the last sounds the octave of the first. Find the frequency of the first and last.
Answer:
As the last is the octave (double) of the first, so the frequencies are ¡n the increasing order.
Let frequency of the first = x
frequencyofthe2nd = x + 4
frequency olthe3rd = x + 2(4)
frequency of the 24th = x + 23 (4)
But this is the octave of the first
∴ frequency of the 24th = 2(x) (given)
∴ x + 23(4) = 2x
or
x = 92
∴ frequency of last tuning fork 2 × 92 = 184 Hz.

Question 9.
A drop of water 2 mm in diameter falling from a height of 50 cm in a bucket generates a sound that can be heard from a 5 m distance. Take all gravitational energy difference equal to sound energy, the transformation being spread in time over 0.2s, deduce the average intensity. Take g = 10 ms².
Answer:
Here, ρ of water = 103 kg m^-3
D = 2mm

∴ radius = r = \(\frac{2}{2}\) = 1 mm = 10^-3 m
h = 50cm = 0.50 m
g = 10 ms^-2
d = 5m
∴ a = area in which sound is heard
=4πd²
I = intensity of sound =?

Now I = \(\frac{\text { energy transference }}{\text { time } \times \text { area }}\)
= \(\frac{\text { P.E. of drop }}{\text { time } \times \text { area }}=\frac{m g h}{t \times a}\) …(1)

Question 10.
A train moves towards a stationary observer with a velocity of \(\frac{1}{30}\)th of the velocity of sound. The whistle of the engine regularly blows after one second. What ¡s the interval between successive sounds of the whistle as heard by the observer?
Answer:
Actual time interval between successive blows of whistle = 1 sec.

∴ Actual frequency of whistle, v = 1 Hz
Let v = velocity of sound
∴ velocity of source, vs = \(\frac{v}{30}\)
∴ apparent frequency of the whistle is
ν’ = \(\frac{v}{v-v_{s}}\) × ν = \(\frac{v}{v-\frac{v}{30}}\) × 1
or
ν’ = \(\frac{30}{29}\) Hz

∴ Apparent time interval between two successive sounds of whistle is
t = \(\frac{1}{v^{\prime}}=\frac{29}{30}\) s.

Question 11.
The splash is heard 4.2,3 s after a stone is dropped into a well which is 78.4 m deep. Find the velocity of sound in the air.
Answer:
Here, Depth of well, h = 78.4 m
v = velocity of sound = ?
t = total time after which splash is heard = 4.23 s.
t₁ = time taken by stone to hit water surface in the well.
t₂ = time the sound takes in reaching top of the well.
∴ t₁ +t₂ = 4.23 s
u = 0, g = 9.8 ms^-2, h = 78.4m, t = t₁

using the relation, s = ut + \(\frac{1}{2}\) at², we get

Question 12.
What is the intensity level in dB of sound whose intensity is 10^-6 watt m^-2. Take zero levels of intensity = 10^-2 watt m^-2.
Answer:
Here,
I = 10-6 w m^-2
I₀ = 10^-12 w m^-2

L =?
L = log10 \(\left(\frac{I}{I_{0}}\right)\) = log10 \(\left(\frac{10^{-6}}{10^{-12}}\right)\)
= log₁₀ 10⁶
= 6 log₁₀ 10 = 6 × 1 = 6B
As 1B = 10 dB
∴ L = 6 × 10 = 60 dB

Question 13.
Two closed organ pipes when sounded together produce 12 beats in 4s at a temperature of 27°C. Find the temperature at which the number of beats produced is 16 during the same period.
Answer:
Let v₁ and v₂ be the frequencies produced by the two organ pipes at 27°C. Let v₂₇ be the velocity of sound at 27°C.
and v_t = velocity of sound at t°C
l₁, l₂ be their lengths respectively.

Question 14.
A police-man on duty detects a drop of 15% in the pitch of the horn of a motor car as it crosses him. If the velocity of sound is 330 ms^-1, calculate the speed of a car.
Answer:
v_s = speed of car = ?
v = velocity of sound = 330 ms^-1
v = frequency of sound emitted by horn
If v’ be the apparent frequency’of sound when car approaches the police man, then
ν’ = \(\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_{\mathrm{s}}}\) × ν …(i)

Also let ν” be the apparent frequency of sound when car recedes away from the police man, then
ν” = \(\frac{\mathrm{v}}{\mathrm{v}+\mathrm{v}_{\mathrm{s}}}\) × ν …(ii)

Question 15.
A wire of length 80 cm has a frequency of 250 Hz. If the length of the wire is increased to 100 cm and tension is reduced to \(\frac{1}{4}\)th of its original value, then calculate the new frequency.
Answer:
l₁ = initial length = 80 cm
ν₁ = 250 Hz

Let T₁ = T be the tension
l₂ = 100 cm
T₂ = \(\frac{1}{4}\)T₁ = \(\frac{T}{4}\).
ν = ?

Using the relation

Question 16.
A tuning fork A of unknown frequency is sounded with a tuning fork B of frequency 512 Hz. 8 beats are heard in 1 second. Tuning fork A is then loaded with a little wax and sounded together with B. Again 8 beats are heard in 1 second. Find the frequency of
Answer:
Let ν = frequency of tuning fork A
No. of beats formed/sec. =8
∴ ν = 512 ± 8 = 520, 504

On loading A with wax, it again produces 8 beats/second with B of frequency 512.
Now if ν_A = 520, then it means its frequency decreases on loading. If v. falls to 504 then it will produce 8 beats/sec. with B.
∴ ν_A = 520

If ν_A is 504, then on loading its frequency falls below 504, so it forms more than 8 beats/sec. when sounded together with B which is not consistent with the given condition.

So the frequency of A cannot be 504.
∴ ν_A = 520 Hz.

Question 17.
Two engines pass each other in opposite directions with a velocity of 60 km ph. One of them is emitting a note of frequency 540 Hz. Calculate the frequencies heard in the other engine before and after they have passed each other. The velocity of sound = 316.67 ms^-1.
Answer:
Here, v_s = v_o = 60 kmph = 60 × \(\frac{5}{18}\) = 16.67 ms^-1
ν = 540 Hz
ν’ = ?
v = velocity of sound = 316.67 ms^-1

Case A: Before passing each other:
v = 316.67 ms^-1
v_s = v_o = 16.67 ms^-1
∴ ν’ = ?

Using the relation

Case B: After passing each other:
v_s = – 16.67 ms^-1
v_o = – 16.67 ms^-1
v = 316.67 ms^-1

Question 18.
The audible frequency range of a human ear is 20 Hz to 20 kHz. Convert this into the corresponding wavelength range. Take the speed of sound in the air to be 340 ms^-1.
Answer:
Here, ν₁ = 20 Hz
ν₂ = 20000 Hz
v = 340 ms^-1
λ₁ = ?
λ₂ = ?

∴ λ₁ = \(\frac{v}{v_{1}}=\frac{340}{20}\) = 17 m
and λ₂ = \(\frac{v}{v_{2}}=\frac{340}{20000}\) = 0.017 m

∴ Corresponding wavelength range is 0.017 to 17 m.

Question 19.
For aluminum, the bulk modulus and the modulus of rigidity are 7.5 × 10¹⁰ Nm^-2 and 2.1 × 10¹⁰ Nm^-2. Find the velocity of longitudinal and transverse waves in the medium. The density of aluminum is 2.7 × 10³ kg m^-3.
Answer:
Here, for aluminium, ρ = 2.7 × 10³ kg m^-3 .
η = 2.1 × 10¹⁰ Nm^-2
k = 7.5 × 10¹⁰ Nm^-2
v_l = velocity of longitudinal waves = ?
v_t = velocity of transverse waves = ?

Using the relation,


Also using the relation, for transverse waves,

Question 20.
The velocity of sound at 27°C is 350 ms^-1. If the density of air at N.T.P. is 1.293 kg m^-3, calculate the ratio of the specific heats of air.
Answer:
Here, T = 27 + 273 = 300k
v₂₇ =. velocity of sound at 27°C
= 350 ms^-1
ρ = 1.293 kg m^-3
T_o = 273 k
v_o = velocity at N.T.P. = ?
P = 76 cm of Hg
= 0.76 × 13600 × 9.8 Nm^-2

Using the relation,

Using the relation,

Question 21.
A tuning fork B produces 6 beats per second with another tuning fork of frequency 288 Hz. The tuning fork of unknown frequency is filed and the number of beats now produced is 4 per second. Calculate the frequency of the tuning fork.
Answer:
Known frequency of the fork =288 Hz
No. of beats/second = 6
∴ Unknown frequency = 288 ± 6 = 294 or 282.

When the prongs of tuning fork B are filed, its frequency increases. If the frequency of B is originally 294 Hz, on filing it will increase. So the difference between the frequencies will increase and hence no. of beats will also increase.

If the frequency of B is originally 282 Hz, then on filing it, its frequency will increase, so the difference between the frequencies will decrease, and hence the no. of beats will decrease.

In this case, when the prongs of B are filed, the no. of beats decreases from 6 to 4. Thus the frequency of the given tuning fork is 282 Hz.

Question 22.
Find the change in the frequency observed by a listener when a source approaching him with a velocity of 54 km h^-1 starts going away from him with the same velocity. Take velocity of sound = 330 ms^-1 and v = 300 Hz.
Answer:
Here, v_s = 54 km h^-1 = 54 × \(\frac{5}{18}\) = 15 ms^-1
v = 330 ms^-1
ν = 300 Hz
Case I: When the source is approaching, then
ν’₁ = \(\frac{\mathbf{v}}{\mathbf{v}-\mathbf{v}_{\mathbf{s}}}\)ν = \(\frac{330}{330-15}\) × 300
= 314 Hz

Case II: When the source reduces then
ν’₂ = \(\frac{\mathbf{v}}{\mathbf{v}+\mathbf{v}_{\mathbf{s}}}\)ν = \(\frac{330}{330+15}\) × 300
= \(\frac{330}{345}\) × 300
= 287 Hz

∴ Change in frequency,
ν’₁ – ν’₂ = 314 – 287 = 27 Hz.

Question 23.
A progressive wave is given by
y = 12 sin (5t – 4x)
On this wave, how far away are the two points having a phase difference of \(\frac{π}{2}\)?
Answer:
Here, ΔΦ = phase difference = \(\frac{π}{2}\)

Let Δx be the corresponding path difference,

Question 24.
The figure here shows the wave, y = A sin (ωt – kx) at any instant traveling in the +x direction. What is the slope of the curve at B?

Answer:
Here, the particle velocity is maximum at B and is given by
v_o = ωA.
Also, wave velocity is given by
C = \(\frac{ω}{k}\)
∴ So the slope \(\frac{v_{0}}{C}=\frac{\omega A}{\omega / k}\) = kA

Question 25.
Two sound waves
y₁ = A₁ sin 1000 π(t – \(\frac{x}{220}\) )
and y₂ = A₂ sin 1010 π(t – \(\frac{x}{220}\) ) are superposed. What is the frequency with which the amplitude varies?
Answer:
Rate of variation of amplitude is equal to the beat frequency.
Here, 2πν₁ = 1000 π
or
ν₁ = 500
and 2πν₂ = 1010 π
or
ν₂ = 505

∴ beat frequency = ν₂ – ν₁
= 505 – 500
= 5.

Value-Based Type:

Question 1.
A group of students went to a place on an excursion. While boating on seawater, the students identified a submerged Torpedo-shaped structure. The boys debated among themselves on what they saw. A student by the name of Sharath considering it as a threat informed the police. The police took necessary steps to protect the country from the enemy submarine. Sharath was rewarded.
(a) What can you say about the qualities exhibited by Sharath?
Answer:
Navigator is a responsible citizen, he is duty-minded, having a presence of mind.

(b) A SONAR system fixed in a submarine operates at a frequency of 40 kHz. An enemy submarine moves towards the
SONAR with a speed of 360 km/hr. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to bel450 m/s.
Answer:
Here, frequency of SONAR (Source) = 40 k Hz
= 4 × 10³ Hz
Speed of the sound wave, V = 1450 m/s
Speed of the observer, V_o = 360 kM/h = 100 m/s

∴ Apparent frequency received by an enemy submarine ;
V’ = \(\left(\frac{V+V_{0}}{V}\right) \cdot V=\left(\frac{1450+100}{1450}\right)\) × 40 × 10³
=4.276 × 10⁴ Hz.

This frequency is reflected by the enemy submarine (Source) and observed by SONAR (Now observer).
In this case, Apparent frequency is given by
V” = \(\left(\frac{V}{V-V_{s}}\right) \times V^{\prime}=\left(\frac{1450}{1450-100}\right)\) × 4.276 × 10⁴
=45.9k Hz

Question 2.
Jagat and Ram are working in the same company. Jagat has noticed that Ram is suffering from Cancer. Ram is not aware of this. When Jagat asks him to go for a checkup, Ram refused. He gets convinced how even when he realizes normal, it is very important to get the checkup done once a year.
(a) What according to you, are the values displayed by Jagat in helping Ram.
Answer:
He has concern for hi^ friend, also he has the knowledge of medical facilities available

(b) A hospital uses an ultrasonic scanner to locate tumors in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km/s? The operating fre¬quency of the scanner is 4.2 MHz.
Answer:

that is λ = 4.05 × 10^-4 m

Question 3.
‘Preeti a student of class XI was reading the newspaper, The Headlines in the Newspaper were about the earthquake that had taken place in Assam on the previous day. She was very depressed seeing the loss of life and property. She approached her physics teacher and got the information about how an earthquake occurs.
(a) What can you say about the inquisitiveness of Preeti?
Answer:
She has concern for society and is sympathetic towards others.

(b) Earthquake generates sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of the S wave is about 4 km/s, and that of the P wave is 8 km/s. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in a straight line, how far away does the earthquake occur?
Answer:
LetV₁ and V₂ be the velocities of S waves and P waves and t₁ , t₂ be the time taken by these waves to travel to the position of seismograph. If l is the distance of occurrence of earthquake from the seismograph, .
∴ l = V₁ t₁ = V₂t₂
⇒ 4t₁ = 8 t₂
or
t₁ = 2 t₂ [∴ V₁ = 4 kmh^-1 ,V₂ = 8 kmh^-1]

Also, t₁ – t₂ = 4 min = 240 S.
2t₂ – t₂ = 240 [Using (i)]
or
t₂ = 240 S and t₁ = 2 × 240 = 480 S.
l = v₁ t₁ = 4 × 480 = 1920 km

Question 4.
Rajesh was waiting for the train on the platform with his parents. They were going to Mumbai and the train arrived half an hour late. He felt that when the train was coining towards the station, the intensity of the sound of the whistle was gradually increasing and on the platform the sound was maximum and when the train passes away the intensity of the whistle was decreasing.
Rajesh got confused and asked his father the reason behind it. His father could not give the correct answer. So, he decided to ask his physics teacher.
(i) What are the values displayed here by Rajesh?
Answer:
Values displayed by Rajesh are:
Awareness, curiosity, creativity, and intelligence,

(ii) Write the answer given by your teacher.
Answer:
The teacher explained that it is due to “Doppler’s effect”. Whenever there is a relative motion between the source and observer O. There is a change in observed frequency. So, the apparent frequencies of sound heard by the listener are different from the actual frequency of the sound of the source, which is given by.
V = V_o\(\left(\frac{V+V_{0}}{V+V_{s}}\right)\)

Here, V is the speed of sound through the j medium, V_o is the velocity of the observer relative to the medium, and Vs is the source velocity relative to the medium.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 14 Oscillations. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 14 Important Extra Questions Oscillations

Oscillations Important Extra Questions Very Short Answer Type

Question 1.
(a) A particle has maximum velocity in the mean position and zero velocity at the extreme position. Is it a sure test for S.H.M.?
Answer:
No.

(b) Is restoring force necessary in S.H.M.?
Answer:
Yes.

Question 2.
Imagine a situation where the motion is not simple harmonic but the particle has maximum velocity in the mean position and zero velocity at the extreme position.
Answer:
Projection of a particle in non-uniform circular motion satisfies all the given conditions.

Question 3.
We know that in S.H.M., the time period is given by
T = 2π\(\sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}\)
Does T depend upon displacement?
Answer:
No. T is independent of displacement as the displacement term is also contained in acceleration.

Question 4.
(a) Two simple pendulums of equal lengths cross each other at the mean position. What is their phase difference?
Answer:
180° i.e. it radians.

(b) Can a simple pendulum vibrate at the center of Earth? Why?
Answer:
No. This is because the value of g at the center of Earth is zero.

Question 5.
(a) A particle is in S.H.M. of amplitude 2 cm. At the extreme position, the force is 4N. What is the force at a mid-point i.e. midway between mean and extreme position?
Answer:
2N.

(b) What happens to the time period of a simple pendulum if its length is doubled?
Answer:
The time period is increased by a factor of 4l.

Question 6.
Can & simple pendulum be used in an artificial satellite? Why?
Answer:
No. This is because there exists a state of weightlessness in the artificial satellite.

Question 7.
What fraction of the total energy is potential energy when the displacement is one-half of the amplitude?
Answer:
\(\frac{1}{4}\left[\because \frac{P . E}{\text { Total energy }}=\frac{\frac{1}{2} \operatorname{m\omega}^{2}\left(\frac{a}{2}\right)^{2}}{\frac{1}{2} m \omega^{2} a^{2}}\right]\)

Question 8.
What fraction of the total energy is kinetic energy, when the displacement is one-half of the amplitude?
Answer:
\(\frac{3}{4}\left[\because \frac{\text { K.E. }}{\text { Total energy }}=\frac{\frac{1}{2} m \omega^{2}\left(a^{2}-\left(\frac{a}{2}\right)^{2}\right)}{\frac{1}{2} m \omega^{2} a^{2}}=\frac{3}{4}\right]\)

Question 9.
(a) When a particle oscillates simply harmonically, its potential energy varies periodically. If v be the frequency of oscillation of the particle, then what is the frequency of vibration of P.E.?
Answer:
2v

(b) A body executes S.H.M. with a period of \(\frac{11}{7}\) seconds and an amplitude of 0.025 m. What is the maximum value of acceleration?
Answer:

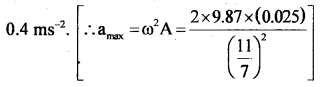
Question 10.
A body of mass m when hung on a spiral spring stretches it by 20 cm. What is its period of oscillation when pulled down, and released?
Answer:
T = 2π\(\sqrt{\frac{20}{980}}=\frac{2 \pi}{7} \mathrm{~s}=\frac{44}{49} \mathrm{~s}\)

Question 11.
A spring-mass system oscillating vertically has a time period T. What shall be the time period if oscillating horizontally?
Answer:
T i.e. it remains the same.

Question 12.
The time period of a body executing S.H.M. is 0.05 s and the amplitude of vibration is 4 cm. What is the maximum velocity of the body?
Answer:
1.6 π ms^-1

Question 13.
A spring-controlled wristwatch is taken from Earth to Moon. What shall be the effect on the watch?
Answer:
There will be no effect on g as the time period of spring is independent of g.

Question 14.
(a) At what displacement, the P.E. of a simple harmonic oscillator is maximum?
Answer:
At the extreme position.

(b) At what displacement, the K.E. of a simple harmonic oscillator is maximum? ‘
Answer:
At the mean position.

Question 15.
What is the total energy of a simple harmonic oscillator?
Answer:
\(\frac{1}{2}\)m ω² r², where r = amplitude, ω = angular frequency, m = mass of the oscillator.

Question 16.
Name the trigonometric functions which are suitable for the analytical treatment of periodic motions. ,
Answer:
Sine and Cosine functions or their linear combination.

Question 17.
How is acceleration (a) related to the displacement (y) in S.H.M.?
Answer:
aα – y.

Question 18.
At what position, the velocity of a particle executing S.H.M. is maximum?
Answer:
At mean position.

Question 19.
What is Force constant (k)? What are its units in the S.I. system?
Answer:
k = Force per unit displacement.
S.I unit of k is Nm^-1

Question 20.
(a) What ¡s the phase difference between displacement and velocity of a particle executing S.H.M.?
Answer:
90° or \(\frac{π}{2}\) radian.

(b) What is the phase difference between displacement and acceleration of a particle executing S.H.M.?
Answer:
180° or π radian.

Question 21.
(a) What will be the change in the time period of a loaded spring when taken to Moon?
Answer:
No change because T = 2π\(\sqrt{\frac{m}{k}}\) i.e. T ¡s independent of g.

(b) Why does the time period (T) of the swing not change when two boys sit on it instead of one?
Answer:
T is independent of the mass of the swing as T = 2π\(\sqrt{\frac{l}{g}}\).

Question 22.
Why are the vibrations of a simple pendulum damped?
Answer:
Because the energy of the pendulum is used to overcome air resistance.

Question 23.
A pendulum clock is taken on a lift moving down with a uniform Velocity. Will it gain dr lose time?
Answer:
It neither gains nor loses time.

Question 24.
What role do shock absorbers play in oscillations of vehicles on a bumpy road?
Answer:
They act as damping devices and save vehicles from resonant oscillations.

Question 25.
When do you apply force as the spring descends while swinging on a swing?
Answer:
To counter the effect of the damping force on the amplitude of oscillations of the swing at an appropriate point.

Question 26.
The time period of oscillation of a sphere hung from a wire attached to a rigid support and given slight rotation about the wire is given by T = 2π\(\sqrt{\frac{I}{C}}\). Which factor out of these is equivalent to the mass factor of an oscillator in S.H.M.?
Answer:
I (moment of inertia) of the sphere is equivalent to m, the mass of an ordinary oscillator in S.H.M.

Question 27.
At what points is the energy entirely K.E. and entirely P.E. in S.H.M.?
Answer:
At mean position and extreme position respectively.

Question 28.
What provides the restoring force for simple harmonic motion in the following cases?
(i) Simple pendulum.
(ii) Spring.
(iii) Column of mercury in a U-tube.
Answer:
The restoring force is provided by:
(a) gravity in simple pendulum i.e. weight of the pendulum.
(b) elasticity in spring.
(c) weight in the column of Hg in a U-tube.

Question 29.
Which single characteristics of a periodic motion distinguishes it as S.H.M?
Answer:
If acceleration is directly proportional to the negative- displacement, then the motion is said to be S.H.M.

Question 30.
(a) Does the bursting of air bubbles at the surface of boiling water show a periodic motion of the surface molecules?
Answer:
No.

(b) Do all periodic motions are S.H.M.?
Answer:
No.

Question 31.
At what point the velocity and acceleration are zero in S.H.M.?
Answer:
The velocity is zero at the extreme points of motion and acceleration is zero at the mean position of motion.

Question 32.
On what factors does the force constant of a spring depend?
Answer:
It Depends Upon the following factors:

1. Nature of the material of the spring.
2. Elasticity (i.e. coefficient of elasticity) of the material of spring.

Question 33.
Which factors determine the natural frequency of an oscillator?
Answer:
The dimensions and the elastic properties of the oscillator.

Question 34.
When a high-speed plane passes by, the windows of the plane start producing sound due to
(i) S.H.M.,
(ii) damped oscillations,
(iii) maintained oscillations. Why?
Answer:
(ii) Damped oscillations are caused due to air pressure on the glass window panes.

Question 35.
A motorcyclist while trying to loop a loop of maximum radius in a death trap goes round in the globe. Is it his projection on diameter in S.H.M.?
Answer:
Yes.

Question 36.
Sometimes on the screen of a cathode-ray oscilloscope, we see rectangular or triangular waves. Are these formed due to S.H.M. of the oscillator connected to it?
Answer:
No, these are not S.H.M. but are periodic waves.

Question 37.
Is oscillation of a mass suspended by a spring simple harmonic?
Answer:
Yes, only if the spring is perfectly elastic.

Question 38.
A diver wearing an electronic digital watch goes down into seawater with terminal velocity v. How will the time in the waterproof watch be affected?
Answer:
It will not be affected as its action is independent of gravity and buoyant force.

Question 39.
When is the tension maximum in the string of a simple pendulum?
Answer:
The tension in the string is maximum at the mean position because the tension in the string = mg cos θ = mg. (∵ θ = 0 at mean position).

Question 40.
Is the damping force constant on a system executing S.H.M.?
Answer:
No, because damping force depends upon velocity and it is more when the system moves fast and is less when the system moves slow.

Question 41.
What is the (a) distance covered by (b) displacement of, a body executing S.H.M. in a time equal to its period if its
amplitude is r?
Answer:
A body executing S.H.M. completes one vibration in a time equal to its period, so the body reaches its initial position after a time equal to its period.
Thus the
(a) total distance traveled is 4r and
(b) displacement is zero.

Question 42.
Can a motion be oscillatory but not simple harmonic? If yes give an example and if no explain, why?
Answer:
Yes. Uniform circular motion is an example of it.

Question 43.
How will the period of a pendulum change when its length is doubled?
Answer:
The time period becomes \(\sqrt{2}\) times the original value as T ∝ \(\sqrt{l}\).

Question 44.
Determine whether or not the following quantities can be in the same direction for a simple harmonic motion;
(a) displacement and velocity,
Answer:
Yes, when the particle in S.H.M. is moving from equilibrium position to extreme position.

(b) velocity and acceleration,
Answer:
Yes, when the particle executing S.H.M. is moving from an extreme position to a mean position.

(c) acceleration and displacement?
Answer:
No, because acceleration is always directed opposite to the displacement.,

Question 45.
Can a body have zero velocity and maximum acceleration in S.H.M.?
Answer:
Yes. In S.H.M., at the extreme position, the velocity of the body is zero and acceleration is maximum.

Question 46.
A passing airplane sometimes causes the rattling of windows of a house. Explain why?
Answer:
When the frequency of the sound waves produced by the engine of the airplane strikes the windows panes, they start vibrating due to forced oscillations. This causes rattling of windows.

Question 47.
Identify periodic, non-periodic, and S.H.M. out of the following:
(a) fluttering tree leaves due to wind.
Answer:
Non-periodic

(b) fluttering of honeybee’s wings for a microsecond.
Answer:
S.H.M.

(c) rising and falling of water drops at the bottom of a waterfall.
Answer:
Non-periodic

(d) the sound produced by a motorcycle in a small interval of time.
Answer:
Periodic

(e) the motion of the wheels of a canon during rapid fire.
Answer:
Periodic

(f) jerks in a machine gun during rapid fire.
Answer:
periodic

(g) vibrations of a drum membrane in a music band.
Answer:
Non-periodic.

Question 48.
Why pendulum clocks are not suitable for spaceships?
Answer:
The time period of a pendulum clock is given by
T = 2π\(\sqrt{\frac{l}{g}}\)

In a spaceship g = 0, so T = ∞,
It means the pendulum clock will not oscillate and hence are not suitable for spaceships.

Question 49.
A glass window may be broken by a distant explosion. Is it correct?
Answer:
Yes. The sound waves can cause forced vibrations in glass due to the difference between the frequency of sound waves and the natural frequency of the glass. This can break the glass window.

Question 50.
The bob of a simple pendulum is positively charged. The pendulum is made to oscillate over a negatively charged plate. How shall the time period change as compared to the natural time period of the simple pendulum?
Answer:
Due to the electric force of attraction between the bob and the plate, the effective value of acceleration due to gravity will increase T = 2π\(\sqrt{\frac{l}{g}}\) therefore T will decrease.

Oscillations Important Extra Questions Short Answer Type

Question 1.
Why does the body of a bus begin to rattle sometimes when the bus is accelerated?
Answer:
At some speed of the bus, the frequency of vibrations produced by the bus-engine is equal to the natural frequency of the bus. This produces resonant vibrations which have quite a large amplitude and\ence the bus begins to rattle.

Question 2.
The displacement of a particle in S.H.M. may be given by x = A sin (ωt + Φ) Show that if the time t is increased by \(\frac{2π}{ω}\), the value of x remains the same.
Answer:
The displacement of a particle in S.H.M. at a time t is given
x = A sin (ωt + Φ) …. (i)

Let x be the displacement of the-particle at time t’ = ( t + \(\frac{2π}{ω}\)),
To prove x₁ = x

From equation (i), we get
x₁ = A sin [ω( t + \(\frac{2π}{ω}\)) + Φ)]
= A sin [ωt + 2π + Φ]
= A sin [2π + (ωt + Φ)]
= A sin (ωt + Φ)
[ ∵ sin (2π + θ) = sin θ]

i.e. the displacement of the particle in S.H.M. is same for times t and t + \(\frac{2π}{ω}\) .
Hence proved.

Question 3.
A hollow sphere is filled with water through a small hole in it. It is hung by a long thread and as water slowly flows out of the hole at the bottom, one finds that the period of oscillations first increases and then decreases. Explain why?
Answer:
When the sphere is filled with water, its C.G. is at the center of the sphere. We know that the time period (T) of oscillation is directly proportional to the square root of the effective length of the pendulum
i.e. T ∝ \(\sqrt{l}\).

Due to the flow out of the water through the hole at the bottom of the sphere, the first effective length l increases, and then it decreases because of the lowering of the center of gravity in the first case and rising up in the second case. The first case corresponds to the lowering of the water level up to the center of the sphere. The second case corresponds to the lowering of the water level from the center of the sphere to its bottom.

Question 4.
A girl is swinging in the sitting position. How will the period ^ of the swing be changed if she stands up?
Answer:
This can be explained using the concept of a simple pendulum.
We know that the time period of a simple pendulum is given by
T = 2π \(\sqrt{\frac{l}{g}}\) i.e. T ∝ \(\sqrt{l}\)

When the girl stands up, the distance between the point of suspension arid the center of mass of the swinging body decreases i. e. l decreases, so l will also decrease.

Question 5.
At what displacement, a particle in S.H.M. possesses half K.E. and half P.E.?
Answer:
We know that in any position for a displacement of y from the mean position, the K.E. and P.E. are given by the expressions:
E_k = \(\frac{1}{2}\) mω² (r² – y²) ….(1)
E_p = \(\frac{1}{2}\)mω²y² …..(2)
Where m = mass of the particle
y = displacement from the mean position
ω = its angular frequency
r = amplitude of oscillation of the particle

Now for E_k = E_p, we get

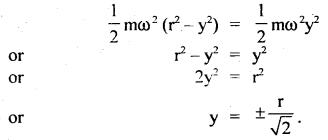
Question 6.
Explain why marching troops are asked to break their steps while crossing a bridge?
Answer:
This is done so as to avoid setting the bridge into resonant oscillations of large amplitude. If troops march in step, then the frequency of the steps of the marching troops may become equal to the natural frequency of vibration of the bridge. Hence it may oscillate with high amplitude due to the phenomenon of resonance, resulting in damage to the bridge.

Question 7.
What is the direction of acceleration at the mean and extreme positions of an oscillating simple pendulum?
Answer:
When the simple pendulum oscillates, its bob moves along a circular path with the point of suspension at its center. At the mean position, bob possesses centripetal acceleration which acts along the thread towards the point of suspension. At an extreme position, the bob is at rest for a moment. The acceleration on the bob acts along the tangent to the circular path and is directed towards its mean position. This acceleration results due to the restoring force arising due to the weight of the bob.

Question 8.
You are provided with a light spring, a meter scale, and a known mass. How will you find the time period of oscillation of mass attached to the spring without the use of a clock?
Answer:
With the help of metre scale, we can note the length and extension produced. Since
F = – kl
and F = mg
or
∴ mg = – k l
or
\(\frac{\mathrm{m}}{\mathrm{k}}=\frac{l}{\mathrm{~g}}\) (numerically)
∴ T = 2π\(\sqrt{\frac{m}{k}}\) = 2π\(\sqrt{\frac{l}{g}}\) …(1)

∴ By knowing the extension l, T can be calculated from equation (1) w ithout the use of clock.

Question 9.
Why does the time period of a pendulum change when taken to the top of a mountain or deep in a mine? Will clocks keep the correct time?
Answer:
Time period of a pendulum is given by
T = 2π\(\sqrt{\frac{l}{g}}\)
As the value of ‘g’ on the top of a mountain or deep in a mine decreases, so the time period of the pendulum increases on the top of a mountain or deep in a mine and hence the pendulum clocks will run slow,

Question 10.
What is the source of potential energy in a loaded elastic spring?
Answer:
As the load is put at the end of the spring, it gets extended. To increase the length, the load does work against the elastic restoring force. This work done is stored in the spring in the form of its potential energy,

Question 11.
Why cannot we construct an ideal simple pendulum?
Answer:
An ideal simple pendulum is made up of a heavy point mass suspended to a weightless, inextensible string fastened to a rigid support. In actual practice geometrical point mass is not realized so is a weightless and inextensible string. Hence ideal simple pendulum cannot be constructed in actual practice.

Question 12.
When a fast railway train passes over a river bridge, we hear a loud sound, why?
Answer:
Fast railway train vibrations are passed to the air column between the bridge and the river water through railway lines and slippers. The vertical air column starts resonating with train vibrations, so a loud sound is heard. ‘

Question 13.
If the amplitude of vibration of an oscillator is made half, how will its time period and energy be affected?
Answer:
Since the time period of an oscillator is independent of its amplitude, so it remains unaffected. However, the total energy is directly proportional to the square of the amplitude, so the energy of the oscillator will become a quarter of its original value on making amplitude half.

Question 14.
A bead is mounted on a vertical stand placed attached to the rim of a record player and its shadow is cast on the wall with the help of light from a lamp. The record player is set in motion. Describe the motion of the shadow of the bead.
Answer:
As the bead executes circular motion with the record player, its shadow on the wall will execute whose period depends on the speed of rotation of the record player.

Question 15.
In Boyle’s law apparatus, if the open end tube is quickly moved up and down what will happen to the mercury column in the closed tube?
Answer:
Due to quick compression and expansion of air column above mercury column in the closed tube, the mercury column is set into damped harmonic motion. Damping is caused due to friction in the air layer and mercury with the glass wall.

Question 16.
Alcohol in a U-tube is executing S.H.M. of time period T. Now alcohol is replaced by water up to the same height in U-tube. What will be the effect on the time period?
Answer:
As the time period (T) of oscillation of a liquid column in a U-tube does not depend upon the density of the liquid, so T is independent of the nature of liquid in a U-tube, hence there will be no effect on the time-period of replacing alcohol by water.

Question 17.
A spring having a force constant k and a mass m is suspended. The spring is cut into three halves and the $ame mass is suspended from one of the halves. Is the frequency of vibration the same before and after the spring is cut? Give reason.
Answer:
No. This can be explained as follows:
The spring constant k = \(\frac{F}{x}\), when the spring is cut inito three parts, the hew force constant will be k’ = \(\frac{\mathrm{F}}{\frac{\mathrm{x}}{3}}=\frac{3 \mathrm{~F}}{\mathrm{x}}\) = 3k.

If v = frequency of oscillation when the spring was not divided,
Then

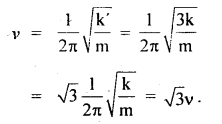
i.e. frequency of oscillation after cutting the spring into 3 parts is \(\sqrt{3}\) times the frequency of oscillation before cutting. It is now clear to us that this is due to the reason that v ∝ \(\sqrt{k}\) and k increases on cutting the spring, so frequency increases.

Question 18.
Oscillatory motion is periodic but the reverse is not always true. Justify.
Answer:
The motion of planets and comets like Hailey’s comet, satellites, merry-go-round, etc. all are periodic but not oscillatory as these are not to and fro motions about a mean position. But the motion of the simple pendulum is not only oscillatory but periodic too as it is also to and fro and repeats itself at regular intervals of time.

Question 19.
Why a restoring force is a must for S.H.M.?
Answer:
A restoring force is a force that restores or tends to restore or bring back a body or particle to its equilibrium position. When a body executing S.H.M. crosses its mean position due to its kinetic energy, the restoring force starts acting towards the equilibrium position and brings the oscillator towards the mean position from the extreme position of motion. The same thing happens when the body goes to the other side of the equilibrium position. So, a restoring force is a must for any oscillatory motion including S.H.M.

Question 20.
What is a periodic function, explain?
Answer:
A mathematical function that repeats itself after a definite period is called a periodic function, e.g. f (t) = f (t + T), here T = period of the function.

Let F(t) fie a periodic function such that F(t) = A sin \(\frac{2π}{T}\) t or F(t) = A cos \(\frac{2π}{T}\) t which are periodic functions. If t is replaced by t + T, we get once again the same value of the function. Thus


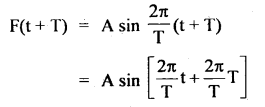
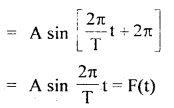
Hence f(t) is a periodic function having a time period T.

Question 21.
Distinguish between forced vibrations and maintained vibrations.
Answer:
A body vibrating under the effect of an external applied periodic force and oscillating with a frequency other than its natural frequency is said to be performing forced vibrations.

If energy is supplied to the oscillator at the same rate at which it is dissipated, the amplitude of the oscillator remains unchanged. Such oscillations are called maintained oscillations e.g. The oscillations of the pendulum clock of a watch or the balance wheel of a watch are examples of maintained oscillations.

Question 22.
Will a pendulum go slower or faster at
(a) Moon,
(b) planet Jupiter?
The time period of oscillation of a pendulum on Earth is given by
T_e = 2π\(\sqrt{\frac{1}{g_{e}}}\)
Answer:
(a) On moon gm = \(\frac{1}{6}\) of the Earth = \(\frac{\mathrm{g}_{\mathrm{c}}}{6}\).Since g_m < g_e, so T_m > T_e. Thus due to increase in time period of oscillation of pendulum, it will go slower on the moon.

(b) The value of acceleration due to gravity g_j on Jupiter is more than g_e, so the time period T_J of oscillation of the pendulum will be less than what it is on the earth. Thus due to a decrease in the time period of oscillation of a pendulum, it will go faster on Jupiter.

Question 23.
The mass M attached to a spring oscillates with a period of 2s. If the mass is increased by 2 kg, the period increases by 1 s. Find the initial mass m assuming that Hooke’s law is obeyed.
Answer:
Let the initial mass and time period be M and T respectively. If the Hook’s law is obeyed, then the oscillations of the spring will be simple harmonic having time period T given by
T = 2π\(\sqrt{\frac{M}{k}}\)

Given T = 2s
∴ 2 = 2π\(\sqrt{\frac{M}{k}}\); k = spring constant ….(1)

On increasing the mass by 2 kg, T’ = 2 + 1 = 3s.
∴ 3 = 2π\(\sqrt{\frac{M+2}{k}}\)

Squaring and dividing equation (2) by (1), we have

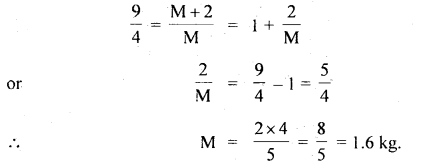
Question 24.
The displacement of a particle having periodic motion is given by
y = r sin ωt
Show that the motion of the particle is simple harmonic for small values of v.
Answer:
Since y = r sin(ωt – Φ) ….(1)
∴ \(\frac{dy}{dt}\) = rω cos(ωt – Φ) …(2)
and \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}\) = – rω² sin(ωt – Φ)
= – ω² y …(3) [by (i)]

where,a = \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}\) is called acceleration.
ω = angular frequency
∴ a = – ω²y

Now as a ∝ y and acts towards mean position. This is the characteristic of S.H.M. Hence the given equation y = r sin (ωt – Φ) represents an S.H.M. of the oscillator.

Question 25.
We have a very strong string and of sufficient length making a pendulum with a metal ball (e.g. a shot put). What will be the effect on the time period if
(a) the length of the pendulum is doubled and
Answer:
If the length of the pendulum is doubled, then
T = 2π\(\sqrt{\frac{2l}{g}}\)
= 2π\(\sqrt{\frac{l}{g}}\) \(\sqrt{2}\) = \(\sqrt{2}\)T.
The period of oscillation will increase.

(b) the ball is replaced by an elephant?
Answer:
Since mass does not come in relation to the time period of oscillation of a pendulum therefore instead of shot put if we make a pendulum of some length with an elephant there will be no effect on the time period of its oscillation.

Question 26.
The angular frequency of damped harmonic motion is given by ω = \(\sqrt{\frac{k}{m}-\left(\frac{b}{2 m}\right)^{2}}\) where b is know as damping constant. The displacement in such a motion is given by x = A e^-bt/2m cos (ωt + Φ) and the retarding force is F = – b v, where v is the speed of the particle. Could you guess from the given equations?
(a) How the amplitude of vibration change?
Answer:
The amplitude of vibration decreases continuously due to damping force. The amplitude decreases exponentially as is evident from the displacement equation the damping force is velocity-dependent.

(b) Does the time period of vibration change with displacement?
Answer:
The time period of oscillation does not change in damped oscillations.

Question 27.
Apart from the danger of being burnt which other factors make the re-entry of a space vehicle difficult in Earth’s atmosphere?
Answer:
The Earth’s thick atmospheric layer offers buoyant force and space vehicles suffer from damped harmonic oscillations, making the re-entry difficult.

Question 28.
If the amplitude of vibration is not small in the simple pendulum experiment will it not be executing periodic harmonic oscillations? How will the time period be affected?
Answer:
The simple pendulum will still be executing periodic harmonic oscillation even if the amplitude is large. However, the time period of oscillation will be slightly greater than what it is for small amplitudes
i.e. T > 2π\(\sqrt{\frac{l}{g}}\) ,

(The derivation of formulae is beyond the scope of this course),

Question 29.
Can you give some examples where an anharmonic oscillator does not possess potential energy?
Answer:
The thermal radiation enclosed in a black body of fixed dimensions and photons in solids behave like harmonic oscillators where they don’t have potential energy.

Question 30.
A man is standing on a platform executing S.H.M. in the vertical direction and attached to a weighing machine. Will there be any change in his weight?
Answer:
Depending on the motion of the platform from its mean position, the weight of the man will change when the platform moves down from the mean position to the lowermost point and return back to the mean position, ‘ the acceleration acts vertically upwards and hence the weight of the man j will increase. But when the platform moves up from its mean position to [ the uppermost point and returns back to the mean position, the acceleration in S.H.M. acts downwards, so the weight of the man is decreased.

Oscillations Important Extra Questions Long Answer Type

Question 1.
(a) What is the effect on the time period of a simple pendulum when:
(i) it is immersed in a liquid of density σ.
Answer:
Let p = density of the material of the pendulum bob.
σ = density of the liquid in which the pendulum bob is immersed such that p > σ. Let it is made oscillate with a time period T’. The effective value of ‘g’ in the liquid is given by

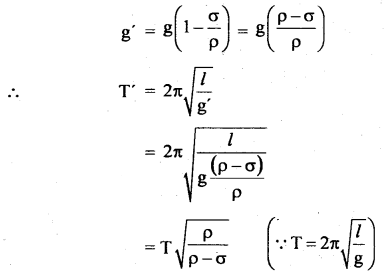
where T = time period of the simple pendulum when it oscillates in air.
or
\(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}=\sqrt{\frac{\rho}{\rho-\sigma}}\)
∴ ρ > σ
or
ρ – σ > 0

∴ \(\frac{\rho}{\rho-\sigma}\) > 1
or
\(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}\) > 1
or
T’ > T
i.e. its time period increases.

(ii) the temperature of wire through which the bob is suspended increased?
Answer:
When the temperature of the wire with which the bob of the pendulum is suspended increases, the length of the wire increases due to its thermal expansion. As
T ∝ \(\sqrt{l}\), so T will also increase as shown below:
Let l = original length of the wire
dθ = rise in its temperature
α = coefficient of linear expansion of the material of the wire
If l’ = new length
and dl = increase in its length = l’ – l, then

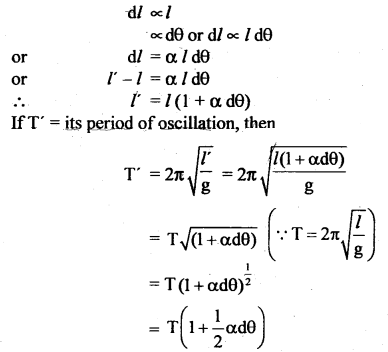
(Using Binomial expansion)
or increase in Time period = T’ – T = \(\frac{\mathrm{T} \alpha \mathrm{d} \theta}{2}\)

(b) Derive the differential equation of Simple Harmonic Oscillation.
Answer:
When an oscillator is displaced, say in the x-direction, the restoring force tends to bring it in its equilibrium position. It is well known that restoring force is directly proportional to the displacement, thus
Fα – x or F = – k x(t) .
where, the negative sign indicates! that the force always acts towards equilibrium position and opposes displacement, k is known as the force constant.

According to Newton’s law of motion if x (t) is the displacement then \(\frac{\mathrm{dx}(\mathrm{t})}{\mathrm{dt}}\) is the velocity and \(\frac{\mathrm{d}^{2} \mathrm{x}(\mathrm{t})}{\mathrm{dt}^{2}}\) is the acceleration of the oscillating particle.

Now Force = mass × acceleration

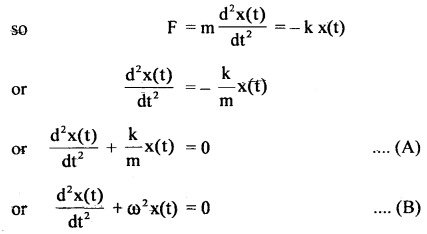
Equations (A) and (B) are known as the differential equations of simple harmonic oscillator, GO is the angular velocity given by
ω = \(\frac{2π}{T}\)
Also
ω = \(\sqrt{\frac{k}{m}}\)

So, the time period of oscillation of the oscillator is given by
\(\frac{2π}{T}\) = \(\sqrt{\frac{k}{m}}\)
or
T = 2π\(\sqrt{\frac{m}{k}}\)

(c) Distinguish briefly between natural, forced and , resonant vibrations. What are damped and undamped / vibrations?
Answer:
Natural vibrations: The vibrations of a body in the absence of any resistive, damping, or external) forces are said to be its natural vibrations. The body once vibrated continues to vibrate with its natùral frequency and undiminished amplitude.

Forced vibrations: A body at rest or vibrating with some frequency changes its frequency of vibration and amplitude when an external force is impressed on it. If the applied force is periodic the body oscillates with a period which is the period of the impressed force.

The vibrations of the body are not natural or free vibrations but are forced vibrations. If the external periodic force is removed, the body executes its natural oscillations after a while.

Resonant vibrations: If a body is set in vibrations such that a periodic force creates vibrations in it and the frequency of such vibrations becomes equal to the natural frequency of vibration of the body (i.e. the frequency of its free vibrations in the absence of the applied periodic force), its amplitude of vibration increases vigorously. The body is said to be in resonance with the second oscillating body or the applied periodic force.

The frequencies of the two oscillators become equal. Resonant oscillations are not only set up in mechanical oscillators but in electrical circuits and atomic oscillators too.

Damped vibrations: If a body vibrates in the presence of a resistive force such as fluid friction or electromagnetic damping force, its amplitude of oscillation decreases, and ultimately the oscillations die out i.e. the body stops oscillating. Such an oscillation is called damped oscillation as shown in the figure. The amplitude of vibration decreases with time.

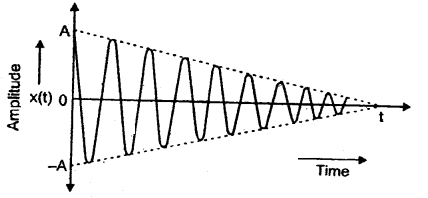
Undamped Oscillations: The free oscillations of an oscillator in the absence of any resistive or damping force have constant amplitude over time. Such oscillations are called undamped oscillations. Most vibrations in ‘ daily life are damped vibrations because the oscillator experiences one or the other type of force acting on it. So, its vibrations become damped.

Question 2.
(a) Discuss the effect of driving force frequency on the driven frequency. How does friction affect the oscillation of an oscillator?
Answer:
Driving force is a time-dependent force represented by
F(t) = f_o cos 2πvt …..(1)
where v = frequency of driving force. This frequency is different from the natural frequency of the oscillation v_n of the oscillator. v_n is also called driven frequency. Thus motion depends on driving force.

Thus the motion of the particle is now under the action of: (a) linear restoring force, (b) time dependent (or periodic) force given in equation (1) so that using Newton’s law, we have for the oscillator:
ma(t) = – k x(t) + f_o cos2πvt …. (2)
and v_n² = \(\frac{1}{\mathrm{~T}^{2}}=\frac{\mathrm{k}}{4 \pi^{2} \mathrm{~m}}\) ….(3)

where m = mass of oscillator,
k = force constant,
v = frequency of the driving force,
ω = 2πvt,
vn = natural frequency of the oscillator,

Let the displacement be given by, x = C cos ωt,
where C = constant, .

This shows that the mass m will execute S.H.M. whose frequency is equal to the frequency of the driving force. The amplitude of oscillation too depends on the frequency of the driving force and is independent of time.

If there is a large difference between v and v_n, then the amplitude of oscillation will be too small. But if v_n ~ v, the amplitude of oscillation will become infinite, which does not actually happen as some sort of unaccounted force breaks the oscillations down. But if v – v_n, the amplitude becomes very large. This phenomenon is called resonance. There are several examples of resonance in daily life such as playing musical instruments, marching of troops in steps, etc.

Effect of the force of friction on S.H.M.: The real oscillations of almost all oscillators are known as damped oscillations. The energy of the system is continuously dissipated but nevertheless, oscillations remain periodic. This dampens oscillations. It is an additional restoring force that is proportional to the velocity of the particle rather than its displacement i.e. F = – bv(t), where b is a positive constant called damping constant. The oscillator is now under the combined action of F(t) and f(t) so that
ma(t) = – k x(t) – bv(t) …. (5)

The solution of this equation gives

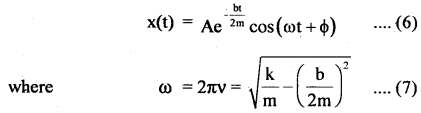
(b) Derive an expression for
(1) angular velocity
(2) time period,
(3) frequency of a particle executing S.H.M. in terms of spring factor and inertia factor.
Answer:
Let m = mass of a particle executing S.H.M. The restoring force F is directly proportional to the displacement and acts opposite to it so that
F ∝ – x
or
F = – k x
where k is called the force constant. If the mass m is attached to an elastic spring, then k is called the spring constant for a given spring. From Newton’s second law of motion,
F = ma
Therefore F = ma = – kx
or
a = – \(\frac{k}{m}\)x
⇒ a ∝ – x

Hence the motion is S.H.M., we can write
a = – ω² x
where ω² = \(\frac{k}{m}\)
or
ω = \(\left(\frac{k}{m}\right)^{\frac{1}{2}}\)

This gives ω in terms of spring and constant mass factor.
we know that ω = \(\frac{2π}{T}\)

⇒ T = \(\frac{2π}{ω}\)

Substituting the value of ω from above we have
T = 2π\(\sqrt{\frac{m}{k}}\)

This is the expression for time period.
The frequency v = \(\frac{1}{T}\) = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\)

If the body executing S.H.M. has angular motion, then mass is replaced by the moment of inertia L and the force constant k is replaced by C, the restoring couple per unit twist, hence ω, T and v become
ω = \(\sqrt{\frac{C}{I}}\)

T = 2π\(\sqrt{\frac{C}{I}}\)
and v = \(\frac{1}{2 \pi} \sqrt{\frac{C}{I}}\)

Thus ω, T and v are found in terms of the spring factor and moment of inertia factor.

Question 3.
Calculate the effective spring constant and time period of a parallel and series combination of two different types of springs that are loaded.
Answer:
(a) When springs are connected in parallel with weight mg, hanging at the lower end.

Both the springs are pulled down through the same displacement say y.

Let F₁ and F₂ be the restoring forces acting on the spring.
Then F₁ = – k₁y
and F₂ = – k₂y

If F = total restoring force, then
F = F₁ + F₂
= – (k₁ + k₂)y ….(1)

Let k = spring constant of the combination, then
F = – ky ….(2)

∴ From (1) and (2), we get
k = k₁ + k₂

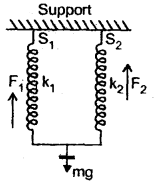
The motion of the weight will be simple harmonic in nature. Its time period is given by
T = 2π\(\sqrt{\frac{m}{k}}\)
= 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}_{1}+\mathrm{k}_{2}}}\)

(b) When the springs are connected in series, the springs suffer different displacement y₁ and y₂ when the weight mg is pulled down. But the restoring force is the same in each spring.
∴ F = – k₁y₁
and F = -k₂y₂

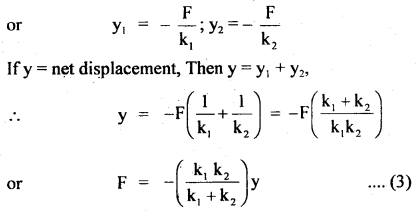
If k be the spring constant of the combination, then
F = -ky …..(4)
∴ From (3) and (4), we get
k = \(\frac{\mathbf{k}_{1} \mathbf{k}_{2}}{\mathbf{k}_{1}+\mathbf{k}_{2}}\) …(5)

If ‘a’ be the acceleration produced in the body of mass m, then
a = \(\frac{\mathrm{F}}{\mathrm{m}}=\frac{-\mathrm{k}}{\mathrm{m}}\)y ⇒ motion of S.H.M. having time period T given by

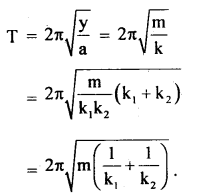
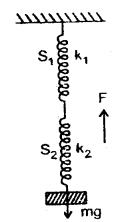
(c) The weight ‘mg’ is connected in between the two springs which themselves are connected in series.

When the weight is pulled to one side, one spring gets compressed and the other is extended by the same amount. The restoring force acts in the same direction due to both the springs.

Let y = extension or compression produced in the springs,
F₁, F₂ = restoring forces produced in the springs, then
F₁ = – k₁y
F₂ = – k₂y
If F = F₁ + F₂ = – (k₁ + k₂)y

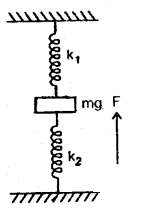
If k = spring constant of the combination, then
F = – ky;
∴ k = k₁ + k₂
a = \(\frac{F}{m}\) = – \(\frac{\left(\mathrm{k}_{1}+\mathrm{k}_{2}\right)}{\mathrm{m}}\)y
and T = 2π\(\sqrt{\frac{M}{k}}\) = 2π\(\sqrt{\frac{M}{k_{1}+k_{2}}}\)

Question 4.
(a) Obtain the expression for a time period of a simple pendulum.
(b) Calculate the total energy of a particle executing S.H.M.
Answer:
(a) Let l = length of the string of the pendulum.
mg = weight of the bob acting vertically downward.
θ = angle by which the bob be displaced from the vertical position.
O = equilibrium position of the bob.

At any position P, the various forces acting on the bobs are:

1. mg, the weight of the bob acting in a vertically downward direction.
2. Tension (T) in the string acting along the string towards the support from which the pendulum is suspended.

mg is resolved into two rectangular components.

1. mg cos θ opposite to T.
2. mg sin θ perpendicular to T and directed towards the mean position O.

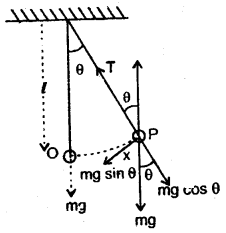
T – mg cos θ provides the centripetal force = \(\frac{\mathrm{mv}^{2}}{l}\) to the bob to move it in the circular path of radius l.

∴ T – mg cos θ = \(\frac{\mathrm{mv}^{2}}{l}\)
At extreme position P, bob is momentarily at rest i.e. v = 0

∴ T – mg cos θ = 0
or
T = mg cos θ ….(1)
mg sin θ provides restoring force (F), i.e.
F = – mg sin θ …. (2)

It acts towards the mean position. Here -ve sign shows that F tends to decrease θ. If θ is small, then
sin θ ~ θ
∴ F = – mg θ
Or
\(\frac{F}{m}\) = – gθ
or
a = – gθ = – g. \(\frac{x}{l}\) (∵ x = lθ)

where a = acceleration produced in the bob.
Now as a ∝ x and acts towards mean position, so its motion is S.H.M. having timC period (T) given by

T = 2π\(\sqrt{\frac{x}{a}}\) = 2π\(\sqrt{\frac{l}{g}}\)

(b) A particle executing S.H.M. has two types of energy

1. P.E. due to its displacement from mean position.
2. K.E. due to its velocity.

Let M = mass of the particle executing S.H.M.
r = amplitude of S.H.M.
ω = angular frequency of S.H.M.
y = displacement after a time t. k = force constant of S.H.M.
F = ky, restoring force acting at any position A.

Let the body is displaced from A to B s.t. AB = dy
If dW = work is done on the body when displaced by dy, then
dW = F dy = ky dy

If W = work done when the body is displaced through y, then

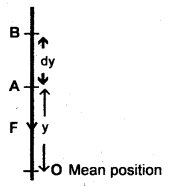
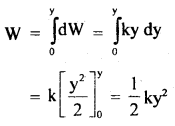
This work is stored in the particle in the form of P.E.
i.e. E₁ = P.E. = \(\frac{1}{2}\)ky²

KE. Let y = velocity of the particle executing S.H.M. at a displacement y from the mean position. Then
v = ω\(\sqrt{r^{2}-y^{2}}\)


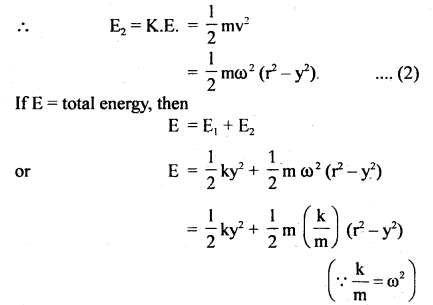
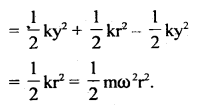
Thus the total energy in S.H.M. remains constant.

Numerical Problems:

Question 1.
A particle executing S.H.M. along a straight line has a velocity of 4 ms^-1 at a distance of 3 m from its mean position and 3 ms^-1 at a distance of 4 m from it. Determine its angular speed and time period of oscillation.
Answer:
Here, y₁ = 3 m
v₁ = 4 ms^-1
y₂ = 4 m
v₂ = 3 ms^-1
ω =?

We know that the velocity of a particle executing S.H.M. is given by

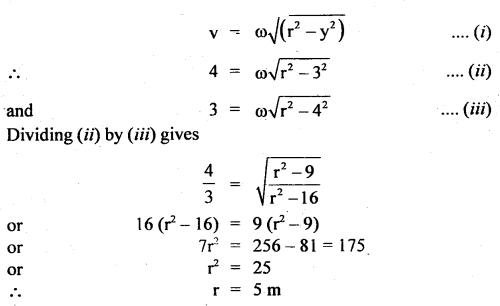
∴ From (ii),
4 = ω \(\sqrt{25-9}\) = 4ω
∴ ω = 1 rad s^-1
∴ T = \(\frac{2π}{ω}\) = 2π second.

Question 2.
A harmonic oscillation is represented by y = 0.34 cos (3000 t + 0.74) where y and t are in cm and s respectively. Deduce
(i) amplitude,
(ii) frequency and angular frequency,
(iii) time period,
(iv) initial phase.
Answer:
The given equation is y 0.34 cos (3000 t + 0.74) …. (1)
Comparing eqn. (i) with the standard equation of displacement of harmonic oscillation,
y = r cos (ωt + Φ_o), we get
r = amplitude = 0.34 cm

Question 3.
A particle vibrates simply harmonically with an amplitude of 4 cm.
(a) Locate the position of the point where its speed is half its maximum speed.
(b) At what displacement ¡s P.E. = K.E.?
Answer:
Here, r = 4 cm
v_max = maximum speed of the particle
m = mass of the particle
(a) let v = speed of the particle when its displacement is y and
v = \(\frac{1}{2}\)v_max …(i)
Let y = required position w.r.t. mean pcsition =?

∴ maximum P.E = \(\frac{1}{2}\)kr²
Also maximum K.E = \(\frac{1}{2}\)mv²_max

According to the law of conservation of energy,

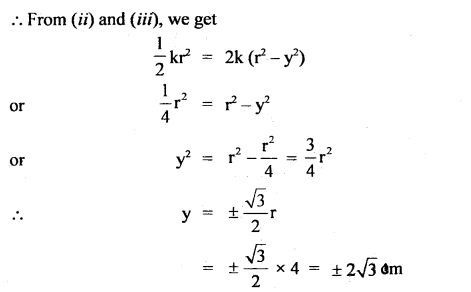
(b) Let y₁ be the displacement from the mean position at which
P.E.=KE.

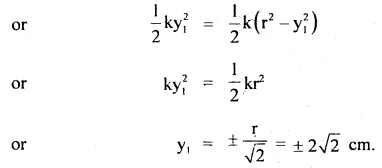
Question 4.
A body of mass 12 kg is suspended by a coil spring of natural length 50 cm and force constant 2.0 × 10³ Nm^-1. What is the stretched length of the spring? 1f the body is pulled down further stretching the spring to a length of 59 cm and then released, what is the frequency of oscillation of the suspended mass? (Neglect the mass of the spring) .
Answer:
Here, k = 2 × 10³ Nm^-1
m = 12 kg
L = original length of the spring
= 50 cm = 0.50 m

Let l = elongation produced in the spring when 12 kg mass is suspended.
∴ F = kl = mg
or
l = \(\frac{\mathrm{mg}}{\mathrm{k}}=\frac{12 \times 9.8}{2 \times 10^{3}}\)
= 0.0588 m = 5.88 cm

∴ stretched length of the spring = L + l = 50.00 + 5.88 = 55.88 cm

The time period of a loaded spring does not change even if the spring is further stretched. So when it is stretched to 59 cm, its time period will be given by
T= 2π\(\sqrt{\frac{m}{k}}\)

∴ Frequency of oscillation is given by

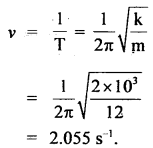
Question 5.
A body of mass of 1.0 kg is suspended from a weightless spring having a force constant of 600 Nm^-1. Another body of mass 0.5 kg moving vertically upward hits the suspended body with a velocity of 3.0 ms^-1 and gets embedded in it. Find the frequency of oscillations and amplitude of motion.
Answer:
Here, m₁ = 1 kg
m₂ = 0.5 kg
k = force constant = 600 Nm^-1
v₁ = 0
v₂ = 3 ms^-1

As the mass m2 gets embedded after collision; so
m = total mass = inertia factor = m₁ + m₂ = 1 + 0.5 = 1.5 kg
If v = frequency of oscillation, then

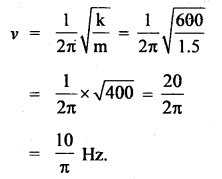
According to the law of conservation of linear momentum, pf = pi.
(m₁ + m₂)V = m₁v₁ + m₂v₂ = m₂v₂ (∵ v₁ = 0)
∴ V = \(\frac{\mathrm{m}_{2} \mathrm{v}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}=\frac{0.5 \times 3}{1.5}\) = 1 ms^-1

Let r = amplitude of motion
Also according to the law of conservation of mechanical energy

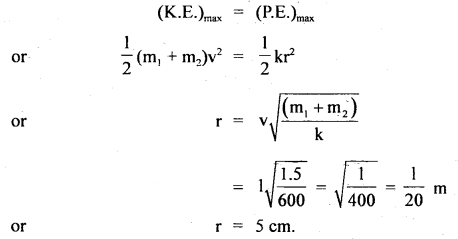
Question 6.
(a) If the length of a second’s pendulum is increased by 1%, how many beats will it lose in one day?
(b) A pendulum clock normally shows the correct time. On an extremely cold day, its length decreases by 0.2%. Compute the error in time per day.
Answer:
(a) Time period of a pendulum is
T = 2π\(\sqrt{\frac{l}{g}}\)

For second’s pendulum, T = 2s
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\) …(i)

Let l’ = new length of the second’s pendulum. When l is increased by 1%, then
l’ = l + l% of l = l +\(\frac{1}{100}\)l

If T’ = new time period, then


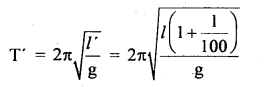
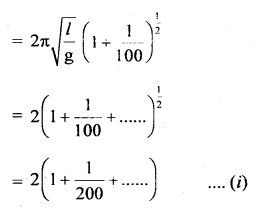
(Using Binomial Expansion Theorem)
= 2 + \(\frac{1}{100}\)

No. of oscillations initially produced by the pendulum is
n = no. of seconds in one day/time
= \(\frac{24 \times 60 \times 60}{2}=\frac{86400}{2}\) …(ii)

No. of oscillations produced by the pendulum after increasing its length.

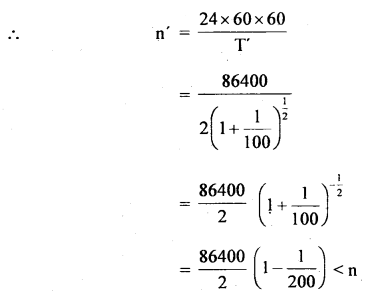
Number of oscillations lost per day = no. of seconds lose per day
= 216 × 2 = 432 s.

(b) The correct time period of the pendulum clock 2s.
Let l be its correct length
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\) ….(iii)

Decrease in length = 0.2% of l = \(\frac{2}{100}\)l
If l’ be the new length than
l’ = l – \(\frac{0.2}{100}\)l = l(1 – \(\frac{0.2}{100}\))

If T’ be the new time period, then

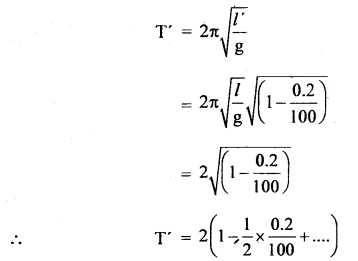
= (2 – \(\frac{0.2}{100}\)) < 2
∴ Clock gains time,
Time gained in 2 seconds = \(\frac{0.2}{100}\)s

∴ Time gained per day = \(\frac{0.2}{100}\) × \(\frac{1}{2}\) × 24 × 60 × 60 = 86.4 s.

Question 7.
A simple pendulum is made by attaching a 1 kg bob to a 5 cm copper wire of diameter 0.08 cm and it has a certain period of oscillation. Next, a 10 kg bob is substituted for a 1 kg bob. Calculate the change in period if any. Young’s modulus of Copper is 12.4 × 1010 Nm^-2.
Answer:
Here, F = mg
A = πr²
The original length of the pendulum, l = 5 m

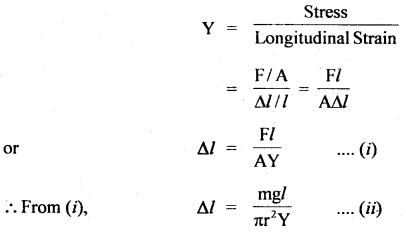
Case I: m = 1 kg, l = 5 m, r = \(\frac{0.08}{2}\) cm = 0.04 cm = 4 × 10^-4 m, Y = 12.4 × 10¹⁰ Nm^-2
∴ Δl1 = \(\frac{1 \times 9.8 \times 5}{3.14 \times(0.04)^{2} \times 12.4 \times 10^{10}}\)
= 0.0787 × 10^-2 m
= 0.00079 m.

∴ Total length of the pendulum,
l₁ = l + Δl₁ = 5 m + 0.00079 m
= 5.00079 m.

If T1 be the initial time period of the pendulum, then
T₁ = 2π\(\sqrt{\frac{l_{1}}{g}}\)
= 2 × \(\frac{22}{7} \sqrt{\frac{5.00079}{9.8}}\)
= 6.28 × 0.714 = 4.486 s

CaseII: M = 10kg, l = 5 m, r = 0.04 × 10^-4m, Y = 12.4 × 1010 Nm^-2
∴ Δl₂ = \(\frac{10 \times 5 \times 9.8}{3.14 \times 16 \times 10^{-8} \times 12.4 \times 10^{10}}\)
= 0.0079 m
∴ l₂ = l + Δl₂ = 5 + 0.0079 = 5.0079 m

If T2 be the new time period of the pendulum, then
T₂ = 2π\(\sqrt{\frac{l_{2}}{g}}\)
= 2 × 3.14\(\sqrt{\frac{5.00079}{9.8}}\)
= 4.489 s.

∴ Increase in time = T₂ – T₁ = 4.489 – 4.486 = 0.003s.

Question 8.
A second’s pendulum is taken in a carriage. Find the period of oscillation when the carriage moves with an acceleration of 4 ms^-2.
(i) Vertically upwards,
(ii) Vertically downwards,
(iii) in a horizontal direction.
Answer:
Here, T = 2s
using T = 2π\(\sqrt{\frac{l}{g}}\), we get
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\)
or
1 = 2π\(\frac{l}{g}\)
or
l = \(\frac{\mathrm{g}}{\pi^{2}}=\frac{9.8}{\pi^{2}}\) …(i)

(i) When carriage moves up, a = 4 ms^-2
∴ If T₁ be the time period, then

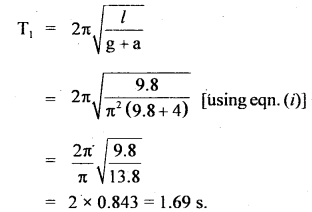
(ii) When the carriage moves down with a = 4 ms^-2
If T₂ be the time period, then

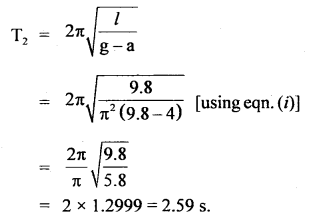
(iii) When the carriage moves horizontally, then g and a are at right angles to each other and hence the net acceleration is

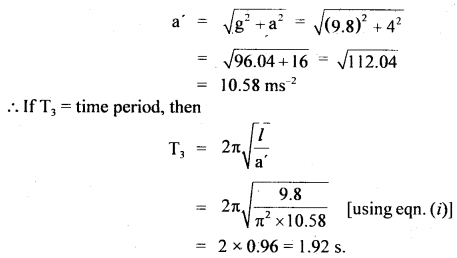
Question 9.
A block is kept on a horizontal table. The table is undergoing S.H.M. of frequency 3 Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. Find the maximum amplitude of the table at which the block does not slip on the surface (g = 10 ms^-2).
Answer:
Here, v = 3 Hz.
μ = 0.72
g = 10 ms^-2

Maximum acceleration of the block is
amax = rω²
where r = amplitude of the table
ω = its angular frequency = 2πv
= 2π × 3

∴ Maximum force on the block is given by
F = mamax = mrω²

Frictional force on the block,
f_s = μmg

The block will not slip on the surface of the table if
F = f_s
or
mrω² = μmg
or
r = \(\frac{\mu g}{\omega^{2}}\)
or
r = \(\frac{0.72 \times 10.0}{(6 \pi)^{2}}\) = 0.02 m

Question 10.
The pendulum bob has a speed of 3 ms^-1 at its lowest position. The pendulum is 0.5 m long. What will be the speed of the bob when the length makes an angle of 60° with the vertical?
Answer:
Let m = mass of the bob
y = speed of the bob at the lowest position = 3ms^-1.

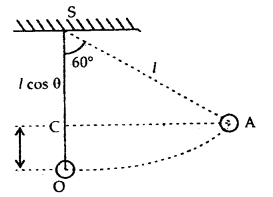
l = length of the pendulum
= 0.5 m = \(\frac{1}{2}\)m

∴ K.E at the lowest position O = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\)m × 3² = \(\frac{9}{2}\)m …(i)

When the length (i) makes an angle O ( 60°) to the vertical, the bob of the pendulum will have both K.E. and P.E.

If v₁ be the velocity of the bob in this position and h= height of the bob with respect to O, then
SC = l cos θ
∴ h = OS – SC = l – l cos θ
= l(l – cos θ)
= l(1 – \(\frac{1}{2}\))
= \(\frac{l}{2}=\frac{1}{2} \times \frac{1}{2}\)m
= \(\frac{1}{4}\)m.

Total energy of the bob = K.E. + P.E.
= \(\frac{1}{2}\)mv₁² + mgh
= \(\frac{1}{2}\)mv₁² + m × 9.8 × \(\frac{1}{4}\) …(iii)

∴ According to the law of conservation of energy,
K.E. at O = Total energy at A
\(\frac{9}{2}\) m = \(\frac{1}{2}\)mv12 + \(\frac{\mathrm{m} \times 9.8}{4}\)
or
v₁² = 9 – \(\frac{9.8}{2}\) = 9 – 4.9 = 4.1
∴ v₁ = 2.025 = 2.03 ms-1.

Question 11.
A person stands on a weighing machine placed on a horizontal platform. The machine reads 60 kg. When the platform executes S.H.M. at a frequency of 2.0 s^-1 and amplitude 5.0 cm, what will be the effect on the reading of the weighing machine? Take g = 10 ms^-2.
Answer:
Here, m = 60 kg
v = 2 s^-1
r = 5 cm = 0.05 m
ω = 2πv = 2π × 2 = 4π rad^-1 s

Here A and B are the extreme positions between which the platform vibrates and O = mean position.
∴ acceleration is maximum at A or B and is given by
a_max = rω² = 0.05 × (4π)²
= 0.05 × 16 × 9.87
= 7.9 ms^-2

∴ restoring force, F = ma_max
= m × 7.9 N
= 7.9 m N

At point A, both weight and restoring force are directed towards the mean position, so the effective weight is maximum at A i.e. reading will be maximum and is given by
W₁ = mg + ma_max = m(g + a_max)
= 60 (10 + 7.9)
= 60 × 17.9 N
= 1074.0 N
= 107.4 kgf

At point B, the weight and the restoring force are opposite to each other, so the effective weight i.e. reading of the weighing machine is minimum at B and is given by

Question 12.
If earth were a homogeneous sphere and a square hole was bored in it through its center, show that a body dropped in the hole will execute S.H.M. and calculate its period if the radius of earth = 6400 km.
Answer:
Let R = radius of earth 6400 × 10³ m
O = center of the earth

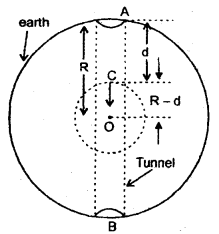
Let AB be a tunnel bored along the diameter of the earth and a body be dropped from point A.

Let it reaches point C at a depth d from the surface of the earth.
∴ OC = R — d = distance of the object from the center of earth displacement of the body.

If gd be the acceleration due to gravity at a depth ‘d’ then we know, that
g_d = g(1 – \(\frac{d}{R}\)) = g\frac{(R-d)}{R}\(\)

If R – d = y = displacement from O, then
g_d = \(\frac{g}{R}\)y

Now as the acceleration of the body is proportional to its displacement from the center of earth i.e. O. Hence the motion of the body is S.H.M. and its time period is given by

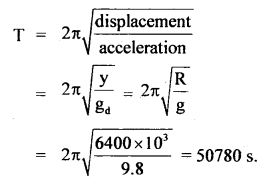
Question 13.
A horizontal spring block system of mass M executes S.H.M. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration.
Answer:
The frequency of oscillation of spring block system of mass M is given by
v = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{M}}}\) …..(i)
where k = force constant of the spring.

Let r = initial amplitude of oscillation.
V_o = velocity of the system in equilibrium position,
according to the law of conservation of energy,
∴ \(\frac{1}{2}\)MV₀² = \(\frac{1}{2}\)kr²
or
V_o = \(\sqrt{\frac{k}{M}}\)r ….(ii)

When mass m is put on the system, then total mass = M + m.

If V = velocity of the combination in equilibrium, then according to the law of conservation of linear momentum,
MV_o = (M + m)V
or
V = \(\frac{\mathrm{MV}_{0}}{\mathrm{M}+\mathrm{m}}\) ….(iii)

Let r₁ be the new amplitude, then


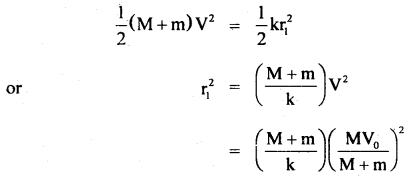
If v’ be the new frequency of oscillation, then
v’ = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{M}+\mathrm{m}}}\)

Question 14.
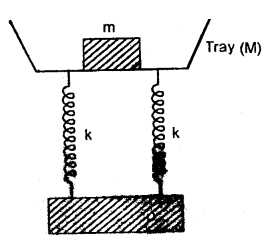
A tray of mass 12 kg is supported by two parallel vertical identical springs. When the tray is pressed down slightly and released, it executes S.H.M. with a time period of 1.5 s. What is the force constant of each spring? When a block of mass m is placed in the tray, the period of S.H.M. changes to 3 s. What is the mass of the block?
Answer:
Let k be the spring constant of each of the identical springs connected in parallel.
M = mass of tray = 12 kg
T₁ = time period of oscillation of the tray = 1.5 s

Let T₂ = time period of oscillation of the tray + block of mass ‘m’
∴ T₂ = 3 s
m = ?
k =?

If k’ = spring constant of the combination, then
k’ = k + k = 2k (a)

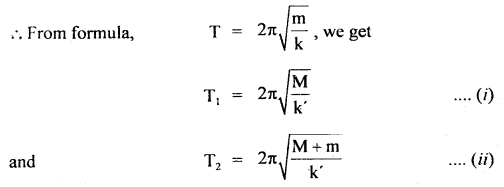
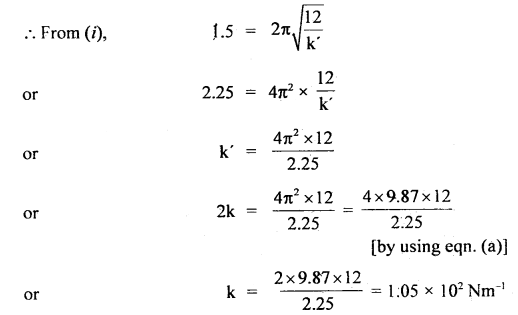
Dividing (ii) and (i), we get

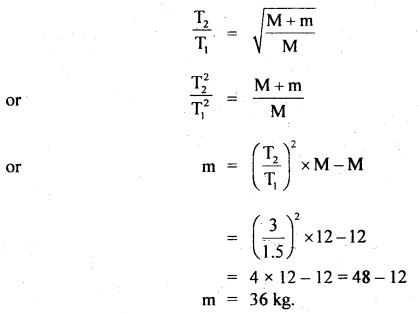
Question 15.
Two pendulums of lengths 100 cm and 110.25 cm start oscillating in phase simultaneously. After how many oscillations will they again be in phase together?
Answer:
Here, l₁ = 100 cm
l₂ = 110.25 cm
using T = 2π\(\sqrt{\frac{l}{g}}\)

For smaller pendulum, T₁ = 2π\(\sqrt{\frac{100}{g}}\) …(i)

For larger pendulum, T₂ = 2π\(\sqrt{\frac{110.25}{g}}\) …(ii)
where T₁ and T₂ are the time periods of the two pendulums.

Let these pendulums oscillate in phase again if the larger pendulum completes n oscilLations, It means the smaller pendulum must complete (n + 1) oscillations.
nT₂ = (n + 1)T₁

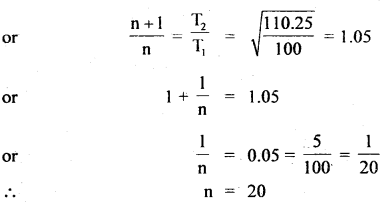
Hence both pendulums will again oscillate in phase after 20 oscillations of the larger or 21 oscillations of the smaller pendulum.

Question 16.
Springs of spring constants k, 2k, 4k., 8k, are connected in series. A mass m kg ¡s attached to the lowér end to the last spring and the system is allowed to vibrate. Calculate the approximate time period of vibration.
Answer:
The time period of vibration of series loaded spring is given by
T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}_{\mathrm{s}}}}\) …(1)
Where k is the force constant of the series combination of springs.

In a series combination of springs, the combined spring constant k is given by

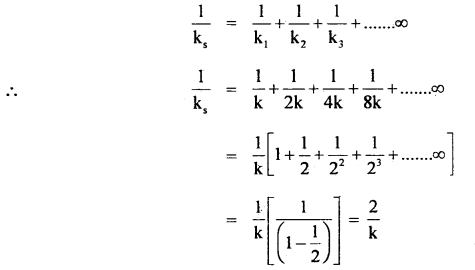
or
ks = \(\frac{k}{2}\)

m mass attached to the lower end of the spring.
∴ From (1) and (2), we get
T = 2π\(\sqrt{\frac{2 m}{k}}\)

Question 17.
A point particle of mass 0.1 kg is executing S.H.M. of amplitude 0.1 m. When the particle passes through the mean position, its kinetic energy is 8 × 10^-2 J. Obtain the equation of motion of this article if the initial phase of oscillation is 45°
Answer:
Since the kinetic energy is maximum at the mean position and is equal to

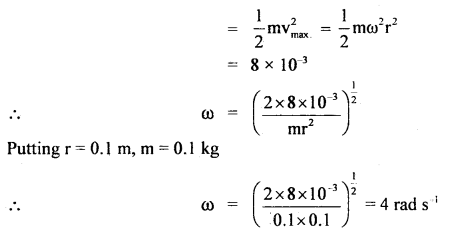
The standard equation of motion of a particle executing S.H.M. is
y = A sin(ωt + Φ₂)
or
x = A cos(ωt + Φ₂)
Given r = 0.1 m, ω = 4 rad s-1 and Φ₂ = 45° = \(\frac{π}{4}\)

∴ The required cquation of motion is
y = 0.1 sin (4t + \(\frac{π}{4}\))
or
x = 0.1 cos (4t + \(\frac{π}{4}\)).

Question 18.
A cubical body (side 0.1 m and mass 0.002 kg) floats in water. It is pressed and then released so that it oscillates vertically. Show that the motion of the body is simple harmonic and And the time period.
Answer:
Here, m = mass of body = 0.002 kg
L = side of body = 0.1 m
In the absence of any given indication it is assumed that the body floats (just sunk), so

The mass of water displaced = volume × density of water
= V ρ = (0.1 )3 ρ.

The upward thrust exerted by water displaced
i.e. buoyant force = Vρg=(0.1 )3 × 10³ × 9.8 (∴ ρ ofwater = 10³ kg m³)
W₁ = Downward weight = mg
Net downward force, F = (0.002 g -Vρg)
or
F = [0.002g – (1)³ × 10³g
= (0.002 – 1)g
= – 0.998 × 9.8 N …. (1)

Suppose the block is depressed by y,
hence restoring force F₁ = – (0.1 + y)k

When the body floats on the water the force acting is F = 0.1 k, where k is the force constant
The net downward force
F – F’ = 0.1 k – (0.1 + y)k
= – yk ….(2)

Thus force ∝ (- y)
Force = ma, where a = acceleration of the body.
∴ ma = – y k
or a = – \(\frac{k}{m}\) y
m
or a ∝ -y …. (3)

Hence the motion-ofthe block is S.H.M.
The time period of oscillation is given by
T = 2π\(\frac{m}{k}\) …(4)

From eqn. (1), k = \(\frac{\mathrm{F}}{\mathrm{L}}=\frac{0.998 \times 9.8}{0.1}\)Nm^-1 …(5)
m = 0.002 kg

∴ T = 2π\(\sqrt{\frac{0.002 \mathrm{~kg} \times 0.1}{0.998 \times 9.8 \mathrm{Nm}_{1}}}\)
= 0.0284 s.

Question 19.
Two simple harmonic motions are represented by the following equations:
y₁ = 10 sin \(\frac{π}{4}\) (12t + 1); y² = 5 (sin 3πt + \(\sqrt{3}\) cos 3πt).
(a) Find out the ratio of their amplitudes.
(b) What are the time periods of two motions?
(c) Also find the phase difference between two motions.
Answer:
The two given displacements may be written as

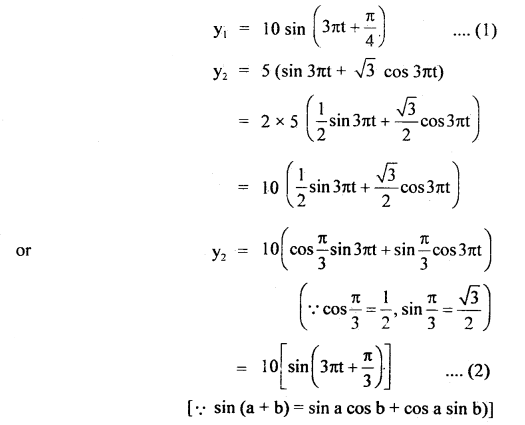
(a) The amplitudes of the two S.H.M. are A₁ = 10 units. and A₂ = 10 units
Hence \(\frac{\mathrm{A}_{1}}{\mathrm{~A}_{2}}=\frac{10}{10}\) = 1

(b) Comparing the given equation with the normal sine function of S.H.M.
i.e. y = A sin(\(\frac{2πt}{T}\) + Φ) …(3)

Here we get \(\frac{2πt}{T}\) = 3πt
or
T = \(\frac{2}{3}\) s

i.e. Time period for two motions is same i.e. T = 0.67 s.

(c) Phase difference between two motions:
Phase (Φ₁) of motion represented by y₁ is
Φ₁ = 3πt + \(\frac{π}{4}\) …(4)

Phase (Φ₂) of motion represented by y₂ is
Φ₂ = 3πt + \(\frac{π}{3}\) …(5)

∴ Phase difference is given by
dΦ = Φ₂ – Φ₁ = (3πt + \(\frac{π}{3}\)) – (3πt + \(\frac{π}{4}\))
= (4 – 3)\(\frac{π}{12}\)
= \(\frac{π}{12}\) = 15°

Question 20.
Two particles execute- S.H.M. of the same amplitude at time period along the same straight line. They cross each other in opposite directions at half the amplitude. What is the phase difference between them?
Answer:
Let the displacement of one particle executing S.H.M. be
y₁ = A sin ωt …. (1)

when y₁ = \(\frac{A}{2}\)
From equation (1), we get.
\(\frac{A}{2}\) = A sin ωt
or
sin ωt = \(\frac{1}{2}\) = sin 30°
∴ ωt = 30° = \(\frac{π}{6}\) radian.

If Φ₁ be the phase of first particle then Φ = \(\frac{π}{6}\) radian. Also let the displacement of second particle executing S.H.M. be
y₁ = r sin (π – ωt) = r sin Φ₂ ….(2)
where Φ₂ = π – ωt = π – \(\frac{π}{6}\) = \(\frac{5}{6}\)π radian

If dΦ be the phase difference between the two particle when they cross each other, then
dΦ = Φ₂ – Φ₁
= \(\frac{5}{6}\)π – \(\frac{π}{6}\) = \(\frac{4π}{6}\) = \(\frac{2}{3}\)π radian
= 120°.

Question 21.
A spring compressed by 10 cm develops a restoring force of 5N. A body of mass of 2 kg is placed on it. Find
(i) Force constant,
(ii) depression of a spring,
(iii) time period and
(iv) the frequency of oscillations, if the body is disturbed.
Answer:
Here, F = 5N
x = 10 cm = 0.1 m
m = 2 kg
(i) k = force constant = \(\frac{F}{x}=\frac{5 N}{0.1}\) = 50 Nm^-1.

(ii) depression, l = \(\frac{\mathrm{mg}}{\mathrm{k}}=\frac{2 \times 9.8}{50}\) = 0.392 m

(iii) T = 2π\(\sqrt{\frac{m}{k}}\) = 2π\(\sqrt{\frac{2}{50}}\) = \(\sqrt{\frac{2π}{5}}\)s

(iv) v = \(\frac{1}{\mathrm{~T}}=\frac{5}{2 \pi}\) Hz

Question 22.
The S.H.M. of a particle is given by the equation y = 3 sin cot + 4 cos cot. Find its amplitude.
Answer:
The equation y = 3 sin ωt + 4 cos ωt is due to the superposition of two waves,
y₁ = 3 sin ωt
and
y₂ = 4 cos ωt = 4 sin(ωt + \(\frac{π}{2}\))

If r₁ and r₂ be the amplitudes of the two w’aves respectively, then r₁= 3 units and r₂ = 4 units.
Φ = phase difference between them = \(\frac{π}{2}\)

If r be the amplitude of the resultant wave, then

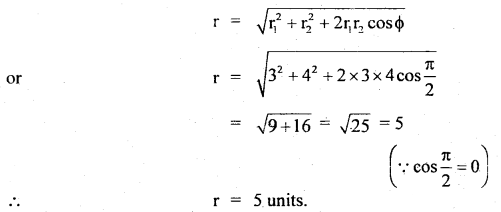
Question 23.
Two masses m₁ = 1.0 kg and m₂ = 0.5 kg arc suspended together by a massless spring of spring constant k as shown in the figure. When masses are in equilibrium, m, is removed without disturbing the system. Calculate the amplitude of oscillation and angular frequency of m2. (g = 10 ms^-2 and k = 12.5 Nm^-1).
Answer:
Let y = extension in length of the spring when both m1 and m2 are suspended with it, then
(m₁ + m₂)g = ky
or
y = \(\frac{\left(m_{1}+m_{2}\right) g}{k}\) …(1)

Let y’ extension in the length of the spring when only m is suspended.
∴ m₂g = ky’
or
y’ = \(\frac{\mathrm{m}_{2} \mathrm{~g}}{\mathrm{k}}\) …(2)

(1) – (2) gives y – y’ = \(\frac{\left(m_{1}+m_{2}\right) g}{k}-\frac{m_{2} g}{k}=\frac{m_{1} g}{k}\)

This represents the amplitude of oscillation (r)
i.e. r = y – y’ = \(\frac{\mathrm{m}_{1} \mathrm{~g}}{\mathrm{k}}\) …(3)
Here, m₁ = 1.0 kg
k = 12.5 Nm^-1
g = 10 ms^-2

Putting these values in equation (3), we get
r = \(\frac{1 \times 10}{12.5}\) = 0.8 m

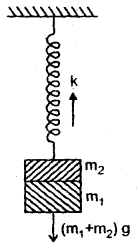
If ω be the angular frequency of m₂, then
ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}_{2}}}=\sqrt{\frac{12.5}{0.5}}\) (∵ m₂ = 0.5 kg)
ω = 5 s^-1.

Question 24.
Prove that T = 84.6 minutes for a simple pendulum of infinite length.
Answer:
T = 2π\(\sqrt{\frac{l}{g}}\) …(1)
eqn. (1) hold good till l << R (radius of the earth).

When l is large, the curvature of the earth had also to be taken into account. In that case,

Question 25.
For damped oscillator, m = 200 gm, k = 90 Nm b = 40 gs^-1.
Calculate (a) time period of oscillation,
(b) time is taken for its amplitude of vibration to become \(\frac{l}{2}\) of its initial value.
(c) time is taken for its mechanical energy to drop to half of its initial value.
Answer:
Here, m = 200 g = 0.200 kg
k = 90 Nm^-1
b = 40gs^-1.
(a) \(\sqrt{km}\) = \(\sqrt{90 \times 0.2}=\sqrt{18}\) = 4.243 kg s^-1
b = 0.04 kg s^-1
∴ b << \(\sqrt{km}\)

(b) Let T_1/2 = time taken for the amplitude to drop to half of its initial value.

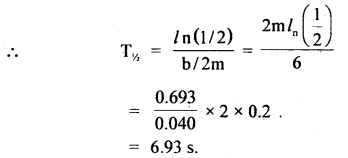
(c) Let T’_1/2 be the time for its mechanical energy to drop to half of its initial value,
∴ Using equation,

which is just half of T_1/2. (i.e. decay period for amplitude).

Value-Based Type:

Question 1.
A sports teacher was training the children to march- past On their way they come across a bridge. Then the physical education teacher stopped the children from marching on the bridge.
(a) Comment upon the values of sports teachers.
Answer:
The sports teacher is responsible, cares not only for public property but also for children.

(b) Also explain what is meant by Resonance.
Answer:
When the frequency of marching coincides with the natural frequency of oscillation of the bridge then the bridge oscillates with maximum amplitude to such an extent that the bridge may even collapse. The condition is called “Resonance”.

Question 2.
The Physics teacher of class XI has assigned the work finding the resultant spring constant when two springs of spring constants K₁, K₂ are joined in series. Two students Sabita and Shirin. Sabita made a theoretical study as well as verified it experimentally. Whereas Shirin could not complete the work. When th~ teacher enquired the next day Sabita could give the answer. Whereas Shirin could not.
(a) Comment upon the qualities of Sabita.
Answer:
Sabita is Sincere and hardworking and has a scientific temper.

(b) Two springs are joined in series and connected to a mass m. If spring constants are Kj and K2, Calculate the period of oscillation of mass m.
Answer:
Since K₁ and K₂ are joined in series.

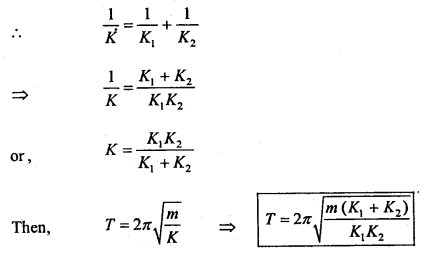
Question 3.
Adarsh a student of class XI has found the factors on which the time period of oscillation of a pendulum depends and arrived at the expression T – (constant) × (l/g)^1/2. He wants to know how the length of the pendulum gets affected on the surface of the moon for the same pendulum and arrived at the conclusion that it is 1/6.
(a) What values does Adarsh possesses?
Answer:
Adarsh is hardworking, thinks logically, having a scientific temper, able to find solutions with patience.

(b) The length of a second pendulum on the surface of the moon?
Answer:
Since l is proportional to ‘g’ the pendulum on the surface of the moon will be 1/6m.

Question 4.
In a physics class, the teacher told that everyone has to finish the homework and assignment within a weak. But only five students including Dinesh did their homework on time. A few questions from the assignment are as under:
(i) Derive the expression for velocity in S.H.M.
Answer:
Let the displacement in S.H.M is given by

(ii) On what factors time period of a simple pendulum depends.
Answer:
The time period of a simple pendulum depends on
(a) Length of the pendulum.
(b) The acceleration due to gravity.

(iii) What values are shown by Dinesh?
Answer:
Values shown by Dinesh are Punctuality and Sincerity.