CBSE Class 10

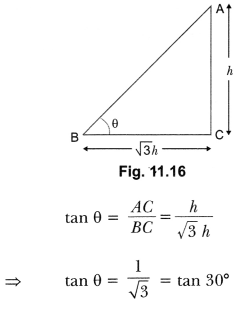
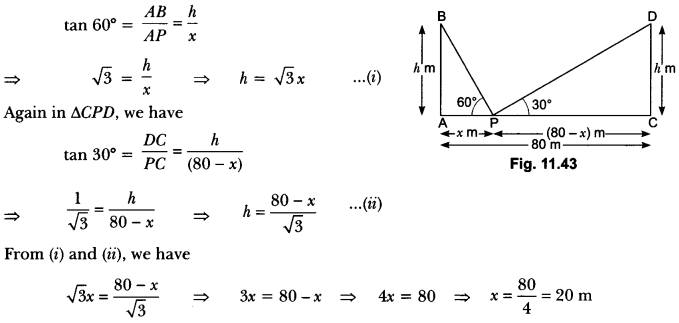
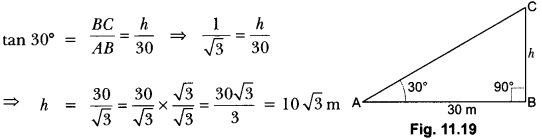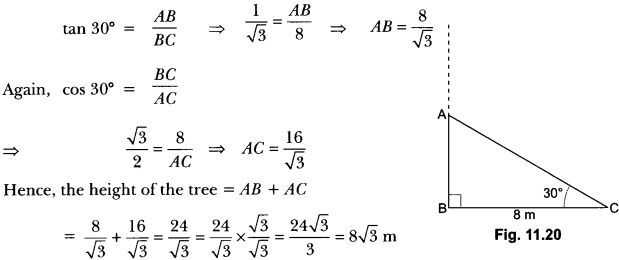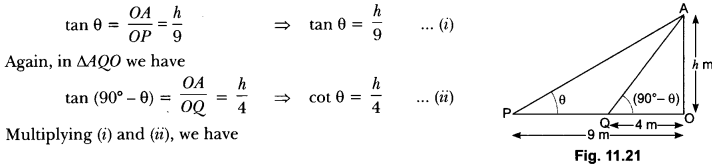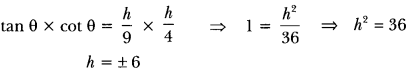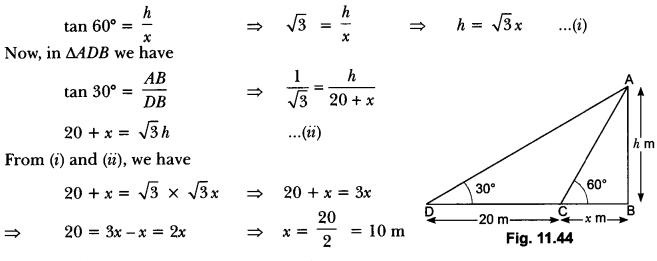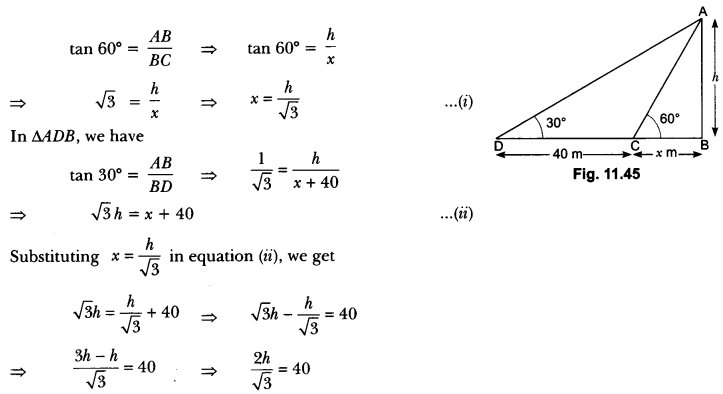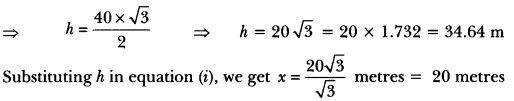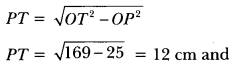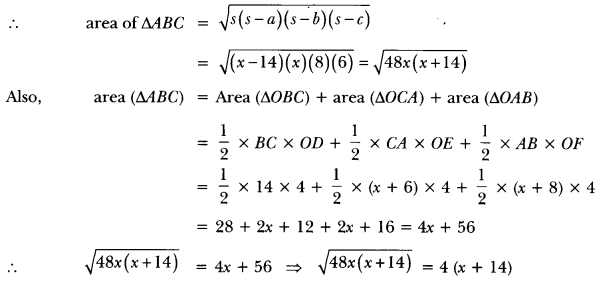Here we are providing Areas Related to Circles Class 10 Extra Questions Maths Chapter 12 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Areas Related to Circles with Answers Solutions

Extra Questions for Class 10 Maths Chapter 12 Areas Related to Circles with Solutions Answers

Areas Related to Circles Class 10 Extra Questions Very Short Answer Type

Question 1.
Find the area of a square inscribed in a circle of diameter p cm.

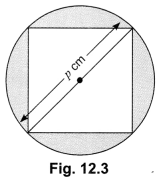
Solution:
Diagonal of the square = p cm
∴ p² = side² + side²
⇒ p² = 2side²
or side² = \(\frac{p^{2}}{2}\) cm² = area of the square

Question 2.
Find the area of the circle inscribed in a square of side a cm.

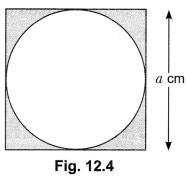
Solution:
Diameter of the circle = a

Question 3.
Find the area of a sector of a circle whose radius is and length of the arc is l.
Solution:
Area ola sector ola circle with radius r

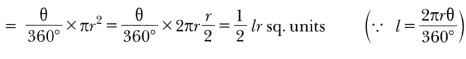
Question 4.
Find the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal.
Solution:

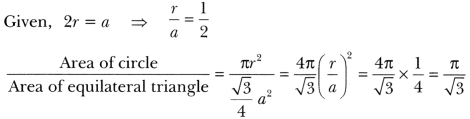
Question 5.
A square inscribed in a circle of diameter d and another square is circumscribing the circle. Show that the area of the outer square is twice the area of the inner square.

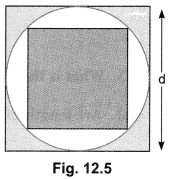
Solution:
Side of outer square = d {Fig. 12.5]
∴ Its area = d
Diagonal of inner square = d
∴ Side = \(\frac{d}{\sqrt{2}}\)
⇒ Area = \(\frac{d^{2}}{2}\)
Area of outer square = 2 × Area of inner square.

Question 6.
If circumference and the area of a circle are numerically equal, find the diameter of the circle.
Solution:
Given, 2πr = πr²
⇒ 2r = r²
⇒ r(r – 2) = 0 or r = 2
i.e. d = 4 units

Question 7.
The radius of a wheel is 0.25 m. Find the number of revolutions it will make to travel a distance of 11 km.
Solution:

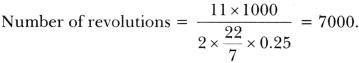
Question 8.
If the perimeter of a semi-circular protractor is 36 cm, find its diameter.
Solution:
Perimeter of a semicircular protractor = Perimeter of a semicircle
= (2r + πr) cm
⇒ 2r + πr = 36
⇒ r\(\left(2+\frac{22}{7}\right)\) = 36
⇒ r = 7cm
Diameter 2r = 2 × 7 = 14 cm.

Question 9.
If the diameter of a semicircular protractor is 14 cm, then find its perimeter.
Solution:
Perimeter of a semicircle = πr + 2r
= \(\frac{22}{7}\) × 7 + 2 × 7 = 22 + 14 = 36cm

Areas Related to Circles Class 10 Extra Questions Short Answer Type 1

Question 1.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?

Solution:
Let radius of the circle be r units.
Then, diagonal of the square = 2r

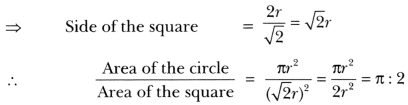
Question 2.
What is the area of the largest triangle that is inscribed in a semi circle of radius r unit?
Solution:

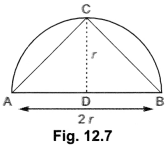
Area of largest ∆ABC = \(\frac{1}{2}\) × AB × CD
\(\frac{1}{2}\) × 2r × r = r² sq. units

Question 3.
What is the angle subtended at the centre of a circle of radius 10 cm by an arc of length 5π cm?
Solution:

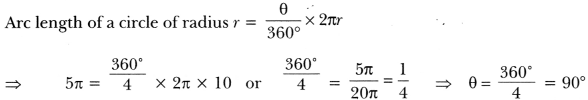
Question 4.
What is the area of the largest circle that can be drawn inside a 4 rectangle of length a cm and breadth b cm (a > b)?

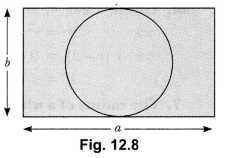
Solution:
Diameter of the largest circle that can be inscribed in the given b
rectangle = b cm
∴ Radius = \(\frac{b}{2}\) cm

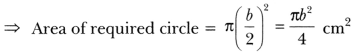
Question 5.
Difference between the circumference and radius of a circle is 37 cm. Find the area of circle.
Solution:
Given 2π r – r = 37
or r (2π – 1) = 37

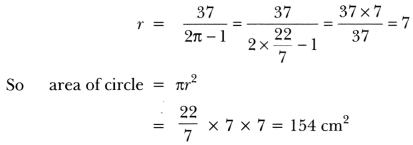
Question 6.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Solution:
Let r be the radius of required circle. Then, we have
πr² = π(8)² + π(6)²
⇒ πr² = 64π + 36π
⇒ πr² = 100π
∴ r² = \(\frac{100 \pi}{\pi}\) = 100
⇒ r = 10cm
Hence, radius of required circle is 10 cm.

Question 7.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Solution:
Let R be the radius of required circle. Then, we have
2πR = 2π(19) + 2π (9)
⇒ 2πR = 2π (19 + 9)
⇒ R = \(\frac{2 \pi \times 28}{2 \pi}\) = 28
⇒ R = 28 cm
Hence, the radius of required circle is 28 cm.

Question 8.
Find the area of a circle whose circumference is 22 cm.
Solution:
Let r be the radius of the circle. Then,
Circumference = 22 cm

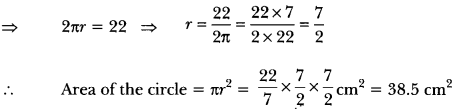
Question 9.
The area of a circular playground is 22176 m². Find the cost of fencing this ground at the rate of ₹50 per m.
Solution:
Area of circular playground = 22176 m²
πr² = 22176
⇒ \(\frac{22}{7}\) r² = 2176
⇒ \(\frac{22176 \times 7}{22}\)
⇒ r = 84 m
∴ Circumference of the playground =2πr = 2 × \(\frac{22}{7}\) × 84 = 44 × 12 = 528 m .
∴ Cost of fencing this ground = ₹ 528 × 50 = ₹ 26400.

Question 10.
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
Solution:
We know that

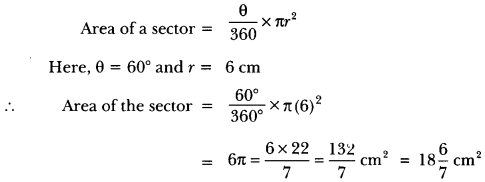
Question 11.
Find the area of a quadrant of a circle whose circumference is 22 cm.
Solution:
Let r be the radius of circle, then circumference = 22 cm

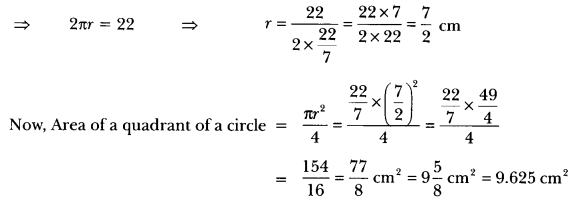
Question 12.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Solution:
Since the minute hand rotates through 6° in one minute, therefore, area swept by the minute hand in one minute is the area of a sector of angle 6° in a circle of radius 14 cm.

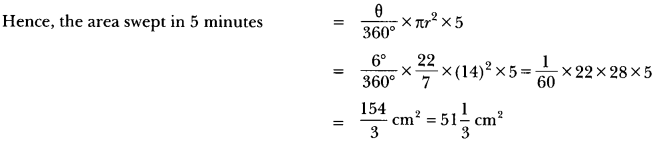
Question 13.
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)
Solution:
We have, r = 16.5 km and 0 = 80°
∴ Area of the sea over which the ships are warned =

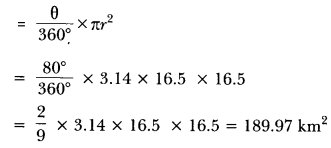
Areas Related to Circles Class 10 Extra Questions Short Answer Type 2

Question 1.
If the perimeter of a semicircular protractor is 66 cm, find the diameter of the protractor
(Take π = \(\frac{22}{7}\)).
Solution:
Let the radius of the protractor be r сm. Then,
Perimeter = 66 cm
= πr + 2r = 66 [∴ Perimeter of a semicircle = πr + 2r]

Question 2.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle.
Solution:
Let the radius of the circle be r сm. Then,
Diameter = 2r cm and Circumference = 2πr cm
According to question,
Circumference = Diameter + 16.8
⇒ 2πr = 2r + 16.8
⇒ 2 × \(\frac{22}{7}\) × r = 2r + 16.8
⇒ 44r = 14r + 16.8 × 7
⇒ 44r – 14r = 117.6 or 30r = 117.6
⇒ r = \(\frac{117.6}{30}\) = 3.92
Hence, radius = 3.92 cm.

Question 3.
A race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.
Solution:
Let the outer and inner radii of the ring be R m and r m respectively. Then,
2πR = 396 and 2πr = 352

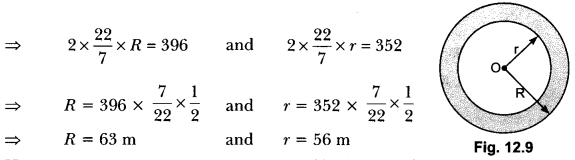
Hence, width of the track = (R – r) m = (63 – 56) m = 7 m

Question 4.
The inner circumference of a circular track [Fig. 12.10] is 220 m. The track is 7 m wide everywhere. Calculate the cost of putting up a fence along the outer circle at the rate of ₹2 per metre.
Solution:

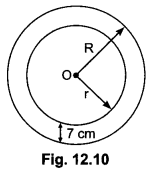
Let the inner and outer radii of the circular track berm and R m respectively. Then,
Inner circumference = 2πr = 220 m

Since the track is 7 m wide everywhere. Therefore,
R = Outer radius = r + 7 = (35 + 7)m = 42 m
∴ Outer circumference = 2πR = 2 × \(\frac{22}{7}\) × 42m = 264m
Rate of fencing = ₹ 2 per metre
∴ Total cost of fencing = (Circumference × Rate) = ₹(264 × 2) = ₹ 528

Question 5.
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Solution:
The diameter of a wheel = 80 cm.
radius of the wheel = 40 cm.
Now, distance travelled in one complete revolution of wheel = 2π × 40 = 80π
Since, speed of the car is 66 km/h
So, distance travelled in 10 minutes = \(\frac{66 \times 100000 \times 10}{60}\)
= 11 × 100000 cm = 1100000 cm.
So, Number of complete revolutions in 10 minutes

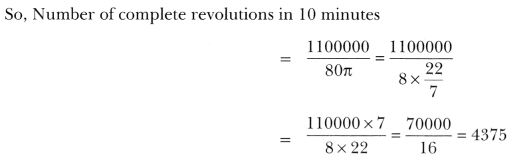
Question 6.
An umbrella has 8 ribs which are equally spaced (Fig. 12.11). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

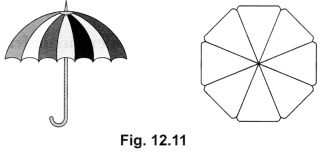
Solution:
We have, r = 45 cm

Question 7.
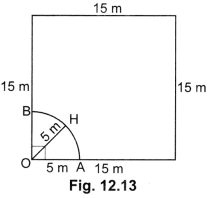
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (Fig. 12.12). Find (i) the area of that part of the field in which the horse can graze;
(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use π = 3.14)

Solution:
Let the horse be tied at point O and the length of the rope is OH (Fig. 12.13).
Thus, (i) the area of the part of the field in which the horse can graze
= Area of the quadrant of a circle (OAHB)

(ii) Now r = 10 m and


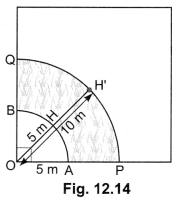
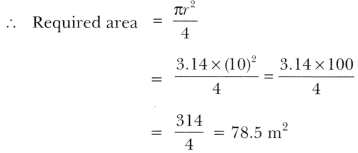
Increase in the grazing area
= (78.5 – 19.625) m²
= 58.875 m²

Question 8.
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115o. Find the total area cleaned at each sweep of the blades.
Solution:
We have, r = 25 cm and θ = 115°.
∴ Total area cleaned at each sweep of the blades
= 2 × (Area of the sector having radius 25 cm and angle θ = 115°).

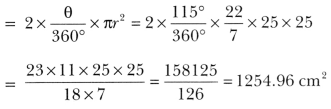
Question 9.
In Fig. 12.15, sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area
of the shaded region.
Solution:
Let A₁ and A₂ be the areas of sectors OAB and OCD respectively. Then, A, = Area of a sector of angle 30° in a circle of radius 7 cm.

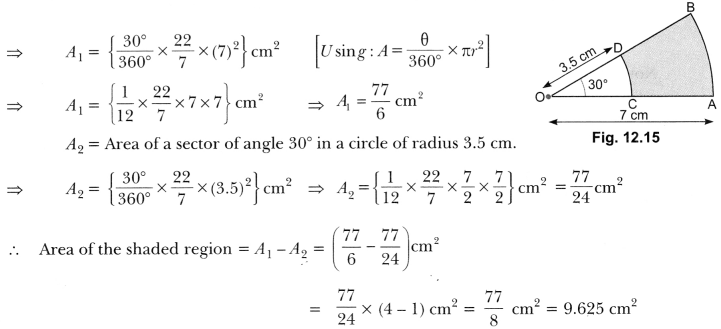
Question 10.
The minute hand of a clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 9 AM and 9.35 AM.
Solution:
We have,
Angle described by the minute hand in one minute = 6°
∴ Angle described by the minute hand in 35 minutes = (6 × 35)° = 210°
Area swept by the minute hand in 35 minutes = Area of a sector of a circle of radius 10 cm

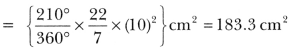
Question 11.
Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector. (Use π = 3.14)
Solution:

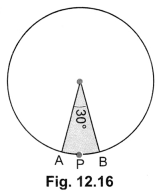
Area of the sector OAPB = \(\frac{\theta}{360^{\circ}} \times \pi r^{2}\)
\(\frac{30^{\circ}}{360^{\circ}}\) × 3.14 × 4 × 4 cm²
= \(\frac{12.56}{3}\)cm²
= 4.19 cm² (approx.)
Area of the corresponding major sector = πr² – Area of sector OAPB
= (3.14 × 4 × 4 – 4.19)cm² = (50.24 – 4.19) cm²
= 46.05 cm² = 46.1 cm² (approx.)

Question 12.
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and √3 = 1.73)
Solution:
We have, r = 15 cm and θ = 60°
Given segment is APB

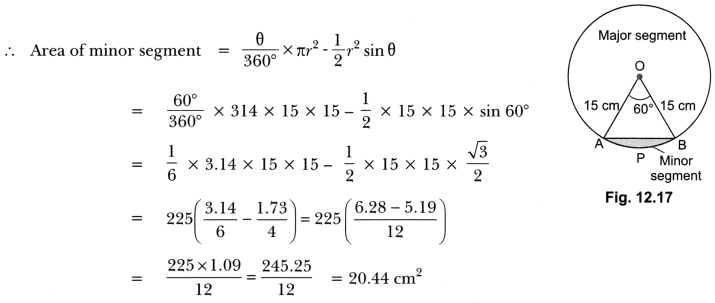
Now, area of major segment = Area of circle – Area of minor segment
= π(15)² – 20.44 = 3.14 × 225 – 20.44
= 706.5 – 20.44 = 686.06 cm

Question 13.
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73)
Solution:
We have, r = 12 cm and θ = 120°
Given segment is APB
Now, area of the corresponding segment of circle
= Area of the minor segment

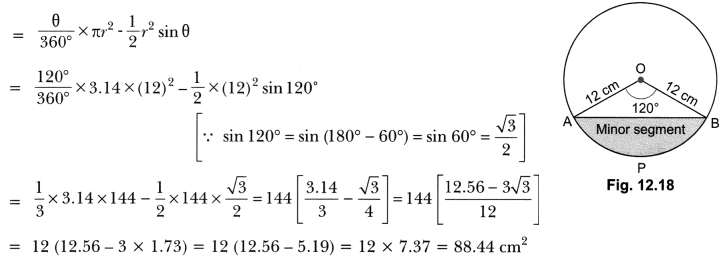
Question 14.
A round table cover has six equal designs as shown in Fig. 12.19. If the radius of the cover is 28 cm?, find the cost of making the designs at the rate of ₹ = 0.35 per cm². (Use √3 = 1.7)
Solution:
Area of one design = Area of the sector OAPB – Area of ΔAOB

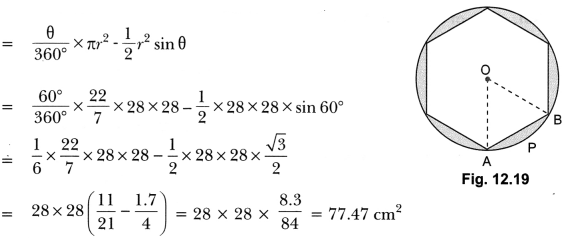
Area of 6 such designs = 77.47 × 6 = 464.8 cm²
Hence, cost of making such designs = ₹ 162.69

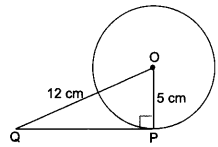
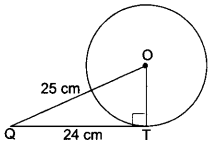
Question 15.
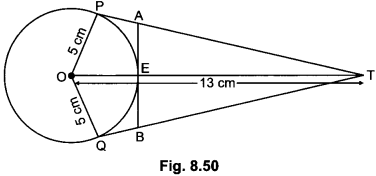
Find the area of the shaded region in Fig. 12.20, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
Solution:

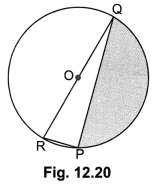
Here, ROQ is the diameter of given circle, therefore ∠RPQ = 90°
Now, in right angled ΔPRQ, we have
RQ² = RP² + PQ² (by Pythagoras Theorem)
RQ² = (7)² + (24)² = 49 + 576 = 625
RQ = \(\sqrt{625}\) = 25 cm
Therefore, radius r = \(\frac{25}{2}\) cm
Now, area of shaded region
= Area of the semi-circle – Area of ARPQ

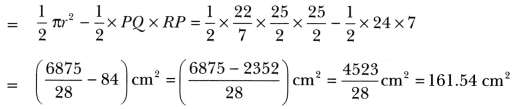
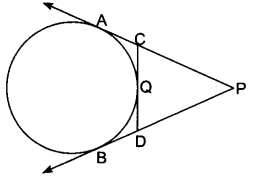
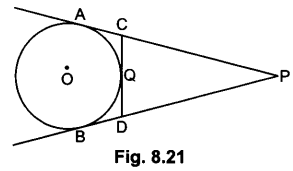
Question 16.
Find the area of the shaded region in Fig. 12.21, if radii of the two concentric circles with centre 0 are 7 cm and 14 cm respectively and ∠AOC = 40°.
Solution:
Area of shaded region
= Area of sector AOC – Area of sector OBD

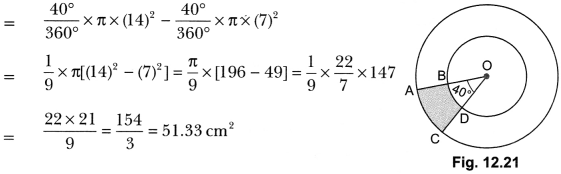
Question 17.
Find the area of the shaded region in Fig. 12.22, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Solution:
We have, radius of semicircles = 7 cm
∴ Area of shaded region
= Area of square ABCD – Area of semi-circles (APD +BPC)

Question 18.
Find the area of the shaded region in Fig. 12.23, where a circular arc of radius 6 cm has been drawn with vertex 0 of an equilateral triangle OAB of side 12 cm as centre.
Solution:
We have, radius of circular region
= 6 cm and each side of ΔOAB = 12 cm.
∴ Area of the circular portion
= Area of circle – Area of the sector

Quesiton 19.
From each corner of a square of side 4 cm, a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.24. Find the area of the remaining portion of the square.
Solution:
We have, the side of the square ABCD = 4 cm
Area of the square ABCD = (4)² = 16 cm²
Since, each quadrant of a circle has radius 1 cm.
∴ The sum of the areas of four quadrants

Question 20.
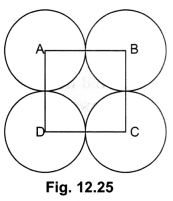
In Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region.

Solution:
We have, each side of square ABCD = 14 cm
∴ Area of square ABCD = (14²)cm² = 196 cm²
Now, radius of each quadrant of circle,
r = \(\frac{14}{2}\) = 7 cm
∴ The sum of the area of the four quadrants at the four corners of the square

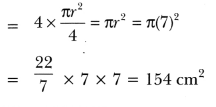
Now, area of shaded portion
= Area of square ABCD – The sum of the areas of four quadrants at the four corners of the square
= (196 – 154) cm² = 42 cm²

Question 21.
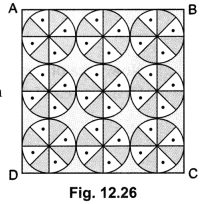
On a square handkerchief, nine circular designs, each of radius 7 cm are made (see Fig. 12.26). Find the area of the remaining portion of the handkerchief.

Solution:
Total area of circular design = 9 × Area of one circular design
= 9 × π × (7)²
= 9 × \(\frac{22}{7}\) × 7 × 7 = 1386 cm²
Now, each side of square ABCD = 3 × diameter of circular design
= 3 × 14 = 42 cm
∴ Area of square ABCD = (42)² = 1764 cm²
∴ Area of the remaining portion of handkerchief
= Area of square ABCD – Total area of circular design
= (1764 – 1386) cm = 378 cm²

Question 22.
In Fig. 12.27, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB, (ii) shaded region.
OR
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
Solution:

Question 23.
In Fig. 12.28, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14).
Solution:
We have,
Radius of quadrant

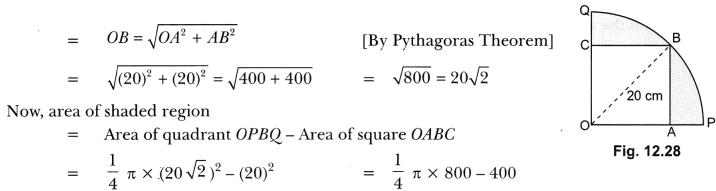
= 200 × 3.14 – 400 = 628 – 400 = 228 cm²

Question 24.
Calculate the area of the designed region in Fig. 12.29, which is common between the two quadrants of circles of radius, 8 cm each.
Solution:
Here, radius of each quadrant ABPD and BQDC = 8 cm

Question 25.
In the given Fig. 12.30, find the area of the shaded region.
Solution:

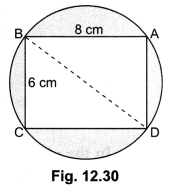
Clearly, diameter of the circle
= Diagonal BD of rectangle ABCD
Now, BD

Let r be the radius of the circle. Then, r = \(\left(\frac{10}{2}\right)\)cm = 5 cm
Hence, area of the shaded region = Area of the circle – Area of rectangle ABCD
= πr² – l × b = (3.14 × 5 × 5) – (8 × 6)
= (78.50 – 48) cm² = 30.50 cm²

Question 26.
A square park has each side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in Fig. 12.31. Find the area of the remaining part of the park.
Solution:

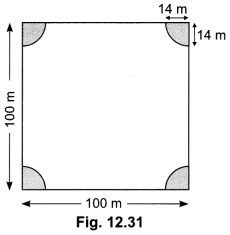
We have,
Area of 4 quadrants of a circle of radius 14 m

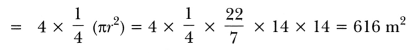
Area of square park having side 100 m long
= (100 × 100) m² = 10,000 m².
Hence, area of the remaining part of the park
= Area of square – Area of 4 quadrants at each corner
= (10,000 – 616) m² = 9384 m²

Question 27.
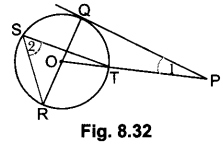
Find the area of the shaded region in Fig. 12.32, where ABCD is a square of side 14 cm each.

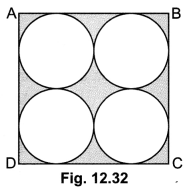
Solution:
Area of square ABCD = 14 × 14 cm² = 196 cm²
Diameter of each circle = \(\frac{14}{2}\) cm = 7 cm
So, radius of each circle = \(\frac{7}{2}\) cm

∴ Area of shaded region = Area of square – Area of 4 circles
= (196 – 154) cm² = 42 cm²

Question 28.
In Fig. 12.33, ABCD is a trapezium of area 24.5 sq. cm. In it, AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π = \(\frac{22}{7}\)
Solution:

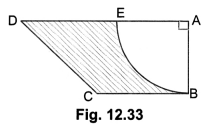
Area of trapezium = 24.5 cm²
\(\frac{1}{2}\)[AD + BC] AB = 24.5
\(\frac{1}{2}\)[10 + 4] × AB = 24.5
AB = 3.5 cm ⇒ r = 3.5 cm
Area of quadrant = \(\frac{1}{4}\)πr²
.025 × \(\frac{22}{7}\) × 3.5 × 3.5 = 9.625 cm²
The area of shaded region = 24.5 – 9.625 = 14.875 cm²

Question 29.
In Fig. 12.34, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
Solution:

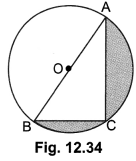
In ΔABC, ∠ACB = 90° (Angle in the semicircle)
∴BC² + AC² = AB²
∴ BC² = AB² – AC²
= 169 – 144 = 25
∴ BC = 5 cm
Area of the shaded region = Area of semicircle – Area of right ΔABC

Question 30.
In Fig. 12.35, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre 0 and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M.
If OP = PQ = 10 cm show that area of shaded region is \(25\left(\sqrt{3}-\frac{\pi}{6}\right)\)cm².
Solution:
Since OP = PQ = QO
⇒ ΔPOQ is an equilateral triangle
∴ ∠POQ = 60°
Area of segment PAQM

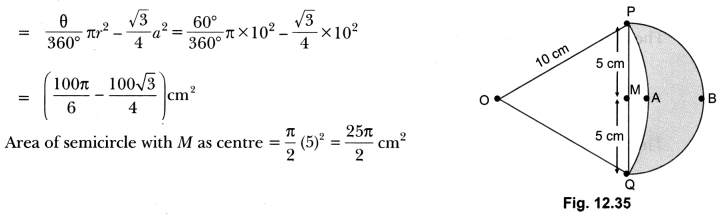
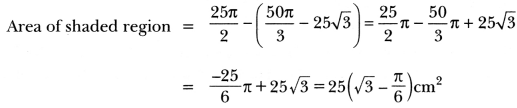
Areas Related to Circles Class 10 Extra Questions Long Answer Type

Question 1.
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn on PQ and QS as diameters is shown in Fig. 12.36. Find the perimeter and area of the shaded region.

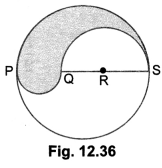
Solution:
We have,
PS = Diameter of a circle of radius 6 cm = 12 cm
∴ PQ = QR = RS = \(\frac{12}{3}\) = 4 cm
Fig. 12.36 QS = QR + RS = (4 + 4) cm = 8 cm
Hence, required perimeter
= Arc of semicircle of radius 6 cm + Arc of semi circle of radius 4 cm + Arc of semi-circle of radius 2 cm
= (π × 6 + π × 4 + π × 2) cm = 12π cm = 12 × = \(\frac{22}{7}\) = \(\frac{264}{7}\) = 37.71 cm.
Required area = Area of semicircle with PS as diameter + Area of semicircle with PQ as diameter – Area of semi-circle with QS as diameter

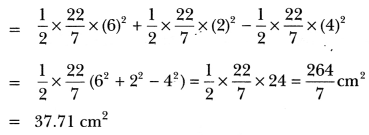
Question 2.
Figure 12.37 depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Solution:

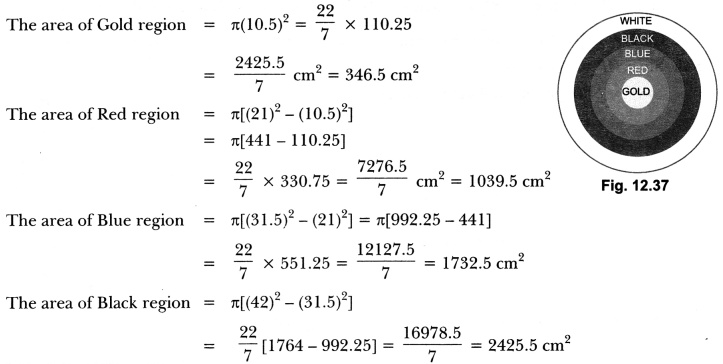
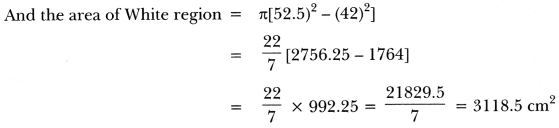
Question 3.
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.
Solution:
In 2 days, the short hand will complete 4 rounds.
Distance moved by its tip = 4 (Circumference of a circle of radius 4 cm)

Question 4.
Fig. 12.38, depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) the distance around the track along its inner edge.
(ii) the area of the track.
Solution:

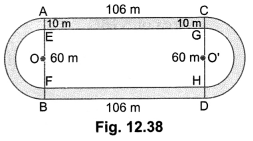
Here, we have
OE = O’G = 30 m
AE = CG = 10 m
OA = O’C = (30 + 10) m = 40 m
AC = EG = FH = BD = 106 m

(i) The distance around the track along its inner edge
= EG + FH + 2 × (circumference of the semicircle of radius OE = 30cm)

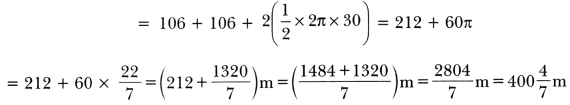
(ii) Area of the track = Area of the shaded region
= Area of rectangle AEGC + Area of rectangle BFHD + 2 (Area of the semicircle of radius 40 m – Area of the semicircle with radius 30 m)

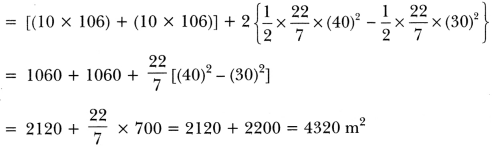
Question 5.
The area of an equilateral triangle ABC is 17320.5 cm. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.39). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)
Solution:

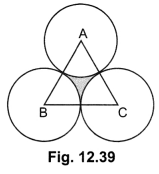
Let each side of the equilateral triangle be x cm. Then,
Area of equilateral triangle ABC = 17320.5 cm (Given)

Question 6.
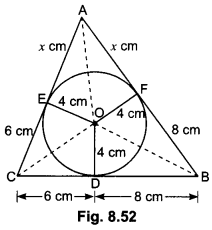
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.40. Find the area of the design.
Solution:
Here, ∆ABC is an equilateral triangle. Let O be the circumcentre of circumcircle.
Radius, r = 32 cm.
Now, area of circle = πr²

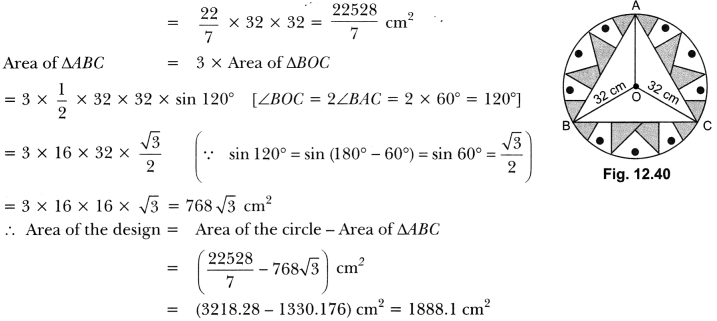
Question 7.
In Fig. 12.41, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Solution:

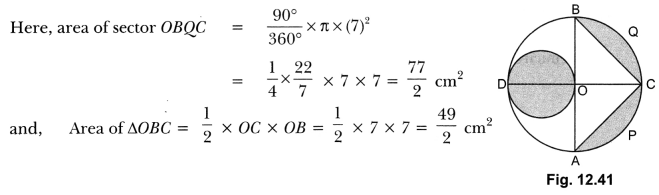
Question 8.
In Fig. 12.42 ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
Solution:
In ∆ABC, we have

Hence, area of the shaded region = Area of the semi-circle BQC – Area of the segment BPC
= (154 – 56)cm² = 98cm²

Question 9.
In Fig 12.43, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use π = 3.14 and √3 = 1.73]

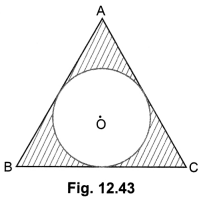
Solution:
Construction:
Join OA, OB and OC
Draw OZ ⊥ BC, OX ⊥ AB and OY ⊥ AC.
Let the radius of the circle be r сm.
Area of ∆ABC = Area of ∆AOB + Area of ∆BOC + Area of ∆AOC


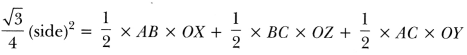
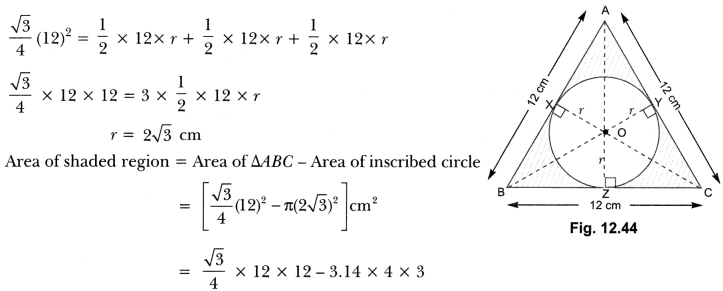
= 1.73 × 3 × 12 – 3.14 × 4 × 3
= 62.28 – 37.68 = 24.6 cm²

Question 10.
In Fig. 12.45, PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [Use π = 3.14]
Solution:

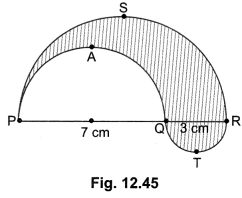
Radius of semicircle PSR = \(\frac{1}{2}\) × 10 cm = 5 cm
Radius of semicircle RTQ = \(\frac{1}{2}\) × 3 cm = 1.5 cm
Radius of semicircle PAQ = \(\frac{1}{2}\) × 7 em = 3.5 cm
Perimeter of shaded region = Circumference of semicircle PSR + Circumference of semicircle RTQ + Circumference of semicircle PAQ.

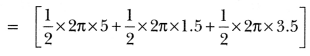
= π[5 + 1.5 + 3.5]= 3.14 × 10 = 31.4cm

Question 11.
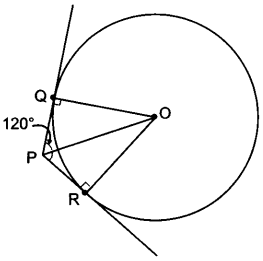
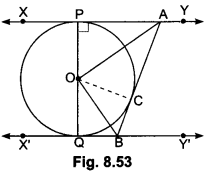
An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 12.46). From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area. (Use π = 3.14 and √3 = 1.73)
Solution:

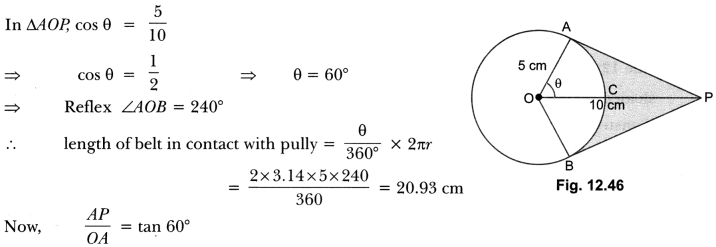
PA = 5√3 cm = BP [Tangents from an external point are equal]

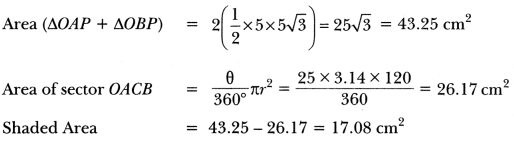
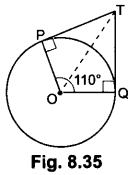
Question 12.
In Fig. 12.47, a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is

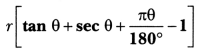
Solution:

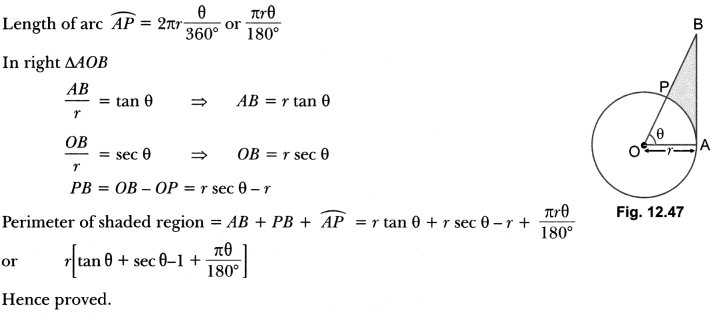
Question 13.
Find the area of the shaded region in Fig. 12.48, where APD, AQB, BRC , CSD are semi-circles of diameter 14 cm, 3.5 cm, 7 cm and 3.5 cm respectively. (Use π = \(\frac{22}{7}\) )
Solution:

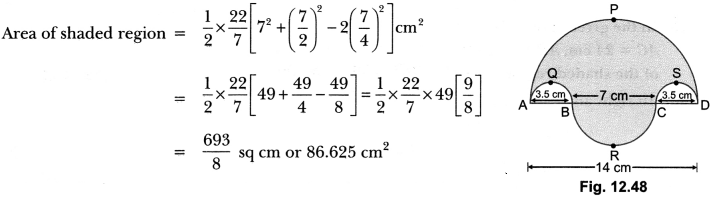
Question 14.
A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the 14 cmcentre of circle. Find the area of major and minor segments of the Fig. 12.48 circle.
Solution:
Area of minor segment
= Area of minor sector having angle 60° at centre – area of equilateral ∆OPQ

Question 15.
In the given figure, ∆ABC is a right-angled triangle in which ∠A is 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region.
Solution:
∵ ABC is right angled triangle

Question 16.
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region.
Solution:
In right angle triangle ABC

Areas Related to Circles Class 10 Extra Questions HOTS

Question 1.
Two circles touch internally. The sum of their areas is 116 ncmo and distance between their centres is 6 cm. Find the radii of the circles.
Solution:

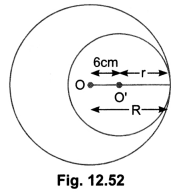
Let R and r be the radii of the circles [Fig. 12.52].
Then, according to question,
⇒ πR² +πr² = 116π
⇒ R² + r² = 116 …..(i)
Distance between the centres = 6 cm
⇒ OO’ = 6 cm
⇒ R – s = 6 …(ii)
Now, (R + r)² + (R – 1)² = 2(R² + m²)
Using the equation (i) and (ii), we get
(R + r)² + 36 = 2 × 116
= (R + r)² = (2 x 116 – 36) = 196
= R + r = 14 …..(iii)
Solving (ii) and (iii), we get R = 10 and r = 4
Hence, radii of the given circles are 10 cm and 4 cm respectively.

Question 2.
A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Solution:
Let the radius of the wheel be r сm.

∴ Diameter = 2r cm = (2 × 35) cm = 70 cm
Hence, the diameter of the wheel is 70 cm.

Question 3.
Find the area of the shaded design of Fig. 12.53, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter (use π = 3.14).

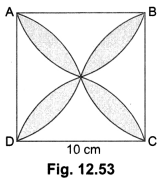
Solution:

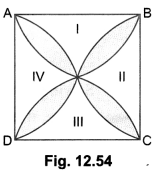
Let us mark the four unshaded regions as I, II, III and IV (Fig. 12.53).
Area of I + Area of III
= Area of ABCD – Areas of two semicircles of radius 5 cm each

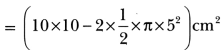
= (100 – 3.14 × 25) cm² = (100 – 78.5) cm² = 21.5 cm²
Similarly, Area of II + Area of IV = 21.5 cm²
So, Area of the shaded design
= Area of ABCD – Area of (I + II + III + IV)
= (100 – 2 × 21.5) cm²
= (100 – 43) cm² = 57 cm²

Question 4.
A copper wire, when bent in the form of a square, encloses an area of 484 cm². If the same wire is bent in the form of a circle, find the area enclosed by it.
Solution:
We have, Area of the square = a² = 484 cm²
∴ Side of the square = √1484 cm = 22 cm
So, Perimeter of the square = 4 (side) = (4 × 22) cm = 88 cm
Let r be the radius of the circle. Then, according to question,
Circumference of the circle = Perimeter of the square

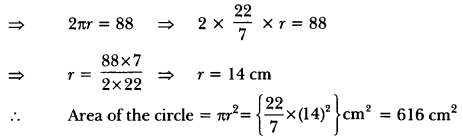
Question 5.
Two circles touch externally. The sum of their areas is 130 r sq. cm and the distance between their centres is 14 cm. Find the radii of the circles.
Solution:

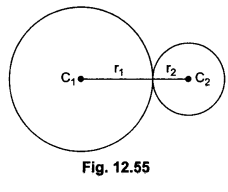
If two circles touch externally, then the distance between their centres is equal to the sum of their radii.
Let the radii of the two circles be r, cm and r² cm respectively [Fig. 12.55).
Let C, and C, be the centres of the given circles. Then,
C₁C₂ = r₁ +r₂
= 14 = r₁ +r₂
[∵ C₁C₂ = 14 cm given]
= r₁ +r₂ = 14
It is given that the sum of the areas of two circles is equal to 130 n cm²

Solving (i) and (iv), we get r₁ = 11 cm and r₂ = 3 cm.
Hence, the radii of the two circles are 11 cm and 3 cm.

Question 6.
In Fig. 12.56, from a rectangular region ABCD with A
AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region. [Use π = 3.14]

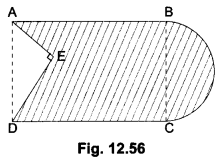
Solution:
Area of shaded region
= Area of rectangle – Area of triangle + Area of semicircle. In right ∆ADE.
AD² = AE² + DE²

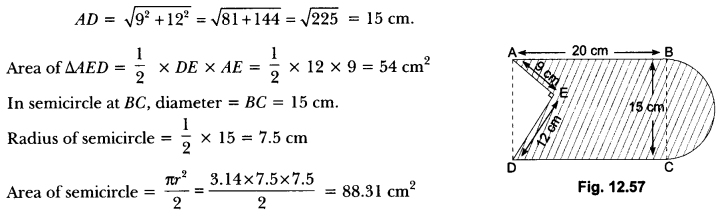
Area of rectangle = AB × BC = 20 × 15 = 300 cm²
Area of shaded region = 300 + 88.31 – 54 = 334.31 cm²

Question 7.
In the given Fig. 12.58, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O’ are centres of the circles. Find the area of shaded region.

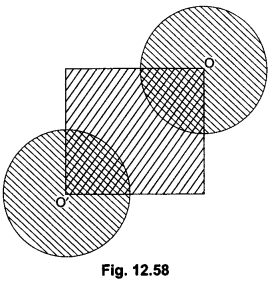
Solution:
Area of shaded region
= Area of square + Area of 2 major sectors having angle 270° at centre

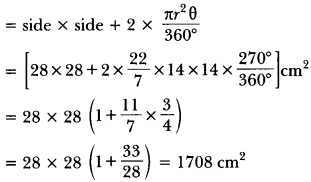
Question 8.
In the given Fig. 12.59, ABCD is a rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
Solution:

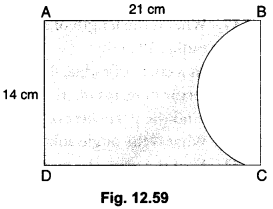
Area of shaded region
Area of shaded region
= Area of rectangle – Area of semicircle
=(l × b) – \(\frac{1}{2}\) × π × r²
= (21 × 14) – \(\frac{1}{2}\) × π × 7 × 7
= 294 – \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7
= 294 – 77 = 217 cm²
Now, perimeter of shaded region = 2l + b + circumference of semicircle i.e.; πr
= 2 × 21 + 14 + \(\frac{22}{7}\) × 7
= 56 + 22 = 78 cm

In this page, we are providing Acids, Bases and Salts Class 10 Extra Questions and Answers Science Chapter 2 pdf download. NCERT Extra Questions for Class 10 Science Chapter 2 Acids, Bases and Salts with Answers will help to score more marks in your CBSE Board Exams.

Class 10 Science Chapter 2 Extra Questions and Answers Acids, Bases and Salts

Extra Questions for Class 10 Science Chapter 2 Acids, Bases and Salts with Answers Solutions

Extra Questions for Class 10 Science Chapter 2 Very Short Answer Type

Question 1.
Write a balanced chemical equation for the reaction between sodium carbonate and hydrochloric acid indicating the physical state of the reactants and products.   [Foreign 2010]
Answer:
Na₂CO₃ (s) + 2HCl (ag) → 2NaCl (aq) + CO₂ (g) + H₂O (l)

Question 2.
During summer season, a milkman usually adds a small amount of baking soda to fresh milk. Give reason.   [CBSE Sample Paper 2009]
Answer:
A milkman adds a very small amount of baking soda so as to prevent spoilage of milk. It leads to change in the pH which does not allow bacteria and enzymes to act and milk does not become sour due to fermentation.

Question 3.
What is the difference between slaked lime and lime water?  [CBSE 2010]
Answer:
A suspension of Ca(OH)₂ in water is called slaked lime. Water containing traces of Ca(OH)₂ is called lime water.

Question 4.
Which acid is present in sour milk or curd?
Answer:
Lactic acid.

Question 5.
Why is potassium iodide added into common salt to use it as table salt?
Answer:
The iodide present in the salt prevents thyroid disorders.

Question 6.
What are the pH values of distilled water and common salt solution?  [CBSE 2010]
Answer:
Both are neutral and have pH close to 7.

Question 7.
A dry pellet of a common base B, when kept in open absorbs moisture and turns sticky. The compound is also a by-product of chloralkali process. Identify B. What type of reaction occurs when B is treated with an acidic oxide? Write a balanced chemical equation for one such solution.  [NCERT Exemplar]
Answer:
Dry pellets of sodium hydroxide absorb moisture and turn sticky when kept in open which is also a by-product of chloralkali process.

When sodium hydroxide is treated with an acidic oxide it produces salt and water.

Question 8.
Which bases are called alkalies? Give an example of an alkali. [CBSE 2009, 2010]
Answer:
Soluble bases are called alkalies. For example, sodium hydroxide (NaOH).

Question 9.
A knife, which is used to cut a fruit, was immediately dipped into water containing drops of blue litmus solution. If the colour of the solution is changed to red, what inference can be drawn about the nature of the fruit and why? [CBSE 2011]
Answer:
Since the colour of the blue litmus has changed to red, this means that the fruit juice is acidic in nature.

Question 10.
How do H⁺ ions exist in water?
Answer:
H⁺ ions in water combine with water (H₂O) molecules and exist as H₃O⁺ ion, called hydronium ion.

Question 11.
What should be done as remedy if stung by leaves of nettle plant in the wild?
Answer:
The area should be rubbed with the leaf of dock plant.

Question 12.
What happens when nitric acid is added to egg shell?  [NCERT Exemplar]
Answer:
Egg shell is made of calcium carbonate. When nitric acid is added to egg shell calcium nitrate, carbon dioxide and water are formed.
CaCO₃ + 2HNO₃ → Ca(NO₃)₂ + CO₂ + H₂O

Question 13.
What is the concentration of H⁺ ion in pure water?
Answer:
10^-7

Question 14.
Which one of these has a higher concentration of H⁺ ions? 1 M HCl or 1 M CH₃COOH.   [CBSE 2009]
Answer:
1 M HCl has higher concentration of H⁺ ions.

Question 15.
Name an example of olfactory indicators.
Answer:
Vanilla.

Question 16.
Name the chemical substance present in thick white and yellowish clouds present in the atmosphere of Venus.
Answer:
Sulphuric acid.

Question 17.
What is acid rain?
Answer:
Rainwater having pH less than 5.6, is called acid rain.

Question 18.
Name the hardest substance in the body.
Answer:
Tooth enamel (Calcium phosphate).

Question 19.
The pH of three solutions A, B and C are 4, 9 and 6 respectively. Arrange them in increasing order of acidic strength. [CBSE 2010]
Answer:
The increasing order of acidic strength is : B < C < A.

Question 20.
Name the chemist who had given the pH scale.
Answer:
S.P.L. Sorensen (1909).

Question 21.
Name the acid present in tomato.
Answer:
Oxalic acid.

Question 22.
Acidic and basic solutions in water conduct electricity. Why?
Answer:
Because they produce hydrogen and hydroxide ions respectively.

Question 23.
What would be the colour of litmus in a solution of sodium carbonate?   [CBSE 2009]
Answer:
Red litmus will change to blue in sodium carbonate solution.

Question 24.
The pH of a sample of vegetable soup was found to be 6.5. How is this soup likely to taste?
Answer:
The taste will be slightly sour as it is weakly acidic.

Question 25.
Name the chemical substance which is used in the manufacture of soap as well as used as a preservative in pickles.
Answer:
Sodium chloride (NaCl).

Question 26.
There are two jars A and B containing food materials. Food in jar ‘A’ is pickled with acetic acid while ‘B’ is not. Food of which of jar will stale first? Explain. Name two synthetic indicators which are used to test acids and bases.
Answer:
Food in jar ‘B’ will stale first because it will undergo oxidation and will also be attacked by microorganisms.
Synthetic indicators: Phenolphthalein, methyl orange.

Question 27.
What is the chemical formula of soda ash?
Answer:
Na₂CO₃

Question 28.
Name the substance used for disinfecting drinking water supply.
Answer:
Bleaching powder.

Question 29.
Name a chemical substance which can be used to detect the presence of moisture in a liquid.
Answer:
Anhydrous copper sulphate.

Question 30.
What is meant by water of crystallisation?
Answer:
Water of crystallisation is the fixed number of water molecules chemically attached to each formula unit of a salt in its crystalline form.

Question 31.
Which one is a stronger acid, with pH = 5 or with pH = 2?
Answer:
The acid with pH = 2 is a stronger acid.

Question 32.
Fresh milk has a pH of 6. When it changes into curd (yogurt), will its pH value increases or decrease? Why?
Answer:
Its pH will decrease because curd (yogurt) is sour in taste due to presence of acid in it.

Extra Questions for Class 10 Science Chapter 2 Short Answer Type I

Question 1.
How would you distinguish between baking powder and washing soda by heating?   [NCERT Exemplar]
Answer:
Baking soda (NaHCO₃) gives carbon dioxide and water vapour on heating at very low temperature. The gas so formed turns lime water milky, which confirms the presence of carbon dioxide gas.

When washing soda (Na₂CO₃) is heated it does not produce carbon dioxide even at high temperatures, but gives off its water of crystallisation to become anhydrous salt.

Question 2.
A sulphate salt of Group 2 element of the Periodic Table is a white, soft substance, which can be moulded into different shapes by making its dough. When this compound is left in the open for some time, it becomes a solid mass and cannot be used for moulding purposes. Identify the sulphate salt and why does it show such a behaviour? Give the reaction involved.   [NCERT Exemplar]
Answer:
Calcium belongs to group 2. Calcium sulphate is a white soft substance. It is known as Plaster of Paris, which can be moulded into different shapes by making its dough.

When Plaster of Paris is left for some time in the open, it turns into a solid mass because of reaction with moisture present in the atmosphere. The solid mass so formed is known as gypsum and cannot be further used for moulding.

The above said group 2 element is calcium sulpahte.

Question 3.
Name the acid present in ant sting and give its chemical formula. Also give the common method to get relief from the discomfort caused by the ant sting.   [NCERT Exemplar]
Answer:
The acid present in ant sting: Methanoic acid
Chemical Formula of methanoic acid: HCOOH
Method to get relief from the discomfort caused by the ant sting: Rubbing baking soda over the area of ant sting.
Explanation: Rubbing baking soda (a base) over ant sting neutralises the methanoic acid present in the ant sting and gives relief from pain.

Question 4.
List two differences between acids and bases on the basis of chemical properties.
Answer:
(i) Dilute acids like HCl and H₂SO₄ evolve H₂ gas on reacting with metals like Zn, Mg and Ca, etc. and dilute bases do not evolve hydrogen gas.
(ii) Acids react with oxides of metals while bases react with oxides of non-metals.

Question 5.
List four main differences between acids and bases.
Answer:

Question 6.
Mention the terms defined by the following sentences:
(a) A soluble base
(b) The insoluble solid formed when two solution are mixed together.
Answer:
(a) Alkali
(b) Precipitate.

Question 7.
Name the product formed in each case when:
(а) hydrochloric acid reacts with caustic soda.
(b) granulated zinc reacts with caustic soda.
Answer:
(a) The product formed is a mixture of sodium chloride and water.
NaOH (ag) + HCl (ag) → NaCl (ag) + H₂O

(b) The product formed is a mixture of sodium zincate and hydrogen gas.
Zn (s) + 2NaOH (ag) → Na₂ZnO₂ (ag) + H₂(g)

Question 8.
Explain why sodium hydroxide solution cannot be kept in aluminium containers? Write equation for the reaction that may take place for the same.
Answer:
Sodium hydroxide solution reacts with aluminium to form sodium metaaluminate and hydrogen is evolved. Therefore, it cannot be kept in a container made of aluminium.

Question 9.
How can you obtain the following gases by using dilute acid and one other substance?
(а) hydrogen
(b) carbon dioxide.
Answer:
(a) Fe + H₂SO₄(dil.) → FeSO₄ + H₂(g)
Mg + 2HCl(dil.) → MgCl₂ + H₂(g)

(b) Na₂CO₃ + 2HCl(dil.) → 2NaCl + H₂O + CO₂(g)
NaHCO₃ + HCl(dil.) → NaCl + H₂O + CO₂(g)

Question 10.
A solution of HCl is taken in a beaker and an electric circuit with a bulb is set up with the solution in series. What happens to the bulb and why?
Answer:
The bulb will start glowing. Glowing of the bulb indicates that there is a flow of electric current through the solution. Electric current is carried through the solution by ions.

Since the cation present in acids is H⁺, this suggests that acids produce hydrogen ions, H⁺(ag), in solution, which are responsible for carrying current through the solution.

Question 11.
If 280 g of washing soda crystals are left in dry air for some time, a loss of weight of 162 g occurs. How can you account for this?
Answer:
Washing soda (Na₂CO₃. 10H₂O) is an efflorescent substance (if exposed to air, it loses most of its water of crystallisation). 280 g of washing soda lose 162 g of its water of crystallisation.

Question 12.
A sample of bleaching powder was kept in an air tight container. After a month, it lost some of its chlorine content. How will you account for it?
Answer:
Bleaching powder if kept even in an air tight container, will slowly decompose on its own and form calcium chlorate and calcium chloride. The reaction is called auto oxidation. This will result in decrease in its chlorine contents.

Question 13.
A compound which is prepared from gypsum has the property of hardening when mixed with proper quantity of water. Identify the compound. Write chemical equation to prepare the compound. Mention one important use of the compound.
Answer:
The compound is Plaster of Paris (CaSO₄. \(\frac { 1 }{ 2 }\) H₂O). It is formed from gypsum (CaSO₄ . \(\frac { 1 }{ 2 }\) H₂O) upon heating to a temperature of 373 K. It changes back to gypsum on adding water. Plaster of Paris is used for setting fractured bones.

Question 14.
A white powder is added while baking breads and cakes to make them soft and fluffy. Write the name of the powder. Name its main ingredients. Explain the function of each ingredient. Write the chemical reaction taking place when the powder is heated during baking.   [CBSE 2012, 2013]
Answer:
The white powder is known as baking powder. The main ingredients are baking soda (NaHCO₃) and tartaric acid (C₄H₆O₆).

Question 15.
Explain giving reasons:
(i) Tartaric acid is a component of baking powder used in making cakes.
(ii) Gypsum (CaSO₄. 2H₂O) is used in the manufacture of cement.
Answer:
(i) Role of tartaric acid in baking powder (mixture of tartaric acid and sodium hydrogencarbonate) is to neutralise sodium carbonate formed upon heating sodium hydrogencarbonate.

In case it is not done, cake will be better and sodium carbonate will also have injurious side effects.

(ii) The role of gypsum (CaSO₄.2H₂O) in the manufacture of cement is to slow down the process of setting of cement.

Extra Questions for Class 10 Science Chapter 2 Short Answer Type II

Question 1.
What will be the action of the following substances on litmus paper?
Dry HCl gas, moistened NH₃ gas, lemon juice, carbonated soft drink, curd, soap solution.  [NCERT Exemplar]
Answer:
Dry HCl gas: No action
Moistened NH₃ gas: Turns red litmus blue.
Lemon juice: Turns blue litmus red.
Carbonated soft drink: Turns blue litmus red.
Curd: Turns blue litmus red.
Soap solution: Turns red litmus blue.

Explanation:

• Dry HCl gas does not liberate hydrogen ion, hence no action takes place with litmus paper.
• NH₃ gas forms ammonium hydroxide with water which turns red litmus paper blue.
• Lemon juice is citric acid, so it turns blue litmus paper red.
• Carbonate soft drink contains carbon dioxide dissolved in water. Carbon dioxide forms carbonic acid with water; which turns blue litmus paper red.
• Curd contains lactic acid and hence turns blue litmus paper red.
• Soap solution is basic in nature hence it turns red litmus paper blue.

Question 2.
When zinc metal is treated with a dilute solution of a strong acid, a gas is evolved, which is utilised in the hydrogenation of oil. Name the gas evolved. Write the chemical equation of the reaction involved and also write a test to detect the gas formed.   [NCERT Exemplar]
Answer:
Zinc metal gives hydrogen gas when it is treated with dilute sulphuric acid. Hydrogen gas is utilised in hydrogenation of oil.
Therefore, the gas evolved is hydrogen.

Test for hydrogen gas: When a burning candle is brought near hydrogen gas, it bums with a pop sound which confirms the presence of hydrogen gas.

Question 3.
(i) Identify the compound of calcium which is a yellowish powder and is used for disinfecting drinking water. Write its chemical name and formulae.
(ii) Write the balanced chemical equation of chlor-alkali process.   [CBSE 2012, 2014]
Answer:
(i) The yellowish white solid is known as bleaching powder. Chemically, it is calcium oxychloride or calcium hypochlorite. Its chemical formula is CaOCl₂.

(ii) Chemical equation for chlor-alkali process is

Question 4.
Explain with suitable reason
(a) Ferric chloride is stored in air tight bottles.
(b) On exposure to atmosphere, Glaublar’s salt loses weight while quicklime gains weight.
(c) Common salt (containing traces of magnesium chloride) becomes sticky during the monsoons.
Answer:
(a) Because ferric chloride is deliquescent in nature.
(b) Glaubar’s salt is efflorescent and loses water of crystallisation whereas quick lime is hygroscopic in nature and absorbs moisture from the air.
(c) This is because magnesium chloride is deliquescent and absorbs moisture from the atmospheric air and becomes moist.

Question 5.
(a) A solution has a pH of 7. Explain how you would
(i) increases its pH
(ii) decrease its pH
(b) If a solution changes the colour of litmus from red to blue, what can you say about its pH?
(c) What can you say about the pH of a solution that liberates CO₂ from sodium carbonate?
Answer:
(a) (i) By adding some alkali like NaOH
(ii) By adding some acid like HCl

(b) Since the solution changes the colour of litmus from red to blue it is alkaline and hence it has pH > 7.

(c) Since the solution liberates CO₂ from sodium carbonate, it should be acidic and has pH < 7.

Question 6.
A compound which is prepared from gypsum has the property of hardening when mixed with proper quantity of water.
(i) Identify the compound.
(ii) Write the chemical equation for its preparation.
(iii) Mention one important use of this compound.
Answer:
(i) Plaster of Paris

(iii) It is used for plastering fractured bones.

Question 7.
Write any three chemical properties of acids.
Answer:
(i) They react with metals to give out hydrogen gas, for example,

(ii) They react with bases to form salt and water, for example,

(iii) They react with metal carbonates to liberate carbon dioxide gas.

Question 8.
Classify the solutions of the following as acids, bases and salts:
Ammonium hydroxide, barium chloride, sodium chloride, sodium hydroxide, sulphuric acid and nitric acid.
Answer:

Question 9.
You are given two solutions A and B. The pH of solution A is 6 and pH of solution B is 8.
(i) Which solution is acidic and which is basic?
(ii) Which solution has more H+ ion concentration?
(iii) Why is HCl a stronger acid than acetic acid?   [CBSE 2011]
Answer:
(i) The solution with pH 6 is acidic while the solution with pH 8 is basic.
(ii) The solution with pH 6 has more H⁺ ion concentration.
(iii) HCl is a stronger acid than CH₃COOH since its degree of dissociation (α) is more or it releases more H+ ions in solution than acetic acid.

Question 10.
What is tooth enamel chemically? State the conditions when it starts corroding. What happens when food particles left in the mouth after eating degrade? Why do doctors suggest use of powder/tooth paste to prevent tooth decay? [CBSE 20011, 2014]
Answer:
(i) The tooth enamel is chemically calcium phosphate with the formula Ca₃(PO₄)₂. It is quite hard.
(ii) The enamel starts corroding when the pH inside our mouth falls below 5.5 because the saliva present in the mouth becomes acidic.
(iii) The bacteria present in the mouth breakdown the food particles into acids which damage our teeth by corroding them.
(iv) The contents of the tooth paste are of basic nature. They neutralise the excess acid present. As a result, the corrosion of enamel and decay of teeth are checked.

Question 11.
(a) Write the name given to bases that are highly soluble in water. Give an example.
(b) How is tooth decay related to pH? How can it be prevented?
(c) Why does bee sting cause pain and irritation? Rubbing of baking soda on the sting area gives relief. How?
Answer:
(a) Alkali, for example, NaOH (Sodium hydroxide).

(b) Lower the pH, more will be tooth decay. Acid formed in the mouth reacts with enamel which is made up of [Ca₃(PO₄)₂] and causes tooth decay.
It can be prevented by brushing our teeth after every meal.

(c) A bee injects formic acid into the skin when it stings which causes pain and irritation. Sodium hydrogencarbonate (baking soda) neutralises formic acid giving relief.

Question 12.
Mention the colour changes observed when the following indicators are added to acids:
(i) Alkaline phenolphthalein solution
(ii) Methyl orange solution
(iii) Neutral litmus solution
Answer:
(i) It gets decolourised
(ii) It turns red or pink
(iii) It turns red.

Question 13.
Choosing only substances from the list given in the box below, write equations for the reactions which you would use in the laboratory to obtain:
(a) Sodium sulphate
(b) Iron (II) sulphate
(c) Zinc carbonate.
Dilute sulphuric acid, copper, iron, copper carbonate, sodium, zinc, sodium carbonate
Answer:
(a) Sodium sulphate
Na₂CO₃ + H₂SO₄ (dil.) → Na₂SO₄ + H₂O + CO₂ (g)

(b) Iron (II) sulphate
Pe + H₂SO₄ (dil.) → FeSO₄ + H₂ (g)

(c) Zinc carbonate
Zn + CuCO₃ → ZnCO₃ + Cu

Question 14.
What is dilution? What precaution should be taken during dilution of a strong acid like sulphuric acid?
Answer:
Dilution is a process in which concentration of a substance decreases by addition of a solvent. Care must be taken while mixing concentrated sulphuric acid with water as the process is a highly exothermic one. The acid must always be added slowly to water with constant stirring. If water is added to a concentrated acid, the heat generated may cause the mixture to splash out and cause burns. The glass container may also break due to excessive local heating.

Question 15.
Write balanced equations to satisfy each statement:
(a) Acid + Chloride → Salt + Hydrochloric acid gas
(b) Acid + Carbonate → Salt + Water + Carbon dioxide
(c) Acid + Sulphite → Salt + Water + Sulphur dioxide
Answer:
(a) H₂SO₄ + NaCl → NaHSO₄ + HCl (g)
(b) 2HCl + Na₂CO₃ → 2NaCl + H₂O + CO₂ (g)
(c) 2HCl + CaSO₃ → CaCl₂ + H₂O + SO₂ (g)

Extra Questions for Class 10 Science Chapter 2 Long Answer Type

Question 1.
What are strong and weak acids? In the following list of acids, separate strong acids from weak acids.  [NCERT Exemplar]
Hydrochloric acid, citric acid, acetic acid, nitric acid, formic acid, sulphuric acid.
Answer:
Strong acid: Strong acids ionise completely in their aqueous solutions to produce a large number of hydrogen ions. Mineral acids are generally strong acids.

Weak acid: Weak acids do not ionise completely in their aqueous solution. Organic acids are generally weak acids.

Strong acid: Hydrochloric acid, nitric acid, sulphuric acid
Weak acid: Citric acid, acetic acid, formic acid

Question 2.
(i) Explain, why is hydrochloric acid a strong acid and acetic acid, a weak acid? How can it be verified?
(ii) Explain, why aqueous solution of an acid conducts electricity?
(iii) You have four solutions A, B, C and D. The pH of solution A is 6, B is 9, C is 12 and D is 7.
(a) Identify the most acidic and most basic solutions.
(b) Arrange the above four solutions in the increasing order of H+ ion concentration.
(c) State the change in colour of pH paper on dipping in solution C and D.   [CBSE 2012, 2013]
Answer:
(i) Hydrochloric acid (HCl) is a stronger acid than acetic acid (CH₃COOH) because it dissociates completely into H⁺ and Cl^– ions in aqueous solution. In order to verify this, add a few drops of universal indicator solution in the test tubes containing the acids. It acquires red colour in hydrochloric acid and yellow in acetic acid which confirms that hydrochloric acid is a stronger acid.

(ii) An aqueous solution of an acid releases ions in aqueous solutions. These ions conduct electricity.

(iii) (a) Most acidic is A (pH = 6) and most basic is C (pH = 12).
(b) The increasing order of H⁺ ion concentration is : C < B < D < A.
(c) The pH paper acquires dark purple colour in solution C and green in solution D.

Question 3.
Fill the missing data in the following table:

Answer:

Question 4.
(a) Explain how antacids give relief from acidity. Write the name of one such antacid.
(b) Fresh milk has a pH of 6. How does the pH change as it turns to curd? Explain your answer.
(c) A milkman adds a very small amount of baking soda to fresh milk. Why does this milk take a longer time to set as curd?
(d) Mention the nature of toothpastes. How do they prevent tooth decay?
Answer:
(a) Our stomach produces hydrochloric acid that helps in digestion of food. During indigestion, our stomach produces excess acid. Antacids neutralise the excess of acid produced and gives relief from hyperacidity. Milk of magnesia (magnesium hydroxide) is one of such antacid.

(b) pH will decrease as it turns to curd because curd is acidic due to the presence of lactic acid.

(c) It takes longer time to set as curd as the presence of baking soda (sodium hydrogen carbonate) makes the milk basic and it does not allow it to become acidic easily.

(d) Toothpastes are basic in nature. They neutralise the acid formed in mouth which causes tooth decay.

Question 5.
(a) Explain the following chemical properties of acids with the help of balanced chemical equations only.
(i) when an acid reacts with a metal carbonate
(ii) when an acid reacts with a metal bicarbonate
(iii) when an acid reacts with a metal oxide.
(b) You are given three solutions A, B and C with pH values 2, 10 and 13 respectively. Write which solution has more hydrogen ion concentration among the three and state the nature ‘acidic or basic’ of each solution.
Answer:
(a) (i) CaCO₃ + 2HCl → CaCl₂ + H₂O + CO₂
(ii) NaHCO₃ + HCl → NaCl + H₂O + CO₂
(iii) Al₂O₃ + 6HCl → 2AlCl₃ + 3H₂O

(b) ‘A’ has maximum [H₃O⁺] equal 10^-2 mol L^-1
‘A’ acidic whereas B and C are basic in nature.

Question 6.
Complete the following reaction:
(i) 2NaCl (aq) + 2H₂O(l) →
(ii) Ca(OH)₂ + Cl₂ →
(iii) NaCl + H₂O + CO₂ + NH₃ →
(iv)
(v) Na₂CO₃ + 10H₂O
Answer:
(i) 2NaCl(aq) + 2H₂O(l) → 2NaOH(aq) + Cl₂(g) + H₂(g)
(ii) Ca(OH)₂ + Cl₂ → CaOCl₂ + H₂O

Acids Bases and Salts HOTS Questions With Answers

Question 1.
A student prepared solutions of (i) an acid and (ii) a base in two separate beakers. She forgot to label the solutions and litmus paper was not available in the laboratory. Since both the solutions were colourless, how would she distinguish between the two?  [NCERT Exemplar]
Answer:
While answering this question, we need to make certain assumptions. Let us assume that laboratory has all the necessary items but no litmus paper. We can use phenolphthalein to check which of the beakers contains acid and which one contains a base. Apart from that, we can also use other natural indicators; like China rose or turmeric.

Question 2.
Salt A commonly used in bakery products on heating gets converted into another salt B which itself is used for removal of hardness of water and a gas C is evolved. The gas C when passed through lime water, turns it milky. Identify A, B and C.  [NCERT Exemplar]
Answer:
Baking powder which is a salt used in bakery products. It give sodium carbonate and carbon dioxide gas on heating. Sodium carbonate is used to remove hardness of water. Carbon dioxide turns lime water milky.

Therefore,

• Salt A, which is sodium bicarbonate and used as baking powder.
• Salt B is sodium carbonate, which is used to remove hardness of water.
• The C is carbon dioxicje gas which turns lime water milky.

Question 3.
In one of the industrial processes used for manufacture of sodium hydroxide, a gas X is formed as by product. The gas X reacts with lime water to give a compound Y which is used as bleaching agent in chemical industry. Identify X and Y giving the chemical equation of the reactions involved.   [NCERT Exemplar]
Answer:
Sodium chloride is used in the manufacture of sodium hydroxide by the Chlor-Alkali process. In this process chlorine and hydrogen gas are formed as by products along with sodium hydroxide. Chlorine gas reacts with lime water to produce bleaching power which is used as bleaching agent in chemical industries.

Therefore,

• The gas ‘X’ is chlorine.
• Compound Y is calcium oxychloride which is commonly known as bleaching powder and used as bleaching agent in chemical industries.

Question 4.
In the following schematic diagram for the preparation of hydrogen gas as shown in Figure. What would happen if following changes are made?   [NCERT Exemplar]
Answer:

(a) In place of zinc granules, same amount of zinc dust is taken in the test tube.
(b) Instead of dilute sulphuric acid, dilute hydrochloric acid is taken.
(c) In place of zinc, copper turnings are taken.
(d) Sodium hydroxide is taken in place of dilute sulphuric acid and the tube is heated.
Answer:
(a) When zinc dust is taken instead of zinc granules to react with sulphuric acid, hydrogen gas is formed. But the rate of reaction increases in the case of zinc dust compared to zinc granules, because of increased surface area of zinc dust which increases the rate of reaction.

Thus, when zinc dust is used in the place of zinc granules, hydrogen gas is produced at a faster rate.

(b) Zinc granules give hydrogen gas; along with zinc chloride; when they react with hydrochloric acid.

Thus, when hydrochloric acid is used in place of sulphuric acid, zinc chloride is formed instead of zinc sulphate; along with hydrogen gas and the reaction takes place at the same rate.

(c) Copper does not react with dilute acids under normal conditions because copper lies at lower position in the reactivity series and does not displace hydrogen from dilute acids.
Thus, if copper turnings are taken in place of zinc granules, no reaction will take place.

(d) If sodium hydroxide is taken in place of dilute sulphuric acid and the tube is heated, sodium zincate is formed along with hydrogen gas. Heating the test tube will increase the rate of formation of hydrogen gas as heating the reaction mixture increases the rate of reaction.

Question 5.
Identify the compound X on the basis of the reactions given below. Also, write the name and chemical formulae of A, B and C.   [NCERT Exemplar]
Answer:

Answer:

Therefore,

• Compound “X’ is sodium hydroxide (NaOH).
• Compound ‘A’ is zinc sulphate (ZnSO₄).
• Compound ‘B’ is sodium chloride (NaCl).
• Compound ‘C’ is sodium acetate (CH₃COONa).

Question 6.
A metal carbonate X on reacting with an acid gives a gas which when passed through a solution Y gives the carbonate back. On the other hand, a gas G that is obtained at the anode during electrolysis of brine is passed on dry Y, it gives a compound Z, used for disinfecting drinking water. Identity X, Y, G and Z.   [NCERT Exemplar]
Answer:
Calcium carbonate gives carbon dioxide gas when it reacts with hydrochloric acid.

Carbon dioxide turns lime water milky when passed through it because of formation of calcium carbonate. When carbon dioxide; so formed; is passed through lime water, it turns milky because of the formation of calcium carbonate.

On electrolysis of brine, chlorine gas is produced at the anode. Therefore G is Cl₂.
Bleaching powder is used in disinfecting drinking water.
Therefore Z can be CaOCl₂.
When chlorine is passed through dry calcium hydroxide [Ca(OH)₂], bleaching powder CaOCl₂ is formed.

Therefore, Y is calcium hydroxide, Ca(OH)₂.
Since Y reacts with a gas to give a carbonate, the gas is CO₂ and the carbonate is CaCO₃.

Therefore, the metal carbonate X is calcium carbonate, CaCO₃.
Therefore,

• Metal carbonate ‘X’ is calcium carbonate.
• Solution ‘Y is lime water (Calcium hydroxide).
• Gas ‘G’ is chlorine gas.
• Dry Y’ is dry calcium hydroxide (dry slaked lime).
• Compound ‘Z’ is bleaching powder (Calcium oxychloride).

Question 7.
A substance X used as an antacid reacts with hydrochloric acid to produce a gas Y which is used in extinguishers.
(а) Name the substances X and Y.
(b) Write a balanced equation of the reaction between X and hydrochloric acid.   [CBSE 2011]
Answer:
(a) Substance X is sodium hydrogencarbonate (X) and the gas evolved Y is carbon dioxide.
(b)

Question 8.
You are provided with the following materials in your laboratory:
Answer:
Hydrochloric acid (HCl), sulphuric acid, (H₂SO₄), nitric acid (HNO₃), acetic acid (CH₃COOH), sodium hydroxide (NaOH), potassium hydroxide (KOH), calcium hydroxide [Ca(OH)₂], magnesium hydroxide [Mg(OH)₃] and ammonium hydroxide (NH₄OH).
If we test each of the above solutions one by one with a drop of the following indicators, what colour change will you observe?
Red litmus, blue litmus, phenophthalein, methyl orange.
Answer:
Acidic substances: HCl, H₂SO₄, HNO₃, CH₃COOH
They will turn blue litmus red and methyl orange red. There will be no effect on red litmus and phenolphthalein.

Basic substances: NaOH, KOH, Ca(OH)₂, Mg(OH)₂, NH₄OH. They will turn red litmus blue and phenolphthalein pink. There will be no effect on blue litmus and methyl orange.

Question 9.
The crystals of a compound A on keeping in air get converted into a white powder. Its solution in water gives blue colour with red litmus. It is used to remove permanent hardness from water.
(a) Identify the substance. Write chemical formula for its crystalline form.
(b) From the given information, identify the nature of the substance.
(c) Write two more uses of the substance.   [CBSE 2013]
Answer:
(a) The substance is washing soda. Its chemical formula is Na₂CO₃.10H₂O.
(b) Since the aqueous solution of the substance in water turns red litmus blue, it is of basic nature.
(c) (i) It is used in laundry for washing clothes.
(ii) It is used in the manufacture of glass, paper and chemicals like caustic soda (NaOH), and borax (Na₂B₄O₇), etc.

Question 10.
A substance X is used as a building material and is insoluble in water. When reacted with dilute HCl, it produces a gas which turns lime water milky. Predict the substance. Write the chemical equations evolved.
Answer:
The substance is probably calcium carbonate (CaCO₃), also called lime stone or marble. It is used as a building material. On reacting with dilute HCl, it evolves CO₂ gas which turns lime water milky.

Question 11.
When electricity is passed through a common salt solution, sodium hydroxide is produced along with the liberation of two gases ‘X’ and T. The gas ‘X’ burns with a pop sound whereas T is used for disinfecting drinking water.  [CBSE 2011]
(i) Identify X and Y.
(ii) Give the chemical equation for the reaction stated above.
(iii) State the reaction of Y with dry slaked lime.
Answer:
(i) The gas X’ is H₂ and gas ‘Y’ is Cl₂.
(ii) The chemical equation for the reaction is:

(iii) Cl₂ reacts with slaked lime to form bleaching powder.
Ca(OH)₂ + Cl₂ → CaOCl₂ + H₂O

Extra Questions for Class 10 Science Chapter 2 Value Based

Question 1.
Aman is fond of eating fast foods and chat. He was suffering from a stomach pain and indigestion for a number of days. Doctor advised him to take antacid tablet after each meal and avoid spicy and junk food. He followed the advice and was cured rapidly.
(i) What is an antacid?
(ii) How are antacid tablets helpful in such indigestion? Justify by the relevant chemical reaction.
(iii) Mention the values exhibited by Aman and the doctor.
Answer:
(i) Antacid is a substance which can neutralise acidity in the stomach.
(ii) The antacid tablets or gels contain base like NaHCO₃ or Mg(OH)₂ which neutralise the effect of excess HCl released in the stomach as
NaHCO₃ + HCl → NaCl + H₂O + CO₂
(iii) Knowledge of Chemistry, caring.

Question 2.
Ayush has cold drinks, chocolates and sweets every day. His teeth were getting damaged. His science teacher asked him to brush his teeth after every meal as well as after eating sweets.
(i) How do the teeth get damaged due to eating chocolates and sweets?
(ii) Brushing of teeth is helpful and prevent tooth decay. Justify.
(iii) Mention the values exhibited by the science teacher.
Answer:
(i) On eating sweets/chocolates the pH of mouth becomes less than 5.5, so tooth enamel gets corroded and tooth decay starts.
(ii) Using toothpaste, which is basic in nature can neutralise the excess acid formed in the mouth and prevent tooth decay.
(iii) Caring, helpful nature, knowledge of Chemistry.

Question 3.
Mohan and Priyanka were playing in the garden. Priyanka was stung by a bee and started crying and returned home. Her mother immediately observed the affected area and applied a thin coating of toothpaste as first aid, then took her to the nearest doctor.
(i) Why did Priyanka cry?
(ii) Name the chemical substance present in bee sting.
(iii) How is toothpaste effective in such incident?
(iv) Mention the values exhibited by Priyanka’s mother.
Answer:
(i) Priyanka cried because the bee injected an acid while stinging which caused pain and irritation.
(ii) Formic acid or Methanoic acid (HCOOH)
(iii) Toothpaste is basic in nature so it neutralise the effect of formic acid and gives relief.
(iv) Knowledge of Chemistry, caring nature.

Question 4.
Manshi is a student of class X in a city school. There was a tall tree at the edge of the garden having a large honeycomb attached to it. Some students were playing cricket in the school playground. Suddenly the cricket ball hit the honeycomb due to which a large number of honey-bees started flying here and there. Manshi was stung on her face by a honey-bee. The sting was so painful that Manshi started crying. One of her classmates Shanti quickly got some baking soda and made a paste of it with water. Then she applied the paste on the stung area of the face. On rubbing baking soda solution, Manshi felt a lot of relief from the pain.
(a) What kind of liquid is injected into the skin when honey-bee strings?
(b) Why did rubbing baking soda solution on the stung area of skin give relief from pain?
(c) What type of chemical reaction takes place when baking soda solution is rubbed on the area stung by honey-bee?
(d) What values are exhibited by Shanti and the classmates?
Answer:
(а) Honey-bee sting injects an acidic liquid into the skin.

(b) Baking soda is a mild base. Being a base, baking soda solution neutralises the acidic liquid injected by honey-bee sting and neutralises its effect. This gives relief from pain.

(c) Neutralisation reaction (between an acid and a base)

(d) The values displayed by Shanti and classmates are

• Awareness
• Knowledge of Chemistry and
• Desire to remove the suffering of others.

In this page, we are providing Chemical Reactions and Equations Class 10 Extra Questions and Answers Science Chapter 1 pdf download. NCERT Extra Questions for Class 10 Science Chapter 1 Chemical Reactions and Equations with Answers will help to score more marks in your CBSE Board Exams.

Class 10 Science Chapter 1 Extra Questions and Answers Chemical Reactions and Equations

Extra Questions for Class 10 Science Chapter 1 Chemical Reactions and Equations with Answers Solutions

Extra Questions for Class 10 Science Chapter 1 Very Short Answer Type

Question 1.
How does the food become rancid?
Answer:
Food becomes rancid when fat and oils present in the food are oxidised.

Question 2.
A student burnt a metal A found in the form of ribbon. The ribbon burnt with a dazzling flame and a white powder B was formed which was basic in nature. Identify A and B. Write the balanced chemical equation.
Answer:
X = Mg,  Y = MgO,  Mg + O₂ → 2MgO

Question 3.
What is a balanced chemical equation?
Answer:
An equation that has equal number of atoms of each element on both the sides of the equation is called a balanced chemical equation, i.e., mass of the reactants is equal to mass of the products.
For example, \(2 \mathrm{Mg}+\mathrm{O}_{2} \stackrel{\Delta}{\longrightarrow} 2 \mathrm{MgO}\)

Question 4.
Write a balanced equation for a chemical reaction that can be characterised as precipitation.
Answer:
BaCl₂(aq) + Na₂SO₄ (aq) → BaSO₄(s) + 2NaCl(aq)

Question 5.
What is rust?
Answer:
It is a brown mass known as hydrated ferric oxide. Its formula is Fe₂O₃. xH₂O.

Question 6.
A zinc rod is left for nearly 20 minutes in a copper sulphate solution. What change would you observe in the zinc rod?
Answer:
The zinc rod will change into zinc sulphate.

Question 7.
Name two salts that are used in black and white photography.
Answer:
Both silver chloride and silver bromide are used in black and white photography.

Question 8.
Which chemical process is used for obtaining a metal from its oxide?
Answer:
The process is known as the reduction of metal oxide.

Question 9.
If you collect silver coins and copper coins you may have seen that after some days a black coating forms on silver coins and a green coating on copper coins. Which chemical phenomenon is responsible for these coatings? Write the chemical name of the black and green coatings.
Answer:
Corrosion is responsible for the formation of this coating. Black coating is due to formation of Ag₂S and green coating is due to formation of CuCO₃.Cu(OH)₂.

Question 10.
When carbon dioxide is passed through lime water, it turns milky, why?
Answer:
Lime water (calcium hydroxide) combines with carbon dioxide to form a suspension of calcium carbonate which makes lime water milky.
Ca(OH)₂ + CO₂ → CaCO₃ + H₂O

Question 11.
Identify the most reactive and least reactive metal: Al, K, Ca, Au.
Answer:
Most reactive metal: K(Potassium); least reactive metal: Au(gold).

Question 12.
X + Y SO₄ → X SO₄ + Y
Y + X SO₄ → No reaction
Of the two elements T and Y which is more reactive and why?
Answer:
‘X’ is more reactive than ‘Y since it has displaced ‘Y’ in the displacement reaction.

Question 13.
Why is it necessary to balance a chemical equation?
Answer:
An equation is balanced in order to satisfy the law of conservation of mass according to which total mass of the reactants is equal to the total mass of the products, i.e., mass can neither be created nor be destroyed during any chemical change.

Question 14.
During electrolysis of water, the gas collected in one test tube is double than the other, why?
Answer:
On electrolysis, water decomposes into hydrogen and oxygen in the ratio 2 : 1 by volume so, H₂ gas collected in one test tube is double than O₂.

Question 15.
Represent decomposition of ferrous sulphate with the help of balanced chemical equation.
Answer:
2FeSO₄ (s) → Fe₂O₃ (s) + SO₂ (g) + SO₃ (g)

Question 16.
What is a chemical equation?
Answer:
A chemical equation is a symbolic notation that uses formulae instead of words to represent a chemical equation.

Question 17.
A teacher took a few crystals of sugar in a dry test tube and heated the test tube over a flame. The colour of sugar turned black. Explain why?
Answer:
Sugar is a complex compound which on heating undergoes decomposition. Water gets evaporated thereby leaving behind black carbon in the test tube.

Question 18.
Name two metals which do not get corroded.
Answer:
Gold (Au) and platinum (Pt) do not get corroded.

Question 19.
Identify the compound oxidised in the following reaction:
H₂S (g) + Cl₂ → S(s) + 2HCl (g)
Answer:
H₂S is oxidised.

Question 20.
Why is a magnesium ribbon cleaned before burning?
Answer:
Magnesium reacts with moist air and forms a layer of oxide, MgO (white), on its surface. So, a magnesium ribbon is cleaned to remove the oxide layer before burning.

Question 21.
State the chemical change that takes place when limestone is heated.
Answer:
Calcium carbonate decomposes on heating to give calcium oxide and carbon dioxide.

Question 22.
On which chemical law, balancing of chemical equation is based?
Answer:
Balancing of a chemical equation is based on the law of conservation of mass.

Question 23.
Name the term used for the solution of the reactants or products when dissolved in water.
Answer:
Aqueous

Question 24.
What happens when magnesium ribbon burns in air?
Ans. When magnesium ribbon burns in air, it combines with the oxygen to form magnesium oxide.
2Mg(s) + O₂(g) → 2MgO(s)

Question 25.
Give an example of an exothermic reaction.
Answer:
CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(g) + Heat (evolved)

Question 26.
What type of reaction is this: Na₂SO₄ + BaCl₂ → BaSO₄ + 2NaCl
Answer:
It is a double displacement reaction.

Question 27.
Give an example of exothermic reaction.
Answer:
N₂ (g) + O₂ (g) → 2NO (g) – Heat (absorbed)

Question 28.
A substance X used for coating iron articles is added to a blue solution of a reddish brown metal Y. The colour of the solution gets discharged. Identify X and Y and also the type of reaction.
Answer:
X = Zn, Y = Cu, Displacement reaction.

Question 29.
Name the gas evolved when zinc reacts with dil. HCl.
Answer:
Hydrogen gas is evolved.

Extra Questions for Class 10 Science Chapter 1 Short Answer Type I

Question 1.
You are given the following materials
(i) Marble chips (ii) dilute hydrochloric acid (iii) Zinc granules
Identify the type of reaction when marble chips and zinc granules are added separately to acid taken in two test tubes.
Answer:
(i) Marble chips react with dilute hydrochloric acid to form calcium chloride and carbon dioxide. It is a double displacement reaction.
CaCO₃ + 2HCl → CaCl₂ + H₂O + CO₂

(ii) Zinc granules react with dilute hydrochloric acid to give hydrogen gas. It is a displacement reaction.
Zn (s) + 2HCl → ZnCl₂ (aq) + H₂ (g)

Question 2.
What do you understand by precipitation reaction? Explain with suitable examples.
Answer:
The reaction in which two compounds in their aqueous state react to form an insoluble compound. When two reactants react and product formed remains insoluble and settles as a solid it is substance (precipitate) is called a precipitation reaction.

For example,
(i) When aqueous solution of sodium sulphate is mixed with an aqueous solution or barium chloride, barium sulphate is obtained as a white precipitate.
Na₂SO₄ (aq) + BaCl₂ (aq) → BaSO₄ (s) + 2NaCl (ag)

(ii) When aqueous solution of sodium chloride is mixed with an aqueous solution of silver nitrate, silver chloride is obtained as a white precipitate.

Question 3.
What happens when aqueous solutions of sodium sulphate and barium chloride are mixed? What type of reaction is it?
Answer:
On mixing the solutions of sodium sulphate and barium chloride, a white precipitate of barium sulphate is obtained.

It is a double displacement reaction.

Question 4.
Explain the following terms with suitable examples.
(a) Oxidation
(b) Reduction
Answer:
(a) Oxidation is a process of addition of oxygen to a substance or removal of hydrogen from a substance, for example,

Copper is oxidised to CuO, as oxygen is added to copper.

(b) It is the process of removal of oxygen from a substance or addition of hydrogen to a substance, for example,

Copper oxide is reduced to copper as it involves removal of oxygen.

Question 5.
Complete the missing components/variables given as x and y in the following reactions.  [NCERT Exemplar]
(a) Pb(NO₃)₂ (aq) + 2Kl (aq) → PbI₂ (x) + 2KNO₃ (y)
(b) Cu (s) + 2AgNO₃ (aq) → Cu(NO₃)₂ (aq) + x (s)
(c) Zn (s) + H₂SO₄ (aq) → ZnSO₄ (x) + H₂ (y)

Answer:
(a) x = (s), y = (aq)
(b) x = 2Ag
(c) x = (aq); y = (g)
(d) x = heat

Question 6.
An iron knife kept dipped in a blue copper sulphate solution turns the blue solution light green. Why?
Answer:
We know that iron is more reactive than copper, so it displaces copper from copper sulphate solution and forms ferrous sulphate which is of light green colour.

Question 7.
A, B and C are three elements which undergo chemical reactions in the following way.
A₂O₃ + 2B → B₂O₃ + 2A
3CSO₄ + 2B → B₂(SO₄)₃ + 3C
3CO + 2A → A₂O₃ + 3C
Answer the following:
(a) Which element is most reactive?
(b) Which element is least reactive?
Answer:
(a) The most reactive element is ‘B’. It has displaced both ‘A’ and ‘C’ from their compounds.
(b) The least reactive element is ‘C’ as it has been displaced by both ‘A’ and ‘B’.

Question 8.
Write the balanced chemical equations for the following reactions and identify the type of reaction in each case.
(a) Nitrogen gas is treated with hydrogen gas in the presence of a catalyst at 773 K to form ammonia gas.
(b) Sodium hydroxide solution is treated with acetic acid to form sodium acetate and water.
(c) Ethanol is warmed with ethanoic acid to form ethyl acetate in the presence of concentrated H₂SO₄.
(d) Ethene is burnt in the presence of oxygen to form carbon dioxide, water and releases heat and light.  [NCERT Exemplar]
Answer:

Question 9.
What is lime water test for the detection of carbon dioxide?
Answer:
When carbon dioxide gas is passed through lime water, it turns milky due to the formation of a milky suspension (precipitate) of calcium carbonate.
Ca(OH)₂ (aq) + CO₂ (g) → CaCO₃ (s) + CO₂ (g)

Question 10.
During the reaction of some metals with dilute hydrochloric acid, following observations were made,
(a) Silver metal does not show any change.
(b) The temperature of the reaction mixture rises when aluminium (Al) is added.
(c) The reaction of sodium metal is found to be highly explosive.
(d) Some bubbles of a gas are seen when lead (Pb) is reacted with the acid.
Explain these observations giving suitable reasons.   [NCERT Exemplar]
Answer:
(a) No change takes place because silver metal does not react with hydrochloric acid in normal situations.
(b) The reaction between hydrochloric acid and aluminium is exothermic, thus the temperature of the reaction mixture rises when aluminium is added.
(c) Since, sodium is a highly reactive metal, thus it reacts with hydrochloric acid vigorously and produces a large amount of heat. Thus, the reaction is exothermic.
(d) Bubbles of hydrogen gas are formed when lead react with dilute hydrochloric acid.
Pb + 2HCl → PbCl₂ + H₂

Question 11.
A copper coin is kept in a solution of silver nitrate for some time. What will happen to the coin and the colour of the solution?
Answer:
We know that copper is more reactive than silver, so it will displace silver from its salt solution.
Cu (s) + 2AgNO₃ (aq) → Cu(NO₃)₂ (aq) + 2Ag (s)
So, the solution will turn blue due to the formation of copper nitrate.

Question 12.
An aqueous solution of metal nitrate P reacts with sodium bromide solution to form yellow ppt. of compound Q which is used in photography. Q on exposure to sunlight undergoes decomposition reaction to form metal present in P along with reddish brown gas. Identify P and Q. Write the chemical reaction and type of chemical reaction.
Answer:
P = Ag NO₃, Q = AgBr
AgNO₃ (aq) + NaBr (aq) → NaNO₃ (aq) + AgBr (s); Double decomposition reaction
2AgBr (s) → 2Ag (s) + Br₂ (g); Photochemical decomposition reaction

Question 13.
What happens when iron nails are immersed in copper sulphate solution? What type of reaction is it?
Answer:
When iron nails are immersed in copper sulphate solution, iron ions displace copper ions and a new compound ferrous sulphate is formed.

It is a diplacement reaction.

Question 14.
Which of the following reaction is possible. Explain giving suitable reason.
(i) Zn (s) + CuSO₄ (aq) → ZnSO₄ (aq) + Cu (s)
(ii) Fe (s) + ZnSO₄ (aq) → FeSO₄ (aq) + Zn (s)
(iii) Zn (s) + FeSO₄ (s) → ZnSO₄ (aq) + Fe (s)
Answer:
Reaction (i) and (iii) are possible.
(i)

Zinc is more reactive than copper, therefore, it can displace copper from copper sulphate solution.

(iii) Zn (s) + FeSO₄ (aq) → ZnSO₄ (aq) + Fe (s)
Zn is more reactive than Fe, therefore, it can displace iron from ferrous sulphate solution.

Reaction (ii) is not possible as iron is less reactive than zinc, hence, it cannot displace Zn.

Question 15.
Which among the following changes are exothermic or endothermic in nature?
(a) Decomposition of ferrous sulphate
(b) Dilution of sulphuric acid
(c) Dissolution of sodium hydroxide in water
(d) Dissolution of ammonium chloride in water  [NCERT Exemplar]
Answer:
(a) endothermic
(b) exothermic
(c) exothermic
(d) endothermic.

Question 16.
State one advantage and one disadvantage of corrosion.
Answer:
Advantage. In some metals a protective layer is formed on its surface due to corrosion which prevent it from further corrosion.

Example, Aluminium (Al) forms a layer of aluminium oxide (Al₂O₃) by corrosion. This layer prevents further corrosion of aluminium.
Disadvantage: Loss of the metal.

Extra Questions for Class 10 Science Chapter 1 Short Answer Type II

Question 1.
What is corrosion? State condiyions necessary for rusting of iron. How is rusting harmful?  [NCERT Exemplar]
Answer:
Corrosion. The process of eating away of the metal surface by the action of atmospheric reagents like water, oxygen and acids changing the metal into its compound is called corrosion.

Rusting of iron. When iron objects are exposed to atmosphere, they are attacked by air and moisture (water) of the atmosphere and a brown and orange coloured layer is formed on the surface. It is called rust which is mainly hydrated iron (III) oxide Fe₂O₃. xH₂O.

Harmful effect of rusting. Hydrated iron (III) oxide is a brittle substance and falls off from the surface of iron and thus the object is damaged. Holes, cavities and roughness of surfaces are the result of rusting of an iron object.

Conditions necessary for rusting:

• Open surface of the metal
• Presence of air (oxygen)
• Presence of moisture (water).

Question 2.
The gases hydrogen and chlorine do not react with each other even if kept together for a long time. However, in the presence of sunlight, they readily combine. What actually happens?   [NCERT Exemplar]
Answer:
In chemical reactions, energy is needed to break the bonds present in the reacting molecules so that they may combine to form the products. In this reaction, sunlight is the source of energy in the form of photons. The energy made available by sunlight helps in breaking the bonds and this leads to chemical reaction between hydrogen and chlorine.

Question 3.
Write the balanced chemical equations for the following reactions and identify the type of reaction in each case.
(a) Thermite reaction, iron (III) oxide reacts with aluminium and gives molten iron and aluminium oxide.
(b) Magnesium ribbon is burnt in an atmosphere of nitrogen gas to form solid magnesium nitride.
(c) Chlorine gas is passed in an aqueous potassium iodide solution to form potassium chloride solution and solid iodine.
(d) Ethanol is burnt in air to form carbon dioxide, water and releases heat.   [NCERT Exemplar]
Answer:
The balanced equations are as under:
(a) Fe₂O₃ (s) + 2Al (s) → 2Fe (l) + Al₂O₃ (s) + Heat
It is a redox reaction / displacement reaction.

(b) 3Mg (s) + N₂ (g) → Mg₃N₂ (s)
It is a combination reaction as well as redox reaction.

(c) Cl₂ (g) + 2KI (aq) → 2KCl (aq) + I₂ (s)
It is a displacement reaction as well as redox reaction.

(d) C₂H₅OH (l) + 3O₂ (g) → 2CO₂ (g) + 3H₂O (l) + Heat
Redox reaction/combustion reaction

Question 4.
What is rancidity? Write the common method to prevent it.
Answer:
When food item are kept unprotected for some time, their smell and taste changes. This process is called rancidity. Actually, the microorganisms oxidise the fat and oils present in them. So oxidation of food items need to be prevented to protect them.

Common methods to prevent rancidity of food item:

• Keeping the food at low temperature.
• Keeping food item in air tight containers.
• By filling nitrogen in the food storage bags.

Question 5.
(a) What happens chemically when quick lime is added to water?
(b) Write the chemical equation in balanced form.
MnO₂ + HCl → MnCl₂ + Cl₂ + H₂O
(c) What is decomposition reaction? Explain it with a suitable example.
Answer:
(a) When quick lime (CaO) is added to water, slaked lime Ca(OH)₂ is formed. The reaction is highly exothermic in nature.

(b) The balanced chemical equation is:
MnO₂ + 4HCl → MnCl₂ + 2H₂O + Cl₂

(c) Decomposition reaction is a chemical reaction in which a single substance splits or breaks into two or more substances under suitable conditions. For example,
2FeSO₄(s) → Fe₂O₃(s) + SO₂(g) + SO₃ (g)

Question 6.
Identify the oxidising agent (oxidant) in the following reactions:
(a) Pb₃O₄ + 8HCl → 3PbCl₂ + Cl₂ + 4H₂O
(b) 2Mg + O₂ → 2MgO
(c) CuSO₄ + Zn → Cu + ZnSO₄
(d) V₂O₅ + 5Ca → 2V + 5CaO
(e) 3Fe + 4H₂O → Fe₃O₄ + 4H₂
(f) CuO + H₂ → Cu + H₂O [NCERT Exemplar]
Answer:
(a) Pb₃O₄
(b) O₂
(c) CuSO₄
(d) V₂O₅
(e) 4H₂O
(f) CuO

Question 7.
Write the balanced chemical equations for the following reactions:  [NCERT Exemplar]
(a) Sodium carbonate on reaction with hydrochloric acid in equal molar concentrations gives sodium chloride and sodium hydrogencarbonate.
(b) Sodium hydrogencarbonate on reaction with hydrochloric acid gives sodium chloride, water and liberates carbon dioxide.
(c) Copper sulphate on treatment with potassium iodide precipitates cuprous iodide (Cu₂I₂), liberates iodine gas and also forms potassium sulphate.
Answer:
(a) Na₂CO₃ + HCl → NaCl + NaHCO₃
(b) NaHCO₃ + HCl → NaCl + H₂O + CO₂
(c) 2CUSO₄ + 4KI → 2K₂SO₄ + Cu₂I₂ + I₂

Question 8.
Write chemical equations for the reactions taking place when:
(i) Iron reacts with steam
(ii) Magnesium reacts with dilute HCl
(iii) Copper is heated in air
Answer:

Question 9.
fialance the following chemical equations and identify the type of chemical reaction.
(a) Mg (s) + Cl₂ (g) → MgCl₂ (s)

(d) TiCl₄ (l) + Mg (s) → Ti (s) + MgCl₂ (s)
(e) CaO (s) + SiO₂ (s) → CaSiO₃ (s)

[NCERT Exemplar]
Answer:
The chemical equation in their balanced form may be written as follows:
(a) Mg (s) + Cl₂ (g) → MgCl₂ (s), Combination reaction

(d) TiCl₄ (l) + 2Mg (s) → Ti (s) + 2MgCl₂ (s); Displacement reaction
(e) CaO (s) + SiO₂ (s) → CaSiO₃ (s); Combination reaction

Question 10.
A silver article generally turns black when kept in the open for a few days. The article when rubbed with toothpaste again starts shining.
(a) Why do silver articles turn black when kept in the open for a few days? Name the phenomenon involved.
(b) Name the black substance formed and give its chemical formula.   [NCERT Exemplar]
Answer:
(a) Silver articles turn black when kept in the air for a few days because H₂S gas present in the air attacks silver forming a coating of black silver sulphide. The phenomenon is called corrosion.

(b) Black substance formed is silver sulphide (Ag₂S)
2Ag (s) + H₂S (g) → Ag₂S (s) + H₂ (g).

Question 11.
Which among the following are physical or chemical changes?
(a) Evaporation of petrol
(b) Burning of Liquefied Petroleum Gas (LPG)
(c) Heating of an iron rod to red hot
(d) Curdling of milk
(e) Sublimation of solid ammonium chloride  [NCERT Exemplar]
Answer:
(a) Physical change
(b) Chemical change
(c) Physical change
(d) Chemical change
(e) Physical change

Extra Questions for Class 10 Science Chapter 1 Long Answer Type

Question 1.
Balance the following equations:
(a) Bacl₂ + H₂SO₄ → BaSO₄ + HCl
(b) CH₄ + O₂ → CO₂ + H₂O



Answer:
(a) Bacl₂ + H₂SO₄ → BaSO₄ + 2HCl
(b) CH₄ + 2O₂ → CO₂ + 2H₂O

Question 2.
On heating blue coloured powder of copper (II) nitrate in a boiling tube, copper oxide (black), oxygen gas and a brown gas X is formed.
(а) Write a balanced chemical equation of the reaction.
(b) Identify the brown gas X evolved.
(c) Identify the type of reaction.
(d) What could be the pH range of aqueous solution of the gas X?  [NCERT Exemplar]
Answer:

(b) Brown gas X is nitrogen dioxide (NO₂).
(c) It is a thermal decomposition reaction.
(d) The gas (NO₂) is an oxide of a non-metal. Hence, its aqueous solution will be acidic, i.e., pH range would be between 0 and 7.

Question 3.
(A) Name the type of chemical reaction represented by the following equation:

(c) Zn(s) + H₂SO₄(ag) → ZnSO₄(aq) + H₂(g)
(B) “A solution of potassium chloride when mixed with silver nitrate solution, and an insoluble white substance is formed”.   [CBSE 2010, 2012]
(i) Translate the above statement into a chemical equation.
(ii) State two types for the classification of this reaction.
Answer:
(A) (a) Decomposition reaction
(b) Combination reaction
(c) Displacement reaction.

(B) (i) KCl (aq) + AgNO₃ (aq) → AgCl (s) + KNO₃ (aq)
(ii) It is a double displacement reaction also called precipitation reaction.

Question 4.
What happens when zinc granules are treated with dilute solution of H₂SO₄, HCl, HNO₃, NaCl and NaOH, also write the chemical equations if reaction occurs.  [NCERT Exemplar]
Answer:

Question 5.
(A) Write the balanced chemical equations for the following chemical reactions:
(i) Hydrogen + Chlorine → Hydrogen chloride
(ii) Lead + Copper chloride → Lead chloride + Copper
(iii) Zinc oxide + Carbon → Zinc + Carbon monoxide
(B) Write balanced chemical equations for the following reactions:
(a) Silver bromide on exposure to sunlight decomposes into silver and bromine.
(b) Sodium metal reacts with water to form sodium hydroxide and hydrogen gas.
Answer:
(A) (i) H₂ + Cl₂ → 2HCl
(ii) Pb + CuCl₂ → PbCl₂ + Cu
(iii) ZnO + C → Zn + CO
(B)

(b) 2Na + 2H₂O→ 2NaOH + H₂

Question 6.
(a) Why cannot a chemical change be normally reversed?
(b) Why is it always essential to balance a chemical equation?
(c) What happens when CO₂ gas is passed through lime water and why does it disappear on passing excess CO₂?
(d) Can rusting of iron takes place in distilled water?
Answer:
(a) In a chemical change some bonds are broken and some bonds are formed. The products are quite different from the reactants. Therefore, it normally can’t be reversed.
(b) A chemical equation has to be balanced to satisfy the law of conservation of mass.
(c) On passing CO₂ gas through lime water, it turns milky due to formation of insoluble calcium carbonate which dissolves on passing excess CO₂ due to formation of soluble calcium bicarbonate.
Ca(OH)₂ + CO₂(g) → CaCO₃(s) + H₂O(l)
CaCO₃(s) + H₂O(l) + CO₂(g) → Ca(HCO₃)₂ (soluble)
(d) No

Question 7.
What happens when a piece of
(a) zinc metal is added to copper sulphate solution?
(b) aluminium metal is added to dilute hydrochloric acid?
(c) silver metal is added to copper sulphate solution?
Also, write the balanced chemical equation if the reaction occurs.  [NCERT Exemplar]
Answer:
(a) Zinc is more reactive than copper. It displaces Cu from CuSO₄ solution forming colourless zinc sulphate. Thus, blue colour of CuSO₄ solution starts fading and ultimately blue colour disappears.

(b) Aluminium reacts with dilute HCl acid forming AlCl₃ along with evolution of bubbles of H₂ gas.

(c) Silver is less reactive than copper. Hence, Ag cannot displace Cu from CuSO₄ solution. Thus, no reaction occurs.

Question 8.
(A) A brown substance ‘X’ on heating in air forms a substance ‘Y’. When hydrogen gas is passed over heated ‘Y’, it again changes back into ‘X’.
(i) Name the substances X and Y.
(ii) Name the chemical processes occurring during both the changes.
(iii) Write the chemical equations.   [CBSE 2011]
(B) A metal is treated with dil. H₂SO₄. The gas evolved is collected by the method shown in the figure. Answer the following:

(i) Name the gas.
(ii) Name the method of collection of the gas.
(iii) Is the gas soluble or insoluble in water?
(iv) Is the gas lighter or heavier than air?
Answer:
(A) (i) The substance X is copper and Y is copper (II) oxide or CuO.
(ii) The process of change of X into Y is oxidation. The process of change of Y into X is reduction.
(iii) The chemical equations are:

(B) (i) The gas evolved is hydrogen.
(ii) The method of collection of the gas is the downward displacement of water.
(iii) The gas is insoluble in water. That is why, it can be collected over water.
(iv) The gas is lighter than air.

Chemical Reactions and Equations HOTS Questions With Answers

Question 1.
The marble statues often slowly get corroded when kept in open for a long time. Assign a suitable explanation.
Answer:
SO₂, NO₂ gases are released into the atmosphere from various sources. These dissolve in rain water to give acid which corrodes marble statues.
2SO₂ + O₂ → 2SO₃
H₂O + SO₃ → H₂SO₄
2NO₂ + H₂O → 2HNO₃
CaCO₃ + H₂SO₄ → CaSO₄ + H₂O + CO₂
CaCO₃ + 2HNO₃ → Ca(NO₃)₂ + H₂O + CO₂

Question 2.
Observe the following activity and identify the following:

(a) Type of chemical reaction.
(b) Write a chemical equation to represent the above change.
(c) Name the gas evolved in the above reaction.
(d) Do you observe any colour change in the above reaction? If yes, mention the colour change.
(e) Name the coloured substance formed.
Answer:
(a) Decomposition reaction.
(b) 2Pb(NO₃)₂ (s) → 2PbO (s) + 4NO₂ (g) + O₂ (g)
(c) Reddish brown fumes of nitrogen dioxide along with oxygen gas is evolved.
(d) The colour of the substance changes from white to yellow due to formation of lead oxide.
(e) Lead oxide which is yellow coloured.

Question 3.
A substance X, which is an oxide of a group 2 element, is used intensively in the cement industry. This element is present in bones also. On treatment with water it forms a solution which turns red litmus blue. Identify X and also write the chemical reactions involved.   [NCERT Exemplar]
Answer:
The above information suggests that the substance ‘A’ is oxide of the element calcium (Ca) which is present in group 2 of the periodic table. Calcium is also a constituent of our bones in the form of calcium phosphate. Calcium oxide (CaO) reacts with water to form calcium hydroxide (basic in nature). It forms a basic solution which turns red litmus blue.
CaO (s) + H₂O (aq) → Ca(OH)₂ (aq)

Question 4.
On adding a drop of barium chloride solution to an aqueous solution of sodium sulphite, a white precipitate is obtained.
(a) Write a balanced chemical equation of the reaction involved.
(b) What other name can be given to this precipitation reaction?
(c) On adding dilute hydrochloric acid to the reaction mixture, white precipitate disappears. Why? [NCERT Exemplar]
Answer:
(a) A white precipitate of barium sulphite is formed when barium chloride is added to the solution of sodium sulphite.
BaCl₂ (aq) + Na₂SO₃ (aq) → BaSO₃ (s) + 2NaCl (aq)

(b) This precipitation reaction is also a double displacement reaction.

(c) Barium chloride, sulphur dioxide and water are formed when dilute hydrochloric acid is added to this solution of barium sulphate and sodium chloride. Since barium chloride is a soluble substance, thus white precipitate of barium sulphite disappears.
BaSO₃ (s) + HCl (ag) → BaCl₂ (ag) + SO₂ (g) + H₂O

Question 5.
A water insoluble substance ‘X’ on reacting with dilute H₂SO₄ released a colourless and odourless gas accompanied by brisk effervescence. When the gas was passed through water, the solution obtained turned blue litmus red. On bubbling the gas through lime water, it initially became milky and the milkiness disappeared when the gas was passed in excess. Identify the substance ‘X’ and write the chemical equations of the reaction involved.
Answer:
The water insoluble substance ‘X’ is most probably the metal carbonate (CaCO₃). The chemical reaction that were involved are given below.
CaCO₃ (s) + H₂SO₄ (aq) → CaSO₄ (ag) + H₂O (aq) + CO₂ (g)
Ca(OH)₂ (aq) + CO₂ (g) → CaCO₃ (s) (milky) + H₂O (l)
CaCO₃ (s) + CO₂ (g) + H₂O (aq) → Ca (HCO₃)₂ (milkiness)

Question 6.
The given set up shows the electrolysis of water taking place.

(a) Identify the gases evolved at cathode and anode.
(b) Why is the amount of gas collected in one of the test tubes double the amount in the other? Name this gas.
(c) How will you test the evolved gases?
Answer:
(a) The gases evolved at anode and cathode are oxygen and hydrogen.

(b) On electrolysis, water decomposes to form hydrogen and oxygen gas in the ratio of 2 : 1 by volume according to the equation given below:

The gas collected in double volume is hydrogen.

(c) Test for oxygen. If we bring a burning splinter near the mouth of test tube containing oxygen gas it burns more brightly.
Test for hydrogen. On bringing a burning splinter near the mouth of the test tube containing hydrogen, the gas burns with a pop sound.

Question 7.
A magnesium ribbon is burnt in oxygen to give a white compound X accompanied by emission of light. If the burning ribbon is now placed in an atmosphere of nitrogen, it continues to burn and forms a compound Y.
(a) Write the chemical formulae of X and Y.
(b) Write a balanced chemical equation, when X is dissolved in water.   [NCERT Exemplar]
Answer:

Question 8.
You are provided with two containers made up of copper and aluminium. You are also provided with solutions of dilute HCl, dilute HNO₃, ZnCl₂ and H₂O. In which of the above containers these solutions can be kept? [NCERT Exemplar]
Answer:
(A) When solutions are kept in copper container
(a) Dilute HCl
Copper does not react with dilute HCl. Therefore, it can be kept.

(b) Dilute HNO₃
Nitric acid acts as a strong oxidising agent and reacts with copper vessel, therefore cannot be kept.

(c) ZnCl₂
Zinc is more reactive than copper (Cu) therefore, no displacement reaction occurs and hence can be kept.

(d) H₂O
Copper does not react with water. Therefore, can be kept.

(B) When solutions are kept in aluminium containers
(a) Dilute HCl
Aluminium reacts with dilute HCl to form its salt and hydrogen is evolved. Therefore, cannot be kept.
2 Al + 6HCl → 2AlCl₃ + 3H₂

(b) Dilute HNO₃
Aluminium gets oxidised by dilute HNO₃ to form a layer of Al₂O₃ and can be kept.

(c) ZnCl₂
Aluminium being more reactive than zinc can displace zinc ion from the solution. Therefore, the solution cannot be kept.
2Al + 3ZnCl₂ → 2AlCl₃ + 3Zn

(d) H₂O
Aluminium does not react with cold or hot water. Therefore, water can be kept.
Aluminium is attacked by steam to form aluminium oxide and hydrogen.
2Al(s) + 3H₂O(g) → Al₂O₃(S) + 3H₂ (g)

Extra Questions for Class 10 Science Chapter 1 Value Based

Question 1.
Rakesh wanted to give a coating of white wash on the walls of his house. He purchased quick lime (CaO) and dropped it in container of water and immediately applied the same on the walls. In this process, he spoiled his hands and even suffered minor bums. His friend Kapil advised him to keep the container overnight before applying a coating on the wall.
(i) What mistake was committed by the Rakesh?
(iii) Why did he suffer from minor bums?
(iii) How was Kapil’s advice useful?
(iv) What values are exhibited by Kapil?
Answer:
(i) Rakesh should have waited for a few hours because when quick lime dissolves in water, slaked lime is formed and the process is highly exothermic (a lot of energy is released).

(ii) Because the reaction is exothermic and a lot of energy is released and container becomes hot so he suffered from minor burns.

(iii) Quick lime (CaO) reacts with water to form Ca(OH)₂ which is known as slaked lime. The dissolution process is highly exothermic. So a large amount of heat is evolved. By keeping container overnight, the chemical reaction subsides and the heat dissipates. So the coating of slaked lime can be applied safely on the walls.

(iv) Knowledge of Chemistry, helpful and caring nature.

Question 2.
Palak is an eleven year old girl. She purchased a packet of potato chips and had a few from it more than a month back. She had kept away the open packet containing the remaining potato chips then. She wanted to eat the remaining potato chips now. Her elder sister Anjali found that the potato chips were giving out an unpleasant odour. When she put one of them in her mouth, she found that it had an unpleasant taste too. Anjali threw away the packet and did not allow Palak to eat the potato chips.
(a) What name is given to the condition in which potato chips kept in the open for a long time give out unpleasant smell and taste?
(b) Which chemical reaction is responsible for the spoilage of potato chips?
(c) Explain the reason for the unpleasant smell as well as unpleasant taste of the potato chips.
(d) Mention the values exhibited by Anjali.
Answer:
(a) Rancidity.
(b) Oxidation reaction.
(c) Potato chips contain oil. The oil present in potato chips (which have been kept exposed to air for a considerable time) gets oxidised by the oxygen of air. The oxidation products have unpleasant smell and taste. The potato chips are then said to have turned rancid. They become unfit to eat.
(d) (i) Awareness (or knowledge of Chemistry)
(ii) Concern for the health of her sister.

Here we are providing Some Applications of Trigonometry Class 10 Extra Questions Maths Chapter 9 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Some Applications of Trigonometry with Answers Solutions

Extra Questions for Class 10 Maths Chapter 9 Some Applications of Trigonometry with Solutions Answers

Some Applications of Trigonometry Class 10 Extra Questions Short Answer Type 1

Question 1.
If a man standing on a platform, 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.

Solution:
False, θ₁ ≠ θ₁ (Fig. 11.15)

Question 2.
Find the angle of elevation of the sun when the shadow of a pole h m high is √3 h m long.
Solution:

In ∆ABC

θ = 30°

Question 3.
The height of a tower is 12 m. What is the length of its shadow when 10 Sun’s altitude is 45°?
Solution:

Let AB be the tower [Fig. 11.17].
Then, ∠C = 45°, AB = 12 m

∴ The length of the shadow is 12 m.

Question 4.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° [Fig. 11.18].
Solution:
Let AB be the vertical pole and AC be the long rope tied to point C.
In right ∆ABC, we have

Therefore, height of the pole is 10 m.

Some Applications of Trigonometry Class 10 Extra Questions Short Answer Type 2

Question 1.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Solution:
Let BC be the tower whose height is h metres and A be the point at a distance of 30 m from the
foot of the tower. The angle of elevation of the top of the tower from point A is given to be 30°.
Now, in right angle ∆CBA we have,

Hence, the height of the tower is 10 √3 m.

Question 2.
A tree breaks due to storm and the broken part bends, so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:
In right angle ∆ABC, AC is the broken part of the tree (Fig. 11.20).
So, the total height of tree = (AB + AC)
Now in right angle ∆ABC,

Question 3.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:

Let OA be the tower of height h metre and P, l be the two points at distance of 9 m and 4 m respectively from the base of the tower.
Now, we have OP = 9 m, OQ = 4 m,
Let ∠APO = θ, ∠AQO = (90° – θ)
and OA = h metre (Fig. 11.21)
Now, in ∆POA, we have


Height cannot be negative.
Hence, the height of the tower is 6 metre.

Question 4.
Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 30° and at a distance 10 km further off from the mountain, along the same line, the angle of elevation is 15o. (Use tan 15° = 0.27)
Solution:
Let AB be the mountain of height h kilometres. Let C be a point at a distance of x km, from the base of the mountain such that the angle of elevation of the top at C is 30°. Let D be a point at a distance of 10 km from C such that angle of elevation at D is of 15°.
In MBC (Fig. 11.22), we have

Substituting x = √3h in equation (i), we get
⇒ 0.27 ( √3h + 10) = h
= 0.27 × √3h + 0.27 × 10 = h
⇒ 2.7 = h – 0.27 × √3h
⇒ 27 = h (1 – 0.27 × √3)
⇒ 27 = h (1 – 0.46)
⇒ h = \(\frac{2.7}{0.54}\) = 5
Hence, the height of the mountain is 5 km.

Question 5.
The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Solution:
In Fig. 11.23, AB is the tower and BC is the length of the shadow when the Sun’s altitude is 60°, i.e., the angle of elevation of the top of the tower from the tip of the shadow is 60° and DB is the length of the shadow, when the angle of elevation is 30°.
Now, let AB be h m and BC be x m.
According to the question, DB is 40 m longer than BC.
So, BD = (40 + x) m
Now, we have two right triangles ABC and ABD.

Using (i) in (ii), we get (x √3 ) √3 = x + 40, i.e., 3x = x + 40
i.e., x = 20
So, h = 20 √3 [From (i)]
Therefore, the height of the tower is 20 √3 m.

Question 6.
From a point P on the ground, the angle of elevation of the top of a 10m tall building is 30°. A flag is hosted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45o. Find the length of the flagstaff and the distance of the building from the point P. (You may take √3 = 1.732).
Solution:

In Fig. 11.24, AB denotes the height of the building, BD the flagstaff and P the given point. Note that there are two right triangles PAB and PAD. We are required to find the length of the flagstaff, i.e., BD and the distance of the building from the point P, i.e., PA.
Since, we know the height of the building AB, we will first consider the right ∆PAB.

i.e., x = 100(√3 – 1) = 7.32
So, the length of the flagstaff is 7.32 m.

Question 7.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:
Let AC be a steep slide for elder children and DE be a slide for younger children. Then AB = 3 m and DB = 1.5 m (Fig. 11.25).
Now, in right angle ∆DBE, we have

So, the length of slide for elder children is 2 √3 m.

Question 8.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
Let AB be the horizontal ground and K be the position of the kite and its height from the ground is 60 m and let length of string AK be x m. (Fig. 11.26)
∠KAB = 60°
Now, in right angle ∆ABK we have

So, the length of string is 40 √3 m.

Question 9.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
Let AB be the building and PQ be the initial position of the boy (Fig. 11.27) such that
∠APR = 30°
and AB = 30 m
Now, let the new position of the boy be P’Q’ at a distance QQ’.
Here, ∠AP’R = 60°
Now, in ∆ARP, we have

Therefore, required distance, QQ = PP’ = PR – P’R
= 28.5 √3 – 9.5 √3 = 19√3
Hence, distance walked by the boy is 19√3 m.

Question 10.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find
the width of the river.
Solution:
In Fig. 11.28, A and B represent points on the bank on opposite sides of the river, so that AB is the width of the river. P is a point on the bridge at a height of 3 m, i.e., DP = 3m. We are interested to determine the width of the river, which is the length of the side AB of the ∆APB.
In right ∆ADP, ∠A = 30°

∴ DB = 3m
Now, AB = BD + AD = 3 + 3 √3 = 3 (1 + √3) m
Therefore, the width of the river is 3(√3 + 1) m.

Question 11.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:

Let AB be the lighthouse of height 75 m and P, Q be the position of the two ships whose angles of depression are 45° and 30°, respectively (Fig. 11.29). Let BP = x m and PQ = y m, we have
∠APB = 45° and ∠AQB = 30°
Now, in ∆ABP we have
tan 45° = \(\frac{AB}{BP}\)
⇒ 1 = \(\frac{70}{x}\)
⇒ x = 75 m …..(i)
Again, in ∆ABQ we have
tan 30° = \(\frac{AB}{BQ}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{75}{x+y}\)
⇒ x + y = 75 √3 ……(ii)
From (i) and (ii), we have
75 + y = 75 √3
y = 75 √3 – 75
⇒ y = 75(√3 – 1)
Hence, the distance between two ships is 75(√3 – 1) metres.

Question 12.
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. (Use √3 = 1.73]
Solution:
Let the distance between the two ships be d.
Let the distance of one ship from the light house be x metres. Then, the distance of the other ship from the light house will be (d – x) metres.

Question 13.
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 30°. If the aeroplane is flying at a constant height of 3000 √3 m, find the speed of the aeroplane.
Solution:
Let A be point of observation and P and Q be positions of the plane. Let ABC be the line through A and it is given that angles of elevation from point A to two positions P and Q are 60° and 30°.
∠PAB = 60°, ∠QAB = 30°
Height = 3000 √3 m
So, in ∆ABP, we have

Question 14.
From the top of a 60 m high building, the angles of depression of the top and the bottom of a tower are 45° and 60° respectively. Find the height of the tower. [Take √3 = 1.73]
Solution:
Let the height of the building be AE = 60 m, the height of the tower is ‘h’. The distance between the base of the building and the tower be ‘d’.
In ∆ADE,

⇒ AC = 34.60 m
Now, height of tower = AE – AC = 60 – 34.60 = 25.4 m

Question 15.
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. (Use √3 = 1.732]
Solution:
Let AD be the light house and its height be h. The distance of one ship from the light house is x and that of other ship is 100 – x.
In ∆ADB,

= 50 × (1.732 – 1)
h = 36.6 m

Question 16.
Two men on either side of a 75 m high building and in line with base of building observe the angle of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use √3 = 1.73)
Solution:

(i) In ∆ABM₁
\(\frac{A B}{B M_{1}}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
⇒ BM₁ = 75 √3 m

(ii) In ∆ABM₂
\(\frac{A B}{B M_{2}}\) = tan 60° = √3
⇒ BM2 = \(\frac{75}{\sqrt{3}}\) = 25 √3 m
∴ M₁ M₂ = M₁B + BM₂
= 75√3 + 25 √3 = 100 √3 m = 173 m
∴ Distance between two men = 173 m.

Question 17.
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
Solution:

Let the speed of boat be x m/min
∴ CD = 2x
In ∆ABC
\(\frac{150}{y}\) = tan 60°
⇒ y =\(\frac{150}{\sqrt{3}}\) = 50√3 m
In ∆ABD
\(\frac{150}{y+2 x}\) = tan 45°
⇒ 150 = 50√3 + 2x
⇒ x = 25(3 – √3)
Speed = 25(3 – √3 ) m/min
∴ = 25 × 60 (3 – √3) m/h = 1500 (3 – √3) m/h

Some Applications of Trigonometry Class 10 Extra Questions Long Answer Type

Question 1.
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60°, respectively. Find the height of the tower.
Solution:
Let AB be a building of height 20 m and BC be the transmission tower of height x m and D be any point on the ground (Fig. 11.36).
Here, ∠BDA = 45° and ∠ADC = 60°
Now, in ∆ADC, we have

⇒ x = 20√3 – 20 = 20 (√3 – 1) = 20 (1.732 – 1) = 20 × 0.732 = 14.64 m
Hence, the height of tower is 14.64 m.

Question 2.
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the bottom of the pedestal is 45°. Find the height of the pedestal.
Solution:
Let AB be the pedestal of height h metres and BC be the statue of height 1.6 m (Fig. 11.37).
Let D be any point on the ground such that,
∠BDA = 45° and ∠CDA = 60°
Now, in ∆BDA, we have


Hence, height of the pedestal is 0.8 (√3 + 1) m.

Question 3.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
OR
From the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of its foot is 45°. Find the height of the tower. (Use √3 = 1.732]
Solution:

Let PQ be the building of height 7 metres and AB be the cable tower. Now it is given that the angle of elevation of the top A of the tower observed from the top P of building is 60° and the angle of depression of the base B of the tower observed from P is 45° (Fig. 11.38).
So, ∠APR = 60° and ∠QBP = 45°
Let QB = x m, AR = h m then, PR = x m
Now, in ∆APR, we have
tan 60° = \(\frac{AR}{PR}\)
⇒ √3 = \(\frac{h}{x}\)
⇒ √3x = h
⇒ h = √3x ……(i)
Again, in ∆PBQ we have
tan 45o = \(\frac{PQ}{QB}\)
⇒ 1 = \(\frac{7}{x}\)
⇒ x = 7 ……(ii)
Putting the value of x in equation (i), we have
h = √3 × 7 = 7 √3
i.e., AR = 7 √3 metres
So, the height of tower = AB = AR + RB = 7 √3 + 7 = 7(√3 + 1) m.

Question 4.
At a point, the angle of elevation of a tower is such that its tangent is \(\frac{5}{12}\) On walking 240 m to the tower, the tangent of the angle of elevation becomes \(\frac{3}{4}\). Find the height of the tower.
Solution:
In the Fig. 11.39, let AB be the tower, C and D be the positions of observation from where given that


Hence, the height of the tower is 225 metres.

Question 5.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (Fig. 11.40). Find the distance travelled by the balloon during the interval.
Solution:
Let A and B be two positions of the balloon and G be the point of observation. (eyes of the girl)
Now, we have
AC = BD = BQ – DQ = 88.2 m – 1.2 m = 87 m .
∠AGC = 60°, ∠BGD = 30°
Now, in ∆AGC, we have

Hence, the balloon travels 58 √3 metres.

Question 6.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:
Let OA be the tower of height h, and P be the initial position of the car when the angle of depression is 30°.
After 6 seconds, the car reaches to such that the angle of depression at Q is 60°. Let the speed of the car be v metre per second. Then,
PQ = 6υ (∵ Distance = speed × time)
and let the car take t seconds to reach the tower OA from Q (Fig. 11.41). Then, OQ = υt metres.
Now, in ∆AQO, we have

Hence, the car will reach the tower from Q in 3 seconds.

Question 7.
In Fig. 11.42, ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ = JK = KP. If AB = 0.5 m and AP = BQ = 1.8 m, find the lengths of AC, BD, RN and LM.
Solution:
We have,
AP = 1.8 m
AJ = JK = KP = 0.6 m
AK = 2AJ = 1.2 m
In ∆ARJ and ∆BNJ’ we have
AJ = BJ, ∠ARJ = ∠BNJ = 60°
and ∠AJR = ∠BJ’N = 90°
∴ ∆ARJ ≅ ∆BNJ
⇒ RJ = NJ (By AAS congruence criterion)
Similarly, ∆ALK ≅ ∆BMK”
⇒ LK = MK”
In ∆ARJ,


Since ∆ACP ≅ ∆BDQ
So, BD = AC = 2.0784 m
Now, RN = RJ + JJ + J’N
= 2RJ + AB [∵ RJ = J’ N and JJ = AB]
= 2 × 0.3464 +0.5 = 1.1928 m
Length of step LM = LK + KK + KM
= 2LK + AB [∵ LK = K M and KK = AB]
= 2 × 0.6928 + 0.5 = 1.8856 m
Thus, length of each leg = 2.0784 m = 2.1 m
Length of step RN = 1.1928 m = 1.2 m
and, length of step LM = 1.8856 m = 1.9 m

Question 8.
Two poles of equal heights are standing opposite to each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Solution:

Let AB and CD be two poles of equal height h metre and let P be any point between the poles, such that
∠APB = 60° and ∠DPC = 30°
The distance between two poles is 80m.(Given)
Let AP = x m, then PC = (80 – x) m.
h’m Now, in ∆APB, we have

Now, putting the value of x in equation (i), we have
h = √3 × 20 = 20 √3
Hence, the height of the pole is 20 √3 m and the distance of the point from first pole is 20 m and that of the second pole is 60 m.

Question 9.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (Fig. 11.44). Find the height of the tower and the width of the canal.
Solution:
Let height of the tower be h metres and width of the canal be x metres, so AB = h m and BC = x m
Now in ∆ABC, we have

Now, putting the value of x in equation (i), we have
h = √3 × 10 = 10√3
⇒ h = 10 73 m
Hence, height of the tower is 10 √3 m and width of the canal is 10 m.

Question 10.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 metres away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and the width of the river.
Solution:
Let AB be the tree of height metres standing on the bank of a river. Let C be the position of man standing on the opposite bank of the river such that BC = x m. Let D be the new position of the man. It is given that CD = 40 m and the angles of elevation of the top of the tree at C and D are 60° and 30°, respectively, i.e.,
∠ACB = 60° and ∠ADB = 30°.
In ∆ACB, we have


Hence, the height of the tree is 34.64 m and width of the river is 20 m.

Question 11.
The angles of elevation and depression of the top and bottom of a lighthouse from the top of a building, 60 m high, are 30° and 60° respectively. Find
(i) the difference between the heights of the lighthouse and the building.
(ii) distance between the lighthouse and the building.
Solution:
Let AB be the building and CE be the lighthouse (Fig. 11.46).
In right-angled ∆ABC,

= √3 DE = 20 √3
⇒ DE = 20
∴ (i) Difference between the heights of lighthouse and building = EC – DC = DE = 20 m
and (ii) Distance between the lighthouse and the building = BC = 34.64 m.

Question 12.
In Fig. 11.47, from the top of a building AB, 60 metres high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60°, respectively. Find
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post.
Solution:
Given AB is the building and CD is the vertical lamp post. Then, DE is the horizontal distance between AB and CD. Let CD = h metres.
Then
∠EDB = 30° and ∠ACB = 60°, AE = CD = h metres and EB = (60 -h) m
Now, in ∆ABC

⇒ 60 – h = 20, i.e., h = 40 m
∴ (i) Horizontal distance between AB and CD = 20 √3 m = 20 × 1.732 = 34.64 m
(ii) The height of lamp post = 40 m

Question 13.
A boy standing on a horizontal plane finds a bird flying at a distance an elevation of 30°. A girl standing on the roof of 20 metre high building, finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.
Solution:
Let B be the position of bird. O and P be the positions of boy and girl respectively and PQ be the building
We have, ∠AOB = 30° and ∠BPM = 45°
Now, in ∆AOB we have

Hence, distance of bird from girl is 30 √2 m.

Question 14.
The angles of depression of the top and the bottom of a 8 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building and the distance between the two buildings.
Solution:
In Fig. 11.49, PC denotes the multi-storeyed building and AB denotes the 8 m tall building. We are interested to determine the height of the multi-storeyed building, i.e., PC and the distance between the two buildings, i.e., AC.
Let PD = x m
In right ∆PDB, we have

From (i), BD = [4(√3 + 1)] √3 = 4(3 + √3 )]
So, the height of the multi-storeyed building is {4( √3 + 1) +8} m = 4(3 + √3) m
and the distance between the two buildings is also 4(3 + √3) m.

Question 15.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [Use √3 = 1.73]
Solution:

Let CD be the tower which is at a distance of 120m from A.
BD = x be the length of flagstaff.

120 √3 = x + 120
= 120 × 1.73 – 120
x = 120 (1.73 – 1) = 120 × 0.73
x = 87.6 m

Question 16.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Let AB be the building of height h m and CD be the tower of height 50 m. We have,
∠ACB = 30° and ∠DAC = 60°
Now, in ∆ACD, we have

Hence, the height of the building is 16\(\frac{2}{3}\)m.

Question 17.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (Take √3 = 1.732)
Solution:
Let height of tower be x m and distance of
point from tower be y m.


= x + 5 = 3x
⇒ x = \(\frac{5}{2}\) = 2.5
Height of tower = 2.5 m
Distance of point from tower = y = √3x
= (2.5 x 1.732) or 4.33 m

Question 18.
From the top of a tower, 100 m high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45o. Find the distance between the cars.[Take √3 = 1.732]
Solution:
Let AQ be the tower of height 100m. Car B and Car Care in opposite direction and at distance
of x m and y m respectively.
In ∆ABO,

Distance between the cars = x + y
= 100 + 100√3 [From equation (i) and (ii)]
= 100 (1 + √3 )
= 100 (1 + 1.732) = 273.2 m

Some Applications of Trigonometry Class 10 Extra Questions HOTS

Question 1.
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
Solution:
In Fig. 11.54, let C represents the position of the man on the deck of the ship, A represents the top of hill and D its base.
Now in right-angled triangle CWD,

Now, AD = AB + BD = 30 m + 10 m = 40 m.
Therefore, the distance of the hill from the ship = 17.3 m and the height of the hill = 40 m

Question 2.
A spherical balloon of radius r subtends an angle θ at the eye of an observer. If the angle of elevation of its centre is Ø, find the height of the centre of the balloon.
Solution:
In Fig. 11.55, O is the centre of balloon, whose radius OP = rand ∠PAQ = 0. Also, ∠OAB = Ø.
Let the height of the centre of the balloon be h. Thus OB = h.
Now, from ∆OAP,

Question 3.
From a window (h metres high above the ground) of a house in a street, the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are θ and Ø respectively. Show that the height of the opposite house is h (1 + tan θ cot Ø).
Solution:
Let W be the window and AB be the house on the opposite side.
Then, WP is the width of the street (Fig. 11.56).
Let AP = h’ m

⇒ h’ = WP tan θ
⇒ h’ = h cot Ø tan θ
∴ Height of house = h’ + h
= h cot Ø tan θ + h = h (1 + tan θ cot Ø)

Question 4.
The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet plane is flying at a constant height of
1500√3 m find the speed of the jet plane.
Solution:
Let P and Q be the two positions of the plane and let A be the point of observation. Let ABC be the horizontal line through A. It is given that angles of elevation of the plane in two positions P and Q from a point A are 60° and 30°, respectively,
Then, ∠PAB = 60°, ∠QAB = 30°
It is also given that PB = 1500√3 metres
In ∆ABP, we have

Question 5.
If the angle of elevation of a cloud from a point h metres above a lake is a and the angle of depression of its reflection in the lake is B, prove that the height of the cloud is \(\frac { h(tanß-tanα) }{ tan ß – tan α }\)

Solution:
Let AB be the surface of the lake and let P be a point of observation (Fig. 11.58) such that AP = h metres. Let C be the position of the cloud and C’ be its reflection in the lake. Then, CB = C’ B. Let PM be perpendicular from P on CB. Then, ∠CPM = a and ∠MPC’ = B.
Let CM = x.
Then, CB = CM + MB = CM + PA = x + h
In ∆CPM, we have

Question 6.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow.
Solution:
Let AB be the flagstaff and BC be the length of its shadow when the Sun rays meet the ground at an angle of 60°. Let o be the angle between the Sun rays and the ground when the length of the shadow of the flagstaff is BD. Let h be the height of the flagstaff (Fig. 11.59).
Let BC = x
∴ BD = 3x and CD = 2x
In ∆ABC, we have

Question 7.
From an aeroplane vertically above a straight horizontal plane, the angles of depression of two consecutive kilometre stones on the opposite sides of the aeroplane are found to be α and β. Show that the height of the aeroplane is = \(\frac { tanα.tanβ }{ tanα+tanβ }\)
Solution:
In Fig. 11.60, let P be the position of plane, A and B be the positions of two stones one kilometre apart. Angles of depression of stones A and B are a and ß respectively.
Let PC = h.
In right-angled triangle ACP, we have

Question 8.
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of the cliff at an angle of Ø, it is found that the angle of elevation is α. Show that the height of the cliff is \(\frac {k(cos\phi-sin\phi cot\alpha)}{cot\theta-cot\alpha}\) metres.
Solution:
Let AB be the cliff and O be the fixed point such that ∠AOB = θ. Let ∠AOC = Ø and OC = k m.
From C, draw CD and CE perpendiculars on AB and OA, respectively. Now, ∠DCB = a. Let h be the height of the cliff AB.
In ∆COE, we have

Hence Proved.

Question 9.
The angle of elevation of the top of a tower from a point A due south of the tower is a and from B due east of the tower is β. if AB = d, show that the height of the tower is \(\frac {d}{\sqrt{{cot}^{2}}\alpha+{cot}^{2}\beta}\).
Solution:
Let OC be the tower. Let height of tower OC be h. A and B be two points due south and east of tower at O.
In ∠AOC, ∠O = 90°

Question 10.
From the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 45° and 30° respectively. Find the height of the hill.
Solution:
Let the height of the hill be hm, C and D are two consecutive stones having distance 1000 m between them and AC = x m.
In ∆ABC,
tan 45° = \(\frac{h}{x}\)
⇒ x = h ….(i)
In ∆ABD,

Hence, the height of the hill = 500(√3 + 1)m.

Here we are providing Circles Class 10 Extra Questions Maths Chapter 10 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Circles with Answers Solutions

Extra Questions for Class 10 Maths Chapter 10 Circles with Solutions Answers

Circles Class 10 Extra Questions Very Short Answer Type

Question 1.
If a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
Solution:

OA ⊥ PA (∵ radius is ⊥ to tangent at point of contact)
∴ In ∆OAP, we have
PO² = PA² + AO²
⇒ (17)² = (PA)² + (8)²
(PA)² = 289 – 64 = 225
⇒ PA = √225 = 15
Hence, the length of the tangent from point P is 15 cm.

Question 2.
The length of the tangent to a circle from a point P, which is 25 cm away from the centre, is 24 cm. What is the radius of the circle?
Solution:

∵ OQ ⊥ PQ
∴ PQ² + QO² = OP²
⇒ 25² = OQ² + 24²
or OQ = √625 – √576
= √49 = 7 cm

Question 3.
In Fig. 8.6, ABCD is a cyclic quadrilateral. If ∠BAC = 50° and ∠DBC = 60° then find ∠BCD.
Solution:

Here ∠BDC = ∠BAC = 50° (angles in same segment are equal)
In ABCD, we have
∠BCD = 180° – (∠BDC + ∠DBC)
= 180° – (50° + 60°)= 70°

Question 4.
In Fig. 8.7, the quadrilateral ABCD circumscribes a circle with centre O. If ∠AOB = 115°, then find ∠COD.
Solution:

∵ ∠AOB = ∠COD (vertically opposite angles)
∴ ∠COD = 115°

Question 5.
In Fig. 8.8, AABC is circumscribing a circle. Find the length of BC.

Solution:
AN = AM = 3 cm [Tangents drawn from an external point]
BN = BL = 4 cm [Tangents drawn from an external point]
CL = CM = AC – AM = 9 – 3 = 6 cm
⇒ BC = BL + CL = 4 + 6 = 10 cm.

Question 6.
In Fig. 8.9, O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ. Find ∠POQ.
Solution:

∠OPQ = 90° – 50° = 40°
OP = OQ [Radii of a circle]
∠OPQ = ∠OQP = 40°
(Equal opposite sides have equal opposite angles)
∠POQ = 180° – ∠OPQ – ∠OQP
= 180° – 40° – 40° = 100°

Question 7.
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then find the length of each tangent.
Solution:

In Fig. 8.10
∆AOP ≅ ∆BOP (By SSS congruence criterion)
∠APO = ∠BPO = \(\frac{60°}{2}\) = 30°
In ∆AOP, OA ⊥ AP
∴ tan 30° = \(\frac{OA}{AP}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{3}{AP}\)
⇒ AP = 3√3 cm

Question 8.
If radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
Solution:

OA = 4 cm, OB = 5 cm
Also, OA ⊥ BC
∴ OB² = OA² + AB²
⇒ 5² = 4² + AB²
⇒ AB = √25 – √16 = 3 cm
⇒ BC = 2 AB = 2 × 3 = 6 cm

Question 9.
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° then find ∠OPQ.
Solution:

∠OQP = 90°
∠QOP = 180° – 120° = 60°
∠OPQ = 180° – ∠OQP – ∠QOP
= 180° – 90° – 60°
= 30°

Question 10.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.

Solution:
∵ PA = PB ⇒ ∠BAP = ∠ABP = 50°
∴ ∠APB = 180° – 50° – 50° = 80°
∴ ∠AOB = 180° – 80° = 100°

Question 11.
In PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.
Solution:

∠ACB = 90° (Angle in the semicircle)
∠CAB = 30° (given)
In ∆ABC,
90° + 30° + ∠ABC = 180°
⇒ ∠ABC = 60°
Now, ∠PCA = ∠ABC (Angles in the alternate segment)
∴ ∠PCA = 60°
or
Construction: Join O to C.
∠PCO = 90° [∵ Line joining centre to point of contact is perpendicular to PQ]
In ∆AOC, OA = OC [Radii of circle]
∴ ∠OAC = ∠OCA = 30° [Equal sides have equal opp. angles]
Now, ∠PCA = ∠PCO – ∠ACO
= 90° – 30° = 60°

Question 12.
In fig. 8.16, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Solution:

PQ = PR = 5 cm [∵ Tangents drawn from external point are equal] PK
∴ PS = 2PQ = 10 cm [∵ Perpendicular drawn from centre to the chord bisects the chord]

Circles Class 10 Extra Questions Short Answer Type 1

State true or false for each of the following and justify your answer (Q. 1 to 3)

Question 1.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Solution:

True, Join OC,
∠ACB = 90° (Angle in semi-circle)
∴ ∠OBC = 180o – (90° + 30°) = 60°
Since, OB = OC = radii of same circle [Fig. 8.16]
∴ ∠OBC = ∠OCB = 60°
Also, ∠OCD = 90°
⇒ ∠BCD = 90° – 60° = 30°
Now, ∠OBC = ∠BCD + ∠BDC (Exterior angle property)
⇒ 60° = 30° + ∠BDC
⇒ ∠BDC = 30°
∵ ∠BCD = ∠BDC = 30°
∴ BC = BD

Question 2.
The length of tangent from an external point P on a circle with centre O is always less than OP.

Solution:
True, let PQ be the tangent from the external point P.
Then ∆PQO is always a right angled triangle with OP as the hypotenuse. So, PQ is always less than OP.

Question 3.
If angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre 0 is 90°, then OP = a√2.

Solution:
True, let PQ and PR be the tangents
Since ∠P = 90°, so ∠QOR = 90°
Also, OR = OQ = a
∴ PQOR is a square

Question 4.
In Fig. 8.20, PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PA = 15 cm, find the perimeter of ∆PCD.

Solution:
∵ PA and PB are tangent from same external point
∴ PA = PB = 15 cm
Now, Perimeter of ∆PCD = PC + CD + DP = PC + CQ + QD + DP
= PC + CA + DB + DP
= PA + PB = 15 + 15 = 30 cm

Question 5.
In Fig. 8.21, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.

Solution:
PA = PC + CA = PC + CQ [∵ CA = CQ (tangents drawn An from external point are equal)]
⇒ 12 = PC + 3 = PC = 9 cm
∵ PA = PB = PA – AC = PB – BD
⇒ PC = PD
∴ PD = 9 cm
Hence, PC + PD = 18 cm

Question 6.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.

Solution:
Let the tangents to a circle with centre O be ABC and XYZ.
Construction : Join OB and OY.
Draw OP||AC
Since AB||PO
∠ABO + ∠POB = 180° (Adjacent interior angles)
∠ABO = 90° (A tangent to a circle is perpendicular to the radius through the point of contact)
90° + ∠POB = 180° = ∠POB = 90°
Similarly ∠POY = 90°
∠POB + ∠POY = 90° + 90° = 180°
Hence, BOY is a straight line passing through the centre of the circle.

Question 7.
If from an external point P of a circle with centre 0, two tangents PQ and PR are drawn such that QPR = 120°, prove that 2PQ = PO.

Solution:
Given, ∠QPR = 120°
Radius is perpendicular to the tangent at the point of contact.
∠OQP = 90°
⇒ ∠QPO = 60°
(Tangents drawn to a circle from an external point are equally inclined to the segment, joining the centre to that point)

2PQ = PO

Question 8.
In Fig. 8.24, common tangents AB and CD to two circles with centres , and 0, intersect at E. Prove that AB = CD.

Solution:
AE = CE and BE = ED [Tangents drawn from an external point are equal]
On addition, we get
AE + BE = CE + ED
∠QPO = 60°
⇒ AB = CD

Question 9.
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
OR
In Fig. 8.25, if AB = AC, prove that BE = EC.
[Note: D, E, F replace by F, D, E]

Solution:

Given, AB = AC
We have, BF + AF = AE + CE ….(i)
AB, BC and CA are tangents to the circle at F, D and E respectively.
∴ BF = BD, AE = AF and CE = CD ….(ii)
From (i) and (ii)
BD + AE = AE + CD (∵ AF = AE)
⇒ BD = CD

Question 10.
In Fig. 8.27, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR.

Solution:
In the given figure,
AP = AR
BR = BQ
XP = XQ [Tangent to a circle from an external point are equal]
XA + AP = XB + BQ
XA + AR = XB + BR [AP = AR, BQ = BR]

Question 11.
In Fig. 8.28, a circle is inscribed in a AABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.

Solution:
Let AD = AF = x
∴ DB = BE = 12 – x
and CF = CE = 10 – x
BC = BE + EC
⇒ 8 = 12 – x + 10 – x
⇒ x = 7
∴ AD = 7 cm, BE = 12 – 7 = 5 cm, CF = 10 – 7 = 3 cm

Question 12.
In Fig. 8.29, AP and BP are tangents to a circle with centre 0, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.

Solution:
PA = PB (Tangents from an external point are equal)
and ∠APB = 60°
⇒ ∠PAB = ∠PBA = 60°
∴ ∆PAB is an equilateral triangle.
Hence AB = PA = 5 cm.

Question 13.
In Fig. 8.30 from an external point P, two tangents PT and PS are drawn to a circle with centre 0 and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°.

Solution:
Let ∠TOP = θ
∴ cos θ = \(\frac{OT}{OP}\) = \(\frac{r}{2r}\) =\(\frac{1}{2}\)
⇒ cos θ = cos 60°
⇒ θ = 60°
Hence, ∠TOS = 120°
In ∆OTS, OT = OS [Radii of circle]
⇒ ∠OTS = ∠OST = \(\frac{60^{\circ}}{2}\) = 30°

Question 14.
In Fig. 8.31, are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP.

Solution:
OA = 6 cm, OB = 4 cm, AP = 8 cm
OP² = OA² + AP² = 36 + 64 = 100
⇒ OP = 10 cm
BP² = OP² – OB² = 100 – 16 = 84
⇒ BP = 2√21 cm

Question 15.
In fig. 8.32, PQ is a tangent from an external point P to a circle with centre ( and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find R 21 + 22.

Solution:
∵ ∠POR = 130o = ∠ROT [∵ Angle subtended by an arc at the centre is double than the angle subtended by it at any part of circumference]
∠2 = \(\frac{1}{2}\) ∠ROT = \(\frac{1}{2}\) × 130° = 65°
∠POQ = 180° – 130° = 50° [Linear pair]
and ∠Q = 90°
∴ ∠1 = 40°[∵ Line drawn from centre to the point of contact is perpendicular to the tangent]
Hence ∠2 + ∠1 = 65° + 40° = 105° .

Circles Class 10 Extra Questions Short Answer Type 2

Question 1.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre 0 at a point so that OQ = 12 cm. Find the length of PQ.

Solution:
We have, ∠OPQ = 90°
OQ = 12 cm and OP = 5 cm
∴ By Pythagoras Theorem
OQ² = OP² + QP²
⇒ 122 = 52 + QP²
⇒ QP² = 144 – 25 = 119
= QP = √119 cm

Question 2.
From a point l, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
Solution:

Let QT be the tangent and OT be the radius of circle. Therefore
OT ⊥ QT i.e., ∠OTQ = 90°
and OQ = 25 cm and QT = 24 cm
Now, by Pythagoras Theorem, we have
OQ² = QT² + OT²
⇒ 25² = 24² + OT²
⇒ OT² = 25² – 24²
⇒ 625 – 576
OT² – 49
∴ OT = 7 cm

Question 3.
In Fig. 8.35, if TP and TQ are the two tangents to a circle with centre 0 so that ∠POQ = 110°, then find ∠PTQ.
Solution:

Since TP and TQ are the tangents to the circle with centre O
So, OPIPT and OQ ⊥ QT
⇒ ∠OPT = 90°, ∠OQT = 90° and ∠POQ = 110°
So, in quadrilateral OPTQ, we have
∠POQ + ∠OPT + ∠PTQ + ∠TQO = 360°
⇒ 110° + 90° + ∠PTQ + 90° = 360°
⇒ ∠PTQ + 290° = 360°
∴ ∠PTQ = 360° – 290°
= ∠PTQ = 70°

Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:

Let AB be the diameter of the given circle with centre O, and two tangents PQ and LM are drawn at the end of diameter AB respectively.
Р. Now, since the tangent at a point to a circle is perpendicular to the radius through the point of contact.
Therefore, OA ⊥ PQ and OB ⊥ LM
i.e., AB ⊥ PQ and also AB ⊥ LM
⇒ ∠BAQ = ∠ABL (each 90°)
∴ PQ||LM (∵ ∠BAQ and ∠ABL are alternate angles)

Question 5.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then find ∠POA.
Solution:

∵ PA and PB are tangents to a circle with centre O,
∴ OA ⊥ AP and OB ⊥ PB
i.e., ∠APB = 80°, ∠OAP = 90°, and ∠OBP = 90°
Now, in quadrilateral OAPB, we have
∠APB + ∠PBO + ∠BOA + ∠OAP = 360°
⇒ 80° + 90° + ∠BOA + 90o = 360°
⇒ 260° + ∠BOA = 360°
∴ ∠BOA = 360° – 260°
⇒ ∠BOA = 100°
Now, in ∆POA and APOB we have
OP = OP (Common)
ОА = ОВ (Radii of the same circle)
∠OAP = ∠OBP = 90°
∴ ∆POA ≅ APOB (RHS congruence condition)
⇒ ∠POA = ∠POB (CPCT)
Now, ∠POA = \(\frac{1}{2}\) = ∠BOA = \(\frac{1}{2}\) × 100 = 50°

Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Solution:
Let O be the centre and P be the point of contact.
Since tangent to a circle is perpendicular to the radius through the point of contact,
∴ ∠OPA = 90° Now, in right ∆OPA we have
OA² = OP² + PA² [By Pythagoras Theorem]
5² = OP² + 4²
= 25 = OP² + 16
⇒ OP² = 25 – 16 = 9
∴ OP = 3cm
Hence, the radius of the circle is 3 cm.

Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:

Let O be the common centre of two concentric circles and let AB be a chord of larger circle
touching the smaller circle at P. Join OP.
Since OP is the radius of the smaller circle and AB is tangent to this circle at P,
∴ OP ⊥ AB
We know that the perpendicular drawn from the centre of a circle to any chord of the circle bisects the chord.
Therefore, AP = BP
In right ∆APO we have
⇒ OA² = AP² + OP²
⇒ 5² = AP² + 3²
⇒ 25 – 9 = AP²
⇒ AP² = 16
⇒ AP = 4
Now, AB = 2.AP = 2 × 4 = 8 [∵ AP = PB]
Hence, the length of the chord of the larger circle which touches the smaller circle is 8 cm.

Question 8.
Prove that the tangents drawn at the ends of a chord of circle make equal angles with the chord.
Solution:

Given: A circle with centre O, PA and PB are tangents drawn at the ends A and B on chord AB.
To prove: ∠PAB = ∠PBA
Construction: Join OA and OB.
Proof: In ∆OAB we have
ОА = ОВ … (i) [Radii of the same circle]
∠2 = ∠1 … (ii) [Angles opposite to equal sides of a A]
Also (∠2 + ∠3 = ∠1 + 24) …(iii) [Both 90° as Radius ⊥ Tangent]
Subtracting (ii) from (iii), we have
∴ ∠3 = ∠4 = ∠PAB = ∠PBA

Question 9.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Solution:
Let LM be tangent drawn at the point P on the circle with centre O. Join OP. If possible, let PQ be perpendicular to LM, not passing through O.
Now, since tangent at a point to a circle is perpendicular to the radius through the point.
∴ OP ⊥ LM ⇒ ∠OPM = 90°
Also, ∠QPM = 90° (as assumed above)
∴ ∠OPM = ∠QPM,
which is possible only when points O and I coincide
Hence, the perpendicular at the point of contact to tangent to a circle passes through the centre.

Question 10.
A quadrilateral ABCD is drawn to circumscribe a circle (Fig. 8.42). Prove that AB + CD = AD + BC.
OR
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA

Solution:
Since lengths of two tangents drawn from an external point of circle are equal,
Therefore, AP = AS, BP = BQ and DR = DS
CR = CQ (Where P, Q, R and S are the points of contact]
Adding all these, we have
(AP + BP) + (CR + RD) = (BQ + CQ) + (DS + AS)
⇒ AB + CD = BC + DA

Question 11.
A circle is touching the side BC of AABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ = \(\frac{1}{2}\) (perimeter of ∆ABC).
Solution:

Since tangents from an exterior point to a circle are equal in length.
∴ BP = BQ [Tangents from B] …(i)
CP = CR [Tangents from C] … (ii)
and, AQ = AR [Tangents from A] …(iii)
From (iii), we have
AQ = AR
⇒ AB + BQ = AC + CR
AB + BP
⇒ AC + CP (Using (i) and (ii)] …(iv)
Now, perimeter of AABC = AB + BC + AC
= AB + (BP.+ PC) + AC
= (AB + BP) + (AC + PC)
= 2(AB + BP) [Uisng (iv)]
= 2(AB + BQ) = 2AQ [Using (i)]
AQ = \(\frac{1}{2}\) (Perimeter of ∆ABC)

Question 12.
The difference between the radii of the smaller circle and the larger circle is 7 cm and the difference between the areas of the two circles is 1078 sq. cm. Find the radius of the smaller circle.
Solution:
Given: r₂ – r₁ = 7 (r₂ > r₁) …(i)
and π(r₂² – r₁²) = 1078
π (r₂ – r₁) (r₂ + r₁) = 1078
π (r₂ + r₁) = 1078 [(From equation (i)]
⇒ r₂ + r₁ = \(\frac{1078 \times 7}{22 \times 7}\) = 49…(ii)
Adding (i) and (ii), we get
2r₂ = 56
⇒ r₂ = 28 cm
r₁ = 21 cm [From equation (ii)]
∴ Radius of smaller circle = 21 cm.

Circles Class 10 Extra Questions Long Answer Type 1

Question 1.
Prove that the tangent to a circle is perpendicular to the radius through the point of contact.
Solution:
Given: A circle C(O,r) and a tangent AB at a point P.
To Prove: OP ⊥ AB.
Construction: Take any point l, other than P, on the tangent AB. Join OQ. Suppose OQ meets the circle at R.
Proof: We know that among all line segments joining the point to a point on AB, the shortest one is perpendicular to AB. So, to prove that OP ⊥ AB it is sufficient to prove that OP is shorter than any other segment joining O to any point of AB.

Clearly, OP = OR [Radii of the same circle]
Now, OQ = OR + RQ
⇒ OQ > OR
⇒ OQ > OP [∵OP = OR]
Thus, OP is shorter than any other segment joining O to any point on AB.
Hence, OP ⊥ AB.

Question 2.
Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Solution:

Given: AP and AQ are two tangents from a point A to a circle C (O, r).
To Prove: AP = AQ
Construction: Join OP, OQ and OA.
Proof: In order to prove that AP = AQ, we shall first prove that ∆OPA ≅ ∆OQA.
Since a tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OP ⊥ AP and OQ ⊥ AQ
⇒ ∠OPA = ∠OQA = 90°
Now, in right triangles OPA and OQA, we have
OP = OQ [Radii of a circle]
∠OPA = ∠OQA [Each 90°]
and OA = OA [Common]
So, by RHS-criterion of congruence, we get
∆OPA ≅ OQA
⇒ AP = AQ [CPCT]
Hence, lengths of two tangents from an external point are equal.

Question 3.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

Let ABCD be a parallelogram such that its sides touch a circle with centre O.
We know that the tangents to a circle from an exterior point are equal in length.
Therefore, we have
AP = AS [Tangents from A]
BP = BQ [Tangents from B] …. (ii)
CR = CQ [Tangents from C] …. (iii)
And DR = DS [Tangents from D] …. (iv)
Adding (i), (ii), (iii) and (iv), we have
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC [∵ ABCD is a parallelogram ∴ AB = CD, BC = DA]
2AB = 2BC ⇒ AB = BC
Thus, AB = BC = CD = AD
Hence, ABCD is a rhombus.

Question 4.
In Fig. 8.47, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
Solution:
Given: PQ = 16 cm
PO = 10 cm

Question 5.
If PQ is a tangent drawn from an external point P to a circle with centre O and QOR is a diameter where length of QOR is 8 cm such that ∠POR = 120°, then find OP and PQ.
Solution:
Let O be the centre and QOR = 8 cm is diameter of a circle. PQ is tangent such that ∠POR = 120°

Question 6.
In Fig. 8.49, two equal circles, with centres O and O’, touch each other at X.OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre 0, at the point C. O’D is perpendicular to AC. Find the value of \(\frac{DO’}{CO}\) .
Solution:

AC is tangent to circle with centre O.
Thus ∠ACO = 90°
In ∆AO’D and ∆AOC
∠ADO’ = ∠ACO = 90°
∠A = ∠A (Common)
∴ ∆AO’D – ∠AOC (By AA similarity)

Question 7.
In Fig. 8.50, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Solution:
In right ∆POT

TE = 8 cm
Let PA = AE = x
(Tangents from an external point to a circle are equal)
In right ∆AET
TA² = TE² + EA²
⇒ (12 – x)² = 64 + x²
⇒ 144 + x² – 24x = 64 + x²
⇒ x = \(\frac{80}{24}\)
⇒ x = 3.3 cm
Thus, AB = 6.6 cm

Circles Class 10 Extra Questions HOTS

Question 1.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:

Let a circle with centre O touches the sides AB, BC, CD and DA of a D quadrilateral ABCD at the points P, Q, R and S respectively. Then, we have to prove that
∠AOB + ∠COD = 180° and ∠AOD + ∠BOC = 180°
Now, Join OP, OQ, OR and OS.
Since the two tangents drawn from an external point to a circle subtend equal angles at the centre.
∴ ∠1 = ∠2, ∠3 = 24, 25 = 26 and 27 = 28 …(i)
Now, 21 + 22 +23 + 24 + 25 +26+ 27 + ∠8 = 360° … (ii)
[sum of all the angles subtended at a point is 360°]
⇒ 2(∠2 + ∠3 + ∠6 + ∠7) = 360° [using equation (i) and (ii)]
= (∠2 + ∠3) + (∠6 + ∠7) = 180°
∠AOB + ∠COD = 180°
again 2(∠1 + ∠8 +∠4 + ∠5) = 360° [from (i) and (ii)]
(∠1 + ∠8) + (∠4 + ∠5) = 180°
∠AOD + ∠BOC = 180°

Question 2.
A triangle ABC [Fig. 8.52] is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
Solution:

Let ∆ABC be drawn to circumscribe a circle with centre O and radius 4 cm and circle touches the sides BC, CA and AB at D, E and 6 cm F respectively.
We have given that CD = 6 cm and BD = 8 cm
∴ BF = BD = 8 cm and CE = CD = 6 cm
{Length of two tangents drawn from an external point of circle are equal}
Now, let AF = AE = x cm
Then, AB = c = (x + 8) cm, BC = a = 14 cm, CA = b = (x + 6) cm
2s = (x + 8) + 14 + (x + 6) 25 = 2x + 28 or s = x + 14
s – a = (x + 14) – 14 = x
s – b = (x + 14) – (x + 6) = 8
s – c = (x + 14) – (x + 8) = 6

Squaring both sides, we have
48x (x + 14) = 16(x + 14)² = 48x (x + 14) – 16 (x + 14)² = 0
16 (x + 14) (3x – (x + 14)] = 0
⇒ 16(x + 14)(2x – 14) = 0
either 16(x + 14) = 0 or 2x – 14 = 0
⇒ x = -14 or 2x = 14
⇒ x = -14 or x = 7
But x cannot be negative so x ≠ – 14 .
∴ x = 7 cm
Hence, the sides AB = x + 8 = 7 + 8 = 15 cm
AC = x + 6 = 7 + 6 = 13 cm.

Question 3.
In Fig. 8.53, XY and X’Y are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and ∠X’Y at B. Prove that ∠AOB = 90°.
Solution:

Join OC. In ∆APO and ∆ACO, we have
AP = AC (Tangents drawn from external point A)
AO = OA (Common)
PO = OC (Radii of the same circle)
∴ ∆APO ≅ ∆ACO (By SSS criterion of congruence)
∴∠PAO = ∠CAO (CPCT)
⇒ ∠PAC = 2∠CAO
Similarly, we can prove that
∆OQB ≅ ∆OCB
∴∠QBO = 2CBO
⇒ ∠CBQ = 22CBO
Now, ∠PAC + ∠CBQ = 180° [Sum of interior angles on the same side of transversal is 180°]
⇒ 2∠CAO + 2∠CBO = 180°
⇒ ∠CAO + ∠CBO = 90°
⇒ 180° – ∠AOB = 90°
[∵ ∠CAO + ∠CBO + ∠AOB = 180°]
⇒ 180° – 90° = ∠AOB
⇒ ∠AOB = 90°

Question 4.
Let A be one point of intersection of two intersecting circles with centres O and Q. The tangents at A to the two circles meet the circles again at B and C respectively. Let the point P be located so that AOPQ is a parallelogram. Prove that P is the circumcentre of the triangle ABC.
Solution:

In order to prove that P is the circumcentre of ∆ABC it is sufficient to show that P is the point of intersection of perpendicular bisectors of the sides of AABC i.e., OP and PQ are perpendicular bisectors of sides AB and AC respectively. Now, AC is tangent at A to the circle with centre at 0 and OA is its radius.
∴ OA ⊥ AC
⇒ PQ ⊥ AC [∵ OAQP is a parallelogram so, OA ||PQ]
Also, Q is the centre of the circle
QP bisects AC [Perpendicular from the centre to the chord bisects the chord]
⇒ PQ is the perpendicular bisector of AC.
Similarly, BA is the tangent to the circle at A and AQ is its radius through A.
∴ BA ⊥ AQ [∵ AQPO is parallelogram]
BA ⊥ OP [∴ OP || AQ]
Also, OP bisects AB [∵ 0 is the centre of the circle]
⇒ OP is the perpendicular bisector of AB. Thus, P is the point of intersection of perpendicular bisectors PQ and PO of sides AC and AB respectively.
Hence, P is the circumcentre of ∆ABC.