Circles Class 10 Extra Questions Maths Chapter 10 with Solutions Answers

Here we are providing Circles Class 10 Extra Questions Maths Chapter 10 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Circles with Answers Solutions

Extra Questions for Class 10 Maths Chapter 10 Circles with Solutions Answers

Circles Class 10 Extra Questions Very Short Answer Type

Question 1.
If a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
Solution:

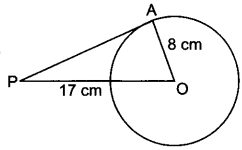
OA ⊥ PA (∵ radius is ⊥ to tangent at point of contact)
∴ In ∆OAP, we have
PO² = PA² + AO²
⇒ (17)² = (PA)² + (8)²
(PA)² = 289 – 64 = 225
⇒ PA = √225 = 15
Hence, the length of the tangent from point P is 15 cm.

Question 2.
The length of the tangent to a circle from a point P, which is 25 cm away from the centre, is 24 cm. What is the radius of the circle?
Solution:

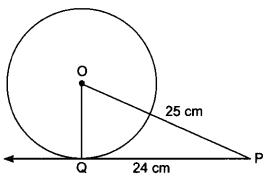
∵ OQ ⊥ PQ
∴ PQ² + QO² = OP²
⇒ 25² = OQ² + 24²
or OQ = √625 – √576
= √49 = 7 cm

Question 3.
In Fig. 8.6, ABCD is a cyclic quadrilateral. If ∠BAC = 50° and ∠DBC = 60° then find ∠BCD.
Solution:

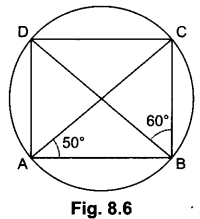
Here ∠BDC = ∠BAC = 50° (angles in same segment are equal)
In ABCD, we have
∠BCD = 180° – (∠BDC + ∠DBC)
= 180° – (50° + 60°)= 70°

Question 4.
In Fig. 8.7, the quadrilateral ABCD circumscribes a circle with centre O. If ∠AOB = 115°, then find ∠COD.
Solution:

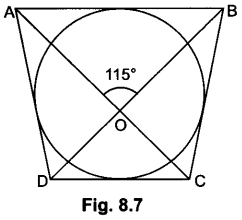
∵ ∠AOB = ∠COD (vertically opposite angles)
∴ ∠COD = 115°

Question 5.
In Fig. 8.8, AABC is circumscribing a circle. Find the length of BC.

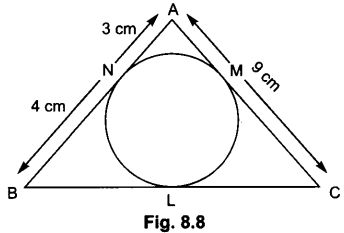
Solution:
AN = AM = 3 cm [Tangents drawn from an external point]
BN = BL = 4 cm [Tangents drawn from an external point]
CL = CM = AC – AM = 9 – 3 = 6 cm
⇒ BC = BL + CL = 4 + 6 = 10 cm.

Question 6.
In Fig. 8.9, O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ. Find ∠POQ.
Solution:

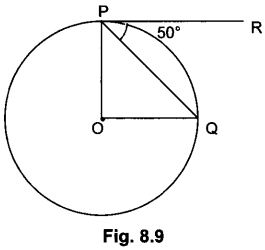
∠OPQ = 90° – 50° = 40°
OP = OQ [Radii of a circle]
∠OPQ = ∠OQP = 40°
(Equal opposite sides have equal opposite angles)
∠POQ = 180° – ∠OPQ – ∠OQP
= 180° – 40° – 40° = 100°

Question 7.
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then find the length of each tangent.
Solution:

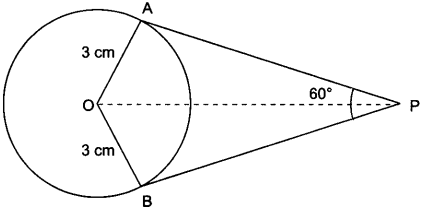
In Fig. 8.10
∆AOP ≅ ∆BOP (By SSS congruence criterion)
∠APO = ∠BPO = \(\frac{60°}{2}\) = 30°
In ∆AOP, OA ⊥ AP
∴ tan 30° = \(\frac{OA}{AP}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{3}{AP}\)
⇒ AP = 3√3 cm

Question 8.
If radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
Solution:

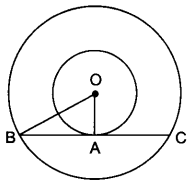
OA = 4 cm, OB = 5 cm
Also, OA ⊥ BC
∴ OB² = OA² + AB²
⇒ 5² = 4² + AB²
⇒ AB = √25 – √16 = 3 cm
⇒ BC = 2 AB = 2 × 3 = 6 cm

Question 9.
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° then find ∠OPQ.
Solution:

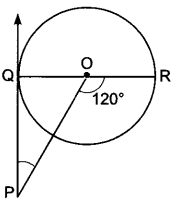
∠OQP = 90°
∠QOP = 180° – 120° = 60°
∠OPQ = 180° – ∠OQP – ∠QOP
= 180° – 90° – 60°
= 30°

Question 10.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.

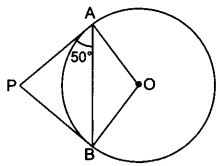
Solution:
∵ PA = PB ⇒ ∠BAP = ∠ABP = 50°
∴ ∠APB = 180° – 50° – 50° = 80°
∴ ∠AOB = 180° – 80° = 100°

Question 11.
In PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.
Solution:

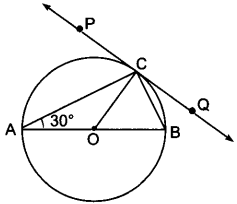
∠ACB = 90° (Angle in the semicircle)
∠CAB = 30° (given)
In ∆ABC,
90° + 30° + ∠ABC = 180°
⇒ ∠ABC = 60°
Now, ∠PCA = ∠ABC (Angles in the alternate segment)
∴ ∠PCA = 60°
or
Construction: Join O to C.
∠PCO = 90° [∵ Line joining centre to point of contact is perpendicular to PQ]
In ∆AOC, OA = OC [Radii of circle]
∴ ∠OAC = ∠OCA = 30° [Equal sides have equal opp. angles]
Now, ∠PCA = ∠PCO – ∠ACO
= 90° – 30° = 60°

Question 12.
In fig. 8.16, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Solution:

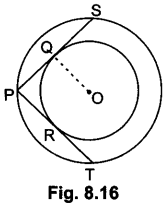
PQ = PR = 5 cm [∵ Tangents drawn from external point are equal] PK
∴ PS = 2PQ = 10 cm [∵ Perpendicular drawn from centre to the chord bisects the chord]

Circles Class 10 Extra Questions Short Answer Type 1

State true or false for each of the following and justify your answer (Q. 1 to 3)

Question 1.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Solution:

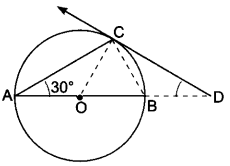
True, Join OC,
∠ACB = 90° (Angle in semi-circle)
∴ ∠OBC = 180o – (90° + 30°) = 60°
Since, OB = OC = radii of same circle [Fig. 8.16]
∴ ∠OBC = ∠OCB = 60°
Also, ∠OCD = 90°
⇒ ∠BCD = 90° – 60° = 30°
Now, ∠OBC = ∠BCD + ∠BDC (Exterior angle property)
⇒ 60° = 30° + ∠BDC
⇒ ∠BDC = 30°
∵ ∠BCD = ∠BDC = 30°
∴ BC = BD

Question 2.
The length of tangent from an external point P on a circle with centre O is always less than OP.

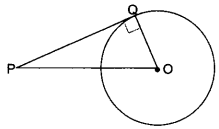
Solution:
True, let PQ be the tangent from the external point P.
Then ∆PQO is always a right angled triangle with OP as the hypotenuse. So, PQ is always less than OP.

Question 3.
If angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre 0 is 90°, then OP = a√2.

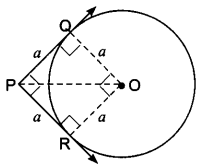
Solution:
True, let PQ and PR be the tangents
Since ∠P = 90°, so ∠QOR = 90°
Also, OR = OQ = a
∴ PQOR is a square

Question 4.
In Fig. 8.20, PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PA = 15 cm, find the perimeter of ∆PCD.

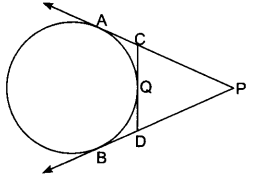
Solution:
∵ PA and PB are tangent from same external point
∴ PA = PB = 15 cm
Now, Perimeter of ∆PCD = PC + CD + DP = PC + CQ + QD + DP
= PC + CA + DB + DP
= PA + PB = 15 + 15 = 30 cm

Question 5.
In Fig. 8.21, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.

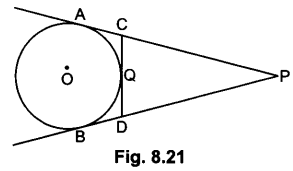
Solution:
PA = PC + CA = PC + CQ [∵ CA = CQ (tangents drawn An from external point are equal)]
⇒ 12 = PC + 3 = PC = 9 cm
∵ PA = PB = PA – AC = PB – BD
⇒ PC = PD
∴ PD = 9 cm
Hence, PC + PD = 18 cm

Question 6.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.

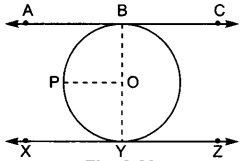
Solution:
Let the tangents to a circle with centre O be ABC and XYZ.
Construction : Join OB and OY.
Draw OP||AC
Since AB||PO
∠ABO + ∠POB = 180° (Adjacent interior angles)
∠ABO = 90° (A tangent to a circle is perpendicular to the radius through the point of contact)
90° + ∠POB = 180° = ∠POB = 90°
Similarly ∠POY = 90°
∠POB + ∠POY = 90° + 90° = 180°
Hence, BOY is a straight line passing through the centre of the circle.

Question 7.
If from an external point P of a circle with centre 0, two tangents PQ and PR are drawn such that QPR = 120°, prove that 2PQ = PO.

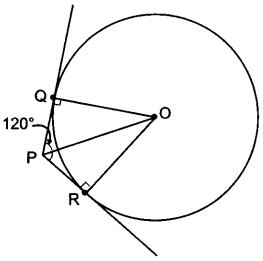
Solution:
Given, ∠QPR = 120°
Radius is perpendicular to the tangent at the point of contact.
∠OQP = 90°
⇒ ∠QPO = 60°
(Tangents drawn to a circle from an external point are equally inclined to the segment, joining the centre to that point)

2PQ = PO

Question 8.
In Fig. 8.24, common tangents AB and CD to two circles with centres , and 0, intersect at E. Prove that AB = CD.

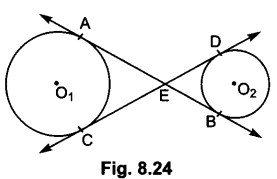
Solution:
AE = CE and BE = ED [Tangents drawn from an external point are equal]
On addition, we get
AE + BE = CE + ED
∠QPO = 60°
⇒ AB = CD

Question 9.
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
OR
In Fig. 8.25, if AB = AC, prove that BE = EC.
[Note: D, E, F replace by F, D, E]

Solution:

Given, AB = AC
We have, BF + AF = AE + CE ….(i)
AB, BC and CA are tangents to the circle at F, D and E respectively.
∴ BF = BD, AE = AF and CE = CD ….(ii)
From (i) and (ii)
BD + AE = AE + CD (∵ AF = AE)
⇒ BD = CD

Question 10.
In Fig. 8.27, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR.

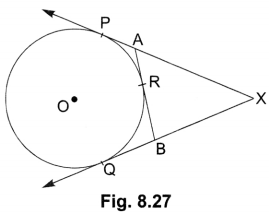
Solution:
In the given figure,
AP = AR
BR = BQ
XP = XQ [Tangent to a circle from an external point are equal]
XA + AP = XB + BQ
XA + AR = XB + BR [AP = AR, BQ = BR]

Question 11.
In Fig. 8.28, a circle is inscribed in a AABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.

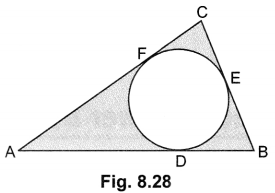
Solution:
Let AD = AF = x
∴ DB = BE = 12 – x
and CF = CE = 10 – x
BC = BE + EC
⇒ 8 = 12 – x + 10 – x
⇒ x = 7
∴ AD = 7 cm, BE = 12 – 7 = 5 cm, CF = 10 – 7 = 3 cm

Question 12.
In Fig. 8.29, AP and BP are tangents to a circle with centre 0, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.

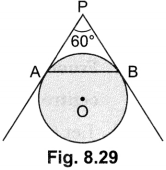
Solution:
PA = PB (Tangents from an external point are equal)
and ∠APB = 60°
⇒ ∠PAB = ∠PBA = 60°
∴ ∆PAB is an equilateral triangle.
Hence AB = PA = 5 cm.

Question 13.
In Fig. 8.30 from an external point P, two tangents PT and PS are drawn to a circle with centre 0 and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°.

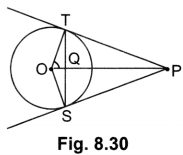
Solution:
Let ∠TOP = θ
∴ cos θ = \(\frac{OT}{OP}\) = \(\frac{r}{2r}\) =\(\frac{1}{2}\)
⇒ cos θ = cos 60°
⇒ θ = 60°
Hence, ∠TOS = 120°
In ∆OTS, OT = OS [Radii of circle]
⇒ ∠OTS = ∠OST = \(\frac{60^{\circ}}{2}\) = 30°

Question 14.
In Fig. 8.31, are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP.

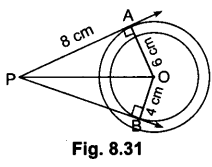
Solution:
OA = 6 cm, OB = 4 cm, AP = 8 cm
OP² = OA² + AP² = 36 + 64 = 100
⇒ OP = 10 cm
BP² = OP² – OB² = 100 – 16 = 84
⇒ BP = 2√21 cm

Question 15.
In fig. 8.32, PQ is a tangent from an external point P to a circle with centre ( and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find R 21 + 22.

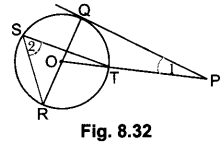
Solution:
∵ ∠POR = 130o = ∠ROT [∵ Angle subtended by an arc at the centre is double than the angle subtended by it at any part of circumference]
∠2 = \(\frac{1}{2}\) ∠ROT = \(\frac{1}{2}\) × 130° = 65°
∠POQ = 180° – 130° = 50° [Linear pair]
and ∠Q = 90°
∴ ∠1 = 40°[∵ Line drawn from centre to the point of contact is perpendicular to the tangent]
Hence ∠2 + ∠1 = 65° + 40° = 105° .

Circles Class 10 Extra Questions Short Answer Type 2

Question 1.
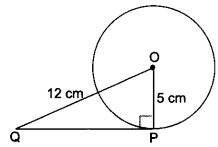
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre 0 at a point so that OQ = 12 cm. Find the length of PQ.

Solution:
We have, ∠OPQ = 90°
OQ = 12 cm and OP = 5 cm
∴ By Pythagoras Theorem
OQ² = OP² + QP²
⇒ 122 = 52 + QP²
⇒ QP² = 144 – 25 = 119
= QP = √119 cm

Question 2.
From a point l, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
Solution:

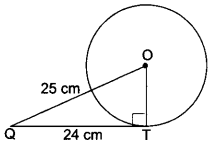
Let QT be the tangent and OT be the radius of circle. Therefore
OT ⊥ QT i.e., ∠OTQ = 90°
and OQ = 25 cm and QT = 24 cm
Now, by Pythagoras Theorem, we have
OQ² = QT² + OT²
⇒ 25² = 24² + OT²
⇒ OT² = 25² – 24²
⇒ 625 – 576
OT² – 49
∴ OT = 7 cm

Question 3.
In Fig. 8.35, if TP and TQ are the two tangents to a circle with centre 0 so that ∠POQ = 110°, then find ∠PTQ.
Solution:

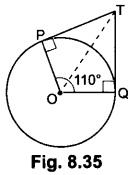
Since TP and TQ are the tangents to the circle with centre O
So, OPIPT and OQ ⊥ QT
⇒ ∠OPT = 90°, ∠OQT = 90° and ∠POQ = 110°
So, in quadrilateral OPTQ, we have
∠POQ + ∠OPT + ∠PTQ + ∠TQO = 360°
⇒ 110° + 90° + ∠PTQ + 90° = 360°
⇒ ∠PTQ + 290° = 360°
∴ ∠PTQ = 360° – 290°
= ∠PTQ = 70°

Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:

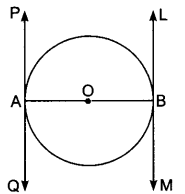
Let AB be the diameter of the given circle with centre O, and two tangents PQ and LM are drawn at the end of diameter AB respectively.
Р. Now, since the tangent at a point to a circle is perpendicular to the radius through the point of contact.
Therefore, OA ⊥ PQ and OB ⊥ LM
i.e., AB ⊥ PQ and also AB ⊥ LM
⇒ ∠BAQ = ∠ABL (each 90°)
∴ PQ||LM (∵ ∠BAQ and ∠ABL are alternate angles)

Question 5.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then find ∠POA.
Solution:

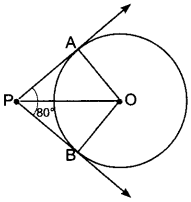
∵ PA and PB are tangents to a circle with centre O,
∴ OA ⊥ AP and OB ⊥ PB
i.e., ∠APB = 80°, ∠OAP = 90°, and ∠OBP = 90°
Now, in quadrilateral OAPB, we have
∠APB + ∠PBO + ∠BOA + ∠OAP = 360°
⇒ 80° + 90° + ∠BOA + 90o = 360°
⇒ 260° + ∠BOA = 360°
∴ ∠BOA = 360° – 260°
⇒ ∠BOA = 100°
Now, in ∆POA and APOB we have
OP = OP (Common)
ОА = ОВ (Radii of the same circle)
∠OAP = ∠OBP = 90°
∴ ∆POA ≅ APOB (RHS congruence condition)
⇒ ∠POA = ∠POB (CPCT)
Now, ∠POA = \(\frac{1}{2}\) = ∠BOA = \(\frac{1}{2}\) × 100 = 50°

Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

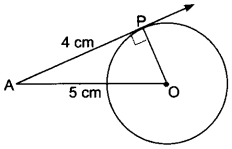
Solution:
Let O be the centre and P be the point of contact.
Since tangent to a circle is perpendicular to the radius through the point of contact,
∴ ∠OPA = 90° Now, in right ∆OPA we have
OA² = OP² + PA² [By Pythagoras Theorem]
5² = OP² + 4²
= 25 = OP² + 16
⇒ OP² = 25 – 16 = 9
∴ OP = 3cm
Hence, the radius of the circle is 3 cm.

Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:

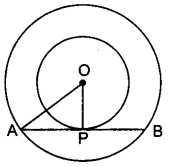
Let O be the common centre of two concentric circles and let AB be a chord of larger circle
touching the smaller circle at P. Join OP.
Since OP is the radius of the smaller circle and AB is tangent to this circle at P,
∴ OP ⊥ AB
We know that the perpendicular drawn from the centre of a circle to any chord of the circle bisects the chord.
Therefore, AP = BP
In right ∆APO we have
⇒ OA² = AP² + OP²
⇒ 5² = AP² + 3²
⇒ 25 – 9 = AP²
⇒ AP² = 16
⇒ AP = 4
Now, AB = 2.AP = 2 × 4 = 8 [∵ AP = PB]
Hence, the length of the chord of the larger circle which touches the smaller circle is 8 cm.

Question 8.
Prove that the tangents drawn at the ends of a chord of circle make equal angles with the chord.
Solution:

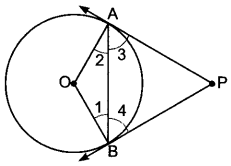
Given: A circle with centre O, PA and PB are tangents drawn at the ends A and B on chord AB.
To prove: ∠PAB = ∠PBA
Construction: Join OA and OB.
Proof: In ∆OAB we have
ОА = ОВ … (i) [Radii of the same circle]
∠2 = ∠1 … (ii) [Angles opposite to equal sides of a A]
Also (∠2 + ∠3 = ∠1 + 24) …(iii) [Both 90° as Radius ⊥ Tangent]
Subtracting (ii) from (iii), we have
∴ ∠3 = ∠4 = ∠PAB = ∠PBA

Question 9.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Solution:
Let LM be tangent drawn at the point P on the circle with centre O. Join OP. If possible, let PQ be perpendicular to LM, not passing through O.
Now, since tangent at a point to a circle is perpendicular to the radius through the point.
∴ OP ⊥ LM ⇒ ∠OPM = 90°
Also, ∠QPM = 90° (as assumed above)
∴ ∠OPM = ∠QPM,
which is possible only when points O and I coincide
Hence, the perpendicular at the point of contact to tangent to a circle passes through the centre.

Question 10.
A quadrilateral ABCD is drawn to circumscribe a circle (Fig. 8.42). Prove that AB + CD = AD + BC.
OR
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA

Solution:
Since lengths of two tangents drawn from an external point of circle are equal,
Therefore, AP = AS, BP = BQ and DR = DS
CR = CQ (Where P, Q, R and S are the points of contact]
Adding all these, we have
(AP + BP) + (CR + RD) = (BQ + CQ) + (DS + AS)
⇒ AB + CD = BC + DA

Question 11.
A circle is touching the side BC of AABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ = \(\frac{1}{2}\) (perimeter of ∆ABC).
Solution:

Since tangents from an exterior point to a circle are equal in length.
∴ BP = BQ [Tangents from B] …(i)
CP = CR [Tangents from C] … (ii)
and, AQ = AR [Tangents from A] …(iii)
From (iii), we have
AQ = AR
⇒ AB + BQ = AC + CR
AB + BP
⇒ AC + CP (Using (i) and (ii)] …(iv)
Now, perimeter of AABC = AB + BC + AC
= AB + (BP.+ PC) + AC
= (AB + BP) + (AC + PC)
= 2(AB + BP) [Uisng (iv)]
= 2(AB + BQ) = 2AQ [Using (i)]
AQ = \(\frac{1}{2}\) (Perimeter of ∆ABC)

Question 12.
The difference between the radii of the smaller circle and the larger circle is 7 cm and the difference between the areas of the two circles is 1078 sq. cm. Find the radius of the smaller circle.
Solution:
Given: r₂ – r₁ = 7 (r₂ > r₁) …(i)
and π(r₂² – r₁²) = 1078
π (r₂ – r₁) (r₂ + r₁) = 1078
π (r₂ + r₁) = 1078 [(From equation (i)]
⇒ r₂ + r₁ = \(\frac{1078 \times 7}{22 \times 7}\) = 49…(ii)
Adding (i) and (ii), we get
2r₂ = 56
⇒ r₂ = 28 cm
r₁ = 21 cm [From equation (ii)]
∴ Radius of smaller circle = 21 cm.

Circles Class 10 Extra Questions Long Answer Type 1

Question 1.
Prove that the tangent to a circle is perpendicular to the radius through the point of contact.
Solution:
Given: A circle C(O,r) and a tangent AB at a point P.
To Prove: OP ⊥ AB.
Construction: Take any point l, other than P, on the tangent AB. Join OQ. Suppose OQ meets the circle at R.
Proof: We know that among all line segments joining the point to a point on AB, the shortest one is perpendicular to AB. So, to prove that OP ⊥ AB it is sufficient to prove that OP is shorter than any other segment joining O to any point of AB.

Clearly, OP = OR [Radii of the same circle]
Now, OQ = OR + RQ
⇒ OQ > OR
⇒ OQ > OP [∵OP = OR]
Thus, OP is shorter than any other segment joining O to any point on AB.
Hence, OP ⊥ AB.

Question 2.
Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Solution:

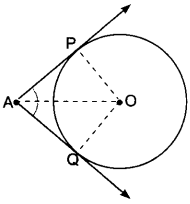
Given: AP and AQ are two tangents from a point A to a circle C (O, r).
To Prove: AP = AQ
Construction: Join OP, OQ and OA.
Proof: In order to prove that AP = AQ, we shall first prove that ∆OPA ≅ ∆OQA.
Since a tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OP ⊥ AP and OQ ⊥ AQ
⇒ ∠OPA = ∠OQA = 90°
Now, in right triangles OPA and OQA, we have
OP = OQ [Radii of a circle]
∠OPA = ∠OQA [Each 90°]
and OA = OA [Common]
So, by RHS-criterion of congruence, we get
∆OPA ≅ OQA
⇒ AP = AQ [CPCT]
Hence, lengths of two tangents from an external point are equal.

Question 3.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

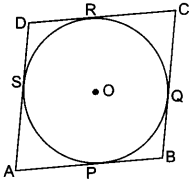
Let ABCD be a parallelogram such that its sides touch a circle with centre O.
We know that the tangents to a circle from an exterior point are equal in length.
Therefore, we have
AP = AS [Tangents from A]
BP = BQ [Tangents from B] …. (ii)
CR = CQ [Tangents from C] …. (iii)
And DR = DS [Tangents from D] …. (iv)
Adding (i), (ii), (iii) and (iv), we have
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC [∵ ABCD is a parallelogram ∴ AB = CD, BC = DA]
2AB = 2BC ⇒ AB = BC
Thus, AB = BC = CD = AD
Hence, ABCD is a rhombus.

Question 4.
In Fig. 8.47, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
Solution:
Given: PQ = 16 cm
PO = 10 cm

Question 5.
If PQ is a tangent drawn from an external point P to a circle with centre O and QOR is a diameter where length of QOR is 8 cm such that ∠POR = 120°, then find OP and PQ.
Solution:
Let O be the centre and QOR = 8 cm is diameter of a circle. PQ is tangent such that ∠POR = 120°

Question 6.
In Fig. 8.49, two equal circles, with centres O and O’, touch each other at X.OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre 0, at the point C. O’D is perpendicular to AC. Find the value of \(\frac{DO’}{CO}\) .
Solution:

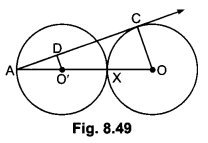
AC is tangent to circle with centre O.
Thus ∠ACO = 90°
In ∆AO’D and ∆AOC
∠ADO’ = ∠ACO = 90°
∠A = ∠A (Common)
∴ ∆AO’D – ∠AOC (By AA similarity)

Question 7.
In Fig. 8.50, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

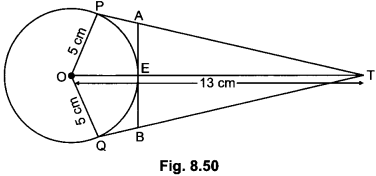
Solution:
In right ∆POT

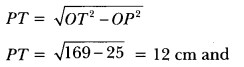
TE = 8 cm
Let PA = AE = x
(Tangents from an external point to a circle are equal)
In right ∆AET
TA² = TE² + EA²
⇒ (12 – x)² = 64 + x²
⇒ 144 + x² – 24x = 64 + x²
⇒ x = \(\frac{80}{24}\)
⇒ x = 3.3 cm
Thus, AB = 6.6 cm

Circles Class 10 Extra Questions HOTS

Question 1.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:

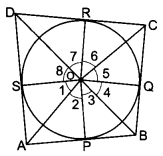
Let a circle with centre O touches the sides AB, BC, CD and DA of a D quadrilateral ABCD at the points P, Q, R and S respectively. Then, we have to prove that
∠AOB + ∠COD = 180° and ∠AOD + ∠BOC = 180°
Now, Join OP, OQ, OR and OS.
Since the two tangents drawn from an external point to a circle subtend equal angles at the centre.
∴ ∠1 = ∠2, ∠3 = 24, 25 = 26 and 27 = 28 …(i)
Now, 21 + 22 +23 + 24 + 25 +26+ 27 + ∠8 = 360° … (ii)
[sum of all the angles subtended at a point is 360°]
⇒ 2(∠2 + ∠3 + ∠6 + ∠7) = 360° [using equation (i) and (ii)]
= (∠2 + ∠3) + (∠6 + ∠7) = 180°
∠AOB + ∠COD = 180°
again 2(∠1 + ∠8 +∠4 + ∠5) = 360° [from (i) and (ii)]
(∠1 + ∠8) + (∠4 + ∠5) = 180°
∠AOD + ∠BOC = 180°

Question 2.
A triangle ABC [Fig. 8.52] is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
Solution:

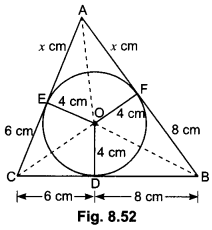
Let ∆ABC be drawn to circumscribe a circle with centre O and radius 4 cm and circle touches the sides BC, CA and AB at D, E and 6 cm F respectively.
We have given that CD = 6 cm and BD = 8 cm
∴ BF = BD = 8 cm and CE = CD = 6 cm
{Length of two tangents drawn from an external point of circle are equal}
Now, let AF = AE = x cm
Then, AB = c = (x + 8) cm, BC = a = 14 cm, CA = b = (x + 6) cm
2s = (x + 8) + 14 + (x + 6) 25 = 2x + 28 or s = x + 14
s – a = (x + 14) – 14 = x
s – b = (x + 14) – (x + 6) = 8
s – c = (x + 14) – (x + 8) = 6

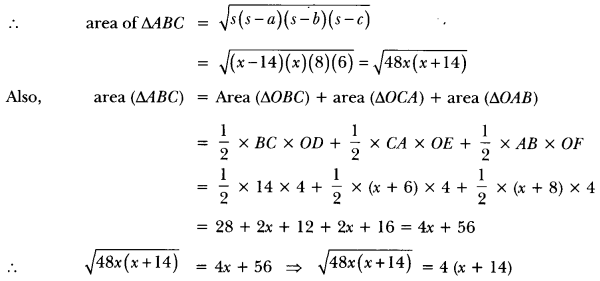
Squaring both sides, we have
48x (x + 14) = 16(x + 14)² = 48x (x + 14) – 16 (x + 14)² = 0
16 (x + 14) (3x – (x + 14)] = 0
⇒ 16(x + 14)(2x – 14) = 0
either 16(x + 14) = 0 or 2x – 14 = 0
⇒ x = -14 or 2x = 14
⇒ x = -14 or x = 7
But x cannot be negative so x ≠ – 14 .
∴ x = 7 cm
Hence, the sides AB = x + 8 = 7 + 8 = 15 cm
AC = x + 6 = 7 + 6 = 13 cm.

Question 3.
In Fig. 8.53, XY and X’Y are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and ∠X’Y at B. Prove that ∠AOB = 90°.
Solution:

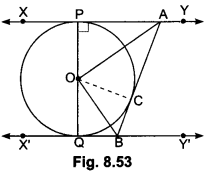
Join OC. In ∆APO and ∆ACO, we have
AP = AC (Tangents drawn from external point A)
AO = OA (Common)
PO = OC (Radii of the same circle)
∴ ∆APO ≅ ∆ACO (By SSS criterion of congruence)
∴∠PAO = ∠CAO (CPCT)
⇒ ∠PAC = 2∠CAO
Similarly, we can prove that
∆OQB ≅ ∆OCB
∴∠QBO = 2CBO
⇒ ∠CBQ = 22CBO
Now, ∠PAC + ∠CBQ = 180° [Sum of interior angles on the same side of transversal is 180°]
⇒ 2∠CAO + 2∠CBO = 180°
⇒ ∠CAO + ∠CBO = 90°
⇒ 180° – ∠AOB = 90°
[∵ ∠CAO + ∠CBO + ∠AOB = 180°]
⇒ 180° – 90° = ∠AOB
⇒ ∠AOB = 90°

Question 4.
Let A be one point of intersection of two intersecting circles with centres O and Q. The tangents at A to the two circles meet the circles again at B and C respectively. Let the point P be located so that AOPQ is a parallelogram. Prove that P is the circumcentre of the triangle ABC.
Solution:

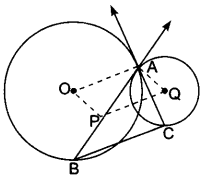
In order to prove that P is the circumcentre of ∆ABC it is sufficient to show that P is the point of intersection of perpendicular bisectors of the sides of AABC i.e., OP and PQ are perpendicular bisectors of sides AB and AC respectively. Now, AC is tangent at A to the circle with centre at 0 and OA is its radius.
∴ OA ⊥ AC
⇒ PQ ⊥ AC [∵ OAQP is a parallelogram so, OA ||PQ]
Also, Q is the centre of the circle
QP bisects AC [Perpendicular from the centre to the chord bisects the chord]
⇒ PQ is the perpendicular bisector of AC.
Similarly, BA is the tangent to the circle at A and AQ is its radius through A.
∴ BA ⊥ AQ [∵ AQPO is parallelogram]
BA ⊥ OP [∴ OP || AQ]
Also, OP bisects AB [∵ 0 is the centre of the circle]
⇒ OP is the perpendicular bisector of AB. Thus, P is the point of intersection of perpendicular bisectors PQ and PO of sides AC and AB respectively.
Hence, P is the circumcentre of ∆ABC.