CBSE Class 10

RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios MCQS

Question 1.
In each of the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.

Solution:
∴ Perpendicular BC – 2 units and
Hypotenuse AC = 3 units
By Phythagoras Theorem, in AABC,
(Hypotenuse)² = (Base)² + (Perpendicular)²
AC² = AB² + BC²
⇒ (3)² = (AB)² + (2)²
⇒ 9 = AB² + 4 ⇒ AB² = 9-4 = 5
AB = √5 units

Question 2.
In a ΔABC, right angled at B, AB = 24 cm, BC = 7 cm. Determine
(i) sin A, cos A
(ii) sin C, cos C.
Solution:

Question 3.
In the figure, find tan P and cot R. Is tan P = cot R ?

Solution:

Question 4.
If sin A = \(\frac { 9 }{ 41 }\), compute cos A and tan A.
Solution:

Question 5.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Question 6.
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
Solution:

Question 7.
If cot 0 = \(\frac { 7 }{ 8 }\), evaluate :

Solution:

Question 8.
If 3 cot A = 4, check whether \(\frac { 1-{ tan }^{ 2 }A }{ 1+{ tan }^{ 2 }A }\) = cos² A – sin² A or not.
Solution:

Question 9.
If tan θ = a/b , Find the Value of \(\frac { cos\theta +sin\theta }{ cos\theta -sin\theta }\).
Solution:

Question 10.
If 3 tan θ = 4, find the value of 4cos θ – sin θ \(\frac { 4cos\theta -sin\theta }{ 2cos\theta +sin\theta }\).
Solution:

Question 11.
If 3 cot 0 = 2, find the value of \(\frac { 4sins\theta -3cos\theta }{ 2sin\theta +6cos\theta }\).
Solution:

Question 12.
If tan θ = \(\frac { a }{ b }\), prove that

Solution:

Question 13.
If sec θ = \(\frac { 13 }{ 5 }\), show that \(\frac { 2sins\theta -3cos\theta }{ 4sin\theta -9cos\theta }\) =3.
Solution:

Question 14.
If cos θ \(\frac { 12 }{ 13 }\), show that sin θ (1 – tan θ) \(\frac { 35 }{ 156 }\).
Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.
If sec θ = \(\frac { 5 }{ 4 }\), find the value of \(\frac { sins\theta -2cos\theta }{ tan\theta -cot\theta }\).
Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21.
If tan θ = \(\frac { 24 }{ 7 }\), find that sin θ + cos θ.
Solution:

Question 22.
If sin θ = \(\frac { a }{ b }\), find sec θ + tan θ in terms of a and b.
Solution:

Question 23.
If 8 tan A = 15, find sin A – cos A.
Solution:

Question 24.

Solution:

Question 25.

Solution:

Question 26.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
∠A and ∠B are acute angles and cos A = cos B
Draw a right angle AABC, in which ∠C – 90°

Question 27.
In a ∆ABC, right angled at A, if tan C =√3 , find the value of sin B cos C + cos B sin C. (C.B.S.E. 2008)
Solution:

Question 28.
28. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = \(\frac { 12 }{ 5 }\) for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = \(\frac { 4 }{ 3 }\) for some angle θ.
Solution:
(i) False, value of tan A 0 to infinity.
(ii) True.
(iii) False, cos A is the abbreviation of cosine A.
(iv) False, it is the cotengent of angle A.
(v) Flase, value of sin θ varies on 0 to 1.

Question 29.

Solution:

Question 30.

Solution:

Question 31.

Solution:

Question 32.
If sin θ =\(\frac { 3 }{ 4 }\), prove that

Solution:

Question 33.

Solution:

Question 34.

Solution:

Question 35.
If 3 cos θ-4 sin θ = 2 cos θ + sin θ, find tan θ.
Solution:

Question 36.
If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
Solution:
∠A and ∠P are acute angles and tan A = tan P Draw a right angled AAPB in which ∠B = 90°

Hope given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

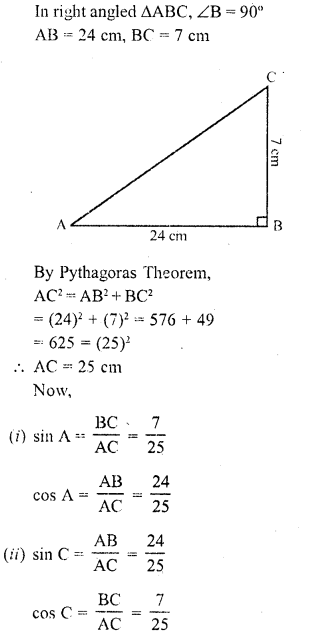
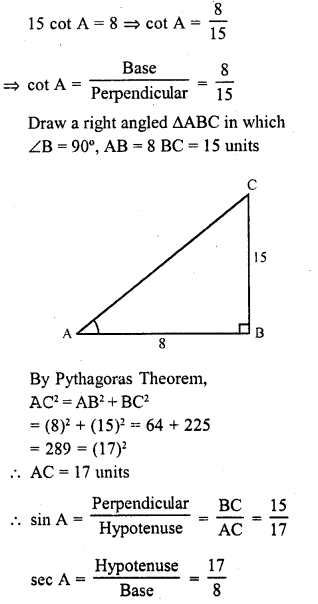
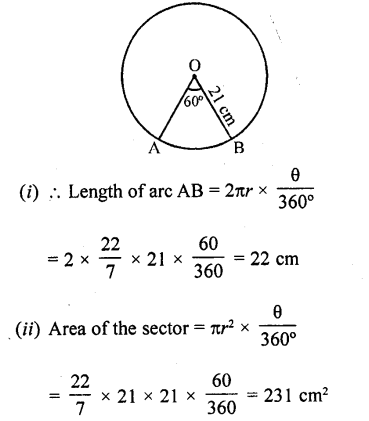
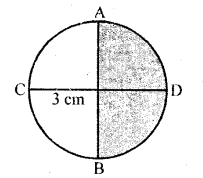
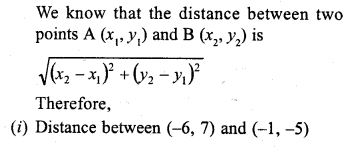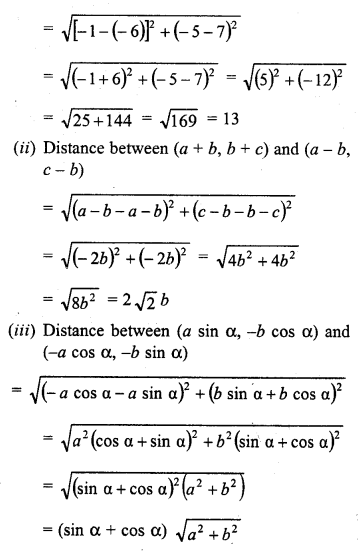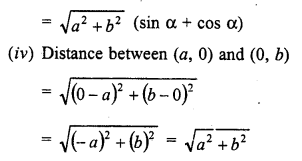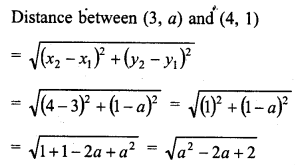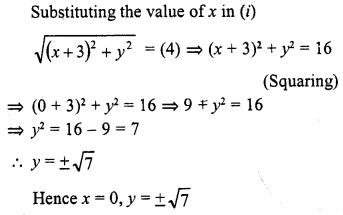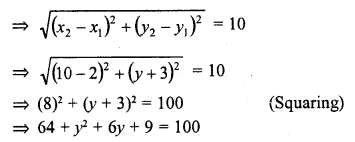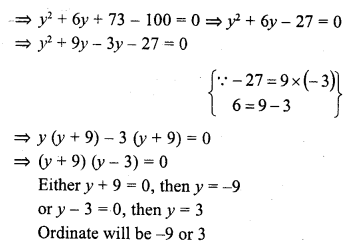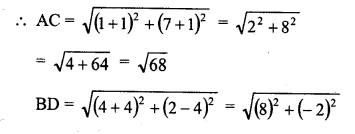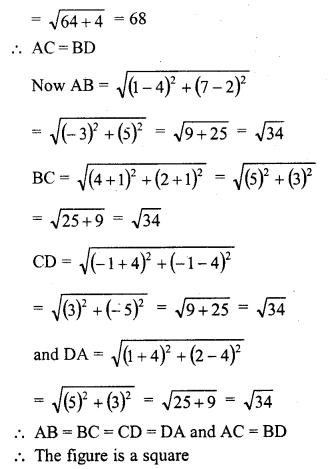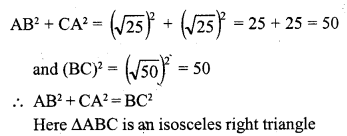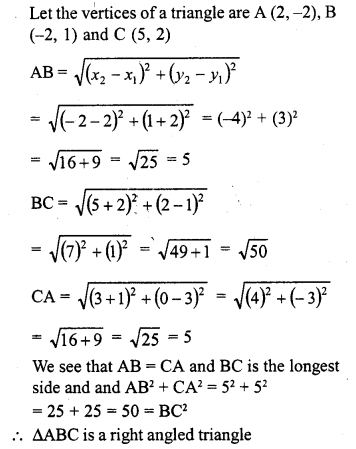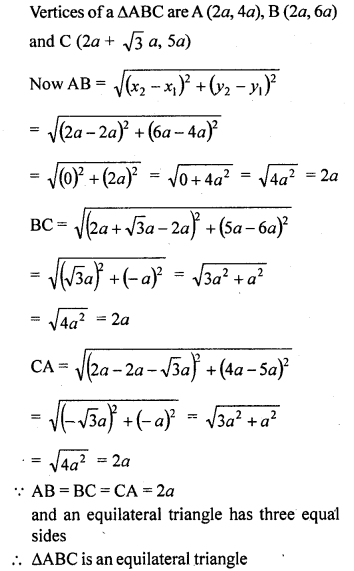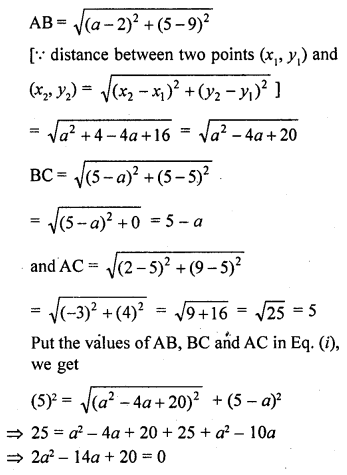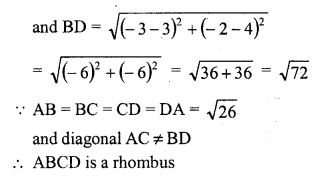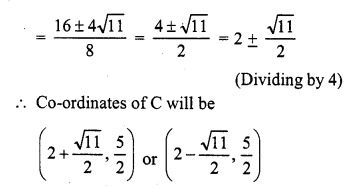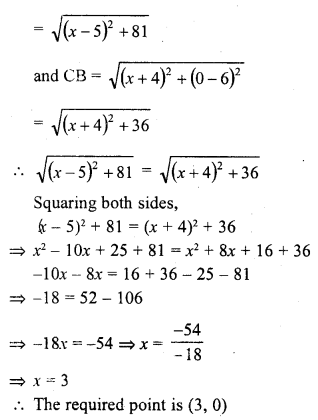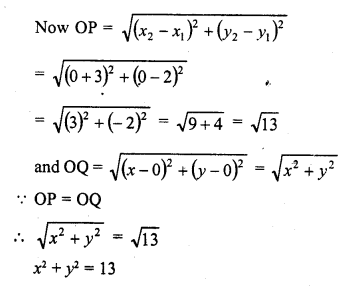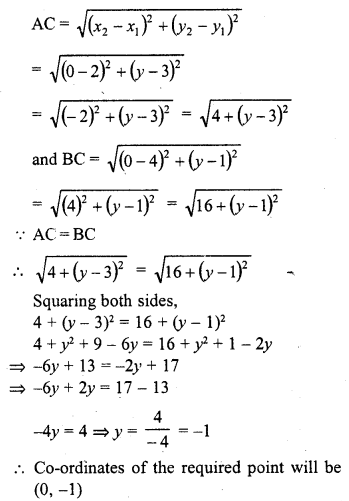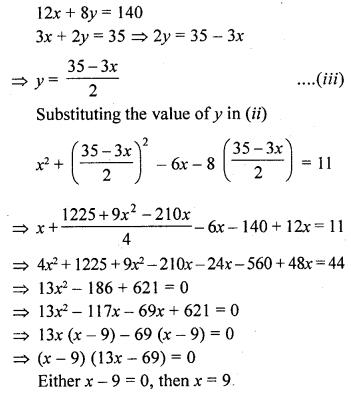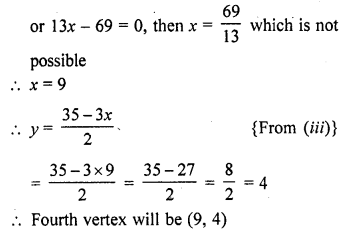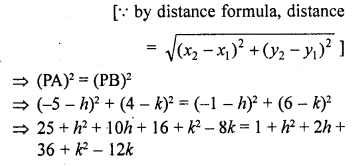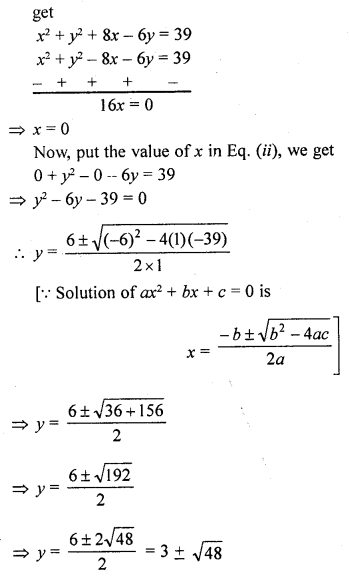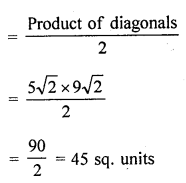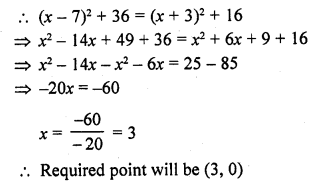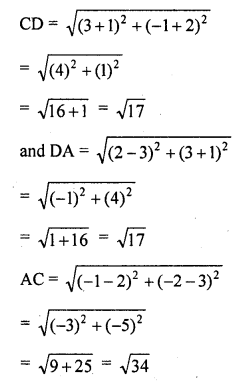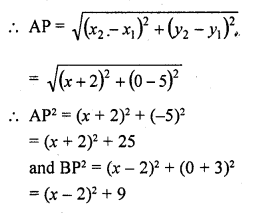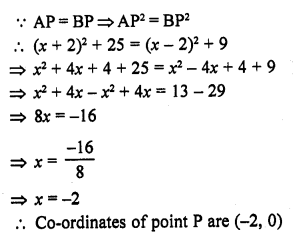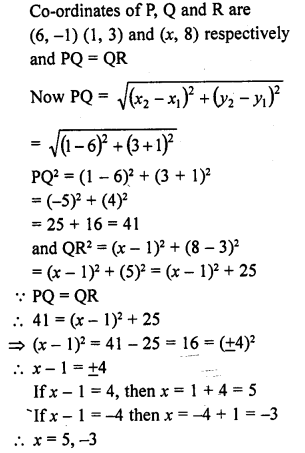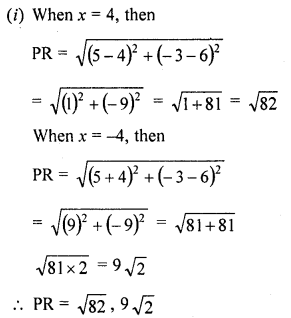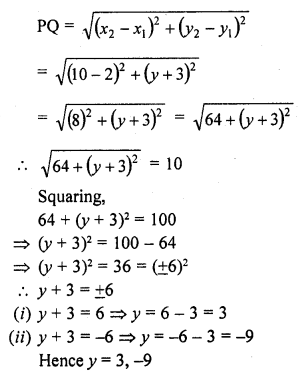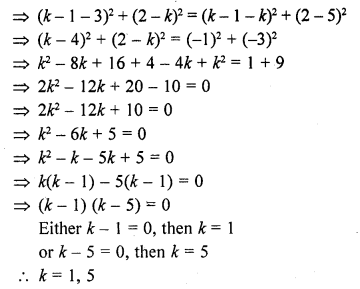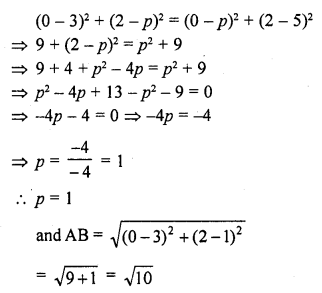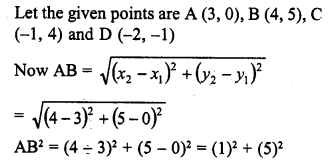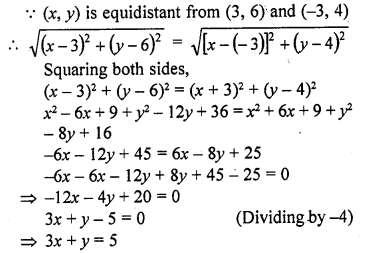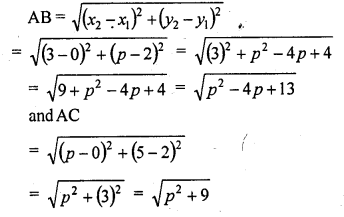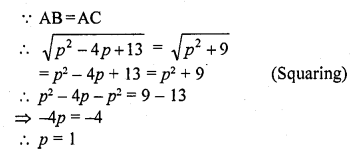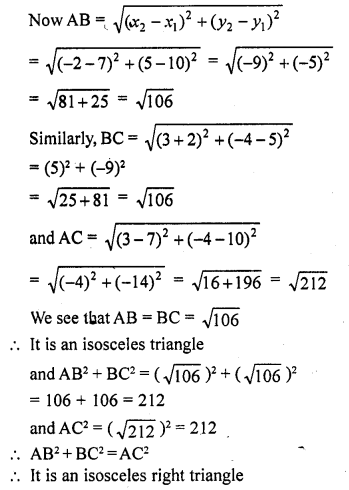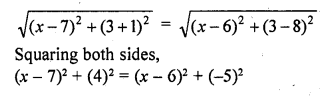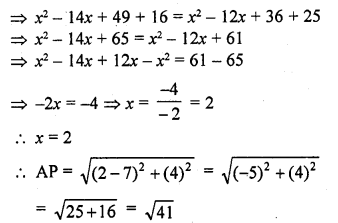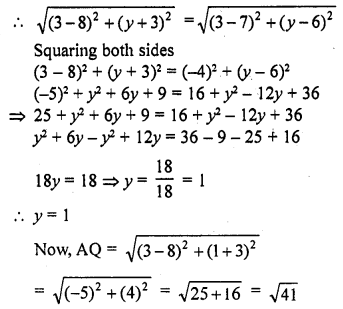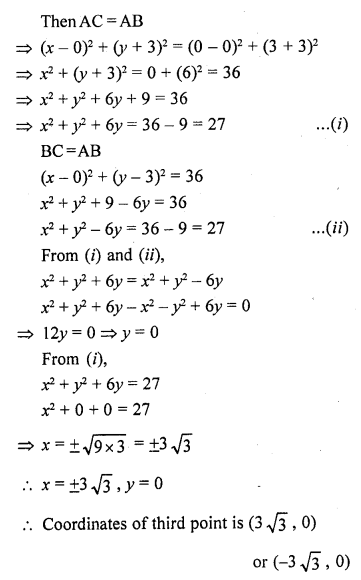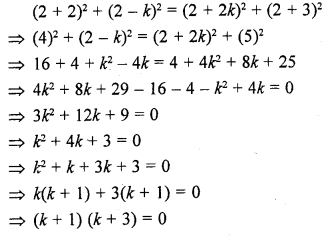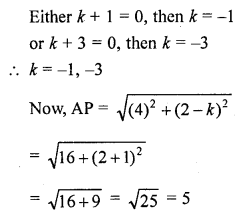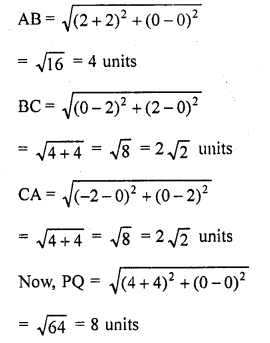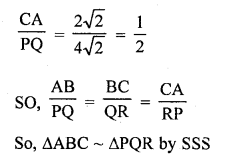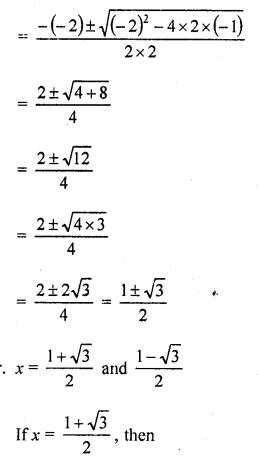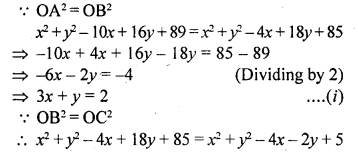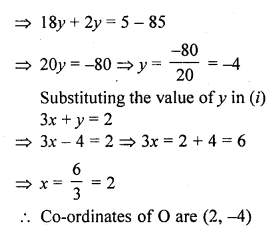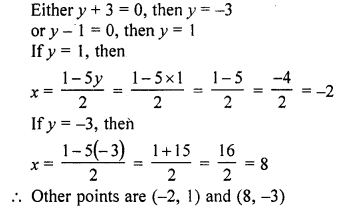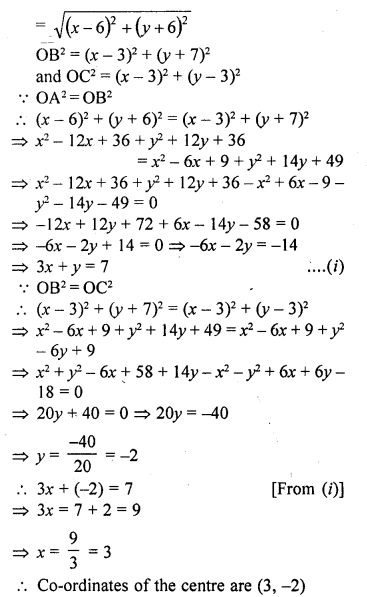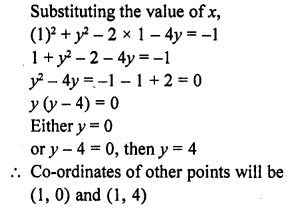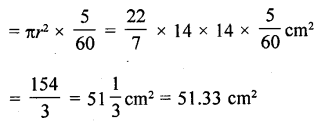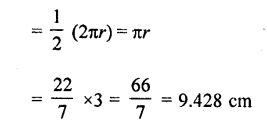RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS

Question 1.
Find the distance between the following pair of points :
(i) (-6, 7) and (-1, -5)
(ii) (a + b, b + c) and (a – b, c – b)
(iii) (a sin α, -b cos α) and (-a cos α, -b sin α)
(iv) (a, 0) and (0, b)
Solution:

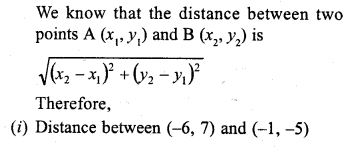
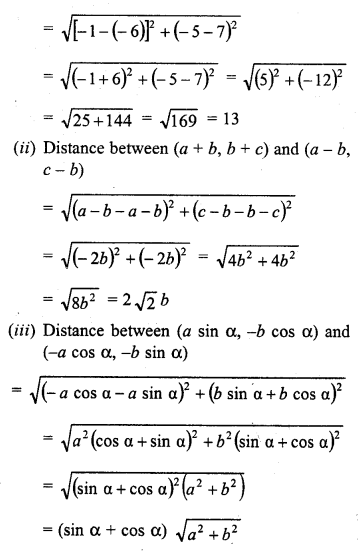
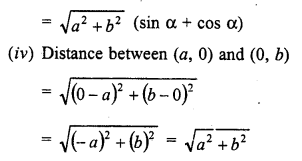
Question 2.
Find the value of a when the distance between the points (3, a) and (4, 1) is √10
Solution:

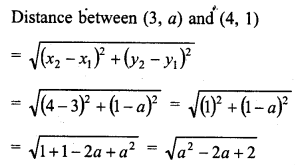
Question 3.
If the points (2, 1) and (1, -2) are equidistant from the point (x, y), show that x + 3y = 0.
Solution:

Question 4.
Find the values of x, y if the distances of the point (x, y) from (-3, 0) as well as from (3, 0) are 4.
Solution:
Distance between (x, y) and (-3, 0) is

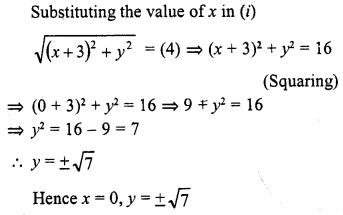
Question 5.
The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end.
Solution:
Let the ordinate of other end by y, then The distance between (2, -3) and (10, y) is

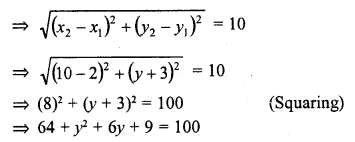
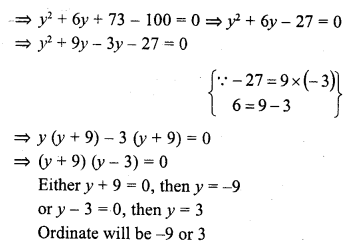
Question 6.
Show that the points (-4, -1), (-2, -4), (4, 0) and (2, 3) are the vertices points of a rectangle. (C.B.S.E. 2006C)
Solution:

AB = CD and AD = BC
and diagonal AC = BD
ABCD is a rectangle

Question 7.
Show that the points A (1, -2), B (3, 6), C (5, 10) and D (3, 2) are the vertices of a parallelogram.
Solution:

Question 8.
Prove that the points A (1, 7), B (4, 2), C (-1, -1) and D (-4, 4) are the vertices of a square. [NCERT]
Solution:
Vertices A (1, 7), B (4, 2), C (-1,-1), D (-4, 4)
If these are the vertices of a square, then its diagonals and sides are equal

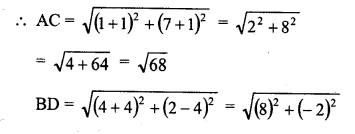
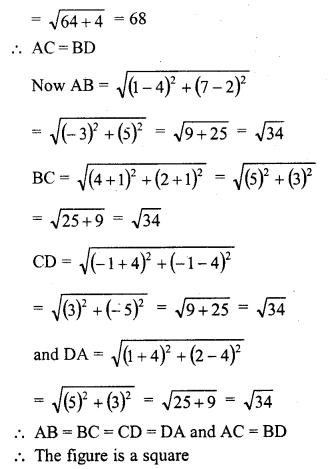
Question 9.
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle. (C.B.S.E. 2006C)
Solution:

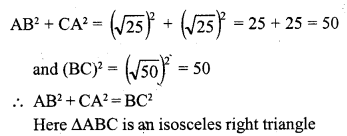
Question 10.
Prove that (2, -2), (-2, 1) and (5, 2) are the vertices of a right angled triangle. Find the area of the triangle and the length of the hypotenuse.
Solution:

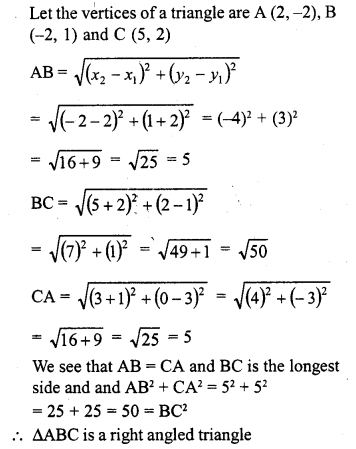
Question 11.
Prove that the points (2a, 4a), (2a, 6a) and (2a + √3 a , 5a) are the vertices of an equilateral triangle.
Solution:

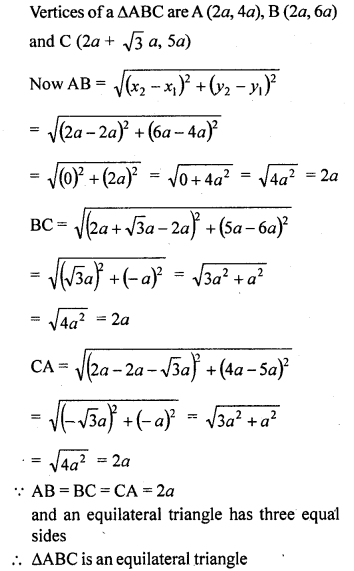
Question 12.
Prove that the points (2, 3), (-4, -6) and (1, \(\frac { 3 }{ 2 }\) )do not form a triangle.
Solution:

Question 13.
The points A (2, 9), B (a, 5) and C (5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC. [NCERT Exemplar]
Solution:
Given that, the points A (2, 9), B (a, 5) and C (5, 5) are the vertices of a ∆ABC right angled at B.
By Pythagoras theorem, AC² = AB² + BC² ………(i)
Now, by distance formula,

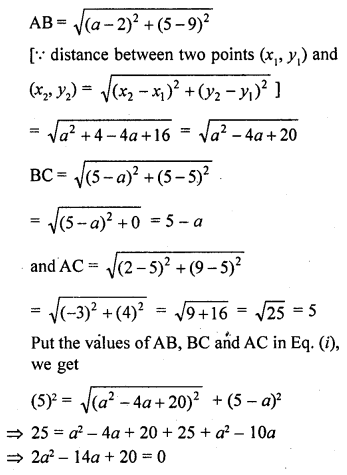
Question 14.
Show that the quadrilateral whose vertices are (2, -1), (3, 4), (-2, 3) and (-3, -2) is a rhombus.
Solution:

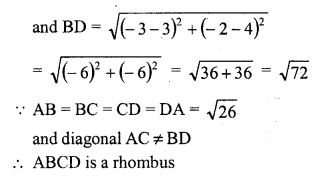
Question 15.
Two vertices of an isosceles triangle are (2, 0) and (2, 5). Find the third vertex if the length of the equal sides is 3.
Solution:
Two vertices of an isosceles ∆ABC are A (2, 0) and B (2, 5). Let co-ordinates of third vertex C be (x, y)

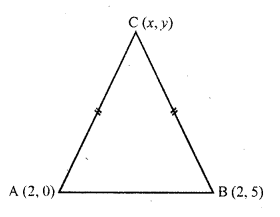
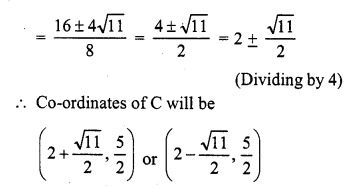
Question 16.
Which point on x-axis is equidistant from (5, 9) and (-4, 6) ?
Solution:
Let co-ordinates of two points are A (5, 9), B (-4, 6)
The required point is on x-axis
Its ordinates or y-co-ordinates will be 0
Let the co-ordinates of the point C be (x, 0)
AC = CB

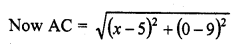
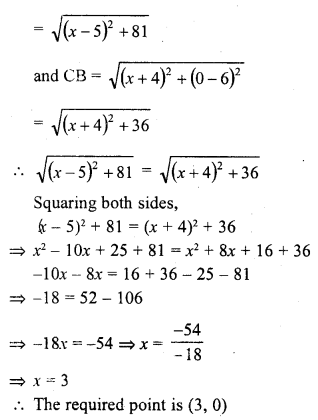
Question 17.
Prove that the point (-2, 5), (0, 1) and (2, -3) are collinear.
Solution:

Now AB + BC = 2√5 +2√5
and CA = 4√5
AB + BC = CA
A, B and C are collinear

Question 18.
The co-ordinates of the point P are (-3,2). Find the co-ordinates of the point Q which lies on the line joining P and origin such that OP = OQ.
Solution:
Co-ordinates of P are (-3, 2) and origin O are (0, 0)
Let co-ordinates of Q be (x, y)
O is the mid point of PQ


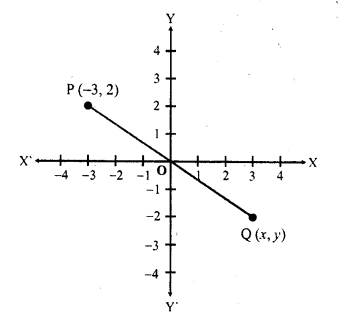
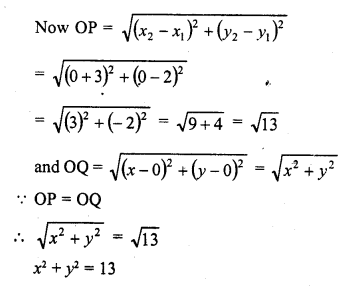
= 9 + 4 = (±3)² + (±2)²
The point will be in fourth quadrant
Its y-coordinates will be negative
and x-coordinates will be positive
Now comparing the equation
x² = (±3)² => x = ±3
y² = (±2)² => y = ±2
x = 3, y = -2
Co-ordinates of the point Q are (3, -2)

Question 19.
Which point on y-axis is equidistant from (2, 3) and (-4, 1) ?
Solution:
The required point lies on y-axis
Its abscissa will be zero
Let the point be C (0, y) and A (2, 3), B (-4, 1)
Now,

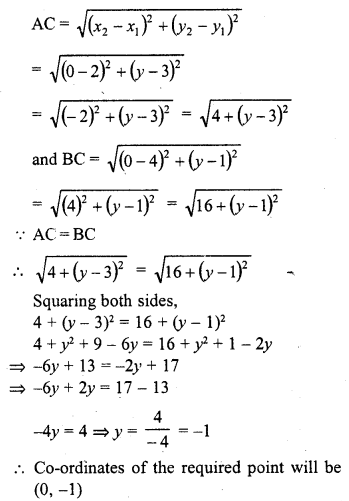
Question 20.
The three vertices of a parallelogram are (3, 4), (3, 8) and (9, 8). Find the fourth vertex.
Solution:
Let ABCD be a parallelogram and vertices will be A (3, 4), B (3, 8), C (9, 8)

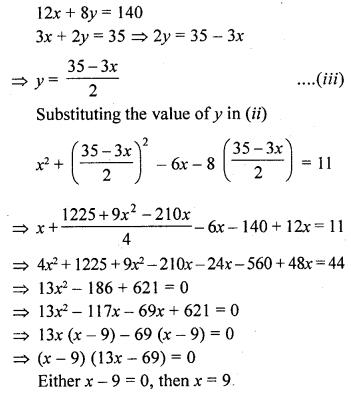
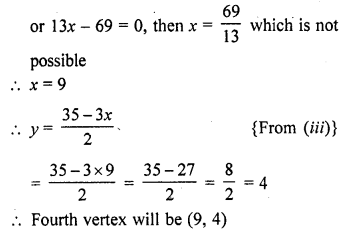
Question 21.
Find a point which is equidistant from the point A (-5, 4) and B (-1, 6). How many such points are there? [NCERT Exemplar]
Solution:
Let P (h, k) be the point which is equidistant from the points A (-5, 4) and B (-1, 6).
PA = PB


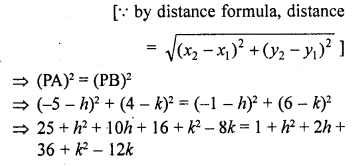
So, the mid-point of AB satisfy the Eq. (i).
Hence, infinite number of points, in fact all points which are solution of the equation 2h + k + 1 = 0, are equidistant from the point A and B.
Replacing h, k, by x, y in above equation, we have 2x + y + 1 = 0

Question 22.
The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, -9) and has diameter 10√2 units. [NCERT Exemplar]
Solution:
By given condition,
Distance between the centre C (2a, a-1) and the point P (11, -9), which lie on the circle = Radius of circle

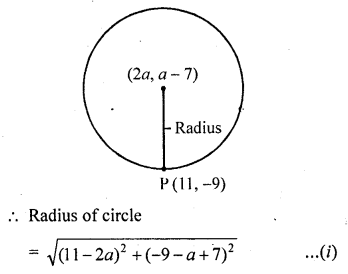
Question 23.
Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. What is the extra distance travelled by Ayush in reaching the office? (Assume that all distance covered are in straight lines). If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at (13, 26) and coordinates are in kilometers. [NCERT Exemplar]
Solution:

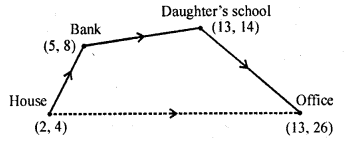
Question 24.
Find the value of k, if the point P (0, 2) is equidistant from (3, k) and (k, 5).
Solution:
Let P (0, 2) is equidistant from A (3, k) and B (k, 5)
PA = PB
=> PA² = PB²

Question 25.
If (-4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the
(i) interior,
(ii) exterior of the triangle. [NCERT Exemplar]
Solution:
Let the third vertex of an equilateral triangle be (x, y).
Let A (-4, 3), B (4,3) and C (x, y).
We know that, in equilateral triangle the angle between two adjacent side is 60 and all three sides are equal.



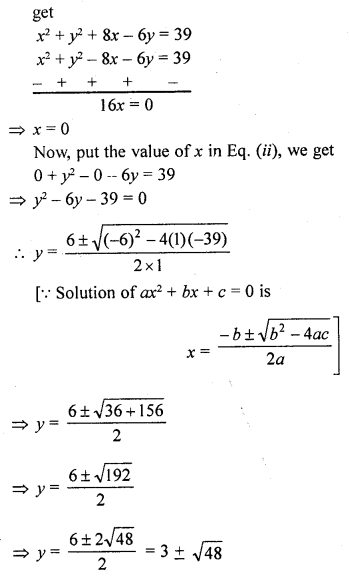
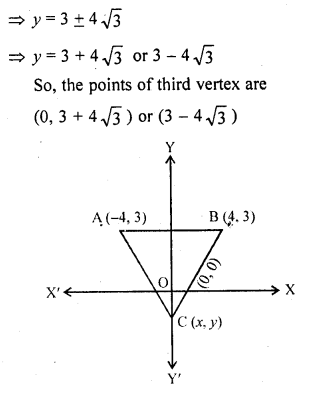
But given that, the origin lies in the interior of the ∆ABC and the x-coordinate of third vertex is zero.
Then, y-coordinate of third vertex should be negative.
Hence, the require coordinate of third vertex,
C = (0, 3 – 4√3). [C ≠ (0, 3 + 4√3)]

Question 26.
Show that the points (-3, 2), (-5, -5), (2, -3) and (4, 4) are the vertices of a rhombus. Find the area of this rhombus.
Solution:
Let the co-ordinates of the vertices A, B, C and D of a rhombus are A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4)

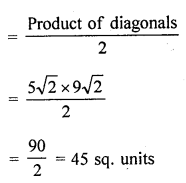
Question 27.
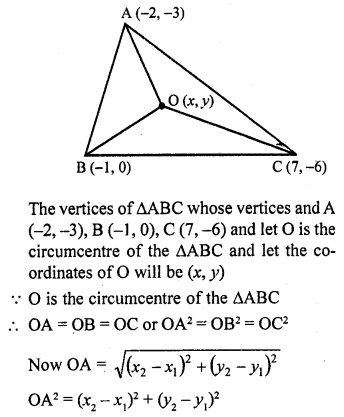
Find the coordinates of the circumcentre of the triangle whose vertices are (3, 0), (-1, -6) and (4, -1). Also, find its circumradius.
Solution:
Let ABC is a triangle whose vertices are A (3, 0), B (-1, -6) and C (4, -1)

Question 28.
Find a point on the x-axis which is equidistant from the points (7, 6) and (-3, 4). [CBSE 2005]
Solution:
The required point is on x-axis
Its ordinate will be O
Let the co-ordinates of the required point P (x, 0)
Let the point P is equidistant from the points A (7, 6) and B (-3, 4)

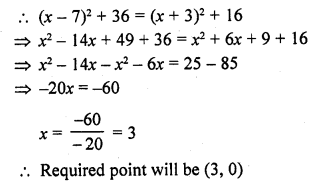
Question 29.
(i) Show that the points A (5, 6), B (1, 5), C (2, 1) and D (6, 2) are the vertices of a square. [CBSE 2004]
(ii) Prove that the points A (2, 3), B (-2, 2), C (-1, -2) and D (3, -1) are the vertices of a square ABCD. [CBSE 2013]
(iii) Name the type of triangle PQR formed by the point P(√2 , √2), Q(- √2, – √2) and R (-√6 , √6 ). [NCERT Exemplar]
Solution:

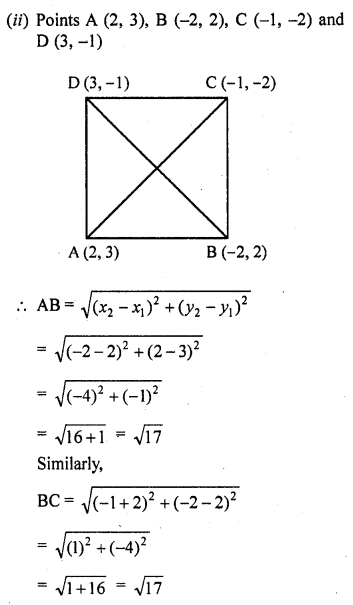
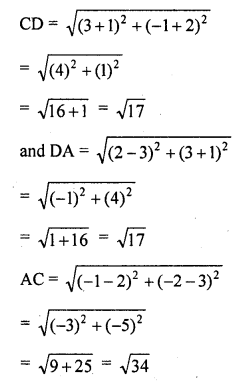
Question 30.
Find the point on x-axis which is equidistant from the points (-2, 5) and (2, -3). [CBSE 2004]
Solution:
The point P lies on x-axis
The ordinates of P will be 0 Let the point P be (x, 0)
Let P is equidistant from A (-2, 5) and B (2, -3)

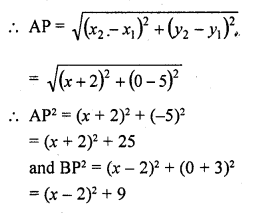
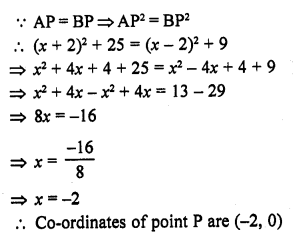
Question 31.
Find the value of x such that PQ = QR where the co-ordinates of P, Q and R are (6, -1) (1, 3) and (x, 8) respectively. [CBSE 2005]
Solution:

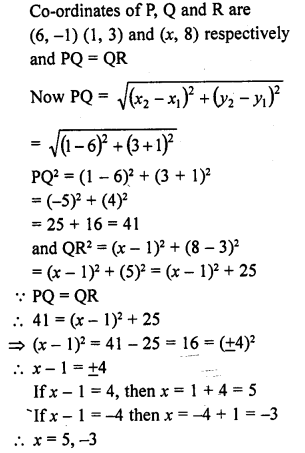
Question 32.
Prove that the points (0, 0), (5, 5) and (-5, 5) are the vertices of a right isosceles triangle. [CBSE 2005]
Solution:
Let the vertices of a triangle be A (0, 0), B (5, 5) and C (-5, 5)

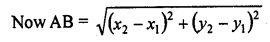
Question 33.
If the points P (x, y) is equidistant from the points A (5, 1) and B (1,5), prove that x = y. [CBSE 2005]
Solution:

Question 34.
If Q (0, 1) is equidistant from P (5, -3) and R (x, 6) find the values of x. Also find the distances QR and PR. [NCERT]
Solution:
Q (0, 1) is equidistant from P (5, -3) and R (x, 6)
PQ = RQ

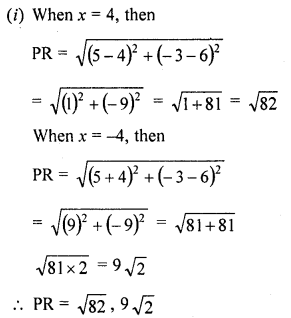
Question 35.
Find the values ofy for which the distance between the points P (2, -3) and Q (10, y) is 10 units. [NCERT]
Solution:
Distance between P (2, -3) and Q (10, y) = 10

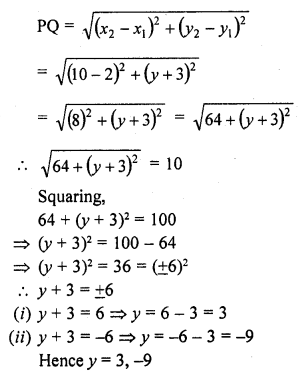
Question 36.
If the point P (k – 1, 2) is equidistant from the points A (3, k) and B (k, 5), find the values of k. [CBSE 2014]
Solution:
Point P (k – 1, 2) is equidistant from A (3, k) and B (k, 5)
PA= PB

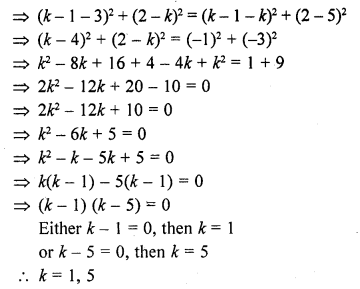
Question 37.
If the point A (0, 2) is equidistant from the point B (3, p) and C (p, 5), find p. Also, find the length of AB. [CBSE 2014]
Solution:
Point A (0, 2) is equidistant from B (3, p) and C (p, 5)
AB = AC

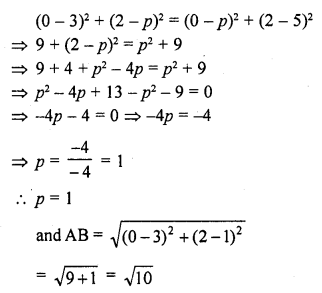
Question 38.
Name the quadrilateral formed, if any, by the following points, and give reasons for your answers :
(i) A (-1, -2), B (1, 0), C (-1, 2), D (-3, 0)
(ii) A (-3, 5), B (3, 1), C (0, 3), D (-1, -4)
(iii) A (4, 5), B (7, 6), C (4, 3), D (1, 2)
Solution:

Question 39.
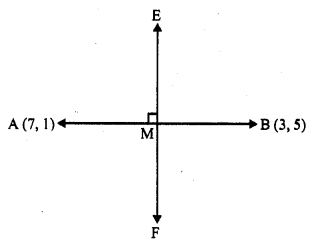
Find the equation of the perpendicular bisector of the line segment joining points (7, 1) and (3, 5).
Solution:
Let the given points are A (7, 1) and B (3, 5) and mid point be M

Question 40.
Prove that the points (3, 0), (4, 5), (-1, 4) and (-2, -1) taken in order, form a rhombus. Also find its area.
Solution:

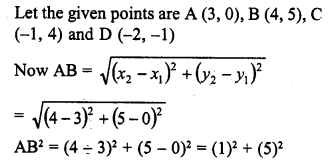
Question 41.
In the seating arrangement of desks in a classroom three students Rohini, Sandhya and Bina are seated at A (3, 1), B (6, 4) and C (8, 6). Do you think they are seated in a line ?
Solution:
A (3, 1), B (6, 4) and C (8, 6)

Question 42.
Find a point ony-axis which is equidistant from the points (5, -2) and (-3, 2).
Solution:
The point lies on y-axis
Its x = 0
Let the required point be (0, y) and let A (5, -2) and B (-3, 2)

Question 43.
Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4). [NCERT]
Solution:

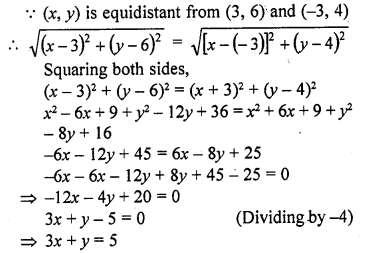
Question 44.
If a point A (0, 2) is equidistant from the points B (3, p) and C (p, 5), then find the value of p. [CBSE 2012]
Solution:
Point A (0, 2) is equidistant from the points B (3, p) and C (p, 5)
AB = AC

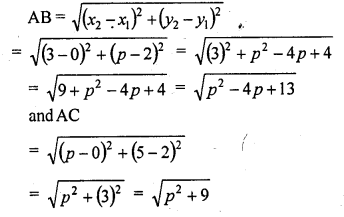
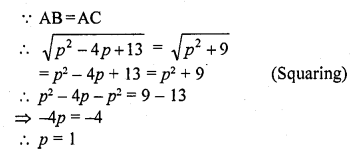
Question 45.
Prove that the points (7, 10), (-2, 5) and (3, -4) are the vertices of an isosceles right triangle. [CBSE 2013]
Solution:
Let points are A (7, 10), B (-2, 5) and C (3, -4)

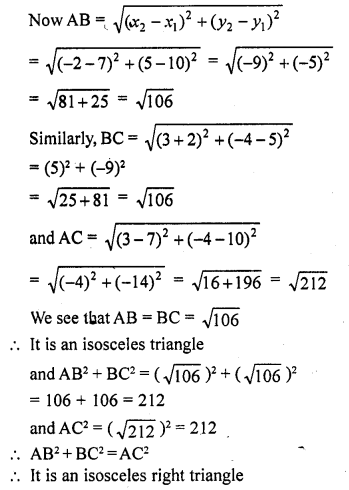
Question 46.
If the point P (x, 3) is equidistant from the points A (7, -1) and B (6, 8), find the value of x and And the distance AP. [CBSE 2014]
Solution:
Point P (x, 3) is equidistant from the points A (7, -1) and B (6, 8)
PA = PB

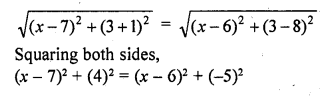
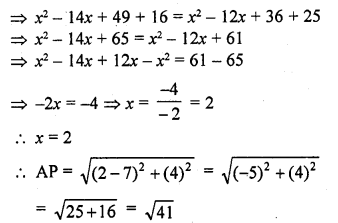
Question 47.
If A (3, y) is equidistant from points P (8, -3) and Q (7, 6), find the value of y and find the distance AQ. [CBSE 2014]
Solution:
Point A (3, y) is equidistant from P (8, -3) and Q (7, 6)
i.e., AP = AQ

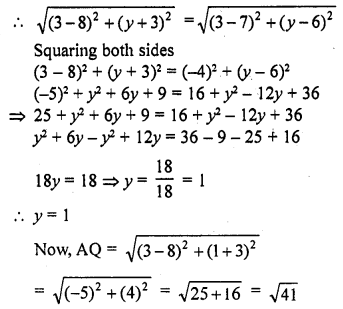
Question 48.
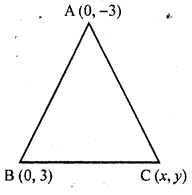
If (0, -3) and (0, 3) are the two vertices of an equilateral triangle, find the coordinates of its third vertex. [CBSE 2014]
Solution:
Let A (0, -3) and B (0, 3) are vertices of an equilateral triangle
Let the coordinates of the third vertex be C (x, y)

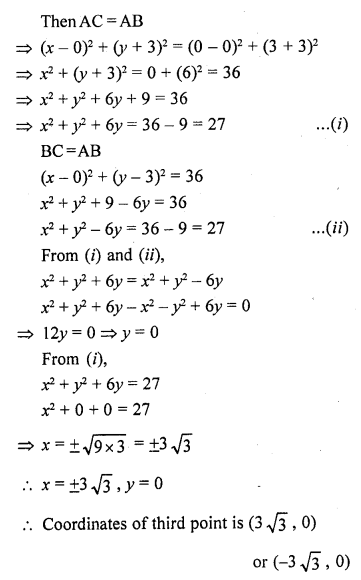
Question 49.
If the point P (2, 2) is equidistant from the points A (-2, k) and B (-2k, -3), find k. Also, find the length of AP.
Solution:
Point P (2, 2) is equidistant from the points A (-2, k) and B (-2k, -3)
AP = BP
Now,

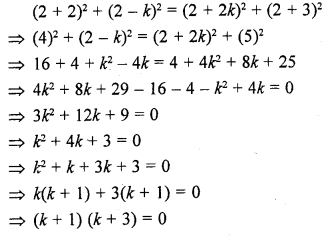
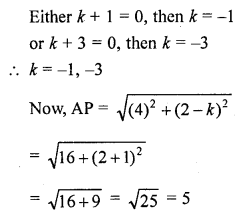
Question 50.
Show that ∆ABC, where A (-2, 0), B (2, 0), C (0, 2) and ∆PQR, where P (-4, 0), Q (4, 0), R (0, 4) are similar.
Solution:

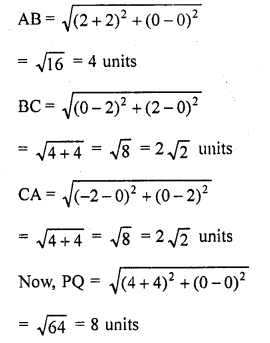
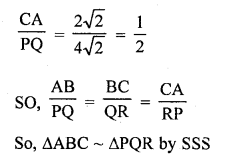
Question 51.
An equilateral triangle has two vertices at the points (3, 4), and (-2, 3). Find the co-ordinates of the third vertex.
Solution:
Let two vertices of an equilateral triangle are A (3,4), and B (-2,3) and let the third vertex be C (x, y)

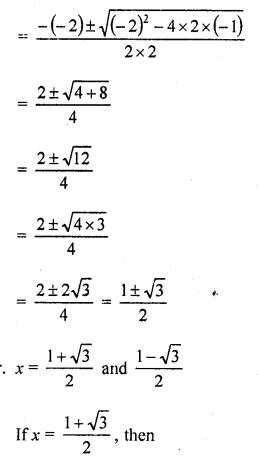
Question 52.
Find the circumcentre of the triangle whose vertices are (-2, -3), (-1, 0), (7, -6).
Solution:

Question 53.
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
Solution:
Let co-ordinates of the end points of a line segment are A (0, 100), B (10, 0) and origin is O (0, 0)
Abscissa of A is 0
It lies on y-axis
Similarly, ordinates of B is 0
It lies on x-axis
But axes intersect each other at right angle
AB will subtended 90° at the origin
Angle is 90° or \(\frac { \pi }{ 2 }\)

Question 54.
Find the centre of the circle passing through (5, -8), (2, -9) and (2, 1).
Solution:

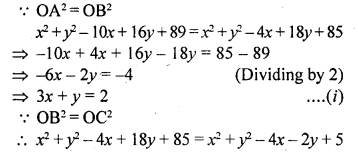
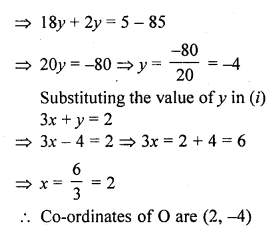
Question 55.
If two opposite vertices of a square are (5, 4) and (1, -6), find the coordinates of its remaining two vertices.
Solution:
Two opposite points of a square are (5, 4) and (1, -6)
Let ABCD be a square and A (5, 4) and C (1, -6) are the opposite points
Let the co-ordinates of B be (x, y). Join AC

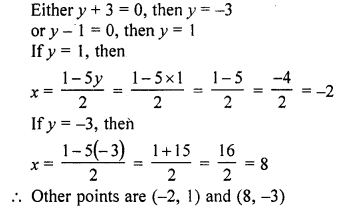
Question 56.
Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3).
Solution:
Let O is the centre of the circle is (x, 7) Join OA, OB and OC

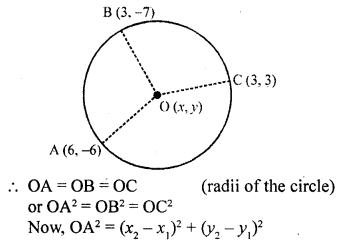
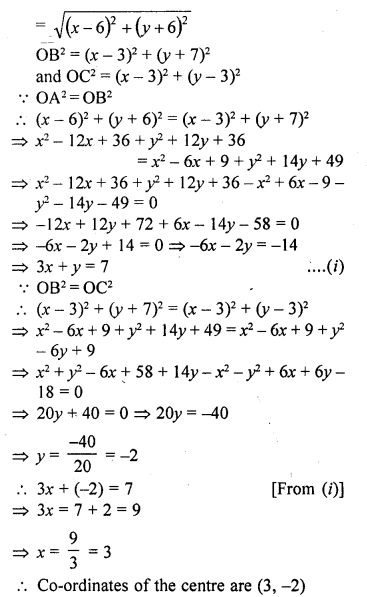
Question 57.
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the co-ordinates of other two vertices.
Solution:

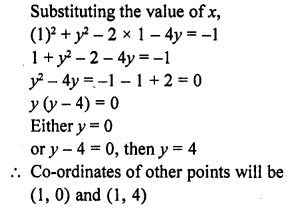
Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.3
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.4
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS

Question 1.
Find, in terms of π the length of the arc that subtends an angle of 30° at the centre of a circle of radius 4 cm.
Solution:
Radius of the circle (r) = 4 cm
Angle at the centre subtended an arc = 30°

Question 2.
Find the angle subtended at the centre of a circle of radius 5 cm by an arc of length \((\frac { 5\pi }{ 3 } \) cm.
Solution:
Radius of the circle (r) = 5 cm 571
Length of arc = \(\frac { 5\pi }{ 3 }\) cm
Let θ be the angle subtended by the arc, then

Question 3.
An arc of length 20tc cm subtends an angle of 144° at the centre of a circle. Find the radius of the circle.
Solution:
Length of an arc = 20π cm
Angle subtended by the arc = 144°
Let r be the radius of the circle, then

Question 4.
An arc of length 15 cm subtends an angle of 45° at the centre of a circle. Find in terms of π ; the radius of the circle.
Solution:
Length of arc = 15 cm
Angle subtended at the centre = 45°
Let r be the radius of the circle, then

Question 5.
Find the angle subtended at the centre of a circle of radius ‘a’  by an arc of length \((\frac { a\pi }{ 4 } )\)  cm.
Solution:
Radius of the circle (r) = a cm
Length of arc = \(\frac { a\pi }{ 4 }\)   cm
Let θ be the angle subtended by the arc at the centre, then

Question 6.
A sector of a circle of radius 4 cm contains an angle of 30°. Find the area of the sector.
Solution:
Radius of the sector of a circle (r) = 4 cm
Angle at the centre (θ) = 30°

Question 7.
A sector of a circle of radius 8 cm contains an angle of 135°. Find the area of the sector.
Solution:
Radius of the sector of the circle (r) = 8 cm
Angle at the centre (θ) = 135°

Question 8.
The area of a sector of a circle of radius 2 cm is 7 is cm². Find the angle contained by the sector.
Solution:
Area of the sector of a circle =π cm²
Radius of the circle (r) = 2 cm
Let 0 be the angle at the centre, then

Question 9.
The area of a sector of a circle of radius 5 cm is 5π cm². Find the angle contained by the sector.
Solution:
Area of the sector of a circle = 5π cm²
Radius of the circle (r) = 5 cm
Let 9 be the angle at the centre, then

Question 10.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm. [NCERT Exemplar]
Solution:
Let the central angle of the sector be θ.
Given that, radius of the sector of a circle (r) = 5 cm
and arc length (l) = 3.5 cm

Question 11.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of the arc and area of the sector.
Solution:
Radius of the circle (r) = 25 cm
Angle at the centre (θ) = 72°

Question 12.
The perimeter of a sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
Solution:
Radius of the circle (r) = 5.7 m
Perimeter of the sector = 27.2 m
Length of the arc = Perimeter – 2r
= (27.2 – 2 x 5.7) m
= 27.2 – 11.4 = 15.8 m
Let θ be the central angle, then

Question 13.
The perimeter of a certain sector of a circle of radius 5.6 cm is 27.2 m. Find the area of the sector.
Solution:
Radius of the sector (r) = 5.6 cm
and perimeter of the sector = 27.2 cm
∴ Length of arc = Perimeter – 2r
= 27.2 – 2 x 5.6
= 27.2- 11.2= 16.0 cm
∴ θ be the angle at the centre, then

Question 14.
A sector is cut-off from a circle of radius 21 cm. The angle of the sector is 120°. Find the length of its arc and the area.
Solution:
Radius of the sector of a circle (r) = 21 cm
Angle at the centre = 120°

Question 15.
The minute hand of a clock is \(\sqrt { 21 } \)  cm long, Find the area described by the minute hand on the face of the clock between 7.00 A.M. and 7.05 A.M.
Solution:
Length of minute hand of a clock (r) = \(\sqrt { 21 }\)  cm
Period = 7 a.m. to 7.05 a.m. 5 minutes

Question 16.
The minute hand of a clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 8.00 A.M. and 8.25 A.M.
Solution:
Length of minute hand of a clock (r) = 10 cm
Period = 8 A.M. to 8.25 A.M. = 25 minutes

Question 17.
The sector of 56° cut out from a circle contains area 4.4 cm², Find the radius of the circle.
Solution:
Area of a sector = 4.4 cm²
Central angle = 56°                                        ‘
Let r be the radius of the sector of the circle, then

Question 18.
Area of a sector of central angle 200° of a circle s 770²cm. Find the length of the corresponding are of this sector.
Solution:
Let the radius of the sector AOBA be r.
Given that, Central angle of sector AOBA = θ = 200°
and area of the sector AOBA = 770 cm²

Question 19.
The length of minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6:05 am and 6:40 am.           [NCERT Exemplar]
Solution:
We know that, in 60 min, minute hand revolving = 360°
In 1 min, minute hand revolving = \(\frac { 360\circ }{ 60\circ }\)

Question 20.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [CBSE 2013]
Solution:
Length of minute hand (r)= 14 cm
Area swept by the minute hand in 5 minutes

Question 21.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find (0 the length of the arc (ii) area of the secter formed by the arc. (Use π = 22/7) [CBSE 2013]
Solution:
Radius of a circle (r) = 21 cm
Angle at the centre = 60°

Question 22.
From a circular piece of cardboard of radius 3 cm two sectors of 90° have been cut off. Find the perimeter of the remaining portion nearest hundredth centimeters (Take π = 22/7).
Solution:
Radius of the circular piece of cardboard (r) = 3 cm

∴ Two sectors of 90° each have been cut off
∴ We get a semicular cardboard piece
∴ Perimeter of arc ACB

Question 23.
The area of a sector is one-twelfth that of the complete circle. Find the angle of the sector.
Solution:
Let r be the radius of the circle and 0 be the central angle of the sector of the circle Then area of circle = πr²

Question 24.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by the chord AB.
Solution:
Radius of the circle with centre O (r) = 4 cm
Length of chord AB = 4 cm

Question 25.
In a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110° at the centre of the circle. Find 
(i)  the circumference of the circle,
(ii) the area of the circle,
(iii) the length of the arc AB,
(iv) the area of the sector OAB.
Solution:
Radius of the circle (r) = 6 cm
Length of chord = 10 cm
and central angle (θ) =110°

Question 26.
Figure, shows a sector of a circle, centre O, containing an angle θ°. Prove that :

Solution:
Radius of the circle = r
Arc AC subtends ∠θ at the centre of the
circle. OAB is a right triangle
In the right ΔOAB,

Question 27.
Figure, shows a sector of a circle of radius r cm containing an angle θ°. The area of the sector is A cm² and perimeter of the sector is 50 cm. Prove that

Solution:
Radius of the sector of the circle = r cm
and angle at the centre = 0
Area of sector OAB = A cm²
and perimeter of sector OAB = 50 cm

Hope given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS
• RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS

Question 1.
On which axis do the following points lie?
(i) P (5, 0)
(ii) Q (0 – 2)
(iii) R (-4, 0)
(iv) S (0, 5)
Solution:
(i) P (5, 0)
Its ordinate or y-axis is 0. It lies on x-axis
(ii) Q (0 – 2)
Its abscissa or x-axis is 0. It lies on y-axis
(iii) R (-4, 0)
Its ordinate is 0 It lies on x-axis
(iv) S (0, 5)
Its abscissa is 0. It lies on y-axis

Question 2.
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when
(i) A coincides with the origin and AB and AD are along OX and OY respectively.
(ii) The centre of the square is at the-origin and coordinate axes are parallel to the sides AB and AD respectively.
Solution:
ABCD is a square whose side is 2a
(i) A coincides with origin (0, 0)
AB and AD are along OX and OY respectively
Co-ordinates of A are (0, 0), of B are (2a, 0) of C are (2a, 2a) and of D are (0, 2a)
(ii) The centre of the square is at the origin (0, 0) and co-ordinates axes are parallel to the sides AB and AD respectively.
Then the co-ordinates of A are (a, a) of B are (-a, a), of C are (-a, -a) and of D are (a, -a) as shown in the figure given below :

Question 3.
The base PQ of two equilateral triangles PQR and PQR’ with side 2a lies along y- axis such.that the mid-point of PQ is at the origin. Find the coordinates of the vertices R and R’ of the triangles.
Solution:
∆PQR and PQR’ are equilateral triangles with side 2a each and base PQ and mid of point of PQ is 0 (0, 0) and PQ lies along y-axis

Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.3
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.4
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS

Question 1.
Find the circumference and area of a circle of radius 4.2 cm.
Solution:
Radius of a circle = 4.2 cm

Question 2.
Find the circumference of a circle whose area is 301.84 cm².
Solution:
Area of a circle = 301.84 cm²
Let r be the radius, then πr² = 301.84

Question 3.
Find the area of a circle whose circum­ference is 44 cm.
Solution:
Circumference of a circle = 44 cm
Let r be the radius,
then 2πr = circumference

Question 4.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the circum­ference of the circle. (C.B.S.E. 1996)
Solution:
Let r be the radius of the circle
∴  Circumference = 2r + 16.8 cm
⇒  2πr = 2r + 16.8
⇒  2πr – 2r = 16.8

Question 5.
A horse is tied to a pole with 28 m long string. Find the area where the horse can graze. (Take π = 22/7)
Solution:
Radius of the circle (r) = Length of the rope = 28 m .
Area of the place where the horse can graze

Question 6.
A steel wire when bent in the form of a square encloses an area of 121 cm². If the same wire is bent in the form of a circle, find the area of the circle.  (C.B.S.E. 1997)
Solution:
Area of square formed by a wire =121 cm²
∴ Side of square (a) = \(\sqrt { Area } \)  = \(\sqrt { 121 } \)  = 11 cm Perimeter of the square = 4 x side = 4 x 11 = 44 cm
∴Circumference of the circle formed by the wire = 44cm
Let r be the radius

Question 7.
The circumference of two circles are in the ratio 2 : 3. Find the ratio of their areas.
Solution:
Let R and r be the radii of two circles and their ratio between them circumference = 2 : 3

Question 8.
The sum of radii of two circles is 140 cm and the difference of their circum­ferences is 88 cm. Find the diameters of the circles.
Solution:
Let R and r be the radii of two circles Then R + r = 140 cm  …….(i)
and difference of their circumferences

Question 9.
Find the radius of a circle whose circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm. [NCERT Exemplar]
Solution:
Let the radius of a circle be r.
Circumference of a circle = 2πr
Let the radii of two circles are r₁ and r₂ whose
values are 15 cm and 18 cm respectively.
i.e., r₁ = 15 cm and r₂ = 18 cm
Now, by given condition,
Circumference of circle = Circumference of first circle + Circumference of second circle
⇒   2πr = 2π r₁ + 2πr₂ =
⇒  r = r₁ + r₂
⇒   r = 15 + 18
∴ r = 33 cm
Hence, required radius of a circle is 33 cm.

Question 10.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having its area equal to the sum of the areas of the two circles.
Solution:
Radius of first circle (r₁) = 8 cm
and radius of second circle (r₂) = 6 cm

Question 11.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius and area of the circle which has its circumference equal to the sum of the circumferences of the two circles.
Solution:
Radius of the first circle (r₁) = 19 cm
and radius of the second circle (r₂) = 9 cm S
um of their circumferences = 2πr₁ + 2πr₂
= 2π (r₁ + r₂) = 2π (19 + 9) cm
= 2π x 28 = 56π cm
Let R be the radius of the circle whose circumference is the sum of the circum­ferences of given two circles, then

Question 12.
The area of a circular playground is 22176 m². Find the cost of fencing this ground at the rate of ₹50 per metre.  [NCERT Exempiar]
Solution:
Given, area of a circular playground  = 22176 m²

Question 13.
The side of a square is 10 cm. Find the area of circumscribed and inscribed circles.
Solution:
ABCD is a square whose each side is 10 cm
∴  AB = BC = CD = DA = 10 cm
AC and BD are its diagonals

Question 14.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
Solution:
Let r be the radius of the circle a be the side of the square

Question 15.
The area of a circle inscribed in an equilateral triangle is 154 cm². Find the perimeter of the triangle. (Use π = 22/7 and \(\sqrt { 3 } \)  = 1.73)
Solution:
Area of the inscribed circle of ΔABC = 154 cm²

Question 16.
A field is in the form of a circle. A fence is to be erected around the field. The cost of fencing would be ₹2640 at the rate of ₹12 per metre. Then, the field is to be thoroughly ploughed at the cost of ₹0.50 per m². What is the amount required to plough the field ? (Take π = 22/7)
Solution:
Cost of the fencing the circular field = ₹2640
Rate = ₹12 per metre 2640
∴ Circumference = \((\frac { 2640 }{ 12 } )\) = 220 m
Let r be the radius of the field, then = 2πr = 220

Question 17.
A park is in the form of a rectangle 120 m x 100 m. At the centre of the park there is a circular lawn. The area of park excluding lawn is 8700 m². Find the radius of the circular lawn. (Use π = 22/7).
Solution:
Area of the park excluding lawn = 8700 m²
Length of rectangular park = 120 m
and width = 100 m

∴ Area of lawn = l x b
= 120 x 100 m² = 12000 m²
Let r be the radius of the circular lawn, then area of lawn = πr²

Question 18.
A car travels 1 kilometre distance in which each wheel makes 450 complete revolutions. Find the radius of the its wheels.
Solution:
Distance covered by the car in 450 revolutions = 1 km = 1000 m
∴ Distance covered in 1 revolution = \((\frac { 1000 }{ 450 } )\)
= \((\frac { 20 }{ 9 } )\) m

Question 19.
The area of enclosed between the concentric circles is 770 cm². If the radius of the outer circle is 21 cm, find the radius of the inner circle.
Solution:
Area of enclosed between two concentric circles = 770 cm²
Radius of the outer circle (R) = 21 cm

Question 20.
An archery target has three regions formed by the concentric circles as shown in the figure. If the diameters of the concentric circles are in the ratio 1:2:3, then find the ratio of the areas of three regions.[NCERT Exemplar]

Solution:
Let the diameters of concentric circles be k, 2k , 3k

Question 21.
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr? [NCERT Exemplar]
Solution:
Given, radius of wheel, r = 35 cm
Circumference of the wheel = 2πr
= 2 x \((\frac { 22 }{ 7 } )\) x 35 = 220 cm
But speed of the wheel = 66 kmh^-1
= \((\frac { 66 x 1000 }{ 60 } )\) m/ mm
= 1100 x 100 cm min^-1
= 110000 cm min^-1
∴ Number of revolutions in 1 min
= \((\frac { 110000 }{ 220 } )\)= 500 revolution
Hence, required number of revolutions per minute is 500.

Question 22.
A circular pond is 17.5 m in diameter. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of ₹25 per m². [NCERT Exemplar]
Solution:
Given that, a circular pond is surrounded by a wide path.
The diameter of circular pond = 17.5 m

Question 23.
A circular park is surrounded by a rod 21 m wide. If the radius of the park is 105 m, find the area of the road. [NCERT Exemplar]
Solution:
Given that, a circular park is surrounded by a road.
Width of the road = 21 m
Radius of the park (r₁) = 105 m

.’. Radius of whole circular portion (park + road),
r_e = 105 + 21 = 126 m
Now, area of road = Area of whole circular portion – Area of circular park
= πr² – πr²             [∵ area of circle = πr²]

Question 24.
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.  [NCERT Exemplar]
Solution:
Let the side of a square be a and the radius of circle be r.
Given that, length of diagonal of square = 8 cm

Question 25.
A path of 4 m width runs round a semi­circular grassy plot whose circumference is 81 \((\frac { 5 }{ 7 } )\)m. Find:
(i) the area of the path
(ii) the cost of gravelling the path at the rate of ₹1.50 per square metre
(iii) the cost of turfing the plot at the rate of 45 paise per m².
Solution:
Width of path around the semicircular grassy plot = 4 m
Circumference of the plot = 81 \((\frac { 5 }{ 7 } )\)m
= \((\frac { 572 }{ 7 } )\) m
Let r be the radius of the plot, then

Question 26.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle, such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles. Find the radius of the third circle correct to one decimal place.
Solution:
Radius of first circle (r₁) = 3.5 cm
Radius of second circle (r₂) = 7 cm

Question 27.
A path of width 3.5 m runs around a semi­circular grassy plot whose perimeter is 72 m. Find the area of the path. (Use π = 22/7)                   [CBSE 2015]
Solution:
Perimeter of semicircle grassy plot = 72 m

Let r be the radius of the plot

Question 28.
A circular pond is of diameter 17.5 m. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of ₹25 per square metre (Use π = 3.14)               [CBSE 2014]
Solution:
Diameter of circular pond (d) = 17.5 m
Radius (r) =\((\frac { 1725 }{ 2 } )\) = 8.75 m
Width of path = 2m
∴  Radius of outer cirlce (R) = 8.75 + 2 = 10.75 m
Area of path = (R² – r²)π
= [(10.75)² – (8.75)²](3.14)
= 3.14(10.75 + 8.75) (10.75 – 8.75)
= 3.14 x 19.5 x 2 = 122.46 m²
Cost of 1 m² for constructing the path ₹25 m²
∴  Total cost = ₹ 122.46 x 25 = ₹3061.50

Question 29.
The outer circumference of a circular race-track is 528 m. The track is every­where 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre (Use π= 22/7).
Solution:
Let R and r be the radii of the outer and inner of track.
Outer circumference of the race track = 528 m

Question 30.
A road which is 7 m wide surrounds a circular park whose circumference is 352 m. Find the area of the road.
Solution:
Width of the road = 7 m

Circumference of the park = 352 m
Let r be the radius, then 2πr = 352

Question 31.
Prove that the area of a circular path of uniform width surrounding a circular region of radius r is πh(2r + h).
Solution:
Radius of inner circle = r
Width of path = h
∴ Outer radius (R) = (r + h)
∴ Area of path = πR² – πr²
= π {(r + h)² – r²}
= π {r² + h² + 2rh – r²}
= π {2rh + h²}
= πh (2r + h) Hence proved.

Hope given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.