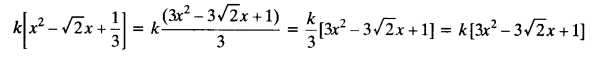CBSE Class 10

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3. https://mcqquestions.guru/ncert-solutions-for-class-10-maths-chapter-2-ex-2-3/

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3

Ex 2.3 Class 10 Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder, in each of the following:
(i) p(x) = x³ – 3x² + 5x -3, g(x) = x²-2
(ii) p(x) =x⁴ – 3x² + 4x + 5, g(x) = x² + 1 -x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 -x²
Solution:
(i) Here p(x) = x³ -3x² + 5x – 3 and g(x) = x² -2
dividing p(x) by g(x) ⇒

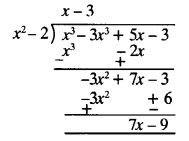
Quotient = x – 3, Remainder = 7x – 9

(ii) Here p(x) = x⁴– 3x² + 4x + 5 and g(x) = x² + 1 -x
dividing p(x) by g(x) ⇒

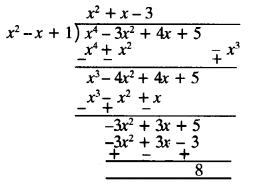
Quotient = x² + x – 3, Remainder = 8

(iii) Herep(x) = x⁴– 5x + 6 and g(x) = 2-x²
Rearranging g(x) = -x² + 2
dividing p(x) by g(x) ⇒
Quotient = -x² – 2
Remainder = -5x + 10.

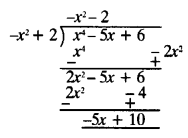
Ex 2.3 Class 10 Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t²-3, 2t⁴ + t³ – 2t² – 9t – 12
(ii) x² + 3x + 1,3x⁴+5x³-7x²+2x + 2
(iii) x³ -3x + 1, x⁵ – 4x³ + x² + 3x + l
Solution:
(i) First polynomial = t² – 3,
Second polynomial = 2t⁴ + 3t³ – 2t² – 9t – 12
dividing second polynomial
by first polynomial ⇒
∵ Remainder is zero.
∴First polynomial is a factor of second polynomial.

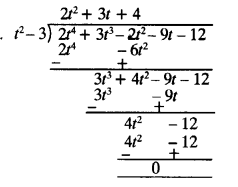
(ii) First polynomial = x² + 3x + 1
Second polynomial = 3x⁴ + 5x³ – 7x² + 2x + 2
dividing second polynomial
by first polynomial ⇒
∵ Remainder is zero.
∴ First polynomial is a factor of second polynomial.

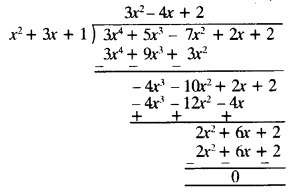
(iii) First polynomial = x³ – 3x + 1
Second polynomial = x⁵ – 4x³ + x² + 3x + 1.
∵ Remainder ≠ 0.
∴ First polynomial is not a factor of second polynomial.

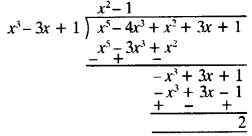
Ex 2.3 Solutions Class 10 Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are \(\sqrt { \frac { 5 }{ 3 } }\) and –\(\sqrt { \frac { 5 }{ 3 } }\)
Solution:

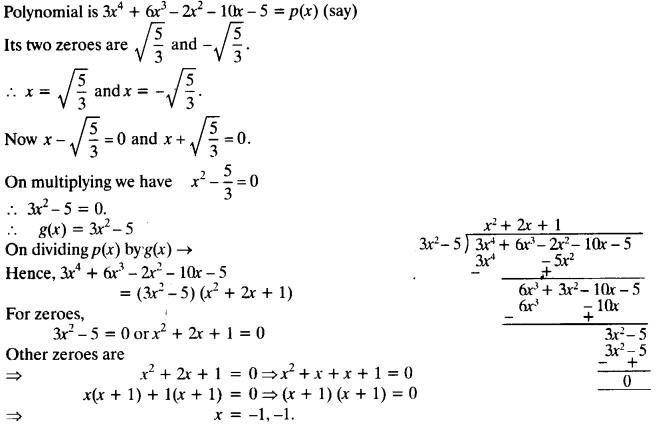
NCERTSolutions Ex 2.3 Class 10 Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Solution:
p(x) = x³ – 3 x 2 + x + 2 g(x) = ?
Quotient = x – 2; Remainder = -2x + 4
On dividing p(x) by g(x), we have
p(x) = g(x) x quotient + remainder
⇒ x³– 3x² + x + 2 = g(x) (x – 2) + (-2x + 4)
⇒ x³ – 3x² + x + 2 + 2 x- 4 = g(x) x (x-2)
⇒ x³ – 3x² + 3x – 2 = g(x) (x – 2)

Exercise 2.3 Class 10 Maths Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i) p(x),g(x),q(x),r(x)
deg p(x) = deg q(x)
∴ both g(x) and r(x) are constant terms.
p(x) = 2x²– 2x + 14; g(x) = 2
q(x) = x² – x + 7; r(x) = 0

(ii) deg q(x) = deg r(x)
∴ this is possible when
deg of both q(x) and r(x) should be less than p(x) and g(x).
p(x) = x³+ x² + x + 1; g(x) = x² – 1
q(x) = x + 1, r(x) = 2c + 2

(iii) deg r(x) is 0.
This is possible when product of q(x) and g(c) form a polynomial whose degree is equal to degree of p(x) and constant term.

We hope the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2. https://mcqquestions.guru/ncert-solutions-for-class-10-maths-chapter-2-ex-2-2/

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2

Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² -15
(vi) 3x² – x – 4
Solution:

Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

Solution:
(i) Zeroes of polynomial are not given, sum of zeroes = \(\frac { 1 }{ 4 }\) and product of zeroes = -1
If ax² + bx + c is a quadratic polynomial, then
α + β = sum of zeroes = \(\frac { -b }{ a }\) = \(\frac { 1 }{ 4 }\) and αβ = product of zeroes = \(\frac { c }{ a }\) = -1
Quadratic polynomial is ax² + bx + c
Let a = k, ∴ b = \(\frac { -k }{ 4 }\) and c = -k
Putting these values, we get

For different values of k, we can have quadratic polynomials all having sum of zeroes as \(\frac { 1 }{ 4 }\) and product of zeroes as -1.

(ii) Sum of zeroes = α + β = √2 = \(\frac { -b }{ a }\); product of zeroes = αβ = \(\frac { 1 }{ 3 }\) = \(\frac { c }{ a }\)
Quadratic polynomial is ax² + bx + c
Let a = k,b = -√2k and c = \(\frac { k }{ 3 }\)
Putting these values we get

For all different real values of k, we can have different quadratic polynomials of the form 3×2 – 3√2x +1 having sum of zeroes = √2 and product of zeroes = \(\frac { 1 }{ 3 }\)

(iii) Sum of zeroes = α + β = 0 = \(\frac { -b }{ a }\); product of zeroes = αβ = √5 = \(\frac { c }{ a }\)
Let quadratic polynomial is ax² + bx + c
Let a = k,b = 0, c = √5 k
Putting these values, we get
k[x² – 0x + √5 ] = k(x² + √5).
For different real values of k, we can have different quadratic polynomials of the form
x² + √5, having sum of zeroes = 0 and product of zeroes = √5

(iv) Sum of zeroes = α + β = 1= \(\frac { -b }{ a }\); product of zeroes = αβ = 1 = \(\frac { c }{ a }\)
Let quadratic polynomial is ax² + bx + c.
Let a=k, c = k, b = -k
Putting these values, we get k[x² -x +1]
Quadratic polynomial is of the form x² -x + 1 for different values of k.

(v) Sum of zeroes = α + β = \(\frac { -1 }{ 4 }\)= \(\frac { -b }{ a }\); product of zeroes = αβ = \(\frac { 1 }{ 4 }\) = \(\frac { c }{ a }\)
Let quadratic polynomial is ax² + bx + c
Let a=k, b= \(\frac { k }{ 4 }\), c= \(\frac { k }{ 4 }\)
Putting these values, we get k

Quadratic polynomial is of the form 4x² +x + 1 for different values of k.

(vi) Sum of zeroes = α + β = 4 = \(\frac { -b }{ a }\); product of zeroes = αβ = 1 = \(\frac { c }{ a }\)
Let quadratic polynomial is ax² + bx + c
Let a = k,b = -4k and c = k
Putting these values, we get
k[x² – 4x + 1]
Quadratic polynomial is of the form x² – 4x + 1 for different values of k.

We hope the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.1. https://mcqquestions.guru/ncert-solutions-for-class-10-maths-chapter-2-1/

LearnInsta.com designed free Maths NCERT Solutions Class 10 to score more marks in your CBSE examination.

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

Exercise 2.1

Question 1.
The graphs of y = p(x) are given in figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Solution:
The number of zeroes of p(x) in each graph given; are

We hope the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.1 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.1, drop a comment below and we will get back to you at the earliest.