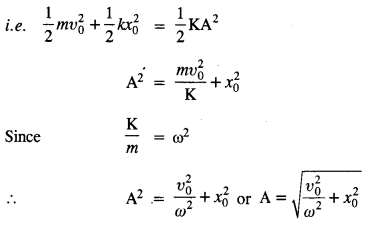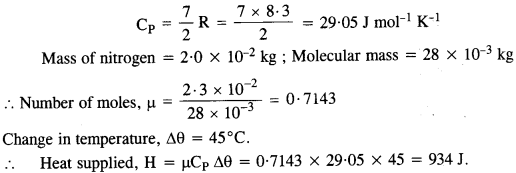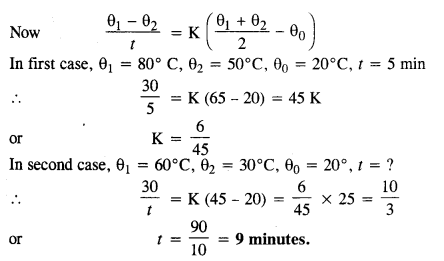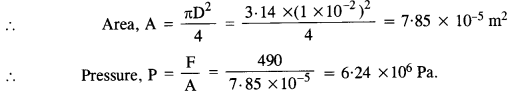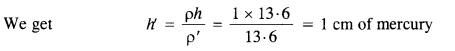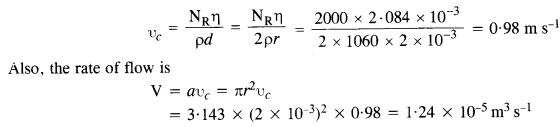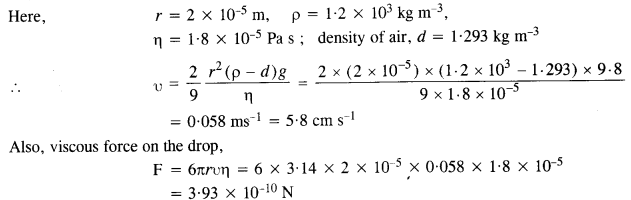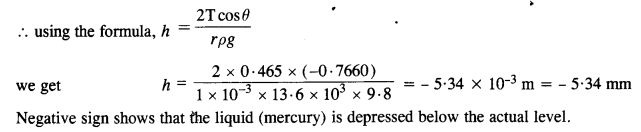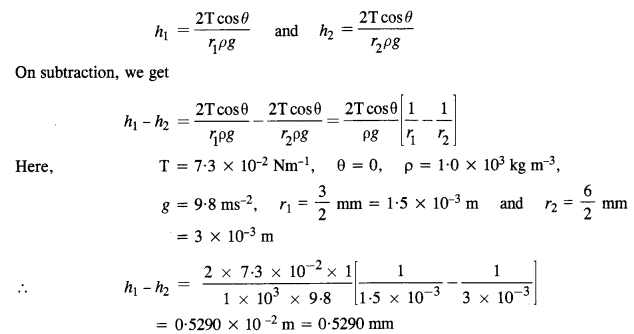Veer

NCERT Solutions for Class 11 Physics Chapter 15 Waves

These Solutions are part of NCERT Solutions for Class 11 Physics. Here we have given NCERT Solutions for Class 11 Physics Chapter 15 Waves

Question 1.
A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 cm. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end ?
Answer:
Tension in the string, T = 200 N ; Mass of string, M = 2.50 kg ;
Length, l= 20.0 cm = 20 x 10^-2 m

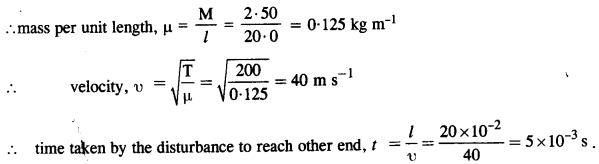
Question 2.
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top? Given that the speed of sound in air is 340 m s^-1. (g = 9.8 m s^-2)
Answer:
Here, h=300 m, g = 9.8 m s^-2 and velocity of sound,υ= 340 m s^-1
Let t₁ be the time taken by the stone to reach the surface of the pond.

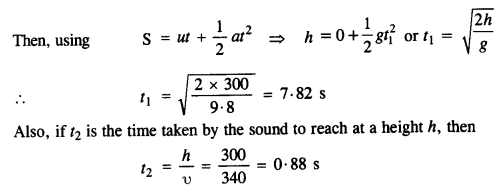
.’. Total time after which sound of splash is heard = t₁+ t₂= 7.82 + 0.88 = 8.7 s.

Question 3.
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that the speed of a transverse wave on the wire equals the speed of sound in dry air at 20°C = 343 m s^-1.
Answer:
Mass, M= 2.10 kg, Length, l = 12.0 m.

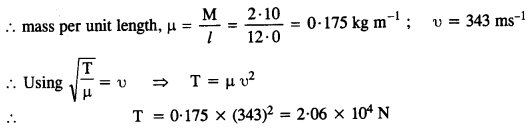
Question 4.
Use the formula

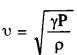
to explain why the speed of sound in air
(a) is independent of pressure.
(b) increases with humidity.
(c) increases with temperature
Answer:


Question 5.
You have learnt that a travelling wave in one dimension is represented by a function y = f(x,t) where x and t must appear in the combination x – υt or x + υt, i.e. y = F(x ± υt.) Is the converse true ? Examine if the following functions for y can possibly represent a travelling wave:
(a) (x – υt)²
(b) log [(x +υt )/x₀]
(c)exp [-(x + υt)/x₀]
(d) 1/(x + υt)
Answer:
The converse of the above statement is not true. For a function to represent a travelling wave, the function must be finite and well defined at any point and at any time. Only the function (C) satisfies this condition and is a wave function.

Question 6.
A bat emits the ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of (a) the reflected sound, (b) the transmitted sound?
Speed of sound in air is 340 m s^-1 and in water 1486 m s-1.
Answer:
Here v = 1000 kHz = 1000 x 10³ Hz = 10⁶ Hz
Velocity of sound in air, υ_a = 340 ms^-1; the velocity of sound in water, υ_w = 1486 ms^-1
(a) For reflected sound, medium remains the same

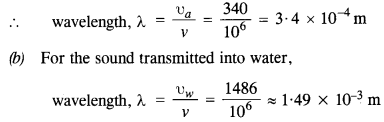
Question 7.
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s^-1 ? The operating frequency of the scanner is 4.2 MHz.
Answer:
Here,υ = 1.7kms^_1 = 1.7 x 1000 ms^_1 = 1700 ms^_1
Frequency, v= 4.2 MHz = 4.2 X 10⁶ Hz

Question 8.
A transverse harmonic wave on a string is described by
y (x, t) = 3.0 sin (361 + 0.018 x + π/4) where x and y are in cm and t in s. The positive direction of x is from left to right.
(a) Is this a travelling wave or a stationary wave?
(b) If it is travelling, what are the speed and direction of its propagation?
(c) What are its amplitude and frequency ?|
(d) What is the initial phase at the origin?
(e) What is the least distance between two successive crests in the wave?
Answer:
(a) It is traveling which is propagating from right to left. Comparing the given equation with y (x, t) = r sin (ωt+kr+φ)

Question 9.
For the wave described in Exercise 8, plot the displacement (y) versus (f) graphs for x = 0, 2, and 4 cm. What is the shape of these graphs? In which aspects do the oscillatory motion in travelling waves differ from one point to another: amplitude, frequency, or phase?
Answer:
The transverse harmonic wave is

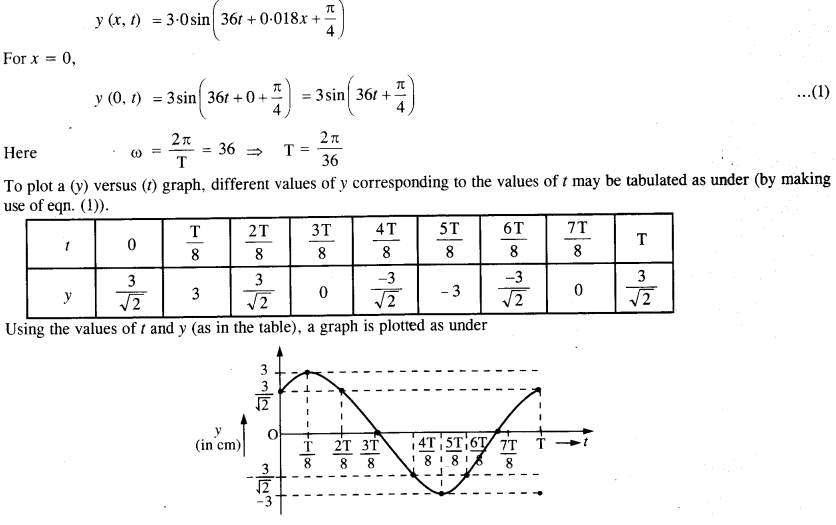
The graph obtained is sinusoidal. Similar graphs are obtained for x = 2 cm and x = 4 cm. The oscillatory motion in the travelling wave only differs in respect of phase. The amplitude and frequency of oscillatory motion remain the same in all the cases.

Question 10.
For the traveling harmonic wave
y (x, t) = 2.0 cos 2π(10t – 0.0080 x + 0.35)
where x and y are in cm and t in s. Calculate the phase difference between the oscillatory motion of two points separated by a distance of
(a)4 m
(b) 0.5 m
(c) λ/2
(d) 3λ/4.
Answer:
Comparing the equation given in the question, with the standard equation of travelling wave:

Question 11.
The transverse displacement of a string (clamped at its both ends) is given by

where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 x 10^-2 kg.
Answer the following:
(a) Does the function represent a travelling wave or a stationary wave?
(b) Interpret the wave as a superposition of two waves traveling in opposite directions. What are the wavelength, frequency, and speed of each wave?
(c) Determine the tension in the string.
Answer:
(a) The function does not represent a travelling wave. It represents a stationary wave.
(b) Using the relation

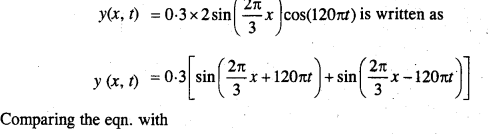
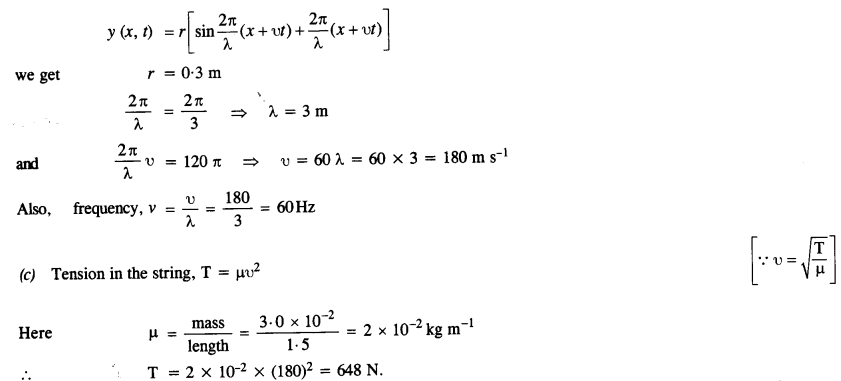
Question 12.
(1) For the wave on a string described in Exercise 11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers, (2) What is the amplitude of a point 0.375 m away from one end?
(a) All the points on the wave have
(b) same frequently everywhere except at the nodes.
(c) same phase everywhere in a loop except at the nodes.
(d) different amplitude.
(2) Here, x = 0.375 m, 1 = 0

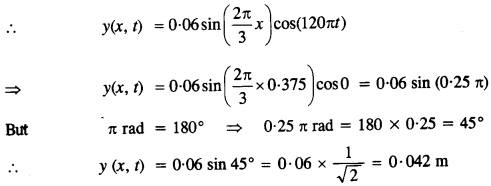
Question 13.
Given below are some functions of x and y to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent
(1) a travelling wave,
(2) a stationary wave or
(3) none at all:
(a) y = 2 cos (3x) sin (10t)
(b)
(c) y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)
(d) y = cos x sin t- cos 2x sin 2t
Answer:
(a) It represents a stationary wave.
(b) It does not represent either a travelling wave or a stationary wave.
(c) It is a representation of the travelling wave.
(d) It is a superposition of two stationary waves.

Question 14.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 x 10^-2 kg and its linear density is
4.0 x 10^-2 kg m^_1. What is
(a) the speed of a transverse wave on the string, and
(b) the tension in the string?
Answer:
Here, v = 45 Hz ; mass of wire, M = 3.5 x 10^-2 kg

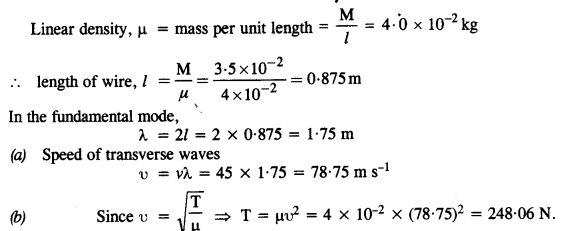
Question 15.
A meter-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when this tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in the air at the temperature of the experiment. The edge effects may be neglected.
Answer:
Let v be the fundamental frequency of the closed-end organ pipe for the length
l_x = 25.5 cm

Question 16.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 kHz. What is the speed of sound in steel?
Answer:
l = 100 cm = 1 m  f = 2.53 kHz
Since the rod is champed at the middle, a node is formed and since the rod is oscillating at a fundamental frequency of 2.53 kHz antinodes are formed at both ends as shown in the figure.
∴ l = λ/4 × 2 = λ/2 ⇒ λ = 2l
λ = 2 × 1 = 2 cm
We know that
v = fλ = 2.53 × 10³ × 2
= 5.06 × 10 ³ ms^-1

Question 17.
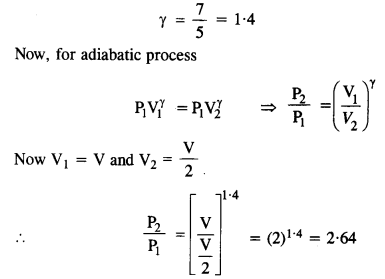
A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source? Will the same source be in resonance with the pipe if both ends are open? (speed of sound in air is 340 ms^-1).
Answer:

This is the first harmonic. The second harmonic is 3v i.e., 1275 Hz, the third harmonic is 5v i.e., 2125 Hz etc. Therefore, only the first harmonic of frequency 425 is rasonantly excited by a 430 Hz source.If both the ends of the pipe are open, the fundamental frequency is given by

The second, third, fourth… etc. harmonics have frequencies 2v’, 3v’, 4v’……. i.e., 1700 Hz, 2550 Hz, 3400 Hz etc.No harmonic can be excited by the 430 Hz source in this case.

Question 18.
Two sitar strings A and B playing the note ‘Ga’ are slightly out of tune and produce beats of frequency 6 Hz. The tension in string A is slightly reduced and the beat frequency is found to reduce to 3 Hz. If the original frequency of A is 324 Hz, what is the frequency of B?
Answer:
Let v₁ and v₂ be the frequencies of strings A and B respectively
Then, v₁= 324 Hz, v₂ = ?
Number of beats, b = 6
v₂ = v₁± b = 324 ± 6
i.e.,   v₂ = 330 Hz or 318Hz.
Since the frequency is directly proportional to square root of tension, on decreasing the tension in the string A, its frequency v₁; will be reduced i.e., number of beats will increase if v₂ = 330 Hz. This is not so because a number of beats becomes 3. Therefore, it is concluded that the frequency v₂ = 318 Hz because on reducing the tension in string A, its frequency may be reduced to 32l Hz, thereby giving 3 beats with v₂ = 318 Hz.

Question 19.
Explain why (or how) :
(a) in a sound wave, a displacement node is a pressure antinode and vice versa.
(b) bats can ascertain distances, directions, nature and sizes of the obstacles without any “eyes”.
(c) a violin note and sitar note may have the same frequency, yet we can distinguish between the two notes.
(d) solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases, and
(e) The shape of a pulse gets distorted during propagation in a dispersive medium.
Answer:
(a) In a sound wave, a decrease in displacement i..e. displacement node causes an increase in the pressure there i.e, a pressure antinode is formed. Also, an increase in displacement is due to the decrease in pressure.

(b) Bats emit ultrasonic waves of high frequency from their mouths. These waves after being reflected back from the obstacles on their path are observed by the bats. These waves give them an idea of distance, direction, nature and size of the obstacles.

(c) The quality of a violin note is different from the quality of sitar. Therefore, they emit different harmonics which can be observed by human ear to differentiate between the two notes.

(d) This is due to the fact that gases have only the bulk modulus of elasticity whereas solids have both, the shear modulus as well as the bulk modulus of elasticity.

(e) A pulse of sound consists of a combination of waves of different wavelength. In a dispersive medium, these waves travel with different velocities giving rise to the distortion in the wave.

Question 20.
A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (1) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 ms^-1, (b) recedes from the platform with a speed of 10 ms^-1 ? (2) What is the speed of sound in each case ? The speed of sound in still air can be taken as 340 ms^-1.
Answer:
Here, frequency of whistle, v = 400 Hz,
Speed of sound, v = 340 ms^-1; Speed of train, v_s = 10 m s^-1,
(1) (a) When the train approaches the platform i.e., the observer at rest,

Question 21.
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station at a speed of 10 ms^-1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 ms^-1? The speed of sound in still air can be taken as 340 ms^-1.
Answer:
Frequency of source of the sound, v = 400 Hz.
Speed of sound, υ= 340 ms^-1; Speed of wind, υ_m = 10 ms^-1.
Effective speed of sound = Speed of sound + Speed of air
= υ + υ_m = 340 + 10 = 350 ms^-1.
The source, as well as the listener, are both at rest. Therefore, there is no relative motion.

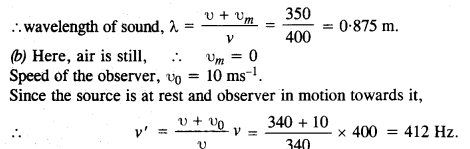
Since the source of sound is at rest, the wavelength A does not change
.’. wavelength = 0.875 m.
Also, speed of sound = 340 + 0 = 340 ms^-1
The situations are altogether different, because both the observer and the source are in motion with respect to the medium in this case.

Question 22.
A traveling harmonic wave on a string is described by
y (x,t) = 7.5 sin (0.0050 x + 12t + π/4)
(a) What are the displacement and velocity of oscillation of a point at x = 1 cm, and t = 1 s? Is this velocity equal to the velocity of wave propagation?
(b) Locate the points of the string which have the same transverse displacements and velocity as the x = 1 cm point at t = 2s, 5s, and 11s.
Answer:
The traveling harmonic wave is

(b) All the point, located at distance nλ, (where n is an integer) from the point x = 1 have the same velocity and displacement.

Question 23.
A narrow sound pulse (for example, a short pip by a whistle) is sent across a medium, (a) Does the pulse have a definite (1) frequency, (2) wavelength, (3) speed of propagation ? (b) If the pulse rate is 1 after every 20 s, (that is the whistle is blown for a split of second after every 20 s), is the frequency of the note produced by the whistle equal to 1/20 or 0.05 Hz? ¹
Answer:
1.  The pulse does not have a definite frequency and definite wavelength but has a definite speed of propagation.
2.  The frequency of the note is not 1/20 Hz or 0.05 Hz. It is only the frequency of repetition of the whistle.

Question 24.
One end of a long string of linear mass density 8.0 x 10^-3 kg m^-1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t = 0, the left end (fork end) of the string x = 0 has zero transverse displacement (y = 0) and is moving along positive y- direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.
Answer:
Here, mass per unit length, m = linear mass density = 8 x 10^-3 kg m³.
Tension in the string, T = 90 kg = 90 x 9.8 = 882 N
Frequency,  v = 256 Hz ; Amplitude, r = 5.0 cm = 5 x 10^-2 m. Hz
The wave produced in the string has velocity υ given by


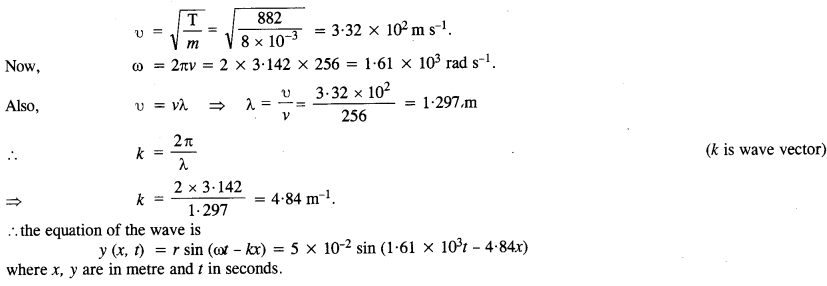
Question 25.
A SONAR system fixed in a submarine operates at a frequency of 40.0 kHz. An enemy submarine moves towards the SONAR with a speed of 360 km h^-1. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 1450 ms^-1.
Answer:
Here, frequency of SONAR(source )=40.0 kHz = 40 x10³

Question 26.
Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of the S wave is about 4.0 kms^-1, and that of P wave is 8.0 kms^-1. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in a straight line, how far away does the earthquake occur?
Answer:
Let υ₁ and υ₂ be the velocities of two waves respectively and t₁ and t₂ is the time taken by them to travel to the position of a seismograph.

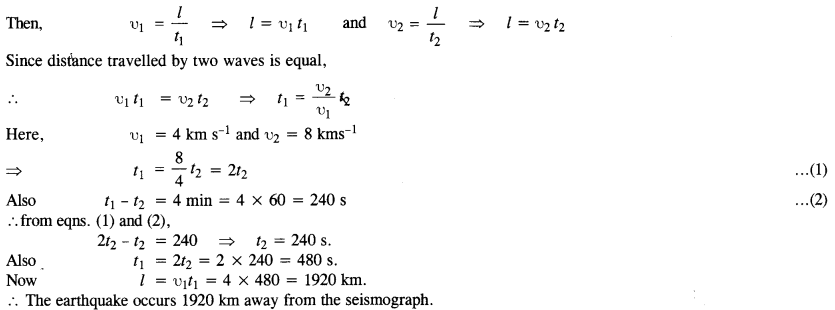
Question 27.
A bat is fitting about in a cave, navigating via ultrasonic bleeps. Assume that the sound emission frequency of the bat is 40 kHz. During one fast swoop directly toward a flat wall surface, the bat is moving at 0.03 times the speed of sound in air. What frequency does the bat hear reflected off the wall ?
Answer:
Here, frequency of sound emitted by bat, v = 40 kHz
Velocity of bat υ_s= 0.03 u, where 0 is the velocity of sound.
The bat is moving towards the flat wall. This is the case of source in motion and the observer at rest. Therefore, the frequency of sound reflected at the wall is

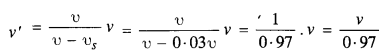
The frequency v’ is reflected by the wall and is again received by the bat moving towards the wall. This is the case of an observer moving towards the source with velocity
υ₀= 0.03υ.
.’. frequency observed by bat,

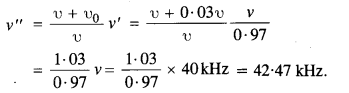
We hope the NCERT Solutions for Class 11 Physics Chapter 15 Waves, help you. If you have any query regarding NCERT Solutions for Class 11 Physics Chapter 15 Waves, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 11 Physics Chapter 14 Oscillations

These Solutions are part of NCERT Solutions for Class 11 Physics. Here we have given NCERT Solutions for Class 11 Physics Chapter 14 Oscillations

Question 1.
Which of the following examples represent periodic motion?
(a) A swimmer completing one (return) trip from one bank of a river to the other and back.
(b) A freely suspended bar magnet displayed from its N-S direction and released.
(c) A hydrogen molecule rotating about its center of mass.
(d) An arrow released from a bow.
Answer:
(b) and (c).
(Swimmer does not repeat trip after regular interval of time. Similarly, arrow released from a bow is not periodic).

Question 2.
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) the rotation of earth about its axis.
(b) motion of an oscillating mercury column in a U-tube.
(c) motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most point.
(d) general vibrations of a polyatomic molecule about its equilibrium position.
Answer:
(b) and (c) represent SHM in particular, (a) represents the period motion, (d) represents a superposition of a number of simple harmonic motions and is a periodic motion not necessarily S.H.M.

Question 3.
Figure depicts’four x-t plots for linear motion of a particle. Which of the plots represents periodic motion ? What is the period of motion (in case of periodic motion) ?

Answer:
Fig (b) and (d) represent periodic motions and the time period of each of these is 2 second, (a) and (c) are non periodic motions.

Question 4.
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion ? Give period for each case of periodic motion : (ω is any positive constant).
(a) sin ωt – cos ωt
(b) sin² ωt
(c) 3 cos (π/4 — 2ωt)
(d) cos ωt + cos 3ωt + cos 5ωt
(e) exp (- ω²t² )
(f) 1 +ωt +ω²t²
Answer:

Question 5.
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is (a) at the end A, (b) at the end B, (c) at the mid-point of AB going towards A, (d) at 2 cm away from B going towards A, (e) at 3 cm away from A going towards B, and (f) at 4 cm away from A going towards A.
Answer:
A and B form the extreme positions and the center of line AB (let it be O) forms the mean position.

(a) At the end A, e., extreme position, velocity is zero, acceleration and force are directed towards O and are positive.

(b) At the end B, e., second extreme position, velocity is zero whereas the acceleration and force are directed towards the point O and are negative.

(c) At the mid point 0, while going towards A, velocity is negative and maximum. The acceleration and force are both zero.

(d) At a distance 2 cm away from B going towards A, velocity is negative. Since acceleration and force are also directed towards O, both of them are negative.

(e) At a distance 3 cm away from A going towards B, velocity is positive. Since the acceleration and force are directed towards 0 from A, both of these are positive.

(f) At a distance of 4 cm away from A and going towards A, velocity is directed along BA, therefore, it is positive.Since acceleration and force are directed towards OB, both of them are positive.

Question 6.
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion ?
(a) a = 0.7x           (b) a = – 200 x²        (c) a = -10x                   (d) a = 100³
Answer:
Only the relation (c) represents the simple harmonic motion because for S.H.M., a a – x.

Question 7.
The motion of a particle executing simple harmonic motion is described by the displacement function, x(t) = A cos (cos ωt + Φ)
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is co cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is n s^_1. If instead of the cosine function, we choose the sine function to describe the SHM : x = B sin (at + a), what are the amplitude and initial phase of the particle with the above initial conditions ?
Answer:

Question 8.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance,,when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body ?
Answer:
Length of scale = 20 cm = 0.20 m
Total scale reading = 50 kg
∴ F = mg = 50 x 9.8 = 490 N
x= 20 cm = 0.20 m

Question 9.
A spring with a spring constant 1200 N m^-1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine
(1) the frequency of oscillations,
(2) maximum acceleration of the mass, and
(3) the maximum speed of the mass.

Answer:
Here k = 1200 N m^_1, m = 3 kg, A = 2.0 cm = 2 x 10^-2 m

Question 10.
In Exercise 9, let us take the position of mass when the spring is unstreched as x= 0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase ?
Answer:
Here, the maximum displacement = Amplitude A = 2 cm
(a) If the time t = 0 at x = 0, the displacement can be expressed as the sine function of t.
x(t) = A sin ωt

Question 11.
Following figures correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e clockwise or anti-clockwise) are indicated on each figure.

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
Answer:

Question 12.
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case (or is in cm and t is in s) :
(a) x = – 2 sin (3t + π/3)
(b) x = cos (π/6 – t)
(c) x = 3 sin (2nt + tc/4)
(d) x = 2 cos πt
Answer:

Question 13.
Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Fig. (b) is stretched by the same force F.

(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released free, what is the period of oscillation in each case ?
Answer:
(a) Let y be the maximum extension produced in the spring in fig. (a).
Then   F = Ay (in magnitude)   ∴y =  \(\frac { F }{ K } \)
In fig. (b), the force on one mass acts as the force of reaction due to the force on the other mass. Therefore, each mass behaves as if it is fixed with respect to the other.

Question 14.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rev/min,
what its maximum speed ?
Answer:

Question 15.
The acceleration due to gravity on the surface of moon is 1.7 ms^-2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s ? (g on the surface of earth is 9.8 ms^-2)
Answer:

Question 16.
Answer the following questions :
(a) Time period of a particle in SHM depends on the force constant k and mass m of the particle :

A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum ?

(b) The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation ,a more involved analysis shows that T is grater than

Think of a qualitative argument to appreciate this results.

(c) A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall ?

(d) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity
Answer:
In case of a spring, k does not depend upon m. However, in case of a simple pendulum, k is directly proportional to

(c) The wrist watch uses an electronic system t>r spring system to give correct time, which does not change with acceleration due to gravity. Therefore, watch gives the correct time.

(d) During free fall of the cabin, the acceleration due to gravity is zero. Therefore, the frequency of oscillations is also zero e., the pendulum will not vibrate at all.

Question 17.
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period ?
Answer:
In this case, the bob of the pendulum is under the action of two accelerations.
(1) Acceleration due to gravity ‘g’ acting vertically downwards.

Question 18.
A cylindrical piece of cork of base area A and height h floats in a liquid of density ρ. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period

where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
Answer:
Let l be the height of the cork which is inside the liquid. Then, at equilibrium,
weight of the cork = upthrust of the portion of cork inside the liquid .

Question 19.
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
Answer:
The suction pump creates the pressure difference, thus mercury rises in one limb of the U-tube. When it is removed, a net force acts on the liquid column due to the difference in levels of mercury in the two limbs and hence the liquid column executes S.H.M. which can be expressed as:
Consider the mercury contained in a vertical U-tube upto the level P and Q in its two limbs.
Let P = density of the mercury.
L = Total length of the mercury column in both the limbs.
A = internal cross-sectional area of U-tube. m = mass of mercury in U-tube = LAP.
Assume, the mercury be depressed in left limb to F by a small distance y, then it rises by the same amount in the right limb to position Q’.
.’. Difference in levels in the two limbs = P’ Q’ = 2y.
:. Volume of mercury contained in the column of length 2y = A X 2y
.•. m – A x 2y x ρ.
If W = weight of liquid contained in the column of length 2y.
Then W = mg = A x 2y x ρ x g
This weight produces the restoring force (F) which tends to bring back the mercury to its equilibrium position.

Question 20.
An air chamber of volume V has a neck area of cross-section a into which a ball of mass m can move up and down without any friction (Fig.). Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig.]

Answer:
When the ball is lying at rest in the long neck, the pressure of air below the ball inside the chamber is equal to the atmospheric pressure outside. If the ball is slightly depressed below through a distance y, then change in volume of air inside the chamber,

Question 21.
You are riding in an automobile of mass 3000 kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15 cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by 50% during one complete oscillation. Estimate the values of (a) the spring constant k and (b) the damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750 kg.
Answer:
(a) Here, mass M = 3000 kg, displacement x = 15 cm = 015 m, g = 10 m/s². There are four spring systems. If k is the spring constant of each spring, then total spring constant of all the four springs in parallel is

Question 22.
Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.
Answer:
Let the SHM be represented as
y = r sin ωt, where r – amplitude…..(1)


Question 23.
A circular disc of mass 10 kg is suspended by a wire attached to its center. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5 s. The radius of the disc is 15 cm. Determine the torsional spring constant of the wire. (Torsional spring constant a is defined by the relation J = – αθ, where J is the restoring couple and 0 the angle of twist).
Answer:
Here, mass of disc, m = 10 kg,
radius r =15 cm = 0.15 m Tortional spring constant a = ?
Time period of tortional oscillations, T = 1.5 s

Question 24.
A body describes a S.H.M. with an amplitude of 5 cm and period of 0.2 s. Find the acceleration and velocity of the body, when displacement is (a) 5 cm, (b) 3 cm, (c) 0 cm.
Answer:
A = 5 cm, T = 0.2 s.

Question 25.
A mass attached to a spring is free to oscillate with angular velocity to in a horizontal plane without friction or damping. It is pulled to a distance x₀ and pushed towards the center with velocity υ₀ at time
t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters oo, x₀ and υ₀ .
Answer:
According to the law of conservation of energy
Total energy at x₀ = Total energy at extreme position.

We hope the NCERT Solutions for Class 11 Physics Chapter 14 Oscillations, help you. If you have any query regarding . NCERT Solutions for Class 11 Physics Chapter 14 Oscillations, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 11 Physics Chapter 12 Thermodynamics

These Solutions are part of NCERT Solutions for Class 11 Physics. Here we have given NCERT Solutions for Class 11 Physics Chapter 12 Thermodynamics

Question 1.
A geyser heats water flowing at the rate of 3.0 liters per minute from 27 °C to 77 °C. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is 4-0 x 10⁴ J/g ?
Answer:

Question 2.
What amount of heat must be supplied to 2.0 x 10^-2 kg of nitrogen (at room temperature) to raise its temperature by 45°C at constant pressure ? (Molecular) mass of N₂ = 28 ; R = 8.3 J mol^-1 K^-1).
Answer:
Nitrogen is a diatomic gas. Therefore its molar specific heat at constant pressure is

Question 3.
Explain why
(a) Two bodies at different temperatures T₁ and T₂ if brought in thermal contact do not necessarily settle to the mean temperature (T₁ + T₂)/2.
(b) The coolant in a chemical or a nuclear plant (i.e., the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat.
(c) Air pressure in a car type increases during driving.
(d) The climate of a harbor town is more temperate than that of a town in a desert at the same latitude.
Answer:
(a) Two bodies would settle at the mean temperature (T₁+ T₂)/2 only if they have equal thermal capacities.
(b) A coolant of high specific heat can withdraw more heat out of the chemical or nuclear plant than a coolant of ordinary specific heat.
(c) During driving, the tyres of the car are heated up due to friction between tyres and road. Since heating of tyres causes an increase in temperature, the pressure in the tyres increases (P a T at constant volume).
(d) The relative humidity in a harbour town is more than the relative humidity in a desert town. Therefore, the climatic conditions of a harbour town do not reach extremes of hot or cold making it a temperate zone.

Question 4.
A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half its original volume?
Answer:
Hydrogen is a diatomic gas. Therefore, for hydrogen, ratio of two specific heats is

Question 5.
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken form state A to B via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case ? [Take 1 cal = 4.19 J]
Answer:
When the state of the gas changes adiabatically from A to B, amount of work done is used to increase the internal energy of the gas.
Increase in internal energy, ΔU = 22.3 J.
In the second case, when state A changes to state B, heat absorbed by the system
ΔQ = 9.35 cal = 9.35 x 4.19J = 39 18 J
Now, using the first law of thermodynamics,
ΔQ =ΔU + ΔW
=> ΔW =ΔQ-ΔU = 39 18-22.3 = 16.88 J

Question 6.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following :
(a) What is the final pressure of the gas in A and B?
(b) What is the change in the internal energy of the gas?
(c) What is the change in the temperature of the gas?
Do the intermediate states of the system (before settling to the final equilibrium state) lie of its P-V-T surface ?
Answer:
(a) Since the final temperature and initial temperature remain the same (isothermal process).

(b) Since the temperature of the system remains unchanged, the change in internal energy is zero.

(c) The system being thermally insulated, there is no change in temperature (because of free expansion)

(d) The expansion is a free expansion. Therefore, the intermediate states are non-equilibrium states and the gas equation is not satisfied in these states. As a result, the gas can not return to an equilibrium state which lie on the P-V-T surface.

Question 7.
A steam engine delivers 5.4 x 10⁸ J of work per minute and services 3.6 x 10⁹ J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
Answer:
Output i.e., useful work done per minute = 5.4 x 10⁸J
Input i.e., heat absorbed per minute = 3.6 X 10⁹ J

Question 8.
An electric heater supplies heat to a system at a rate of 100 W. If the system performs work at a rate of 75 joules per second, at what rate is the internal energy increasing?
Answer:
Rate of heat supplied to the system is 100 W = 100 Js^-1
Rate of work done by the system is 75Js^-1.
From the first law of thermodynamics, we have
∆ Q = ∆ U + ∆ W ……..(1)
If the above parameters are observed for a time‘∆ t’,
\(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{t}}=\frac{\Delta \mathrm{U}}{\Delta \mathrm{t}}+\frac{\Delta \mathrm{W}}{\Delta \mathrm{t}}\) …….(2)
where \(\frac{\Delta Q}{\Delta t}\) is the rate of heat supplied to the system for the given time, \(\frac{\Delta U}{\Delta t}\) is the rate of increase in internal energy of the system for the given time and \(\frac{\Delta W}{\Delta t}\) is the
rate of work done by the system in the given time.
∴ From equation (2), we have
100 = \(\frac{\Delta U}{\Delta t}\) + 75
∴ \(\frac{\Delta U}{\Delta t}\) = 25 Js^-1
Therefore the internal energy increases at rate of 25 Joules per second.

Question 9.
A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in Fig.

Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the work done by the gas from D to E to F.
Answer:
As is clear from above Fig.,
Change in pressure, dP = EF = 5.0 – 2.0 = 3.0 N m^-2
Change in volume, dW = DF = 600 – 300 = 300 m³
Work done by the gas from D to E to F = area of ADEF

Question 10.
A refrigerator is to remove heat from the eatables kept inside at 10°C. Calculate the coefficient of performance, if room temperature is 36°C.
Answer:
Here, T₁ = 36°C = 36 + 273 = 309 K
T₂ = 10°C = 10 + 273 = 283 K

We hope the NCERT Solutions for Class 11 Physics Chapter 12 Thermodynamics, help you. If you have any query regarding NCERT Solutions for Class 11 Physics Chapter 12 Thermodynamics, drop a comment below and we will get back to you at the earliest

NCERT Solutions for Class 11 Physics Chapter 11 Thermal Properties of Matter

These Solutions are part of NCERT Solutions for Class 11 Physics. Here we have given NCERT Solutions for Class 11 Physics Chapter 11 Thermal Properties of Matter

Question 1.
The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales.
Answer:
The relation between Kelvin scale and Celcius scale is

Question 2.
Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between T_A and T_B?
Answer:
The triple point of water is T = 273.16 K

Question 3.
The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law:
R = R₀ [1 + 5 x 10^-3 (T – T₀)]
The resistance is 101.6 Ω at the triple-point of water, and 165.5 Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4 Ω ?
Answer:
At the triple point of water, T = 273.16 K and R = 101.6 Ω(given)
R = R₀ [1 + 5 X 10^-3  (T – T0)]
=>  101.6 = Ro [1 + 5 X 10^-3 (273-16-T₀)]  …(1)
At temperature T = 600.5 K, R = 165.5 Q
165.5 = Ro [1 + 5 X 10^-3 (600-5 – T0)]……………(2)


Answer the following:
(a) The triple-point of water is a standard fixed point in modern thermometry. Why? What is wrong with taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale)?
(b) There were two fixed points in the original Celsius scale as mentioned above which were assigned the number 0 °C and 100 °C respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the kelvin absolute scale is assigned the number 273.16 K. What is the other fixed point on this (Kelvin) scale?
(c) The absolute temperature (Kelvin scale) T is related to the temperature t_c on the Celsius scale by
t_c = T – 273.15
(d) Why do we have 273.15 in this relation, and not 273.16?
What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale?
Answer:
(a) Triple point of water has a unique value e. 273.16 K. The melting point and boiling points of ice, and water respectively do not have unique values and change with the change in pressure.
(b) The other fixed point is absolute zero of temperature.
(c) On the Celcius scale 0 °C corresponds to the melting point of ice at normal pressure and the value of absolute temperature is 273.15 K. The temperature 273.16 K corresponds to the triple point of water.
(d) The Fahrenheit scale and Absolute scale are related as

Question 5.
Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made :

(a) What is the absolute temperature of the normal melting point of sulphur as read by thermometers A and B?
(b) What do you think is the reason for the slightly different answers from A and B? (The thermometers are not faulty). What further procedure is needed in the experiment to reduce the discrepancy between the two readings?
Answer:

(b) The discrepancy between the two readings is due to the fact that the gases are not perfectly ideal gases. To reduce the discrepancy, the readings should be taken at low pressures so that the gases could show prefect behaviour.

Question 6.
A steel tape 1 m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is 27.0°C? Coefficient of linear expansion of steel = 1.20 x 10^-5 °C^_1.
Answer:
The length of the steel tape at 27 °C is 100 cm
∴  L = 100 m and T = 27°

Length of the same steel rod shall again be 63 cm when measured by the same steel tape at 27°.

Question 7.
A large steel wheel is to be fitted onto a shaft of the same material. At 27°C, the outer diameter of the shaft is 8.70 cm and the diameter of the central holes in the wheel is 8.69 cm. The shaft is cooled using ‘dry ice’. At what temperature of the shaft does the wheel slip on the shaft? Assume the coefficient of linear expansion of the steel to be constant over the required temperature range.
Answer:

Question 8.
A hole is drilled in copper steel. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the steel is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 x 10^-5 °C¹
Answer:
Given α = 1.70 × 10^-5K^-1
β = 2α = 3.40 × 10^-5K^-1
d₁ = 4.24 cm
Initial area A₁ at 27°C = 300K = T₁
is \(\pi\left(\frac{\mathrm{d}_{1}}{2}\right)^{2}=\pi\left(\frac{4.24}{2}\right)^{2}\)
⇒ A₁ = 4.4944 π cm²
Area A₂ at 227°C = 500K = T₂ is
∆₁ [1 + β(T₂ – T₁)]
i.e. A₂ = 4.4944 π [1 + 3.40 × 10^-5 (500 – 300)]
A₂ = 4.5250 π cm²
⇒ \(\pi\left(\frac{\mathrm{d}_{2}}{2}\right)^{2}\) = 4.5250 π cm²
⇒ d₂ = \(\sqrt{18.100}\) =4.2544 cm
∴ Change in diameter = d₂ – d₁
= 4.2544 – 4.25 = 0.0144 cm

Question 9.
A brass wire 1.8 m long at 27°C is held taut with little tension between two rigid supports. If the wire is cooled to a temperature of – 39 °C, what is the tension developed in the wire, if its diameter is 2.0 mm? Co-efficient of linear expansion of brass = 2.0 x 10^-5 °C’ ; Young’s modulus of brass = 0.91 x 10¹¹ Pa.
Answer:

Question 10.
A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40*0 °C? Is there a ‘thermal stress’ developed at the junction? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 x 10^-5 °C¹, steel = 1.2 x 10⁵ °C¹.
Answer:

Question 11.
The coefficient of volume expansion of glycerin is 49 x 10^-5 °C^-1. What is the fractional change in its density for a 30 °C rise in temperature?
Answer:

Question 12.
A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in beating the machine itself or lost to the surroundings? Specific heat of aluminium = 0.91Jg^-1°C^-1.
Answer:

Question 13.
A copper block of mass 2.5 kg is heated in a furnace to a temperature of 500°C and then placed on a large ice block. What is the maximum amount of ice that cari melt?
(Specific heat of copper = 0.39J g^-1 °C^-1, and heat of fusion of water = 335 J g^-1).
Answer:
Let m be the mass of ice melted when hot copper block is placed over an ice block.
Heat lost of copper block = Heat gained by ice

Question 14.
In an experiment on the specific heat of a metal, a 0.20 kg block of metal at 150°C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm³ of water at 27°C. The final temperature is 40°C. Compute the specific heat of the metal.
Answer:

Question 15.
Given below are observations on molar-specific heats at room temperature of some common gases.

The measured molar specific heats of these gases are markedly different from those for monoatomic gases. [Typically, the molar specific heat of a monoatomic gas is 2.92 cal/mol K, as you must have worked out in 16.] Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine?
Answer:
All the gases mentioned above are diatomic, and hence have other degrees of freedom in addition to the translational degrees of freedom. To raise the temperature of the gas, heat has to be supplied to increase the average energy of all the modes.

Consequently, the molar specific heats for diatomic gases is higher than that for monoatomic gases. The higher value of the molar specific heat of chlorine indicates that at room temperature, vibrational modes are also present In addition to the rotational modes of freedom.

Question 16.
Answer the following questions based on the P – T phase diagram of carbon dioxide (Figure shown below) :

(a) At what temperature and pressure can the solid, liquid and vapour phase of CO2 co-exist in equilibrium ?
(b) What is the effect of decrease of pressure on the fusion and boiling point of CO₂ ?
(c) What are the critical temperature and pressure for CO₂ ? What is their significance ?
(d) Is CO₂ solid, liquid or gas at

(a) – 70 °C under 1 atm,
(b) – 60 °C under 10 atm
(c) 15 °C under 56 atm ?

Answer:
(a) Liquid and vapour phases coexist with solid phase at the triple point temperature – 56.6 °C and a pressure of 5.11 atm.
(b) The boiling point as well as freezing point decrease with the decrease in pressure.
(c) The critical temperature is 3T1 °C and critical pressure is’73.0 atm.
(d) (a) It is vapour (b) It is solid and (c) It is liquid.

Question 17.
Answer the following questions based on the P – T phase diagram of CO₂ (Fig. of question 17).
(a) CO₂ at 1 atm pressure and temperature – 60 °C is compressed isothermally. Does it go through a liquid phase?
(b) What happens when CO₂ at 4 atm pressure is cooled from room temperature at constant pressure?
(c) Describe qualitatively the changes in a given mass of solid CO₂ at 10 atm pressure and temperature – 65 °C as it is heated up at room temperature at constant pressure.
(d) CO₂ is heated to a temperature of 70° C and compressed isothermally. What changes in its properties do you expect to observe?
Answer:

1. When subjected to isothermal compression, Co₂ will condense to solid directly without passing through the liquid phase.
2. When cooled at constant pressure, Co₂ will condense directly to solid phase without passing through the liquid phase,
3. As the solid Co₂ is heated up, it first turns to liquid phase and then solid phase. The fusion and boiling points can be obtained from finding out the points of intersection between the horizontal 10 atm line on the P-T diagram with the fusion and vaporization curves.
4. Co₂ will not exhibit any clear transition to the liquid phase but will deviate more and more from ideal behaviour ps the pressure increases.

Question 18.
A child running a temperature of 101 °F is given an antipyrin (i. e. a medicine that lowers fever) which causes an increase in the rate of evaporation of sweat from his body. If the fever is brought down to 98 °F in 20 min, what is the average Irate of extra evaporation caused by the drug? Assume the evaporation mechanism to be the only way by which heat is lost. The mass of the child is 30 kg. The specific heat of the human body is approximately the same as that of water, and the latent heat of evaporation of water at that temperature is about 580 cal g^_1.
Answer:

Question 19.
A cubical icebox of thermocouples has each side = 30 cm and a thickness of 5 cm. 4 kg of ice is put in the box. If the outside temp is 45° C and coeff. of thermal conductivity = 0.01 Js^-1 mf¹ °C^-1, calculate the mass of ice left after 6 hours. Take latent heat of fusion of ice = 335 x 10³ J/kg.
Answer:


Question 20.
A brass boiler has a base area of 0.15 m² and a thickness of 1.0 cm. It boils water at the rate of 6.0 kg/min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass = 609 Js^-1 m^-1 °C^-1. Heat of vaporisation of water = 2256 Jg^-1.
Answer:

Question 21.
Explain why :
(a) a body with large reflectivity is a poor emitter
(b) a brass tumbler feels much colder than a wooden tray on a chilly day
(c) an optical pyrometer (for measuring high temperatures) calibrated for ideal black body radiation gives too low a value for the temperature of a read hot iron piece in the open, but gives a correct value for the temperature when the same piece is in the furnace
(d) the earth without its atmosphere would be inhospitably cold
(e) Heat systems based on the circulation of steam are more efficient in warming a building than those based on circu|ation of hot water.
Answer:
(a) According to Kirchhoff s law of black body radiations, good emitters are good absorbers and bad emitters are bad absorbers. A body with large reflectivity is a poor absorber of heat and consequently, it is also a poor emitter.

(b) Brass is a good conductor of heat, while wood is a bad conductor. When we touch the brass tumbler on a chilly day, heat starts flowing from our body to the tumbler and we feel it cold. However, when the wooden tray is touched, heat does mot flow from our hands to the tray and we do not feel cold.

(c) An optical pyrometer is based on the principle that the brightness of a glowing surface of a body depends upon its temperature. Therefore, if the temperature of the body is less than 600°C, the image formed by the optical pyrometer is not brilliant and we do not get a reliable result. It is for this reason that the pyrometer gives a too low value for the temperature of red hot iron in the open.

(d) The atmosphere of earth acts as an insulator to stop the infrared radiations which fall on the surface of earth during day time, to escape during the night. If there were no atmosphere, the whole of heat radiated by the earth during night would escape to the universe leaving it under the intense cold.

(e) Steam at a temperature of 100°C has more heat (because its latent heat is 540 cal g^-1) compared to the same amount of water at the same temperature. Therefore, heating systems based on the circulation of steam are more efficient in warming a building than those based on the circulation of hot water.

Question 22.
A body cools from 80°C to 50°C in 5 minutes. Calculate the time it takes to cool from 60°C to 30°C. The temperature of the surroundings is 20°C.
Answer:
If θ₀ is the temperature of surrounding, time taken t to cool a body from temperature θ₁, to θ₂ is given by

We hope the NCERT Solutions for Class 11 Physics Chapter 11 Thermal Properties of Matter, help you. If you have any query regarding NCERT Solutions for Class 11 Physics Chapter 11 Thermal Properties of Matter, drop a comment below and we will get back to you at the earliest

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids

These Solutions are part of NCERT Solutions for Class 11 Physics. Here we have given NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids

Question 1.
Explain why
1. The blood pressure In humans is greater at the feet than at the brain.
Answer:
The height of the blood column in the human body is more at the feet than at the brain. As the pressure increases with the height of the column, blood exerts  more pressure at the feet than at the brain (P = ρgh)

2. Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km.
Answer:
The density of air is maximum near the surface of the earth (at sea level) and it decreases rapidly with height. The density of air at a height of 6 km reduces to almost half it’s value at sea level. Hence the atmospheric pressure at a height of 6 km decreases to nearly half of its value at sea level even though the height of the atmosphere is more than 100km.

3. Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.
Answer:
The pressure created while applying a force on a liquid is transmitted equally in all direction inside the liquid. That is why there is no fixed direction for the pressure transmitted. Hence we can say that hydrostatic pressure is a scalar quantity.

Question 2.
Explain why
(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute.
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets the glass while mercury does not.)
(c) Surface tension of a liquid is independent of the area of the surface.
(d) Detergents should have small angles of contact.
(e) A drop of liquid under no external forces is always spherical in shape.
Answer:
(a) The cohesive force between mercury molecules is greater than the adhesive force between mercury and glass molecules. Therefore, the meniscus of mercury in a glass tube is convex and hence the angle of contact is obtuse. In the case of water, the cohesive force between water molecules is less than the adhesive force between water and glass molecules. Therefore, the meniscus of water in the glass tube is concave and hence the angle of contact is acute.
(b) The cohesive force between water molecules is less than the adhesive force between glass and water molecules. On the other hand, the cohesive force between mercury molecules is greater than the adhesive force between glass and mercury molecules.
(c) Surface tension is defined as the force per unit length of an imaginary line drawn tangentially on the surface of the liquid at rest. Therefore, surface tension is also independent of the area of the liquid surface.
(d) So that the detergent has low surface tension and greater ability to wet a surface.
(e) In the absence of external force, liquid drop takes a spherical shape due to surface tension.

Question 3.
Fill in the blanks using the words from the list appended with each statement:
(a) Surface tension of liquids generally……………. with temperature (increases/decreases)
(b) Viscosity of gases……………… with temperature, whereas viscosity of liquids………………. with temperature (increases/decreases)
(c) For solids with the elastic modulus of rigidity, the shearing force is proportional to………………….. while for fluids it is proportional to…………. (shear strain/rate of shear strain)
(d) For a fluid in steady flow, the increase in flow speed at a constriction follows from…………….. while the decrease of pressure there follows from………….. (conservation of mass/Bernoulli’s principle)
(e) For the model of a plane in a wind tunnel, turbulence occurs at a…………………… speed than the critical speed for turbulence for an actual plane (greater/smaller)
Answer:
(a) decreases
(b) increases ; decreases
(c) shear strain ; rate of shear strain
(d) conservation of mass ; Bernoulli’s principle

Question 4.
Explain why
(a) To keep a piece of paper horizontal, you should blow over, not under, it.
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers.
(c) The size of a needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection.
(d) A fluid flowing out of a small hole in a vessel results in a backward thurst on the vessel.
(e) a spinning cricket ball in air does not follow a parabolic trajectory.
Answer:
(a) When we blow over the piece of paper, the velocity of air increases. As a result, the pressure over it decreases in accordance with the Bernoulli’s theorem whereas the pressure below it is higher (atmospheric pressure) which keeps the paper horizontal.

(b) This is due to the continuity equation of flow of the liquids. When we close the water tap, the area of cross-section decreases and according to the equation of continuity (aυ= constant), the velocity of flow of the liquid increases.

(c) For a> constant height, the Bernoulli’s theorem is expressed as
p + \(\frac { 1}{ 2 } \) pυ² = constant
In this equation, the pressure P occur with a single power whereas the velocity occurs with a square power. Therefore, the velocity has more effect compared to the pressure. It is for this reason that needle of the syringe controls flow rate better than the thumb pressure exerted by the doctor.

(d) When a fluid flows out of a small hole, it carries momentum with it. According to the law of conservation of momentum, the vessel gets a recoil momentum. Thus, there is a change in momentum of the vessel which means that a backward thurst acts on it.

(e) When ball is given spin at the top, the velocity of air above the ball is higher than below the ball. According to Bernoulli’s theorem, die pressure above the ball is less than the pressure below the ball. Thus, there is net upward force on the spinning ball and hence the ball follows a curved path. This effect is known as the Magnus effect.

Question 5.
A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Answer:
Mass of girl, m= 50 kg.
Force on the heel, F = mg = 50 x 9.8 = 490 N
Diameter, D = 1.0 cm = 1 x 10^-2 m

Question 6.
Toricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m^-3. Determine the height of the wine column for normal atmospheric pressure.
Answer:
At normal pressure of atmosphere,


Question 7.
A vertical off-shore structure is built to withstand maximum stress of 10⁹ Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.
Answer:
Maximum stress that can be taken by the off-share structure, P_max = 10⁹Pa.
density of water = 10³ kg /m³ and g = 9.8 m/s² and h = 3km (depth of the sea)
∴ Pressure exerted by seawater, P = ρgh
= 10³ × 9.8 × 3 × 10³
P = 2.94 × 10⁷ Pa
Note that, P < P_max
Since the pressure exerted by the seawater is less than the maximum pressure the structure can withstand, the structure is suitable for putting on the top of the oil well.

Question 8.
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm². What maximum pressure would the smaller piston have to bear?
Answer:
Maximum mass, m= 3000 kg ; Area, A = 425 cm² = 425 x 10^-4 m².

Question 9.
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?
Answer:

Since the mercury column in the two arms is in level, therefore,
Pressure due to spirit = Pressure due to water

Question 10.
In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6)
Answer:
If p_m be the density of mercury, then

Question 11.
Can Bernoulli’s equation be used to describe the flow of water through a rapid motion in a river? Explain.
Answer:
No. The flow of water through a rapid in a river is turbulent and hence Bernoulli’s principle cannot be applied.

Question 12.
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
Answer:
If the pressures at the two places where Bernoulli’s theorem is applied are not much different, it does not matter if one uses gauge pressure instead of absolute pressure.

Question 13.
Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 x 10^-3 kg s^-1, what is the pressure difference between the two ends of the tube? Density of glycerine = 1.3 X 10³ kg m^-3 and viscosity of
glycerine = 0.83 N s m^-2 to
Answer:
Here, l= 1.5 m, r =1.0 cm = 10^-2 q = 0.83 N s m^-2

Question 14.
In a test experiment on a model airplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s^-1 and 63 m s^-1 respectively. What is the lift on the wing if its area is 2.5 m² ? Take the density of air to be 1.3 kg m^-3.
Answer:
Here υ₁ 70 ms^-1, υ₂ = 63 ms ‘, p = 1.3 kg m ³ and A = 2.5 m².
Now, using Bernoulli’s theorem (for constant height),

Question 15.
Figures (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect? Why?

Answer:
Figure (a) is incorrect. It is because of the fact that at the kink, the velocity of flow of liquid is large and hence using the Bernoulli’s theorem the pressure is less. As a result, the water should not rise higher in the tube where there is a kink (i. e. where the area of cross-section is small).

Question 16.
The cylindrical tube of a spray pump has a cross-section of 8.0 cm² one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min^-1, what is the speed of ejection of the liquid through the holes ?
Answer:
Here, area of cylindrical tube, a_x = 8.0 cm² = 8 x 10^-4 m²

Question 17.
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 x 10^-2 N (which includes the small weight of the silder). The length of the silder is 30 cm. What is the surface tension of the film ?
Answer:
Force on the silder, F= 1.5 x 10^-2 N

Question 18.
(a) shows a thin liquid film supporting a small weight = 4.5 x 10^-2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c) ? Explain your answer physically.

Answer:
As shown in fig(a)

Question 19.
What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature ? Surface tension of mercury at that temperature (20 °C) is 4.65 x 10^-1 N m^_1. The atmospheric pressure is 1.01 x 10⁵ Pa. Also give the excess pressure inside the drop.
Answer:
Here, surface tension, T = 4.65 x 10^-1 Nm^-1
Radius of drop, r =3.00 mm = 3 x 10^-3 m.
Outside pressure, p₀ = 1.01 x 10⁵ Pa.
Using the relation,

Question 20.
What is the excess pressure inside a bubble of soap solution of radius 5-00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 x 10^-2 N m^-1 ? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 x 10^s Pa).
Answer:
Here, surface tension, T = 2.50 x 10^-2 N m^-1
Radius, r= 5.00 mm = 5 x 10^-3 m.

Question 21.
A tank with a square base of area 1.0 m² is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20 cm². The tank is filled with water in one compartment, and an acid (or relative density 1.7) in the other, both to a height of 4.0 m. compute the force necessary to keep the door close.
Answer:

Question 22.
A manometer reads the pressure of a gas in an enclosure as shown in Fig. (a). When a pump removes some of the gas, the manometer reads as in Fig. (b). The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).

Answer:
The atmospheric pressure, P = 76 cm of mercury
(a) From figure (a),
Pressure head, h = 20 cm of mercury
∴ Absolute pressure = P + h = 76 + 20 = 96 cm of mercury
Also, Gauge pressure = h =20 cm of mercury
From figure (b),
Pressure head,h = -18 cm of mercury
∴ Absolute pressure = P + h = 76 + (- 18) = 58 cm of mercury
Also, (Gauge pressure = h = – 18 cm of mercury
(b) When 13.6 cm of water is poured into the right limb of the manometer of figure (b), then, using the relation : pressure, p = pgh = p’g’h’,

Therefore, pressure at the point B,
P_B = P + h’ = 76 + 1 = 77 cm of mercury
If h is the difference in the mercury levels in the two limbs, then taking P_A = P_B
=>  58 + h” = 11 => h” = 77 – 58 = 19 cm of mercury.

Question 23.
Two vessels have the same area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill upto a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?
Answer:

Question 24.
During blood transfusion, the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein ? [Use the density of whole blood as 1.06 x 10³ kg m^-3 ]
Answer:

Question 25.
In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy,
(a) How does the pressure change as the fluid moves along the tube if dissipative forces are present?
(b) Do the dissipative forces become more important as the fluid velocity increases? Discuss qualitatively.
Answer:
(a) If the dissipative forces are present, some of the pressure energy of the liquid is used in doing some work against these forces. Hence, the fluid pressure decreases.
(b) With the increase in velocity, the rate of loss of energy also increases. As a result, the dissipative forces become more significant.

Question 26.
(a) What is the largest average velocity of blood flow in an artery of radius 2 x 10^-3 m if the flow must remain steady? (b) What is the corresponding flow rate?
(Take viscosity of blood to be 2.084 x 10^-3 Pa s). Take the density of blood as 1.06 kg m^-3.
Answer:
Here, r = 2 x 10^-3 m, η = 2.084 x 10^-3 Pa s
Taking the maximum value of Reynold number for streamlined flow as N_R = 2000, the maximum velocity is

Question 27.
A plane is in level flight at constant speed and each of its two wings has an area of 25 m². If the speed of the air is 180 km/h over the lower wing and 234 km/h over the upper wing surface, determine the plane’s mass. (Take air density to be 1 kg m^-3).
Answer:

Question 28.
In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 x 10^-5 m and density 1.2 x 10³ kg m^-3. Take the viscosity of air at the temperature of the experiment to be
1.8 x 10^-5 How much is the viscous force on the drop at that speed ? Neglect buoyancy of the drop due to air.
Answer:

Question 29.
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside ? Surface tension of mercury at the temperature of the experiment is 0.465 N m^_1. Density of mercury = 13.6 x 10³ kg m³.
Answer:
Here, angle of contact, θ = 140°                 .’. cos θ= cos 140° = – 0.7660
Also,  r = 1.00 mm = 1 x 10^-3 m, surface tension, T = 0.465 N nr¹
density ρ= 13.6 x 10³ kg m^-3

Question 30.
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube ? Surface tension of water at the temperature of the experiment is 7.3 x 10^-2 N m^-1. Take the angle of contact to be zero and density of water to be 1.0 x 10³ kg m^-3 (g = 9.8 ms’²)
Answer:
Let r_x be the radius of one bore and r₂ be the radius of second bore of the U-tube. Then, if h_x and h₂ are the heights of water on two sides,

Question 31.
(a) It is known that density p of air decreases with height y (in metres) as

where ρo = 1.25 kg m^-3 is the density at sea level, and y₀ is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of the atmosphere remains constant (isothermal conditions). Also, assume that the value of g remains constant.
(b) A large He balloon of volume 1425 m³ is used to lift a payload of 400 kg. Assume that the balloon maintains a constant radius as it rises. How high does it rise?
[Take yo = 8000 m and p_He = 0.18 kg m^-3]
Answer:
(a) Consider an imaginary cylinder of air having an area ‘a’ of a cross-section of each end face and placed vertically above the surface of the earth. Let the cap I of the cylinder be at a height of y and the cap II be at the height y + dy. Let P and P + dP be the pressures at caps I and II respectively. Then, the net force acting on the cap due to gravity is the weight of the cylinder i. e.,
W = mass of cylinder xg = ady.pg    …(1)
Since the cylinder is considered to be placed in the air, therefore, the force due to the difference in pressure is balanced by the weight of the cylinder under the equilibrium conditions.

We hope the NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids, help you. If you have any query regarding NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids, drop a comment below and we will get back to you at the earliest