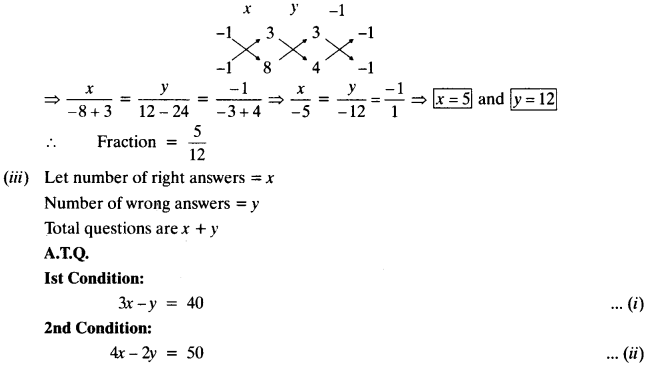
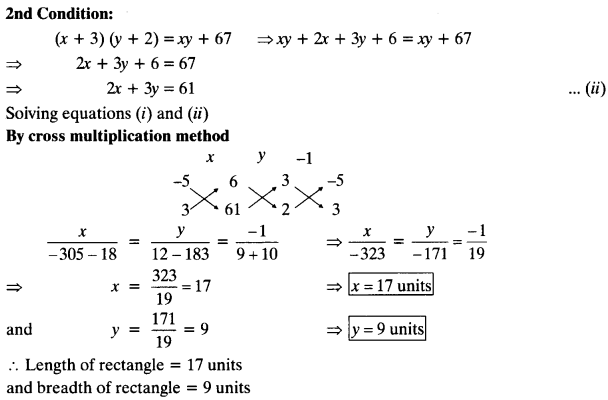
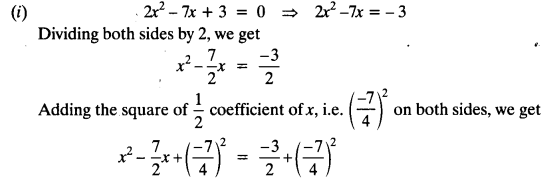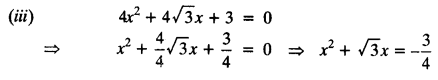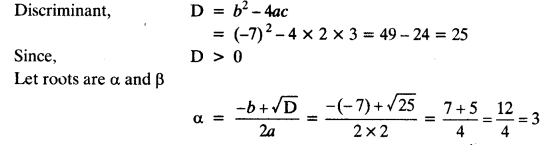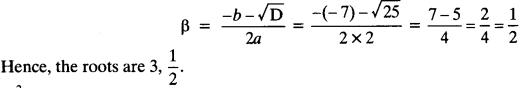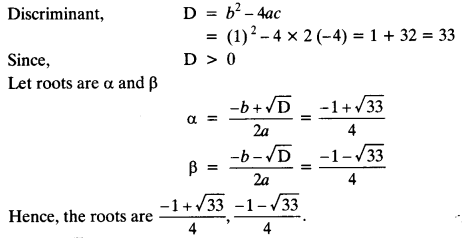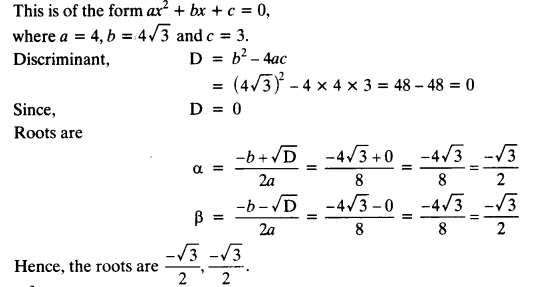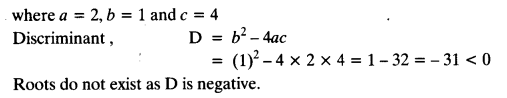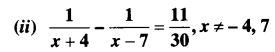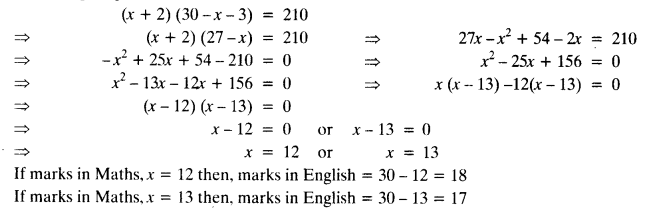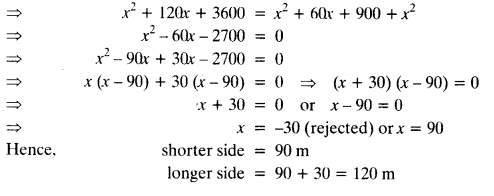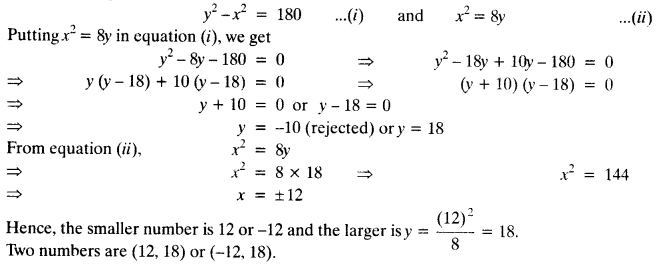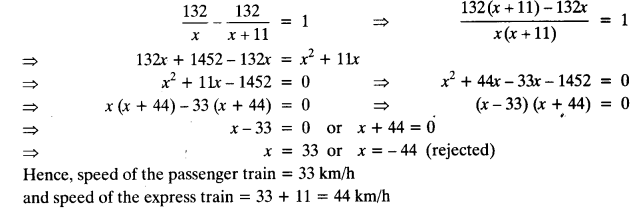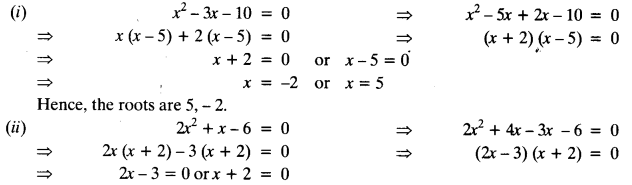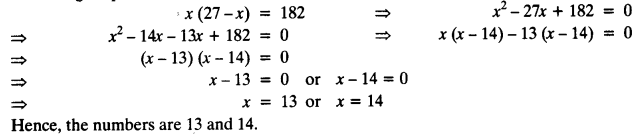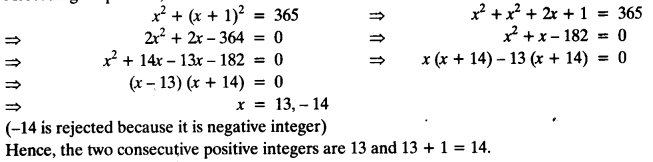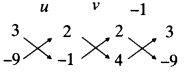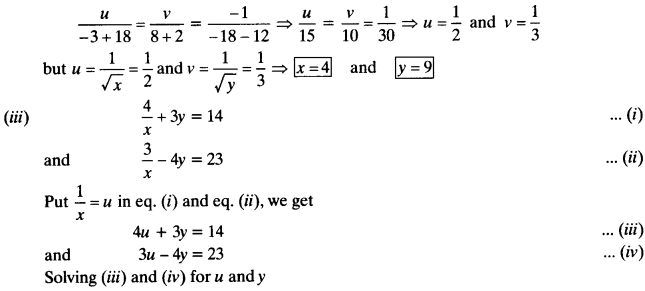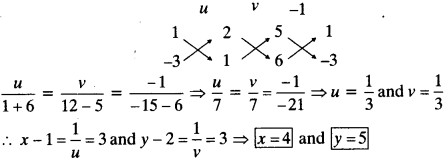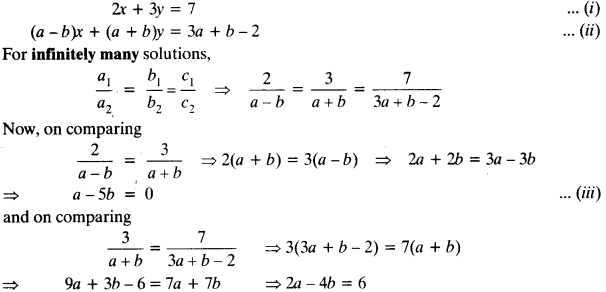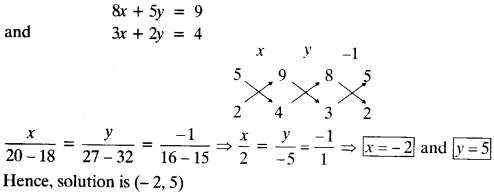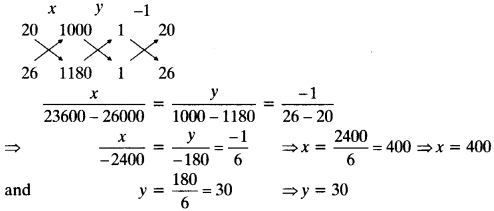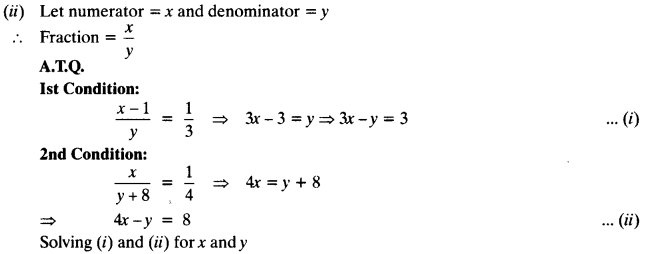NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2. https://mcqquestions.guru/ncert-solutions-for-class-10-maths-chapter-5-ex-5-2/
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | Arithmetic Progressions |
| Exercise | Ex 5.2 |
| Number of Questions Solved | 20 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Ex 5.2 Class 10 Maths Solutions Question 1.
Fill in the blanks in the following table, given that a is the first term, d the common difference and an the nth term of the AP:
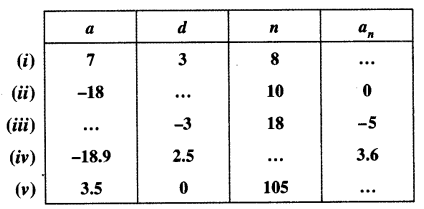
Solution:
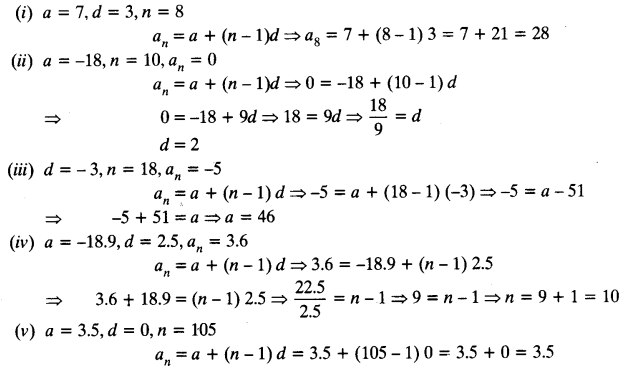
Class 10 Maths Chapter 5 Exercise 5.2 Question 2.
Choose the correct choice in the following and justify:
(i) 30th term of the AP: 10, 7, 4, …, is
(A) 97
(B) 77
(C) -77
(D) -87
(ii) 11th term of the AP: -3, \(\frac { -1 }{ 2 }\) , 2, …, is
(A) 28
(B) 22
(C) -38
(D) -48
Solution:
(i) 10, 7, 4, …,
a = 10, d = 7 – 10 = -3, n = 30
an = a + (n – 1)d
⇒ a30 = a + (30 – 1) d = a + 29 d = 10 + 29 (-3) = 10 – 87 = – 77
Hence, correct option is (C).
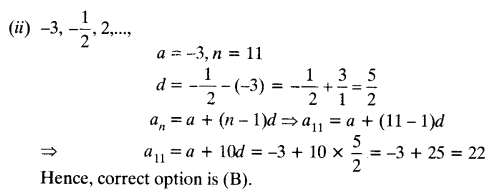
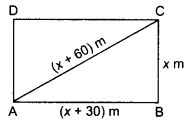
Class 10 Maths Chapter 5 Exercise 5.2 Question 3.
In the following APs, find the missing terms in the boxes:
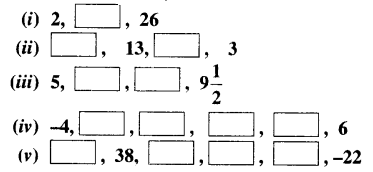
Solution:

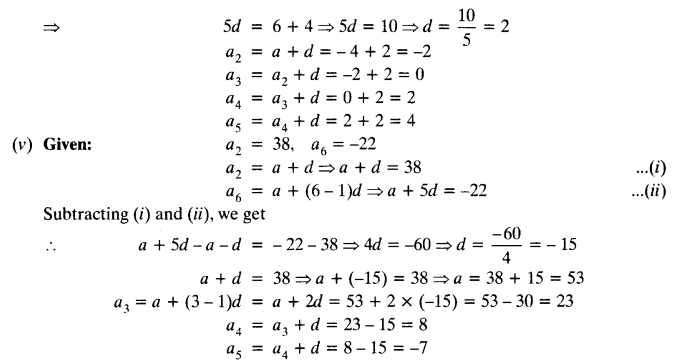
Class 10 Maths Chapter 5 Exercise 5.2 Question 4.
Which term of the AP: 3, 8, 13, 18, …, is 78?
Solution:
Given: 3, 8, 13, 18, ………,
a = 3, d = 8 – 3 = 5
Let nth term is 78
an = 78
a + (n – 1) d = 78
⇒ 3 + (n – 1) 5 = 78
⇒ (n – 1) 5 = 78 – 3
⇒ (n – 1) 5 = 75
⇒ n – 1 = 15
⇒ n = 15 + 1
⇒ n = 16
Hence, a16 = 78
Class 10 Maths Chapter 5 Exercise 5.2 Question 5.
Find the number of terms in each of the following APs:
(i) 7, 13, 19, …, 205
(ii) 18, 15\(\frac { 1 }{ 2 }\), 13, …, -47
Solution:

Class 10 Ex 5.2 Solutions Question 6.
Check, whether -150 is a term of the AP: 11, 8, 5, 2, ….
Solution:
11, 8, 5, 2, …….
Here, a = 11, d = 8 – 11= -3, an = -150
a + (n – 1) d = an
⇒ 11 + (n – 1) (- 3) = -150
⇒ (n – 1) (- 3) = -150 – 11
⇒ -3 (n – 1) = -161
⇒ n – 1 = \(\frac { -161 }{ -3 }\)
⇒ n = \(\frac { 161 }{ 3 }\) + 1 = \(\frac { 164 }{ 3 }\) = 53\(\frac { 4 }{ 3 }\)
Which is not an integral number.
Hence, -150 is not a term of the AP.
Maths NCERT Solutions Class 10 Arithmetic Progression Exercise 5.2 Question 7.
Find the 31st term of an AP whose 11th term is 38 and the 16th term is 73.
a11 = 38 and a16 = 73
⇒ a11 = a + (11 – 1) d ⇒ a + 10d = 38 ….. (i)
⇒ a16 = a + (16 – 1 )d ⇒ a + 15d = 73 …(ii)
Subtracting eqn. (i) from (ii), we get
a + 15d – a – 10d = 73 – 38
⇒ 5d = 35
⇒ d = 1
From (i), a + 10 x 7 = 38
⇒ a = 38 – 70 = – 32
a31 = a + (31 – 1) d = a + 30d = – 32 + 30 x 7 = – 32 + 210 = 178
Class 10 Maths Chapter 5 Exercise 5.2 Question 8.
An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
Solution:
Given:
a50 = 106
a50 = a + (50 – 1) d
⇒ a + 49d = 106 …(i)
and a3 = 12 ⇒ a3 = a + (3 – 1 )d ⇒ a + 2d = 12 …(ii)
Subtracting eqn. (ii) from (i), we get
a + 49d – a – 2d = 106 – 12
⇒ 47d = 94
⇒ d = \(\frac { 94 }{ 47 }\) = 2
a + 2d = 12
⇒ a + 2 x 2 = 12
⇒ a + 4 = 12
⇒ a = 12 – 4 = 8
a29 = a + (29 – 1) d = a + 28d = 8 + 28 x 2 = 8 + 56 = 64
Ex 5.2 Class 10 NCERT Solutions Question 9.
If the 3rd and the 9th term of an AP are 4 and -8 respectively, which term of this AP is zero?
Solution:
Given: a3 = 4 and a9 = – 8
⇒ a3 = a + (3 – 1 )d ⇒ a + 2d = 4 …(i)
a9 = a + (9 – 1) d ⇒ a + 8d = -8 ….(ii)
Subtracting eqn. (i) from (ii), we get
a + 8d – a – 2d = -8 – 4
⇒ 6d = -12.
⇒ d = -2
Now,
a + 2d = 4
⇒ a + 2(-2) = 4
⇒ a – 4 = 4
⇒ a = 4 + 4 = 8
Let an = 0
⇒ a + (n – 1) d = 0
⇒ 8 + (n – 1) (- 2) = 0
⇒ 8 = 2 (n – 1)
⇒ n – 1 = 4
⇒ n = 4 + 1 = 5
Hence, 5th term is zero.
Exercise 5.2 Class 10 NCERT Solutions Question 10.
The 17th term of an AP exceeds its 10th term by 7. Find the common difference.
Solution:
Given: a17 – a10 = 7
⇒ [a + (17 – 1 ) d] – [a + (10 – 1 ) d] = 7
⇒ (a + 16d) – (a + 9d) = 7
⇒ 7d = 7
⇒ d = 1
Class 10 Maths Chapter 5 Exercise 5.2 Question 11.
Which term of the AP: 3, 15, 27, 39, … will be 132 more than its 54th term?
Solution:
3, 15, 27, 39, …..
Here, a = 3, d = 15 – 3 = 12
Let an = 132 + a54
⇒ an – a54 = 132
⇒ [a + (n – 1) d] – [a + (54 – 1) d] = 132
⇒ a + nd – d – a – 53d = 132
⇒ 12n – 54d = 132
⇒ 12n – 54 x 12 = 132
⇒ (n – 54)12 = 132
⇒ n – 54 = 11
⇒ n = 11 + 54 = 65
Class 10 Maths Chapter 5 Exercise 5.2 Question 12.
Two APs have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms?
Solution:
Let a and A be the first term of two APs and d be the common difference.
Given:
a100 – A100 = 100
⇒ a + 99d – A – 99d = 100
⇒ a – A = 100
⇒ a1000 – A1000 = a + 999d – A – 999d
⇒ a – A = 100
⇒ a1000 – A1000 = 100
NCERT Solutions Class 10 Maths Ch 5 Ex 5.2 Question 13.
How many three-digit numbers are divisible by 7?
Solution:
The three-digit numbers which are divisible by 7 are 105, 112, 119, ………., 994
Here, a = 105, d = 112 – 105 = 7 , an = 994
a + (n – 1) d = 994
⇒ 105 + (n – 1) 7 = 994
⇒ (n – 1) 7 = 994 – 105
⇒ 7 (n – 1) = 889
⇒ n – 1 = 127
⇒ n = 127 + 1 = 128
CBSE Class 10 Maths Ex 5.2 Solutions Question 14.
How many multiples of 4 lie between 10 and 250?
Solution:
The multiples of 4 between 10 and 250 be 12, 16, 20, 24,…., 248
Here, a = 12, d = 16 – 12 = 4, an = 248
an = a + (n – 1) d
⇒ 248 = 12 + (n – 1) 4
⇒ 248 – 12 = (n – 1) 4
⇒ 236 = (n – 1) 4
⇒ 59 = n – 1
⇒ n = 59 + 1 = 60
NCERT Solutions For Class 10 Maths Ch 5 Ex 5.2 Question 15.
For what value of n, the nth term of two APs: 63, 65, 61,… and 3, 10, 17,… are equal?
Solution:
First AP
63, 65, 67,…
Here, a = 63, d = 65 – 63 = 2
an = a + (n – 1) d = 63 + (n – 1) 2 = 63 + 2n – 2 = 61 + 2n
Second AP
3, 10, 17, …
Here, a = 3, d = 10 – 3 = 7
an = a + (n – 1) d = 3 + (n – 1)7 = 3 + 7n – 7 = 7n – 4
Now, an = an
⇒ 61 + 2n = 7n – 4
⇒ 61 + 4 = 7n – 2n
⇒ 65 = 5n
⇒ n = 13
Class 10 Maths Chapter 5.2 Question 16.
Determine the AP whose 3rd term is 16 and 7th term exceeds the 5th term by 12.
Solution:
Given: a3 = 16
⇒ a + (3 – 1)d = 16
⇒ a + 2d = 16
and a7 – a5 = 12
⇒ [a + (7 – 1 )d] – [a + (5 – 1 )d] = 12
⇒ a + 6d – a – 4d = 12
⇒ 2d = 12
⇒ d = 6
Since a + 2d = 16
⇒ a + 2(6) = 16
⇒ a + 12 = 16
⇒ a = 16 – 12 = 4
a1 = a = 4
a2 = a1 + d = a + d = 4 + 6 = 10
a3 = a2 + d = 10 + 6 = 16
a4 = a3 + d = 16 + 6 = 22
Thus, the required AP is a1, a2, a3, a4,…, i.e. 4, 10, 16, 22
Class 10 Maths Chapter 5 Exercise 5.2 Question 17.
Find the 20th term from the last term of the AP: 3, 8, 13, …, 253.
Solution:
Given: AP is 3, 8, 13,…….. ,253
On reversing the given A.P., we have
253, 248, 243 ,………, 13, 8, 3.
Here, a = 253, d = 248 – 253 = -5
a20 = a + (20 – 1)d = a + 19d = 253 + 19 (-5) = 253 – 95 = 158
Exercise 5.2 Class 10 Solutions Question 18.
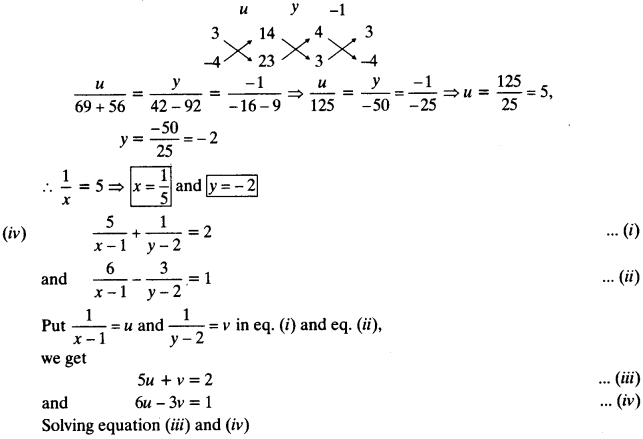
The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
Solution:
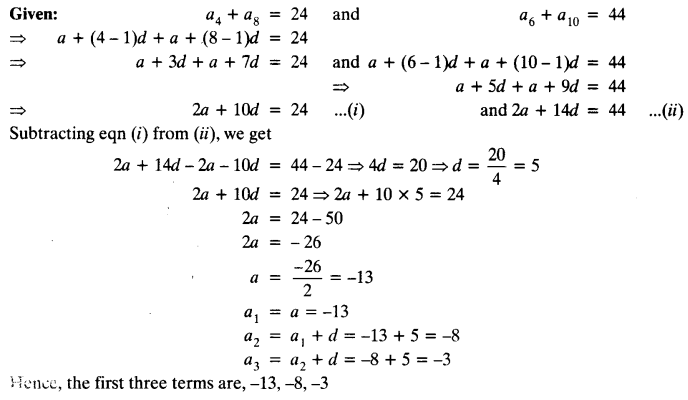
Solution Of Ex 5.2 Class 10 Question 19.
Subba Rao started work in 1995 at an annual salary of ₹ 5000 and received an increment of ₹ 200 each year. In which year did his income reach ₹ 7000 ?
Solution:
a = ₹ 5000, d = ₹ 200
Let an = ₹ 7000
We have, a + (n – 1) d = 7000
⇒ 5000 + (n – 1) 200 = 7000
⇒ (n – 1) 200 = 7000 – 5000
⇒ (n – 1) 200 = 2000
⇒ (n- 1) = 10
⇒ n = 11
⇒ 1995 + 11 = 2006
Hence, in 2006 Subba Rao’s income will reach ₹ 7000.
NCERT Solutions For Class 10 Maths 5.2 Question 20.
Ramkali saved ₹ 5 in the first week of a year and then increased her weekly saving by ₹ 1.75. If in the nth week, her weekly saving become ₹ 20.75, find n.
Solution:
Given: a = ₹ 5, d = ₹ 1.75
an = ₹ 20.75
a + (n – 1) d – 20.75
⇒ 5 + (n – 1) 1.75 = 20.75
⇒ (n – 1) x 1.75 = 20.75 – 5
⇒ (n – 1) 1.75 = 15.75
⇒ n – 1 = 9
⇒ n = 9 + 1
⇒ n = 10
Hence, in 10th week Ramkali’s saving will be ₹ 20.75.
We hope the NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2, drop a comment below and we will get back to you at the earliest.