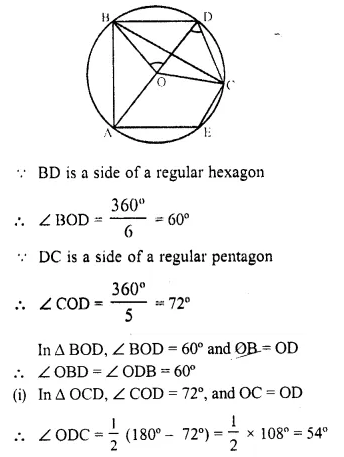
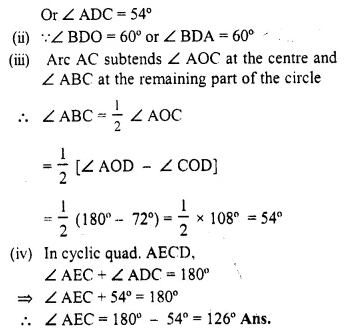These Sample papers are part of CBSE Sample Papers for Class 12 History Here we have given CBSE Sample Papers for Class 12 History Paper 2.
CBSE Sample Papers for Class 12 History Paper 2
| Board | CBSE |
| Class | XII |
| Subject | History |
| Sample Paper Set | Paper 2 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 2 of Solved CBSE Sample Paper for Class 12 History is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 80
General Instructions:
(i) Answer all the questions. Some questions have internal choice. Marks are indicated against each question.
(ii) Answer to question nos 1 to 3 carrying 2 marks should not exceed 30 words each.
(iii) Answer to question nos. 4 to 9 carrying 4 marks should not exceed 100 words. Students should attempt only 5 questions in this section.
(iv) Question 10 (for 4 marks) is a value based question and compulsory question.
(v) Answer to question nos 11 to 13 carrying 8 marks should not exceed 350 words.
(vi) Questions 14 -16 are source based questions and have no internal choice.
(vii) Question 17 is a map question includes ‘identification’ and significant’ test items.
PART-A
Answer all the questions given below:
Question 1:
Give two reasons why the sixth century BCE is often regarded as a major turning point in early Indian History?
Question 2:
Who were Alvars and Nayanars? In which languages did they sing?
Question 3:
State the significance of Gandhiji’s speech at Banaras Hindu University?
PART-B
Section-I
Answer any five of the following questions:
Question 4:
Discuss whether the Mahabharata could have been the work of single author.
Question 5:
Describe the growth of temple architectures in the ancient period.
Question 6:
Describe the position of untouchables in ancient society?
Question 7:
Explain the basic ideas of Jaina philosophy.
Question 8:
Describe the life of village artisans during the Mughal period.
Question 9:
Describe the results of India’s overseas trade under the Mughals.
Section-II
Value Based Questions
Read the following passage and answer the question that follow.
The rebel proclamations in 1857 repeatedly appealed to all sections of the population, irrespective of their caste and creed. Many of the Proclamations were issued by Muslim princes or in their names but even these took care to address the sentiments of Hindus. The rebellion was seen as a war in which both Hindus and Muslims had equally to lose or gain. The ishtahars worked back to the pre-British Hindu-Muslim part and glorified the co existence of different communities under the Mughal empire.
Question 10:
What type of values were developed in 1857 in both Muslims and Hindus?
PART-C
Answer all the questions given below:
Question 11:
Discuss the ways in which panchayats and village headman regulated rural society.
OR
Explain how the fortification and roads in the city of Vijayanagar were unique and impressive.
Question 12:
Explain the main events of the Dandi March. What is its significance in the history of the Indian national movement?
OR
What are the salient features of town planning in Calcutta during the British period?
Question 13:
How did the message about the Revolt of 1857 spread?
OR
Discuss the religious causes for the Revolt of 1857.
PART-D
Source Based Questions
Question 14:
Read the following excerpt carefully and answer the questions that follows.
The poor peasants of the vast tracts of country constituting the empire of Hindustan, many are little more than sand, or barren mountains, badly cultivated, and thinly populated. Even a considerable portion of the good land remains unfilled for want of labourers; many of whom perish in consequence of the bad treatment they experience from Governors. The poor people, when they become incapable of discharging the demands of their rapacious lords, are not only often deprived of the means of subsistence, but are also made to lose their children, who are carried away as slaves. Thus, it happens that the peasantry, driven to despair by so excessive a tyranny, abandon the country.
In this instance, Bernier was participating in contemporary debates in Europe concerning the , nature of state and society, and intended that his description of Mughal India would serve as warning to those who did not recognise the “merits” of private property.
(i) What were the problems about cultivating the land, according to Bernier?
(ii) Why did peasantry abandon the land?
(iii) Explain the reasons given by Bernier for the exploitation of the peasants.
Question 15:
Read the following excerpt carefully and answer the questions that follows.
There cannot be any divided loyalty
Govind Ballabh Pant argued that in order to become loyal citizens people had to stop focusing only on the community and the self. For the success of democracy one must train himself in the art of self-discipline. In democracies one should care less for himself and more for others. There cannot be any divided loyalty. All loyalties must exclusively be centered round the state.
If in a democracy, you create rival loyalties, or you create a system in which any individual or group, instead of suppressing his extravagance, cares naught for larger or other interests, then democracy is doomed.
(i) What do you understand by ‘Separate Electorate’?
(ii) Why was the demand for separate electorate made during the drafting of the constitution?
(iii) Why was G. B Pant against this demand? Give two reasons.
Question 16:
Read the following excerpt carefully and answer the questions that follows.
How artefacts are identified
Processing of food required grinding equipment as well as vessels for mixing, blending and cooking. These were made of stone, metal and terracotta. This is an excerpt from one of the earliest reports on excavations at Mohenjodaro, the best known Harappan site:
Saddle quem … are found in considerable numbers … and they seem to have been the only means in use for grinding cereals. As a rule, they were roughly made of hard, gritty, igneous rock or sandstone and mostly show signs of hard usage. As their bases are usually convex, they must have been set in the earth or in mud to prevent their rocking. Two main types have been found: those on which another smaller stone was pushed or rolled to and fro, and others with which a second stone was used as a pounder, eventually making a large cavity in the .nether stone. Querns of the former type were probably used solely for grain; the second type possibly only for pounding herbs and spices for making curries. In fact, stones of this latter type are dubbed ‘curry stones” by our workmen and our cook asked for the loan of one from the museum for use in the kitchen
(i) What are the two types of querns?
(ii) What materials were these querns made of? Why are they described as “curry stones”
(iii) What are two kinds of saddle?
Question 17:
(17.1). On the given political outline map of India, locate and label the following with appropriate symbols:
(a) Shravasti, ancient Buddhist site
(b) Champa, an early state
(17.2). On the same outline map of India, three places related to the 14 – 18th century South India have been marked as A, B and C. Identify them and write their correct names on the lines drawn near them.
Answers
Answer 1:
(i) Rise of states, cities, widespread use of iron and coins.
(ii) Witnessed the growth of different religions viz. Buddhism and Jainism.
Answer 2:
(i) Alvars – worshippers of Vishnu.
Nayanars – devotees of Shiva.
(ii) They sang in Tamil language.
Answer 3:
(i) Indian Nationalism was elitist in nature (factual).
(ii) His desire to make it a mass movement.
Answer 4:
The original story was composed by charioteer bard’s named as Sutras.
In the 5th BCE, Brahmans took over the story and began to commit it to writing called itihasa.
- Between 200 BCE and 200 CE worship of Vishnu was growing in importance.
- Between 200 BCE and 400 CE large didactic sections were added.
- Verses increased to 1,00,000.
- Sage Vyasa was considered to be the original composer of Mahabharata.
Answer 5:
Temple architecture:
- Temples built at the same pattern as that of the Sanchi Stupa.
- Temples had square room – Garbhagriha -with single doorway, for the worshipper to enter. Tall structure called as Shikhara was built.
- Temple walls were decorated with beautiful sculptures. Temples had assembly halls, huge walls, gateways etc.
- Some of these were made out of rocks as artificial caves, e.g Kailashnatha Temple.
Answer 6:
Untouchables: Brahmans considered some people as outside the system.
- They were those people who indulged in polluting activities such as handling corpses and dead animals. These people were called Chandalas.
- They lived outside the cities. They used discarded utensils.
- They wore ornaments of iron. They could not walk about in villages and cities at night.
- They served as executioners. They had to sound clapper in the streets.
Answer 7:
The entire world is animated. Ahimsa or non-injury to living beings.
- Cycle of birth and rebirth is shaped through Karma.
- Asceticism and penance required to free oneself from the cycle of karma.
- Moksha can be achieved by renouncing the world and adopting monastic life.
- 5 vows to abstain from killing, stealing and lying to observe celibacy and to abstain from possessing property.
Answer 8:
(i) Marathi documents make a mention of 32.5% of the village constituted artisans. Distinction between peasants and artisans a fluid one.
(ii) They engaged in various types of craft production especially in between different agricultural activity.
(iii) For their services they were compensated by villages in variety of ways. Cultivated waste given to them called Miras or Nathan in Maharashtra.
(iv) 18lh century zamindars of Bengal paid the artisans small daily allowance called jajmani system.
Answer 9:
This trade brought in silver bullion into Asia.
- A large part of the bullion gravitated towards India. Commodity composition expanded.
- Stability in the availability of metal currency silver Rupiah in India.
- Expansion of minting of coins and circulation of money in the economy.
- Voyages of discovery led to expansion of Asia’s trade.
Answer 10:
Expected values:
- Vision of unity
- Common Harmony
- Coordination
- Mutual faith
- Nationalism
- Peaceful Coexistence
- Desire for freedom
- Sacrifice for motherland in Hindu-Muslim unity
Answer 11:
Village panchayat consisted of an assembly of elders. Its decision was binding on its members.
- The head of the panchayat was the Mandal.
- To prepare the village accounts with the help of the panchayat.
- The members of the village made contributions to a common financial pool.
- To administer the conduct of the members of the village.
- Panchayat could also levy fines and even expel a person from the community.
- Teach caste or jati in the village had its ownjati panchayat.
- The panchayat was also regarded as the government of appeal.
- In cases of excessive revenue demands, the panchyat suggested compromise.
OR
Roads and fortifications-Razzaq greatly impressed by fortification-seven lines of forts encircled and agricultural hinterland, massive masonty, no mortar used.
- Square or rectangular bastions projected outwards.
- Second fortifications went round their inner core of the urban complex.
- Roads wound around the valley avoiding rocky terrain.
- Some roads extended from temple gateways.
- It enclosed vast agricultural fields.
- Canals system helped to irrigate these fields.
- Roads were extended from temple gateways and bazars.
Answer 12:
On the 12th March 1930 Gandhi began the Dandi March-followed by 78 followers. It is at a distance of 375 km on foot from Sabarmati Ashram to Dandi.
- News of the progress of the March spread to various parts-many of the common people j oined/supported.
- People paid their respect by spinning Khadi.
- On 6th April he broke the salt law.
- He launched the Civil Disobedience Movement which spread to most parts of the country especially NWFP where Abdul Gaffar Khan played an active role.
- It focused the attention on Gandhiji’s philosophy and action. It was conveyed by the European/American press.
- Women participated in large numbers, especially Kamala Devi. It made the British realize the depth of nationalist feelings.
- Their rule could not last forever. Devolving some power to Indians through the Indian Act of 1935.
OR
Planning required a layout of the entire urban space and regulation of urban land use.
- Defence – after the Battle of Plassey in 1757 they decided to build a new fort taking village of Sutanati, Kolkata and Govindpur.
- Vast space around the fort was left known as maidan reason-to fire in a straight line from the fort against an advancing army.
- Later they moved out of the fort and building residences along the maidan.
- Lord Wellesley built a massive palace, government house. He felt the need for town planning.
- Many bazars, ghats, burial grounds were removed.
- This work was later taken up by lottery committee. They made a new map of the city and took up activities of road building and
cleaning Indian areas. - To save the area from the treatment of epidemics, bustis were demolished.
- Frequent fires led to stricter building regulations. Finally all town planning activities were taken up by the government.
Answer 13:
(i) The Revolt of 1857 was associated not only with the people of the court but also with ordinary men and women.
(ii) Besides the ranis, rajas, nawabs and taluqdars, many common people, religious persons and self-styled prophets participated in it.
(iii) The message of rebellion was carried by ordinary men and women.
(iv) At some places, even the religious people spread the message of the Revolt of 1857. For example; in Meerut, a fakir used to ride on elephant. Many sepoys met him time and again.
(v) After the annexation of Awadh, Lucknow had many religious leaders and self-styled prophets who preached the destruction of British rule.
(vi) At many places, the local leaders played an important role. They urged the peasants, zamindars and tribals to revolt.
(vii) In Uttar Pradesh, Shahu Mai motivated and mobilised the residents of Barout Paragana.
(viii) Similarly Ganoo, a tribal who cultivated in Singhbhum in Chotanagpur, became a rebel leader of the kol tribals.
OR
(i) The Christian missionaries were assuring material benefits to Indians to convert them to Christianity. So, many people of India became antagonistic towards the British.
(ii) Lord William Bentinck, the Governor-General of India, initiated reforms in the Indian society.
(iii) He abolished customs like Sati and permitted remarriage of the Hindu widows. Many Hindus viewed these steps against the ideology of Hinduism.
(iv) The British introduced western education, western ideas and western institutions in India. They set up English medium educational institutions but many Hindus considered these steps as attempts to encourage religious conversion.
(v) Many people felt that the British were destroying their sacred ideals that they had long cherished.
(vi) Many Hindus were enraged when the Christian missionaries criticized their scriptures on religious books.
(vii) In accordance with the law passed in 1856, the Hindus could be sent across the sea to fight a war. During those days, the Hindus considered it a sin to cross the sea.
(viii) The Sepoys were were given cartridges coated with the fat of the cows and the pigs. At this the Indian soldiers lost patience and revolted against the British.
Answer 14:
(i) Most of the land was sand, barren mountain, badly cultivated & thinly populated.
considerable portion of the good land remains unfilled for want of labourers.
(ii) Incapable of discharging the demands of their rapacious lords the peasants are deprived of the means of subsistence-their land. So they abandon them.
(iii) The absence of private property in land which remained in the hands of landlords. Landlords could not pass on their land to their children. The serfs who tilled the land could not produce much.
Answer 15:
1. A separate electorate meant that in certain constituencies seats were reserved only for members of a particular community or religion.
2. The demand was made to protect the rights of the minorities. It was felt that this was possible only if the minorities were properly represented within the political system, their voices be heard and view taken into account.
3. He felt that it would permanently isolate the minorities, make them vulnerable and deprive them of any effective role within the government.
Answer 16:
(i) Two types of quems have been found-those on which another smaller stone was pushed or rolled to and fro and other with which a second stone was used as a pounder eventually making a large cavity in the nether stone.
(ii) Made of hard, gritty, igneous rock or sand stone. Because they were used to grind species for making curries.
(iii) (a) Saddle – one on which another small stone was pushed or rolled to and fro. Those saddle were used to grind cereals were caller grinding saddle.
(b) If another type of saddle a second stone was used as a pounder. These saddles were used to pound herbs and spices.
Answer 17:

We hope the CBSE Sample Papers for Class 12 History Paper 2 help you. If you have any query regarding CBSE Sample Papers for Class 12 History Paper 2, drop a comment below and we will get back to you at the earliest.