Prasanna

RD Sharma Class 8 Solutions Chapter 22 Mensuration III (Surface Area and Volume of a Right Circular Cylinder) Ex 22.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1
• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Question 1.
Find the volume of a cuboid whose
(i) r = 3.5 cm, h = 40 cm
(ii) r = 2.8 m, h = 15 m
Solution:
(i) Radius (r) = 3.5 cm
Height (h) = 40 cm
Volume of cylinder = πr²h

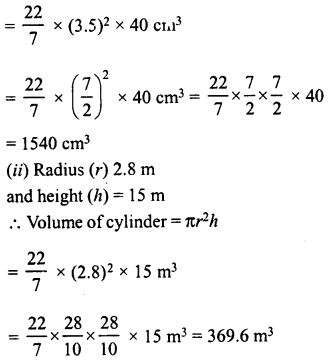
Question 2.
Find the volume of a cylinder, if the diameter (d) of its base and its altitude (h) are:
(i) d= 21 cm, h = 10 cm
(ii) d = 7 m, h = 24 m.
Solution:
(i) Diameter (d) = 21 cm

Question 3.
The area of the base of a right circular cylinder is 616 cm3 and its height is 25 cm. Find the volume of the cylinder.
Solution:
Base area of cylinder = 616 cm²
Height (h) = 25 cm.
∴ Volume = Area of base x height
= 616 x 25 cm³ = 15400 cm³

Question 4.
The circumference of the base of a cylinder is 88 cm and its height is 15 cm. Find the volume of the cylinder.
Solution:
Circumference of the base of cylinder = 88 cm
Let r be the radius

Question 5.
A hollow cylindrical pipe is 21 dm long. Its outer and inner diameters are 10 cm and 6 cm respectively. Find the volume of the copper used in making the pipe.
Solution:
Length (Height) of hollow cylindrical pipe = 21 dm = 210 cm
Inner diameter = 6 cm
Outer diameter = 10 cm

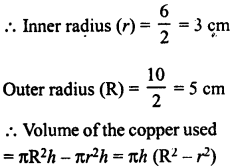
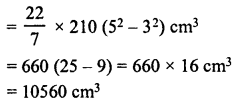
Question 6.
Find the (i) curved surface area (ii) total surface area and (iii) volume of a right circular cylinder whose height is 15 cm and the radius of the base is 7 cm
Solution:
Radius of the cylider (r) = 7 cm
and height (h) = 15 cm
(i) Curved surface area = 2πrh

Question 7.
The diameter of the base of a right circular cylinder is 42 cm and its height is 10 cm. Find the volume of the cylinder.
Solution:
Diameter of the base of cylinder = 42 cm

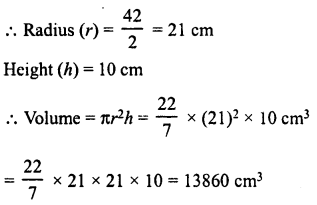
Question 8.
Find the volume of a cylinder, the diameter of whose base is 7 cm and height being 60 cm. Also, find the capacity of the cylinder in litres.
Solution:
Diameter of cylinder = 7 cm

Question 9.
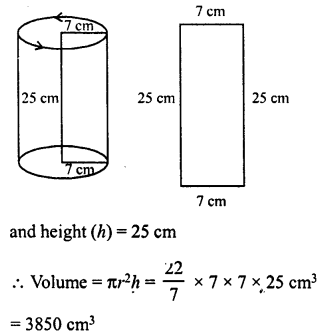
A rectangular strip 25 cm x 7 cm is rotated about the longer side. Find the volume of the solid, thus generated.
Solution:
Size of rectangular strip = 25 cm x 7 cm
By rotating, about the longer side, we find a right circular cylinder,
then the radius of cylinder (r) = 7 cm

Question 10.
A rectangular sheet of paper 44 cm x 20 cm, is rolled along its length to form a cylinder. Find the volume of the cylinder so formed.
Solution:
Size of sheet of paper = 44 cm x 20 cm
By rolling along length, a cylinder is formed in which circumference of its base = 20 cm
and height (h) = 44 cm

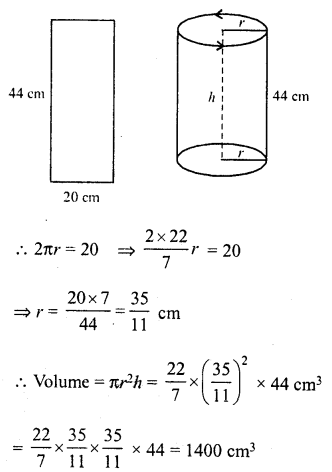
Question 11.
The volume and the curved surface area of a cylinder are 1650 cm3 and 660 cm2 respectively. Find the radius and height of the cylinder.
Solution:
Volume of cylinder = 1650 cm³
and curved surface area = 660 cm²
Let r be the radius and h be the height of the cylinder, then

Question 12.
The radii of two cylinders are in the ratio 2 :3 and their heights are in the ratio 5 : 3. Calculate the ratio of their volumes.
Solution:
Ratio in radii = 2:3
and in heights = 5:3
Let r₁,h₁ and r₂, h₂ are the radii and heights of two cylinders respectively.

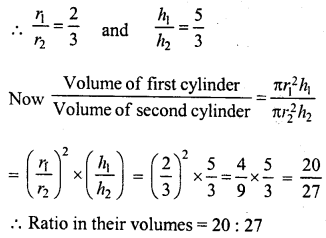
Question 13.
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1 : 2. Find the volume of the cylinder, if its total surface area is 616 cm².
Solution:
Ratio in curved surface are and total surface area =1 : 2
Let r be the radius and h be the height.
Then 2πrh : 2πr (h + r)= 1 : 2

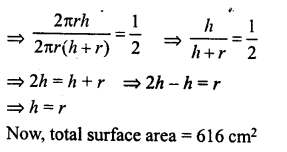
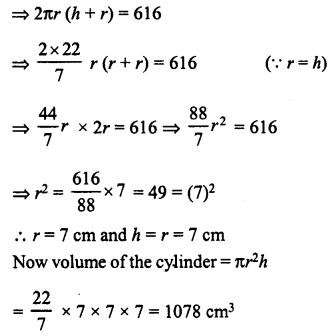
Question 14.
The curved surface area of a cylinder is 1320 cm2 and its base has diameter 21 cm. Find the volume of the cylinder.
Solution:
Curved surface area of a cylinder = 1320 cm²
Diameter of base = 21 cm

Question 15.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. Find the total surface area of the cylinder, if its volume is 1617 cm³.
Solution:
Ratio between radius and height of a cylinder = 2:3
Volume = 1617 cm³
Let r be the radius and A be the height of the cylinder, then

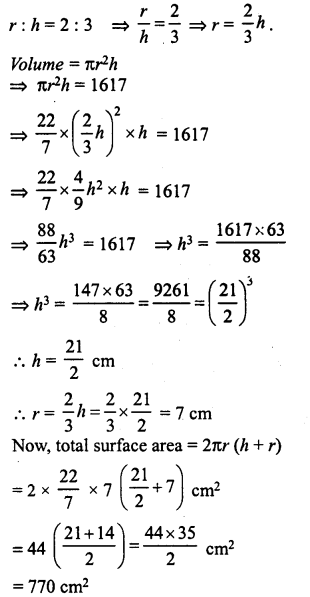
Question 16.
The curved surface area of a cylindrical pillar is 264 m² and its volume is 924 m³. Find the diameter and the height of the pillar.
Solution:
Let r be the radius and A be the height of the cylinder, then
2πrh = 264 …(i)
and πr2h= 924 …(ii)
Dividing (ii) by (i),

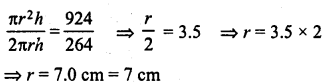
Question 17.
Two circular cylinders of equal volumes have their heights in the ratio 1 : 2. Find the ratio of their radii.
Solution:
Volumes of two cylinders are equal.
Let r1, r2 are the radii and h₁, h₂ are their heights, then

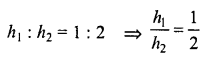
Now, volume of first cylinder = πr₁²h₁
and Volume of second cylinder = πr₂²h₂
Their volumes are equal

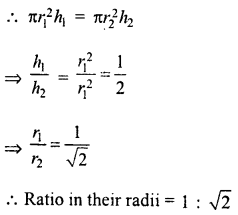
Question 18.
The height of a right circular cylinder is 10.5 m. Three times the sum of the areas of its two circular faces is twice the area of the curved surface. Find the volume of the cylinder.
Solution:
Height of cylinder (A) = 10.5 m.
Let r be the radius, then
Sum of areas of two circular faces = 2π²
and curved surface area = 2πrh
According to the condition,

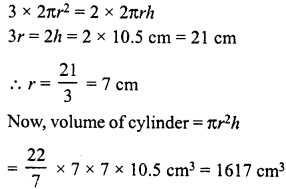
Question 19.
How many cubic metres of earth must be dug-out to sink a well 21 m deep and 6 m diameter ?
Solution:
Diameter of well = 6 m

Question 20.
The trunk of a tree is cylindrical and its circumference is 176 cm. If the length of the trunk is 3 m, find the volume of the timber that can be obtained from the trunk.
Solution:
Circumference of cylindrical trunk = 176 cm

Question 21.
A well is dug 20 m deep and it has a diameter of 7 m. The earth which is so dug out is spread out on a rectangular plot 22 m long and 14 m broad, what is the height of the platform so formed ?
Solution:
Diameter of the well = 7 m
∴ Radius (r) = \(\frac { 7 }{ 2 }\) m
Depth (h) = 20 m
= Volume of earth dug out = πr²h

Question 22.
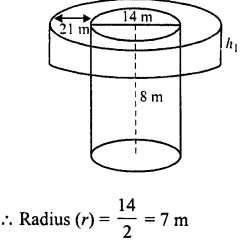
A well with 14 m diameter is dug 8 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 14 m

Question 23.
A cylindrical container with diameter of base 56 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 32 cm x 22 cm x 14 cm. Find the rise in the level of the water when the solid is completely submerged.
Solution:
Diameter of the base of a cylindrical container = 56 cm

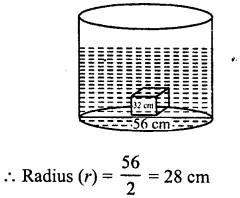
Dimensions of the rectangular solid = 32 cm x 22 cm x 14 cm
∴ Volume of solid = 32 x 22 x 14 cm³ = 9856 cm³
∴Volume of water rose up = 9856 cm³
Let h be the height of water, then πr²h = 9856

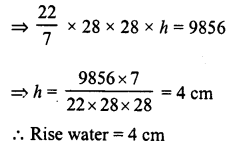
Question 24.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways Le., either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinders thus formed.
Solution:
Size of paper = 30 cm and 18 cm.

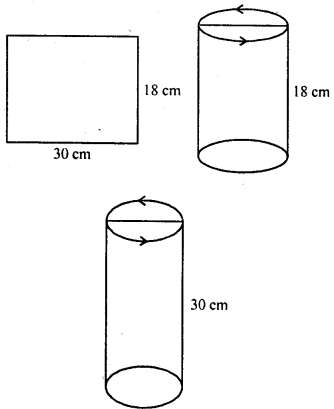
(i) By rolling length wise,
The circumference of base = 30 cm

Question 25.
The rain which falls on a roof 18 m long and 16.5 m wide is allowed to be stored in a cylindrical tank 8 m in diameter. If it rains 10 cm on a day, what is the rise of water level in the tank due to it.
Solution:
Length of roof (l) = 18 m
Breadth (b) = 16.5 m
Height of water on the roof = 10 cm
∴ Volume of water collected

Question 26.
A Piece of ductile metal is in the form of a cylinder of diameter 1 cm and length 5 cm. It is drawnout into a wire of diameter 1 mm. What will be the length of the wire so formed ?
Solution:
Diameter of ductile metal = 1 cm
and length (h) = 5 cm
and radius (r) = \(\frac { 1 }{ 2 }\) cm

Question 27.
Find the length of 13.2 kg of copper wire of diameter 4 mm when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Weight of wire = 13.2 kg
Diameter of wire = 4 mm

Question 28.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:
Volume of brass = 2.2 cu.dm
= 2.2 x 10 x 10 x 10 = 2200 cm²
Diameter of wire = 0.25 cm

Question 29.
The difference between inside and outside surfaces of a cylindrical tube 14 cm long is 88 sq. cm. If the volume of the tube is 176 cubic cm, find the inner and outer radii of the tube.
Solution:
Let r and R be the radii of inner and outer surfaces of a cylindrical tube,

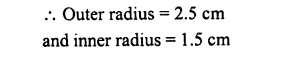
Question 30.
Water flows out through a circular pipe whose internal diameter is 2 cm, at the rate of 6 metres per second into a cylindrical tank, the radius of whose base is 60 cm. Find the rise in the level of water in 30 minutes.
Solution:
Diameter of pipe = 2 cm
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm = 0.01 m
Length of flow of water in 1 second = 6 m Length of flow in 30 minutes = 6 x 30 x 60 m = 10800 m
∴ Volume of water = πr²h

Question 31.
A cylindrical tube, open at both ends, is to made of metal. The internal diameter of the tube is 10.4 cm and its length is 25 cm. The thickness of the metal tube is 8 mm everywhere. Calculate the volume of the metal.
Solution:
Length of metal tube (h) = 25 cm
Internal diameter = 10.4 cm
∴ Internal radius (r) = \(\frac { 10.4 }{ 2 }\) = 5.2 cm
Thickness of metal = 8 mm = 0.8 cm
∴ Outer radius = 5.2 + 0.8 = 6 cm
Now volume of the metal

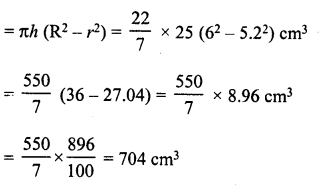
Question 32.
From a tap of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in one hour.
Solution:
Inner radius of pipe (r) = 0.75 cm
Rate of water flow = 7 m per second
∴ Length of water flow in 1 hour (h)
= 7 x 3600 m = 25200 m
∴ Volume of water in 1 hour

Question 33.
A cylindrical water tank of diameter 1. 4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled ?
Solution:
Diameter of cylindrical tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) = 0.7 m
Height (h) = 2.1m.

Question 34.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways Le. either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinder thus formed.
Solution:
In first case,
By rolling the paper along its length,
the circumference of the base = 30 cm
and height (h) = 18 cm

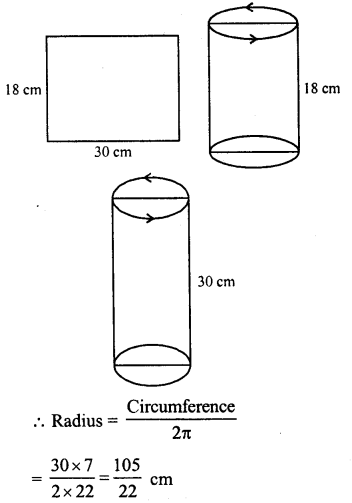
Note: See Q.No. 24 this exercise

Question 35.
How many litres of water flow out of a pipe having an area of cross-section of 5 cm2 in one minute, if the speed of water in the pipe is 30 cm/sec ?
Solution:
Speed of water = 30 cm/sec
∴ Water flow in 1 minute = 30 cm x 60 = 1800 cm
Area of cross-section = 5 cm²
∴ Volume of water = 1800 x 5 = 9000 cm³
Capacity of water in litres = 9000 x l ml

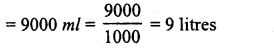
Question 36.
A solid cylinder has a total surface area of 231 cm². Its curved surface area is \(\frac { 2 }{ 3 }\) of the total surface area. Find the volume of the cylinder.
Solution:
Total surface area of a solid cylinder = 231 cm²
Curved surface area = \(\frac { 2 }{ 3 }\) of 231 cm² = 2 x 77 = 154 cm²
and area of two circular faces = 231-154 = 77 cm²
Let r be the radius, then

Question 37.
Find the cost of sinking a tubewell 280 m deep, having diameter 3 m at the rate of Rs 3.60 per cubic metre. Find also the cost of cementing its inner curved surface at Rs 2.50 per square metre.
Solution:
Diameter of well = 3 m
∴ Radius (r) = \(\frac { 3 }{ 2 }\) m
and depth (h) = 280 m
(i) Volume of earth dug out = πr²h

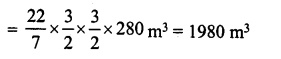
Rate of sinking the well = Rs 3.60 per m³
∴ Total cost of sinking = Rs 1980 x 3.60 = Rs 7,128
(ii) Inner curved surface area = 2πrh

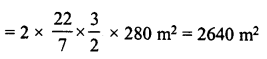
Rate of cementing = Rs 2.50 per m²
∴ Total cost of cementing = Rs 2.50 x 2640
= Rs 6,600

Question 38.
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Note : See Q.No. 27 of this exercise

Question 39.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:
Note: See Q.No. 28 of this exercise.

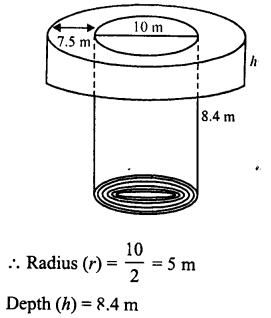
Question 40.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 10 m

Question 41.
A hollow garden roller, 63 cm wide with a girth of 440 cm, is made of 4 cm thick iron. Find the volume of the iron.
Solution:
Width of roller (h) = 63 cm.

Outer circumference of roller = 440 cm

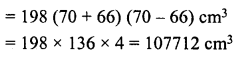
Question 42.
What length of a solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of length 16 cm, external diameter 20 cm and thickness 2.5 mm ?
Solution:
Length of hollow cylinder (h) = 16 cm
External diameter = 20 cm
∴ External radius (R) = \(\frac { 20 }{ 2 }\) = 10 cm
Thickness of iron = 2.5 mm
∴ Internal radius (r) = 10 – 0.25 = 9.75 cm
∴ Volume of iron = πh (R² – r²)

Question 43.
In the middle of rectangular field measuring 30 m x 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
Solution:
Diameter of well = 7 m
∴ Radius (r) = \(\frac { 7 }{ 2 }\) m
Depth (h) = 10 m.
∴ Volume of earth dug out = πr²h

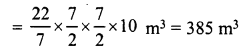
Hope given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.