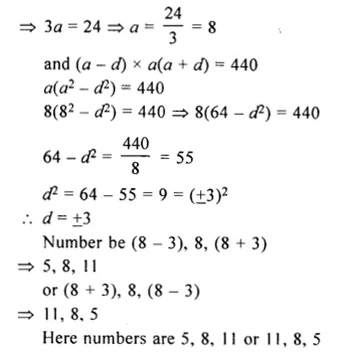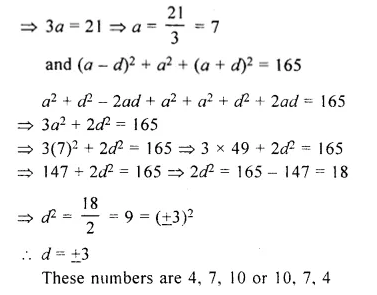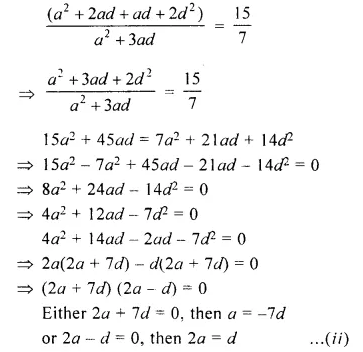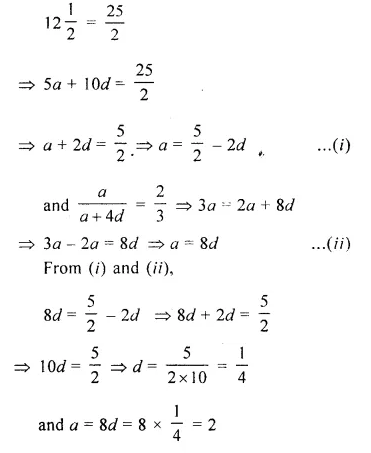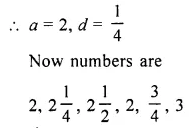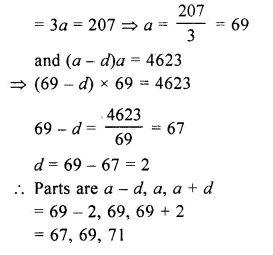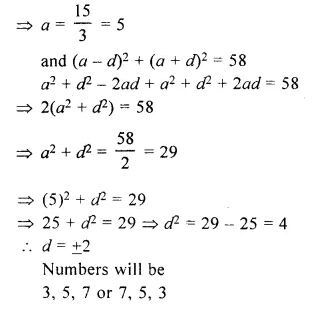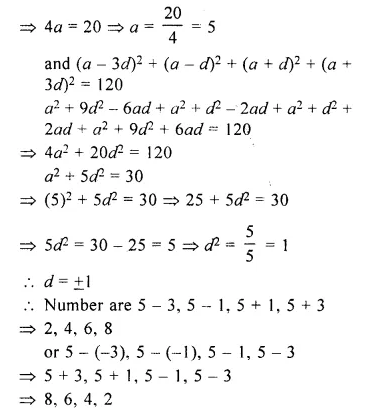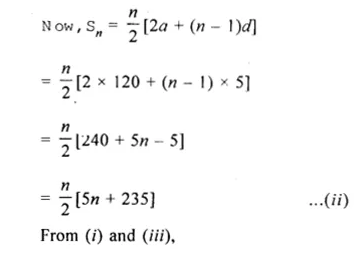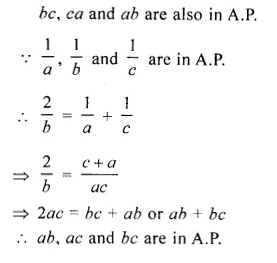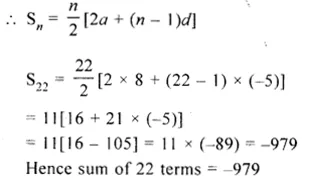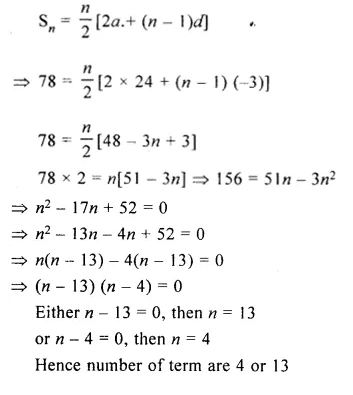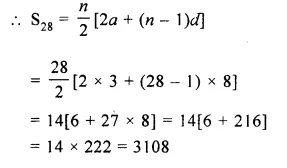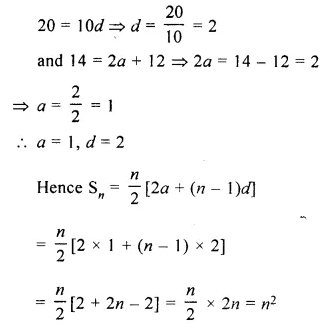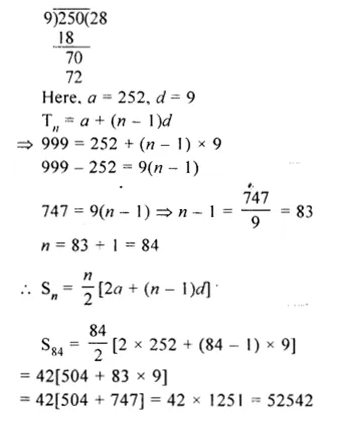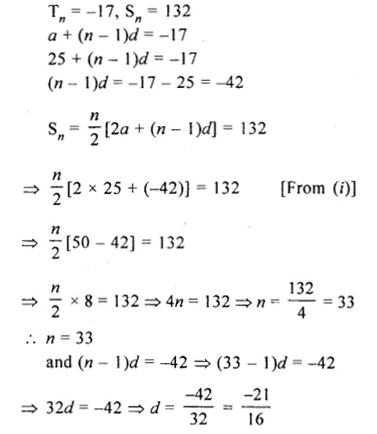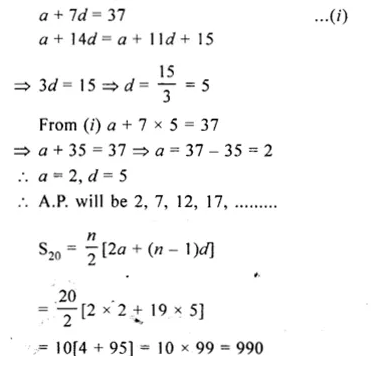HOTS Questions for Class 10 Science Chapter 12 Electricity
These Solutions are part of HOTS Questions for Class 10 Science. Here we have given HOTS Questions for Class 10 Science Chapter 12 Electricity
Question 1.
Following table gives the resistivity of three samples in (Ωm)
![]()
Which of them is a good conductor ? And which of them is an insulator ? Explain why ? (CBSE 2012)
Answer:
A material having low resistivity is a good conductor. Since, resistivity of sample A is the least among all other materials, so sample A is a good conductor. A material having high value of resistivity is an insulator. Therefore, sample C is an insulator.
More Resources
- HOTS Questions for Class 10 Science
- NCERT Solutions for Class 10 Science
- Value Based Questions in Science for Class 10
- NCERT Exemplar Solutions for Class 10 Science
- Previous Year Question Papers for CBSE Class 10 Science
Question 2.
The electrical resistivity of few materials is given below in ohm-meter. Which of these materials can be used for making element of a heating device ?

(CBSE Sample Paper, CBSE 2012, Similar CBSE 2014)
Answer:
For making element of a heating device, we use alloy instead of pure metals.The resistivity of material D lies in the range of resistivities of alloys. Therefore, material D can be used for making element of a heating device.
Question 3.
Electrical resistivities of some substances at 20°C are given below :
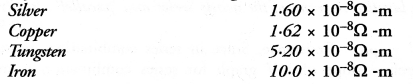
![]()
Answer the following questions in relation to them :
- Among silver and copper, which one is a better conductor ? Why ?
- Which material would you advise to be used in electrical heating devices ? Why ? (CBSE 2012)
Answer:
- A material whose electrical resistivity is low is a good conductor of electricity. Since the electrical resistivity of silver is less than that of the copper, so silver is a better conductor than the copper.
- For making the elements of heating devices, alloy is used instead of a pure metal. This is because the resistivity of an alloy is more than that of a metal and alloy does not burn (or oxidise) even at higher temperature. Out of the given substances, nichrome is an alloy, so nichrome is used in electrical heating devices.
Question 4.
The following table gives the resistivity of three samples :
![]()
Which of them is suitable for heating elements of electrical appliances and why ? (CBSE, 2010, 2012)
Answer:
For making the heating elements of electrical appliances, alloy is used instead of a pure metal. This is because alloy does not burn even at higher temperature. The resistivity of sample C is of the order of an alloy, so sample C is suitable for heating elements of electrical appliances.
Question 5.
Two metallic wires A and B are connected in series. Wire A has length l and radius r, while wire B has length 2l and radius 2r. Find the ratio of the total resistance of series combination and the resistance of wire A, if both the wires are of same material
Answer:
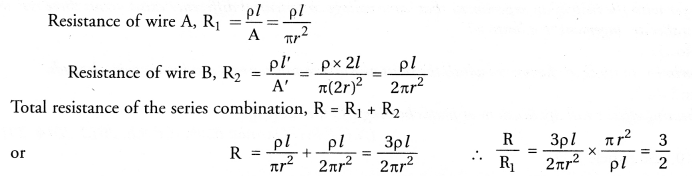
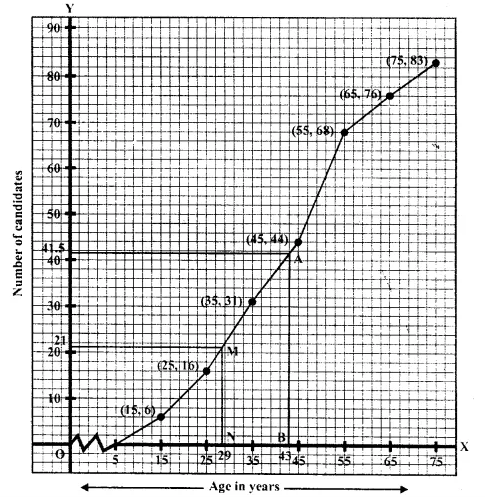
Question 6.
Two metallic wires A and B of same material are connected in parallel. Wire A has length l and radius r and wire B has length 2l and radius 2r. Compute the ratio of the total resistance of parallel combination and the resistance of wire A.
(CBSE Sample Paper)
Answer:
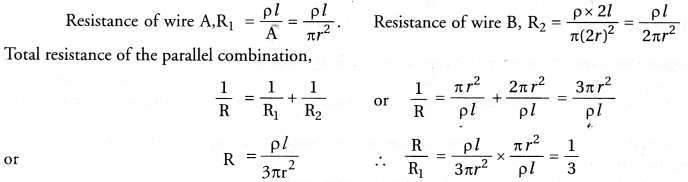
Question 7.
Two students perform the experiments on series and parallel combinations of two given resistors R1 and R2 and plot the following V-I graphs.
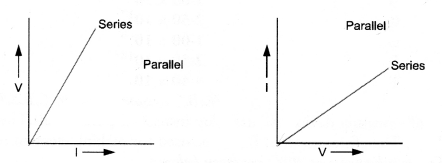
Which of the graphs is (are) correctly labelled in terms of the words ‘series’ and ‘parallel’. Justify your answer.
(CBSE Sample Paper, 2012)
Answer:
In first graph, slope of I-V graph = Resistance.
Since in series combination, resistance is more than the resistance in parallel combination, therefore slope of I-V graph for series combination is more than the slope of resistance.
![]()
Hence, graph is correctly labelled. In second graph, slope of resistance
Question 8.
Two electric circuits I and II are shown in figure.
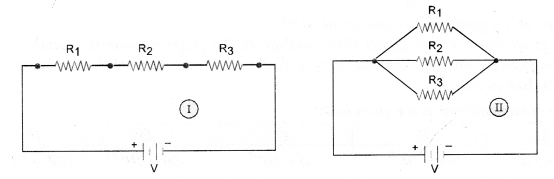
(i) Which of the two circuits has more resistance ?
(ii) Through which circuit, more current passes ?
(iii) In which circuit, the potential difference across each resistor is equal.
Answer:
(i) Equivalent resistance of series combination of resistors is more than the equivalent resistance of the parallel combination of resistors. So, the resistance of circuit I is more than the resistance of circuit II.
![]()
∴ So current in circuit II is more than the current in circuit I.
(iii) Potential difference across each resistor is equal in circuit II.
Question 9.
An electrician puts a fuse of rating 5 A in that part of domestic electrical circuit in which an electrical heater of rating 1.5 kW, 220 V is operating. What is likely to happen in this case and why ? What change, if any needs to be made ?
(CBSE Sample Paper)
Answer:
The fuse will melt and the circuit breaks if electric current more than the rating of fuse (i.e., 5 A) flows in the circuit. Electric current flowing in the circuit,
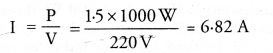
Since, current flowing in the circuit (6.82 A) is more than the rating of fuse (5 A), therefore, the fuse will melt and the electrical heater does not work. To operate the heater, fuse of rating 10 A is to be put in the circuit.
Question 10.
The electric power consumed by a device may be calculated by using either of the two expressions: P = I2R or P = V2/R . The first expression indicates that the power is directly proportional to R,whereas the second expression indicates inverse proportionality. How can the seemingly different dependence of P on R in these expressions be explained ?
(CBSE Sample Paper)
Answer:
P = I2R is used when current flowing in every component of the circuit is constant. This is the case of series combination of the devices in the circuit.
P = V2/R is used when potential difference (V) across every component of the circuit is constant. This expression is used in case of parallel combination in the circuit. In series combination, R is greater than the value of R in parallel combination.
Question 11.
Three V-I graphs are drawn individually for two resistors and their series combination. Out of A, B, C which one represents the graph for series combination of the other two. Give reason for y or ansiver. (CBSE 2011)
Answer:
Slope of V-I graph = resistance of a resistor.
When two resistors are connected in series,Volts the resistance of this combination (R = R1 + R2) is more than the resistance of both the resistors.
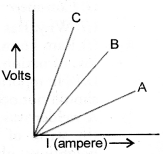
Since, slope of C is greater than the slopes of A and B. Therefore, C represents the graph for series combination of the other two.
Question 12.
V-I graphs for the two wires A and B are shown in the figure. If we connect both the wires one by one to the same battery, which of the two will produce more heat per unit time ? Give justification for your answer (CBSE 2014, 2015)
Answer:
Heat produced per unit time = V2/R
Now slope of V-I graph = R (resistance of wire).
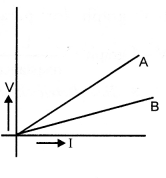
Since slope of V-I graph for wire A is greater than the slope of V-I graph for wire B, therefore, resistance of wire A is greater than the resistance of wire B. Hence, more heat will be produced per unit time in wire B than in wire A.
Question 13.
The resistivities of some substances are given below :

Answer the following questions in relation to them giving justification for each :
(i) Which material is best for making connecting cords ?
(ii) Which material do you suggest to be used in heater elements ?
(iii) You have two wires of same length and same thickness. One is made of material A and another of material D. If the resistance of wire made of A is 2 Ω, what is the resistance of the other wire ?
Answer:
(i) Material A is best for making connecting cords as its resistivity is the lowest one.
(ii) For heater elements, material of high resistivity is used. Therefore, the material E is to be used in heater elements.
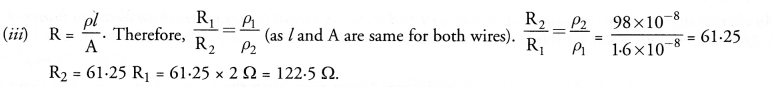
Hope given HOTS Questions for Class 10 Science Chapter 12 Electricity are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.