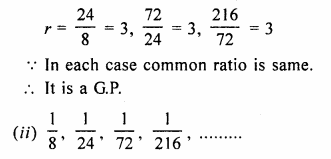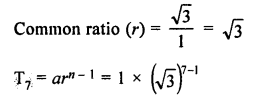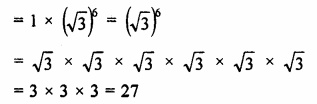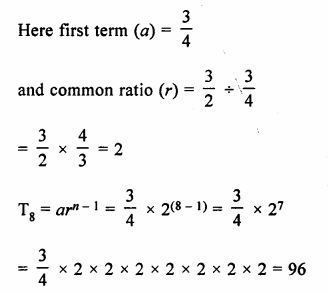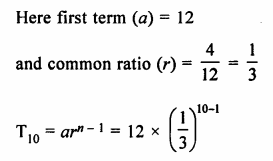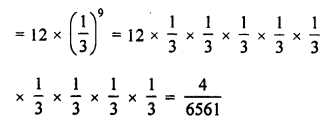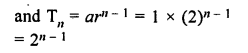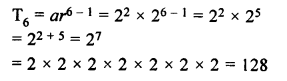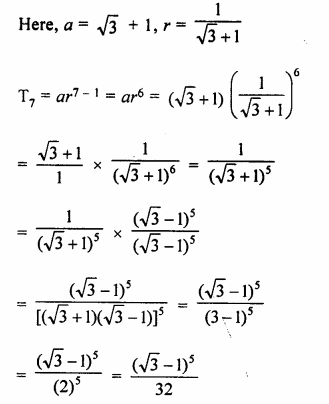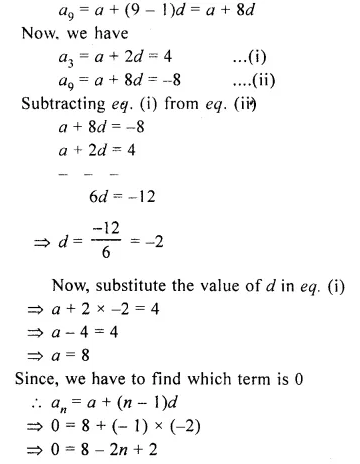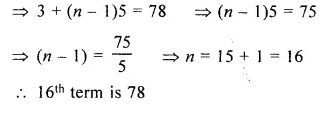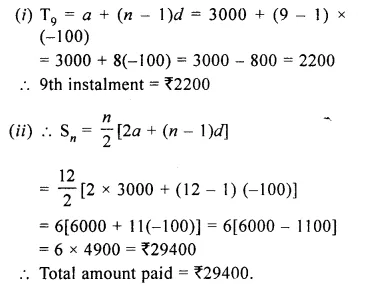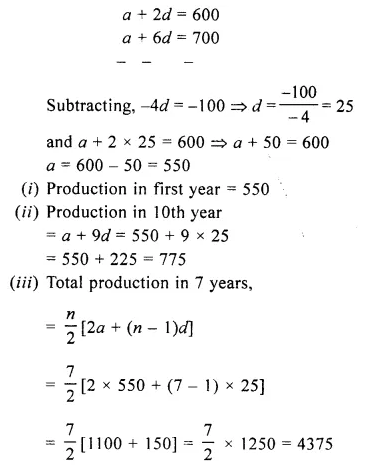Prasanna

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Question 1.
Which term of the G.P. :
– 10, \(\frac { 5 }{ \surd 3 } ,-\frac { 5 }{ 6 } ,….-\frac { 5 }{ 72 } ? \)
Solution:
– 10, \(\frac { 5 }{ \surd 3 } ,-\frac { 5 }{ 6 } ,….\)
Here a = – 10
r = \(\frac { 5 }{ \surd 3 } \div \left( -10 \right) \)

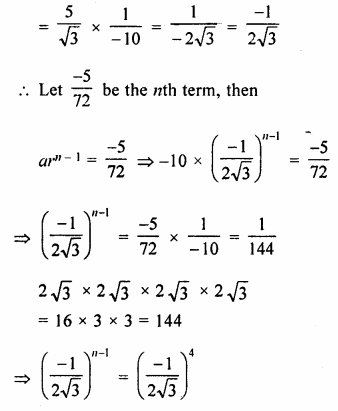
n – 1 = 4
=> n = 4 + 1 = 5
It is 5th term

Question 2.
The fifth term of a G.P. is 81 and its second term is 24. Find the geometric progression.
Solution:
In a G.P.
T₅ = ar⁴ = 81
T₂ = ar = 24

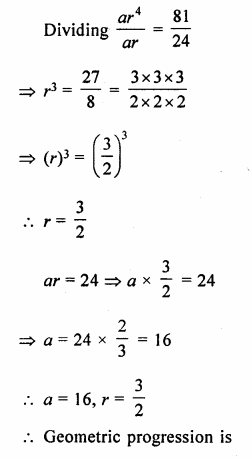
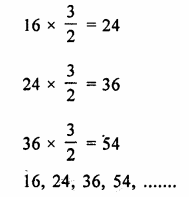
Question 3.
Fourth and seventh terms of a G.P. \(\\ \frac { 1 }{ 18 } \) are \(– \frac { 1 }{ 486 } \) respectively. Find the GP.
Solution:
In a G.P.

Question 4.
If the first and the third terms of a G.P. are 2 and 8 respectively, find its second term
Solution:
In a G.P.
T₁ = 2, and T₃ = 8
=>a = 2 and ar² = 8
Dividing, we get
r² = \(\\ \frac { 8 }{ 2 } \) = 4 = (2)²
r = 2
Second term = ar = 2 x 2 = 4

Question 5.
The product of 3rd and 8th terms of a G.P. is 243. If its 4th term is 3, find its 7th term.
Solution:
Let a be first term and r be common ratio, then
T₃ = ar²
T₈ = ar⁷
T₃ x T₈ = ar² x ar⁷
= 243

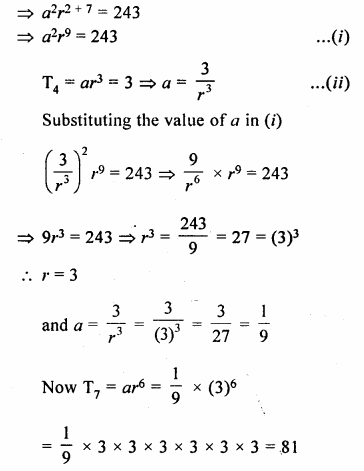
Question 6.
Find the geometric progression with 4th term = 54 and 7th term = 1458.
Solution:
In a G.P.
T₄ = 54 and T₇ = 1458
Let a be the first term and r be the common
ratio, then

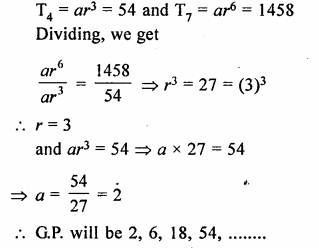
Question 7.
Second term of a geometric progression is 6 and its fifth term is 9 times of its third term. Find the geometric progression. Consider that each term of the G.P. is positive.
Solution:
In a G.P.
T₂ = 6,
T₅ = 9 x T₃
Let a be the first term and r be the common ratio

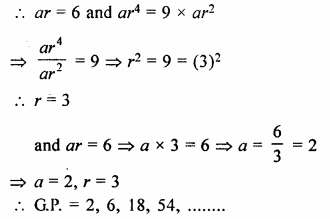
Question 8.
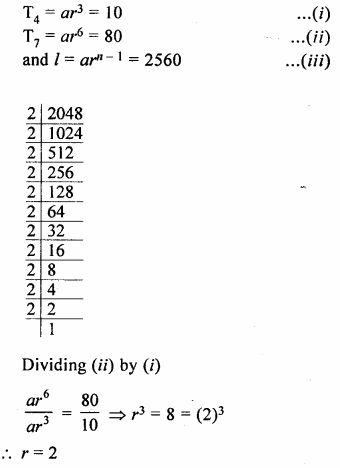
The fourth term, the seventh term and the last term of a geometric progression are 10, 80 and 2560 respectively. Find its first term, common ratio and number of terms.
Solution:
In a G.P.
T₄= 10,
T₇ = 80 and l = 2560
Let a be the first term and r be the common ratio. Therefore

Question 9.
If the 4th and 9th terms of a G.P. are 54 and 13122 respectively, find the GP. Also, find its general term.
Solution:
In a G.P.
T₄ = 54 and T₉ = 13122
Let a be the first term and r be the common ratio

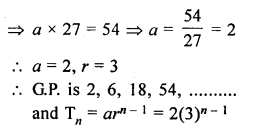
Question 10.
The fifth, eight and eleventh terms of a geometric progression are p, q and r respectively. Show that : q² = pr.
Solution:
In a G.P.
T₅ = p,
T₈ = q and T₁₁ = r
To show that q² = pr
Let a be the first term and r be the common ratio, therefore
ar⁴ = p, ar⁷ = q and ar¹⁰ = r
Squaring the ar⁷ = q

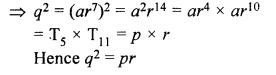
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Question 1.
Find, which of the following sequence form a G.P. :
(i) 8, 24, 72, 216, ……
(ii) \(\\ \frac { 1 }{ 8 } \),\(\\ \frac { 1 }{ 24 } \),\(\\ \frac { 1 }{ 72 } \),\(\\ \frac { 1 }{ 216 } \)
(iii) 9, 12, 16, 24,…..
Solution:
(i) 8, 24, 72, 216,……
Here, a = 8

Question 2.
Find the 9th term of the series :
1, 4, 16, 64,…….
Solution:
In G.P. 1, 4, 16, 64,….
Here first term (a) = 1
and common ratio (r) = \(\\ \frac { 4 }{ 1 } \) = 4,
T₉ = ar^{n – 1} = 1 x 4^{9 – 1} = 1 x 4⁸ = 4⁸
= 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4
= 65536

Question 3.
Find the seventh term of the G.P. :
1 , √3, 3, 3√3…….
Solution:
G.P. is 1 , √3, 3, 3√3
Here first term (a) = 1

Question 4.
Find the 8th term of the sequence :
\(\\ \frac { 3 }{ 4 } \),\(1 \frac { 1 }{ 2 } \),3……
Solution:
G.P. = \(\\ \frac { 3 }{ 4 } \),\(1 \frac { 1 }{ 2 } \),3…….
= \(\\ \frac { 3 }{ 4 } \),\(\\ \frac { 3 }{ 2 } \),3…….

Question 5.
Find the 10th term of the G.P. :
12, 4, \(1 \frac { 1 }{ 3 } \),……
Solution:
G.P. = 12, 4, \(1 \frac { 1 }{ 3 } \),……..
= 12, 4, \(\\ \frac { 4 }{ 3 } \),…..

Question 6.
Find the nth term of the series :
1, 2, 4, 8 …….
Solution:
1, 2, 4, 8,……
Here, a = 1,r = \(\\ \frac { 2 }{ 1 } \) = 2

Question 7.
Find the next three terms of the sequence :
√5, 5, 5√5…..
Solution:
√5, 5, 5√5……
Here a = √5 and r = \(\frac { 5 }{ \surd 5 }\) = √5

Question 8.
Find the sixth term of the series :
2², 2³, 2⁴,….
Solution:
2², 2³, 2⁴,……
Here, a = 2², r = 2³ ÷ 2² = 2^{3 – 2} = 2¹ = 2

Question 9.
Find the seventh term of the G.P. :
√3 + 1, 1, \(\frac { \surd 3-1 }{ 2 } \),…….
Solution:
√3 + 1, 1, \(\frac { \surd 3-1 }{ 2 } \),…….

Question 10.
Find the G.P. whose first term is 64 and next term is 32.
Solution:
First term of a G.P. (a) = 64
and second term (ar) = 32
G.P. will be 64, 32, 16, 8, 4, 2, 1,…….

Question 11.
Find the next three terms of the series:
\(\\ \frac { 2 }{ 27 } \),\(\\ \frac { 2 }{ 9 } \),\(\\ \frac { 2 }{ 3 } \),…..
Solution:
G.P. is \(\\ \frac { 2 }{ 27 } \),\(\\ \frac { 2 }{ 9 } \),\(\\ \frac { 2 }{ 3 } \),…..
a = \(\\ \frac { 2 }{ 27 } \)

Question 12.
Find the next two terms of the series
2 – 6 + 18 – 54…..
Solution:
G.P. is 2 – 6 + 18 – 54 +………
Here a = 2 and r = \(\\ \frac { -6 }{ 2 } \) = – 3
Next two terms will be
– 54 x ( – 3) = + 162
162 x ( – 3) = – 486
Next two terms are 162 – 486

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Question 1.
The 6th term of an A.P. is 16 and the 14th term is 32. Determine the 36th term.
Solution:
Let the first term and common difference of an A.P. be a and d
As, we know that,

Question 2.
If the third and the 9th terms of an A.P. term is 12 and the last term is 106. Find the 29th term of the A.P.
Solution:
Let the first term and common difference of an A.P. be a and d.
As, we know that,
a_n = a + (n – 1 )d
a₃ = a + (3 – 1 )d = a + 2d
Similarly,

Question 3.
An A.P. consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term of the A.P.
Solution:
Number of terms in an A.P. = 50
T₃= 12, l = 106
To find T₂₉
Let a be the first term and d be the common difference
=> a + 2d = 12 …(i)

Question 4.
Find the arithmetic mean of :
(i) – 5 and 41
(ii) 3x – 2y and 3x + 2y
(iii) (m + n)² and (m – n)²
Solution:
(i) Arithmetic mean between – 5 and 41
= \(\\ \frac { -5+41 }{ 2 } \)
= \(\\ \frac { 36 }{ 2 } \)
= 18

Question 5.
Find the sum of first 10 terms of the A.P. 4 + 6 + 8 +…..
Solution:
A.P. = 4 + 6 + 8 +…….
Here, a = 4, d = 6 – 4 = 2, n = 10

Question 6.
Find the sum of first 20 terms of an A.P. whose first term is 3 and the last term is 60.
Solution:
Sum of first 20 terms of an A.P. in which
a = 3 and a₂₀ = 60
a₂₀ = a + (20 – 1) x d
60 = 3 + 19 x d
19d = 60 – 3
d = \(\\ \frac { 57 }{ 19 } \)
= 3

Question 7.
How many terms of the series 18 + 15 + 12 +…..when added together will give 45 ?
Solution:
A.P. is 18 + 15 + 12 +…..
Here, a = 18, d = 15 – 18 = – 3
Given : S_n = 45

Question 8.
The nth term of a sequence is 8 – 5n. Show that the sequence is an A.P.
Solution:
Given, a_n = 8 – Sn
a₁ = 8 – 5 x (1) = 8 – 5 = 3
a₂ = 8 – 5 x (2) = 8 – 10 = – 2
a₃ = 8 – 5 x (3) = 8 – 15 = – 7
We see that

Question 9.
The the general term (nth term) and 23rd term of the sequence 3, 1, – 1, – 3,……
Solution:
The progression 3, 1, – 1, – 3,…..is A.P.
with first term (a) = 3 and common difference (d) = 1 – 3 = – 2

Question 10.
Which term of the sequence 3, 8, 13,…..is 78 ?
Solution:
Let 78 be the nth term
a = 3, d = 8 – 3 = 5, a_n = 78, n = ?
a + (n – 1)d = a_n

Question 11.
Is – 150 a term of 11, 8, 5, 2,….. ?
Solution:
11, 8, 5, 2,….1st term, a = 11
Common difference, d = 8 – 11 = – 3
a_n = – 150
=> a + (n – 1 )d = – 150
=> 11 + (n – 1) ( – 3) = – 150

Question 12.
How many two digit numbers are divisible by 3 ?
Solution:
Numbers divisible by 3 are 3, 6, 9, 12,….
Hence, lowest two digit number divisible by 3 = 12
and highest two digit number divisible by 3 = 99

Question 13.
How many multiples of 4 lie between 10 and 250 ?
Solution:
Multiples of 4 between 10 and 250 are
12, 16, 20, 24,……, 248
Here, a = 12, d = 4, l = 248

Question 14.
The sum of the 4th term and the 8th term of an A.P. is 24 and the sum of 6th term and the 10th term is 44. Find the first three terms of the A.P.
Solution:
In an A.P.
T₄ + T₈ = 24
T₆ + T₁₀ = 44
Let a be the first term and d be the common difference

Question 15.
The sum of first 14 terms of an A.P. is 1050 and its 14th term is 140. Find the 20th term.
Solution:
Given a₁₄ = 140
we know, a_n = a + (n – 1) x d

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Question 1.
Two cars start together in the same direction from the same place. The first car goes at uniform speed of 10 km h^-1. The second car goes at a speed of 8 km h^-1 in the first hour and thereafter increasing the speed by 0.5 km h^-1 each succeeding hour. After how many hours will the two cars meet ?
Solution:
Speed of first car = 10 km/hr
Speed of second car = 8 km/hr in first hour

Question 2.
A sum of Rs 700 is to be paid to give seven cash prizes to the students of a school for their overall academic performance. If the cost of each prize is Rs 20 less than its preceding prize; find the value of each of the prizes.
Solution:
Total amount (S_n) = Rs 700
Cost of each prize is Rs 20 less than its preceding price or d = – 20
d = – 20 and n = 7
\({ S }_{ n }=\frac { n }{ 2 } \left[ 2a+(n-1)d \right] \)

Question 3.
An article can be bought by paying Rs 28,000 at once or by making 12 monthly installments. If the first installment paid is Rs 3,000 and every other installment is Rs 100 less than the previous one, find :
(i) amount of installment paid in the 9th month
(ii) total amount paid in the installment scheme.
Solution:
Total price of an article = Rs 28000
No. of installments (n) = 12
First installment (a) = RS 3000
d = Rs 100

Question 4.
A manufacturer of TV sets produces 600 units in the third year and 700 units in the 7th year. Assuming that the production increases uniformly by a fixed number every year, find :
(i) the production in the first year.
(ii) the production in the 10th year.
(iii) the total production in 7 years.
Solution:
A manufacture of TV sets, he produces
No. of units in 3rd year = 600
No. of units in 7th year = 700
Let a be the first term and d be the common difference, then

Question 5.
Mrs. Gupta repays her total loan of Rs 1.18,000 by paying installments every month. If the installment for the first month is Rs 1,000 and it increases by RS 100 every month, what amount will she pay as the 30th installment of loan? What amount of loan she still has to pay after the 30th installment?
Solution:
Total loan to be paid by Mrs. Gupta = Rs 118000
Installment for the first month (a) = Rs 1000

Question 6.
In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be five times of the class to which the respective section belongs. If there are 1 to 10 classes in the school and each class has three sections, find how many trees were planted by the students?
Solution:
Number of classes = 10
Number of sections of each class = 3
Total number of sections = 10 x 3 = 30
Each section plant tree = 5 times of the class
Each section of 1st class will plant = 1 x 15 = 15

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.