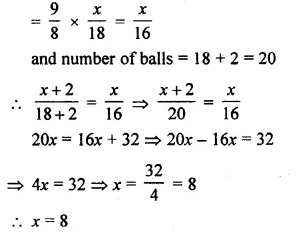Prasanna

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test

Question 1.
A game consists of spinning an arrow which comes to rest at one of the regions 1, 2 or 3 (shown in the given figure). Are the outcomes 1, 2 and 3 equally likely to occur? Give reasons.

Solution:
In a game,
No, the outcomes are not equally likely.
Outcome 3 is more likely to occur than the outcomes of 1 and 2.

Question 2.
In a single throw of a die, find the probability of getting
(i) a number greater than 5
(ii) an odd prime number
(iii) a number which is multiple of 3 or 4.
Solution:
In a single throw of a die
Number of total outcomes = 6 (1, 2, 3, 4, 5, 6)
(i) Numbers greater than 5 = 6 i.e., one number
Probability = \(\\ \frac { 1 }{ 6 } \)
(ii) An odd prime number 2 i.e., one number
Probability = \(\\ \frac { 1 }{ 6 } \)
(iii) A number which is a multiple of 3 or 4 which are 3, 6, 4 = 3 numbers
Probability = \(\\ \frac { 3 }{ 6 } \) = \(\\ \frac { 1 }{ 2 } \)

Question 3.
A lot consists of 144 ball pens of which 20 are defective and the others are good. Rohana will buy a pen if it is good, but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that :
(i) She will buy it?
(ii) She will not buy it?
Solution:
In a lot, there are 144 ball pens in which defective ball pens are = 20
and good ball pens are = 144 – 20 = 124
Rohana buys a pen which is good only.
(i) Now the number of possible outcomes = 144
and the number of favourable outcomes = 124

Question 4.
A lot consists of 48 mobile phones of which 42 are good, 3 have only minor defects and 3 have major defects. Varnika will buy a phone if it is good but the trader will only buy a mobile if it has no major defect. One phone is selected at random from the lot. What is the probability that it is
(i) acceptable to Varnika?
(ii) acceptable to the trader?
Solution:
Number of total mobiles = 48
Number of good mobiles = 42
Number having minor defect = 3
Number having major defect = 3
(i) Acceptable to Varnika = 42
Probability = \(\\ \frac { 42 }{ 48 } \) = \(\\ \frac { 7 }{ 8 } \)
(ii) Acceptable to trader = 42 + 3 = 45
Probability = \(\\ \frac { 45 }{ 48 } \) = \(\\ \frac { 15 }{ 16 } \)

Question 5.
A bag contains 6 red, 5 black and 4 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is
(i) white
(ii) red
(iii) not black
(iv) red or white.
Solution:
Total number of balls = 6 + 5 + 4 = 15
Number of red balls = 6
Number of black balls = 5
Number of white balls = 4
(i) Probability of a white ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 4 }{ 15 } \)
(ii) Probability of red ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 6 }{ 15 } \) = \(\\ \frac { 2 }{ 5 } \)
(iii) Probability of not black ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 15-5 }{ 15 } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)
(iv) Probability of red or white ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+4 }{ 15 } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)

Question 6.
A bag contains 5 red, 8 white and 7 black balls. A ball is drawn from the bag at random. Find the probability that the drawn ball is:
(i) red or white
(ii) not black
(iii) neither white nor black
Solution:
Total number of balls in a bag = 5 + 8 + 7 = 20
(i) Number of red or white balls = 5 + 8 = 13
Probability of red or white ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 20 } \)
(ii) Number of ball which are not black = 20 – 7 = 13
Probability of not black ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 20 } \)
(iii) Number of ball which are neither white nor black
= Number of ball which are only red = 5
Probability of neither white nor black ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 20 } \)
= \(\\ \frac { 1 }{ 4 } \)

Question 7.
A bag contains 5 white balls, 7 red balls, 4 black balls and 2 blue balls. One ball is drawn at random from the bag. What is the probability that the ball drawn is :
(i) white or blue
(ii) red or black
(iii) not white
(iv) neither white nor black ?
Solution:
Number of total balls = 5 + 7 + 4 + 2 = 18
Number of white balls = 5
number of red balls = 7
number of black balls = 4
and number of blue balls = 2.
(i) Number of white and blue balls = 5 + 2 = 7
Probability of white or blue balls will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 7 }{ 18 } \)
(ii) Number of red and black balls = 7 + 4 = 11
Probability of red or black balls will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 11 }{ 18 } \)
(iii) Number of ball which are not white = 7 + 4 + 2 = 13
Probability of not white balls will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 18 } \)
(iv) Number of balls which are neither white nor black = 18 – (5 + 4) = 18 – 9 = 9
Probability of ball which is neither white nor black will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 9 }{ 18 } \) = \(\\ \frac { 1 }{ 2 } \)

Question 8.
A box contains 20 balls bearing numbers 1, 2, 3, 4,……, 20. A ball is drawn at random from the box. What is the probability that the number on the ball is
(i) an odd number
(ii) divisible by 2 or 3
(iii) prime number
(iv) not divisible by 10?
Solution:
In a box, there are 20 balls containing 1 to 20 number
Number of possible outcomes = 20
(i) Numbers which are odd will be,
1, 3, 5, 7, 9, 11, 13, 15, 17, 19 = 10 balls.
Probability of odd ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 10 }{ 20 } \) = \(\\ \frac { 1 }{ 2 } \)
(ii) Numbers which are divisible by 2 or 3 will be
2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20 = 13 balls
Probability of ball which is divisible by 2 or 3 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 20 } \)
(iii) Prime numbers will be 2, 3, 5, 7, 11, 13, 17, 19 = 8
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 8 }{ 20 } \) = \(\\ \frac { 2 }{ 5 } \)
(iv) Numbers not divisible by 10 will be
1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19 = 18
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 18 }{ 20 } \) = \(\\ \frac { 9 }{ 10 } \)

Question 9.
Find the probability that a number selected at random from the numbers 1, 2, 3,……35 is a
(i) prime number
(ii) multiple of 7
(iii) multiple of 3 or 5.
Solution:
Numbers are 1, 2, 3, 4, 5,…..30, 31, 32, 33, 34, 35
Total = 35
(i) Prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31
which are 11
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 11 }{ 35 } \)
(ii) Multiple of 7 are 7, 14, 21, 28, 35 which are 5
Probability of multiple of 7 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 5 }{ 35 } \) = \(\\ \frac { 1 }{ 7 } \)
(iii) Multiple of 3 or 5 are 3, 5, 6, 9, 10, 12 ,15, 18, 20, 21, 24, 25, 27, 30, 33, 35.
Which are 16 in numbers
Probability of multiple of 3 or 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 16 }{ 35 } \)

Question 10.
Cards marked with numbers 13, 14, 15,…..60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the card is
(i) divisible by 5
(ii) a number which is a perfect square.
Solution:
Number of cards which are marked with numbers
13, 14, 15, 16, 17,….to 59, 60 are = 48
(i) Numbers which are divisible by 5 will be
15, 20, 25, 30, 35, 40, 45, 50, 55, 60 = 10
Probability of number divisible by 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 10 }{ 48 } \) = \(\\ \frac { 5 }{ 24 } \)
(ii) Numbers which is a perfect square are 16, 25, 36, 49 which are 4 in numbers.
Probability of number which is a perfect square will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 4 }{ 48 } \) = \(\\ \frac { 1 }{ 12 } \)

Question 11.
The box has cards numbered 14 to 99. Cards are mixed thoroughly and a card is drawn at random from the box. Find the probability that the card drawn from the box has
(i) an odd number
(ii) a perfect square number.
Solution:
Cards in a box are from 14 to 99 = 86
No. of total cards = 86
One card is drawn at random
Cards bearing odd numbers are 15, 17, 19, 21, …, 97, 99
Which are 43
(i) P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 43 }{ 86 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) Cards bearing number which are a perfect square
= 16, 25, 36, 49, 64, 81
Which are 6
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 6 }{ 86 } \)
= \(\\ \frac { 3 }{ 43 } \)

Question 12.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is four times that of a red ball, find the number of balls in the bags.
Solution:
Number of red balls = 5
and let number of blue balls = x
Total balls in the bag = 5 + x
and that of red balls = \(\\ \frac { 5 }{ 5+x } \)
According to the condition,
\(\frac { x }{ 5+x } =4\times \frac { 5 }{ 5+x } =>\frac { x }{ 5+x } =\frac { 20 }{ 5+x } \)
x ≠ – 5
x = 20
Hence, number of blue balls = 20
and number of balls in the bag = 20 + 5 = 25

Question 13.
A bag contains 18 balls out of which x balls are white.
(i) If one ball is drawn at random from the bag, what is the probability that it is white ball?
(ii) If 2 more white balls are put in the bag, the probability of drawing a white ball will be \(\\ \frac { 9 }{ 8 } \) times that of probability of white ball coming in part (i). Find the value of x.
Solution:
Total numbers of balls in a bag = 18
No. of white balls = x
(i) One ball is drawn a random
Probability of being a white ball = \(\\ \frac { x }{ 18 } \)
(ii) If 2 more white balls an put, then number of white balls = x + 2
and probability is \(\\ \frac { 9 }{ 8 } \) times

Question 14.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is :
(i) a red face card
(ii) neither a club nor a spade
(iii) neither an ace nor a king of red colour
(iv) neither a red card nor a queen
(v) neither a red card nor a black king.
Solution:
Number of cards in a pack of well-shuffled cards = 52
(i) Number of a red face card = 3 + 3 = 6
Probability of red face card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 6 }{ 52 } \) = \(\\ \frac { 3 }{ 26 } \)
(ii) Number of cards which is neither a club nor a spade = 52 – 26 = 26
Probability of card which’ is neither a club nor a spade will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 26 }{ 52 } \) = \(\\ \frac { 1 }{ 2 } \)
(iii) Number of cards which is neither an ace nor a king of red colour
= 52 – (4 + 2) = 52 – 6 = 46
Probability of card which is neither ace nor a king of red colour will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 46 }{ 52 } \) = \(\\ \frac { 23 }{ 26 } \)
(iv) Number of cards which are neither a red card nor a queen are
= 52 – (26 + 2) = 52 – 28 = 24
Probability of card which is neither red nor a queen will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 24 }{ 52 } \) = \(\\ \frac { 6 }{ 13 } \)
(v) Number of cards which are neither red card nor a black king
= 52 – (26 + 2) = 52 – 28 = 24
Probability of cards which is neither red nor a black king will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 24 }{ 52 } \) = \(\\ \frac { 6 }{ 13 } \)

Question 15.
From pack of 52 playing cards, blackjacks, black kings and black aces are removed and then the remaining pack is well-shuffled. A card is drawn at random from the remaining pack. Find the probability of getting
(i) a red card
(ii) a face card
(iii) a diamond or a club
(iv) a queen or a spade.
Solution:
Total number of cards = 52
Black jacks, black kings and black aces are removed
Now number of cards = 52 – (2 + 2 + 2) = 52 – 6 = 46
One card is drawn
(i) No. of red cards = 13 + 13 = 26
∴Probability = \(\\ \frac { 26 }{ 46 } \) = \(\\ \frac { 13 }{ 23 } \)
(ii) Face cards = 4 queens, 2 red jacks, 2 kings = 8
∴Probability = \(\\ \frac { 8 }{ 46 } \) = \(\\ \frac { 4 }{ 23 } \)
(iii) a diamond on a club = 13 + 10 = 23
∴Probability = \(\\ \frac { 23 }{ 46 } \) = \(\\ \frac { 1 }{ 2 } \)
(iv) A queen or a spade = 4 + 10 = 14
∴Probability = \(\\ \frac { 14 }{ 46 } \) = \(\\ \frac { 7 }{ 23 } \)

Question 16.
Two different dice are thrown simultaneously. Find the probability of getting:
(i) sum 7
(ii) sum ≤ 3
(iii) sum ≤ 10
Solution:
(i) Numbers whose sum is 7 will be (1, 6), (2, 5), (4, 3), (5, 2), (6, 1), (3, 4) = 6
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 6 }{ 36 } \) = \(\\ \frac { 1 }{ 6 } \)
(ii) Sum ≤ 3
Then numbers can be (1, 2), (2, 1), (1, 1) which are 3 in numbers
∴Probability will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 3 }{ 36 } \) = \(\\ \frac { 1 }{ 12 } \)
(iii) Sum ≤ 10
The numbers can be,
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, .6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5),
(6, 1), (6, 2), (6, 3), (6, 4) = 33
Probability will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 33 }{ 36 } \) = \(\\ \frac { 11 }{ 12 } \)

Question 17.
Two dice are thrown together. Find the probability that the product of the numbers on the top of two dice is
(i) 6
(ii) 12
(iii) 7
Solution:
Two dice are thrown together
Total number of events = 6 × 6 = 36
(i) Product 6 = (1, 6), (2, 3), (3, 2). (6, 1) = 4
Probability = \(\\ \frac { 4 }{ 36 } \) = \(\\ \frac { 1 }{ 9 } \)
(ii) Product 12 = (2, 6), (3, 4), (4, 3), (6, 2) = 4
Probability = \(\\ \frac { 4 }{ 36 } \) = \(\\ \frac { 1 }{ 9 } \)
(iii) Product 7 = 0 (no outcomes)
Probability = \(\\ \frac { 0 }{ 36 } \) = 0

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test

Choose the correct answer from the given four options (1 to 28):

Question 1.
Which of the following cannot be the probability of an event?
(a) 0.7
(b) \(\\ \frac { 2 }{ 3 } \)
(c) – 1.5
(d) 15%
Solution:
– 1.5 (negative) can not be a probability as a probability is possible 0 to 1. (c)

Question 2.
If the probability of an event is p, then the probability of its complementary event will be
(a) p – 1
(b) p
(c) 1 – p
(d) \(1- \frac { 1 }{ p } \)
Solution:
Complementary of p is 1 – p
Probability of complementary even of p is 1 – p. (c)

Question 3.
Out of one digit prime numbers, one selecting an even number is
(a) \(\\ \frac { 1 }{ 2 } \)
(b) \(\\ \frac { 1 }{ 4 } \)
(c) \(\\ \frac { 4 }{ 9 } \)
(d) \(\\ \frac { 2 }{ 5 } \)
Solution:
One digit prime numbers are 2, 3, 5, 7 = 4
Probability of an even prime number (i.e , 2) = \(\\ \frac { 1 }{ 4 } \) (b)

Question 4.
Out of vowels, of the English alphabet, one letter is selected at random. The probability of selecting ‘e’ is
(a) \(\\ \frac { 1 }{ 26 } \)
(b) \(\\ \frac { 5 }{ 26 } \)
(c) \(\\ \frac { 1 }{ 4 } \)
(d) \(\\ \frac { 1 }{ 5 } \)
Solution:
Vowels of English alphabet are a, e, i, o, u = 4
One letter is selected at random.
The probability of selecting ’e’ = \(\\ \frac { 1 }{ 5 } \) (d)

Question 5.
When a die is thrown, the probability of getting an odd number less than 3 is
(a) \(\\ \frac { 1 }{ 6 } \)
(b) \(\\ \frac { 1 }{ 3 } \)
(c) \(\\ \frac { 1 }{ 2 } \)
(d) 0
Solution:
A die is thrown
Total number of events = 6
Odd number less than 3 is 1 = 1
Probability = \(\\ \frac { 1 }{ 6 } \) (a)

Question 6.
A fair die is thrown once. The probability of getting an even prime number is
(a) \(\\ \frac { 1 }{ 6 } \)
(b) \(\\ \frac { 2 }{ 3 } \)
(c) \(\\ \frac { 1 }{ 3 } \)
(d) \(\\ \frac { 1 }{ 2 } \)
Solution:
A fair die is thrown once
Total number of outcomes = 6
Prime numbers = 2, 3, 5 and even prime is 2
Probability of getting an even prime number = \(\\ \frac { 1 }{ 6 } \) (a)

Question 7.
A fair die is thrown once. The probability of getting a composite number is
(a) \(\\ \frac { 1 }{ 3 } \)
(b) \(\\ \frac { 1 }{ 6 } \)
(c) \(\\ \frac { 2 }{ 3 } \)
(d) 0
Solution:
A fair die is thrown once
Total number of outcomes = 6
Composite numbers are 4, 6 = 2
Probability = \(\\ \frac { 2 }{ 6 } \) = \(\\ \frac { 1 }{ 3 } \) (a)

Question 8.
If a fair dice is rolled once, then the probability of getting an even number or a number greater than 4 is
(a) \(\\ \frac { 1 }{ 2 } \)
(b) \(\\ \frac { 1 }{ 3 } \)
(c) \(\\ \frac { 5 }{ 6 } \)
(d) \(\\ \frac { 2 }{ 3 } \)
Solution:
A fair dice is thrown once.
Total number of outcomes = 6
Even numbers or a number greater than 4 = 2, 4, 5, 6 = 4
Probability = \(\\ \frac { 4 }{ 6 } \) = \(\\ \frac { 2 }{ 3 } \) (d)

Question 9.
Rashmi has a die whose six faces show the letters as given below :

If she throws the die once, then the probability of getting C is
(a) \(\\ \frac { 1 }{ 3 } \)
(b) \(\\ \frac { 1 }{ 4 } \)
(c) \(\\ \frac { 1 }{ 5 } \)
(d) \(\\ \frac { 1 }{ 6 } \)
Solution:
A die having 6 faces bearing letters A, B, C, D, A, C
Total number of outcomes = 4
Probability of getting C = \(\\ \frac { 2 }{ 6 } \) = \(\\ \frac { 1 }{ 3 } \) (a)

Question 10.
If a letter is chosen at random from the letters of English alphabet, then the probability that it is a letter of the word ‘DELHI’ is
(a) \(\\ \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 26 } \)
(c) \(\\ \frac { 5 }{ 26 } \)
(d) \(\\ \frac { 21 }{ 26 } \)
Solution:
Total number of English alphabets = 26
Letter of Delhi = D, E, L, H, I. = 5
Probability = \(\\ \frac { 5 }{ 26 } \) (c)

Question 11.
A card is drawn from a well-shuffled pack of 52 playing cards. The event E is that the card drawn is not a face card. The number of outcomes favourable to the event E is
(a) 51
(b) 40
(c) 36
(d) 12
Solution:
Number of playing cards = 52
Probability of a card which is not a face card = (52 – 12) = 40
Number of possible events = 40 (b)

Question 12.
A card is drawn from a deck of 52 cards. The event E is that card is not an ace of hearts. The number of outcomes favourable to E is
(a) 4
(b) 13
(c) 48
(d) 51
Solution:
Total number of cards = 52
Balance 52 – 1 = 51
Number of possible events = 51 (d)

Question 13.
If one card is drawn from a well-shuffled pack of 52 cards, the probability of getting an ace is
(a) \(\\ \frac { 1 }{ 52 } \)
(b) \(\\ \frac { 4 }{ 13 } \)
(c) \(\\ \frac { 2 }{ 13 } \)
(d) \(\\ \frac { 1 }{ 13 } \)
Solution:
Total number of cards = 52
Number of aces = 4
Probability of card being an ace = \(\\ \frac { 4 }{ 52 } \) = \(\\ \frac { 1 }{ 13 } \) (d)

Question 14.
A card is selected at random from a well- shuffled deck of 52 cards. The probability of its being a face card is
(a) \(\\ \frac { 3 }{ 13 } \)
(b) \(\\ \frac { 4 }{ 13 } \)
(c) \(\\ \frac { 6 }{ 13 } \)
(d) \(\\ \frac { 9 }{ 13 } \)
Solution:
Total number of cards = 52
No. of face cards = 3 × 4 = 12
.’. Probability of face card = \(\\ \frac { 12 }{ 52 } \) = \(\\ \frac { 3 }{ 13 } \) (a)

Question 15.
A card is selected at random from a pack of 52 cards. The probability of its being a red face card is
(a) \(\\ \frac { 3 }{ 26 } \)
(b) \(\\ \frac { 3 }{ 13 } \)
(c) \(\\ \frac { 2 }{ 13 } \)
(d) \(\\ \frac { 1 }{ 2 } \)
Solution:
Total number of card = 52
No. of red face card = 3 × 2 = 6
.’. Probability = \(\\ \frac { 6 }{ 52 } \) = \(\\ \frac { 3 }{ 26 } \) (a)

Question 16.
If a card is drawn from a well-shuffled pack of 52 playing cards, then the probability of this card being a king or a jack is
(a) \(\\ \frac { 1 }{ 26 } \)
(b) \(\\ \frac { 1 }{ 13 } \)
(c) \(\\ \frac { 2 }{ 13 } \)
(d) \(\\ \frac { 4 }{ 13 } \)
Solution:
Total number of cards 52
Number of a king or a jack = 4 + 4 = 8
.’. Probability = \(\\ \frac { 8 }{ 52 } \) = \(\\ \frac { 2 }{ 13 } \) (c)

Question 17.
The probability that a non-leap year selected at random has 53 Sundays is.
(a) \(\\ \frac { 1 }{ 365 } \)
(b) \(\\ \frac { 2 }{ 365 } \)
(c) \(\\ \frac { 2 }{ 7 } \)
(d) \(\\ \frac { 1 }{ 7 } \)
Solution:
Number of a non-leap year 365
Number of Sundays = 53
In a leap year, there are 52 weeks or 364 days
One days is left
Now we have to find the probability of a Sunday out of remaining 1 day
∴ Probability = \(\\ \frac { 1 }{ 7 } \) (d)

Question 18.
A bag contains 3 red balk, 5 white balls and 7 black balls. The probability that a ball drawn from the bag at random will be neither red nor black is
(a) \(\\ \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 3 } \)
(c) \(\\ \frac { 7 }{ 15 } \)
(d) \(\\ \frac { 8 }{ 1 } \)
Solution:
In a bag, there are
3 red balls + 5 white balls + 7 black balls
Total number of balls = 15
One ball is drawn at random which is neither
red not black
Number of outcomes = 5
Probability = \(\\ \frac { 5 }{ 15 } \) = \(\\ \frac { 1 }{ 3 } \) (b)

Question 19.
A bag contains 4 red balls and 5 green balls. One ball is drawn at random from the bag. The probability of getting either a red ball or a green ball is
(a) \(\\ \frac { 4 }{ 9 } \)
(b) \(\\ \frac { 5 }{ 9 } \)
(c) 0
(d) 1
Solution:
In a bag, there are
4 red balls + 5 green balls
Total 4 + 5 = 9
One ball is drawn at random
Probability of either a red or a green ball = \(\\ \frac { 9 }{ 9 } \) = 1 (d)

Question 20.
A bag contains 5 red, 4 white and 3 black balls. If a. ball is drawn from the bag at random, then the probability of the ball being not black is
(a) \(\\ \frac { 5 }{ 12 } \)
(b) \(\\ \frac { 1 }{ 3 } \)
(c) \(\\ \frac { 3 }{ 4 } \)
(d) \(\\ \frac { 1 }{ 4 } \)
Solution:
In a bag, there are
5 red + 4 white + 3 black balls = 12
One ball is drawn at random
Probability of a ball not black = \(\\ \frac { 5+4 }{ 12 } \) = \(\\ \frac { 9 }{ 12 } \) = \(\\ \frac { 3 }{ 4 } \) (c)

Question 21.
One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 5 is
(a) \(\\ \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 3 }{ 5 } \)
(c) \(\\ \frac { 4 }{ 5 } \)
(d) \(\\ \frac { 1 }{ 3 } \)
Solution:
There are t to 40 = 40 tickets in a bag
No. of tickets which is multiple of 5 = 8
(5, 10, 15, 20, 25, 30, 35, 40)
Probability = \(\\ \frac { 8 }{ 40 } \) = \(\\ \frac { 1 }{ 5 } \) (a)

Question 22.
If a number is randomly chosen from the numbers 1,2,3,4, …, 25, then the probability of the number to be prime is
(a) \(\\ \frac { 7 }{ 25 } \)
(b) \(\\ \frac { 9 }{ 25 } \)
(c) \(\\ \frac { 11 }{ 25 } \)
(d) \(\\ \frac { 13 }{ 25 } \)
Solution:
There are 25 number bearing numbers 1, 2, 3,…,25
Prime numbers are 2, 3, 5, 7, 11, 13, 17 19, 23 = 9
Probability being a prime number = \(\\ \frac { 9 }{ 25 } \) (b)

Question 23.
A box contains 90 cards numbered 1 to 90. If one card is drawn from the box at random, then the probability that the number on the card is a perfect square is
(a) \(\\ \frac { 1 }{ 10 } \)
(b) \(\\ \frac { 9 }{ 100 } \)
(c) \(\\ \frac { 1 }{ 9 } \)
(d) \(\\ \frac { 1 }{ 100 } \)
Solution:
In a box, there are
90 cards bearing numbers 1 to 90
Perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 81 = 9
Probability of being a perfect square = \(\\ \frac { 9 }{ 90 } \) = \(\\ \frac { 1 }{ 10 } \) (a)

Question 24.
If a (fair) coin is tossed twice, then the probability of getting two heads is
(a) \(\\ \frac { 1 }{ 4 } \)
(b) \(\\ \frac { 1 }{ 2 } \)
(c) \(\\ \frac { 3 }{ 4 } \)
(d) 0
Solution:
A coin is tossed twice
Number of outcomes = 2 x 2 = 4
Probability of getting two heads (HH = 1) = \(\\ \frac { 1 }{ 4 } \) (a)

Question 25.
If two coins are tossed simultaneously, then the probability of getting atleast one head is
(a) \(\\ \frac { 1 }{ 4 } \)
(b) \(\\ \frac { 1 }{ 2 } \)
(c) \(\\ \frac { 3 }{ 4 } \)
(d) 1
Solution:
Two coins are tossed
Total outcomes = 2 × 2 = 4
Probability of getting atleast one head (HT,TH,H,H) = \(\\ \frac { 3 }{ 4 } \) (c)

Question 26.
Lakshmi tosses two coins simultaneously. The probability that she gets almost one head
(a) 1
(b) \(\\ \frac { 3 }{ 4 } \)
(c) \(\\ \frac { 1 }{ 2 } \)
(d) \(\\ \frac { 1 }{ 7 } \)
Solution:
Two coins are tossed
Total number of outcomes = 2 × 2 = 4
Probability of getting atleast one head = (HT, TH, RH = 3) = \(\\ \frac { 3 }{ 4 } \) (b)

Question 27.
The probability of getting a bad egg in a lot of 400 eggs is 0.035. The number of bad eggs in the lot is
(a) 7
(b) 14
(c) 21
(d) 28
Solution:
Total number of eggs 400
Probability of getting a bad egg = 0.035
Number of bad eggs = 0.035 of 400 = \(400 \times \frac { 35 }{ 1000 } \) = 14 (b)

Question 28.
A girl calculates that the probability of her winning the first prize in a lottery is 0.08. If 6000 tickets are sold, how many tickets she has bought?
(a) 40
(b) 240
(c) 480
(d) 750
Solution:
For a girl,
Winning a first prize = 0.08
Number of total tickets = 6000
Number of tickets she bought = 0.08 of 6000 = \(6000 \times \frac { 8 }{ 100 } \) = 480 (c)

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test

Question 1.
A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. Anjali takes out a ball from the bag without looking into it. What is the probability that she takes out
(i) yellow ball ?
(ii) red ball ?
(iii) blue ball ?
Solution:
Number of balls in the bag = 3.
(i) Probability of yellow ball = \(\\ \frac { 1 }{ 3 } \)
(ii) Probability of red ball = \(\\ \frac { 1 }{ 3 } \)
(iii) Probability of blue ball = \(\\ \frac { 1 }{ 3 } \)

Question 2.
A box contains 600 screws, one-tenth are rusted. One screw is taken out at random from this box. Find the probability that it is a good screw.
Solution:
Number of total screws = 600
Rusted screws = \(\\ \frac { 1 }{ 10 } \) of 600 = 60
∴ Good screws = 600 – 60 = 540
Probability of a good screw
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 540 }{ 600 } \)
= \(\\ \frac { 9 }{ 10 } \)

Question 3.
In a lottery, there are 5 prized tickets and 995 blank tickets. A person buys a lottery ticket. Find the probability of his winning a prize.
Solution:
Number of prized tickets = 5
Number of blank tickets = 995
Total number of tickets = 5 + 995 = 1000
Probability of prized ticket
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 1000 } \)
= \(\\ \frac { 1 }{ 200 } \)

Question 4.
12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution:
Number of defective pens = 12
Number of good pens = 132
Total number of pens =12 + 132 = 144
Probability of good pen
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 132 }{ 144 } \)
= \(\\ \frac { 11 }{ 12 } \)

Question 5.
If the probability of winning a game is \(\\ \frac { 5 }{ 11 } \), what is the probability of losing ?
Solution:
Probability of winning game = \(\\ \frac { 5 }{ 11 } \)
⇒ P(E) = \(\\ \frac { 5 }{ 11 } \)
We know that P (E) + P (\(\overline { E } \)) = 1
where P (E) is the probability of losing the game.
\(\\ \frac { 5 }{ 11 } \) + P (\(\overline { E } \)) = 1
⇒ P (\(\overline { E } \)) = \(1- \frac { 5 }{ 11 } \)
= \(\\ \frac { 11-5 }{ 11 } \)
= \(\\ \frac { 6 }{ 11 } \)

Question 6.
Two players, Sania and Sonali play a tennis match. It is known that the probability of Sania winning the match is 0.69. What is the probability of Sonali winning ?
Solution:
Probability of Sania’s winning the game = 0.69
Let P (E) be the probability of Sania’s winning the game
and P (\(\overline { E } \)) be the probability of Sania’s losing
the game or probability of Sonali, winning the game
P (E) + P (\(\overline { E } \)) = 1
⇒ 0.69 + P (\(\overline { E } \)) = 1
⇒ P(\(\overline { E } \)) = 1 – 0.69 = 0.31
Hence probability of Sonali’s winning the game = 0.31

Question 7.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random’ from in bag. What is the probability that the ball drawn is .
(i) red ?
(ii) not red ?
Solution:
Number of red balls = 3
Number of black balls = 5
Total balls = 3 + 5 = 8
Let P (E) be the probability of red balls,
then P (\(\overline { E } \)) will be the probability of not red balls.
P (E) + P (\(\overline { E } \)) = 1
(i) But P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 8 } \)
(ii) P (\(\overline { E } \)) = 1 – P(E)
= \(1- \frac { 6 }{ 11 } \)
= \(\\ \frac { 8-3 }{ 8 } \)
= \(\\ \frac { 5 }{ 8 } \)

Question 8.
There are 40 students in Class X of a school of which 25 are girls and the.others are boys. The class teacher has to select one student as a class representative. She writes the name of each student on a separate card, the cards being identical. Then she puts cards in a bag and stirs them thoroughly. She then draws one card from the bag. What is the probability that the name written on the card is the name of
(i) a girl ?
(ii) a boy ?
Solution:
Number of total students = 40
Number of girls = 25
Number of boys = 40 – 25 = 15
(i) Probability of a girl
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 25 }{ 40 } \)
= \(\\ \frac { 5 }{ 8 } \)
(ii) Probability of a boy
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 15 }{ 40 } \)
= \(\\ \frac { 3 }{ 8 } \)

Question 9.
A letter is chosen from the word ‘TRIANGLE’. What is the probability that it is a vowel ?
Solution:
There are three vowels: I, A, E
.’. The number of letters in the word ‘TRIANGLE’ = 8.
Probability of vowel
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 8 } \)

Question 10.
A letter of English alphabet is chosen at random. Determine the probability that the letter is a consonant.
Solution:
No. of English alphabet = 26
No. of vowel = 5
No. of constant = 25 – 5 = 21
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 21 }{ 26 } \)

Question 11.
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn at random from the bag, find the probability that the ball drawn is:
(i) red
(ii) black or white
(iii) not black.
Solution:
In a bag,
Number of black balls = 5
Number of red balls = 7
and number of white balls = 3
Total number of balls in the bag
= 5 + 7 + 3 = 15
(i) Probability of red balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7 }{ 15 } \)
(ii) Probability of black or white balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5+3 }{ 15 } \)
= \(\\ \frac { 8 }{ 15 } \)
(iii) Probability of not black balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7+3 }{ 15 } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)

Question 12.
A box contains 7 blue, 8 white and 5 black marbles. If a marble is drawn at random from the box, what is the probability that it will be
(i) black?
(ii) blue or black?
(iii) not black?
(iv) green?
Solution:
Total number of marbles in the box
= 7 + 8 + 5 = 20
Since, a marble is drawn at random from the box
(i) Probability (of a black Marble)
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 20 } \)
= \(\\ \frac { 1 }{ 4 } \)
(ii) Probability (of a blue or black marble)
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7+5 }{ 20 } \)
= \(\\ \frac { 12 }{ 20 } \)
= \(\\ \frac { 3 }{ 5 } \)
(iii) Probability (of not black marble)
= 1 – P (of black 1)
= \(1- \frac { 1 }{ 4 } \)
= \(\\ \frac { 4-1 }{ 4 } \)
= \(\\ \frac { 3 }{ 4 } \)
(iv) P (of a green marble) = 0
(∴ Since, a box does not contain a green marble,
so the probability of green marble will be zero)

Question 13.
A bag contains 6 red balls, 8 white balls, 5 green balls and 3 black balls. One ball is drawn at random from the bag. Find the probability that the ball is :
(i) white
(ii) red or black
(iii) not green
(iv) neither white nor black.
Solution:
In a bag,
Number of red balls = 6
Number of white balls = 8
Number of green balls = 5
and number of black balls = 3
Total number of balls in the bag
= 6 + 8 + 5 + 3 = 22
(i) Probability of white balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 22 } \)
= \(\\ \frac { 4 }{ 11 } \)
(ii) Probability of red or black balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+3 }{ 22 } \)
= \(\\ \frac { 9 }{ 22 } \)
(iii) Probability of not green balls i.e. having red, white and black balls.
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+8+3 }{ 22 } \)
= \(\\ \frac { 17 }{ 22 } \)
(iv) Probability of neither white nor black balls i.e. red and green balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+5 }{ 22 } \)
= \(\\ \frac { 11 }{ 22 } \)
= \(\\ \frac { 1 }{ 2 } \)

Question 14.
A piggy bank contains hundred 50 p coins, fifty Rs 1 coins, twenty Rs 2 coins and ten Rs 5 coins. It is equally likely that one of the coins will fall down when the bank is turned upside down, what is the probability that the coin
(i) will be a 50 p coin?
(ii) will not be Rs 5 coin?
Solution:
In a piggy bank, there are
100, 50 p coin
50, Rs 1 coin
20, Rs 2 coin
10, Rs 5 coin
Total coins = 100 + 50 + 20 + 10 = 180
One coin is drawn at random Probability of
(i) 50 p coins = \(\\ \frac { 100 }{ 180 } \)
= \(\\ \frac { 5 }{ 9 } \)
(ii) Will not be Rs 5 coins
= 100 + 50 + 20 = 170
Probability = \(\\ \frac { 170 }{ 180 } \) = \(\\ \frac { 17 }{ 18 } \)

Question 15.
A carton consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Peter, a trader, will only accept the shirts which are good, but Salim, another trader, will only reject the shirts which have major defects. One shirts is drawn at random from the carton. What is the probability that
(i) it is acceptable to Peter ?
(ii) it is acceptable to Salim ?
Solution:
In a carton, there the 100 shirts.
Among these number of shirts which are good = 88
number of shirts which have minor defect = 8
number of shirt which have major defect = 4
Total number of shirts = 88 + 8 + 4 = 100
Peter accepts only good shirts i.e. 88
Salim rejects only shirts which have major defect i.e. 4
(i) Probability of good shirts which are acceptable to Peter
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 88 }{ 100 } \)
= \(\\ \frac { 22 }{ 25 } \)
(ii) Probability of shirts acceptable to Salim
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 88+8 }{ 100 } \)
= \(\\ \frac { 96 }{ 100 } \)
= \(\\ \frac { 24 }{ 25 } \)

Question 16.
A die is thrown once. What is the probability that the
(i) number is even
(ii) number is greater than 2 ?
Solution:
Dice is thrown once
Sample space = {1, 2, 3, 4, 5, 6}
(i) No. of ways in favour = 3
(∵ Even numbers are 2, 4, 6)
Total ways = 6
Probability = \(\\ \frac { 3 }{ 6 } \) = \(\\ \frac { 1 }{ 2 } \)
(ii) No. of ways in favour = 4
(Numbers greater than 2 are 3, 4, 5, 6)
Total ways = 6
Probability = \(\\ \frac { 4 }{ 6 } \) = \(\\ \frac { 2 }{ 2 } \)

Question 17.
In a single throw of a die, find the probability of getting:
(i) an odd number
(ii) a number less than 5
(iii) a number greater than 5
(iv) a prime number
(v) a number less than 8
(vi) a number divisible by 3
(vii) a number between 3 and 6
(viii) a number divisible by 2 or 3.
Solution:
A die is thrown and on its faces, numbers 1 to 6 are written.
Total numbers of possible outcomes = 6
(i) Probability of an odd number,
odd number are 1, 3 and 5
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 6 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) A number less them 5 are 1, 2, 3, 4
Probability of a number less than 5 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 6 } \)
= \(\\ \frac { 2 }{ 3 } \)
(iii) A number greater than 5 is 6
Probability of a number greater than 5 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 6 } \)
(iv) Prime number is 2, 3, 5
Probability of a prime number is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 6 } \)
= \(\\ \frac { 1 }{ 2 } \)
(v) Number less than 8 is nil
P (E) = 0
(vi) A number divisible by 3 is 3, 6
Probability of a number divisible by 3 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 6 } \)
= \(\\ \frac { 1 }{ 3 } \)
(vii) Numbers between 3 and 6 is 4, 5
Probability of a number between 3 and 6 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 6 } \)
= \(\\ \frac { 1 }{ 3 } \)
(viii) Numbers divisible by 2 or 3 are 2, 4 or 3,
Probability of a number between 2 or 3 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 6 } \)
= \(\\ \frac { 1 }{ 3 } \)

Question 18.
A die has 6 faces marked by the given numbers as shown below:

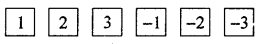
The die is thrown once. What is the probability of getting
(i) a positive integer.
(ii) an integer greater than – 3.
(iii) the smallest integer ?
Solution:
Total outcomes n(S)= 6
(i) a positive integer = (1, 2, 3)
No. of favourables n(E) = 3
Probability = \(\\ \frac { n(E) }{ n(S) } \)
= \(\\ \frac { 3 }{ 6 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) Integer greater than -3
= (1, 2, 3, -1, -2)
No. of favourables n(E) = 5
Probability = \(\\ \frac { n(E) }{ n(S) } \)
= \(\\ \frac { 5 }{ 6 } \)
(iii) Smallest integer = -3
No. of favourables n(E) = 1
Probability = \(\\ \frac { n(E) }{ n(S) } \)
= \(\\ \frac { 1 }{ 6 } \)

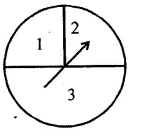
Question 19.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (shown in the adjoining figure) and these are equally likely outcomes. What is the probability that it will point at
(i) 8 ?
(ii) an odd number ?
(iii) a number greater than 2?
(iv) a number less than 9?

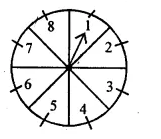
Solution:
On the face of a game, numbers 1 to 8 is shown.
Possible outcomes = 8
(i) Probability of number 8 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 8 } \)
(ii) Odd number are 1, 3, 5, 7
Probability of a number which is an odd will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 8 } \)
= \(\\ \frac { 1 }{ 2 } \)
(iii) A number greater than 2 are 3, 4, 5, 6, 7, 8 which are 6
Probability of number greater than 2 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 8 } \)
= \(\\ \frac { 3 }{ 4 } \)
(iv) A number less than 9 is 8.
Probability of a number less than 9 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 8 } \)

Question 20.
Find the probability that the month of January may have 5 Mondays in
(i) a leap year
(ii) a non-leap year.
Solution:
In January, there are 31 days and in an ordinary year,
there are 365 days but in a leap year, there are 366 days.
(i) In January of an ordinary year, there are 31 days i.e. 4 weeks and 3 days.
Probability of Monday will be = \(\\ \frac { 3 }{ 7 } \)
(ii) In January of a leap year, there are 31 days i.e. 4 weeks and 3 days
Probability of Monday will be = \(\\ \frac { 3 }{ 7 } \)

Question 21.
Find the probability that the month of February may have 5 Wednesdays in
(i) a leap year
(ii) a non-leap year.
Solution:
In the month of February, there are 29 days in a leap year
while 28 days in a non-leap year,
(i) In a leap year, there are 4 complete weeks and 1 day
Probability of Wednesday = P (E) = \(\\ \frac { 1 }{ 7 } \)
(ii) and in a non leap year, there are 4 complete weeks and 0 days
Probability of Wednesday P (E) = \(\\ \frac { 0 }{ 7 } \) = 0

Question 22.
Sixteen cards are labelled as a, b, c,…, m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is:
(i) a vowel
(ii) a consonant
(iii) none of the letters of the word median.
Solution:
Here, sample space (S) = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p)
∴n(S) = 16
(i) Vowels (V) = {a, e, i, o}
∴n(V) = 4
∴P(a vowel) = \(\\ \frac { n(V) }{ n(S) } \) = \(\\ \frac { 4 }{ 16 } \) = \(\\ \frac { 1 }{ 4 } \)
(ii) Consonants (C) = {b, c, d, f, g, h, j, k, l, m, n, p}
∴n(C) = 12
∴P (a consonant) = \(\\ \frac { n(C) }{ n(S) } \) = \(\\ \frac { 12 }{ 16 } \) = \(\\ \frac { 3 }{ 4 } \)
(iii) None of the letters of the word MEDIAN (N) = {b, c, f, g, h, j, k, l, o, p)
∴n(N) = 10
∴P (N) = \(\\ \frac { n(N) }{ n(S) } \) = \(\\ \frac { 10 }{ 16 } \) = \(\\ \frac { 5 }{ 8 } \)

Question 23.
An integer is chosen between 0 and 100. What is the probability that it is
(i) divisible by 7?
(ii) not divisible by 7?
Solution:
Integers between 0 and 100 = 99
(i) Number divisible by 7 are
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98 = 14
Probability = \(\\ \frac { 14 }{ 99 } \)
(ii) Not divisible by 7 are 99 – 14 = 85
Probability = \(\\ \frac { 85 }{ 99 } \)

Question 24.
Cards marked with numbers 1, 2, 3, 4, 20 are well shuffled and a card is drawn at random.
What is the probability that the number on the card is
(i) a prime number
(ii) divisible by 3
(iii) a perfect square ? (2010)
Solution:
Number cards is drawn from 1 to 20 = 20
One card is drawn at random
No. of total (possible) events = 20
(i) The card has a prime number
The prime number from 1 to 20 are 2, 3, 5, 7, 11, 13, 17, 19
Actual No. of events = 8
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 8 }{ 20 } \)
= \(\\ \frac { 2 }{ 5 } \)
(ii) Numbers divisible by 3 are 3, 6, 9, 12, 15, 18
No. of actual events = 6
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 6 }{ 20 } \)
= \(\\ \frac { 3 }{ 10 } \)
(iii) Numbers which are perfect squares = 1, 4, 9, 16 = 4
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 4 }{ 20 } \)
= \(\\ \frac { 1 }{ 5 } \)

Question 25.
A box contains 25 cards numbered 1 to 25. A card is drawn from the box at random. Find the probability that the number on the card is :
(i) even
(ii) prime
(iii) multiple of 6
Solution:
Number of card in a box = 25 numbered 1 to 25
(i) Even numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24
i.e. number of favourable outcomes = 12
Probability of an even number will be
P(E) = \(\\ \frac { 12 }{ 25 } \)
(ii) Prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23
i.e. number of primes = 9
Probability of primes will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 25 } \)
(iii) Multiples of 6 are 6, 12, 18, 24
Number of multiples = 4
Probability of multiples of 6 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 25 } \)

Question 26.
A box contains 15 cards numbered 1, 2, 3,…..15 which are mixed thoroughly. A card is drawn from the box at random. Find the probability that the number on the card is :
(i) Odd
(ii) prime
(iii) divisible by 3
(iv) divisible by 3 and 2 both
(v) divisible by 3 or 2
(vi) a perfect square number.
Solution:
Number of cards in a box =15 numbered 1 to 15
(i) Odd numbers are 1, 3, 5, 7, 9, 11, 13, 15
Number of odd numbers = 8
Probability of odd numbers will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 15 } \)
(ii) Prime number are 2, 3, 5, 7, 11, 13
Number of primes is 6
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 15 } \)
= \(\\ \frac { 2 }{ 5 } \)
(iii) Numbers divisible by 3 are 3, 6, 9, 12, 15
which are 5 in numbers
Probability of number divisible by 3 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 15 } \)
= \(\\ \frac { 1 }{ 3 } \)
(iv) Divisible by 3 and 2 both are 6, 12
which are 2 in numbers.
Probability of number divisible by 3 and 2
Both will be = \(\\ \frac { 2 }{ 15 } \)
(v) Numbers divisible by 3 or 2 are
2, 3, 4, 6, 8, 9, 10, 12, 14, 15 which are 10 in numbers
Probability of number divisible by 3 or 2 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)
(v) Perfect squares number are 1, 4, 9 i.e., 3 number
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 15 } \)
= \(\\ \frac { 1 }{ 5 } \)

Question 27.
A box contains 19 balls bearing numbers 1, 2, 3,…., 19. A ball is drawn at random
from the box. Find the probability that the number on the ball is :
(i) a prime number
(ii) divisible by 3 or 5
(iii) neither divisible by 5 nor by 10
(iv) an even number.
Solution:
In a box, number of balls = 19 with number 1 to 19.
A ball is drawn
Number of possible outcomes = 19
(i) Prime number = 2, 3, 5, 7, 11, 13, 17, 19
which are 8 in number
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 19 } \)
(ii) Divisible by 3 or 5 are 3, 5, 6, 9, 10, 12, 15, 18
which are 8 in number
Probability of number divisible by 3 or 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 19 } \)
(iii) Numbers which are neither divisible by 5 nor by 10 are
1, 2, 3, 4, 6, 7, 8, 9, 11, 12,
13, 14, 16, 17, 18, 19
which are 16 in numbers
Probability of there number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 16 }{ 19 } \)
(iv) Even numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18
which are 9 in numbers.
Probability of there number will be
Number of favourable outcome
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 19 } \)

Question 28.
Cards marked with numbers 13, 14, 15, …, 60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the card drawn is
(i) divisible by 5
(ii) a perfect square number.
Solution:
Number of card bearing numbers 13,14,15, … 60 = 48
One card is drawn at random.
(i) Card divisible by 5 are 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 = 10
Probability = \(\\ \frac { 10 }{ 48 } \)
= \(\\ \frac { 5 }{ 24 } \)
(ii) A perfect square = 16, 25, 36, 49 = 4
Probability = \(\\ \frac { 4 }{ 48 } \)
= \(\\ \frac { 1 }{ 12 } \)

Question 29.
Tickets numbered 3, 5, 7, 9,…., 29 are placed in a box and mixed thoroughly. One ticket is drawn at random from the box. Find the probability that the number on the ticket is
(i) a prime number
(ii) a number less than 16
(iii) a number divisible by 3.
Solution:
In a box there are 14 tickets with number
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29
Number of possible outcomes = 14
(i) Prime numbers are 3, 5, 7, 11, 13, 17, 19, 23, 29
which are 9 in number
Probability of prime will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 14 } \)
(ii) Number less than 16 are 3, 5, 7, 9, 11, 13, 15
which are 7 in numbers,
Probability of number less than 16 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7 }{ 14 } \)
= \(\\ \frac { 1 }{ 2 } \)
(iii) Numbers divisible by 3 are 3, 9, 15, 21, 27
which are 5 in number
Probability of number divisible by 3 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 14 } \)

Question 30.
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
(i) a two-digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Solution:
There are 90 discs in a box containing numbered from 1 to 90.
Number of possible outcomes = 90
(i) Two digit numbers are 10 to 90 which are 81 in numbers.
Probability of two digit number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 81 }{ 90 } \)
= \(\\ \frac { 9 }{ 10 } \)
(ii) Perfect squares are 1, 4, 9, 16, 25, 36,49, 64, 81
which are 9 in numbers.
Probability of square will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 90 } \)
= \(\\ \frac { 1 }{ 10 } \)
(iii) Number divisible by 5 are
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90
which are 18 in numbers.
Probability of number divisible by 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 18 }{ 90 } \)
= \(\\ \frac { 1 }{ 5 } \)

Question 31.
Cards marked with numbers 2 to 101 are placed in a box and mixed thoroughly. One card is drawn at random from this box. Find the probability that the number on the card is
(i) an even number
(ii) a number less than 14
(iii) a number which is a perfect square
(iv) a prime number less than 30.
Solution:
Number of cards with numbered from 2 to 101 are placed in a box
Number of possible outcomes = 100 one card is drawn
(i) Even numbers are 2, 4, 6, 8, 10, 12, 14, 16,….., 96, 98, 100
which are 50 in numbers.
Probability of even number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 50 }{ 100 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) Numbers less than 14 are 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
which are 12 in numbers
Probability of number less than 14 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 12 }{ 100 } \)
= \(\\ \frac { 3 }{ 25 } \)
(iii) Perfect square are 4, 9, 16, 25, 36, 49, 64, 81, 100 which are 9 in numbers
Probability of perfect square number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 100 } \)
(iv) Prime numbers less than 30 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
which are 10 in numbers Probability of prime numbers, less than 30 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 10 }{ 100 } \)
= \(\\ \frac { 1 }{ 10 } \)

Question 32.
A bag contains 15 balls of which some are white and others are red. If the probability of drawing a red ball is twice that of a white ball, find the number of white balls in the bag.
Solution:
In a bag, there are 15 balls.
Some are white and others are red.
Probability of red ball = 2 probability of white ball
Let number of white balls = x
Then, number of red balls = 15 – x
\(2\times \frac { 15-x }{ 15 } =\frac { x }{ 15 } \)
⇒ 2(15 – x) = x
⇒ 30 – 2x = x
⇒ 30 = x + 2x
⇒ x = \(\\ \frac { 30 }{ 3 } \) = 10
Number of red balls = 10
and Number of white balls = 15 – 10 = 5

Question 33.
A bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball is twice that of a red ball, find the number of balls in the bag.
Solution:
In a bag, there are 6 red balls, and some blue balls
Probability of blue ball = 2 × probability of red ball
Let number of blue balls = x
and number of red balls = 6
Total balls = x + 6
Probability of a blue ball = 2
⇒ \(\frac { x }{ x+6 } =2\times \frac { 6 }{ x+6 } \)
⇒ \(\frac { x }{ x+6 } =\frac { 12 }{ x+6 } \)
⇒ x = 12
Number of balls = x + 6 = 12 + 6 = 18

Question 34.
A bag contains 24 balls of which x are red, 2x are white and 3x are blue. A blue is selected at random. Find the probability that it is
(i) white
(ii) not red.
Solution:
In a bag, there are 24 balls
Since, there are x balls red, 2 × balls white and 3 × balls blue
x + 2x + 3x = 24

Question 35.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability of getting:
(i) ‘2’ of spades
(ii) a jack .
(iii) a king of red colour
(iv) a card of diamond
(v) a king or a queen
(vi) a non-face card
(vii) a black face card
(viii) a black card
(ix) a non-ace
(x) non-face card of black colour
(xi) neither a spade nor a jack
(xii) neither a heart nor a red king
Solution:
In a playing card, there are 52 cards
Number of possible outcome = 52
(i) Probability of‘2’ of spade will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 52 } \)
(ii) There are 4 jack card Probability of jack will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 52 } \)
= \(\\ \frac { 1 }{ 13 } \)
(iii) King of red colour are 2 in number
Probability of red colour king will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 52 } \)
= \(\\ \frac { 1 }{ 26 } \)
(iv) Cards of diamonds are 13 in number
Probability of diamonds card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 13 }{ 52 } \)
= \(\\ \frac { 1 }{ 4 } \)
(v) Number of kings and queens = 4 + 4 = 8
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 52 } \)
= \(\\ \frac { 2 }{ 13 } \)
(vi) Non-face cards are = 52 – 3 × 4 = 52 – 12 = 40
Probability of non-face card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 40 }{ 52 } \)
= \(\\ \frac { 10 }{ 13 } \)
(vii) Black face cards are = 2 × 3 = 6
Probability of black face card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 52 } \)
= \(\\ \frac { 3 }{ 26 } \)
(viii) No. of black cards = 13 x 2 = 26
Probability of black card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 26 }{ 52 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ix) Non-ace cards are 12 × 4 = 48
Probability of non-ace card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 48 }{ 52 } \)
= \(\\ \frac { 12 }{ 13 } \)
(x) Non-face card of black colours are 10 × 2 = 20
Probability of non-face card of black colour will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 20 }{ 52 } \)
= \(\\ \frac { 5 }{ 13 } \)
(xi) Number of card which are neither a spade nor a jack
= 13 × 3 – 3 = 39 – 3 = 36
Probability of card which is neither a spade nor a jack will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 36 }{ 52 } \)
= \(\\ \frac { 9 }{ 13 } \)
(xii) Number of cards which are neither a heart nor a red king
= 3 × 13 = 39 – 1 = 38
Probability of card which is neither a heart nor a red king will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 38 }{ 52 } \)
= \(\\ \frac { 19 }{ 26 } \)

Question 36.
All the three face cards of spades are removed from a well-shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting
(i) a black face card
(ii) a queen
(iii) a black card
(iv) a heart
(v) a spade
(vi) ‘9’ of black colour
Solution:
In a pack of 52 cards
All the three face cards of spade are = 3
Number of remaining cards = 52 – 3 = 49
One card is drawn at random
(i) Probability of a black face card which are = 6 – 3 = 3
Probability = \(\\ \frac { 3 }{ 49 } \)
(ii) Probability of being a queen which are 4 – 1 = 3
Probability = \(\\ \frac { 3 }{ 49 } \)
(iii) Probability of being a black card = (26 – 3 = 23)
Probability = \(\\ \frac { 23 }{ 49 } \)
(iv) Probability of being a heart = \(\\ \frac { 13 }{ 49 } \)
(v) Probability of being a spade = (13 – 3 = 10)
Probability = \(\\ \frac { 10 }{ 49 } \)
(vi) Probability of being 9 of black colour (which are 2) = \(\\ \frac { 2 }{ 49 } \)

Question 37.
From a pack of 52 cards, a blackjack, a red queen and two black kings fell down. A card was then drawn from the remaining pack at random. Find the probability that the card drawn is
(i) a black card
(ii) a king
(iii) a red queen.
Solution:
In a pack of 52 cards, a blackjack, a red queen, two black being felt down.
Then number of total out comes = 52 – (1 + 1 + 2) = 48
(i) Probability of a black card (which are 26 – 3 = 23) = \(\\ \frac { 23 }{ 48 } \)
(ii) Probability of a being (4 – 2 = 2) = \(\\ \frac { 2 }{ 48 } \) = \(\\ \frac { 1 }{ 24 } \)
(iii) Probability of a red queen = (2 – 1 = 1) = \(\\ \frac { 1 }{ 48 } \)

Question 38.
Two coins are tossed once. Find the probability of getting:
(i) 2 heads
(ii) at least one tail.
Solution:
Total possible outcomes are . HH, HT, TT, TH, i.e., 4
(i) Favourable outcomes are HH, i.e., 1
So, P(2 heads)
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(ii) Favourable outcomes are HT, TT, TH, i.e., 3
So, P (at least one tail) = \(\\ \frac { 3 }{ 4 } \)

Question 39.
Two different coins are tossed simultaneously. Find the probability of getting :
(i) two tails
(ii) one tail
(iii) no tail
(iv) atmost one tail.
Solution:
Two different coins are tossed simultaneously
Number of possible outcomes = (2)² = 4
Number of event having two tails = 1 i.e. (T, T)
(i) Probability of two tails will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(ii) Number of events having one tail = 2 i.e. (TH) and (HT)
Probability of one tail will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(iii) Number of events having no tail = 1 i.e. (HH)
Probability of having no tail will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(iv) Atmost one tail
Number Of events having at the most one tail = 3 i.e. (TH), (HT, (TT)
Probability of at the most one tail will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 4 } \)

Question 40.
Two different dice are thrown simultaneously. Find the probability of getting:
(i) a number greater than 3 on each dice
(ii) an odd number on both dice.
Solution:
When two different dice are thrown simultaneously,
then the sample space S of the random experiment =
{(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) .
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
It consists of 36 equally likely outcomes.
(i) Let E be the event of ‘a number greater than 3 on each dice’.
E = {(4, 4), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
No. of favourable outcomes (E) = 9
P (number greater than 3 on each dice) = \(\\ \frac { 9 }{ 36 } \) = \(\\ \frac { 1 }{ 4 } \)
(ii) Let E be the event of ‘an odd number on both dice’.
E = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}
No. of favourable outcomes (E) = 9
∴ P (Odd on both dices) = \(\\ \frac { 9 }{ 36 } \) = \(\\ \frac { 1 }{ 4 } \)

Question 41.
Two different dice are thrown at the same time. Find the probability of getting :
(i) a doublet
(ii) a sum of 8
(iii) sum divisble by 5
(iv) sum of atleast 11.
Solution:
Two different dice are thrown at the same time
Possible outcomes will be (6)² i.e. 36
(i) Number of events which doublet = 6
i.e. (1, 1), (2, 2) (3, 3), (4, 4), (5, 5) and (6, 6)
.’. Probability of doublets will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 36 } \)
= \(\\ \frac { 1 }{ 6 } \)
(ii) Number of event in which the sum is 8 are
(2, 6), (3, 5), (4, 4), (5, 3), (6, 2) = 5
Probability of a sum of 8 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 36 } \)
(iii) Number of event when sum is divisible by
5 are (1, 4), (4, 1), (2, 3), (3, 2), (4, 6),
(5, 5) = 7 in numbers
Probability of sum divisible by 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7 }{ 36 } \)
(iv) Sum of atleast 11, will be in following events
(5, 6), (6, 5), (6, 6)
Probability of sum of atleast 11 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 36 } \)
= \(\\ \frac { 1 }{ 12 } \)

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
Arun scored 36 marks in English, 44 marks in Civics, 75 marks in Mathematics and x marks in Science. If he has scored an average of 50 marks, find x.
Solution:
Marks in English = 36
Marks in Civics = 44
Marks in Mathematics = 75
Marks in Science = x
Total marks in 4 subjects = 36 + 44 + 75 + x = 155 + x
average marks = \(\\ \frac { 155+x }{ 4 } \)
But average marks = 50 (given)
\(\\ \frac { 155+x }{ 4 } \) = 50
⇒ 155 + x = 200
⇒ x = 200 – 155 = 45

Question 2.
The mean of 20 numbers is 18. If 3 is added to each of the first ten numbers, find the mean of new set of 20 numbers.
Solution:
Mean of 20 numbers =18
Total number = 18 × 20 = 360
By adding 3 to first 10 numbers,
The new sum will be = 360 + 3 × 10 = 360 + 30 = 390
New Mean = \(\\ \frac { 390 }{ 20 } \) = 19.5

Question 3.
The average height of 30 students is 150 cm. It was detected later that one value of 165 cm was wrongly copied as 135 cm for computation of mean. Find the correct mean.
Solution:
In first case,
Average height of 30 students = 150 cm
Total height = 150 × 30 = 4500 cm
Difference in copying the number = 165 – 135 = 30 cm
Correct sum = 4500 + 30 = 4530 cm
Correct mean = \(\\ \frac { 4530 }{ 30 } \) = 151 cm

Question 4.
There are 50 students in a class of which 40 are boys and the rest girls. The average weight of the students in the class is 44 kg and average weight of the girls is 40 kg. Find the average weight of boys.
Solution:
Total students of a class = 50
No. of boys = 40
No. of girls = 50 – 40 = 10
Average weight of 50 students = 44 kg
Total weight = 44 × 50 = 2200 kg
Average weight of 10 girls = 40 kg
.’. Total weight of girls = 40 × 10 = 400 kg
Then the total weight of 40 boys = 2200 – 400 = 1800kg
Average weight of boys = \(\\ \frac { 1800 }{ 40 } \) = 45kg

Question 5.
The contents of 50 boxes of matches were counted giving the following results

Calculate the mean number of matches per box.
Solution:

Question 6.
The heights of 50 children were measured (correct to the nearest cm) giving the following results :

Solution:
Calculate the mean height for this distribution correct to one place of decimal.

Mean = \(\frac { \sum { fx } }{ \sum { f } } =\frac { 3459 }{ 50 } \) = 69.18 = 69.2

Question 7.
Find the value of p for the following distribution whose mean is 20.6 :

Solution:

Question 8.
Find the value of p if the mean of the following distribution is 18.

Solution:

Question 9.
Find the mean age in years from the frequency distribution given below:

Solution:
Arranging the classes in proper form

Question 10.
Calculate the Arithmetic mean, correct to one decimal place, for the following frequency distribution :

Solution:

Question 11.
The mean of the following frequency distribution is 62.8. Find the value of p.

Solution:
Mean = 62.8

Hence p = 10

Question 12.
The daily expenditure of 100 families are given below. Calculate f1, and f2, if the mean daily expenditure is Rs 188.

Solution:
Mean = 188,
No. of families = 100

Question 13.
The measures of the diameter of the heads of 150 screw is given in the following table. If the mean diameter of the heads of the screws is 51.2 mm, find the values of p and q

Solution:
Mean = 51.2
No. of screws = 150

Question 14.
The median of the following numbers, arranged in ascending order is 25. Find x, 11, 13, 15, 19, x + 2, x + 4, 30, 35, 39, 46
Solution:
Here, n = 10, which is even

Question 15.
If the median of 5, 9, 11, 3, 4, x, 8 is 6, find the value of x.
Solution:
Arranging in ascending order, 3, 4, 5, x, 8, 9, 11,
Here n = 7 which is odd.
∴ Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 7+1 }{ 2 } \) = 4th term = x
∴ but median = 6
∴ x = 6

Question 16.
Find the median of: 17, 26, 60, 45, 33, 32, 29, 34, 56 If 26 is replaced by 62, find the new median.
Solution:
Arranging the given data in ascending order
17, 26, 29, 32, 33, 34, 45, 56, 60
Here n = 9 which is odd
∴Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 9+1 }{ 2 } \) = \(\\ \frac { 10 }{ 2 } \) = 5th term = 33
(ii) If 26 is replaced by 62, their the order will be
17, 29, 32, 33, 34, 45, 56, 60, 62
Here 5th term is 34
∴ Median = 34

Question 17.
The marks scored by 16 students in a class test are : 3, 6, 8, 13, 15, 5, 21, 23, 17, 10, 9, 1, 20, 21, 18, 12
Find
(i) the median
(ii) lower quartile
(iii) upper quartile
Solution:
Arranging the given data in ascending order:
1, 3, 5, 6, 8, 9, 10, 12, 13, 15, 17, 18, 20, 21, 21, 23
Here n = 16 which is even.

Question 18.
Find the median and mode for the set of numbers : 2, 2, 3, 5, 5, 5, 6, 8, 9
Solution:
Here n = 9 which is odd.
∴Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 9+1 }{ 2 } \) = \(\\ \frac { 10 }{ 2 } \) = 5th term = 5
Here 5 occur maximum times
∴Mode = 5

Question 19.
Calculate the mean, the median and the mode of the following distribution :

Solution:

Question 20.
The daily wages of 30 employees in an establishment are distributed as follows :

Estimate the modal daily wages for this distribution by a graphical method.
Solution:

Taking daily wages on x-axis and No. of employees on the y-axis
and draw a histogram as shown. Join AB and CD intersecting each other at M.
From M draw ML perpendicular to x-axis, L is the mode
∴ Mode = Rs 23

Question 21.
Using the data given below, construct the cumulative frequency table and draw the ogive. From the ogive, estimate ;
(i) the median
(ii) the inter quartile range.

Also state the median class
Solution:

Question 22.
Draw a cumulative frequency curve for the following data :

Hence determine:
(i) the median
(ii) the pass marks if 85% of the students pass.
(iii) the marks which 45% of the students exceed.
Solution:

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test, drop a comment below and we will get back to you at the earliest.